Home Physical Sciences Balloonless spinning spindle head shape optimisation
Article Open Access

Balloonless spinning spindle head shape optimisation

  • Robert Drobina EMAIL logo , Stanisław Płonka , Jacek Rysiński and Aleksandra Jarco
Published/Copyright: July 23, 2024
Download Article (PDF)
AUTEX Research Journal
From the journal AUTEX Research Journal Volume 24 Issue 1

Abstract

The article presents a procedure for assessing and selecting the shape of the ring spinner spindle head that is optimum for yarn manufacturing using the balloonless system, considering multiple criteria. This procedure consists of two stages: the Pareto-optimal method and the distance function method. Twelve spindle head variants were designed and manufactured of 100Cr6 bearing steel composed of C (0.93–1.05%), Si (0.15–0.35%), Mn (0.25–0.45%) along with aluminium alloys EN AW-6060 (AlSi1MgMn) containing Si (0.70–1.3%), Mg (0.6–1.2%), Mn (0.4–1.0%) and EN AW-6060 (AlMgSi) containing Si (0.30–0.60%) and Mg (0.35–0.60%). The shapes of the heads were developed on the basis of the design solutions used previously by the leading ring-spinning machine and spinning spindle manufacturers. Four design variants of spindle heads, made of AlMgSi wrought aluminium alloy, have a unique shape that enables shaping their teeth (notches) by extrusion on a hydraulic press. The assessment criteria were production cost per unit, head weight, maximum surface hardness HV0.1, and four yarn technological quality criteria: maximum yarn tension values during the formation of the base, body and head of the package, and the tension amplitude. The assessment values for the criteria obtained through calculations and measurements were normalized. Then, a set of Pareto-optimal solutions was determined using seven criteria. Due to the fact that this set consisted of six variants, the distance function was used to select the best one. The best design variant of the head is the one corresponding to the lowest distance function value. In our case, the variant is a unique shape, made of AlMgSi alloy, with teeth thickened on the outer diameter of the head, ensuring the lowest yarn tension value at the height during the formation of the package.

Keywords: Multi-objective optimisation; balloon-less spinning spindle head; ring-spinning machine; optimisation; manufacturing processes; manufacturing cost; product quality

1 Introduction

The purpose of the spinning process is to produce a uniform yarn characterized by appropriate quality parameters, with the lowest possible number of breakages occurring during spinning. Depending on the type of raw material and the spinning technique used, the yarns differ in terms of quality, appearance, and suitability for further processes [1]. There are two types of ring-spinning machines that can be distinguished: one with a ballooning twist and wind gear (used in combed and carded systems for cotton spinning and worsted wool spinning systems) and one with a balloonless twist and wind gear (used in the semi-worsted systems for wool and wool-like chemical fibres as well as carded systems).

In the worsted system, the yarn should be characterized by purity, uniformity, smoothness, and thinness, as well as strength [1,2,3,4]. Obtaining these physical properties of yarns is only possible using ring-spinning machines equipped with a ballooning twist and wind gear. Where such rigorous physical properties of the yarn fibres are not required, it is possible to use ring-spinning machines equipped with a balloonless twist and wind gear. The advantages of using such a yarn-forming method include, above all, the possibility of increasing the rotational speed of the spindles, which results in the reduction of the necessary number of twists and thus increasing the production capacity, as well as the dimensions of the formed spinning packages, i.e. cops [1,4]. The latter benefit is related to

  1. shortening of the spinning process, which is translated into economic benefits,

  2. a reduction in the number of cop exchanges during the winding operation, and thus a reduction in the number of knotted or spliced joints of the thread ends after a breakage is eliminated.

One of the most important problems occurring during yarn production is maintaining the proper yarn tension while winding the yarn on the tube and creating the spinning package (cheese). Improper tension during the formation of the yarn package results in excessive and undesirable yarn breakage.

Changes in yarn tension depend on many factors and, in the most general case, can be divided into two main groups:

  1. tension changes depending on the movement of the traveller on the ring, its own vibrations, vibrations of the spindles, and the yarn itself,

  2. tension changes depending on the winding angle, balloon height, linear mass of the yarn, as well as on the rotational speed of the spindles.

The rotational speed of the spindles is one of the factors influencing overall yarn tension, with the approximate value of tension being directly proportional to the square of the rotational speed of the spindles.

In ring-spinning machines, in the twisting zone, the fibres assembly, after leaving the delivery rollers of the drawing mechanism, passes through a guide and a groove in the spindle head. The traveller-ring arrangement twists the fibres assembly.

The twist multiplier is a measure of twist that takes into accounts both the yarn radius and the twist level. The twist multiplier is an expression of the twist level adjusted for yarn count (tex) [1].

As a result of twisting, it is transformed into yarn and wound in the form of a package (cop) on a bobbin [1,2,3,4,5]. The use of collapse balloon spindles causes the balloon to be formed only in the section from the head of the bobbin to the traveller, which significantly reduces the tension of the yarn and allows using high packages (320–520 mm), as well as increasing the rotational speed of the spindles up to 11,000 rpm, thus significantly improving the production capacity of these machines.

The amount of yarn tension occurring in the twisting and winding system of a balloon-less ring-spinning machine depends not only on the characteristic dimensions of the head, but also, inter alia, on the type of material from which the head is made [4,6,7,8,9,10,11,12,13,14,15,16] as it has a direct impact on its weight.

Taking into account the fact that the spindle blade is placed vertically during operation, and the needle is placed in a bearing insert flooded with oil and supported in two places: sliding on an alloy bearing and rolling at the height of the driving belt against the spinning top [4,11]. Therefore, the weight of the head may have a significant impact on the trajectory of the spindle blade axis and, consequently, on the changes in yarn tension, as well as the number of yarn thick and thin spots.

The key problem in balloonless ring spinning is the proper design of the head, also known as the rosette. The yarn does not hold its position in one groove of the head. With too much tension, the yarn jumps to the next groove, opposite to the direction of spindle movement, which then reduces its tension [1,2,3,4,5,17]. There are many design variants of spindle heads.

Based on the analysis of the design solutions of spindle heads for balloonless spinning previously used by leading manufacturers of ring-spinning machines and spinning spindles [5,6,17,18,19,20,21,22], 12 structural variants of spindle heads were designed and manufactured. These variants included four original spindle head designs made of EN AW-6060 aluminium alloy (AlMgSi), shaping their teeth (notches) being made possible using extrusion on hydraulic presses.

The operating conditions of the traveller and the ring spinner spindle head require the material to be abrasion-resistant, resulting in high hardness at the appropriate depth.

A list of references describing the research on developing the theory of multi-objective optimisation, as well as its applications, mainly in economics and resource management, is presented in the study of Stadler [23]. The problem of multi-objective assessment of a structure with regard to two or more criteria, on the other hand, has been presented in numerous papers, which are briefly discussed in the literature [12,13,25,28]. The issue of multi-objective optimization is also discussed in more detail, e.g. in previous research studies [18,25,26,27,28,29,30]. Only a few works on structure optimization employ three types of criteria: deterministic, probabilistic-statistical, and fuzzy, to select the best solution (also called the most preferred solution) [13,18,24,25].

Optimization criteria which are often treated as deterministic in conventional models, e.g. cost, in the design phase must often be treated as non-deterministic, i.e. as subjective scores [13,24]. In general, however, the optimization criteria of a probabilistic and statistical nature are in most cases rather rarely used in the optimization of product design and manufacturing processes. Therefore, in order to simplify the procedure, they are treated as deterministic, and the validity of the criteria is captured using the collective Saaty’s matrix [30].

The purpose of this article is to present the procedure for assessing design solutions based on multiple criteria, the values of which were determined by calculations and measurements, to select the best design variant for the shape of the ring spinner spindle head to be used in the production of yarn in a balloonless system.

2 Assessment and multi-criteria selection procedure

The analysis of literature reports [3,13,23,25,26,27,28,29,30] indicates that the research which enables modelling yarn properties can employ statistical models based on linear, orthogonal, or multiple regression or through alternative programmable computational techniques using elements of fuzzy logic, as well as by searching for the Pareto optimum. Multi-objective assessment and selection of the best design variant are usually solved in two stages: determination of the Pareto-optimal set of variants and then selection of the best variant in this set using one criterion. A new criterion may be employed here – one that could not have been taken into account before, e.g. due to formalization difficulties – or a simplified form of a criterion already used in the multi-objective optimization phase [13,24].

2.1 Pareto-optimum method

The Pareto-optimum method, which consists of determining a set of non-dominated variants or a set of Pareto-optimal variants, was used in the assessment and selection of the optimal shape of the ring spinner head used for the production of yarn in a balloonless system, taking into account multiple criteria [13,24,26,27,28,29]. If A denotes the set of possible variants of the ring spinner head shape:

(1) A = { a 1 , a 2 , … , a n } ,

and K (d) represents a set of deterministic criteria from 1 to m:

(2) K ( d ) = { k 1 ( d ) , k 2 ( d ) , … , k m ( d ) } .

The assessment table of the ring-spinning machine head shape variants for the production of yarn using the balloonless system in relation to individual criteria is as follows:

(3) k 11 ( d ) , k 12 ( d ) , … , k 1 i ( d ) , … , k 1 s ( d ) k 21 (d) , k 22 ( d ) , … , k 2 i (d) , … , k 2 s (d) .................................... . k j 1 (d) , k j 2 (d) , … , k j i (d) , … , k j s (d) ..................................... . k m 1 (d) , k m 2 (d) , … , k m i (d) , … , k m s (d) ,

where k ji (d) = k j (d)(a i ) represents the assessment of the ith variant according to the jth criterion, j = 1,…,m.

The ideal shape of the spindle head a i (id) is a shape variant that simultaneously extremizes each criterion.

In the case of minimization, a i (id) is the ideal shape of the head if for every a i belonging to the set A, there is an a i (id) belonging to this set, such that

(4) k ( d ) ( a i ( id ) ) ≤ k ( d ) ( a i ) ,

where k (d)(a i ) represents the assessment vector of the ith variant of the spindle head shape in relation to each of the criteria.

Since these criteria are usually conflicting, in this case the ideal variant does not exist.

The non-dominated variant a i (nd) is a variant of the spindle head shape for which no criterion can be improved without at least one of the others being deteriorated.

In the case of minimization, a i (nd) is a non-dominated head shape variant if for each criterion k j (d) it is not true that there is a criteria vector k (d)(a i ) that belongs to the criteria set K such that k j (d) (a i ) ≤ k j (d)(a i (nd)) and there is a criterion k j (d) that satisfies k j (d)(a i (nd)) < k j (d)(a i ).

The set of non-dominated variants ZA is also called the set of Pareto-optimal variants. A set of criteria – compromise assessments ZK□K (d) – is assigned to set ZA.

The set of Pareto-optimal variants usually contains multiple variants, and it is from them that the best (optimal) one a i (opt)□ ZA is usually selected based on an additional criterion.

The non-dominated variant a i (nd) is a solution to the Pareto multi-objective assessment problem if the corresponding criterion vector k (d)(a i (nd)) is the smallest one in the sense of partial ordering.

This formula assumes that all criteria are to be minimized. If in a multi-objective assessment problem the k j (d)(a i ) criterion is to be maximized, then such a problem can be reduced to a minimization problem by changing the sign of the criterion

(5) max j k ji ( d ) = − min j ( − k ji ( d ) ) .

To determine the set of Pareto-optimal variants of the spindle head shape, the POLOPT.2 program, written specifically in the Pascal language, was used. This program, based on a dialogue with a computer, enables determining a set of Pareto-optimal variants from a set consisting of a maximum of 100 admissible variants, assessed according to a maximum of 10 criteria each. The program developed in this way allows us to determine the set of Pareto-optimal variants according to any number of criteria in the range from 2 to 10.

The program consists of the following modules: creating a set of criteria, reading a set of criteria, selecting criteria for determining the Pareto-optimal set, and determining the Pareto set, sorting, viewing, and printing the Pareto set.

2.2 Choosing the best solution from the Pareto set using the distance function

The distance function methods, according to their classic approach, allow us to determine one compromise solution, which usually leads to the determination of one non-dominated variant. A large number of different assessment criteria characterizing the variants translates into vector quality indicators. In a situation where some of these indicators are minimized and the others are maximized, and considering the fact that most of these indicators are expressed in different units, the problem of correctly selecting the best variant proves to be difficult [13]. In order to be independent of the influence of different units of individual criteria, and since the set of criteria contains assessments of which some are to be minimized, and the others maximized, the following distance function f l(i) was designed:

(6) f d ( i ) = ∑ j = 1 m [ c i ( j ) * − c id ( j ) * ] 2 → min ,

where c i ( j ) * represents the normalized value of the jth criterion for individual variants and c i d ( j ) * represents the normalized value of the j criterion for the ideal value.

The best variant from the set of Pareto-optimal variants is the one for which the value of the distance function f d(i) is minimum.

3 An example of selecting the optimal variant of the ring-spinning machine spindle head

The starting point for the assessment and selection of the best solution is determining the set of acceptable design variants (in our case, the set of design variants of the spindle head) considered and analysed in the light of the designated criteria and then adopting an appropriate algorithm to select the best variant.

3.1 Set of acceptable spindle head variants

Assessment and testing of the design solutions of the spindle head were carried out on an experimental bench equipped with a prototype ring-spinning machine for spinning using a balloonless system and with measuring equipment.

The shapes of the heads were developed on the basis of the design solutions used previously by the leading ring-spinning machine and spinning spindle manufacturers [5,6,12,19,20,21,22]. Twelve design variants of the balloonless spinning machine spindle head shape were designed and manufactured in order to ensure the lowest possible yarn tension during package formation, thus obtaining the best quality yarn. Also, minimizing the number of breaks and thus increasing the efficiency in the spinning process of ring spinners were to be obtained as a result. Design variants of the spindle head shape are presented in Figure 1, and the characteristic dimensions of each of the heads are given in Table 1.

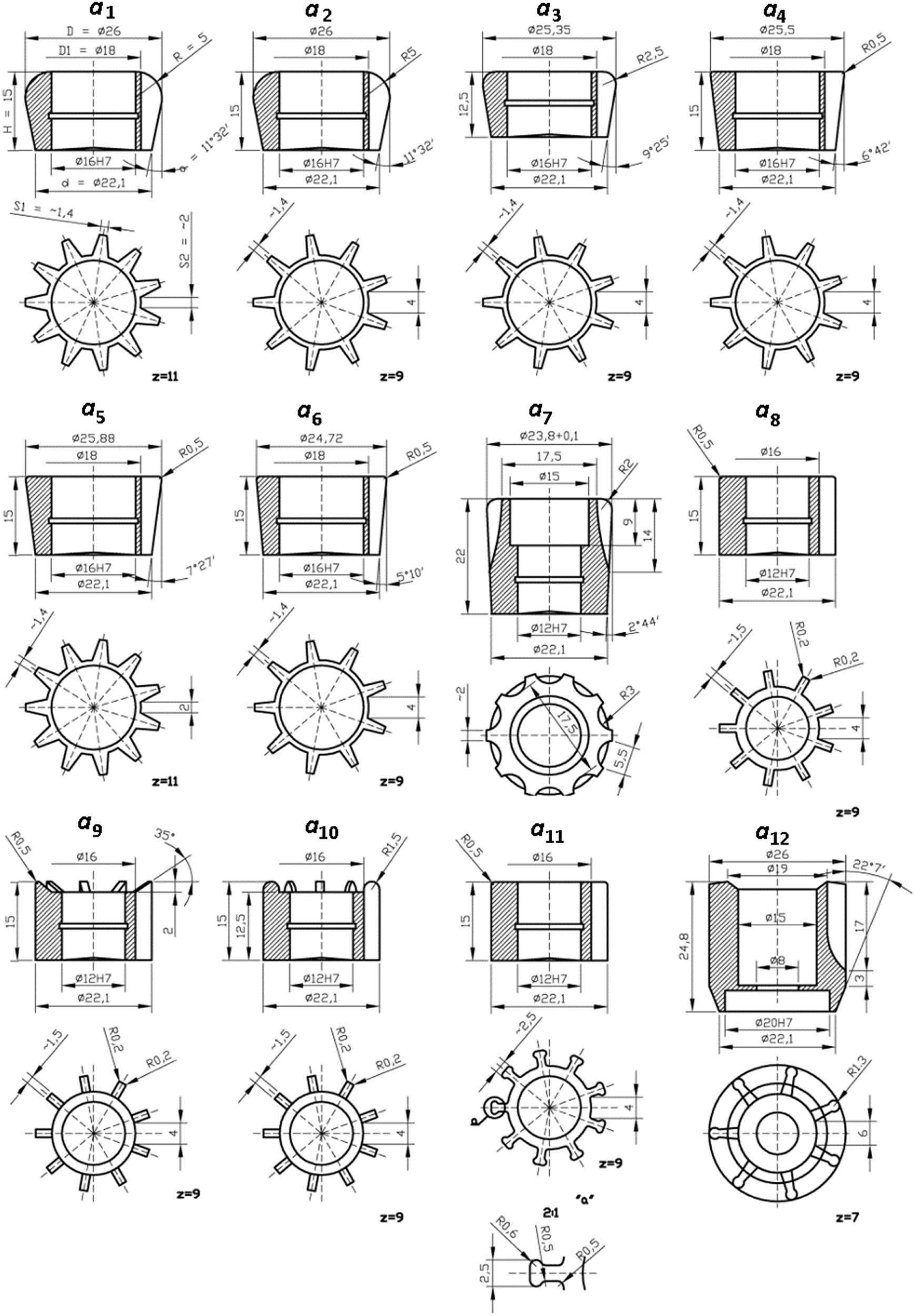
Figure 1 Design variants of the ring spinner machine spindle head shape used in the production of yarn with the balloonless system.
Figure 1

Design variants of the ring spinner machine spindle head shape used in the production of yarn with the balloonless system.

Table 1

Characteristic dimensions of the balloon control head (rosette) of the ring-spinning machine spindle

Variant number Material Characteristic dimensions of the head (mm) Angle α Number of teeth z
d D D 1 H R s 1 s 2
a 1 100Cr6 22.1 26 18 15 5 1.4 2 11°32′ 11
a 2 100Cr6 22.1 26 18 15 5 1.4 4 11°32′ 9
a 3 100Cr6 22.1 25.35 18 12.5 2.5 1.4 4 9°25′ 9
a 4 AlSi1MgMn 22.1 25.5 18 15 0.5 1.4 4 6°42′ 9
a 5 AlSi1MgMn 22.1 25.88 18 15 0.5 1.4 2 7°27′ 11
a 6 AlSi1MgMn 22.1 24.72 18 15 0.5 1.4 4 5°10′ 9
a 7 AlSi1MgMn 22.1 23.8 17.5 22 2 2 5.5 2°44′ 10
a 8 AlMgSi 22.1 22.1 16 15 0.5 1.5 4 0° 9
a 9 AlMgSi 22.1 22.1 16 15 0.5 1.5 4 0° 9
a 10 AlMgSi 22.1 22.1 16 15 1.5 1.5 4 0° 9
a 11 AlMgSi 22.1 22.1 16 15 0.5 2.5 4 0° 9
a 12 Fe–C–Cu–Ni–Mo 22.1 26 19 24.8 1.3 2.6 6 22°7′ 7

Three design variants of the spindle head were designed and manufactured of 100Cr6 bearing steel and then heat-treated, hardened, and tempered to a hardness of 58 ± 2 HRC (Rockwell hardness scale). The next four variants were made of EN AW-6082 wrought alloy (AlSi1MgMn). Subsequently, four design variants of spindle heads of unique shape were designed and manufactured of EN AW-6060 (AlMgSi) wrought aluminium alloy, shaping their teeth (notches) being made possible using extrusion on hydraulic presses. Aluminium alloy variants were hard anodized to increase their abrasion resistance. The last of the variants was made by pressing and sintering metal powders: iron, carbon, copper, nickel, and molybdenum, and by hardening heat treatment to a hardness of 40HRC.

3.2 A set of criteria assessments of the spinning machine spindle head

To assess the design variants of the ring spinner machine spindle head shape, the production cost per unit, head weight, hardness, and the following four technological yarn quality criteria were used:

  • cost of production per unit K w, Euro,

  • weight m n, g,

  • maximum hardness on the surface of the top layer HV0.1, MPa,

  • maximum value of yarn tension at the base of the package F p, cN,

  • maximum value of yarn tension in the body part at 1/2 of the package height F z, cN,

  • maximum value of yarn tension at the head of the package F w, cN,

  • maximum value of the tension amplitude A np, cN,

Calculations of production costs per unit for various design variants of the spindle head shape were based on the multi-stage job order costing algorithm, according to workstation costs presented in the literature [31,32].

The second criterion was the weight of the spindle head since the minimum and maximum values, as well as the amplitude of the yarn tension in each phase of the package formation, increase with the increase in the head weight. The measurement of the spindle head weights was carried out using WA32-type PRL TAI3 analytical balance.

In the assessment of the physical properties of the surface layer, only the maximum hardness in the surface layer HV0.1 was adopted. This is due to the fact that, as a result of several years of observations and research in industrial conditions, it was found that parts of ring and open-end spinning machines that are in direct contact with the fibres assembly or yarn wear less as the hardness on the surface and the top layer of those parts is increased [24]. The second parameter, i.e. the hardening depth of the surface layer g ww, was omitted, because the spindle is in rotation and the contact of the fibres assembly with the head is only temporary. For the rotational speed from 8,500 to 10,000 rpm, collapse balloon spindles with 10 teeth, generally moving at a speed of 0.42–0.58 m/s and a maximum tension of up to 37 cN from one notch to the next, the travel time of the fibres assembly ranges from 0.00060 to 0.000706 s. Measurements of the hardness distribution at the depth of the surface layer HV 0.1 = f(g ww) of the heads were carried out using the Vickers method and a Leitz Wetzlar microhardness tester on oblique microsections with an angle of 1°30′ (0.026 rad), and an indenter load of 0.98 N. During the hardness measurements, at least threefold repeatability was applied. All measurement results were checked for statistical homogeneity to eliminate gross errors using the Grubbs’ test for this purpose. The critical value of the test function T kr was read from Table 51 in Statistical tables [32] depending on the number of trials n p = 5, the number of repetitions n p = 3, and the adopted significance level α = 0.05 (5%). After the elimination of gross errors, average values for individual design variants of the spindle head were calculated and are presented in Table 2.

Table 2

Values of the c ij criteria for the collapse balloon spindle head (rosette) of the ring-spinning machine

Variant number Material Manuf. cost per unit Wt. m n (g) Max. hardness on the surface The minimum and maximum yarn tension values (cN) The amplitude of tension changes A np (cN)
K w (Euro) HV 0.1 (MPa) Base F p Body F z Head F w
Min Max Min Max Min Max
a 1 100Cr6 9.70 17.07 5950 8.00 12.00 20.00 24.00 10.00 23.00 16.00
a 2 100Cr6 9.15 15.36 5950 6.00 8.00 8.00 17.00 22.00 23.00 17.00
a 3 100Cr6 8.93 13.26 5950 2.00 4.00 3.00 6.00 10.00 13.00 11.00
a 4 AlSi1MgMn 5.80 5.69 6840 2.00 3.00 4.00 6.00 6.00 9.00 7.00
a 5 AlSi1MgMn 6.35 6.20 6840 3.00 4.00 3.50 5.00 6.00 8.00 5.00
a 6 AlSi1MgMn 5.79 5.84 6840 3.00 4.00 3.00 8.00 17.00 19.00 16.00
a 7 AlSi1MgMn 6.15 5.42 6840 5.00 6.00 6.00 9.50 10.00 14.00 9.00
a 8 AlMgSi 3.70 4.99 6950 4.40 6.40 8.00 12.60 11.00 13.00 8.60
a 9 AlMgSi 3.90 4.30 6950 4.20 6.60 3.00 7.20 7.00 7.80 4.80
a 10 AlMgSi 4.00 4.39 6950 5.00 7.00 3.00 7.50 9.00 10.00 7.00
a 11 AlMgSi 4.30 5.59 6950 2.40 4.00 3.50 5.00 5.30 6.00 3.60
a 12 Fe–C–Cu–Ni–Mo 1.40 41.46 3960 5.00 6.00 8.00 10.50 15.00 20.00 15.00

During the yarn tension measurements, constant parameters of the spinning process were used for all 12 tested spindle heads:

  1. rotational speed of the spindles n wrz = 8,000 rpm,

  2. rotational and linear speed of the delivery rollers n w = 200 rpm and v w = 31.4 rpm, respectively,

  3. traveller type: type C with a weight of m b = 110 mg.

The subject of the study was a 100% wool yarn with a linear density of 60.6 tex (Nm 16.5). In order to capture the changes in yarn tension during the spinning process caused by the influence of simultaneous changes in the mass of the spindle head and the phases of the spinning process, wool yarn from the lower range of masses of linear carded yarns was used for testing [15].

A number of yarn twists per 1 m, T m = 254.7 1/m TPM. This yarn was made of New Zealand wool with a nominal fibre diameter of 28 µm.

Due to the nature of the yarn formation process and yarn quality, the criteria of yarn tension occurring during the formation of the spinning package were the ones adopted for the assessment of the heads.

The yarn tension was measured on a prototype balloonless ring-spinning machine using Rothschild measuring equipment, featuring the C-1386 measuring head (probe) with a range of 0–100 g, the R-1092 Electronic Tensometer, and the Helco Scriptor recorder.

The measuring head was mounted on a specially made stand below the delivery roller clamps, halfway between the delivery roller clamp and the upper frontal plane of the spindle attachment and connected to the meter and recorder. The distance of the guidewire from the upper frontal plane of the attachments was 9 mm for each measurement (Figure 2).

Figure 2 Technological lay-out of the PG-7A ring-spinning frame: (a) the run of fibre stream from the unrolling shaft of the roving to the lap of the yarn; (b) the run of fibre stream from the guide to the lap of the yarn; 1 – roving, 2 – unrolling shaft, 3 – roving guide, 4 – feed rollers, 5 – false twist spiral, 6 – delivery rollers, 7 – suction cleaner, 8 – yarn guide, 9 – crown, 10 – spinning spindle, 11 – bobbin, 12 – traveller, 13 – ring, 14 – lap of yarn, 15 – ring frame, T – electronic tensometer [33].
Figure 2

Technological lay-out of the PG-7A ring-spinning frame: (a) the run of fibre stream from the unrolling shaft of the roving to the lap of the yarn; (b) the run of fibre stream from the guide to the lap of the yarn; 1 – roving, 2 – unrolling shaft, 3 – roving guide, 4 – feed rollers, 5 – false twist spiral, 6 – delivery rollers, 7 – suction cleaner, 8 – yarn guide, 9 – crown, 10 – spinning spindle, 11 – bobbin, 12 – traveller, 13 – ring, 14 – lap of yarn, 15 – ring frame, T – electronic tensometer [33].

Before each subsequent measurement, the meter and the recording device were zeroed and calibrated with a 50 g weight. The yarn tension was recorded continuously on the graph at the tape speed of 10 mm/s, in three formation planes, namely: at the base of the package, in the main part, at ½ of the package height, and at the head of the package.

3.3 Selection of the optimal variant of the spindle head with regard to the production cost per unit, weight, and hardness, as well as the technological quality criteria of the yarn

The criteria assessment values obtained from the calculations and measurements of the analysed design variants of the spindle head shape are presented in Table 2. Subsequently, the values obtained from the calculations and measurements were normalized to the range of ≤ 0.1; 0.9 ≥ using the function described by formula (7):

(7) c ij * = 0.1 + c ij − min 1 ≤ s ≤ n ( c ij ) [ max 1 ≤ s ≤ n ( c ij ) − min 1 ≤ s ≤ n ( c ij ) ] ∙ 1.25 ,

where c ij is the assessment values of considered variants in relation to particular criteria, i = 1, …, n; j = 1, …, m. n is the number of variants; m is the number of criteria.

The obtained scores, c ij * normalized according to formula (7), are fractions in the range of ≤0.1; 0.9≥. This method of normalization excludes extreme scores of 0 and 1.

In the contemplated example, the criteria to be minimized include the cost [32] of producing one piece of the spindle head K w, the weight of the head m n, the maximum value of the yarn tension at the base of the package F p, the maximum value of the yarn tension in the main part at 1/2 of the package height F z, the maximum value of the yarn tension at the head of the package F w, and the maximum value of the tension amplitude A np, while the maximum hardness of the surface layer HV0.1 is the criterion to be maximized.

The assessment values, after normalization for individual criteria and each design variant of the spindle head shape, are presented in Table 3.

Table 3

Criteria assessment values after c ij * normalization

a 1 a 2 a 3 a 4 a 5 a 6
k 1 0.9000 0.8470 0.8258 0.5241 0.5771 0.5231
k 2 0.3749 0.3381 0.2929 0.1299 0.1409 0.1332
k 3 0.6324 0.6324 0.6324 0.8706 0.8706 0.8706
k 4 0.9000 0.5444 0.1889 0.1000 0.1889 0.1889
k 5 0.9000 0.6053 0.1421 0.1421 0.1000 0.2263
k 6 0.9000 0.9000 0.4294 0.2412 0.1941 0.7118
k 7 0.8403 0.9000 0.5418 0.3030 0.1836 0.8403
a 7 a 8 a 9 a 10 a 11 a 12
k 1 0.5578 0.3217 0.3410 0.3506 0.3795 0.1000
k 2 0.1241 0.1149 0.1000 0.1019 0.1278 0.9000
k 3 0.8706 0.9000 0.9000 0.9000 0.9000 0.1000
k 4 0.3667 0.4022 0.4200 0.4556 0.1889 0.3667
k 5 0.2895 0.4200 0.1926 0.2053 0.1000 0.3316
k 6 0.4765 0.4294 0.1847 0.2882 0.1000 0.7588
k 7 0.4224 0.3985 0.1716 0.3030 0.1000 0.7806

In the next step, using the POLOPT.2 program, the Pareto-optimal set was determined for the analysed set of acceptable variants, consisting of 12 spindle head variants. The Pareto-optimal set with regard to seven criteria: production cost per unit K w, weight m n, maximum hardness HV0.1, and four yarn technological quality criteria, consists of six variants. The Pareto-optimal variants are the following: a 4, a 7, a 8, a 9, a 11, and a 12.

To select the best variant from the Pareto-optimal set, the distance function defined by the formula (8) was used. For the seven criteria, the form of this function is as follows:

(8) f d ( i ) = [ c i ( 1 ) * − c id ( 1 ) * ] 2 + [ c i ( 2 ) * − c id ( 2 ) * ] 2 + ,   … ,   + [ c i ( 7 ) * − c id ( 7 ) * ] 2 .

Depending on whether the criterion is to be minimized or maximized in the problem, the coordinates of the ideal spot were determined:

(9) c id ( j ) * = ( 0.1 ; 0.1 ; 0.9 ; 0.1 ; 0.1 ; 0.1 ; 0.1 ) .

Values c i j * for the Pareto-optimal variants are presented in Table 3, and the values of the distance function f d(i) for these six variants are presented in Table 4.

Table 4

Value of the distance function f d(i) for six Pareto-optimal variants

Variant number Distance from the ideal variant
a 4 0.4945
a 7 0.7508
a 8 0.4794
a 9 0.4259
a 11 0.2946
a 12 1.4755

The best variant is the one for which the value of the distance function f d(i) is the lowest. In our case, it is variant a 11, i.e. the variant of the head made of AlMgSi aluminium alloy with nine teeth thickened on the outer diameter. It was hard-anodized with the corresponding value of the distance function of f d( a 11) = 0.2946. The criteria assessment values for the optimal variant are as follows: K w = 4.30 EUR/pc.; m n = 5.59 g; HV0.1 = 6950 MPa; F p = 4.00 cN; F z = 5.00 cN; F w = 6.00 cN; A np = 3.60 cN.

4 Conclusions

In determining the best shape of the spindle head according to two or more assessment criteria, if specifying the values of the criteria adopted for assessment with sufficient accuracy is possible, positive results are obtained when using a two-stage multi-objective optimization procedure. In the first stage, it involves the determination of a set of the Pareto-optimal variants (a set of non-dominated variants), and in the second stage, the selection of the best variant from this set using the distance function. The advantage of this procedure is that the same assessment criteria are used in both stages of the optimization procedure. Therefore, determining an additional (usually a new) criterion becomes redundant, which greatly facilitates and accelerates the selection of the optimal solution.

The optimal shape of the ring spinner machine spindle head was found to be the head with nine teeth thickened on the outer diameter, having the same diameter over the entire height. As a result, the removal of the yarn that is torn off and wound around the winding sleeve lining does not cause any problems during the operation of ring-spinning machines. The optimally shaped head is made of EN AW-6060 aluminium–silicon–magnesium alloy and hard anodized to increase its abrasion resistance. It is characterized by a relatively low production cost per unit, low weight, the highest surface hardness, and, above all, the lowest yarn tension amplitudes along the entire height of the package during its formation. The considerations contained in the article and the conclusions arising from it may be applicable when using a balloon-less spinning system for the production of recycled yarns and recycled fibres. Currently, efforts are being made to produce products that use recycled materials. The quality of these products varies and depends on the customer’s expectations. Where good quality yarn from recycled or re-fibres is required, the use of appropriate anti-balloon rosettes (spindle heads) to improve the efficiency and quality of the produced yarns is of great importance. The presented research is applicable to existing machinery of older generations, where modernization or replacement of the entire spinning machine may prove too expensive.

  1. Funding information: Authors state no funding involved.

  2. Author contributions: All authors have accepted responsibility for the entire content of this manuscript and consented to its submission to the journal, reviewed all the results and approved the final version of the manuscript. RD – Development of the experimental plan, development of experimental results, numerical analysis, manuscript editing. SP – Development of experimental results, development of the experimental plan, numerical analysis, manuscript editing. JR – Numerical analysis, manuscript editing. AJ – Numerical analysis, editing in the development of statistics.

  3. Conflict of interest: Authors state no conflict of interest.

  4. Ethical approval: The conducted research is not related to either human or animal use.

  5. Data availability statement: The datasets generated during and/or analysed during the current study are available from the corresponding author on reasonable request.

References

[1] Lawrence Carl, A. (2003). Fundamentals of Spun Yarn technology. Boca Raton London, New York, Washington, D.C., CRC Press, Leeds.10.1201/9780203009581Search in Google Scholar

[2] Hossain, M., Abdkader, A., Cherif, C. (2018). Analysis of yarn properties in the superconducting magnetic bearing based ring spinning process. Textile Research Journal, 88(22), 2624–2638. 10.1177/0040517517725122.Search in Google Scholar

[3] Hossain, M, Telke, C., Sparing, M., Abdkader, A., Nocke, A., Unger, R., et al. (2017). Mathematical modeling, simulation and validation of the dynamic yarn path in a superconducting magnet bearing (SMB) ring spinning system. Textile Research Journal, 87(8), 1011–1022. 10.1177/0040517516641363.Search in Google Scholar

[4] Hossain, M., Abdkader, A., Nocke, A., Unger, R., Krzywinski, F., Hasan, MMB., et al. (2016). Measurement methods of dynamic yarn tension in a ring spinning process. Fibres & Textiles in Eastern Europe, 24, 1(115), 36–43. 10.5604/12303666.1172098.Search in Google Scholar

[5] Bigagli Woollen Ring Spinning Frame. Royal Westa (Canada). www.https://royalwesta.com/ Web site: 04.04. 2022.Search in Google Scholar

[6] Complete spindles - Saurer. https://saurer.com/en/products/components/texparts/spindles/complete-spindles Web site: 04.04. 2022.Search in Google Scholar

[7] Fraser, W. B. (1993). On the theory of ring spinning Philosophical Transactions of the Royal Society of London. Series A: Physical and Engineering Sciences, 342, 439–468. 10.1098/rsta.1993.0028.Search in Google Scholar

[8] Gao, S., Nakane, K., Ohgoshi, A., Isaji, T., Ozawa, M. (2018). Development of superam-phiphobic alumina nanofiber mats using trimethoxysilane with a short perfluoroalkyl chain. Textile Research Journal, 88, 1803–1811. 10.1177/0040517517712093.Search in Google Scholar

[9] Gaudino Company M-4707 (1988). Semi-worsted Ring Spinning Machine (Italy).Search in Google Scholar

[10] ISO 25178-2:2021(E) – Geometrical product specifications (GPS) – Surface texture: Areal – Part 2: terms, definitions and surface texture parameters.Search in Google Scholar

[11] Oczoś, K. E., Kawalec, A. (2012). Forming of light metals. PWN Polish-English Dictionary, Warsaw.Search in Google Scholar

[12] Płonka, S, Postrożny, J., Drobina, R. (2021). Methodology of optimum selection of material and semi-folded products for rotors of open-end spinning machine. AUTEX Research Journal, 21(4), 393–402. 10.2478/aut-2020-0040.Search in Google Scholar

[13] Płonka, S. (2017). Multicriteria optimization of manufacturing processes of machinery elements. WNT, Warsaw.Search in Google Scholar

[14] PN-EN 755-2: 2016-05 – Aluminum and aluminum alloys–Rods, pipes and extruded sections. Part II: Mechanical properties.Search in Google Scholar

[15] Jackowski, T., Chylewska, B. (1999). Spinning - construction and technology of yarns. Lodz University of Technology, Lodz.Search in Google Scholar

[16] Shao, R., Cheng, L., Xue, W. (2019). Theoretical study of the effects on yarn strength in a modified ring spinning system. Textile Research Journal, 89(23–24), 5014–5023. 10.1177/0040517519846071.Search in Google Scholar

[17] Murugesan, M, Senthilkumar, T., Nayar, R. C. (2015). A study of collapsed balloon spinning and its effect on cotton yarn properties. IOSR Journal of Polymer and Textile Engineering (IOSR-JPTE), 2(3), 44–49.Search in Google Scholar

[18] Nguyen, N. T., Trawiński, B., Knosala, R. (2015). Multi objective optimization of bioactive compound extraction process via evolutionary strategies. Lecture Notes in Computer Science (pp. 13–21). Switzerland, Springer International Publishing. 10.1007/978-3-319-15705-4_2.Search in Google Scholar

[19] Delpiano Company FD-104 (1987). Woollen ring spinning (Italy). ITMA’87.Search in Google Scholar

[20] Galan. Semi-worsted Ring Spinning Machine CP 7072 type (1980). Talleres Galan firm (Spain).Search in Google Scholar

[21] NSC Schlumberger Semi-worsted lines. http://www.nsc-schlumberger.com/production-line/semi-worsted-lines. Designer of industrial equipment for textiles of all types Web site: 04.04. 2022.Search in Google Scholar

[22] Houget Duesberg Bosson CBY3 (1988). Semi-worsted Ring Spinning machine (Belgium).Search in Google Scholar

[23] Stadler, W. (1981). Stability implications and the equivalence of stability and optimality conditions in the optimal design of uniform shallow arches. Proc. Symp. Of Sruct. Optimiz., 11th Naval Struct. Mech. Symp., Univ. of Arizona, Tucson, Arizona.Search in Google Scholar

[24] Płonka, S. (1998). Methods of evaluation and selection of the optimal structure of the technological process. Scientific Dissertations 48. Construction and Operation of Machines 31. Lodz University of Technology Branch in Bielsko-Biała.Search in Google Scholar

[25] Breiing, A., Knosala, R. (1997). Bewerten technischen Systeme (Theoretische Und methodische grundlagen bewertungstechnischer Entscheidungshilfen). Springer – Verlag, Berlin – Heidelberg.10.1007/978-3-642-59229-4Search in Google Scholar

[26] Osyczka, A. (2002). Evolutionary algorithms for single and multi-criteria design optimization. Physical – Verlag Heidelberg, New York.Search in Google Scholar

[27] Montusiewicz, J. (2004). Evolutionary multi-criteria analysis in technical issues. Habilitation thesis. Institute of Fundamental Technological Research of the Polish Academy of Sciences, Warsaw.Search in Google Scholar

[28] Montusiewicz, J. (2012). Supporting the design and production planning processes in the construction and operation of machines with multi-criteria analysis methods. Monographs. Lublin University of Technology, Lubin.Search in Google Scholar

[29] Kaliszewski, J. (2008). Multi-criteria decision making. Soft calculations for complex decision problems. WNT, Warsaw.Search in Google Scholar

[30] Saaty, T. L. (1980). The analytic hierarchy processes. McGraw-Hill, New York.10.21236/ADA214804Search in Google Scholar

[31] Matuszek, J., Kłosowski, M., Krokosz-Krynke, Z. (2011). Cost accounting for engineers. PWE, Warsaw.Search in Google Scholar

[32] Zieliński, W., Zieliński, R. (1990). Statistical tables. PWN, Warsaw.Search in Google Scholar

[33] Płonka, S., Hajduga, M. (2008). Assesing the wear of spindle neck coating made of AlCu4Mg1 alloy of ring spinning spindles with an anti-balloon crown. Fibres & Textiles in Eastern Europe, 16(3), 33–38.Search in Google Scholar
Received: 2023-12-04
Revised: 2024-04-18
Accepted: 2024-05-29
Published Online: 2024-07-23

© 2024 by the authors, published by De Gruyter

This work is licensed under the Creative Commons Attribution 4.0 International License.

Articles in the same Issue

  2. Characterization of viscoelastic properties of yarn materials: Dynamic mechanical analysis in the transversal direction
  3. Analysis of omni-channel implementations that are preferred by consumers in clothing sector
  4. Structural modeling and analysis of three-dimensional cross-linked braided preforms
  5. An experimental study of mechanical properties and comfortability of knitted imitation woven shirt fabrics
  6. Technology integration to promote circular economy transformation of the garment industry: a systematic literature review
  7. Research on T-shirt-style design based on Kansei image using back-propagation neural networks
  8. Research on She nationality clothing recognition based on color feature fusion with PSO-SVM
  9. Accuracy prediction of wearable flexible smart gloves
  10. Preparation and performance of stainless steel fiber/Lyocell fiber-blended weft-knitted fabric
  11. Development of an emotional response model for hospital gown design using structural equation modeling
  12. Preparation and properties of stainless steel filament/pure cotton woven fabric
  13. Facemask comfort enhancement with graphene oxide from recovered carbon waste tyres
  14. Use of enzymatic processes in the tanning of leather materials
  15. Optical-related properties and characterization of some textile fibers using near-infrared spectroscopy
  16. Network modeling of aesthetic effect for Chinese Yue Opera costume simulation images
  17. Predicting consumers’ garment fit satisfactions by using machine learning
  18. Non-destructive identification of wool and cashmere fibers based on improved LDA using NIR spectroscopy
  19. Study on the relationship between structure and moisturizing performance of seamless knitted fabrics of protein fibers for autumn and winter
  20. Antibacterial and yellowing performances of sports underwear fabric with polyamide/silver ion polyurethane filaments
  21. Numerical and experimental analysis of ballistic performance in hybrid soft armours composed of para-aramid triaxial and biaxial woven fabrics
  22. Phonetic smart clothing design based on gender awareness education for preschoolers
  23. Determination of anthropometric measurements and their application in the development of clothing sizing systems for women in the regions of the Republic of Croatia
  24. Research on optimal design of pleated cheongsam based on Kano–HOQ–Pugh model
  25. Numerical investigation of weaving machine heald shaft new design using composite material to improve its performance
  26. Corrigendum to “Use of enzymatic processes in the tanning of leather materials”
  27. Shaping of thermal protective properties of basalt fabric-based composites by direct surface modification using magnetron sputtering technique
  28. Numerical modeling of the heat flow component of the composite developed on the basis of basalt fabric
  29. Weft insertion guideway design based on high-temperature superconducting levitation
  30. Ultrasonic-assisted alkali hydrolysis of polyethylene terephthalate fabric and its effect on the microstructure and dyeing properties of fibers
  31. Comparative study on physical properties of bio-based PA56 fibers and wearability of their fabrics
  32. Investigation of the bias tape roll change time efficiency in garment factories
  33. Analysis of foot 3D scans of boys from Polish population
  34. Optimization of garment sewing operation standard minute value prediction using an IPSO-BP neural network
  35. Influence of repeated switching of current through contacts made of electroconductive fabrics on their resistance
  36. Numerical calculation of air permeability of warp-knitted jacquard spacer shoe-upper materials based on CFD
  37. Compact Spinning with Different Fibre Types: An Experimental Investigation on Yarn Properties in the Condensing Zone with 3D-Printed Guiding Device
  38. Modeling of virtual clothing and its contact with the human body
  39. Advances in personalized modelling and virtual display of ethnic clothing for intelligent customization
  40. Investigation of weave influence on flame retardancy of jute fabrics
  41. Balloonless spinning spindle head shape optimisation
  42. Research on 3D simulation design and dynamic virtual display of clothing flexible body
  43. Turkish textile and clothing SMEs: Importance of organizational learning, digitalization, and internationalization
  44. Corrigendum To: “Washing characterization of compression socks”
  45. Study on the promotion multiple of blood flow velocity on human epidermal microcirculation of volcanic rock polymer fiber seamless knitted fabric
  46. Bending properties and numerical analysis of nonorthogonal woven composites
  47. Bringing the queen mother of the west to life: Digital reconstruction and analysis of Taoist Celestial Beings Worshiping mural’s apparel
  48. Modeling process for full forming sports underwear
  49. Retraction of: Ionic crosslinking of cotton
  50. An observational study of female body shape characteristics in multiracial Malaysia
  51. Study on theoretical model and actual deformation of weft-knitted transfer loop based on particle constraint
  52. Design and 3D simulation of weft-knitted jacquard plush fabrics
  53. An overview of technological challenges in implementing the digital product passport in the textile and clothing industry
  54. Understanding and addressing the water footprint in the textile sector: A review
  55. Determinants of location changes in the clothing industry in Poland
  56. Influence of cam profile errors in a modulator on the dynamic response of the heald frame
  57. Quantitative analysis of wool and cashmere fiber mixtures using NIR spectroscopy
  58. 3D simulation of double-needle bar warp-knitted clustered pile fabrics on DFS
  59. Finite element analysis of heat transfer behavior in glass fiber/metal composite materials under constant heat load
  60. Price estimation and visual evaluation of actual white fabrics used for dress shirts and their photographic images
  61. Effect of gluing garment materials with adhesive inserts on their multidirectional drape and bending rigidity
  62. Optimization analysis of carrier-track collision in braiding process
  63. Numerical and experimental analysis of the ballistic performance of soft bulletproof vests for women
  64. The antimicrobial potential of plant-based natural dyes for textile dyeing: A systematic review using prisma
  65. Influence of sewing parameters on the skin–fabric friction
  66. Validation by experimental study the relationship between fabric tensile strength and weave structures
  67. Optimization of fabric’s tensile strength and bagging deformation using surface response and finite element in stenter machine
  68. Analysis of lean manufacturing waste in the process flow of ready-to-wear garment production in Nigeria
  69. An optimization study on the sol–gel process to obtain multifunctional denim fabrics
  70. Drape test of fully formed knitted flared skirts based on 3D-printed human body posture
  71. Supplier selection models using fuzzy hybrid methods in the clothing textile industry
https://doi.org/10.1515/aut-2023-0041
Keywords for this article
Multi-objective optimisation; balloon-less spinning spindle head; ring-spinning machine; optimisation; manufacturing processes; manufacturing cost; product quality
Creative Commons
BY 4.0

Articles in the same Issue

  2. Characterization of viscoelastic properties of yarn materials: Dynamic mechanical analysis in the transversal direction
  3. Analysis of omni-channel implementations that are preferred by consumers in clothing sector
  4. Structural modeling and analysis of three-dimensional cross-linked braided preforms
  5. An experimental study of mechanical properties and comfortability of knitted imitation woven shirt fabrics
  6. Technology integration to promote circular economy transformation of the garment industry: a systematic literature review
  7. Research on T-shirt-style design based on Kansei image using back-propagation neural networks
  8. Research on She nationality clothing recognition based on color feature fusion with PSO-SVM
  9. Accuracy prediction of wearable flexible smart gloves
  10. Preparation and performance of stainless steel fiber/Lyocell fiber-blended weft-knitted fabric
  11. Development of an emotional response model for hospital gown design using structural equation modeling
  12. Preparation and properties of stainless steel filament/pure cotton woven fabric
  13. Facemask comfort enhancement with graphene oxide from recovered carbon waste tyres
  14. Use of enzymatic processes in the tanning of leather materials
  15. Optical-related properties and characterization of some textile fibers using near-infrared spectroscopy
  16. Network modeling of aesthetic effect for Chinese Yue Opera costume simulation images
  17. Predicting consumers’ garment fit satisfactions by using machine learning
  18. Non-destructive identification of wool and cashmere fibers based on improved LDA using NIR spectroscopy
  19. Study on the relationship between structure and moisturizing performance of seamless knitted fabrics of protein fibers for autumn and winter
  20. Antibacterial and yellowing performances of sports underwear fabric with polyamide/silver ion polyurethane filaments
  21. Numerical and experimental analysis of ballistic performance in hybrid soft armours composed of para-aramid triaxial and biaxial woven fabrics
  22. Phonetic smart clothing design based on gender awareness education for preschoolers
  23. Determination of anthropometric measurements and their application in the development of clothing sizing systems for women in the regions of the Republic of Croatia
  24. Research on optimal design of pleated cheongsam based on Kano–HOQ–Pugh model
  25. Numerical investigation of weaving machine heald shaft new design using composite material to improve its performance
  26. Corrigendum to “Use of enzymatic processes in the tanning of leather materials”
  27. Shaping of thermal protective properties of basalt fabric-based composites by direct surface modification using magnetron sputtering technique
  28. Numerical modeling of the heat flow component of the composite developed on the basis of basalt fabric
  29. Weft insertion guideway design based on high-temperature superconducting levitation
  30. Ultrasonic-assisted alkali hydrolysis of polyethylene terephthalate fabric and its effect on the microstructure and dyeing properties of fibers
  31. Comparative study on physical properties of bio-based PA56 fibers and wearability of their fabrics
  32. Investigation of the bias tape roll change time efficiency in garment factories
  33. Analysis of foot 3D scans of boys from Polish population
  34. Optimization of garment sewing operation standard minute value prediction using an IPSO-BP neural network
  35. Influence of repeated switching of current through contacts made of electroconductive fabrics on their resistance
  36. Numerical calculation of air permeability of warp-knitted jacquard spacer shoe-upper materials based on CFD
  37. Compact Spinning with Different Fibre Types: An Experimental Investigation on Yarn Properties in the Condensing Zone with 3D-Printed Guiding Device
  38. Modeling of virtual clothing and its contact with the human body
  39. Advances in personalized modelling and virtual display of ethnic clothing for intelligent customization
  40. Investigation of weave influence on flame retardancy of jute fabrics
  41. Balloonless spinning spindle head shape optimisation
  42. Research on 3D simulation design and dynamic virtual display of clothing flexible body
  43. Turkish textile and clothing SMEs: Importance of organizational learning, digitalization, and internationalization
  44. Corrigendum To: “Washing characterization of compression socks”
  45. Study on the promotion multiple of blood flow velocity on human epidermal microcirculation of volcanic rock polymer fiber seamless knitted fabric
  46. Bending properties and numerical analysis of nonorthogonal woven composites
  47. Bringing the queen mother of the west to life: Digital reconstruction and analysis of Taoist Celestial Beings Worshiping mural’s apparel
  48. Modeling process for full forming sports underwear
  49. Retraction of: Ionic crosslinking of cotton
  50. An observational study of female body shape characteristics in multiracial Malaysia
  51. Study on theoretical model and actual deformation of weft-knitted transfer loop based on particle constraint
  52. Design and 3D simulation of weft-knitted jacquard plush fabrics
  53. An overview of technological challenges in implementing the digital product passport in the textile and clothing industry
  54. Understanding and addressing the water footprint in the textile sector: A review
  55. Determinants of location changes in the clothing industry in Poland
  56. Influence of cam profile errors in a modulator on the dynamic response of the heald frame
  57. Quantitative analysis of wool and cashmere fiber mixtures using NIR spectroscopy
  58. 3D simulation of double-needle bar warp-knitted clustered pile fabrics on DFS
  59. Finite element analysis of heat transfer behavior in glass fiber/metal composite materials under constant heat load
  60. Price estimation and visual evaluation of actual white fabrics used for dress shirts and their photographic images
  61. Effect of gluing garment materials with adhesive inserts on their multidirectional drape and bending rigidity
  62. Optimization analysis of carrier-track collision in braiding process
  63. Numerical and experimental analysis of the ballistic performance of soft bulletproof vests for women
  64. The antimicrobial potential of plant-based natural dyes for textile dyeing: A systematic review using prisma
  65. Influence of sewing parameters on the skin–fabric friction
  66. Validation by experimental study the relationship between fabric tensile strength and weave structures
  67. Optimization of fabric’s tensile strength and bagging deformation using surface response and finite element in stenter machine
  68. Analysis of lean manufacturing waste in the process flow of ready-to-wear garment production in Nigeria
  69. An optimization study on the sol–gel process to obtain multifunctional denim fabrics
  70. Drape test of fully formed knitted flared skirts based on 3D-printed human body posture
  71. Supplier selection models using fuzzy hybrid methods in the clothing textile industry
Sign up now to receive a 20% welcome discount
Institutional Access
How does access work?
Have an idea on how to improve our website?
Please write us.
© 2026 De Gruyter Brill
Downloaded on 17.1.2026 from https://www.degruyterbrill.com/document/doi/10.1515/aut-2023-0041/html?lang=en
Scroll to top button