Abstract
Numerical simulation basic steps are making a model and recreating the course of the examined process. The article presents numerical modeling of the component of heat flow through a composite developed on the basis of basalt fabric. The composite consisted of the following components: basalt fabric, modified with a composite coating consisting of 1 µm thick aluminum with a mixture of 1 µm zirconia and titanium dioxide, silicone, and Mylar® film modified with the same coating as the basalt fabric. Numerical modeling was performed using the ANSYS 2022 R1 program. The performed numerical simulations of the temperature gradient represented the contact heat resistance test for the contact temperature of 250°C for the basalt fabric and the composite. The proposed model reproduced the exact course and results of the actual study. Each of the layers making up the composite had a thickness and was mapped in accordance with the physical model.
1 Introduction
Modeling is a process of creating mathematical and physical representations of real systems, taking into account the accuracy and cost of this modeling. The purpose of simulation is recreating the course of the examined process or phenomenon and is performed on the basis of its model. At present, the following methods of process modeling are distinguished: statistical modeling [1,2], physical modeling [3,4], using artificial neural networks [5,6], as well as modeling that is a combination of physical and mathematical modeling [7,8,9,10,11,12]. The created models are to be used for process analysis, especially for their optimization. Each of the modeling methods, properly carried out and performed, allows for the analysis of the research object, leading as a result to its control in order to obtain the planned effects. All of the modeling methods, apart from the physical and mathematical connection, require experimental research [13,14].
Scientists are constantly working on modeling the flow of heat through textiles or material packages. Onofrei et al. [15] studied the effect of moisture on heat transfer through single-layer fabrics exposed to low flux density (1100 W/m2) radiant heat. Researchers developed a mathematical model of heat transfer that used the finite-element method. The obtained calculations of the numerical model indicated changes in temperature during the action of the radiant heat flux on a single-layer fabric with different moisture levels, which was consistent with experimental research. The model was developed as a result of work on COMSOL Multiphysics® modeling software. The resulting heat transfer model was developed to predict the temperature in the protective clothing of a firefighter exposed to low-intensity thermal radiation [15].
Another example of numerical modeling is the modeling of the thermal insulation properties of a multi-layer system of materials intended for protective clothing exposed to thermal radiation. The multi-layer protective clothing consisted of five layers. Computer software (computer-aided design [CAD]) was used in the research to analyze the thermal insulation of the multi-layer system used in the protective clothing. First, the three-dimensional geometry of the selected material arrangement was modeled. In the next stage of the work, the finite-volume method was used to estimate the thermal insulation properties of the system subjected to thermal radiation. In the final stage, the simulation results were compared with the experimental results. Based on the simulation result and experimental results obtained for a multi-layer textile system, the parameters of protective clothing were specified, which directly affect the protective properties against heat. The results of experimental measurements differed from the simulation results. Differences could occur depending on the intensity of the thermal radiation acting on the multi-layer system.
In addition, differences may occur due to modeling problems (mainly related to the simplification of the complex geometry of textile materials). One of the simplifications is the model of a fabric with an elliptical yarn cross-section, while in reality, the fabric changes its cross-section, which results from the friction forces occurring between the interlacing of the warp and the weft. Another example of the resulting differences may be the mutual contact of the layers of materials, which affects the interlayer thermal conductivity, because for the designed model it can be completely different from the model of the actual material arrangement. Despite the use of simplifications, the software used and the developed geometric model of the multi-layer system make it possible to predict the heat transfer coefficient with an error of 3–20% [16].
Research in terms of the analysis of thermal comfort and safety of protective clothing used by firefighters was conducted by Puszkarz and Machnowski [17]. The multi-layer material packages used in the protective clothing were modeled using CAD computer design software. Geometric models of individual yarns were designed for the fabric model and homogenization was performed for the nonwoven fabric model. The finite-volume method was used to simulate heat transfer through a textile bundle caused by the effect of a flame on the bundle. A comparison of the results obtained from the simulation with the experimental results carried out according to the EN ISO 9151 standard was made. On the basis of the obtained experimental and simulation results, the parameters describing the protective features of the tested clothing, which have a direct impact on the firefighter’s safety, were indicated.
Numerical modeling was used to determine the convection coefficient of knitted fabrics based on finite-element methods [18]. The main objective of the work was to investigate the applicability of finite-volume analysis software to the textile sector. Experimental studies were carried out on the natural convective heat transfer coefficient of a cotton jersey fabric in specific conditions. The next step was to model the smooth weft knitted fabric using CATIA V5R16 and perform numerical analyses using the FLUENT software. As a result of the conducted research, a good agreement was obtained between the numerical and experimental values, with an uncertainty of 11% of the heat transfer coefficient for cotton-knitted fabrics.
The process of transporting heat and moisture through protective fabrics used by firefighters was modeled by Zhu and Zhou [19]. The authors relied on a theoretical–physical one-dimensional model to study the transfer of heat and moisture through the porous system of protective clothing materials during exposure to the flame jet, taking Fourier’s law and Fick’s law as the basis. Nomex fabrics were selected for the tests. The obtained results showed that the transfer of heat and moisture by flash fire exposed to contact with a wet fabric can be considered a drying process resulting from dynamic diffusion. It was found that the developed drying model can be used to estimate the thermal reaction of wetted fabrics. The obtained model should be the theoretical basis for the ergonomic construction of thermal protective clothing for firefighters.
Subsequent researchers developed simulations of heat transfer through the fabric based on a model of its geometry. The finite-element method was used to predict heat transfer through fabrics. Based on the thickness of the fabric and the cross-sectional shape of the yarn, geometric models of a 5/3 satin fabric, a 2/2 plain weave, and a 2/2 twill fabric made of glass fiber were made. The obtained models of fabric geometry are very close to real fabrics. The numerical temperatures obtained were very close to the experimental test temperatures for glass fiber fabrics, which means that the developed finite-element model makes it possible to predict the heat transfer properties of the fabric [20].
Heat flow simulations were performed for basalt fabric and aluminized basalt fabric and the clothing system based on research results obtained on the Alambeta device worked by Gilewicz et al. [21]. The tested clothing system consisted of aluminum layer, glue, basalt fabric, woolen fabric, and underwear. In addition, the author took into account the air in the upper part of the Alambeta device, the air layer between the basalt fabric and the glue on one side, and the layer between the glue and the woolen fabric on the other side. Numerical simulations were performed using Ansys CFX software. The coefficient of thermal conductivity for the basalt fabric, aluminized basalt fabric, and the clothing system was determined on the basis of experimental tests performed on the Alambeta device. The obtained numerical model was made for a specific experiment and a specific clothing system; however, the test results obtained and the developed simulations can be used as auxiliary material when testing similar clothing systems for thermal conductivity testing.
The aim of the research was to perform a numerical simulation of basalt fabric and composite based on experimental tests performed on an OTI device for testing thermal insulation.
2 Materials and methods
The preparation of the geometric model of the basalt fabric was based on measurements carried out using the Olympus microscope.
Table 1 presents the geometric dimensions obtained from the arithmetic means of five measurements made for warp yarns, five for weft yarns, and six clearances in the basalt fabric. According to the data obtained, tests were carried out to recreate the weave of the basalt fabric.
Average geometric dimensions of the 2/2 twill weave of the basalt fabric measured with a microscope and used in the model
| Thickness of the warp yarn (mm) | Thickness of the weft yarn (mm) | Gaps in the fabric (mm) | |
|---|---|---|---|
| Yarn width in interlacing | 0.90 | 2.58 | 0.28 |
| Yarn length in interlacing | 2.68 | 0.99 | 0.20 |
2.1 Determination of resistance to contact heat
The contact heat resistance test was carried out according to the PN-EN ISO 12127-1:2016-02 standard [22]. The test involves exposing the tested sample, placed on a calorimeter, to contact with a heating cylinder heated to a temperature of 250°C. During the test, the threshold time t t is measured, which is the time from the moment of first contact with the heating cylinder until the calorimeter temperature increases by 10°C compared to the initial value. For gloves, tests are carried out on three samples of each fabric. The arithmetic mean is calculated from the three obtained values of the threshold time t t, which is the test result according to which the gloves are classified to the appropriate level of effectiveness.
According to the PN-EN 407:2020-10 standard [23], in terms of resistance to contact heat, there are four levels of effectiveness to which gloves are classified based on laboratory tests.
The composite with the best contact heat resistance for the contact temperature of 250°C was selected for the simulation. The composite consisted of the following components: basalt fabric, modified with a composite coating consisting of 1 µm thick aluminum with a mixture of 1 µm zirconia and titanium dioxide, silicone, and Mylar® foil modified with the same coating as the basalt fabric. Composite coatings were applied using the magnetron sputtering method due to the review of the literature on the use of PVD methods in textiles [24].
As a result of the test of resistance to contact heat at a contact temperature of 250°C in the case of the basalt fabric, a threshold time of 4 s was obtained, while in the case of the composite produced, the t t was 17 s.
2.2 Numerical modeling of heat flow through a composite developed on the basis of basalt fabric
Numerical modeling showing the temperature gradient through the composite reflects the simulation of contact heat resistance testing for a contact temperature of 250°C, which was performed in accordance with PN-EN ISO 12127-1:2016-02 [23] and PN-EN 407:2020-10 [24] determined the level of composite protection effectiveness. Numerical modeling was carried out using a program dedicated to numerical simulations ANSYS 2022 R1 and was divided into three stages.
Building a geometric model of the research object was divided into sub-stages:
Modeling the distribution of fibers assuming a constant diameter in the yarn;
Preparation of basalt fabric geometry;
Creation of a geometric model for the composite, taking into account five components: basalt fabric, composite coating with which the fabric was modified, silicone, Mylar® foil, and composite coating with which the foil was modified, the same as in the case of fabric modification.
In computer simulations, it is very often necessary to homogenize the analyzed materials. The introduced simplifications in the structure of textile products significantly improve the accuracy of the model.
During the simulation of heat transfer through the composite, the conditions adopted were the same as those used during the contact heat resistance test.
The first stage of the work was to determine the differences in heat transfer through the basalt fabric. The basalt fabric selected for the tests was one of the components of the composite intended, for example, for use in a glove protecting against high temperature and hot factors.
The second stage of the work consisted in an attempt to recreate the mutual arrangement of the yarns and their arrangement in the fabric in order to reproduce its actual weave. Reproducing the actual image of the arrangement of the yarn in the weave of the fabric using a geometric model was a very complicated task. This was due to the fact that the yarn is made of many fibers that are joined together during the spinning process. It should also be noted that the fibers in the yarn are constantly working, sliding, and moving due to the bending or stretching of the finished textile product.
The twill weave of the basalt fabric, characterized by a high complexity of the structure, made it necessary to use structural simplifications for the assumptions of the thermal simulations. Such a simplification is referred to as “submodeling” – which may take the form of a section of the general model. As a result of using such a model, we are looking for an exact solution, assuming on the appropriate edges or planes of the model, as boundary conditions, the results obtained in the general model. In the numerical modeling, an object representing a basalt fabric with a 2/2 twill weave was presented.
The third and final stage of preparing the geometry of the composite was very complicated and complex. The composite was divided into five computational domains due to the five component layers from which it was built. In the geometric model, a structural simplification was also used – isotropy of components due to the variety of materials that make up the composite.
Due to the complexity of the structure of the basalt fabric with a 2/2 twill weave, structural simplifications related to the assumptions of the simulation were applied. A variant of fiber distribution was made for a single yarn. The structure of the fabric shows the arrangement of interwoven yarns made of warp and weft yarns. Interlaces in the fabric resulting from the structure of the weave create thermal bridges that increase the flow of heat. The contact heat resistance test for the contact temperature of 250°C was carried out separately for the basalt fabric, and the composite was developed with the use of a basalt fabric with a 1/1 µm composite coating.
Table 2 shows the properties of the individual layers of the composite intended for the palm part of the protective glove. Density, thermal conductivity coefficient, and specific heat for the composite coating were calculated using appropriate formulas and relationships. For the remaining layers forming the composite, the values of the thermal conductivity coefficient and specific heat were read from the material tables. The time of heat flow through the composite was assumed to be the average threshold time calculated from three measurements made for testing the resistance to contact heat at a contact temperature of 250°C.
Parameter values adopted for individual layers of the composite
| Material | Density (kgm−3) | Thermal conductivity coefficient (Wm−1K−1) | Specific heat (Jkg−1K−1) |
|---|---|---|---|
| Composite coating | 3,830 | 1.20 | 727 |
| Mylar® film | 1,390 | 0.14 | 960 |
| Silicon | 1,250 | 0.40 | 1,000 |
| Basalt fabric | 2,650 | 1.30 | 860 |
3 Results
3.1 Geometric model and numerical model of basalt fabric
The process of building a geometric model of a basalt fabric consisted in making a model of a single yarn and then using a tool for duplicating the resulting elements. Based on this, two sets of yarns were made: warp and weft, and in the next stage, an elementary report of the 2/2 twill weave for the basalt fabric was made. Weft and warp yarns are characterized by a fibrous structure with a varied distribution of fibers. On this basis, for the simulation of heat flow through the basalt fabric, it was assumed that the fabric should be represented in the form of a homogeneous matter. At this point in the formation of the geometric model of the warp and weft yarns, the homogenization process was carried out. The model with the given properties characterizing the basalt fabric, namely density, thermal conductivity coefficient, and specific heat, was the basis for making the geometry of the basalt fabric with a 2/2 twill weave.
In order to create an appropriate numerical grid used for calculations, rounding of the contact edge between the weft and warp yarns was performed. Changing the contact surface does not affect the simulation of heat flow for the model.
Basalt twill weave fabric has a complex structure, because the fibers are in slight point contact or surface contact. Taking into account these considerations related to the simulation of heat flow, it was necessary to take into account the occurrence of the compressive force of the fabric (resulting from the measurements carried out on the device for testing thermal insulation of the OTI type). For this reason, during the implementation of the geometric model of the basalt fabric, a simplification was used consisting in the homogenization of fibers in the yarn. This was due to the lack of information about the deformation and distribution of fiber diameters in the yarn and the actual course of the fibers that occurs as a result of the compression process.
At this stage, a geometric model of the basalt fabric with a twill weave was built in the ANSYS 2022 R1 program (Figure 1), while the next figure shows a cross-section of the basalt fabric (Figure 2).

Model of a geometric basalt fabric with a 2/2 twill weave.

Cross-sectional view of a 2/2 twill basalt fabric.
In the next stage of modeling, submodeling was performed – a fragment of the fabric was cut out from the solid model of the fabric, on which a contact heat resistance test was simulated for a contact temperature of 250°C.
The numerical model of the basalt fabric after the submodeling process was presented in the form of one yarn with dimensions 0.004 m × 0.0003 m × 0.0006 m, because, in the case of thermal flows, the simulation performed on a small section of the object reflects the heat flow for the entire surface of the model. For the prepared fabric model, its selected properties were introduced in order to simulate heat flow, i.e., a density of 2,650 kgm−3, a thermal conductivity of 1.3 Wm−1K−1, and a specific heat of −860 Jkg−1K−1.
For the fabric model made in the ANSYS – Transient Thermal module, in the “Mesh” option, the model was divided into finite volumes. Due to the complex geometry of the fabric, the space was divided by the use of square elements – preferred in thermal flows. For the model, tests of the impact of mesh density on the simulated heat flow were carried out. The mesh was refined for the entire volume of the model. Due to the needs of the model, the mesh made included elements of various sizes. In order to generate the mesh correctly, the sizes of the largest elements had to be defined. Smaller elements showing smaller sizes are generated for areas of the model with large differences in parameters that can occur for heat flow simulations. Calculations were made and the results were analyzed in order to obtain stabilization of the observed parameters.
Numerical simulations for a steady-state process of heat flow through the basalt fabric and composite model were performed in the ANSYS 2022 R1 program – Transient Thermal module. For the basalt fabric model, a simulation was performed taking into account the conditions prevailing during the contact heat resistance measurement for the contact temperature of 250°C. The following boundary conditions were adopted: the temperature of the upper heating cylinder was 250°C, the temperature of the lower cylinder was 35°C, and the heat flow through the fabric took 4 s.
3.2 Numerical model of the temperature gradient in relation to the heat flow through the composite developed on the basis of basalt fabric
The third stage of the work was to simulate the composite model, which consisted of the following components: basalt fabric, composite coating with which the fabric was modified, silicone, Mylar® film, and a composite coating for which the foil was modified (Figure 3). Due to the very complicated structure of the thin coating, silicone, and Mylar® film, spatial homogenization was used for these components in the overall general shape of the composite structure with given dimensions and thicknesses (Figure 4).

Scheme and arrangement of layers forming the composite.

Section of the elementary cell model of the composite used in the numerical simulation.
The geometric model of the composite was made entirely in the ANSYS program (SpaceClaim). The model representing the produced composite was presented in the form of one yarn with dimensions of 0.004 m × 0.0003 m × 0.0006 m.
The composite model was divided into five computational domains:
Composite coating consisting of aluminum and a mixture of zirconium dioxide and titanium dioxide;
Mylar® film;
Silicone;
Composite coating consisting of aluminum and a mixture of zirconium dioxide and titanium dioxide, the same as in the first layer; and
Basalt fabric.
In order to create a numerical model of the composite, mesh refinement using the “Mesh” option (Workbench) was carried out individually for each of the five layers that make up the composite (Figure 5). In addition, each component was characterized by determining its density, thermal conductivity coefficient, and specific heat. The mesh density for the entire composite was based on square elements. The large size of the mesh was caused by adjusting the size of the mesh elements to the elements corresponding to the composite coating, because it was the thinnest component of the composite, equal to 2 µm.

Geometric model of a composite package consisting of five components.
For the resulting composite model consisting of five computational domains, a simulation was performed taking into account the conditions prevailing during the measurement of resistance to contact heat for a contact temperature of 250°C, which was carried out on an OTI device for testing thermal insulation.
Accordingly, as in the case of the simulation performed only for the layer of basalt fabric, the same boundary conditions were adopted for the entire composite. The temperature of 250°C was assumed for the outer layer of the composite – a composite coating consisting of aluminum with a thickness of 1 µm and a mixture of zirconium dioxide and titanium dioxide with a thickness of 1 µm. On the other hand, for the bottom layer, which was a basalt fabric, a temperature value of 35°C was assumed. In addition, it was assumed that the heat flow occurred in 17 s, which is confirmed by experimental tests carried out for this variant of the composite. The symmetry condition was assumed on the side walls of the composite.
4 Results and analysis of simulation tests
4.1 Analysis of results for basalt fabric
Figure 6 shows the temperature gradient inside the tested basalt fabric structure in the case of mapping the contact heat resistance measurement for the contact temperature of 250°C. The temperature gradient for the tested fabric was presented after 4 s. Due to the fact that after 4 s the contact heat resistance test was completed, the basalt fabric was not resistant to the contact temperature of 250°C.

Temperature gradient obtained for the basalt fabric after the fourth second of operation of the heating cylinder heated to 250°C.
Applying a heating cylinder with a temperature of 250°C to the surface of the basalt fabric after 4 s resulted in a temperature gradient in the range of 35–250°C. There is a rapid change in temperature during the simulation. In the middle section of the basalt fabric (in its central part), there is a linear temperature change. In the fourth second of operation of the set temperature, the flow of heat through the basalt fabric ended because from the side of the calorimeter, it showed a temperature of 35°C.
4.2 Analysis of the results for the composite developed on the basis of basalt fabric
The temperature gradient inside the tested composite structure after the threshold time (17 s) is shown in Figure 7. For the upper part of the domain, from the heating cylinder, there is a high-temperature area. The temperature change occurring in the cross-section of the composite, in the global range, changes in a linear way from the heating cylinder to the calorimeter. The scale of temperature changes was selected based on the lowest and highest values obtained in the simulation.
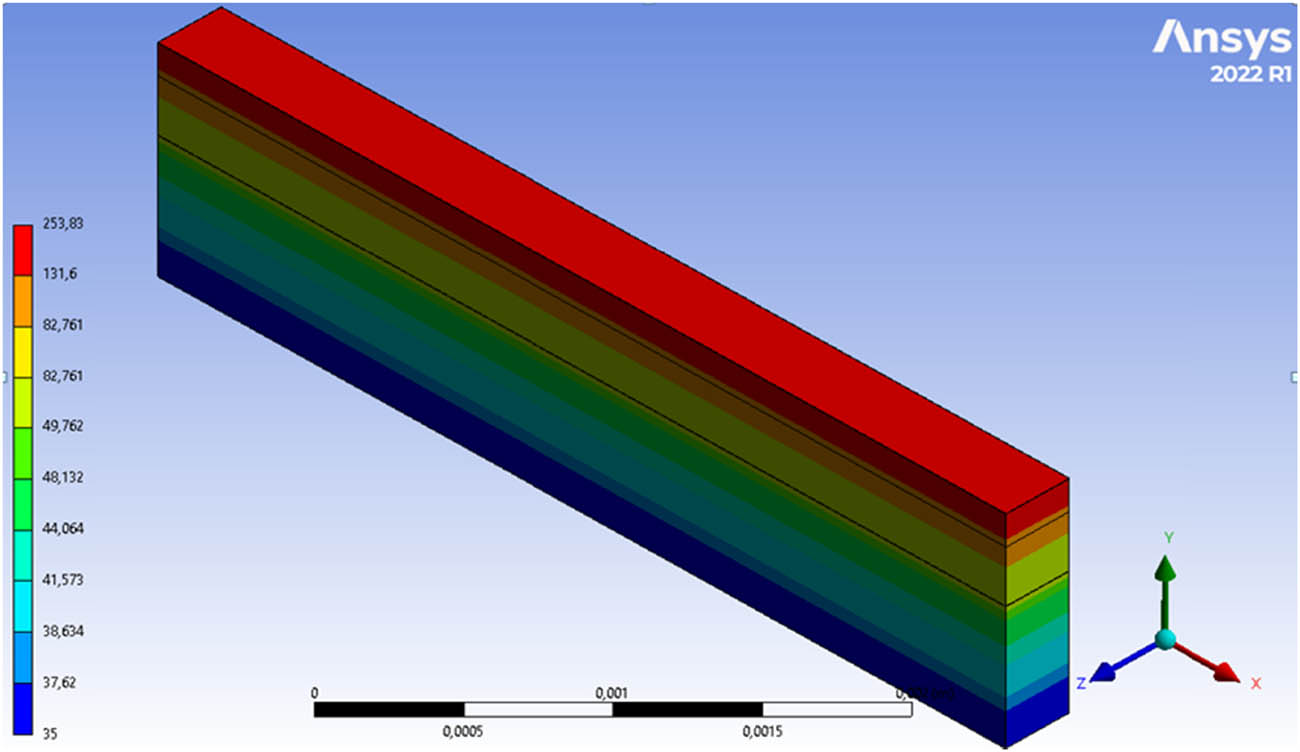
Temperature gradient obtained for the composite after the threshold time from the operation of the heating cylinder heated to 250°C.
In the upper part of the domain, heated by a heating cylinder reaching a temperature of 250°C, we observe the area of operation of the highest temperature that affects the composite coating. Mylar® film is exposed to temperatures ranging from 82.76 to 250°C. For silicone, it is in the drop from 49.76 to 82.76°C, while the composite coating deposited on the surface of the basalt fabric reaches a temperature of 48.13°C. The basalt fabric, after the threshold time (17 s) from the application of the heating cylinder, shows a temperature in the drop of 35–48.13°C.
5 Conclusions
Each of the layers making up the composite had a thickness and was mapped in accordance with the physical model.
Due to the complex and complicated structure of the entire composite consisting of five components, “submodeling,” i.e., a simplified model of the composite, was used to perform a numerical simulation.
A series of numerical simulations were performed using the ANSYS Transient Thermal software to determine the temperature gradient for the basalt fabric and then for the entire composite. The values of the average threshold time for the fabric and for the composite were determined based on experimental tests of contact heat resistance for the contact temperature of 250°C. The experimental test results were used to reflect the course of testing the resistance to contact heat at a temperature of 250°C for the basalt fabric and the composite.
The numerical model of the composite can be presented as an innovative approach in terms of numerical modeling of heat flow not only through textiles but also other materials that can form a composite for use in personal protective equipment.
The performed numerical simulations of the temperature gradient reproduced the contact heat resistance test for the contact temperature of 250°C for the basalt fabric and the composite. The model reproduces the exact course and results of the actual test.
-
Conflict of interest: Authors state no conflict of interest.
References
[1] Lee, S., Obendorf, S. K. (2005). Statistical model of pesticide penetration through woven work clothing fabrics. Archives of Environmental Contamination and Toxicology, 49, 266–273.10.1007/s00244-004-0127-8Search in Google Scholar PubMed
[2] Schiavon, S., Ho Lee, K. (2013). Dynamic predictive clothing insulation models based on outdoor air and indoor operative temperatures. Building and Environment, 59, 250–260.10.1016/j.buildenv.2012.08.024Search in Google Scholar
[3] Hrynyk, R., Frydrych, I., Irzmińska, E. A., Stefko A. (2012). Thermal properties of aluminized and non-aluminized basalt fabrics. Textile Research Journal, 83(17), 1860–1872.10.1177/0040517512447517Search in Google Scholar
[4] Hrynyk, R., Frydrych, I. (2015). Study on textile assemblies with aluminized basalt fabrics destined for protective gloves. International Journal of Clothing Science and Technology, 27(5), 1–17.10.1108/IJCST-09-2014-0112Search in Google Scholar
[5] Wong, A. S. W., Yeung, L., Lee, P. W. H. (2003). Neural network predictions of human psychological perceptions of clothing sensory comfort. Textile Research Journal, 73(1), 31–37.10.1177/004051750307300106Search in Google Scholar
[6] Yian, S., Kyung-shik, S. (2019). Hierarchical convolutional neural networks for fashion image classification. Expert Systems with Applications, 116, 328–339.10.1016/j.eswa.2018.09.022Search in Google Scholar
[7] Shen, H., Xie, K., Tu, L., Xu, Y., Wang, J. (2019). Analysis of heat transfer characteristics in textiles and factors affecting thermal properties by modeling. Textile Research Journal, 89, 21–22.10.1177/0040517519842790Search in Google Scholar
[8] Puszkarz, A. K., Korycki, R., Krucinska, I. (2016). Simulations of heat transport phenomena in a three-dimensional model of knitted fabric. Autex Research Journal, 16, 128–137.10.1515/aut-2015-0042Search in Google Scholar
[9] Barauskas, R., Abraitiene, A. (2011). A model for numerical simulation of heat and water vapor exchange in multilayer textile packages with three-dimensional spacer fabric ventilation layer. Textile Research Journal, 81, 1195–1215.10.1177/0040517510392468Search in Google Scholar
[10] Ghazy, A., Bergstrom, D. J. (2010). Numerical simulation of transient heat transfer in a protective clothing system during a flash fire exposure. Numerical Heat Transfer, Part A: Applications. 58, 702–724.10.1080/10407782.2010.516691Search in Google Scholar
[11] Zhu, Q. Y., Li, Y. (2010). Numerical simulation of the transient heat and liquid moisture transfer through porous textiles with consideration of electric double layer. International Journal of Heat and Mass Transfer, 53, 1417–1425.10.1016/j.ijheatmasstransfer.2009.12.014Search in Google Scholar
[12] Ye, C., Huang, H., Fan, J., Sun, W. (2008). Numerical study of heat and moisture transfer in textile materials by a finite volume method. Communications in Computational Physics, 4, 929–948.Search in Google Scholar
[13] Gotowała, K., Patyk, R. (2016). The use of modern modeling and simulation methods in the design of machines and devices. Buses: Technology, Operation, Transport Systems, 8, 275–280.Search in Google Scholar
[14] Miśkiewicz, P., Puszkasz, A. K. (2023). Assessment of insulation against contact heat and radiant heat of composites with TiO2-ZrO2-Al and parylene C coatings Intended for protective gloves supported by computational fluid dynamics. Applied Sciences, 13(22), 12420.10.3390/app132212420Search in Google Scholar
[15] Onofrei, E., Petrusic, S., Bedek, G., Dupont, D., Saulat, D., Cadau, T. C. (2014). Modeling of heat transfer through multilayer firefighter protective clothing. Industria Textila, 5, 277–282.Search in Google Scholar
[16] Puszkarz, A. K., Machnowski, W., Błasińska, A. (2020). Modeling of thermal performance of multilayer protective clothing exposed to radiant heat. Heat and Mass Transfer, 56, 1767–1775.10.1007/s00231-020-02820-1Search in Google Scholar
[17] Puszkarz, A. K., Machnowski, W. (2022). Simulations of heat transfer through multilayer protective clothing exposed to flame. Autex Research Journal, 22(3), 298–304.10.2478/aut-2020-0041Search in Google Scholar
[18] Duru Cimilli, S., Deniz, E., Candan, C., Nergis, B. U. (2012). Determination of natural convective heat transfer coefficient for plain knitted fabric via CFD modeling. Fibres & Textiles in Eastern Europe, 1, 90, 42–46.Search in Google Scholar
[19] Zhu, F. L., Zhou, Y. (2013). Modelling heat-moisture transport through firefighters’ protective fabrics from an impinging flame jet by simulating the drying process. Fibres & Textiles in Eastern Europe, 5, 101, 85–90.Search in Google Scholar
[20] Zheng, Z., Zhang, N., Zhao, X. (2017). Simulation of heat transfer through woven fabrics based on the fabric geometry model. Thermal Science, 22(6B), 2815–2825.10.2298/TSCI160507128ZSearch in Google Scholar
[21] Gilewicz, P., Obidowski, D., Sobczak, K., Frydrych, I., Cichocka, A. (2021). Analysis of heat transfer through a protective clothing package. Autex Research Journal, 23(1), 29–38.10.2478/aut-2021-0044Search in Google Scholar
[22] EN ISO 12127-1:2016-02. (2016). Heat and flame protective clothing - Determination of contact heat transfer through protective clothing or protective clothing materials – Part 1: Contact heat generated by a heating cylinder.Search in Google Scholar
[23] PN-EN 407:2020-10. (2020). Protective gloves and other hand protection against thermal hazards (heat and/or fire). ISO, Geneva, Switzerland.Search in Google Scholar
[24] Miśkiewicz, P., Frydrych, I., Cichocka, A. (2022). Application of physical vapor deposition in textile industry. Autex Research Journal, 22(1), 1–13.10.2478/aut-2020-0004Search in Google Scholar
© 2024 by the authors, published by De Gruyter
This work is licensed under the Creative Commons Attribution 4.0 International License.
Articles in the same Issue
- Characterization of viscoelastic properties of yarn materials: Dynamic mechanical analysis in the transversal direction
- Analysis of omni-channel implementations that are preferred by consumers in clothing sector
- Structural modeling and analysis of three-dimensional cross-linked braided preforms
- An experimental study of mechanical properties and comfortability of knitted imitation woven shirt fabrics
- Technology integration to promote circular economy transformation of the garment industry: a systematic literature review
- Research on T-shirt-style design based on Kansei image using back-propagation neural networks
- Research on She nationality clothing recognition based on color feature fusion with PSO-SVM
- Accuracy prediction of wearable flexible smart gloves
- Preparation and performance of stainless steel fiber/Lyocell fiber-blended weft-knitted fabric
- Development of an emotional response model for hospital gown design using structural equation modeling
- Preparation and properties of stainless steel filament/pure cotton woven fabric
- Facemask comfort enhancement with graphene oxide from recovered carbon waste tyres
- Use of enzymatic processes in the tanning of leather materials
- Optical-related properties and characterization of some textile fibers using near-infrared spectroscopy
- Network modeling of aesthetic effect for Chinese Yue Opera costume simulation images
- Predicting consumers’ garment fit satisfactions by using machine learning
- Non-destructive identification of wool and cashmere fibers based on improved LDA using NIR spectroscopy
- Study on the relationship between structure and moisturizing performance of seamless knitted fabrics of protein fibers for autumn and winter
- Antibacterial and yellowing performances of sports underwear fabric with polyamide/silver ion polyurethane filaments
- Numerical and experimental analysis of ballistic performance in hybrid soft armours composed of para-aramid triaxial and biaxial woven fabrics
- Phonetic smart clothing design based on gender awareness education for preschoolers
- Determination of anthropometric measurements and their application in the development of clothing sizing systems for women in the regions of the Republic of Croatia
- Research on optimal design of pleated cheongsam based on Kano–HOQ–Pugh model
- Numerical investigation of weaving machine heald shaft new design using composite material to improve its performance
- Corrigendum to “Use of enzymatic processes in the tanning of leather materials”
- Shaping of thermal protective properties of basalt fabric-based composites by direct surface modification using magnetron sputtering technique
- Numerical modeling of the heat flow component of the composite developed on the basis of basalt fabric
- Weft insertion guideway design based on high-temperature superconducting levitation
- Ultrasonic-assisted alkali hydrolysis of polyethylene terephthalate fabric and its effect on the microstructure and dyeing properties of fibers
- Comparative study on physical properties of bio-based PA56 fibers and wearability of their fabrics
- Investigation of the bias tape roll change time efficiency in garment factories
- Analysis of foot 3D scans of boys from Polish population
- Optimization of garment sewing operation standard minute value prediction using an IPSO-BP neural network
- Influence of repeated switching of current through contacts made of electroconductive fabrics on their resistance
- Numerical calculation of air permeability of warp-knitted jacquard spacer shoe-upper materials based on CFD
- Compact Spinning with Different Fibre Types: An Experimental Investigation on Yarn Properties in the Condensing Zone with 3D-Printed Guiding Device
- Modeling of virtual clothing and its contact with the human body
- Advances in personalized modelling and virtual display of ethnic clothing for intelligent customization
- Investigation of weave influence on flame retardancy of jute fabrics
- Balloonless spinning spindle head shape optimisation
- Research on 3D simulation design and dynamic virtual display of clothing flexible body
- Turkish textile and clothing SMEs: Importance of organizational learning, digitalization, and internationalization
- Corrigendum To: “Washing characterization of compression socks”
- Study on the promotion multiple of blood flow velocity on human epidermal microcirculation of volcanic rock polymer fiber seamless knitted fabric
- Bending properties and numerical analysis of nonorthogonal woven composites
- Bringing the queen mother of the west to life: Digital reconstruction and analysis of Taoist Celestial Beings Worshiping mural’s apparel
- Modeling process for full forming sports underwear
- Retraction of: Ionic crosslinking of cotton
- An observational study of female body shape characteristics in multiracial Malaysia
- Study on theoretical model and actual deformation of weft-knitted transfer loop based on particle constraint
- Design and 3D simulation of weft-knitted jacquard plush fabrics
- An overview of technological challenges in implementing the digital product passport in the textile and clothing industry
- Understanding and addressing the water footprint in the textile sector: A review
- Determinants of location changes in the clothing industry in Poland
- Influence of cam profile errors in a modulator on the dynamic response of the heald frame
- Quantitative analysis of wool and cashmere fiber mixtures using NIR spectroscopy
- 3D simulation of double-needle bar warp-knitted clustered pile fabrics on DFS
- Finite element analysis of heat transfer behavior in glass fiber/metal composite materials under constant heat load
- Price estimation and visual evaluation of actual white fabrics used for dress shirts and their photographic images
- Effect of gluing garment materials with adhesive inserts on their multidirectional drape and bending rigidity
- Optimization analysis of carrier-track collision in braiding process
- Numerical and experimental analysis of the ballistic performance of soft bulletproof vests for women
- The antimicrobial potential of plant-based natural dyes for textile dyeing: A systematic review using prisma
- Influence of sewing parameters on the skin–fabric friction
- Validation by experimental study the relationship between fabric tensile strength and weave structures
- Optimization of fabric’s tensile strength and bagging deformation using surface response and finite element in stenter machine
- Analysis of lean manufacturing waste in the process flow of ready-to-wear garment production in Nigeria
- An optimization study on the sol–gel process to obtain multifunctional denim fabrics
- Drape test of fully formed knitted flared skirts based on 3D-printed human body posture
- Supplier selection models using fuzzy hybrid methods in the clothing textile industry
Articles in the same Issue
- Characterization of viscoelastic properties of yarn materials: Dynamic mechanical analysis in the transversal direction
- Analysis of omni-channel implementations that are preferred by consumers in clothing sector
- Structural modeling and analysis of three-dimensional cross-linked braided preforms
- An experimental study of mechanical properties and comfortability of knitted imitation woven shirt fabrics
- Technology integration to promote circular economy transformation of the garment industry: a systematic literature review
- Research on T-shirt-style design based on Kansei image using back-propagation neural networks
- Research on She nationality clothing recognition based on color feature fusion with PSO-SVM
- Accuracy prediction of wearable flexible smart gloves
- Preparation and performance of stainless steel fiber/Lyocell fiber-blended weft-knitted fabric
- Development of an emotional response model for hospital gown design using structural equation modeling
- Preparation and properties of stainless steel filament/pure cotton woven fabric
- Facemask comfort enhancement with graphene oxide from recovered carbon waste tyres
- Use of enzymatic processes in the tanning of leather materials
- Optical-related properties and characterization of some textile fibers using near-infrared spectroscopy
- Network modeling of aesthetic effect for Chinese Yue Opera costume simulation images
- Predicting consumers’ garment fit satisfactions by using machine learning
- Non-destructive identification of wool and cashmere fibers based on improved LDA using NIR spectroscopy
- Study on the relationship between structure and moisturizing performance of seamless knitted fabrics of protein fibers for autumn and winter
- Antibacterial and yellowing performances of sports underwear fabric with polyamide/silver ion polyurethane filaments
- Numerical and experimental analysis of ballistic performance in hybrid soft armours composed of para-aramid triaxial and biaxial woven fabrics
- Phonetic smart clothing design based on gender awareness education for preschoolers
- Determination of anthropometric measurements and their application in the development of clothing sizing systems for women in the regions of the Republic of Croatia
- Research on optimal design of pleated cheongsam based on Kano–HOQ–Pugh model
- Numerical investigation of weaving machine heald shaft new design using composite material to improve its performance
- Corrigendum to “Use of enzymatic processes in the tanning of leather materials”
- Shaping of thermal protective properties of basalt fabric-based composites by direct surface modification using magnetron sputtering technique
- Numerical modeling of the heat flow component of the composite developed on the basis of basalt fabric
- Weft insertion guideway design based on high-temperature superconducting levitation
- Ultrasonic-assisted alkali hydrolysis of polyethylene terephthalate fabric and its effect on the microstructure and dyeing properties of fibers
- Comparative study on physical properties of bio-based PA56 fibers and wearability of their fabrics
- Investigation of the bias tape roll change time efficiency in garment factories
- Analysis of foot 3D scans of boys from Polish population
- Optimization of garment sewing operation standard minute value prediction using an IPSO-BP neural network
- Influence of repeated switching of current through contacts made of electroconductive fabrics on their resistance
- Numerical calculation of air permeability of warp-knitted jacquard spacer shoe-upper materials based on CFD
- Compact Spinning with Different Fibre Types: An Experimental Investigation on Yarn Properties in the Condensing Zone with 3D-Printed Guiding Device
- Modeling of virtual clothing and its contact with the human body
- Advances in personalized modelling and virtual display of ethnic clothing for intelligent customization
- Investigation of weave influence on flame retardancy of jute fabrics
- Balloonless spinning spindle head shape optimisation
- Research on 3D simulation design and dynamic virtual display of clothing flexible body
- Turkish textile and clothing SMEs: Importance of organizational learning, digitalization, and internationalization
- Corrigendum To: “Washing characterization of compression socks”
- Study on the promotion multiple of blood flow velocity on human epidermal microcirculation of volcanic rock polymer fiber seamless knitted fabric
- Bending properties and numerical analysis of nonorthogonal woven composites
- Bringing the queen mother of the west to life: Digital reconstruction and analysis of Taoist Celestial Beings Worshiping mural’s apparel
- Modeling process for full forming sports underwear
- Retraction of: Ionic crosslinking of cotton
- An observational study of female body shape characteristics in multiracial Malaysia
- Study on theoretical model and actual deformation of weft-knitted transfer loop based on particle constraint
- Design and 3D simulation of weft-knitted jacquard plush fabrics
- An overview of technological challenges in implementing the digital product passport in the textile and clothing industry
- Understanding and addressing the water footprint in the textile sector: A review
- Determinants of location changes in the clothing industry in Poland
- Influence of cam profile errors in a modulator on the dynamic response of the heald frame
- Quantitative analysis of wool and cashmere fiber mixtures using NIR spectroscopy
- 3D simulation of double-needle bar warp-knitted clustered pile fabrics on DFS
- Finite element analysis of heat transfer behavior in glass fiber/metal composite materials under constant heat load
- Price estimation and visual evaluation of actual white fabrics used for dress shirts and their photographic images
- Effect of gluing garment materials with adhesive inserts on their multidirectional drape and bending rigidity
- Optimization analysis of carrier-track collision in braiding process
- Numerical and experimental analysis of the ballistic performance of soft bulletproof vests for women
- The antimicrobial potential of plant-based natural dyes for textile dyeing: A systematic review using prisma
- Influence of sewing parameters on the skin–fabric friction
- Validation by experimental study the relationship between fabric tensile strength and weave structures
- Optimization of fabric’s tensile strength and bagging deformation using surface response and finite element in stenter machine
- Analysis of lean manufacturing waste in the process flow of ready-to-wear garment production in Nigeria
- An optimization study on the sol–gel process to obtain multifunctional denim fabrics
- Drape test of fully formed knitted flared skirts based on 3D-printed human body posture
- Supplier selection models using fuzzy hybrid methods in the clothing textile industry

