Home Finite element analysis of heat transfer behavior in glass fiber/metal composite materials under constant heat load
Article Open Access

Finite element analysis of heat transfer behavior in glass fiber/metal composite materials under constant heat load

  • Ke Wang EMAIL logo , Ting Zhu , Qian Ma EMAIL logo , Shudong Wang EMAIL logo , Hongtao Zhou , Jumei Zhao and Limin Jin
Published/Copyright: November 21, 2024
Download Article (PDF)
AUTEX Research Journal
From the journal AUTEX Research Journal Volume 24 Issue 1

Abstract

A finite element analysis model was employed to analyze the heat conduction behavior of glass fiber/metal (stainless steel, aluminum, or oxygen-free copper) composite materials under a constant thermal load of 100°C on the metal surface, i.e., the temperature distribution after reaching thermal equilibrium. By comparing and analyzing the effects of different metal materials, different air convection heat transfer capabilities, and different metal phase thicknesses, the heat transfer mechanism is elaborated. The results indicate that the metal with stronger heat conduction capacity induces more uniform temperature distribution, while the temperature uniformity on the fiber is relatively worse. Besides, with the increase of the air convection heat transfer coefficient, the temperature on the fiber phase shows a significant downward trend, however, the impact on the metal phase remains limited. In addition, the metal thickness primarily affects the weight or rigidity of the composite material, with minimal impact on temperature distribution.

Keywords: glass fiber; composite materials; thermal conductivity; finite element analysis

1 Introduction

It is well known that metal materials are often used in engineering structural components that require high rigidity and strength. Generally, these metals serve as the framework materials, providing the entire structure with high strength and fracture toughness, allowing it to meet various working condition demands, thus leading to their widespread applications [1,2,3,4]. However, it is important to note that since metal materials are typically good conductors of heat, when exposed to high-temperature conditions and subjected to external thermal loads for extended periods, heat tends to be efficiently conducted within the structure. This results in high surface temperatures, which can negatively affect the temperature comfort and operability of the structural component [5,6,7]. To reduce the surface temperature of structural components to a suitable range, one or more layers of materials with lower thermal conductivity can be bonded to the surface of the metal material, forming a composite material that can be used in high-temperature environments [8,9,10,11]. Compared to metals, glass fiber has a much lower thermal conductivity, typically only a few hundredths of that of metals, which can effectively lower the surface temperature of structural components to a suitable range, thereby benefiting engineering applications [12].

In this study, finite element analysis (FEA) was used to conduct a steady-state thermal analysis of glass fiber/metal (stainless steel, aluminum or oxygen-free copper) composites under a constant metal-phase temperature of 100°C. The analysis explained the temperature distribution after the system reaches thermal equilibrium. Additionally, by comparing the effects of different metal materials, thermal convection conditions, and material thicknesses on temperature distribution, the study discussed the performance of such composite materials as thermal insulators, providing reference and guidance for the optimal design of high-temperature-resistant structural components.

2 Materials, FEA model, and theory

2.1 Materials

This work studies the composite material composed of glass fiber and metal (stainless steel, aluminum, or oxygen-free copper). The properties of these materials are listed in Table 1. The 3D structure of the composite is shown in Figure 1. The size of metal phase is 22.5 × 300 × 5 mm3, and the size of glass fiber assembly phase is 37.5 × 300 × 5 mm3.

Table 1

Properties of the materials

Material Density/g cm−3 Elastic modulus/GPa Poisson’s ratio Thermal conductivity/W m⁻1°C⁻1
Glass fiber 2.50 70.00 0.20 1.26
Steel 7.80 200.00 0.30 60.5
Aluminum 2.7 70 0.33 207
Oxygen-free copper 8.9 122.08 0.343 391
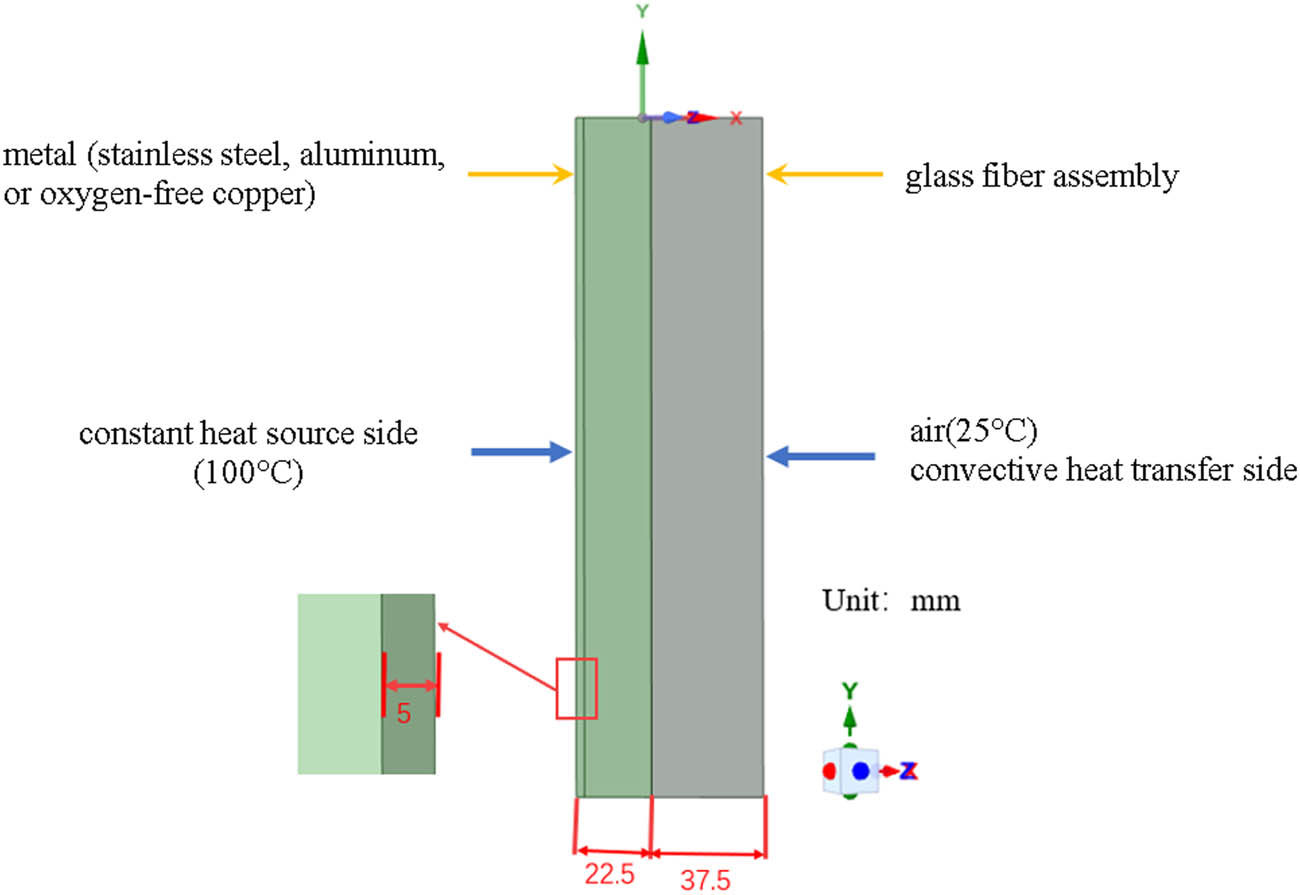
Figure 1 Structure of the 3D model.
Figure 1

Structure of the 3D model.

2.2 FEA model

FEA model of the metal/glass fiber composite material under constant thermal load conditions was created using ANSYS Workbench, as shown in Figure 2. ANSYS is a powerful commercial FEA software. It has a strong ability to conduct effective analysis for various physical fields and excels in thermal analysis. This software can accurately simulate the heat transfer modes such as heat conduction, heat convection and heat radiation of the analysis objects, and predict indicators such as the temperature distribution and heat release situation of the object under various working conditions. This helps to discover potential problems in advance, and then through optimized design, ensure the reliable working performance of materials or structural components, it is widely used in many fields such as aerospace and automobile manufacturing.

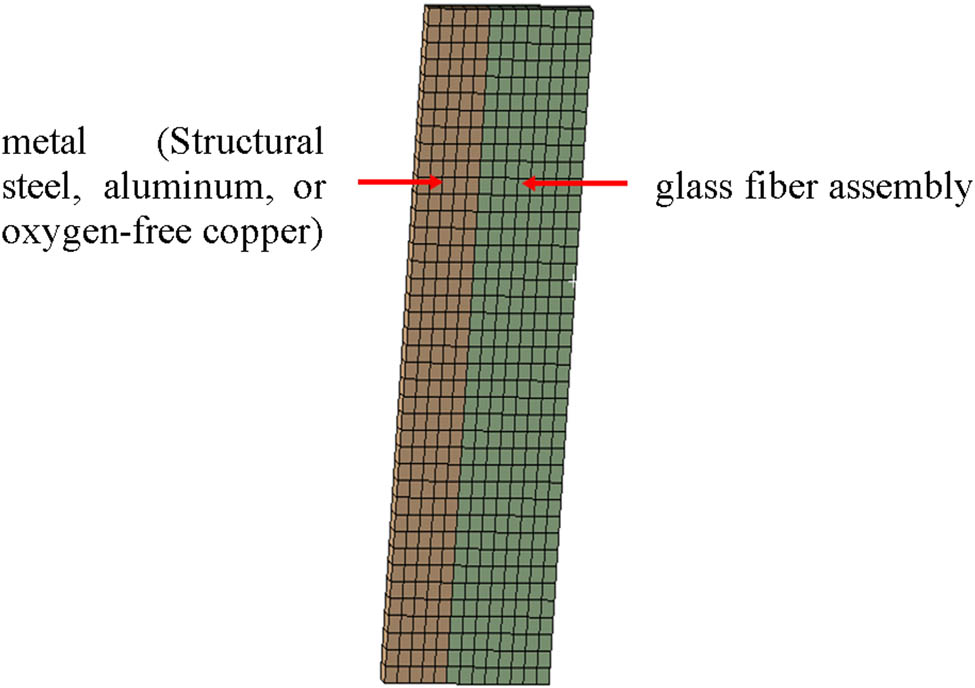
Figure 2 FEA model.
Figure 2

FEA model.

As indicated in Figures 1 and 2, in this model, a constant heat source with a temperature of 100°C is applied to the free side of the metal phase, while the free side of the glass fiber assembly is exposed to air at the room temperature of 25°C, involving the convective heat transfer. Heat will be conducted from the metal phase to the fiber assembly phase and then be carried away by air thermal convection. Regarding the contact property between the two phases, the “bonded” setting is used to ensure good thermal conductivity at the interface.

For this model, the meshing size is set to 5 mm, with a total of 520 elements, and the type used is hexahedral.

2.3 Heat transfer theory

As mentioned above, in the system, heat conduction and heat convection are mainly involved, while the influence of heat radiation is ignored. Therefore, the theoretical explanations of heat conduction and heat convection are given.

2.3.1 Thermal conduction

Heat conduction can be defined as the exchange of internal energy between two objects in complete contact or between different parts of an object due to a temperature gradient. Heat conduction follows Fourier’s law [13]:

(1) q ″ = − k d T d x ,

where q″ is the heat flow density (W m−2), k is the coefficient of thermal conductivity (W m−1 °C−1), and “–” indicates that the heat flows in the direction of decreasing temperature.

2.3.2 Thermal convection

Thermal convection refers to the exchange of heat caused by the temperature difference between the surface of a solid and the fluid in contact with it. It can be divided into two categories: natural convection and forced convection. Thermal convection is described by the Newton’s law of cooling equation [14]:

(2) q ″ = h ( T S − T B ) ,

where h is the convective heat transfer coefficient (W m−2 °C−1), T S is the solid surface temperature (°C), and T B is the temperature of the surrounding fluid (°C).

Natural convective heat transfer, in this issue, occurs between the free side of glass fiber assembly and air. The magnitude of the air convection heat transfer coefficient mainly depends on the flow velocity of the air medium. The air convection heat transfer coefficient has been calculated according to the following equations below [15,16,17]:

(3) R e = ρ v L μ ,

(4) P r = μ C p k ,

(5) N u = 0.453 R e 0.5 ⋅ P r 1 / 3 ,

(6) h = N u ⋅ k L ,

where Re is the Reynolds number, Pr is the Prandtl number, and N u is the Nusselt number. Besides, ρ, v, μ, and C p are the density (kg m−3), velocity (m s−1), viscosity (Pa s), and specific heat (J kg−1 °C−1) of the air, respectively. And L is the feature length (m).

3 Results and discussions

3.1 Influence of metal material type

To investigate the impact of different metal materials on thermal conductivity, Figure 3 presents the temperature distributions for different composites, i.e., glass fiber/structural steel, glass fiber/aluminum, and glass fiber/oxygen-free copper. Specifically, Figure 4 provides the quantitative analysis curves reflecting the temperature distribution characteristics within the materials (from the heat source side a to the heat dissipation side b). Herein, it should be noted that considering that the applied metal material and glass fiber are both isotropic materials, line a–b connecting the middle positions of the two phases is taken as a representative for illustration. The temperature distribution on any line parallel to line a–b is consistent with it.

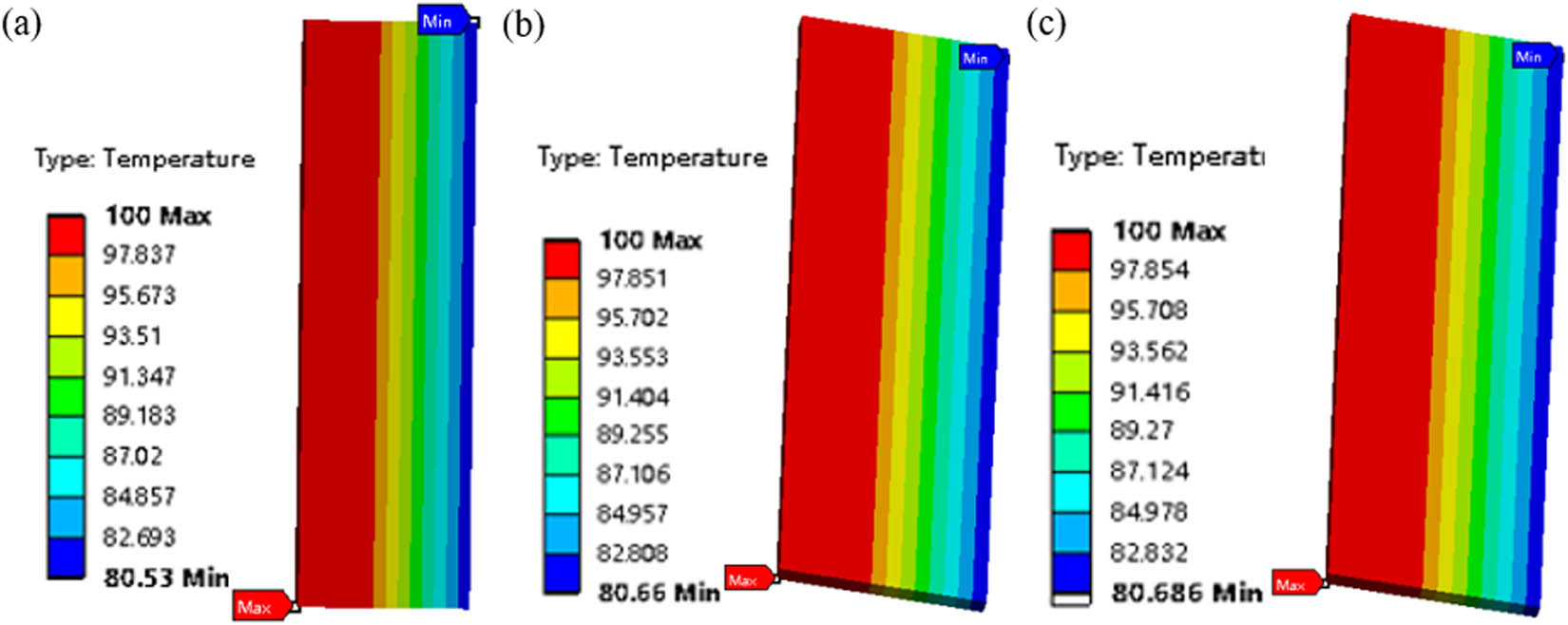
Figure 3 Temperature distributions of different metal/fiber composites: (a) glass fiber/structural steel, (b) glass fiber/aluminum, (c) glass fiber/oxygen-free copper.
Figure 3

Temperature distributions of different metal/fiber composites: (a) glass fiber/structural steel, (b) glass fiber/aluminum, (c) glass fiber/oxygen-free copper.

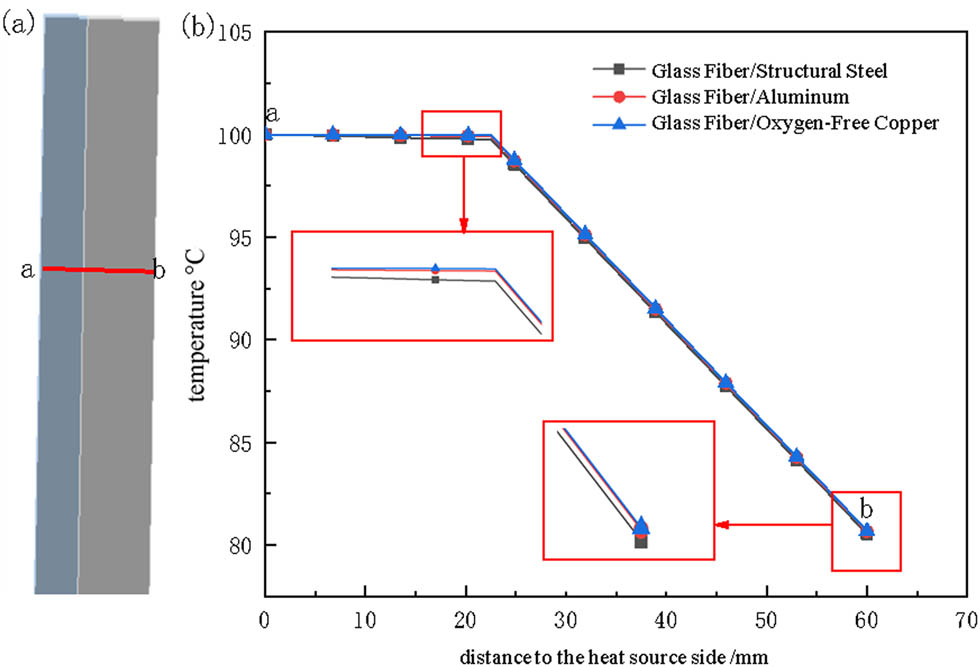
Figure 4 Temperature variation curve along the path a–b within the material: (a) location of path a–b, and (b) temperature variation curve.
Figure 4

Temperature variation curve along the path a–b within the material: (a) location of path a–b, and (b) temperature variation curve.

It can be observed that the higher thermal conductivity of the metal material results in a more uniform temperature distribution on the metal phase when reaching thermal equilibrium. Since a higher thermal conductivity means faster heat transfer and smaller temperature differences between different parts of the metal, the resulting temperature distribution is more uniform. On the contrary, due to the low thermal conductivity of glass fiber assembly, heat is less able to spread effectively within the fiber phase. As a result, even temperature at the “metal–glass fiber” interface is relatively high, the temperature uniformity on the fiber phase remains relatively poor.

3.2 Influence of convective heat transfer coefficient

To investigate the impact of the convective heat transfer coefficient on the thermal conductivity of composite materials, the cases for the glass fiber/structural steel composite are selected and analyzed. Figure 5 presents the temperature distributions when the convective heat transfer coefficients are 12, 25, and 40 W m−2 °C−1, respectively. Similarly, Figure 6 provides the quantitative analysis reflecting the temperature distribution characteristics within the material (from the heat source surface a to the heat dissipation surface b).

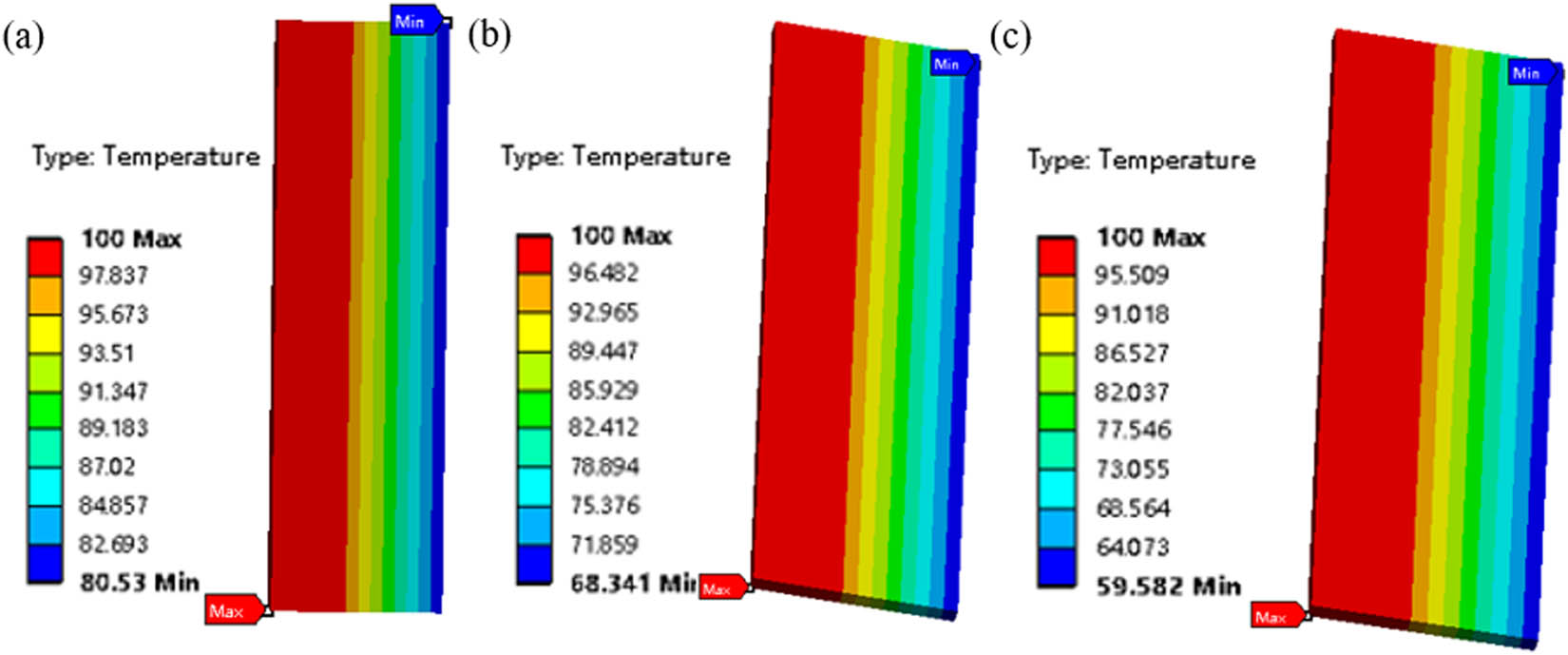
Figure 5 Temperature distributions of glass fiber/stainless steel composite with different convective heat transfer coefficients: (a) 12 W m−2 °C−1, (b) 25 W m−2 °C−1, and (c) 40 W m−2 °C−1.
Figure 5

Temperature distributions of glass fiber/stainless steel composite with different convective heat transfer coefficients: (a) 12 W m−2 °C−1, (b) 25 W m−2 °C−1, and (c) 40 W m−2 °C−1.

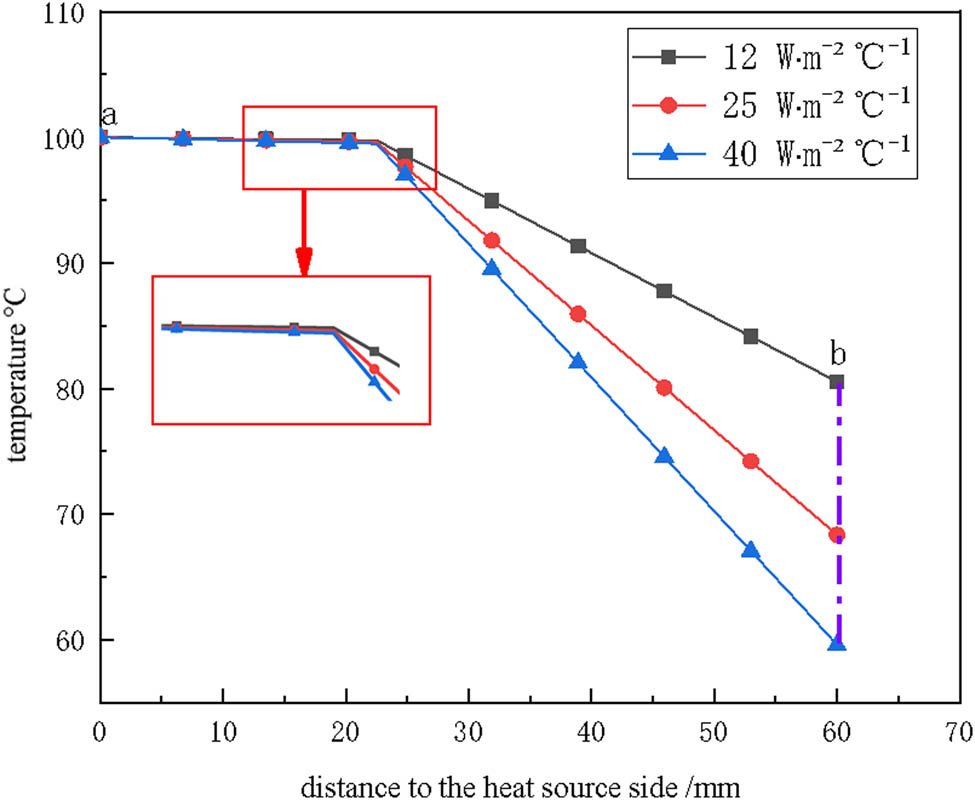
Figure 6 Temperature variation curve along path a–b inside the glass fiber/stainless steel composite under different convective heat transfer coefficients.
Figure 6

Temperature variation curve along path a–b inside the glass fiber/stainless steel composite under different convective heat transfer coefficients.

It can be seen that the convective heat transfer is located on the surface of the fiber assembly. It significantly influences the temperature of the fiber component. As the convective heat transfer coefficient increases, indicating enhanced heat dissipation capability, the temperature of the fiber phase shows a significant downward trend. Quantitatively, when the convective heat transfer coefficient increases from 12 to 25 W m−2 °C−1, representing 2.083 times increase in convective heat transfer capability, the temperature on the convective heat transfer surface decreases by 15.136%. As the coefficient increases from 25 to 40 W m−2 °C−1, representing 1.6 times increase in convective heat transfer capability, the temperature on the convective heat transfer surface decreases by 12.817%.

Nevertheless, the increase in convective heat transfer capability mainly affects the temperature drop in the fiber phase, with only a limited impact on the temperature of the metal phase. This phenomenon is clearly visible in Figure 6. The reason is that the continuous heat load on the metal, coupled with the high thermal conductivity of the metal, allows its internal temperature to remain around 100°C, making it less susceptible to the temperature changes in the fiber component, which has much lower thermal conductivity. In addition, this factor is also the reason why all three curves show a slow decline first and then a significant downward trend.

3.3 Influence of metal thickness on temperature distribution

In some cases, the composite material also needs to have properties such as high rigidity and weight to meet the requirements of overall strength and structural stability under specific working conditions. Generally, it can be achieved by increasing the volume of the metal phase. In this case, it is achieved by increasing the metal thickness. To investigate the impact of metal component thickness on the thermal conductivity of composite materials, the cases of the glass fiber/structural steel composite are analyzed. Figure 7 presents the temperature distributions for structural steel with thicknesses of 20, 22.5, and 25 mm, respectively. Similarly, Figure 8 provides the quantitative analysis reflecting the temperature distribution characteristics (from the heat source surface a to the heat dissipation surface b).

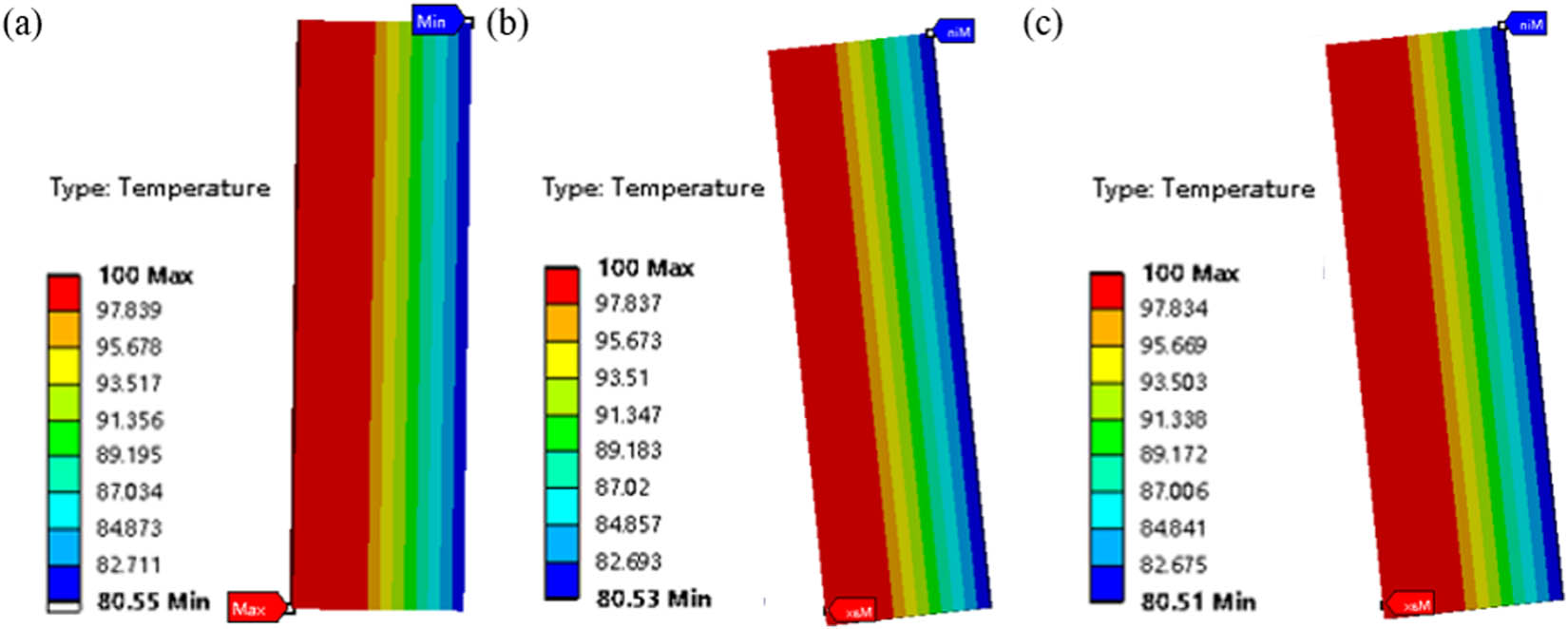
Figure 7 Temperature distributions of glass fiber/structural steel composites under different structural steel thicknesses: (a) 20 mm, (b) 22.5 mm, and (c) 25 mm.
Figure 7

Temperature distributions of glass fiber/structural steel composites under different structural steel thicknesses: (a) 20 mm, (b) 22.5 mm, and (c) 25 mm.

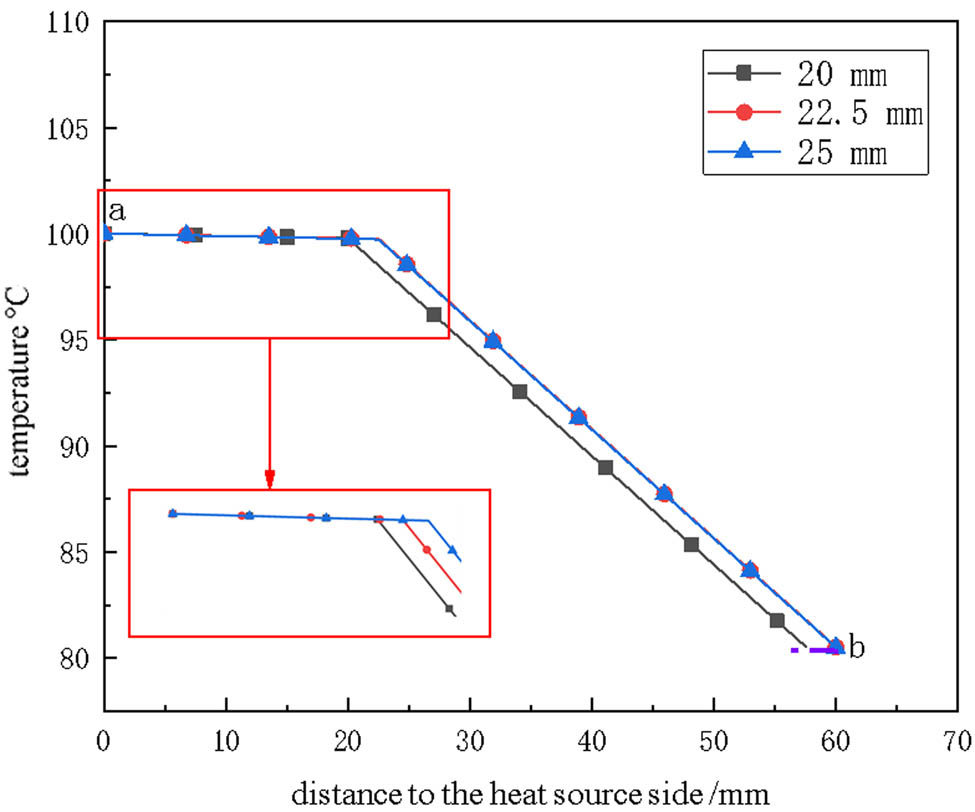
Figure 8 Temperature variation curve along path a–b inside the composite with different structural steel thicknesses.
Figure 8

Temperature variation curve along path a–b inside the composite with different structural steel thicknesses.

It can be seen that thickness of the structural steel increases, the heat transfer path becomes longer, resulting in a decrease in the initial temperature at the “structural steel–glass fiber” interface, which in turn leads to the corresponding decrease in the temperature at the “glass fiber-convective heat transfer” surface. Quantitatively, when the thickness of the structural steel increases from 20 to 22.5 mm, representing 1.125 times increase in weight, the temperature at the “glass fiber-convective heat transfer” surface decreases by 0.025% only. Besides, when the thickness of the structural steel increases from 22.5 to 25 mm, representing 1.11 times increase in weight, the temperature at the “glass fiber-convective heat transfer” surface decreases by 0.0248% only.

This indicates that the thickness of the metal phase primarily affects the weight or rigidity of the composite material and has minimal impact on the temperature distribution.

4 Conclusions

In this study, the heat conduction behavior of glass fiber/metal (stainless steel, aluminum, or oxygen-free copper) composites under a steady 100°C surface temperature was analyzed through FEA. The temperature distribution reaching thermal equilibrium status was examined. Additionally, by conducting a comparative analysis of the effects of different metal materials, varying air convective heat transfer capabilities, and different metal phase thicknesses, the heat transfer mechanisms were elucidated. The following conclusions were drawn:

  1. The higher thermal conductivity of the metal material leads to a more uniform temperature distribution in the metal phase at thermal equilibrium. However, due to the low thermal conductivity of glass fiber assembly, heat diffusion within the fiber phase is limited, resulting in relatively poor temperature uniformity in the fiber phase.

  2. As the air convective heat transfer coefficient increases, indicating enhanced heat dissipation capability, the temperature of the fiber phase shows a significant downward trend. However, the increase in air convective heat transfer capability mainly affects the temperature drop in the fiber phase, with only a limited impact on the temperature of the metal phase.

  3. The thickness of the metal phase primarily affects the weight or rigidity of the composite material, with minimal impact on the temperature distribution.

# These authors have contributed equally to this work.

Acknowledgements:

The authors acknowledge the financial supports from Qinglan Project (Jiangsu Teacher 2024 No. 14 and 2022 No. 29), the Excellent Scientific and Technological Innovation Team (Jiangsu Teaching and Research 2023 No. 3), and the Brand Major of International Talents Training (Jiangsu International Cooperation and Exchange, 2022 No. 12) of Jiangsu Provincial Department of Education.

  1. Funding information: This work was financially supported by the Natural Science Foundation (No. YCBK2023019) of Yancheng. The authors also acknowledge the financial supports from the Major Program of the Natural Science Foundation (No. 24KJA540005) of Jiangsu Higher Education Institutions and the Visiting Scholar Research Program (2024 No. 4) of Jiangsu Teachers Training Center of Higher Vocational Education.

  2. Author contributions: Conceptualization, Ke Wang, Ting Zhu and Limin Jin; methodology, Ke Wang, Ting Zhu and Limin Jin; analysis of data/investigation, Qian Ma, Ting Zhu and Shudong Wang; writing–original draft preparation, Ke Wang and Ting Zhu; writing–review and editing, Hongtao Zhou and Jumei Zhao; project administration, Ke Wang, Qian Ma and Shudong Wang; funding acquisition, Ke Wang, Shudong Wang, Hongtao Zhou and Jumei Zhao.

  3. Conflict of interest: Authors state no conflict of interest.

  4. Ethical approval: The conducted research is not related to either human or animal use.

  5. Data availability statement: The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.

References

[1] Maleki, E., Bagherifard, S., Bandini, M., Guagliano, M. (2021). Surface post-treatments for metal additive manufacturing: Progress, challenges, and opportunities. Additive Manufacturing, 37, 101619.10.1016/j.addma.2020.101619Search in Google Scholar

[2] Yang, Y., Luo, M., Zhang, W., Sun, Y., Chen, X., Guo, S. (2018). Metal surface and interface energy electrocatalysis: fundamentals, performance engineering, and opportunities. Chem, 4(9), 2054–2083.10.1016/j.chempr.2018.05.019Search in Google Scholar

[3] Latif, M. T., Baharudin, N. H., Velayutham, P., Awang, N., Hamdan, H., Mohamad, R., et al. (2011). Composition of heavy metals and airborne fibers in the indoor environment of a building during renovation. Environmental Monitoring and Assessment, 181, 479–489.10.1007/s10661-010-1843-3Search in Google Scholar PubMed

[4] Çakan, A., Kiren, B., Ayas, N. (2023). Hydrodeoxygenation of safflower oil over cobalt-doped metal oxide catalysts for bio-aviation fuel production. Molecular Catalysis, 546, 113219.10.1016/j.mcat.2023.113219Search in Google Scholar

[5] Karna, P., Giri, A. (2023). Effect of intense laser irradiation on the thermal transport properties of metals. Physical Review B, 107, 094301.10.1103/PhysRevB.107.094301Search in Google Scholar

[6] Zhang, A., Li, Y. (2023). Thermal conductivity of aluminum alloys-A review. Materials, 16(8), 2972.10.3390/ma16082972Search in Google Scholar PubMed PubMed Central

[7] Du, Z., Liu, G., Huang, X., Xiao, T., Yang, X., He, Y. L. (2023). Numerical studies on a fin-foam composite structure towards improving melting phase change. International Journal of Heat and Mass Transfer, 208, 124076.10.1016/j.ijheatmasstransfer.2023.124076Search in Google Scholar

[8] Raj, A., Paul, G. (2024). A simulation based analysis for enhancement of performances of turbine blades in turbo jet engines with thermal barrier coatings (TBCs). Numerical Heat Transfer, Part A: Applications, 1–15. 10.1080/10407782.2024.2376314.Search in Google Scholar

[9] Wahlquist, S., Hansel, J., Sabharwall, P., Ali, A. (2023). A critical review of heat pipe experiments in nuclear energy applications. Nuclear Science and Engineering, 5, 719–752.10.1080/00295639.2022.2082230Search in Google Scholar

[10] Akhil, U. V., Radhika, N., Rajeshkumar, L. (2023). A comprehensive review on ceramic coating on steel and centrifugal thermite process: Applications and future trends. Journal of Bio- and Tribo-Corrosion, 9, 41.10.1007/s40735-023-00765-6Search in Google Scholar

[11] Xu, F., Ye, P., Peng, J., Geng, H., Cui, Y., Bao, D., et al. (2023). Cerium methacrylate assisted preparation of highly thermally conductive and anticorrosive multifunctional coatings for heat conduction metal protection. Nano-Micro Letters, 15, 201.10.1007/s40820-023-01163-wSearch in Google Scholar PubMed PubMed Central

[12] Ma, Q., Wang, K., Wang, S., Zhou, H., Jin, L., Yi, H., et al. (2023). FEA-based structural heat transfer characteristic of 3-D orthogonal woven composite subjected to the non-uniform heat load. Autex Research Journal, 23(1), 110–115.10.2478/aut-2021-0046Search in Google Scholar

[13] Fourier, J. B. J. (1822). Équations du Mouvement de la Chaleur. Théorie Analytique de La Chaleur, Cambridge University Press, p. 99–158.Search in Google Scholar

[14] Newton, I. (1701). Scala graduum caloris. Philosophical Transactions, 22, 824–829.10.1098/rstl.1700.0082Search in Google Scholar

[15] Churchill, S. W., Ozoe, H. (1973). Correlations for laminar forced convection in flow over an isothermal flat plate and in developing and fully developed flow in an isothermal tube. Journal of Heat Transfer, 95(3), 416–419.10.1115/1.3450078Search in Google Scholar

[16] Staton, D. A., Cavagnino, A. (2008). Convection heat transfer and flow calculations suitable for electric machines thermal models. IEEE Transactions on Industrial Electronics, 55(10), 3509–3516.10.1109/TIE.2008.922604Search in Google Scholar

[17] Mills, A. F. (1979). Average Nusselt numbers for external flows. Journal of Heat Transfer, 101(4), 734–735.10.1115/1.3451066Search in Google Scholar
Received: 2024-08-15
Revised: 2024-10-09
Accepted: 2024-10-13
Published Online: 2024-11-21

© 2024 the author(s), published by De Gruyter

This work is licensed under the Creative Commons Attribution 4.0 International License.

Articles in the same Issue

  2. Characterization of viscoelastic properties of yarn materials: Dynamic mechanical analysis in the transversal direction
  3. Analysis of omni-channel implementations that are preferred by consumers in clothing sector
  4. Structural modeling and analysis of three-dimensional cross-linked braided preforms
  5. An experimental study of mechanical properties and comfortability of knitted imitation woven shirt fabrics
  6. Technology integration to promote circular economy transformation of the garment industry: a systematic literature review
  7. Research on T-shirt-style design based on Kansei image using back-propagation neural networks
  8. Research on She nationality clothing recognition based on color feature fusion with PSO-SVM
  9. Accuracy prediction of wearable flexible smart gloves
  10. Preparation and performance of stainless steel fiber/Lyocell fiber-blended weft-knitted fabric
  11. Development of an emotional response model for hospital gown design using structural equation modeling
  12. Preparation and properties of stainless steel filament/pure cotton woven fabric
  13. Facemask comfort enhancement with graphene oxide from recovered carbon waste tyres
  14. Use of enzymatic processes in the tanning of leather materials
  15. Optical-related properties and characterization of some textile fibers using near-infrared spectroscopy
  16. Network modeling of aesthetic effect for Chinese Yue Opera costume simulation images
  17. Predicting consumers’ garment fit satisfactions by using machine learning
  18. Non-destructive identification of wool and cashmere fibers based on improved LDA using NIR spectroscopy
  19. Study on the relationship between structure and moisturizing performance of seamless knitted fabrics of protein fibers for autumn and winter
  20. Antibacterial and yellowing performances of sports underwear fabric with polyamide/silver ion polyurethane filaments
  21. Numerical and experimental analysis of ballistic performance in hybrid soft armours composed of para-aramid triaxial and biaxial woven fabrics
  22. Phonetic smart clothing design based on gender awareness education for preschoolers
  23. Determination of anthropometric measurements and their application in the development of clothing sizing systems for women in the regions of the Republic of Croatia
  24. Research on optimal design of pleated cheongsam based on Kano–HOQ–Pugh model
  25. Numerical investigation of weaving machine heald shaft new design using composite material to improve its performance
  26. Corrigendum to “Use of enzymatic processes in the tanning of leather materials”
  27. Shaping of thermal protective properties of basalt fabric-based composites by direct surface modification using magnetron sputtering technique
  28. Numerical modeling of the heat flow component of the composite developed on the basis of basalt fabric
  29. Weft insertion guideway design based on high-temperature superconducting levitation
  30. Ultrasonic-assisted alkali hydrolysis of polyethylene terephthalate fabric and its effect on the microstructure and dyeing properties of fibers
  31. Comparative study on physical properties of bio-based PA56 fibers and wearability of their fabrics
  32. Investigation of the bias tape roll change time efficiency in garment factories
  33. Analysis of foot 3D scans of boys from Polish population
  34. Optimization of garment sewing operation standard minute value prediction using an IPSO-BP neural network
  35. Influence of repeated switching of current through contacts made of electroconductive fabrics on their resistance
  36. Numerical calculation of air permeability of warp-knitted jacquard spacer shoe-upper materials based on CFD
  37. Compact Spinning with Different Fibre Types: An Experimental Investigation on Yarn Properties in the Condensing Zone with 3D-Printed Guiding Device
  38. Modeling of virtual clothing and its contact with the human body
  39. Advances in personalized modelling and virtual display of ethnic clothing for intelligent customization
  40. Investigation of weave influence on flame retardancy of jute fabrics
  41. Balloonless spinning spindle head shape optimisation
  42. Research on 3D simulation design and dynamic virtual display of clothing flexible body
  43. Turkish textile and clothing SMEs: Importance of organizational learning, digitalization, and internationalization
  44. Corrigendum To: “Washing characterization of compression socks”
  45. Study on the promotion multiple of blood flow velocity on human epidermal microcirculation of volcanic rock polymer fiber seamless knitted fabric
  46. Bending properties and numerical analysis of nonorthogonal woven composites
  47. Bringing the queen mother of the west to life: Digital reconstruction and analysis of Taoist Celestial Beings Worshiping mural’s apparel
  48. Modeling process for full forming sports underwear
  49. Retraction of: Ionic crosslinking of cotton
  50. An observational study of female body shape characteristics in multiracial Malaysia
  51. Study on theoretical model and actual deformation of weft-knitted transfer loop based on particle constraint
  52. Design and 3D simulation of weft-knitted jacquard plush fabrics
  53. An overview of technological challenges in implementing the digital product passport in the textile and clothing industry
  54. Understanding and addressing the water footprint in the textile sector: A review
  55. Determinants of location changes in the clothing industry in Poland
  56. Influence of cam profile errors in a modulator on the dynamic response of the heald frame
  57. Quantitative analysis of wool and cashmere fiber mixtures using NIR spectroscopy
  58. 3D simulation of double-needle bar warp-knitted clustered pile fabrics on DFS
  59. Finite element analysis of heat transfer behavior in glass fiber/metal composite materials under constant heat load
  60. Price estimation and visual evaluation of actual white fabrics used for dress shirts and their photographic images
  61. Effect of gluing garment materials with adhesive inserts on their multidirectional drape and bending rigidity
  62. Optimization analysis of carrier-track collision in braiding process
  63. Numerical and experimental analysis of the ballistic performance of soft bulletproof vests for women
  64. The antimicrobial potential of plant-based natural dyes for textile dyeing: A systematic review using prisma
  65. Influence of sewing parameters on the skin–fabric friction
  66. Validation by experimental study the relationship between fabric tensile strength and weave structures
  67. Optimization of fabric’s tensile strength and bagging deformation using surface response and finite element in stenter machine
  68. Analysis of lean manufacturing waste in the process flow of ready-to-wear garment production in Nigeria
  69. An optimization study on the sol–gel process to obtain multifunctional denim fabrics
  70. Drape test of fully formed knitted flared skirts based on 3D-printed human body posture
  71. Supplier selection models using fuzzy hybrid methods in the clothing textile industry
https://doi.org/10.1515/aut-2024-0011
Keywords for this article
glass fiber; composite materials; thermal conductivity; finite element analysis
Creative Commons
BY 4.0

Articles in the same Issue

  2. Characterization of viscoelastic properties of yarn materials: Dynamic mechanical analysis in the transversal direction
  3. Analysis of omni-channel implementations that are preferred by consumers in clothing sector
  4. Structural modeling and analysis of three-dimensional cross-linked braided preforms
  5. An experimental study of mechanical properties and comfortability of knitted imitation woven shirt fabrics
  6. Technology integration to promote circular economy transformation of the garment industry: a systematic literature review
  7. Research on T-shirt-style design based on Kansei image using back-propagation neural networks
  8. Research on She nationality clothing recognition based on color feature fusion with PSO-SVM
  9. Accuracy prediction of wearable flexible smart gloves
  10. Preparation and performance of stainless steel fiber/Lyocell fiber-blended weft-knitted fabric
  11. Development of an emotional response model for hospital gown design using structural equation modeling
  12. Preparation and properties of stainless steel filament/pure cotton woven fabric
  13. Facemask comfort enhancement with graphene oxide from recovered carbon waste tyres
  14. Use of enzymatic processes in the tanning of leather materials
  15. Optical-related properties and characterization of some textile fibers using near-infrared spectroscopy
  16. Network modeling of aesthetic effect for Chinese Yue Opera costume simulation images
  17. Predicting consumers’ garment fit satisfactions by using machine learning
  18. Non-destructive identification of wool and cashmere fibers based on improved LDA using NIR spectroscopy
  19. Study on the relationship between structure and moisturizing performance of seamless knitted fabrics of protein fibers for autumn and winter
  20. Antibacterial and yellowing performances of sports underwear fabric with polyamide/silver ion polyurethane filaments
  21. Numerical and experimental analysis of ballistic performance in hybrid soft armours composed of para-aramid triaxial and biaxial woven fabrics
  22. Phonetic smart clothing design based on gender awareness education for preschoolers
  23. Determination of anthropometric measurements and their application in the development of clothing sizing systems for women in the regions of the Republic of Croatia
  24. Research on optimal design of pleated cheongsam based on Kano–HOQ–Pugh model
  25. Numerical investigation of weaving machine heald shaft new design using composite material to improve its performance
  26. Corrigendum to “Use of enzymatic processes in the tanning of leather materials”
  27. Shaping of thermal protective properties of basalt fabric-based composites by direct surface modification using magnetron sputtering technique
  28. Numerical modeling of the heat flow component of the composite developed on the basis of basalt fabric
  29. Weft insertion guideway design based on high-temperature superconducting levitation
  30. Ultrasonic-assisted alkali hydrolysis of polyethylene terephthalate fabric and its effect on the microstructure and dyeing properties of fibers
  31. Comparative study on physical properties of bio-based PA56 fibers and wearability of their fabrics
  32. Investigation of the bias tape roll change time efficiency in garment factories
  33. Analysis of foot 3D scans of boys from Polish population
  34. Optimization of garment sewing operation standard minute value prediction using an IPSO-BP neural network
  35. Influence of repeated switching of current through contacts made of electroconductive fabrics on their resistance
  36. Numerical calculation of air permeability of warp-knitted jacquard spacer shoe-upper materials based on CFD
  37. Compact Spinning with Different Fibre Types: An Experimental Investigation on Yarn Properties in the Condensing Zone with 3D-Printed Guiding Device
  38. Modeling of virtual clothing and its contact with the human body
  39. Advances in personalized modelling and virtual display of ethnic clothing for intelligent customization
  40. Investigation of weave influence on flame retardancy of jute fabrics
  41. Balloonless spinning spindle head shape optimisation
  42. Research on 3D simulation design and dynamic virtual display of clothing flexible body
  43. Turkish textile and clothing SMEs: Importance of organizational learning, digitalization, and internationalization
  44. Corrigendum To: “Washing characterization of compression socks”
  45. Study on the promotion multiple of blood flow velocity on human epidermal microcirculation of volcanic rock polymer fiber seamless knitted fabric
  46. Bending properties and numerical analysis of nonorthogonal woven composites
  47. Bringing the queen mother of the west to life: Digital reconstruction and analysis of Taoist Celestial Beings Worshiping mural’s apparel
  48. Modeling process for full forming sports underwear
  49. Retraction of: Ionic crosslinking of cotton
  50. An observational study of female body shape characteristics in multiracial Malaysia
  51. Study on theoretical model and actual deformation of weft-knitted transfer loop based on particle constraint
  52. Design and 3D simulation of weft-knitted jacquard plush fabrics
  53. An overview of technological challenges in implementing the digital product passport in the textile and clothing industry
  54. Understanding and addressing the water footprint in the textile sector: A review
  55. Determinants of location changes in the clothing industry in Poland
  56. Influence of cam profile errors in a modulator on the dynamic response of the heald frame
  57. Quantitative analysis of wool and cashmere fiber mixtures using NIR spectroscopy
  58. 3D simulation of double-needle bar warp-knitted clustered pile fabrics on DFS
  59. Finite element analysis of heat transfer behavior in glass fiber/metal composite materials under constant heat load
  60. Price estimation and visual evaluation of actual white fabrics used for dress shirts and their photographic images
  61. Effect of gluing garment materials with adhesive inserts on their multidirectional drape and bending rigidity
  62. Optimization analysis of carrier-track collision in braiding process
  63. Numerical and experimental analysis of the ballistic performance of soft bulletproof vests for women
  64. The antimicrobial potential of plant-based natural dyes for textile dyeing: A systematic review using prisma
  65. Influence of sewing parameters on the skin–fabric friction
  66. Validation by experimental study the relationship between fabric tensile strength and weave structures
  67. Optimization of fabric’s tensile strength and bagging deformation using surface response and finite element in stenter machine
  68. Analysis of lean manufacturing waste in the process flow of ready-to-wear garment production in Nigeria
  69. An optimization study on the sol–gel process to obtain multifunctional denim fabrics
  70. Drape test of fully formed knitted flared skirts based on 3D-printed human body posture
  71. Supplier selection models using fuzzy hybrid methods in the clothing textile industry
Sign up now to receive a 20% welcome discount
Institutional Access
How does access work?
Have an idea on how to improve our website?
Please write us.
© 2025 De Gruyter Brill
Downloaded on 6.9.2025 from https://www.degruyterbrill.com/document/doi/10.1515/aut-2024-0011/html
Scroll to top button