Home Joint optimization of two-dimensional warranty period and maintenance strategy considering availability and cost constraints
Article Open Access

Joint optimization of two-dimensional warranty period and maintenance strategy considering availability and cost constraints

  • Junkai Cheng EMAIL logo
Published/Copyright: December 31, 2023
Download Article (PDF)
Open Physics
From the journal Open Physics Volume 21 Issue 1

Abstract

Warranty can improve customer satisfaction and increase product sales, but it will bring additional economic burden to manufacturers, so making reasonable warranty decisions is particularly important. The current research focuses more on the interests of manufacturers, while there is less attention paid to indicators that consumers are concerned about, such as system availability. To solve this problem, a joint optimization model of the two-dimensional warranty period and preventive maintenance (PM) strategy considering availability and cost constraints was established. Based on the failure dependence analysis of multi-component systems, the actual failure rate function is constructed by using the failure dependence coefficient matrix. Based on the comprehensive consideration of imperfect PM and minimum maintenance, the two-dimensional warranty cost model and system availability model are established, respectively. Aiming at maximum availability and considering the warranty cost budget constraint, a joint optimization model of the two-dimensional warranty period and PM strategy was built, and a model-solving algorithm combining grid search and binary search was introduced. The effectiveness of the model is verified by the case analysis, and the necessity of the PM strategy and considering failure dependence are reflected in the model comparative analysis and parameter sensitivity analysis. Finally, reasonable suggestions are put forward for manufacturers’ warranty decisions through the result analysis.

Keywords: two-dimensional warranty; preventive maintenance strategy; joint optimization; availability; binary search

1 Introduction

1.1 Background and motivation

Warranty refers to the maintenance service provided by the manufacturer for the failure of the sold products due to quality problems within a certain period [1]. As the structure and function of products become more and more complex, the corresponding warranty cost and difficulty also continue to increase [2]. Product warranty service has become one of the key factors affecting consumers’ decision to buy products [3]. The warranty period specifies the time limit for the manufacturer (seller) to maintain, replace, and return the product. Under the condition of the market economy, the length of the warranty period has become a key factor affecting the customer’s satisfaction and loyalty to the product [4]. So manufacturers need to determine a reasonable warranty period and make a scientific warranty decision scheme to control cost, improve reputation, and retain more users. Warranties can be divided into one- and two-dimensional warranties based on the number of variables used to define warranties. The one-dimensional warranty is usually defined by age or usage, while a two-dimensional warranty can be characterized as a two-dimensional region, usually represented by age and usage. Now, two-dimensional warranties have been adopted in many complex products [5].

For a long time, scholars have often regarded the research object as a whole and neglected the dependence between various components within the system when researching two-dimensional warranty decision-making models [6]. In fact, with the progress of manufacturing technology and the improvement of system functionality, the dependence between various components within the system is becoming increasingly close. According to the mainstream view in the current academic community, the dependence between components can be divided into economic dependence, structural dependence, and failure dependence, among which the research on failure dependence is the most extensive [7]. Failure dependence widely exists in multi-component systems. Taking a gearbox as an example, if the gearbox spindle fails, it will enhance the vibration of the gearbox and further exacerbate the gear wear, which means that there is a failure dependence between the spindle and the gear. From this perspective, the existence of failure dependence changes the inherent failure patterns of components, thus affecting the formulation of the optimal warranty decision plan. However, the current two-dimensional warranty decision-making model neglects the exploration of failure dependence in multi-component systems, and this study attempts to fill this gap.

The high availability of systems has always been an important goal pursued by engineers [8], which is also closely monitored by users. High availability means that equipment has a higher proportion of the normal working time and is less prone to malfunctions. Availability is crucial for large and complex equipment. For example, the breakdown of the production workshop will cause immeasurable economic losses, so the high availability of the manufacturing systems will bring greater profits to manufacturing enterprises. The breakdown of the weaponry will threaten the safety of soldiers and lead to war failure, so the high availability of the weaponry will increase the probability of successful warfare. Two-dimensional warranty equipment is usually capital intensive [9], and users often have high requirements for the availability of two-dimensional warranty equipment. However, most of the current research on two-dimensional warranty decision-making has not considered the availability of equipment but focuses more on product prices, profits, and costs.

To address the above challenges, this study proposes a two-dimensional warranty period and maintenance strategy joint optimization model considering availability and cost constraints. The innovation of this article mainly lies in the following:

  1. This article takes maximizing system availability as the decision objective and establishes a decision model with budget as the constraint condition.

  2. Considering the failure dependence between multiple components, a multi-component system failure rate model is established based on a failure chain model.

  3. A novel binary method has been developed for model solving.

The research of the article is mainly under the umbrella of social and economic physics, statistics, and nonlinear physics. In this article, mathematical modeling and algorithm development are mainly used to solve problems in engineering physics, and important suggestions are provided for manufacturers to carry out warranty activities. The fitting of the failure rate function of power plants involves probability theory, mathematical statistics, and random process knowledge. The solution of the entire model involves nonlinear programming problems. The developed binary method is a commonly used sorting algorithm in computer algorithms, which has enlightening significance for solving this engineering problem. So, the article is under the umbrella of social and economic physics, statistics, and nonlinear physics.

1.2 Relevant literature

The determination of warranty period has always been a concern of scholars. Wu et al. established a model of free renewal warranty cost for components before the operation time reaches the specified value, which was used to determine the optimal warranty price and length when maximizing profit [10]. Chien divided the failure of repairable products into minor failure and serious failure, determined the optimal warranty period based on the minimization of the cost function, and obtained the age replacement interval outside the optimal warranty period from the perspective of consumers and manufacturers [11]. Huang et al. established a model of sales price, warranty period, and product reliability under the strategy of free replacement or maintenance [12]. Liu et al. optimized the product’s warranty period and reliability based on the free replacement or maintenance strategy for repairable products [13]. Xie et al. developed a model to evaluate the overall profitability of components within and outside the warranty period [14]. He et al. defined an attraction index based on available warranty areas to describe the degree of attraction of the two-dimensional warranty period to customers with different usage rates. From the manufacturer’s point of view, the optimal two-dimensional basic warranty period was designed to maximize the expected profit, and the effectiveness of the method is demonstrated by numerical examples [15]. Chen and Popova proposed a two-dimensional warranty strategy, which is free replacement within the limited area and minimal maintenance beyond the limited area but within the warranty area. With the lowest cost as the goal, the warranty period and the limited area were obtained [16]. Baik et al. put forward two models: the faulty system is always carried out with minimum maintenance, and the faulty system is always replaced in the context of the two-dimensional warranty, and the model is used to carry out cost analysis and give the optimal warranty period [17]. Taleizadeh and Mokhtarzadeh designed a value-risk method for dual-channel (online and offline) sales manufacturers to optimize the two-dimensional warranty scheme and pricing simultaneously, and higher profits were obtained by considering the covariance between product warranty claims [18]. Park et al. studied the method for determining the optimal warranty period of products from the manufacturer’s perspective under specific lemon law regulations [19].

It can be seen that most studies only stand on the manufacturer’s point and take the lowest warranty cost or the highest profit as the goal to make the warranty period decision, ignoring the needs of consumers to some extent. At present, the two-dimensional warranty decision model based on the win–win perspective of both manufacturers and consumers has been preliminarily studied. Huang et al. classified customers according to their usage conditions in the basic warranty period and provided two-dimensional extended warranty schemes for different types of customers to reduce warranty costs and improve marketing competitiveness [20]. He et al. established a two-dimensional extended warranty cost model based on the product failure process considering consumers’ different usage rates, purchase time, and maintenance options of the extended warranty and obtained the isoline of win–win warranty area and win–win extended warranty interval [21]. Dong et al. considered the consumer utility function of different warranty periods and obtained a two-dimensional warranty period that both manufacturers and consumers won [22]. Salmasnia et al. studied the optimal two-dimensional warranty policy for second-hand products by considering the two-dimensional warranty areas in both L-shaped and rectangular cases [23]. Peng et al. studied the optimal cost allocation ratio for preventive maintenance (PM) of two-dimensional warranty equipment from the user’s perspective [24]. Wang studied the design and pricing of customized two-dimensional extended warranty solutions from the perspective of suppliers, allowing each consumer to match suitable warranty solutions based on their usage rate [25]. Gupta et al. designed a new optimal extended warranty policy based on the price curve and demonstrated the advantages of the two-dimensional warranty policy compared to the one-dimensional warranty policy [26]. Ruan et al. considered the learning effectiveness of users and manufacturers during the warranty period and studied the problem of “the PM and the two-dimensional warranty design,” proving that considering both the PM planning and the two-dimensional warranty design is a win–win strategy for both manufacturers and users [27]. Zhang et al. considered the differences in user usage rates and studied the optimal two-dimensional extended warranty policy in stable and dynamic markets [28]. Although the above research paid attention to the interests of consumers to some extent, the essence of their decision is to hope that manufacturers can sell more products or warranty services. For users, the improvement of the availability of warranty objects means the reduction of unexpected failure, which is the ideal state expected by users [29]. As an important performance index measuring the probability of systems being in the working state, system availability can effectively guide maintenance decisions and has always been a hot topic in the field of reliability engineering [30].

The application of different maintenance strategies during the warranty period is another research focus besides the decision on the warranty period. Varnosafaderani and Chukova divided the warranty area into several sub-areas, used the failure rate rollback method to describe the maintenance degree of imperfect maintenance, and stipulated that minimum maintenance should be carried out in the first sub-area and the last sub-area, imperfect maintenance should be carried out in the first failure of the remaining sub-areas, and minimum maintenance should be carried out in the subsequent failure. The sub-areas were identified by minimizing manufacturer maintenance costs [31]. Based on the imperfect PM strategy, Shahanaghi et al. established a two-dimensional extended warranty decision model intending to minimize the cost of the two-dimensional extended warranty to obtain the optimal number and degree of PM [32]. Yu and Chen divided the warranty area into three sub-areas, adopted the minimum maintenance strategy, and proposed the optimal two-dimensional warranty scheme for products with the goal of the lowest warranty cost [33]. Wang and Song designed a two-dimensional PM and replacement strategy. Under the strategy, PM was carried out according to calendar time or usage, and if the product withstood (n − 1)th shock, it was replaced with a new product at the nth shock. From the manufacturer’s point, the average warranty cost for the whole warranty period was obtained by using the renewal theory [34]. Gupta and Chattopadhyay proposed the labor code priority index and studied the identification of early reliability problems in two-dimensional warranty equipment [35]. Wei et al. studied a new burn-in policy for repairable products with a two-dimensional combination warranty based on the assumption of product heterogeneity [36]. PM has been paid more and more attention to by researchers because it can prevent failure or serious consequences of failure and reduce the loss caused by failure downtime. However, there are relatively few studies on the joint optimization of the warranty period and PM interval.

At present, most of the research objects are single-component systems, and the dependence between the components of multi-component systems is rarely considered. For multi-component systems, there are three forms of dependence between components, namely, economic dependence, failure dependence, and structural dependence [37,38]. Failure dependence, also known as stochastic dependence, means that the failure of one component affects the status of other components in the system. Generally, it can be divided into three categories [39,40]: Class I failure dependence refers to that when one component fails in the system, other components will fail with a certain probability a ( 0 ≤ a ≤ 1 ); Class II failure dependence is failure rate dependence in essence, that is, when a component fails, it will increase the failure rate of other components to a certain extent, but it will not directly cause the component failure; and Class III failure dependence is related to impact damage, that is, when a component fails, it will cause random damage to other components of the system to a certain extent. When the impact damage accumulates to a certain extent, it will lead to the component failure. The current study does not provide sufficient support for the warranty decision of failure-dependence multi-component systems.

1.3 Overview of the study

Based on the above analysis, this study introduced a PM strategy into complex product warranty. For the multi-component system with failure dependence, a joint optimization model of two-dimensional warranty and PM strategy based on cost and availability is established, which effectively integrated PM and corrective maintenance and provided a decision scheme for complex products warranty considering PM strategy, to achieve the product warranty decision scientific and effective.

The main contributions of this work are listed as follows:

  1. Taking the multi-component system as the warranty object, the warranty decision-making model of the multi-component system is established based on the analysis of the failure dependence of each component in the multi-component system.

  2. The warranty decision model integrates corrective maintenance and PM effectively, considering the warranty cost and the system availability simultaneously.

  3. The joint optimization of the two-dimensional warranty period and PM interval for a failure-dependence multi-component system is carried out.

The remainder of this article is organized as follows. Section 2 introduces the model formulation, including six aspects: problem description, working assumptions and notations, the system failure rate function, the imperfect PM strategy, the system availability, and the expected warranty costs. Section 3 presents the model optimization analysis including joint optimization model and algorithms. Section 4 provides the corresponding case study. Finally, the conclusions and research perspectives are offered in Section 5.

2 Model formulation

2.1 Problem description

The multi-component system with failure dependence adopts the two-dimensional warranty policy. K B 1 and K B 2 represent time and usage limits, respectively, as shown in Figure 1. During the warranty period, the manufacturer shall carry out post-failure corrective maintenance and regular PM for the multi-component system. The study assumes that the usage rate of the multi-component system by different consumers is a random variable, but for a given consumer, it is a certain value during the warranty period [41]. The distribution function of the usage rate is G ( r ) = P ( R ≤ r ) , r min ≤ r ≤ r max . The distribution of usage rate can be determined by records of similar products or customer surveys [42]. During the product design phase, the desired reliability of the product is ensured in the nominal usage rate r 0 .

Figure 1 Two-dimensional warranty.
Figure 1

Two-dimensional warranty.

During the warranty period, the manufacturer expects to control the warranty cost, and the consumer expects to obtain higher product availability. Therefore, how to take into account the interests and needs of both manufacturers and consumers and scientifically determining the warranty period and PM interval of the failure dependence multi-component system is the problem that the manufacturer needs to solve.

2.2 Assumptions and notations

To construct the model, the assumptions of this article are as follows:

  1. The failure-dependence multi-component system consists of Y single components in series.

  2. The failure-dependence multi-component system is a repairable system, and its failure rate increases with time and usage [43].

  3. Corrective maintenance is minimum maintenance, and PM is imperfect maintenance.

  4. Each component in a multi-component system has unidirectional failure dependence, which belongs to Class Ⅱ failure dependence.

  5. Failure under the nominal usage rate and the consumer usage rates are subject to Weibull distribution [44].

The notations that appeared in the study are presented in Table 1.

Table 1

Model notations

Notation Description
K B 1 The time limit of the two-dimensional warranty
K B 2 The usage limit of the two-dimensional warranty
r 0 The nominal usage rate of the system
G ( r ) The distribution function of the usage rate
g ( r ) The probability density function of the usage rate
r min The minimum value of usage rates
r max The maximum value of usage rates
r The actual usage rate of the system
I 1 The first failure time under the nominal usage rate
I 2 The first failure time under the actual usage rate
f I 1 i ( t ) The probability density function of I 1 for component i
F I 1 i ( t ) The cumulative distribution function of I 1 for component i
h I 1 i ( t ) The failure rate function of I 1 for component i
γ The AFT parameter
β r The scale parameter under the actual usage rate
F ( t | r ) The cumulative distribution function of I 2 for component i
h ( t | r ) The failure rate function of I 2 for component i
h real i ( t | r ) The actual failure rate of component i
h s ( t | r ) The failure rate of the system
T 0 PM interval
d The level of imperfect PM
χ ( d ) The PM improvement factor under level d
Y The number of components in the system
n a The number of PM during the two-dimensional warranty for the system
A z The expected availability of the system
EC The expected warranty cost for the system

2.3 System failure rate function

In the two-dimensional warranty, the calendar time and usage of the product are the key factors affecting the failure rate. There are three main fitting methods for the two-dimensional warranty product failure rate function, namely, the bivariate method, composite method, and marginal approach. The marginal approach transforms the usage rate into a function of calendar time, effectively changes the two-dimensional problem into a one-dimensional problem, and is widely used at present. The accelerated failure time (AFT) model is one of the marginal approaches. In this study, the AFT model is used to fit the failure rate function of a single component.

I 1 and I 2 indicate the first failure time under the nominal usage rate and actual usage rate, respectively. For component I, the probability density function, cumulative distribution function, and failure rate function of I 1 are f I 1 i ( t ) , F I 1 i ( t ) and h I 1 i ( t ) , respectively, then

(1) f I 1 i ( t ) = α β t β α − 1 e − ( t β ) α ,

(2) F I 1 i ( t ) = 1 − e − t β α ,

(3) h I 1 i ( t ) = α β t β α − 1 ,

where α is the shape parameter and β is the scale parameter. According to the AFT model [45], the quantitative relation between I 1 and I 2 is

(4) I 1 I 2 = r 0 r γ ,

where γ is the AFT parameter and γ ≥ 1 . Under the actual usage rate r, the scale parameter turns into

(5) β r = β r 0 r γ .

Then, the cumulative distribution function and failure rate function of I 2 for component i are

(6) F i ( t | r ) = 1 − exp − r r 0 γ α t α β α ,

(7) h i ( t | r ) = F I 2 ' ( t ) F I 2 ( t ) ¯ = α r r 0 γ α t α − 1 β α .

The failure chain model is used to describe the unidirectional failure dependence of components [46]. The failure chain model is shown in Figure 2.

Figure 2 The failure chain model.
Figure 2

The failure chain model.

Each component is numbered, as shown in Table 2.

Table 2

Component numbers

Component Number
A 1
B 2
C 3
D 4
E 5

The failure dependence coefficient is introduced to describe the degree of failure dependence between components. The failure dependence coefficient φ i j means the impact of the failure rate of component j on the failure rate of component i. The failure dependence matrix in Figure 2 can be constructed as

(8) φ = 0 0 0 0 0 φ 21 0 0 0 0 0 φ 32 0 0 0 φ 41 0 0 0 0 0 0 φ 53 φ 54 0 .

Then, considering the failure dependence, the actual failure rate of component i can be expressed as follows:

(9) h r e a l i ( t | r ) = { I } { h i ( t | r ) } + { φ } { h i ( t | r ) } ,

where h real i ( t | r ) is the matrix of Y × 1 , 1 ≤ i ≤ Y , which represents the actual failure rate of component i, I is the Y-order unit matrix, and h i ( t | r ) is the matrix of Y × 1 , 1 ≤ i ≤ Y , which represents the inherent failure rate of each component. Then, the failure rate function of the system is

(10) h s ( t | r ) = ∑ i = 1 Y h real i ( t | r ) .

2.4 Imperfect PM strategy

The manufacturer shall carry out regular imperfect PM of the system within the warranty period and the PM interval is T 0 . Imperfect PM leaves the repaired system in a state between as good as new and as bad as old. Imperfect PM is widely used because the maintenance cost is reasonable and the system state can be improved [32]. The effect of imperfect PM is modeled by the virtual age method and the failure-rate regression method. d represents the level of imperfect PM, and 0 ≤ d ≤ D . d = 0 corresponds to the state of the system without PM. M is the upper limit of PM. Let PM improvement factor be χ ( d ) . According to Gupta et al. [35]:

(11) χ ( d ) = ( 1 + d ) ⋅ e − d .

The virtual age of the system after the qth PM is [47]

(12) θ q = θ q − 1 + χ ( d ) ⋅ T 0 ,

where θ q − 1 represents the virtual age of the system after the (q − 1)-th PM. The change in system failure rate under imperfect PM is shown in Figure 3.

Figure 3 The system failure rate under imperfect PM.
Figure 3

The system failure rate under imperfect PM.

2.5 System availability

Based on the calculation method of the average availability proposed by Li et al. [48], the long-term availability of the system in this study was modeled. The combination of the PM interval and the level of imperfect maintenance is [ T 0 , d ] . The minimum maintenance time is T f , and the PM time under different PM levels is T p ( d ) . As shown in Figure 1, the actual length of the system warranty varies with different usage rates. The actual length of the system warranty is

(13) K r = min ( K B 1 , K B 2 / r ) .

Then, during the two-dimensional warranty period, the number of PM under usage rate r of the system is

(14) n a = K r / T 0 .

During the two-dimensional warranty period, the number of corrective maintenance under usage rate r of the system is

(15) L = ∑ u = 0 n a − 1 ∫ u ⋅ χ ( d ) ⋅ T 0 u ⋅ χ ( d ) ⋅ T 0 + T 0 h s ( t | r ) d t + ∫ n a ⋅ χ ( d ) ⋅ T 0 n a ⋅ χ ( d ) ⋅ T 0 + K r − n a ⋅ T 0 h s ( t | r ) d t .

Under usage rate r, the expected downtime of the system is

(16) T d = T f ⋅ L + n a ⋅ T p ( d ) .

Then, the expected availability of the system during the warranty is

(17) A s = K r − T d K r .

Based on the above analysis, the expected availability of all consumers within the two-dimensional warranty period can be expressed as

(18) A z = ∫ r min r max A s ⋅ g ( r ) d r .

2.6 Expected warranty costs

The minimum maintenance cost is C f , and the PM time under different PM levels is C p ( d ) . Under usage rate r, the expected warranty cost of the system is

(19) C d = C f ⋅ L + n a ⋅ C p ( d ) .

The expected warranty cost of all consumers within the two-dimensional warranty period can be expressed as

(20) EC = ∫ r min r max C d ⋅ g ( r ) d r .

3 Model optimization analysis

Given the warranty cost budget, this study is devoted to finding the two-dimensional warranty period that maximizes availability. Then, by changing the PM interval and level, the final plan of the two-dimensional warranty period, PM interval, and level that maximizes system availability are determined, thus achieving joint optimization of the two-dimensional warranty period, PM interval, and level. This section first establishes a joint optimization model and then provides a detailed introduction to the algorithm for solving the model.

3.1 Joint optimization model

Let the manufacturer’s warranty cost budget be C a . Under equal cost C a , the two-dimensional warranty period optimization model aiming at maximizing system availability is as follows:

(21) arg K B 1 , K B 2 max A z A z = ∫ r min r max A s ⋅ g ( r ) d r A s = K r − T d K r = K r − T f ⋅ ∑ u = 0 n a − 1 ∫ u ⋅ χ ( d ) ⋅ T 0 u ⋅ χ ( d ) ⋅ T 0 + T 0 h s ( t | r ) d t + ∫ n a ⋅ χ ( d ) ⋅ T 0 n a ⋅ χ ( d ) ⋅ T 0 + K r − n a ⋅ T 0 h s ( t | r ) d t + n a ⋅ T p ( d ) K r subject to : EC = C a C a = ∫ r min r max C d ⋅ g ( r ) d r = ∫ r min r max C f ⋅ ∑ u = 0 n a − 1 ∫ u ⋅ χ ( d ) ⋅ T 0 u ⋅ χ ( d ) ⋅ T 0 + T 0 h s ( t | r ) d t + ∫ n a ⋅ χ ( d ) ⋅ T 0 n a ⋅ χ ( d ) ⋅ T 0 + K r − n a ⋅ T 0 h s ( t | r ) d t + n a ⋅ C p ( d ) ⋅ g ( r ) d r

Through the above model, the joint optimization of the two-dimensional warranty period and PM strategy is realized. PM strategy includes PM interval and imperfect PM level. Under the fixed PM strategy, the optimal two-dimensional warranty period can be obtained by maximizing the availability, but the PM strategy is not necessarily optimal. Therefore, by changing the PM strategy, the system’s availability could get even higher, and then the joint optimization of the two-dimensional warranty period and PM interval period can be realized. The specific solving algorithm is discussed in detail in Section 3.2.

3.2 Algorithms

There are three main steps to solving the joint optimization model.

Step 1: Given the PM strategy and warranty cost budget, the two-dimensional warranty period scheme that maximizes system availability under the PM strategy and the constraint of warranty cost is solved.

Step 2: Since the PM level is limited and the PM interval can be discretized, the optimal two-dimensional warranty period of the system can be obtained by transforming the PM strategy and applying the same method and principle in Step 1.

Step 3: The PM strategy and two-dimensional warranty period, which make the system reach the highest availability, are selected, thus realizing the joint optimization of the two-dimensional warranty period and PM strategy.

The main process of solving the model is shown in Figure 4.

Figure 4 The main process of solving the model.
Figure 4

The main process of solving the model.

The key to Step 1 is the calculation of expected warranty cost and system availability. As can be seen from Figure 1, when the usage rate is greater than K B 2 / K B 1 , the warranty period of the system varies with the usage rate. It is difficult to directly obtain the expected warranty cost and availability of the system under all usage rates by the calculus method. Therefore, when the usage rate is greater than K B 2 / K B 1 , the method of transforming continuous to discrete is adopted, and the usage rate is divided into 20 equal minizones on the interval [ K B 2 / K B 1 , r max ]. The probability of each usage rate and the warranty cost and availability under the utilization rate are calculated, respectively. Then, the warranty cost and expected availability of the system with a usage rate greater than K B 2 / K B 1 are obtained according to the calculation method of mathematical expectation. Finally, the total expected warranty cost and availability of the system are obtained by considering the usage rate greater than K B 2 / K B 1 and less than K B 2 / K B 1 comprehensively. The pseudo-code for warranty costs is shown in Appendix A. The pseudo-code for system availability is shown in Appendix B [49].

Next, we need to find all two-dimensional warranty periods under this cost budget. This article mainly adopts Binary Search to solve this problem. Binary search is a search algorithm that looks for a specific element in an ordered array. The basic idea is to divide the array into two parts, determine which part the target element is in, and then continue searching in that part until you find the target element or determine that it does not exist [50]. Combined with this model, the basic logic of binary search is shown in Figure 5.

Figure 5 The application process of binary search.
Figure 5

The application process of binary search.

The solution process shown in Figure 5 can be used to obtain the optimal two-dimensional warranty period under a specific PM strategy and warranty cost budget. Since the PM interval and maintenance level are discrete, the optimal PM strategy and two-dimensional warranty period under a specific cost budget can be obtained by changing the PM strategy a limited number of times [51,52]. By repeating Steps 1 to Step 3, the joint optimization of the two-dimensional warranty period and maintenance strategy can be achieved.

4 Case analysis

In this section, the study illustrates the application of the proposed model through a case study of a power plant in China. The power plant has adopted the two-dimensional warranty, whose one dimension is calendar time (years), and one dimension is usage (km). It is necessary to decide the optimal warranty period and PM strategy to realize the improvement of system availability based on controlling the warranty cost. The power plant can be regarded as a multi-component system consisting of three components. There is failure dependence between components, and the failure chain model is shown in Figure 6.

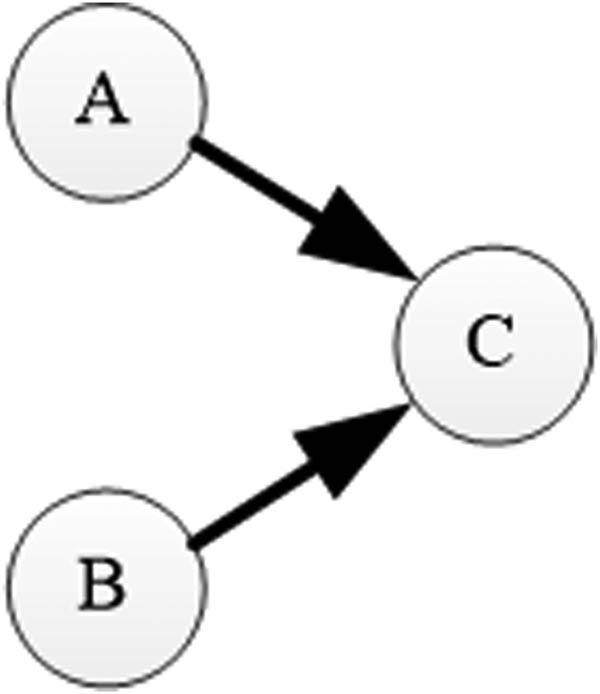
Figure 6 The failure chain model of the power plant.
Figure 6

The failure chain model of the power plant.

The failure dependence coefficient matrix is

φ = 0 0 0 0 0 0 0.02 0.01 0 .

Consumer usage rates r in [0, 6] follows Weibull distribution, and

r : W ( η = 2.2 , θ = 0.5 )

The first failure time of each component under the nominal usage rate is subject to Weibull distribution, and

I 1 : W ( α = 1.5 , β = 0.6 ) .

The unit usage rate is 104 km/year.

The nominal usage rate r 0 is 2 × 104 km/year. The imperfect PM level d ∈ [ 0 , 1 , 2 , 3 , 4 , 5 ] , the corresponding imperfect PM cost C p ∈ [ 0 , 10 , 30 , 60 , 100 , 160 ] , and the corresponding imperfect PM time T p ∈ [ 0 , 5 , 10 , 15 , 20 , 30 ] . The corrective maintenance cost C f = 250 , and the corrective maintenance time T f = 40 . The unit of T p and T f is “Day” and the unit of C p and C f is “CNY.”

4.1 Model validity analysis

The PM strategy d = 3 T 0 = 9 months is taken as an example to test the validity of the model. The value range K B 1 is [1,10], and the value step is 0.2. The value range K B 2 is [1,5], and the value step is 0.2. Costs and availability under different warranties can be calculated separately. The variation trend three-dimensional graph of cost and availability under different warranty periods can be drawn by using the data obtained in the calculation, as shown in Figures 7 and 8.

Figure 7 The availability trends under different warranty periods.
Figure 7

The availability trends under different warranty periods.

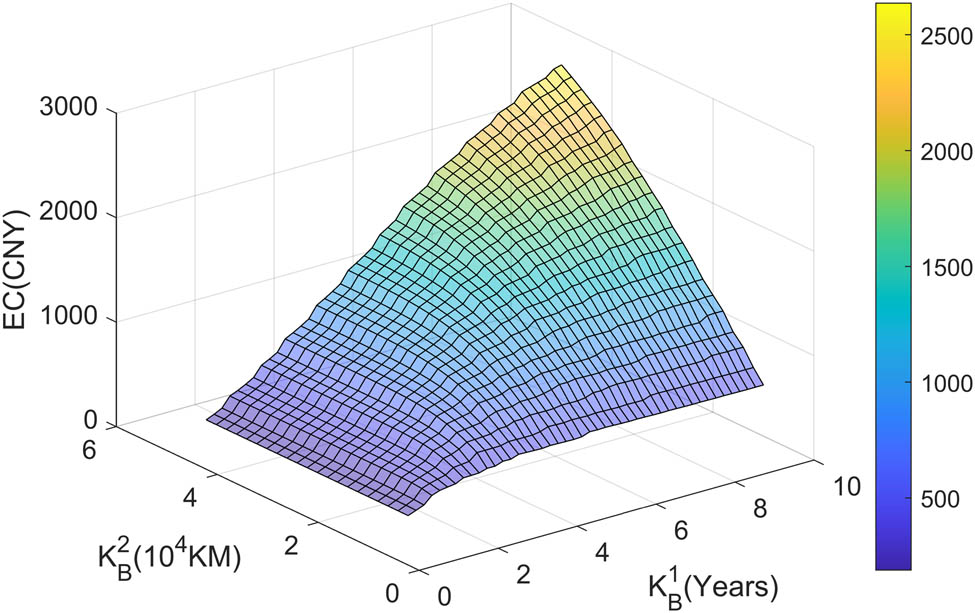
Figure 8 The cost trends under different warranty periods.
Figure 8

The cost trends under different warranty periods.

The cost budget for C a is 700 CNY. First, the binary search method is used to find all the combinations [ K B 1 , K B 2 ] satisfying the conditions on the equal cost curve (C a = 700), as shown in Figure 9.

Figure 9 Schematic diagram of two-dimensional warranty combination.
Figure 9

Schematic diagram of two-dimensional warranty combination.

In Figure 9, the blue dots represent the combination of [ K B 1 , K B 2 ] with budget 700 CNY, and the red dot indicates that no K B 2 matches K B 1 so that meets the budget. The variation trend of availability K B 1 is shown in Figure 10.

Figure 10 The variation trend of availability with K B 1 {K}_{\text{B}}^{1} .
Figure 10

The variation trend of availability with K B 1 .

By calculating the availability of each valid point, the optimal two-dimensional warranty period [ K B 1 , K B 2 ] is found. That is [9.9, 1.33], and the availability is 0.9625. The PM strategy is changed, that is, the value of PM level d and PM interval T 0 are changed, and the optimal two-dimensional warranty period and corresponding system availability are found under different PM strategies. The value of T 0 is in the range of [1 month, 15 months], and its step is 1 month. Figure 11 shows the variation of maximum system availability under different PM strategies.

Figure 11 The variation of maximum system availability.
Figure 11

The variation of maximum system availability.

As can be seen from Figure 11, when the PM interval is small, the system availability is low, mainly because frequent PM leads to increased system downtime. This suggests that manufacturers should determine the PM interval scientifically and reasonably to prevent the maintenance surplus. The combination of the optimal two-dimensional warranty period and system availability under the partial PM strategy is shown in Table 3.

Table 3

Optimization of the two-dimensional warranty period and availability

Preventive strategy C a = 700 CNY
d T 0 (months) K B 1 (years) K B 2 (104 km) A z
5 6 1.9 7.4 0.82
5 8 3.3 1 0.8936
5 13 10 1.3 0.9667
4 4 2.3 1 0.8392
4 6 5.5 1 0.9338
4 15 10 1.35 0.9668
3 2 1.6 1.32 0.73
3 4 9.4 1 0.9545
3 11 9.8 1.38 0.9626
2 1 1.5 1.04 0.6285
2 2 3.8 1 0.8651
2 9 10 1.4 0.9624
1 1 8.8 1 0.9259
1 2 9.9 1.19 0.9511
1 15 9.9 1.4 0.9666

Bold values represent the optimal solution among all candidate solutions.

According to the actual situation of manufacturers and consumers, the alternative PM strategy (d, T 0) is determined as (5, 6), (4, 15), (3, 4), (2, 9), and (1, 2). As shown in Table 3, the optimal PM strategy can be determined as (4, 15), and the optimal two-dimensional warranty is (10 years, 1.35 × 104 km). In this case, the availability is 0.9668.

4.2 Model comparative analysis

When the failure dependence among components of a multi-component system is not considered, the failure dependence coefficient matrix φ becomes a zero matrix. The same parameter settings as 4.1 when considering failure dependence are adopted. The variation trend three-dimensional graph of cost and availability under different warranty periods are shown in Figures 12 and 13, respectively.

Figure 12 The availability trends when failure dependence is not considered.
Figure 12

The availability trends when failure dependence is not considered.

Figure 13 The cost trends when failure dependence is not considered.
Figure 13

The cost trends when failure dependence is not considered.

The binary search is used to solve the optimal two-dimensional warranty period and availability without considering failure dependence. The optimal two-dimensional warranty period [ K B 1 , K B 2 ] is [9.8, 1.34], and the availability is 0.9607. Compared with considering failure dependence, the optimal two-dimensional warranty period changes, indicating that the existence of failure dependence will affect the two-dimensional warranty decision of the system, so managers should consider the impact of failure dependence when making decisions. Tables 4 and 5, respectively, show the system availability and warranty cost under different two-dimensional warranties.

Table 4

System availability under different two-dimensional warranties

Failure dependence is not considered
K B 2 ( 10 4 km ) K B 1 ( years )
1 1.2 1.4 1.6 1.8 2 2.2 2.4 2.6
1 0.9034 0.9089 0.9126 0.8968 0.9006 0.9082 0.9148 0.9125 0.9194
1.2 0.9032 0.9079 0.9102 0.8902 0.8953 0.9015 0.9069 0.9017 0.9084
1.4 0.9032 0.9077 0.9093 0.8870 0.8925 0.8973 0.9015 0.8934 0.8989
1.6 0.9032 0.9077 0.9091 0.8859 0.8912 0.8950 0.8980 0.8873 0.8928
1.8 0.9032 0.9077 0.9091 0.8854 0.8906 0.8938 0.8960 0.8837 0.8868
2 0.9032 0.9077 0.9090 0.8854 0.8904 0.8933 0.8950 0.8816 0.8848
Failure dependence is considered
K B 2 ( 10 4 km ) K B 1 ( years )
1 1.2 1.4 1.6 1.8 2 2.2 2.4 2.6
1 0.9028 0.9083 0.9121 0.8962 0.9001 0.9077 0.9143 0.9120 0.9189
1.2 0.9026 0.9073 0.9096 0.8896 0.8947 0.9010 0.9064 0.9011 0.9079
1.4 0.9026 0.9071 0.9087 0.8864 0.8919 0.8967 0.9009 0.8928 0.8983
1.6 0.9026 0.9071 0.9085 0.8852 0.8905 0.8944 0.8974 0.8866 0.8922
1.8 0.9026 0.9071 0.9084 0.8848 0.8900 0.8932 0.8953 0.8830 0.8862
2 0.9026 0.9071 0.9084 0.8848 0.8898 0.8927 0.8943 0.8809 0.8841
Table 5

System warranty cost under different two-dimensional warranties (unit: CNY)

Failure dependence is not considered
K B 2 ( 10 4 km ) K B 1 ( years )
1 1.2 1.4 1.6 1.8 2 2.2 2.4 2.6
1 186.7 215.7 245.2 315.8 342.2 353.6 363.6 399.3 401.5
1.2 187.1 218.3 253.1 336.4 362.9 382.9 401.4 452.0 459.7
1.4 187.1 218.9 255.8 345.9 374.2 401.4 427.9 492.2 508.8
1.6 187.1 219.0 256.6 349.4 379.5 411.8 444.7 521.0 541.5
1.8 187.1 219.0 256.7 350.7 381.7 416.9 454.5 538.4 570.6
2 187.1 219.0 256.7 350.8 382.4 419.2 459.4 548.7 582.2
Failure dependence is considered
K B 2 ( 10 4 km ) K B 1 ( years )
1 1.2 1.4 1.6 1.8 2 2.2 2.4 2.6
1 187.9 217.2 247.1 317.9 344.5 356.0 366.1 401.9 404.2
1.2 188.3 219.9 255.0 338.6 365.4 385.6 404.2 454.9 462.8
1.4 188.4 220.5 257.8 348.1 376.8 404.2 431.0 495.5 512.2
1.6 188.4 220.6 258.5 351.7 382.1 414.7 447.9 524.5 545.2
1.8 188.4 220.6 258.7 353.0 384.3 419.9 457.8 542.0 574.5
2 188.4 220.6 258.7 353.1 385.1 422.2 462.7 552.5 586.2

It can be seen from Tables 4 and 5 that the existence of failure dependence will increase the warranty cost and reduce the system availability. Therefore, in the design and manufacturing stage of the system, efforts should be made to reduce the failure dependence coefficient between components, reduce the warranty cost, and increase the system availability as much as possible.

When PM strategies are not carried out during the warranty period, i.e., when T 0 = 10, the warranty cost and availability of the system during the warranty period can be calculated separately. Then, the average warranty cost at all sampling points is obtained and compared with the PM strategy adopted during the warranty period, as shown in Figure 14. Through comparison, it can be found that PM reduces warranty costs; therefore, it is necessary to implement PM during the warranty period.

Figure 14 Comparison of warranty costs.
Figure 14

Comparison of warranty costs.

4.3 Parameter sensitivity analysis

In the optimization of the two-dimensional warranty period, the distribution of consumers’ usage rates will have a great impact on the final two-dimensional warranty period. In Section 4.1, consumer usage rates follow the Weibull distribution with shape parameter η = 2.2 and scale parameter θ = 0.5 . The values of shape parameters and scale parameters were changed, and the other parameters were set in the same way as in Section 4.1. The change of optimal two-dimensional warranty period with usage rate distribution was studied.

Figures 15–18, respectively, show all qualified two-dimensional warranties and the optimal two-dimensional warranties on the C a = 700 curve under different usage rate distributions. It can be seen that the optimal two-dimensional warranty period under different usage rate distributions is not the same. So, the usage rate distribution of consumers has an important effect on the optimization of the two-dimensional warranty period. This tells us in two-dimensional warranty period design, effective prediction and distribution fitting of consumers’ usage rate is an important basis for optimization of the two-dimensional warranty period.

Figure 15 Schematic diagram of two-dimensional warranty combination ( η = 2.3 , θ = 0.4 \eta =2.3,\theta =0.4 ).
Figure 15

Schematic diagram of two-dimensional warranty combination ( η = 2.3 , θ = 0.4 ).

Figure 16 Schematic diagram of two-dimensional warranty combination ( η = 2.1 , θ = 0.6 \eta =2.1,\theta =0.6 ).
Figure 16

Schematic diagram of two-dimensional warranty combination ( η = 2.1 , θ = 0.6 ).

Figure 17 Schematic diagram of two-dimensional warranty combination ( η = 1.7 , θ = 0.9 \eta =1.7,\theta =0.9 ).
Figure 17

Schematic diagram of two-dimensional warranty combination ( η = 1.7 , θ = 0.9 ).

Figure 18 Schematic diagram of two-dimensional warranty combination ( η = 1.7 , θ = 0.8 \eta =1.7,\theta =0.8 ).
Figure 18

Schematic diagram of two-dimensional warranty combination ( η = 1.7 , θ = 0.8 ).

The warranty cost budget is another important factor affecting the optimization of the two-dimensional warranty period. In Section 4.1, the warranty cost budget is 700 CNY. The cost is [700, 2,100], and the step size is 200. The optimal two-dimensional warranty period and system availability under different warranty cost budgets are shown in Table 6.

Table 6

Sensitivity analysis of warranty cost budgets

C a = 700 CNY
K B 1 (years) 9.9
K B 2 (104 km) 1.33
A z 0.9625
C a = 900 CNY
K B 1 (years) 10
K B 2 (104 km) 1.68
A z 0.9529
C a = 1,100 CNY
K B 1 (years) 10
K B 2 (104 km) 1.96
A z 0.9421
C a = 1,300 CNY
K B 1 (years) 10
K B 2 (104 km) 2.28
A z 0.9321
C a = 1,500 CNY
K B 1 (years) 10
K B 2 (104 km) 2.63
A z 0.9223
C a = 1,700 CNY
K B 1 (years) 10
K B 2 (104 km) 2.95
A z 0.9121
C a = 1,900 CNY
K B 1 (years) 10
K B 2 (104 km) 3.32
A z 0.9024
C a = 2,100 CNY
K B 1 (years) 10
K B 2 (104 km) 3.74
A z 0.8930

Figure 19 shows the trend of K B 2 and A z changing with warranty cost budgets. From Figure 18, it can be seen that a higher warranty cost budget can lead to a longer warranty period for the mileage dimension. Simultaneously, it can be seen that system availability decreases with the increase of warranty cost budget, indicating that more warranty cost budget is not always better. Therefore, determining a reasonable warranty cost budget is also particularly important for manufacturers.

Figure 19 The trend of K B 2 {K}_{\text{B}}^{2} and A z changing with warranty cost budgets.
Figure 19

The trend of K B 2 and A z changing with warranty cost budgets.

5 Conclusion

In this article, a joint optimization model of the two-dimensional warranty period and PM interval for failure-dependence multi-component systems was established. The model integrated PM and corrective maintenance effectively and considered the warranty cost and availability simultaneously, giving concern to the interests of both consumers and manufacturers. First, the failure dependence analysis of multi-component systems was conducted, and the actual failure rate model of the multi-component system was constructed. On this basis, the multi-component system warranty cost model and availability model were established. Aiming at maximum availability and considering the warranty cost budget constraint, a joint optimization model of the two-dimensional warranty period and PM strategy was built, and a model-solving algorithm combining grid search and binary search was introduced. The case analysis results indicated that the model established in this article could provide technical support for the decision-making of the two-dimensional warranty period and PM interval for failure-dependence multi-component systems. Through comparative analysis and sensitivity analysis, the findings are listed as follows:

  1. The failure dependence between various components in a multi-component system cannot be ignored when making warranty decisions.

  2. PM is beneficial for cost savings for the manufacturer, so it is necessary.

  3. The distribution of consumer usage rate has a significant impact on warranty decisions; therefore, effective prediction and distribution fitting of consumers’ usage rate is an important basis for optimization of the two-dimensional warranty period.

  4. Manufacturers need to reasonably determine the warranty cost budget to improve warranty quality and efficiency.

The research done in the article enriches the study of social and economic physics, statistics, and nonlinear physics. The mathematical model and the algorithm developed have potential applications in the fields of engineering physics and computational physics. There are still some problems related to our analysis that could be further studied. The study only considers failure dependence. The situation is more interesting when economic dependence and structural dependence are considered. And, joint optimization of the two-dimensional extended warranty period and PM interval is also a very interesting direction to be studied in the future.

Acknowledgments

The authors are very grateful to the associate editor and anonymous reviewers for their valuable and constructive comments and suggestions.

  1. Funding information: The authors state no funding involved.

  2. Author contributions: All authors have accepted responsibility for the entire content of this manuscript and approved its submission.

  3. Conflict of interest: The authors state no conflict of interest.

Appendix A Pseudo-code for warranty costs

Function: The warranty cost is obtained through this program
Parameters： K B 1 , K B 2 , C f , C p ( d ) , d , T 0 , etc.
if r min ≤ r ≤ K B 2 / K B 1
n a = floor ( K B 1 / T 0 )
EC1 = ∫ r min K B 2 / K B 1 C d ⋅ g ( r ) d r
else
r low = K B 2 / K B 1 ;
M = 20;
r c = (r max – r low)/M;
r 1 = r low : r c : (r low + (M – 1) * r c);
r 2 = r 1 + r c;
r m = r low : r c : (r low + M * r c);
for q = 1: M
n a = floor [ K B 2 / r m ( q ) T 0 ]
EC2 = C d [ r m ( q ) ] ⋅ g [ r m ( q ) ]
EC3 = ∑ M EC 2
end for
end if
EC = EC1 + EC3
print EC
end procedure

Appendix B Pseudo-code for system availability

Function: The system availability is obtained through this program
Parameters： K B 1 , K B 2 , T f , T p ( d ) , d , T 0 , etc.
if r min ≤ r ≤ K B 2 / K B 1
n a = floor ( K B 1 / T 0 )
A z1 = ∫ r min K B 2 / K B 1 A s ⋅ g ( r ) d r
else
r low = K B 2 / K B 1 ;
M = 20;
r c = (r max – r low)/M;
r 1 = r low : r c: (r low + (M – 1) * r c);
r 2 = r 1 + r c;
r m = r low : r c : (r low + M * r c);
for q = 1: M
n a = floor [ K B 2 / r m ( q ) T 0 ]
A z2 = { [ K B 2 / r m ( q ) ] − T d [ r m ( q ) ] ⋅ g [ r m ( q ) ] } / [ K B 2 / r m ( q ) ]
A z3 = ∑ M A z 2
end for
end if
A z = A z1 + A z3
print A z
end procedure

References

[1] Dong FQ, Wang HQ, Men F, Liang LJ. Customized preventive maintenance strategies for products sold with two-dimensional warranty. Math Probl Eng. 2021;2021:5576455.10.1155/2021/5576455Search in Google Scholar

[2] Zhao X, He SG, Xie M. Utilizing experimental degradation data for warranty cost optimization under imperfect repair. Reliab Eng Syst Saf. 2018;177:108–19.10.1016/j.ress.2018.05.002Search in Google Scholar

[3] Wang X, Ye ZS. Design of customized two-dimensional extended warranties considering use rate and heterogeneity. IISE Trans. 2021;53(3):341–51.10.1080/24725854.2020.1768455Search in Google Scholar

[4] Lin KS, Chen YX. Analysis of two-dimensional warranty data considering global and local dependence of heterogeneous marginals. Reliab Eng Syst Saf. 2021;207:107327.10.1016/j.ress.2020.107327Search in Google Scholar

[5] Zheng R, Su C. A flexible two-dimensional basic warranty policy with two continuous warranty regions. Qual Reliab Eng Int. 2020;36(6):2003–18.10.1002/qre.2670Search in Google Scholar

[6] Salmasnia A, Hatami A, Maleki MR. Joint optimization of two-dimensional preventive maintenance parameters, technology level and product price under continuous usage rate and agent warranty services. Int J Model Simul. 2023 early access. 10.1080/02286203.2023.2180602.Search in Google Scholar

[7] Zhao F, Peng R, Zhang N. Inspection policy optimization for a k-out-of-n system considering failure dependence: a case study. Reliab Eng Syst Saf. 2023;237:109331.10.1016/j.ress.2023.109331Search in Google Scholar

[8] Guo LH, Li RY, Wang Y, Yang J, Liu Y, Chen YM, et al. Availability for multi-component k-out-of-n: G warm-standby system in series with shut-off rule of suspended animation. Reliab Eng Syst Saf. 2023;233:109106.10.1016/j.ress.2023.109106Search in Google Scholar

[9] Wang XL, Xie W. Two-dimensional warranty: A literature review. P I Mech Eng O-J Ris. 2018;232(3):284–307.10.1177/1748006X17742776Search in Google Scholar

[10] Wu CC, Lin PC, Chou CY. Determination of price and warranty length for a normal lifetime distributed product. Int J Prod Econ. 2006;102(1):95–107.10.1016/j.ijpe.2005.02.002Search in Google Scholar

[11] Chien YH. Determining optimal warranty periods from the seller’s perspective and optimal out-of-warranty replacement age from the buyer’s perspective. Int J Syst Sci. 2005;36(10):631–7.10.1080/00207720500219054Search in Google Scholar

[12] Huang HZ, Liu ZJ, Murthy DNP. Optimal reliability, warranty and price for new products. IIE Trans. 2007;39(8):819–27.10.1080/07408170601091907Search in Google Scholar

[13] Liu ZJ, Huang HZ, Murthy DNP. Optimal reliability and price choices for products under warranty. Reliability and Maintainability Symposium, 2006. RAMS'06. Annual. IEEE; 2006. p. 146–51.Search in Google Scholar

[14] Xie W, Liao HT, Zhu XY. Estimation of gross profit for a new durable product considering warranty and post-warranty repairs. IIE Trans. 2014;46(2):87–105.10.1080/0740817X.2012.761370Search in Google Scholar

[15] He SG, Zhang ZM, Zhang GH, He Z. Two-dimensional base warranty design based on a new demand function considering heterogeneous usage rate. Int J Prod Res. 2017;55(23):7058–72.10.1080/00207543.2017.1346837Search in Google Scholar

[16] Chen T, Popova E. Maintenance policies with two-dimensional warranty. Reliab Eng Syst Safe. 2002;77(1):61–9.10.1016/S0951-8320(02)00031-5Search in Google Scholar

[17] Baik J, Murthy DNP, Jack N. Two-dimensional failure modeling with minimal repair. Nav Res Log. 2004;51(3):345–62.10.1002/nav.10120Search in Google Scholar

[18] Taleizadeh AA, Mokhtarzadeh M. Pricing and two-dimensional warranty policy of multi-products with online and offline channels using a value-at-risk approach. Comput Ind Eng. 2020;148(3):106674.10.1016/j.cie.2020.106674Search in Google Scholar

[19] Park M, Iskandar BP, Park DH. Optimization of two-dimensional warranty policy for repairable products based on age and usage, applicable to lemon law conditions. Appl Stoch Model Bus. 2022;38(6):1144–57.10.1002/asmb.2720Search in Google Scholar

[20] Huang YS, Huang CD, Ho JW. A customized two-dimensional extended warranty with preventive maintenance. Eur J Oper Res. 2017;257(3):45–62.10.1016/j.ejor.2016.07.034Search in Google Scholar

[21] He Z, Wang DF, He SG, Zhang YW, Dai AS. Two-dimensional extended warranty strategy including maintenance level and purchase time: A win-win perspective. Comput Ind Eng. 2020;141(4):56–72.10.1016/j.cie.2020.106294Search in Google Scholar

[22] Dong FQ, Liu ZX, Hao JH, Men F. The design and optimization of two-dimensional warranty period with considering preventive maintenance strategy. Ind Eng Manag Syst. 2019;24(4):64–71.Search in Google Scholar

[23] Salmasnia A, Doroudi A, Kohan F. A flexible two-dimensional warranty in optimizing the dealer and customer satisfaction. Int J Reliab Qual Saf Eng. 2022;29(6):2250009.10.1142/S0218539322500097Search in Google Scholar

[24] Peng SZ, Jiang W, Wei L, Wang XL. A new cost-sharing preventive maintenance program under two-dimensional warranty. Int J Prod Econ. 2022;254:108580.10.1016/j.ijpe.2022.108580Search in Google Scholar

[25] Wang XL. Design and pricing of usage-driven customized two-dimensional extended warranty menus. IISE Trans. 2023;55(9):873–85.10.1080/24725854.2022.2104972Search in Google Scholar

[26] Gupta SK, Mukhopadhyay I, Chatterjee A. Two-dimensional extended warranty length design from incomplete warranty data based on a new price curve considering different maintenance policies. Comput Ind Eng. 2022;170:108323.10.1016/j.cie.2022.108323Search in Google Scholar

[27] Ruan YP, Wu GC, Luo XG. Optimal joint design of two-dimensional warranty and preventive maintenance policies for new products considering learning effects. Comput Ind Eng. 2022;166:107958.10.1016/j.cie.2022.107958Search in Google Scholar

[28] Zhang ZM, He SG, He Z, Wang DF, Dong FQ. A systematic warranty-reliability-price decision model for two-dimensional warranted products with heterogeneous usage rates. Comput Ind Eng. 2022;163:107820.10.1016/j.cie.2021.107820Search in Google Scholar

[29] Dong EZ, Cheng ZH, Wang RC, Zhang YX. Extended warranty decision model of failure dependence wind turbine system based on cost-effectiveness analysis. Open Phys. 2022;20(1):616–31.10.1515/phys-2022-0057Search in Google Scholar

[30] Qiu QG, Liu BL, Lin C, Wang JJ. Availability analysis and maintenance optimization for multiple failure mode systems considering imperfect repair. P I Mech Eng O-J Ris. 2021;235(6):982–97.10.1177/1748006X211012792Search in Google Scholar

[31] Varnosafaderani S, Chukova S. A two-dimensional warranty servicing strategy based on reduction in product failure intensity. Comput Math Appl. 2012;63(1):201–13.10.1016/j.camwa.2011.11.011Search in Google Scholar

[32] Shahanaghi K, Noorossana R, Jalali-Naini SG, Heydari M. Failure modeling and optimizing preventive maintenance strategy during two-dimensional extended warranty contracts. Eng Fail Anal. 2013;28(3):90–102.10.1016/j.engfailanal.2012.09.006Search in Google Scholar

[33] Yu J, Chen XZ. Research on a two-dimensional warranty strategy based on minimal and imperfect repairs. Ind Eng Manag Syst. 2009;14(3):65–9.Search in Google Scholar

[34] Wang LY, Song YS. Optimization of preventive maintenance and replacement strategies for nonrenewing two-dimensional warranty products experiencing degradation and external shocks. Math Probl Eng. 2022;32(7):89–110.10.1155/2022/9524204Search in Google Scholar

[35] Gupta SK, Chattopadhyay G. Early detection of reliability related problems from two-dimensional warranty data considering labour code priority index. Reliab Eng Syst Saf. 2022;225:108588.10.1016/j.ress.2022.108588Search in Google Scholar

[36] Wei YZ, Liu SY, Ling XL, Shen LJ. Optimal burn-in policy for mixed population of products under two-dimensional combination warranty. Appl Stoch Model Bus. 2022;38(4):651–76.10.1002/asmb.2680Search in Google Scholar

[37] Thomas LC. A survey of maintenance and replacement models for maintainability and reliability of multi-item systems. Reliab Eng. 1986;16(4):297–309.10.1016/0143-8174(86)90099-5Search in Google Scholar

[38] Dao CD, Zuo MJ. Selective maintenance of multi-state systems with structural dependence. Reliab Eng Sys Saf. 2017;159:184–95.10.1016/j.ress.2016.11.013Search in Google Scholar

[39] Zhang N, Fouladirad M, Barros A, Zhang J. Condition-based maintenance for a K-out-of-N deteriorating system under periodic inspection with failure dependence. Eur J Oper Res. 2020;287:159–67.10.1016/j.ejor.2020.04.041Search in Google Scholar

[40] Qian Q, Jiang ZH. Preventive maintenance strategy and maintenance time of multi-component system. Ind Eng. 2020;23:95–100.Search in Google Scholar

[41] Ye ZS, Murthy DNP. Warranty menu design for a two-dimensional warranty. Reliab Eng Syst Saf. 2016;155:21–9.10.1016/j.ress.2016.05.013Search in Google Scholar

[42] Su C, Wang XL. A two-stage preventive maintenance optimization model incorporating two-dimensional extended warranty. Reliab Eng Syst Saf. 2016;155:169–78.10.1016/j.ress.2016.07.004Search in Google Scholar

[43] Wang DF, He Z, He SG, Zhang ZM, Zhang YW. Dynamic pricing of two-dimensional extended warranty considering the impacts of product price fluctuations and repair learning. Reliab Eng Syst Saf. 2021;210:107516.10.1016/j.ress.2021.107516Search in Google Scholar

[44] Dai AS, Wei GZ, Wang DF, He Z, He SG. The opportunity study of PM strategy for second-hand products sold with a two-dimensional warranty. Reliab Eng Syst Saf. 2021;214(3):107699.10.1016/j.ress.2021.107699Search in Google Scholar

[45] Laeless J, Hu J, Cao J. Methods for estimation of failure distributions and rates from automobile warranty data. Lifetime Data Anal. 1995;1(3):227–40.10.1007/BF00985758Search in Google Scholar PubMed

[46] Wang H, Du WX, Liu ZL, Yang XZ, Li ZX. Integrating failure and economic dependence for maintenance of electric multiple unit multi-component system. J Shanghai Jiaotong Univ Sci. 2016;50(5):660–7.Search in Google Scholar

[47] Wang YK, Liu YL, Liu ZX, Li XP. On reliability improvement program for second-hand products sold with a two-dimensional warranty. Reliab Eng Syst Saf. 2017;167:452–63.10.1016/j.ress.2017.06.029Search in Google Scholar

[48] Li X, Makis V, Zhao ZD, Zuo HF, Duan CQ, Zhang YY. Optimal Bayesian maintenance policy for a gearbox subject to two dependent failure modes. Qual Reliab Eng Int. 2019;35:659–76.10.1002/qre.2428Search in Google Scholar

[49] Dong E, Cheng Z, Shuai Y, Zhao JM. Optimal block replacement policy for two-dimensional products considering imperfect maintenance with improved Salp swarm algorithm. Open Phys. 2022;20(1):1062–79.10.1515/phys-2022-0199Search in Google Scholar

[50] Niu Q, Mo R, Wan N. Algorithm of multi-cause process quality diagnosis based on dichotomy. J Mech Eng. 2014;50(02):202–6.10.3901/JME.2014.02.202Search in Google Scholar

[51] Alharbi KAM, Farooq U, Waqas H, Imran M, Noreen S, Akgül A, et al. Numerical solution of maxwell-sutterby nanofluid flow inside a stretching sheet with thermal radiation, exponential heat source/sink, and bioconvection. Int J Thermofluid. 2023;18:100339.10.1016/j.ijft.2023.100339Search in Google Scholar

[52] Li PL, Gao R, Xu CJ, Li Y, Akgül A, Baleanu D. Dynamics exploration for a fractional-order delayed zooplankton-phytoplankton system. Chaos Solit Fract. 2023;166:112975.10.1016/j.chaos.2022.112975Search in Google Scholar
Received: 2023-05-22
Revised: 2023-11-26
Accepted: 2023-12-04
Published Online: 2023-12-31

© 2023 the author(s), published by De Gruyter

This work is licensed under the Creative Commons Attribution 4.0 International License.

Articles in the same Issue

  1. Regular Articles
  2. Dynamic properties of the attachment oscillator arising in the nanophysics
  3. Parametric simulation of stagnation point flow of motile microorganism hybrid nanofluid across a circular cylinder with sinusoidal radius
  4. Fractal-fractional advection–diffusion–reaction equations by Ritz approximation approach
  5. Behaviour and onset of low-dimensional chaos with a periodically varying loss in single-mode homogeneously broadened laser
  6. Ammonia gas-sensing behavior of uniform nanostructured PPy film prepared by simple-straightforward in situ chemical vapor oxidation
  7. Analysis of the working mechanism and detection sensitivity of a flash detector
  8. Flat and bent branes with inner structure in two-field mimetic gravity
  9. Heat transfer analysis of the MHD stagnation-point flow of third-grade fluid over a porous sheet with thermal radiation effect: An algorithmic approach
  10. Weighted survival functional entropy and its properties
  11. Bioconvection effect in the Carreau nanofluid with Cattaneo–Christov heat flux using stagnation point flow in the entropy generation: Micromachines level study
  12. Study on the impulse mechanism of optical films formed by laser plasma shock waves
  13. Analysis of sweeping jet and film composite cooling using the decoupled model
  14. Research on the influence of trapezoidal magnetization of bonded magnetic ring on cogging torque
  15. Tripartite entanglement and entanglement transfer in a hybrid cavity magnomechanical system
  16. Compounded Bell-G class of statistical models with applications to COVID-19 and actuarial data
  17. Degradation of Vibrio cholerae from drinking water by the underwater capillary discharge
  18. Multiple Lie symmetry solutions for effects of viscous on magnetohydrodynamic flow and heat transfer in non-Newtonian thin film
  19. Thermal characterization of heat source (sink) on hybridized (Cu–Ag/EG) nanofluid flow via solid stretchable sheet
  20. Optimizing condition monitoring of ball bearings: An integrated approach using decision tree and extreme learning machine for effective decision-making
  21. Study on the inter-porosity transfer rate and producing degree of matrix in fractured-porous gas reservoirs
  22. Interstellar radiation as a Maxwell field: Improved numerical scheme and application to the spectral energy density
  23. Numerical study of hybridized Williamson nanofluid flow with TC4 and Nichrome over an extending surface
  24. Controlling the physical field using the shape function technique
  25. Significance of heat and mass transport in peristaltic flow of Jeffrey material subject to chemical reaction and radiation phenomenon through a tapered channel
  26. Complex dynamics of a sub-quadratic Lorenz-like system
  27. Stability control in a helicoidal spin–orbit-coupled open Bose–Bose mixture
  28. Research on WPD and DBSCAN-L-ISOMAP for circuit fault feature extraction
  29. Simulation for formation process of atomic orbitals by the finite difference time domain method based on the eight-element Dirac equation
  30. A modified power-law model: Properties, estimation, and applications
  31. Bayesian and non-Bayesian estimation of dynamic cumulative residual Tsallis entropy for moment exponential distribution under progressive censored type II
  32. Computational analysis and biomechanical study of Oldroyd-B fluid with homogeneous and heterogeneous reactions through a vertical non-uniform channel
  33. Predictability of machine learning framework in cross-section data
  34. Chaotic characteristics and mixing performance of pseudoplastic fluids in a stirred tank
  35. Isomorphic shut form valuation for quantum field theory and biological population models
  36. Vibration sensitivity minimization of an ultra-stable optical reference cavity based on orthogonal experimental design
  37. Effect of dysprosium on the radiation-shielding features of SiO2–PbO–B2O3 glasses
  38. Asymptotic formulations of anti-plane problems in pre-stressed compressible elastic laminates
  39. A study on soliton, lump solutions to a generalized (3+1)-dimensional Hirota--Satsuma--Ito equation
  40. Tangential electrostatic field at metal surfaces
  41. Bioconvective gyrotactic microorganisms in third-grade nanofluid flow over a Riga surface with stratification: An approach to entropy minimization
  42. Infrared spectroscopy for ageing assessment of insulating oils via dielectric loss factor and interfacial tension
  43. Influence of cationic surfactants on the growth of gypsum crystals
  44. Study on instability mechanism of KCl/PHPA drilling waste fluid
  45. Analytical solutions of the extended Kadomtsev–Petviashvili equation in nonlinear media
  46. A novel compact highly sensitive non-invasive microwave antenna sensor for blood glucose monitoring
  47. Inspection of Couette and pressure-driven Poiseuille entropy-optimized dissipated flow in a suction/injection horizontal channel: Analytical solutions
  48. Conserved vectors and solutions of the two-dimensional potential KP equation
  49. The reciprocal linear effect, a new optical effect of the Sagnac type
  50. Optimal interatomic potentials using modified method of least squares: Optimal form of interatomic potentials
  51. The soliton solutions for stochastic Calogero–Bogoyavlenskii Schiff equation in plasma physics/fluid mechanics
  52. Research on absolute ranging technology of resampling phase comparison method based on FMCW
  53. Analysis of Cu and Zn contents in aluminum alloys by femtosecond laser-ablation spark-induced breakdown spectroscopy
  54. Nonsequential double ionization channels control of CO2 molecules with counter-rotating two-color circularly polarized laser field by laser wavelength
  55. Fractional-order modeling: Analysis of foam drainage and Fisher's equations
  56. Thermo-solutal Marangoni convective Darcy-Forchheimer bio-hybrid nanofluid flow over a permeable disk with activation energy: Analysis of interfacial nanolayer thickness
  57. Investigation on topology-optimized compressor piston by metal additive manufacturing technique: Analytical and numeric computational modeling using finite element analysis in ANSYS
  58. Breast cancer segmentation using a hybrid AttendSeg architecture combined with a gravitational clustering optimization algorithm using mathematical modelling
  59. On the localized and periodic solutions to the time-fractional Klein-Gordan equations: Optimal additive function method and new iterative method
  60. 3D thin-film nanofluid flow with heat transfer on an inclined disc by using HWCM
  61. Numerical study of static pressure on the sonochemistry characteristics of the gas bubble under acoustic excitation
  62. Optimal auxiliary function method for analyzing nonlinear system of coupled Schrödinger–KdV equation with Caputo operator
  63. Analysis of magnetized micropolar fluid subjected to generalized heat-mass transfer theories
  64. Does the Mott problem extend to Geiger counters?
  65. Stability analysis, phase plane analysis, and isolated soliton solution to the LGH equation in mathematical physics
  66. Effects of Joule heating and reaction mechanisms on couple stress fluid flow with peristalsis in the presence of a porous material through an inclined channel
  67. Bayesian and E-Bayesian estimation based on constant-stress partially accelerated life testing for inverted Topp–Leone distribution
  68. Dynamical and physical characteristics of soliton solutions to the (2+1)-dimensional Konopelchenko–Dubrovsky system
  69. Study of fractional variable order COVID-19 environmental transformation model
  70. Sisko nanofluid flow through exponential stretching sheet with swimming of motile gyrotactic microorganisms: An application to nanoengineering
  71. Influence of the regularization scheme in the QCD phase diagram in the PNJL model
  72. Fixed-point theory and numerical analysis of an epidemic model with fractional calculus: Exploring dynamical behavior
  73. Computational analysis of reconstructing current and sag of three-phase overhead line based on the TMR sensor array
  74. Investigation of tripled sine-Gordon equation: Localized modes in multi-stacked long Josephson junctions
  75. High-sensitivity on-chip temperature sensor based on cascaded microring resonators
  76. Pathological study on uncertain numbers and proposed solutions for discrete fuzzy fractional order calculus
  77. Bifurcation, chaotic behavior, and traveling wave solution of stochastic coupled Konno–Oono equation with multiplicative noise in the Stratonovich sense
  78. Thermal radiation and heat generation on three-dimensional Casson fluid motion via porous stretching surface with variable thermal conductivity
  79. Numerical simulation and analysis of Airy's-type equation
  80. A homotopy perturbation method with Elzaki transformation for solving the fractional Biswas–Milovic model
  81. Heat transfer performance of magnetohydrodynamic multiphase nanofluid flow of Cu–Al2O3/H2O over a stretching cylinder
  82. ΛCDM and the principle of equivalence
  83. Axisymmetric stagnation-point flow of non-Newtonian nanomaterial and heat transport over a lubricated surface: Hybrid homotopy analysis method simulations
  84. HAM simulation for bioconvective magnetohydrodynamic flow of Walters-B fluid containing nanoparticles and microorganisms past a stretching sheet with velocity slip and convective conditions
  85. Coupled heat and mass transfer mathematical study for lubricated non-Newtonian nanomaterial conveying oblique stagnation point flow: A comparison of viscous and viscoelastic nanofluid model
  86. Power Topp–Leone exponential negative family of distributions with numerical illustrations to engineering and biological data
  87. Extracting solitary solutions of the nonlinear Kaup–Kupershmidt (KK) equation by analytical method
  88. A case study on the environmental and economic impact of photovoltaic systems in wastewater treatment plants
  89. Application of IoT network for marine wildlife surveillance
  90. Non-similar modeling and numerical simulations of microploar hybrid nanofluid adjacent to isothermal sphere
  91. Joint optimization of two-dimensional warranty period and maintenance strategy considering availability and cost constraints
  92. Numerical investigation of the flow characteristics involving dissipation and slip effects in a convectively nanofluid within a porous medium
  93. Spectral uncertainty analysis of grassland and its camouflage materials based on land-based hyperspectral images
  94. Application of low-altitude wind shear recognition algorithm and laser wind radar in aviation meteorological services
  95. Investigation of different structures of screw extruders on the flow in direct ink writing SiC slurry based on LBM
  96. Harmonic current suppression method of virtual DC motor based on fuzzy sliding mode
  97. Micropolar flow and heat transfer within a permeable channel using the successive linearization method
  98. Different lump k-soliton solutions to (2+1)-dimensional KdV system using Hirota binary Bell polynomials
  99. Investigation of nanomaterials in flow of non-Newtonian liquid toward a stretchable surface
  100. Weak beat frequency extraction method for photon Doppler signal with low signal-to-noise ratio
  101. Electrokinetic energy conversion of nanofluids in porous microtubes with Green’s function
  102. Examining the role of activation energy and convective boundary conditions in nanofluid behavior of Couette-Poiseuille flow
  103. Review Article
  104. Effects of stretching on phase transformation of PVDF and its copolymers: A review
  105. Special Issue on Transport phenomena and thermal analysis in micro/nano-scale structure surfaces - Part IV
  106. Prediction and monitoring model for farmland environmental system using soil sensor and neural network algorithm
  107. Special Issue on Advanced Topics on the Modelling and Assessment of Complicated Physical Phenomena - Part III
  108. Some standard and nonstandard finite difference schemes for a reaction–diffusion–chemotaxis model
  109. Special Issue on Advanced Energy Materials - Part II
  110. Rapid productivity prediction method for frac hits affected wells based on gas reservoir numerical simulation and probability method
  111. Special Issue on Novel Numerical and Analytical Techniques for Fractional Nonlinear Schrodinger Type - Part III
  112. Adomian decomposition method for solution of fourteenth order boundary value problems
  113. New soliton solutions of modified (3+1)-D Wazwaz–Benjamin–Bona–Mahony and (2+1)-D cubic Klein–Gordon equations using first integral method
  114. On traveling wave solutions to Manakov model with variable coefficients
  115. Rational approximation for solving Fredholm integro-differential equations by new algorithm
  116. Special Issue on Predicting pattern alterations in nature - Part I
  117. Modeling the monkeypox infection using the Mittag–Leffler kernel
  118. Spectral analysis of variable-order multi-terms fractional differential equations
  119. Special Issue on Nanomaterial utilization and structural optimization - Part I
  120. Heat treatment and tensile test of 3D-printed parts manufactured at different build orientations
https://doi.org/10.1515/phys-2023-0164
Keywords for this article
two-dimensional warranty; preventive maintenance strategy; joint optimization; availability; binary search
Creative Commons
BY 4.0

Articles in the same Issue

  1. Regular Articles
  2. Dynamic properties of the attachment oscillator arising in the nanophysics
  3. Parametric simulation of stagnation point flow of motile microorganism hybrid nanofluid across a circular cylinder with sinusoidal radius
  4. Fractal-fractional advection–diffusion–reaction equations by Ritz approximation approach
  5. Behaviour and onset of low-dimensional chaos with a periodically varying loss in single-mode homogeneously broadened laser
  6. Ammonia gas-sensing behavior of uniform nanostructured PPy film prepared by simple-straightforward in situ chemical vapor oxidation
  7. Analysis of the working mechanism and detection sensitivity of a flash detector
  8. Flat and bent branes with inner structure in two-field mimetic gravity
  9. Heat transfer analysis of the MHD stagnation-point flow of third-grade fluid over a porous sheet with thermal radiation effect: An algorithmic approach
  10. Weighted survival functional entropy and its properties
  11. Bioconvection effect in the Carreau nanofluid with Cattaneo–Christov heat flux using stagnation point flow in the entropy generation: Micromachines level study
  12. Study on the impulse mechanism of optical films formed by laser plasma shock waves
  13. Analysis of sweeping jet and film composite cooling using the decoupled model
  14. Research on the influence of trapezoidal magnetization of bonded magnetic ring on cogging torque
  15. Tripartite entanglement and entanglement transfer in a hybrid cavity magnomechanical system
  16. Compounded Bell-G class of statistical models with applications to COVID-19 and actuarial data
  17. Degradation of Vibrio cholerae from drinking water by the underwater capillary discharge
  18. Multiple Lie symmetry solutions for effects of viscous on magnetohydrodynamic flow and heat transfer in non-Newtonian thin film
  19. Thermal characterization of heat source (sink) on hybridized (Cu–Ag/EG) nanofluid flow via solid stretchable sheet
  20. Optimizing condition monitoring of ball bearings: An integrated approach using decision tree and extreme learning machine for effective decision-making
  21. Study on the inter-porosity transfer rate and producing degree of matrix in fractured-porous gas reservoirs
  22. Interstellar radiation as a Maxwell field: Improved numerical scheme and application to the spectral energy density
  23. Numerical study of hybridized Williamson nanofluid flow with TC4 and Nichrome over an extending surface
  24. Controlling the physical field using the shape function technique
  25. Significance of heat and mass transport in peristaltic flow of Jeffrey material subject to chemical reaction and radiation phenomenon through a tapered channel
  26. Complex dynamics of a sub-quadratic Lorenz-like system
  27. Stability control in a helicoidal spin–orbit-coupled open Bose–Bose mixture
  28. Research on WPD and DBSCAN-L-ISOMAP for circuit fault feature extraction
  29. Simulation for formation process of atomic orbitals by the finite difference time domain method based on the eight-element Dirac equation
  30. A modified power-law model: Properties, estimation, and applications
  31. Bayesian and non-Bayesian estimation of dynamic cumulative residual Tsallis entropy for moment exponential distribution under progressive censored type II
  32. Computational analysis and biomechanical study of Oldroyd-B fluid with homogeneous and heterogeneous reactions through a vertical non-uniform channel
  33. Predictability of machine learning framework in cross-section data
  34. Chaotic characteristics and mixing performance of pseudoplastic fluids in a stirred tank
  35. Isomorphic shut form valuation for quantum field theory and biological population models
  36. Vibration sensitivity minimization of an ultra-stable optical reference cavity based on orthogonal experimental design
  37. Effect of dysprosium on the radiation-shielding features of SiO2–PbO–B2O3 glasses
  38. Asymptotic formulations of anti-plane problems in pre-stressed compressible elastic laminates
  39. A study on soliton, lump solutions to a generalized (3+1)-dimensional Hirota--Satsuma--Ito equation
  40. Tangential electrostatic field at metal surfaces
  41. Bioconvective gyrotactic microorganisms in third-grade nanofluid flow over a Riga surface with stratification: An approach to entropy minimization
  42. Infrared spectroscopy for ageing assessment of insulating oils via dielectric loss factor and interfacial tension
  43. Influence of cationic surfactants on the growth of gypsum crystals
  44. Study on instability mechanism of KCl/PHPA drilling waste fluid
  45. Analytical solutions of the extended Kadomtsev–Petviashvili equation in nonlinear media
  46. A novel compact highly sensitive non-invasive microwave antenna sensor for blood glucose monitoring
  47. Inspection of Couette and pressure-driven Poiseuille entropy-optimized dissipated flow in a suction/injection horizontal channel: Analytical solutions
  48. Conserved vectors and solutions of the two-dimensional potential KP equation
  49. The reciprocal linear effect, a new optical effect of the Sagnac type
  50. Optimal interatomic potentials using modified method of least squares: Optimal form of interatomic potentials
  51. The soliton solutions for stochastic Calogero–Bogoyavlenskii Schiff equation in plasma physics/fluid mechanics
  52. Research on absolute ranging technology of resampling phase comparison method based on FMCW
  53. Analysis of Cu and Zn contents in aluminum alloys by femtosecond laser-ablation spark-induced breakdown spectroscopy
  54. Nonsequential double ionization channels control of CO2 molecules with counter-rotating two-color circularly polarized laser field by laser wavelength
  55. Fractional-order modeling: Analysis of foam drainage and Fisher's equations
  56. Thermo-solutal Marangoni convective Darcy-Forchheimer bio-hybrid nanofluid flow over a permeable disk with activation energy: Analysis of interfacial nanolayer thickness
  57. Investigation on topology-optimized compressor piston by metal additive manufacturing technique: Analytical and numeric computational modeling using finite element analysis in ANSYS
  58. Breast cancer segmentation using a hybrid AttendSeg architecture combined with a gravitational clustering optimization algorithm using mathematical modelling
  59. On the localized and periodic solutions to the time-fractional Klein-Gordan equations: Optimal additive function method and new iterative method
  60. 3D thin-film nanofluid flow with heat transfer on an inclined disc by using HWCM
  61. Numerical study of static pressure on the sonochemistry characteristics of the gas bubble under acoustic excitation
  62. Optimal auxiliary function method for analyzing nonlinear system of coupled Schrödinger–KdV equation with Caputo operator
  63. Analysis of magnetized micropolar fluid subjected to generalized heat-mass transfer theories
  64. Does the Mott problem extend to Geiger counters?
  65. Stability analysis, phase plane analysis, and isolated soliton solution to the LGH equation in mathematical physics
  66. Effects of Joule heating and reaction mechanisms on couple stress fluid flow with peristalsis in the presence of a porous material through an inclined channel
  67. Bayesian and E-Bayesian estimation based on constant-stress partially accelerated life testing for inverted Topp–Leone distribution
  68. Dynamical and physical characteristics of soliton solutions to the (2+1)-dimensional Konopelchenko–Dubrovsky system
  69. Study of fractional variable order COVID-19 environmental transformation model
  70. Sisko nanofluid flow through exponential stretching sheet with swimming of motile gyrotactic microorganisms: An application to nanoengineering
  71. Influence of the regularization scheme in the QCD phase diagram in the PNJL model
  72. Fixed-point theory and numerical analysis of an epidemic model with fractional calculus: Exploring dynamical behavior
  73. Computational analysis of reconstructing current and sag of three-phase overhead line based on the TMR sensor array
  74. Investigation of tripled sine-Gordon equation: Localized modes in multi-stacked long Josephson junctions
  75. High-sensitivity on-chip temperature sensor based on cascaded microring resonators
  76. Pathological study on uncertain numbers and proposed solutions for discrete fuzzy fractional order calculus
  77. Bifurcation, chaotic behavior, and traveling wave solution of stochastic coupled Konno–Oono equation with multiplicative noise in the Stratonovich sense
  78. Thermal radiation and heat generation on three-dimensional Casson fluid motion via porous stretching surface with variable thermal conductivity
  79. Numerical simulation and analysis of Airy's-type equation
  80. A homotopy perturbation method with Elzaki transformation for solving the fractional Biswas–Milovic model
  81. Heat transfer performance of magnetohydrodynamic multiphase nanofluid flow of Cu–Al2O3/H2O over a stretching cylinder
  82. ΛCDM and the principle of equivalence
  83. Axisymmetric stagnation-point flow of non-Newtonian nanomaterial and heat transport over a lubricated surface: Hybrid homotopy analysis method simulations
  84. HAM simulation for bioconvective magnetohydrodynamic flow of Walters-B fluid containing nanoparticles and microorganisms past a stretching sheet with velocity slip and convective conditions
  85. Coupled heat and mass transfer mathematical study for lubricated non-Newtonian nanomaterial conveying oblique stagnation point flow: A comparison of viscous and viscoelastic nanofluid model
  86. Power Topp–Leone exponential negative family of distributions with numerical illustrations to engineering and biological data
  87. Extracting solitary solutions of the nonlinear Kaup–Kupershmidt (KK) equation by analytical method
  88. A case study on the environmental and economic impact of photovoltaic systems in wastewater treatment plants
  89. Application of IoT network for marine wildlife surveillance
  90. Non-similar modeling and numerical simulations of microploar hybrid nanofluid adjacent to isothermal sphere
  91. Joint optimization of two-dimensional warranty period and maintenance strategy considering availability and cost constraints
  92. Numerical investigation of the flow characteristics involving dissipation and slip effects in a convectively nanofluid within a porous medium
  93. Spectral uncertainty analysis of grassland and its camouflage materials based on land-based hyperspectral images
  94. Application of low-altitude wind shear recognition algorithm and laser wind radar in aviation meteorological services
  95. Investigation of different structures of screw extruders on the flow in direct ink writing SiC slurry based on LBM
  96. Harmonic current suppression method of virtual DC motor based on fuzzy sliding mode
  97. Micropolar flow and heat transfer within a permeable channel using the successive linearization method
  98. Different lump k-soliton solutions to (2+1)-dimensional KdV system using Hirota binary Bell polynomials
  99. Investigation of nanomaterials in flow of non-Newtonian liquid toward a stretchable surface
  100. Weak beat frequency extraction method for photon Doppler signal with low signal-to-noise ratio
  101. Electrokinetic energy conversion of nanofluids in porous microtubes with Green’s function
  102. Examining the role of activation energy and convective boundary conditions in nanofluid behavior of Couette-Poiseuille flow
  103. Review Article
  104. Effects of stretching on phase transformation of PVDF and its copolymers: A review
  105. Special Issue on Transport phenomena and thermal analysis in micro/nano-scale structure surfaces - Part IV
  106. Prediction and monitoring model for farmland environmental system using soil sensor and neural network algorithm
  107. Special Issue on Advanced Topics on the Modelling and Assessment of Complicated Physical Phenomena - Part III
  108. Some standard and nonstandard finite difference schemes for a reaction–diffusion–chemotaxis model
  109. Special Issue on Advanced Energy Materials - Part II
  110. Rapid productivity prediction method for frac hits affected wells based on gas reservoir numerical simulation and probability method
  111. Special Issue on Novel Numerical and Analytical Techniques for Fractional Nonlinear Schrodinger Type - Part III
  112. Adomian decomposition method for solution of fourteenth order boundary value problems
  113. New soliton solutions of modified (3+1)-D Wazwaz–Benjamin–Bona–Mahony and (2+1)-D cubic Klein–Gordon equations using first integral method
  114. On traveling wave solutions to Manakov model with variable coefficients
  115. Rational approximation for solving Fredholm integro-differential equations by new algorithm
  116. Special Issue on Predicting pattern alterations in nature - Part I
  117. Modeling the monkeypox infection using the Mittag–Leffler kernel
  118. Spectral analysis of variable-order multi-terms fractional differential equations
  119. Special Issue on Nanomaterial utilization and structural optimization - Part I
  120. Heat treatment and tensile test of 3D-printed parts manufactured at different build orientations
Sign up now to receive a 20% welcome discount
Institutional Access
How does access work?
Have an idea on how to improve our website?
Please write us.
© 2025 De Gruyter Brill
Downloaded on 12.9.2025 from https://www.degruyterbrill.com/document/doi/10.1515/phys-2023-0164/html
Scroll to top button