New soliton solutions of modified (3+1)-D Wazwaz–Benjamin–Bona–Mahony and (2+1)-D cubic Klein–Gordon equations using first integral method

Shumaila Javeed; Tayyab Imran; Hijaz Ahmad; Fairouz Tchier; Yun-Hui Zhao

doi:10.1515/phys-2022-0229

Article Open Access

New soliton solutions of modified (3+1)-D Wazwaz–Benjamin–Bona–Mahony and (2+1)-D cubic Klein–Gordon equations using first integral method

Shumaila Javeed , Tayyab Imran , Hijaz Ahmad , Fairouz Tchier and Yun-Hui Zhao

Published/Copyright: March 30, 2023

Published by

Become an author with De Gruyter Brill

Submit Manuscript Author Information Explore this Subject

From the journal Open Physics Volume 21 Issue 1

Abstract

In this article, first integral method (FIM) is used to acquire the analytical solutions of (3+1)-D Wazwaz–Benjamin–Bona–Mahony and (2+1)-D cubic Klein–Gordon equation. New soliton solutions are obtained, such as solitons, cuspon, and periodic solutions. FIM is a direct method to acquire soliton solutions of nonlinear partial differential equations (PDEs). The proposed technique can be used for solving higher dimensional PDEs. FIM can be implemented to solve integrable and ion-integrable equations.

Keywords: first integral method; (3+1)-D WBBM equation; (2+1)-D cubic Klein–Gordon-equation

1 Introduction

Nonlinearity exists in various applications such as biology, physics, fluid dynamics, chemical, and process engineering. Various real-world phenomena can be studied by solving the nonlinear partial differential equations (PDEs) with the help of analytical solution. Researchers applied first integral method (FIM) for finding analytical solutions of nonlinear PDEs such as in refs [1–4].

Different accurate and efficient numerical methods already exist in the literature, but still finding analytical solutions is important. Analytical solutions provide the physical information about the physical behaviour of a system. Different analytical and numerical techniques have been applied for solving PDEs such as the Sardar-subequation method [5], the extended rational sine–cosine and rational sinh–cosh methods [6], the extended ( G ′ ∕ G 2 ) -expansion technique [7], the sine-Gordon expansion method [8], the inverse scattering transform [9], Hirota’s bilinear method [10], the sine–cosine method [11], the homotopy perturbation method [12], the homotopy analysis method [13,14], the variational iteration method [15–17], the extended tanh-function method [18], the exponential function method [19–22], and meshless methods [23–27]. Many researchers obtained analytical solution in the field of mechanical and thermal engineering [28–31].

Feng presented FIM for finding the soliton solutions of nonlinear PDEs [32]. The suggested algorithm is related to commutative algebra and ring theory. FIM is a direct mathematical method for acquiring soliton solutions of nonlinear PDEs. FIM have been implemented to solve both equations integrable and nonintegrable [33–37].

This study is new as we implemented FIM to the models, namely, variants of (3+1)-D Wazwaz–Benjamin–Bona–Mahony (WBBM) equations, and (2+1)-D cubic Klein–Gordon (CKG) equation, for the first time and obtained new analytical solutions. FIM can produce precise outcomes consisting of no arbitrary constants. In comparing with other methods, the selected algorithm has many benefits, for example, FIM provides exact and explicit solutions and avoids for complex calculations. In this work, we applied FIM to different variants of WBBM equation and CKG equation.

Firstly, we apply FIM to extract the solutions of variants of WBBM equation. The WBBM equation is

(1) ν t + ν x + ν ν x − ν x x t = 0

proposed in refs [22,38] and is used in modelling surface waves of long wave length in liquids. The modified form of WBBM equation is

(2) ν t + ν x + ν 2 ν x − ν x x t = 0 .

Moreover, it is realistic to study higher dimensional and different modification of Eq. (2). Three types of modifications of Eq. (2) are given as follows:

(3) ν t + ν x + ν 2 u y − ν x z t = 0 .

(4) ν t + ν z + ν 2 ν x − ν x y t = 0 .

(5) ν t + ν y + ν 2 ν z − ν x x t = 0 .

Secondly, we will extract the analytical solution of (2+1)-D CKG equation using the proposed method.

(6) v x x + v y y + v t t + α v + β v 3 = 0 .

In the quantum field theory, the Klein–Gordon equation is amongst the most significant mathematical models. Dispersive wave processes in relativistic physics are explained by this equation. Plasma physics and nonlinear optics are two more fields where it might be found. The solution of the Klein–Gordon equation was also extracted using the inverse scattering and Backlund-transformation method.

The following is the layout of this article. The procedure of FIM are discussed in Section 2. Analytical solutions of three variations of the WBBM equation and the Klein–Gordon equation are given in Section 3. Summary of the work is discussed in Section 4.

2 Procedure of FIM

Step 1: Consider a nonlinear PDE:

(7) E ( ν , ν x , ν t , ν x x , ν x t , … ) = 0 .

Using the following variable, the travelling wave solutions of Eq. (7) can be obtained.

(8) ζ = x − c t .

(9) ν ( x , t ) = ν ( ζ ) .

We make the following modifications as a result of this.

(10) ∂ ∂ x ( ⋅ ) = ∂ ∂ ζ ( ⋅ ) , ∂ ∂ t ( ⋅ ) = − c 2 ∂ ∂ ζ ( ⋅ ) , ∂ 2 ∂ x 2 ( ⋅ ) = ∂ 2 ∂ ζ 2 ( ⋅ ) , ∂ 2 ∂ t ∂ x ( ⋅ ) = − c 2 ∂ 2 ∂ ζ 2 ( ⋅ )

Eq. (10) changes the PDE (7) to an ODE:

(11) G ν , ∂ ν ∂ ζ , ∂ 2 ν ∂ ζ 2 , … = 0 .

Here, ν = ν ( ζ ) represents an unknown function.

Step 2: The solution of above mentioned ODE (c.f. Eq. (11)) is presented as follows:

(12) ν ( x , t ) = f ( ζ ) .

Furthermore, the following variable is introduced and the presented as follows:

(13) x ( ζ ) = f ( ζ ) , y ( ζ ) = ∂ f ( ζ ) ∂ ζ .

Step 3: Applying conditions of the aforementioned step, Eq. (11) can be transformed into a following system of ODEs:

(14) x ′ ( ζ ) = y ( ζ ) , y ′ ( ζ ) = F ( x ( ζ ) , y ( ζ ) ) .

The general solution of Eq. (14) can be acquired subject to the existence of the integral. The division theorem can be used to obtain first integral of Eq. (14), which reduces Eq. (11) to a first-order integrable ODE. Afterwards, the acquired equation is solved to obtain an analytical solution of Eq. (7).

Division theorem: Suppose that A ( ξ , ϖ ) and B ( ξ , ϖ ) are two polynomials in complex domain C ( ξ , ϖ ) , such that A ( ξ , ϖ ) represents an irreducible polynomial in C ( ξ , ϖ ) . If B ( ξ , ϖ ) vanishes all zeros of A ( ξ , ϖ ) , then a polynomial D ( ξ , ϖ ) exists in C ( ξ , ϖ ) such that

(15) B [ ξ , ϖ ] = A [ ξ , ϖ ] D [ ξ , ϖ ] .

3 The first integral method’s applications

3.1 (3+1)-D WBBM equation of type 1

3.1.1 (3+1)-D WBBM equation of type 1

Consider type 1 (3+1)-D WBBM equation:

(16) ν t + ν x + ν 2 ν y − ν x z t = 0 .

Applying the following transformation,

(17) ν ( x , y , z , t ) = ν ( ζ ) ζ = k x + λ y + μ z − c t .

Using Eqs. (16) and (17) leads to the subsequent ODE:

(18) ( k − c ) ν ′ + λ ν 2 ν ′ + k μ c ν ‴ = 0 .

Applying integration with respect to ζ , we have

(19) ν ″ = − k − c k μ c ν − λ 3 μ c k ν 3 .

Variables are defined as x = ν ( ζ ) and y = ν ′ ( ζ ) . Eq. (19) is identical to the autonomous system.

(20) d x d ζ = y d y d ζ = − k − c k μ c x − λ 3 μ c k x 3 .

Here, x ( ζ ) and y ( ζ ) are supposed to nontrivial solutions of Eq. (20). Moreover, irreducible polynomial is denoted by r ( x , y ) = ∑ m = 0 n e m ( x ) y m in C ; thus,

(21) r ( x ( ζ ) , y ( ζ ) ) = ∑ m = 0 n e m ( x ( ζ ) ) y ( ζ ) m = 0 .

Here, e m ( x ) , m = 0 , 1 , 2 … , n are polynomial of x and e n ( x ) ≠ 0 . Moreover, Eq. (21) is known as the first integral of Eq. (20). A polynomial such as, q ( x ) + l ( x ) y is obtained from division theorem.

(22) d r d ζ = ∂ r ∂ x ∂ x ∂ ζ + ∂ r ∂ y ∂ y ∂ ζ = [ q ( x ) + l ( x ) y ] ∑ m = 0 n e m ( x ) y m .

We obtain n = 1 from Eq. (21). Letting n = 1 for equalizing coefficients of y m ( m = 0 , 1 , 2 ) in Eq. (22), we obtain the following equations:

(23) e 1 ′ ( x ) = l ( x ) e 1 ( x ) ,

(24) e 0 ′ ( x ) = q ( x ) e 1 ( x ) + l ( x ) e 0 ( x ) ,

(25) q ( x ) e 0 ( x ) = e 1 ( x ) c − k k μ c x − λ 3 μ c k x 3 .

Here, e m ( x ) are polynomials of x . From Eq. (22), we obtain that e 1 ( x ) is a constant. As a result, l ( x ) = 0 . Furthermore, we suppose that e 1 ( x ) = 1 . Afterwards, balancing the degree of q ( x ) and e 0 ( x ) and utilizing these results lead to deg ( q ( x ) ) = 1 . Consider q ( x ) = A 1 x + B 0 , and Eq. (24) is re-written as follows:

(26) e 0 ( x ) = 1 2 A 1 x 2 + B 0 x + A 0 .

The solution of Eq. (25) is acquired using the values of e 0 ( x ) , q ( x ) , l ( x ) , and e 1 ( x ) . We acquire a system of nonlinear algebraic equations. The solution of obtained algebraic equations leads to the following constants.

Case i:

(27) B 0 = 0 , A 1 = − 2 λ 3 μ c k , A 0 = 3 k μ c − 2 λ c − k k μ c .

The following result is obtained: considering Eqs. (27) and (21):

(28) y 1 ( ζ ) = − − 2 λ 3 μ c k x 2 2 − 3 k μ c − 2 λ ( c − k ) k μ c .

By using Eqs. (28) and (20), the first solution of ( 3 + 1 ) -D WBBM equation of type 1 is obtained.

(29) ν 1 ( x , y , z , t ) = 3 ( c − k ) − λ tan c − k 2 k μ c ( k x + λ y + μ z − c t ) + ξ 0 .

Case ii: We obtain

(30) B 0 = 0 , A 1 = − − 2 λ 3 μ c k , A 0 = − 3 k μ c − 2 λ c − k k μ c .

The following result is acquired considering Eqs. (30) and (21).

(31) y 2 ( ζ ) = − 2 λ 3 μ c k x 2 2 + 3 k μ c − 2 λ ( c − k ) k μ c .

By using Eqs. (31) and (20), the second solution of (3+1)-D WBBM equation of type 1 is achieved.

(32) ν 2 ( x , y , z , t ) = − 3 ( c − k ) − λ tan × c − k 2 k μ c ( k x + λ y + μ z − c t ) + ξ 0 .

Figures 1, 2, 3 depict the graphical representation of the solution ν 1 ( x , y , z , t ) of the WBBM equation using different values of ν , k , λ , and c . These figures show that amplitude is decreasing towards left, right, or central position, and for large distance, these solitaires are asymptotically zero.

$Figure 1 Solution ν 1 ( x , y , z , t ) {\nu }_{1}\left(x,y,z,t) of first (3+1)-D WBBM equation at k = 3 k=3 , c = 2 c=2 , t = 1 t=1 , x = 1 x=1 , λ = 2 \lambda =2 , and μ = 1 \mu =1 .$

Figure 1

Solution ν 1 ( x , y , z , t ) of first (3+1)-D WBBM equation at k = 3 , c = 2 , t = 1 , x = 1 , λ = 2 , and μ = 1 .

$Figure 2 Solution ν 1 ( x , y , z , t ) {\nu }_{1}\left(x,y,z,t) of first (3+1)-D WBBM equation at k = 3 k=3 , c = 2 c=2 , y = 1 y=1 , x = 1 x=1 , λ = 2 \lambda =2 , and μ = 1 \mu =1 .$

Figure 2

Solution ν 1 ( x , y , z , t ) of first (3+1)-D WBBM equation at k = 3 , c = 2 , y = 1 , x = 1 , λ = 2 , and μ = 1 .

$Figure 3 Solution ν 1 ( x , y , z , t ) {\nu }_{1}\left(x,y,z,t) of first (3+1)-D WBBM equation at k = 3 k=3 , c = 2 c=2 , z = 1 z=1 , x = 1 x=1 , λ = 2 \lambda =2 , and μ = 1 \mu =1 .$

Figure 3

Solution ν 1 ( x , y , z , t ) of first (3+1)-D WBBM equation at k = 3 , c = 2 , z = 1 , x = 1 , λ = 2 , and μ = 1 .

3.2 (3+1)-D WBBM equation of type 2

3.2.1 (3+1)-D WBBM equation of type 2

Consider type 2 (3+1)-D WBBM equation:

(33) ν t + ν z + ν 2 ν x − ν x y t = 0 .

Applying the following transformation:

(34) ν ( x , y , z , t ) = ν ( ζ ) ζ = k x + λ y + μ z − c t .

Eq. (33) takes the subsequent form of ODE:

(35) ( μ − c ) ν ′ + k ν 2 ν ′ + k λ c ν ‴ = 0 .

By applying integration with respect to ζ , we have

(36) ν ″ = c − μ k λ c ν − k 3 λ c k ν 3 .

Introducing variables x = ν ( ζ ) and y = ν ′ ( ζ ) , Eq. (36) is identical to the autonomous system.

(37) d x d ζ = y , d y d ζ = c − μ k λ c x − k 3 λ c k x 3 .

Suppose that x ( ζ ) and y ( ζ ) represent nontrivial form of solutions of Eq. (37). Moreover, irreducible polynomial is denoted by r ( x , y ) = ∑ m = 0 n e m ( x ) y m in C ; thus,

(38) r ( x ( ζ ) , y ( ζ ) ) = ∑ m = 0 n e m ( x ( ζ ) ) y ( ζ ) m = 0 .

where e m ( x ) , m = 0 , 1 , 2 … , n represent polynomial of x and e n ( x ) ≠ 0 . Furthermore, Eq. (38) is a first integral of Eq. (37). Implementing division theorem on a polynomial such as, q ( x ) + l ( x ) y , leads to the subsequent results:

(39) d r d ζ = ∂ r ∂ x ∂ x ∂ ζ + ∂ r ∂ y ∂ y ∂ ζ = [ q ( x ) + l ( x ) y ] ∑ m = 0 n e m ( x ) y m .

By using Eq. (38), we obtain n = 1 . Equating coefficients of y m ( m = 0 , 1 , 2 ) into Eq. (39) and using n = 1 lead to the following equations:

(40) e 1 ′ ( x ) = l ( x ) e 1 ( x ) ,

(41) e 0 ′ ( x ) = q ( x ) e 1 ( x ) + l ( x ) e 0 ( x ) ,

(42) q ( x ) e 0 ( x ) = e 1 ( x ) c − μ k λ c x − k 3 λ c k x 3 .

Here, e j ( x ) are polynomials in x . From Eq. (40), e 1 ( x ) is a constant and l ( x ) = 0 . We assume that e 1 ( x ) = 1 . Balancing the degree of q ( x ) and e 0 ( x ) . After putting these values, we obtain that deg ( q ( x ) ) = 1 . Furthermore, q ( x ) = A 1 x + B 0 ; therefore, Eq. (41) gives,

(43) e 0 ( x ) = 1 2 A 1 x 2 + B 0 x + A 0 .

The solution of Eq. (42) is acquired by putting the values of e 0 ( x ) , q ( x ) , l ( x ) , and e 1 ( x ) . Finally, a system of algebraic equations is acquired. The solution of obtained algebraic equations leads to the following constants.

Case i:

(44) B 0 = 0 , A 1 = − 2 k 3 λ c k , A 0 = 3 k λ c − 2 k ( c − μ ) k λ c .

The following result is acquired considering Eqs. (44) and (38).

(45) y 1 ( ζ ) = − − 2 3 λ c x 2 2 − c − μ k λ c ( 3 λ c ) 2 .

By using Eqs. (45) and (37), the first solution of WBBM equation of type 2 is obtained.

(46) ν 1 ( x , y , z , t ) = 3 ( c − μ ) − k tan c − μ 2 k λ c ( k x + λ y + μ z − c t ) + ξ 0 .

Case ii:

(47) B 0 = 0 , A 1 = − − 2 k 3 λ c k , A 0 = − 3 k λ c − 2 k ( c − μ ) k λ c .

The following result is obtained by substituting Eq. (47) into Eq. (38).

(48) y 2 ( ζ ) = − 2 3 λ c x 2 2 + c − μ k λ c ( 3 λ c ) 2 .

Using Eqs. (48) and (37), the solution of (3+1)-Dim WBBM equation of type 2 is expressed as follows:

(49) ν 2 ( x , y , z , t ) = − 3 ( c − μ ) − k tan c − μ 2 k λ c ( k x + λ y + μ z − c t ) + ξ 0 .

Figures 4, 5, 6 show a graphs for the various values of μ , k , λ , and c in the function ν 1 ( x , y , z , t ) . These solitons are cuspons.

$Figure 4 Solution ν 1 ( x , y , z , t ) {\nu }_{1}\left(x,y,z,t) of second (3+1)-D WBBM equation at k = 3 k=3 , c = 2 c=2 , t = 1 t=1 , x = 1 x=1 , λ = 2 \lambda =2 , and μ = 1 \mu =1 .$

Figure 4

Solution ν 1 ( x , y , z , t ) of second (3+1)-D WBBM equation at k = 3 , c = 2 , t = 1 , x = 1 , λ = 2 , and μ = 1 .

$Figure 5 Solution ν 1 ( x , y , z , t ) {\nu }_{1}\left(x,y,z,t) of second (3+1)-D WBBM equation at k = 3 k=3 , c = 2 c=2 , y = 1 y=1 , x = 1 x=1 , λ = 2 \lambda =2 , and μ = 1 \mu =1 .$

Figure 5

Solution ν 1 ( x , y , z , t ) of second (3+1)-D WBBM equation at k = 3 , c = 2 , y = 1 , x = 1 , λ = 2 , and μ = 1 .

$Figure 6 Solution ν 1 ( x , y , z , t ) {\nu }_{1}\left(x,y,z,t) of second (3+1)-D WBBM equation at k = 3 k=3 , c = 2 c=2 , z = 1 z=1 , x = 1 x=1 , λ = 2 \lambda =2 , and μ = 1 \mu =1 .$

Figure 6

Solution ν 1 ( x , y , z , t ) of second (3+1)-D WBBM equation at k = 3 , c = 2 , z = 1 , x = 1 , λ = 2 , and μ = 1 .

3.3 The (3+1)-D WBBM equation of type 3

3.3.1 (3+1)-D WBBM equation of type 3

Consider type 3 (3+1)-D WBBM equation:

(50) ν t + ν y + ν 2 ν z − ν x x t = 0 .

Applying the following transformation:

(51) ν ( x , y , z , t ) = ν ( ζ ) ζ = k x + λ y + μ z − c t ,

Eq. (50) leads to the ODE as follows:

(52) ( λ − c ) ν + μ 3 ν 3 + k 2 c ν ‴ = 0 .

By applying integration with respect to ζ , we have

(53) ν ″ = c − λ k 2 c ν − μ 3 k 2 c ν 3 .

Introducing variables x = ν ( ζ ) and y = ν ′ ( ζ ) , Eq. (53) is identical to the autonomous system.

(54) d x d ζ = y , d y d ζ = c − λ k 2 c x − μ 3 k 2 c x 3 .

We suppose that x ( ζ ) and y ( ζ ) are nontrivial solutions of Eq. (54). Moreover, irreducible polynomial is denoted by r ( x , y ) = ∑ m = 0 n e m ( x ) y m in C ; thus,

(55) r ( x ( ζ ) , y ( ζ ) ) = ∑ m = 0 n e m ( x ( ζ ) ) y ( ζ ) m = 0 .

Here, e m ( x ) , m = 0 , 1 , 2 … , n are polynomial of x and e n ( x ) ≠ 0 . Moreover, Eq. (55) is a first integral of Eq. (54). Considering division theorem with q ( x ) + l ( x ) y leads to the following results:

(56) d r d ζ = ∂ r ∂ x ∂ x ∂ ζ + ∂ r ∂ y ∂ y ∂ ζ = [ q ( x ) + l ( x ) y ] ∑ m = 0 n e m ( x ) y m .

We suppose that n = 1 in Eq. (55). As n = 1 and equalizing coefficients of y m ( m = 0 , 1 , 2 ) in Eq. (56), the following equation is obtained.

(57) e 1 ′ ( x ) = l ( x ) e 1 ( x ) ,

(58) e 0 ′ ( x ) = q ( x ) e 1 ( x ) + l ( x ) e 0 ( x ) ,

(59) q ( x ) e 0 ( x ) = e 1 ( x ) c − λ k 2 c x − μ 3 k 2 c x 3 .

Here, e m ( x ) represent polynomials in x . From Eq. (57), we analyze that e 1 ( x ) is a constant. As a result, l ( x ) = 0 . Furthermore, e 1 ( x ) = 1 and balance the degree of q ( x ) and e 0 ( x ) , and after substituting these values, we obtain deg ( q ( x ) ) = 1 . Consider q ( x ) = A 1 x + B 0 , therefore Eq. (59) gives,

(60) e 0 ( x ) = 1 2 A 1 x 2 + B 0 x + A 0 .

By using values of e 0 ( x ) , q ( x ) , l ( x ) , and e 1 ( x ) , Eq. (59) is solved. By equating coefficients of x , we obtain a system of algebraic equations. By using the solutions of nonlinear algebraic equations, unknown constants are acquired. Case i:

(61) B 0 = 0 , A 1 = − 2 μ 3 k 2 c , A 0 = 3 k 2 c − 2 μ ( c − λ ) k 2 c .

Following results are acquired by substituting Eq. (61) into Eq. (55).

(62) y 1 ( ζ ) = − − 2 μ 3 k 2 c x 2 2 − 3 k 2 c − 2 k ( c − λ ) k 2 c .

By using Eqs. (62) and (54), the first solution of (3+1)-D WBBM equation is expressed as follows:

(63) ν 1 ( x , y , z , t ) = − 3 ( λ − c ) μ tan × c − λ 2 k 2 c ( k x + λ y + μ z − c t ) + ξ 0 .

Case ii:

(64) B 0 = 0 , A 1 = − − 2 μ 3 k 2 c , A 0 = − 3 k 2 c − 2 μ ( c − λ ) k 2 c .

By using Eqs. (64) and (55), the following results are obtained.

(65) y 2 ( ζ ) = − 2 μ 3 k 2 c x 2 2 + 3 k 2 c − 2 k c − λ k 2 c .

By using Eqs. (65) and (54), the second solution of (3+1)-D WBBM equation of type 3 is expressed as follows:

(66) ν 2 ( x , y , z , t ) = 3 ( λ − c ) μ tan × c − λ 2 k 2 c ( k x + λ y + μ z − c t ) + ξ 0 .

Figures 7, 8, 9 presents the solution ( ν 1 ( x , y , z , t ) ) of WBBM equation considering values of μ , k , λ , and c . These figures show kink soliton solutions.

$Figure 7 Solution ν 1 ( x , y , z , t ) {\nu }_{1}\left(x,y,z,t) of third (3+1)-D WBBM equation at k = 3 k=3 , c = 2 c=2 , t = 1 t=1 , x = 1 x=1 , λ = 3 \lambda =3 , and μ = 1 \mu =1 .$

Figure 7

Solution ν 1 ( x , y , z , t ) of third (3+1)-D WBBM equation at k = 3 , c = 2 , t = 1 , x = 1 , λ = 3 , and μ = 1 .

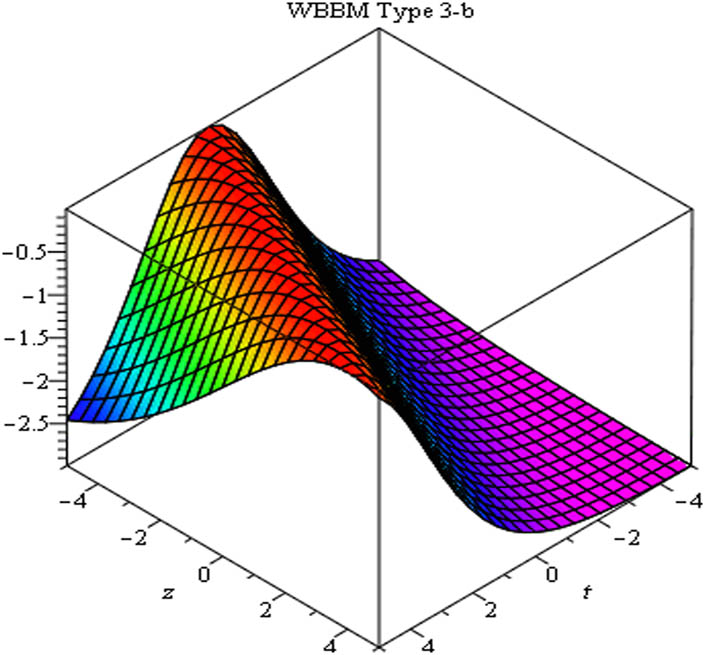
$Figure 8 Solution ν 1 ( x , y , z , t ) {\nu }_{1}\left(x,y,z,t) of third (3+1)-D WBBM equation at k = 3 k=3 , c = 2 c=2 , y = 1 y=1 , x = 1 x=1 , λ = 3 \lambda =3 , and μ = 1 \mu =1 .$

Figure 8

Solution ν 1 ( x , y , z , t ) of third (3+1)-D WBBM equation at k = 3 , c = 2 , y = 1 , x = 1 , λ = 3 , and μ = 1 .

$Figure 9 Solution ν 1 ( x , y , z , t ) {\nu }_{1}\left(x,y,z,t) of third (3+1)-D WBBM equation at k = 3 k=3 , c = 2 c=2 , z = 1 z=1 , x = 1 x=1 , λ = 3 \lambda =3 , and μ = 1 \mu =1 .$

Figure 9

Solution ν 1 ( x , y , z , t ) of third (3+1)-D WBBM equation at k = 3 , c = 2 , z = 1 , x = 1 , λ = 3 , and μ = 1 .

3.4 The ( 2 + 1 ) -D CKG equation

Consider ( 2 + 1 ) -D CKG equation:

(67) v x x + v y y − v t t + α v + β v 3 = 0 .

The following transformations are used.

(68) v ( x , y , t ) = v ( ζ ) , ζ = x + y − λ t .

Here, λ represents a constant. Using Eqs. (68), (67) leads to the ODE as follows:

(69) ( 2 − λ 2 ) v ″ + α v + β v 3 = 0 .

By applying integration with respect to ζ , we have

(70) ν ″ = − α 2 − λ 2 v − β 2 − λ 2 v 3 .

Introducing new variables x = ν ( ζ ) and y = ν ′ ( ζ ) , Eq. (70) is identical to the autonomous system.

(71) d x d ζ = y , d y d ζ = − α 2 − λ 2 x − β 2 − λ 2 x 3 .

We suppose that x ( ζ ) and y ( ζ ) are nontrivial solutions of Eq. (71). Moreover, irreducible polynomial is denoted by r ( x , y ) = ∑ m = 0 n e m ( x ) y m in complex domain C ( x , y ) ; thus,

(72) r ( x ( ζ ) , y ( ζ ) ) = ∑ m = 0 n e m ( x ( ζ ) ) y ( ζ ) m = 0 .

Here, e m ( x ) , m = 0 , 1 , 2 … , n denote polynomial in x and e n ( x ) ≠ 0 . Moreover, Eq. (72) is a first integral of Eq. (71). Division theorem and a polynomial q ( x ) + l ( x ) y as follows:

(73) d r d ζ = ∂ r ∂ x ∂ x ∂ ζ + ∂ r ∂ y ∂ y ∂ ζ = [ q ( x ) + l ( x ) y ] ∑ m = 0 n e m ( x ) y m .

We assume that n = 1 in Eq. (72). Suppose n = 1 and equating coefficients of y m ( m = 0 , 1 , 2 ) in Eq. (73), we obtain the following equations:

(74) e 1 ′ ( x ) = l ( x ) e 1 ( x ) ,

(75) e 0 ′ ( x ) = q ( x ) e 1 ( x ) + l ( x ) e 0 ( x ) ,

(76) q ( x ) e 0 ( x ) = e 1 ( x ) − α 2 − λ 2 x − β 2 − λ 2 x 3 .

Here, e m ( x ) represents polynomials in x . From Eq. (74), we analyze that e 1 ( x ) is a constant leads to l ( x ) = 0 . We further assume that e 1 ( x ) = 1 . Balancing the degree of q ( x ) and e 0 ( x ) , we conclude deg ( q ( x ) ) = 1 . Take q ( x ) = A 1 x + B 0 , therefore Eq. (76) gives,

(77) e 0 ( x ) = 1 2 A 1 x 2 + B 0 x + A 0 .

By using the values of e 0 ( x ) , q ( x ) , l ( x ) , and e 1 ( x ) , Eq. (76) is solved. Finally, a system of nonlinear algebraic equations are obtained. By solving the acquired system of equations, unknown constant values are obtained.

Case i:

(78) A 1 = − 2 β 2 − λ 2 , B 0 = 0 , A 0 = − α 2 − λ 2 ( 2 − λ 2 ) − 2 β .

Following results are obtained using Eqs. (78) and (72).

(79) y 1 ( ζ ) = − − 2 β 2 − λ 2 x 2 2 − 2 − λ 2 − 2 β ( − α ) 2 − λ 2 .

By using Eqs. (79) and (71), we obtain the first solution of CKG equation and is expressed as follows:

(80) ν 1 ( x , y , t ) = − α β ( 2 − λ 2 ) tan × − α 2 − λ 2 ( x + y − λ t ) + ξ 0 .

Case ii:

(81) B 0 = 0 , A 1 = − − 2 β 2 − λ 2 , A 0 = − − α 2 − λ 2 ( 2 − λ 2 ) − 2 β .

The following results are obtained using Eqs. (78) and (72).

(82) y 2 ( ζ ) = − 2 β 2 − λ 2 x 2 2 + 2 − λ 2 − 2 β ( − α ) 2 − λ 2 .

By using Eqs. (82) and (71), the second solution of CKG equation solution is presented as follows:

(83) ν 2 ( x , y , t ) = α β ( 2 − λ 2 ) tan − α 2 − λ 2 ( x + y − λ t ) + ξ 0 .

Figure 10 displays the solution function ν 1 ( x , y , z , t ) considering the values of α , β , and λ . Figure 10 displays kink-type of solutions. Solitary wave solutions for WBBM type 1 and cuspons for WBBM type 2 were obtained. Solitons and kink-type solutions of WBBM type 3 and the (2+1)-D CKG equation are obtained. All presented soliton solutions satisfy their respective models.

$Figure 10 Solution ν 1 ( x , y , t ) {\nu }_{1}\left(x,y,t) of (2+1)-D CKG equation using t = 1 t=1 , β = 1 \beta =1 , λ = 1 \lambda =1 , and α = 2 \alpha =2 .$

Figure 10

Solution ν 1 ( x , y , t ) of (2+1)-D CKG equation using t = 1 , β = 1 , λ = 1 , and α = 2 .

4 Conclusion

The solutions of nonlinear (3+1)-D WBBM and (2+1)-D CKG equation were obtained using FIM. New solitary wave solutions for WBBM type 1 and cuspons for WBBM type 2 were obtained. Solitons and kink-type solutions were acquired for WBBM type 3 and the (2+1)-D CKG equations, respectively. The suggested method allows us to easily conduct tedious and difficult algebraic computations with the assistance of a computer. FIM is a straightforward and concise method and capable of solving nonlinear system arises in mathematical physics and engineering.

Funding information: This study was supported by Project Number (RSP2023R401), King Saud University, Riyadh, Saudi Arabia.
Author contributions: All authors have accepted responsibility for the entire content of this manuscript and approved its submission.
Conflict of interest: The authors state no conflict of interest.

References

[1] Ahmad I, Khan MN, Inc M, Ahmad H, Nisar KS. Numerical simulation of simulate an anomalous solute transport model via local meshless method. Alexandr Eng J. 2020;59(14):2827–38. 10.1016/j.aej.2020.06.029Search in Google Scholar

[2] Wang F, Ahmad I, Ahmad H, Alsulami MD, Alimgeer KS, Cesarano C, et al. Meshless method based on RBFS for solving three-dimensional multi-term time fractional PDEs arising in engineering phenomenons. J King Saud Univ-Sci. 2021;33(8):101604. 10.1016/j.jksus.2021.101604Search in Google Scholar

[3] Liu X, Ahsan M, Ahmad M, Nisar M, Liu X, Ahmad I, et al. Applications of Haar wavelet-finite difference hybrid method and its convergence for hyperbolic nonlinear Schrödinger equation with energy and mass conversion. Energies. 2021;14(23):7831. 10.3390/en14237831Search in Google Scholar

[4] Ahmad I, Ahmad H, Abouelregal AE, Thounthong P, Abdel-Aty M. Numerical study of integer-order hyperbolic telegraph model arising in physical and related sciences. Europ Phys J Plus. 2020;135(9):1–14. 10.1140/epjp/s13360-020-00784-zSearch in Google Scholar

[5] Rezazadeh H, Inc M, Baleanu D. New solitary wave solutions for variants of (3+1)-dimensional Wazwaz-Benjamin-Bona-Mahony equations. Front Phys. 2020;8:332. 10.3389/fphy.2020.00332Search in Google Scholar

[6] Vahidi J, Zekavatmand SM, Rezazadeh H, Inc M, Akinlar MA, Chu YM. New solitary wave solutions to the coupled Maccarias system. Results Phys. 2021;21:103801. 10.1016/j.rinp.2020.103801Search in Google Scholar

[7] Jhangeer A, Rezazadeh H, Seadawy A. A study of travelling, periodic, quasiperiodic and chaotic structures of perturbed Fokas-Lenells model. Pramana. 2021;95(1):1–11. 10.1007/s12043-020-02067-9Search in Google Scholar

[8] Kallel W, Almusawa H, Mirhosseini-Alizamini SM, Eslami M, Rezazadeh H, Osman MS. Optical soliton solutions for the coupled conformable Fokas-Lenells equation with spatio-temporal dispersion. Results Phys. 2021;26:104388. 10.1016/j.rinp.2021.104388Search in Google Scholar

[9] Zhang X, Chen Y. Inverse scattering transformation for generalized nonlinear Schrödinger equation. Appl Math Lett. 2019;98:306–13. 10.1016/j.aml.2019.06.014Search in Google Scholar

[10] Hirota R. The direct method in soliton theory. No. 155. United Kingdom: Cambridge University Press; 2004. 10.1017/CBO9780511543043Search in Google Scholar

[11] Yusufoğlu E, Bekir A, Alp M. Periodic and solitary wave solutions of Kawahara and modified Kawahara equations by using sine–cosine method. Chaos Soliton Fractal. 2008;37(4):1193–7. 10.1016/j.chaos.2006.10.012Search in Google Scholar

[12] Dehghan M, Manafian J. The solution of the variable coefficients fourth-order parabolic partial differential equations by the homotopy perturbation method. Zeitschrift für Naturforschung A. 2009;64(7–8):420–30. 10.1515/zna-2009-7-803Search in Google Scholar

[13] Wang F, Ali SN, Ahmad I, Ahmad H, Alam KM, Thounthong P. Solution of Burgers’ equation appears in fluid mechanics by multistage optimal homotopy asymptotic method. Thermal Sci. 2022;26(1 Part B):815–21. 10.2298/TSCI210302343WSearch in Google Scholar

[14] Ali SN, Ahmad I, Abu-Zinadah H, Mohamed KK, Ahmad H. Multistage optimal homotopy asymptotic method for the K (2, 2) equation arising in solitary waves theory. Thermal Sci. 2021;25(Spec. issue 2):199–205. 10.2298/TSCI21S2199ASearch in Google Scholar

[15] Anjum N, He JH. Laplace transform: making the variational iteration method easier. Appl Math Lett. 2019;92:134–8. 10.1016/j.aml.2019.01.016Search in Google Scholar

[16] Ahmad H, Khan TA, Ahmad I, Stanimirović PS, Chu YM. A new analyzing technique for nonlinear time fractional Cauchy reaction-diffusion model equations. Results Phys. 2020;19:103462. 10.1016/j.rinp.2020.103462Search in Google Scholar

[17] Ahmad H, Khan TA, Stanimirović PS, Chu YM, Ahmad I. Modified variational iteration algorithm-II: convergence and applications to diffusion models. Complexity. 2020;2020:1–14. 10.1155/2020/8841718Search in Google Scholar

[18] Fan E. Extended tanh-function method and its applications to nonlinear equations. Phys Lett A. 2000;277(4):212–8. 10.1016/S0375-9601(00)00725-8Search in Google Scholar

[19] He JH, Wu XH. Exp-function method for nonlinear wave equations. Chaos Solitons Fractal. 2006;30(3):700–8. 10.1016/j.chaos.2006.03.020Search in Google Scholar

[20] Heris JM, Bagheri M Exact solutions for the modified KdV and the generalized KdV equations via exp-function method. J Math Extension. 2020;4(2):75–95.Search in Google Scholar

[21] Javeed S, Baleanu D, Nawaz S, Rezazadeh H. Soliton solutions of nonlinear Boussinesq models using the exponential function technique. Phys Scr. 2021;96(10):105209. 10.1088/1402-4896/ac0e01Search in Google Scholar

[22] Javeed S, Saleem Alimgeer K, Nawaz S, Waheed A, Suleman M, Baleanu D, et al. Soliton solutions of mathematical physics models using the exponential function technique. Symmetry. 2020;12(1):176. 10.3390/sym12010176Search in Google Scholar

[23] Ahmad I, Ahsan M, Elamin AEA, Abdel-Khalek S, Inc M. Numerical simulation of 3-D Sobolev equation via local meshless method. Thermal Sci. 2022;26(Spec. issue 1):457–62. 10.2298/TSCI22S1457ASearch in Google Scholar

[24] Ahmad I, Abdel-Khalek S, Alghamdi AM, Inc M. Numerical simulation of the generalized Burger’s-Huxley equation via two meshless methods. Thermal Sci. 2022;26(Spec. issue 1):463–8. 10.2298/TSCI22S1463ASearch in Google Scholar

[25] Wang F, Hou E, Ahmad I, Ahmad H, Gu Y. An efficient meshless method for hyperbolic telegraph equations in (1+1) dimensions. Comput Model Eng Sci. 2021;128(2):687–98. 10.32604/cmes.2021.014739Search in Google Scholar

[26] Ahmad I, Seadawy AR, Ahmad H, Thounthong P, Wang F. Numerical study of multi-dimensional hyperbolic telegraph equations arising in nuclear material science via an efficient local meshless method. Int J Nonlinear Sci Numer Simulat. 2022;23(1):115–22. 10.1515/ijnsns-2020-0166Search in Google Scholar

[27] Wang F, Zhang J, Ahmad I, Farooq A, Ahmad H. A novel meshfree strategy for a viscous wave equation with variable coefficients. Front Phys. 2021;9:701512. 10.3389/fphy.2021.701512Search in Google Scholar

[28] Samadi H, Mohammadi NS, Shamoushaki M, Asadi Z, Ganji DD. An analytical investigation and comparison of oscillating systems with nonlinear behavior using AGM and HPM. Alexandr Eng J. 2022;61(11):8987–96. 10.1016/j.aej.2022.02.036Search in Google Scholar

[29] Hosseinzadeh S, Hosseinzadeh K, Hasibi A, Ganji DD. Hydrothermal analysis on non-Newtonian nanofluid flow of blood through porous vessels. Proceedings of the Institution of Mechanical Engineers, Part E: Journal of Process Mechanical Engineering. 2022;236(4):1604–15.10.1177/09544089211069211Search in Google Scholar

[30] Alaraji A, Alhussein H, Asadi Z, Ganji DD. Investigation of heat energy storage of RT26 organic materials in circular and elliptical heat exchangers in melting and solidification process. Case Stud Thermal Eng. 2021;28:101432. 10.1016/j.csite.2021.101432Search in Google Scholar

[31] Hosseinzadeh S, Hosseinzadeh K, Hasibi A, Ganji DD. Thermal analysis of moving porous fin wetted by hybrid nanofluid with trapezoidal, concave parabolic and convex cross sections. Case Stud Thermal Eng. 2022;30:101757. 10.1016/j.csite.2022.101757Search in Google Scholar

[32] Feng ZS. The first integral method to study the Burgers-Korteweg-de Vries equation. J Phys A Math Gen. 2002;35(2):343–9. 10.1088/0305-4470/35/2/312Search in Google Scholar

[33] Javeed S, Abbasi MA, Imran T, Fayyaz R, Ahmad H, Botmart T. New soliton solutions of simplified modified Camassa Holm equation, Klein-Gordon-Zakharov equation using first integral method and exponential function method. Results Phys. 2022;38:105506. 10.1016/j.rinp.2022.105506Search in Google Scholar

[34] Lu B. The first integral method for some time fractional differential equations. J Math Anal Appl. 2012;395(2):684–93. 10.1016/j.jmaa.2012.05.066Search in Google Scholar

[35] Mirzazadeh M, Eslami M. Exact solutions of the Kudryashov-Sinelshchikov equation and nonlinear telegraph equation via the first integral method. Nonlinear Anal Model Control. 2012;17(4):481–8. 10.15388/NA.17.4.14052Search in Google Scholar

[36] Taghizadeh N, Mirzazadeh M, Farahrooz F. Exact solutions of the nonlinear Schrodinger equation by the first integral method. J Math Anal Appl. 2011;374(2):549–53. 10.1016/j.jmaa.2010.08.050Search in Google Scholar

[37] Feng Z, Wang X. The first integral method to the two-dimensional Burgers-Korteweg-de Vries equation. Phys Lett A. 2003;308(2):173–8. 10.1016/S0375-9601(03)00016-1Search in Google Scholar

[38] Wu XHB, He JH. Exp-function method and its application tononlinear equations. Chaos Soliton Fractal. 2008;38(3):903–10. 10.1016/j.chaos.2007.01.024Search in Google Scholar

Received: 2021-10-31

Revised: 2023-01-09

Accepted: 2023-01-20

Published Online: 2023-03-30

This work is licensed under the Creative Commons Attribution 4.0 International License.

Articles in the same Issue

https://doi.org/10.1515/phys-2022-0229

Keywords for this article

first integral method; (3+1)-D WBBM equation; (2+1)-D cubic Klein–Gordon-equation

Creative Commons

BY 4.0