Abstract
This article features the buoyancy-driven electro-magnetohydrodynamic micropolar nanomaterial flow subjected to motile microorganisms. The flow is engendered via an elongating surface, and the energy relation includes heat source generation, magnetohydrodynamics, and radiation. A Buongiorno nanomaterial model (which includes thermophoretic and Brownian diffusions) together with chemical reaction and bioconvection aspects is pondered. The nonlinear governing expressions are transfigured into a dimensionless system, and the dimensionless expressions are computed using the numerical differential-solve scheme. Graphical analyses are conducted to examine the liquid flow, microrotation velocity, microorganism concentration, and temperature in relation to secondary variables. It is observed that a higher Hartman number has an opposite influence on temperature and velocity profiles. A rise in material variables engenders a decline in microrotation velocity. The temperature is enhanced through radiation. The concentration shows conflicting trends for both thermophoretic and random factors. The presence of motile microorganisms reduces the bioconvection Lewis and Peclet numbers.
1 Introduction
In recent times, the inspection of micropolar materials has been remarkable because of its abundant engineering and industrials usages like cervical flows, radial diffusive paint rheology, colloids, and thrust bearing technologies. A micropolar model captures translation along with rotational motions of fluid particles. It has distinct real-world usages in biological fluids and microorganisms (e.g., cilia motion, flagella, and other microorganisms in biological systems), lubrication and bearings (the micropolar model can be applied to evaluate the characteristics of lubricants in bearings and other mechanical components, where the rotational movements of fluid particles play a noteworthy role in the overall fluid dynamics), suspensions and colloidal systems (in suspensions of particles or colloidal systems, the micropolar model can provide insights into the interactions between particles, comprising both translational and rotational aspects), advanced materials processing (understanding micropolar fluid behavior can be beneficial in processes encompassing advanced materials, for illustration composite manufacturing along with additive printing, where the accurate mechanism of fluid flows is essential) and astrophysical fluids (the micropolar model can be utilized in astrophysics to scrutinize the fluid behavior in celestial bodies and space environments). The Naiver–Stokes’ equation that has only a drastic limitation does not adequately describe (by definition) the flow properties for fluids with microstructure. The hypothesis of micropolar material was first given by Eringen [1,2], dealing with fluids that unveil microscopic characteristics appearing from local structure and fundamental motion of liquid elements. The micropolar material is non-Newtonian liquid containing a suspension of small body liquid and colloidal liquid particles like giant dumbbell molecules. Solutal and heat transport analyses for magnetized micropolar liquid flow considering dissipation toward a stretchable wall are elaborated by Saidulu and Reddy [3]. They computed numeric outcomes and found an increment in temperature subjected to higher Eckert number values, while concentration declines with higher Schmidt number values. Kumar et al. [4] investigated the entropy feature for micropolar nanomaterial flow subject to Ohmic heating. They utilized a homotopic scheme for nonlinear analysis. They further reported a rise in angular velocity for the increasing squeezed factor. Magneto-hydrodynamic impact in micropolar nanomaterial flow considering thermal analysis subject to stretchable permeable medium is illuminated by Bilal et al. [5]. They employed the Shooting algorithm for numerical outcomes. Their findings indicate a decline in micro-rotational velocity when the magnetic (Hartman) factor is augmented. Shahzad et al. [6] reported the radiating bioconvective flow of nanomaterial subject to Darcy–Forchheimer rotating disks and generalized heat-mass fluxes. They obtained numeric results through the bvp4c algorithm. The nanoparticle concentration is enlarged when the thermophoresis factor is enlarged. Activation energy characteristics for micropolar material flow featuring varying fluid (viscosity) and thermal (temperature-dependent conductivity) aspects are demonstrated by Saraswathy et al. [7]. They utilized a response surface scheme for solution development. They reported a rise in shear-stress and couple-stress subjected to the increasing viscosity variation factor. Thermal aspects of magnetized flow Williamson micropolar material subject to non-Darcy permeable surface are illustrated by Mishra et al. [8]. They utilized the Runge–Kutta algorithm for computational results. They witnessed a reduction in material velocity against non-Darcian and magnetic factors. Bian et al. [9], Zhang et al. [10], and Yang et al. [11] scrutinized the dynamics of bio-inspired magneto-responsive hybrid type microstructure materials, formulation of a sandwich micro-shell and electromagnetic interference shielding, and electrical performance, respectively. Few important analyses regarding non-Newtonian fluid flow are demonstrated in previous studies [12–15].
A living thing that is so small can be seen only through a microscope. Microorganisms consist of algae, fungi, and bacteria. It helps in processing food digestion, antibiotic development, cleansing environment, farming, nitrogen cycle, and also in the fixation of nitrogen. Bioconvection phenomenon appears due to swimming of motile microorganisms in a liquid. Microorganisms perform incredibly an influential task in the development of pharmaceuticals, engine cooling, agricultural and industrials processes such as biotechnology fields, biofuel, biomedicine, biofertilizers, and bioconvective secondary metabolites. Motile microorganisms have a vital role in biotechnology, medical sciences, micro-systems, micro-fluidic techniques, and many others. One of the most important microorganisms (algae) has the ability to produce more rapid biomass, which can be converted into biodiesel and biofuel [16]. To investigate particular characteristics of these microorganisms in the literature, numerous struggles have been done. Kuznetsov [17] reported the bioconvective flow of nanomaterial containing motile microorganisms considering random and thermophoretic diffusions. He acquired perturbed solutions for nonlinear mathematical expressions and declared that the presence of nanoparticles upsurges the critical Rayleigh factor by a considerable quantity. Avramenko et al. [18] illustrated the magnetized bioconvective flow of viscous liquid including motile microorganisms. They used a Lorenz procedure and reported the bioconvective flow instability. According to them, when the Schmidt number exceeds 8, then variations in viscosity or diffusion exert a more pronounced influence on the oscillations than the microorganism-specific shape. An impact of the Marangoni convective radiating flow of the Williamson nanoliquid containing microorganisms subjected to moving surface is illustrated by Kairi et al. [19]. They applied the Runge–Kutta–Fehlberg algorithm and computed numeric outcomes. They noted a decline in heat–mass transfer rates when the material variable is enlarged. Aziz et al. [20] highlighted features of motile microorganisms with the suspension of nanoparticles in the viscous fluid flow. They computed numerical results and reported that the buoyancy factor has a noteworthy influence on dimensionless physical quantities. Ghachem et al. [21] highlighted features of heat source in bio-convective dissipative flow of nanoliquid considering convective condition. Here, the nonlinear expressions are computed numerically through the shooting scheme. The consideration of convective along with slip boundary constraints effectually improved the transference phenomenon. Zhang et al. [22] examined micro-structural and mechanical characteristics of alkali-activated nanocomposites. Xu et al. [23], Zheng et al. [24], and Hu et al. [25] recently explored the behavior of bio-mimetic nanomaterials as fluorescent sensors, dielectric barrier discharge plasma actuator, and hybrid liquid flow with the multiphysics coupling model. Few important investigations about gyrotactic microorganism and other flow assumptions are presented in previous studies [26–31].
Nanofluids are deployed to intensify the thermal transportation phenomenon of base liquid that leads to enhance the heat transfer coefficient. They have many biomedical and engineering applications in cancer therapy, cooling industry, and process industry. Enhancement in thermal conductivity increases the performance of thermal systems. In some cases, specific heat capacity of nanofluid declines with the addition of nanoparticles in the base fluid. Nanofluids represent those fluids that contains nanometer-sized particles. The nanoparticles have exceptionally smaller size or similar to coherent or de Brogile waves. Due to this phenomenon, nanoparticles exhibit behaviors akin to energy materials. Their size should be in the range of 1–100 nm. These particles are utilized to upsurge or decline the heat transference. In recent times, scientists have been increasingly captivated by nanoliquids owing to their crucial thermal properties. Enhancing the thermal efficiency of their transport stands is one of the several applications of such substances. Nanoliquids can be applied in vehicle cooling, nanowires, artificial intelligence, fuel cells, radiotherapy, brain tumors, inorganic lungs, nanofibers, surgery, pharmaceutical processes, engine cooling, electronic chilling system, cancer therapy, domestic refrigerators, and radiators. Choi et al. [32,33] introduced the concept of nanofluids. In his work, he delved into the nanomaterial thermal conductivity. Buongiorno [34] presented the concept of thermal conduction improvement of liquid. The Buongiorno model offers a comprehensive framework to study the behavior of nanofluids by considering interactions between the base materials and dispersed nanoparticles. It provides insights into heat transfer and fluid dynamics in nanofluid-based systems, impacting a range of practical applications. Kalpana et al. [35] highlighted the magnetohydrodynamic time-dependent flow of the nanomaterial subject to thermophoresis and random diffusions. They utilized the finite difference algorithm, quasilinear approach, and Thomas scheme for simulation. Significant findings reveal that increasing the wavy wall amplitude has a noticeable impact on flow. Few related studies regarding nanofluid are presented in previous studies [36–45].
In this study, the subsequent dimensionless couple systems are calculated numerically via numerical differential (ND)-solve technique. Features of liquid flow, concentration, microrotation velocity, motile microorganisms, and temperature against emerging variables are graphically analyzed.
2 Constitutive relations
The fundamental expressions governing the micropolar fluid are as follows [46]:
where
The aforementioned expressions yield [46]:
3 Formulation
Here, electromagnetohydrodynamics two-dimensional bioconvection flow of micropolar nanomaterial containing microorganisms toward a stretched wall is considered. Boungiorno’s model is deployed to inspect the nanofluid significance by thermophoretic and random diffusions. Heat generation, chemical reaction, Ohmic heating, and radiation are taken into account. Uniform electric

Schematic flow analysis.
The related equations subjected to considered rheological characteristics are as follows [47]:
with the following conditions [47]:
Here,
Letting [47]:
Finally, we have
In the aforementioned expressions,
4 Engineering quantities
4.1 Heat transference rate (Nusselt number)
The heat-transference rate is given by [38]:
where heat flux
A dimensionless form is given by
4.2 Mass transference rate (Sherwood number)
The Sherwood number is given by [38]:
The mass flux
A nondimensional form is given by
5 Numerical computation
This section provides an overview of the numerical techniques used in this study. The computational approach employed in this investigation utilizes the ND-solve method, a boundary value problem solver implemented in MATHEMATICA. This method, also known as the “Shooting” method, is specifically designed for solving various flow problems (e.g., Navier–Stokes expressions) under distinct conditions. The governing mathematical expressions expressed in a nondimensional mathematical form are developed from Navier–Stokes expressions. To effectually compute such nonlinear expressions, the “shooting” method employs a series of carefully selected similarity transformations. These transformations allow for the manipulation and the solution of governing flow rheological expressions in a more efficient manner.
In this study, a crucial step in the transformation process involves converting the coupled systems (i.e., Eqs. (21)–(26)) into first-order mathematical systems via transformations. This conversion from higher-order mathematical expressions to first-order mathematical one simplifies the problem and makes it more well suited with the deployed numerical schemes. The interpretation of these novel transformational mathematical systems is described in detail below.
with
6 Analysis
This section elaborates nondimensional parameters impact on dimensionless parameters such as velocity
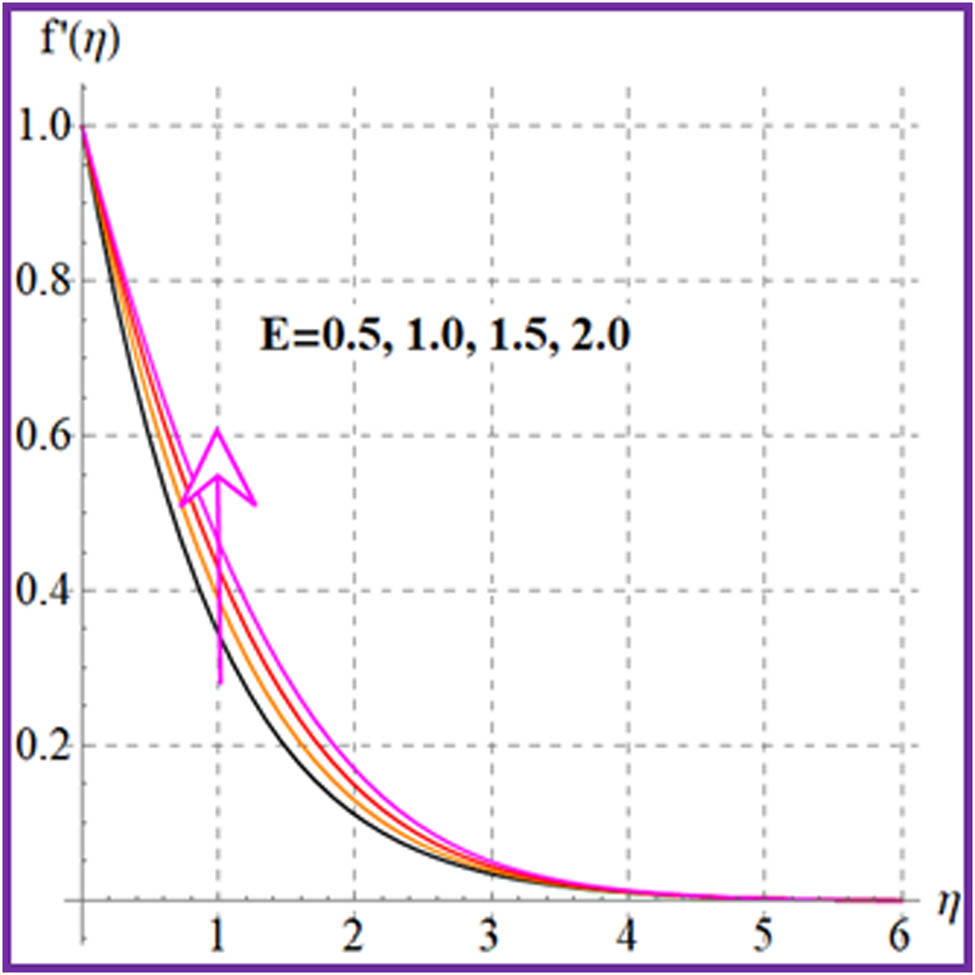




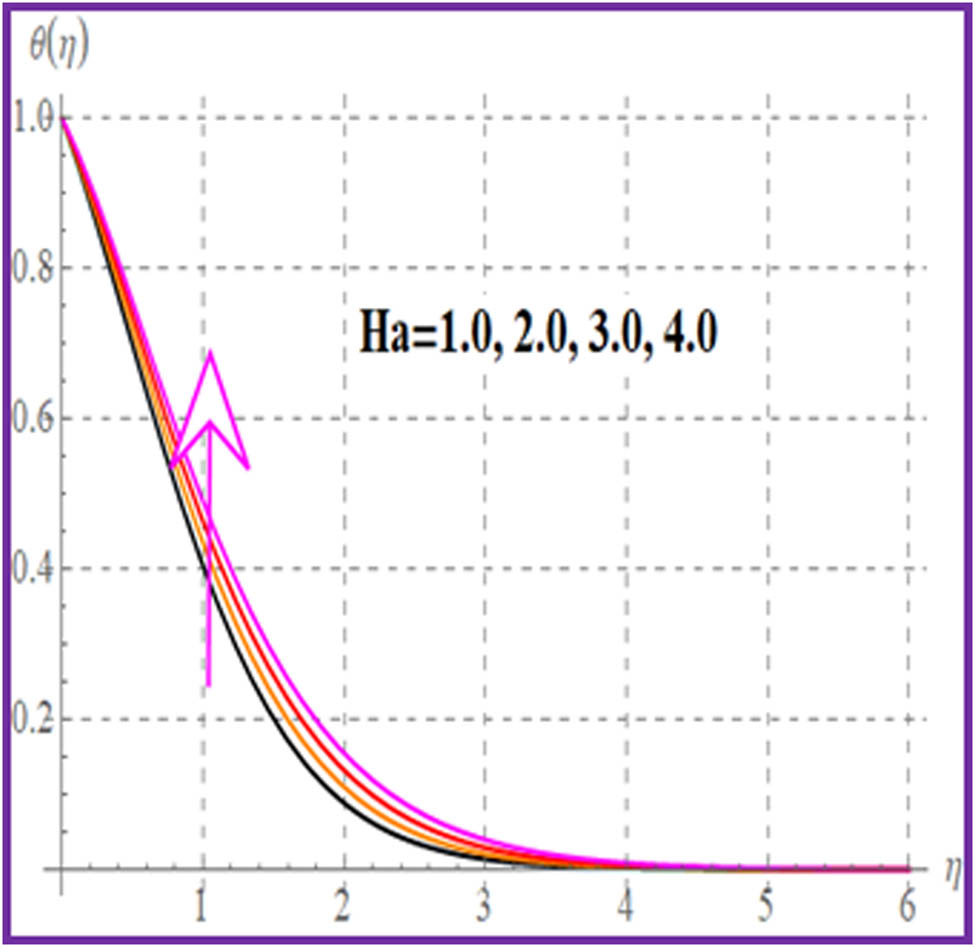


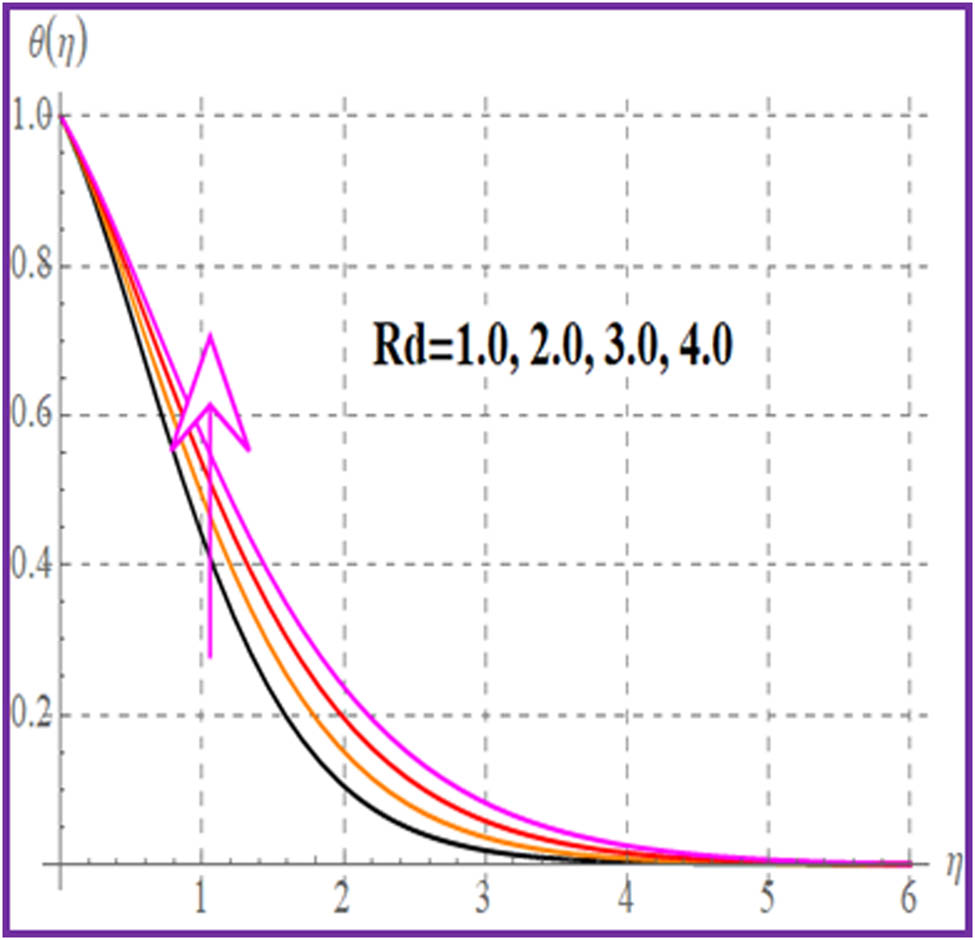





The electric field
Table 1 exhibits a comparative study about results acquired here with those from the research of Waqas et al. [43], and it is evident that the obtained results are in strong agreement. Such agreement between independent studies enhances the reliability and validity of the utilized methodology.
Comparative outcomes of
|
|
Waqas et al. [43] | Current study |
|---|---|---|
| 0.0 | −1.00000 | −1.00000 |
| 0.5 | −1.1180 | −1.11803 |
| 1.0 | −1.4141 | −1.41421 |
7 Closing remarks
The present analysis has provided several key findings:
Fluid flow decays as the Hartmann number increases, while the reverse trend is observed for temperature.
A larger estimation of the electric field variable enhances the velocity.
Higher material variables lead to a reverse behavior in fluid flow and microrotation velocity.
Microrotation velocity increases against an unknown variable.
Temperature exhibits opposite behavior for larger radiation and Prandtl numbers.
The thermal field shows an increasing behavior with random and thermophoresis variables.
An increase in concentration is observed against the thermophoresis variable.
Variation in the Schmidt number yields concentration reduction.
Concentration decreases for Brownian and thermophoresis variables.
Motile microorganisms decay for higher unknown variable.
Motile microorganisms shrink against higher Peclet numbers.
Variation in the bioconvective Lewis number engenders a decline in motile microorganisms.
These findings provide useful understandings regarding fluid flow, temperature, microrotation velocity, concentration, and motile microorganisms under different variables. Further research can be conducted to explore the underlying mechanisms and extend the analysis to more complex systems.
Acknowledgments
The authors extend their appreciation to the Deputyship for Research & Innovation, Ministry of Education in Saudi Arabia for funding this research work through the project number RI-44-0332.
-
Funding information: The authors extend their appreciation to the Deputyship for Research & Innovation, Ministry of Education in Saudi Arabia for funding this research work through the project number RI-44-0332.
-
Author contributions: All authors have accepted responsibility for the entire content of this manuscript and approved its submission.
-
Conflict of interest: The authors state no conflict of interest.
References
[1] Eringen AC. Simple microfluids. Int J Eng Sci. 1964;2:205–17.10.1016/0020-7225(64)90005-9Search in Google Scholar
[2] Eringen AC. Theory of micropolar fluids. J Math Mech. 1966;16:1–18.10.1512/iumj.1967.16.16001Search in Google Scholar
[3] Saidulu B, Reddy KS. Evaluation of combined heat and mass transfer in hydromagnetic micropolar flow along a stretching sheet when viscous dissipation and chemical reaction is present. Partial Differ Equ Appl Math. 2023;7:100467. 10.1016/j.padiff.2022.100467.Search in Google Scholar
[4] Kumar NN, Sastry DRVSRK, Shaw S. Irreversibility analysis of an unsteady micropolar CNT-blood nanofluid flow through a squeezing channel with activation energy-Application in drug delivery. Comput Methods Prog Biomed. 2022;226:107156. 10.1016/j.cmpb.2022.107156.Search in Google Scholar PubMed
[5] Bilal M, Ramzan M, Siddique I, Sajjad A. Magneto-micropolar nanofluid flow through the convective permeable channel using Koo-Kleinstreuer-Li model. J Magn Magn Mater. 2023;565:170288. 10.1016/j.jmmm.2022.170288.Search in Google Scholar
[6] Shahzad A, Imran M, Tahir M, Khan SA, Akgül A, Abdullaev S, et al. Brownian motion and thermophoretic diffusion impact on Darcy-Forchheimer flow of bioconvective micropolar nanofluid between double disks with Cattaneo-Christov heat flux. Alex Eng J. 2023;62:1–15.10.1016/j.aej.2022.07.023Search in Google Scholar
[7] Saraswathy M, Prakash D, Muthtamilselvan M, Mdallal QMA. Arrhenius energy on asymmetric flow and heat transfer of micropolar fluids with variable properties: A sensitivity approach. Alex Eng J. 2022;61:12329–52.10.1016/j.aej.2022.06.015Search in Google Scholar
[8] Mishra P, Kumar D, Kumar J, Aty AHA, Park C, Yahia IS. Analysis of MHD Williamson micropolar fluid flow in non-Darcian porous media with variable thermal conductivity. Case Stud Therm Eng. 2022;36:102195. 10.1016/j.csite.2022.102195.Search in Google Scholar
[9] Bian Y, Zhu S, Li X, Tao Y, Nian C, Zhang C, et al. Bioinspired magnetism-responsive hybrid microstructures with dynamic switching toward liquid droplet rolling states. Nanoscale. 2023;15:11945–54.10.1039/D3NR02082GSearch in Google Scholar PubMed
[10] Zhang M, Jiang X, Arefi M. Dynamic formulation of a sandwich microshell considering modified couple stress and thickness-stretching. Eur Phys J Plus. 2023;138:227.10.1140/epjp/s13360-023-03753-4Search in Google Scholar
[11] Yang B, Wang H, Zhang M, Jia F, Liu Y, Lu Z. Mechanically strong, flexible, and flame-retardant Ti3C2Tx MXene-coated aramid paper with superior electromagnetic interference shielding and electrical heating performance. Chem Eng J. 2023;476:146834.10.1016/j.cej.2023.146834Search in Google Scholar
[12] Fares ME, Salem MG, Atta D, Elmarghany MK. Mixed variational principle for micropolar elasticity and an accurate two-dimensional plate model. Eur J Mech A Solids. 2023;99:104870. 10.1016/j.euromechsol.2022.104870.Search in Google Scholar
[13] Shabbir T, Mushtaq M, Khan MI, Hayat T. Modeling and numerical simulation of micropolar fluid over a curved surface: Keller box method. Comput Methods Prog Biomed. 2022;187:105220. 10.1016/j.cmpb.2019.105220.Search in Google Scholar PubMed
[14] Faisal M, Mabood F, Asogwa KK, Badruddin IA. Bidirectional radiative transport of magnetic Maxwell nanofluid mobilized by Arrhenius energy and prescribed thermal/concentration conditions: Significance of Ludwig-Soret and pedesis effects. Ain Shams Eng J. 2023;14:101933.10.1016/j.asej.2022.101933Search in Google Scholar
[15] Waqas M, Sadiq MA, Bahaidarah HMS. Gyrotactic bioconvection stratified flow of magnetized micropolar nanoliquid configured by stretchable radiating surface with Joule heating and viscous dissipation. Int Commun Heat Mass Transf. 2022;138:106229. 10.1016/j.icheatmasstransfer.2022.106229.Search in Google Scholar
[16] Singh SP, Singh P. Effect of temperature and light on the growth of algae species: A review. Renew Sustain Energy Rev. 2015;50:431–44.10.1016/j.rser.2015.05.024Search in Google Scholar
[17] Kuznetsov AV. The onset of nanofluid bioconvection in a suspension containing both nanoparticles and gyrotactic microorganisms. Int Commun Heat Mass Trans. 2010;37:1421–5.10.1016/j.icheatmasstransfer.2010.08.015Search in Google Scholar
[18] Avramenko AA, Kovetska YY, Shevchuk IV. Lorenz approach for analysis of bioconvection instability of gyrotactic motile microorganisms. Chaos Solit Fractals. 2023;166:112957. 10.1016/j.chaos.2022.112957.Search in Google Scholar
[19] Kairi RR, Roy S, Raut S. Stratified thermosolutal Marangoni bioconvective flow of gyrotactic microorganisms in Williamson nanofluid. Eur J Mech B/Fluids. 2023;97:40–52.10.1016/j.euromechflu.2022.09.004Search in Google Scholar
[20] Aziz A, Khan WA, Pop I. Free convection boundary layer flow past a horizontal flat plate embedded in porous mediumfilled by nanofluid containing gyrotactic microorganisms. Int J Therm Sci. 2012;56:48–57.10.1016/j.ijthermalsci.2012.01.011Search in Google Scholar
[21] Ghachem K, Ahmad B, Noor S, Abbas T, Khan SU, Anjum S, et al. Numerical simulations for radiated bioconvection flow of nanoparticles with viscous dissipation and exponential heat source. J Indian Chem Soc. 2023;100(1):100828. 10.1016/j.jics.2022.100828.Search in Google Scholar
[22] Zhang C, Khorshidi H, Najafi E, Ghasemi M. Fresh, mechanical and microstructural properties of alkali-activated composites incorporating nanomaterials: A comprehensive review. J Clean Prod. 2023;384:135390.10.1016/j.jclepro.2022.135390Search in Google Scholar
[23] Xu P, Liu X, Zhao Y, Lan D, Shin I. Study of graphdiyne biomimetic nanomaterials as fluorescent sensors of ciprofloxacin hydrochloride in water environment. Desalin Water Treat. 2023;302:129–37.10.5004/dwt.2023.29723Search in Google Scholar
[24] Zheng B, Lin D, Qi S, Hu Y, Jin Y, Chen Q, et al. Turbulent skin-friction drag reduction by annular dielectric barrier discharge plasma actuator. Phys Fluids. 2023;35:125129.10.1063/5.0172381Search in Google Scholar
[25] Hu G, Ying S, Qi H, Yu L, Li G. Design, analysis and optimization of a hybrid fluid flow magnetorheological damper based on multiphysics coupling model. Mech Syst Signal Process. 2023;205:110877.10.1016/j.ymssp.2023.110877Search in Google Scholar
[26] Tham L, Nazar R, Pop I. Mixed convection flow over a solid sphere embedded in a porous medium filled by a nanofluid containing gyrotactic microorganisms. Int Commun Heat Mass Transf. 2013;62:647–60.10.1016/j.ijheatmasstransfer.2013.03.012Search in Google Scholar
[27] Ali A, Sulaiman M, Islam S, Shah Z, Bonyah E. Three-dimensional magnetohydrodynamic (MHD) flow of Maxwell, nanofluid containing gyrotactic micro-organisms with heat source/sink. AIP Adv. 2018;8:085303. 10.1063/1.5040540.Search in Google Scholar
[28] Asogwa KK, Goud BS, Shah NA, Yook S-J. Rheology of electromagnetohydrodynamic tangent hyperbolic nanofluid over a stretching riga surface featuring dufour effect and activation energy. Sci Rep. 2022;12:14602.10.1038/s41598-022-18998-9Search in Google Scholar PubMed PubMed Central
[29] Garg A, Sharma YD, Jain SK. Stability analysis of thermo-bioconvection flow of Jeffrey fluid containing gravitactic microorganism into an anisotropic porous medium. Forces Mech. 2023;10:100152. 10.1016/j.finmec.2022.100152.Search in Google Scholar
[30] Ali A, Sarkar S, Das S. Bioconvective chemically reactive entropy optimized Cross-nano-material conveying oxytactic microorganisms over a flexible cylinder with Lorentz force and Arrhenius kinetics. Math Comput Simul. 2023;205:1029–51.10.1016/j.matcom.2022.11.002Search in Google Scholar
[31] Goud BS, Reddy YD, Asogwa KK. Chemical reaction, Soret and Dufour impacts on magnetohydrodynamic heat transfer Casson fluid over an exponentially permeable stretching surface with slip effects. Int J Mod Phys B. 2023;37:2350124.10.1142/S0217979223501242Search in Google Scholar
[32] Choi SUS. Enhancing thermal conductivity of fluids with nanoparticles. ASME J Fluids Eng Publ Fed. 1995;231:99–106.Search in Google Scholar
[33] Eastman JA, Choi SUS, Li S, Yu W, Thompson LJ. Anomalously increased effective thermal conductivities of ethylene glycol-based nanofluids containing copper nanoparticles. Appl Phys Lett. 2001;78:718–20.10.1063/1.1341218Search in Google Scholar
[34] Buongiorno J. Convective transport in nanofluids. ASME. J. Heat Transf. 2006;128:240–50.10.1115/1.2150834Search in Google Scholar
[35] Kalpana G, Madhura KR, Kudenatti RB. Numerical study on the combined effects of Brownian motion and thermophoresis on an unsteady magnetohydrodynamics nanofluid boundary layer flow. Math Comput Simul. 2022;200:78–96.10.1016/j.matcom.2022.04.010Search in Google Scholar
[36] Oudina FM, Aissa A, Mahanthesh B, Oztop HF. Heat transport of magnetized Newtonian nanoliquids in an annular space between porous vertical cylinders with discrete heat source. Int Commun Heat Mass Transf. 2020;117:104737.10.1016/j.icheatmasstransfer.2020.104737Search in Google Scholar
[37] Ahmed S, Xu H, Zhou Y, Yu Q. Modelling convective transport of hybrid nanofluid in a lid driven square cavity with consideration of Brownian diffusion and thermophoresis. Int Commun Heat Mass Transf. 2022;137:106226. 10.1016/j.icheatmasstransfer.2022.106226.Search in Google Scholar
[38] Farooq S, Khan MI, Riahi A, Chammam W, Khan WA. Modeling and interpretation of peristaltic transport in single wall carbon nanotube flow with entropy optimization and Newtonian heating. Comput Methods Prog Biomed. 2020;192:105435.10.1016/j.cmpb.2020.105435Search in Google Scholar PubMed
[39] Kalpana G, Madhura KR, Kudenatti RB. Magnetohydrodynamic boundary layer flow of hybrid nanofluid with the thermophoresis and Brownian motion in an irregular channel: A numerical approach. Eng Sci Technol Int J. 2022;32:101075. 10.1016/j.jestch.2021.11.001.Search in Google Scholar
[40] Ahmed MF, Zaib A, Ali F, Bafakeeh OT, Tag-ElDin ESM, Guedri K, et al. Numerical computation for gyrotactic microorganisms in MHD radiative Eyring–Powell nanomaterial flow by a static/moving wedge with Darcy–Forchheimer relation. Micromachines. 2022;13:1768. 10.3390/mi13101768.Search in Google Scholar PubMed PubMed Central
[41] Muruganandam M, Kumar PM. Experimental analysis on internal combustion engine using MWCNT/water nanofluid as a coolant. Mater Today Proc. 2020;21:248–52.10.1016/j.matpr.2019.05.411Search in Google Scholar
[42] Patil S, Kataria C, Kumar A, Kumar A. Effect of segregation and advection governed heterogeneous distribution of nanoparticles on NEPCM discharging behavior. J Energy Storage. 2023;57:106230. 10.1016/j.est.2022.106230.Search in Google Scholar
[43] Waqas M, Khan WA, Pasha AA, Islam N, Rahman MM. Dynamics of bioconvective Casson nanoliquid from a moving surface capturing gyrotactic microorganisms, magnetohydrodynamics and stratifications. Therm Sci Eng Prog. 2022;36:101492.10.1016/j.tsep.2022.101492Search in Google Scholar
[44] Dutta S, Bhattacharyya S, Pop I. Effect of hybrid nanoparticles on conjugate mixed convection of a viscoplastic fluid in a ventilated enclosure with wall mounted heated block. Alex Eng J. 2023;62:99–111.10.1016/j.aej.2022.06.042Search in Google Scholar
[45] Bafakeeh OT, Raza A, Khan SU, Khan MI, Nasr A, Khedher NB, et al. Physical interpretation of nanofluid (copper oxide and silver) with slip and mixed convection effects: Applications of fractional derivatives. Appl Sci. 2022;12:10860.10.3390/app122110860Search in Google Scholar
[46] Waqas M. Modeling and analysis for nonlinear flows due to stretched surface. 2018. http://142.54.178.187:9060/xmlui/handle/123456789/11062.Search in Google Scholar
[47] Li Y, Anwar MI, Katbar NM, Prakash M, Saqlain M, Waqas M, et al. Analysis of magnetized micropolar fluid subjected to generalized heat-mass transfer theories. Open Phys. 2023;21:20230117.10.1515/phys-2023-0117Search in Google Scholar
© 2023 the author(s), published by De Gruyter
This work is licensed under the Creative Commons Attribution 4.0 International License.
Articles in the same Issue
- Regular Articles
- Dynamic properties of the attachment oscillator arising in the nanophysics
- Parametric simulation of stagnation point flow of motile microorganism hybrid nanofluid across a circular cylinder with sinusoidal radius
- Fractal-fractional advection–diffusion–reaction equations by Ritz approximation approach
- Behaviour and onset of low-dimensional chaos with a periodically varying loss in single-mode homogeneously broadened laser
- Ammonia gas-sensing behavior of uniform nanostructured PPy film prepared by simple-straightforward in situ chemical vapor oxidation
- Analysis of the working mechanism and detection sensitivity of a flash detector
- Flat and bent branes with inner structure in two-field mimetic gravity
- Heat transfer analysis of the MHD stagnation-point flow of third-grade fluid over a porous sheet with thermal radiation effect: An algorithmic approach
- Weighted survival functional entropy and its properties
- Bioconvection effect in the Carreau nanofluid with Cattaneo–Christov heat flux using stagnation point flow in the entropy generation: Micromachines level study
- Study on the impulse mechanism of optical films formed by laser plasma shock waves
- Analysis of sweeping jet and film composite cooling using the decoupled model
- Research on the influence of trapezoidal magnetization of bonded magnetic ring on cogging torque
- Tripartite entanglement and entanglement transfer in a hybrid cavity magnomechanical system
- Compounded Bell-G class of statistical models with applications to COVID-19 and actuarial data
- Degradation of Vibrio cholerae from drinking water by the underwater capillary discharge
- Multiple Lie symmetry solutions for effects of viscous on magnetohydrodynamic flow and heat transfer in non-Newtonian thin film
- Thermal characterization of heat source (sink) on hybridized (Cu–Ag/EG) nanofluid flow via solid stretchable sheet
- Optimizing condition monitoring of ball bearings: An integrated approach using decision tree and extreme learning machine for effective decision-making
- Study on the inter-porosity transfer rate and producing degree of matrix in fractured-porous gas reservoirs
- Interstellar radiation as a Maxwell field: Improved numerical scheme and application to the spectral energy density
- Numerical study of hybridized Williamson nanofluid flow with TC4 and Nichrome over an extending surface
- Controlling the physical field using the shape function technique
- Significance of heat and mass transport in peristaltic flow of Jeffrey material subject to chemical reaction and radiation phenomenon through a tapered channel
- Complex dynamics of a sub-quadratic Lorenz-like system
- Stability control in a helicoidal spin–orbit-coupled open Bose–Bose mixture
- Research on WPD and DBSCAN-L-ISOMAP for circuit fault feature extraction
- Simulation for formation process of atomic orbitals by the finite difference time domain method based on the eight-element Dirac equation
- A modified power-law model: Properties, estimation, and applications
- Bayesian and non-Bayesian estimation of dynamic cumulative residual Tsallis entropy for moment exponential distribution under progressive censored type II
- Computational analysis and biomechanical study of Oldroyd-B fluid with homogeneous and heterogeneous reactions through a vertical non-uniform channel
- Predictability of machine learning framework in cross-section data
- Chaotic characteristics and mixing performance of pseudoplastic fluids in a stirred tank
- Isomorphic shut form valuation for quantum field theory and biological population models
- Vibration sensitivity minimization of an ultra-stable optical reference cavity based on orthogonal experimental design
- Effect of dysprosium on the radiation-shielding features of SiO2–PbO–B2O3 glasses
- Asymptotic formulations of anti-plane problems in pre-stressed compressible elastic laminates
- A study on soliton, lump solutions to a generalized (3+1)-dimensional Hirota--Satsuma--Ito equation
- Tangential electrostatic field at metal surfaces
- Bioconvective gyrotactic microorganisms in third-grade nanofluid flow over a Riga surface with stratification: An approach to entropy minimization
- Infrared spectroscopy for ageing assessment of insulating oils via dielectric loss factor and interfacial tension
- Influence of cationic surfactants on the growth of gypsum crystals
- Study on instability mechanism of KCl/PHPA drilling waste fluid
- Analytical solutions of the extended Kadomtsev–Petviashvili equation in nonlinear media
- A novel compact highly sensitive non-invasive microwave antenna sensor for blood glucose monitoring
- Inspection of Couette and pressure-driven Poiseuille entropy-optimized dissipated flow in a suction/injection horizontal channel: Analytical solutions
- Conserved vectors and solutions of the two-dimensional potential KP equation
- The reciprocal linear effect, a new optical effect of the Sagnac type
- Optimal interatomic potentials using modified method of least squares: Optimal form of interatomic potentials
- The soliton solutions for stochastic Calogero–Bogoyavlenskii Schiff equation in plasma physics/fluid mechanics
- Research on absolute ranging technology of resampling phase comparison method based on FMCW
- Analysis of Cu and Zn contents in aluminum alloys by femtosecond laser-ablation spark-induced breakdown spectroscopy
- Nonsequential double ionization channels control of CO2 molecules with counter-rotating two-color circularly polarized laser field by laser wavelength
- Fractional-order modeling: Analysis of foam drainage and Fisher's equations
- Thermo-solutal Marangoni convective Darcy-Forchheimer bio-hybrid nanofluid flow over a permeable disk with activation energy: Analysis of interfacial nanolayer thickness
- Investigation on topology-optimized compressor piston by metal additive manufacturing technique: Analytical and numeric computational modeling using finite element analysis in ANSYS
- Breast cancer segmentation using a hybrid AttendSeg architecture combined with a gravitational clustering optimization algorithm using mathematical modelling
- On the localized and periodic solutions to the time-fractional Klein-Gordan equations: Optimal additive function method and new iterative method
- 3D thin-film nanofluid flow with heat transfer on an inclined disc by using HWCM
- Numerical study of static pressure on the sonochemistry characteristics of the gas bubble under acoustic excitation
- Optimal auxiliary function method for analyzing nonlinear system of coupled Schrödinger–KdV equation with Caputo operator
- Analysis of magnetized micropolar fluid subjected to generalized heat-mass transfer theories
- Does the Mott problem extend to Geiger counters?
- Stability analysis, phase plane analysis, and isolated soliton solution to the LGH equation in mathematical physics
- Effects of Joule heating and reaction mechanisms on couple stress fluid flow with peristalsis in the presence of a porous material through an inclined channel
- Bayesian and E-Bayesian estimation based on constant-stress partially accelerated life testing for inverted Topp–Leone distribution
- Dynamical and physical characteristics of soliton solutions to the (2+1)-dimensional Konopelchenko–Dubrovsky system
- Study of fractional variable order COVID-19 environmental transformation model
- Sisko nanofluid flow through exponential stretching sheet with swimming of motile gyrotactic microorganisms: An application to nanoengineering
- Influence of the regularization scheme in the QCD phase diagram in the PNJL model
- Fixed-point theory and numerical analysis of an epidemic model with fractional calculus: Exploring dynamical behavior
- Computational analysis of reconstructing current and sag of three-phase overhead line based on the TMR sensor array
- Investigation of tripled sine-Gordon equation: Localized modes in multi-stacked long Josephson junctions
- High-sensitivity on-chip temperature sensor based on cascaded microring resonators
- Pathological study on uncertain numbers and proposed solutions for discrete fuzzy fractional order calculus
- Bifurcation, chaotic behavior, and traveling wave solution of stochastic coupled Konno–Oono equation with multiplicative noise in the Stratonovich sense
- Thermal radiation and heat generation on three-dimensional Casson fluid motion via porous stretching surface with variable thermal conductivity
- Numerical simulation and analysis of Airy's-type equation
- A homotopy perturbation method with Elzaki transformation for solving the fractional Biswas–Milovic model
- Heat transfer performance of magnetohydrodynamic multiphase nanofluid flow of Cu–Al2O3/H2O over a stretching cylinder
- ΛCDM and the principle of equivalence
- Axisymmetric stagnation-point flow of non-Newtonian nanomaterial and heat transport over a lubricated surface: Hybrid homotopy analysis method simulations
- HAM simulation for bioconvective magnetohydrodynamic flow of Walters-B fluid containing nanoparticles and microorganisms past a stretching sheet with velocity slip and convective conditions
- Coupled heat and mass transfer mathematical study for lubricated non-Newtonian nanomaterial conveying oblique stagnation point flow: A comparison of viscous and viscoelastic nanofluid model
- Power Topp–Leone exponential negative family of distributions with numerical illustrations to engineering and biological data
- Extracting solitary solutions of the nonlinear Kaup–Kupershmidt (KK) equation by analytical method
- A case study on the environmental and economic impact of photovoltaic systems in wastewater treatment plants
- Application of IoT network for marine wildlife surveillance
- Non-similar modeling and numerical simulations of microploar hybrid nanofluid adjacent to isothermal sphere
- Joint optimization of two-dimensional warranty period and maintenance strategy considering availability and cost constraints
- Numerical investigation of the flow characteristics involving dissipation and slip effects in a convectively nanofluid within a porous medium
- Spectral uncertainty analysis of grassland and its camouflage materials based on land-based hyperspectral images
- Application of low-altitude wind shear recognition algorithm and laser wind radar in aviation meteorological services
- Investigation of different structures of screw extruders on the flow in direct ink writing SiC slurry based on LBM
- Harmonic current suppression method of virtual DC motor based on fuzzy sliding mode
- Micropolar flow and heat transfer within a permeable channel using the successive linearization method
- Different lump k-soliton solutions to (2+1)-dimensional KdV system using Hirota binary Bell polynomials
- Investigation of nanomaterials in flow of non-Newtonian liquid toward a stretchable surface
- Weak beat frequency extraction method for photon Doppler signal with low signal-to-noise ratio
- Electrokinetic energy conversion of nanofluids in porous microtubes with Green’s function
- Examining the role of activation energy and convective boundary conditions in nanofluid behavior of Couette-Poiseuille flow
- Review Article
- Effects of stretching on phase transformation of PVDF and its copolymers: A review
- Special Issue on Transport phenomena and thermal analysis in micro/nano-scale structure surfaces - Part IV
- Prediction and monitoring model for farmland environmental system using soil sensor and neural network algorithm
- Special Issue on Advanced Topics on the Modelling and Assessment of Complicated Physical Phenomena - Part III
- Some standard and nonstandard finite difference schemes for a reaction–diffusion–chemotaxis model
- Special Issue on Advanced Energy Materials - Part II
- Rapid productivity prediction method for frac hits affected wells based on gas reservoir numerical simulation and probability method
- Special Issue on Novel Numerical and Analytical Techniques for Fractional Nonlinear Schrodinger Type - Part III
- Adomian decomposition method for solution of fourteenth order boundary value problems
- New soliton solutions of modified (3+1)-D Wazwaz–Benjamin–Bona–Mahony and (2+1)-D cubic Klein–Gordon equations using first integral method
- On traveling wave solutions to Manakov model with variable coefficients
- Rational approximation for solving Fredholm integro-differential equations by new algorithm
- Special Issue on Predicting pattern alterations in nature - Part I
- Modeling the monkeypox infection using the Mittag–Leffler kernel
- Spectral analysis of variable-order multi-terms fractional differential equations
- Special Issue on Nanomaterial utilization and structural optimization - Part I
- Heat treatment and tensile test of 3D-printed parts manufactured at different build orientations
Articles in the same Issue
- Regular Articles
- Dynamic properties of the attachment oscillator arising in the nanophysics
- Parametric simulation of stagnation point flow of motile microorganism hybrid nanofluid across a circular cylinder with sinusoidal radius
- Fractal-fractional advection–diffusion–reaction equations by Ritz approximation approach
- Behaviour and onset of low-dimensional chaos with a periodically varying loss in single-mode homogeneously broadened laser
- Ammonia gas-sensing behavior of uniform nanostructured PPy film prepared by simple-straightforward in situ chemical vapor oxidation
- Analysis of the working mechanism and detection sensitivity of a flash detector
- Flat and bent branes with inner structure in two-field mimetic gravity
- Heat transfer analysis of the MHD stagnation-point flow of third-grade fluid over a porous sheet with thermal radiation effect: An algorithmic approach
- Weighted survival functional entropy and its properties
- Bioconvection effect in the Carreau nanofluid with Cattaneo–Christov heat flux using stagnation point flow in the entropy generation: Micromachines level study
- Study on the impulse mechanism of optical films formed by laser plasma shock waves
- Analysis of sweeping jet and film composite cooling using the decoupled model
- Research on the influence of trapezoidal magnetization of bonded magnetic ring on cogging torque
- Tripartite entanglement and entanglement transfer in a hybrid cavity magnomechanical system
- Compounded Bell-G class of statistical models with applications to COVID-19 and actuarial data
- Degradation of Vibrio cholerae from drinking water by the underwater capillary discharge
- Multiple Lie symmetry solutions for effects of viscous on magnetohydrodynamic flow and heat transfer in non-Newtonian thin film
- Thermal characterization of heat source (sink) on hybridized (Cu–Ag/EG) nanofluid flow via solid stretchable sheet
- Optimizing condition monitoring of ball bearings: An integrated approach using decision tree and extreme learning machine for effective decision-making
- Study on the inter-porosity transfer rate and producing degree of matrix in fractured-porous gas reservoirs
- Interstellar radiation as a Maxwell field: Improved numerical scheme and application to the spectral energy density
- Numerical study of hybridized Williamson nanofluid flow with TC4 and Nichrome over an extending surface
- Controlling the physical field using the shape function technique
- Significance of heat and mass transport in peristaltic flow of Jeffrey material subject to chemical reaction and radiation phenomenon through a tapered channel
- Complex dynamics of a sub-quadratic Lorenz-like system
- Stability control in a helicoidal spin–orbit-coupled open Bose–Bose mixture
- Research on WPD and DBSCAN-L-ISOMAP for circuit fault feature extraction
- Simulation for formation process of atomic orbitals by the finite difference time domain method based on the eight-element Dirac equation
- A modified power-law model: Properties, estimation, and applications
- Bayesian and non-Bayesian estimation of dynamic cumulative residual Tsallis entropy for moment exponential distribution under progressive censored type II
- Computational analysis and biomechanical study of Oldroyd-B fluid with homogeneous and heterogeneous reactions through a vertical non-uniform channel
- Predictability of machine learning framework in cross-section data
- Chaotic characteristics and mixing performance of pseudoplastic fluids in a stirred tank
- Isomorphic shut form valuation for quantum field theory and biological population models
- Vibration sensitivity minimization of an ultra-stable optical reference cavity based on orthogonal experimental design
- Effect of dysprosium on the radiation-shielding features of SiO2–PbO–B2O3 glasses
- Asymptotic formulations of anti-plane problems in pre-stressed compressible elastic laminates
- A study on soliton, lump solutions to a generalized (3+1)-dimensional Hirota--Satsuma--Ito equation
- Tangential electrostatic field at metal surfaces
- Bioconvective gyrotactic microorganisms in third-grade nanofluid flow over a Riga surface with stratification: An approach to entropy minimization
- Infrared spectroscopy for ageing assessment of insulating oils via dielectric loss factor and interfacial tension
- Influence of cationic surfactants on the growth of gypsum crystals
- Study on instability mechanism of KCl/PHPA drilling waste fluid
- Analytical solutions of the extended Kadomtsev–Petviashvili equation in nonlinear media
- A novel compact highly sensitive non-invasive microwave antenna sensor for blood glucose monitoring
- Inspection of Couette and pressure-driven Poiseuille entropy-optimized dissipated flow in a suction/injection horizontal channel: Analytical solutions
- Conserved vectors and solutions of the two-dimensional potential KP equation
- The reciprocal linear effect, a new optical effect of the Sagnac type
- Optimal interatomic potentials using modified method of least squares: Optimal form of interatomic potentials
- The soliton solutions for stochastic Calogero–Bogoyavlenskii Schiff equation in plasma physics/fluid mechanics
- Research on absolute ranging technology of resampling phase comparison method based on FMCW
- Analysis of Cu and Zn contents in aluminum alloys by femtosecond laser-ablation spark-induced breakdown spectroscopy
- Nonsequential double ionization channels control of CO2 molecules with counter-rotating two-color circularly polarized laser field by laser wavelength
- Fractional-order modeling: Analysis of foam drainage and Fisher's equations
- Thermo-solutal Marangoni convective Darcy-Forchheimer bio-hybrid nanofluid flow over a permeable disk with activation energy: Analysis of interfacial nanolayer thickness
- Investigation on topology-optimized compressor piston by metal additive manufacturing technique: Analytical and numeric computational modeling using finite element analysis in ANSYS
- Breast cancer segmentation using a hybrid AttendSeg architecture combined with a gravitational clustering optimization algorithm using mathematical modelling
- On the localized and periodic solutions to the time-fractional Klein-Gordan equations: Optimal additive function method and new iterative method
- 3D thin-film nanofluid flow with heat transfer on an inclined disc by using HWCM
- Numerical study of static pressure on the sonochemistry characteristics of the gas bubble under acoustic excitation
- Optimal auxiliary function method for analyzing nonlinear system of coupled Schrödinger–KdV equation with Caputo operator
- Analysis of magnetized micropolar fluid subjected to generalized heat-mass transfer theories
- Does the Mott problem extend to Geiger counters?
- Stability analysis, phase plane analysis, and isolated soliton solution to the LGH equation in mathematical physics
- Effects of Joule heating and reaction mechanisms on couple stress fluid flow with peristalsis in the presence of a porous material through an inclined channel
- Bayesian and E-Bayesian estimation based on constant-stress partially accelerated life testing for inverted Topp–Leone distribution
- Dynamical and physical characteristics of soliton solutions to the (2+1)-dimensional Konopelchenko–Dubrovsky system
- Study of fractional variable order COVID-19 environmental transformation model
- Sisko nanofluid flow through exponential stretching sheet with swimming of motile gyrotactic microorganisms: An application to nanoengineering
- Influence of the regularization scheme in the QCD phase diagram in the PNJL model
- Fixed-point theory and numerical analysis of an epidemic model with fractional calculus: Exploring dynamical behavior
- Computational analysis of reconstructing current and sag of three-phase overhead line based on the TMR sensor array
- Investigation of tripled sine-Gordon equation: Localized modes in multi-stacked long Josephson junctions
- High-sensitivity on-chip temperature sensor based on cascaded microring resonators
- Pathological study on uncertain numbers and proposed solutions for discrete fuzzy fractional order calculus
- Bifurcation, chaotic behavior, and traveling wave solution of stochastic coupled Konno–Oono equation with multiplicative noise in the Stratonovich sense
- Thermal radiation and heat generation on three-dimensional Casson fluid motion via porous stretching surface with variable thermal conductivity
- Numerical simulation and analysis of Airy's-type equation
- A homotopy perturbation method with Elzaki transformation for solving the fractional Biswas–Milovic model
- Heat transfer performance of magnetohydrodynamic multiphase nanofluid flow of Cu–Al2O3/H2O over a stretching cylinder
- ΛCDM and the principle of equivalence
- Axisymmetric stagnation-point flow of non-Newtonian nanomaterial and heat transport over a lubricated surface: Hybrid homotopy analysis method simulations
- HAM simulation for bioconvective magnetohydrodynamic flow of Walters-B fluid containing nanoparticles and microorganisms past a stretching sheet with velocity slip and convective conditions
- Coupled heat and mass transfer mathematical study for lubricated non-Newtonian nanomaterial conveying oblique stagnation point flow: A comparison of viscous and viscoelastic nanofluid model
- Power Topp–Leone exponential negative family of distributions with numerical illustrations to engineering and biological data
- Extracting solitary solutions of the nonlinear Kaup–Kupershmidt (KK) equation by analytical method
- A case study on the environmental and economic impact of photovoltaic systems in wastewater treatment plants
- Application of IoT network for marine wildlife surveillance
- Non-similar modeling and numerical simulations of microploar hybrid nanofluid adjacent to isothermal sphere
- Joint optimization of two-dimensional warranty period and maintenance strategy considering availability and cost constraints
- Numerical investigation of the flow characteristics involving dissipation and slip effects in a convectively nanofluid within a porous medium
- Spectral uncertainty analysis of grassland and its camouflage materials based on land-based hyperspectral images
- Application of low-altitude wind shear recognition algorithm and laser wind radar in aviation meteorological services
- Investigation of different structures of screw extruders on the flow in direct ink writing SiC slurry based on LBM
- Harmonic current suppression method of virtual DC motor based on fuzzy sliding mode
- Micropolar flow and heat transfer within a permeable channel using the successive linearization method
- Different lump k-soliton solutions to (2+1)-dimensional KdV system using Hirota binary Bell polynomials
- Investigation of nanomaterials in flow of non-Newtonian liquid toward a stretchable surface
- Weak beat frequency extraction method for photon Doppler signal with low signal-to-noise ratio
- Electrokinetic energy conversion of nanofluids in porous microtubes with Green’s function
- Examining the role of activation energy and convective boundary conditions in nanofluid behavior of Couette-Poiseuille flow
- Review Article
- Effects of stretching on phase transformation of PVDF and its copolymers: A review
- Special Issue on Transport phenomena and thermal analysis in micro/nano-scale structure surfaces - Part IV
- Prediction and monitoring model for farmland environmental system using soil sensor and neural network algorithm
- Special Issue on Advanced Topics on the Modelling and Assessment of Complicated Physical Phenomena - Part III
- Some standard and nonstandard finite difference schemes for a reaction–diffusion–chemotaxis model
- Special Issue on Advanced Energy Materials - Part II
- Rapid productivity prediction method for frac hits affected wells based on gas reservoir numerical simulation and probability method
- Special Issue on Novel Numerical and Analytical Techniques for Fractional Nonlinear Schrodinger Type - Part III
- Adomian decomposition method for solution of fourteenth order boundary value problems
- New soliton solutions of modified (3+1)-D Wazwaz–Benjamin–Bona–Mahony and (2+1)-D cubic Klein–Gordon equations using first integral method
- On traveling wave solutions to Manakov model with variable coefficients
- Rational approximation for solving Fredholm integro-differential equations by new algorithm
- Special Issue on Predicting pattern alterations in nature - Part I
- Modeling the monkeypox infection using the Mittag–Leffler kernel
- Spectral analysis of variable-order multi-terms fractional differential equations
- Special Issue on Nanomaterial utilization and structural optimization - Part I
- Heat treatment and tensile test of 3D-printed parts manufactured at different build orientations

