Home Vibration sensitivity minimization of an ultra-stable optical reference cavity based on orthogonal experimental design
Article Open Access

Vibration sensitivity minimization of an ultra-stable optical reference cavity based on orthogonal experimental design

  • Jing Gao , Dongdong Jiao , Linbo Zhang , Guanjun Xu EMAIL logo , Xue Deng , Qi Zang , Honglei Yang , Ruifang Dong EMAIL logo , Tao Liu EMAIL logo and Shougang Zhang
Published/Copyright: July 29, 2023
Download Article (PDF)
Open Physics
From the journal Open Physics Volume 21 Issue 1

Abstract

The ultra-stable optical reference cavity (USORC) is a key element for a variety of applications. In this work, based on the orthogonal experimental design method, we study the vibration sensitivity optimization of a classical USORC with a 100 mm length. According to a test of 4 levels and 3 factors, the L 16 (43) orthogonal table is established to design orthogonal experiments. The vibration sensitivities under different parameters are simulated and analyzed. The vibration sensitivities in three directions of the USORC are used as three single-object values, and the normalized sum of the three vibration sensitivities is selected as comprehensive object values. Through the range analysis of the object values, the influence degrees of the parameters on the three single objects and the comprehensive object are determined. The optimal parameter combination schemes are obtained by using the comprehensive balance method and the comprehensive evaluation method, respectively. Based on the corresponding fractional frequency stability of ultra-stable lasers, the final optimal parameter combination scheme A1B3C3 is determined and verified. This work is the first to use an orthogonal experimental design method to optimize vibration sensitivities, providing an approach to vibration sensitivities optimization and is also beneficial for the vibration sensitivity design of a transportable USORC.

Keywords: ultra-stable optical reference cavity; optimization; vibration sensitivity; orthogonal experimental design; ultra-stable laser

1 Introduction

Ultra-stable lasers have important applications, such as high-precision spectroscopy, gravitational redshift measurement, relativistic test, gravitational wave detection, and coherent communication [1,2,3,4,5,6]. Currently, ultra-stable lasers are often achieved by using the Pound–Drever–Hall method based on an ultra-stable optical reference cavity (USORC) [7,8,9,10,11,12,13,14,15]. A USORC is the reference of the laser frequency, so the stability of the optical length of USORCs primarily determines the fractional frequency stability of ultra-stable lasers [7,8,9,10].

The main factors affecting the stability of the optical length of USORCs include vibration [9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24], temperature [25,26], and thermal noise [27,28,29,30], where the latter two can be well solved by controlling temperature and increasing USORC’s length. In general, the index to assess the impact of vibration on the stability of the optical length of USORCs is vibration sensitivity [7,8,9,10]. In order to reduce this impact, the finite element method plays an important role [7,8,9]. Benefiting from this, the vibration sensitivity of USORC is reduced from 10−9/g to 10−11/g by the passive method [7,8,9,10,11,13,14,15,17,18,19]. Furthermore, the fractional frequency stability of state-of-the-art laboratory ultra-stable lasers [25,26] and transportable ultra-stable laser systems [14,19,22,23] approach an order of magnitude of 10−17 in 1 s and an order of magnitude of 10−16 in 1 s, respectively.

However, in order to design the USORC with low vibration sensitivity, a large number of numerical simulations are often required to obtain a better combination of parameters, and it is difficult to compare the influence degree of parameters on vibration sensitivity under the same conditions. In addition, with the improvement of ultra-stable laser performance requirements, it has changed from focusing mainly on vibration sensitivity in the vertical direction in the past to paying attention to the three directions (X-axis, Y-axis, and Z-axis). In this case, it is obviously very difficult to obtain the optimal parameter combination of the lowest vibration sensitivity in the three directions only by the commonly used single-factor and single-object analysis and calculation, as well as the commonly used observation method. The orthogonal experimental design method [31] can greatly reduce the number of tests without reducing the test feasibility. Through range analysis, the influence degree of each factor on the object can be obtained, and the optimal parameter combination required for the multi-object can be determined. The orthogonal experimental design method can be used to optimize the USORC’s parameters to achieve the least vibration sensitivity, but as far as we know, related research has not been reported.

In this work, based on the orthogonal experimental design method with multi-object, we optimize the parameters of a classic cylindrical USORC with a 100 mm length to achieve the minimum effect induced by the vibration sensitivity. According to the vibration characteristics of the USORC, the finite element model of quasi-static mechanics is established to simulate and calculate the vibration sensitivities. The L 16 (43) orthogonal table is adopted to design the orthogonal experiment based on a test of 4 levels and 3 factors including the position Zc of the support point in the Z-axis direction, the support point position Yp in the Y-axis direction, and the support pad area Ps. We simulate and analyze the vibration sensitivities under the three parameters. The vibration sensitivities in three directions are determined as three single-object values, and the normalized sum of the three vibration sensitivities is the comprehensive object value. Based on the range analysis, we analyze and discuss the influence degree of the three parameters on the object values. The optimal parameter combination schemes are obtained by using the comprehensive balance method and the comprehensive evaluation method, respectively. According to the corresponding fractional frequency stability of the ultra-stable laser, the final optimal parameter combination scheme A1B3C3 (Zc = 3 mm, Yp = 10 mm, and Ps = 3 mm) is determined and verified by the finite element method. This work provides a method of vibration sensitivities optimization for USORCs and is also beneficial for the vibration sensitivity design of a transportable USORC, which is affected by more factors.

This article is structured as follows: We present the design of the cylindrical USORC with a 100 mm length in Section 2. In Section 3, we design an orthogonal experiment including the determination of test indexes, design variables, orthogonal experimental table, and test results. Optimization of vibration sensitivity based on a comprehensive balance method and a comprehensive evaluation method is provided in Section 4. The final optimization results are determined in Section 4.3. The conclusions are summarized in Section 5.

2 Design of the USORC

In this work, we consider the cylindrical USORC designed by Millo et al. [7], which is widely used in related fields. The geometric model of the USORC is shown in Figure 1, which is supported by four square pads with a thickness of 1 mm. Both the length and diameter of the USORC are 100 mm. The diameter of the optical channel along the Y-axis is 10 mm. There are two mirrors with a diameter of 25.4 mm and a thickness of 6.3 mm. The venting hole with a 6 mm diameter is drilled in the upper half along the Z-axis. The position of the four support pads requires extensive calculation simulations to design the USORC with the lowest vibration sensitivity. Two square “cutouts” are machined along the Y-axis of the cylindrical spacer to provide the contact planes for these support points. The four support pads are symmetrically distributed across the spacer and are all located on the same horizontal plane. To have the least vibration sensitivity, the USORC should ideally be a perfect cylinder supported at the horizontal midplane XY, with contact points placed on the surface of the USORC. Because the cavity and support points are entirely symmetrical, vibration will not result in mirror translations. Mirror translation owing to vertical vibration is no longer guaranteed by the symmetry as a result of the cutouts disrupting the cavity symmetry about the XY plane. For some cutout designs, the simulation can, however, be used to determine a specific location for the support points to achieve the least vibration sensitivity. The cuts for the support points are positioned as follows [7]: Xc with respect to the YZ plane and Zc with respect to the XY plane. The distance from the USORC’s end along the Y-axis is indicated by Yp.

Figure 1 Geometric model of the cylindrical USORC [7]. Black triangles are used to indicate each of the four support points. (a) Front view and (b) side view.
Figure 1

Geometric model of the cylindrical USORC [7]. Black triangles are used to indicate each of the four support points. (a) Front view and (b) side view.

3 Test design

3.1 Simulation analysis model

The cylindrical USORC is analyzed by a quasi-static mechanical model, which is commonly used in the vibration sensitivity analysis [7,8,9,10,17,18,19]. The USORC is regarded as a single elastic body in the finite element analysis model. In the elastic limit, simulation deformations are determined. Elastic deformations of the USORC cause a cavity length change when the cavity is loaded by vibration acceleration. As shown in Table 1, the mechanical characteristics of the ultra-low expansion (ULE) glass have been used in simulation models. In order to save computational time, a quarter model is used in the calculation of vibration sensitivity along the Z-axis direction, and two half models are used in the analysis of vibration sensitivities along the X-axis and the Y-axis direction vibration. The geometry of the USORC is meshed with tetrahedral elements, where each tetrahedral element has 4 nodes and the side length of each tetrahedral element is about 1.5 mm. When calculating the vibration sensitivity, the USORC is subjected to 1 g of vibration acceleration. The calculation method of vibration sensitivity is based on the definition of Chen et al. [8].

Table 1

Material properties of the USORC [7]

Material properties Elastic modulus (GPa) Poisson ratio Density (kg/m3)
ULE 67.6 0.17 2,210

3.2 Determination of test indexes

Vibration sensitivity (including X-axis, Y-axis, and Z-axis) is the key index of USORC. For the same material and the same shape of the USORC, different parameters have different influence rules on vibration sensitivities. The vibration sensitivities will eventually affect the stability of the ultra-stable laser. In this work, vibration sensitivities along three directions ( S z , S x , and S y ) and the normalized sum (S) of the three vibration sensitivities are selected as three single-object values and comprehensive object values, respectively.

3.3 Design variables and values

For the USORC in this work, the main parameters affecting the vibration sensitivities include the position of the support point in the Z-axis direction (Zc), the position of the support point in the X-axis direction (Xc), the position of the support point in the Y-axis direction (Yp), and the support pad area (Ps), which affect the USORC vibration sensitivities to varying degrees. In the optimization process of these parameters, the range of design variables is very important, which not only affects whether the selected range has an optimal solution or a suboptimal solution but also affects the search efficiency of the optimization process. Referring to the study by Millo et al. [7], the position of the support point in the X-axis direction (Xc) is 47 mm. In order to meet the requirements of minimum vibration sensitivities and better parameters, the range of design variables in Table 2 is adopted. There are three design variables, the position of the support point in the Z-axis direction (Zc), the position of the support point in the Y-axis direction (Yp), and the support pad area (Ps), each of which is divided into four levels. A, B, and C denote Zc, Yp, and Ps, respectively.

Table 2

Factors and levels of orthogonal test

Level Position of support point in the Z-axis direction Position of support point in the Y-axis direction Support pad area
A B C
Zc (mm) Yp (mm) Ps (mm2)
1 3 2 1
2 5 6 2
3 7 10 3
4 9 14 4

3.4 Orthogonal experimental table and test results

The test of all different combinations of test conditions is called a comprehensive test. In this test, the full-scale test contains 64 different combinations of tests, to be conducted one by one, which is obviously time-consuming and unnecessary. This work is a test of 3 factors and 4 levels. We select L 16 (43) orthogonal table to design an orthogonal experiment, and only 16 tests are needed, which is 75% less than the comprehensive test. In the test, the vibration sensitivity values under the combination of different parameters are obtained. The test scheme and test results are shown in Table 3. S z , S x , and S y present the absolute values of vibration sensitivities along three directions, Z-axis, X-axis, and Y-axis. The normalized sum of vibration sensitivities in three directions is represented by S, which is also the comprehensive object value. Generally, the vibration in the Z-axis direction is dominant in the laboratory environment [32,33,34,35]. Therefore, in the normalization process, it is assumed that S z accounts for 80% and the other two items each account for 10%.

Table 3

Orthogonal table of experiment L 16 (43) and simulation test data

Number A B C S z S x S y S
Zc (mm) Yp (mm) Ps (mm2) 10−10/g 10−12/g 10−12/g
1 3 2 1 5.04 7.10 2.18 55.16
2 3 6 2 1.72 3.91 6.04 18.14
3 3 10 3 0.12 9.29 10.37 1.70
4 3 14 4 1.81 2.82 0.71 18.65
5 5 2 2 6.23 31.01 4.14 72.78
6 5 6 1 1.38 4.51 0.70 14.22
7 5 10 4 0.93 6.23 26.32 10.92
8 5 14 3 2.89 4.05 21.57 31.90
9 7 2 3 7.37 27.02 6.15 84.73
10 7 6 4 1.61 2.80 162.56 25.01
11 7 10 1 1.38 14.65 40.16 18.17
12 7 14 2 4.29 57.32 4.66 56.22
13 9 2 4 6.62 41.56 49.22 81.40
14 9 6 3 1.57 16.12 189.49 28.44
15 9 10 2 2.36 17.41 3.75 27.56
16 9 14 1 5.18 32.52 9.57 61.76

4 Optimization of vibration sensitivity

To obtain the optimal parameter combination of minimum vibration sensitivities, a comprehensive balance method and a comprehensive evaluation method are adopted for the optimization of vibration sensitivity in this work. The optimization process is as follows: First, the optimal combinations of three single objects are obtained by range analysis, and then the global optimal combination is selected by the comprehensive balance method. Second, through the range analysis of the normalization S, the optimal combination of parameters is determined. According to the comparison of the corresponding fractional frequency stability of the ultra-stable laser based on the optimal parameter combination schemes (including the comprehensive balance method and comprehensive evaluation method), the final optimal parameter combination scheme is obtained.

4.1 Comprehensive balance method

The three vibration sensitivities ( S z , S x , and S y ) are calculated and analyzed by single index one by one. For each vibration sensitivity index, the optimal combination of three design parameters is given. According to the importance of each vibration sensitivity index and the primary and secondary factors in each index, the overall optimal combination is finally determined. In this work, we use the range method to analyze the data to obtain the relationship between various factors and indicators.

Through the calculation and analysis of the range of the vibration sensitivity, the influence of various parameters on the vibration sensitivity S z of the USORC is obtained. The position Yp of the support point in the Y-axis direction has the greatest influence on vibration sensitivity S z , and the support pad area Ps has the least influence on vibration sensitivity S z , namely, B > A > C. The results are shown in Table 4 and Figure 2(a). In Table 4, L 1-1, L 2-1, L 3-1, and L 4-1 denote the sums of the vibration sensitivity S z for four levels, respectively. L 1-1-M , L 2-1-M , L 3-1-M , and L 4-1-M represent the means of L 1-1, L 2-1, L 3-1, and L 4-1, respectively. The range of the vibration sensitivity S z is denoted by D 1. According to the requirements of the USORC, the smaller the vibration sensitivity S z the better. The optimized combination of various parameters is A1B3C4, that is, the position Zc of the support point in the Z-axis direction is 3 mm, the position Yp of the support point in the Y-axis direction is 10 mm, the support pad area Ps is 4 mm2.

Table 4

Results of the ranges analysis of S z

Mean values and ranges of level scores Factors
A B C
L 1-1 8.69 25.26 12.98
L 2-1 11.43 6.28 14.6
L 3-1 14.65 4.79 11.95
L 4-1 15.73 14.17 10.97
L 1-1-M 2.17 6.32 3.25
L 2-1-M 2.86 1.57 3.65
L 3-1-M 3.66 1.20 2.99
L 4-1-M 3.93 3.54 2.74
D 1 1.76 5.12 0.91
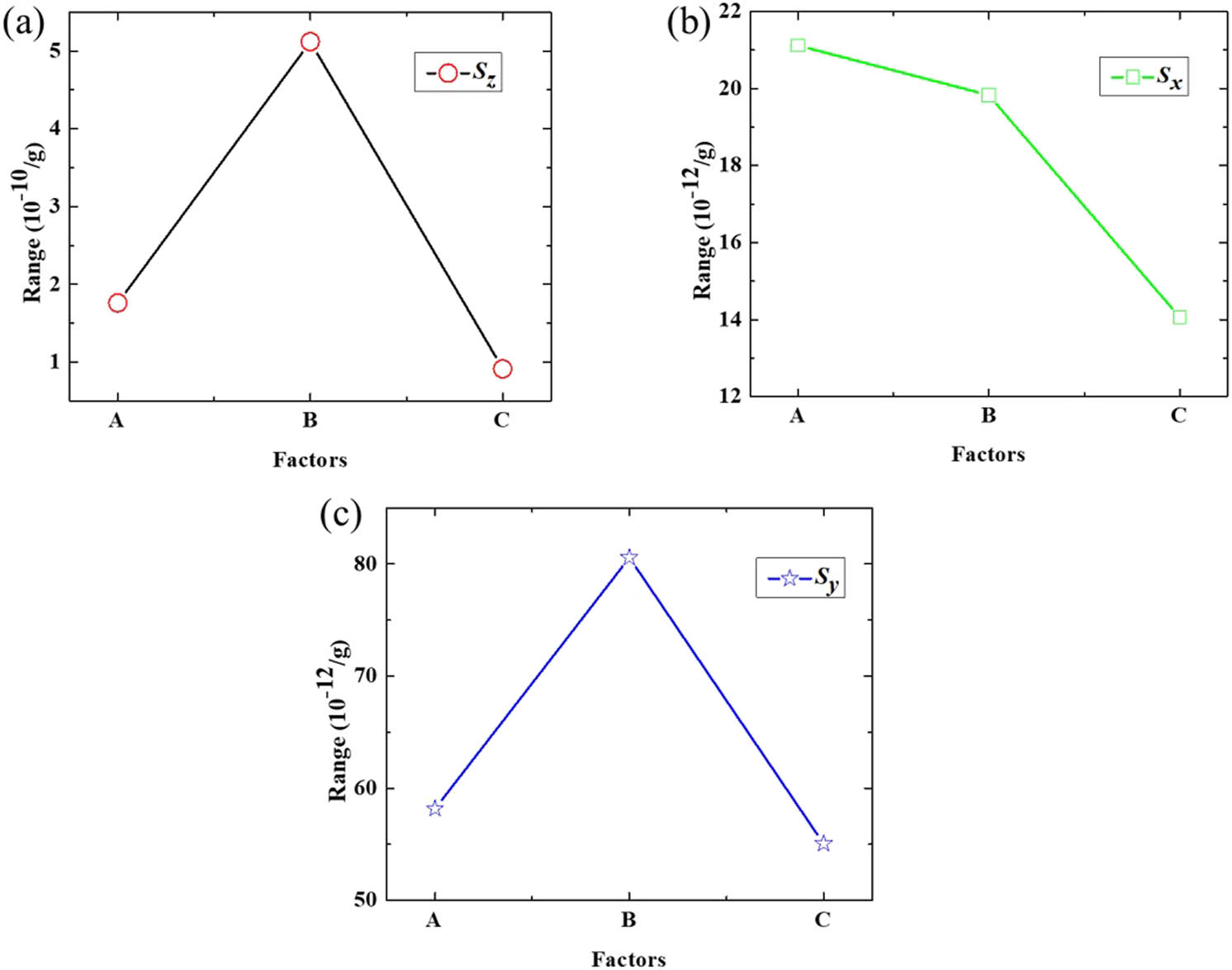
Figure 2 Range of the vibration sensitivity. (a) The Z-axis direction. (b) The X-axis direction. (c) The Y-axis direction.
Figure 2

Range of the vibration sensitivity. (a) The Z-axis direction. (b) The X-axis direction. (c) The Y-axis direction.

As shown in Table 5 and Figure 2(b), the impact of different parameters on the vibration sensitivity S x of the USORC is determined through the computation and examination of the vibration sensitivity range. In Table 5, the sums of the vibration sensitivity S x for four levels are expressed as L 1-2, L 2-2, L 3-2, and L 4-2, respectively. The mean values of L 1-2, L 2-2, L 3-2, and L 4-2 are represented by L 1-2-M , L 2-2-M , L 3-2-M , and L 4-2-M , correspondingly. D 2 represents the range of the vibration sensitivity S x . The support point’s position Zc in the Z-axis direction has the biggest impact on vibration sensitivity S x , while the support pad area Ps has the least vibration sensitivity S x , with A > B > C as the order of importance. The USORC requires that the vibration sensitivity S x should be as low as possible. The optimal combination of different parameters is A1B2C4, which means that the support point’s position Zc in the Z-axis direction is 3 mm, its position in the Y-axis direction is 6 mm, and the support pad area Ps is 4 mm2.

Table 5

Results of the ranges analysis of S x

Mean values and ranges of level scores Factors
A B C
L 1-2 23.12 106.69 58.78
L 2-2 45.8 27.34 109.65
L 3-2 101.79 47.58 56.48
L 4-2 107.61 96.71 53.41
L 1-2-M 5.78 26.67 14.70
L 2-2-M 11.45 6.84 27.41
L 3-2-M 25.45 11.90 14.12
L 4-2-M 26.90 24.18 13.35
D 2 21.12 19.83 14.06

As seen in Table 6 and Figure 2(c), the computation and analysis of the vibration sensitivity range are used to determine the effects of various factors on the USORC’s vibration sensitivity S y . The sums of the vibration sensitivity S y are represented as L 1-3, L 2-3, L 3-3, and L 4-3 in Table 5, correspondingly, for four levels. L 1-3-M , L 2-3-M , L 3-3-M , and L 4-3-M , respectively, indicate the means of L 1-3, L 2-3, L 3-3, and L 4-3. The range of the vibration sensitivity S y is represented by D 3. The most influence on vibration sensitivity S y comes from the support point’s position Yp along the Y-axis, while the least influence comes from the support pad area Ps, with B > A > C being the order of significance. The vibration sensitivity S y should meet the USORC’s requirements for minimum values. The ideal arrangement of the various parameters is A1B4C2, which specifies that the support point’s position Zc in the Z-axis direction, its position Yp in the Y-axis direction, and the support pad area Ps are 3 mm, 14 mm, and 2 mm2, respectively.

Table 6

Results of the ranges analysis of S y

Means and ranges of level scores Factors
A B C
L 1-3 19.3 61.69 52.61
L 2-3 52.73 358.79 18.59
L 3-3 213.53 80.6 227.58
L 4-3 252.03 36.51 238.81
L 1-3-M 4.83 15.42 13.15
L 2-3-M 13.18 89.70 4.65
L 3-3-M 53.38 20.15 56.90
L 4-3-M 63.01 9.13 59.70
D 3 58.18 80.57 55.05

In the vibration sensitivity analysis, the primary and secondary relationships of the three factors on the three indicators are: the vibration sensitivity S z along the Z-axis direction: B > A > C; the vibration sensitivity S x along the X-axis direction: A > B > C; the vibration sensitivity S y along the Y-axis direction: B > A > C. The three optimal schemes: The optimal scheme with the lowest vibration sensitivity S z as the evaluation objective is A1B3C4; the optimal solution with the minimal vibration sensitivity S x as the evaluation object is A1B2C4; and the optimal solution with the least vibration sensitivity S y is A1B4C2. A1 is in all the three optimal schemes, so A1 is first determined. Factor B has a great influence on all three vibration sensitivities, and it has the greatest influence on the vibration sensitivities S z and S y , which should be analyzed first. Compared with the other two indicators, S z is the most important indicator, so to ensure that it is the lowest first, B3 is selected. C4 appears in the optimal combination of the two optimal schemes, so C4 is selected. Finally, A1B3C4 is determined as the optimal combination by the comprehensive balance method.

4.2 Comprehensive evaluation method

Table 7 demonstrates how the computation and analysis of the comprehensive object values range are utilized to ascertain the influence of different parameters on the USORC’s comprehensive object S. The S for the four levels are denoted in Table 7 as L 1, L 2, L 3, and L 4, respectively. The means of L 1, L 2, L 3, and L 4 are represented by L 1-M , L 2-M , L 3-M , and L 4-M , correspondingly. D represents the range of the comprehensive object S. The support point’s position along the Y-axis, Yp, has the greatest impact on the overall object S, while the support pad area, Ps, has the least impact. B > A > C is the order of significance. The minimum values of the USORC must be satisfied by the comprehensive object S. The effect of C1, C3, and C4 on comprehensive object S is basically the consistency. Eventually, A1B3C1, A1B3C3, and A1B3C4 are selected.

Table 7

Results of the ranges analysis of the comprehensive evaluation

Mean values and ranges of level scores Factors
A B C
L 1 93.65 294.07 149.31
L 2 129.82 85.81 174.7
L 3 184.13 58.35 146.77
L 4 199.16 168.53 135.98
L 1-M 23.41 73.52 37.33
L 2-M 32.46 21.45 43.68
L 3-M 46.03 14.59 36.69
L 4-M 49.79 42.13 34.00
D 26.38 58.93 9.68

4.3 Optimization results

In order to obtain the final optimal scheme, we use the fractional frequency stability of the ultra-stable laser as the criterion indicator. The frequency relative variation in the laser due to the vibration sensitivity of a USORC can be expressed as follows [19,32]:

(1) ∆ v v = ∑ i = x , y , z ( S i × a i ) 2 1 2 ,

where v is the laser frequency, and Δv is the laser frequency change. We denote S i as the sensitivities of the USORC length to vibration acceleration along the X-axis, Y-axis, or Z-axis.

Most laboratory environments have vibrations of approximately 1 μg (or even lower) [32,33,34,35], so it is assumed that the vibration along the Z-axis direction is 1 μg and the vibration along the horizontal direction (X-axis and Y-axis) is 0.5 μg. According to Eq. (1), the fractional frequency stabilities of the ultra-stable laser based on the above optimal schemes are shown in Table 8.

Table 8

Fractional frequency stability of the ultra-stable laser based on the above optimal schemes

Number A B C S z S x S y Relative frequency stability
Zc (mm) Yp (mm) Ps (mm2) 10−10/g 10−12/g 10−12/g
A1B3C1 3 10 1 0.16 9.45 50.31 3.02 × 10−17
A1B3C3 3 10 3 0.12 9.29 10.37 1.39 × 10−17
A1B3C4 3 10 4 0.30 4.45 1.71 3.01 × 10−17

According to Table 8, it is easy to understand that the A1B3C3 is the optimal scheme, and the corresponding fractional frequency stability of the ultra-stable laser is 1.39 × 10−17. When the A1B3C3 is selected as the optimal combination, the USORC’s displacement in the optical axis is shown in Figure 3.

Figure 3 The USORC’s displacement in the optical axis when the A1B3C3 is selected as the optimal combination. Note that the undeformed USORC is displayed in gray. (a) 1 g acceleration along the Z-axis direction. (b) 1 g acceleration along the X-axis direction. (c) 1 g acceleration along the Y-axis direction.
Figure 3

The USORC’s displacement in the optical axis when the A1B3C3 is selected as the optimal combination. Note that the undeformed USORC is displayed in gray. (a) 1 g acceleration along the Z-axis direction. (b) 1 g acceleration along the X-axis direction. (c) 1 g acceleration along the Y-axis direction.

5 Conclusion

The vibration sensitivity is one of the core performance indicators of USORCs. To get wonderful performances of ultra-stable lasers, the vibration sensitivity is required to be as low as possible. In this work, taking a classical USORC with a 100 mm length as an example, we optimize its vibration sensitivities by using the orthogonal experimental design method with multi-object. Based on a test of 3 factors (including the position Zc of the support point in the Z-axis direction, the position Yp of the support point in the Y-axis direction, and the support pad area Ps) and 4 levels, the L 16 (43) orthogonal table is selected to design an orthogonal experiment. The vibration sensitivities under three important parameters are simulated and analyzed by the finite element method. We select the vibration sensitivity in three directions (X-axis, Y-axis, and Z-axis) as three single-object, and the comprehensive object value is the normalized sum of the three vibration sensitivities. According to the range analysis of the single-object value and the comprehensive object value, the influence degree of the three parameters on the object values is determined. The optimal parameter combination schemes are obtained by using the comprehensive balance method and the comprehensive evaluation method. By comparing the corresponding fractional frequency stability of the ultra-stable laser based on the above optimal parameter combination schemes, the final optimal parameter combination scheme is A1B3C3 (Zc = 3 mm, Yp = 10 mm, and Ps = 3 mm2), which is also verified by the finite element method. As far as we know, this is the first time to use the orthogonal experimental design method with multi-object on vibration sensitivity optimization of UROSC and verify its effectiveness. This work aims to provide a reference for vibration sensitivities optimization of an USORC, especially a transportable USORC affected by more factors, such as a squeezing force, a length-to-diameter ratio, and weight.

# These authors contributed equally to this work and should be considered first co-authors.

Acknowledgments

The authors would like to acknowledge the contribution of X. Zhang of Northwestern Polytechnical University to this work.

  1. Funding information: The project is partially supported by the Youth Innovation Promotion Association of the Chinese Academy of Sciences (Grant No. 1188000XGJ), the Chinese National Natural Science Foundation (Grant No. 11903041), and the Young Innovative Talents of the National Time Service Center of the Chinese Academy of Sciences (Grant No. Y917SC1).

  2. Author contributions: Conceptualization: G.X. and J.G.; methodology: D.J.; software: J.G.; validation: D.J. and H.Y.; investigation: G.X.; data curation: J.G. and X.D.; writing – original draft preparation: G.X.; writing – review and editing: G.X. and J.G.; visualization: L.Z. and Q.Z.; supervision: R.D.; project administration: T.L. and S.Z. All authors have accepted responsibility for the entire content of this manuscript and approved its submission.

  3. Conflict of interest: The authors state no conflict of interest.

References

[1] Predehl K, Grosche G, Raupach SMF, Droste S, Terra O, Alnis J, et al. A 920-kilometer optical fiber link for frequency metrology at the 19th decimal place. Science. 2012;336:441–4.10.1126/science.1218442Search in Google Scholar PubMed

[2] Kennedy CJ, Oelker E, Robinson JM, Bothwell T, Kedar D, Milner WR, et al. Precision metrology meets cosmology: improved constraints on ultralight dark matter from atom-cavity frequency comparisons. Phys Rev Lett. 2020;125:201302.10.1103/PhysRevLett.125.201302Search in Google Scholar PubMed

[3] Müller H, Peters A, Chu S. A precision measurement of the gravitational red shift by the interference of matter waves. Nature. 2010;463:926–9.10.1038/nature08776Search in Google Scholar PubMed

[4] Müller H, Stanwix P, Tobar M, Ivanov E, Herrmann S, Senger A, et al. Tests of relativity by complementary rotating Michelson-Morley experiments. Phys Rev Lett. 2007;99:050401.10.1103/PhysRevLett.99.050401Search in Google Scholar PubMed

[5] Luo J, Sheng L, Duan H, Gong Y, Hu S, Ji J, et al. TianQin: a space-borne gravitational wave detector. Class Quantum Gravity. 2016;33(3):035010.10.1088/0264-9381/33/3/035010Search in Google Scholar

[6] Chou CW, Hume DB, Rosenband T, Wineland DJ. Optical clocks and relativity. Science. 2010;329:1630–3.10.1126/science.1192720Search in Google Scholar PubMed

[7] Millo J, Magalhaes DV, Mandache C, Coq YL, English EML, Westergaard PG, et al. Ultrastable lasers based on vibration insensitive cavities. Phys Rev A. 2009;79:053829.10.1103/PhysRevA.79.053829Search in Google Scholar

[8] Chen L, Hall JL, Ye J, Yang T, Zang E, Li T. Vibration-induced elastic deformation of Fabry-Perot Cavities. Phys Rev A. 2006;74:053801.10.1103/PhysRevA.74.053801Search in Google Scholar

[9] Nazarova T, Riehle F, Sterr U. Vibration-insensitive reference cavity for an ultra-narrow-linewidth laser. Appl Phys B. 2006;83:531–6.10.1007/s00340-006-2225-ySearch in Google Scholar

[10] Webster SA, Oxborrow M, Gill P. Vibration insensitive optical cavity. Phys Rev A. 2007;75:011801.10.1103/PhysRevA.75.011801Search in Google Scholar

[11] Argence B, Prevost E, Lévèque T, Le Goff R, Bize S, Lemonde P, et al. Prototype of an ultra-stable optical cavity for space applications. Opt Express. 2012;20:25409–20.10.1364/OE.20.025409Search in Google Scholar PubMed

[12] Leibrandt D, Bergquist J, Rosenband T. Cavity-stabilized laser with acceleration sensitivity below 10−12 g-1. Phys Rev A. 2013;87:023829.10.1103/PhysRevA.87.023829Search in Google Scholar

[13] Leibrandt DR, Thorpe MJ, Notcutt M, Drullinger RE, Rosenband T, Bergquist JC. Spherical reference cavities for frequency stabilization of lasers in non-laboratory environments. Opt Express. 2011;19:3471–82.10.1364/OE.19.003471Search in Google Scholar PubMed

[14] Häfner S, Herbers S, Vogt S, Lisdat C, Sterr U. Transportable interrogation laser system with an instability of mod σy = 3 × 10−16. Opt Express. 2020;28(11):16407–16.10.1364/OE.390105Search in Google Scholar PubMed

[15] Chen Q, Nevsky A, Cardace M, Schiller S, Legero T, Häfner S, et al. A compact, robust, and transportable ultra-stable laser with a fractional frequency instability of 1 × 10−15. Rev Sci Instrum. 2014;85:113107.10.1063/1.4898334Search in Google Scholar PubMed

[16] Xu G, Jiao D, Chen L, Zhang L, Dong R, Liu T, et al. Analysis of vibration sensitivity induced by the elastic deformation of vertical optical reference cavities. IEEE Access. 2020;8:194466–76.10.1109/ACCESS.2020.3033311Search in Google Scholar

[17] Webster S, Gill. P. Force-insensitive optical cavity. Opt Lett. 2011;36(18):3572–4.10.1364/OL.36.003572Search in Google Scholar PubMed

[18] Tao B, Chen Q. A vibration-sensitive-cavity design holds impact of higher than 100g. Appl Phys B. 2018;124:228.10.1007/s00340-018-7096-5Search in Google Scholar

[19] Chen X, Jiang Y, Li B, Yu H, Jiang H, Wang T, et al. Laser frequency instability of 6 × 10−16 using 10-cm-long cavities on a cubic spacer. Chin Opt Lett. 2020;18:030201.10.3788/COL202018.030201Search in Google Scholar

[20] Cao J, Wang S, Yuan J, Liu D, Shu H, Huang X. Integrated multiple wavelength stabilization on a multi-channel cavity for a transportable optical clock. Opt Express. 2020;28(8):11852–60.10.1364/OE.383115Search in Google Scholar PubMed

[21] Xu G, Jiao D, Chen L, Zhang L, Dong R, Liu T, et al. Vibration modes of a transportable optical cavity. Opt Express. 2021;29(15):24264–77.10.1364/OE.422182Search in Google Scholar PubMed

[22] Herbers S, Häfner S, Dörscher S, Lücke T, Sterr U, Lisdat C. Transportable clock laser system with an instability of 1.6 × 10−16. Opt Lett. 2022;47:5441–4.10.1364/OL.470984Search in Google Scholar PubMed

[23] Xiao R, Xu Y, Wang Y, Sun H, Chen Q. Transportable 30 cm optical cavity based ultrastable lasers with beating instability of 2 × 10−16. Appl Phys B. 2022;128:220.10.1007/s00340-022-07938-0Search in Google Scholar

[24] Jiao D, Deng X, Gao J, Zhang L, Xu G, Liu T, et al. Highly vibration-resistant sub-Hertz ultra-stable laser passing over 1700 km transport test. Infrared Phys Technol. 2023;130:104608.10.1016/j.infrared.2023.104608Search in Google Scholar

[25] Häfner S, Falke S, Grebing C, Vogt S, Legero T, Merimaa M, et al. 8 × 10−17 fractional laser frequency instability with a long room-temperature cavity. Opt Lett. 2015;40:2112–5.10.1364/OL.40.002112Search in Google Scholar PubMed

[26] Matei DG, Legero T, Häfner S, Grebing C, Weyrich R, Zhang W, et al. 1.5 μm Lasers with Sub-10 mHz Linewidth. Phys Rev Lett. 2017;118:263202.10.1364/CLEO_SI.2017.SW1J.1Search in Google Scholar

[27] Cole GD, Zhang W, Martin MJ, Ye J, Aspelmeyer M. Tenfold reduction of Brownian noise in high-reflectivity optical coatings. Nat Photonics. 2013;67:46–650.10.1038/nphoton.2013.174Search in Google Scholar

[28] Xu G, Zhang L, Liu J, Gao J, Chen L, Dong R, et al. Estimation of thermal noise for spindle optical reference cavities. Opt Commun. 2016;360:61–7.10.1016/j.optcom.2015.10.029Search in Google Scholar

[29] Robinson JM, Oelker E, Milner WR, Kedar D, Zhang W, Legero T, et al. Thermal noise and mechanical loss of SiO2/Ta2O5 optical coatings at cryogenic temperatures. Opt Lett. 2021;46:592–5.10.1364/OL.413758Search in Google Scholar PubMed

[30] Xu G, Jiao D, Chen L, Zhang L, Dong R, Liu T, et al. Thermal noise in cubic optical cavities. Photonics. 2021;8:261.10.3390/photonics8070261Search in Google Scholar

[31] Taguchi G. Introduction to Quality Engineering. Tokyo: Asian Productivity Organization; 1990.Search in Google Scholar

[32] Hafiz MA, Ablewski P, Masoudi AA, Martínez HÁ, Balling P, Barwood G, et al. Guidelines for developing optical clocks with 10-18 fractional frequency uncertainty; 2019. https://arxiv.org/abs/1906.11495.Search in Google Scholar

[33] Jiao D. Research on Key Technologies of Engineering Ultrastable Laser in Communication Band and its Application. China: University of Chinese Academy of Sciences; 2020.Search in Google Scholar

[34] Newell DB, Richman SJ, Nelson PG, Stebbins RT, Bender PL, Faller JE, et al. An ultra-low-noise, low-frequency, six degrees of freedom active vibration isolator. Rev Sci Instrum. 1997;68:3211–9.10.1063/1.1148269Search in Google Scholar

[35] Álvarez MD. Optical cavities for optical atomic clocks, atom interferometry and gravitational-wave detection. England: National Physical Laboratory and University of Birmingham; 2018.10.1007/978-3-030-20863-9Search in Google Scholar
Received: 2023-03-07
Revised: 2023-06-13
Accepted: 2023-06-19
Published Online: 2023-07-29

© 2023 the author(s), published by De Gruyter

This work is licensed under the Creative Commons Attribution 4.0 International License.

Articles in the same Issue

  1. Regular Articles
  2. Dynamic properties of the attachment oscillator arising in the nanophysics
  3. Parametric simulation of stagnation point flow of motile microorganism hybrid nanofluid across a circular cylinder with sinusoidal radius
  4. Fractal-fractional advection–diffusion–reaction equations by Ritz approximation approach
  5. Behaviour and onset of low-dimensional chaos with a periodically varying loss in single-mode homogeneously broadened laser
  6. Ammonia gas-sensing behavior of uniform nanostructured PPy film prepared by simple-straightforward in situ chemical vapor oxidation
  7. Analysis of the working mechanism and detection sensitivity of a flash detector
  8. Flat and bent branes with inner structure in two-field mimetic gravity
  9. Heat transfer analysis of the MHD stagnation-point flow of third-grade fluid over a porous sheet with thermal radiation effect: An algorithmic approach
  10. Weighted survival functional entropy and its properties
  11. Bioconvection effect in the Carreau nanofluid with Cattaneo–Christov heat flux using stagnation point flow in the entropy generation: Micromachines level study
  12. Study on the impulse mechanism of optical films formed by laser plasma shock waves
  13. Analysis of sweeping jet and film composite cooling using the decoupled model
  14. Research on the influence of trapezoidal magnetization of bonded magnetic ring on cogging torque
  15. Tripartite entanglement and entanglement transfer in a hybrid cavity magnomechanical system
  16. Compounded Bell-G class of statistical models with applications to COVID-19 and actuarial data
  17. Degradation of Vibrio cholerae from drinking water by the underwater capillary discharge
  18. Multiple Lie symmetry solutions for effects of viscous on magnetohydrodynamic flow and heat transfer in non-Newtonian thin film
  19. Thermal characterization of heat source (sink) on hybridized (Cu–Ag/EG) nanofluid flow via solid stretchable sheet
  20. Optimizing condition monitoring of ball bearings: An integrated approach using decision tree and extreme learning machine for effective decision-making
  21. Study on the inter-porosity transfer rate and producing degree of matrix in fractured-porous gas reservoirs
  22. Interstellar radiation as a Maxwell field: Improved numerical scheme and application to the spectral energy density
  23. Numerical study of hybridized Williamson nanofluid flow with TC4 and Nichrome over an extending surface
  24. Controlling the physical field using the shape function technique
  25. Significance of heat and mass transport in peristaltic flow of Jeffrey material subject to chemical reaction and radiation phenomenon through a tapered channel
  26. Complex dynamics of a sub-quadratic Lorenz-like system
  27. Stability control in a helicoidal spin–orbit-coupled open Bose–Bose mixture
  28. Research on WPD and DBSCAN-L-ISOMAP for circuit fault feature extraction
  29. Simulation for formation process of atomic orbitals by the finite difference time domain method based on the eight-element Dirac equation
  30. A modified power-law model: Properties, estimation, and applications
  31. Bayesian and non-Bayesian estimation of dynamic cumulative residual Tsallis entropy for moment exponential distribution under progressive censored type II
  32. Computational analysis and biomechanical study of Oldroyd-B fluid with homogeneous and heterogeneous reactions through a vertical non-uniform channel
  33. Predictability of machine learning framework in cross-section data
  34. Chaotic characteristics and mixing performance of pseudoplastic fluids in a stirred tank
  35. Isomorphic shut form valuation for quantum field theory and biological population models
  36. Vibration sensitivity minimization of an ultra-stable optical reference cavity based on orthogonal experimental design
  37. Effect of dysprosium on the radiation-shielding features of SiO2–PbO–B2O3 glasses
  38. Asymptotic formulations of anti-plane problems in pre-stressed compressible elastic laminates
  39. A study on soliton, lump solutions to a generalized (3+1)-dimensional Hirota--Satsuma--Ito equation
  40. Tangential electrostatic field at metal surfaces
  41. Bioconvective gyrotactic microorganisms in third-grade nanofluid flow over a Riga surface with stratification: An approach to entropy minimization
  42. Infrared spectroscopy for ageing assessment of insulating oils via dielectric loss factor and interfacial tension
  43. Influence of cationic surfactants on the growth of gypsum crystals
  44. Study on instability mechanism of KCl/PHPA drilling waste fluid
  45. Analytical solutions of the extended Kadomtsev–Petviashvili equation in nonlinear media
  46. A novel compact highly sensitive non-invasive microwave antenna sensor for blood glucose monitoring
  47. Inspection of Couette and pressure-driven Poiseuille entropy-optimized dissipated flow in a suction/injection horizontal channel: Analytical solutions
  48. Conserved vectors and solutions of the two-dimensional potential KP equation
  49. The reciprocal linear effect, a new optical effect of the Sagnac type
  50. Optimal interatomic potentials using modified method of least squares: Optimal form of interatomic potentials
  51. The soliton solutions for stochastic Calogero–Bogoyavlenskii Schiff equation in plasma physics/fluid mechanics
  52. Research on absolute ranging technology of resampling phase comparison method based on FMCW
  53. Analysis of Cu and Zn contents in aluminum alloys by femtosecond laser-ablation spark-induced breakdown spectroscopy
  54. Nonsequential double ionization channels control of CO2 molecules with counter-rotating two-color circularly polarized laser field by laser wavelength
  55. Fractional-order modeling: Analysis of foam drainage and Fisher's equations
  56. Thermo-solutal Marangoni convective Darcy-Forchheimer bio-hybrid nanofluid flow over a permeable disk with activation energy: Analysis of interfacial nanolayer thickness
  57. Investigation on topology-optimized compressor piston by metal additive manufacturing technique: Analytical and numeric computational modeling using finite element analysis in ANSYS
  58. Breast cancer segmentation using a hybrid AttendSeg architecture combined with a gravitational clustering optimization algorithm using mathematical modelling
  59. On the localized and periodic solutions to the time-fractional Klein-Gordan equations: Optimal additive function method and new iterative method
  60. 3D thin-film nanofluid flow with heat transfer on an inclined disc by using HWCM
  61. Numerical study of static pressure on the sonochemistry characteristics of the gas bubble under acoustic excitation
  62. Optimal auxiliary function method for analyzing nonlinear system of coupled Schrödinger–KdV equation with Caputo operator
  63. Analysis of magnetized micropolar fluid subjected to generalized heat-mass transfer theories
  64. Does the Mott problem extend to Geiger counters?
  65. Stability analysis, phase plane analysis, and isolated soliton solution to the LGH equation in mathematical physics
  66. Effects of Joule heating and reaction mechanisms on couple stress fluid flow with peristalsis in the presence of a porous material through an inclined channel
  67. Bayesian and E-Bayesian estimation based on constant-stress partially accelerated life testing for inverted Topp–Leone distribution
  68. Dynamical and physical characteristics of soliton solutions to the (2+1)-dimensional Konopelchenko–Dubrovsky system
  69. Study of fractional variable order COVID-19 environmental transformation model
  70. Sisko nanofluid flow through exponential stretching sheet with swimming of motile gyrotactic microorganisms: An application to nanoengineering
  71. Influence of the regularization scheme in the QCD phase diagram in the PNJL model
  72. Fixed-point theory and numerical analysis of an epidemic model with fractional calculus: Exploring dynamical behavior
  73. Computational analysis of reconstructing current and sag of three-phase overhead line based on the TMR sensor array
  74. Investigation of tripled sine-Gordon equation: Localized modes in multi-stacked long Josephson junctions
  75. High-sensitivity on-chip temperature sensor based on cascaded microring resonators
  76. Pathological study on uncertain numbers and proposed solutions for discrete fuzzy fractional order calculus
  77. Bifurcation, chaotic behavior, and traveling wave solution of stochastic coupled Konno–Oono equation with multiplicative noise in the Stratonovich sense
  78. Thermal radiation and heat generation on three-dimensional Casson fluid motion via porous stretching surface with variable thermal conductivity
  79. Numerical simulation and analysis of Airy's-type equation
  80. A homotopy perturbation method with Elzaki transformation for solving the fractional Biswas–Milovic model
  81. Heat transfer performance of magnetohydrodynamic multiphase nanofluid flow of Cu–Al2O3/H2O over a stretching cylinder
  82. ΛCDM and the principle of equivalence
  83. Axisymmetric stagnation-point flow of non-Newtonian nanomaterial and heat transport over a lubricated surface: Hybrid homotopy analysis method simulations
  84. HAM simulation for bioconvective magnetohydrodynamic flow of Walters-B fluid containing nanoparticles and microorganisms past a stretching sheet with velocity slip and convective conditions
  85. Coupled heat and mass transfer mathematical study for lubricated non-Newtonian nanomaterial conveying oblique stagnation point flow: A comparison of viscous and viscoelastic nanofluid model
  86. Power Topp–Leone exponential negative family of distributions with numerical illustrations to engineering and biological data
  87. Extracting solitary solutions of the nonlinear Kaup–Kupershmidt (KK) equation by analytical method
  88. A case study on the environmental and economic impact of photovoltaic systems in wastewater treatment plants
  89. Application of IoT network for marine wildlife surveillance
  90. Non-similar modeling and numerical simulations of microploar hybrid nanofluid adjacent to isothermal sphere
  91. Joint optimization of two-dimensional warranty period and maintenance strategy considering availability and cost constraints
  92. Numerical investigation of the flow characteristics involving dissipation and slip effects in a convectively nanofluid within a porous medium
  93. Spectral uncertainty analysis of grassland and its camouflage materials based on land-based hyperspectral images
  94. Application of low-altitude wind shear recognition algorithm and laser wind radar in aviation meteorological services
  95. Investigation of different structures of screw extruders on the flow in direct ink writing SiC slurry based on LBM
  96. Harmonic current suppression method of virtual DC motor based on fuzzy sliding mode
  97. Micropolar flow and heat transfer within a permeable channel using the successive linearization method
  98. Different lump k-soliton solutions to (2+1)-dimensional KdV system using Hirota binary Bell polynomials
  99. Investigation of nanomaterials in flow of non-Newtonian liquid toward a stretchable surface
  100. Weak beat frequency extraction method for photon Doppler signal with low signal-to-noise ratio
  101. Electrokinetic energy conversion of nanofluids in porous microtubes with Green’s function
  102. Examining the role of activation energy and convective boundary conditions in nanofluid behavior of Couette-Poiseuille flow
  103. Review Article
  104. Effects of stretching on phase transformation of PVDF and its copolymers: A review
  105. Special Issue on Transport phenomena and thermal analysis in micro/nano-scale structure surfaces - Part IV
  106. Prediction and monitoring model for farmland environmental system using soil sensor and neural network algorithm
  107. Special Issue on Advanced Topics on the Modelling and Assessment of Complicated Physical Phenomena - Part III
  108. Some standard and nonstandard finite difference schemes for a reaction–diffusion–chemotaxis model
  109. Special Issue on Advanced Energy Materials - Part II
  110. Rapid productivity prediction method for frac hits affected wells based on gas reservoir numerical simulation and probability method
  111. Special Issue on Novel Numerical and Analytical Techniques for Fractional Nonlinear Schrodinger Type - Part III
  112. Adomian decomposition method for solution of fourteenth order boundary value problems
  113. New soliton solutions of modified (3+1)-D Wazwaz–Benjamin–Bona–Mahony and (2+1)-D cubic Klein–Gordon equations using first integral method
  114. On traveling wave solutions to Manakov model with variable coefficients
  115. Rational approximation for solving Fredholm integro-differential equations by new algorithm
  116. Special Issue on Predicting pattern alterations in nature - Part I
  117. Modeling the monkeypox infection using the Mittag–Leffler kernel
  118. Spectral analysis of variable-order multi-terms fractional differential equations
  119. Special Issue on Nanomaterial utilization and structural optimization - Part I
  120. Heat treatment and tensile test of 3D-printed parts manufactured at different build orientations
https://doi.org/10.1515/phys-2022-0269
Keywords for this article
ultra-stable optical reference cavity; optimization; vibration sensitivity; orthogonal experimental design; ultra-stable laser
Creative Commons
BY 4.0

Articles in the same Issue

  1. Regular Articles
  2. Dynamic properties of the attachment oscillator arising in the nanophysics
  3. Parametric simulation of stagnation point flow of motile microorganism hybrid nanofluid across a circular cylinder with sinusoidal radius
  4. Fractal-fractional advection–diffusion–reaction equations by Ritz approximation approach
  5. Behaviour and onset of low-dimensional chaos with a periodically varying loss in single-mode homogeneously broadened laser
  6. Ammonia gas-sensing behavior of uniform nanostructured PPy film prepared by simple-straightforward in situ chemical vapor oxidation
  7. Analysis of the working mechanism and detection sensitivity of a flash detector
  8. Flat and bent branes with inner structure in two-field mimetic gravity
  9. Heat transfer analysis of the MHD stagnation-point flow of third-grade fluid over a porous sheet with thermal radiation effect: An algorithmic approach
  10. Weighted survival functional entropy and its properties
  11. Bioconvection effect in the Carreau nanofluid with Cattaneo–Christov heat flux using stagnation point flow in the entropy generation: Micromachines level study
  12. Study on the impulse mechanism of optical films formed by laser plasma shock waves
  13. Analysis of sweeping jet and film composite cooling using the decoupled model
  14. Research on the influence of trapezoidal magnetization of bonded magnetic ring on cogging torque
  15. Tripartite entanglement and entanglement transfer in a hybrid cavity magnomechanical system
  16. Compounded Bell-G class of statistical models with applications to COVID-19 and actuarial data
  17. Degradation of Vibrio cholerae from drinking water by the underwater capillary discharge
  18. Multiple Lie symmetry solutions for effects of viscous on magnetohydrodynamic flow and heat transfer in non-Newtonian thin film
  19. Thermal characterization of heat source (sink) on hybridized (Cu–Ag/EG) nanofluid flow via solid stretchable sheet
  20. Optimizing condition monitoring of ball bearings: An integrated approach using decision tree and extreme learning machine for effective decision-making
  21. Study on the inter-porosity transfer rate and producing degree of matrix in fractured-porous gas reservoirs
  22. Interstellar radiation as a Maxwell field: Improved numerical scheme and application to the spectral energy density
  23. Numerical study of hybridized Williamson nanofluid flow with TC4 and Nichrome over an extending surface
  24. Controlling the physical field using the shape function technique
  25. Significance of heat and mass transport in peristaltic flow of Jeffrey material subject to chemical reaction and radiation phenomenon through a tapered channel
  26. Complex dynamics of a sub-quadratic Lorenz-like system
  27. Stability control in a helicoidal spin–orbit-coupled open Bose–Bose mixture
  28. Research on WPD and DBSCAN-L-ISOMAP for circuit fault feature extraction
  29. Simulation for formation process of atomic orbitals by the finite difference time domain method based on the eight-element Dirac equation
  30. A modified power-law model: Properties, estimation, and applications
  31. Bayesian and non-Bayesian estimation of dynamic cumulative residual Tsallis entropy for moment exponential distribution under progressive censored type II
  32. Computational analysis and biomechanical study of Oldroyd-B fluid with homogeneous and heterogeneous reactions through a vertical non-uniform channel
  33. Predictability of machine learning framework in cross-section data
  34. Chaotic characteristics and mixing performance of pseudoplastic fluids in a stirred tank
  35. Isomorphic shut form valuation for quantum field theory and biological population models
  36. Vibration sensitivity minimization of an ultra-stable optical reference cavity based on orthogonal experimental design
  37. Effect of dysprosium on the radiation-shielding features of SiO2–PbO–B2O3 glasses
  38. Asymptotic formulations of anti-plane problems in pre-stressed compressible elastic laminates
  39. A study on soliton, lump solutions to a generalized (3+1)-dimensional Hirota--Satsuma--Ito equation
  40. Tangential electrostatic field at metal surfaces
  41. Bioconvective gyrotactic microorganisms in third-grade nanofluid flow over a Riga surface with stratification: An approach to entropy minimization
  42. Infrared spectroscopy for ageing assessment of insulating oils via dielectric loss factor and interfacial tension
  43. Influence of cationic surfactants on the growth of gypsum crystals
  44. Study on instability mechanism of KCl/PHPA drilling waste fluid
  45. Analytical solutions of the extended Kadomtsev–Petviashvili equation in nonlinear media
  46. A novel compact highly sensitive non-invasive microwave antenna sensor for blood glucose monitoring
  47. Inspection of Couette and pressure-driven Poiseuille entropy-optimized dissipated flow in a suction/injection horizontal channel: Analytical solutions
  48. Conserved vectors and solutions of the two-dimensional potential KP equation
  49. The reciprocal linear effect, a new optical effect of the Sagnac type
  50. Optimal interatomic potentials using modified method of least squares: Optimal form of interatomic potentials
  51. The soliton solutions for stochastic Calogero–Bogoyavlenskii Schiff equation in plasma physics/fluid mechanics
  52. Research on absolute ranging technology of resampling phase comparison method based on FMCW
  53. Analysis of Cu and Zn contents in aluminum alloys by femtosecond laser-ablation spark-induced breakdown spectroscopy
  54. Nonsequential double ionization channels control of CO2 molecules with counter-rotating two-color circularly polarized laser field by laser wavelength
  55. Fractional-order modeling: Analysis of foam drainage and Fisher's equations
  56. Thermo-solutal Marangoni convective Darcy-Forchheimer bio-hybrid nanofluid flow over a permeable disk with activation energy: Analysis of interfacial nanolayer thickness
  57. Investigation on topology-optimized compressor piston by metal additive manufacturing technique: Analytical and numeric computational modeling using finite element analysis in ANSYS
  58. Breast cancer segmentation using a hybrid AttendSeg architecture combined with a gravitational clustering optimization algorithm using mathematical modelling
  59. On the localized and periodic solutions to the time-fractional Klein-Gordan equations: Optimal additive function method and new iterative method
  60. 3D thin-film nanofluid flow with heat transfer on an inclined disc by using HWCM
  61. Numerical study of static pressure on the sonochemistry characteristics of the gas bubble under acoustic excitation
  62. Optimal auxiliary function method for analyzing nonlinear system of coupled Schrödinger–KdV equation with Caputo operator
  63. Analysis of magnetized micropolar fluid subjected to generalized heat-mass transfer theories
  64. Does the Mott problem extend to Geiger counters?
  65. Stability analysis, phase plane analysis, and isolated soliton solution to the LGH equation in mathematical physics
  66. Effects of Joule heating and reaction mechanisms on couple stress fluid flow with peristalsis in the presence of a porous material through an inclined channel
  67. Bayesian and E-Bayesian estimation based on constant-stress partially accelerated life testing for inverted Topp–Leone distribution
  68. Dynamical and physical characteristics of soliton solutions to the (2+1)-dimensional Konopelchenko–Dubrovsky system
  69. Study of fractional variable order COVID-19 environmental transformation model
  70. Sisko nanofluid flow through exponential stretching sheet with swimming of motile gyrotactic microorganisms: An application to nanoengineering
  71. Influence of the regularization scheme in the QCD phase diagram in the PNJL model
  72. Fixed-point theory and numerical analysis of an epidemic model with fractional calculus: Exploring dynamical behavior
  73. Computational analysis of reconstructing current and sag of three-phase overhead line based on the TMR sensor array
  74. Investigation of tripled sine-Gordon equation: Localized modes in multi-stacked long Josephson junctions
  75. High-sensitivity on-chip temperature sensor based on cascaded microring resonators
  76. Pathological study on uncertain numbers and proposed solutions for discrete fuzzy fractional order calculus
  77. Bifurcation, chaotic behavior, and traveling wave solution of stochastic coupled Konno–Oono equation with multiplicative noise in the Stratonovich sense
  78. Thermal radiation and heat generation on three-dimensional Casson fluid motion via porous stretching surface with variable thermal conductivity
  79. Numerical simulation and analysis of Airy's-type equation
  80. A homotopy perturbation method with Elzaki transformation for solving the fractional Biswas–Milovic model
  81. Heat transfer performance of magnetohydrodynamic multiphase nanofluid flow of Cu–Al2O3/H2O over a stretching cylinder
  82. ΛCDM and the principle of equivalence
  83. Axisymmetric stagnation-point flow of non-Newtonian nanomaterial and heat transport over a lubricated surface: Hybrid homotopy analysis method simulations
  84. HAM simulation for bioconvective magnetohydrodynamic flow of Walters-B fluid containing nanoparticles and microorganisms past a stretching sheet with velocity slip and convective conditions
  85. Coupled heat and mass transfer mathematical study for lubricated non-Newtonian nanomaterial conveying oblique stagnation point flow: A comparison of viscous and viscoelastic nanofluid model
  86. Power Topp–Leone exponential negative family of distributions with numerical illustrations to engineering and biological data
  87. Extracting solitary solutions of the nonlinear Kaup–Kupershmidt (KK) equation by analytical method
  88. A case study on the environmental and economic impact of photovoltaic systems in wastewater treatment plants
  89. Application of IoT network for marine wildlife surveillance
  90. Non-similar modeling and numerical simulations of microploar hybrid nanofluid adjacent to isothermal sphere
  91. Joint optimization of two-dimensional warranty period and maintenance strategy considering availability and cost constraints
  92. Numerical investigation of the flow characteristics involving dissipation and slip effects in a convectively nanofluid within a porous medium
  93. Spectral uncertainty analysis of grassland and its camouflage materials based on land-based hyperspectral images
  94. Application of low-altitude wind shear recognition algorithm and laser wind radar in aviation meteorological services
  95. Investigation of different structures of screw extruders on the flow in direct ink writing SiC slurry based on LBM
  96. Harmonic current suppression method of virtual DC motor based on fuzzy sliding mode
  97. Micropolar flow and heat transfer within a permeable channel using the successive linearization method
  98. Different lump k-soliton solutions to (2+1)-dimensional KdV system using Hirota binary Bell polynomials
  99. Investigation of nanomaterials in flow of non-Newtonian liquid toward a stretchable surface
  100. Weak beat frequency extraction method for photon Doppler signal with low signal-to-noise ratio
  101. Electrokinetic energy conversion of nanofluids in porous microtubes with Green’s function
  102. Examining the role of activation energy and convective boundary conditions in nanofluid behavior of Couette-Poiseuille flow
  103. Review Article
  104. Effects of stretching on phase transformation of PVDF and its copolymers: A review
  105. Special Issue on Transport phenomena and thermal analysis in micro/nano-scale structure surfaces - Part IV
  106. Prediction and monitoring model for farmland environmental system using soil sensor and neural network algorithm
  107. Special Issue on Advanced Topics on the Modelling and Assessment of Complicated Physical Phenomena - Part III
  108. Some standard and nonstandard finite difference schemes for a reaction–diffusion–chemotaxis model
  109. Special Issue on Advanced Energy Materials - Part II
  110. Rapid productivity prediction method for frac hits affected wells based on gas reservoir numerical simulation and probability method
  111. Special Issue on Novel Numerical and Analytical Techniques for Fractional Nonlinear Schrodinger Type - Part III
  112. Adomian decomposition method for solution of fourteenth order boundary value problems
  113. New soliton solutions of modified (3+1)-D Wazwaz–Benjamin–Bona–Mahony and (2+1)-D cubic Klein–Gordon equations using first integral method
  114. On traveling wave solutions to Manakov model with variable coefficients
  115. Rational approximation for solving Fredholm integro-differential equations by new algorithm
  116. Special Issue on Predicting pattern alterations in nature - Part I
  117. Modeling the monkeypox infection using the Mittag–Leffler kernel
  118. Spectral analysis of variable-order multi-terms fractional differential equations
  119. Special Issue on Nanomaterial utilization and structural optimization - Part I
  120. Heat treatment and tensile test of 3D-printed parts manufactured at different build orientations
Sign up now to receive a 20% welcome discount
Institutional Access
How does access work?
Have an idea on how to improve our website?
Please write us.
© 2025 De Gruyter Brill
Downloaded on 11.9.2025 from https://www.degruyterbrill.com/document/doi/10.1515/phys-2022-0269/html
Scroll to top button