Multiple Lie symmetry solutions for effects of viscous on magnetohydrodynamic flow and heat transfer in non-Newtonian thin film

Muhammad Safdar; Safia Taj; Muhammad Bilal; Shoaib Ahmed; Muhammad Ijaz Khan; Sana Ben Moussa; Bandar M. Fadhl; Basim M. Makhdoum; Sayed M. Eldin

doi:10.1515/phys-2022-0244

Article Open Access

Multiple Lie symmetry solutions for effects of viscous on magnetohydrodynamic flow and heat transfer in non-Newtonian thin film

Muhammad Safdar , Safia Taj , Muhammad Bilal , Shoaib Ahmed , Muhammad Ijaz Khan , Sana Ben Moussa , Bandar M. Fadhl , Basim M. Makhdoum and Sayed M. Eldin

Published/Copyright: May 10, 2023

Published by

Become an author with De Gruyter Brill

Submit Manuscript Author Information Explore this Subject

From the journal Open Physics Volume 21 Issue 1

Abstract

Numerous flow and heat transfer studies have relied on the construction of similarity transformations which map the nonlinear partial differential equations (PDEs) describing the flow and heat transfer, to ordinary differential equations (ODEs). For these reduced equations, one finds multiple analytic and approximate solution procedures as compared to the flow PDEs. Here, we aim at constructing multiple classes of similarity transformations that are different from those already existing in the literature. We adopt the Lie symmetry method to derive these new similarity transformations which reveal new classes of ODEs corresponding to flow equations when applied to them. With these multiple classes of similarity transformations, one finds multiple reductions in the flow PDEs to ODEs. On solving these ODEs analytically or numerically, we obtain different kinds of flow and heat transfer patterns that help in determining optimized solutions in accordance with the physical requirements of a problem. For the said purpose, we derive Lie point symmetries for the magnetohydrodynamic Casson fluid flow and heat transfer in a thin film on an unsteady stretching sheet with viscous dissipation. Linear combinations of these Lie symmetries that are again the Lie symmetries of the flow model are employed here to construct new similarity transformations. We derive multiple Lie similarity transformations through the proposed procedure which lead us to more than one class of reduced ODEs obtained by applying the deduced transformations. We analyze the flow and heat transfer by deriving analytic solutions for the obtained classes of systems of ODEs using the homotopy analysis method. Magnetic parameters and viscous dissipation influences on the flow and heat transports are investigated and presented in graphical and tabulated formats.

Keywords: Casson fluid; viscous dissipation; magnetic field; Lie symmetry; similarity transformations; homotopy analysis method and analytic solution

1 Introduction

In a thin liquid film on an unsteady stretching surface, fluid flow and transfer of heat remained a field that received an enormous amount of attention over the past few decades [1,2,3,4,5,6,7,8,9,10,11,12,13]. These studies have been conducted by researchers working in different areas, e.g., engineering, pharmaceutical, physical sciences, and biology. The contributions signify the importance of fluid flows and heat transfers in thin films. To mention a few applications of fluid flows and heat transfers in thin films, one may consider coating wires as well as fibers, transpiration cooling, processing of food, reactor fluidization, and heat exchangers. Therefore, these problems are studied extensively under different physical conditions to acquire the optimum flow and heat transfer needed for a specific quality of a product. These studies are conducted experimentally as well as theoretically. For theoretical investigations, an approach that is adopted in many attempts is the conversion of the flow models that are genuinely non-linear partial differential equations (PDEs), to ordinary differential equations (ODEs). Similarity transformations enable such a reduction. Hence, through the construction of such similarity transformation, new solvable classes of the flow and heat transfer problems are revealed [14,15,16,17]. Reduction of PDEs defining these transports to ODEs eases derivations of solutions using approximate or analytic methods [18,19]. Because there are several well-established approximate and analytic solution schemes that are available for ODEs as compared to PDEs. Similarity transformations are invertible maps, i.e., they transform the flow PDEs to ODEs that are solved analytically or numerically and then these solutions can be inverted to obtain solutions for the flow PDEs. There exists a specific relation between velocity and temperature of the stretching surface and the similarity transformations. It assists in the reduction of the associated conditions to the desired format. Lie symmetry method systematically builds such similarity transformations [20].

In this article, first, we obtain Lie symmetries for the magnetohydrodynamic (MHD) Casson fluid flow and heat transfer in a thin film on an unsteady stretching sheet with viscous dissipation. These are point transformations that are invertible mappings of the dependent and independent variables of the flow equations which leave the flow equations to form invariant. The associated conditions also remain invariant under the admitted Lie point symmetries. This invariance criterion helps us in determining the stretching sheet velocity and temperature that initially are arbitrary functions of the time and one space variable. Second, invariants corresponding to linear combinations of the derived Lie symmetries are determined which provide similarity transformations to map PDEs describing the flow problem, to ODEs.

We use MAPLE here for the derivation of Lie symmetries as it includes Lie algebraic procedure to construct symmetries in PDEtools package. We obtain five Lie symmetries for the flow equations which constitute a five -dimensional Lie symmetry algebra. A linear combination of the Lie point symmetries is also a Lie point symmetry. Consideration of the Lie symmetries or their linear combinations for the construction of the similarity transformations depends on the form of the stretching sheet velocity and temperature they provide. Therefore, based on this, we present more than one reduction of the flow equations to ODEs, through similarity transformations as there exists more than one combination of the Lie symmetries which leaves the stretching sheet velocity and temperature as functions of time and space variables. On the obtained systems of ODEs, we apply the homotopy analysis method (HAM) to deduce the analytic solutions. The obtained solutions are interpreted with the help of figures and tables to demonstrate the effects of Prandtl number Pr , magnetic parameter Mn , Eckert number Ec , Casson parameter β , and the unsteadiness parameter S , on the velocity and temperature.

This article is organized as follows. The second section presents a review of the MHD flow and heat transfer in a Casson fluid thin film on an unsteady stretching surface with viscous dissipation and its Lie point symmetry generators. The subsequent section is on the construction of similarity transformations and reductions corresponding to them. The fourth section contains the derivation of the analytic solutions. The last section concludes this work.

2 MHD flow equations

The flow and heat transfer in the thin film of Casson fluid on an unsteady stretching sheet under the magnetic and viscous effects is written in terms of the following equations:

∂ u ∂ x + ∂ v ∂ y = 0 ,

∂ u ∂ t + u ∂ u ∂ x + v ∂ u ∂ y − ν 1 + 1 β ∂ 2 u ∂ y 2 − σ B 2 ρ u = 0 ,

(1) ∂ T ∂ t + u ∂ T ∂ x + v ∂ T ∂ y − κ ρ C p ∂ 2 T ∂ y 2 − μ ρ C p 1 + 1 β ∂ u ∂ y 2 = 0 ,

with the conditions

u ( t , x , 0 ) = U ( t , x ) , v ( t , x , 0 ) = 0 ,

T ( t , x , 0 ) = T s ( t , x ) ,

∂ u ( t , x , h ( t ) ) ∂ y = ∂ T ( t , x , h ( t ) ) ∂ y = 0 ,

(2) v ( t , x , h ( t ) ) = d h d t .

The same has been studied by Vijaya et al. [21] along with internal heating where a schematic diagram of the flow is provided. Lie point symmetries for the flow model (1) are given in Table 1. These are derivable from MAPLE using the package “PDEtools” and the built-in command “Infinitesimals.” For a detailed algebraic procedure to derive Lie symmetries for such systems of PDEs, readers are referred to the study by Safdar et al. [22]. Equations of the system (1) remain invariant under Lie symmetry generators and the transformations corresponding to these symmetries also leave equations of system (1) form invariant. These Lie transformations are given in Table 1. Furthermore, all the associated conditions (2) also remain invariant under the Lie point symmetry generators and Lie transformations given in Table 1. For verification of this, we use each symmetry generator on every condition in (2) through the following invariance criterion

(3) X j [ i ] ( ζ k ) | ζ k = 0 = 0 ,

Table 1

Lie symmetry generators and Lie symmetry transformations

Lie symmetry generator	Lie symmetry transformations
X 1 = ∂ ∂ x	t = t ̅ , x = x ̅ + ϵ , y = y ̅ , u = u ̅ , v = v ̅ , T = T ̅
X 2 = ∂ ∂ T	t = t ̅ , x = x ̅ , y = y ̅ , u = u ̅ , v = v ̅ , T = T ̅ + ϵ
X 3 = x ∂ ∂ x + 2 T ∂ ∂ T + u ∂ ∂ u	t = t ̅ , x = x ̅ e ϵ , y = y ̅ , u = u ̅ e ϵ , v = v ̅ , T = T ̅ e 2 ϵ
X 4 = t ∂ ∂ t + y 2 ∂ ∂ y − 2 T ∂ ∂ T − u ∂ ∂ u − v 2 ∂ ∂ v	t = t ̅ e ϵ , x = x ̅ , y = y ̅ e ϵ , u = u ̅ e − ϵ , v = v ̅ e ϵ , T = T ̅ e − 2 ϵ
X 5 = t − σ B 0 2 + α ρ α ρ ∂ ∂ x + ( − σ B 0 2 + α ρ ) t − σ B 0 2 + α ρ α ρ α ρ t ∂ ∂ u	t = t ̅ , x = x ̅ + ϵ t ( α ρ − σ B 0 2 ) / ( α ρ ) , y = y ̅ , u = u ̅ + ϵ ( α ρ − σ B 0 2 ) t α ρ − σ B 0 2 α ρ / ( α ρ t ) , v = v ̅ , T = T ̅

where i denotes the extension of the symmetry generator, and here, we require the first extension of X j . Further, j = 1,2 , … , 5 , and ζ k denotes the conditions (2) for k = 1,2 , … , 6 , e.g., ζ 1 ≔ u ( t , x , 0 ) = U ( t , x ) and vice versa. The above invariance criterion leads to specific formats of U ( t , x ) , T s ( t , x ) , and h ( t ) , corresponding to each symmetry of the flow model.

3 Lie similarity transformations of the flow equations

In this section, we investigate and construct all possible Lie similarity transformations corresponding to Lie symmetries X 1 − X 5 . We call them Lie similarity transformations which have been constructed [22,23,24,25] and authors [26–29] highlight some industrial applications of recent studies for flow models of this kind. Here, only X 3 , and X 4 are suitable to construct the similarity transformations [24] when one symmetry is used separately from the listed five symmetries in Table 1. Here, we use linear combinations of X 1 − X 5 of these generators to construct Lie similarity transformations. A few of these linear combinations are selected for derivation of Lie similarity transformations based upon the format they yield for stretching sheet velocity and temperature. In the studies conducted earlier on this type of fluid and heat transports [22,23,24,25], both the said quantities are set to be dependent on both t and x . We are also taking only those linear combinations of X 1 − X 5 into consideration which leave both the said quantities as functions of time and space variables. These linear combinations of the symmetry generators when employed on the stretching sheet velocity U ( t , x ) and temperature T s ( t , x ) lead to functions depending on both x and t . Hence, they yield the desired form along with h ( t ) .

In a study by Taj et al. [24], the following similarity transformations are derived using X 3 and X 4

y = δ α ν t b η , u = − bx α t d f d η ,

(4) v = δ b ν α t f , T = x 2 t 2 θ ,

which transform the flow Eq. (1) to

1 + 1 β d 3 f d η 3 + S δ 2 d f d η − δ 2 f d 2 f d η 2 + δ 2 d f d η 2 + S η δ 2 2 d 2 f d η 2 − δ 2 M n d f d η = 0 ,

(5) 1 Pr d 2 θ d η 2 + 2 S δ 2 θ + S η δ 2 2 d θ d η + 2 δ 2 θ d f d η − δ 2 f d θ d η + Ec 1 + 1 β d 2 f d η 2 2 = 0 .

The associated conditions (2) under (4) map to

f ( 0 ) = 0 , d f ( 0 ) d η = θ ( 0 ) = 1 ,

(6) f ( 1 ) = S 2 , d 2 f ( 1 ) d η 2 = d θ ( 1 ) d η = 0 .

The above system is similar to the one obtained by Taj et al. [24] except only the Casson parameter. In the present work, we deduce a few more cases by constructing linear combinations of symmetries from Table 1.

We derive similarity transformations for Z 1 = C 1 X 3 + C 2 X 4 . Applying this linear combination of two Lie point symmetries X 3 and X 4 provides the following formats of U ( t , x ) , T s ( t , x ) and h ( t ) :

U ( t , x ) = t C 1 C 2 − 1 f 1 x t − C 1 C 2 ,

(7) T s ( t , x ) = t 2 C 1 C 2 − 2 f 2 x t − C 1 C 2 ,

h ( t ) = C 5 t .

The constraint imposed on these functions that they remain functions of all their variables when Lie symmetries or combinations of these symmetries act on them has been satisfied as evident from Eq. (7). This type of constraint on these functions enables a comparison with the studies already conducted on this type of flow. The forms given in Eq. (7) are obtained when the linear combination Z 1 is applied through the following invariance criteria:

Z 1 ( u − U ( t , x ) ) | u − U ( t , x ) = 0 = 0 ,

Z 1 ( T − T s ( t , x ) ) | T − T s ( t , x ) = 0 = 0 ,

(8) Z 1 ( y − h ( t ) ) | y − h ( t ) = 0 = 0 .

The following equation

(9) Z 1 J ( t , x , y , T , u , v ) = 0 ,

yields invariants

x t − C 1 C 2 = m 1 , y t = m 2 , T t 2 C 1 C 2 − 1 = P ,

(10) u t C 1 C 2 − 1 = Q , v = R t .

These invariants transform Eq. (1) and conditions (2) through (7) to

∂ Q ∂ m 1 + ∂ R ∂ m 2 = 0 ,

C 1 C 2 − 1 Q − C 1 m 1 C 2 ∂ Q ∂ m 1

− m 2 2 ∂ Q ∂ m 2 + Q ∂ Q ∂ m 1 + R ∂ Q ∂ m 2 − ν 1 + 1 β ∂ 2 Q ∂ m 2 2 + σ B 0 2 α ρ Q = 0 ,

(11) 2 C 1 C 2 − 1 P − C 1 m 1 C 2 ∂ P ∂ m 1 − m 2 2 ∂ P ∂ m 2 + Q ∂ P ∂ m 1 + R ∂ P ∂ m 2 − κ ρ C p ∂ 2 P ∂ m 2 2 − μ ρ C p 1 + 1 β ∂ Q ∂ m 2 2 = 0 ,

and

m 2 = 0 :

Q = f 1 ( m 1 ) , R = 0 , P = f 2 ( m 1 ) ,

m 2 = C 5 :

(12) ∂ Q ∂ m 2 = ∂ P ∂ m 2 = 0 , R = C 5 2 .

The system (11) further has one Lie point symmetry

(13) Y = m 1 ∂ ∂ m 1 + 2 P ∂ ∂ P + Q ∂ ∂ Q ,

that reduces the conditions (12) to

m 2 = 0 :

Q = C 3 m 1 , R = 0 , P = C 4 m 1 2 ,

m 2 = C 5 :

(14) ∂ Q ∂ m 2 = ∂ P ∂ m 2 = 0 , R = C 5 2 ,

and provides the following invariants

m 2 = τ , P = m 1 2 N ,

(15) Q = m 1 L , R = M .

Using these invariants in system (11), one obtains

L + d M d τ = 0 ,

L + m 2 2 − M d L d τ + ν 1 + 1 β d 2 L d τ 2 − σ B 0 2 α ρ L = 0 ,

(16) ρ C p 2 N + m 2 2 − M d N d τ − 2 LN + μ 1 + 1 β d L d τ 2 + κ d 2 N d τ 2 = 0 .

The conditions (Eq. (14)) reduce to

τ = 0 : L = C 3 , M = 0 , N = C 4 ,

(17) τ = C 5 : d L d τ = ∂ P d τ = 0 , M = C 5 2 ,

by considering

τ = δ α ν b η , L = − b α f ′ ,

(18) M = δ b ν α f , N = θ .

The system (16) transforms to system (5) and associated conditions (17) to (6) if C 3 = − b α , C 4 = 1 , C 5 = δ α ν b for systems corresponding to all except Z 2 , while for system obtained via this generator, these constants read as C 3 = − b α C 2 , C 4 = 1 , C 5 = δ α ν b .

In Table 2, we provide all those linear combinations which yields the desired forms of the stretching sheet velocity and temperature along with the film thickness. Including this case, we present five cases namely similarity transformations corresponding to Z 1 , … , Z 5 . However, velocity and temperature profiles are sketched with HAM for reductions obtained through Z 1 , Z 2 , Z 4 , and Z 5 . Reduced system of ODEs provided by similarity transformation through Z 3 , is not investigated further as it does not possess the conditions of the type (Eq. (6)) to which conditions of all the other cases reduce.

Table 2

Systems of ODEs for all linear combinations

Case	Double reduction
(i)	Linear combination	Z 2 = C 1 X 1 + C 2 X 3
	Conditions	h = δ α ν t b η , u = − b ( C 1 + C 2 x ) α t C 2 , T = ( C 1 + C 2 x ) 2 t 2
	Similarity transformations	η = y δ b α ν t , u = − b ( C 1 + C 2 x ) f ′ α t C 2 , v = δ b ν α t f , T = ( C 1 + C 2 x ) 2 θ t 2
	System of ODEs	(6)
(ii)	Linear combination	Z 3 = C 1 X 1 + C 2 X 4
	Conditions	h = δ α ν t b η , u = − b α t , T = 1 t 2
	Similarity transformations	η = y δ b α ν t , u = − bf α t , v = δ b ν α t , T = θ t 2
	System of ODEs	1 + 1 β d 2 f d η 2 + δ 2 Sf − d f d η + S η 2 d f d η − Mn f = 0 ,
	System of ODEs	1 Pr d 2 θ d η 2 + δ 2 2 S θ + S η 2 d θ d η − d θ d η + Ec 1 + 1 β d f d η 2 = 0
(iii)	Linear combination	Z 4 = C 1 X 2 + C 2 X 3
	Conditions	h = δ α ν t b η , u = − bx α t , T = x 2 t 2 − C 1 2 C 2
	Similarity transformations	η = y δ b α ν t , u = − bx α t f ′ , v = δ b ν α t f , T = x 2 θ t 2 − C 1 2 C 2
	System of ODEs	1 + 1 β d 3 f d η 3 + δ 2 S d f d η − f d 2 f d η 2 + d f d η 2 + S η 2 d 2 f d η 2 − M n d f d η = 0 ,
	System of ODEs	1 Pr d 2 θ d η 2 + δ 2 2 S θ + S η 2 d θ d η + 2 C 2 θ d f d η − f d θ d η + Ec 1 + 1 β d 2 f d η 2 2 = 0
(iv)	Linear combination	Z 5 = C 1 X 2 + C 2 X 4
	Conditions	h = δ α ν t b η , u = − bx α t , T = x 2 t 2 + C 1 2 C 2
	Similarity transformations	η = y δ b α ν t , u = − b xf ′ α t , v = δ b ν α t f , T = x 2 θ t 2 + C 1 2 C 2
	System of ODEs	(6)

4 Analytic solutions and discussion

Analytic solutions are derived here using HAM [18] on the reduced system of ODEs (5). We adopt a series expansion approach to construct the deformation equations up to order 10. Hence, we insert the following

(19) d n 1 f ( η ) d η n 1 = ∑ i = 0 m q i d n 1 f i ( η ) d η n 1 , d n 2 θ ( η ) d η n 2 = ∑ i = 0 m q i d n 2 θ i ( η ) d η n 2 , δ 2 = γ = ∑ i = 0 m q i γ i ,

where n 1 = 0 , 1 , 2 , 3 , n 2 = 0 , 1 , 2 , and m is the order of HAM, in the system (5). The associated conditions (6) become

∑ i = 0 m 1 + 1 β q i f i ″ ′ = ∑ i = 0 m q i γ i ∑ i = 0 m q i f i f i ″ − S f i ′ − f i ′ 2 − S η 2 f i ″ + Mn f i ′ ,

(20) 1 Pr ∑ i = 0 m q i θ i ″ = ∑ i = 0 m q i γ i ∑ i = 0 m q i − 2 S θ i − S η 2 θ i ′ − 2 θ i f i ′ + f i θ i ′ − Ec 1 + 1 β ∑ i = 0 m q i f i ″ 2 .

Equating coefficients of q , starting with q 0 , in above equations, to zero we obtain deformation equations of different orders. Here, we derive HAM analytic solutions through the deformation equations obtained by equating coefficients of q 0 , … , q 10 , to zero, in the expanded forms of Eq. (20).

We denote such deformation equations by ω 1 , i − 1 , and ω 2 , i − 1 , obtained by applying the said procedure on the first and second equation of system (5), respectively, i.e., equating coefficients of q 0 , in both equations we derive ω 1 , 0 and ω 2 , 0 . After derivation of these deformation equations, we use them in the following expressions:

f i ( η ) − λ i f i − 1 ( η ) = h f H f ( η ) ∭ ω 1 , i − 1 d η d η d η ,

(21) θ i ( η ) − λ i θ i − 1 ( η ) = h θ H θ ( η ) ∬ ω 1 , i − 1 d η d η ,

for i = 1 , 2 , … , 10 . In these equations, λ i = 0 , for i = 1 , and λ i = 1 , for i > 1 . Moreover, h f and h θ are HAM parameters, and H f ( η ) and H θ ( η ) are HAM auxiliary functions. After integrating Eq. (21), we finally obtain

(22) f i ( η ) − λ i f i − 1 ( η ) = h f H f ( η ) Ω 1 , i − 1 + C 11 + C 12 η + C 13 η 2 , θ i ( η ) − λ i θ i − 1 ( η ) , = h θ H θ ( η ) Ω 2 , i − 1 + C 14 + C 15 η ,

where C 11 , C 12 , … , C 15 are constants of integration. These equations are completely solved by integration and applying the following conditions:

∑ i = 0 m q i f i ( 0 ) = 0 ,

∑ i = 0 m q i f i ′ ( 0 ) = ∑ i = 0 m q i θ i ( 0 ) = 1 ,

∑ i = 0 m q i f i ( 1 ) = S 2 ,

(23) ∑ i = 0 m q i f i '' ( 1 ) = ∑ i = 0 m q i θ i ′ ( 1 ) = 0 .

We obtain tenth-order HAM solutions with this procedure, for a range of parameters S , Mn , β , Pr , and Ec . The HAM parameters h f and h θ that are introduced in Eq. (21) to control convergence of the solution are adjusted through the h-curves while auxiliary functions H f ( η ) = H θ ( η ) = 1 . With these solutions, we construct the velocity and temperature profiles against multiple values of the Prandtl number, magnetic parameter, Eckert number, Casson parameter, and unsteadiness parameter.

4.1 Homotopy solutions for system of ODEs derived using Z 1 , Z 2 , & Z 5

First, we draw h -curves for the HAM parameter h f , to obtain a range of this parameter for which one obtains a convergent analytic solution for velocity. Moreover, these h -curves provide the dimensionless film thickness γ . We draw these curves in Figures 1–3 by varying the magnetic, Casson, and unsteadiness parameters, respectively. These figures show a variation in the dimensionless film thickness due to variations in these parameters. While the horizontal portion in these figures provides us with the values of the HAM parameter h f , in which we obtain convergent solution for the first equation in the system (5). In Figures 1–3, h f -curves are plotted and it is evident from these figures that the fluid film gets thinner with an increase in Mn , β , and S , respectively.

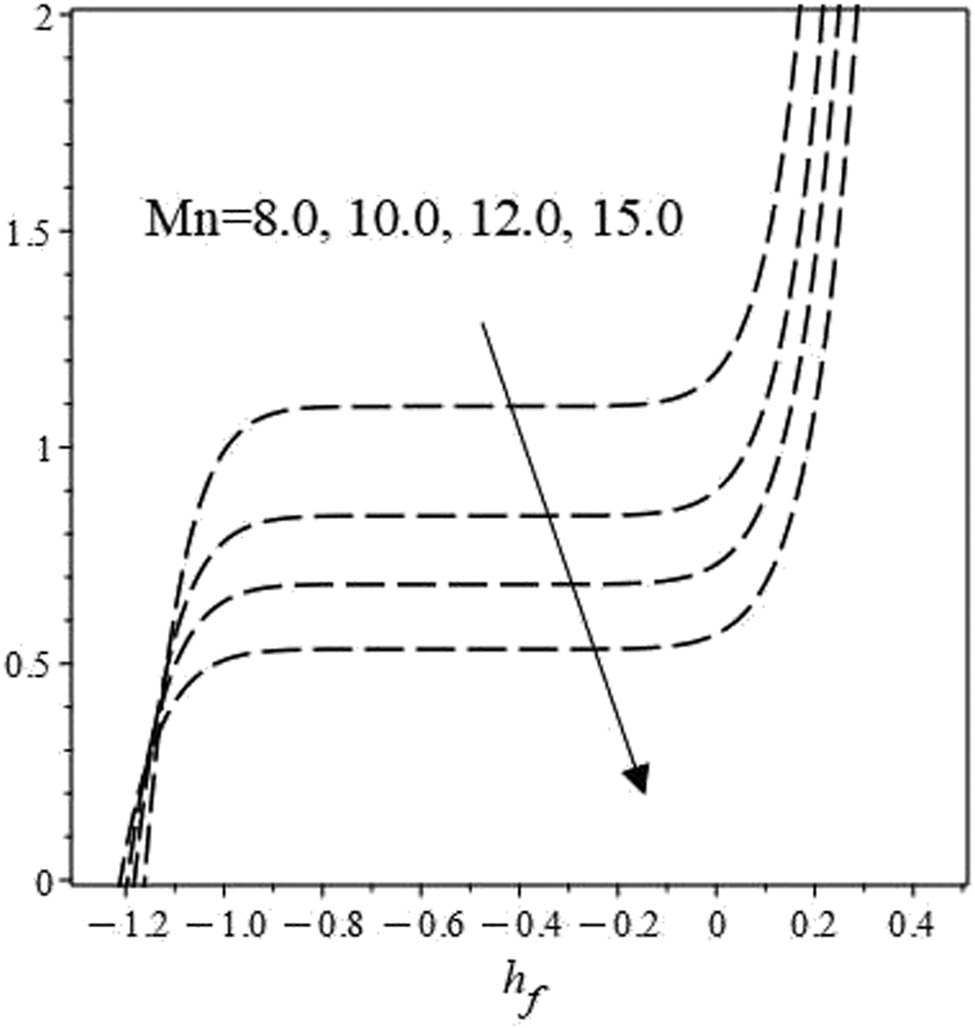
$Figure 1 Variation in γ \gamma with ( S = 0 . 8 , β = 5 . 0 S=0.8,\beta =5.0 ) and a variation in Mn {\rm{Mn}} .$

Figure 1

Variation in γ with ( S = 0 . 8 , β = 5 . 0 ) and a variation in Mn .

$Figure 2 Variation in γ \gamma with ( S = 0 . 8 , Mn = 7 . 0 S=0.8,{\rm{Mn}}=7.0 ) and a variation in β \beta .$

Figure 2

Variation in γ with ( S = 0 . 8 , Mn = 7 . 0 ) and a variation in β .

$Figure 3 Variation in γ \gamma with ( Mn = 7 . 0 , β = 5 . 0 {\rm{Mn}}=7.0,\beta =5.0 ) and a variation in S S .$

Figure 3

Variation in γ with ( Mn = 7 . 0 , β = 5 . 0 ) and a variation in S .

Similarly, in Figures 4 and 5, same trends for the dimensionless film thickness are obtained with a variation, i.e., an increase in Mn , and S , by keeping h f = − 0.5 , i.e., the value identified in the h f -curves. These figures show thinning of the film with an increment in these parameters that is comparatively rapid for higher values of the magnetic and unsteadiness parameters. These figures also demonstrate the effects of the Casson parameter on the film thickness which when increased reduces film thickness. In Table 3, the behavior of the free surface velocity with an increment in the magnetic parameter is given that shows a slow response of the free surface velocity versus the magnetic field. In Figure 6, a variation in the velocity is studied with respect to the Casson parameter which shows that the fluid slows down with the Casson parameter, i.e., an increment in this parameter turns the fluid more resistant to the flow and the same is demonstrated in the said figure. In Figure 7, a variation in f ′ ( η ) is shown due to the unsteadiness parameter S . Increasing this parameter causes a turbulence in the fluid, and in the considered range of the unsteadiness parameter, we observe an increment in the fluid velocity. Figure 7 indicates that the velocity increases with the increase in unsteadiness. We draw h θ -curves for different combinations of the parameters (magnetic, Casson, and unsteadiness) and the Eckert number. A few of these curves are shown in Figure 8 for specific values of these quantities that are mentioned in the figure caption. The horizontal region in these curves stretches in a small neighborhood of h θ = − 0.04 . Therefore, temperature profiles are constructed by considering h θ = − 0.037 to − 0.035 . In Figure 9, the first study of the free surface temperature is conducted by taking this value of the HAM second parameter and with a variation in the Casson parameter which shows that increments in the Casson parameter reduce the temperature θ ( η ) . The Casson parameter indirectly affects the heat transfer phenomena in a thin film as it affects the fluid behavior. A variation in this parameter varies the fluid viscosity and hence influences the heat transfers, and here, it is observed to reduce the fluid’s temperature. Figures 10–12 present the temperature profiles and show that with an increment in the Eckert number, i.e., when the kinetic energy dominates, then the fluid temperature increases. In these figures, the magnetic parameter is also varied. A comparison of all these figures asserts that strengthening the magnetic field suppresses the heat transfer, and it also is an indirect influence through alterations of the fluid properties when the magnetic field varies. Likewise, we draw temperature profiles in Figures 13–15 for a variation in the Prandtl number and the unsteadiness parameter. In each of these figures, it is evident that the increase in the Prandtl number causes an increase in θ ( η ) . Though a rise in the Prandtl number implies a decrease in the thermal diffusivity which causes a slow rate of heat transfer as compared to the transfer of momentum, here these effects are coupled with other parameters and numbers hence one observes the opposite to the effects in a physical sense. Keeping all these in front of us helps in predicting a decrease in θ ( η ) , when the unsteadiness is increased that is a trend opposite to what is observed for the variation in Pr . In the case of unsteadiness, the same is happening as is reported for the Prandtl number. The turbulence and mixing offered due to the increase in the unsteadiness affects the transfer of heat within fluid. Here, it gives a decrease in θ ( η ) .

$Figure 4 Variation in γ \gamma with ( S = 0 . 8 , h f = − 0 . 5 S=0.8,{h}_{f}=-0.5 ) and a variation in Mn {\rm{Mn}} .$

Figure 4

Variation in γ with ( S = 0 . 8 , h f = − 0 . 5 ) and a variation in Mn .

$Figure 5 Variation in γ \gamma with ( Mn = 7 . 0 , h f = − 0 . 5 {\rm{Mn}}=7.0,{h}_{f}=-0.5 ) and a variation in S S .$

Figure 5

Variation in γ with ( Mn = 7 . 0 , h f = − 0 . 5 ) and a variation in S .

Table 3

Variation in velocity with S = 1.2 , β = 0.1 , h f = 0.5 and a variation in Mn

Mn	f ' ( η )
5 . 0	0 . 416187904683275
6 . 0	0 . 417207947598479
7 . 0	0 . 417830885334903
8 . 0	0 . 418250847848063
9 . 0	0 . 418553149481099
10 . 0	0 . 418781164287947

$Figure 6 Variation in f ′ ( η ) {f}^{^{\prime} }(\eta ) with ( Mn = 15 . 0 , S = 0 . 8 , h f = − 0 . 5 {\rm{Mn}}=15.0,S=0.8,{h}_{f}=-0.5 ) and a variation in β \beta .$

Figure 6

Variation in f ′ ( η ) with ( Mn = 15 . 0 , S = 0 . 8 , h f = − 0 . 5 ) and a variation in β .

$Figure 7 Variation in f ′ ( η ) {f}^{^{\prime} }(\eta ) with ( Mn = 7 . 0 , β = 1 . 0 , h f = − 0 . 5 {\rm{Mn}}=7.0,\beta =1.0,{{h}}_{f}=-0.5 ) and a variation in S S .$

Figure 7

Variation in f ′ ( η ) with ( Mn = 7 . 0 , β = 1 . 0 , h f = − 0 . 5 ) and a variation in S .

$Figure 8 h θ − {h}_{\theta }- Curves with ( Mn = 7 . 0 , Ec = 0 . 5 , β = 2 . 0 , h f = − 0 . 5 , S = 0 . 8 {\rm{Mn}}=7.0,{\rm{Ec}}=0.5,\beta =2.0,{h}_{f}=-0.5,S=0.8 ) and a variation in Pr {\rm{\Pr }} .$

Figure 8

h θ − Curves with ( Mn = 7 . 0 , Ec = 0 . 5 , β = 2 . 0 , h f = − 0 . 5 , S = 0 . 8 ) and a variation in Pr .

$Figure 9 Variation in θ ( η ) \theta (\eta ) with ( Mn = 15 . 0 , Ec = 1 . 0 , S = 0 . 8 , Pr = 0 . 045 , {\rm{Mn}}=15.0,{\rm{Ec}}=1.0,S=0.8,{\rm{Pr}}=0.045, h f = − 0 . 5 , h θ = − 0 . 035 {h}_{f}=-0.5,{\rm{\ }}{h}_{\theta }=-0.035 ) and a variation in β \beta .$

Figure 9

Variation in θ ( η ) with ( Mn = 15 . 0 , Ec = 1 . 0 , S = 0 . 8 , Pr = 0 . 045 , h f = − 0 . 5 , h θ = − 0 . 035 ) and a variation in β .

$Figure 10 Variation in θ ( η ) \theta \left(\eta ) with S = 0 . 8 S=0.8 , Pr = 0 . 035 {\rm{\Pr }}=0.035 , Mn = 10 . 0 {\bf{Mn}}{\boldsymbol{=}}{\bf{10}}{\boldsymbol{.}}{\bf{0}} , β = 1 . 0 \beta =1.0 , h f = − 0 . 5 {h}_{f}=-0.5 , h θ = − 0 . 037 {h}_{\theta }=-0.037 and a variation in Ec {\rm{Ec}} .$

Figure 10

Variation in θ ( η ) with S = 0 . 8 , Pr = 0 . 035 , Mn = 10 . 0 , β = 1 . 0 , h f = − 0 . 5 , h θ = − 0 . 037 and a variation in Ec .

$Figure 11 Variation in θ ( η ) \theta (\eta ) with S = 0 . 8 S=0.8 , Pr = 0 . 035 {\rm{\Pr }}=0.035 , Mn = 12 . 0 {\bf{Mn}}{\boldsymbol{=}}{\bf{12}}{\boldsymbol{.}}{\bf{0}} , β = 1 . 0 \beta =1.0 , h f = − 0 . 5 {h}_{f}=-0.5 , h θ = − 0 . 037 {h}_{\theta }=-0.037 and a variation in Ec {\rm{Ec}} .$

Figure 11

Variation in θ ( η ) with S = 0 . 8 , Pr = 0 . 035 , Mn = 12 . 0 , β = 1 . 0 , h f = − 0 . 5 , h θ = − 0 . 037 and a variation in Ec .

$Figure 12 Variation in θ ( η ) \theta (\eta ) with S = 0 . 8 S=0.8 , Pr = 0 . 035 {\rm{\Pr }}=0.035 , Mn = 15 . 0 {\bf{Mn}}{\boldsymbol{=}}{\bf{15}}{\boldsymbol{.}}{\bf{0}} , β = 1 . 0 \beta =1.0 , h f = − 0 . 5 {h}_{f}=-0.5 , h θ = − 0 . 037 {h}_{{\rm{\theta }}}=-0.037 and a variation in Ec {\rm{Ec}} .$

Figure 12

Variation in θ ( η ) with S = 0 . 8 , Pr = 0 . 035 , Mn = 15 . 0 , β = 1 . 0 , h f = − 0 . 5 , h θ = − 0 . 037 and a variation in Ec .

$Figure 13 Variation in θ ( η ) \theta (\eta ) with S = 0 . 8 {\boldsymbol{S}}{\boldsymbol{=}}{\bf{0}}{\boldsymbol{.}}{\bf{8}} , Ec = 0 . 5 {\rm{Ec}}=0.5 , Mn = 7 . 0 {\rm{Mn}}=7.0 , β = 1 . 0 \beta =1.0 , h f = − 0 . 5 {h}_{f}=-0.5 , h θ = − 0 . 037 {h}_{{\rm{\theta }}}=-0.037 and a variation in Pr {\rm{\Pr }} .$

Figure 13

Variation in θ ( η ) with S = 0 . 8 , Ec = 0 . 5 , Mn = 7 . 0 , β = 1 . 0 , h f = − 0 . 5 , h θ = − 0 . 037 and a variation in Pr .

$Figure 14 Variation in θ ( η ) \theta (\eta ) with S = 1 . 2 {\boldsymbol{S}}{\boldsymbol{=}}{\bf{1}}{\boldsymbol{.}}{\bf{2}} , Ec = 0 . 5 {\rm{Ec}}=0.5 , Mn = 7 . 0 {\rm{Mn}}=7.0 , β = 1 . 0 \beta =1.0 , h f = − 0 . 5 {h}_{f}=-0.5 , h θ = − 0 . 037 , {h}_{{\rm{\theta }}}=-0.037, and a variation in Pr {\rm{\Pr }} .$

Figure 14

Variation in θ ( η ) with S = 1 . 2 , Ec = 0 . 5 , Mn = 7 . 0 , β = 1 . 0 , h f = − 0 . 5 , h θ = − 0 . 037 , and a variation in Pr .

$Figure 15 Variation in θ ( η ) \theta (\eta ) with S = 1 . 5 {\boldsymbol{S}}{\boldsymbol{=}}{\bf{1}}{\boldsymbol{.}}{\bf{5}} , Ec = 0 . 5 {\rm{Ec}}=0.5 , Mn = 7 . 0 {\rm{Mn}}=7.0 , β = 1 . 0 \beta =1.0 , h f = − 0 . 5 {h}_{f}=-0.5 , h θ = − 0 . 037 , {h}_{{\rm{\theta }}}=-0.037, and a variation in Pr {\rm{\Pr }} .$

Figure 15

Variation in θ ( η ) with S = 1 . 5 , Ec = 0 . 5 , Mn = 7 . 0 , β = 1 . 0 , h f = − 0 . 5 , h θ = − 0 . 037 , and a variation in Pr .

4.2 Homotopy solutions for system of ODEs derived using Z 4

The system in this case contains an arbitrary constant C 2 , in the second equation which affects the convergence of the homotopic solution. Hence, it can be used to control the convergence of the temperature profiles. For these solutions, we draw h θ -curves and the corresponding temperature profiles. In Figures 16 and 17, a rise in the h θ -curves and temperature can be seen due to a rise in the Casson parameter β . Similar trends are shown in Figures 18 and 19 where we study the effects of the Eckert number Ec , on the temperature profiles. For different values of Pr , we draw the h θ -curves in Figure 20 and temperature profiles in Figure 21. From these figures, we conclude that an increase in the Prandtl number results in a decrease in the temperature. In Figures 22 and 23, variations in the temperature profiles are studied with a variation in the magnetic parameter Mn . We observe that the temperature is directly proportional to the magnetic parameter. We draw the h θ -curves for different values of the unsteadiness parameter S . Increasing the unsteadiness causes an increase in the h θ -curves as shown in Figure 24. We present temperature profiles for some values of the unsteadiness parameter and temperature is shown to rise with the unsteadiness parameter in Figure 25.

$Figure 16 h θ − {h}_{\theta }- Curves with ( Mn = 15 . 0 , Ec = 1 . 0 , S = 0 . 8 , h f = − 0 . 5 , Pr = 0 . 045 {\rm{Mn}}=15.0,{\rm{Ec}}=1.0,{\rm{\ }}S=0.8,{h}_{f}=-0.5,{\rm{Pr}}=0.045 ) and a variation in β \beta .$

Figure 16

h θ − Curves with ( Mn = 15 . 0 , Ec = 1 . 0 , S = 0 . 8 , h f = − 0 . 5 , Pr = 0 . 045 ) and a variation in β .

$Figure 17 Variation in θ ( η ) \theta (\eta ) with ( Mn = 15 . 0 , Ec = 1 . 0 , S = 0 . 8 , Pr = 0 . 045 , h f = − 0 . 5 , h θ = − 0 . 035 {\rm{Mn}}=15.0,{\rm{Ec}}=1.0,{\rm{\ }}S=0.8,{\rm{Pr}}=0.045,{h}_{{\rm{f}}}=-0.5,{\rm{\ }}{h}_{{\rm{\theta }}}=-0.035 ), and a variation in β \beta .$

Figure 17

Variation in θ ( η ) with ( Mn = 15 . 0 , Ec = 1 . 0 , S = 0 . 8 , Pr = 0 . 045 , h f = − 0 . 5 , h θ = − 0 . 035 ), and a variation in β .

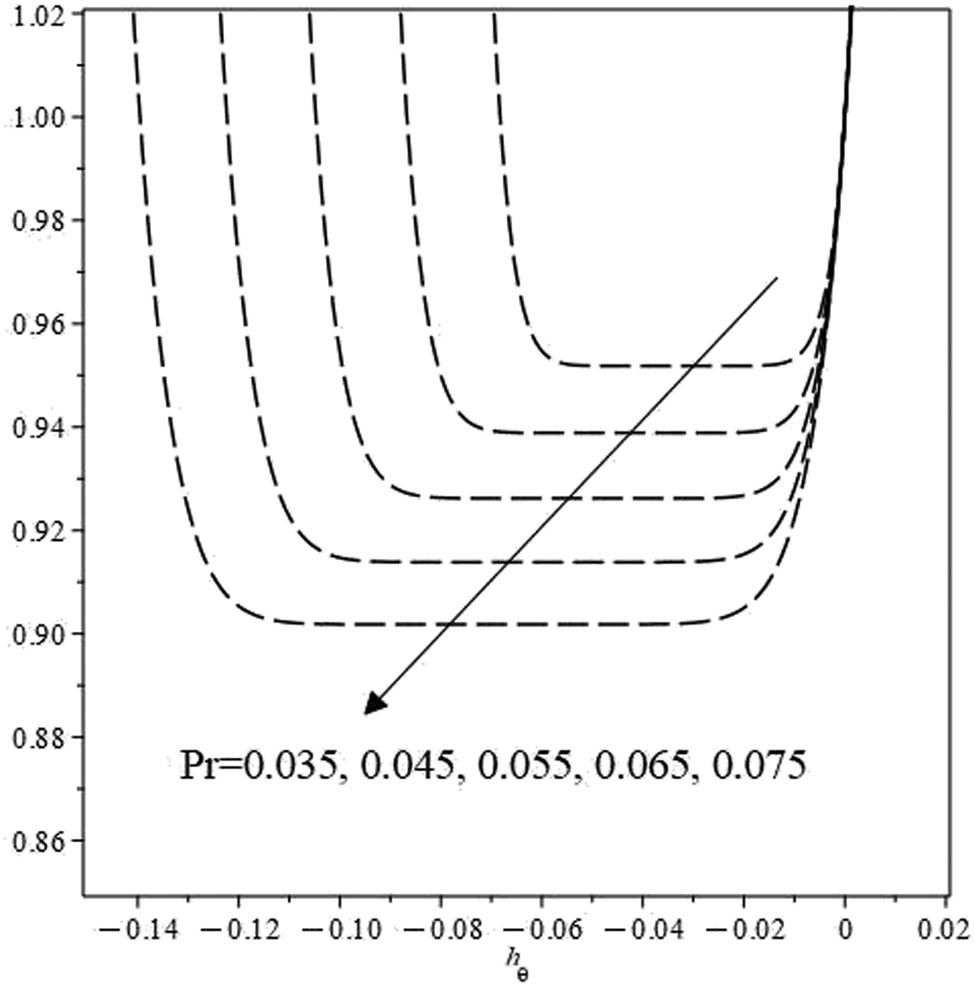
$Figure 18 h θ − {h}_{\theta }- Curves with ( Mn = 15 . 0 , β = 2 . 0 , S = 0 . 8 , h f = − 0 . 5 , Pr = 0 . 075 {\rm{Mn}}=15.0,\beta =2.0,{\rm{\ }}S=0.8,{h}_{f}=-0.5,{\rm{Pr}}=0.075 ) and a variation in Ec {\rm{Ec}} .$

Figure 18

h θ − Curves with ( Mn = 15 . 0 , β = 2 . 0 , S = 0 . 8 , h f = − 0 . 5 , Pr = 0 . 075 ) and a variation in Ec .

$Figure 19 Variation in θ ( η ) \theta (\eta ) with ( Mn = 15 . 0 , β = 2 . 0 , S = 0 . 8 , Pr = 0 . 075 , h f = − 0 . 5 , h θ = − 0 . 06 {\rm{Mn}}=15.0,{\rm{\ }}\beta =2.0,{\rm{\ }}S=0.8,{\rm{Pr}}=0.075,{h}_{{\rm{f}}}=-0.5,{\rm{\ }}{h}_{{\rm{\theta }}}=-0.06 ) and a variation in Ec {\rm{Ec}} .$

Figure 19

Variation in θ ( η ) with ( Mn = 15 . 0 , β = 2 . 0 , S = 0 . 8 , Pr = 0 . 075 , h f = − 0 . 5 , h θ = − 0 . 06 ) and a variation in Ec .

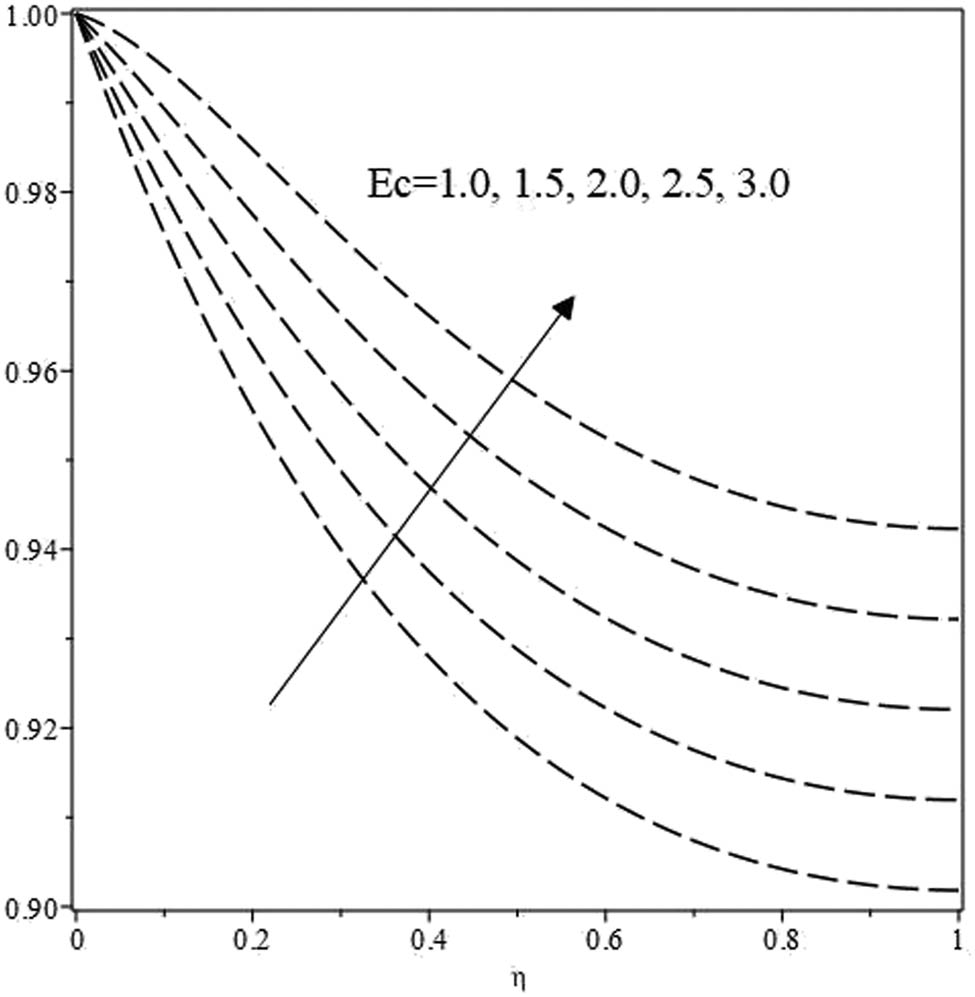
$Figure 20 h θ − {h}_{\theta }- Curves with ( Mn = 15 . 0 , β = 2 . 0 , S = 0 . 8 , h f = − 0 . 5 , Ec = 1 . 0 {\rm{Mn}}=15.0,\beta =2.0,{\rm{\ }}S=0.8,{h}_{{\rm{f}}}=-0.5,{\rm{Ec}}=1.0 ) and a variation in Pr {\rm{\Pr }} .$

Figure 20

h θ − Curves with ( Mn = 15 . 0 , β = 2 . 0 , S = 0 . 8 , h f = − 0 . 5 , Ec = 1 . 0 ) and a variation in Pr .

$Figure 21 Variation in θ ( η ) \theta (\eta ) with ( Mn = 15 . 0 , β = 2 . 0 , S = 0 . 8 , Ec = 1 . 0 , h f = − 0 . 5 , h θ = − 0 . 045 {\rm{Mn}}=15.0,{\rm{\ }}\beta =2.0,{\rm{\ }}S=0.8,{\rm{Ec}}=1.0,{h}_{{\rm{f}}}=-0.5,{h}_{\theta }=-0.045 ) and a variation in Pr {\rm{\Pr }} .$

Figure 21

Variation in θ ( η ) with ( Mn = 15 . 0 , β = 2 . 0 , S = 0 . 8 , Ec = 1 . 0 , h f = − 0 . 5 , h θ = − 0 . 045 ) and a variation in Pr .

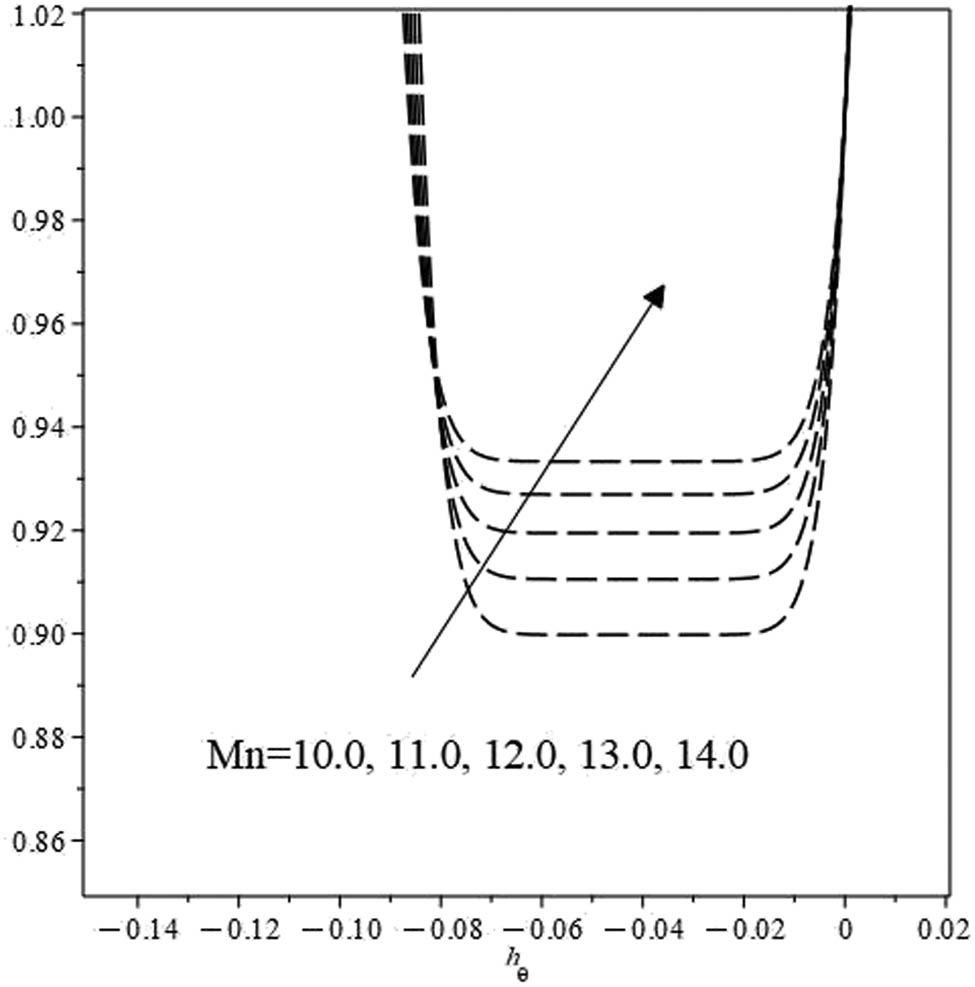
$Figure 22 h θ − {h}_{\theta }- Curves with ( Pr = 0 . 045 , β = 2 . 0 , S = 0 . 8 , h f = − 0 . 5 , Ec = 1 . 0 {\rm{\Pr }}=0.045,\beta =2.0,S=0.8,{h}_{{\rm{f}}}=-0.5,{\rm{Ec}}=1.0 ) and a variation in Mn . {\rm{Mn}}.$

Figure 22

h θ − Curves with ( Pr = 0 . 045 , β = 2 . 0 , S = 0 . 8 , h f = − 0 . 5 , Ec = 1 . 0 ) and a variation in Mn .

$Figure 23 Variation in θ ( η ) \theta (\eta ) with ( Pr = 0 . 045 , β = 2 . 0 , S = 0 . 8 , Ec = 1 . 0 , h f = − 0 . 5 , h θ = − 0 . 045 {\rm{\Pr }}=0.045,\beta =2.0,S=0.8,{\rm{Ec}}=1.0,{h}_{{\rm{f}}}=-0.5,{h}_{\theta }=-0.045 ) and a variation in Mn {\rm{Mn}} .$

Figure 23

Variation in θ ( η ) with ( Pr = 0 . 045 , β = 2 . 0 , S = 0 . 8 , Ec = 1 . 0 , h f = − 0 . 5 , h θ = − 0 . 045 ) and a variation in Mn .

$Figure 24 h θ − {h}_{\theta }- curves with ( Pr = 0 . 045 , β = 2 . 0 , Mn = 10 . 0 , h f = − 0 . 5 , Ec = 1 . 0 {\rm{\Pr }}=0.045,\beta =2.0,{\rm{Mn}}=10.0,{h}_{{\rm{f}}}=-0.5,{\rm{Ec}}=1.0 ) and a variation in S S .$

Figure 24

h θ − curves with ( Pr = 0 . 045 , β = 2 . 0 , Mn = 10 . 0 , h f = − 0 . 5 , Ec = 1 . 0 ) and a variation in S .

$Figure 25 Variation in θ ( η ) \theta (\eta ) with ( Pr = 0 . 045 , β = 2 . 0 , Mn = 10 . 0 , Ec = 1 . 0 , h f = − 0 . 5 , h θ = − 0 . 035 {\rm{\Pr }}=0.045,\beta =2.0,{\rm{Mn}}=10.0,{\rm{Ec}}=1.0,{h}_{{\rm{f}}}=-0.5,{h}_{\theta }=-0.035 ) and a variation in S S .$

Figure 25

Variation in θ ( η ) with ( Pr = 0 . 045 , β = 2 . 0 , Mn = 10 . 0 , Ec = 1 . 0 , h f = − 0 . 5 , h θ = − 0 . 035 ) and a variation in S .

A comparison of both the cases in (4.1) and (4.2) shows that in response to an increase in the Casson parameter both the reduced systems corresponding to Z 1 , Z 2 , Z 5 , and Z 4 behave differently. The former exhibits a decrease in temperature while the latter shows an increment in temperature. For a variation in the Eckert number Ec , both the systems provide an increase in the temperature with a rise in this number. In the case of the variation in the Prandtl number Pr , the system in case (4.1) provides an increase with higher values of this number while the system in case (4.2) shows a decrease in the temperature. With an increase in the unsteadiness parameter both systems behave differently. In the first case, the temperature drops while in the second case, it rises.

5 Conclusion

We study flow and heat transfer in a Casson fluid thin film on an unsteady stretching sheet. A magnetic field is imposed on the considered flow model along with the viscous dissipation. One approach out of many that are practiced for these kinds of flow problems is the reduction of the flow model equations to their simplest possible forms. That is a transformation of the PDEs to ODEs. This is achieved with similarity transformations. The problem we are dealing with has been considered earlier, and the same procedure has been applied to it to construct corresponding velocity and temperature profiles. In this article, we derive new classes of similarity transformations using the Lie symmetry method. It provides us with more than one such transformation that enables different kinds of reductions of the flow PDEs to ODEs. The similarity transformation used here is named Lie similarity transformation. By employing it, we provide an invertible conversion of the flow PDEs to ODEs on which we apply the homotopy analysis method to construct and analyze the flow and heat transfer. The purpose of obtaining multiple classes for the similarity transformations is the optimization of the flow and heat transfer within a liquid film. Multiple similarity transformations yield different types of reductions of the flow PDEs, and hence, different kinds of flow and heat transfer patterns are revealed through analytic solutions of the obtained systems of ODEs. We presented variations in velocity and temperature profiles due to the magnetic, Casson and unsteadiness parameters, Prandtl, and Eckert numbers with the derived analytic solutions. All these dimensionless parameters and numbers are imposed in our study due to the form of similarity transformations we provided. Furthermore, the particular ranges for these parameters and numbers that are considered in this study are determined through the h -curves of HAM.

To extend this study, one may construct an optimal system for the Lie symmetries of such flow equations to deduce all reducible inequivalent classes of systems of ODEs corresponding to flow PDEs. In this way, all distinct analytic solutions can be deduced which exist due to the Lie similarity procedure and HAM. As mentioned earlier with the distinct multiple solutions of a flow problem, an optimization or in other words a control on the flow and heat transfer can be attained according to the requirements of the flow problem under consideration.

Acknowledgments

The authors extend their appreciation to the Deanship of Scientific Research at King Khalid University for funding this work through a large group Research Project under grant number RGP2/47/44.

Funding information: Research Project under grant number RGP2/47/44 from Deanship of Scientific Research at King Khalid University.
Author contributions: All authors have accepted responsibility for the entire content of this manuscript and approved its submission.
Conflict of interest: The authors state no conflict of interest.

References

[1] Abel MS, Mahesha N, Tawade J. Heat transfer in a liquid film over an unsteady stretching surface with viscous dissipation in presence of external magnetic field. Appl Math Model. 2009;33(8):3430–41.Search in Google Scholar

[2] Abel MS, Tawade J, Nandeppanavar MM. Effect of non-uniform heat source on MHD heat transfer in a liquid film over an unsteady stretching sheet. Int J Non-Linear Mech. 2009;44(9):990–8.Search in Google Scholar

[3] Andersson HI, Aarseth JB, Dandapat BS. Heat transfer in a liquid film on an unsteady stretching surface. Int J Heat Mass Transf. 2000;43(1):69–74.Search in Google Scholar

[4] Aziz R, Hashim I, Abbasbandy S. Flow and heat transfer in a nanofluid thin film over an unsteady stretching sheet. Sains Malaysiana. 2018;47(7):1599–605.Search in Google Scholar

[5] Aziz RC, Hashim I, Alomari A. Thin film flow and heat transfer on an unsteady stretching sheet with internal heating. Meccanica. 2011;46(2):349–57.Search in Google Scholar

[6] Char MI. Heat transfer of a continuous, stretching surface with suction or blowing. J Math Anal Appl. 1988;135(2):568–80.Search in Google Scholar

[7] Chen CH. Effect of viscous dissipation on heat transfer in a non-Newtonian liquid film over an unsteady stretching sheet. J Non-Newtonian Fluid Mech. 2006;135(2–3):128–35.Search in Google Scholar

[8] Chen CH. Heat transfer in a power-law fluid film over a unsteady stretching sheet. Heat Mass Transf. 2003;39(8):791–6.Search in Google Scholar

[9] Crane LJ. Flow past a stretching plate. Zeitschrift für angewandte Mathematik und Physik. ZAMP. 1970;21(4):645–7.Search in Google Scholar

[10] Gupta P, Gupta A. Heat and mass transfer on a stretching sheet with suction or blowing. Can J Chem Eng. 1977;55(6):744–6.Search in Google Scholar

[11] Liu IC, Andersson HI. Heat transfer in a liquid film on an unsteady stretching sheet. Int J Therm Sci. 2008;47(6):766–72.Search in Google Scholar

[12] Mahmoud MA, Megahed AM. MHD flow and heat transfer in a non-Newtonian liquid film over an unsteady stretching sheet with variable fluid properties. Can J Phys. 2009;87(10):1065–71.Search in Google Scholar

[13] Megahed A. Effect of slip velocity on Casson thin film flow and heat transfer due to unsteady stretching sheet in presence of variable heat flux and viscous dissipation. Appl Math Mech. 2015;36(10):1273–84.Search in Google Scholar

[14] Ali L, Liu X, Ali B, Mujeed S, Abdal S. Finite element simulation of multi-slip effects on unsteady MHD bioconvective micropolar nanofluid flow over a sheet with solutal and thermal convective boundary conditions. Coatings. 2019;9(12):842.Search in Google Scholar

[15] Ali L, Ali B, Liu X, Iqbal T, Zulqarnain RM, Javid M. A comparative study of unsteady MHD Falkner–Skan wedge flow for non-Newtonian nanofluids considering thermal radiation and activation energy. Chin J Phys. 2022;77:1625–38.Search in Google Scholar

[16] Ali L, Ali B, Ghori MB. Melting effect on Cattaneo–Christov and thermal radiation features for aligned MHD nanofluid flow comprising microorganisms to leading edge: FEM approach. Comput Math Appl. 2022;109:260–9.Search in Google Scholar

[17] Kumar P, Poonia H, Ali L, Areekara S. The numerical simulation of nanoparticle size and thermal radiation with the magnetic field effect based on tangent hyperbolic nanofluid flow. Case Stud Therm Eng. 2022;37:102247.Search in Google Scholar

[18] Liao S. Beyond perturbation: introduction to the homotopy analysis method. New York: Chapman and Hall/CRC; 2003.Search in Google Scholar

[19] Wang C. Analytic solutions for a liquid film on an unsteady stretching surface. Heat Mass Transf. 2006;42(8):759–66.Search in Google Scholar

[20] Aziz T, Mahomed F. Applications of group theoretical methods to non-newtonian fluid flow models: survey of results. Math Probl Eng. 2017;2017:6847647.Search in Google Scholar

[21] Vijaya N, Sreelakshmi K, Sarojamma G. Effect of magnetic field on the flow and heat transfer in a Casson thin film on an unsteady stretching surface in the presence of viscous and internal heating. Open J Fluid Dyn. 2016;6(4):303–20.Search in Google Scholar

[22] Safdar M, Khan MI, Taj S, Malik MY, Shi QH. Construction of similarity transformations and analytic solutions for a liquid film on an unsteady stretching sheet using lie point symmetries. Chaos Solitons Fractals. 2021;150:111115.Search in Google Scholar

[23] Safdar M, Ijaz Khan M, Khan RA, Taj S, Abbas F, Elattar S, et al. Analytic solutions for the MHD flow and heat transfer in a thin liquid film over an unsteady stretching surface with Lie symmetry and homotopy analysis method. Waves Random Complex Media. 2022;1–19.Search in Google Scholar

[24] Taj S, Khan MI, Safdar M, Elattar S, Galal AM. Lie symmetry analysis of heat transfer in a liquid film over an unsteady stretching surface with viscous dissipation and external magnetic field. Waves Random Complex Media. 2022;1–16.Search in Google Scholar

[25] Wang F, Safdar M, Jamil B, Khan MI, Taj S, Malik MY, et al. One-dimensional optimal system of Lie sub-algebra and analytic solutions for a liquid film fluid flow. Chin J Phys. 2022;78:220–33.Search in Google Scholar

[26] Li X, Dong Z, Wang L, Niu X, Yamaguchi H, Li D, et al. A magnetic field coupling fractional step lattice Boltzmann model for the complex interfacial behavior in magnetic multiphase flows. Appl Math Model. 2023;117:219–50. 10.1016/j.apm.2022.12.025.Search in Google Scholar

[27] Liu W, Zhao C, Zhou Y, Xu X, Rakkesh RA. Modeling of Vapor-Liquid equilibrium for electrolyte solutions based on COSMO-RS interaction. J Chem. 2022;2022:9070055. 10.1155/2022/9070055.Search in Google Scholar

[28] Pang X, Zhao Y, Gao X, Wang G, Sun H, Yin J, et al. Two-step colloidal synthesis of micron-scale Bi2O2Se nanosheets and their electrostatic assembly for thin-film photodetectors with fast response. Chin Chem Lett. 2021;32(10):3099–104.Search in Google Scholar

[29] Yao J, Kong J, Kong L, Wang X, Shi W, Lu C. The phosphorescence nanocomposite thin film with rich oxygen vacancy: Towards sensitive oxygen sensor. Chin Chem Lett. 2022;33(8):3977–80.Search in Google Scholar

Received: 2023-01-31

Revised: 2023-03-28

Accepted: 2023-04-13

Published Online: 2023-05-10

This work is licensed under the Creative Commons Attribution 4.0 International License.

Articles in the same Issue

https://doi.org/10.1515/phys-2022-0244

Keywords for this article

Casson fluid; viscous dissipation; magnetic field; Lie symmetry; similarity transformations; homotopy analysis method and analytic solution

Creative Commons

BY 4.0