Continuum percolation of the realistic nonuniform ITZs in 3D polyphase concrete systems involving the aggregate shape and size differentiation

1 Introduction

Percolation is a commonly used physical definition reflecting the global connectivity of individual phases in the composite system [1,2], and it can be roughly divided into two groups: lattice percolation [3,4,5] and continuum percolation [6,7,8,9] according to the characteristics of study objects. Especially, the continuum percolation has always been applied by domestic and foreign researchers to explore the connectivity of various components in materials such as the pore phase (i.e., the soft particles) [10,11,12,13] and the interface phase (i.e., the rigid particles) [14,15,16] in a wide range of fields. For example, for the polyphase concrete materials in civil engineering, the interfacial transition zone (ITZ) surrounding the aggregate particles is commonly deemed to be a weak phase in concrete because of its higher porosity and greater permeability compared with the aggregates and cement paste [17,18,19]. According to the continuum percolation theory in the study by Stauffer and Aharony [1], when the effective fraction of the ITZs in concrete reaches the critical percolation condition (i.e., the connected path of ITZ through the whole systems can be formed), the great change of macroscopic properties of materials may occur. That is to say, the percolation of ITZs may have a significant influence on the mechanical and transport properties of concrete structures. Hence, the relevant issues about the ITZ percolation have always drawn the attention in recent years.

Because of the variability and complexity of the ITZ phase around the aggregates, a series of its characteristics including its percolation are always very difficult to be identified and quantified accurately by experiments. To compensate for the aforementioned shortcoming, the numerical simulation methods have been developed recently and become an effective research toolkit for the ITZ percolation. As of now, a large number of numerical investigations have been carried out to clarify the dependence of the ITZ percolation properties on the characteristics of aggregate particles as well as their effect on the macroscopic performance. For instance, by assuming all the aggregates in concrete as the group of polydisperse convex particles with the smooth surface (e.g., spheres [20,21], ellipsoids [22,23], and ovoids [24]), the influence of both uniform ITZ thickness and particle morphologies on the critical percolation thresholds ϕ _agg,c of uniform ITZs is evaluated recently. The findings reveal that (a) whatever the aggregate shape is, the ITZ thickness always presents the dominant impact on the critical threshold ϕ _agg,c; (b) as the specific surface area (SSA) of aggregates increases, the threshold ϕ _agg,c generally possesses an increasing trend; and (c) as the aspect ratio of aggregates deviates from 1.0, the value of ϕ _agg,c would reduce dramatically. Besides, in view of the realistic morphology of gravels (one of the commonly used coarse aggregates) in concrete, the concrete is assumed as three-phase systems consisting of polyhedral aggregates, uniform ITZs, and homogeneous cement paste, and the sensitivity of the critical percolation of the ITZ phase to the polyhedral particles is further studied in the studies by Lin et al. [25,26]. On the one hand, several interesting conclusions that are similar to those in the literature [20,21,22,23,24] are obtained. On the other hand, the value of ϕ _agg,c also shows an obviously declining tendency with the decrease of the face of these regular particles. This is mainly because the ITZs around the polyhedral particles with their shape far from the spherical are easier to form the global percolation paths than the ITZs around the spherical particles. According to the aforementioned studies, it can be concluded that the geometric features of aggregates have the crucial effect on ITZ percolation. However, it should also be pointed out that, in most previous studies, both coarse aggregates and fine aggregates are usually simplified as the convex-shaped particles with the identical morphologies and the geometric differences between them are generally not considered. Strictly speaking, the morphologies of gravels in concrete are more similar to the two-dimensional (2D)/three-dimensional (3D) convex fillers with the limited number of faces. But the shapes of sands are much closer to the fillers with the smooth morphology, as described in the studies by Lin et al. [27,28]. To explore the ITZ percolation with the response of the diversities of aggregate shapes, the four-component polyphase models of concrete are developed by assuming the aggregate particles as a mixture of ovals/ovoids and polygons/polyhedrons in different dimensions. Based on the obtained results, the corresponding empirical expressions of ϕ _agg,c are also derived in these studies [27,28].

Up till now, the specific relationship between the regular aggregate morphologies and the ITZ percolation has been clarified. However, there are still some serious oversimplifications in previous studies, which may lead to the great deviation between the predictions and the realities. It is well known that the effective thickness of the ITZs in cementitious materials may generally fluctuate within a certain range (e.g., [0.1 mm, 0.2 mm] in Ref. [29], [0.015 mm, 0.05 mm] in Ref. [30], and [0.05 mm, 0.2 mm] in Ref. [31]), which would be affected by a variety of factors such as the compositions, spatial distribution, and hydration degree of cement. Moreover, according to the study by Elsharief et al. [32] and Lyu et al. [33], the aggregate size is also a critical parameter that determines the ITZ thickness. Thus, it may not be very appropriate for the prediction of ITZ percolation to adopt the simplistic uniform ITZs, rather than the realistic differential ITZs in the modeling of concrete. Recently, the ITZ percolation involving the differential thickness has been studied by us in 2D space [34], and the results show that the critical threshold ϕ _agg,c can be greatly overestimated once the uniform ITZs are applied. However, whether this finding can also be applicable in 3D cases is still unknown, which is an issue of concern for many researchers and reviewers.

To clarify the ITZ percolation with the response of different phases, especially the effect of the nonuniform ITZs in a more realistic way, a variety of 3D polyphase composite models of concrete materials containing gravels as regular polyhedrons and sands as ovoids are presented by referring to description in the study by Lin et al. [28]. Moreover, the more realistic nonuniform ITZs are further assigned for all the aggregates according to their equivalent diameters and the water–cement (W/C) ratio. Afterward, by combining these polyphase models with the theory of continuum percolation, the percolation behavior of nonuniform ITZs surrounding the mixture of ovoidal and polyhedral particles is simulated explicitly, and the effect of individual phases (e.g., aggregate shape- and size-differentiation, sand ratio, W/C) on the critical threshold ϕ _agg,c in concrete is explored numerically. Simultaneously, the critical threshold ϕ _agg,c for the realistic nonuniform ITZs is also in comparison with the corresponding ϕ _agg,c for the simplistic uniform ITZs through the whole process of analysis. Based on the numerical results and comparisons, several significant findings are clarified finally.

2 3D polyphase models of concrete materials

As described in the study by Lin et al. [26], the regular polyhedron, also known as “Platonic particle” is a general term for a variety of 3D regular particles with the limited number of faces, such as regular icosahedrons, dodecahedrons, octahedrons, cubes, and tetrahedrons, as shown in Figure 1, and they have been widely adopted by researchers to represent the particulate components in the modeling of granular composites in the literature [26,35,36]. Mathematically, the surfaces of all these particles can be expressed by the collections of their vertices, edges, and faces, and the specific expressions have been elaborated in the study by Lin and Chen [37]. In view of their similar morphologies to the gravels in concrete, they are also be applied here to represent the coarse aggregates.

Figure 1

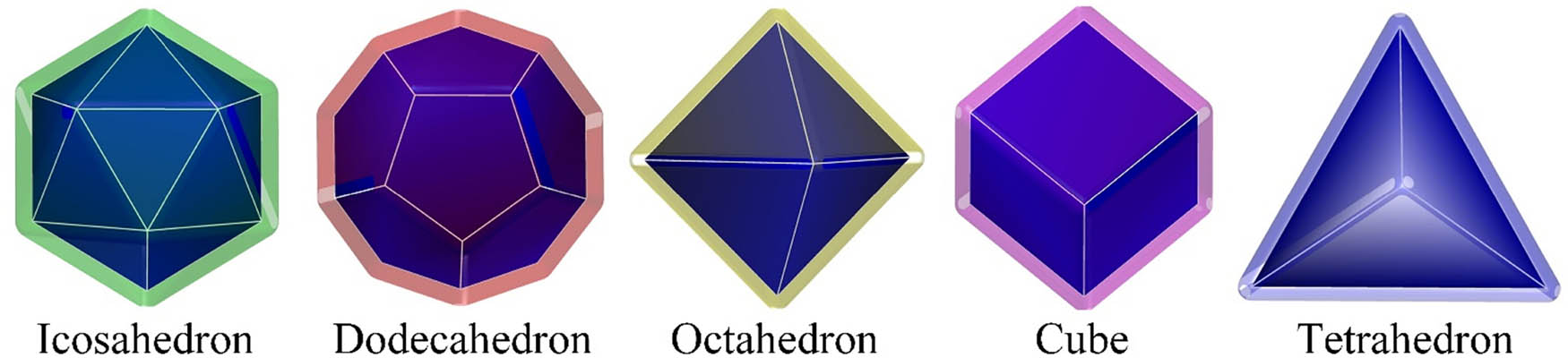
The surface of five kinds of 3D regular polyhedrons along with the interfaces.

By comparison, the ovoid, which is generally used to stand for the fine aggregates, can be considered as the catch-all name for a variety of particles with the smooth surface such as spheres, egg-like particles, ellipsoids, etc., and the surfaces of these particles could be simply expressed by the extension of the formula (i.e., equation (1)) for the ellipsoids, as given in the study by Lin et al. [28]:

where a, b, and c are the measures of particle sizes in the x-, y- and z-axis direction, respectively, and the ratio of c to a (i.e. c/a) is defined as the aspect ratio of these particles. The parameter ζ is termed as the tapering coefficient that can also determine the geometric morphology of ovoid. In this work, the values of c/a in [0.2, 2.0] and ζ in [0.0, 0.6] are applied by reference to our previous paper [28]. Moreover, to reduce the complexity of particle shapes, the ratio b/a is always set to be 1.0. Figure 2 illustrates an example of the ovoid with c/a = 1.5 and ζ = 0.3.

Figure 2

The surface of 3D ovoidal particle (c/a = 1.5, ζ = 0.3) along with the interfaces.

In most of numerical simulation of concrete materials, their ITZ phase is commonly assumed to be an identical-thickness layer around the aggregates, and the ITZs for different aggregates can be overlapped freely. However, as stated in Section 1, the ITZ thickness in realistic concrete is not a fixed quantity. Naija and Miled [38] stated that the ITZ thickness t _ITZ in concrete can be simplistically formulized as a function of both the W/C and aggregate sizes, and its applicability has also been verified by comparison with the experimental data. To explore the influence of nonuniform ITZs on its percolation, the formula of ITZ thickness t _ITZ is adopted from the study by Naija and Miled [38], as expressed by equation (2).

where D _eq is the equivalent diameter of aggregate particles.

In addition, to explore the sensitivity of ITZ percolation to the aggregate size gradations, two mathematical gradation functions (i.e., equations (3) and (4)), which are commonly adopted in the area of cement-based composites are also utilized to express the size gradations (PSG) of both gravels and sands in the work.

where D _eq,min and D _eq,max represent the minimum and maximum equivalent diameters of these 3D nonspherical aggregates, respectively. F _V (D _eq) is the volume-based cumulative probability function.

Finally, by incorporating the aforementioned formulas (i.e., equations (2)–(4)) into the RSA algorithm in the literature [28], the simplified 3D polyphase models of concrete specimen containing the smaller-sized ovoidal sands (i.e., fine aggregates), larger-sized polyhedral gravels (i.e., coarse aggregates), and nonuniform ITZs can be quickly constructed by using computer simulation technology, as shown in Figure 3.

Figure 3

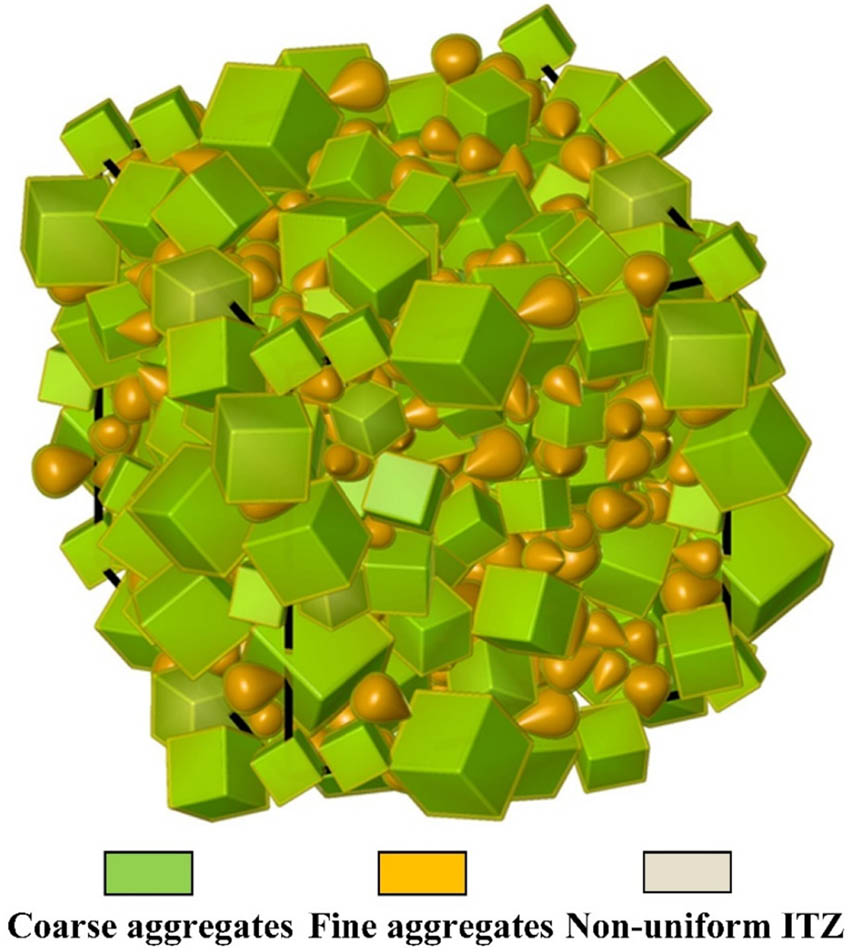
An example of the 3D polyphase model of concrete containing the polyhedral coarse aggregates, ovoidal fine aggregates and nonuniform ITZs (W/C = 0.42, for cubes, D _eq = Fuller 5–10 mm, for ovoids, D _eq = Fuller 2.0–4.5 mm, and the sand ratio β _s = 0.42).

3 Percolation simulation of nonuniform ITZs

As depicted in Figure 4, the ITZ percolation mainly reflects the global connectivity of the ITZs through the whole system and the critical threshold is generally represented by the total relative content ϕ _agg,c of aggregate particles when the ITZ percolation is exactly emerged. For a 3D polyphase model with the finite size length L, the existence or not of the effective ITZ percolation paths is random, which can be expressed by the binominal distribution function, as given in the previous studies [27,39,40]. With the increase of the number N _total of the specimen models, a new parameter P _ITZ(ϕ _agg), which is termed the percolation probability, is proposed to represent the probability of the emergence of the percolation paths for the given model of L and aggregate fraction ϕ _agg, and its value can be approximated by the number ratio N _pcl/N _total of the percolated samples to the total samples, as expressed in equation (5). For instance, it is assumed that there is a total of 200 models of concrete specimen (i.e., N _total = 200). If the ITZ percolation paths can be formed in 50 models (i.e., N _pcl = 50), the value of P _ITZ can be considered to be approximately equal to the number ratio N _pcl/N _total (i.e., P _ITZ ≈ 50/200 = 0.25). Moreover, to guarantee the stability of P _ITZ, both the size length L and the sample number N _total should be large enough. According to the description in the study by Lin et al. [28] as well as the criterion for the REV in [41], the values of N _total and L are, respectively, set to 1,000 and to be at least four times as wide as the value of D _eq,max,p for the polyhedral coarse aggregates.

where ϕ _agg is the volume fraction of aggregate particles in the model of concrete, N _total is the total number of generated sample models, and N _pcl is the number of samples in which the ITZ percolation paths can be found.

Figure 4

The schematic diagram of the percolation path of nonuniform ITZs in the polyphase model in Figure 3.

Afterward, as the statistical results of P_ITZ for a wide range of aggregate fraction ϕ _agg (i.e., the curves of P _ITZ vs ϕ _agg) are obtained, the critical percolation threshold ϕ _agg,c could be obtained easily through the curve-fitting analysis of these P _ITZ vs ϕ _agg curves by equation (6).

where Δ is the percolation transition and ϕ _agg,c is the critical percolation threshold, which corresponds to the total aggregate fraction when the ITZ phase is exactly at the critical percolation state.

4 Results and discussion

In this section, the systematic simulations of the ITZ percolation under the different cases are carried out one after another, and the corresponding numerical predictions of ϕ _agg,c are analyzed and compared with the analytical solutions predicted by the analytical formulas in the study by Lin et al. [28]. In what follows, a brief recall of the formula is presented first.

In our previous study [28], the gravels and sands in concrete are separately simplified as the larger-sized polyhedrons and smaller-sized ovoids, and the critical percolation of the uniform ITZs around them is simulated. Based on the simulated results, the quantitative relationship between the percolation threshold ϕ _agg,c and the geometrical characteristics of these aggregate particles is derived, and the detailed expression of ϕ _agg,c is written as equation (7).

where t _ITZ is the ITZ thickness; s _3D,P and s _3D,O are the sphericities of polyhedrons and ovoids, respectively; S _V,P and S _V,O denote the SSA of polyhedrons and ovoids, respectively; and β _s is the sand ratio of aggregates.

In view of that the effective thickness of the ITZs in equation (7) is assigned as a constant for all the aggregates, to compare our obtained results of ϕ _agg,c here with the analytical predictions, the effective average thickness t ITZ avg of the nonuniform ITZs in the work is firstly obtained by equation (8) and the corresponding solutions of ϕ _agg,c with the same average thickness are evaluated by substituting the value of t ITZ avg into equation (7).

where D _eq,p and D _eq,o are the equivalent diameter of polyhedrons and ovoids, respectively; f _N is the number-based probability function; D _eq,max,p and D _eq,min,p are the maximum and minimum equivalent diameters of polyhedral aggregates, respectively; and D _eq,max,o and D _eq,min,o are the maximum and minimum equivalent diameters of ovoidal aggregates, respectively.

By using the aforementioned technique, a range of the parametric studies are conducted hereafter to investigate the influence of the microstructural characteristics of individual phases on the percolation thresholds of these nonuniform ITZs in concrete.

4.1 Aggregate shape effect on ITZ percolation

Figure 5 shows the sensitivity of the critical threshold ϕ _agg,c of both nonuniform and uniform ITZs to the geometrical shapes of polyhedral gravels and ovoidal sands. It is found that all the variations of ϕ _agg,c with the morphology shift of aggregate particles for the nonuniform ITZs are consistent with the variations of ϕ _agg,c for the uniform ITZs. In Figure 5(a), when the shape of ovoidal particles is given, ϕ _agg,c shows an apparently declining trend along with the shift of polyhedral aggregate from sphere to tetrahedron for both nonuniform and uniform ITZs. It means that the fewer the number of the face of polyhedral aggregates is, the effective percolation paths of the ITZ phase would be easier to be formed. As shown in Figure 5(b), when the shape of polyhedron is given, the threshold ϕ _agg,c can be deemed as an obvious ζ- and c/a-dependent parameter. On the one hand, ϕ _agg,c decays slightly with the increasing ζ from 0.0 to 0.6. On the other hand, the evolution curve of ϕ _agg,c with c/a in [2.0, 0.2] is generally divided into two stages (i.e., the slowly declining stage and the rapidly growing stages) by the inflection point c/a = 1.0. The maximum threshold ϕ _agg,c is roughly reached when ζ = 0.0 and c/a = 1.0. That is to say, when the spheres are used to stand for the sands in concrete, the ITZ percolation threshold ϕ _agg,c may generally be larger than realities. Essentially, the influence of particle morphology on the value of ϕ _agg,c can be attributed to the aggregate sphericity s _3D. No matter for polyhedral coarse aggregates or ovoidal fine aggregates, the threshold ϕ _agg,c in both Figure 5(a) and (b) presents the roughly declining variation with the decrease of particle sphericities (i.e., s _3D,P and s _3D,O). This is due to that the smaller the aggregate sphericities (s _3D,P or s _3D,O) are, the greater the circumradius of aggregates and the effective content of the ITZ phase for a single particle would be, which would result in the increase of the collision probabilities of adjacent ITZs around the different aggregates.

Figure 5

The sensitivity of ϕ _agg,c of nonuniform and uniform ITZs to the geometric shapes of (a) regular polyhedral gravels and (b) ovoidal sands.

According to the results presented in Figure 5, it is observed that whatever the geometric shape of polyhedrons or ovoids is, when the same average ITZ thickness is given for all the aggregate particles, the corresponding ϕ _agg,c predicted by the models in the literature [28] would be commonly greatly overestimated than that for the realistic nonuniform ITZs, and the overestimation degree of ϕ _agg,c is not sensitive to the specific shapes of particles. The above trends of ϕ _agg,c further emphasizes the necessity and importance of the realistic nonuniform ITZ thickness for the prediction of its percolation.

Figure 6 illustrates the evolution of ϕ _agg,c of the nonuniform ITZs with the increasing W/C in [0.3, 0.66]. It is shown that no matter what the aggregate shape is, ϕ _agg,c always decrease with the increasing W/C ratio in a linear manner, and its attenuation amplitude is also not sensitive to the specific shapes of both polyhedral and ovoidal aggregates. This is mainly because in the proposed model of t _ITZ, the ITZ thickness is formulized as a linear function of W/C, and consequently, the linear increase of ITZ thickness in concrete can naturally result in a regularly linear decline for the percolation of these nonuniform ITZs.

Figure 6

Impact of W/C ratio on the percolation threshold ϕ _agg,c of nonuniform ITZs.

4.2 Sand ratio effect on ITZ percolation

In the cases of W/C = 0.30, 0.42, and 0.54, Figure 7 further presents the evolution of ϕ _agg,c of both the realistic nonuniform ITZs and the simplistic uniform ITZs along with the increase of β _s from 0.30 to 0.70. It can be seen that, on the one hand, the influence of the W/C ratio on ϕ _agg,c here is also consistent with the proposed trend shown in Figure 6 (i.e., the greater the value of W/C is, the smaller the value of ϕ _agg,c is), which is untouched by the sand ratio β _s. This is a logical and expected trend, which is mainly due to that the larger W/C ratio would correspond to the greater value of t ITZ avg and then the higher collision probabilities of ITZs around the different aggregates. On the other hand, as the variable ITZ thickness is replaced by the equivalent uniform ITZ thickness t ITZ avg , the critical percolation threshold ϕ _agg,c also significantly decreases here.

Figure 7

The variation of the percolation threshold ϕ _agg,c of both nonuniform and uniform ITZs with the increasing β _s in [0.3, 0.7] under the cases of different W/C.

In addition, the obviously different curves of ϕ _agg,c-β _s are presented in Figure 7 when the nonuniform and uniform ITZs are considered, respectively. For the simplistic uniform ITZs, ϕ _agg,c shows the perfectly linear declining tendency with the increase of β _s in [0.3, 0.7]. By referring to the description by Naija and Miled [38], the aforementioned phenomenon can be explained by the fact that as the sand ratio β _s increases, the total number of aggregate particles would be greatly increased for the same aggregate fraction ϕ _agg, which in turn leads to the greater contact surface between the aggregates and the cement matrix. However, for the realistic nonuniform ITZs in Figure 7, all the curves of ϕ _agg,c-β _s present a slightly increasing trend first and then decreasing trend with the increase of β _s. On the one hand, the growth of the total contact surface of aggregate particles along with the increasing β _s in concrete is conducive to the formation of the ITZ percolation paths (i.e., the lower threshold ϕ _agg,c). On the other hand, under a constant W/C, the smaller-sized aggregate corresponds to the thinner ITZ thickness according to the expression in equation (2), which would be unfavorable to the formation of ITZ percolation path and may in turn lead to the larger percolation threshold ϕ _agg,c. Actually, the percolation of the nonuniform ITZs here would be subjected to the synergetic influence of the aforementioned two factors. Hence, the assumption (i.e., the nonuniform ITZs) gives the different results from that for the uniform ITZs.

4.3 Aggregate size gradation effect on ITZ percolation

In Figure 8, the effect of aggregate size gradation on the percolation threshold ϕ _agg,c of both nonuniform ITZs and uniform ITZs under W/C = 0.30, 0.42 and 0.54 is explored. One can see that whatever the aggregate size gradation is, the threshold ϕ _agg,c always shows the rapid declining tendency with the increase of W/C. The value of ϕ _agg,c for the realistic nonuniform ITZs is still much lower than the predicted solutions obtained by substituting the same average thickness t ITZ avg into the previous prediction models, as illustrated in Figure 7. Besides, the results in Figure 8 clearly show that the critical thresholds for the Fuller gradation are always greater than those for the EVF gradation, which is not conditioned by the W/C ratio and the ITZ thickness. This can be mainly attributed to the variation of the SSA of aggregate particles or the total contact surfaces between cement matrix and aggregate particles. As stated in Ref. [22], for the aggregate particles with EVF gradation, there are much more small particles than that with the Fuller gradation, which can in turn lead to the larger SSA of aggregates as well as the greater total contact surface. Both of the aforementioned variations can promote the formation of ITZ percolation paths. In addition to all of the aforementioned trends, a new noticeable phenomenon (i.e., the sensitivity of ϕ _agg,c to the PSG for the nonuniform ITZs is much slighter than that for the simplistic uniform ITZs) is shown in this figure, which can be explained by another fact that, for the realistic nonuniform ITZs given by equation (2), the effective thickness t _ITZ would decrease with the decrease of the aggregate equivalent diameter D _eq. In this sense, the number growth of the smaller-sized particles with the same aggregate fraction (e.g., EVF gradation) may make the total effective ITZ thickness be thinner, and then presents the unfavorable effect to the formation of the ITZ percolation paths. The composite effect of a series of the aforementioned factors eventually results in the decline of the sensitivity of ϕ _agg,c to the PSG for the realistic nonuniform ITZs.

Figure 8

Effect of PSG on the percolation threshold ϕ _agg,c of both nonuniform and uniform ITZs under the cases of different W/C values.

4.4 Maximum aggregate diameter effect on ITZ percolation

Under the case of D _eq,o = Fuller 1.0–4.5 mm, Figure 9 further displays the evolution of ϕ _agg,c with the increase of maximum equivalent diameter D _eq,max,p of polyhedral aggregates. It is shown that whatever the W/C or ITZ thickness is, the ITZ percolation threshold ϕ _agg,c shows the slightly upward trend as the aggregate size D _eq,max,p increases. This is also an expected and logical result. It can be explained by the fact that as the value of D _eq,max,p increases, the contact surface between the cement matrix and aggregate particles would decrease, which can be not conducive to the formation of the ITZ percolation (i.e., the more fraction of aggregate particles is needed to form the global percolation paths of the ITZ phase). Besides, the aforementioned phenomenon can also be explained by the variation of the SSA of these aggregates (i.e., the aggregate fineness). According to our previous study [26], the larger maximum diameter of aggregates can result in the greater value of SSA, which corresponds to the higher ITZ percolation threshold ϕ _agg,c. In addition, it should be noticeable that the sensitivity of ϕ _agg,c to D _eq,max,p for the realistic nonuniform ITZs in this figure is also obviously lighter than that for the simplistic uniform ITZs. All in all, for the realistic ITZs with the differential thickness, the influence of the microstructural factors on the ITZ percolation is much more complicated than that reported in the previously published studies [20,22,26,27,28].

Figure 9

Effect of maximum aggregate diameter D _eq,max,p on the percolation threshold ϕ _agg,c of both nonuniform and uniform ITZs under the cases of different W/C values.

By using the computer simulation technology, a variety of 3D polyphase composite models of concrete materials that are closer to the realistic structure of concrete are generated in this work and the critical percolation behavior (i.e., the global connectivity) of the ITZ phase around different aggregates is further simulated based on the combination of percolation theory and Hard core-soft shell network. Afterward, the percolation property of the ITZ phase in different polyphase systems is explored numerically, and the sensitivity of the critical percolation threshold ϕ _agg,c of ITZ to the geometric features of both aggregate particles and nonuniform ITZs is clarified. All of the aforementioned processes are implemented through our own programming and the numerical results are obtained by the computer technique. According to the continuum percolation theory, the ITZ percolation is mainly applied to represent the global connectivity of the ITZ phase through the whole concrete. The relevant researches here can be generally regarded as a pre-phase preparation for exploring the influence of ITZ percolation on the macroscopic properties of concrete and thus may provide some meaning guide for the optimization of a variety of material properties.

5 Conclusions

In the work, a variety of more realistic 3D polyphase composite model of concrete are developed, in which the gravels and sands are separately simplified as the regular polyhedrons and ovoids according to their actual morphologies. In this way, the geometric difference between them becomes a major consideration here. Moreover, on the basis of the specific aggregate size and the W/C for the cement paste, the differential ITZ thickness for the nonuniform ITZs is also assigned for each aggregate in these models. By coupling these polyphase models with the continuum percolation theory, the sensitivities of the percolation threshold ϕ _agg,c of nonuniform ITZs to the microstructural features of individual phases are studied by the simulation. Furthermore, a range of the numerical comparisons of the threshold ϕ _agg,c for both the realistic nonuniform ITZs and simplistic uniform ITZs are also presented through the whole process of analysis. According to the obtained results and comparisons, several noticeable conclusions are obtained here.

• For the nonuniform ITZs, the value of W/C has a dominant influence on the ITZ percolation. The ITZ percolation threshold ϕ _agg,c would significantly decrease along with the increase of W/C.

• When the realistic ITZs with the nonuniform thickness are replaced by their average value, their percolation threshold ϕ _agg,c would be greatly overestimated in varying degrees than the reality (i.e., the nonuniform ITZs).

• The sensitivity of ϕ _agg,c to the aggregate size distribution for the realistic nonuniform ITZs is much lighter than that for the simplistic uniform ITZs.

• For the nonuniform ITZs, ϕ _agg,c shows a slightly increasing first and then decreasing trend with the increase of sand ratio β _s, which is distinctly different from the curves of ϕ _agg,c-β _s for the uniform ITZs.