Fast prediction of concrete equivalent modulus based on the random aggregate model and image quadtree SBFEM

1 Introduction

Concrete is a main construction material with excellent performance, which has widely used in civil and hydraulic engineering [1,2,3]. It is an artificial composite material generated by mixing cement, sand, coarse aggregate, water, and other admixtures, followed by evenly stirring, compacting, curing, and hardening. The mechanical properties of concrete are directly related to the water/cement ratio, pores, aggregate content, and aggregate type [4,5] The traditional researches on mechanical properties of concrete mostly focus on experimental tests. The test not only provides basic parameters for numerical simulation and theoretical analysis but also offers a significant method of verification of the rationality and accuracy of theories [6,7,8]. However, it usually requires a lot of manpower and material costs to accommodate the changes in test conditions and site factors. What’s worse, with the operation of engineering structures, the germination of internal defects results in a certain degree discreteness in experimental data.

To efficiently evaluate the mechanical properties of concrete, especially including defects, it is necessary to develop the prediction model. Based on a three-phase spherical model and a hollow cylindrical rod model, the influence of porosity on the macroscopic mechanical properties of concrete has been studied and given the quantitative relationships between the porosity and the effective bulk and shear moduli [9]. The results indicate that the effect of pore-water on concrete tensile strength is significant and should not be neglected in design. On the basis of homogenization techniques and failure criteria, Greco et al. [10] proposed an innovative micro-mechanical approach to investigate the effects of micro-crack initiation and evolution on the macroscopic response of elastic periodic composite materials, where the initially undamaged inclusion and matrix interface were considered in the fibre-reinforced composite. The innovative approach with robust capability and efficiency is also helpful to study the mechanical properties of composite materials like concrete. Considering the porosity and pore size, Li et al. [11] established a micromechanical model to predict the macroscopic of concrete through two equivalent processes and discussed the influence of the elastic modulus of coarse aggregate, the coarse aggregate content, and the elastic modulus of the interfacial transition zone (ITZ) on the yield strength. In the later work, explicit formulae of porous concrete effective tensile and compressive strengths were given out and detailed the total influence coefficient of porosity and pore size [12]. As a basic mechanical index of concrete, the equivalent elastic modulus plays an important role in governing the mechanical properties and especially in terms of stiffness and deformation capacity. Many studies have been carried out to estimate the effective elastic modulus based on the theoretical and experimental analyses [13,14,15]. The influences on the effective elastic modulus also have been studied by considering the maximum aggregate size, aggregate gradation, hydration, water-to-binder ratio (w/b), coarse aggregate content, steel fibre shape, and so on.

With the development of meso-mechanics and computer technology, numerical simulation has become a popular method to study the relationship between meso-components and macroscopic mechanical properties of concrete [16,17]. When establishing the numerical model of the meso-concrete structure, the finite element method is commonly utilized with quite fine meshes to fit well with heterogeneous geometric boundaries for avoiding the appearance of the hanging nodes [18]. It greatly increases the workload of grid partition and subsequent structural numerical calculation. To avoid remeshing processes, Ammendolea et al. [19] present a novel finite element (FE) modelling approach based on the moving mesh technique to reproduce crack propagation mechanisms. The comparison results show that the proposed method has high reliability and robustness, which could represent a valid tool to simulate concrete fracture property. Recently, the scaled boundary finite element method (SBFEM) with a semi-analytical accuracy in the calculation is developed [20], which exhibits outstanding works on crack propagation modelling [21,22]. What is more, the computational domain of SBFEM only discretizes in the boundary of elements so that the method becomes more alternative for the simulation of complex heterogeneous materials due to its accuracy and low computational cost [23]. On the other hand, the quadtree is a tree data structure that starts with the initial root unit, and each unit can be divided into four subunits until all units meet the requirements [24]. When the quadtree data structure is used for the meshing, an automatic partition of the model is fulfilled and achieves a rapid transition of the junction of different mesh sizes [25]. Combining the quadtree algorithm and SBFEM, a novel approach was proposed for the mesoscopic fracture modelling of concrete [26]. There are only six types of unique node subdomains, and all the shapes are square. When assembling the overall stiffness matrix of the model, only six types of subdomain stiffness matrices are calculated and other element stiffness matrices are directly obtained by multiplying the scale factor. Because of the same features with the corner node in SBFEM, the handing node does not affect the calculation accuracy, which is flexible and robust on element meshing with irregular boundaries for composite materials like concrete to study the mechanical property of concrete with the quadtree data structure.

The aim of this article is to propose a fast prediction model for evaluating the effective modulus of 2D mesoscopic concrete based on the random aggregate model. Herein, SBFEM is employed to calculate the mesoscopic response of concrete with the quadtree data structure. First, the mesoscopic components of concrete are generated and distributed randomly by the random aggregate model. Then, the mesoscopic concrete model is transferred into a data matrix and divided in accord with the quadtree data structure to follow. Combining the advantages of image quadtree algorithm, the representative volume element (RVE) of meso-concrete is established, and the stress–strain field efficiently based on SBFEM was analysed. The equivalent modulus is predicted by using the numerical homogenization method. Finally, several numerical examples are conducted to verify the prediction model. What is more, the effects of aggregate gradation, particle shape, porosity, and pore water are analysed on the concrete equivalent modulus.

2 Construction of meso-concrete model

In general, meso-concrete is regarded as a three-phase material containing mortar, aggregate, and ITZ. The coarse aggregate of the concrete structure is the crushed stone or gravel with a convex shape. The area, equivalent radius, size distribution, and other characteristics of aggregates in the concrete specimen are analysed by using the statistic method before constructing the meso-concrete model. Herein, the 2D meso-concrete model is considered, and the shape of polygonal aggregates is generated that usually consists of two steps, namely, aggregate generating and distributing [27]. In the first step, several circles are randomly generated with different quantities and sizes according to the descending order of aggregate sizes. The size of each circle approximates the size of the corresponding gradation aggregate. An original triangle is drawn by connecting three random points located in the trisection arc of the circle. The triangle is then extended to be polygon by governing the thresholds of the size of the longest edge and the total area of the polygon. Finally, that polygon is regarded as the polygon aggregate, and the detailed generation process is shown in Figure 1.

Figure 1

Generation of random polygonal aggregate.

In the governing of the edge size, a maximum threshold l _max is employed, and the aggregate will extend from this edge when the value is larger than the threshold (l _i > l _max). The new vertex is obtained randomly in the semicircular area according to the current longest edge l(x _i , x _i−1), as shown in Figure 2, and the coordinate vector x _p is given as follows:

where x _i and x _i+1 denote the two vertices coordinate vector of the longest edge, γ is a random value between 0 and 1, r x i x i + 1 denotes the radius of a semicircle, where the edge x _i x _i+1 is the diameter, and e is a random unit vector.

Figure 2

Generation of vertex x _p.

To ensure the particle sizes of generated aggregates belong to the region of the aggregate gradation, statistics on the particle size of the generated aggregate is performed according to the geometric method. First, each edge of the aggregate is selected as the baseline and the vertical line is drawn from each vertex to the edge. The corresponding length of each vertical line is then calculated and sorted. Finally, the minimum value of all maximum lengths is the particle size of the aggregate, which means that the minimum threshold of the sieve pore can successfully get through for classifying aggregate gradation. For example, orthogonal lines from each vertex to edge i and i + 1 are drawn, and each maximum value max _i and max _i+1 is sorted out, as shown in Figure 3. If max _i > max _i+1, then the aggregate can get through the sieve pore along the edge i + 1 and the size of the sieve pore is max _i+1. Thus, the particle size D of the aggregate is the minimum value of all maximum lengths, which is expressed as follows:

Figure 3

Identifying method of aggregate particle size.

In the second step, the obtained aggregate is randomly distributed over the model based on the Monte Carlo method. The distribution process also adheres to the descending order of aggregate sizes. An inspection of the mutual overlap between any two aggregates is performed to verify the aggregate distribution. To increase efficiency, the inspection is divided into coarse and fine strategies. A minimal rectangle is employed to envelop the aggregate by using the minimum and maximum values of aggregate coordinates in the coarse strategy. If any two rectangles do not overlap with each other, the aggregate distribution proceeds. Otherwise, the vertex will be tracked to check the location. If the vertex located in another aggregate or the aggregate overlaps with another one, the new aggregate will be rotated by a random angle around its centroid up to 360 degree and the vertex locations are tracked and checked again. The aggregate would be discarded unless a certain angle is obtained to make the aggregate not overlap any other aggregate. The coordinate of vertex after rotating is expressed as follows:

where x ′ y ′ is the new coordinate of the vertex, x 0 y 0 is the original ones, and θ is the rotation angle around its centroid.

3 Numerical model for meso-concrete

3.1 Image quadtree mesh

Quadtree data structure is a hierarchical data structure that recursively divides each parent data into four child data. Quadtree mesh can quickly complete the element transition at the junction of different material areas, and the divided elements are all squares with high quality, as shown in Figure 4. The original square is the root element, and each square is divided into four equivalent squares by the quadtree mesh algorithm until the square size reaches the threshold. Handing nodes are inevitably generated during the mesh partition and hence it is hard to combine the finite element method for simulation [28]. Fortunately, the handing node is common with the corner node in the SBFEM element, and only six types of unique subdomains may occur in the numerical model by implementing the 2:1 rule during the quadtree meshing, as shown in Figure 5. These subdomain stiffness matrices can be precalculated and stored for fast data invocation.

Figure 4

Hanging nodes in quadtree mesh.

Figure 5

Unique subdomains when implemented 2:1 rule.

Before the quadtree mesh partition, the element size and pixel threshold of the image model are set first. The numbers in the pixel matrix range are 0–255, where 1 represents black colour and 255 represents white colour, respectively. The larger the number, the lighter the colour. Different colours represent different materials. The meso-concrete model is then transformed to be a grayscale image and stored as a digital matrix, as shown in Figure 6. The white colour is the aggregate and the black colour is the mortar. Taking a local region as example, the element size is set as one pixel and the grey colour denotes the ITZ. The transformation process is shown in Figure 6. During the quadtree mesh partition, the digital matrix is divided into four square subdomains in the first step, as shown in Figure 7(a). Then a check is carried out to the difference value between any two adjacent pixels in each subdomain. If the difference value is larger than the threshold value, the subdomain will be divided into four smaller square subdomains again. This process is repeated until the difference value in each element meets the pixel threshold and the quadtree mesh is shown in Figure 7(b). Finally, a further partition is implemented to ensure that the size ratio of adjacent subdomains is not greater than 2:1, namely, the balanced quadtree mesh [29]. The dividing step of the quadtree meshes of the meso-concrete model is shown in Figure 7.

Figure 6

Transformation process of meso-concrete to pixel matrix model. (a) Meso-concrete RVE model. (b) Local region with mortar, aggregate and ITZ. (c) Pixel image of the local region. (d) Pixel matrix model.

Figure 7

Dividing steps of quadtree meshes with 2:1 rule. (a) Digital matrix divided into four square. (b) Quadtree mesh satisfying the pixel threshold. (c) Final balanced quadtree meshes of local region. (d) Overall quadtree meshes of meso-concrete model.

3.2 SBFEM formulation

When conducting the numerical simulation of the meso-concrete, the quadtree meshing algorithm is employed to divide the model automatically and each square element with uncertain hanging nodes is modelled as scaled boundary finite element (SBFE) subdomain. The SBFEM is a radially analytical numerical method, which was first proposed by Wolf and Song [30]. In the SBFE subdomain, polygon edges with any number of nodes can be used as conventional line elements so that the hanging node does not affect the solution accuracy. As shown in Figure 8, the so-called scaling centre O places in the geometric centre of the quadtree SBFE subdomain, and only boundaries are discretized as line elements. Herein, the SBFE subdomain contains four corner nodes and two handing nodes, where the handing node divides the corresponding edge. There are six line elements in this subdomain, and the handing nodes are called as regular nodes in the scaled boundary coordinates (ξ, η).

Figure 8

SBFE subdomain with local coordinates (ξ, η).

In each SBFE subdomain, any point (x, y) in the line element can be described as follows:

(4) x = ξ x b ( η ) = ξ N ( η ) x b y = ξ y b ( η ) = ξ N ( η ) y b ,

where ( x _b , y _b ) is the nodal coordinate vectors in Cartesian coordinate, b denotes the number of line elements, N (η) is the shape function of the line element, ξ is the dimensionless radial coordinate pointing from the scaling centre (ξ = 0) to the boundary (ξ = 1), and η is the local coordinate in the circumferential direction along each line element. The whole area is covered by scaling the line elements on the boundary, which is shown by the dot-dashed line (ξ < 1) in Figure 8.

It is noted that only two-node line element is employed in the quadtree SBFE subdomain so that the vectors can be described directly by the two-node coordinates of the line element on the boundary with x _b = [x _i , x _i+1] and y _b = [y _i , y _i+1]. With the coordinate transformation to the scaled boundary coordinate, the displacements at the point inside the subdomain are formed as follows:

(5) u ( ξ , η ) = N ( η ) u ( ξ ) ,

where u ( ξ ) is the analytical displacements on the radial direction.

The static SBFEM equilibrium in displacement can be derived by applying the principle of virtual work.

(6) E 0 ξ 2 u ( ξ ) , ξ ξ + ( E 0 + E 1 T − E 1 ) ξ u ( ξ ) , ξ − E 2 u ( ξ ) = 0 ,

where E 0 , E 1 , and E 2 are coefficient matrices and depend on the geometry of the boundary.

(7) E 0 = ∫ η B 1 ( η ) T D B 1 ( η ) ∣ J ∣ d η E 1 = ∫ η B 2 ( η ) T D B 1 ( η ) ∣ J ∣ d η E 2 = ∫ η B 2 ( η ) T D B 2 ( η ) ∣ J ∣ d η .

Equation (6) is the Euler–Cauchy equation, which can be transformed into a first-order differential equation.

(8) ξ u ( ξ ) q ( ξ ) , ξ = − Z u ( ξ ) q ( ξ ) ,

where q ( ξ ) is the equivalent internal force vector and the Hamiltonian coefficient matrix Z is expressed as follows:

(9) Z = E 0 − 1 E 1 T − E 0 − 1 − E 2 + E 1 E 0 − 1 E 1 T − E 1 E 0 − 1 .

The Hamiltonian matrix Z can be solved using an eigenvalue decomposition [26], so the solutions for displacements u ( ξ ) and nodal forces q ( ξ ) are therefore expressed as follows:

(10) u ( ξ ) = Ψ 11 ξ − S 11 c ,

(11) q ( ξ ) = Ψ 21 ξ − S 11 c ,

where c is the integral constant vector, S ₁₁ is the positive real part of the eigenvalue vector of the modes, and Ψ ₁₁ and Ψ ₂₁ denote the displacement and force modes, respectively. The stiffness matrix of each S element is defined as follows:

(12) K S = Ψ 21 Ψ 11 − 1 .

For the elastic problem, the stiffness matrices of all S elements are assembled to form the global stiffness matrix, which are similar to the static stiffness matrices in FEM [31].

4 Prediction scheme of concrete equivalent modulus

A three-step analysis scheme is proposed to predict the equivalent modulus rapidly. First, the RVE of the meso-concrete model is constructed according to the aggregate content, gradation, and shape. Aggregates are randomly extended and distributed by using the randomized algorithm, which is detailed in Section 2. The square RVE model is exported as a grayscale image. Second, the grayscale image containing different colour is stored as a digital matrix and divided into quadtree meshes with 2:1 rule. SBFEM is then employed to analyse the stress–strain field with the static uniform compressive load. Finally, the numerical homogenization method is employed to evaluate the equivalent modulus. During the simulation, the average stress and average strain of RVE of meso-concrete are calculated as follows:

where σ ¯ and ε ¯ represent the average values of stress and strain fields, respectively. Ω denotes the domain of RVE. The effective properties of meso-concrete formed by the homogenization field theory is described as follows:

5 Numerical examples

5.1 Verification of equivalent modulus

To verify the proposed prediction model, several groups of meso-concrete RVE are generated with polygonal aggregates. Each group contains three numerical specimens, and the specimen size is 450 mm × 450 mm. Aggregates are generated and classified into three aggregate gradations according to the Fuller gradation curve and the aggregate standard [32]. The sizes of the three gradations are in ranges of 10–25, 25–40, and 40–50 mm, respectively, where the particle size of each aggregate is calculated using Equation (2). The aggregate contents are set to be 20, 30, 40, 50, 60, and 70%. The typical RVE models are shown in Figure 9. Concrete is generally simulated as a three-phase composite material, and the ITZ thickness is determined by the cement particle size. ITZ thickness is quite small, and the value is approximately between 30 and 80 μm [33]. For the sake of simplicity, only aggregate and mortar matrices are considered in this meso-concrete numerical model. The grayscale image of the meso-concrete model is set to be 1,024 pixel × 1,024 pixel and one pixel denote 0.44 mm. The white colour represents the aggregate with E = 7.0 × 10¹⁰Pa and v = 0.16. The black colour is the mortar matrix with E = 3.0 × 10¹⁰ Pa and v = 0.2. The model is partitioned by the image quadtree algorithm for the SBFEM analysis, and the minimum element size is 1 pixel. A static uniform compressive load is imposed on the top edge of the model and the bottom edge is restrained by several rollers, where the value is 1.0 × 10⁶ N/m.

Figure 9

Typical RVE models with contents of 20, 40, and 60%. (a) 20% aggregate content. (b) 30% aggregate content. (c) 40% aggregate content.

The quadtree mesh of the concrete RVE model with 30% aggregate content is shown in Figure 10(a). Mesh partition and all subsequent calculations are completed on a desktop PC configured with Intel(R) Core(TM) i7-8700 CPU @ 3.20 GHz and 64 GB memory. The total number of SBFE subdomains is 87670, and the mesh partition process only takes 0.21 s. Due to implementing the 2:1 rule, only six unique SBFE subdomain stiffness matrices are calculated, and hence, the calculation cost is quite low, wherein the static solution for simulating the concrete RVE with 30% aggregate content takes 5.02 s. The displacement in the direction of the compressive load and normal stress contour plots are, respectively, shown in Figure 10(b) and (c).

Figure 10

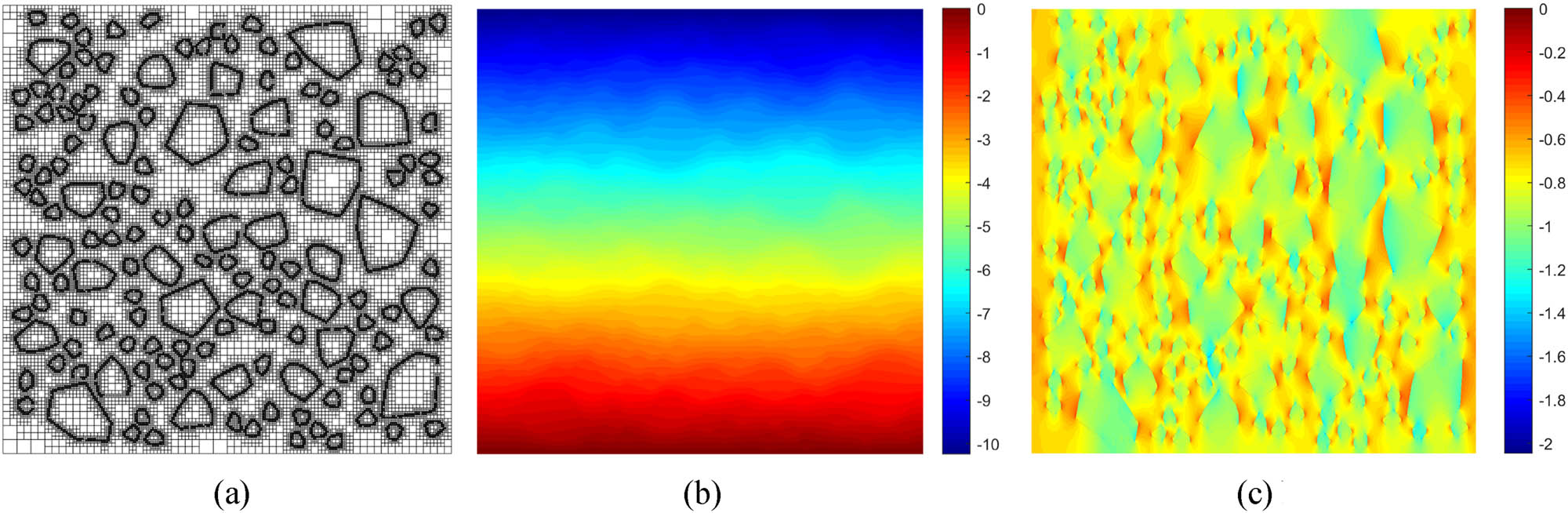
Quadtree mesh, displacement, and stress contour plots of concrete RVE with 30% aggregate content. (a) Quadtree meshes. (b) Displacement contour in vertical direction/μm. (c) Normal stress contour in vertical direction/MPa.

Based on the numerical results of concrete RVE, the average values of stress σ ¯ and strain ε ¯ are first calculated according to the numerical homogenization method using Equation (13). Then, the equivalent modulus is calculated using Equation (14), and the value variation over the aggregate content is detailed in Figure 11. Furthermore, the prediction values are compared with other existing methods, such as Voigt model, Reuss model, Mori–Tanaka model, and Hirsch model [34]. As shown in Figure 11, the value of the equivalent elastic modulus increases with the aggregate content, and the results always range between the ones calculated by the Voigt and Reuss method. The predicted equivalent elastic modulus agrees well with the values of the Mori–Tanaka method, and all relative errors are calculated, as shown in Figure 12. The maximum values of the relative errors to each other methods always occur in the region of 40–60% aggregate content. The maximum relative error occurs in 40% aggregate content when comparing with the Voigt method and the value is13.18%. When compared with the Mori–Tanaka method, the maximum relative error is only 1.20%, where the aggregate content is 60%. All the trend curves of the relative errors appear as the Gaussian distribution. It is indicated that SBFEM with the image quadtree algorithm is suitable for calculating and analysing the equivalent elastic modulus of concrete materials. The bulk modulus and shear modulus of concrete materials also have been calculated, and the variation with aggregate content is noted. With the aggregate content increasing, both the bulk modulus and shear modulus of concrete increase, which is consistent with the actual situation, as shown in Figure 13.

Figure 11

Comparison of equivalent elastic modulus under different methods.

Figure 12

Relative error of equivalent elastic modulus compared with other methods.

Figure 13

Variation of bulk modulus and shear modulus with aggregate content.

5.2 Effect of aggregate gradation and shape

To reveal the effect of aggregate gradation and shape on the equivalent modulus, the meso-concrete RVE models with 50% polygonal and circular aggregates are considered under different gradation compositions. Taking the aggregate content to be 50%, the aggregates are classified into four gradations according to the particle size, wherein the sizes are in ranges of 10–25, 25–40, 40–50, and 50–63 mm [32]. If the concrete aggregates consist of two smaller gradations, the gradation composition aggregate is called to be two-graded aggregate. Herein, two-, three-, and fully-graded aggregates are designed to construct the meso-concrete RVE model. The automatic analyses are then carried out by using the image quadtree algorithm and SBFEM. The predicted values of the equivalent elastic modulus are detailed in Table 1.

Table 1

Comparison of aggregate gradation and shape on equivalent elastic modulus of concrete

Aggregate gradation	Average equivalent elastic modulus (GPa)
	Polygonal aggregate	Circular aggregate
Secondary graded	44.4327	44.2659
Tertiary graded	44.3799	44.1961
Fully graded	44.3691	44.2151

Under the same aggregate content, the equivalent elastic modulus of concrete with polygonal aggregates is slightly larger than the one of concrete with circular aggregates. The main reason is that polygonal aggregate with sharp corners often leads to stress concentration, so that the calculated results are magnified by using the stress–strain field based on the numerical homogenization method. In addition, the irregular shape of polygonal aggregates increases the variability due to the rotation, which induces a larger standard deviation on the equivalent elastic modulus. The maximum value of the standard deviation for the polygonal aggregate model is 11.75%, and the value tends to be smaller with the increasing aggregate gradation, as shown in Figure 14. The discontinuous aggregate gradation plays the same role as polygonal aggregates, which induces a “stress concentration” in the whole domain, so that the predicted results present the same overestimate on the equivalent modulus. On the other hand, the standard deviation for the circular aggregate model tends to be larger with the increasing aggregate gradation, and the minimum value is 5.83%. It is concluded that aggregates with smoother aggregate gradation distribution form more compact concrete, which causes a slighter effect on the prediction of concrete equivalent modulus. If the aggregate composition is consistent with a quite ideal aggregate gradation, the effect of gradation would be zero and the standard deviation is a constant, which may be induced by the random distribution of aggregates.

Figure 14

Standard deviation of equivalent elastic modulus for different aggregate shape and gradation.

5.3 Effect of porosity and pore water

Due to the presence of defects like pores and microcracks, concrete material is inevitably permeated by water. The pore water pressure is imposed on the pore wall and the performance of concrete deteriorates steadily, especially under dynamic loading. To study the impact of porosity and pore water on the equivalent modulus of concrete, the moduli of the mortar matrix need to be reduced considering the volume fraction of the pores or pore water. The effective bulk and shear moduli are given based on the three-phase spherical model in the work of Jin et al. [9]. The reduction values of the Young’s modulus and Poisson’s ratio of the mortar matrix are calculated by the relationship with the bulk and shear moduli. Taking the random aggregate model of the fully graded concrete with 50% aggregate content as example, the equivalent modulus of dry and saturated concrete is calculated, and the variation curves of the equivalent elastic modulus are analysed with respect to the mortar matrix porosity from 0 to 30%. The equivalent elastic modulus decreases with the increasing porosity as shown in Figure 15(a). The decreasing values are divided by the elastic modulus value of nonporous concrete, and the relative reduction rates are calculated and shown in Figure 15(b). When the porosity of the concrete is 25%, the relative reduction rates on the equivalent elastic modulus are 7.13 and 5.78% for the dry concrete and saturated concrete, respectively. The pore water plays a positive role to restrain concrete from deteriorating the compression performance in a certain degree, and the positive impact becomes larger as the porosity increases.

Figure 15

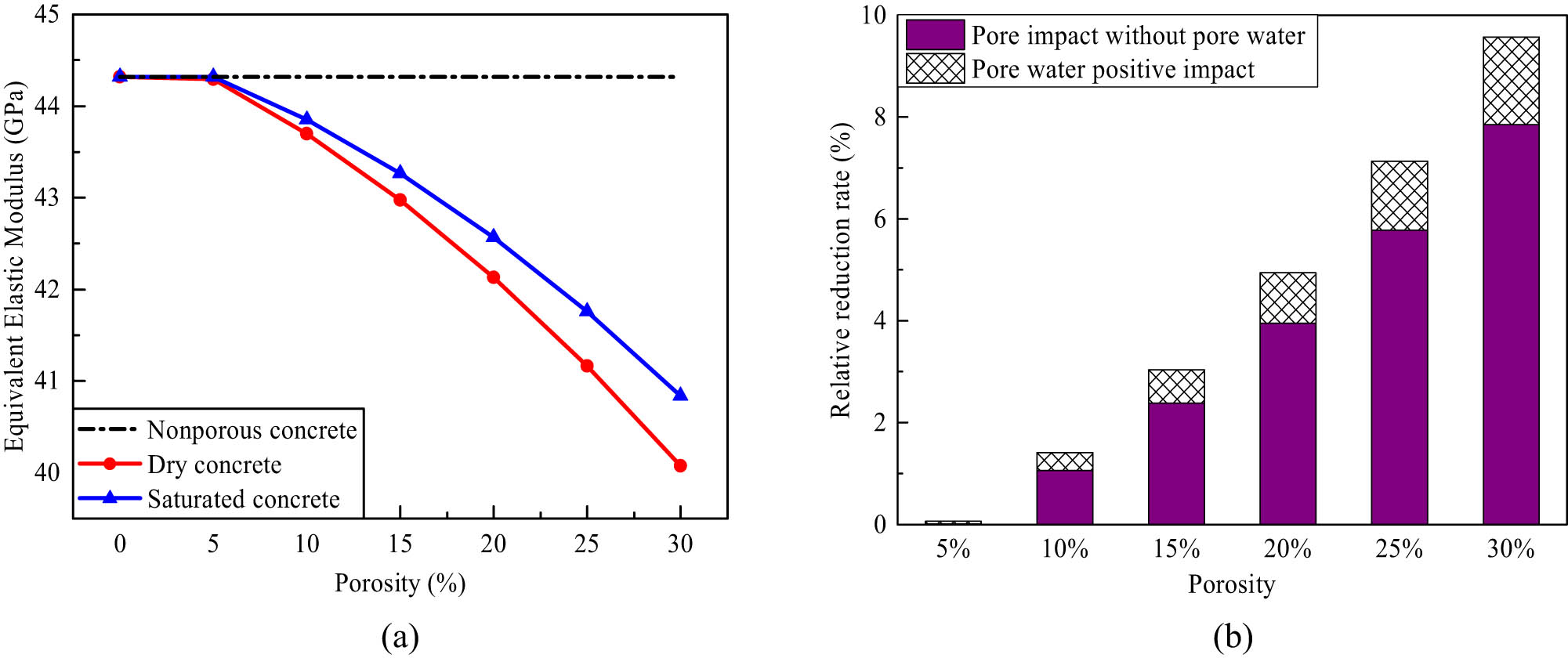
Variations on equivalent elastic modulus of concrete with porosity and pore water. (a) Comparison with dry and saturated concrete. (b) Relative reduction rate.

6 Conclusions

Combining the random aggregate model of meso-concrete and the quadtree SBFEM, a fast prediction scheme is proposed for determining the equivalent modulus based on the numerical homogenization method. Several numerical examples are studied to verify the predicted results, and the comparison with other methods is analysed with different aggregate contents. Furthermore, the effects of the aggregate gradation, shape, porosity, and pore water are studied in our work. The simulation results indicate the potential of the proposed model for predicting the equivalent modulus of concrete, and the model is also applicable to other composite materials. The conclusions can be drawn as follows:

1. The prediction model consists of a random aggregate model, the image quadtree method, and SBFEM. The equivalent modulus of concrete can be determined fast according to the aggregate content, gradation, shape, porosity, and pore water. The predicted results agree well with the values of the Mori–Tanaka method, and the maximum relative error is only 1.20%.

2. In the process of solving the equivalent modulus of concrete, the 2:1 rule of quadtree mesh partition is adopted, so there are only six unique subdomains in the whole calculation. Consequently, the overall stiffness matrix required for the solution can be assembled directly with the element stiffness matrix of these six modes. This approach significantly reduces the calculation work of the stiffness matrix, resulting in lower costs and greater automation.

3. The discontinuous aggregate gradation plays the same role as polygonal aggregates, which induces a “stress concentration” in the whole domain, so that the predicted results present the same overestimate on the equivalent modulus. Smoother aggregate gradation distribution forms more compact concrete, which causes a slighter effect on the prediction of concrete equivalent modulus. The effect of gradation would be zero with the aggregate fitting with a quite ideal aggregate gradation.

4. The porosity of concrete deteriorates the mechanic compression performance, while the pore water plays a positive role to restrain concrete from deteriorating to a certain degree and the positive impact becomes larger as the porosity increases. Therefore, the saturated concrete is recommended in pressure-bearing structures rather than dry concrete.