Home Research on the ingot shrinkage in the electroslag remelting withdrawal process for 9Cr3Mo roller
Article Open Access

Research on the ingot shrinkage in the electroslag remelting withdrawal process for 9Cr3Mo roller

  • Wanming Li , Ximin Zang EMAIL logo , Haiyang Qi , Dejun Li and Xin Deng
Published/Copyright: June 28, 2019
Download Article (PDF)
Become an author with De Gruyter Brill
Submit Manuscript Author Information
High Temperature Materials and Processes
From the journal High Temperature Materials and Processes Volume 38 Issue 2019

Abstract

In order to reduce the air gap between ingot and mould in the electroslag remelting withdrawal (ESRW) process, the taper of the mould should be consistent with the ingot shrinkage.Athree-dimensional mathematical model was developed to describe the interaction of multiple-physical fields (Joule heat, electromagnetic field, velocity field, and temperature field) and ingot shrinkage during the ESRW process. The variations of material thermal and mechanical properties, as well as the yield function with temperature, were considered. The shrinkage behavior of 9Cr3Mo roller in the ESRW process was simulated using the sequential coupling method. A good agreement between the calculated value and the measured valuewas obtained in the temperature field and stress field. Numerical results showed that maximum values of current density, Joule heat, and electromagnetic forcewere at the electrode corner of the slag bath. The direction of the magnetic flux density was tangential to the slag bath and had a clockwise rotation. There were two pairs of vortices and two high temperature zones in the slag bath. The shrinkage displacement was obtained through thermal-stress analysis. As the distance from the mould outlet decreases, the shrinkage displacement of ingot increases. As for the electroslag remelting withdrawal process for 9Cr3Mo roller, the variation of the shrinkage displacement from the slag/metal interface to the mould outlet was 0.0028 m. The maximum shrinkage displacement is at the mould outlet, and the value was 0.0089 m.

Keywords: ESRW; air gap; temperature field; ingot shrinkage; mould taper

1 Introduction

Electroslag remelting (ESR) products are characterized by compact structure, uniform composition and superior purity. The products are widely used in the aerospace, chemical, and energy industries, as well as for military and other applications [1]. Compared with the traditional ESR, the electroslag remelting withdrawal (ESRW) process has many advantages, such as increased productivity, yield, and decreased cost. Because of the large temperature gradient in the ESR process, there is an air gap between the ingot and the mould, which affects heat transfer of the ingot in the mould. In order to reduce the air gap, an inverted taper should be used [2]. If the mould taper is not suitable, the process would not proceed efficiently. If the inverted taper is too small, the heat transfer of the ingot will slow down, and if the taper is too large, the ingot will be difficult to demould. Leakage of molten steel and slag can also occur in serious cases when the taper is large [3]. The hydrostatic pressure of liquid steel acts vertically on the slag film during the ESRW process. Under normal circumstances, a slag film with molten steel wrapped inside is close to the inner wall of the mould, and the slag film will not be broken due to the internal support of the mould. However, if the taper is not reasonable, the air gap between the ingot and the mould will become larger under the action of ingot shrinkage. When the air gap extends upward to initial solidification shell near the slag-steel interface, the slag film will be crushed under the action of hydrostatic pressure of liquid steel, resulting in the leakage of steel and slag. Thus, the optimum design of the mould taper should be consistent with the volume change during ingot shrinkage. Therefore, it is important to study ingot shrinkage to develop ways to optimize the taper and minimize the leakage of molten steel and slag. As the requirement on product quality becomes more and stringent steadily, more detailed and precise approaches to the production technology should be adopted.

The temperature field is the basis of study for ingot shrinkage in the ESRW process. It is not possible to observe the melting and solidification process at the scene. A repeated trial and error method is very inefficient and expensive, so it is not suitable for system studies in ESR [4]. The numerical simulation method is a more effective method for studying the temperature field. In order to obtain an accurate temperature field, it is necessary to study Joule heat, the electromagnetic field, and the velocity field in the ESRW process. Many scholars have studied various mathematical models using the traditional ESR process. A. Kharicha et al. [5] and E.Karimi Sibaki et al. [6] described the effect of current variation in the ESR process, but their model is a two-dimensional (2D) numerical model, so the accuracies of the simulation results were constrained. Li et al. [7] built a three-dimensional (3D) finite element model, considering the skin effect of alternating current (AC), but only the electromagnetic field and Joule heat were simulated and analyzed. In order to make the results more realistic, some scholars [8, 9, 10, 11, 12] considered the effect of droplet dripping in the ESR process. However, the study of the ingot shrinkage and mould taper design based on 3D multi-physics field distribution is rarely reported in the ESR process.

The numerical simulation of the ingot shrinkage in a 2D continuous casting mould has become mature, but no one has studied the 3D numerical model of ingot shrinkage in the ESRW process. Thomas et al. [13] developed a CON2D finite element model, using the elastic-viscoplastic creep constitutive equation to calculate the stress field both inside and outside of ingot in continuous casting mould. Koric [14] calculated the temperature field and stress field of the billet using two different elastomeric constitutive models. Some scholars [15, 16] studied the solidification shrinkage of molten steel in moulds. Cai et al. [17, 18] established a transient model of solidification heat transfer and elastic-plastic stress for 2D molten steel using the ANSYSTM software, and the deformation of steel was simulated by the indirect coupling method.

In our research, we developed a three-dimensional numerical model for multiple-physical fields (Joule heat, electromagnetic field, velocity field, and temperature field) and ingot shrinkage in the ESRW process for 9Cr3Mo roller. The multiple-physical fields and ingot shrinkage in the ESRW process were calculated using ANSYS finite-element analysis (FEA) software and computational fluid dynamics (CFD) software, including the consideration of the effect of metal droplets on the process. The ingot shrinkage rule in the mould of the ESRW process was analyzed by shrinkage displacement of ingot, which provides a theoretical basis for solving the problem of leakage of molten steel and slag.

2 Numerical Model

2.1 Geometric model

In our research, the electroslag remelting withdrawal process of 9Cr3Mo roller steel was simulated. The slag composition used in the ESRW process is 60% CaF2, 20% CaO, and 20% Al2O3. The diagram of the ESRW process is shown in Figure 1. The process includes a consumable electrode, a slag bath, a liquid metal pool, a solidified ingot, and a mould. In order to simplify the calculations, the geometric model is simplified and the grid model is shown in Figure 2. The geometrical properties, specific process parameters, and physical parameters of materials are shown in Table 1.

Figure 1 Principle diagram of ESRW process
Figure 1

Principle diagram of ESRW process

Figure 2 Grid model of the calculation domain
Figure 2

Grid model of the calculation domain

Table 1

Geometrical properties, operating conditions, physical properties of the ESRW system

ParameterValue
Geometry
Electrode (diameter / height), m0.48/0.5
Electrode immersed depth, m0.01
Ingot diameter, m0.6
Ingot inside mould height, m0.37
Ingot outside mould height, m1
Slag (diameter / height), m0.6/0.18
Operating conditions
Current amplitude, A16500
Frequency, Hz50
Physical properties of metal
Density, kg·m−37800
Specific heat, J·kg−1·K−1753
Thermal conductivity, W·m−1·K−1781 K1344 K1572 K1673 K1723 K
24.182931.1831.8130.51
Electric conductivity, Ω−1·m−17.14×105
Latent heat of fusion, KJ·Kg−1267.1
Liquidus / solidus, K1564/1727
Magnetic permeability, H·m−11.26×10−6
Elasticity modulus, GPa573 K873 K1423 K1679 K1732 K
209178.671.322.82.4
Coefficient of linear expansion576 K986 K1191 K1421 K1667 K
1.3×10−51.4×10−51.1×10−51.3×10−51.5×10−5
Poisson ratio576 K1911 K1625 K1653 K1676 K
0.27590.27590.28680.29980.3199
Yield stress, GPa523 K1173 K1423 K1639 K1679 K
0.0190.0180.0070.0030.0003
Physical properties of slag
Density, kg·m−32594
Specific heat, J·kg−1·K−1837
Thermal conductivity, W·m−1·K−110.46
Liquidus, K1668
Thermal expansion coefficient, K−11×10−4
Magnetic permeability, H·m−11.26×10−6
Viscosity, Pa·s−11623 K1673 K1723 K1773 K1823 K
0.03690.02250.02020.0180.0178
Electric conductivity, Ω−1·m−11723 K1773 K1823 K1973 K
166.4200.9240275

2.2 Basic assumptions

In order to make the simulation more accurate and efficient, the following assumptions were made:

  1. The ESRW process is a quasi-steady state.

  2. The slag/metal interface of the ESRW is horizontal.

  3. The thermal physical properties of the slag and ingot are related only to temperature.

  4. The heat of the molten droplets is generated by the internal heat source.

  5. Neglecting the influence of creep, the thermal stress analysis of the steel ingot is carried out by using the thermo-elastic-plastic model.

  6. The high temperature mechanical properties of the ingot are related only to temperature.

2.3 Governing equation

2.3.1 Equations for the electromagnetic field

The current density distribution is calculated using Ampere’s law, where the current displacement is ignored:

(1)∇×H=J
(2)∇⋅B=0
(3)∇⋅J=0
(4)B=μaH

The current density is determined by Ohm’s law:

(5)J=σE

The potential distribution equation is:

(6)∇⋅σ∇ϕk=0

The Lorentz force and Joule heating therefore are described:

(7)Q=J⋅Jσ
(8)F=J×B=μaJ×H

where H is the magnetic field intensity; J is the current density; B is the magnetic flux density; μa is the magnetic permeability of free space; σ is the electrical conductivity; E is the electric field intensity; φk is the potential; Q is the Joule heating; F is the Lorentz force.

2.3.2 Fluid-flow equations

The continuity equation and the Navier-Stokes equations can describe the flow phenomena in the slag pool as follows:

(9)∇⋅v=0
(10)ρhv⋅∇v=−∇P+∇⋅μeff⋅∇v+F

The effective viscosity is the sum of molecular viscosity and turbulent viscosity, then:

(11)μeff=μ+μt

The turbulent viscosity can be calculated, by the following κ − ε equations:

Turbulent kinetic energy κ satisfies the equation:

(12)ρh∂κνj∂xj=∂∂xjμeffσε∂κ∂xj+G−ρε

Turbulent dissipation rate ε satisfies the equations:

(13)ρh∂εvj∂xj=∂∂xjμeffσε∂ε∂xj+εκC1G−C2ρε
(14)G=μt∂vi∂xj∂vi∂xj+∂vj∂xi

The relation of turbulent viscosity μt to κ, ε can be described as:

(15)μt=ρhCμκ2ε

where ρh is the density of molten; v is the velocity vector; P is the pressure; μeff is the effective viscosity of molten-metal; F is the body force; μt is the turbulent viscosity; C1, C2 are constant in the κ − ε model; G is the generation term for turbulent kinetic energy; σκ, σϵ are the Prandtl Numeral for the equation of κ and ϵ; Cμ is the dissipation rate constant. The model constants were assigned the values proposed by Launder and Spading [19].

2.3.3 Heat transfer equations

The heat transfer equation for the slag bath as follows:

(16)ρhCpv⋅∇T=∇⋅keff∇T+Q

Because the flow phenomenon of a metal molten bath is very complex, heat transfer of the bath can be simplified as conduction heat transfer, and the heat-transfer phenomenon can be described by an effective heat-transfer coefficient. The heat-conduction equation can be described as:

(17)ρdCPdvz∂T∂z=λd∂2T∂x2+∂2T∂y2+∂2T∂z2+qd

Where Cp is the heat capacity at a constant pressure; keff is the effective thermal conductivity of the slag pool; Q is the joule heat generated by the current; λd is the coefficient of thermal conductivity; vz is the drawing speed; d stands for different regions, and d = l, m, s, where l is the metallic bath, m is the mushy zone, and s is the solidified ingot.

2.3.4 The thermo-elastic-plastic constitutive equations

The plastic processing is quite complicated in the thermoelastic-plastic model. When the ingot enters the plastic state, there is no one-to-one correspondence between stress and strain. Strain not only depends on the current stress state, but it also depends on the entire loading history. It is impossible to establish the full relationship between the final stress and the strain, so the incremental theory must be used to establish the incremental relationship between stress and strain that is reflected in the loading history [20].

Considering the influence of temperature and strain rate, the total strain increment from the elastic-plastic theory is

(18)dε=dεe+dεp+dεθ

Where ϵ is the total strain; ϵe is the elastic strain; ϵp is the plastic strain; ϵθ is the thermal strain.

The elastic strain obeys Hook’s law. Considering the changes in the material parameters with temperature and strain rate, the incremental form is

(19)dεe=De−1dσ+∂De−1∂θσdθ+∂De−1∂ε˙σdε˙

According to the plastic flow rule of correlation, the plastic strain increment is

(20)dεp=dλ∂F∂σ

The thermal strain increment is

(21)dεθ=αdθ

Similarly, the yield function F should also consider the effects of temperature, strain rate, and the work hardening parameter K. The mathematical expression is

(22)F=Fσ,K,θ,ε˙

2.4 Calculation method and boundary conditions

2.4.1 Calculation method

Based on the size of the electroslag furnace, a three-dimensional (3D) geometric model was developed. The finite element mesh is divided by the mapping principle. According to the mathematical model and the process parameter table, the boundary conditions and initial conditions are applied to the whole system. The current density and Joule heat distribution of the whole system are calculated by thermoelectric coupling analysis unit (solid 69). The calculation results for the current density are introduced into the electromagnetic analysis unit (solid 97) to calculate the magnetic flux density and the electromagnetic force distribution of the whole system. Finally, the Joule heat is taken as the heat source and the electromagnetic force is taken as the driving force into the ANSYS CFX program. Using the CFX fluid-solid conjugate heat transfer module and the standard k-ϵ model, the velocity field and the temperature field are calculated. In the calculation of the stress analysis, the simulated ingot temperature field results are introduced into the thermal stress analysis unit. The ingot is subjected to thermal stress analysis. The flow chart of the calculation method is shown in Figure 3.

Figure 3 The flow chart of the calculation method
Figure 3

The flow chart of the calculation method

2.4.2 Electromagnetism and fluid flow

A consumable electrode is introduced into the current, and the bottom of the ingot is defined as zero potential. The magnetic induction intensity of the ESRW system is restrained. The slag/electrode interface, the slag bath side wall, and the slag/metal interface have no-slip boundary conditions. The slag /air interface has a free slip boundary condition.

2.4.3 Heat transfer and thermal stress

The consumable electrode is immersed in the slag bath as the liquidus temperature of the electrode. Radiation heat transfer and convective heat transfer between the slag bath and the air are simplified to the effective thermal conductivity.

The heat transfer between the slag pool and the mould conformed to the following equation:

(23)qcon=hconT−Tw

The heat transfer of the ingot surface in the mould conformed to the following equation:

(24)ke∂T∂x=hcovT−Tw

The heat transfer of the outside ingot surface of the mould conformed to the following equation:

(25)ke∂T∂y=hocT−Tc

The thermal conductivity of the outside ingot surface of the mould is divided into two parts, convective heat conduction and radiant heat conduction:

(26)hoc=hoca+hocb

Where hcon is the thermal conductivity between the slag bath and the mould; ke is the thermal conductivity of the ingot; hcov is the comprehensive thermal conductivity between the ingot side and the mould.

The heat-transfer boundary conditions used in the model are as follows. The heat transfer coefficient between the air and the electrode was 25.1 W·m−1·K−1. The heat transfer coefficient between the air and slag was 985 W·m−1·K−1. The heat transfer coefficient at the side of the slag bath was 1352 W·m−1·K−1. With increasing distance between the slag/metal interface and the outlet of the mould, the heat transfer coefficient of ingot sides decreased linearly from 271 to 8 W·m−1·K−1. The ingot sides outside the mould was 6 W·m−1·K−1 [21]. The metal material obeyed the Von Mises yield criterion, and the ingot surface was a free surface.

3 Simulation results analysis and validation

3.1 Electromagnetic field and Joule heat

Figure 4 shows the potential distribution of the longitudinal section in the ESRW. Because the slag bath is the largest resistance, most of the voltage-drop occurs in the slag bath. The electrode immersed in the slag bath has the largest potential gradient. The potential of the slag/metal interface approached zero.

Figure 4 The potential distribution of longitudinal section of the ESRW
Figure 4

The potential distribution of longitudinal section of the ESRW

Figure 5 shows the current density distribution of the longitudinal section in the ESRW. The current flows into the electrode and flows out of the ingot from top to bottom. The current density distribution in the electrode and ingot area is more regular. Because the electrical conductivity of the slag bath is much less than for the electrode and ingots, the current density changes rapidly in the slag bath. When the current flows into the slag bath, it is redistributed. The current density of the electrode corner in the slag bath has the highest value of 378078 A·m−2. Figure 5 also verifies the distribution of the potential in the slag pool. Therefore, the electrode corner is the main heating zone for the electrode melting in the slag bath.

Figure 5 The current density distribution of longitudinal section of the ESRW
Figure 5

The current density distribution of longitudinal section of the ESRW

Figure 6 shows the Joule heat distribution in the slag bath. The Joule heating depends on the distribution of the current density and the electrical conductivity of the materials, so the Joule heating of the electrode and the ingot are smaller than the Joule heating of the slag bath. Because of the maximum current density near the electrode corner in the slag bath, the Joule heat of the electrode corner in the slag bath has the highest value of 0.596×108 W·m−3.

Figure 6 The Joule heat distribution in the slag bath
Figure 6

The Joule heat distribution in the slag bath

Figure 7 shows the magnetic flux density distribution of cross section in the slag bath. The direction of the magnetic flux density is tangential to the slag bath and has a clockwise rotation. Its direction and the direction of the current density correspond to the right-hand rule. The magnetic flux density is the smallest at the center of the slag bath, where the value is 0.52×10−4 T. It is noted that the magnetic flux density increases from the center to the periphery in the slag bath. The maximum value is 0.013 T.

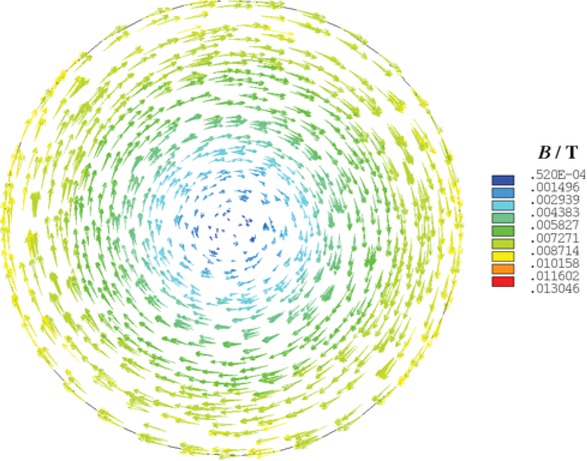
Figure 7 The magnetic flux density distribution of cross section in the slag bath
Figure 7

The magnetic flux density distribution of cross section in the slag bath

Figure 8 shows the electromagnetic force distribution in the cross-section and the longitudinal section of the slag bath in the ESRW system. Figure 8 (a) shows that the electromagnetic force points to the center of the slag bath. Figure 8 (b) shows that the electromagnetic force is tangential direction to the current density and follows the left-hand rule for the direction of the current density and the direction of the magnetic flux density. The electromagnetic force is divided into two components in the axial and radial directions near the electrode corner of the slag pool. The electromagnetic force becomes smaller and smaller in the radial direction, reaching a minimum value of 0.199×10−5 N. The maximum value near the electrode corner is 0.001 N.

Figure 8 The electromagnetic force distribution in (a) the cross-section and (b) the longitudinal section of the slag bath
Figure 8

The electromagnetic force distribution in (a) the cross-section and (b) the longitudinal section of the slag bath

3.2 Velocity field

Figure 9 shows the velocity distribution of the longitudinal section of the slag bath in the ESRW system. There are two pairs of vortices, a pair of large ones at the center of the slag bath under the electrode and another pair of small ones near the electrode corner. The large vortices have a counter-clockwise rotation due to the influence of the Lorentz force and the metal droplets dripping traction. The small vortices have a clockwise rotation due to the effects of buoyancy and temperature gradients. The calculated vortices are 0 to 0.08 m·s−1 in the slag bath. The maximum value and the minimum value occur close to the central axis of the slag bath and near the center of the vortices.

Figure 9 The velocity distribution of longitudinal section of the slag bath
Figure 9

The velocity distribution of longitudinal section of the slag bath

3.3 Temperature field and shape of the molten-metal pool

Figure 10 shows the temperature distribution of the longitudinal section in the ESRW system. Due to uneven distribution of the current density in the slag bath and the flow of the slag, the temperature field is distributed unevenly in the slag bath. There are two high temperature zones (1990 K) that are found on both sides of the central line in the slag bath. This is mainly due to two factors. First, the speed of the center of the large vortices is small in the slag bath, so the slag will not spread out and lose its heat. Second, the metal droplets absorb the heat of the slag in the slag pool, so the high temperature zones of the slag bath move to the nearby center of the vortices. The temperature closer to the electrode is lower than in the slag bath. Because the slag pool is cooled by the mould, the temperature gradient is large at the sidewall of slag.

Figure 10 The temperature distribution of longitudinal section of the ESRW system
Figure 10

The temperature distribution of longitudinal section of the ESRW system

Figure 11 shows the shape of the molten-metal pool for the temperature field in the ESRW system. Figure 10 and 11 show that the metal droplets carry a large amount of heat into the molten-metal pool, the temperature is high in the middle of ingot. The ingot cools near the mould, so the temperature gradient of ingot surface increasing distance from the center, and the faster heat transfer leads to lower the temperature. The molten-metal pool has the appearance of a “bowl”. The ingot is air cooling outside the mould, so the temperature gradient of the ingot is small. Figure 11 shows that the depth of the liquidus line is 0.12 m and the depth of solidus line is 0.20 m. The maximum depth of the two-phase region is 0.08 m.

Figure 11 The shape of metal pool in longitudinal section of the ESRW process
Figure 11

The shape of metal pool in longitudinal section of the ESRW process

The experiment using the ESRW process (Current amplitude 16500 A, Frequency 50 Hz, Electrode immersed depth 0.01 m, slag height 0.18 m) for producing an ingot of 9Cr3Mo roller was done by using the slag system with 60% CaF2, 20% CaO, and 20% Al2O3 and the technological parameters listed in Table 1. It was very difficult to measure the surface temperature of the ingot in the mould, so the surface temperature of the ingot outside mould was measured by an HY63 infrared thermometer. Figure 12 shows the temperature-measured position on the ingot surface. Figure 13 shows the comparison of the numerical simulation values and the actual measured values of the surface temperature of the ingot, which shows that the calculated values are in good agreement with the measured values.

Figure 12 Line of the ingot surface for measuring temperature
Figure 12

Line of the ingot surface for measuring temperature

Figure 13 The calculated temperature and the measured temperature of the ingot surface below the mould outlet
Figure 13

The calculated temperature and the measured temperature of the ingot surface below the mould outlet

3.4 Numerical simulation and model validation of ingot shrinkage

Figure 14(a) shows the shrinkage displacement of the longitudinal section of the ingot in the mould. Figure 14(b) is a shrinkage curve drawn from the shrinkage displacement of the left side surface of the ingot. Figure 14(a) shows that the shrinkage displacement of the ingot increases gradually from the center of ingot to the surface. Figure 14(b) shows that the variation of the shrinkage displacement between the slag/metal interface and the mould outlet is 0.0028m. Figures 14(a) and 14(b) show that as the distance from the mould outlet decreases, the shrinkage displacement of the ingot increase. The maximum value of the shrinkage displacement is about 0.00894 m at the mould outlet. Due to cooling effect of the mould, the surface temperature of the ingot is lower than the center, so the shrinkage in the boundary layers is greatest. Closer to the ingot axis, the change of shrinkage displacement is considerably slower. This results from the variation of the thermal flux. On account of rapid shrinkage at the corners of ingot, the gap increases sharply, and hence the thermal flux is sharply reduced. In turn, it slows the shrinkage and the gap begins to slowly decrease in mold cross section.

Figure 14 (a) The shrinkage displacement of longitudinal section of the ingot and (b) ingot shrinkage curve in the mould
Figure 14

(a) The shrinkage displacement of longitudinal section of the ingot and (b) ingot shrinkage curve in the mould

To verify the accuracy of the simulation results of ingot shrinkage, shrinkage displacement of five electroslag ingot under the same process conditions as Table 1 were measured. Figure 15 shows the comparison between the measured values (A, B, C, D, E) of the shrinkage displacement of the ingot at the mould outlet for different furnace times and the calculated value (F) of the ESRW (Current amplitude 16500 A, Frequency 50 Hz, Electrode immersed depth 0.01 m, slag height 0.18m) for the same working conditions. The calculated value is in good agreement with the measured values.

Figure 15 The comparison between the measured values (A, B, C, D, E) of the shrinkage displacement of the ingot at the mould outlet for different furnace times and calculated value (F) of the ESRW
Figure 15

The comparison between the measured values (A, B, C, D, E) of the shrinkage displacement of the ingot at the mould outlet for different furnace times and calculated value (F) of the ESRW

4 Conclusions

  1. The potential drop is the greatest in the slag bath. The maximum values of the current density, the Joule heating, and the electromagnetic force are found near the electrode corner in the slag bath. The magnetic flux density increases from the center to the periphery in the slag bath.

  2. The velocity field has two pairs of vortices in the slag pool, a large pair with counterclockwise rotation, and another small pair with clockwise rotation. There are two high temperature zones in the slag bath, which are distributed on both sides of the central line in the slag bath.

  3. The shrinkage displacement of the ingot increases gradually from the center of the ingot to the surface. As the distance from the mould outlet decreases, the shrinkage displacement of ingot increases. The maximum shrinkage displacement is at the mould outlet, and the value was 0.0089 m

Acknowledgement

This work is supported by National Natural Science Foundation of China (No.51604149, No.U1560203). Also, this project is supported by national key laboratory of marine engineering of China (No. SKLMEA-USTL-201707).

References

[1] Z.B. Li, China Foundry, 1 (2004) 7-16.Search in Google Scholar

[2] S.W. Cai, T.M. Wang, J. Li, J.J. Xu, Y.Y. Du, Z.Q. Cao, and T.J. Li, Special Casting & Nonferrous Alloys, 8 (2009) 709-712.Search in Google Scholar

[3] X.M. Zang, Z.H. Jiang, L. Medovar, and H.L. Jiang, J. Mat. Metall., 10S1 (2011) 81-85.Search in Google Scholar

[4] L. Fubin, Z. Ximin, J. Zhouhua, G. Xin, and Y. Man, J. Univ. Sci. Technol. B, 4 (2012) 303-311.Search in Google Scholar

[5] A. Kharicha, A. Ludwig, and M. Wu, Mater. Sci. Eng., A, 6 (2005) 129-134.10.1016/j.msea.2005.08.212Search in Google Scholar

[6] E. K. Sibaki, A. Kharicha, M. Wu, A. Ludwig, H. Holzgruber, B. Ofner, and M. Ramprecht, Proceedings of the 2013 International Symposium on Liquid Metal Processing & Casting September 22-25, 2013, Austin, Texas, TMS, USA, (2013) , pp. 13-19.10.1007/978-3-319-48102-9_2Search in Google Scholar

[7] B.K. Li, F. Wang, and F. Tsukihashi, ISIJ Int., 7 (2012) 1289-1295.10.2355/isijinternational.52.1289Search in Google Scholar

[8] X.H. Wang and Y. Li, Metall. Mater. Trans. B, 2 (2015) 800-812.10.1007/s11663-014-0227-4Search in Google Scholar

[9] F. Wang, Y.C. Lou, R. Chen, Z.W. Song, and Q. Wang, TMS 2015 144th Annual Meeting & Exhibition: Supplemental Proceedings March 15-19, 2015, Orlando, Florida, TMS, USA, (2015), pp. 783-790.10.1007/978-3-319-48127-2_95Search in Google Scholar

[10] F. Wang, Q. Wang, Y.C. Lou, R. Chen, Z.W. Song, and B.K. Li, JOM, 1 (2016) 410-420.10.1007/s11837-015-1684-1Search in Google Scholar

[11] Q. Wang, Z. He, B.K. Li, and F. Tsukihashi, Metall. Mater. Trans. B, 6 (2014) 2425-2441.10.1007/s11663-014-0158-0Search in Google Scholar

[12] Q. Wang, W.J. Rong, and B.K. Li, JOM, 11 (2015) 2705-2713.10.1007/s11837-015-1621-3Search in Google Scholar

[13] C.S. Li and B.G. Thomas, Metall. Mater. Trans. B, 6 (2004) 827-834.Search in Google Scholar

[14] S. Koric and B.G. Thomas, J. Mater. Process. Tech., 1 (2008) 408-418.10.1016/j.jmatprotec.2007.06.060Search in Google Scholar

[15] B.F. Wang, G. Ding, and J.W. Zhao, Special Steel, 2(2005) 38-40.Search in Google Scholar

[16] W.H. Wang, Y. Liu, and W.J. Wang, Iron Steel Res., 6 (2014) 26-29.10.1179/1743281212Y.0000000096Search in Google Scholar

[17] T.M.Wang, S.W. Cai, J. Li and T.J. Li, China Foundry, 1 (2010) 61-67.Search in Google Scholar

[18] S.W. Cai, T.M. Wang, J.J. Xu, J. Li, Z.Q. Cao, and T.J. Li, Mater. Res. Innov., 1 (2011) 29-35.10.1179/143307511X12922272563707Search in Google Scholar

[19] B. E. Launder and D. B. Spading, Mathematical Models of Turbulence, Academic Press, London, (1972).Search in Google Scholar

[20] E.G. Wang, J.C. He, Z.K. Yang, H.G. Chen, J. Northeast. Univ., 6(1998) 555-557.Search in Google Scholar

[21] M. Choudhary and J. Szekely, Metall. Trans. B, 3 (1980) 439-453.10.1007/BF02676888Search in Google Scholar

Received: 2018-10-02
Accepted: 2018-12-25
Published Online: 2019-06-28
Published in Print: 2019-02-25

© 2019 W. Li et al., published by De Gruyter

This work is licensed under the Creative Commons Attribution 4.0 Public License.

Articles in the same Issue

  1. Frontmatter
  2. Review Article
  3. Research on the Influence of Furnace Structure on Copper Cooling Stave Life
  4. Influence of High Temperature Oxidation on Hydrogen Absorption and Degradation of Zircaloy-2 and Zr 700 Alloys
  5. Correlation between Travel Speed, Microstructure, Mechanical Properties and Wear Characteristics of Ni-Based Hardfaced Deposits over 316LN Austenitic Stainless Steel
  6. Factors Influencing Gas Generation Behaviours of Lump Coal Used in COREX Gasifier
  7. Experiment Research on Pulverized Coal Combustion in the Tuyere of Oxygen Blast Furnace
  8. Phosphate Capacities of CaO–FeO–SiO2–Al2O3/Na2O/TiO2 Slags
  9. Microstructure and Interface Bonding Strength of WC-10Ni/NiCrBSi Composite Coating by Vacuum Brazing
  10. Refill Friction Stir Spot Welding of Dissimilar 6061/7075 Aluminum Alloy
  11. Solvothermal Synthesis and Magnetic Properties of Monodisperse Ni0.5Zn0.5Fe2O4 Hollow Nanospheres
  12. On the Capability of Logarithmic-Power Model for Prediction of Hot Deformation Behavior of Alloy 800H at High Strain Rates
  13. 3D Heat Conductivity Model of Mold Based on Node Temperature Inheritance
  14. 3D Microstructure and Micromechanical Properties of Minerals in Vanadium-Titanium Sinter
  15. Effect of Martensite Structure and Carbide Precipitates on Mechanical Properties of Cr-Mo Alloy Steel with Different Cooling Rate
  16. The Interaction between Erosion Particle and Gas Stream in High Temperature Gas Burner Rig for Thermal Barrier Coatings
  17. Permittivity Study of a CuCl Residue at 13–450 °C and Elucidation of the Microwave Intensification Mechanism for Its Dechlorination
  18. Study on Carbothermal Reduction of Titania in Molten Iron
  19. The Sequence of the Phase Growth during Diffusion in Ti-Based Systems
  20. Growth Kinetics of CoB–Co2B Layers Using the Powder-Pack Boriding Process Assisted by a Direct Current Field
  21. High-Temperature Flow Behaviour and Constitutive Equations for a TC17 Titanium Alloy
  22. Research on Three-Roll Screw Rolling Process for Ti6Al4V Titanium Alloy Bar
  23. Continuous Cooling Transformation of Undeformed and Deformed High Strength Crack-Arrest Steel Plates for Large Container Ships
  24. Formation Mechanism and Influence Factors of the Sticker between Solidified Shell and Mold in Continuous Casting of Steel
  25. Casting Defects in Transition Layer of Cu/Al Composite Castings Prepared Using Pouring Aluminum Method and Their Formation Mechanism
  26. Effect of Current on Segregation and Inclusions Characteristics of Dual Alloy Ingot Processed by Electroslag Remelting
  27. Investigation of Growth Kinetics of Fe2B Layers on AISI 1518 Steel by the Integral Method
  28. Microstructural Evolution and Phase Transformation on the X-Y Surface of Inconel 718 Ni-Based Alloys Fabricated by Selective Laser Melting under Different Heat Treatment
  29. Characterization of Mn-Doped Co3O4 Thin Films Prepared by Sol Gel-Based Dip-Coating Process
  30. Deposition Characteristics of Multitrack Overlayby Plasma Transferred Arc Welding on SS316Lwith Co-Cr Based Alloy – Influence ofProcess Parameters
  31. Elastic Moduli and Elastic Constants of Alloy AuCuSi With FCC Structure Under Pressure
  32. Effect of Cl on Softening and Melting Behaviors of BF Burden
  33. Effect of MgO Injection on Smelting in a Blast Furnace
  34. Structural Characteristics and Hydration Kinetics of Oxidized Steel Slag in a CaO-FeO-SiO2-MgO System
  35. Optimization of Microwave-Assisted Oxidation Roasting of Oxide–Sulphide Zinc Ore with Addition of Manganese Dioxide Using Response Surface Methodology
  36. Hydraulic Study of Bubble Migration in Liquid Titanium Alloy Melt during Vertical Centrifugal Casting Process
  37. Investigation on Double Wire Metal Inert Gas Welding of A7N01-T4 Aluminum Alloy in High-Speed Welding
  38. Oxidation Behaviour of Welded ASTM-SA210 GrA1 Boiler Tube Steels under Cyclic Conditions at 900°C in Air
  39. Study on the Evolution of Damage Degradation at Different Temperatures and Strain Rates for Ti-6Al-4V Alloy
  40. Pack-Boriding of Pure Iron with Powder Mixtures Containing ZrB2
  41. Evolution of Interfacial Features of MnO-SiO2 Type Inclusions/Steel Matrix during Isothermal Heating at Low Temperatures
  42. Effect of MgO/Al2O3 Ratio on Viscosity of Blast Furnace Primary Slag
  43. The Microstructure and Property of the Heat Affected zone in C-Mn Steel Treated by Rare Earth
  44. Microwave-Assisted Molten-Salt Facile Synthesis of Chromium Carbide (Cr3C2) Coatings on the Diamond Particles
  45. Effects of B on the Hot Ductility of Fe-36Ni Invar Alloy
  46. Impurity Distribution after Solidification of Hypereutectic Al-Si Melts and Eutectic Al-Si Melt
  47. Induced Electro-Deposition of High Melting-Point Phases on MgO–C Refractory in CaO–Al2O3–SiO2 – (MgO) Slag at 1773 K
  48. Microstructure and Mechanical Properties of 14Cr-ODS Steels with Zr Addition
  49. A Review of Boron-Rich Silicon Borides Basedon Thermodynamic Stability and Transport Properties of High-Temperature Thermoelectric Materials
  50. Siliceous Manganese Ore from Eastern India:A Potential Resource for Ferrosilicon-Manganese Production
  51. A Strain-Compensated Constitutive Model for Describing the Hot Compressive Deformation Behaviors of an Aged Inconel 718 Superalloy
  52. Surface Alloys of 0.45 C Carbon Steel Produced by High Current Pulsed Electron Beam
  53. Deformation Behavior and Processing Map during Isothermal Hot Compression of 49MnVS3 Non-Quenched and Tempered Steel
  54. A Constitutive Equation for Predicting Elevated Temperature Flow Behavior of BFe10-1-2 Cupronickel Alloy through Double Multiple Nonlinear Regression
  55. Oxidation Behavior of Ferritic Steel T22 Exposed to Supercritical Water
  56. A Multi Scale Strategy for Simulation of Microstructural Evolutions in Friction Stir Welding of Duplex Titanium Alloy
  57. Partition Behavior of Alloying Elements in Nickel-Based Alloys and Their Activity Interaction Parameters and Infinite Dilution Activity Coefficients
  58. Influence of Heating on Tensile Physical-Mechanical Properties of Granite
  59. Comparison of Al-Zn-Mg Alloy P-MIG Welded Joints Filled with Different Wires
  60. Microstructure and Mechanical Properties of Thick Plate Friction Stir Welds for 6082-T6 Aluminum Alloy
  61. Research Article
  62. Kinetics of oxide scale growth on a (Ti, Mo)5Si3 based oxidation resistant Mo-Ti-Si alloy at 900-1300∘C
  63. Calorimetric study on Bi-Cu-Sn alloys
  64. Mineralogical Phase of Slag and Its Effect on Dephosphorization during Converter Steelmaking Using Slag-Remaining Technology
  65. Controllability of joint integrity and mechanical properties of friction stir welded 6061-T6 aluminum and AZ31B magnesium alloys based on stationary shoulder
  66. Cellular Automaton Modeling of Phase Transformation of U-Nb Alloys during Solidification and Consequent Cooling Process
  67. The effect of MgTiO3Adding on Inclusion Characteristics
  68. Cutting performance of a functionally graded cemented carbide tool prepared by microwave heating and nitriding sintering
  69. Creep behaviour and life assessment of a cast nickel – base superalloy MAR – M247
  70. Failure mechanism and acoustic emission signal characteristics of coatings under the condition of impact indentation
  71. Reducing Surface Cracks and Improving Cleanliness of H-Beam Blanks in Continuous Casting — Improving continuous casting of H-beam blanks
  72. Rhodium influence on the microstructure and oxidation behaviour of aluminide coatings deposited on pure nickel and nickel based superalloy
  73. The effect of Nb content on precipitates, microstructure and texture of grain oriented silicon steel
  74. Effect of Arc Power on the Wear and High-temperature Oxidation Resistances of Plasma-Sprayed Fe-based Amorphous Coatings
  75. Short Communication
  76. Novel Combined Feeding Approach to Produce Quality Al6061 Composites for Heat Sinks
  77. Research Article
  78. Micromorphology change and microstructure of Cu-P based amorphous filler during heating process
  79. Controlling residual stress and distortion of friction stir welding joint by external stationary shoulder
  80. Research on the ingot shrinkage in the electroslag remelting withdrawal process for 9Cr3Mo roller
  81. Production of Mo2NiB2 Based Hard Alloys by Self-Propagating High-Temperature Synthesis
  82. The Morphology Analysis of Plasma-Sprayed Cast Iron Splats at Different Substrate Temperatures via Fractal Dimension and Circularity Methods
  83. A Comparative Study on Johnson–Cook, Modified Johnson–Cook, Modified Zerilli–Armstrong and Arrhenius-Type Constitutive Models to Predict Hot Deformation Behavior of TA2
  84. Dynamic absorption efficiency of paracetamol powder in microwave drying
  85. Preparation and Properties of Blast Furnace Slag Glass Ceramics Containing Cr2O3
  86. Influence of unburned pulverized coal on gasification reaction of coke in blast furnace
  87. Effect of PWHT Conditions on Toughness and Creep Rupture Strength in Modified 9Cr-1Mo Steel Welds
  88. Role of B2O3 on structure and shear-thinning property in CaO–SiO2–Na2O-based mold fluxes
  89. Effect of Acid Slag Treatment on the Inclusions in GCr15 Bearing Steel
  90. Recovery of Iron and Zinc from Blast Furnace Dust Using Iron-Bath Reduction
  91. Phase Analysis and Microstructural Investigations of Ce2Zr2O7 for High-Temperature Coatings on Ni-Base Superalloy Substrates
  92. Combustion Characteristics and Kinetics Study of Pulverized Coal and Semi-Coke
  93. Mechanical and Electrochemical Characterization of Supersolidus Sintered Austenitic Stainless Steel (316 L)
  94. Synthesis and characterization of Cu doped chromium oxide (Cr2O3) thin films
  95. Ladle Nozzle Clogging during casting of Silicon-Steel
  96. Thermodynamics and Industrial Trial on Increasing the Carbon Content at the BOF Endpoint to Produce Ultra-Low Carbon IF Steel by BOF-RH-CSP Process
  97. Research Article
  98. Effect of Boundary Conditions on Residual Stresses and Distortion in 316 Stainless Steel Butt Welded Plate
  99. Numerical Analysis on Effect of Additional Gas Injection on Characteristics around Raceway in Melter Gasifier
  100. Variation on thermal damage rate of granite specimen with thermal cycle treatment
  101. Effects of Fluoride and Sulphate Mineralizers on the Properties of Reconstructed Steel Slag
  102. Effect of Basicity on Precipitation of Spinel Crystals in a CaO-SiO2-MgO-Cr2O3-FeO System
  103. Review Article
  104. Exploitation of Mold Flux for the Ti-bearing Welding Wire Steel ER80-G
  105. Research Article
  106. Furnace heat prediction and control model and its application to large blast furnace
  107. Effects of Different Solid Solution Temperatures on Microstructure and Mechanical Properties of the AA7075 Alloy After T6 Heat Treatment
  108. Study of the Viscosity of a La2O3-SiO2-FeO Slag System
  109. Tensile Deformation and Work Hardening Behaviour of AISI 431 Martensitic Stainless Steel at Elevated Temperatures
  110. The Effectiveness of Reinforcement and Processing on Mechanical Properties, Wear Behavior and Damping Response of Aluminum Matrix Composites
https://doi.org/10.1515/htmp-2019-0014
Keywords for this article
ESRW; air gap; temperature field; ingot shrinkage; mould taper
Creative Commons
BY 4.0

Articles in the same Issue

  1. Frontmatter
  2. Review Article
  3. Research on the Influence of Furnace Structure on Copper Cooling Stave Life
  4. Influence of High Temperature Oxidation on Hydrogen Absorption and Degradation of Zircaloy-2 and Zr 700 Alloys
  5. Correlation between Travel Speed, Microstructure, Mechanical Properties and Wear Characteristics of Ni-Based Hardfaced Deposits over 316LN Austenitic Stainless Steel
  6. Factors Influencing Gas Generation Behaviours of Lump Coal Used in COREX Gasifier
  7. Experiment Research on Pulverized Coal Combustion in the Tuyere of Oxygen Blast Furnace
  8. Phosphate Capacities of CaO–FeO–SiO2–Al2O3/Na2O/TiO2 Slags
  9. Microstructure and Interface Bonding Strength of WC-10Ni/NiCrBSi Composite Coating by Vacuum Brazing
  10. Refill Friction Stir Spot Welding of Dissimilar 6061/7075 Aluminum Alloy
  11. Solvothermal Synthesis and Magnetic Properties of Monodisperse Ni0.5Zn0.5Fe2O4 Hollow Nanospheres
  12. On the Capability of Logarithmic-Power Model for Prediction of Hot Deformation Behavior of Alloy 800H at High Strain Rates
  13. 3D Heat Conductivity Model of Mold Based on Node Temperature Inheritance
  14. 3D Microstructure and Micromechanical Properties of Minerals in Vanadium-Titanium Sinter
  15. Effect of Martensite Structure and Carbide Precipitates on Mechanical Properties of Cr-Mo Alloy Steel with Different Cooling Rate
  16. The Interaction between Erosion Particle and Gas Stream in High Temperature Gas Burner Rig for Thermal Barrier Coatings
  17. Permittivity Study of a CuCl Residue at 13–450 °C and Elucidation of the Microwave Intensification Mechanism for Its Dechlorination
  18. Study on Carbothermal Reduction of Titania in Molten Iron
  19. The Sequence of the Phase Growth during Diffusion in Ti-Based Systems
  20. Growth Kinetics of CoB–Co2B Layers Using the Powder-Pack Boriding Process Assisted by a Direct Current Field
  21. High-Temperature Flow Behaviour and Constitutive Equations for a TC17 Titanium Alloy
  22. Research on Three-Roll Screw Rolling Process for Ti6Al4V Titanium Alloy Bar
  23. Continuous Cooling Transformation of Undeformed and Deformed High Strength Crack-Arrest Steel Plates for Large Container Ships
  24. Formation Mechanism and Influence Factors of the Sticker between Solidified Shell and Mold in Continuous Casting of Steel
  25. Casting Defects in Transition Layer of Cu/Al Composite Castings Prepared Using Pouring Aluminum Method and Their Formation Mechanism
  26. Effect of Current on Segregation and Inclusions Characteristics of Dual Alloy Ingot Processed by Electroslag Remelting
  27. Investigation of Growth Kinetics of Fe2B Layers on AISI 1518 Steel by the Integral Method
  28. Microstructural Evolution and Phase Transformation on the X-Y Surface of Inconel 718 Ni-Based Alloys Fabricated by Selective Laser Melting under Different Heat Treatment
  29. Characterization of Mn-Doped Co3O4 Thin Films Prepared by Sol Gel-Based Dip-Coating Process
  30. Deposition Characteristics of Multitrack Overlayby Plasma Transferred Arc Welding on SS316Lwith Co-Cr Based Alloy – Influence ofProcess Parameters
  31. Elastic Moduli and Elastic Constants of Alloy AuCuSi With FCC Structure Under Pressure
  32. Effect of Cl on Softening and Melting Behaviors of BF Burden
  33. Effect of MgO Injection on Smelting in a Blast Furnace
  34. Structural Characteristics and Hydration Kinetics of Oxidized Steel Slag in a CaO-FeO-SiO2-MgO System
  35. Optimization of Microwave-Assisted Oxidation Roasting of Oxide–Sulphide Zinc Ore with Addition of Manganese Dioxide Using Response Surface Methodology
  36. Hydraulic Study of Bubble Migration in Liquid Titanium Alloy Melt during Vertical Centrifugal Casting Process
  37. Investigation on Double Wire Metal Inert Gas Welding of A7N01-T4 Aluminum Alloy in High-Speed Welding
  38. Oxidation Behaviour of Welded ASTM-SA210 GrA1 Boiler Tube Steels under Cyclic Conditions at 900°C in Air
  39. Study on the Evolution of Damage Degradation at Different Temperatures and Strain Rates for Ti-6Al-4V Alloy
  40. Pack-Boriding of Pure Iron with Powder Mixtures Containing ZrB2
  41. Evolution of Interfacial Features of MnO-SiO2 Type Inclusions/Steel Matrix during Isothermal Heating at Low Temperatures
  42. Effect of MgO/Al2O3 Ratio on Viscosity of Blast Furnace Primary Slag
  43. The Microstructure and Property of the Heat Affected zone in C-Mn Steel Treated by Rare Earth
  44. Microwave-Assisted Molten-Salt Facile Synthesis of Chromium Carbide (Cr3C2) Coatings on the Diamond Particles
  45. Effects of B on the Hot Ductility of Fe-36Ni Invar Alloy
  46. Impurity Distribution after Solidification of Hypereutectic Al-Si Melts and Eutectic Al-Si Melt
  47. Induced Electro-Deposition of High Melting-Point Phases on MgO–C Refractory in CaO–Al2O3–SiO2 – (MgO) Slag at 1773 K
  48. Microstructure and Mechanical Properties of 14Cr-ODS Steels with Zr Addition
  49. A Review of Boron-Rich Silicon Borides Basedon Thermodynamic Stability and Transport Properties of High-Temperature Thermoelectric Materials
  50. Siliceous Manganese Ore from Eastern India:A Potential Resource for Ferrosilicon-Manganese Production
  51. A Strain-Compensated Constitutive Model for Describing the Hot Compressive Deformation Behaviors of an Aged Inconel 718 Superalloy
  52. Surface Alloys of 0.45 C Carbon Steel Produced by High Current Pulsed Electron Beam
  53. Deformation Behavior and Processing Map during Isothermal Hot Compression of 49MnVS3 Non-Quenched and Tempered Steel
  54. A Constitutive Equation for Predicting Elevated Temperature Flow Behavior of BFe10-1-2 Cupronickel Alloy through Double Multiple Nonlinear Regression
  55. Oxidation Behavior of Ferritic Steel T22 Exposed to Supercritical Water
  56. A Multi Scale Strategy for Simulation of Microstructural Evolutions in Friction Stir Welding of Duplex Titanium Alloy
  57. Partition Behavior of Alloying Elements in Nickel-Based Alloys and Their Activity Interaction Parameters and Infinite Dilution Activity Coefficients
  58. Influence of Heating on Tensile Physical-Mechanical Properties of Granite
  59. Comparison of Al-Zn-Mg Alloy P-MIG Welded Joints Filled with Different Wires
  60. Microstructure and Mechanical Properties of Thick Plate Friction Stir Welds for 6082-T6 Aluminum Alloy
  61. Research Article
  62. Kinetics of oxide scale growth on a (Ti, Mo)5Si3 based oxidation resistant Mo-Ti-Si alloy at 900-1300∘C
  63. Calorimetric study on Bi-Cu-Sn alloys
  64. Mineralogical Phase of Slag and Its Effect on Dephosphorization during Converter Steelmaking Using Slag-Remaining Technology
  65. Controllability of joint integrity and mechanical properties of friction stir welded 6061-T6 aluminum and AZ31B magnesium alloys based on stationary shoulder
  66. Cellular Automaton Modeling of Phase Transformation of U-Nb Alloys during Solidification and Consequent Cooling Process
  67. The effect of MgTiO3Adding on Inclusion Characteristics
  68. Cutting performance of a functionally graded cemented carbide tool prepared by microwave heating and nitriding sintering
  69. Creep behaviour and life assessment of a cast nickel – base superalloy MAR – M247
  70. Failure mechanism and acoustic emission signal characteristics of coatings under the condition of impact indentation
  71. Reducing Surface Cracks and Improving Cleanliness of H-Beam Blanks in Continuous Casting — Improving continuous casting of H-beam blanks
  72. Rhodium influence on the microstructure and oxidation behaviour of aluminide coatings deposited on pure nickel and nickel based superalloy
  73. The effect of Nb content on precipitates, microstructure and texture of grain oriented silicon steel
  74. Effect of Arc Power on the Wear and High-temperature Oxidation Resistances of Plasma-Sprayed Fe-based Amorphous Coatings
  75. Short Communication
  76. Novel Combined Feeding Approach to Produce Quality Al6061 Composites for Heat Sinks
  77. Research Article
  78. Micromorphology change and microstructure of Cu-P based amorphous filler during heating process
  79. Controlling residual stress and distortion of friction stir welding joint by external stationary shoulder
  80. Research on the ingot shrinkage in the electroslag remelting withdrawal process for 9Cr3Mo roller
  81. Production of Mo2NiB2 Based Hard Alloys by Self-Propagating High-Temperature Synthesis
  82. The Morphology Analysis of Plasma-Sprayed Cast Iron Splats at Different Substrate Temperatures via Fractal Dimension and Circularity Methods
  83. A Comparative Study on Johnson–Cook, Modified Johnson–Cook, Modified Zerilli–Armstrong and Arrhenius-Type Constitutive Models to Predict Hot Deformation Behavior of TA2
  84. Dynamic absorption efficiency of paracetamol powder in microwave drying
  85. Preparation and Properties of Blast Furnace Slag Glass Ceramics Containing Cr2O3
  86. Influence of unburned pulverized coal on gasification reaction of coke in blast furnace
  87. Effect of PWHT Conditions on Toughness and Creep Rupture Strength in Modified 9Cr-1Mo Steel Welds
  88. Role of B2O3 on structure and shear-thinning property in CaO–SiO2–Na2O-based mold fluxes
  89. Effect of Acid Slag Treatment on the Inclusions in GCr15 Bearing Steel
  90. Recovery of Iron and Zinc from Blast Furnace Dust Using Iron-Bath Reduction
  91. Phase Analysis and Microstructural Investigations of Ce2Zr2O7 for High-Temperature Coatings on Ni-Base Superalloy Substrates
  92. Combustion Characteristics and Kinetics Study of Pulverized Coal and Semi-Coke
  93. Mechanical and Electrochemical Characterization of Supersolidus Sintered Austenitic Stainless Steel (316 L)
  94. Synthesis and characterization of Cu doped chromium oxide (Cr2O3) thin films
  95. Ladle Nozzle Clogging during casting of Silicon-Steel
  96. Thermodynamics and Industrial Trial on Increasing the Carbon Content at the BOF Endpoint to Produce Ultra-Low Carbon IF Steel by BOF-RH-CSP Process
  97. Research Article
  98. Effect of Boundary Conditions on Residual Stresses and Distortion in 316 Stainless Steel Butt Welded Plate
  99. Numerical Analysis on Effect of Additional Gas Injection on Characteristics around Raceway in Melter Gasifier
  100. Variation on thermal damage rate of granite specimen with thermal cycle treatment
  101. Effects of Fluoride and Sulphate Mineralizers on the Properties of Reconstructed Steel Slag
  102. Effect of Basicity on Precipitation of Spinel Crystals in a CaO-SiO2-MgO-Cr2O3-FeO System
  103. Review Article
  104. Exploitation of Mold Flux for the Ti-bearing Welding Wire Steel ER80-G
  105. Research Article
  106. Furnace heat prediction and control model and its application to large blast furnace
  107. Effects of Different Solid Solution Temperatures on Microstructure and Mechanical Properties of the AA7075 Alloy After T6 Heat Treatment
  108. Study of the Viscosity of a La2O3-SiO2-FeO Slag System
  109. Tensile Deformation and Work Hardening Behaviour of AISI 431 Martensitic Stainless Steel at Elevated Temperatures
  110. The Effectiveness of Reinforcement and Processing on Mechanical Properties, Wear Behavior and Damping Response of Aluminum Matrix Composites
Sign up now to receive a 20% welcome discount
Institutional Access
How does access work?
Have an idea on how to improve our website?
Please write us.
© 2025 De Gruyter Brill
Downloaded on 13.9.2025 from https://www.degruyterbrill.com/document/doi/10.1515/htmp-2019-0014/html
Scroll to top button