Analytical and numerical investigation of free vibration for stepped beam with different materials

Suadad Noori Ghani; Raghad Azeez Neamah; Ali Talib Abdalzahra; Luay S. Al-Ansari; Husam Jawad Abdulsamad

doi:10.1515/eng-2022-0031

Article Open Access

Analytical and numerical investigation of free vibration for stepped beam with different materials

Suadad Noori Ghani , Raghad Azeez Neamah , Ali Talib Abdalzahra , Luay S. Al-Ansari and Husam Jawad Abdulsamad

Published/Copyright: March 16, 2022

Published by

Become an author with De Gruyter Brill

Submit Manuscript Author Information

From the journal Open Engineering Volume 12 Issue 1

Abstract

This work describes the application of classical Rayleigh method (CRM), modified Rayleigh method (MRM), and ANSYS finite element method (FEM) to calculate the natural frequency of non-homogenous cantilever beam. Two-step cantilever stepped beam was investigated through six studied cases. Each step has different material properties and the same cross section area. Results showed that the combination of materials is useful in order to increase the natural frequencies and reduce the weight of the beam at the same time when the cantilever beam is fixed by the side of the stronger material. There is a good agreement between the CRM and FEM for the region with length larger than half length of beam, on the other hand, there is an excellent agreement between the MRM and FEM for the region with length smaller than half length of beam.

Keywords: free vibration; natural frequency; stepped beam; classical Rayleigh method; modified Rayleigh method; finite element method; ANSYS software

1 Introduction

Beams and beam-like elements are main constituent of structures widely used in different engineering applications like aerospace, high speed machinery, light weight structure, etc. Generally, it undergoes a wide variety of loads (static and/or dynamic loads). The dynamic load of certain frequency of vibration leads to the beam failure due to resonance. Therefore, many researchers studied the dynamics of beams because of the importance of its industrial applications in many engineering areas.

In an effort to achieve improved distribution of weight and strength, beams with non-uniform inertia, mass distribution, and variable cross section have been used extensively in many fields. General closed form solutions are more difficult to be obtained for the static and dynamic responses of beams with arbitrary varying cross sections and arbitrary non-homogeneity, because the governing equations of these beams contain variable coefficients.

Generally, the dynamic response of non-uniform Euler–Bernoulli beams was studied using different methods like the dynamic method in conjunction with modal analysis, the dynamic stiffness method, the transformed dynamic stiffness method combined with the Laplace transform, the step reduction method, the finite element method (FEM), the boundary element method, the semi-analytic method, and the transfer matrix method.

Since the stepped beams are used widely in engineering applications and structures, their vibration characteristics was of great interest for research [1,2,3,4,5,6,7,8,9,10,11,12,13]. Kisa and Gurel [14] analyzed the free vibration of stepped cracked and uniform beams with circular cross section using a novel numerical technique. Mao and Pietrzko [15] used the Adomian decomposition method (ADM) in order to investigate the free vibration of a stepped Euler–Bernoulli beam consisting of two uniform sections. Mao [16] explained that ADM provides an effective and accurate method for analysis of free vibration of multiple stepped beams with arbitrary boundary conditions. Suddoung et al. [17] studied free vibration response of stepped beams with functionally graded materials and found that the governing differential equations for these beams can be effectively solved by differential transformation method. Lee [18] used the Chebyshev-tau method to analyze the free vibration of stepped beams based on Timoshenko and Euler–Bernoulli beam theories. Tong et al. [19] presented an analytical solution for free and forced vibrations of stepped beam based on Timoshenko theory. They expressed the frequency equation of free vibration at one end of the beam in terms of some initial parameters. In forced vibration, they solved a set of algebraic equations to obtain the solution with only two unknowns. Rajasekaran and Khaniki [20] presented a comprehensive study on mechanical behaviors of non-homogenous non-uniform size dependent Axially – Functionally Graded Material beams with different types of materials using FEM. Also, Walaa Mohammed Hashim et al. [21] analyzed the static deflection of non-prismatic axially functionally graded beam under distribution load using ANSYS workbench (17.2). They used three supporting types, namely, free-clamped, clamped-free, and simply supported. The elastic modulus of the beam varies continuously in the axial direction of the beam according to a power law model.

In this work, the natural frequency of non-homogenous cantilever beam was calculated by modified Rayleigh method (MRM), classical Rayleigh method (CRM), and ANSYS FEM. The circular and rectangular cross section cantilever stepped beams are considered in this work, and three sets of materials (Steel-Aluminum, copper–Steel and copper–Aluminum) are used to calculate the natural frequencies when the length of each part increases from zero to length of the beam.

2 Problem description

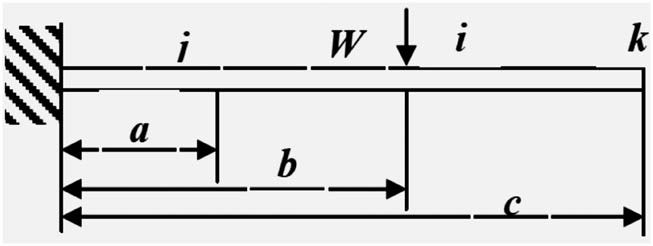
Figure 1 shows the two-step cantilever stepped beam. Each step has different material properties (modulus of elasticity [E] and density [ρ]) and the same cross section area (A) (i.e., same second moment of inertia [I]). The equation of motion of beam (Euler–Bernoulli and Timoshenko equations) cannot be solved analytically in this case because of varying material properties along the length of the beam (ρ and E).

Figure 1

Geometry and material properties of stepped beam used in this work.

For calculation of the natural frequency of this type of beam, CRM, MRM, and the FEM (ANSYS software) are used in this work in order to avoid the complexity in governing equation and its solution [12,13,20,21,22,23].

3 Rayleigh method (RM)

The general formula of Rayleigh method was derived to equate the potential and kinetic energy of any system. The fundamental natural frequency of this system can be calculated by the following equation [12,13,20,21,22,23].

(1) ω 2 = ∫ o l E I d 2 y ( x ) d x 2 2 d x ∫ 0 l ρ A ( y ( x ) ) 2 d x = g ∑ i = 1 n + 1 M i y i ∑ i = 1 n + 1 M i ( y i ) 2 ,

where

ω – frequency (rad/s),

y – deflection (m),

M – mass (kg),

A – cross section area (m²),

ρ – density (kg/m³),

E – modulus of elasticity (N/m²), and

I – second moment of inertia (m⁴).

As mentioned previously, the main problem of the vibration of stepped beam is the variation in the material properties along the beam. Therefore, the methods described in refs. [12,13,20–23] are used in order to calculate the equivalent stiffness (EI) of beam and these methods are:

3.1 Classical method

The equivalent second moment of inertia for stepped beam with two internal steps can be found using the following equation [12,13,20,21,22,23]:

(2) ( I E ) eq = ( L Total ) 3 ( L 2 ) 3 ( I E ) 2 + ( L Total ) 3 − ( L 2 ) 3 ( I E ) 1 ,

where (L _Total = L ₁ + L ₂) is the length of the beam.

3.2 Modified method

According to the idea described in refs. [12,20], at any point at the stepped beam, the equivalent moment of inertia can be calculated by applying the following:

(3) ( I E ) eq ( x ) = ( L Total ) 3 ( L S ( x ) ) 3 ( E I ) S + ( L Total ) 3 − ( L S ( x ) ) 3 ( E I ) L ,

where L _S(x) is the distance from any point to the free edge.

4 Programming Rayleigh methods

The Rayleigh methods (i.e., CRM and MRM) were programmed using MATLAB code [12,13,21,22,23,24,25]. The general steps are:

Input the material properties of each step (i.e., density and modulus of elasticity) and beam dimensions (Figure 1).
Input number of divisions (N).
Calculate the equivalent stiffness of beam using equation (2) for CRM and equation (3) for MRM.
Calculate the mass matrix [m]_(N+1).
Using Table 1 calculate the delta matrix [δ]_{((N+1)*(N+1))}
Calculate the deflection at each node using the following equation and apply the boundary conditions:

[ y ] ( N + 1 ) = [ δ ] ( N + 1 ⁎ ( N + 1 ) ) [ m ] ( N + 1 ) .

Table 1

Formula of the deflections of the cantilever beam [22,25]

δ j i = W a 2 ( 3 b − a ) 6 E I	δ i i = W b 3 3 E I	δ k i = W b 2 ( 3 c − b ) 6 E I

5 FEM

In order to build a 3D finite element model as shown in Figure 2, ANSYS Version 17.2 was used. Cantilever beams with square (Figure 2) and circular (Figure 3) cross section were used in this work.

Figure 2

Geometry and meshing of square stepped beam used in this work.

Figure 3

Meshing and geometry of circular stepped beam used in this work.

6 Cases studied

In this work, the length of the beam is 0.84 m and two types of cross section area are used (square and circular). In the circular shaft, the considered diameter values of the cross section area are 10, 20, 30, 40, and 50 mm. While the considered width values and depth of square cross section area are 10, 20, 30, 40, and 50 mm. Three types of materials are used, and their properties are summarized in Table 2.

Table 2

The material properties used in this work

Property	Unit	Material 1	Material 2	Material 3
Property	Unit	Steel alloy	Cu alloy	Al alloy
Modulus of elasticity	GPa	197	120	68
Poisson ratio	—	0.3	0.3	0.33
Density	kg/m³	7,800	8,500	2,700

The natural frequencies of six studied cases are calculated using three methods (CRM, MRM, and FEM) as in Table 3.

Table 3

The cases studied details

No.	Diameter or width of beam (m)	Material at fixed end	Material at free end	Length of part at fixed end	Length of part at free end	Case no.	Cross section area
1	0.01, 0.02, 0.03, 0.04, and 0.05	Steel alloy	Al alloy	0.84, 0.72, 0.6, 0.48, 0.36, 0.24, 0.12, and 0	0, 0.12, 0.24, 0.36, 0.48, 0.6, 0.72, and 0.84	Case 1	Circular and square
2	0.01, 0.02, 0.03, 0.04, and 0.05	Al alloy	Steel alloy	0.84, 0.72, 0.6, 0.48, 0.36, 0.24, 0.12, and 0	0, 0.12, 0.24, 0.36, 0.48, 0.6, 0.72, and 0.84	Case 2	Circular and square
3	0.01	Steel alloy	Cu alloy	0.84, 0.72, 0.6, 0.48, 0.36, 0.24, 0.12, and 0	0, 0.12, 0.24, 0.36, 0.48, 0.6, 0.72, and 0.84	Case 1	Square
4	0.01	Cu–alloy	Steel alloy	0.84, 0.72, 0.6, 0.48, 0.36, 0.24, 0.12, and 0	0, 0.12, 0.24, 0.36, 0.48, 0.6, 0.72, and 0.84	Case 2	Square
5	0.01	Cu alloy	Al alloy	0.84, 0.72, 0.6, 0.48, 0.36, 0.24, 0.12, and 0	0, 0.12, 0.24, 0.36, 0.48, 0.6, 0.72, and 0.84	Case 1	Square
6	0.01	Al–alloy	Cu–Alloy	0.84, 0.72, 0.6, 0.48, 0.36, 0.24, 0.12, and 0	0, 0.12, 0.24, 0.36, 0.48, 0.6, 0.72, and 0.84	Case 2	Square

7 Results and discussion

Figure 4 shows the comparison among the first natural frequencies calculated by FEM, CRM, and MRM due to the change in the length of steel part for different diameters of circular beam when the material at the fixed end is the stronger material (steel alloy) (Case 1). When the length of stronger material (steel alloy) increases, the first natural frequency will also increase until the length of the stronger material reaches 0.42 m (i.e., half of beam length). Since the beam has uniform cross section, the second moment of inertia is constant. Therefore, the equivalent stiffness of beam (IE)_eq depends on the equivalent modulus of elasticity (E)_eq. But the equivalent modulus of elasticity (E)_eq is maximum and equals the modulus of elasticity of stronger material (steel alloy), when the length of the stronger material equals the length of the beam (equations 2 and 3). That means, the maximum stiffness is found when the beam is made of steel alloy only. This is not completely correct because the frequency depends on stiffness of beam and mass of beam. When the length of the stronger material (steel alloy) increases, the total mass of beam (m) will also increase. The increment in total mass of beam (m) is smaller than that in equivalent modulus of elasticity (E)_eq when the length of the stronger material is smaller than 0.42 m, therefore, the natural frequency will increase. When the stronger material length is greater than 0.42 m, the increase in the total mass of beam (m) is larger than that in equivalent modulus of elasticity (E)_eq, and this leads to the decrease in the natural frequency. The same behavior can be seen in Figure 5, where the beam has a square cross section area and different values of beam width are used.

Figure 4

Comparison among first natural frequencies calculated by FEM, CRM, and MRM due to change in the length of steel part for different diameters of the circular beam (Case 1).

Figure 5

Comparison among first natural frequencies calculated by FEM, CRM, and MRM due to change in the length of steel part for different widths of the square beam (Case 1).

From Figures 4 and 5, the comparison among the three calculating methods shows an excellent agreement between the FEM results (i.e., ANSYS) and MRM results when the length of the stronger material is smaller than 0.42 m. But when the length of the stronger material is larger than 0.42 m, there is a good agreement between the FEM results and CRM results.

Figure 6 shows the comparison among first natural frequencies calculated by FEM, CRM, and MRM due to change in the length of the steel part for different diameters of circular beam when the material at the free end is the stronger material (steel alloy) (Case 2). When the length of the stronger material (steel alloy) increases, the first natural frequency will decrease until the length of the stronger material (steel alloy) reaches 0.42 m (i.e., half of beam length) and then the first natural frequency begins to increase. In other words, the minimum natural frequency is found when the length of stronger material is 0.42 m The increase in length of stronger material causes increment in the equivalent stiffness (IE)_eq and mass (m)_eq of the beam. But the increment in the equivalent stiffness (IE)_eq is smaller than the increment in the total mass of beam (m) when the length of stronger material is smaller than 0.42 m. While the increment in the equivalent stiffness (IE)_eq is larger than the increment in the total mass of beam (m) when the length of stronger material is larger than 0.42 m.

Figure 6

Comparison among first natural frequencies calculated by FEM, CRM, and MRM due to change in the length of steel part for different diameters of the circular beam (Case 2).

From Figures 6 and 7, the comparison among the three calculating method shows an excellent agreement between the MRM and FEM results when the stronger material length is smaller than 0.42 m. Also, there is a good agreement between the FEM and CRM results, when the length of stronger material is larger than 0.42 m.

Figure 7

Comparison among first natural frequencies calculated by FEM, CRM, and MRM due to change in the length of steel part for different widths of square beam (Case 2).

Figures 8 and 9 show the effect of the diameter or width of the beam on the first natural frequency calculated by CRM, MRM, and FEM. Because of the considered uniform cross section of the beam, the effect of increase in diameter or width of the beam appears as the value of the natural frequency increases and it does not affect the relationship between the natural frequency and the length of the stronger material.

Figure 8

Comparison among first natural frequencies calculated by FEM, CRM, and MRM due to change in the length of steel part for different circular beams (Case 1 and Case 2).

Figure 9

Comparison among first natural frequencies calculated by FEM, CRM, and MRM due to change in the length of steel part for different square beams (Case 1 and Case 2).

In Figure 10, the comparison among the first five natural frequencies of the square beams are shown. These beams are:

Steel alloy–Al alloy (Case 1) and Al alloy–Steel alloy (Case 2).
Steel alloy–Cu alloy (Case 1) and Cu alloy–Steel alloy (Case 2).
Cu alloy–Al alloy (Case 1) and Al alloy–Cu alloy (Case 2).

Figure 10

The comparison among five natural frequencies calculated by ANSYS due to change in the length of the first material part (material at the fixed end) for different materials of square beam.

These beams are used to study the effect of modulus ratio (E _Strong/E _Weak), density ratio (ρ _Strong/ρ _Weak) on the natural frequencies. In the first type of beam (steel alloy–Al alloy), the modulus ratio equals density ratio and the frequency ratio equals 1. Then, the maximum and minimum first natural frequencies is found when the length of the stronger material equals half of the beam length. In the second type of beam (steel alloy–Cu alloy), the modulus ratio is 1.641667, the density ratio is 0.917647, and the frequency of pure steel alloy is larger than the frequency of pure Cu alloy with the frequency ratio being 1.337546. In this case, the combination of these two materials in beam is not useful. In the third type of beam (Cu alloy–Al alloy), the modulus ratio is 1.764706, the density ratio is 3.148148, and the frequency of pure steel alloy is larger than the frequency of pure Cu alloy with the frequency ratio being 0.748483. In this case, there is a shifting in the positions of maximum and minimum natural frequency. The position of maximum frequency is at a distance of 0.36 m, while the position of minimum frequency is at a distance of 0.48 m.

From Figure 10, the maximum effect of materials combination is noted in the first natural frequency and this effect appears sharply in the first type of beam (steel alloy–Al alloy) and then in the third type (Cu alloy–Al alloy). Also, this effect decreases when the mode increases.

8 Conclusion

By the obtained results, it can be concluded that:

In cantilever beam, the combination of materials is useful in order to increase the natural frequencies and reduce the weight of the beam at the same time.
The following conditions are essential to increase the natural frequencies of the cantilever combined beam:
1. The modulus ratio and density ratio of any pair of materials are greater than 1, and the modulus ratio is greater than the density ratio.
2. The cantilever beam is fixed by the side of the stronger material.
If the beam has uniform cross-section area (i.e., constant second moment of inertia), the effect of materials combination is not dependent on the shape of the cross-section area and diameter (or width) of the beam.
The results show that there is a good agreement between the CRM and FEM for the region larger than half length of the beam. Also, there is an excellent agreement between the MRM and FEM for the region smaller than half length of the beam.

In future, experimental work will be done in order to measure the natural frequencies of different combined cantilever beams. on the other hand, the dynamic response of combined cantilever beam will be studied theoretically and experimentally.

Conflict of interest: Authors state no conflict of interest.

References

[1] Jang SK, Bert CW. Free vibration of stepped beams: exact and numerical solutions. J Sound Vib. 1989;130:342–6.10.1016/0022-460X(89)90561-0Search in Google Scholar

[2] Jang SK, Bert CW. Free vibration of stepped beams: higher mode frequencies and effects of steps on frequency. J Sound Vib. 1989;132:164–8.10.1016/0022-460X(89)90882-1Search in Google Scholar

[3] Wang JI. Vibration of stepped beams on elastic foundations. J Sound Vib. 1991;149:315–22.10.1016/0022-460X(91)90640-6Search in Google Scholar

[4] Lee HP, Ng TY. Vibration and buckling of a stepped beam. Appl Acoust. 1994;42:257–66.10.1016/0003-682X(94)90113-9Search in Google Scholar

[5] Lee J, Bergman LA. The vibration of stepped beams and rectangular plates by an elemental dynamic flexibility method. J Sound Vib. 1994;171(5):617–40.10.1006/jsvi.1994.1145Search in Google Scholar

[6] Naguleswaran S. Vibration of an Euler–Bernoulli beam on elastic end supports and with up to three step changes in cross-section. Int J Mech Sci. 2002;44(12):2541–55.10.1016/S0020-7403(02)00190-XSearch in Google Scholar

[7] Naguleswaran S. Vibration and stability of an Euler–Bernoulli beam with up to three-step changes in cross-section and in axial force. Int J Mech Sci. 2003;45:1563–79.10.1016/j.ijmecsci.2003.09.001Search in Google Scholar

[8] Maurini C, Porfiri M, Pouget J. Numerical methods for modal analysis of stepped piezoelectric beams. J Sound Vib. 2006;298(4–5):918–33.10.1016/j.jsv.2006.05.041Search in Google Scholar

[9] Kukla S, Zamojska I. Frequency analysis of axially loaded stepped beams by Green’s function method. J Sound Vib. 2007;300(3–5):1034–41.10.1016/j.jsv.2006.07.047Search in Google Scholar

[10] Jaworski JW, Dowell EH. Free vibration of a cantilevered beam with multiple steps: comparison of several theoretical methods with experiment. J Sound Vib. 2008;312(4–5):713–25.10.1016/j.jsv.2007.11.010Search in Google Scholar

[11] Lu ZR, Huang M, Liu JK, Chen WH, Liao WY. Vibration analysis of multiple-stepped beams with the composite element model. J Sound Vib. 2009;322(4–5):1070–80.10.1016/j.jsv.2008.11.041Search in Google Scholar

[12] Al-Ansari LS. Calculating of natural frequency of stepping cantilever beam. Int J Mech Mechatron Eng IJMME-IJENS. 2012;12(5):59–68.Search in Google Scholar

[13] Al-Ansari LS. Calculating static deflection and natural frequency of stepped cantilever beam using modified Rayleigh method. Int J Mech Prod Eng Res Dev (IJMPERD). Oct 2013;3(4):113–24.Search in Google Scholar

[14] Kisa M, Gurel MA. Free vibration analysis of uniform and stepped cracked beams with circular cross sections. Int J Eng Sci. 2007;45(2–8):364–80.10.1016/j.ijengsci.2007.03.014Search in Google Scholar

[15] Mao Q, Pietrzko S. Free vibration analysis of stepped beams by using Adomian decomposition method. Appl Math Comput. 2010;217(7):3429–41.10.1016/j.amc.2010.09.010Search in Google Scholar

[16] Mao Q. Free vibration analysis of multiple-stepped beams by using Adomian decomposition method. Math Computer Model. 2011;54:756–64.10.1016/j.mcm.2011.03.019Search in Google Scholar

[17] Suddoung K, Charoensuk J, Wattanasakulpong N. Vibration response of stepped FGM beams with elastically end constraints using differential transformation method. Appl Acoust. 2014;77:20–8.10.1016/j.apacoust.2013.09.018Search in Google Scholar

[18] Lee J. Application of Chebyshev-tau method to the free vibration analysis of stepped beams. Int J Mech Sci. 2015;101–102:411–20.10.1016/j.ijmecsci.2015.08.012Search in Google Scholar

[19] Tong X, Tabarrok B, Yeh KY. Vibration analysis of Timoshenko beams with nonhomogeneity and varying cross-section. J Sound Vib. 1995;186(5):821–35.10.1006/jsvi.1995.0490Search in Google Scholar

[20] Rajasekaran S, Khaniki HB. Finite element static and dynamic analysis of axially functionally graded nonuniform small-scale beams based on nonlocal strain gradient theory. Mech Adv Mater Struct. 2019;26:14. 10.1080/15376494.2018.1432797.Search in Google Scholar

[21] Hashim WM, Alansari LS, Aljanabi M. Investigating of static deflection of non-prismatic axially functionally graded beam. The 7th International Conference on Renewable Energy and Materials Technology (ICOREMT 2021). in press.10.1155/2022/7436024Search in Google Scholar

[22] Luay SA, Muhannad A, Ali MHY. Vibration analysis of hyper composite material beam utilizing shear deformation and rotary inertia effects. Int J Mech Mechatron Eng IJMME-IJENS. 2012;12(4):76–87.Search in Google Scholar

[23] Alansari LS, Zainy HZ, Yaseen AA, Aljanabi M. Calculating the natural frequency of hollow stepped cantilever beam. Int J Mech Eng Technol (IJMET). January 2019;10(1):898–914. Article ID: IJMET_10_01_093.Search in Google Scholar

[24] Zainy HZ, Al-Ansari LS, Al-Hajjar AMH, Shareef MMS. Analytical and numerical approaches for calculating the static deflection of functionally graded beam under mechanical load. Int J Eng Technol. 2018;7(4):3889–96.Search in Google Scholar

[25] Al-Ansari LS, Al-Hajjar AMH, Husam Jawad A. Calculating the natural frequency of cantilever tapered beam using classical Rayleigh, modified Rayleigh and finite element methods. Int J Eng Technol. 2018;7(4):4866–72.Search in Google Scholar

Received: 2021-07-30

Revised: 2021-08-27

Accepted: 2021-09-12

Published Online: 2022-03-16

This work is licensed under the Creative Commons Attribution 4.0 International License.

Articles in the same Issue

https://doi.org/10.1515/eng-2022-0031

Keywords for this article

free vibration; natural frequency; stepped beam; classical Rayleigh method; modified Rayleigh method; finite element method; ANSYS software

Creative Commons

BY 4.0