Pre-determination of prediction of yield-line pattern of slabs using Voronoi diagrams

1 Introduction

Voronoi diagrams are widely used in many fields such as anthropology, astronomy, archaeology, biology, cartography, chemistry, crystallography, ecology, forestry, geography, geology, linguistics, marketing, metallography, meteorology, operations research, physics, physiology, remote sensing, statistics, urban planning, and architecture. Voronoi diagrams can be used to understand the structure of the universe in astronomy, estimate the precipitation process in meteorology, and locate public schools in urban planning [1]. The last spectacular applications of Voronoi diagrams include a description of the natural fracture pattern of basalt rocks [2], recently in the study of the microstructure of materials, route planning for unmanned vehicles, in goods loading management, in modelling the range of anisotropic transmitters, archaeological reconstructions, and representation of ligand-binding sites in proteins [3,4,5,6,7,8]. However, the use of Voronoi diagrams in the design of a solid waste landfill with a given basis can be found in the paper [9].

Geometrical studies on roof (straight skeleton) geometry [10,11,12] and geometric embankments (on the Voronoi diagrams for a polygon) [9,13] have pointed out the authors’ attention to similarities with yield-lines of statically loaded slabs. The authors verified their observations with photographs of a laboratory series of destroyed slabs. Sawczuk and Jaeger [14] made a series of experiments to confirm the use of limit-bearing capacity theory In recent years, this topic has been devoted to work [15,16,17,18,19,20,21,22,23]. The authors of this article compared their results with the result obtained by discontinuity layout optimisation (DLO) procedure [15]. The comparison is highly promising, considering the simplicity of the method presented here. It would be interesting to check the experimental destruction of the slab with the shape and nature of support described in the work [15]. The approach presented here refers to the results obtained in the work of Wüst and Wagner [24]. The method proposed here is purely geometric and can be used to pre-determine the shape of the yield-lines. It allows you to predict the yield-lines of the polygon plate with any differentiated (segment line, point) way of support. In addition, the support does not have to cover all sides of the polygon. It is also worth noting that Wüst and Wagner used straight skeletons, but called it differently ([24], Figures 8, 17, and 20). However, the Authors of the paper [24] do not use Voronoi diagrams. The predicted yield-lines have only the shape of straight sections [24]. Already from the geometric form of the slab and from the geometry of the support, the shape of the yield-lines can be derived. It is a relatively simple tool when it comes to the software used. In addition, it is possible to accurately read the coordinates defining the predicted yield-lines of the slab.

The aim of this article is to present a new method of predicting the yield-lines of statically loaded slabs, based on roof geometry (straight skeletons) and Voronoi diagrams for a polygon.

2 Methodology

The following research plan was adopted in the article. First, the assumptions defining the kinematic mechanism leading to the determination of the geometry of the yield-lines were formulated (Section 3). Then, the relationships between the concept of a geometric roof as a polyhedral surface, a geometric embankment over a polygon as a surface being the sum of a polyhedral surface and surface fragments of rotating cones, and a model of the actual embankment resulting from the behaviour of loose material freely falling onto a flat polygon are discussed. The methods of creating embankments were presented: geometric in the AutoCAD environment, and real in the laboratory (Section 4). In order to demonstrate the above mentioned relationships, the geometric structure of the roof with constraints is given (Subsection 4.1), the essence of the process of the formation of the yield-line (Section 5) and the method of geometric and laboratory modelling of the yield-line (Section 6) are discussed. Then, the created geometric models of the crease lines were visually compared with the available photos of the damaged plates (Section 7). For greater reliability, geometrical (AutoCAD) and laboratory models of the yield-lines were presented for several examples of plates with complex support (Section 8), including geometric and laboratory models for the example of a slab, the yield-lines of which were obtained by the DLO method. A special comparative visual analysis was performed on the plate and yield-line model obtained by the DLO method and the geometric and laboratory models obtained with the methods proposed in this article (Figures 18 and 19).

3 Geometric basics of yield-lines theory of slabs

The theory (method) of yield-lines was created from the synthesis in the lines of plastic joints of the layouts of yield-lines observed in reinforced concrete slabs.

The theory is based on the following assumptions [25]:

1. Plastic deformations in the plate are concentrated in the yield-lines forming the grid of destruction. The grid of destruction becomes a kinematically admissible mechanism.

2. The yield-lines connect unformed parts of the board that are moving as rigid bodies.

3. The bending moment on the boundary line reaches the limit value. For a homogeneous polygonal slab, the authors additionally formulate the following two principles.

4. In the kinematic mechanism, the rigid parts of the plate rotate around the segments of the support lines (i.e. sides of the polygon) or around the segment lines going through support points (i.e. vertices of the concave angles of the polygon) and perpendicular to the bisectrices of the concave angles. In the second case, the rigid parts of the plate adopt an elastic conical shape.

5. The yield-lines between two rotating rigid parts of the kinematic mechanism are composed of points equally distant from the support elements (rotation axes of the rigid parts of the mechanism).

The condition 5 is assumed similar to the simple beam – uniformly distributed load. The beam fixed at both ends – uniformly distributed load has the largest bending moment in the midpoint. In this case, the plastic deformation of the concrete beam will focus at the midpoint. Thus, naturally the yield-line of the slab will be placed on the symmetry line of the respective support segment lines. If one of the rigid parts is flat and the other is conical, then the symmetry line is a parabola. If both rigid parts have conical surface, then the symmetry line is a hyperbola (in the orthogonal projection as a straight line) (Figure 3).

The consquence of the adopted assumptions 4 and 5 is the straight-line or parabolic shape of the yield-lines. More generally, assumptions 4 and 5 imply a Voronoi diagram for the polygon as the shape of yield-lines. In the case of a convex polygon, it is a roof, i.e. a straight skeleton (Figure 2).

The hypothetical mechanism of slab behaviour adopted here has its precise implementation in the case of the mechanics of loose materials, namely, it is an analogue of the shape that creates loose material falling freely on a given base (polygon). Hence, when interpreting the yield-lines, the embankment shape is simultaneously illustrated. The ridge line of the embankment indicates the topology of the yield-line pattern. It can be said that the deformed plate has the shape of an inverted embankment (flat “sunken” roof) with very small angles of inclination to the horizontal plane.

4 Geometry of roofs and Voronoi diagrams for a polygon

Roofs discussed in this article are defined as polyhedral surfaces on the basis of two assumptions: (1) all eaves of a roof form a planar (simply connected or k-connected) polygon called the base of the roof, (2) every hipped roof end makes the same angle with the (horizontal) plane which contains the base. Thus, every roof, and equivalently the orthographic projection of this roof onto a plane (parallel to the base), is uniquely defined by its base. Then, it is a straight skeleton, the edges are the axis of symmetry of the respective sides of the polygon. The orthographic projection of the roof, i.e. the skeleton of the roof (in the literature since 1995) called the straight skeleton [10] as the object that can be unequivocally generated from a polygon, was known in descriptive geometry for a very long time [11]. The skeleton of a roof in recent years has been the object of interest of many authors dealing with computational geometry [26,27,28,29,30,31,32,33]. The rectangular projection of the roof is obtained as a chain of segments (polygonal chains) containing bisecting lines of angles of the polygon. The straight skeleton of a polygon is defined by a continuous shrinking process: edges of the polygon are moved inwards parallel to themselves at a constant speed. The straight skeleton may be computed by simulating the shrinking process by which it is defined [10]. In three-dimensional terms, the roof is formed of polygons inclined at the same angle to the base. The structure of roof geometry is closely related to Voronoi diagrams [11,13,34].

Assuming that 〈M, d〉 is an arbitrary metric space and Λ₁, Λ₂,…, Λ _n are n subsets (sites) of M, the Voronoi diagram is defined as follows. For any point X ∈ M, d(X, Λ _i ) denotes the distance from the point X to the site Λ _i . The region of dominance of Λ _i over Λ _j is defined by

The Voronoi region for Λ _i is defined by V(Λ _i ) = ⋂ i ≠ j Dom ( i , j ) . The partition of M into V(Λ _i ), V(Λ _i ),…, V(Λ _n ) is called the generalised Voronoi diagram [35]. If the sets Λ₁, Λ₂,…, Λ _n are points of a Euclidean plane (with a Euclidean metric), then the (ordinary) Voronoi diagram is obtained (Figure 1a); if the sets Λ₁, Λ₂,…, Λ _n are sides of a polygon, then the Voronoi diagram for the polygon is obtained (Figure 1b).

Figure 1

Voronoi diagrams: (a) a Voronoi diagram for a set of points and (b) a Voronoi diagram for a polygon and a Voronoi region for a side of a polygon [34].

For a convex polygon, a straight skeleton coincides with the Voronoi diagram. Elements forming it are bisectors of the polygon angles (Figures 2 and 5, and Table 1). For concave polygon, parabolic arcs appear in addition to the line segments (Figure 5). Parabolic arcs are common parts of planes forming the roof and the surface of the right circular cones. These cones have their vertices at the vertices of the concave angles of the polygon. The angle of opening of these cones is equal to the inclination angle of planes. Then, as common parts of the planes and the surface of the cone, parabolas and, as parts of the two cones, hyperbole are obtained. These conical surfaces and planes model the behaviour of bulk material with an angle of internal friction equal to the angle of opening of the cone [13]. The effect of the embankment formation experiment is illustrated in Figures 2 and 3. The geometric model of the embankment (geometric embankment with visible parabolic arcs and hyperbolic arc) is found in Table 2. A projection of a geometric embankment is presented in Table 2 in the right column and a natural embankment – an experimental effect in Figure 3. Tables 1 and 2 contain the roof skeleton and the associated Voronoi diagram – the objects in the right columns as well as the geometric roof and the geometric embankment – objects in the left columns (Figure 4).

Figure 2

Roof (top view – straight skeleton) over a convex polygon, coinciding with the Voronoi diagram for a polygon, realised with 3D commands: EXTRUDE, TAPER FACES in the AutoCAD software environment in 2013 (source: own edition).

Table 1

Roof and roof plan – accepted terminology (source: own edition)

The roof in 3D	Orthogonal projection on the plane of the roof base
A polyhedral surface (or a solid)	Roof skeleton, roof projection, or straight skeleton

Figure 3

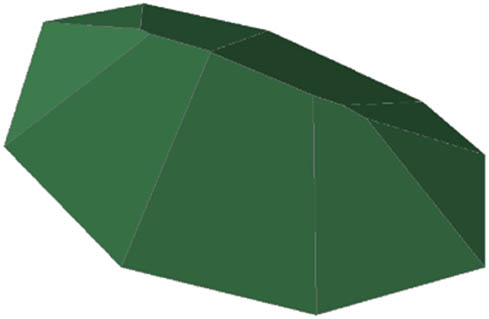
Roof (a straight skeleton) over the convex polygon from Figure 1 in 3D visualisation, realised with 3D commands: EXTRUDE, TAPER FACES in the AutoCAD software environment in 2013.

Table 2

Embankment and Voronoi diagram – adopted terminology (source: own edition)

Embankment in 3D	Orthogonal projection on the base plane of the embankment
A solid containing flat walls and surfaces of a circular cone	Voronoi diagram for the embankment base polygon

Figure 4

Embankment obtained experimentally resting on the polygon (source: own edition).

AutoCAD versions starting from the AutoCAD version v.12 and, with some break, later starting from the AutoCAD version in 2007, allow automatically build a roof in the form of a 3D solid (Figure 5). The creation of the embankment is also possible, but requires manual control or development of a suitable application.

Figure 5

Top view (horizontal projection) of the embankment obtained experimentally resting on a polygon with four concave angles, including two facing each other. The spine line is made up of line segments: ab, bc, ef, jl, and op; parabolic arcs: cd, de, fh, ij, lm, mn, and no (fg, jk – parabolic arcs as parts of corner edges); straight line segment (hyperbolic arc in 3D) hi, a thin line indicates the roof – a straight skeleton [13].

The terminology and meaning of the concepts of roofs and geometric embankments adopted in the work are presented in Tables 1 and 2, and (Photo 1).

Photo 1

Experimental embankment resting on a polygon with four concave angles, including two opposite each other [13].

Figure 6

Designing a roof with constraints by immersion in an ordinary roof and trimming using Boolean operations (stages of roof design in AutoCAD software environment): (r) roof base and water outflow directions, (r1) roof base extension (immersion in an ordinary roof); (r2) the base of a new auxiliary ordinary roof; (r3) design of an ordinary roof (straight skeleton); (r4) truncation by performing Boolean operations; and (r5) projection roof design with restrictions; five views of the roof model project [11].

In Voronoi diagrams, for the polygon, line segments and parabolas are obtained as dividing lines [11,13]. Why is there no hyperbola appearing in a 3D model (Table 2, Figure 5)? Well, a hyperbola (i.e. hyperbolic arc) being a component of the ridge line in embankment models lies in a plane perpendicular to the horizontal plane. Thus, the horizontal projection of the hyperbolic arc, i.e. the top view, is the line segment (Figure 5).

4.1 Roofs with restrictions

Roofs with restrictions (also called “roofs with neighbours”) constitute a special type of roof. It is assumed that certain sides of the polygon of the roof base or parts thereof cannot be eaves. These line segments in the drawings are marked with a double line (Figure 6). In practice, this means that water cannot flow down towards the side (given edge or part of the side) (Figure 6). In order to properly drain the water, additional hipped roof ends (and thus eaves) must be introduced after marking the direction of water drainage. The water in a given plane runs perpendicular to the contours of this plane. Each eave is a contour line of a hipped roof end. Thus, water flows perpendicular to the eaves. The direction of the water flow forces the adoption of new eaves perpendicular to the straight line defining this direction (runoff) (Figure 6(r1)). Taking into account the new eaves, the polygon of the base of the roof is expanded (Figures 6r1-r2). After solving the regular roof (Figure 6r3) and applying the Boolean operation - intersection (Figure 6r4), the final solution is obtained (Figure 6r5).

Figure 7

Diagrams of the main scratches in rectangular, triangular, and trapezoidal slabs supported along the perimeter (own edition on the basis of ref. [36], Figure 2-23).

5 Yield-lines

Mechanics specialists have long started discussion on each case of yield-lines (e.g. rectangular plate) with a sketch of the roof ridge (orthogonal projection) (Figures 7 and 8). Why not use the Voronoi diagram lines if the essence of them lies in many structures of the reality that surrounds us? Even an approximate determination of the topology of the yield-lines will definitely facilitate their thorough examination by another method.

Figure 8

Arrangement of the yield-line of a homogeneously loaded plate (own edition on the basis of ref. [37], Figure 5.117).

Exceeding the limit state of a statically loaded slab takes place in reality during building breakdowns and construction disasters or laboratory experiments. Then, the destruction of the reinforced concrete slab is carried out along the expected yield-lines [36,38]. To calculate the reaction of supports of rectangular boards, with a uniformly distributed load as load sharing lines, hypothetical boundaries very close to the shape of the hipped roof edge are assumed ([37], p. 15, Figure 5.19). Thus, whenever in static analysis and construction calculations the yield-lines are used, everywhere there is a sketch of hypothetical, expected yield-lines resembling the edges of flat roofs [14,25,36,37,39]. This prompted the author of a monograph on roofs [11] to address this issue as an important application of roof geometry. This study proposes a method for assisting in the determination of the expected yield-lines of slabs loaded uniformly, using Voronoi diagrams. There is an extension of the results obtained at work [11] based on the geometry of roofs with different slope angles (Figure 9).

Figure 9

The yield-lines of a homogeneous slab loaded uniformly (supported along the perimeter and centrally with a circular cross-section), analysed in the paper ([14], p. 498): (a) and (b) lines determined by the limit-load method; and (c) yield-lines of the slab obtained as a result of the experiment.

Koźniewski, through the application of mathematical theory of roofs [11], showed the possibility of obtaining a similar shape of the yield-lines in supported slab (Figure 10). He verified his solutions using two methods: the method of the power balance of external loads and internal forces based on the roof skeleton line as a yield-line and determining the load distribution by means of the bending surface by the double sine series with reference to the one-point support. As a central support, he adopted the square described on the circle (Figure 10c), which facilitated the use of the power balance method. In the first case, the results of the load absorbed by the pole differed by 2.1%, and in the second one the point support took over a load differing 0.5%.

Figure 10

Scheme of the slab loaded uniformly and three ways of obtaining yield-lines (a) (freely supported along the circumference and centrally located column with a circular cross-section), analysed in the paper [14], dimensions of the slab is in cm; (b) yield-lines created as a result of experimental destruction of the slab; (c) expected yield-lines obtained as the edges of the natural roof solution ([11], p. 166); and (d) layout of yield-lines obtained as a result of calculations using the method of the power balance of external loads and internal forces on the basis of the natural roof ridge lines ([11], p. 170).

The results obtained were the starting point for the research presented later in this section. The yield-lines, obtained with the help of roof theory, matched quite well in relation to the experimental destruction of the slab in the aspect of numerical results of taking over loads by a supporting pole. However, visually the skeleton lines of the roof slightly differed from the yield-lines created as a result of the slab’s destruction (Figure 10d). Anyway, straightforward schemes of solutions adopted in the monograph [14] also differed considerably. The research carried out in 2012 on the shape of the embankment obtained from homogeneous bulk material, based on any flat figure [13], led to the conclusion that the obtained embankment shape has a Voronoi-shaped projection of a polygon inscribed in a given figure (single- or multiple-connected). CAD technology (e.g. AutoCAD) allows you to create such Voronoi diagrams in 3D representation for a given figure in the base (Figures 11a, 12c–17c, 14d–17d, 18c, and 19d).

Figure 11

(on the left) “Embankment” model as a model of the inverted slab with the base defined in the drawing, the ridge lines have the shape of sections and parabola; (on the right) a visual comparison of empirically obtained test lines [14] with boundary lines of Voronoi diagrams for a rectangle with a centrally located circular hole (the line is a rectangular projection of the “embankment” edge) (source: own edition).

Figure 12

Analysis of the yield-lines of a rectangular slab 1 based on three edges: (a) the result of the theoretical analysis of slab 1 ([14], p. 495), (b) yield-lines of the destroyed slab 1 ([14], p. 495), (c) the model of the Voronoi diagram (source: own edition), (d) the model of the Voronoi diagram with different inclination angles (source: own edition).

Figure 13

Analysis of the yield-lines of a rectangular slab 2 based on three edges and half the length of the fourth edge: (a) the result of the theoretical analysis of slab 2 ([14], p. 477), (b) yield-lines of the destroyed slab 2 ([14], p. 477), (c) the model of the Voronoi diagram (source: own edition), and (d) the model of the Voronoi diagram with the same inclination angles (source: own edition).

Figure 14

Model of embankment associated with a roof with constraints along two edges of the base, shaping the expected yield-lines of a slab supported by two edges: (a) slab supporting scheme, (b) (photo) laboratory model of the embankment in a top view (Voronoi diagram), (c) geometric model in the top view (Voronoi diagram), and (d) axonometry of the inverted geometric model of the embankment illustrating the method of supporting the slab (source: own edition).

Figure 15

Embankment model associated with a roof with two yards, shaping the expected yield-lines of the slab freely supported circumferentially on the edges and on two columns: (a) slab supporting scheme, (b) (photo) laboratory model of the embankment in a top view (Voronoi diagram), (c) a geometric model in a top view (Voronoi diagram), and (d) axonometry of the inverted geometric model of the embankment illustrating the method of supporting the slab (source: own edition).

Figure 16

Embankment model associated with a roof with one yard, shaping the expected yield-lines of the slab freely supported circumferentially on the edges and on one column: (a) slab supporting scheme, (b) (photo) laboratory model of the embankment in a top view (Voronoi diagram), (c) a geometric model in a top view (Voronoi diagram), and (d) axonometry of the inverted geometric model of the embankment illustrating the method of supporting the slab (source: own edition).

Figure 17

Embankment model associated with a roof with full limitation with five trigger points, shaping the expected yield-lines of the slab freely supported by points in five places: (a) slab supporting scheme (five columns), (b) (photo) laboratory model of the embankment in a top view (Voronoi diagram), (c) a geometric model in a top view (Voronoi diagram), and (d) axonometry of the inverted geometric model of the embankment illustrating the method of supporting the slab (source: own edition).

Figure 18

Drawing marks indicating how to find the expected yield-lines of the slab using the method discussed in the article “Automatic yield-line analysis of slabs using discontinuity layout optimisation” [15]: (a) designation of the slab supporting scheme adopted in the article [15], (b) (photo) laboratory model of the embankment in a top view (Voronoi diagram), (c) designation with double lines for the roof with neighbours (embankment) solution, and (d) expected yield-lines obtained by the Voronoi diagram method (source: own edition).

Figure 19

A model of the embankment associated with the roof, shaping the expected lines of the slab breaks discussed in the article: “Automatic yield-line analysis of slabs using discontinuity layout optimisation” [15]: (a) slab supporting scheme, (b) (photo) laboratory model of the embankment in a top view (Voronoi diagram), (c) expected yield-lines obtained by the Voronoi diagram method, and (d) axonometry of the inverted geometric model of the embankment illustrating the method of supporting the slab.

6 The procedure of identifying the yield-lines by means of the 3D model of the “geometric embankment”

To construct the model, any polygonal outline of the slab is accepted: (1) if it is supported along a line segment of the boundary line, in the model this line segment is the eaves of the roof – graphically a single line (in the laboratory model, the bulk material slides freely); (2) if there is no support at a particular section, then there is a limitation on this section – graphically, the double line is assumed (the bulk material is blocked by the wall); (3) if there is a point support, then there is a trigger point – a top of the cone with an angle of opening equal to the slope of the roof slopes is assumed (the material slides over the circular cone).

Modelling of the expected yield-lines of slab is understood as follows. The embankment obtained in laboratory conditions is (by nature) a 3D object. Similarly, the geometric “embankment” constructed as a virtual geometric model in the AutoCAD software environment is also a 3D solid. However, only the top views of these objects will be interesting (Figures 14b–17b, 14c–17c, and 19b and c). From the point of view of orthographic projection theory (Monge), the geometric “embankment” will be horizontal projections of objects created in the laboratory and virtually. The two-dimensional (2D) objects thus obtained are Voronoi diagrams for: a polygon, and a multi-connected domain (i.e. a polygon with openings of different shapes), or for any set of figures (line segments, points, circles) limited to a polygon (or more generally an area) constituting the perimeter of the slab.

However, in order to show only the method of supporting the slab, the geometric model was reversed and supplemented with appropriate support elements: pillars, walls (Figures 14d–17d and 19d). The axonometric interpretation of the inverted model (3D) of the geometric embankment should not be treated as a faithful model (3D) of the “destroyed” slab (Figures 14d–18d). The edges (including ridge lines) of the inverted model (in axonometric terms), including the aforementioned agreement, illustrate the expected lines of the edges of the slab under consideration (Figures 11a, 12c–17c, and 19c).

In cases where orthotropic plate reinforcement is used, the condition mentioned in Section 4 does not have to be met. Then, the analysis of the bending of statically loaded slabs in such situations leads to roof geometry with different slope angles [11]. Let us assume that a plastically orthotropic slab has the dimensions a and b with the edges on the axes Ox and Oy of the coordinate system, with the boundary bending points M _x and M _y . Let us denote Λ = M x M y the coefficient of orthotropy and β = b a the ratio of the lengths of the edges of the slab. Taking into account the designations adopted in Figure 20, as a result of reasoning based on the theory of limit-bearing capacity, taken from a monograph [14], the parameter of the mechanism of slab destruction is obtained.

Figure 20

The lines of the elevations of an orthotropic rectangular slab loaded uniformly (own edition based on [14]).

Then,

Therefore, in the examples discussed in Section 8, two ways of modelling the yield-lines are presented (Figures 12c and d, 13c and d).

7 Analysis of the yield-lines of rectangular slabs with different support geometry

This section presents models – geometric solutions of predicted yield-lines for examples of laboratory destroyed plates. The models were made using the method proposed in this article. In order to make a comparative analysis, examples of slabs with the pattern and support geometry adopted in the monograph were considered [14]. The individual figures contain the result of the theoretical analysis, the photograph of slab destruction, and the geometrical model.

8 Models of selected embankments obtained on the basis of roofs

This section presents models – geometric solutions of the predicted yield-lines in correspondence with laboratory obtained solids of embankments. This is an illustration on the examples of the theory presented in Section 3 and the considerations in Sections 4–7.

Figures 14–17 and 19 show various cases of shaping (modelling) embankments in the aspect of predicting the yield-lines of slab. Figure 19 is a comparative drawing; it stands out from the others by the presence of the model presented in the paper [15].

9 Conclusion

Comparing the method presented in this work with reference to the method and type of the slab discussed in ref. [15] indicates a high similarity of both results. It seems that before applying any method of determining the yield-lines for a given slab, it is worth starting with the construction of the Voronoi diagram.

This method has been verified on many examples of experimental damage to the plates and far-reaching similarity has been noticed everywhere. In addition, the solution to the problem presented by the method is done using standard AutoCAD software working on any notebook. The task can be performed by the student after completing the first semester in the field of descriptive geometry.

1. Visual comparative analysis of the models constructed by the authors with the results of research on a natural scale and/or numerical calculations contained in the literature indicates a very good agreement of the obtained Voronoi diagrams for a polygon with yield-lines. Due to the knowledge of the theory of Voronoi diagrams, a more difficult to determine shape of the expected scratches of a slab (e.g. the ceiling of an exploited building) is possible. It will also be helpful in analysing the reinforcement of complex-shaped slabs when designing a building.

2. The proposal for the computer creation (in the CAD software environment) of embankment models is a good general geometric method of predicting the yield-lines. These lines are precisely defined in the CAD software environment. In the AutoCAD coordinate system, it is possible to read the coordinates of the points that make up these lines.

3. The results of the research presented in the article are an interesting development of geometric theory in the field of structural mechanics, also in the field of potential applications in the diagnostics of structures (e.g. for detecting yield-lines of ceiling slabs). After a properly developed computer application (e.g. for a mobile phone), on the basis of a photograph of the object’s geometry, it is possible to read the places where the scratches appear, without carrying out complicated calculations, often requiring high-power computers.

4. The method presented here can be used to recognize a completely preliminary scheme of the yield-line shape of the tested slab. In the case of a significant demand for frequent use of this method, it would be advisable to automate the procedure presented here by developing a suitable application, e.g. in AutoLISP in the AutoCAD software environment.