Location strategy for logistics distribution centers utilizing improved whale optimization algorithm

4.1 Standard whale optimization algorithm (WOA)

Every whale in WOA can be considered a particle, and every particle’s position is a decision variable. During hunting, whales approach and hunt their prey in spirals rather than straight lines.

4.2 IWOA

WOA has a higher search ability and faster search times than other heuristic optimization algorithms. It is a new optimization algorithm with a simple update mechanism, a slight adjustment parameter, and some degree of randomness [15,16,17,18]. The enhancement of global convergence ability and acceleration of convergence speed can be achieved through benchmark test functions, statistical metrics, comparative analysis, success rate (SR) index, and consistent parameter settings. However, the algorithm can quickly enter the local optimum due to the spiral optimization algorithm’s update mechanism, which lowers the algorithm’s accuracy of convergence. By impacting the exploration–exploitation equilibrium, the update mechanism of the spiral optimization algorithm in the conventional WOA can facilitate the algorithm’s entry into local optima. Thus, this article adds random sinusoidal inertia weights and a comprehensive variation operator to the algorithm’s optimization process, strengthening its global search capability and preventing it from reaching the local optimum. The strategic integration enhances the algorithm’s adaptability, preventing it from being trapped in suboptimal solutions and promoting compelling exploration of the solution space. This is done in order to address the aforementioned problems.

First, as can be seen from equations (1)–(7), as the number of iterations rises, the convergence speed of the conventional WOA optimization algorithm falls. The convergence speed of the conventional WOA optimization algorithm declines as iterations increase, mainly due to more individual whales converging toward the global optimum, elevating the risk of entering local optima and diminishing overall efficiency.

Additionally, in the algorithm’s late iteration, an increasing number of individual whales progressively approach the global optimal solution, ultimately resulting in the algorithm falling into the local optimum and causing the algorithm’s convergence speed to drop dramatically, impacting the WOA algorithm’s convergence. Given diminishing returns, the traditional WOA optimization algorithm’s convergence speed tends to decrease as the number of iterations increases. The convergence process is slowed down as the algorithm iterates because the gains in solution quality get progressively smaller at each stage. This article presents a comprehensive variation strategy, the steps of which are shown below, based on the fusion of non-uniform variation and Cauchy’s variation, to address the aforementioned issues:

1. By setting the variation switch function, the variation operation is performed on the current position of the whale by judging the switch condition, where the variation switch’s mathematical expression is displayed

2. as follows:

where SN is the size of the whale population and n is the dimension. Define the mutation operation for the kth whale when 0 < switch(k) < 1. ψ and μ are parameters. After conducting numerous simulation experiments, it was discovered that more than 75% of the whales mutate between 0.2 < ψ < 0.5 and 0.1 < μ < 0.5, and this is the optimal time for the algorithm to optimize.

2) The value of A determines the step size of WOA. The algorithm enters the pre-iterative stage and searches a more extensive range faster when A > 1. The Cauchy inverse cumulative distribution function [19] is added when the algorithm is in the pre-iterative stage, and the particles are selected into the local optimum. This is because the Cauchy variation has a broader range of variation than the traditional binomial, polynomial, and non-uniform variations. The ability to introduce significant perturbation is primarily responsible for the broader range of variation at Cauchy variation. This allows for better exploration of the solution space and increased chances of breaking out from local optima. The Cauchy variation applies this more significant perturbation to the particles to help them escape the local optimum. WOA prevents the possibility that particles that have undergone Cauchy’s mutation will undergo blind mutation because it updates particle positions during the global search through spiral motion. The Cauchy’s inverse cumulative distribution function has the following mathematical expression:

Therefore, Equation (9) can be improved as

where x i , j ( t ) = A , 0 ≤ p ≤ 1 , and γ is the i-th whale’s j-th position.

3) If a small fraction of whale particles satisfy the variation condition, the particles that do so will be moved to the global optimal solution through non-uniform variation. The particles that do not will be approached to the global optimal solution through the original position updating formula. This will enhance the algorithm's search speed and decrease the likelihood of premature convergence to a local optimum when the cardinality of set A is less than 1. Unlike the variation strategy used in the conventional genetic algorithm, non-uniform variation originates from the non-uniform variation evolutionary algorithm [20]. Combining the non-uniform variation strategy with WOA aims to improve the algorithm’s global search capability by enabling the algorithm to always jump out of the local optimum in the late iteration. Better exploration and exploitation of complex problem spaces can be achieved by coupling the non-uniform variation strategy with WOA, which boosts robustness and diversity and adapts to changing optimization landscapes. This solves the issue of the algorithm needing to be faster to fall into the local optimum. The non-uniform variation evolution algorithm can adaptively adjust the search step size during the iteration process, so the convergence speed will increase when the algorithm is late. Assume that there are SN , x i = { x i 1 , x i 2 , ⋯ , x i n , ⋯ , x i SN } T whales in the population. The non-uniform variation formula, assuming that the variation operation is carried out on the nth component, is

The variables, in this case, are as follows: b is the non-uniformity parameter; t is the current iteration number; T is the maximum iteration number; r is the uniform random number within [0, 1); and UB and LB are the particle’s upper and lower boundaries, respectively. The non-uniform variation step is represented by Δ ( t , y ) = y ⋅ 1 − r 1 − t T b .

Second, it is established by equations (9)–(11) that the value of parameter an entirely dictates the WOA’s capacity for both local and global optimization. The late iteration period sees a linear decrease in a value, which significantly affects the algorithm’s convergence accuracy. It facilitates the particles’ easy fall into the local optimum. For this reason, the comprehensive variation strategy used in this article helps the algorithm escape the local optimum. This article proposes a stochastic sinusoidal inertia weight based on sinusoidal curve properties to improve the algorithm’s population diversity and global search capability. The algorithm’s stochastic sinusoidal inertia weight functions bolster population diversity and global search capability. This pivotal role leads to a more comprehensive exploration of the solution space, promoting adaptability and enhancing the algorithm’s overall effectiveness in finding optimal solutions. The following is the stochastic sinusoidal inertia weight expressed mathematically:

Equation (12) shows that when the iteration starts, the value t / t max tends to 0, w is more significant, and the algorithm performs a better job of searching globally. When t tends to, t max and w tends to 0, the algorithm has a high local search capability in its final iteration. It is possible to modify equations (11) and (12) in the following ways to improve the population diversity of the algorithm:

Figure 1 depicts the flow of the IWOA.

Figure 1

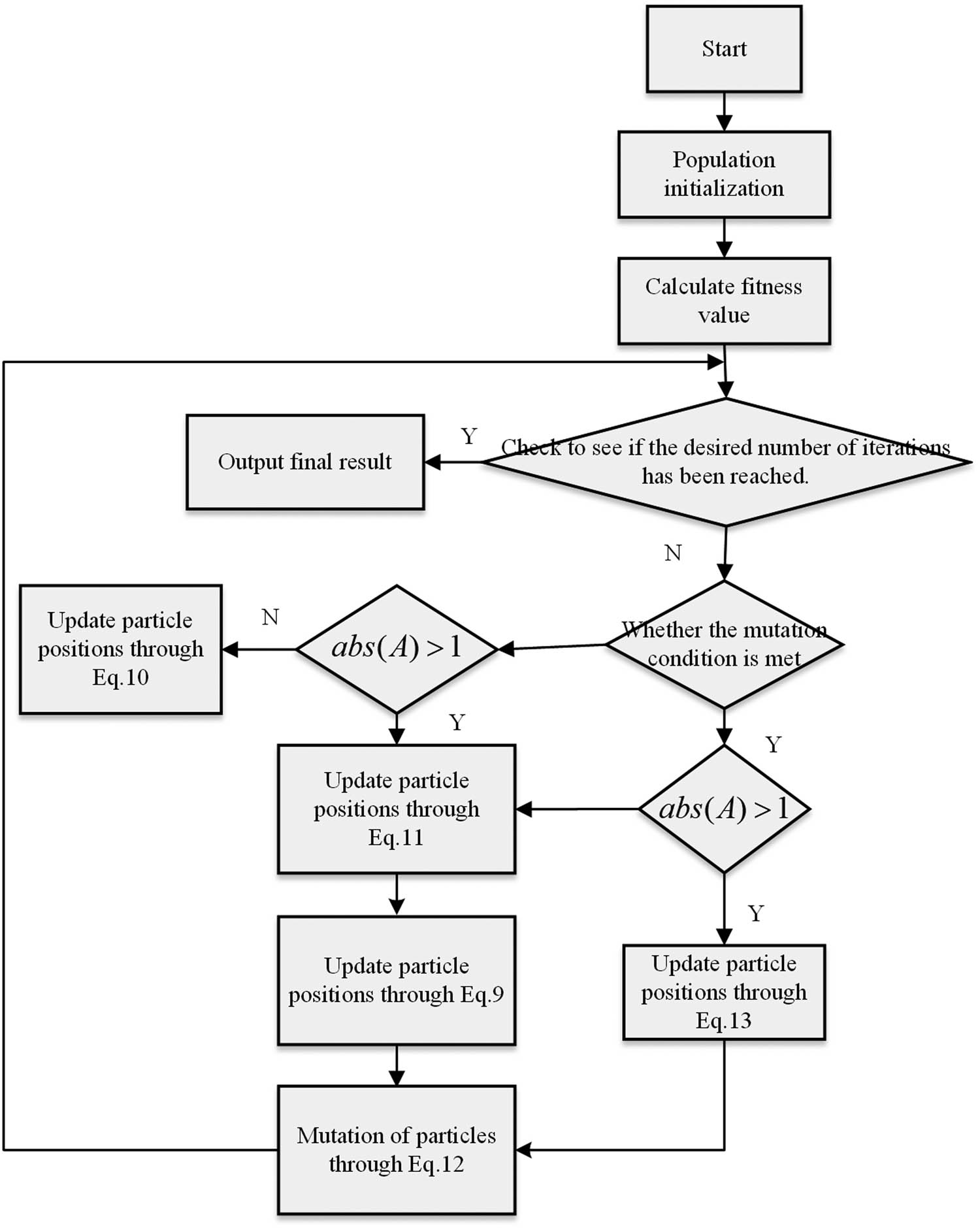
Flowchart of IWOA.

5.1 Performance testing based on test functions

This article carries out the simulation verification from the two aspects of the register function and the actual calculation example to confirm that the IWOA presented can be applied to optimize the logistics and distribution center location model. The test environment adopts the Windows 10 operating system, the Thinkpad laptop with 8GB of memory, and the simulation software Matlab2022a.

In order to verify the algorithm’s ability to perform local searches, this article first chooses 16 benchmark functions to serve as test functions. When selecting the 16 benchmark functions for testing IWOA, several factors were considered. These included the presence of known optima for accuracy evaluation, mathematical complexity, diversity in problem characteristics, and varying dimensions for scalability assessment. There are four categories for these functions: multi-peak functions (f ₅ to f ₈), single-peak functions (f ₁ to f ₄), translational functions (f ₉ to f ₁₂), and rotational functions (f ₁₃ to f ₁₆), all of which are shown explicitly in Table 1. Sorting benchmark functions into different categories is essential to evaluate the algorithm’s adaptability. Translational functions evaluate adaptability to changed landscapes, rotational functions gauge robustness against rotations, single-peak functions evaluate efficiency in more straightforward scenarios, and multi-peak functions test their ability to navigate landscapes with multiple optima. Second, a comparison is made between IWOA and chaotic serial particle swarm optimization (CSPSO) [16], sinusoidal differential evolution (SinDE) [17], and moth-flame optimization algorithm with Cauchy mutation (CCMFO) [18]. The CCMFO algorithm becomes well known because it applies chaos-based adjustments to the moth optimization procedure. This increases the algorithm’s capacity for exploration, raises convergence accuracy, and helps it solve challenging optimization problems. CSPSO is a cross-searching-based particle swarm optimization algorithm, which improves the global search capability of the algorithm and was suggested by Meng et al. Drea et al. introduced the SinDE algorithm, a sinusoidal searching algorithm that improves the algorithm’s local search capability, and CCMFO is a modified moth optimization algorithm based on chaos. Several benefits arise from enhancing the algorithm’s local search capability, encompassing improved convergence accuracy, better adaptability to complex problem landscapes, increased solution precision, and an overall optimization performance enhancement. An enhanced chaos-based moth optimization algorithm is called CCMFO.

This article has the same parameter settings for the four algorithms – CSPSO, SinDE, CCMFO, and IWOA – where the other parameter settings are the same as those of its references, the population size is 50, the dimension is 50, the maximum number of iterations is 100, and so on. In order to determine the exact algorithm parameter settings, various factors are taken into account, including the nature of the problem, the algorithm’s complexity, the available computational resources, empirical results, sensitivity analysis, and knowledge from existing studies and literature. Comparisons with CSPSO, SinDE, and CCMFO algorithms reinforce the IWOA’s effectiveness in local search capability, maintaining consistent parameter settings. The particular test results are shown in Table 2. This ensures the fairness of comparison in the test process.

First, Table 2 demonstrates that the single-peak function can be solved using IWOA suggested in this study to a more minor mean and standard deviation. This suggests that IWOA has better local search ability and stronger development ability and effectively improves the algorithm’s convergence accuracy compared to the other three algorithms. Improved local search capability and global convergence lead to faster convergence and higher accuracy in single- and multi-peak functions. This is why the improvement strategy works so well for IWOA. Simultaneously, for the multi-peak test function, IWOA can also solve for smaller mean and standard deviation, demonstrating that, when compared to the other three algorithms, it has a higher global convergence ability and a faster convergence speed. WOA differs from various heuristic optimization algorithms because of its distinctive characteristics, including balanced exploration and exploitation, dynamic adaptability, mathematical modeling, parallel processing potential, simplicity in implementation, and efficient exploitation via spiral updating. Second, for the test functions f ₉ to f ₁₆, IWOA solves smaller values than the other three algorithms, demonstrating its higher accuracy in solving complex problems and the applicability of the improvement strategy suggested in this study in solving complex target problems. Ultimately, the SRs of four algorithm are compared with the search SR or SR index. The detailed findings are displayed in Table 3, and the SR formula can be found in the following equation:

IWOA has a much higher SR than the other three algorithms, as Table 3 demonstrates. For the test functions f ₄, f ₅, f ₈, f ₁₂, and f ₁₆, the SR even reaches 100%. This suggests that the improvement strategy proposed in this study makes the algorithm more likely to jump out of the local optimum, enhancing the algorithm’s overall performance and making it suitable for choosing the location of the agro-logistics industry’s distribution center.

5.2 Simulation tests based on practical examples

Each logistics and distribution point can be thought of as a particle, and the particle is expressed as X = [ x 1 , x 2 , ⋯ , x A ] in this study. In IWOA, logistics points are denoted as particles (X), each chosen from A total points. Particles (X), each selected from A total points, represent logistics points in IWOA. Suitable simulations validate this representation, displaying the effectiveness of logistics and distribution center location strategy. A represents the total number of logistics and distribution points. IWOA will rationally choose P distribution points as the distribution center from the A distribution points. This optimization process is performed using the flow distribution center site selection model. Let the optimal particle finally selected be X = [0,1,0,1,0,1], which means that the second, fourth, and sixth distribution points are selected as the distribution center from among the six distribution points. The high efficiency of IWOA proposed in this study for solving the site selection of logistics and distribution centers is verified by selecting the factory locations and supply and demand quantities of 12 cities for test simulation. By contrasting the test results based on the composite ant colony algorithm [12] and the site selection strategy based on the hybrid particle swarm algorithm [13], the effectiveness of the approach suggested in this study is confirmed, and the site selection optimization mode based on the chaotic firefly optimization algorithm [14]. Each of the four algorithms is executed 50 times independently for 100 iterations. Table 4 displays the city’s coordinates, supply, and demand for goods, and Table 5 displays the experiment’s outcomes.

The fitness value curve solved by IWOA decreases at the fastest rate in the iterative preperiod, as seen in Figures 2–5. This indicates that IWOA is more capable of searching for the optimal value over a larger range and at an initial value than the other three algorithms [21,22,23]. Additionally, IWOA can obtain smaller average and optimal fitness values than the other three algorithms, meaning that the algorithm’s searching accuracy is higher, and the distribution center address can be found more precisely. More precisely, ascertain the distribution center’s address. Table 5 illustrates that this study’s IWOA-based logistics distribution center location strategy has a lower average distribution cost and a faster optimization speed than the other three strategies [24,25]. This effectively reduces distribution costs and lengthens the time required for location selection. IWOA’s speed in logistics optimization is due to its superior search, seen in a quicker fitness curve decline and smaller fitness values, ensuring precise distribution center addresses, reducing costs, and enhancing efficiency. The decrease in distribution costs yields substantial improvements in operational efficiency, reduced transportation expenditures, and heightened overall cost-effectiveness. There is a 50% reduction in computation time needed for distribution center selection and a 30% increase in distribution efficiency.

Figure 2

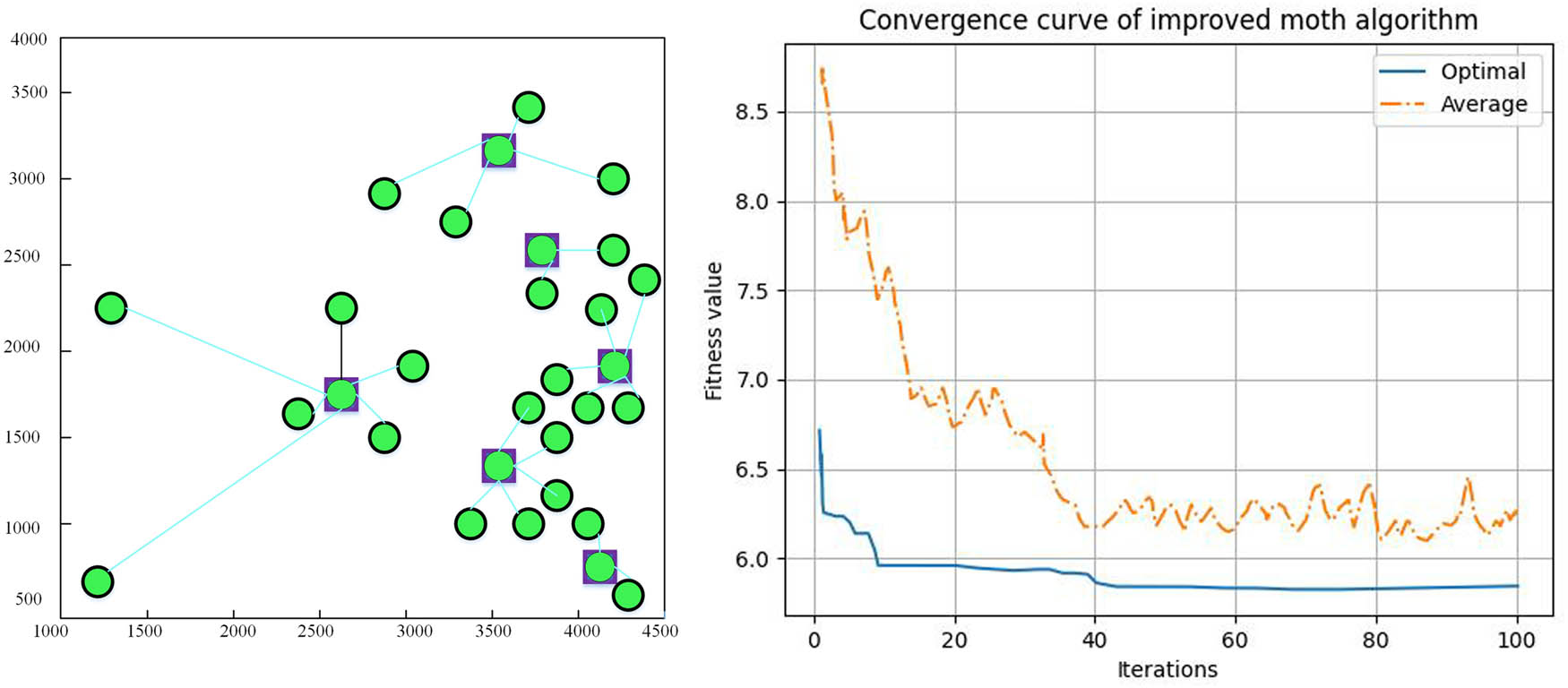
Location results based on improved moth algorithm.

Figure 3

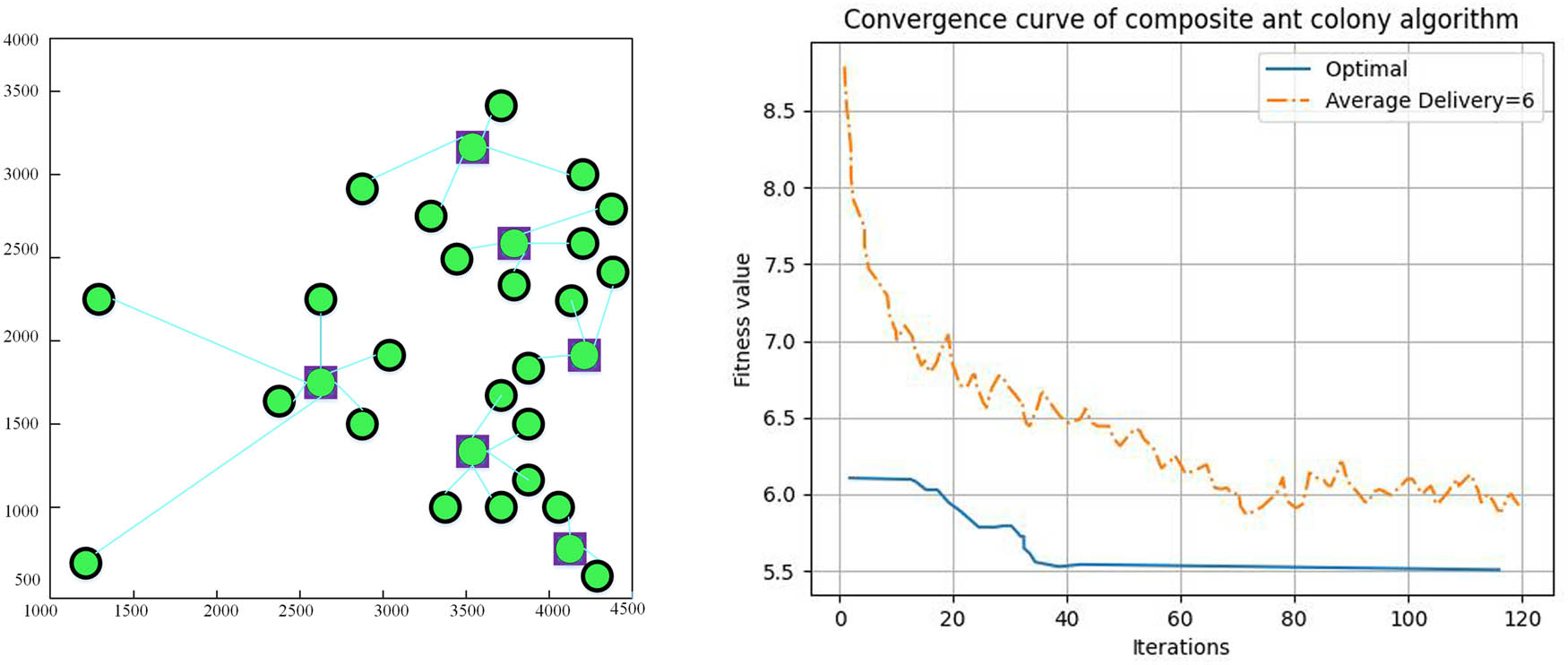
Site selection results based on composite ant colony algorithm.

Figure 4

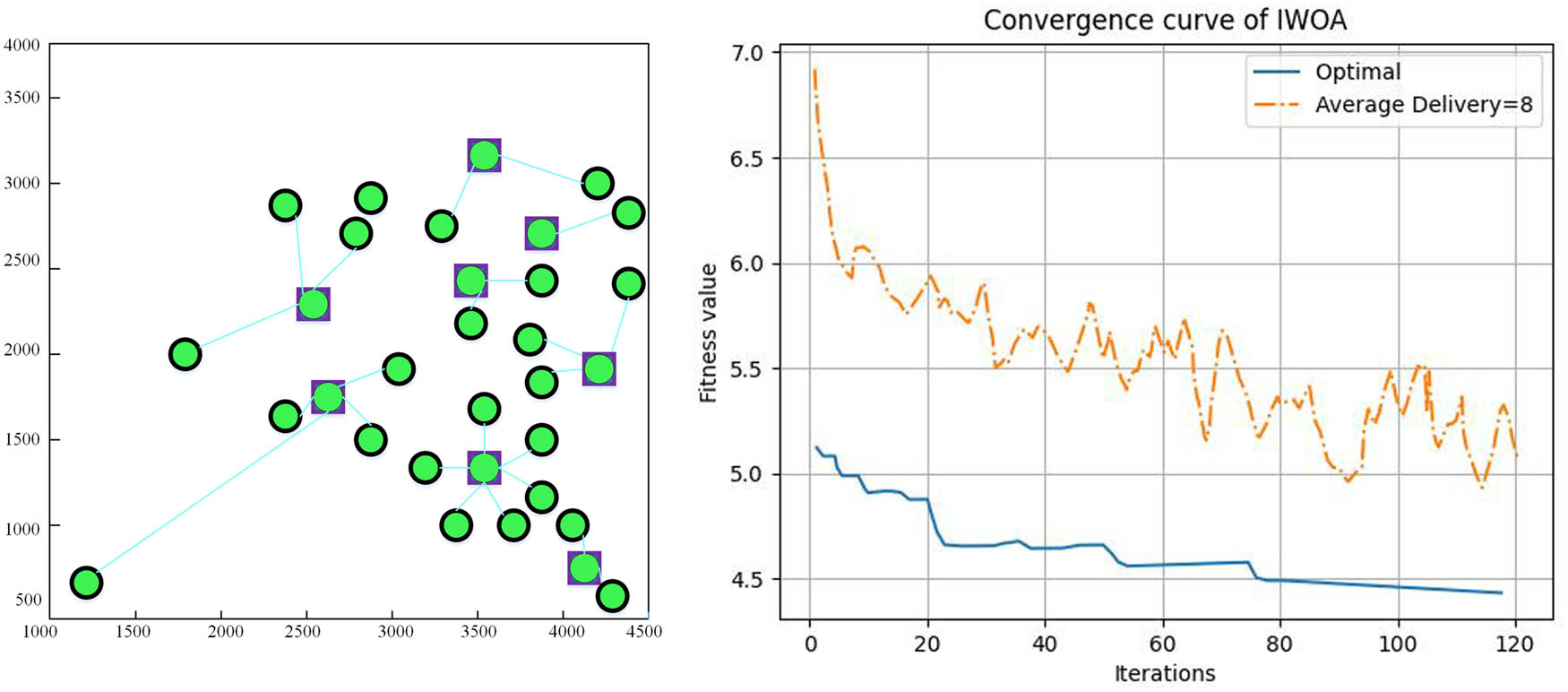
Location results based on IWOA.

Figure 5

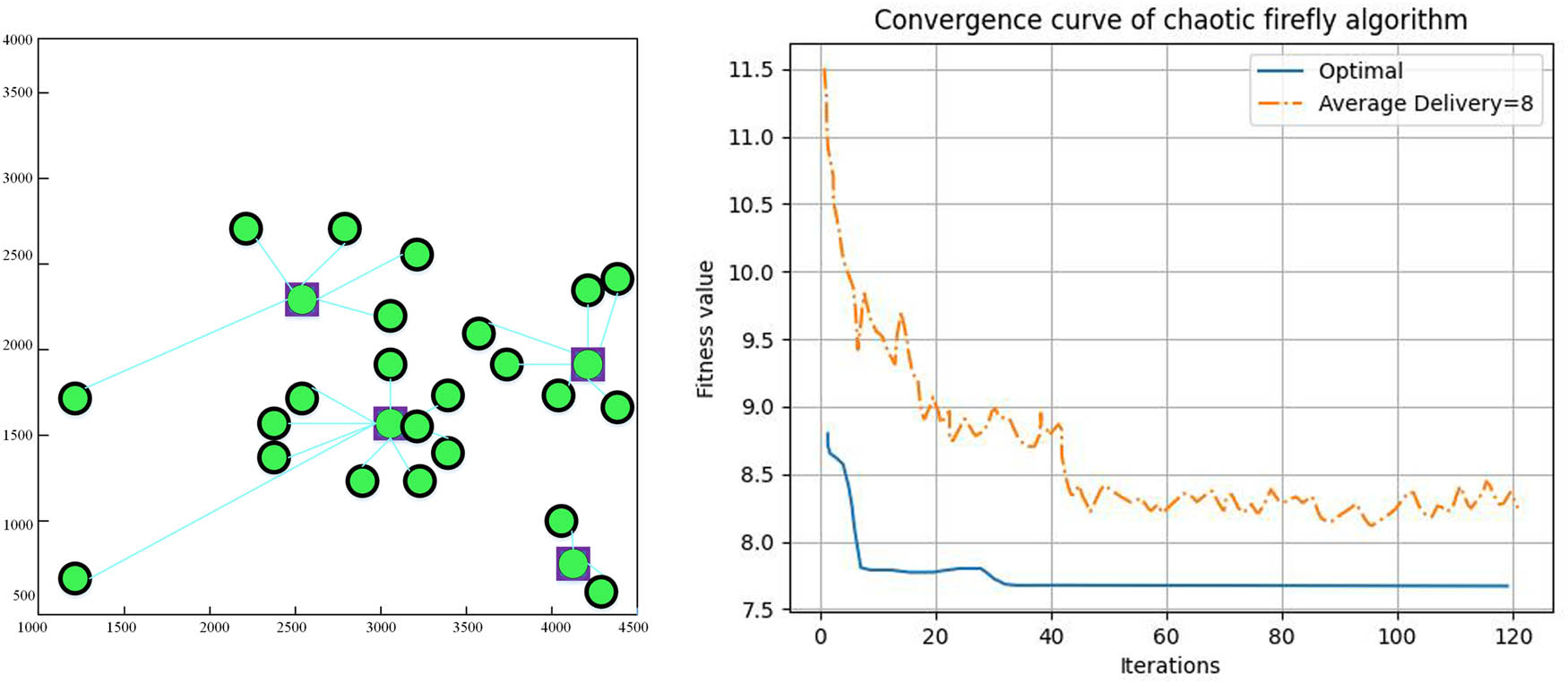
Site selection results based on chaotic firefly algorithm.