Abstract
Resource-constrained problems for technology-based applications/services are common due to pervasive utilization and in-definite user/demand densities. Traditional resource allocation methods consume high allocation time and make it difficult to predict the possible solutions from the collection of resources. Various range of solutions through optimizations are provided for addressing the issues that, however, result in imbalanced solutions. This article assimilates genetic algorithm (GA) and fuzzy clustering process and introduces resource-constrained reduction framework. The proposed framework utilizes a GA for mutating the allocation and availability possibilities of the resources for different problems. The possibilities of solutions are tailored across various demands preventing replications. Post this process, the fuzzy clustering segregates the optimal, sub-optimal, and non-optimal solutions based on the mutation rate from the genetic process. This reduces the complexity of handling heterogeneous resources for varying demand, user, and problem densities. Based on the clustering process, the crossover features are tailored across multiple resource allocation instances that mitigate the existing constraints. This proposed framework improves the problem-addressing ability (11.44%) and improves resource allocation (8.08%), constraint mitigation (11.1%), and allocation time (11.85%).
1 Introduction
Resource constraints occur when a project manager does not have the proper resources to fulfill the demand or command. Resource constraints cause damages during resource allocation and resource scheduling processes that reduce the outcome of a project [1]. Human resources, equipment, finance, and materials are the necessary elements which are needed to create a project [2]. Resource-constrained project problems have mostly occurred during the insufficient range of elements. Resource-constrained project scheduling problems (RCPSP) are a major issue which is faced by a project [3]. The RCPSP is a subclass of constrained resources to perform the tasks. A simulated annealing algorithm is used in RCPSP to solve the problems. The annealing algorithm analyzes the limited resources that are required for a project [4]. The limited resources are scheduled based on the priority level of the tasks. Both single and multimode-constrained problems are identified and managed by the annealing algorithm-based technique [5]. Different objective functions are analyzed to classify the exact types of project problems. The annealing algorithm-based approach increases the accuracy and efficiency of the scheduling process [6].
Genetic approaches are used for problem-solving processes in real-time projects. Genetic approaches are mainly used here to improve the overall performance level of projects. A hybrid genetic algorithm (HGA) is used to solve project scheduling problems [7]. The HGA-based approach commonly uses a classification operator to classify the types of problems. The classification operator identifies the scheduling problems which are presented in a project [8]. The HGA approach increases the quality range of the projects which minimizes the delay in finishing the demand of customers [9]. The HGA approach schedules the limited resources for real-time projects. A two-phase strategy is also used in HGA to evaluate the accuracy of the resource scheduling process [10]. The two-phase strategy reviews the resources that are necessary for project work. The two-phase strategy helps the users to solve the problems based on severity. The two-phase strategy improves the performance level of resource-constrained projects [11]. A genetic algorithm (GA)-based time decomposition approach is used for RCPSP. The GA algorithm changes the structure of the project based on the productivity level of data. The decomposition approach improves the discipline strategies for real-time projects [12].
Fuzzy optimization is a method that is used to solve problems in an application or system. The Fuzzy optimization methods are used for resource-constrained problem-solving processes. A fuzzy theory-based optimization method is used in RCPSP [13]. The fuzzy theory detects the necessary activities that are relevant for real-time projects. The fuzzy theory constructs a proper problem-solving strategy for RCPSP [14]. A fuzzy optimization model is also used in the resource constraints problem-solving process. The severity of problems is identified based on available renewable resources [15]. The exact severity level of the problems is identified, which produces the necessary information for solving the process. The fuzzy optimization model improves the service quality range of the projects [16]. The fuzzy optimization model minimizes the energy consumption level in the problem-solving process. The fuzzy optimization model reduces the computation cost ratio of the problem-solving process [17]. A fuzzy clustering technique-based optimization model is used to solve complex resource-constrained problems in a project. The fuzzy clustering technique uses a multi-patent crossover operator to detect the problems in a project. The fuzzy clustering technique reduces and increases the efficiency level in providing solutions for the problems [4,18].
The proposed resource-constrained reduction framework (RSRF) introduces a novel approach combining fuzzy clustering and GAs to optimize resource allocation in project scheduling. The key differences lie in the RSRF’s unique methodology and focus in handling heterogeneous resources through the fuzzy clustering and GAs. The necessity of the proposed method is crucial because the framework addresses the research gap identified in the literature by providing a comprehensive solution for heterogeneous resources, optimizing through fuzzy clustering, mitigating imbalanced solutions, dynamically adapting to constraints, and offering practical solutions for real-world application in different fields. In contrast, the existing references offered a broader perspective on resource-constrained project scheduling approaches.
The study innovates by introducing the RSRF, integrating GAs and fuzzy clustering. Key contributions include handling heterogeneous resources, precise constraint mitigation, dynamic adaptation to constraints, and real-world applicability. The RSRF addresses shortcomings by effectively handling resource constraints, preventing imbalanced solutions, mitigating various constraints, reducing resource replications in multi-objective network management scheduling, and providing optimization for practical challenges in cloud computing.
The contributions are:
Designing a resource-constrained reduction framework using genetic and fuzzy algorithm combinations for improving the allocation rate;
Identifying the maximum possible combinations of availability and allocations of the resources and thereby classifying the optimal solution from a set of genetic outputs;
Performing a comparative and data analysis for verifying the proposed framework’s efficiency irrespective of different constraints.
2 Related works
Wang et al. [19] proposed a delay-tolerant constrained online convex optimization (DTC-OCO) for long-term constraints. The main aim of the method is to solve the issues in network and resource allocation processes. The proposed DTC-OCO method identifies the exact reason for the constraints that provide relevant data for resource allocation. The proposed DTC-OCO method reduces the time-varying convex in the accumulation process.
Huang et al. [20] introduced an improved simplified swarm optimization (ISSO) based fuzzy constraint model. The introduced method is mostly used to solve the redundancy allocation problem (RAP) in projects. The RAP causes severe damage to the systems that leads to consuming huge amounts of energy to perform tasks. The ISSO method detects the severity range of RAP, which minimizes the latency in performing tasks. The ISSO method increases the sustainability and feasibility range of the systems. The introduced ISSO improves the accuracy of the RAP detection process.
Su et al. [21] developed a multi-objective evolutionary algorithm (MOEA) based model for the constraint handling process. The main aim of the model is to detect multi-objective testing resource allocation (MOTRA) problems. MOEA produces feasible information for a project manager that reduces the time consumption level in the detection process. The evolutionary algorithm creates a proper bond between tasks and resources. The developed MOEA model reduces the testing and computational cost level of the systems.
Liu et al. [22] proposed a heuristic optimization model for robust resource-constrained flexible project scheduling problems (RRCFPSP). The float weight optimization frame (FWOF) algorithm is used in the model which understands the necessity of the tasks. The FWOF algorithm identifies the duration that is required to perform a task in the project. When compared with other models, the proposed model solves the RRCFPSP, which is presented in a project.
Rauf et al. [23] designed a raccoon family optimization (RFO) algorithm-based integrated planning process. The main aim of the method is to identify the exact resource content that is required for the project. The designed method is also used for project scheduling processes that provide optimal scheduling service for multi-projects. The RFO algorithm enhances the performance level of the projects. The designed RFO-based method increases the effective range of the systems.
Shi et al. [24] proposed a boredom-aware dual-resource constrained flexible job shop scheduling problem. The proposed method is an investigation method that investigates the negativity range in the scheduling process. A particle swarm optimization (PSO) algorithm is implemented in the method that searches for the necessary details for the scheduling process. The proposed method is a two-stage problem-solving technique that solves the problems in the projects. The proposed method improves the flexibility and significance level of the systems.
Li et al. [25] developed a new exact approach for service network design problems with heterogeneous resource constraints (SNDHRC). The actual goal of the approach is to schedule the route to perform tasks in the systems. The exact approach minimizes the transportation cost ratio of the systems. The SNDHRC provides relevant services for the users that enhance the performance range of the systems. The developed exact approach increases the efficacy and feasibility range of the problem-solving process.
Liu et al. [26] introduced a bi-objective model for finance-based and resource-constrained robust project scheduling problems. A GA is used in the model to extract the important features for the optimization process. The GA reduces the finance-based scheduling problem in a project that maximizes the reliability level of the systems. The GA is mainly used here to evaluate the determinate range of the problems. The introduced model improves the overall robustness level of the projects.
Wang et al. [27] designed a new multi-subpopulation parallel computing genetic algorithm (MSPCGA) for the semiconductor packaging scheduling problem (SPSP). The actual goal of the algorithm is to schedule the task based on the resources. The SPSP causes various damages to the projects that reduce the quality level of the outcome. MSPCGA identifies the constraints that are presented in a project. The designed MSPCGA increases the effective range of the projects.
Ren et al. [28] introduced a branch and bound embedded GA for resource-constrained project scheduling problems. A linear mathematical model is used in the method that identifies the structure of the problems. The mathematical model provides optimal scheduling services for the projects. The introduced method reduces the time consumption in the problem-solving process. Experimental results show that the introduced algorithm maximizes the accuracy in solving the scheduling problems.
Pan et al. [29] proposed a dynamic resource allocation strategy for collaborative constraints. The actual goal of the strategy is to guide the resources to perform tasks in the systems. The dynamic allocation strategy provides optimal services for the users in the project development process. The proposed strategy also adjusts the evolutionary state of the project which improves the return on investment (ROI) level of the systems. The proposed strategy increases the accuracy range in the resource allocation process.
Gao et al. [30] designed a parallel test task scheduling method using constraint satisfaction. An artificial bee colony (ABC) algorithm is implemented in the method which tackles the problems. The ABC algorithm utilizes the sequence that is relevant to the scheduling process. The ABC minimizes the time consumption range in the evaluation process. The designed method maximizes the efficiency level in task scheduling and enhances the performance range of the systems.
Morin et al. [31] proposed a new project scheduling method to solve the problems in the projects. The proposed method is mostly used in periodic aggregated resource-constraints systems. The main aim of the method is to reduce the time-consuming range in the scheduling process. The exact number of nodes is detected, which minimizes the complexity level in the scheduling process. The proposed method improves the scalability and feasibility range of the systems.
Alipouri [32] introduced a resource flow branch and bound algorithm for fuzzy stochastic resource-constrained project scheduling problems. The introduced algorithm utilizes a search tree to construct a proper scheduling process for the systems. The developed algorithm solves the problems based on the functions. The introduced algorithm minimizes the makespan ratio of the project that provides high-quality service to the users.
Ali et al. [33] explored transfer learning in the machine learning concept to maximize performance while handling tasks in various applications like natural language processing, speech recognition, and computer vision. The main aim of this work is to reduce the data availability issues in task handling. The learning process minimizes the overfitting issues and maximizes the overall target task performance when compared to other methods.
Chai et al. [34] suggested an innovative approach for strategizing overtaking tactics in self-driving land vehicles. The method employs a desensitized trajectory optimization strategy with the goal of reducing the effects of uncertainties and fluctuations in the environment. The authors describe their findings, highlighting the efficacy of the suggested strategy in augmenting the resilience and flexibility of autonomous cars during overtaking scenarios. The study makes a valuable contribution to the field of autonomous vehicle planning by providing insights on how to effectively resolve uncertainties, hence enhancing the reliability and safety of vehicle movement.
Chai et al. [35] examined the utilization of deep neural networks for the automation of parking procedures. The study entails creating and executing a control system utilizing deep neural networks to improve the effectiveness and precision of the parking procedure. The research examines the technique, implementation specifics, and performance of the suggested control system that utilizes deep learning. The method enhances the progress of autonomous parking systems by utilizing the capabilities of deep neural networks to enhance maneuvering in parking situations.
Yaseen et al. [36] analyzed the advantages of artificial intelligence and machine learning ideas to optimize the boundaries of human and technology to enhance the communication. The influence of robots and non-linear systems predicts the resources opted for various classification purpose. Also, the research focused on various cutting-edge technologies in multi-disciplinary applications.
The analysis of the existing framework to solve problems in the genetic process was poor in segregating optimal, sub-optimal, and non-optimal solutions due to pervasive resource utilization and indefinite user/demand densities. To overcome this problem, the RSRF is tailored to improve resource allocation and availability based on the varying users and their demands observed from the genetic process. The resource-constrained reduction framework using a fuzzy clustering process is designed to improve the problem-addressing ability. In a conventional method, the proposed RSR framework is applied for segregating solutions to assist validated crossover mutation for utilizing multiple resources for varying user, demand, and problem densities to improve problem-addressing ability with less time. Instead, the fuzzy clustering process is performed to obtain the maximum solution segregating process for demand allocation. The integration of GAs with fuzzy clustering capitalizes on the advantages of both methodologies. GAs facilitate a comprehensive exploration of the most favorable solutions, whereas fuzzy clustering deals with the inherent uncertainties and complexity associated with resource allocation issues. This collaborative method enhances the development of stronger, flexible, and efficient resource allocation solutions in many fields, including project management, cloud computing, and network optimization. Table 1 discusses the main contributions, advantages, and disadvantages of the related works.
Contributions, advantages, and disadvantages of the related works
| References no. | Contributions | Advantages | Disadvantages |
|---|---|---|---|
| [19] | DTC-OCO for long-term constraints | Efficiently addressed feedback delays and time-varying constraints | Complexity and potential sensitivity to assumptions |
| [20] | ISSO method for RAP | The severity range of RAP was detected | Specific project characteristics need to be fine-tuned |
| [21] | MOEA model for MOTRA | Produced feasible information for the project manager | Does not scale well for large projects |
| [22] | FWOF for RRCFPSP | Necessary task duration was identified | Effectiveness depends on project complexity |
| [23] | RFO for the integrated planning process | Identified distinct resource constraints for various projects | Limited to particular project types |
| [24] | PSO for boredom-aware dual-resource constrained flexible job shop scheduling problem | Investigated negativity range in the scheduling process | Need parameter tuning for different projects |
| [25] | SNDHRC for route scheduling | Minimized transportation scheduling cost ratio | Need adjustments for different service network structures |
| [26] | GA for finance-based resource scheduling problem | Evaluated determinate range of problems | Effectiveness varies on project finance structures |
| [27] | MSPCGA for SPCP | Identified project scheduling constraints | Need customization for different packaging scenarios |
| [28] | Branch and bound GA for resource-constrained project scheduling problems. | Provided optimal scheduling services | Time consumption reduction was not significant |
| [29] | Dynamic resource allocation strategy for collaborative constraints | Improved accuracy and ROI | Required adaptability to changing project constraints |
| [30] | Parallel test task scheduling approach using ABC | Minimized time consumption | Different test scenarios need adjustment |
| [31] | Project scheduling method for periodic aggregated resource-constraints systems | Reduced time consumption in the scheduling process | Lack of adaptability for different scheduling scenarios |
| [32] | Resource flow branch and bound algorithm for fuzzy stochastic resource-constrained project scheduling | Proper utilization of search tree for scheduling | Complexity due to large scheduling problems |
| [33] | Transfer learning for handling tasks in various applications | Improved overall performance in distinct applications | Lack of sufficient data for transfer learning |
| [34] | Desensitized trajectory optimization for overtaking tactics in self-driving land vehicles | Reduced effect of uncertainties and fluctuations | Constraints may vary in different environments, and vehicle constraints |
| [35] | Deep neural networks for the automation of parking procedures | Improved precision and overall effectiveness | Large dependency on the availability and accuracy of models |
3 Data reference
Van Eynde and Vanhoucke [37] addressed the resource constraint problem in multi-objective project scheduling. In particular, a project with 24 instances with 720 activities under four global scheduling activities is utilized in this article for analysis. The optimal results for resource allocation and varying instances are presented in Figure 1(a) and (b).
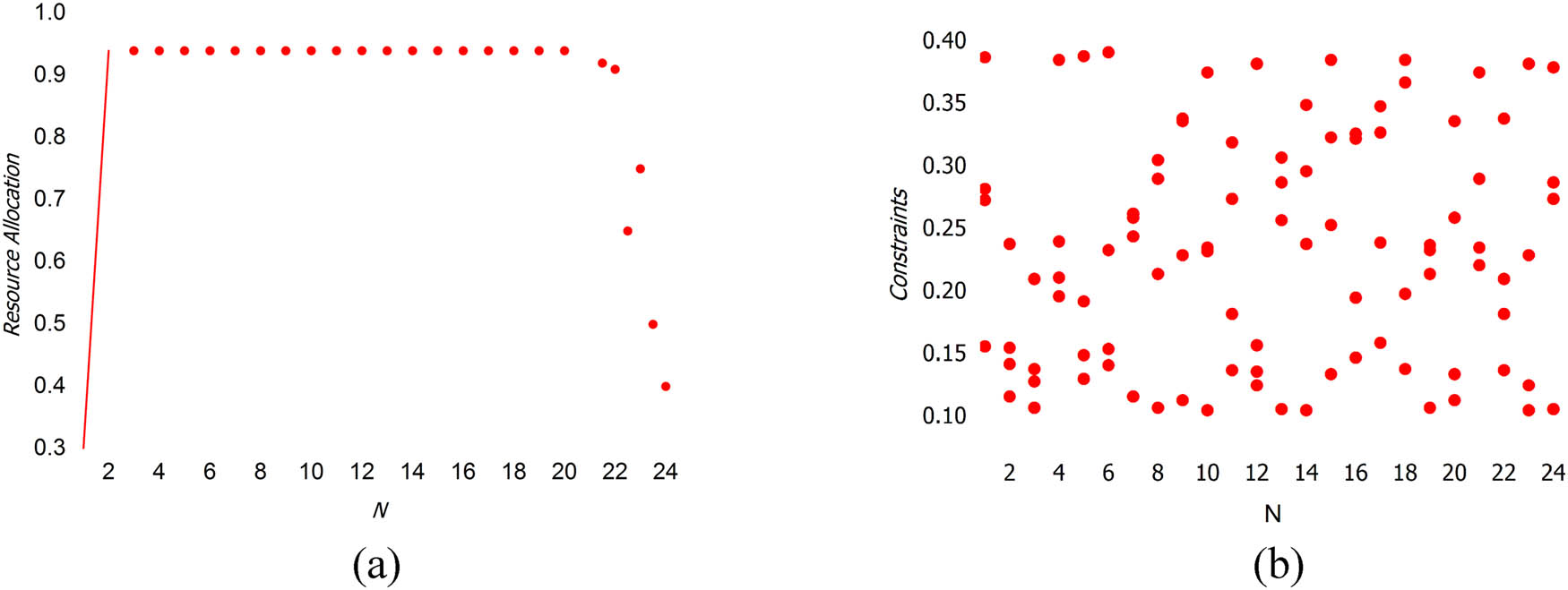
(a) Resource allocation and (b) constraints.
The representation in Figure 1 is the validated output for the above generated data. In this representation, the resource allocation distribution is optimal if the maximum constraints are satisfied in any instance
3.1 RSRF
Fuzzy clustering is applied in this proposed framework for improving resource allocation, constraint mitigation, and allocation time based on crossover mutation for precisely addressing the problems. An efficient resource allocation is indeed a crucial aspect in technology applications facing resource constraints and varying user demands. The proposed RSRF approach overcomes this challenge by integrating GAs and fuzzy clustering for optimizing the resource allocation, thereby ensuring that the available resources are utilized effectively during the accommodation of diverse user demands. Thus, the proposed framework requires better handling of heterogeneous resources to prevent replications. An illustration of the proposed framework is given in Figure 2.
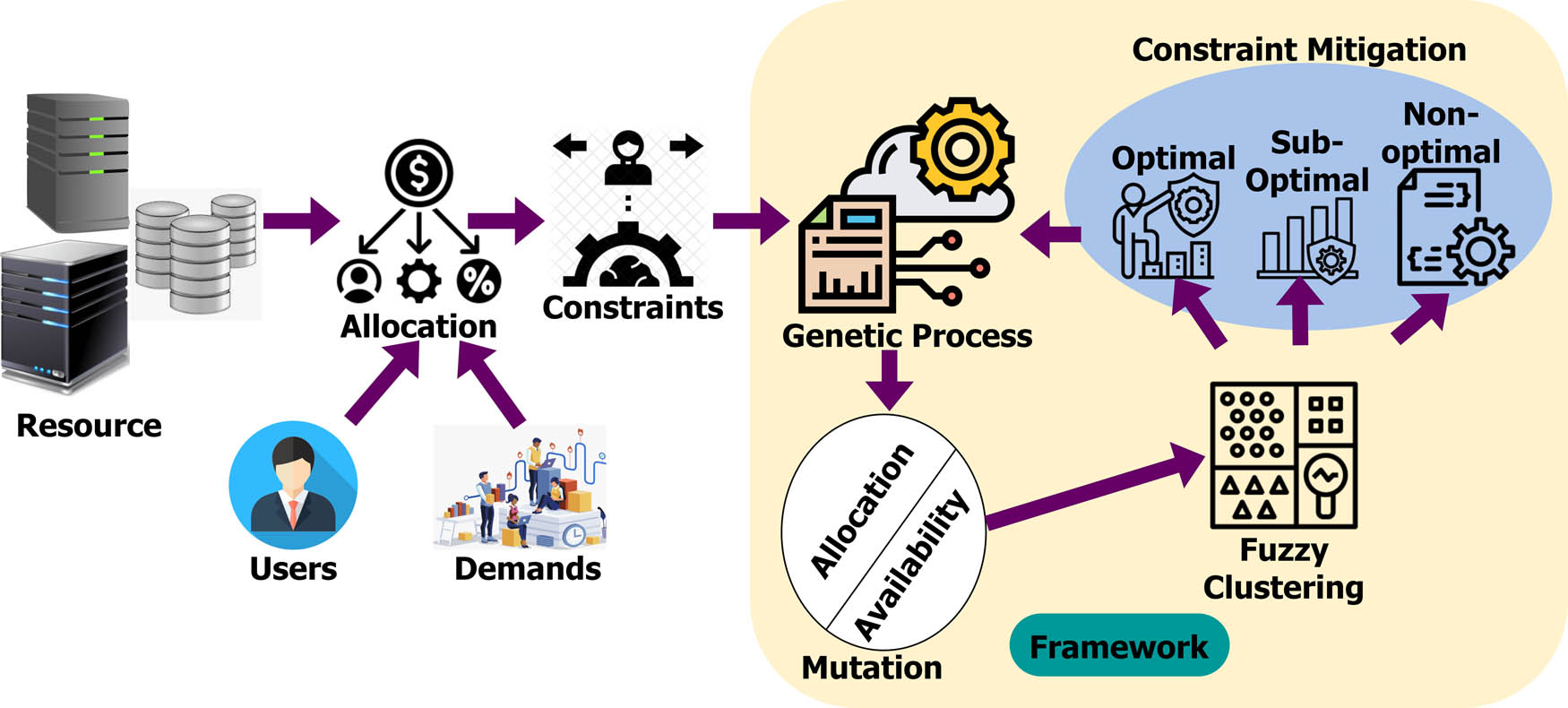
Illustration of the proposed framework.
The overall problems addressed with RSRF using fuzzy clustering are pursued for segregating solutions for retaining non-optimal solutions for mitigating the constraints with maximum demand allocation and allocation time. The RSRF-assisted fuzzy clustering process is applied in the genetic process to highly observe optimal and sub-optimal solutions based on the crossover features, preventing imbalanced solutions. The RSRF-assisted fuzzy clustering process first computes the resource allocation for varying users and requirements. Then, the process identifies different problems in the genetic process. This assists RSRF in using the fuzzy clustering process to improve the problem-addressing ability, and resource allocation is the tallying factor. The GA-assisted fuzzy clustering framework to solve resource-constrained project problems is briefly explained in Section 3.2.
3.2 Genetic process
The RSRF-assisted fuzzy clustering process exploits allocating the resources for varying users, and demand is a considered factor for constraint mitigation in the genetic process. The resources are utilized for allocation using RSRF-assisted fuzzy clustering to improve the addressing of issues mentioned above through optimization for reducing imbalanced solutions. The proposed framework determines the solution possibilities based on mutating the allocation and availability possibilities of the resources for different problems across various demands and users, and segregating solutions contrary to existing constraints is identified in the first level. Therefore, the various range of solutions is satisfied through optimization for segregating the solutions. In the second level, the crossover features are tailored based on a fuzzy clustering process across multiple resource allocations performed to reduce complexity and allocation time.
The study employed a fuzzy and adaptive learning clustering method to capture the progressive shift of data points between clusters accurately. The membership function employed a hybrid methodology, integrating Gaussian and triangular functions. It facilitated the seamless movement of data points and a more precise definition of boundaries, improving the clustering outcomes’ reliability. The clustering criteria focused on achieving both cluster compactness and separation. It was done by optimizing a multi-objective function to reduce the variation inside each cluster and maximize the separation between clusters. It promotes internal unity and clear groupings, making allocating resources more efficient. The study sought to improve their clustering method’s flexibility, precision, and resilience by integrating these distinctive components. With the help of resource allocation and availability, the RSRF computes the crossover mutation for varying users and demands from the genetic process. The proposed framework verifies multiple resource allocation for the instance is 1 to N If the constraint is true, then a genetic process is performed for constraint mitigation and crossover mutation computes using fuzzy clustering to address the issues. Otherwise, if the crossover feature is not tailored for resource allocation, then the RSRF-assisted fuzzy clustering process attains imbalanced solutions across various demands, preventing replications.
The study utilized the fuzzy C-means (FCM) algorithm as the chosen method for fuzzy clustering. The FCM algorithm is a widely recognized clustering method that assigns fuzzy membership values to data points, reflecting the extent to which each point belongs to each cluster. It enables the data to be divided into separate groups, where each data point can be a member of numerous clusters with different levels of affiliation. The FCM algorithm updates cluster centroids and membership values iteratively by minimizing the objective function quantifying the fuzzy partitioning quality. By iteratively improving cluster centroids and membership values, FCM can accurately represent the data’s fundamental organization and offer a versatile framework for clustering. The fuzzy clustering technique in this work employs the Gaussian membership function. The Gaussian membership function is commonly used in fuzzy clustering because of its smooth and symmetrical structure, enabling a gradual transition between cluster memberships. The function is characterized by its mean and standard deviation parameters, which determine the average and variability of the membership values, respectively. The Gaussian membership function offers an inherent method to represent the uncertainty in the clustering process, enabling a seamless and uninterrupted allocation of membership values to data points.
A GA comprising 50 population size as individuals has been employed in the research implementation to determine an acceptable balance between exploration and exploitation. To improve diversity of genes and convergence, 0.1 as mutation rate and 0.8 as crossover rate are considered as parameter settings. These ranges are used to generate new generations by exchanging from two distinct locations on the chromosome that were chosen at chance. Using a mutation approach that incorporates a mutation value that is created randomly from a Gaussian approach, the operator for mutation generated unpredictable modifications to genetic levels. By adjusting the operators of selection, crossover, and mutation, the GA opted for resource allocation with the goals of optimizing resource utilization, minimizing constraint violations, and minimizing the time for allocations.
Let us consider the available resources are represented as
where the variable
where the variables
By using equation (3), the outputs of resource allocation constraint are processed using a genetic process based on varying users and demands in different time intervals. The study employed a population size of 50 people to maintain a balance between the ability to explore and exploit while ensuring that the survey’s computational aspects were manageable. A crossover rate of 0.8 and a mutation rate of 0.1 were selected to enhance genetic diversity and convergence. The maximum number of iterations was set at 100 to ensure convergence. The selection of the cluster number and degree of fuzziness was made to achieve a compromise between the quality of the solution and the computational efficiency. The minimize-variance goal function was selected to optimize resource allocation and reduce the solution’s variability. The GA was executed utilizing selection methods. With the estimated genetic process, the proposed RSRF accurately identifies the issues through optimization that outputs an imbalanced solution. Solution segregation is performed for constraint mitigation to overcome this type of issue. The constraint mitigation process is briefly explained in Section 3.4.
3.3 Crossover mutation
After performing the genetic process, the RSRF-assisted fuzzy clustering process computes crossover mutation and mitigates the resource constraints. In this process, the required solutions are segregated, namely, optimal, sub-optimal, and non-optimal, based on the allocation and availability possibilities of the multiple resources computed by the proposed framework. This work employed a hybrid approach that combined fuzzy clustering results with objective function evaluations to categorize solutions into optimal, suboptimal, and non-optimal categories. Optimal solutions have high membership values in clusters corresponding to desirable features such as maximum resource usage, minimal constraint violations, and low allocation time. These solutions are the most optimal configurations determined by the optimization process. Suboptimal solutions refer to solutions with moderate membership values in clusters but demonstrate sufficient performance based on the objective function. Although suboptimal solutions are not as desired as optimal solutions, they provide acceptable performance and can be used as alternatives in some situations. Non-optimal solutions refer to solutions that have low membership values in clusters or significant deviations from ideal solution features. These solutions are considered suboptimal configurations and are unlikely to achieve the specified objectives and may need more modification or rejection.
Fuzzy clustering process shows the extent that eachpoint is a part of the individual cluster. The most optimal solutions identified by optimization technique with selected mutation rate are those with high values for membership in clusters that correlate to factors such as low allocation time, limited constraint violations, and maximum utilization of resources.
Even with suboptimal solutions, the objective function nevertheless finds them to be good in terms of efficiency, as they have moderate group membership levels and can be used as substitutes if needed. Contrarily, non-optimal solutions either have low cluster values for membership that differ greatly from the qualities of an ideal response solution. The adjustments to these solutions with this framework efficiently use objective function evaluation and fuzzy clustering to classify the optimal, suboptimal, or non-optimal solutions according to mutation rate. This allows for efficient allocation of resources and mitigation of constraints.
In this first level, the existing constraint takes maximum allocation time and results in imbalanced solutions. To compute level 1, the crossover mutation is estimated and the possibilities of the solution are tailored across various demands for reducing issues. Post this process, the required solutions are classified and carried out for constraint mitigation, continuously segregating solutions using RSRF. Sequential solution classification is performed based on utilizing the GA for mutating the allocation and availability possibilities to improve the resource allocation and allocation time as compared to the conventional method. In this proposed framework, both solution segregation and crossover mutation are performed. The crossover mutations are tailored to meet the maximum resource allocation and constraint mitigation from the genetic process using fuzzy clustering to reduce complexity.
The two-point crossover operator produces offspring from parent individuals by swapping genetic material between two randomly selected locations along the chromosome. It fosters biodiversity and safeguards genetic data. The mutation operator introduces random changes to gene values in the chromosome, following a predetermined mutation rate and employing a Gaussian mutation method. This process entails incorporating a randomly generated mutation value, drawn from a Gaussian distribution with a mean of zero and a modest standard deviation, to every gene. It enables detailed exploration of the solution space while minimizing the likelihood of significant disruptions to favorable solutions. The continuous constraint mitigation performed in this article is presented here.
The multiple resource allocation based on the constraint is computed in different instances as the sample input. The fuzzy clustering is performed with crossover mutation, resulting in less replication. Three types of solutions are utilized for constraint mitigation across varying users and demand through optimization. From that, the allocation and availability possibilities are expressed as follows:
where
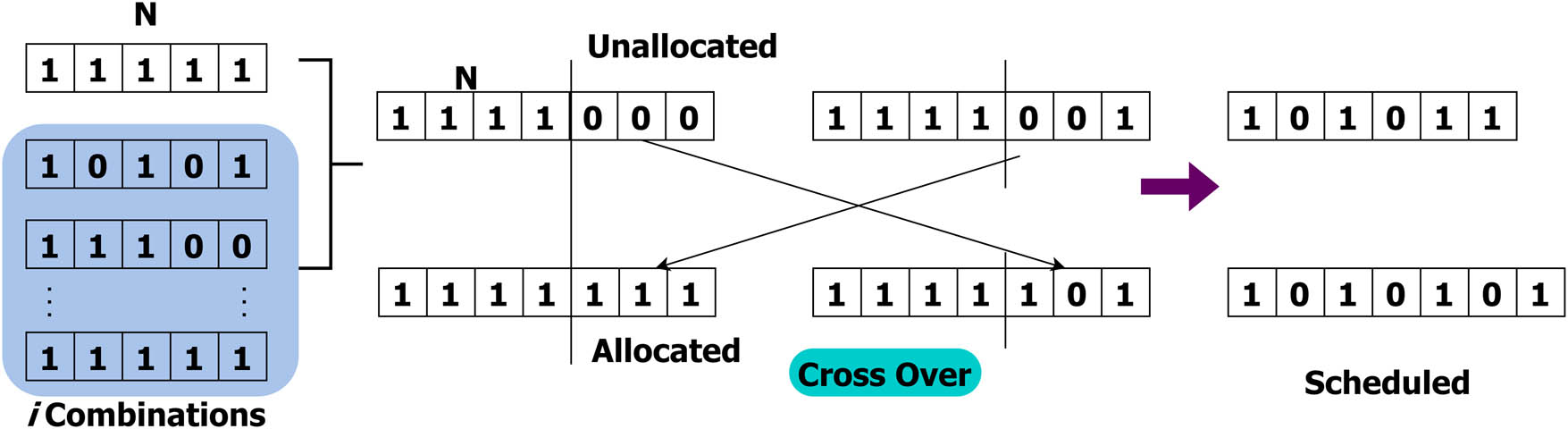
Genetic process illustration.
The study meticulously chose the population size to balance exploration and exploitation within the search space. A bigger population size allows for more extensive exploration of the solution space, but it also increases computational overhead. On the other hand, a smaller population size may reach a standard solution rapidly but runs the danger of reaching poor options too early. The study concluded, following experimentation, that a population size of 50 individuals achieved an optimal equilibrium between exploration and exploitation within the issue domain. This population size enables fast solution space exploration while maintaining variety to avoid premature convergence. The population is initialized using
where
where
and
In equations 7(a) and (b), where the variable
Equation (8) is used to mitigate the constraints to segregate the solutions based on optimal, sub-optimal, and non-optimal for reducing complexity. In this process, the arg max function is used for improving multiple resource allocations from the genetic process. The fuzzy clustering for the three solutions is illustrated in Figure 4.
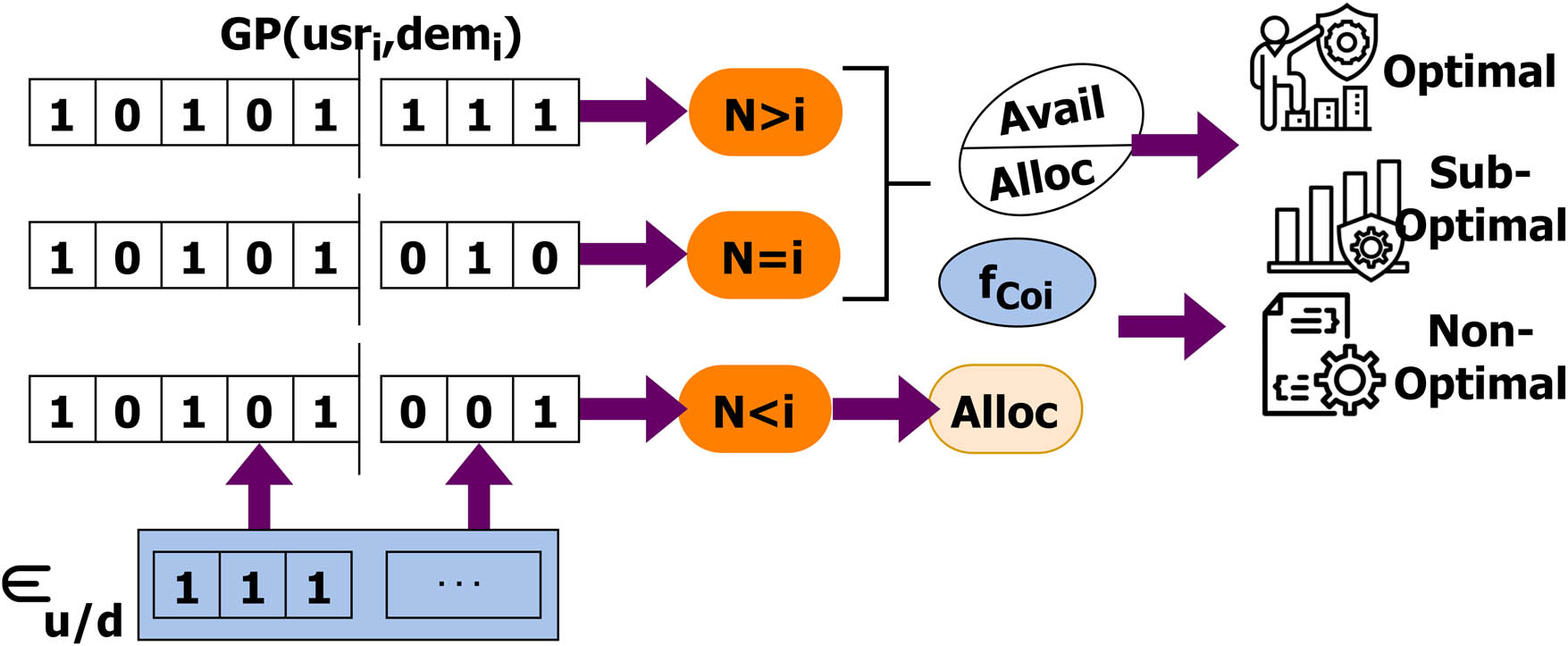
Fuzzy clustering for
The fuzzy clustering process intakes
where
3.4 Constraint mitigation
The objective function of this proposed framework is to mitigate resource constraints based on crossover mutation from the genetic process. The optimal, sub-optimal, and non-optimal solutions are segregated by fuzzy clustering to reduce resource-constraint and allocation time, respectively, then
such that
where the constraint
Equation (12) identifies the allocation and availability possibilities of the resources for the control of different problems in a genetic process using fuzzy clustering. It is used to maximize the mutation rate with
such that
Equations (13) and (14) are used to segregate solutions for continuous resource allocation until a non-optimal solution is identified from the fuzzy clustering process. The fitness function was devised to assess the merit of each solution in the population by measuring its effectiveness in solving the resource allocation problem. The fitness function considered several objectives: minimizing resource duplication, maximizing resource usage, addressing restrictions, and decreasing allocation time. The objectives were assigned weights based on their importance in the optimization problem. This work employed a hybrid fitness function that integrated fuzzy clustering into the fitness evaluation process. The clustering findings were used to assign fuzzy membership values to each solution. It enables the incorporation of the inherent uncertainty in the resource allocation problem and facilitates the generation of more informed judgments throughout the optimization process. The fuzzy clustering classifies the solutions based on the mutation rate until non-optimal solutions are detected from the instances. In this process, the resource constraint concerning availability and allocation possibility from the instances is to improve constraint-less allocation. Besides, the constraint mitigation is to be instantaneous to meet the maximum resource allocation and constraint mitigation. The proposed framework’s main aim is to satisfy constraint-less resource allocation through fuzzy clustering, thereby reducing allocation time. The constraint mitigation sequence based on equation (4) is analyzed in Table 2.
Constraint mitigation sequence
| Conditions |
|
|
|
|
|
||||
|---|---|---|---|---|---|---|---|---|---|
| 2 | 3 | 4 |
|
|
|
||||
|
|
1 | 0 | 11 | 110 | 1,110 | 0 | 0.79 | 0.82 | 0.85 |
| 0 | 1 | 11 | 101 | 1,011 | 0 | 0.85 | 0.89 | 0.91 | |
| 1 | 1 | 11 | — | 1,101 | 0 | 0.81 | 0.92 | 0.94 | |
|
|
1 | 0 | 10 | 10 | 1,100 | 1 | 0.52 | 0.63 | 0.71 |
| 0 | 1 | 01 | 0 | 1,001 | 1 | 0.58 | 0.69 | 0.72 | |
| 1 | 1 | — | 1 | 1,010 | 1 | 0.61 | 0.71 | 0.73 | |
|
|
1 | 0 | 0 | 100 | 1,000 | 3 | 0.19 | 0.24 | 0.32 |
| 0 | 1 | 0 | — | — | 3 | 0.26 | 0.32 | 0.46 | |
| 1 | 1 | 0 | — | — | 3 | 0.31 | 0.42 | 0.46 | |
In Table 2, the outputs for

(a)
The intermediate
(a)
The above analysis is presented based on
Actual and mitigated
| Conditions |
|
|
|
|
|
|---|---|---|---|---|---|
|
|
0.4 | 0.6 | 14 | 0.92 | 10 |
| 0.6 | 0.65 | 12 | 0.852 | 8 | |
| 0.8 | 0.71 | 13 | 0.82 | 6 | |
|
|
0.4 | 0.78 | 10 | 0.85 | 7 |
| 0.6 | 0.81 | 8 | 0.74 | 5 | |
| 0.8 | 0.85 | 9 | 0.82 | 6 | |
|
|
0.4 | 0.86 | 5 | 0.65 | 4 |
| 0.6 | 0.87 | 4 | 0.57 | 3 | |
| 0.8 | 0.91 | 3 | 0.74 | 3 |
In Table 3, the actual
The proposed algorithm is evaluated both with and without model uncertainty. In the absence of uncertainty, it efficiently allocates resources and mitigates constraints. When uncertainty is introduced, the algorithm adapts well, showcasing resilience in optimizing resource allocation under dynamic and unpredictable conditions. The proposed technique is well-suited for practical use in a variety of settings due to its ability to effectively manage uncertainties through the combination of GAs and fuzzy clustering.
Under the influence of model uncertainty, the algorithm consistently demonstrates its ability to optimize resource allocation and effectively mitigate constraints dynamically. The algorithm’s robustness is demonstrated under model uncertainty, showcasing its adaptability and consistent optimization of resource allocation. The detailed analysis emphasizes its resilience and effectiveness in handling diverse uncertainties, making it suitable for dynamic real-world scenarios with changing resource requirements. The comprehensive assessment underscores the algorithm’s suitability and effectiveness across a spectrum of conditions, affirming its practical applicability in dynamic and uncertain resource allocation environments.
The targeted technology applications include resource allocation in cloud computing for dynamic machine allocation and optimization. Also, in network resource management, reduces constraint violations and maximizes the network allocation efficiency. The resource allocation problems RSRF designed for cloud computing and task scheduling in distributed systems can be applied for dynamic optimization of allocating the machines, routing the allocated process, mitigating the latency, and optimizing the utilization of bandwidth.
4 Performance assessment
The performance assessment is validated using the problem-addressing ability, resource allocation, constraint mitigation, allocation time, and constraint failure metrics. The number of constraints and the demand factor are alone varied in this analysis. For an effective assessment, the methods SNDHRC [25], RAP-ISSO [20], and RS-ABC [30] are used in this comparative analysis. During the implementation, GA uses the 50 individuals (population size), 0.8 as cross rate (probability of crossover between individuals), 0.1 as mutation rate, maximum generation is 100, dynamically selected cluster number (assume c = 3), degree of fuzziness is 2, Gaussian membership function, minimize-variance as objective function and 0.001 as utilized as tolerance while utilizing the fuzzy clustering.
The proposed RSRF performance evaluation methodology includes sensitivity analysis to investigate the way distinct GA and fuzzy clustering settings influenced the outcome of the study. This investigation shed light on the effects of changing these parameters on the implemented performance over other existing works like SNDHRC [25]; RAP-ISSO [20], and RS-ABC [30] are used in this comparative analysis.
The assessment procedure was greatly aided by benchmark datasets with scenarios of real-world resource distribution when resources are constrained in a predefined manner while utilizing the fuzzy clustering. The included dataset covered a broad range of problem challenges and limits, making sure the framework’s capabilities were thoroughly tested.
Utilizing predetermined indicators and metrics, the metrics evaluated are ability of addressing the problems, allocation efficiency, mitigating constraints, allocation time, and failure of constraints. The capacity of the framework to successfully handle various problem situations was used to evaluate problem-solving skills. The ideal deployment of resources and the minimization of resource loss were used to evaluate the efficiency of the utilization of resources.
The effectiveness of the framework in identifying and resolving limitations was evaluated by the minimal effect they had on the process of optimization. The time needed to allocate resources was measured by allocation time, an important parameter for applications that run in real time. In situations requiring decisions, reduced allocation duration is indicative of better performance. In order to measure the overall success of the framework, we also quantified constraint failure, which is the number of failures to meet the limits on resource distribution.
The study performed a comparative analysis to evaluate the effectiveness of the suggested RSRF framework compared to established approaches, specifically SNDHRC, RAP-ISSO, and RS-ABC. The assessment was conducted using a predefined set of indicators to gauge different facets of performance, such as problem-solving capability, resource distribution, constraint management, allocation duration, and constraint noncompliance. The framework’s performance may be evaluated by considering crucial metrics such as problem-solving abilities, resource allocation efficiency, ability to mitigate constraints, allocation time, and metrics related to constraint failure. Greater levels imply superior problem-solving capabilities, whereas higher values suggest effective resource usage. The framework’s capacity to alleviate limitations during the optimization process is also vital. Allocation time is a metric that quantifies the duration needed for resource allocation. A lower allocation time suggests superior performance for real-time applications. Constraint failures indicate a lower number of violations, which means improved performance. The study utilized benchmark datasets that accurately represented real-life situations with limited resources to conduct a thorough assessment. These datasets were selected meticulously to encompass a broad spectrum of problem difficulties and restrictions. The benchmark datasets comprised synthetic datasets created to replicate different resource allocation scenarios and real-world information acquired from pertinent literature or industry sources. The framework’s performance was thoroughly assessed under diverse settings by characterizing each dataset with unique restrictions, including resource availability, demand variables, and problem densities.
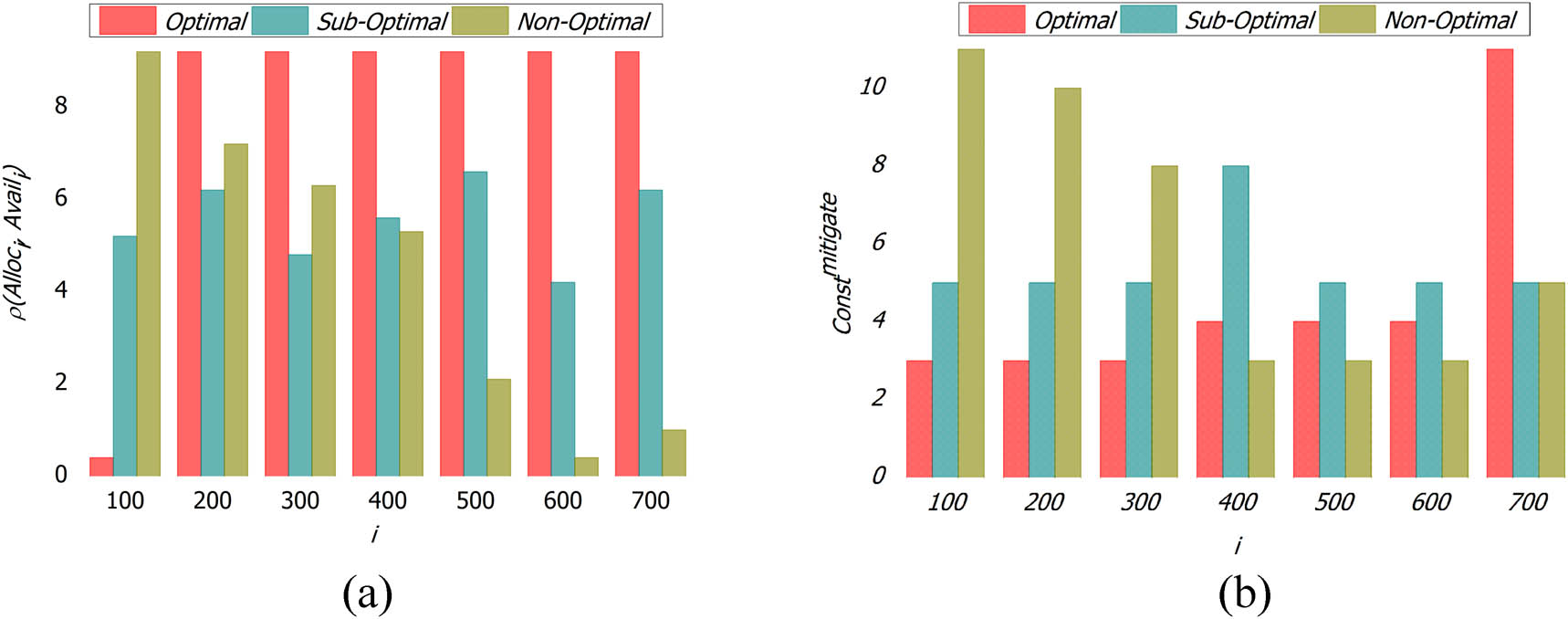
4.1 Problem-addressing ability
In Figure 7(a) and (b), the resource allocation constraint problems are addressed through optimizations and GAs across varying users, and demands for preventing replications are to improve the problem-addressing ability. The solution possibilities are observed from the genetic process for mutating the allocation and availability of the resources leads to different problems. To overcome this issue, fuzzy clustering process is performed. The different problems are addressed at the time of solution segregation for improving the multiple resource allocation instances in technology-based applications/services. Depending upon the availability and allocation possibilities, fuzzy clustering segregates the optimal, sub-optimal, and non-optimal solutions from the genetic process at different time intervals. The fuzzy clustering segregates the solutions based on varying users, and they demand to enhance the constraint mitigation. This problem-addressing ability in the GA-assisted fuzzy clustering process is prominent in identifying constraint failure, wherein the resource-constrained problems are due to pervasive utilization and in-definite user/demand densities. This crossover mutation is computed using fuzzy clustering to satisfy high problem-addressing ability as compared to the other factors.
(a) Problem-addressing ability w. r. t. Constraints; (b) Problem-addressing ability w. r. t. Demand Factor.
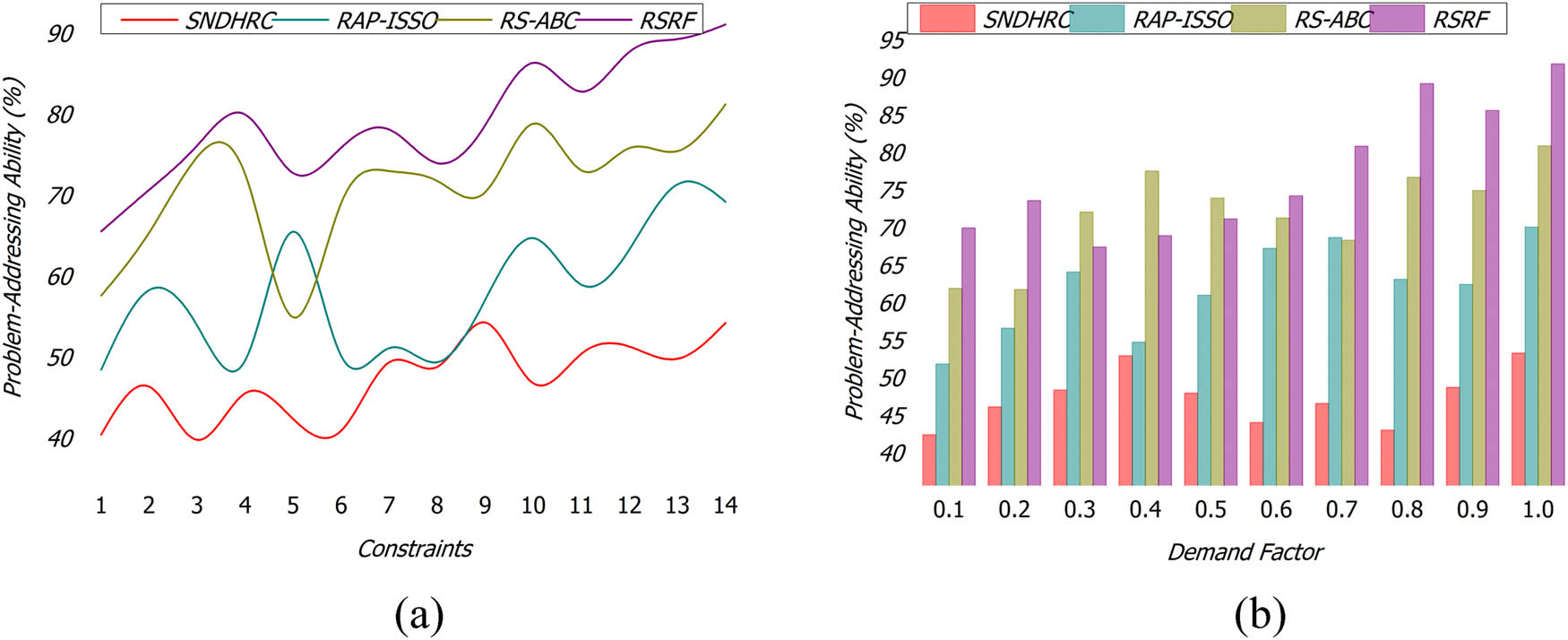
4.2 Resource allocation
This proposed framework achieves high resource allocation across varying users and demands with allocation constraints; the failures are mitigated by filtering fuzzy clustering solutions from the genetic process (Figure 8(a) and (b)). The input users and demands may vary, that is addressed for modifying the constraint through proposed RSRF and fuzzy clustering of the resources, where the maximum constraint failure is identified. Based on the availability and allocation possibilities, the difference between the crossover features is analyzed; the solution possibilities are tailored, and complexity is reduced. The fuzzy clustering first classifies the solutions for performing possible resource allocation with less allocation time. The replication is addressed for varying demand, user, and problem densities using a clustering process, preventing imbalanced solutions. Therefore, the fuzzy clustering process is pursued to improve the multiple resource allocation for varying demands and user densities at different time intervals. Therefore, this process satisfies maximum resource allocation using constraints. In this proposed framework, the imbalanced solutions are retained with fuzzy clustering in an independent manner without modifying the genetic process to reduce complexity.
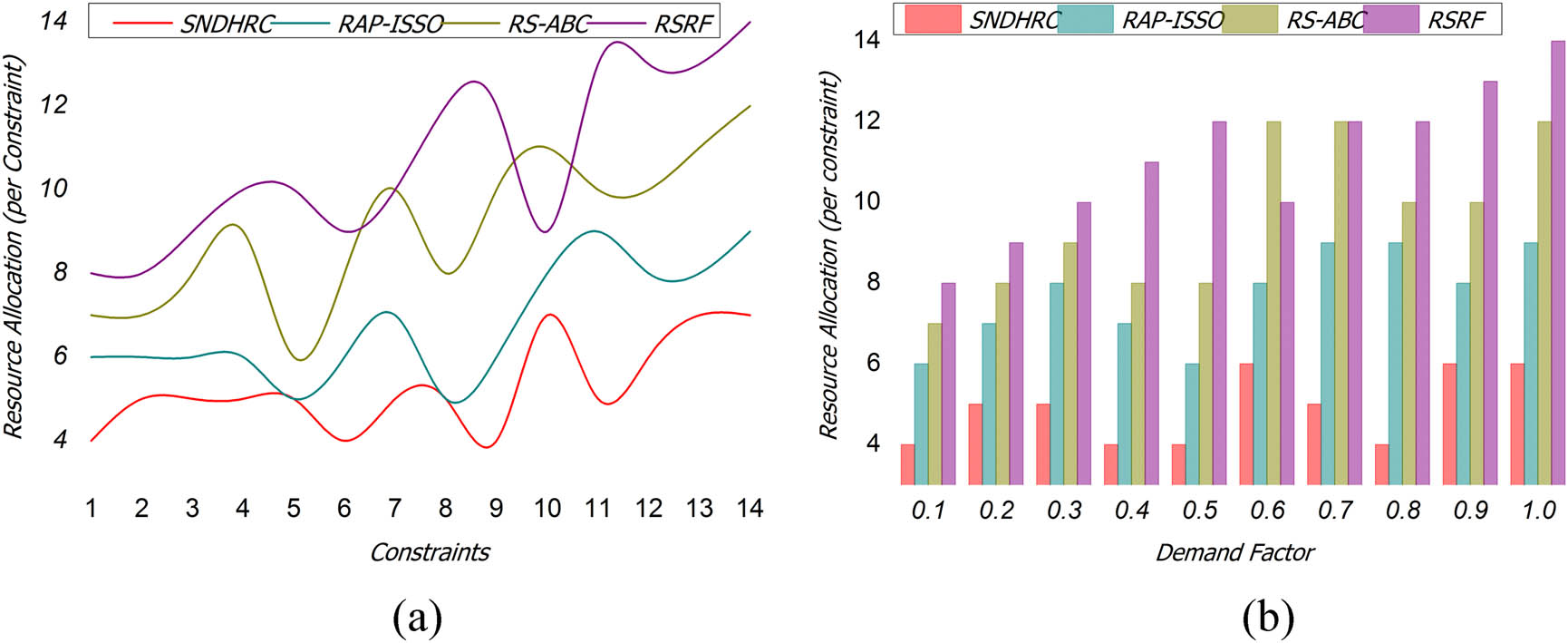
(a) Resource Allocation w. r. t. Constraints; (b) Resource Allocation w. r. t. Demand Factor.
4.3 Constraint mitigation
The multiple resource allocation sequences are performed to address minimum or maximum allocation time across varying demands using fuzzy clustering. The addressing of imbalanced solutions from the genetic process is difficult to identify constraint failures and it reduces complexity by handling heterogeneous resources for different users, demands, and problem densities. The resource availability and allocation complexities reduced using the crossover mutation solution. The failures were mitigated using resource-constrained processes at the time of continuous resource allocation; this failure occurrence is identified through fuzzy clustering. From the crossover features in the genetic process, the varying user demands and problem densities are correlated for addressing the replications. The multiple resource allocation is performed with constraints for improving allocation time. In this proposed framework, fuzzy clustering is segregated for achieving maximum constraint mitigation, as illustrated in Figure 9(a) and (b).
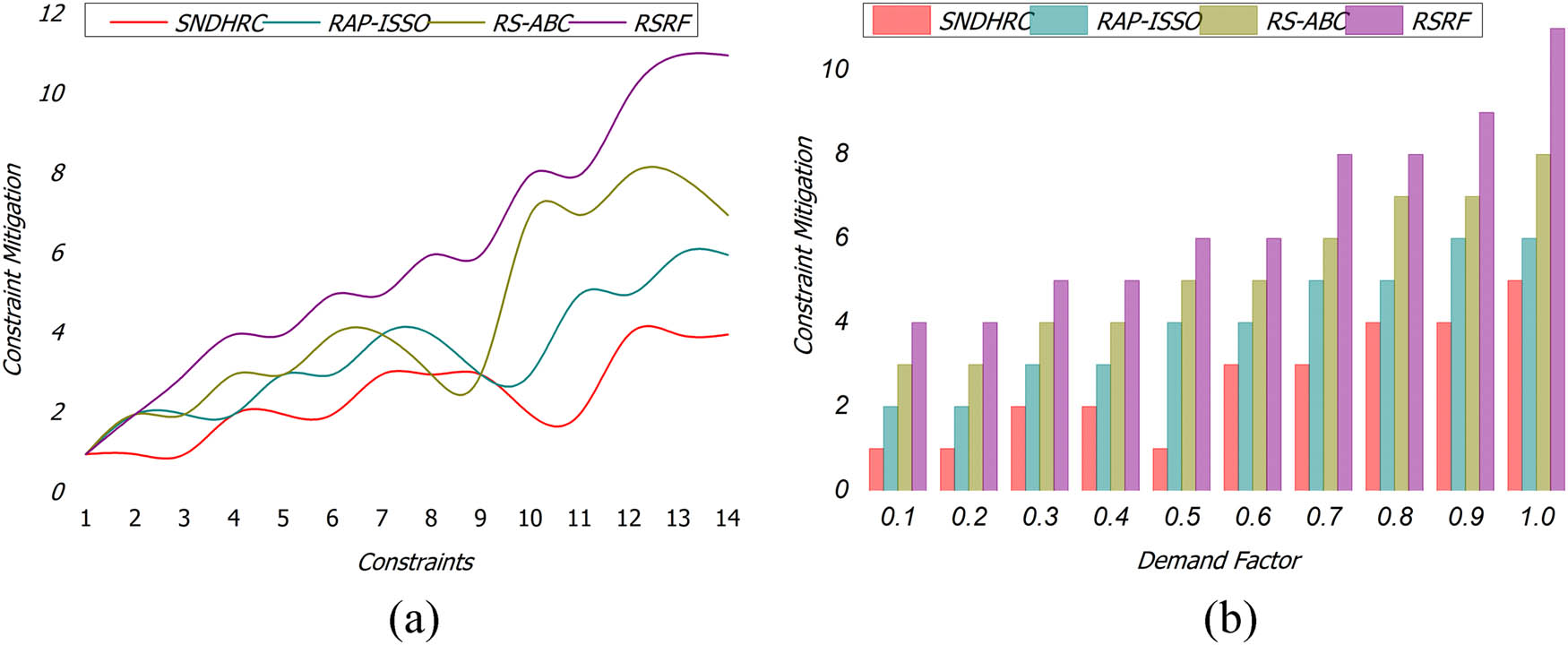
(a) Constraint Mitigation w. r. t. Constraints; (b) Constraint Mitigation w. r. t. Demand Factor.
4.4 Allocation time
This proposed RSRF-assisted fuzzy clustering process used for addressing the different problems in the genetic process with precise constraints satisfies less resource allocation time compared to the other factors, as represented in Figure 10(a) and (b). The constraint-less allocation is achieved for identifying the imbalanced solutions using fuzzy clustering. In contrast, the non-optimal solutions are observed for reducing time. This process performs sequentially until identifying the non-optimal solutions from the fuzzy clustering process. Based on the crossover mutation validation, the extracted features and available resources are processed for improving constraint mitigation. The constraints are mitigated through solutions and possibilities identification from the genetic process of the resources. It is difficult to identify imbalanced solutions for varying users and demands. In this framework, multiple resource allocation constraints are required to reduce allocation time. Thus, the proposed framework estimates fuzzy clustering across varying demands with less constraint failure.
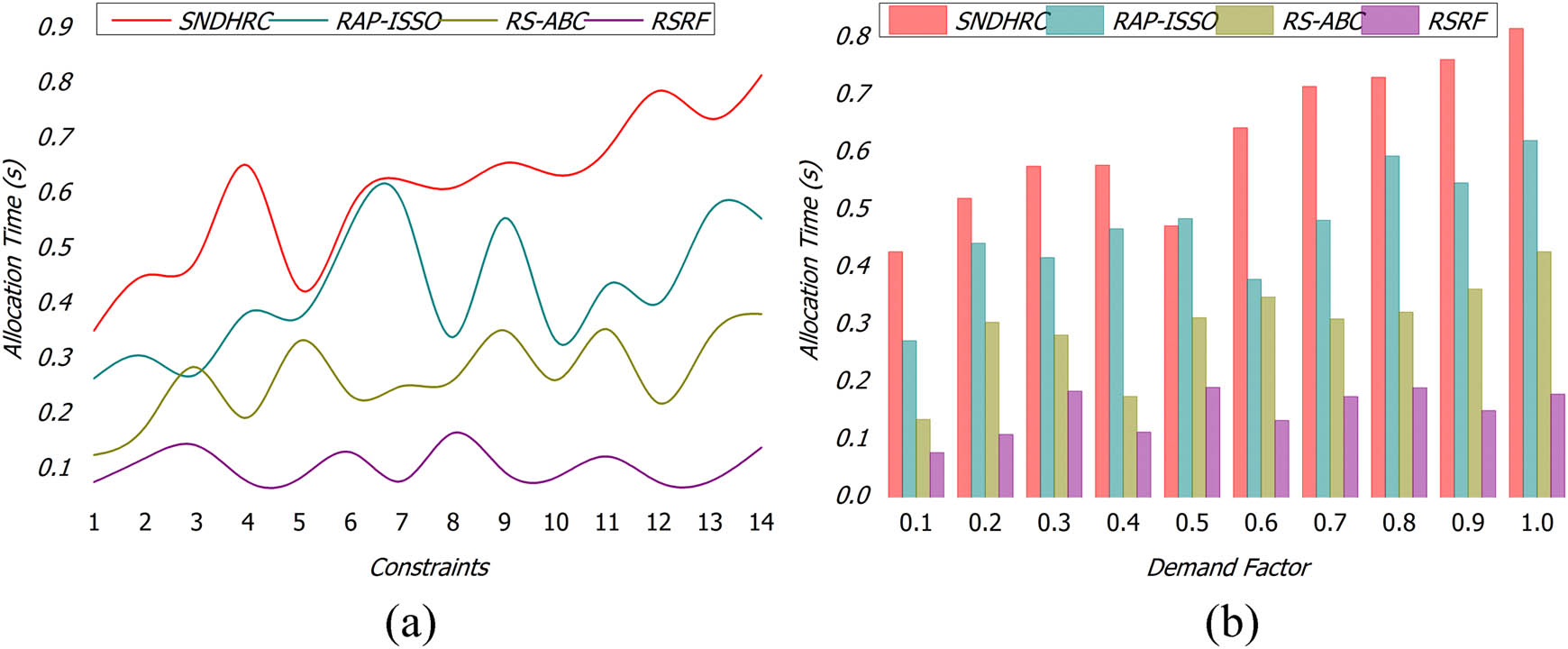
(a) Allocation Time w. r. t. Constraints; (b) Allocation Time w. r. t. Demand Factor.
4.5 Constraint failure
In this proposed fuzzy clustering-based solution segregation for varying users, demands, and problem densities to identify the minimum/maximum resource constrained based on the availability and allocation possibilities is computed for retaining imbalanced solutions (Figure 11(a) and (b)). This process improving multiple resource allocation and constraint mitigation using fuzzy clustering does not mitigate the pervasive utilization and in-definite user/demand densities. The high problem-addressing ability is achieved for varying users and demands of the resources. This constraint mitigation is performed across multiple resource allocation instances, and hence, the solution segregation is increased based on the mutation rate from the genetic process. The proposed framework utilizing both optimal and sub-optimal solutions helps to improve multiple resource allocation, constraint mitigation, and allocation time. In this manner, the constraint-less allocation is satisfied by the proposed framework, whereas the maximum constraint mitigation leads to improved multiple resource allocation with less time. Hence, less allocation time is achieved using fuzzy clustering and RSRF.
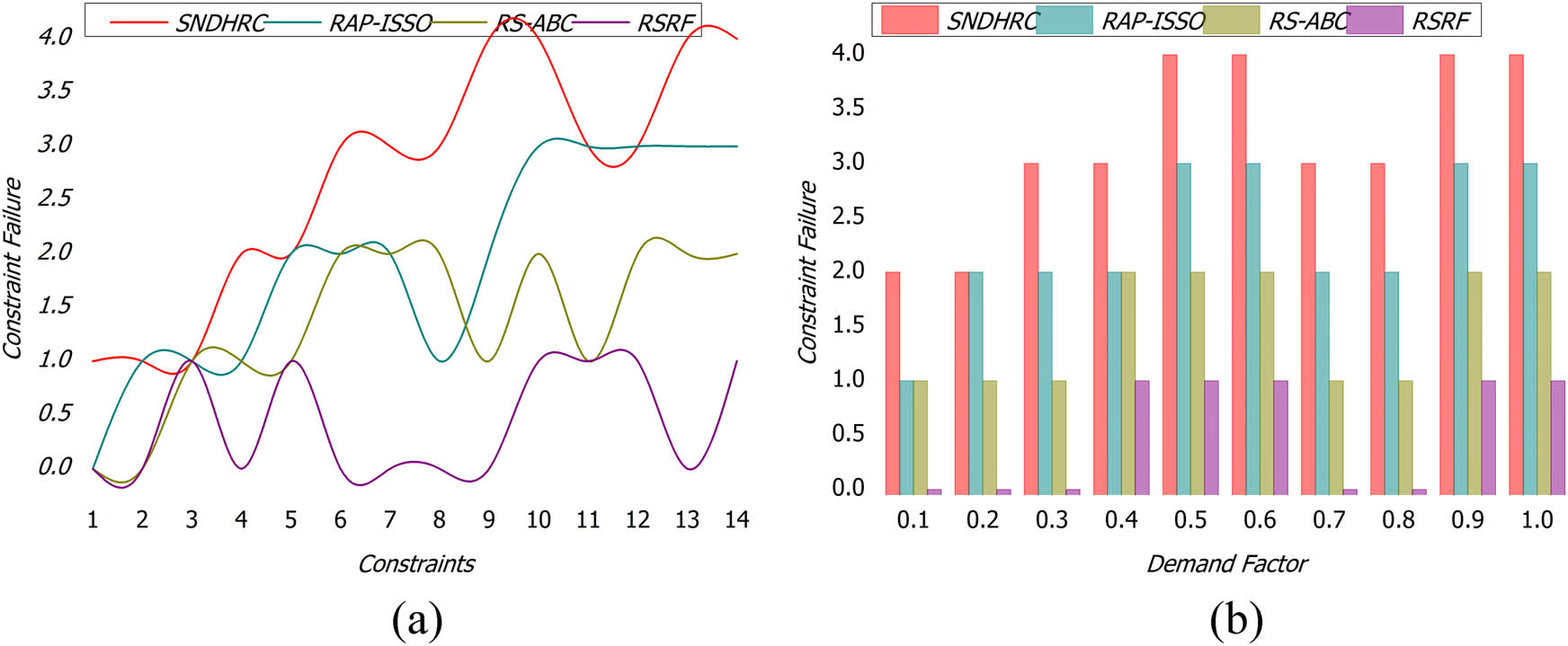
(a) Constraint Failure w. r. t. Constraints; (b) Constraint Failure w. r. t. Demand Factor.
4.6 Sensitivity analysis
The sensitivity analysis is performed to evaluate the impact of varying parameter settings of the GA, including population size and crossover rate, using the metric resource allocation efficiency. For various population sizes, the resource allocation indicator is tested and shows gradual changes in resource distribution as the population grows. By changing the GA’s population size, we can see how it affects the distribution of resources (y-axis). Varieties in population size are depicted on the x-axis. Finding the ideal values for the parameters that maximize the efficiency of resource allocation is the objective of sensitivity analysis.
One important metric for evaluating the algorithm’s resource utilization across a range of population size and crossover rate with the values 0.6–1.0 as parameter values is the resource allocation efficiency, which can be as high as 50, as shown in Figure 12(a) and (b). Likewise, the parameters of fuzzy clustering algorithm such as number of clusters and degree of fuzziness are evaluated using sensitivity analysis to prove the performance of the proposed framework, as shown in Figure 13(a) and (b).
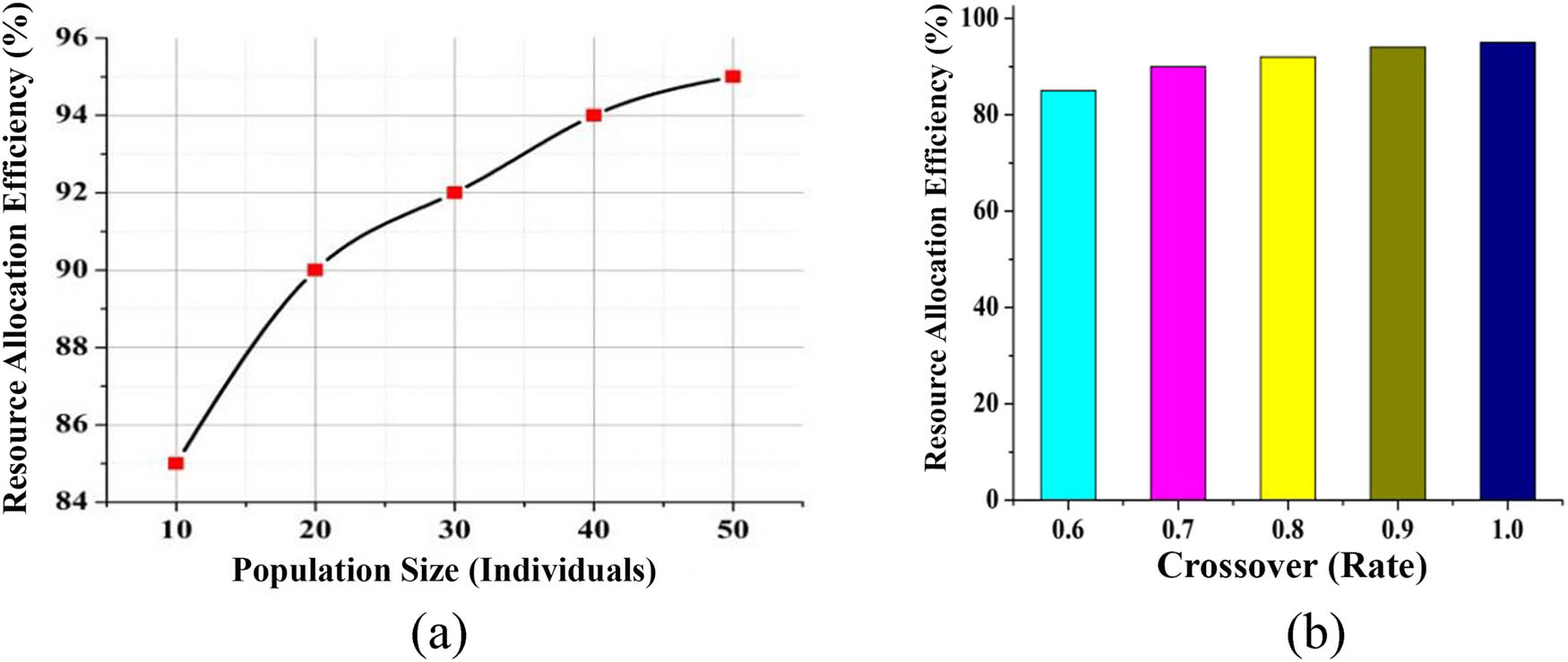
(a) Sensitivity analysis on GA parameters w.r.t. Population Size; (b) Sensitivity analysis on GA parameters w.r.t. Crossover.
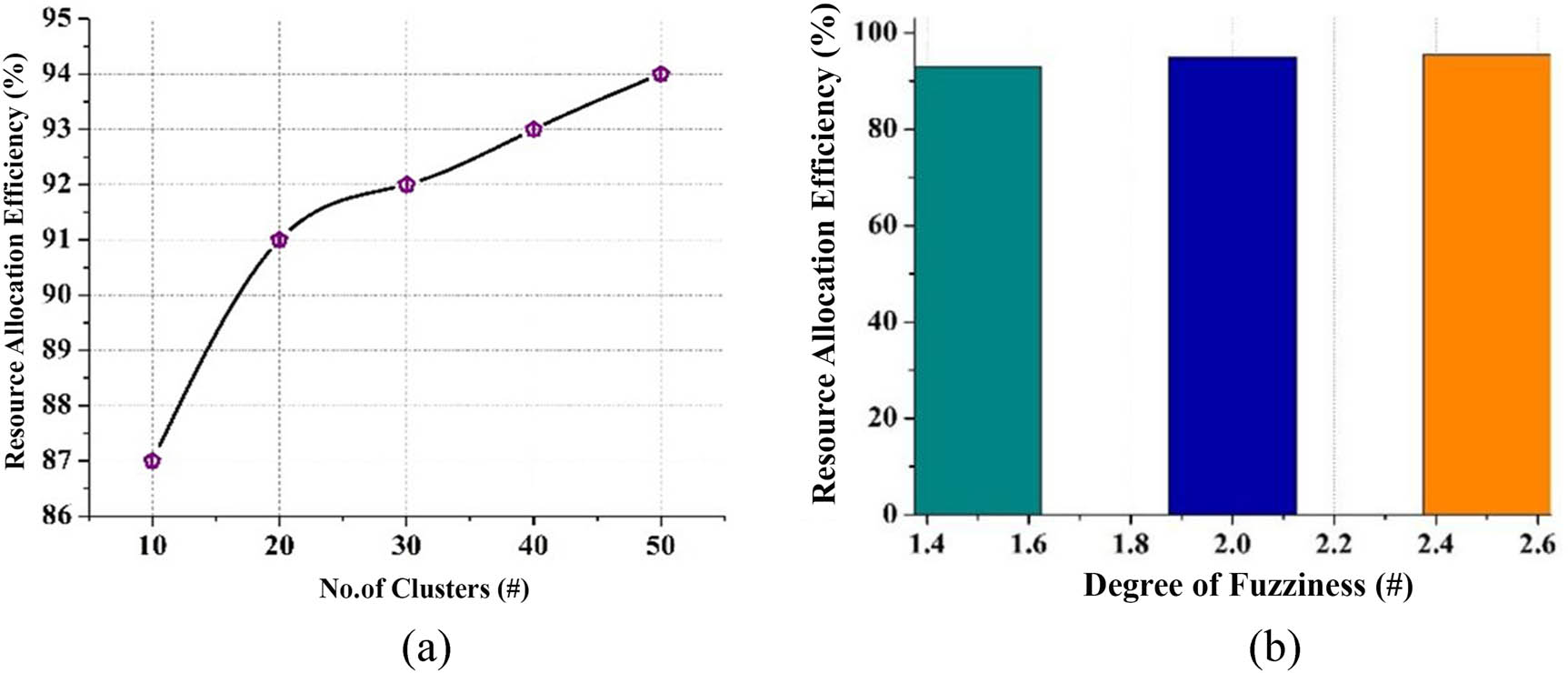
(a) Sensitivity analysis on fuzzy clustering algorithm parameters w.r.t. No.of Clusters; (b) Sensitivity analysis on fuzzy clustering algorithm parameters w.r.t. Degree of Fuzziness.
Sensitivity analysis is carried out by repeating the process with different values for the RSRF framework parameters to improve the generalizability of the framework. The effect of parameter modifications on performance across different problem cases can be better understood in this way.
The experimental evaluation is extended with the consideration of different fields like wireless sensor network (WSN) resource components analyzed by Huang et al. [20] that include cost and weight constraints under uncertain environments consisting of 14 subsystems in the network environment. The assessment includes cost and weight constraint variations comparison of benchmark schemes with the proposed algorithm. The proposed RSRF showed that the performance on both constraints is high in contrast to other works. Figure 14(a) and (b) illustrate the performance evaluation of constraint mitigation on two factors. This scenario of WSN demonstrates that the performance of the proposed framework in this domain is high and proves the generalizability of the framework by implementing it in diverse fields. Other than this, the generalizability of the framework is demonstrated by implementing the sensitivity analysis with the impact of varying parameters of the GAs and fuzzy clustering.
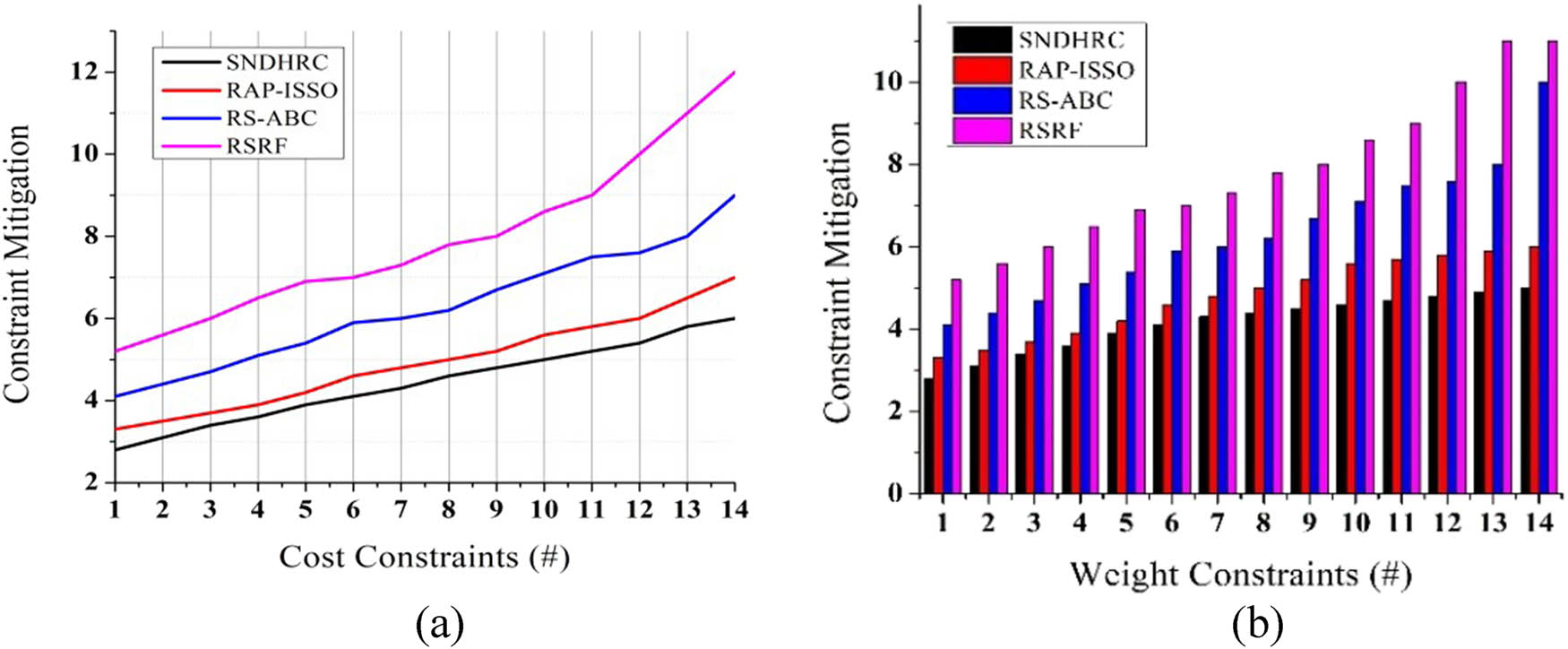
Constraint mitigation on (a) cost factor and (b) weight factor.
Tables 4 and 5 present the comparative analysis results for varying constraints and demand factors.
Comparative analysis result for varying constraints
| Metrics | SNDHRC | RAP-ISSO | RS-ABC | RSRF | Improvements |
|---|---|---|---|---|---|
| Problem-addressing ability (%) | 54.56 | 69.54 | 81.55 | 91.421 | 11.44% High |
| Resource allocation (per constraint) | 7 | 9 | 12 | 14 | 11.1% High |
| Constraint mitigation | 4 | 6 | 7 | 11 | 8.08% High |
| Allocation time (s) | 0.816 | 0.556 | 0.383 | 0.1403 | 12.67% Less |
| Constraint failure | 4 | 3 | 2 | 1 | 11.1% Less |
Comparative analysis result for varying demand factor
| Metrics | SNDHRC | RAP-ISSO | RS-ABC | RSRF | Improvements |
|---|---|---|---|---|---|
| Problem-addressing ability (%) | 53.63 | 70.41 | 81.22 | 92.146 | 11.86% High |
| Resource allocation (per constraint) | 6 | 9 | 12 | 14 | 11.9% High |
| Constraint mitigation | 5 | 6 | 8 | 11 | 7.07% High |
| Allocation time (s) | 0.817 | 0.622 | 0.428 | 0.1801 | 11.85% Less |
| Constraint failure | 4 | 3 | 2 | 1 | 11.1% Less |
The proposed RSRF introduces several innovations and improvements compared to the design methods mentioned in the references SNDHRC, RAP-ISSO, and RS-ABC. The key differentiations are: Unlike the methods SNDHRC [25], RAP-ISSO [20], and RS-ABC [30], the proposed RSRF combines the global search capabilities of GAs with the uncertainty management of fuzzy clustering, providing a resilient methodology. The RSRF exhibits a superior problem-addressing ability, addressing resource allocation constraint problems effectively through optimizations and GAs. Comparatively, the existing references lack the same level of adaptability and precision in addressing diverse problems in resource allocation scenarios. Also, this method faces challenges in achieving comparable resource allocation efficiency, especially in dynamic and complex scenarios; rather, the proposed approach mitigates failures and achieves high resource allocation efficiency. RSRF introduces a constraint mitigation sequence using fuzzy clustering to improve allocation time by identifying optimal, sub-optimal, and non-optimal solutions compared to existing methods. Fuzzy clustering helps RSRF separate solutions and improves numerous resource allocations, which in turn minimizes constraint failures. The existing approaches fall short in their attempt to minimize constraint failures because they are not as thorough as the proposed solution. The RSRF framework offers a comprehensive and flexible approach to resource allocation by combining GAs with fuzzy clustering. The innovation lies in its ability to address diverse problems, enhance resource allocation efficiency, mitigate constraints effectively, reduce allocation time, and minimal constraint failures in comparison to existing design methods.
5 Conclusion
In this article, the study presents a novel framework that effectively tackles resource-constrained challenges in genetic processes by integrating GAs and fuzzy clustering. The proposed approach exhibits significant improvements, including 11.44% boost in the problem-addressing ability, 8.08% enhancement in constraint mitigation, and 11.1% reduction in constraint failure when compared to the existing methods such as SNDHRC, RAP-ISSO, and RS-ABC. The framework’s ability is to dynamically mutate resource allocations and availability, preventing replications and addressing imbalanced solutions, demonstrating its efficacy in handling varying users, demands, and problem densities. However, the study acknowledges the impact of parameter choices on the proposed approach, highlighting the need for careful consideration in handling dynamic and complex constrained project problems. The future research directions include the development of a real-world project management adaptation framework, incorporating metaheuristic optimization techniques for scalability and robust analysis of large project problems. The study’s key findings emphasize this framework’s potential to address the resource constraints in genetic processes and underscore the significance of parameter optimization for its successful implementation.
Future scope involves deployment of real-world applications with advanced strategies, adopting the dynamic constraints, multi-objective optimization techniques, integrated with blockchain, IoT devices, human-centric design ideas, and across cross disciplines. With these enhancements, the research idea enhances the present knowledge level and address practical challenges by making the decisions about the resource allocation matches with the goals and preferences of the people involved.
-
Funding information: No funding was used for this study.
-
Author contributions: Yangyang Ji contributed to the conceptualization, formal analysis, methodology, data curation, validation, visualization, writing the draft and review and editing.
-
Conflict of interest: The author declares that there is no conflict of interest.
-
Data availability statement: The data used to support the findings of this study are available from the corresponding author upon request.
References
[1] Guo X, Zhou M, Liu S, Qi L. Lexicographic multiobjective scatter search for the optimization of sequence-dependent selective disassembly subject to multiresource constraints. IEEE Trans Cybern. 2019;50(7):3307–17.10.1109/TCYB.2019.2901834Search in Google Scholar PubMed
[2] Geng K, Ye C, Liu L. Research on multiobjective hybrid flow shop scheduling problem with dual resource constraints using improved memetic algorithm. IEEE Access. 2020;8:104527–42.10.1109/ACCESS.2020.2999680Search in Google Scholar
[3] Salman SA, Dheyab SA, Salih QM, Hammood WA. Parallel machine learning algorithms. Mesopotamian Journal of Big Data. 2023;2023:12–5.10.58496/MJBD/2023/002Search in Google Scholar
[4] Zhou B, Bian J. A bi-objective salp swarm algorithm with sine cosine operator for resource constrained multi-manned disassembly line balancing problem. Appl Soft Comput. 2022;131:109759.10.1016/j.asoc.2022.109759Search in Google Scholar
[5] Akopov AS, Beklaryan LA, Beklaryan AL. Cluster-based optimization of an evacuation process using a parallel bi-objective real-coded genetic algorithm. Cybern Inf Technol. 2020;20(3):45–63.10.2478/cait-2020-0027Search in Google Scholar
[6] Liu K, Gao H, Liang Z, Zhao M, Li C. Optimal charging strategy for large-scale electric buses considering resource constraints. Transport Res Part D: Transp Environ. 2021;99:103009.10.1016/j.trd.2021.103009Search in Google Scholar
[7] Li X, Ding Y, Pan K, Jiang D, Aneja YP. Single-path service network design problem with resource constraints. Transport Res Part E: Logist Transport Rev. 2020;140:101945.10.1016/j.tre.2020.101945Search in Google Scholar
[8] He W, Li W, Meng X. Scheduling optimization of prefabricated buildings under resource constraints. KSCE J Civil Eng. 2021;25(12):4507–19.10.1007/s12205-021-0444-8Search in Google Scholar
[9] de Azevedo GHI, Pessoa AA, Subramanian A. A satisfiability and workload-based exact method for the resource constrained project scheduling problem with generalized precedence constraints. Eur J Operational Res. 2021;289(3):809–24.10.1016/j.ejor.2019.07.056Search in Google Scholar
[10] Wang D, Wang Y, Dong S, Huang G, Liu J, Gao W. On delay-aware resource control with statistical QoS provisioning by dual connectivity in heterogeneous aeronautical network. IEEE Trans Veh Technol. 2020;69(3):2915–27.10.1109/TVT.2020.2965983Search in Google Scholar
[11] Bargetto R, Garaix T, Xie X. A branch-and-price-and-cut algorithm for operating room scheduling under human resource constraints. Comput Oper Res. 2023;152:106136.10.1016/j.cor.2022.106136Search in Google Scholar
[12] Yang CH, Lee KC, Li SE. A mixed activity-based costing and resource constraint optimal decision model for IoT-oriented intelligent building management system portfolios. Sustain Cities Soc. 2020;60:102142.10.1016/j.scs.2020.102142Search in Google Scholar
[13] Guo H, Sun J, Pang ZH. Stealthy false data injection attacks with resource constraints against multi-sensor estimation systems. ISA Trans. 2022;127:32–40.10.1016/j.isatra.2022.02.045Search in Google Scholar PubMed
[14] Lin C, Li Y, Ahmed M, Song C. Piece-wise pricing optimization with computation resource constraints for parked vehicle edge computing. Peer-to-Peer Network Appl. 2023;16:709–26.10.1007/s12083-022-01427-zSearch in Google Scholar
[15] Wang Z, Hu Z, Tang Y. Float-based resource leveling optimization of linear projects. IEEE Access. 2020;8:176997–7020.10.1109/ACCESS.2020.3027058Search in Google Scholar
[16] Liu H, Fang Z, Li R. Credibility-based chance-constrained multimode resource-constrained project scheduling problem under fuzzy uncertainty. Comput Ind Eng. 2022;171:108402.10.1016/j.cie.2022.108402Search in Google Scholar
[17] Watermeyer K, Zimmermann J. A branch-and-bound procedure for the resource-constrained project scheduling problem with partially renewable resources and general temporal constraints. Spectr. 2020;42:427–60.10.1007/s00291-020-00583-zSearch in Google Scholar
[18] Alinezhad R, Ansari R, Mahdikhani M, Banihashemi SA. Multi-phase projects selection and scheduling problem: a multiobjective optimization approach. Iran J Sci Technology, Trans Civ Eng. 2022;46:2575–91.10.1007/s40996-021-00721-9Search in Google Scholar
[19] Wang J, Dong M, Liang B, Boudreau G, Abou-Zeid H. Delay-tolerant OCO with long-term constraints: Algorithm and its application to network resource allocation. IEEE/ACM Trans Network. 2022;31(1):147–63.10.1109/TNET.2022.3188285Search in Google Scholar
[20] Huang CL, Jiang Y, Yeh WC. Developing model of fuzzy constraints based on redundancy allocation problem by an improved swarm algorithm. IEEE Access. 2020;8:155235–47.10.1109/ACCESS.2020.3018860Search in Google Scholar
[21] Su Z, Zhang G, Yue F, Zhan D, Li M, Li B, et al. Enhanced constraint handling for reliability-constrained multiobjective testing resource allocation. IEEE Trans Evolut Comput. 2021;25(3):537–51.10.1109/TEVC.2021.3055538Search in Google Scholar
[22] Liu Y, Li R, Liu H. Heuristic optimization for robust resource-constrained flexible project scheduling problem. IEEE Access. 2020;8:142269–81.10.1109/ACCESS.2020.3013375Search in Google Scholar
[23] Rauf M, Guan Z, Yue L, Guo Z, Mumtaz J, Ullah S. Integrated planning and scheduling of multiple manufacturing projects under resource constraints using raccoon family optimization algorithm. IEEE Access. 2020;8:151279–95.10.1109/ACCESS.2020.2971650Search in Google Scholar
[24] Shi J, Chen M, Ma Y, Qiao F. A new boredom-aware dual-resource constrained flexible job shop scheduling problem using a two-stage multiobjective particle swarm optimization algorithm. Inf Sci. 2023;643:119141.10.1016/j.ins.2023.119141Search in Google Scholar
[25] Li X, Wei K, Guo Z, Wang W, Aneja YP. An exact approach for the service network design problem with heterogeneous resource constraints. Omega. 2021;102:102376.10.1016/j.omega.2020.102376Search in Google Scholar
[26] Liu W, Zhang J, Liu C, Qu C. A bi-objective optimization for finance-based and resource-constrained robust project scheduling. Expert Syst Appl. 2023;231:120623.10.1016/j.eswa.2023.120623Search in Google Scholar
[27] Wang HK, Lin YC, Liang CJ, Wang YH. Multi-subpopulation parallel computing genetic algorithm for the semiconductor packaging scheduling problem with auxiliary resource constraints. Appl Soft Comput. 2023;142:110349.10.1016/j.asoc.2023.110349Search in Google Scholar
[28] Ren Y, Lu Z, Liu X. A branch-and-bound embedded genetic algorithm for resource-constrained project scheduling problem with resource transfer time of aircraft moving assembly line. Optim Lett. 2020;14(8):2161–95.10.1007/s11590-020-01542-xSearch in Google Scholar
[29] Pan X, Wang L, Zhang M, Qiu Q. A dynamic resource allocation strategy for collaborative constrained multiobjective optimization algorithm. Appl Intell. 2023;53:10176–201.10.1007/s10489-022-03820-wSearch in Google Scholar
[30] Gao J, Zhu X, Zhang R. Optimization of parallel test task scheduling with constraint satisfaction. J Supercomputing. 2023;79(7):7206–27.10.1007/s11227-022-04943-0Search in Google Scholar
[31] Morin PA, Artigues C, Haït A, Kis T, Spieksma FC. A project scheduling problem with periodically aggregated resource-constraints. Comput Oper Res. 2022;141:105688.10.1016/j.cor.2021.105688Search in Google Scholar
[32] Alipouri Y. A resource flow-based branch-and-bound algorithm to solve fuzzy stochastic resource-constrained project scheduling problem. Soft Comput. 2021;25(22):14315–31.10.1007/s00500-021-06147-9Search in Google Scholar
[33] Ali AH, Yaseen MG, Aljanabi M, Abed SA. Transfer learning: A new promising techniques. Mesopot J Big Data. 2023;2023:29–30.10.58496/MJBD/2023/004Search in Google Scholar
[34] Chai R, Tsourdos A, Chai S, Xia Y, Savvaris A, Chen CLP. Multiphase overtaking maneuver planning for autonomous ground vehicles via a desensitized trajectory optimization approach. IEEE Trans Ind Inform. 2023;19(1):74–87.10.1109/TII.2022.3168434Search in Google Scholar
[35] Chai R, Tsourdos A, Savvaris A, Chai S, Xia Y, Chen CLP. Design and implementation of deep neural network-based control for automatic parking maneuver process. IEEE Trans Neural Network Learn Syst. 2022;33(4):1400–13.10.1109/TNNLS.2020.3042120Search in Google Scholar PubMed
[36] Yaseen MG, Aljanabi M, Ali AH, Abd SA. Current cutting-edge research in computer science. Mesop J Comput Sci. 2022;2022:1–4.10.58496/MJCSC/2022/001Search in Google Scholar
[37] Van Eynde R, Vanhouck M. Resource-constrained multi-project scheduling: benchmark datasets and decoupled scheduling. J Sched. 2020;23:301–25.10.1007/s10951-020-00651-wSearch in Google Scholar
© 2024 the author(s), published by De Gruyter
This work is licensed under the Creative Commons Attribution 4.0 International License.
Articles in the same Issue
- Research Articles
- A study on intelligent translation of English sentences by a semantic feature extractor
- Detecting surface defects of heritage buildings based on deep learning
- Combining bag of visual words-based features with CNN in image classification
- Online addiction analysis and identification of students by applying gd-LSTM algorithm to educational behaviour data
- Improving multilayer perceptron neural network using two enhanced moth-flame optimizers to forecast iron ore prices
- Sentiment analysis model for cryptocurrency tweets using different deep learning techniques
- Periodic analysis of scenic spot passenger flow based on combination neural network prediction model
- Analysis of short-term wind speed variation, trends and prediction: A case study of Tamil Nadu, India
- Cloud computing-based framework for heart disease classification using quantum machine learning approach
- Research on teaching quality evaluation of higher vocational architecture majors based on enterprise platform with spherical fuzzy MAGDM
- Detection of sickle cell disease using deep neural networks and explainable artificial intelligence
- Interval-valued T-spherical fuzzy extended power aggregation operators and their application in multi-criteria decision-making
- Characterization of neighborhood operators based on neighborhood relationships
- Real-time pose estimation and motion tracking for motion performance using deep learning models
- QoS prediction using EMD-BiLSTM for II-IoT-secure communication systems
- A novel framework for single-valued neutrosophic MADM and applications to English-blended teaching quality evaluation
- An intelligent error correction model for English grammar with hybrid attention mechanism and RNN algorithm
- Prediction mechanism of depression tendency among college students under computer intelligent systems
- Research on grammatical error correction algorithm in English translation via deep learning
- Microblog sentiment analysis method using BTCBMA model in Spark big data environment
- Application and research of English composition tangent model based on unsupervised semantic space
- 1D-CNN: Classification of normal delivery and cesarean section types using cardiotocography time-series signals
- Real-time segmentation of short videos under VR technology in dynamic scenes
- Application of emotion recognition technology in psychological counseling for college students
- Classical music recommendation algorithm on art market audience expansion under deep learning
- A robust segmentation method combined with classification algorithms for field-based diagnosis of maize plant phytosanitary state
- Integration effect of artificial intelligence and traditional animation creation technology
- Artificial intelligence-driven education evaluation and scoring: Comparative exploration of machine learning algorithms
- Intelligent multiple-attributes decision support for classroom teaching quality evaluation in dance aesthetic education based on the GRA and information entropy
- A study on the application of multidimensional feature fusion attention mechanism based on sight detection and emotion recognition in online teaching
- Blockchain-enabled intelligent toll management system
- A multi-weapon detection using ensembled learning
- Deep and hand-crafted features based on Weierstrass elliptic function for MRI brain tumor classification
- Design of geometric flower pattern for clothing based on deep learning and interactive genetic algorithm
- Mathematical media art protection and paper-cut animation design under blockchain technology
- Deep reinforcement learning enhances artistic creativity: The case study of program art students integrating computer deep learning
- Transition from machine intelligence to knowledge intelligence: A multi-agent simulation approach to technology transfer
- Research on the TF–IDF algorithm combined with semantics for automatic extraction of keywords from network news texts
- Enhanced Jaya optimization for improving multilayer perceptron neural network in urban air quality prediction
- Design of visual symbol-aided system based on wireless network sensor and embedded system
- Construction of a mental health risk model for college students with long and short-term memory networks and early warning indicators
- Personalized resource recommendation method of student online learning platform based on LSTM and collaborative filtering
- Employment management system for universities based on improved decision tree
- English grammar intelligent error correction technology based on the n-gram language model
- Speech recognition and intelligent translation under multimodal human–computer interaction system
- Enhancing data security using Laplacian of Gaussian and Chacha20 encryption algorithm
- Construction of GCNN-based intelligent recommendation model for answering teachers in online learning system
- Neural network big data fusion in remote sensing image processing technology
- Research on the construction and reform path of online and offline mixed English teaching model in the internet era
- Real-time semantic segmentation based on BiSeNetV2 for wild road
- Online English writing teaching method that enhances teacher–student interaction
- Construction of a painting image classification model based on AI stroke feature extraction
- Big data analysis technology in regional economic market planning and enterprise market value prediction
- Location strategy for logistics distribution centers utilizing improved whale optimization algorithm
- Research on agricultural environmental monitoring Internet of Things based on edge computing and deep learning
- The application of curriculum recommendation algorithm in the driving mechanism of industry–teaching integration in colleges and universities under the background of education reform
- Application of online teaching-based classroom behavior capture and analysis system in student management
- Evaluation of online teaching quality in colleges and universities based on digital monitoring technology
- Face detection method based on improved YOLO-v4 network and attention mechanism
- Study on the current situation and influencing factors of corn import trade in China – based on the trade gravity model
- Research on business English grammar detection system based on LSTM model
- Multi-source auxiliary information tourist attraction and route recommendation algorithm based on graph attention network
- Multi-attribute perceptual fuzzy information decision-making technology in investment risk assessment of green finance Projects
- Research on image compression technology based on improved SPIHT compression algorithm for power grid data
- Optimal design of linear and nonlinear PID controllers for speed control of an electric vehicle
- Traditional landscape painting and art image restoration methods based on structural information guidance
- Traceability and analysis method for measurement laboratory testing data based on intelligent Internet of Things and deep belief network
- A speech-based convolutional neural network for human body posture classification
- The role of the O2O blended teaching model in improving the teaching effectiveness of physical education classes
- Genetic algorithm-assisted fuzzy clustering framework to solve resource-constrained project problems
- Behavior recognition algorithm based on a dual-stream residual convolutional neural network
- Ensemble learning and deep learning-based defect detection in power generation plants
- Optimal design of neural network-based fuzzy predictive control model for recommending educational resources in the context of information technology
- An artificial intelligence-enabled consumables tracking system for medical laboratories
- Utilization of deep learning in ideological and political education
- Detection of abnormal tourist behavior in scenic spots based on optimized Gaussian model for background modeling
- RGB-to-hyperspectral conversion for accessible melanoma detection: A CNN-based approach
- Optimization of the road bump and pothole detection technology using convolutional neural network
- Comparative analysis of impact of classification algorithms on security and performance bug reports
- Cross-dataset micro-expression identification based on facial ROIs contribution quantification
- Demystifying multiple sclerosis diagnosis using interpretable and understandable artificial intelligence
- Unifying optimization forces: Harnessing the fine-structure constant in an electromagnetic-gravity optimization framework
- E-commerce big data processing based on an improved RBF model
- Analysis of youth sports physical health data based on cloud computing and gait awareness
- CCLCap-AE-AVSS: Cycle consistency loss based capsule autoencoders for audio–visual speech synthesis
- An efficient node selection algorithm in the context of IoT-based vehicular ad hoc network for emergency service
- Computer aided diagnoses for detecting the severity of Keratoconus
- Improved rapidly exploring random tree using salp swarm algorithm
- Network security framework for Internet of medical things applications: A survey
- Predicting DoS and DDoS attacks in network security scenarios using a hybrid deep learning model
- Enhancing 5G communication in business networks with an innovative secured narrowband IoT framework
- Quokka swarm optimization: A new nature-inspired metaheuristic optimization algorithm
- Digital forensics architecture for real-time automated evidence collection and centralization: Leveraging security lake and modern data architecture
- Image modeling algorithm for environment design based on augmented and virtual reality technologies
- Enhancing IoT device security: CNN-SVM hybrid approach for real-time detection of DoS and DDoS attacks
- High-resolution image processing and entity recognition algorithm based on artificial intelligence
- Review Articles
- Transformative insights: Image-based breast cancer detection and severity assessment through advanced AI techniques
- Network and cybersecurity applications of defense in adversarial attacks: A state-of-the-art using machine learning and deep learning methods
- Applications of integrating artificial intelligence and big data: A comprehensive analysis
- A systematic review of symbiotic organisms search algorithm for data clustering and predictive analysis
- Modelling Bitcoin networks in terms of anonymity and privacy in the metaverse application within Industry 5.0: Comprehensive taxonomy, unsolved issues and suggested solution
- Systematic literature review on intrusion detection systems: Research trends, algorithms, methods, datasets, and limitations
Articles in the same Issue
- Research Articles
- A study on intelligent translation of English sentences by a semantic feature extractor
- Detecting surface defects of heritage buildings based on deep learning
- Combining bag of visual words-based features with CNN in image classification
- Online addiction analysis and identification of students by applying gd-LSTM algorithm to educational behaviour data
- Improving multilayer perceptron neural network using two enhanced moth-flame optimizers to forecast iron ore prices
- Sentiment analysis model for cryptocurrency tweets using different deep learning techniques
- Periodic analysis of scenic spot passenger flow based on combination neural network prediction model
- Analysis of short-term wind speed variation, trends and prediction: A case study of Tamil Nadu, India
- Cloud computing-based framework for heart disease classification using quantum machine learning approach
- Research on teaching quality evaluation of higher vocational architecture majors based on enterprise platform with spherical fuzzy MAGDM
- Detection of sickle cell disease using deep neural networks and explainable artificial intelligence
- Interval-valued T-spherical fuzzy extended power aggregation operators and their application in multi-criteria decision-making
- Characterization of neighborhood operators based on neighborhood relationships
- Real-time pose estimation and motion tracking for motion performance using deep learning models
- QoS prediction using EMD-BiLSTM for II-IoT-secure communication systems
- A novel framework for single-valued neutrosophic MADM and applications to English-blended teaching quality evaluation
- An intelligent error correction model for English grammar with hybrid attention mechanism and RNN algorithm
- Prediction mechanism of depression tendency among college students under computer intelligent systems
- Research on grammatical error correction algorithm in English translation via deep learning
- Microblog sentiment analysis method using BTCBMA model in Spark big data environment
- Application and research of English composition tangent model based on unsupervised semantic space
- 1D-CNN: Classification of normal delivery and cesarean section types using cardiotocography time-series signals
- Real-time segmentation of short videos under VR technology in dynamic scenes
- Application of emotion recognition technology in psychological counseling for college students
- Classical music recommendation algorithm on art market audience expansion under deep learning
- A robust segmentation method combined with classification algorithms for field-based diagnosis of maize plant phytosanitary state
- Integration effect of artificial intelligence and traditional animation creation technology
- Artificial intelligence-driven education evaluation and scoring: Comparative exploration of machine learning algorithms
- Intelligent multiple-attributes decision support for classroom teaching quality evaluation in dance aesthetic education based on the GRA and information entropy
- A study on the application of multidimensional feature fusion attention mechanism based on sight detection and emotion recognition in online teaching
- Blockchain-enabled intelligent toll management system
- A multi-weapon detection using ensembled learning
- Deep and hand-crafted features based on Weierstrass elliptic function for MRI brain tumor classification
- Design of geometric flower pattern for clothing based on deep learning and interactive genetic algorithm
- Mathematical media art protection and paper-cut animation design under blockchain technology
- Deep reinforcement learning enhances artistic creativity: The case study of program art students integrating computer deep learning
- Transition from machine intelligence to knowledge intelligence: A multi-agent simulation approach to technology transfer
- Research on the TF–IDF algorithm combined with semantics for automatic extraction of keywords from network news texts
- Enhanced Jaya optimization for improving multilayer perceptron neural network in urban air quality prediction
- Design of visual symbol-aided system based on wireless network sensor and embedded system
- Construction of a mental health risk model for college students with long and short-term memory networks and early warning indicators
- Personalized resource recommendation method of student online learning platform based on LSTM and collaborative filtering
- Employment management system for universities based on improved decision tree
- English grammar intelligent error correction technology based on the n-gram language model
- Speech recognition and intelligent translation under multimodal human–computer interaction system
- Enhancing data security using Laplacian of Gaussian and Chacha20 encryption algorithm
- Construction of GCNN-based intelligent recommendation model for answering teachers in online learning system
- Neural network big data fusion in remote sensing image processing technology
- Research on the construction and reform path of online and offline mixed English teaching model in the internet era
- Real-time semantic segmentation based on BiSeNetV2 for wild road
- Online English writing teaching method that enhances teacher–student interaction
- Construction of a painting image classification model based on AI stroke feature extraction
- Big data analysis technology in regional economic market planning and enterprise market value prediction
- Location strategy for logistics distribution centers utilizing improved whale optimization algorithm
- Research on agricultural environmental monitoring Internet of Things based on edge computing and deep learning
- The application of curriculum recommendation algorithm in the driving mechanism of industry–teaching integration in colleges and universities under the background of education reform
- Application of online teaching-based classroom behavior capture and analysis system in student management
- Evaluation of online teaching quality in colleges and universities based on digital monitoring technology
- Face detection method based on improved YOLO-v4 network and attention mechanism
- Study on the current situation and influencing factors of corn import trade in China – based on the trade gravity model
- Research on business English grammar detection system based on LSTM model
- Multi-source auxiliary information tourist attraction and route recommendation algorithm based on graph attention network
- Multi-attribute perceptual fuzzy information decision-making technology in investment risk assessment of green finance Projects
- Research on image compression technology based on improved SPIHT compression algorithm for power grid data
- Optimal design of linear and nonlinear PID controllers for speed control of an electric vehicle
- Traditional landscape painting and art image restoration methods based on structural information guidance
- Traceability and analysis method for measurement laboratory testing data based on intelligent Internet of Things and deep belief network
- A speech-based convolutional neural network for human body posture classification
- The role of the O2O blended teaching model in improving the teaching effectiveness of physical education classes
- Genetic algorithm-assisted fuzzy clustering framework to solve resource-constrained project problems
- Behavior recognition algorithm based on a dual-stream residual convolutional neural network
- Ensemble learning and deep learning-based defect detection in power generation plants
- Optimal design of neural network-based fuzzy predictive control model for recommending educational resources in the context of information technology
- An artificial intelligence-enabled consumables tracking system for medical laboratories
- Utilization of deep learning in ideological and political education
- Detection of abnormal tourist behavior in scenic spots based on optimized Gaussian model for background modeling
- RGB-to-hyperspectral conversion for accessible melanoma detection: A CNN-based approach
- Optimization of the road bump and pothole detection technology using convolutional neural network
- Comparative analysis of impact of classification algorithms on security and performance bug reports
- Cross-dataset micro-expression identification based on facial ROIs contribution quantification
- Demystifying multiple sclerosis diagnosis using interpretable and understandable artificial intelligence
- Unifying optimization forces: Harnessing the fine-structure constant in an electromagnetic-gravity optimization framework
- E-commerce big data processing based on an improved RBF model
- Analysis of youth sports physical health data based on cloud computing and gait awareness
- CCLCap-AE-AVSS: Cycle consistency loss based capsule autoencoders for audio–visual speech synthesis
- An efficient node selection algorithm in the context of IoT-based vehicular ad hoc network for emergency service
- Computer aided diagnoses for detecting the severity of Keratoconus
- Improved rapidly exploring random tree using salp swarm algorithm
- Network security framework for Internet of medical things applications: A survey
- Predicting DoS and DDoS attacks in network security scenarios using a hybrid deep learning model
- Enhancing 5G communication in business networks with an innovative secured narrowband IoT framework
- Quokka swarm optimization: A new nature-inspired metaheuristic optimization algorithm
- Digital forensics architecture for real-time automated evidence collection and centralization: Leveraging security lake and modern data architecture
- Image modeling algorithm for environment design based on augmented and virtual reality technologies
- Enhancing IoT device security: CNN-SVM hybrid approach for real-time detection of DoS and DDoS attacks
- High-resolution image processing and entity recognition algorithm based on artificial intelligence
- Review Articles
- Transformative insights: Image-based breast cancer detection and severity assessment through advanced AI techniques
- Network and cybersecurity applications of defense in adversarial attacks: A state-of-the-art using machine learning and deep learning methods
- Applications of integrating artificial intelligence and big data: A comprehensive analysis
- A systematic review of symbiotic organisms search algorithm for data clustering and predictive analysis
- Modelling Bitcoin networks in terms of anonymity and privacy in the metaverse application within Industry 5.0: Comprehensive taxonomy, unsolved issues and suggested solution
- Systematic literature review on intrusion detection systems: Research trends, algorithms, methods, datasets, and limitations

