Abstract
Due to the limitations of the initial rapidly exploring random tree (RRT) algorithm, robotics faces challenges in path planning. This study proposes the integration of the metaheuristic salp swarm algorithm (SSA) to enhance the RRT algorithm, resulting in a new algorithm termed IRRT-SSA. The IRRT-SSA addresses issues inherent in the original RRT, enhancing efficiency and path-finding capabilities. A detailed explanation of IRRT-SSA is provided, emphasizing its distinctions from the core RRT. Comprehensive insights into parameterization and algorithmic processes contribute to a thorough understanding of its implementation. Comparative analysis demonstrates the superior performance of IRRT-SSA over the basic RRT, showing improvements of approximately 49, 54, and 54% in average path length, number of nodes, and number of iterations, respectively. This signifies the enhanced effectiveness of the proposed method. Theoretical and practical implications of IRRT-SSA are highlighted, particularly its influence on practical robotic applications, serving as an exemplar of tangible benefits.
1 Introduction
With the development of artificial intelligence, robot applications are broadly implemented in numerous areas, such as industry, agriculture, surveillance, search and rescue, environmental monitoring, and traffic control [1,2]. Path planning is one of the most sufficient and challenging aspects in the robotic field, in which the main objective is to find a moving sequence for an agent from the starting point to the target point in accordance with particular constraints (such as obstacles or computation time) [3,4,5]. Many path planning methods, including classical methods, exist, as classified in Figure 1. One of the famous algorithms is the rapidly exploring random tree (RRT) or metaheuristic methods, such as ant colony algorithm, particle swarm algorithm, and firefly algorithm [6,7,8]. Path planning comprises two types: one is global, which searches for the optimal path and gives the best performance with the existing static environment known to the robot, and the other is local path planning, which is best in dynamic or unknown environments [9,10,11].
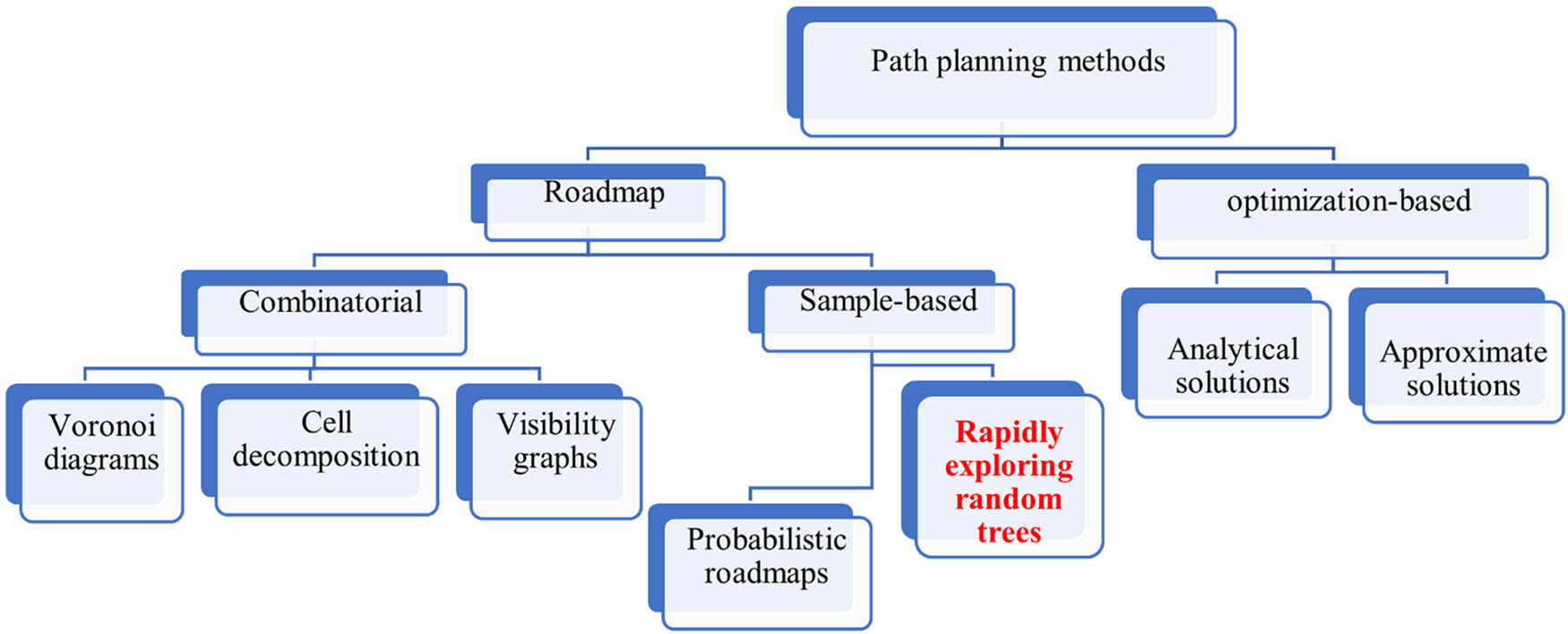
Classification of path planning methods.
Research on robotic path planning has persisted for quite some time, with the original RRT algorithm serving as a rock-solid solution to relevant problems. However, constant development is required to circumvent inherent constraints to keep up with the dynamic nature of robotic applications. In light of the problems with the original RRT and the demands of modern robotics, this work presents an iterative RRT with salp swarm algorithm (IRRT-SSA). Autonomous vehicles and industrial automation are only two examples of the ever-changing field of robotics. Given this variety, fixing the shortcomings of current path planning algorithms is a top priority. Despite its robustness, RRT encounters difficulties with computational efficiency and path quality in complicated and uncertain contexts.
In particular, this study fixes the original RRT algorithm’s inefficiencies about computing iterations, path length, and the number of nodes. Moreover, the SSA is integrated into the path planning framework, considering that improved flexibility in complicated terrain has prompted research into metaheuristic algorithms. The contributions of this work are summarized as follows:
This study proposes improving the RRT algorithm by using the metaheuristic SSA and calls it IRRT-SSA.
Overcoming the limitation of the RRT algorithm in solving path planning problems in robotics, specifically addressing its inability to generate the optimal path.
The final results demonstrate that the newly proposed IRRT-SSA outperforms the essential RRT algorithm regarding the average path length, number of nodes, and number of iterations by approximately 49, 54, and 54%, respectively.
The results indicate improved path quality and the best shortest paths to targets at less cost compared with the original RRT algorithm.
The rest of this work is structured such that the suggested IRRT-SSA can be deeply understood. Section 2 examines the relevant literature, drawing attention to the gaps in existing knowledge. Section 3 presents the basic idea of the RRT algorithm and how it is used in path planning. Section 4 explains SSA, specifically its architecture. The newly proposed IRRT-SSA is described in detail, including how to use it for enhancing performance, in Section 5. Section 6 indicates the results and discussions. Section 7 discusses the performance of IRRT-SSA, its influence on the practical deployment of robotics, and the limitations of the study. In Section 8, conclusions and possible future study options are given.
2 Related works
The efficiency and flexibility of autonomous systems have been greatly enhanced by the many algorithms that have contributed to path planning in robotics. We develop IRRT-SSA in response to specific research gaps in the existing literature, which offers a rich tapestry of approaches. The original RRT technique is crucial for solving path planning problems. It generates pathways that can adjust to complicated environments by effectively exploring the configuration space. Though useful, it has restrictions regarding computing efficiency and flexibility in real-time situations. Metaheuristic algorithm integration has been the subject of recent research to improve the efficiency of path planning algorithms. Particularly impressive is the capacity of swarm intelligence to imitate natural behavior. Metaheuristics, such as SSA, mimic salps’ foraging behavior.
Many studies have been conducted in the domain of path planning algorithm improvement, particularly those considering the RRT algorithm. Some of such studies are indicated in this section.
In [12] (2016), the new development of the RRT algorithm by hybridization with ACO was presented to improve its functioning. The benefit from this hybrid function was described as a trade-off between exploiting the present solution and exploring the state space. The ACO-RRT* algorithm and the original RRT and RRT* algorithms were compared in three challenging scenarios. A faster optimal solution was obtained. The experiment results illustrated that the newly proposed algorithm surpassed the RRT and RRT* algorithms by assessing the performance means of the cost and time to locate the first path and evaluating the path quality with the number of iterations.
In [13] (2021), a new development in the RRT algorithm called Adapted-RRT was proposed. The developed algorithm combines three familiar metaheuristic algorithms: gray wolf optimization (GWO), incremental GWO, and expanded GWO. This combination of methods helps solve the problem of the sampled RRT method in terms of not detecting the optimal path. They attempt to detect solutions near optimal without collision while granting good execution time, decreased space complexities, and optimal path costs. Experiments were conducted by simulating four dissimilar maps for three unmanned aerial vehicles and various sets of points at the start and end. The simulation outcomes were compared with those of other metaheuristic algorithms, and the proposed algorithm outperformed them.
In [14] (2021), a new development in the RRT algorithm through quack expanding a random tree toward the target and avoiding obstacles by using an artificial potential field was introduced. The proposed algorithm raises the number of nodes in a single growth and chooses nodes by integrating the target gravity of a point and obstacle repulsion. The simulation results demonstrated that the proposed algorithm has more power than the essential RRT algorithm regarding the search ability and computation time in various environments.
In [15] (2022), a new path planning algorithm named PSO-RRT, which merges the RRT algorithm and the particle swarm optimization algorithm, was proposed. This algorithm solved the RRT algorithm’s significant shortcoming; it can create a faster path, although this path is not optimal. PSO-RRT enhances convergence, costs less, requires few iterations, and generates a near-optimal path superior to RRT* and informed RRT* in clutter and square field environments.
Several research gaps were identified through a rigorous evaluation of the available literature, which motivated the present investigation. First, improvements are necessary to address problems encountered in real-world circumstances, such as changing terrain and dynamic barriers, even though the traditional RRT algorithm works well. Second, research on the use of SSA as a metaheuristic in path planning algorithms, especially in iterative RRT frameworks, is limited. To address these shortcomings, IRRT-SSA incorporates SSA into the iterative RRT framework to improve the efficiency and adaptability. Considering that contemporary robotic applications are inherently dynamic, this study seeks to address the need for a highly sophisticated path planning method. With regard to the combination of metaheuristic algorithms, such as SSA, with traditional RRT frameworks, there is still much unexplored ground to cover, even though previous research has established a basis for path planning approaches. Along with helping close these knowledge gaps, this study thoroughly compares the suggested IRRT-SSA with the foundational RRT method, illuminating its strengths and weaknesses in terms of practical application.
3 RRT algorithm
The RRT algorithm was introduced as a randomized data structure, which is one of the sample-based path planning algorithms used for solving problems in path planning [16,17,18]. It is constructed and designed as a quick and efficient method to explore high-dimensional spaces. Specifically, it deals with nonconvex spaces. The basic advantage of RRT is that it has efficient computation and the capability of finding a possible solution in the case of configurations for complex obstacles [19]. The RRT algorithm is implemented to explore an environment’s specific M × N matrix space by expanding a random branch from the root node in the tree as a starting point to the goal point. RRT is often used in path planning for robots [20]. It randomly creates a sample in the configuration space and selects one node close to this random sample to construct a tree. If the random sample position is nearer than the step length, then the new node is generated and added to expand the tree until the goal point is reached. The steps of RRT are shown in Alg. 1 in Figure 3 [21]. Figure 2 illustrates the tree expansion toward a q random configuration point. A point near this q random point, named q nearer, defined as a vertex of the tree, is selected. Then, the tree continues in its expansion from the q nearer point to the q random point stopping at a q new point, specified radius r from the q nearer point [22].
![Figure 2
RRT working mechanism [22].](/document/doi/10.1515/jisys-2023-0219/asset/graphic/j_jisys-2023-0219_fig_002.jpg)
RRT working mechanism [22].
![Figure 3
Pseudocode of RRT [21].](/document/doi/10.1515/jisys-2023-0219/asset/graphic/j_jisys-2023-0219_fig_003.jpg)
Pseudocode of RRT [21].
One common and well-liked technique for robotic motion planning is the RRT algorithm. The core principle of RRT, which was developed to solve path planning difficulties, is to construct a tree incrementally by randomly sampling a robot’s configuration space. The algorithm iteratively develops the tree by selecting new configurations at random, exploring space in the direction of these configurations, and linking them to the existing tree. The process begins with an initial configuration. The procedure terminates when a goal configuration is reached or until another preset termination condition is satisfied.
3.1 Key steps of the RRT algorithm
The robot’s basic setup is the only node in the tree initially.
Iteration is carried out through the robot’s configuration space, and a new, random configuration is generated each time.
The current tree structure closest to the randomly selected one is identified.
We can generate a new configuration by guiding the robot from its closest neighbor to the randomly sampled configuration.
Whether the updated setup does not conflict with the current tree is verified. The setup is disregarded and another trial is performed if a collision happens.
The new configuration is connected to its nearest neighbor and added to the tree if collision will not occur.
The process keeps going until something triggers it to end, such as when we attain a certain configuration objective or when the number of iterations is reached.
3.2 Limitations of the RRT algorithm
The sampling approach greatly affects the efficiency of RRTs, and they may provide pathways that are not optimal.
Two factors that can impact the algorithm’s efficiency are how complex is the robot’s geometry and how many dimensions there are in the configuration space.
The performance of RRTs can change depending on the starting configuration and the objective’s location, and they do not ensure that the optimal path will be found.
Adapting RRTs to contexts where barriers are constantly shifting might be challenging.
4 SSA algorithm
SSA is one of the swarm-based metaheuristic algorithms inspired by the behavior of salps flocking in oceans for foraging and navigating. The basic idea is dividing the salps into two kinds. One is considered a leader, and the remaining are followers; they construct a chain with the leader at the front and the followers at the back, as indicated in Figure 4 [23,24,25]. The fundamental concept of SSA is working in two stages, one for global exploration and the other for local exploitation, as illustrated in Alg. 2 in Figure 5. At first, the search operation initializes a random population to assist the algorithm in locating the optimal solution. Then, the exploitation stage starts to search accurately in the specified region detected by the previous stage to enhance the precision of convergence. SSA is extremely competitive, but its limitations comprise unbalanced exploration and exploitation processes and slow convergence [26,27].
![Figure 4
Salp swarm chain [23].](/document/doi/10.1515/jisys-2023-0219/asset/graphic/j_jisys-2023-0219_fig_004.jpg)
Salp swarm chain [23].

Pseudocode of SSA algorithm.
The work of the salp chain is foraging for the target, which is the food source that directs the leader to update its position by equation (1), representing the new node position in RRT.
where t is the recent iteration, and T refers to the maximum iterations. The followers are updated by
where j ≥ 2 and Xi (j) represents the location of the ith follower salp in the jth dimension search space [28,29].
5 IRRT-SSA algorithm
The new improvement of the RRT algorithm is to solve robot path planning using SSA and is called IRRT-SSA. It combines the benefits of these two algorithms to find an optimal path from the start to the goal while avoiding obstacles. The basic RRT algorithm is good at exploring large areas of the search space, but it can get stuck in narrow passages or converge to suboptimal solutions. Meanwhile, salp swarm optimization is good at escaping local optima and finding globally optimal solutions. The proposed IRRT-SSA can more effectively explore the search space and converge to a globally optimal path. SSA also provides a mechanism to explore undiscovered space areas efficiently. The contribution of SSA to the RRT algorithm is mainly improving the exploration and coverage of the configuration space, which can result in faster convergence to a feasible path and better avoidance of obstacles. If an obstacle exists in the path, no new nodes are created. Moreover, no line connects two nodes and passes through any object. SSA’s role in IRRT-SSA is to generate new possible movement paths and guide toward unexplored areas of the environment by selecting a new node in the tree as in Alg. 3 in Figure 6. This algorithm helps find a good path to reach the goal faster and more efficiently.

Pseudocode of IRRT-SSA algorithm.
By using SSA as a metaheuristic, IRRT-SSA aims to overcome the drawbacks of the conventional RRT approach. A comprehensive review of the approach, including the steps of the algorithm, important parameters, and the reasoning for the integration, is given in this section.
5.1 Algorithmic steps
The algorithm starts with the robotic system’s initial configuration by initializing the RRT tree.
An assortment of SSA parameters are defined, including the salp count, convergence criterion, and exploration–exploitation balance. IRRT-SSA employs an iterative expansion technique. On the basis of the conventional RRT procedure, the RRT tree is expanded in each iteration by connecting nodes and randomly sampling them.
SSA guides the exploration procedure. The salps’ actions collectively drive the tree’s growth toward more favorable areas in the configuration space.
IRRT-SSA incorporates a step to enhance the path in each iteration, unlike the typical RRT. SSA is used for refinement to improve the quality and flexibility of the generated pathways for dynamic situations.
Convergence is evaluated using established criteria to guarantee that the algorithm exits after a good solution is achieved. This step entails checking whether the RRT tree has converged and whether the optimization is successful with SSA.
We explain the important parameters of IRRT-SSA to help with thorough understanding and reproducibility.
The number of salps (N) controls the swarm’s size and impacts its exploration ability.
A convergence threshold (CT) specifies the minimum value at which the RRT and SSA parts must converge.
A steady equilibrium is maintained in the iterative expansion’s exploration vs exploitation debate.
Two goals are achieved by including SSA in the RRT architecture. Exploration is improved by SSA’s adaptations, modeled after the group behavior of salps. In line with the ever-changing nature of real-world robotic applications, RRT’s iterative structure permits path improvement with each iteration.
IRRT-SSA deftly blends the benefits of SSA with those of the traditional RRT algorithm. With its iterative nature and SSA-guided path refinement, IRRT-SSA shows promise as a solution to the problems of robotic path planning in dynamic and complicated situations.
The RRT limitations include a lack of assurances about optimality, potentially inefficient path length and computing resources, and inadequate path quality. Improving these areas and streamlining the path planning process are IRRT-SSA’s primary goals.
5.2 Utilization of SSA for improvement
SSA is a metaheuristic that IRRT-SSA introduces to improve the optimization and exploration capabilities of the classic RRT. It is an optimization technique that takes its cues from the way salps, a type of marine invertebrates, work together. The system simulates the behavior of ocean salps, which change their locations depending on local and global data.
Several improvements are realized by integrating SSA into IRRT.
SSA uses the swarm’s collective intelligence to facilitate a more effective exploration of the configuration space. Two possible outcomes are a more complete picture and a more rapid convergence toward ideal solutions.
SSA balances discovery and exploitation by integrating global and local search tactics, finding good pathways in complicated and multimodal situations.
A swarm-based approach such as SSA makes it easy to adjust to changing conditions. This algorithm outperforms the conventional RRTs in terms of versatility given its ability to react to changes in the configuration space.
IRRT-SSA aims to solve the suboptimality problems with conventional RRTs by including SSA to enhance the quality of generated pathways.
6 Results and discussions
To prove the efficiency of the proposed algorithm and to conduct a comparison with the RRT algorithm, we implemented RRT and IRRT-SSA using the Python programming language. The implementation was performed on a two-dimensional environment with two obstacles. The algorithms were run for many iterations, and the performance was evaluated on the basis of the number of nodes generated and the path length. In accordance with the randomness of the RRT algorithm, 20 repeated tests were achieved for the basic RRT algorithm and the proposed RRT algorithm in a known environment. The first test was done by setting the starting point at (1, 1) and the target point at (9, 9), as shown in Figure 7; the second test was done by setting the starting point at (2, 1) and the target point at (2, 5), as depicted in Figure 8. The results showed that IRRT-SSA generated fewer nodes than the original RRT. Specifically, RRT generated 1,065 and 854 nodes on average, whereas IRRT-SSA generated only 458 and 229 nodes in the first and second tests, respectively. This finding indicates that IRRT-SSA has a more efficient search strategy and explores the space more effectively. Furthermore, the path length (red line) generated by IRRT-SSA was significantly shorter than that by RRT. In particular, the average path length generated by RRT was 146 and 105 units, whereas those by IRRT-SSA was 73 and 45 units in the first and second tests, respectively. Thus, IRRT-SSA is better at finding optimal smoothing paths and has a higher global search ability. Both tests are demonstrated in Table 1.
Average path planning with starting point (1, 1) and target point (9, 9). (a) RRT. (b) IRRT-SSA.
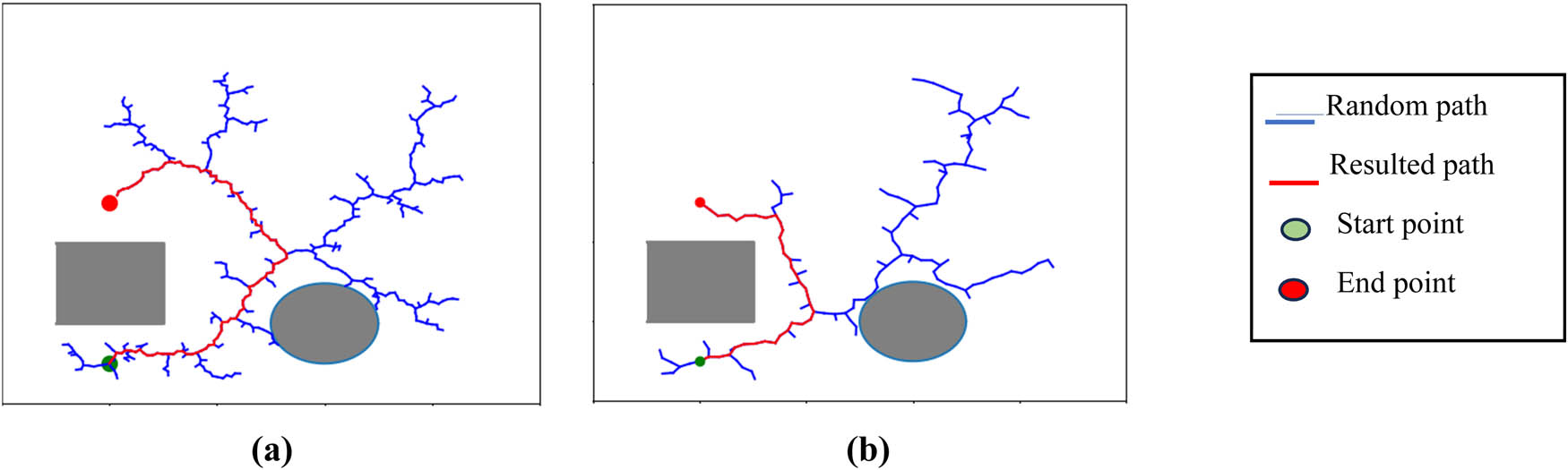
Average path planning with starting point (2, 1) and target point (2, 5). (a) RRT. (b) IRRT-SSA.
Comparison between RRT and IRRT-SSA
| Starting and goal points | RRT | IRRT-SSA | ||||
|---|---|---|---|---|---|---|
| Path length | Number of nodes | Iteration | Path length | Number of nodes | Iteration | |
| Starting = (1, 1), Goal = (9, 9) | 136 | 1,059 | 1,260 | 72 | 561 | 670 |
| 148 | 920 | 1,105 | 72 | 355 | 480 | |
| 140 | 929 | 1,160 | 73 | 328 | 431 | |
| 154 | 956 | 1,183 | 76 | 366 | 411 | |
| 159 | 1,005 | 1,147 | 70 | 434 | 545 | |
| 137 | 1,103 | 1,336 | 73 | 328 | 444 | |
| 151 | 1,073 | 1,290 | 69 | 320 | 377 | |
| 148 | 1,663 | 1,906 | 73 | 322 | 390 | |
| 156 | 1,273 | 1,494 | 70 | 416 | 484 | |
| 142 | 845 | 1,033 | 74 | 405 | 476 | |
| 148 | 902 | 1,115 | 75 | 822 | 952 | |
| 144 | 1,015 | 1,181 | 76 | 453 | 592 | |
| 147 | 1,200 | 1,508 | 74 | 900 | 1,043 | |
| 148 | 1,082 | 1,315 | 73 | 394 | 509 | |
| 143 | 807 | 1,021 | 75 | 410 | 461 | |
| 144 | 923 | 1,167 | 75 | 430 | 524 | |
| 146 | 1,552 | 1,776 | 76 | 638 | 806 | |
| 142 | 978 | 1,182 | 76 | 462 | 549 | |
| 139 | 894 | 1,152 | 72 | 442 | 535 | |
| 148 | 1,128 | 1,348 | 69 | 374 | 486 | |
| Average | 146 | 1,065 | 1315.45 | 73 | 458 | 558.25 |
| Starting = (2, 1), Goal = (2, 5) | 110 | 909 | 1,117 | 51 | 200 | 262 |
| 83 | 512 | 605 | 41 | 304 | 358 | |
| 91 | 312 | 379 | 46 | 160 | 217 | |
| 116 | 603 | 752 | 40 | 173 | 192 | |
| 123 | 849 | 1,000 | 50 | 236 | 282 | |
| 106 | 477 | 536 | 44 | 238 | 271 | |
| 109 | 1,441 | 1,666 | 45 | 293 | 334 | |
| 111 | 1,414 | 1,635 | 45 | 246 | 264 | |
| 84 | 298 | 343 | 37 | 182 | 233 | |
| 122 | 795 | 977 | 50 | 278 | 343 | |
| 115 | 697 | 886 | 48 | 159 | 204 | |
| 125 | 900 | 1,034 | 51 | 285 | 321 | |
| 128 | 1,147 | 1,314 | 46 | 122 | 133 | |
| 109 | 1,031 | 1,167 | 48 | 147 | 180 | |
| 94 | 1,084 | 1,284 | 46 | 250 | 277 | |
| 85 | 1,056 | 1,205 | 41 | 138 | 212 | |
| 97 | 540 | 650 | 55 | 629 | 703 | |
| 90 | 1,278 | 1,484 | 40 | 158 | 200 | |
| 101 | 535 | 616 | 38 | 130 | 153 | |
| 113 | 1,209 | 1,363 | 40 | 260 | 313 | |
| Average | 105.6 | 854 | 1000.65 | 45.1 | 229 | 258.1 |
Finally, the proposed IRRT-SSA was tested on ten robots’ starting and target points, and five implementations were applied to each pair of points. The results are presented in Table 2, where the average path length, number of nodes, and number of iterations are illustrated. The ratios of enhancement are represented by
Average of measurements for enhancement by IRRT-SSA
| Start point | Goal point | RRT | IRRT-SSA | Enhancement ratio | ||||
|---|---|---|---|---|---|---|---|---|
| Average path length | Average number of nodes | Average number of iterations | Average path length | Average number of nodes | Average number of iterations | |||
| (2, 1) | (2, 8) | 119 | 471 | 568 | 60 | 226.8 | 267 | Path length: 50% |
| No. of nodes: 52% | ||||||||
| No. of iterations: 53% | ||||||||
| (8, 6) | (4, 1) | 90 | 1,027 | 1,140 | 48 | 416 | 459 | Path length: 47% |
| No. of nodes: 60% | ||||||||
| No. of iterations: 60% | ||||||||
| (1, 6) | (7, 1) | 106 | 732 | 814 | 59 | 369 | 408 | Path length: 45% |
| No. of nodes: 50% | ||||||||
| No. of iterations: 50% | ||||||||
| (7, 6) | (1, 1) | 106 | 1,409 | 1,562 | 54 | 598 | 669 | Path length: 50% |
| No. of nodes: 58% | ||||||||
| No. of iterations: 58% | ||||||||
| (1, 1) | (4, 4) | 78 | 135 | 228 | 32 | 51 | 92 | Path length: 59% |
| No. of nodes: 63% | ||||||||
| No. of iterations: 60% | ||||||||
| (8, 8) | (5, 5) | 52 | 177 | 182 | 28 | 54 | 51 | Path length: 48% |
| No. of nodes: 69% | ||||||||
| No. of iterations: 70% | ||||||||
| (3, 1) | (8, 7) | 105 | 409 | 474 | 53 | 242 | 263 | Path length: 50% |
| No. of nodes: 41% | ||||||||
| No. of iterations: 45% | ||||||||
| (9, 1) | (1, 5) | 128 | 749 | 786 | 63 | 299 | 333 | Path length: 51% |
| No. of nodes: 60% | ||||||||
| No. of iterations: 58% | ||||||||
| (1, 1) | (6, 6) | 92 | 171 | 266 | 48 | 100 | 147 | Path length: 48% |
| No. of nodes: 42% | ||||||||
| No. of iterations: 45% | ||||||||
| (4, 5) | (9, 1) | 84 | 811 | 921 | 42 | 488 | 545 | Path length: 40% |
| No. of nodes: 50% | ||||||||
| No. of iterations: 41% | ||||||||
Total enhancement in the average path length: 49%. Total enhancement in the average no. of nodes: 54%. Total enhancement in the average no. of iterations: 54%.
With the total average of 10 points for 50 implementations (5 for each pair of starting and goal points), IRRT-SSA enhances the average path length, number of nodes, and number of iterations by approximately 49, 54, and 54%, respectively, compared with the original RRT algorithm. These results lead to the best paths and less cost. The newly proposed IRRT-SSA enhances the efficiency of the original RRT algorithm by optimization. This step represents the role of SSA in selecting a new node instead of that selected by the RRT algorithm. When the new node is best selected, then it selects the best nearest random point. The idea of selecting a new node by SSA is determining the leader that has the best fitness from the generated population, tracking by the remaining salps as the followers, and updating the leader and followers’ positions to achieve convergence. Several essential metrics are used to evaluate IRRT-SSA, and its efficacy and efficiency are shown by comparing it with the original RRT. These metrics demonstrate how far IRRT-SSA has enhanced the route planning procedure. To measure efficiency, we use the following measures.
6.1 Improvement in average path length
Significant implications exist for real-world robotic applications of IRRT-SSA with 49% improvement in average path length. The practical value of this enhancement in improving the overall efficiency and performance of robotic systems in varied settings is substantial, going beyond its status as a purely statistical parameter. To further explain the relevance, we consider the following points:
A robotic system can navigate from the starting point to the destination with a significantly lower trip distance, as shown by the 49% reduction in average path length. Robotic systems that are short on resources, such as energy, or functioning in a time-sensitive environment must prioritize this optimization.
Robotic mobility uses less energy when pathways are shorter. The capacity to accomplish the same task with less energy increases operational endurance. It aligns with sustainable and cost-effective practices, especially in energy-intensive applications such as mobile robots or autonomous drones.
Faster traversal times are achieved with shorter average path lengths. Reaching destinations faster improves a robot’s responsiveness and overall work efficiency in time-critical scenarios such as emergency response or manufacturing processes.
In confined areas, robots can move more efficiently along shorter routes. This characteristic is especially helpful in settings where the robot must be accurate in its movements, such as hospitals, warehouses, or locations hit by natural disasters, where it must navigate narrow passages to reach the objective.
A robot’s capacity to detect and avoid risks and barriers is enhanced when it can identify shorter paths. Autonomous vehicles and robotic systems operating in unpredictable and dynamic surroundings are two examples of applications where this capacity is crucial for safety reasons.
An indication of IRRT-SSA’s adaptation across varied contexts is the improvement in average path length. The algorithm’s capacity to locate shorter paths efficiently increases its versatility and practicality in various real-world circumstances, whether navigating through crowded locations or open areas.
The overall improvement in average path length of 49% is a real step forward that will have far-reaching effects on robotic systems rather than only a numerical one. A significant advancement in robotics and autonomous systems, IRRT-SSA enables robots to function more economically, efficiently, and safely in real-world environments.
6.2 Impact of 54% reduction in the number of nodes
IRRT-SSA cuts the number of nodes by 54% compared with the original RRT, which has various important consequences on the algorithm’s performance and efficiency. The number of nodes is the sum of all the points along the built tree. This reduction indicates a search space that is more streamlined and efficient with resources. As the number of nodes drops, the computational load also decreases. The algorithm’s memory and processing requirements are reduced, improving the computational efficiency given the fewer nodes to assess. For applications requiring instantaneous decisions, this improvement is of utmost importance. A reduced number of nodes allows for a more targeted search of the configuration space, which speeds up the discovery of good pathways. Faster path planning is the outcome of the algorithm’s improved navigation of the search space. Situations requiring quick responses and decisions benefit from this acceleration.
One way to improve memory utilization is by reducing the number of nodes. This aspect is crucial for robots that must function in settings with limited resources or applications where memory is an issue. Because it can accomplish its goals with fewer nodes, the algorithm is more flexible and can be used in different computational environments. The scalability of IRRT-SSA is improved by reducing the number of nodes. Without experiencing an exponential rise in computing needs, it can efficiently handle search areas that are larger and more complicated. Applications that require the algorithm to adapt to different robotic platforms and environmental situations must have this scalability.
Reducing the number of nodes also allows the algorithm to zero down on areas of the configuration space where optimum pathways are more probable. The algorithm’s ability to locate high-quality pathways effectively, even in situations with limited computational resources, is enhanced by this targeted investigation. The needs of real-time systems are met by reducing the number of nodes. The capacity to design pathways with fewer nodes improves the system’s overall stability and guarantees quick responses in applications such as autonomous vehicles or robotics in dynamic environments. IRRT- SSA’s 54% reduced node count demonstrates computational efficiency and offers practical advantages, such as optimized memory utilization, faster path planning, enhanced scalability, and compatibility with real-time applications. Because of these benefits, IRRT-SSA is an attractive algorithm for many robotic applications prioritizing efficiency and resource utilization.
6.3 Implications of 54% decrease in iterations
The time and computational resources needed for path planning are significantly affected by the remarkable 54% reduction in iterations achieved by IRRT-SSA compared with the fundamental RRT. A decrease in iterations indicates an improvement in efficiency and resource utilization. The following are important points about its consequences:
Convergence toward optimal pathways is accelerated with fewer iterations. The time it takes for the algorithm to search for possible configurations and find ones that work is reduced. When making decisions and responding quickly are of the utmost importance, time-sensitive applications greatly benefit from this acceleration in path planning.
The computational workload decreases directly proportional to the decrease in iterations. The algorithm’s processing power and computational resource requirements are reduced with the decreased number of iterations. This reduction is important in situations in which computing resources are limited or making the most of what is available is of the utmost importance.
Reduced iterations meet the needs of real-time systems. The algorithm’s capacity to accomplish its goals with fewer iterations guarantees more responsive and prompt decision-making in applications such as autonomous vehicles and robotics that operate in dynamic situations, which contributes to the system’s overall reliability.
The scalability of IRRT-SSA is improved by reducing iterations. Without a corresponding rise in computing needs, it can efficiently manage search areas that are larger and more complicated. Applications requiring the algorithm to adapt to different environmental conditions and robotic platforms rely on scalability.
Fewer iterations indicate a more targeted and resource-efficient planning approach. By focusing its computing power on the most promising regions of the configuration space, the program can efficiently explore and identify the best paths. In situations in which the processing capacity is limited, this optimization of resources is highly valuable.
Fewer iterations mean less power usage, particularly for robotic systems that run on batteries. By reducing the number of computation cycles needed to accomplish its path planning goals, the algorithm helps preserve energy and prolongs the operating life of the robotic platform.
The time savings achieved by IRRT-SSA – a 54% reduction in iterations – are accompanied by practical benefits, such as greater scalability, lower processing needs, improved real-time capabilities, effective resource utilization, and energy conservation. For tasks in which optimizing path planning within a limited time and computational resources is critical, IRRT-SSA stands out as an attractive approach given its many benefits.
6.4 Enhancements in path quality by IRRT-SSA
Compared with the original RRT, IRRT-SSA significantly improves path quality, promoting the construction of efficient and optimal paths. Several important factors contribute to path quality enhancement.
The generated pathways are fine-tuned using IRRT-SSA, allowing the robotic system to move continuously and smoothly. By directing the search toward more gradual configurations and less abrupt directional shifts, SSA aids in path optimization. This optimization is crucial for robotic platforms for tasks requiring reliable and controlled navigation. The trajectory will be more linear and uninterrupted because the algorithm can smooth out bumps in the road. This characteristic becomes especially useful when dealing with robotic systems navigating varied terrains or environments. Navigational stability and dependability are enhanced as a result of reduced path disturbances.
By improving the exploration process, IRRT-SSA successfully reduces the travel distance. Finding shorter routes that minimize unwanted deviations is the main emphasis of the algorithm. When saving energy or resources is paramount, this enhancement is important. By prioritizing safety, the system finds routes with fewer obstructions. With the help of SSA, IRRT-SSA can intelligently move around the configuration space, staying away from obstacles and avoiding collisions. This feature is crucial for uses in settings where hazards are constantly changing or the weather is erratic. IRRT-SSA can produce routes that are more resistant to environmental changes and disturbances. The algorithm’s improved exploration approach ensures consistent performance in real-world circumstances, which SSA drives. This strategy helps create pathways that adapt effectively to fluctuations.
By skillfully negotiating the trade space between finding new configurations and exploiting promising paths, IRRT-SSA achieves a balanced exploration–exploitation trade-off. The technique is designed to converge toward optimal solutions without getting stuck in local minima, which improves the overall quality of the pathways generated. This balance is maintained throughout the process. As a result of these improvements, we can realize the shortest pathways for less cost than those with the original RRT. The paths produced by IRRT-SSA are of high quality due to a combination of factors, including the optimized trajectory smoothness, minimized path discontinuities, reduced travel distance, improved obstacle clearance, consistent path robustness, and balanced exploration–exploitation trade-off. This optimization guarantees a higher degree of dependability, safety, and adaptability in real-world applications and produces shorter pathways. Finding the optimal shortest pathways is of the utmost importance. IRRT-SSA is a great option because of the lowered cost, which includes energy usage, computational resources, and overall system performance.
6.5 Comparison between RRT and IRRT-SSA within a highly complex environment
RRT and IRRT-SSA were implemented using a different known environment, which is highly complex, including many obstacles and narrow passages. The algorithms were run for many iterations, and the performance was evaluated on the basis of the number of nodes generated and the path length. In accordance with the randomness of the RRT algorithm, 20 repeated tests were achieved. The first test was done by setting the starting point at (1, 1) and the target point at (7, 5.5), as shown in Figure 9; the second test was done by setting the starting point at (2, 8) and the target point at (7, 5.5), as presented in Figure 10. The results showed that IRRT-SSA generated fewer nodes than the original RRT. Specifically, RRT generated 1,578 and 1,027 nodes on average, whereas IRRT-SSA generated only 608 and 511 nodes in the first and second tests, respectively. This finding indicates that IRRT-SSA has a more efficient search strategy and explores the space more effectively.
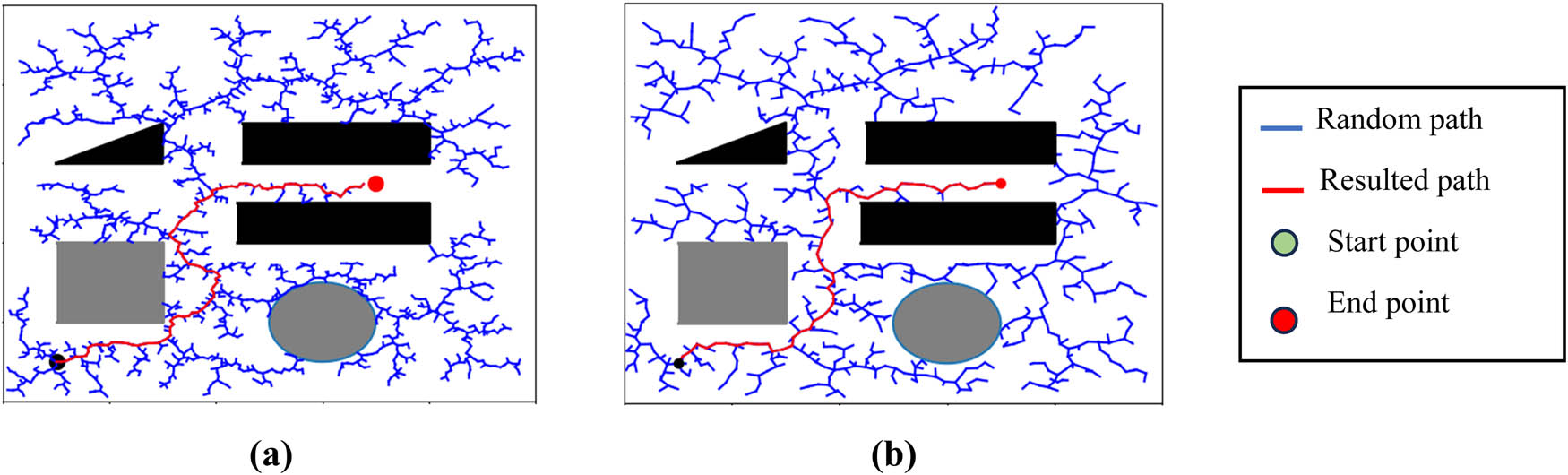
Average path planning with starting point (1, 1) and target point (7, 5.5). (a) RRT and (b) IRRT-SSA.
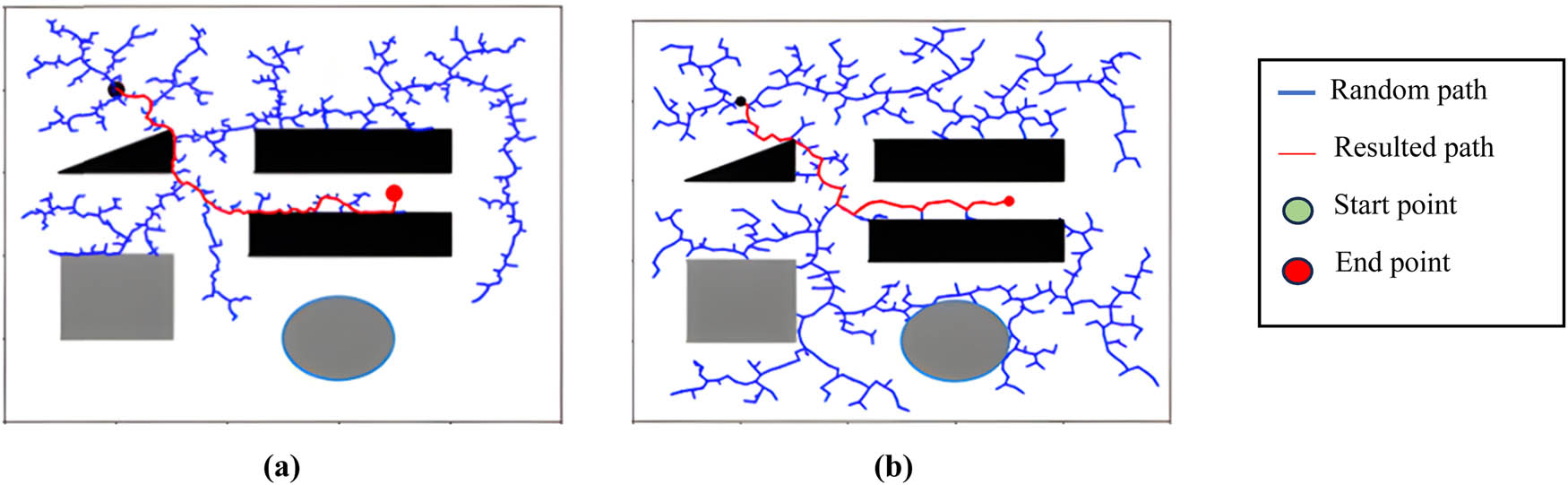
Average path planning with starting point (2, 8) and target point (7, 5.5). (a) RRT and (b) IRRT-SSA.
Furthermore, the path length generated by IRRT-SSA was significantly shorter than that by RRT. Particularly, the average path length generated by RRT was 148.65 and 93.25 units, whereas that by IRRT-SSA was 57.6 and 47.25 units in the first and second tests, respectively. Therefore, IRRT-SSA is better at finding optimal smoothing paths and has a more global search ability. Both tests are demonstrated in Table 3.
Comparison between RRT and IRRT-SSA within a highly complex environment
| Starting and goal points | RRT | IRRT-SSA | ||||
|---|---|---|---|---|---|---|
| Path length | Number of nodes | Iteration | Path length | Number of nodes | Iteration | |
| Starting = (1, 1), Goal = (7, 5.5) | 132 | 1,844 | 2,471 | 52 | 456 | 586 |
| 127 | 932 | 1,270 | 62 | 266 | 447 | |
| 127 | 674 | 1,192 | 54 | 951 | 1,347 | |
| 125 | 1,277 | 1,647 | 59 | 169 | 285 | |
| 128 | 1,388 | 1,895 | 66 | 762 | 1,080 | |
| 135 | 2,023 | 2,605 | 61 | 247 | 570 | |
| 137 | 1,647 | 2,157 | 58 | 706 | 948 | |
| 134 | 1,041 | 1,594 | 66 | 554 | 734 | |
| 144 | 1,283 | 1,967 | 55 | 704 | 1,003 | |
| 112 | 1,795 | 2,279 | 55 | 825 | 1,365 | |
| 132 | 2,016 | 2,739 | 56 | 769 | 1,018 | |
| 109 | 2,557 | 3,408 | 58 | 1,156 | 1,641 | |
| 116 | 1,753 | 2,584 | 53 | 295 | 436 | |
| 127 | 1,357 | 1,895 | 64 | 629 | 846 | |
| 129 | 1,427 | 2,151 | 59 | 831 | 1,134 | |
| 111 | 1,598 | 2,161 | 54 | 125 | 235 | |
| 128 | 903 | 1,351 | 56 | 791 | 1,121 | |
| 192 | 2,836 | 3,815 | 56 | 755 | 972 | |
| 143 | 1,677 | 2,733 | 54 | 187 | 302 | |
| 117 | 1,531 | 2,094 | 54 | 988 | 1,299 | |
| Average | 148.65 | 1,578 | 2200.4 | 57.6 | 608 | 868.45 |
| Starting = (2, 8), Goal = (7, 5.5) | 82 | 1,217 | 1,523 | 39 | 720 | 992 |
| 83 | 1,224 | 1,662 | 55 | 243 | 476 | |
| 119 | 1,948 | 2,594 | 37 | 982 | 1,318 | |
| 83 | 2,275 | 2,994 | 40 | 1,110 | 1,475 | |
| 77 | 673 | 971 | 40 | 699 | 904 | |
| 87 | 1,220 | 1,734 | 57 | 563 | 762 | |
| 120 | 1,260 | 1,947 | 40 | 383 | 513 | |
| 111 | 1,665 | 2,144 | 37 | 212 | 297 | |
| 86 | 851 | 1,155 | 41 | 236 | 313 | |
| 86 | 743 | 955 | 53 | 997 | 1,419 | |
| 118 | 1,021 | 1,621 | 41 | 621 | 846 | |
| 83 | 897 | 1,623 | 36 | 536 | 782 | |
| 78 | 348 | 526 | 41 | 341 | 445 | |
| 72 | 251 | 312 | 59 | 741 | 953 | |
| 87 | 355 | 531 | 42 | 804 | 1,048 | |
| 81 | 533 | 772 | 39 | 133 | 218 | |
| 114 | 718 | 1,239 | 40 | 123 | 167 | |
| 101 | 1,352 | 1,788 | 40 | 379 | 599 | |
| 118 | 1,201 | 1,618 | 38 | 284 | 374 | |
| 79 | 789 | 1,082 | 36 | 120 | 169 | |
| Average | 93.25 | 1,027 | 1439.55 | 47.25 | 511 | 703.5 |
Several significant changes between RRT and its improved version, IRRT-SSA, are noted. As shown by the outcomes, the variations in efficiency, path length, number of nodes, and iterations are apparent.
When exploring the configuration space, RRT-SSA outperforms the core RRT. With SSA, the exploration method becomes smarter and more flexible, which speeds up the convergence to optimal solutions. The results show that IRRT-SSA significantly optimizes path length. Paths produced by the method are, on average, shorter than those produced by the fundamental RRT because it uses SSA’s global and local optimization capabilities. A smaller number of nodes is needed to build the exploration tree using IRRT-SSA. Compared with the fundamental RRT, the simplified and less complicated tree structure is a product of SSA’s swarm intelligence, which aids in the efficient selection of nodes. In IRRT-SSA, as opposed to the fundamental RRT, the number of iterations required for path design is significantly reduced. A faster identification of optimal paths with fewer repetitions is made possible by SSA’s better exploration capabilities, which is responsible for this reduction.
Compared with the essential RRT, IRRT-SSA is more adaptable to changing conditions. In situations in which the environment changes, SSA’s swarm-based approach makes it more robust by allowing the algorithm to alter its exploration technique constantly. SSA’s capacity to integrate global and local optimization techniques allows IRRT-SSA to accomplish a more optimal exploration–exploitation balance. This equilibrium leads to superior path planning with regard to robustness and quality in comparison with the fundamental RRT.
These distinctions demonstrate how IRRT-SSA outperforms the core RRT algorithm and offers a better alternative for robotic path planning by overcoming its inherent limits.
6.6 Comparison of IRRT-SSA with other current sample-based algorithms
A comparative analysis of IRRT-SSA with other sample-based techniques may provide insights into its potential applications and enhanced performance in robotic path planning. The comparisons in Table 4 cover the capabilities of IRRT-SSA in various configurations due to the use of numerous scenarios with diverse beginnings and ends. The mean path length is a fundamental algorithmic metric for path planning. This value denotes the target-chasing distance of the automaton. The IRRT-SSA method reduces path length more effectively than alternative high-tech approaches in all cases. Real-world applications place significant emphasis on energy and resource efficiency, which makes reducing path length indispensable.
Comparison of IRRT-SSA with other current sample-based algorithms
| Starting point and goal point | Criteria | Sample-based methods | |||||
|---|---|---|---|---|---|---|---|
| IRRT-SSA | RRT [17] | RRT- connect [30] | RRT* [31] | Informed RRT* [32] | Smart RRT* [33] | ||
| (2, 1), (2, 8) | Path length avg. | 60 | 119 | 102 | 85 | 76 | 75 |
| Node number avg. | 226 | 471 | 262 | 314 | 1,012 | 947 | |
| Iteration avg. | 267 | 568 | 617 | 447 | 1,354 | 5,365 | |
| (8, 6), (4, 1) | Path length avg. | 48 | 90 | 72 | 67 | 59 | 59 |
| Node number avg. | 416 | 1,027 | 158 | 698 | 1,552 | 1,202 | |
| Iteration avg. | 459 | 1,140 | 168 | 782 | 1,676 | 1,270 | |
| (1, 1), (6, 6) | Path length avg. | 48 | 92 | 84 | 78 | 69 | 72 |
| Node number avg. | 100 | 171 | 216 | 214 | 471 | 394 | |
| Iteration avg. | 147 | 266 | 633 | 459 | 835 | 6,672 | |
| (7, 6), (1, 1) | Path length avg. | 54 | 106 | 90 | 83 | 75 | 75 |
| Node number avg. | 598 | 1,409 | 192 | 1,275 | 4,567 | 3,397 | |
| Iteration avg. | 669 | 1,562 | 512 | 1,483 | 5,344 | 4,389 | |
| (1, 1), (4, 4) | Path length avg. | 32 | 78 | 56 | 52 | 47 | 46 |
| Node number avg. | 51 | 135 | 205 | 77 | 240 | 243 | |
| Iteration avg. | 92 | 228 | 611 | 197 | 756 | 7,637 | |
IRRT-SSA performs better than established sample-based algorithms, including RRT, RRT-connect, RRT*, Informed RRT*, and Smart RRT*, in numerous aspects, such as node exploration, computational efficiency, and path length. IRRT-SSA poses significant competition for robotic path planning implementation given its adaptability and various successful achievements.
Bold values indicates to highlight the results of the proposed algorithm.
The average number of nodes indicates the exploratory efficacy of an algorithm. IRRT-SSA expedites research in comparison with alternative methodologies through the progressive reduction of nodes. IRRT-SSA could transverse the search space and identify the optimal paths. Node exploration reduction improves computational efficiency in real-time applications, where making fast decisions requires less data.
The computation efficacy of an algorithm can be indicative of the average number of iterations performed. Its low number of iterations indicates that IRRT-SSA can converge to optimal solutions while conserving computational resources. The IRRT-SSA method successfully identifies feasible solutions. The significance of robot computer efficiency in real-time applications lies in the correlation between the pace at which decisions are made and the robot’s ability to react and navigate.
The previously mentioned results illuminate the algorithm’s prospective practical implementations and validate its efficacy compared with previous methodologies. The effective trajectory determination facilitated by IRRT-SSA is critical for autonomous robotics and other utilizations [34,35].
7 IRRT-SSA performance
IRRT-SSA outperforms the original RRT in several ways.
When optimizing paths, RRT-SSA performs much better. On average, the pathways generated by SSA are shorter than those generated by the fundamental RRT because it includes a sophisticated global and local optimization mechanism. For robotic navigation to be efficient and resource-effective, this improvement is vital.
Including SSA in IRRT-SSA significantly reduces the number of nodes needed to build the exploration tree. By navigating the configuration space selectively, SSA’s swarm intelligence helps the algorithm avoid using excessive nodes. Compared with that using the fundamental RRT, this reduction helps make the path planning process more streamlined and computationally efficient.
The number of iterations required for path planning is significantly reduced using IRRT-SSA. The adaptive exploration strategy made possible by SSA enables the algorithm to converge toward optimal solutions with fewer iterations and higher efficiency compared with those with the fundamental RRT. The decrease in iterations demonstrates the algorithm’s enhanced computational efficiency.
By incorporating SSA’s increased exploration strategy, RRT-SSA performs better than the essential RRT. Using SSA’s swarm-based technique, IRRT-SSA can adapt to an environment’s features while intelligently exploring configuration space. In complicated and ever-changing situations, this flexibility increases the probability of finding optimal paths and improves the quality of those solutions.
In contrast to the fundamental RRT, IRRT-SSA demonstrates improved resilience in constantly changing contexts. Even in situations in which the environment changes over time, the generated pathways will remain relevant and ideal because of IRRT-SSA’s dynamic adaptability of SSA.
An important component of SSA’s role in the improved performance of IRRT-SSA is its adaptive exploration method. The algorithm adapts its search strategy to changes in its surroundings. This adaptability is helpful for path planning when traversing across settings with different levels of complexity, impediments, or dynamic changes. Because SSA is adaptive, it can handle a wide variety of situations with ease.
Given that it is swarm-based, SSA can converge to optimal solutions efficiently. The salp algorithm converges toward optimal paths more effectively than standard exploration methods because individuals collaborate to explore and utilize the search space. With its efficiency, IRRT-SSA can quickly converge to high-quality solutions with fewer iterations than the fundamental RRT.
Improving IRRT-SSA’s resilience in dynamic settings is one of SSA’s most significant accomplishments. The algorithm’s ability to adjust to new conditions, made possible by SSA’s swarm intelligence, guarantees that the produced paths will remain optimal and relevant regardless of how the environment changes. This ability is a key advantage in real-world scenarios because the environment might change over time.
When searching, SSA makes sure to balance exploiting and exploring. This balance is critical to ensure that the algorithm explores the configuration space completely and prevents early convergence to inferior solutions. An effective exploitation–exploration balance enhances the diversity of created paths, increasing the possibility of locating the best-suited path for each given case.
To sum up, SSA adds sophisticated optimization and flexibility to IRRT-SSA, allowing it to surpass the restrictions of the initial RRT. As a result of the salp swarm’s combined intelligence, IRRT-SSA is an effective tool for robotic path planning in complex and varied situations, offering advantages in computational efficiency, resilience, and path quality.
7.1 Influence on the practical deployment of robotics
In situations that need fast path planning and navigation, the improvements achieved by IRRT-SSA have far-reaching consequences on the real-world application of robotics. The following examples show how these enhancements can benefit practical uses:
Real-time navigation is made more efficient with IRRT-SSA because of its optimized path creation. This algorithm is perfect for situations that require quick decisions and responses because it can efficiently explore and modify courses in dynamic settings, allowing robotic devices to travel efficiently.
Robots’ ability to navigate complicated situations is strengthened by the enhanced path quality, defined by less abrupt trajectories and fewer interruptions. IRRT-SSA is well suited for deployment in settings with varied terrain, barriers, or uncertain conditions due to its ability to evaluate safety margins and adjust to perturbations, guaranteeing reliable performance.
Resource-efficient path design is aided by RRT-SSA’s emphasis on minimizing path length and computational overhead. For real-world applications, this aspect means less strain on robotic systems, better use of computing resources, and optimized energy use. Applications dealing with limited resources must prioritize these variables.
Path length, number of nodes, and iterations are just a few of the metrics this algorithm can handle, making it suitable for various robotics tasks. The advancements made to IRRT-SSA apply to a wide range of deployment scenarios, whether the objective is to optimize pathways for efficiency, preserve energy, or navigate through crowded settings safely.
The capacity of IRRT-SSA to create pathways with shorter travel distances and enhanced energy efficiency results in lower operational and maintenance costs. By reducing mechanical stress and optimizing wear and tear on robotic components, the optimized pathways save energy and contribute to a lengthened lifespan of the system.
The algorithm uses SSA to improve the precision and accuracy of navigation. With the help of SSA’s intelligent exploration method, IRRT-SSA can move and position robotic devices precisely by navigating complicated configuration spaces.
The breakthroughs made by IRRT-SSA greatly aids autonomous robotic systems. Robots can now navigate and plan their paths efficiently with this algorithm, allowing them to work autonomously in various settings with minimal human oversight. This feature is of paramount importance for uses such as driverless cars, drone surveillance, and robotic exploration.
Overall, the advancements made possible by IRRT-SSA should have a major impact on the actual implementation of robots. The algorithm’s versatility, efficiency, resilience, optimization of resources, and capacity to handle complicated real-world scenarios make it a great tool for improving intelligent robotic systems and autonomous navigation.
7.2 Limitations of the study
IRRT-SSA would not construct pathways efficiently if the hyperparameters are not ideal. Finding the optimal hyperparameters for diverse situations remains difficult.
The proposed study may struggle with changing environmental dynamics. The algorithm’s versatility might be tested in changing environments or dynamically imposed hurdles during path planning.
The performance of IRRT-SSA, which assumes homogeneous terrain, may be affected by environments with severely nonuniform surfaces, different friction characteristics, or intricate terrains.
Initial configuration space data precision affects algorithm performance. Suboptimal route planning can occur from erroneous or missing environmental data, highlighting the importance of high-quality input data.
8 Conclusion
The proposed IRRT-SSA solves the limitations of the RRT path planning algorithm in terms of the lack of global search ability and the tendency to generate suboptimal paths by using the metaheuristic SSA. The new algorithm outperforms the original RRT algorithm in generating paths for a robot from the starting point position to the target point. Specifically, IRRT-SSA improves the original RRT in terms of average path length, number of nodes, and number of iterations by approximately 49, 54, and 54%, respectively. These enhancement ratios improve the path quality, realizing the best smoothness paths close to the optimal solution at less cost. For robotic path planning to be more efficient and successful, IRRT-SSA’s practical benefits are crucial. Compared with the baseline RRT, IRRT-SSA shows a significant improvement in average path length, decreasing it by 49%, through its integration of SSA. This reduction in the number of paths that robots must travel has real-world relevance for maximizing efficiency and minimizing operational expenses. In real-world situations in which computational resources and time restrictions are critical, the algorithm’s efficiency is further shown by the large drop of approximately 54% in the number of nodes and iterations. Because of these real-world benefits, IRRT-SSA is regarded as a potential answer for situations and sectors that need rapid and accurate path planning for robotic system deployment. Several obstacles and ways exist to improve the performance and applicability of IRRT-SSA, which offers remarkable advances in robotic path planning for highly complicated applications. Further testing in real-world settings is required to verify the algorithm’s performance in practical situations. Extensive field trials and validations across varied environments and application domains could be the focus of future research efforts to evaluate the robustness, dependability, and generalizability of IRRT-SSA. In conclusion, improving IRRT-SSA by tackling these issues and following the mentioned improvement paths will help intelligent and adaptive robotic systems continue to evolve and be more useful in complicated robotic applications.
-
Funding information: The authors received no specific funding for this study.
-
Author contributions: Dena Kadhim Muhsen: Conceptualization, Methodology, Formal analysis, programming, Investigation, Writing – review & editing. Firas Abdulrazzaq Raheem: Conceptualization, Formal analysis, Data curation, Supervision, review & editing. Ahmed T. Sadiq: Conceptualization, Formal analysis, Data curation, Supervision, review & editing.
-
Conflict of interest: The authors declare no conflict of interest.
-
Data availability statement: Data sharing is not applicable to this article as no datasets were generated or analysed during the current study.
References
[1] Lin S, Liu A, Wang J, Kong X. A review of path-planning approaches for multiple mobile robots. Machines. 2022;10(9):773. 10.3390/machines10090773.Search in Google Scholar
[2] Shihab BS, Abdullah HN, Hassnawi LA. Improved artificial bee colony algorithm-based path planning of unmanned aerial vehicle using late acceptance hill climbing. Int J Intell Eng Syst. 2022;15(6):431–42. 10.22266/ijies2022.1231.39.Search in Google Scholar
[3] Sadiq AT, Hasan AN. Robot path planning based on PSO and D algorithms in dynamic environment. In 2017 International Conference on Current Research in Computer Science and Information Technology (ICCIT); 2017. 10.1109/crcsit.2017.7965550.Search in Google Scholar
[4] Wang Y, Jha DK, Akemi Y. A two-stage RRT path planner for automated parking. 2017 13th IEEE Conference on Automation Science and Engineering (CASE). Xi’an, China; 2017. p. 496–502.10.1109/COASE.2017.8256153Search in Google Scholar
[5] Denk M, Bickel S, Steck P, Goetz S, Völkl H, Wartzack S. Generating digital twins for path-planning of autonomous robots and drones using constrained homotopic shrinking for 2D and 3D environment modeling. Appl Sci. 2022;13(1):105. 10.3390/app13010105.Search in Google Scholar
[6] Ding J, Zhou Y, Huang X, Song K, Lu S, Wang L. An improved RRT∗ algorithm for robot path planning based on path expansion heuristic sampling. J Comput Sci. 2023;67:101937. 10.1016/j.jocs.2022.101937.Search in Google Scholar
[7] Raafat SM, Raheem FA. Intelligent and robust path planning and control of robotic systems. In Springer eBooks. Switzerland: Springer Nature; 2017. p. 291–317. 10.1007/978-3-319-43901-3_13.Search in Google Scholar
[8] El-kenawy EM, Shafi Khan Z, Ibrahim A, Abdullah Aloyaydi B, Arafat Ali H, et al. Metaheuristic optimization for mobile robot navigation based on path planning. Computers Mater Continua. 2022;73(2):2241–55.10.32604/cmc.2022.026672Search in Google Scholar
[9] Karur K, Sharma N, Dharmatti C, Siegel JE. A survey of path planning algorithms for mobile robots. Vehicles. 2021;3(3):448–68. 10.3390/vehicles3030027.Search in Google Scholar
[10] Raheem FA, Raafat SM, Mahdi SM. Robot path-planning research applications in static and dynamic environments. In: Furze JN, Eslamian S, Raafat SM, Swing K, editors. Earth systems protection and sustainability. Cham: Springer; 2022. 10.1007/978-3-030-85829-2_12.Search in Google Scholar
[11] Yuan C, Shuai C, Zhang WA. Dynamic multiple-query RRT planning algorithm for manipulator obstacle avoidance. Appl Sci. 2023;13(6):3394. 10.3390/app13063394.Search in Google Scholar
[12] Viseras A, Losada RO, Merino L. Planning with ants. Int J Adv Rob Syst. 2016;13(5):172988141666407. 10.1177/1729881416664078.Search in Google Scholar
[13] Kiani F, Seyyedabbasi A, Aliyev R, Gulle MU, Basyildiz H, Shah MM. Adapted-RRT: Novel hybrid method to solve three-dimensional path planning problem using sampling and metaheuristic-based algorithms. Neural Comput Appl. 2021;33(22):15569–99. 10.1007/s00521-021-06179-0.Search in Google Scholar
[14] Wang X, Yang S. Improved RRT algorithm path planning combined with artificial potential field algorithm. The 11th International Workshop on Computer Science and Engineering (WCSE 2021), Shanghai, China; 2021. p. 133–7. 10.18178/wcse.2021.06.020.Search in Google Scholar
[15] Malik A, Pohan M. The development of a path planning algorithm combining the rapidly-exploring random tree algorithm and the particle swarm optimization algorithm. J Eng Sci Technol. 2022;17(6):3742–54.Search in Google Scholar
[16] LaValle SM. Rapidly-exploring random trees: A new tool for path planning. The Annual Research Report; 1998.Search in Google Scholar
[17] Rasheed AA, Al-Araji AS, Abdullah MN. Static and dynamic path planning algorithms design for a wheeled mobile robot based on a hybrid technique. Int J Intell Eng Syst. 2022;15(4):167–81. 10.22266/ijies2022.0831.16.Search in Google Scholar
[18] Amin J, Bo JD, Mehra RK. A fast and efficient approach to path planning for unmanned vehicles. In AIAA Guidance, Navigation, and Control Conference and Exhibit; 2006. 10.2514/6.2006-6103.Search in Google Scholar
[19] Tang BZ, Zheng S, Ren Y, Du D. Path planning based on the improved RRT* algorithm for the mining truck. CMC. 2022;71(2):3571–87. 10.32604/cmc.2022.022183.Search in Google Scholar
[20] Lonklang A, Botzheim J. Improved rapidly exploring random tree with bacterial mutation and node deletion for offline path planning of mobile robot. Electronics. 2022;11(9):1459. 10.3390/electronics11091459.Search in Google Scholar
[21] Kang JU, Choi Y, Jung J. A method of enhancing rapidly-exploring random tree robot path planning using midpoint interpolation. Appl Sci. 2021;11(18):8483. 10.3390/app11188483.Search in Google Scholar
[22] Pham QC. Trajectory Planning. In: Nee, A, editor. Handbook of Manufacturing Engineering and Technology. London: Springer. https://doi.org/10.1007/978-1-4471-4976-7_92-1.Search in Google Scholar
[23] Dagal I, Akın B, Akboy E. MPPT mechanism based on novel hybrid particle swarm optimization and salp swarm optimization algorithm for battery charging through simulink. Sci Rep. 2022;12:1–17. 10.1038/s41598-022-06609-6.Search in Google Scholar PubMed PubMed Central
[24] Romeh AE, Mirjalili S. Multi-robot exploration of unknown space using combined meta-heuristic salp swarm algorithm and deterministic coordinated multi-robot exploration. Sensors. 2023;23(4):2156. 10.3390/s23042156.Search in Google Scholar PubMed PubMed Central
[25] Alrowais F, Alotaibi SS, Al-Wesabi FN, Negm N, Alabdan R, Marzouk R, et al. Deep transfer learning enabled intelligent object detection for crowd density analysis on video surveillance systems. Appl Sci. 2022;12(13):6665. 10.3390/app12136665.Search in Google Scholar
[26] Mirjalili S, Gandomi AH, Mirjalili S, Saremi S, Faris H, Mirjalili S. Salp Swarm Algorithm: A bio-inspired optimizer for engineering design problems. Adv Eng Softw. 2017;114:163–91. 10.1016/j.advengsoft.2017.07.002.Search in Google Scholar
[27] Cheng X, Zhu L, Lu H, Wei J, Wu N. Robot path planning based on an improved salp swarm algorithm. J Sens. 2022;12:1–16. 10.1155/2022/2559955.Search in Google Scholar
[28] Alotaibi SS, Mengash HA, Negm N, Marzouk R, Hilal AM, Shamseldin MA, et al. Swarm intelligence with deep transfer learning driven aerial image classification model on UAV networks. Appl Sci. 2022;12(13):6488. 10.3390/app12136488.Search in Google Scholar
[29] Khajehzadeh M, Iraji A, Majdi A, Keawsawasvong S, Nehdi ML. Adaptive salp swarm algorithm for optimization of geotechnical structures. Appl Sci. 2022;12(13):6749. 10.3390/app12136749.Search in Google Scholar
[30] Kuffner JJ, LaValle SM. RRT-connect: An efficient approach to single-query path planning. Proceedings 2000 ICRA. Millennium Conference. IEEE International Conference on Robotics and Automation. Symposia Proceedings (Cat. No.00CH37065). Vol. 2. San Francisco, CA, USA; 2000. p. 995–1001. 10.1109/ROBOT.2000.844730.Search in Google Scholar
[31] Karaman S, Walter MR, Perez A, Frazzoli E, Teller S. Anytime motion planning using the RRT*. IEEE International Conference on Robotics and Automation. Shanghai, China; 2011. p. 1478–83. 10.1109/ICRA.2011.5980479.Search in Google Scholar
[32] Gammell JD, Srinivasa SS, Barfoot TD. Informed RRT*: Optimal sampling-based path planning focused via direct sampling of an admissible ellipsoidal heuristic. IEEE/RSJ International Conference on Intelligent Robots and Systems. Chicago, IL, USA: 2014. p. 2997–3004. 10.1109/IROS.2014.6942976.Search in Google Scholar
[33] Nasir J, Islam F, Malik U, Ayaz Y, Hasan O, Khan M, et al. RRT*-SMART: A rapid convergence implementation of RRT*. Int J Adv Rob Syst. 2013;10(7):299. 10.5772/56718.Search in Google Scholar
[34] Al-Azzawi S, Hasan AM. A new 4D hidden hyperchaotic system with higher largest Lyapunov exponent and its synchronization. Int J Math Stat Computer Sci. 2023;2:63–74. 10.59543/ijmscs.v2i.8469.Search in Google Scholar
[35] Yassine S, Stanulov A. A comparative analysis of machine learning algorithms for the purpose of predicting Norwegian air passenger traffic. Int J Math Stat Computer Sci. 2024;2:28–43. 10.59543/ijmscs.v2i.7851.Search in Google Scholar
© 2024 the author(s), published by De Gruyter
This work is licensed under the Creative Commons Attribution 4.0 International License.
Articles in the same Issue
- Research Articles
- A study on intelligent translation of English sentences by a semantic feature extractor
- Detecting surface defects of heritage buildings based on deep learning
- Combining bag of visual words-based features with CNN in image classification
- Online addiction analysis and identification of students by applying gd-LSTM algorithm to educational behaviour data
- Improving multilayer perceptron neural network using two enhanced moth-flame optimizers to forecast iron ore prices
- Sentiment analysis model for cryptocurrency tweets using different deep learning techniques
- Periodic analysis of scenic spot passenger flow based on combination neural network prediction model
- Analysis of short-term wind speed variation, trends and prediction: A case study of Tamil Nadu, India
- Cloud computing-based framework for heart disease classification using quantum machine learning approach
- Research on teaching quality evaluation of higher vocational architecture majors based on enterprise platform with spherical fuzzy MAGDM
- Detection of sickle cell disease using deep neural networks and explainable artificial intelligence
- Interval-valued T-spherical fuzzy extended power aggregation operators and their application in multi-criteria decision-making
- Characterization of neighborhood operators based on neighborhood relationships
- Real-time pose estimation and motion tracking for motion performance using deep learning models
- QoS prediction using EMD-BiLSTM for II-IoT-secure communication systems
- A novel framework for single-valued neutrosophic MADM and applications to English-blended teaching quality evaluation
- An intelligent error correction model for English grammar with hybrid attention mechanism and RNN algorithm
- Prediction mechanism of depression tendency among college students under computer intelligent systems
- Research on grammatical error correction algorithm in English translation via deep learning
- Microblog sentiment analysis method using BTCBMA model in Spark big data environment
- Application and research of English composition tangent model based on unsupervised semantic space
- 1D-CNN: Classification of normal delivery and cesarean section types using cardiotocography time-series signals
- Real-time segmentation of short videos under VR technology in dynamic scenes
- Application of emotion recognition technology in psychological counseling for college students
- Classical music recommendation algorithm on art market audience expansion under deep learning
- A robust segmentation method combined with classification algorithms for field-based diagnosis of maize plant phytosanitary state
- Integration effect of artificial intelligence and traditional animation creation technology
- Artificial intelligence-driven education evaluation and scoring: Comparative exploration of machine learning algorithms
- Intelligent multiple-attributes decision support for classroom teaching quality evaluation in dance aesthetic education based on the GRA and information entropy
- A study on the application of multidimensional feature fusion attention mechanism based on sight detection and emotion recognition in online teaching
- Blockchain-enabled intelligent toll management system
- A multi-weapon detection using ensembled learning
- Deep and hand-crafted features based on Weierstrass elliptic function for MRI brain tumor classification
- Design of geometric flower pattern for clothing based on deep learning and interactive genetic algorithm
- Mathematical media art protection and paper-cut animation design under blockchain technology
- Deep reinforcement learning enhances artistic creativity: The case study of program art students integrating computer deep learning
- Transition from machine intelligence to knowledge intelligence: A multi-agent simulation approach to technology transfer
- Research on the TF–IDF algorithm combined with semantics for automatic extraction of keywords from network news texts
- Enhanced Jaya optimization for improving multilayer perceptron neural network in urban air quality prediction
- Design of visual symbol-aided system based on wireless network sensor and embedded system
- Construction of a mental health risk model for college students with long and short-term memory networks and early warning indicators
- Personalized resource recommendation method of student online learning platform based on LSTM and collaborative filtering
- Employment management system for universities based on improved decision tree
- English grammar intelligent error correction technology based on the n-gram language model
- Speech recognition and intelligent translation under multimodal human–computer interaction system
- Enhancing data security using Laplacian of Gaussian and Chacha20 encryption algorithm
- Construction of GCNN-based intelligent recommendation model for answering teachers in online learning system
- Neural network big data fusion in remote sensing image processing technology
- Research on the construction and reform path of online and offline mixed English teaching model in the internet era
- Real-time semantic segmentation based on BiSeNetV2 for wild road
- Online English writing teaching method that enhances teacher–student interaction
- Construction of a painting image classification model based on AI stroke feature extraction
- Big data analysis technology in regional economic market planning and enterprise market value prediction
- Location strategy for logistics distribution centers utilizing improved whale optimization algorithm
- Research on agricultural environmental monitoring Internet of Things based on edge computing and deep learning
- The application of curriculum recommendation algorithm in the driving mechanism of industry–teaching integration in colleges and universities under the background of education reform
- Application of online teaching-based classroom behavior capture and analysis system in student management
- Evaluation of online teaching quality in colleges and universities based on digital monitoring technology
- Face detection method based on improved YOLO-v4 network and attention mechanism
- Study on the current situation and influencing factors of corn import trade in China – based on the trade gravity model
- Research on business English grammar detection system based on LSTM model
- Multi-source auxiliary information tourist attraction and route recommendation algorithm based on graph attention network
- Multi-attribute perceptual fuzzy information decision-making technology in investment risk assessment of green finance Projects
- Research on image compression technology based on improved SPIHT compression algorithm for power grid data
- Optimal design of linear and nonlinear PID controllers for speed control of an electric vehicle
- Traditional landscape painting and art image restoration methods based on structural information guidance
- Traceability and analysis method for measurement laboratory testing data based on intelligent Internet of Things and deep belief network
- A speech-based convolutional neural network for human body posture classification
- The role of the O2O blended teaching model in improving the teaching effectiveness of physical education classes
- Genetic algorithm-assisted fuzzy clustering framework to solve resource-constrained project problems
- Behavior recognition algorithm based on a dual-stream residual convolutional neural network
- Ensemble learning and deep learning-based defect detection in power generation plants
- Optimal design of neural network-based fuzzy predictive control model for recommending educational resources in the context of information technology
- An artificial intelligence-enabled consumables tracking system for medical laboratories
- Utilization of deep learning in ideological and political education
- Detection of abnormal tourist behavior in scenic spots based on optimized Gaussian model for background modeling
- RGB-to-hyperspectral conversion for accessible melanoma detection: A CNN-based approach
- Optimization of the road bump and pothole detection technology using convolutional neural network
- Comparative analysis of impact of classification algorithms on security and performance bug reports
- Cross-dataset micro-expression identification based on facial ROIs contribution quantification
- Demystifying multiple sclerosis diagnosis using interpretable and understandable artificial intelligence
- Unifying optimization forces: Harnessing the fine-structure constant in an electromagnetic-gravity optimization framework
- E-commerce big data processing based on an improved RBF model
- Analysis of youth sports physical health data based on cloud computing and gait awareness
- CCLCap-AE-AVSS: Cycle consistency loss based capsule autoencoders for audio–visual speech synthesis
- An efficient node selection algorithm in the context of IoT-based vehicular ad hoc network for emergency service
- Computer aided diagnoses for detecting the severity of Keratoconus
- Improved rapidly exploring random tree using salp swarm algorithm
- Network security framework for Internet of medical things applications: A survey
- Predicting DoS and DDoS attacks in network security scenarios using a hybrid deep learning model
- Enhancing 5G communication in business networks with an innovative secured narrowband IoT framework
- Quokka swarm optimization: A new nature-inspired metaheuristic optimization algorithm
- Digital forensics architecture for real-time automated evidence collection and centralization: Leveraging security lake and modern data architecture
- Image modeling algorithm for environment design based on augmented and virtual reality technologies
- Enhancing IoT device security: CNN-SVM hybrid approach for real-time detection of DoS and DDoS attacks
- High-resolution image processing and entity recognition algorithm based on artificial intelligence
- Review Articles
- Transformative insights: Image-based breast cancer detection and severity assessment through advanced AI techniques
- Network and cybersecurity applications of defense in adversarial attacks: A state-of-the-art using machine learning and deep learning methods
- Applications of integrating artificial intelligence and big data: A comprehensive analysis
- A systematic review of symbiotic organisms search algorithm for data clustering and predictive analysis
- Modelling Bitcoin networks in terms of anonymity and privacy in the metaverse application within Industry 5.0: Comprehensive taxonomy, unsolved issues and suggested solution
- Systematic literature review on intrusion detection systems: Research trends, algorithms, methods, datasets, and limitations
Articles in the same Issue
- Research Articles
- A study on intelligent translation of English sentences by a semantic feature extractor
- Detecting surface defects of heritage buildings based on deep learning
- Combining bag of visual words-based features with CNN in image classification
- Online addiction analysis and identification of students by applying gd-LSTM algorithm to educational behaviour data
- Improving multilayer perceptron neural network using two enhanced moth-flame optimizers to forecast iron ore prices
- Sentiment analysis model for cryptocurrency tweets using different deep learning techniques
- Periodic analysis of scenic spot passenger flow based on combination neural network prediction model
- Analysis of short-term wind speed variation, trends and prediction: A case study of Tamil Nadu, India
- Cloud computing-based framework for heart disease classification using quantum machine learning approach
- Research on teaching quality evaluation of higher vocational architecture majors based on enterprise platform with spherical fuzzy MAGDM
- Detection of sickle cell disease using deep neural networks and explainable artificial intelligence
- Interval-valued T-spherical fuzzy extended power aggregation operators and their application in multi-criteria decision-making
- Characterization of neighborhood operators based on neighborhood relationships
- Real-time pose estimation and motion tracking for motion performance using deep learning models
- QoS prediction using EMD-BiLSTM for II-IoT-secure communication systems
- A novel framework for single-valued neutrosophic MADM and applications to English-blended teaching quality evaluation
- An intelligent error correction model for English grammar with hybrid attention mechanism and RNN algorithm
- Prediction mechanism of depression tendency among college students under computer intelligent systems
- Research on grammatical error correction algorithm in English translation via deep learning
- Microblog sentiment analysis method using BTCBMA model in Spark big data environment
- Application and research of English composition tangent model based on unsupervised semantic space
- 1D-CNN: Classification of normal delivery and cesarean section types using cardiotocography time-series signals
- Real-time segmentation of short videos under VR technology in dynamic scenes
- Application of emotion recognition technology in psychological counseling for college students
- Classical music recommendation algorithm on art market audience expansion under deep learning
- A robust segmentation method combined with classification algorithms for field-based diagnosis of maize plant phytosanitary state
- Integration effect of artificial intelligence and traditional animation creation technology
- Artificial intelligence-driven education evaluation and scoring: Comparative exploration of machine learning algorithms
- Intelligent multiple-attributes decision support for classroom teaching quality evaluation in dance aesthetic education based on the GRA and information entropy
- A study on the application of multidimensional feature fusion attention mechanism based on sight detection and emotion recognition in online teaching
- Blockchain-enabled intelligent toll management system
- A multi-weapon detection using ensembled learning
- Deep and hand-crafted features based on Weierstrass elliptic function for MRI brain tumor classification
- Design of geometric flower pattern for clothing based on deep learning and interactive genetic algorithm
- Mathematical media art protection and paper-cut animation design under blockchain technology
- Deep reinforcement learning enhances artistic creativity: The case study of program art students integrating computer deep learning
- Transition from machine intelligence to knowledge intelligence: A multi-agent simulation approach to technology transfer
- Research on the TF–IDF algorithm combined with semantics for automatic extraction of keywords from network news texts
- Enhanced Jaya optimization for improving multilayer perceptron neural network in urban air quality prediction
- Design of visual symbol-aided system based on wireless network sensor and embedded system
- Construction of a mental health risk model for college students with long and short-term memory networks and early warning indicators
- Personalized resource recommendation method of student online learning platform based on LSTM and collaborative filtering
- Employment management system for universities based on improved decision tree
- English grammar intelligent error correction technology based on the n-gram language model
- Speech recognition and intelligent translation under multimodal human–computer interaction system
- Enhancing data security using Laplacian of Gaussian and Chacha20 encryption algorithm
- Construction of GCNN-based intelligent recommendation model for answering teachers in online learning system
- Neural network big data fusion in remote sensing image processing technology
- Research on the construction and reform path of online and offline mixed English teaching model in the internet era
- Real-time semantic segmentation based on BiSeNetV2 for wild road
- Online English writing teaching method that enhances teacher–student interaction
- Construction of a painting image classification model based on AI stroke feature extraction
- Big data analysis technology in regional economic market planning and enterprise market value prediction
- Location strategy for logistics distribution centers utilizing improved whale optimization algorithm
- Research on agricultural environmental monitoring Internet of Things based on edge computing and deep learning
- The application of curriculum recommendation algorithm in the driving mechanism of industry–teaching integration in colleges and universities under the background of education reform
- Application of online teaching-based classroom behavior capture and analysis system in student management
- Evaluation of online teaching quality in colleges and universities based on digital monitoring technology
- Face detection method based on improved YOLO-v4 network and attention mechanism
- Study on the current situation and influencing factors of corn import trade in China – based on the trade gravity model
- Research on business English grammar detection system based on LSTM model
- Multi-source auxiliary information tourist attraction and route recommendation algorithm based on graph attention network
- Multi-attribute perceptual fuzzy information decision-making technology in investment risk assessment of green finance Projects
- Research on image compression technology based on improved SPIHT compression algorithm for power grid data
- Optimal design of linear and nonlinear PID controllers for speed control of an electric vehicle
- Traditional landscape painting and art image restoration methods based on structural information guidance
- Traceability and analysis method for measurement laboratory testing data based on intelligent Internet of Things and deep belief network
- A speech-based convolutional neural network for human body posture classification
- The role of the O2O blended teaching model in improving the teaching effectiveness of physical education classes
- Genetic algorithm-assisted fuzzy clustering framework to solve resource-constrained project problems
- Behavior recognition algorithm based on a dual-stream residual convolutional neural network
- Ensemble learning and deep learning-based defect detection in power generation plants
- Optimal design of neural network-based fuzzy predictive control model for recommending educational resources in the context of information technology
- An artificial intelligence-enabled consumables tracking system for medical laboratories
- Utilization of deep learning in ideological and political education
- Detection of abnormal tourist behavior in scenic spots based on optimized Gaussian model for background modeling
- RGB-to-hyperspectral conversion for accessible melanoma detection: A CNN-based approach
- Optimization of the road bump and pothole detection technology using convolutional neural network
- Comparative analysis of impact of classification algorithms on security and performance bug reports
- Cross-dataset micro-expression identification based on facial ROIs contribution quantification
- Demystifying multiple sclerosis diagnosis using interpretable and understandable artificial intelligence
- Unifying optimization forces: Harnessing the fine-structure constant in an electromagnetic-gravity optimization framework
- E-commerce big data processing based on an improved RBF model
- Analysis of youth sports physical health data based on cloud computing and gait awareness
- CCLCap-AE-AVSS: Cycle consistency loss based capsule autoencoders for audio–visual speech synthesis
- An efficient node selection algorithm in the context of IoT-based vehicular ad hoc network for emergency service
- Computer aided diagnoses for detecting the severity of Keratoconus
- Improved rapidly exploring random tree using salp swarm algorithm
- Network security framework for Internet of medical things applications: A survey
- Predicting DoS and DDoS attacks in network security scenarios using a hybrid deep learning model
- Enhancing 5G communication in business networks with an innovative secured narrowband IoT framework
- Quokka swarm optimization: A new nature-inspired metaheuristic optimization algorithm
- Digital forensics architecture for real-time automated evidence collection and centralization: Leveraging security lake and modern data architecture
- Image modeling algorithm for environment design based on augmented and virtual reality technologies
- Enhancing IoT device security: CNN-SVM hybrid approach for real-time detection of DoS and DDoS attacks
- High-resolution image processing and entity recognition algorithm based on artificial intelligence
- Review Articles
- Transformative insights: Image-based breast cancer detection and severity assessment through advanced AI techniques
- Network and cybersecurity applications of defense in adversarial attacks: A state-of-the-art using machine learning and deep learning methods
- Applications of integrating artificial intelligence and big data: A comprehensive analysis
- A systematic review of symbiotic organisms search algorithm for data clustering and predictive analysis
- Modelling Bitcoin networks in terms of anonymity and privacy in the metaverse application within Industry 5.0: Comprehensive taxonomy, unsolved issues and suggested solution
- Systematic literature review on intrusion detection systems: Research trends, algorithms, methods, datasets, and limitations

