Home Technology Effect of excitation type on vibration characteristics of typical ship grillage structure
Article Open Access

Effect of excitation type on vibration characteristics of typical ship grillage structure

  • Tongda Zou , Yuhang Tang , Xuhong Miao EMAIL logo , Yuan Du , Fuxin Jia and Yanhe Shan
Published/Copyright: August 30, 2022
Download Article (PDF)
Become an author with De Gruyter Brill
Submit Manuscript Author Information
REVIEWS ON ADVANCED MATERIALS SCIENCE
From the journal REVIEWS ON ADVANCED MATERIALS SCIENCE Volume 61 Issue 1

Abstract

Aiming at the present situation that the effect of excitation type on typical ship grillage structure vibration is not fully revealed, different excitations are applied on typical ship grillage structure to study the effect of different excitation. Finite element method (FEM) is introduced to solve grillage vibration and sound radiation, and a test model is used to verify the effectiveness of the simulation method by comparing test results and simulation results. Mean square vibration velocity and acoustic power are compared to explore the effect of excitation type on grillage vibration. The research shows that the simulation method (FEM) is effective in grillage vibration and sound radiation; the peak frequency of acoustic power and mean square velocity of grillage structure under different excitation are basically the same; uniform distribution excitation is a better way to reduce structure vibration and noise.

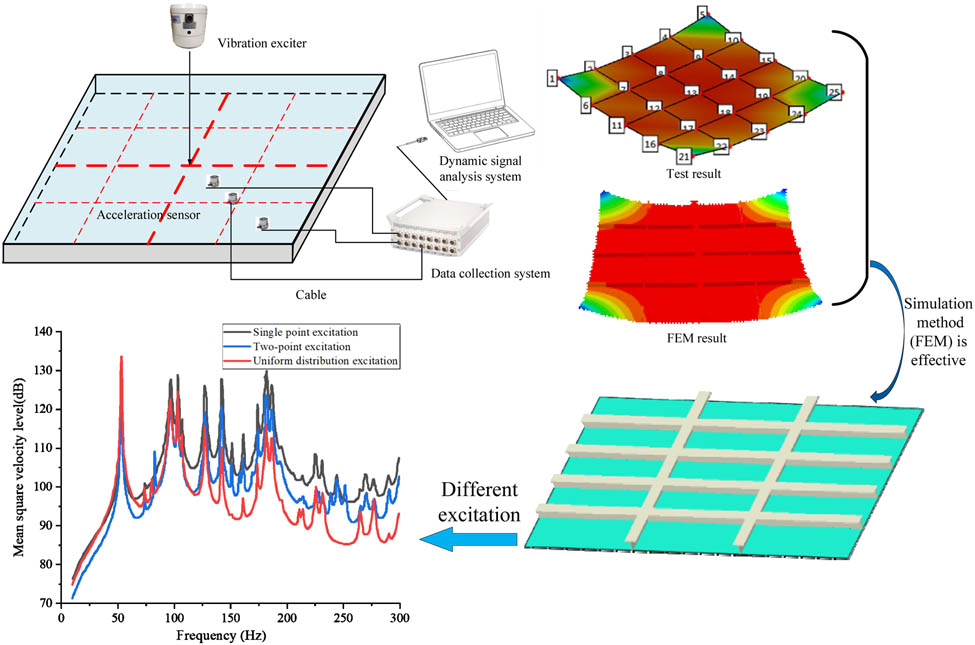
Graphical abstract

Keywords: ship grillage; vibration characteristics; model tests; excitation type; FEM

1 Introduction

Ship is one of the main means of transportation on the sea, reducing ship vibration, and noise has gradually become the main breakthrough direction for ship designers [1,2], and it is particularly important to explore the vibration transmission characteristics of ship structure. The hull structure can be seen as the coupling connection of numerous grillage structures [3]. Grillage structure is complex in form and has coupling vibration problems of beam structure and plate structure [4]. At the same time, the grillage structure is the main transmission path and response area of vibration energy [5]. Therefore, it is of great practical significance to research the vibration transmission characteristics of typical ship grillage structures for vibration and noise reduction. A vibration test of a typical ship grillage structure is carried out to verify the effectiveness of the simulation method. Furthermore, considering many kinds of excitation exist in practical engineering, the research studies the influence of excitation types on grillage vibration, and it also provides support for vibration protection of ship structure.

In the research studies of ship vibration and vibration tests, Zhang et al. [6] calculated natural frequencies of local grillage structures for high-speed ships and analyzed the influence of propulsion on local vibration. Zou et al. [7] carried out an acoustic optimal design of a 1,500-ton small waterplane area twin hull ship with only a small increase in the structure weight. Wang et al. [8,9] investigated vibration characteristics of a wide flat ship and a river-sea-going container ship under different excitations by experiments and numerical calculation. Considering the low frequency and flowing noise characteristics of a ship, Han et al. [10] estimated the vibration and noise in ship cabins. McVicar et al. [11] researched the influence of slam force duration on the vibration response of a high-speed catamaran. Tang et al. [12] investigated the longitudinal vibration of a trimaran in regular waves. Some model tests are also carried out by many scholars; Gao et al. [13] applied the direct testing method to analyze underwater vibration characteristics of a typical stiffened cylindrical shell, and the result showed that mechanical force is the main influence of the high frequency.

Due to the fact that the size of whole ship is very large, and it is difficult to analyze ship vibration quickly, lots of research studies pay much attention to vibration characteristics of typical ship grillage. In the research studies of forced vibration characteristics of typical ship grillage structures, Du et al. [14] introduced auxiliary sine functions and virtual boundary spring stiffness technique to analyze vibration characteristics of typical stiffened plates, and a forced vibration test was carried out to verify the effectiveness of the proposed method. Gao et al. [15,16] studied the steady and transient vibration response of stiffened plates and stepped annular/circular plates through theoretical and experimental methods, the research showed that the proposed semi-analytical method is reliable. Bo et al. [17] applied the time-variant reliability method to evaluate the reliability of ship grillage structure effectively. Sahoo et al. [18] analyzed time-dependent deflection responses of composite plate, model tests, and simulation methods were combined to conclude the influence of each structure parameter. Gong and Zhang [19] used the local cabin finite element method (FEM) model to analyze grillage structure mode accurately. Aiming at the statistical energy method, Wang et al. [20] proposed a simplified method for grillage structure to improve calculation efficiency. Pandey et al. [21] carried out a bending characteristics comparison research of experimental and numerical analysis for composite materials. The validity of the numerical model is verified, and the effect of different variables on mechanical characteristics is concluded. Korgesaar et al. [22] carried out the response research for ice-strengthened grillage frames under a range of pressure. To investigate natural frequencies and vibration response, Sharma et al. [23] proposed a general mathematical model for doubly curved laminated composite shell panels, and the research shows that support conditions and the lamination scheme have a great influence on the response. He et al. [24] combined the power flow theory of two-dimensional plates and FEM, and they studied vibration transmission characteristics of the coupled plates under medium- to low-frequency excitation. Lu [25] used frequency spectrum analysis methods to analyze vibration characteristics of ship grillage and optimize the dynamic characteristics of a grillage. Lin et al. [26] separated out mode shapes and frequencies whose contribution is largest to the acoustic radiation peaks and optimized structure parameters. Kryzhevich et al. [27] optimized the structure layout of a large-span deck grillage based on ship design approaches. Aiming at vibration response analysis for smart composite curved shell panels, Singh et al. [28] developed a nonlinear mathematical model and applied it to structure design.

For free vibration analysis of typical structure, Cho et al. [29] applied numerical procedure and in-house code on free vibration analysis of a stiffened plate with lumped masses, the results showed that this method has high accuracy and practical application value. Nguyen-Minh et al. [30] proposed a cell-based smoothed discrete shear gap method (CS-FEM-DSG3) to analyze the free vibration of grillage structure, and the method showed some advantages in the calculation. Sahoo and Barik [31] carried out a parametric study for free vibration characteristics of grillage structure under various boundary conditions; some numerical examples were introduced for validation. To analyze free vibration characteristics of laminated plates, Hirwani et al. [32] developed a mathematical analysis model based on higher-order shear deformable kinematic models. Different geometries are introduced to verify the convergence of the numerical models. Qing et al. [33] developed a novel mathematical model for stiffened laminated plate free vibration analysis, numerical examples demonstrated the method had the excellent predictive capability. Jadee et al. [34] studied the free vibration characteristics of isotropic plates by FEM and experiment method. Based on a multi-segment partitioning strategy and semi-analytical method, Pang et al. [35,36] researched free vibration behaviors of doubly curved revolution shells and combined composite laminated shells and compared them with simulation results; the proposed method showed great convergence and stability. Li et al. [37,38] analyzed free vibration characteristics of functionally graded porous cylindrical shells and uniform and stepped circular cylindrical shells with arbitrary boundary conditions. They first proposed Jacobi-Ritz method for typical ship structure vibration analysis in the world, and a unified model of ship structure for vibration analysis was established; the proposed method improved the analysis efficiency and had a positive effect on ship vibration research studies. To simplify the complex ship geometry model, Pang et al. [39] also carried out the free vibration research of spherical–cylindrical–spherical shell based on semi-analytical method.

Aiming at the influence of different load on vibration characteristics, a large number of scholars carried out related research studies. Lin and Pan [40] presented a closed-form solution to research the vibration response of stiffened plates under point force excitation. Sahoo and Barik [41] developed an efficient solution for stiffened plate vibration analysis under different excitations, including single and multiple moving loads. Srivastava et al. [42] studied vibration characteristics of stiffened plates under in-plane and edge loads; the research presented the stresses all over the region under different loads. Song et al. [43] carried out the research on typical ship structure vibration and acoustic radiation under different excitations. Yang et al. [44] researched the effect of blade loading on fluid-induced exciting force and noise of the pump. Tamijani and Kapania [45] proposed an element-free Galerkin formulation to analyze the random response of stiffened plates, and the effects of beam stiffness and in-plane load on spectral density were also investigated.

According to the above research summary, some deficiencies of the existing research studies are concluded. Most research studies are carried out based on the simulation method, and few scholars combined the test method with the simulation method in grillage dynamic characteristics analysis. Point excitation and uniform distribution excitation are common in engineering; however, research studies on vibration characteristics of grillage structure under various classic excitation conditions are rarely published. Few scholars studied the effect of excitation type on grillage structure vibration and sound radiation.

In view of the shortcomings of other research studies, this article introduces a model test to verify the effectiveness of the simulation method (FEM). Single-point excitation, multi-point excitation, and uniform distribution excitation are common excitation kinds in engineering applications, to analyze if dynamic characteristics of grillage, acoustic-structure coupling theory, and FEM are innovatively combined. And the research results can be referred to by ship practical low-noise design.

The research idea of this article is described as follows. Considering the accuracy of grillage structure vibration simulation, a model test is introduced to verify the effectiveness of the simulation method (FEM) by comparing test results and simulation results. The test result shows that FEM is effective in vibration and sound radiation analysis. Different excitation types are applied to a simple grillage, the calculated results are compared with each other to discuss the effect of excitation type on grillage vibration. The flow diagram is shown in the graphical abstract.

2 Theoretical model

2.1 Vibration model of stiffened plate

Ship typical structure is mainly composed of plates and beams; therefore, the vibration of beams and plates directly affects the ship's overall vibration. By analyzing vibration characteristics of basic structures, the analysis method of complex structure vibration can be concluded.

Differential equation of bending vibration for the homogeneous thin plate under external load F(x,y) is shown below:

(1) D ∂ 4 ω ∂ x 4 + 2 ∂ 4 ω ∂ 2 x ∂ 2 y + ∂ 4 ω ∂ y 4 = F ( x , y ) ,

where ω signifies displacement function of plate, which is expressed as ω = ω(x,y); D represents bending stiffness, which is expressed as D = Eh 3/(12(1 − ν 2)). And E, ν, h denote, respectively, elastic modulus, Poisson’s ratio and plate thickness.

According to d’Alembert’s principle, inertia force of plate transverse vibration is introduced to the equation, which is expressed as F = − γ h g ∂ 2 ω ∂ t 2 . And the differential equation of plate transverse vibration is expressed as below:

(2) D ∂ 4 ω ∂ x 4 + 2 ∂ 4 ω ∂ 2 x ∂ 2 y + ∂ 4 ω ∂ y 4 + γ h g ∂ 2 ω ∂ t 2 = F ( x , y , t ) .

Bending vibration differential equation of orthotropic plate under excitation q(x,y,t) is shown as follows:

(3) D 1 ∂ 4 ω ∂ x 4 + 2 D 3 ∂ 4 ω ∂ 2 x ∂ 2 y + D 2 ∂ 4 ω ∂ y 4 = q ( x , y , t ) ,

where D 1, D 2 are respectively bending stiffness at x and y directions, and D 1, D 2, D 3 can be expressed as below:

(4) D 1 = E 1 h 3 12 ( 1 − ν 1 ν 2 ) ,

(5) D 2 = E 2 h 3 12 ( 1 − ν 1 ν 2 ) ,

(6) D 3 = D 1 ν 2 + 2 G h 3 12 .

Stiffened plate is a common structure in ship structure, aiming at actual engineering needs, and different section beams are applied in plate structure. T-section beams are common in stiffeners; for stiffened plates with T-section beams, the stiffness of stiffened plate can be expressed as follows:

(7) D 1 = E h 3 12 ( 1 − ν 2 ) + E h e x 2 1 − ν 2 + E I o x a x ,

(8) D 2 = E h 3 12 ( 1 − ν 2 ) + E h e y 2 1 − ν 2 + E I o y a y ,

(9) D 3 = E h 3 12 ( 1 − ν 2 ) + G 6 + ∑ d i 3 t i a x + ∑ d i 3 t i a y ,

where I ax and I oy denote moment of inertia in x and y directions; d 1 and t 1 signify thickness and length of the web plate in x and y directions; d 2 and t 2 represent thickness and length of the plate in x and y directions.

2.2 Mean square velocity and radiated sound power

According to the boundary element theory, the velocity of the radiant surface is given, the sound pressure at the node can be calculated, and the radiated sound power can be obtained [46]. Therefore, the vibration velocity of the structure surface is calculated using the FEM, and the vibration velocity of the structure surface is taken as the boundary condition of boundary element calculation; then the radiated sound power of the structure can be analyzed and obtained.

The average square vibration velocity of the surface of the grillage can show the overall vibration characteristics of the grillage structure. According to the definition of the mean square vibration velocity, it can be known as:

(10) v 2 = 1 S ∬ s ∣ V ∣ 2 d s ,

where S is the surface area of the vibration of the structure; V is the normal vibration velocity distribution function of a vibrating surface.

Similarly, according to the definition of vibration velocity level, it can be known that:

(11) L v = 10 × log ( v 2 / v 0 2 ) ,

where v is the effective value of the mean square vibration velocity of the structure; v 0 = 1 × 10−9 m·s−1 is the reference speed value.

Radiated sound power refers to the average sound energy radiated outward in unit time through an area S, which is perpendicular to the direction of sound propagation. Therefore, the radiated sound power can be expressed as:

(12) W = I ⁎ S = S T ∫ 0 T Re ( p ) Re ( v ) d t ,

where I is the sound intensity, and its unit is W·s−2; Re refers to the real part.

Similarly, the sound power level is defined as follows:

(13) L W = 10 × log w w 0 ,

where w is the radiated sound power, and the reference sound power value is w 0 = 1 × 10−12 Pa.

3 Model test verification

The vibration test model of grillage structure is designed to verify the effectiveness of the simulation method. The modes and vibration transmission characteristics of the grillage model are tested. By comparing simulation results and test results, the grillage vibration characteristics and effectiveness of simulation method can be concluded.

3.1 Test model

The test model is a steel grillage structure model with length a = 2.0 m, width b = 2.0 m, and thickness h = 6 mm. Half of the side length is set with T-section ⊥ 6 × 62 8 × 60 beam, and the other 1/4 position is set with T-section ⊥ 7 × 17 5 × 50 beam. The model is set with simple support boundary conditions as shown in Figure 1.

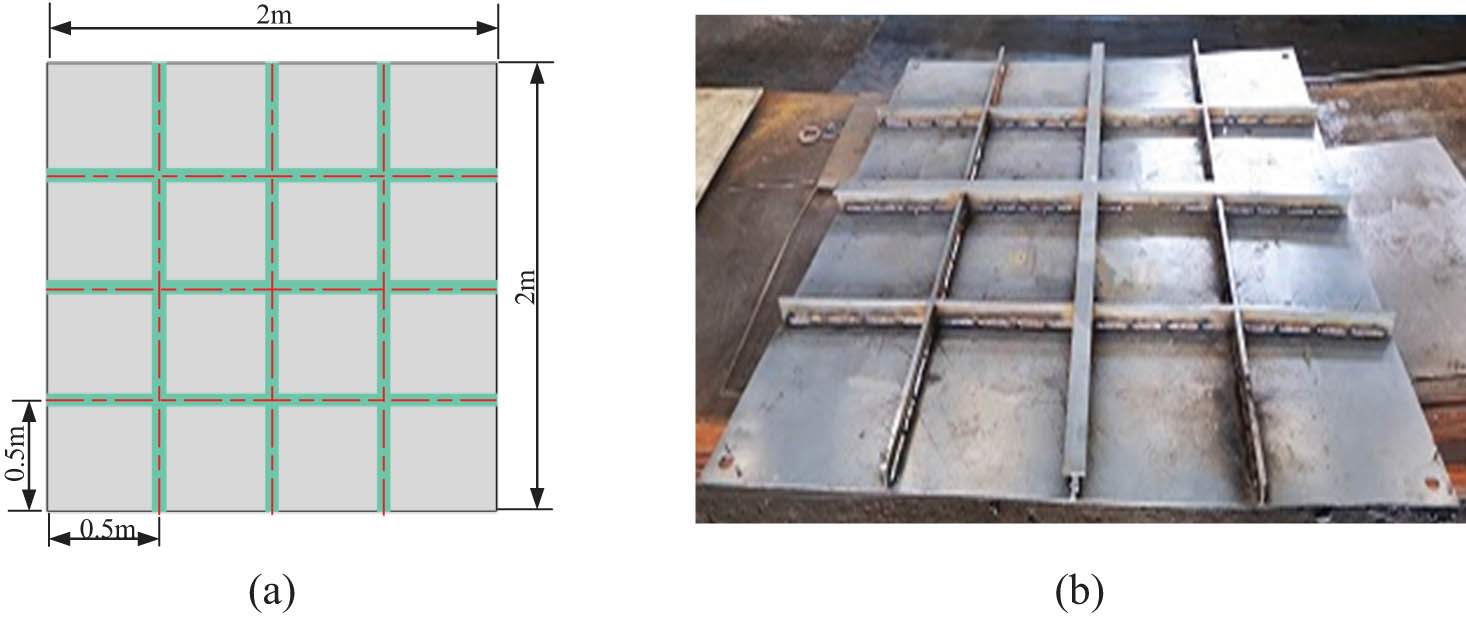
Figure 1 Test model: (a) diagram of test model; (b) physical drawing of test model.
Figure 1

Test model: (a) diagram of test model; (b) physical drawing of test model.

3.2 Test principle

3.2.1 Test principle of mode

Differential equation of motion for multi-degree-of-freedom vibration system is calculated as follows:

(14) M x ̈ ( t ) + C x ̇ ( t ) + K x ( t ) = F ( t ) ,

where M, C, and K, respectively, represent mass matrix, damping matrix, and stiffness matrix. F(t) and x(t) denote external load vector and displacement vector.

Fourier transformation is applied to theoretical model; x(t) and F(t) are expressed as x(t) = Xe jωt , F(t) = Fe jωt .

(15) X ( t ) = H ( ω ) F ( t ) ,

where frequency response transfer function is expressed as:

(16) H ( ω ) = ( K − ω 2 M + j ω C ) − 1 .

φ r represents r-order mode of the structure, and frequency response function matrix is expressed as follows:

(17) H ( ω ) = ∑ r = 1 n φ r φ r T ( k r − ω 2 m r + j ω c r ) ,

where m r , k r , c r , respectively, denote mass matrix, stiffness matrix, and damping matrix of r-order mode. Any element of H(ω) can be expressed as follows:

(18) H i j ( ω ) = ∑ r = 1 n φ i r φ j r ( k r − ω 2 m r + j ω c r ) ,

where H ij (ω) means that the response function of point j under excitation of point i. And the specific line of the response matrix is shown:

(19) [ H i 1 , H i 2 … … H i n ] = ∑ r = 1 n φ i r ( k r − ω 2 m r + j ω c r ) [ φ 1 r , φ 2 r … … φ n r ] .

Therefore, all the parameters of mode are shown in the response function matrix, and every line of the matrix corresponds to a specific mode. A fixed test point is set at the test structure surface, and every test point is excited by the same load. By this way, all the parameters of the mode can be analyzed.

3.2.2 Test principle of transfer function

A structure is excited at a specific location (point A) by a load F A(ω), and vibration response at point B is X B(ω); the vibration transfer function from point A to point B is expressed as follows:

(20) H AB ( ω ) = X B ( ω ) F A ( ω ) .

Therefore, some acceleration sensors are placed at test points to collect vibration response, by changing different loads; transfer function of grillage structure under different excitation can be calculated.

3.3 Test process

Because this test is carried out to study vibration transmission characteristics and modes of the grillage structure, it is necessary to use the vibration exciter to load. In addition, vibration acceleration at different positions of the grillage structure needs to be tested. For this reason, test points are arranged at the intersection of the vertical and horizontal strength members, and the structure mode is measured by excitation at the geometric center of the structure. Test points are uniformly arranged on the diagonal at the of the grillage structure, excitation position locates the geometric center of the structure. The vibration transfer function of the structure is measured. The test schematic diagram of mode and vibration transmission characteristics is shown in Figure 2, and the arrangement of test points is shown in Figure 3.

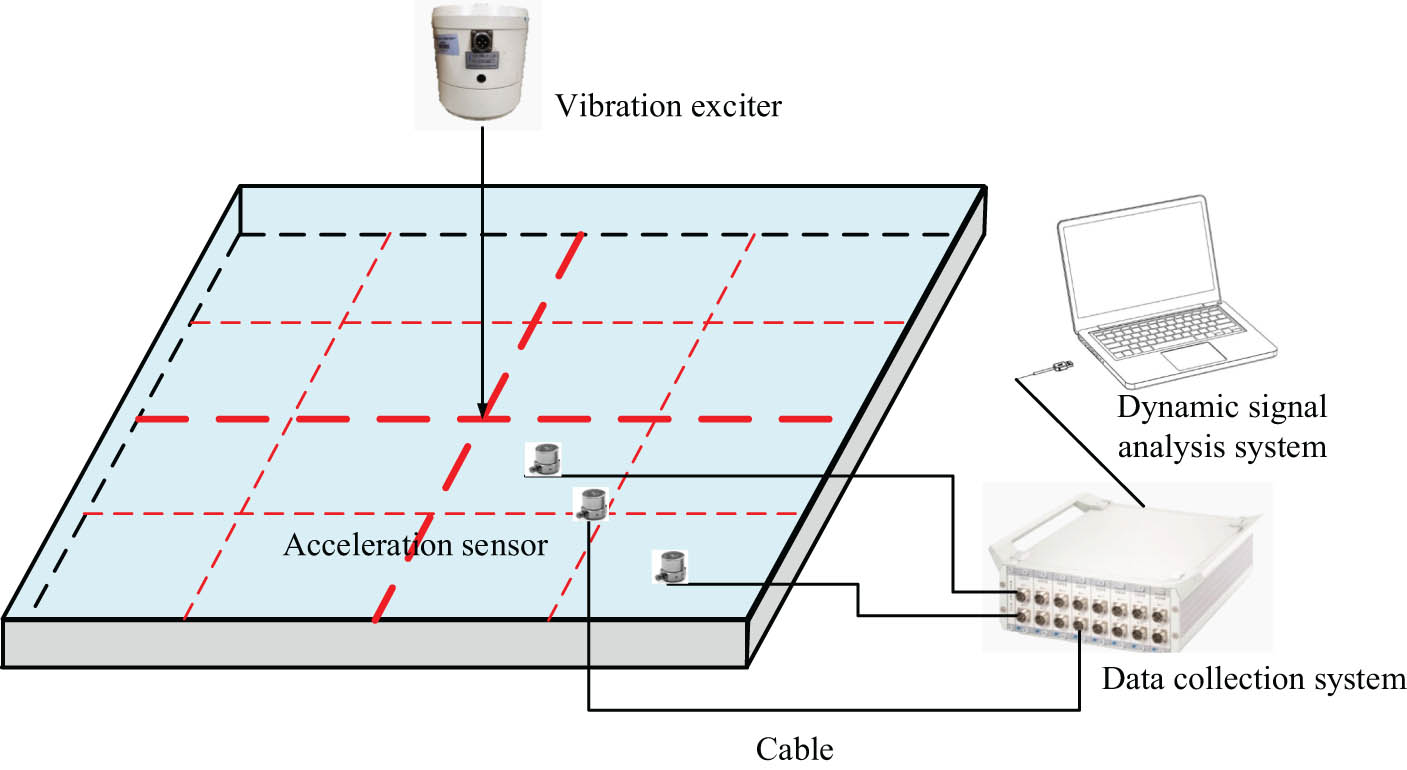
Figure 2 Schematic diagram of test.
Figure 2

Schematic diagram of test.

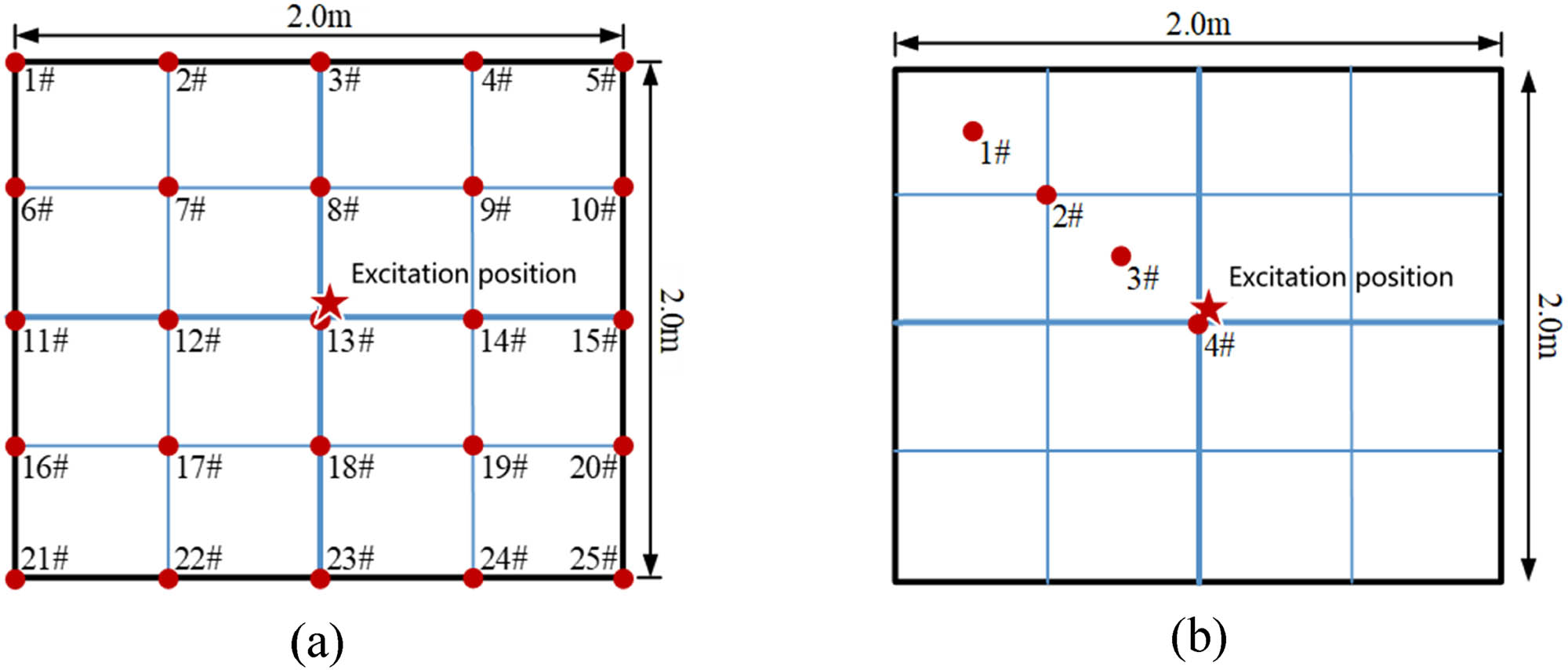
Figure 3 Schematic diagram of measuring point layout: (a) modal test points arrangement; (b) transmission characteristic test points arrangement.
Figure 3

Schematic diagram of measuring point layout: (a) modal test points arrangement; (b) transmission characteristic test points arrangement.

Test process is shown in the test schematic diagram: vibration exciter is arranged at the center of the structure, and the exciter is secured with rope. Acceleration sensors, which are set at the surface of the structure, connect with the data collection system. Under the excitation, vibration signal is tested by sensors and collected by collection system, and then, dynamic signal analysis system on a computer starts data processing and analyzes characteristics. The vibration exciter is placed as shown in Figure 4. To simulate simple boundary conditions, the four corners of the test model are respectively placed on a piece of wood, as shown in Figure 5.

Figure 4 Arrangement of vibration exciter.
Figure 4

Arrangement of vibration exciter.

Figure 5 Simulation of simple boundary conditions.
Figure 5

Simulation of simple boundary conditions.

Time history signal generated by the exciter and the vibration acceleration response time history signal of each test point are collected in the test. The excitation force frequency domain signal and response frequency domain signal are obtained by the fast Fourier transform method, and the vibration transfer function of different test points under the excitation force is obtained. The vibration time history curves of some signal channels are shown in Figure 6.

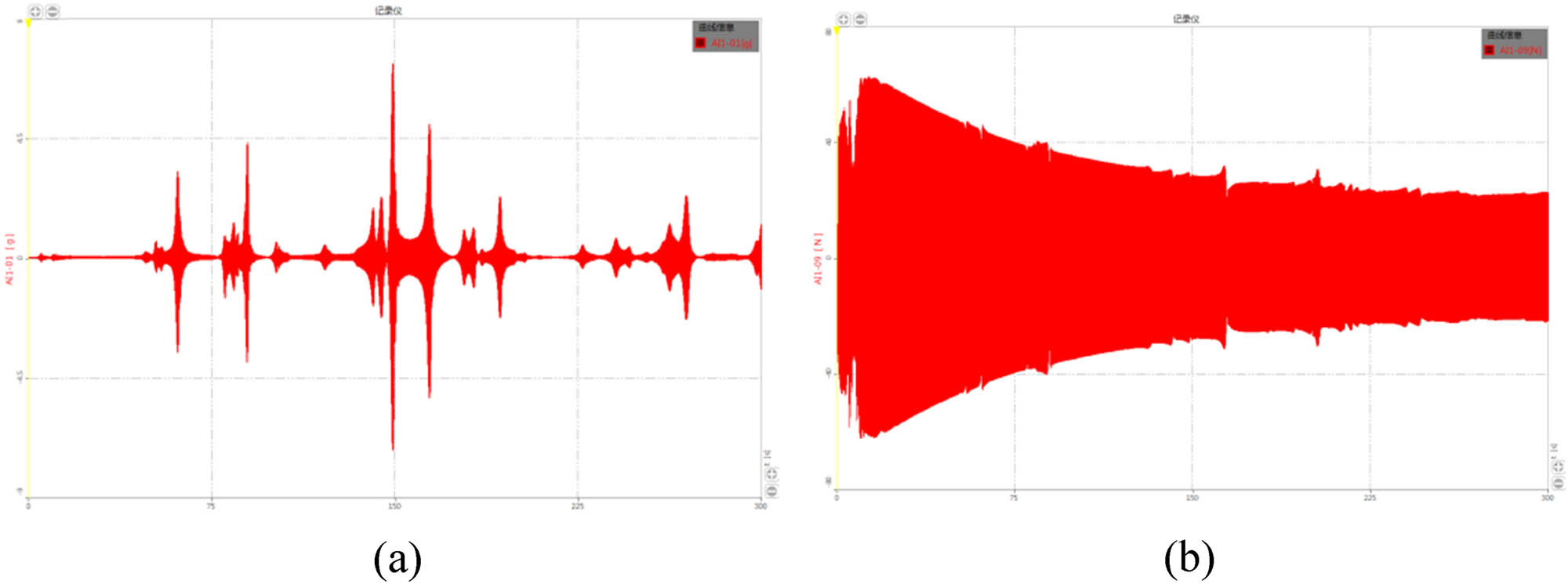
Figure 6 Time history signal curve: (a) acceleration time history signal of channel #1; (b) excitation force time history signal of channel #4.
Figure 6

Time history signal curve: (a) acceleration time history signal of channel #1; (b) excitation force time history signal of channel #4.

3.4 Test results

Based on the test model, the four corners of the structure are simply supported. Some modes are obtained by simulation method (FEM), as shown in Figure 7. Some modes of the structure are obtained by the data processing of the test results. The tested mode results are shown in Figure 8. It is observed that the natural frequencies of the structure obtained from the test are different from the natural frequencies of the corresponding mode shape of the structure obtained from the simulation, but the difference is relatively small. The tested modes correspond to the simulation mode basically.

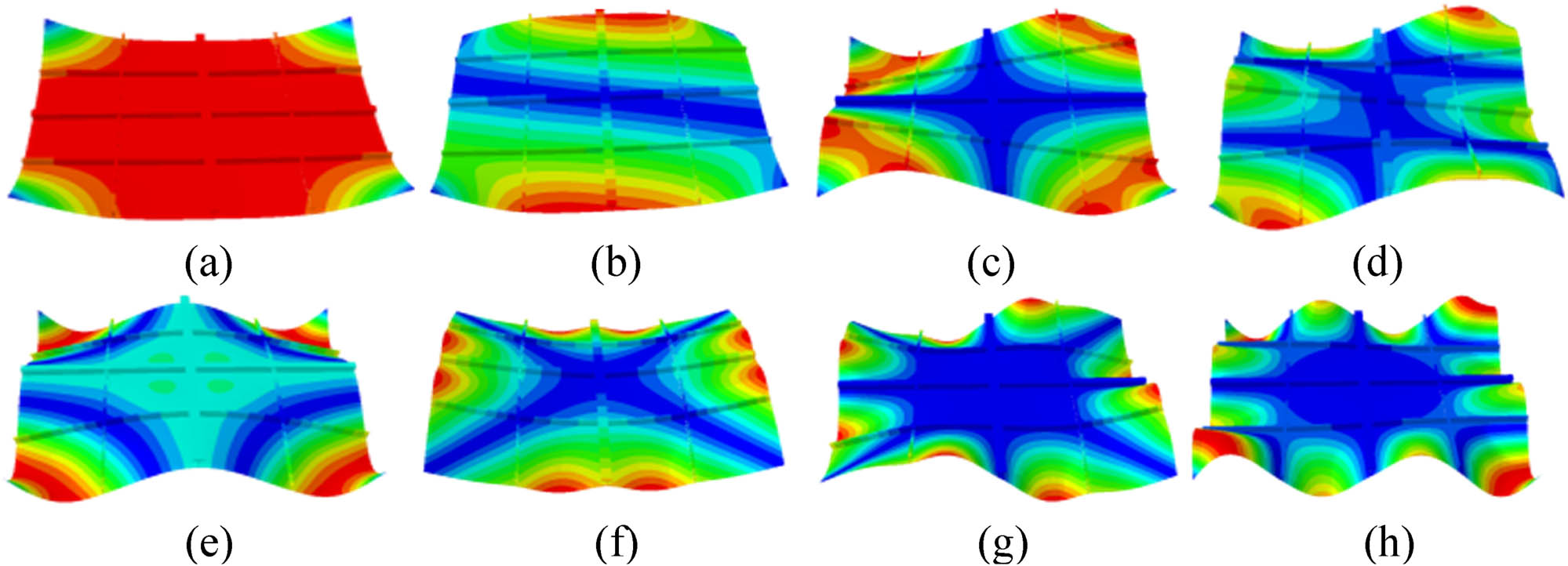
Figure 7 Structural mode simulation results: (a) 4.2 Hz, (b) 8.0 Hz, (c) 17.5 Hz, (d), 43.5 Hz, (e) 47.7 Hz, (f) 51.9 Hz, (g) 73.3 Hz, and (h) 73.9 Hz.
Figure 7

Structural mode simulation results: (a) 4.2 Hz, (b) 8.0 Hz, (c) 17.5 Hz, (d), 43.5 Hz, (e) 47.7 Hz, (f) 51.9 Hz, (g) 73.3 Hz, and (h) 73.9 Hz.

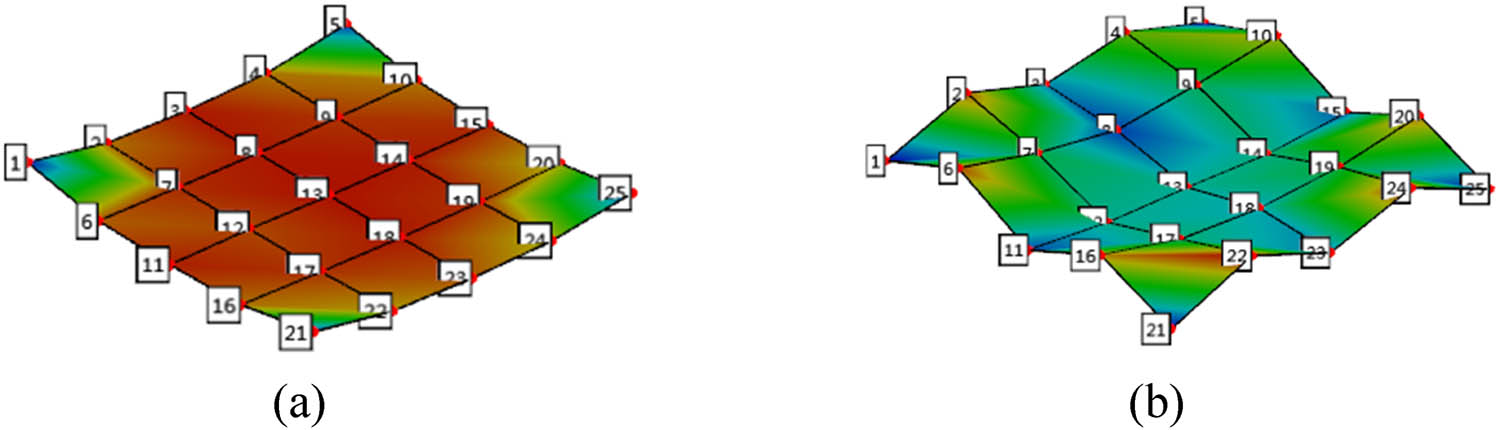
Figure 8 Structural mode test results: (a) 4.4 Hz; (b) 48.7 Hz.
Figure 8

Structural mode test results: (a) 4.4 Hz; (b) 48.7 Hz.

The test and simulation results of structural vibration transmission characteristics are shown in Figure 9. It can be observed that the tested structural vibration transmission characteristics curve is basically consistent with the simulation curve, but the tested curve is more complex and has more peak points. Compared with the simulation results, the peak value of test results deviates.

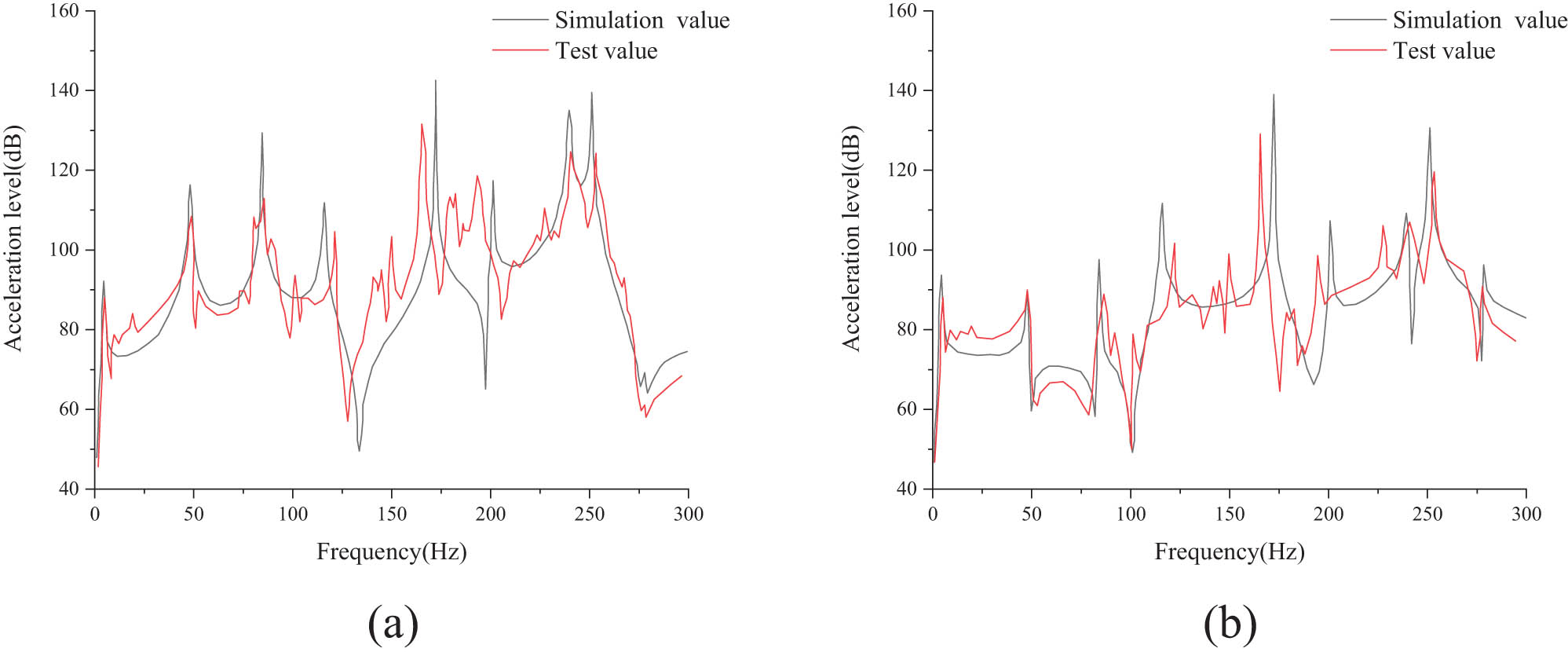
Figure 9 Vibration transmission test results of structure: (a) test point 1#; (b) test point 2#.
Figure 9

Vibration transmission test results of structure: (a) test point 1#; (b) test point 2#.

The vibration transmission characteristic curve of each test point has no obvious peak in the 5–48 Hz frequency band, and only a small vibration peak appears in the test results around 19 Hz. This is because the excitation position is located near the node line of 8.0, 17.5, and 43.5 Hz modes of the grillage structure, which is not easy to cause strong vibration of the structure at these modal frequencies. At 4.4 Hz, strong vibration at each test point is caused, and the difference in vibration amplitude is small. This is because the structural mode near this frequency is the overall vibration of the grillage. At 49 Hz, strong vibration of all test points was caused, and the vibration response of test point 1# was the largest because the mode of the structure near this frequency was mainly manifested as the subpanel vibration near the test point 1#.

When the excitation force frequency is close to the overall mode frequency of the structure, the structural vibration is shown as the overall strong vibration. When the excitation frequency is close to the local plate mode frequency of the structure, the vibration of the structure is dominated by the plate position vibration. The vibration response of the grillage structure is larger only at the resonant frequency, but smaller at other frequencies. Therefore, the vibration response of the structure at the resonant frequency should only be considered when carrying out vibration protection. When the first natural frequency of the structure is higher than a certain range of excitation force frequency, the vibration response of the structure can be relatively small.

The results obtained from the test are consistent with the simulation results, which verifies the effectiveness of the simulation method (FEM). And the effect of excitation type on grillage vibration will be researched with FEM.

4 The effect of excitation type on grillage vibration characteristics

4.1 Research subject

The length of the grillage structure model is L = 3.6 m, its width is B = 2.5 m, and the thickness of the plate is t = 5 mm; the length direction is provided with a beam with an interval of 1.2 m, and the cross section size of the beam is ⊥ 6 × 125 9 × 125 ; the width direction is provided with a longitudinal bone with an interval of 0.5 m, and the cross-section size of the longitudinal bone is L100 × 63 × 7; the diagram of grillage structure model is shown in Figure 10. The structural material parameters are as follows: the elastic modulus is E = 2.1 × 1011 N·m−2, the Poisson ratio is µ = 0.3, and the density is ρ = 7,850 kg·m−3.

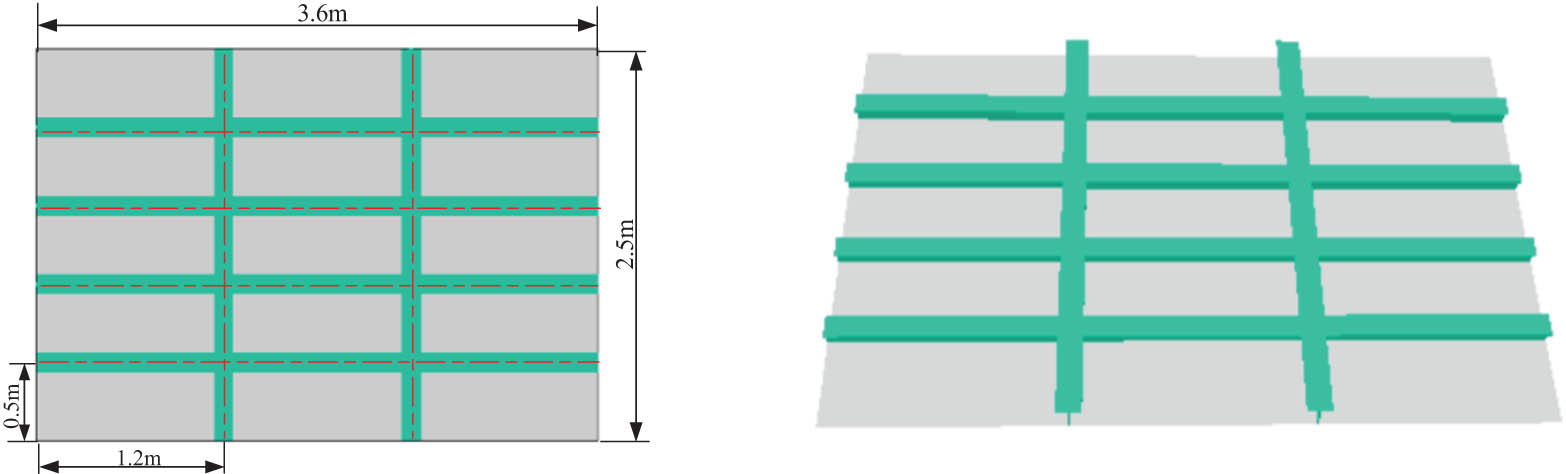
Figure 10 Grillage geometry model.
Figure 10

Grillage geometry model.

4.2 Vibration characteristics of grillage under different excitations

In order to research grillage structure vibration characteristics under different excitations, a unit force is applied to the structure by means of single-point excitation, two-point excitation, and uniform distribution excitation. In single point excitation, vertical unit force is applied to the center of the subpanel. In two-point excitation, vertical force (0.5 N) is set at the intersection of longitudinal bone, beam, and the center of the subpanel, respectively. In uniform distribution excitation, vertical force (1 N) is uniformly distributed over the whole center subpanel. The loading position of different excitation forces is shown in Figure 11.

Figure 11 Loading position of different kinds of excitation: (a) single-point excitation, (b) two-point excitation, and (c) uniform distribution excitation.
Figure 11

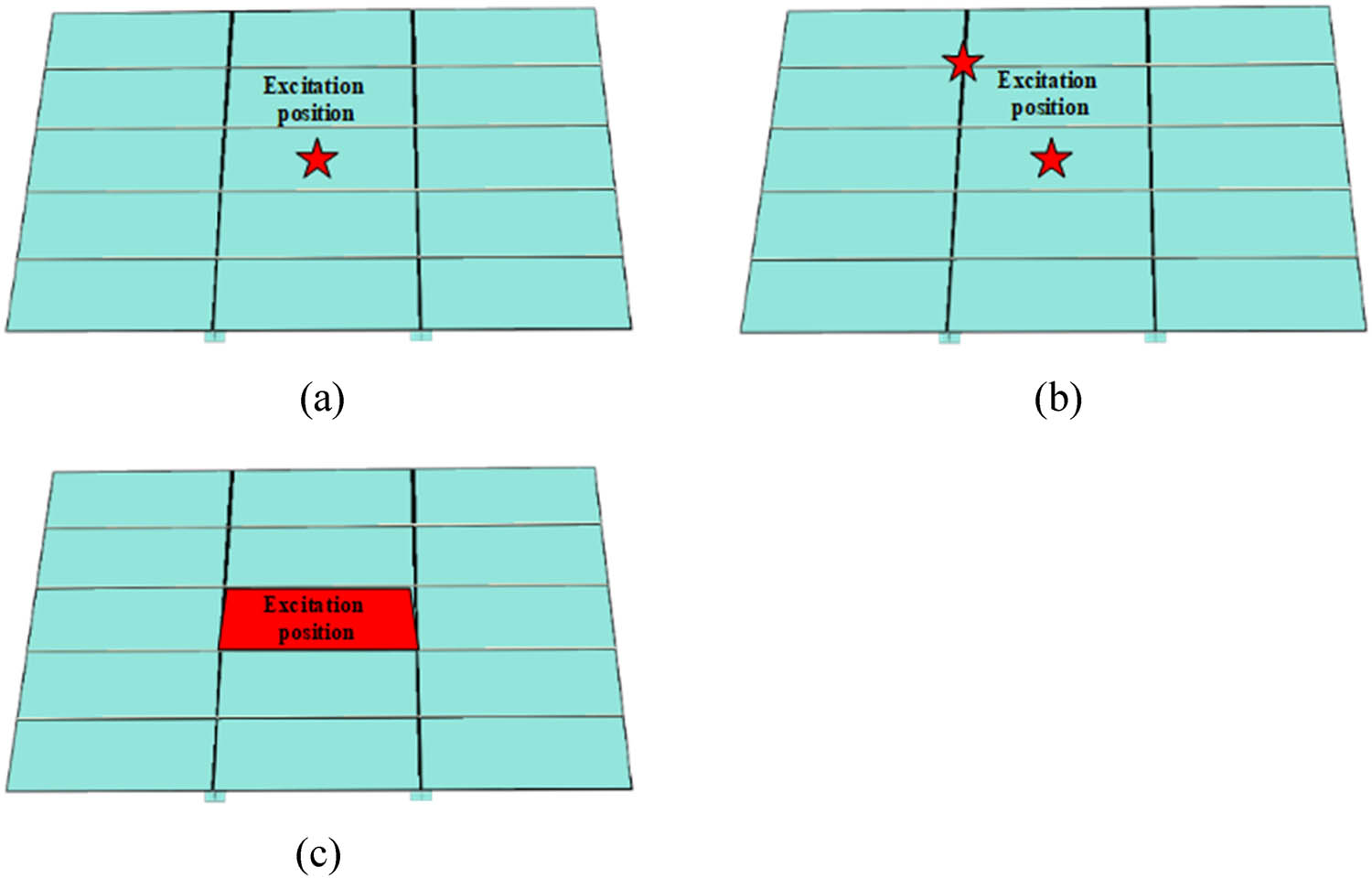
Loading position of different kinds of excitation: (a) single-point excitation, (b) two-point excitation, and (c) uniform distribution excitation.

In the simulation part, the FEM is used for calculation. The plate structure is simulated by a two-dimensional shell element; the longitudinal bone structure is simulated by a one-dimensional beam element. The two-dimensional shell element type is S4R element, and the one-dimensional beam element type is the B31 element. To ensure the accuracy of the analysis process, the basic grid size is set to 0.02 m. Totally, the number of S4R shell elements is 22,500, and the number of B31 beam elements is 970. And the grillage structure is surrounded by simple boundary conditions. FEM simulation model of grillage structure is shown in Figure 12.

Figure 12 FEM simulation model of grillage structure.
Figure 12

FEM simulation model of grillage structure.

The vibration velocity response of different excitation is calculated using FEM, and the vibration velocity response diagrams of different excitations are shown in Figures 13–15.

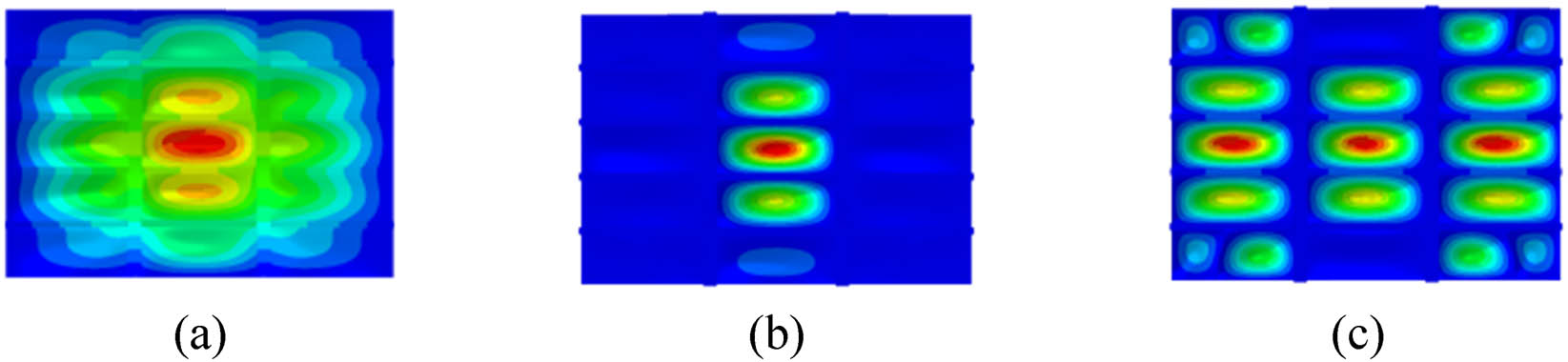
Figure 13 Vibration velocity response diagram of single point excitation: (a) 53 Hz, (b) 97 Hz, and (c) 103 Hz.
Figure 13

Vibration velocity response diagram of single point excitation: (a) 53 Hz, (b) 97 Hz, and (c) 103 Hz.

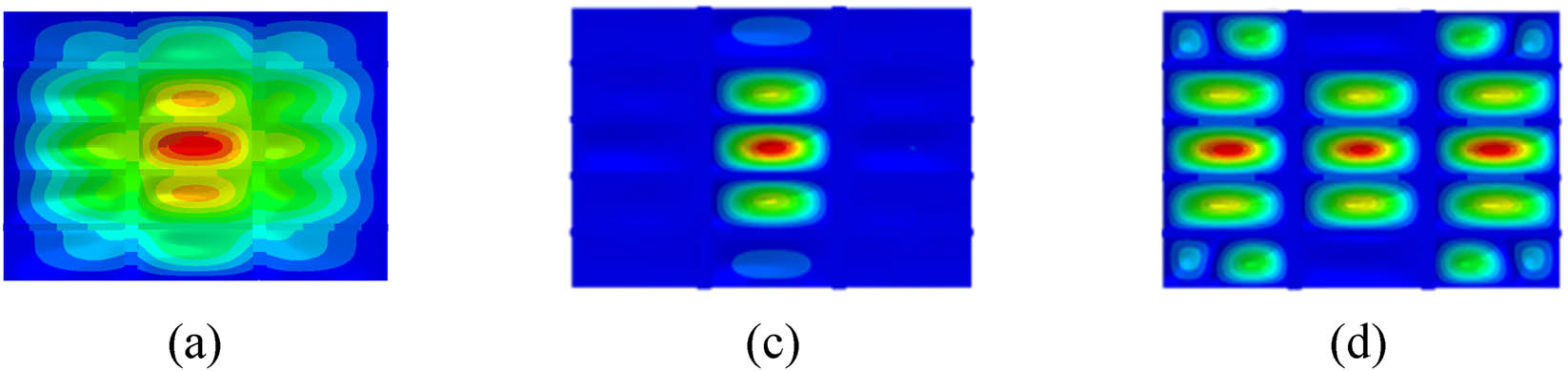
Figure 14 Vibration velocity response diagram of two-point excitation: (a) 53 Hz, (b) 97 Hz, and (c) 103 Hz.
Figure 14

Vibration velocity response diagram of two-point excitation: (a) 53 Hz, (b) 97 Hz, and (c) 103 Hz.

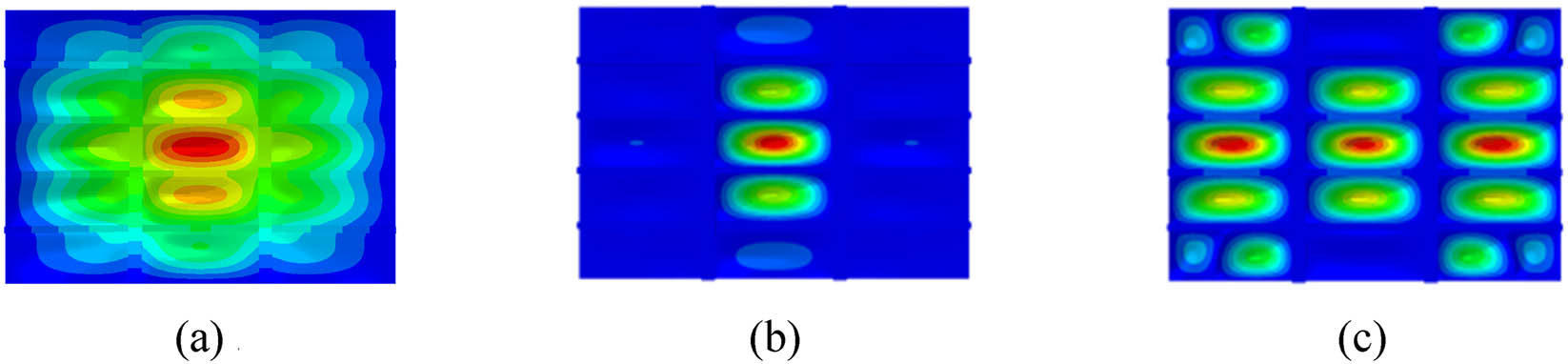
Figure 15 Vibration velocity response diagram of uniform distribution excitation: (a) 53 Hz, (b) 97 Hz, and (c) 103 Hz.
Figure 15

Vibration velocity response diagram of uniform distribution excitation: (a) 53 Hz, (b) 97 Hz, and (c) 103 Hz.

It is observed that 53 Hz mainly causes the overall vibration of the grillage, 97 Hz mainly causes the vibration of the middle subpanels, and 103 Hz mainly causes the vibration of the stiffened plate. According to the analysis results of the forced vibration characteristics of grillage structure with simple boundary conditions, the vibration response distribution of the grillage structure under the peak frequency is basically the same regardless of the single-point excitation, two-point excitation, or uniform distribution excitation. Therefore, the peak frequency of structural vibration transmission is less related to the type of excitation force.

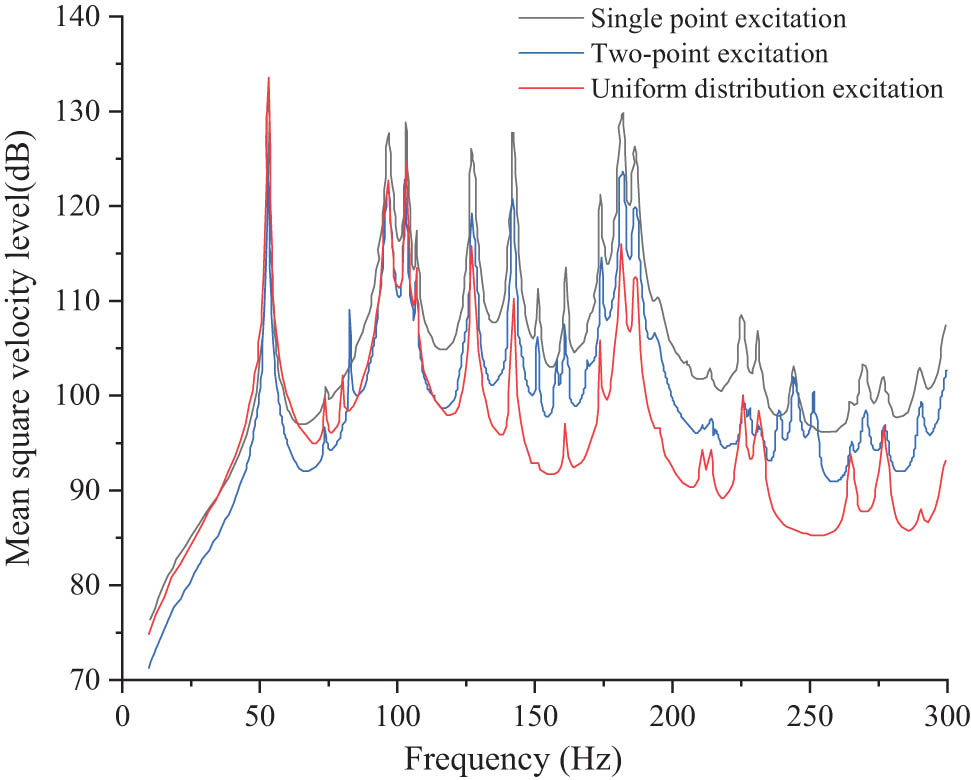
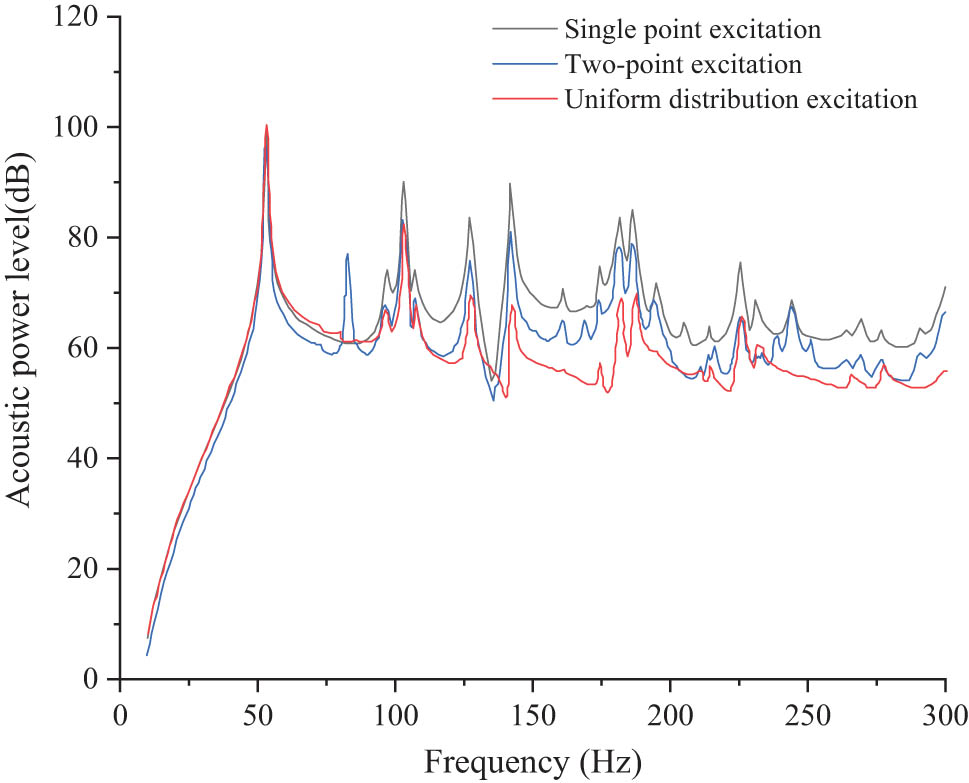
Under different excitation, the calculation results of the mean square velocity of the grillage structure are shown in Figure 16, and the calculation results of acoustic power level are shown in Figure 17.

Figure 16 Mean square velocity level under different excitation.
Figure 16

Mean square velocity level under different excitation.

Figure 17 Acoustic power level under different excitation.
Figure 17

Acoustic power level under different excitation.

It is noted that all the mean square velocity curve has large peak values at 53, 97, 103, 127, 142, 182, and 186 Hz, while the curve of two-point excitation has a peak value at 83 Hz, which is different from others. The maximum value of mean square velocity level is 133 dB, which is under uniform distribution excitation. In 0–75 Hz frequency band, the mean square velocity value of two-point excitation is less than others. Generally, comparing the mean square velocity value of different excitations, for most frequency bands (75–300 Hz), the mean square velocity of single point excitation is larger than others, and uniform distribution excitation has a minimum value of mean square velocity. Therefore, uniform distribution excitation is a better way to control structure mean square velocity generally.

It also shows that all the acoustic power level curves have large peak values at 53, 103, 127, 142, 182, and 186 Hz, while the curve of two-point excitation has a peak value at 83 Hz, which is different from others. The maximum value of acoustic power under different excitation is 100 dB. In 75–300 Hz frequency band, the acoustic power-level value of uniform distribution excitation is less than other values of single-point and two-point excitation. And in 0–75 Hz frequency band, the acoustic power-level value under different excitation is close to each other. Therefore, for most frequency bands, uniform distribution excitation is a better way to control structure acoustic power generally.

It is observed that the peak frequency of the mean square vibration velocity function and acoustic power function of the grillage structure are less related to the type of excitation force. For mean square velocity and acoustic power, by comparing curves of different excitation, the trend of the same function is basically consistent with other excitation, but the phenomenon of peak offset exists in different curves.

5 Conclusion

Aiming at the present situation that the effect of excitation type on typical ship grillage structure vibration is not fully revealed, this article takes simple grillage structure as a test model to explore the effectiveness of the simulation method (FEM). Modal test and vibration transmission characteristics test of typical ship grillage structures are carried out. And mean square velocity level and acoustic power level are compared to research on the effect of excitation type on grillage vibration. The main conclusions are as follows:

  1. The results of mode and transmission characteristics test is basically consistent with simulation results, which verifies the effectiveness of simulation method (FEM).

  2. Under different excitation, the peak frequency of acoustic power and mean square velocity of grillage structure is basically the same.

  3. For most frequency bands, compared with single-point excitation and two-point excitation, uniform distribution excitation has less value of acoustic power and mean square velocity.

  4. In engineering practice, various kinds of loads should be transformed to uniform distribution loads in order to control structure vibration and sound radiation.

  1. Funding information: This study was funded by the National Natural Science Foundation of China (U2006229, 52101351), Key Research and Development Program of Shandong Province (2019JZZY010125, 2020CXGC010701, and 2020CXGC010702), Natural Science Foundation of Jiangsu Province (BK20190962).

  2. Author contributions: Tongda Zou: methodology, software, and manuscript writing. Yuhang Tang: experiment and simulation validation. Xuhong Miao: Supervision. Yuan Du: related research investigation. Fuxin Jia: manuscript revision. Yanhe Shan: data processing and analysis.

  3. Conflict of interest: The authors declare that they have no conflict of interest.

References

[1] Cheng, L. and J. L. He. Anti-vibration design method for 300 000 DWT FPSO engine room. Chinese Journal of Ship Research, Vol. 15, No. S1, 2020, pp. 68–73.Search in Google Scholar

[2] Choi, W. S., S. Y. Hong, H. W. Kwon, J. H. Seo, S. H. Rhee, and J. H. Song. Estimation of turbulent boundary layer induced noise using energy flow analysis for ship hull designs. Proceedings of the Institution of Mechanical Engineers Part M-Journal of Engineering for the Maritime Environment, Vol. 234, No. 1, 2020, pp. 196–208.10.1177/1475090219852195Search in Google Scholar

[3] Tatsumi, A., H. Han, and M. Fujikubo. Ultimate strength of container ships subjected to combined hogging moment and bottom local loads. Marine Structures, Vol. 71, 2020, id. 102738.10.1016/j.marstruc.2020.102738Search in Google Scholar

[4] Ozcelik, Y. and P. M. Clayton. Behavior of columns of steel plate shear walls with beam-connected web plates. Engineering Structures, Vol. 172, 2018, pp. 820–832.10.1016/j.engstruct.2018.06.087Search in Google Scholar

[5] Bolbotowski, K., L. He, and M. Gilbert. Design of optimum grillages using layout optimization. Structural and multidisciplinary optimization, Vol. 58, No. 3, 2018, pp. 851–868.10.1007/s00158-018-1930-6Search in Google Scholar

[6] Zhang, X., H. L. Ren, G. Q. Feng, Y. F. Liu, and Z. N. Wu. Analysis of local vibration and strength of water jet propulsion unit of high speed ship. Proceedings of the Asme 37th International Conference on Ocean, Offshore and Arctic Engineering, 2018, American Society of Mechanical Engineers, Vol. 3, 2018. 10.1115/OMAE2018-77340.Search in Google Scholar

[7] Zou, M. S., C. G. Lin, L. B. Qi, and S. X. Liu. The low-noise optimization of a swath ship’s structures based on the three-dimensional sono-elasticity of ships. Journal of Ship Research, Vol. 62, No. 2, 2018, pp. 89–99.10.5957/JOSR.170042Search in Google Scholar

[8] Wang, Y. W., W. G. Wu, and C. G. Soares. Experimental and numerical study of the hydroelastic response of a river-sea-going container ship. Journal of Marine Science and Engineering, Vol. 8, No. 12, 2020, id. 978.10.3390/jmse8120978Search in Google Scholar

[9] Wang, Y. W., W. G. Wu, and C. Zheng. The springing investigation of the wide flat ship type. Journal of Vibration and Shock, Vol. 39, No. 18, 2020, pp. 174–180.Search in Google Scholar

[10] Han, H., C. Lee, K. Lee, S. H. Jeon, and S. Park. Estimation of the sound in ship cabins considering low frequency and flowing noise characteristics of HVAC duct. Applied Acoustics, Vol. 141, 2018, pp. 261–270.10.1016/j.apacoust.2018.07.011Search in Google Scholar

[11] McVicar, J. J., G. Thomas, J. Lavroff, and M. R. Davis. Effect of slam force duration on the vibratory response of a lightweight high-speed wave-piercing catamaran. Journal of Ship Research, Vol. 59, 2015, pp. 69–84.10.5957/jsr.2015.59.2.69Search in Google Scholar

[12] Tang, H., H. Ren, and Q. Wan. Investigation of longitudinal vibrations and slamming of a trimaran in regular waves. Journal of Ship Research, Vol. 61, No. 3, 2017, pp. 153–166.10.5957/JOSR.170001Search in Google Scholar

[13] Gao, C., H. Zhang, H. C. Li, F. Z. Pang, and H. F. Wang. Numerical and experimental investigation of vibro-acoustic characteristics of a submerged stiffened cylindrical shell excited by a mechanical force. Ocean Engineering, Vol. 249, 2022, id. 110913.10.1016/j.oceaneng.2022.110913Search in Google Scholar

[14] Du, Y., D. Jia, H. C. Li, C. Gao, and H. F. Wang. A unified method to analyze free and forced vibration of stiffened plates under various edge conditions. European Journal of Mechanics a-Solids, Vol. 94, 2022, id. 104573.10.1016/j.euromechsol.2022.104573Search in Google Scholar

[15] Gao, C., F. Pang, H. Li, D. Jia, and Y. Tang. Steady and transient vibration analysis of uniform and stepped annular/circular plates based on FSDT. Acta Mechanica, Vol. 233, No. 3, 2022, pp. 1061–1082.10.1007/s00707-022-03157-ySearch in Google Scholar

[16] Gao, C., F. Pang, H. Li, and D. Jia. A semi-analytical method for the dynamic characteristics of stiffened plate with general boundary conditions. Thin-Walled Structures, Vol. 178, 2022, id. 109513.10.1016/j.tws.2022.109513Search in Google Scholar

[17] Bo, S., L. Huang, T. Ye, and K. C. Yung. Time-variant reliability analysis of ship grillage structure. First International Conference on Reliability Systems Engineering (ICRSE), 2015. pp. 1–9. 10.1109/ICRSE.2015.7366464.Search in Google Scholar

[18] Sahoo, S. S., S. K. Panda, T. R. Mahapatra, and C. K. Hirwani. Numerical analysis of transient responses of delaminated layered structure using different mid-plane theories and experimental validation. Iranian Journal of Science and Technology-Transactions of Mechanical Engineering, Vol. 43, No. 1, 2019, pp. 41–56.10.1007/s40997-017-0111-3Search in Google Scholar

[19] Gong, H. and S. L. Zhang. Study on the simplified modeling methods of ship grillage for modal analysis. Ship & Ocean Engineering, Vol. 45, No. 03, 2016, pp. 47–49 + 54.Search in Google Scholar

[20] Wang, X. C., G. X. Wu, and D. Q. Wang. Research of simplified modeling method for ship grillage structure based on statistical energy. Analysis. Ship Engineering, Vol. 4101, 2019, pp. 40–47.Search in Google Scholar

[21] Pandey, H. K., H. Agrawal, S. K. Panda, C. K. Hirwani, P. V. Katariya, and H. C. Dewangan. Experimental and numerical bending deflection of cenosphere filled hybrid (Glass/Cenosphere/Epoxy) composite. Structural Engineering and Mechanics, Vol. 73, No. 6, 2020, pp. 715–724.Search in Google Scholar

[22] Korgesaar, M., P. Kujala, and J. Romanoff. Load carrying capacity of ice-strengthened frames under idealized ice load and boundary conditions. Marine Structures, Vol. 58, 2018, pp. 18–30.10.1016/j.marstruc.2017.10.011Search in Google Scholar

[23] Sharma, N., T. R. Mahapatra, S. K. Panda, and C. K. Hirwani. Acoustic radiation and frequency response of higher-order shear deformable multilayered composite doubly curved shell panel - An experimental validation. Applied Acoustics, Vol. 133, 2018, pp. 38–51.10.1016/j.apacoust.2017.12.013Search in Google Scholar

[24] He, P., Y. Xiang, Y. Zhou, and H. R. Li. Vibration energy distribution and transfer characteristics of coupled plates under medium-low frequency excitation. Noise and Vibration Control, Vol. 4002, 2020, pp. 13–22.Search in Google Scholar

[25] Lu, Z. Z. Dynamic optimization design of the plate frame structure of large ships. Ship Science and Technology, Vol. 4302, 2021, pp. 4–6.Search in Google Scholar

[26] Lin, C. G., J. G. Sun, Y. Yu, and A. G. Zhou. Research on low noise optimization of ship grillages. Ship Science and Technology, Vol. 41, No. 05, 2019, pp. 24–30.Search in Google Scholar

[27] Kryzhevich, G., E. Norkov, and A. Filatov. Principles and optimal design methods for large ship grillages. Transactions Of The Krylov State Research Centre, Vol. S-I, No. 2, 2020, pp. 83–88.10.24937/2542-2324-2020-2-S-I-83-88Search in Google Scholar

[28] Singh, V. K., C. K. Hirwani, S. K. Panda, T. R. Mahapatra, and K. Mehar. Numerical and experimental nonlinear dynamic response reduction of smart composite curved structure using collocation and non-collocation configuration. Proceedings of the Institution of Mechanical Engineers Part C-Journal of Mechanical Engineering Science, Vol. 233, No. 5, 2019, pp. 1601–1619.10.1177/0954406218774362Search in Google Scholar

[29] Cho, D. S., B. H. Kim, J. H. Kim, T. M. Choi, and N. Vladimir. Free vibration analysis of stiffened panels with lumped mass and stiffness attachments. Ocean Engineering, Vol. 124, 2016, pp. 84–93.10.1016/j.oceaneng.2016.07.055Search in Google Scholar

[30] Nguyen-Minh, N., T. Nguyen-Thoi, T. Bui-Xuan, and T. Vo-Duy. Static and free vibration analyses of stiffened folded plates using a cell-based smoothed discrete shear gap method (CS-FEM-DSG3). Applied Mathematics and Computation, Vol. 266, 2015, pp. 212–234.10.1016/j.amc.2015.05.042Search in Google Scholar

[31] Sahoo, P. R. and M. Barik. Free vibration analysis of stiffened plates. Journal of Vibration Engineering & Technologies, Vol. 8, No. 6, 2020, pp. 869–882.10.1007/s42417-020-00196-4Search in Google Scholar

[32] Hirwani, C. K., R. K. Patil, S. K. Panda, S. S. Mahapatra, S. K. Mandal, L. Srivastava, et al. Experimental and numerical analysis of free vibration of delaminated curved panel. Aerospace Science and Technology, Vol. 54, 2016, pp. 353–370.10.1016/j.ast.2016.05.009Search in Google Scholar

[33] Qing, G. H., J. J. Qiu, and Y. H. Liu. Free vibration analysis of stiffened laminated plates. International Journal of Solids and Structures, Vol. 43, No. 6, 2006, pp. 1357–1371.10.1016/j.ijsolstr.2005.03.012Search in Google Scholar

[34] Jadee, K. J., B. H. Abed, and A. A. Battawi. Free vibration of isotropic plates with various cutout configurations using finite elements and design of experiments. IOP Conference Series Materials Science and Engineering, Vol. 745, 2020, p. 012080.10.1088/1757-899X/745/1/012080Search in Google Scholar

[35] Pang, F. Z., H. C. Li, H. L. Chen, and Y. H. Shan. Free vibration analysis of combined composite laminated cylindrical and spherical shells with arbitrary boundary conditions. Mechanics of Advanced Materials and Structures, Vol. 28, No. 2, 2021, pp. 182–199.10.1080/15376494.2018.1553258Search in Google Scholar

[36] Pang, F. Z., H. C. Li, X. R. Wang, X. H. Miao, and S. Li. A semi analytical method for the free vibration of doubly-curved shells of revolution. Computers & Mathematics with Applications, Vol. 75, No. 9, 2018, pp. 3249–3268.10.1016/j.camwa.2018.01.045Search in Google Scholar

[37] Li, H. C., F. Z. Pang, H. L. Chen, and Y. Du. Vibration analysis of functionally graded porous cylindrical shell with arbitrary boundary restraints by using a semi analytical method. Composites Part B-Engineering, Vol. 164, 2019, pp. 249–264.10.1016/j.compositesb.2018.11.046Search in Google Scholar

[38] Li, H. C., F. Z. Pang, X. H. Miao, and Y. H. Li. Jacobi-Ritz method for free vibration analysis of uniform and stepped circular cylindrical shells with arbitrary boundary conditions: A unified formulation. Computers & Mathematics with Applications, Vol. 77, No. 2, 2019, pp. 427–440.10.1016/j.camwa.2018.09.046Search in Google Scholar

[39] Pang, F. Z., H. C. Li, J. Cui, Y. Du, and C. Gao. Application of flugge thin shell theory to the solution of free vibration behaviors for spherical-cylindrical-spherical shell: A unified formulation. European Journal of Mechanics a-Solids, Vol. 74, 2019, pp. 381–393.10.1016/j.euromechsol.2018.12.003Search in Google Scholar

[40] Lin, T. R. and J. Pan. A closed form solution for the dynamic response of finite ribbed plates. The Journal of the Acoustical Society of America, Vol. 119, No. 2, 2006, pp. 917–925.10.1121/1.2146111Search in Google Scholar

[41] Sahoo, P. R. and M. J. S. Barik. A numerical investigation on the dynamic response of stiffened plated structures unssssder moving loads. Structures, Vol. 28, 2020, pp. 1675–1686.10.1016/j.istruc.2020.09.056Search in Google Scholar

[42] Srivastava, A. K., P. K. Datta, and A. H. Sheikh. Buckling and vibration of stiffened plates subjected to partial edge loading. International Journal of Mechanical Sciences, Vol. 45, No. 1, 2003, pp. 73–93.10.1016/S0020-7403(03)00038-9Search in Google Scholar

[43] Song, C., Y. Zhao, J. T. Liu, Q. K. Zhang, and C. Gao. Research on the effect of typical excitation mode on ship structure vibration and acoustic radiation. Ship Science and Technology, Vol. 42, No. 21, 2020, pp. 24–29.Search in Google Scholar

[44] Yang, A. L., Y. Xu, G. P. Li, and Y. Zhang. Effect of blade loading on fluid-induced exciting force and noise in centrifugal pumps. Journal of Drainage and Irrigation Machinery Engineering, Vol. 32, No. 01, 2014, pp. 23–28.Search in Google Scholar

[45] Tamijani, A. Y. and R. K. Kapania. Random response analysis of curvilinearly-stiffened plate using element free Galerkin method. The 51st Aiaa/asme/asce/ahs/asc Structures, Structural Dynamics, & Materials Conference Aiaa/asme/ahs Adaptive Structures Conference, April 12–15, 2010, Orlando, Florida, 2010. 10.2514/6.2010-3035.Search in Google Scholar

[46] Mana, A. A. and V. R. Sonti. Sound radiation from a finite perforated panel set in a rigid baffle: A fully coupled analysis. Wave Motion, Vol. 85, 2019, pp. 144–164.10.1016/j.wavemoti.2018.11.004Search in Google Scholar
Received: 2022-04-27
Revised: 2022-06-23
Accepted: 2022-07-07
Published Online: 2022-08-30

© 2022 Tongda Zou et al., published by De Gruyter

This work is licensed under the Creative Commons Attribution 4.0 International License.

Articles in the same Issue

  1. Review Articles
  2. State of the art, challenges, and emerging trends: Geopolymer composite reinforced by dispersed steel fibers
  3. A review on the properties of concrete reinforced with recycled steel fiber from waste tires
  4. Copper ternary oxides as photocathodes for solar-driven CO2 reduction
  5. Properties of fresh and hardened self-compacting concrete incorporating rice husk ash: A review
  6. Basic mechanical and fatigue properties of rubber materials and components for railway vehicles: A literature survey
  7. Research progress on durability of marine concrete under the combined action of Cl− erosion, carbonation, and dry–wet cycles
  8. Delivery systems in nanocosmeceuticals
  9. Study on the preparation process and sintering performance of doped nano-silver paste
  10. Analysis of the interactions between nonoxide reinforcements and Al–Si–Cu–Mg matrices
  11. Research Articles
  12. Study on the influence of structural form and parameters on vibration characteristics of typical ship structures
  13. Deterioration characteristics of recycled aggregate concrete subjected to coupling effect with salt and frost
  14. Novel approach to improve shale stability using super-amphiphobic nanoscale materials in water-based drilling fluids and its field application
  15. Research on the low-frequency multiline spectrum vibration control of offshore platforms
  16. Multiple wide band gaps in a convex-like holey phononic crystal strip
  17. Response analysis and optimization of the air spring with epistemic uncertainties
  18. Molecular dynamics of C–S–H production in graphene oxide environment
  19. Residual stress relief mechanisms of 2219 Al–Cu alloy by thermal stress relief method
  20. Characteristics and microstructures of the GFRP waste powder/GGBS-based geopolymer paste and concrete
  21. Development and performance evaluation of a novel environmentally friendly adsorbent for waste water-based drilling fluids
  22. Determination of shear stresses in the measurement area of a modified wood sample
  23. Influence of ettringite on the crack self-repairing of cement-based materials in a hydraulic environment
  24. Multiple load recognition and fatigue assessment on longitudinal stop of railway freight car
  25. Synthesis and characterization of nano-SiO2@octadecylbisimidazoline quaternary ammonium salt used as acidizing corrosion inhibitor
  26. Perforated steel for realizing extraordinary ductility under compression: Testing and finite element modeling
  27. The influence of oiled fiber, freeze-thawing cycle, and sulfate attack on strain hardening cement-based composites
  28. Perforated steel block of realizing large ductility under compression: Parametric study and stress–strain modeling
  29. Study on dynamic viscoelastic constitutive model of nonwater reacted polyurethane grouting materials based on DMA
  30. Mechanical behavior and mechanism investigation on the optimized and novel bio-inspired nonpneumatic composite tires
  31. Effect of cooling rate on the microstructure and thermal expansion properties of Al–Mn–Fe alloy
  32. Research on process optimization and rapid prediction method of thermal vibration stress relief for 2219 aluminum alloy rings
  33. Failure prevention of seafloor composite pipelines using enhanced strain-based design
  34. Deterioration of concrete under the coupling action of freeze–thaw cycles and salt solution erosion
  35. Creep rupture behavior of 2.25Cr1Mo0.25V steel and weld for hydrogenation reactors under different stress levels
  36. Statistical damage constitutive model for the two-component foaming polymer grouting material
  37. Nano-structural and nano-constraint behavior of mortar containing silica aggregates
  38. Influence of recycled clay brick aggregate on the mechanical properties of concrete
  39. Effect of LDH on the dissolution and adsorption behaviors of sulfate in Portland cement early hydration process
  40. Comparison of properties of colorless and transparent polyimide films using various diamine monomers
  41. Study in the parameter influence on underwater acoustic radiation characteristics of cylindrical shells
  42. Experimental study on basic mechanical properties of recycled steel fiber reinforced concrete
  43. Dynamic characteristic analysis of acoustic black hole in typical raft structure
  44. A semi-analytical method for dynamic analysis of a rectangular plate with general boundary conditions based on FSDT
  45. Research on modification of mechanical properties of recycled aggregate concrete by replacing sand with graphite tailings
  46. Dynamic response of Voronoi structures with gradient perpendicular to the impact direction
  47. Deposition mechanisms and characteristics of nano-modified multimodal Cr3C2–NiCr coatings sprayed by HVOF
  48. Effect of excitation type on vibration characteristics of typical ship grillage structure
  49. Study on the nanoscale mechanical properties of graphene oxide–enhanced shear resisting cement
  50. Experimental investigation on static compressive toughness of steel fiber rubber concrete
  51. Study on the stress field concentration at the tip of elliptical cracks
  52. Corrosion resistance of 6061-T6 aluminium alloy and its feasibility of near-surface reinforcements in concrete structure
  53. Effect of the synthesis method on the MnCo2O4 towards the photocatalytic production of H2
  54. Experimental study of the shear strength criterion of rock structural plane based on three-dimensional surface description
  55. Evaluation of wear and corrosion properties of FSWed aluminum alloy plates of AA2020-T4 with heat treatment under different aging periods
  56. Thermal–mechanical coupling deformation difference analysis for the flexspline of a harmonic drive
  57. Frost resistance of fiber-reinforced self-compacting recycled concrete
  58. High-temperature treated TiO2 modified with 3-aminopropyltriethoxysilane as photoactive nanomaterials
  59. Effect of nano Al2O3 particles on the mechanical and wear properties of Al/Al2O3 composites manufactured via ARB
  60. Co3O4 nanoparticles embedded in electrospun carbon nanofibers as free-standing nanocomposite electrodes as highly sensitive enzyme-free glucose biosensors
  61. Effect of freeze–thaw cycles on deformation properties of deep foundation pit supported by pile-anchor in Harbin
  62. Temperature-porosity-dependent elastic modulus model for metallic materials
  63. Effect of diffusion on interfacial properties of polyurethane-modified asphalt–aggregate using molecular dynamic simulation
  64. Experimental study on comprehensive improvement of shear strength and erosion resistance of yellow mud in Qiang Village
  65. A novel method for low-cost and rapid preparation of nanoporous phenolic aerogels and its performance regulation mechanism
  66. In situ bow reduction during sublimation growth of cubic silicon carbide
  67. Adhesion behaviour of 3D printed polyamide–carbon fibre composite filament
  68. An experimental investigation and machine learning-based prediction for seismic performance of steel tubular column filled with recycled aggregate concrete
  69. Effects of rare earth metals on microstructure, mechanical properties, and pitting corrosion of 27% Cr hyper duplex stainless steel
  70. Application research of acoustic black hole in floating raft vibration isolation system
  71. Multi-objective parametric optimization on the EDM machining of hybrid SiCp/Grp/aluminum nanocomposites using Non-dominating Sorting Genetic Algorithm (NSGA-II): Fabrication and microstructural characterizations
  72. Estimating of cutting force and surface roughness in turning of GFRP composites with different orientation angles using artificial neural network
  73. Displacement recovery and energy dissipation of crimped NiTi SMA fibers during cyclic pullout tests
https://doi.org/10.1515/rams-2022-0053
Keywords for this article
ship grillage; vibration characteristics; model tests; excitation type; FEM
Creative Commons
BY 4.0

Articles in the same Issue

  1. Review Articles
  2. State of the art, challenges, and emerging trends: Geopolymer composite reinforced by dispersed steel fibers
  3. A review on the properties of concrete reinforced with recycled steel fiber from waste tires
  4. Copper ternary oxides as photocathodes for solar-driven CO2 reduction
  5. Properties of fresh and hardened self-compacting concrete incorporating rice husk ash: A review
  6. Basic mechanical and fatigue properties of rubber materials and components for railway vehicles: A literature survey
  7. Research progress on durability of marine concrete under the combined action of Cl− erosion, carbonation, and dry–wet cycles
  8. Delivery systems in nanocosmeceuticals
  9. Study on the preparation process and sintering performance of doped nano-silver paste
  10. Analysis of the interactions between nonoxide reinforcements and Al–Si–Cu–Mg matrices
  11. Research Articles
  12. Study on the influence of structural form and parameters on vibration characteristics of typical ship structures
  13. Deterioration characteristics of recycled aggregate concrete subjected to coupling effect with salt and frost
  14. Novel approach to improve shale stability using super-amphiphobic nanoscale materials in water-based drilling fluids and its field application
  15. Research on the low-frequency multiline spectrum vibration control of offshore platforms
  16. Multiple wide band gaps in a convex-like holey phononic crystal strip
  17. Response analysis and optimization of the air spring with epistemic uncertainties
  18. Molecular dynamics of C–S–H production in graphene oxide environment
  19. Residual stress relief mechanisms of 2219 Al–Cu alloy by thermal stress relief method
  20. Characteristics and microstructures of the GFRP waste powder/GGBS-based geopolymer paste and concrete
  21. Development and performance evaluation of a novel environmentally friendly adsorbent for waste water-based drilling fluids
  22. Determination of shear stresses in the measurement area of a modified wood sample
  23. Influence of ettringite on the crack self-repairing of cement-based materials in a hydraulic environment
  24. Multiple load recognition and fatigue assessment on longitudinal stop of railway freight car
  25. Synthesis and characterization of nano-SiO2@octadecylbisimidazoline quaternary ammonium salt used as acidizing corrosion inhibitor
  26. Perforated steel for realizing extraordinary ductility under compression: Testing and finite element modeling
  27. The influence of oiled fiber, freeze-thawing cycle, and sulfate attack on strain hardening cement-based composites
  28. Perforated steel block of realizing large ductility under compression: Parametric study and stress–strain modeling
  29. Study on dynamic viscoelastic constitutive model of nonwater reacted polyurethane grouting materials based on DMA
  30. Mechanical behavior and mechanism investigation on the optimized and novel bio-inspired nonpneumatic composite tires
  31. Effect of cooling rate on the microstructure and thermal expansion properties of Al–Mn–Fe alloy
  32. Research on process optimization and rapid prediction method of thermal vibration stress relief for 2219 aluminum alloy rings
  33. Failure prevention of seafloor composite pipelines using enhanced strain-based design
  34. Deterioration of concrete under the coupling action of freeze–thaw cycles and salt solution erosion
  35. Creep rupture behavior of 2.25Cr1Mo0.25V steel and weld for hydrogenation reactors under different stress levels
  36. Statistical damage constitutive model for the two-component foaming polymer grouting material
  37. Nano-structural and nano-constraint behavior of mortar containing silica aggregates
  38. Influence of recycled clay brick aggregate on the mechanical properties of concrete
  39. Effect of LDH on the dissolution and adsorption behaviors of sulfate in Portland cement early hydration process
  40. Comparison of properties of colorless and transparent polyimide films using various diamine monomers
  41. Study in the parameter influence on underwater acoustic radiation characteristics of cylindrical shells
  42. Experimental study on basic mechanical properties of recycled steel fiber reinforced concrete
  43. Dynamic characteristic analysis of acoustic black hole in typical raft structure
  44. A semi-analytical method for dynamic analysis of a rectangular plate with general boundary conditions based on FSDT
  45. Research on modification of mechanical properties of recycled aggregate concrete by replacing sand with graphite tailings
  46. Dynamic response of Voronoi structures with gradient perpendicular to the impact direction
  47. Deposition mechanisms and characteristics of nano-modified multimodal Cr3C2–NiCr coatings sprayed by HVOF
  48. Effect of excitation type on vibration characteristics of typical ship grillage structure
  49. Study on the nanoscale mechanical properties of graphene oxide–enhanced shear resisting cement
  50. Experimental investigation on static compressive toughness of steel fiber rubber concrete
  51. Study on the stress field concentration at the tip of elliptical cracks
  52. Corrosion resistance of 6061-T6 aluminium alloy and its feasibility of near-surface reinforcements in concrete structure
  53. Effect of the synthesis method on the MnCo2O4 towards the photocatalytic production of H2
  54. Experimental study of the shear strength criterion of rock structural plane based on three-dimensional surface description
  55. Evaluation of wear and corrosion properties of FSWed aluminum alloy plates of AA2020-T4 with heat treatment under different aging periods
  56. Thermal–mechanical coupling deformation difference analysis for the flexspline of a harmonic drive
  57. Frost resistance of fiber-reinforced self-compacting recycled concrete
  58. High-temperature treated TiO2 modified with 3-aminopropyltriethoxysilane as photoactive nanomaterials
  59. Effect of nano Al2O3 particles on the mechanical and wear properties of Al/Al2O3 composites manufactured via ARB
  60. Co3O4 nanoparticles embedded in electrospun carbon nanofibers as free-standing nanocomposite electrodes as highly sensitive enzyme-free glucose biosensors
  61. Effect of freeze–thaw cycles on deformation properties of deep foundation pit supported by pile-anchor in Harbin
  62. Temperature-porosity-dependent elastic modulus model for metallic materials
  63. Effect of diffusion on interfacial properties of polyurethane-modified asphalt–aggregate using molecular dynamic simulation
  64. Experimental study on comprehensive improvement of shear strength and erosion resistance of yellow mud in Qiang Village
  65. A novel method for low-cost and rapid preparation of nanoporous phenolic aerogels and its performance regulation mechanism
  66. In situ bow reduction during sublimation growth of cubic silicon carbide
  67. Adhesion behaviour of 3D printed polyamide–carbon fibre composite filament
  68. An experimental investigation and machine learning-based prediction for seismic performance of steel tubular column filled with recycled aggregate concrete
  69. Effects of rare earth metals on microstructure, mechanical properties, and pitting corrosion of 27% Cr hyper duplex stainless steel
  70. Application research of acoustic black hole in floating raft vibration isolation system
  71. Multi-objective parametric optimization on the EDM machining of hybrid SiCp/Grp/aluminum nanocomposites using Non-dominating Sorting Genetic Algorithm (NSGA-II): Fabrication and microstructural characterizations
  72. Estimating of cutting force and surface roughness in turning of GFRP composites with different orientation angles using artificial neural network
  73. Displacement recovery and energy dissipation of crimped NiTi SMA fibers during cyclic pullout tests
Sign up now to receive a 20% welcome discount
Institutional Access
How does access work?
Have an idea on how to improve our website?
Please write us.
© 2025 De Gruyter Brill
Downloaded on 18.12.2025 from https://www.degruyterbrill.com/document/doi/10.1515/rams-2022-0053/html
Scroll to top button