Basic mechanical and fatigue properties of rubber materials and components for railway vehicles: A literature survey

Wei Kang; Jiefu Liu; Wei Xiong; Tianyu You; Xinxin Wang; Kexin Zeng; Yingao Deng; Zichao Guo; Ke Yuan

doi:10.1515/rams-2022-0054

Article Open Access

Basic mechanical and fatigue properties of rubber materials and components for railway vehicles: A literature survey

Wei Kang , Jiefu Liu , Wei Xiong , Tianyu You , Xinxin Wang , Kexin Zeng , Yingao Deng , Zichao Guo and Ke Yuan

Published/Copyright: September 26, 2022

Published by

Become an author with De Gruyter Brill

Submit Manuscript Author Information

From the journal REVIEWS ON ADVANCED MATERIALS SCIENCE Volume 61 Issue 1

Abstract

Rubber material is widely used in railway vehicles due to its superior damping performance. The testing methods, fatigue, and aging theories of rubber materials are of great significance to improve the design, manufacture, and application of rubber components for railway vehicles. This work systematically introduces the constitutive theory, mechanical testing standards, and testing methods of rubber materials. Then, the aging mechanism is described and the research progress of rubber fatigue properties is reviewed from the perspectives of fatigue crack initiation and fatigue crack propagation. Moreover, the reinforcement methods of rubber materials are presented. Finally, according to the working conditions of rubber components in railway vehicle, the technical difficulties and future research trends of fatigue characteristics analysis of rubber materials and components are pointed out.

Keywords: rubber; railway vehicle; test method; fatigue; aging; life prediction

Acronyms

CDM: continuum damage mechanics
CED: cracking energy density
EFI: energy field intensity
ML: machine learning
NR: natural rubber
SBR: styrene–butadiene rubber
SED: strain energy density
SVM: support vector machine

1 Introduction

The development of science and technology is inseparable from the discovery and application of various new materials. Rubber materials and products have shown good elasticity, insulation, waterproof, and wear resistance in recent years. It is widely used in industry, agriculture, national defense, transportation, machinery manufacturing, medical, and health fields [1]. As shown in Figure 1, different rubber products invented in rail engineering greatly improved the service life, safety, and comfort of the rail vehicles and superior damping performance [2]. Using rubber products in track engineering construction can effectively increase the elasticity of track structure, reduce the dynamic stress of track structure and the load and stress, and reduce the vibration and noise caused by wheel–rail interaction [3,4]. The rubber components with superior damping performance make the train run more smoothly.

Figure 1

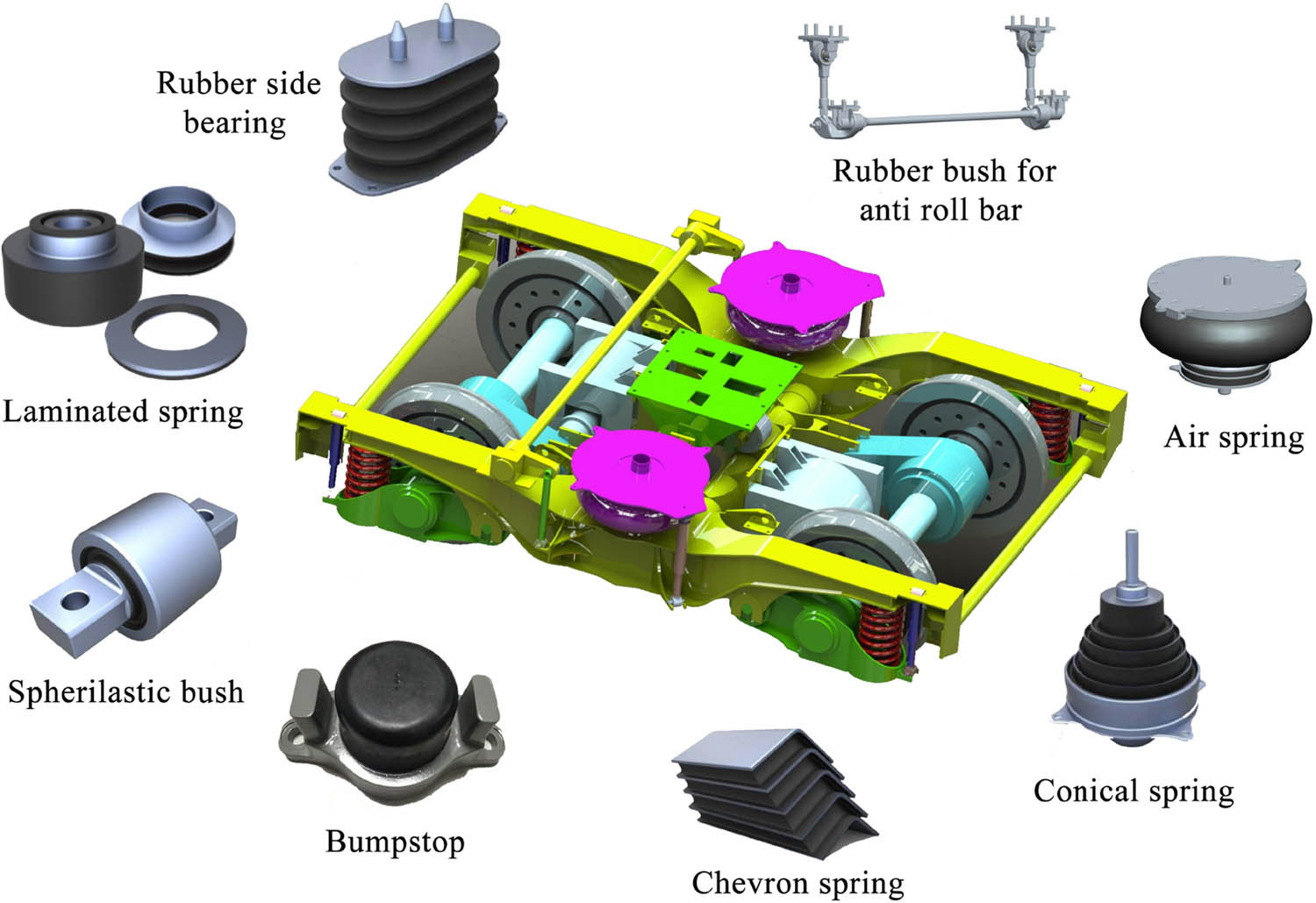
Rubber components in railway vehicle.

Due to being directly related to the ride comfort and running safety of the railway vehicle, the design and development process of the rubber components is extremely complicate. With the promotion of rail transport in remote areas and the increasing speed of rail vehicles, the service environment of the rubber components is becoming more and more severe [5,6,7]. The failure modes of rubber components are complex and the fatigue life is affected by many factors [8,9,10,11]. Testing technology is important for understanding the mechanical properties of rubber materials and components. Much progress has been made in the study of rubber aging and fatigue. Besides, rubber reinforcement technology has recently developed rapidly. Carbon black, nanomaterials, and other fillers have made rubber show more powerful properties [12,13,14,15,16,17]. On the other hand, it is found that the structural design of rubber components also determines their function and durability [18,19,20], and there is a large space for optimization.

With the urgent demand for better material properties and longer durability of rubber in the industry, a large number of works have been published recently. Although there are many state-of-the-art papers on rubber materials, few address specifically for railway vehicles application. The designers of rubber elastic components are still facing more challenges than ever. The present work focuses on systematically collecting and analyzing the vast amount of works on constitutive theories, test standards and methods, aging and fatigue studies, reinforcement, and structural design in the last decades. This detailed survey aims to fill the information gap and provide an informative overview of the railway vehicles field. This work may be of interest to the railway community and inspire in improving the measuring and testing technique, improving the designing ability, sorting out and innovating theory, test, and simulation methods in the rail vehicle industry and rubber industry.

2 Constitutive theory of rubber materials

The mechanical properties of rubber materials are different from those of conventional elastic materials. The deformation of elastic materials under tensile or compression loads is a reversible process, and the internal energy of elastic materials is equivalent to the strain energy. In the case of hyperplastic materials at a constant temperature, the free energy and strain energy are equivalent, that is, there is strain energy to a certain extent [21]. Rubber materials can be classified as hyperplastic in this definition and have incompressible properties [22,23]. Different physical models of rubber materials have different strain energy functions [24,25,26,27]. The Cauchy Green stress tensor σ can be determined by the value of the strain energy function [28]:

(1) σ = − pI + 2 ∂ W ∂ I 1 B − 2 ∂ W ∂ I 2 B − 1 ,

where σ represents the Cauchy Green stress tensor; I represents the unit stress deformation tensor; p stands for static pressure; and I i is a variable determined by B :

(2) I 1 = B , I 2 = 1 2 [ I 1 2 − tr ( B 2 ) ] , I 3 = det B .

I i is mainly determined by the elongation λ i :

(3) I 1 = λ 1 2 + λ 2 2 + λ 3 2 ,

(4) I 2 = λ 1 2 λ 2 2 + λ 2 2 λ 3 2 + λ 1 2 λ 3 2 ,

(5) I 3 = λ 1 2 λ 2 2 λ 3 2 ,

(6) I 3 = λ 1 λ 2 λ 3 = 1 ,

where I 1 , I 2 , and I 3 are the three strain invariant tensors, λ 1 , λ 2 , and λ 3 are the stretch ratio in the three principal directions.

The commonly used constitutive model of rubber is clarified as follows:

2.1 Reduced polynomial model

The reduced polynomial model is a special form of the polynomial model in which the main parameter C ij is set to 0, and I 1 of the higher-order term is taken as the modified parameter of the strain energy function. The strain energy function of the reduced polynomial is shown as follows:

(7) U = ∑ i = 1 N C i 0 ( I 1 ¯ − 3 ) i + ∑ i = 0 N 1 D 1 ( J − 1 ) 2 i ,

where N is the order of the strain density function polynomial; since rubber is usually regarded as an incompressible material, the value of D 1 is 0; J is the volume ratio before and after deformation.

The neo-Hookean model is a reduced polynomial hyperplastic constitutive model when it is a first-order polynomial. Its form is expressed as follows:

(8) U = C 10 ( I 1 − 3 ) ,

where C 10 is the model parameter, 2 C 10 = μ , μ is the shear modulus.

When the structural deformation is relatively small, the stress–strain curves obtained from a single test can be used to model the material parameters and measure other deformations. Occasionally, the component has multiple strains, or the strain of the component is large. Under this circumstance, if there is a large error between the strain energy calculated by the neo-Hookean model and the actual data, another rubber hyperelastic constitutive model should be used.

When N = 3 , the reduced polynomial model is the Yeoh model [23], which is a special form of the reduced polynomial:

(9) U = ∑ i = 1 3 C i 0 ( I 1 ¯ − 3 ) i + ∑ i = 0 3 1 D 1 ( J − 1 ) 2 i .

Because the higher order of the first strain invariant is used as the variable of strain energy density (SED) function, Yeoh model can accurately simulate rubber deformation in a wide range. The stress–strain curve of S-shaped rubber material can be obtained by Yeoh model.

2.2 Ogden model

The strain energy of the Ogden model [29] has three variables, namely, the principal elongation λ 1 , λ 2 , and λ 3 . Its strain energy is in the form of the following equation:

(10) U = ∑ i = 1 N 2 μ i α i 2 ( λ 1 ¯ α i + λ 2 ¯ α i + λ 3 ¯ α i − 3 ) + ∑ i = 1 N 1 D i ( J − 1 ) 2 i ,

where λ i ¯ = J − 1 3 λ i → λ 1 ¯ λ 2 ¯ λ 3 ¯ = 1 ; N is the order of Ogden model; The initial shear modulus μ 0 can be obtained by calculating the sum of μ i .

The Ogden model believes that the independent function of the three main elongations is the SED, so the deformation of different rubbers can be described as a simple polynomial form. Usually, N = 3 or N = 4 can meet the accuracy requirements, and it has good simulation ability for all deformation. When N = 1, α 1 = 2 , that is the expression of neo–Hookean model. When N = 1 , α 1 = 2 , α 2 = − 2 , that is the expression of the Mooney–Rivlin model.

2.3 Mooney–Rivlin model

Based on the theory of phase change material and through many experiments, Mooney established the strain energy function of the rubber hyperplastic constitutive model:

(11) W = C 10 ( I 1 − 3 ) + C 01 ( I 2 − 3 ) .

Since the volume parameter K 0 of the n-order polynomial depends on the order of the polynomial, for the case of the first-order polynomial, the strain energy function of the Mooney–Rivlin model is shown as follows:

(12) U = C 10 ( I 1 ¯ − 3 ) + C 01 ( I 2 ¯ − 3 ) + 1 D 1 ( J − 1 ) 2 .

Mooney–Rivlin model can better express the stress–strain characteristics of rubber materials under the condition of small strain energy [30,31]. It is noted that Mooney–Rivlin model cannot well represent the behavior of steep rise of rubber material under large strain load. Because of the simplicity of the expression and the material parameters can be easily obtained by fitting constitutive test data, Mooney-Rivlin model is most widely used in finite element analysis (Table 1).

Table 1

Comparison of rubber constitutive models

Model	Scope of application	Advantage
Neo-Hookean	Small and medium deformation	Simple expression and simple computation
Yeoh	Various deformation	Simple expression and wide applicability
Ogden	Various deformation	High adaptability
Mooney–Rivlin	Small deformation	Simple expression and wide applicability

3 Test standards and methods of rubber materials

At present, there are many testing standards and methods to obtain the mechanical properties of rubber materials and components. Taking the standard of rubber elastic components for railway vehicles in China as an example, TB/T 2843-2007 “General technical conditions for rubber elastic components for rolling stock” is the current standard of railway industry standard in China. This standard stipulates the basic performance and requirements of rubber elastic components and rubber materials for different kinds of rolling stock. Performance tested methods and inspection rules for rubber materials, metal materials, and products are also included. In addition, the service environment requirements and packaging, storage, and transportation regulations of rubber elastic components are also mentioned.

The rubber elastic components test contains the static performance test, dynamic performance test, bonding strength test, compression creep test, and fatigue performance test. The standard provides principles of the test environment, test principle, test method, test equipment, specimen failure judgment, and data processing method, etc.

The standards of different countries/regions are: Chinese standard TB/T2843-2007 “General technical conditions of rubber elastic components for locomotive and rolling stock,” European standard EN 13913-2003 “Elastic foundation components of rubber suspension components for railway,” and Japanese industrial standard JISE 4710-1995, “General rules of rubber vibration isolators for railway locomotive and rolling stock.”

The main differences between TB/T 2843-2007 and EN13913-2003 are shown as follows: the dynamic creep test and test method are not specified; static and dynamic stress relaxation tests and test methods are not specified. Moreover, the main differences between TB/T 2843-2007 and JISE 4710-1995 are as follows: hardness test and test method are not specified; insulation resistance test and test method are not specified.

This standard TB/T 2843-2007 replaced TB/T 2843-1997 “General technical conditions for rubber elastic components of locomotive and rolling stock” and TB/T 2589-1995 “General technical conditions for rubber pile of electric locomotive.” The main changes are as follows: the basic properties and requirements of rubber materials used for rubber elastic components are different; the dynamic performance test of rubber elastic components is added; the static creep test of rubber elastic components is added. Besides, different test methods for static performance, bonding performance, and fatigue performance of rubber elastic components are provided.

Rubber components used in rolling stock are vulcanized rubber. In addition to the abovementioned standard TB/T 2843-2007 “General technical conditions of rubber elastic components for locomotives and rolling stock,” vulcanized rubber tensile properties, compressive properties, shear properties, tear strength, wear resistance, and low-temperature brittleness have been formulated in other standards. For example, GB/T 39693-2020 “Vulcanized rubber or thermoplastic rubber hardness determination” and GB/T 15256-2014 “vulcanized rubber or thermoplastic rubber low-temperature brittleness determination (multi-sample method)” are designed. An international standard example is ISO 3384 AMD-2019 “vulcanized rubber or thermoplastic rubber compression stress relaxation determination.” Meanwhile, some countries may also formulate standards that suit their own national conditions, such as Japan JIS K6253-2012 “vulcanized rubber or thermoplastic rubber hardness determination” and France NF T46-009-2013 “vulcanized rubber or thermoplastic rubber under constant elongation conditions of tensile permanent deformation, and under the constant tensile load of tensile permanent deformation, elongation, and creep.”

For some specific rubber elastic component standards, such as rubber spring vibration isolator, rubber suspension spring, rubber shock absorber, brake hose, oil-resistant rubber pad, rubber sealing strip, etc., we have developed more detailed independent standards, which are also in line with the railway industry standards of the People’s Republic of China.

Each country has its own standards, according to which components are manufactured or tested to ensure maximum accuracy. However, these standards will be updated to better adapt to new application with the development of science and technology.

3.1 Static mechanical property test

The basic mechanical test of rubber elastic components of locomotive and rolling stock is divided into static mechanical test and dynamic mechanical test. There are eight kinds of static mechanical properties tests for rubber materials, including uniaxial, biaxial, planar, and volumetric tests under the conditions of tensile and compression (Figure 2). Many studies have found that the data obtained from the uniaxial tensile, biaxial tensile, plane tensile, and volumetric compression tests can accurately represent the basic mechanical properties of rubber materials [32,33,34]. Therefore, uniaxial tensile, biaxial tensile, plane tensile, and volumetric compression tests are internationally defined as the basic mechanical behavior of rubber materials.

Figure 2

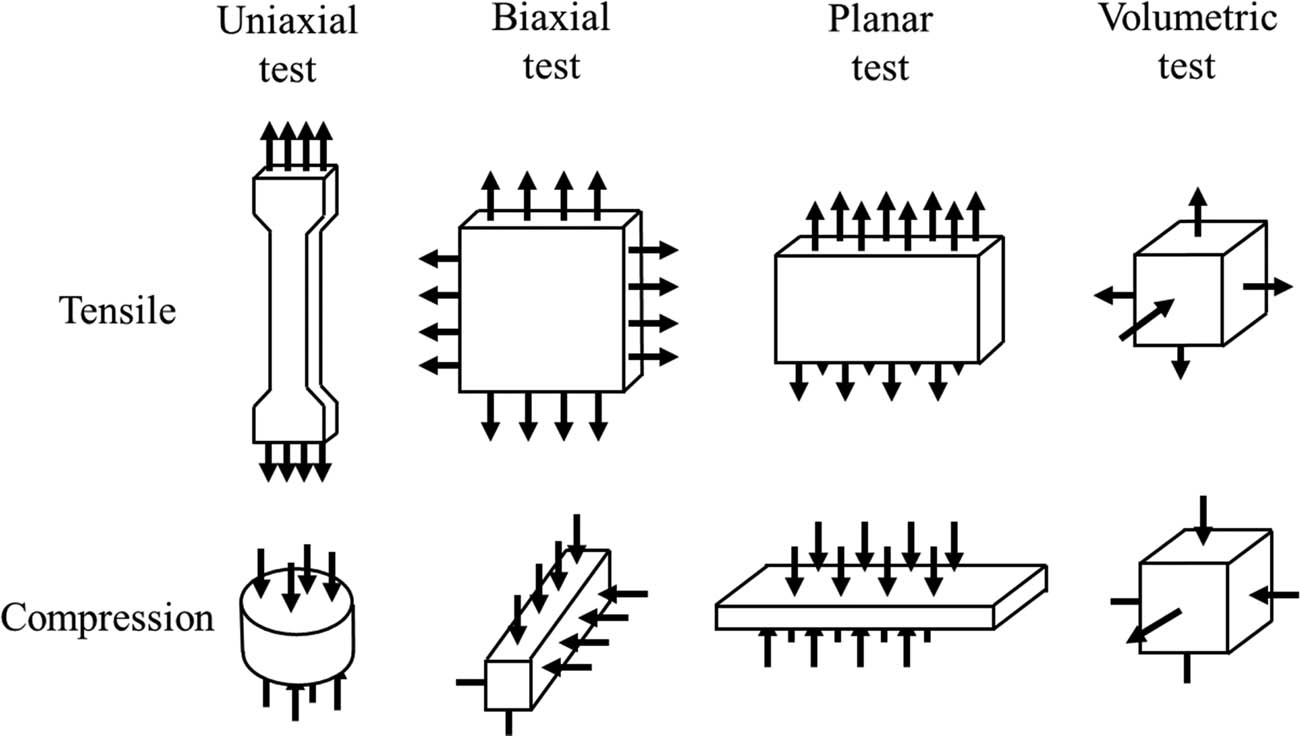
Static mechanical test of rubber material.

The uniaxial tensile test is widely used due to its simple test method, there are many standards for the uniaxial tensile test of rubber material. However, these standards cannot meet the test requirements of rubber material finite element analysis. The rubber material sample side is still restricted, and cannot reach the test requirements of the pure tensile state [35,36,37].

It is difficult for rubber materials to achieve a completely unidirectional compressive strain. Due to the influence of friction factors, rubber materials cannot expand freely, and obvious shear strain will occur on the side of rubber materials, which frequently cause the maximum shear strain exceed the maximum compressive strain [38]. In order to obtain the ideal uniaxial compression data, the biaxial tensile test can be used which is exactly equivalent to the ideal compression test.

Brieu et al. [39] proposed a new mechanism for the biaxial tensile test, which can simultaneously load in-plane specimens in two main directions. The mechanism can also be adapted to any single axial tensile testing machine, thereby reducing the cost of testing on expensive test machines.

The uniaxial and equiaxial tensile test data for rubber materials were determined by Sasso et al. [40]. It is based on optical methods, and has the highest accuracy. Besides, it shows good agreement between simulation and experiment, even when it is applied to additional states of tension (such as planes).

Ru et al. [41] designed a new equiaxial tensile testing machine using a novel rope and pulley loading system that can automatically ensure equal stress in both directions and minimizes possible installation bias. The new rubber biaxial and uniaxial experiments proposed by these researchers improve the accuracy of the classical hyperplastic model by measuring more accurate parameters [42].

The plane tensile test of rubber material is similar to the uniaxial tensile test, but the difference was that the rubber specimen used in the plane tensile test was wider [43]. The results showed that when the width of the rubber specimen is more than ten times its length, the complete tensile strain can be achieved in the plane tensile strain state of the rubber material surface.

Xia et al. [44] proposed a new plane tensile test method that modified plane tension to evaluate the predictive ability of the rubber constitutive model under moderately finite deformation. The results verified that the plane tensile test was a kind of non-uniform deformation, that is, the deformation of the central region of the specimen was uniform, but the deformation of the whole region was not uniform.

The rubber material is almost incompressible. If the compressibility of rubber is considered, the cylindrical rubber specimen should be placed in a fixed rigid container for compression. Radek et al. found that the volume modulus of rubber material was 2–3 orders of magnitude higher than the shear modulus by experimenting [45].

3.2 Dynamic mechanical property test

Different from the static mechanical properties of rubber materials, the dynamic properties are the properties of rubber elastic components, mainly including stiffness and damping properties [46,47]. If the frequency of the interfering force is far less than the natural frequency of the structure, the dynamic stiffness and static stiffness are basically the same [48,49]. When the frequency of the interference force is much greater than the natural frequency of the structure, the deformation of the structure is relatively small, that is, the dynamic stiffness is relatively large. When the frequency of the interference force is close to the natural frequency of the structure, there is a resonance phenomenon, and the dynamic stiffness is the smallest, that is, the deformation is the easiest. The dynamic deformation can reach several times or even more than ten times the static deformation [50,51,52,53]. The response of the structure under dynamic load largely depended on the damping characteristics [54,55,56,57,58,59,60]. Because of the Mullins effect and hysteresis curve, rubber elastic components are widely used in train vibration reduction.

Lie et al. [61] used an artificial neural network to conduct simulation and experiment under different chamfering sizes and axial preloading.

Lee et al. [62] proposed an approximate hybrid method based on finite element analysis and empirical modeling to analyze the dynamic characteristics of the rubber bushing. This method can predict the dynamic stiffness of rubber bushings without an iterative test, but the calculation cost is high. It is suitable for the analysis of full-size vehicles with many rubber bushings under various vibration loads.

Based on the superposition principle, Luo et al. [63] established a nonlinear dynamic model of a rubber shock absorber in a railway fastening system. It simulated its nonlinear vibration behavior, and obtained all model parameters through dynamic experiments. The frequency dependence and amplitude dependence of nonlinear dynamic stiffness were further studied. The results showed that the nonlinear dynamic stiffness characteristics were closely related to the displacement amplitude and frequency, but the frequency correlation was not as great as the amplitude correlation.

4 Aging of rubber materials

Polymer materials in the process of processing, transportation, storage, and service are inevitably affected by internal and external factors. These factors lead to deterioration of material performance or even failure. This phenomenon is usually called aging. Rubber aging is often a complex and multi-factor coupling process, and different factors have different performance characteristics. According to the different influencing factors, rubber aging can be divided into natural air aging, ozone aging, chemical aging, radiation aging, etc., [64,65].

4.1 Aging mechanism

4.1.1 Thermal oxygen aging

The damage of thermal oxygen to the mechanical properties of rubber is obvious in an oxygen environment [63,64,65,66,67,68,69,70,71]. The mechanism of the thermal oxygen aging reaction of rubber is that oxygen automatically catalyzes free radical chain reaction, in which oxygen is the main factor causing aging. Heat plays a role in activating oxidation and accelerating oxidation, and oxygen-containing groups, like ketones, aldehydes, epoxides, etc., are generated in this aging reaction [72,73,74,75,76,77]. The aging process can be divided into the following four periods [78]: (1) induction period, (2) rapid oxidation period, (3) slow oxidation period, and (4) diffusion-forbidden period (Table 2).

Table 2

The thermal oxygen aging reaction of rubber

Aging process	Mechanism of thermal oxygen aging reaction
Induction period	RH → R ∙ + ∙ H
Induction period	(Heat, oxygen, light, or catalyst)
Rapid oxidation period	R ∙ + O 2 → ROO
Rapid oxidation period	ROO ∙ + HR → ROOH + R ∙
Slow oxidation period	ROOH → RO ∙ + ∙ OH
Slow oxidation period	2 ROOH → RO ∙ + ROO ∙ + H 2 O
Diffusion-forbidden period	R ∙ + R ∙ → R − R
	ROO ∙ + ROO ∙ → Stable product + O 2
	R ∙ + ROO ∙ → ROOR

RH stands for rubber macromolecules, R ∙ stands for free radicals, RO ∙ stands for oxidizing radicals, and ROO ∙ stands for peroxide free radical.

4.1.2 Ozone aging

Ozone is an extremely rare gas in the atmosphere, but it is extremely destructive to plastic materials. Ozone can have an irreversible chemical reaction with unsaturated bonds and reductive groups in the chemical structure of plastic materials, resulting in oxidative degradation of plastic materials [79]. Ozone aging of natural rubber is a process from surface to interior and from middle to both sides [80]. Rubber ozone aging first begins on the surface, especially in the stress concentration or compound particles and rubber interface [81]. The aging process usually begins with generating a thin film, and then the film cracks. If it is used under dynamic conditions, the film is more likely to constantly break and expose the fresh surface, making ozone aging worse. The cracking molecular chain in the double bond is more likely to participate in ozone aging, and produces more carbon and oxygen bonds until destruction [82]. Unsaturated rubber is the least resistant to ozone because ozone is most likely to undergo rapid electrophilic addition reactions with the double bonds on the main chain. The oxidation resistance of rubber is enhanced using antioxidants with added chemical elements [83,84].

In addition, there are mechanical stress, moisture, and light radiation, which are important factors in rubber aging (Figure 3).

Figure 3

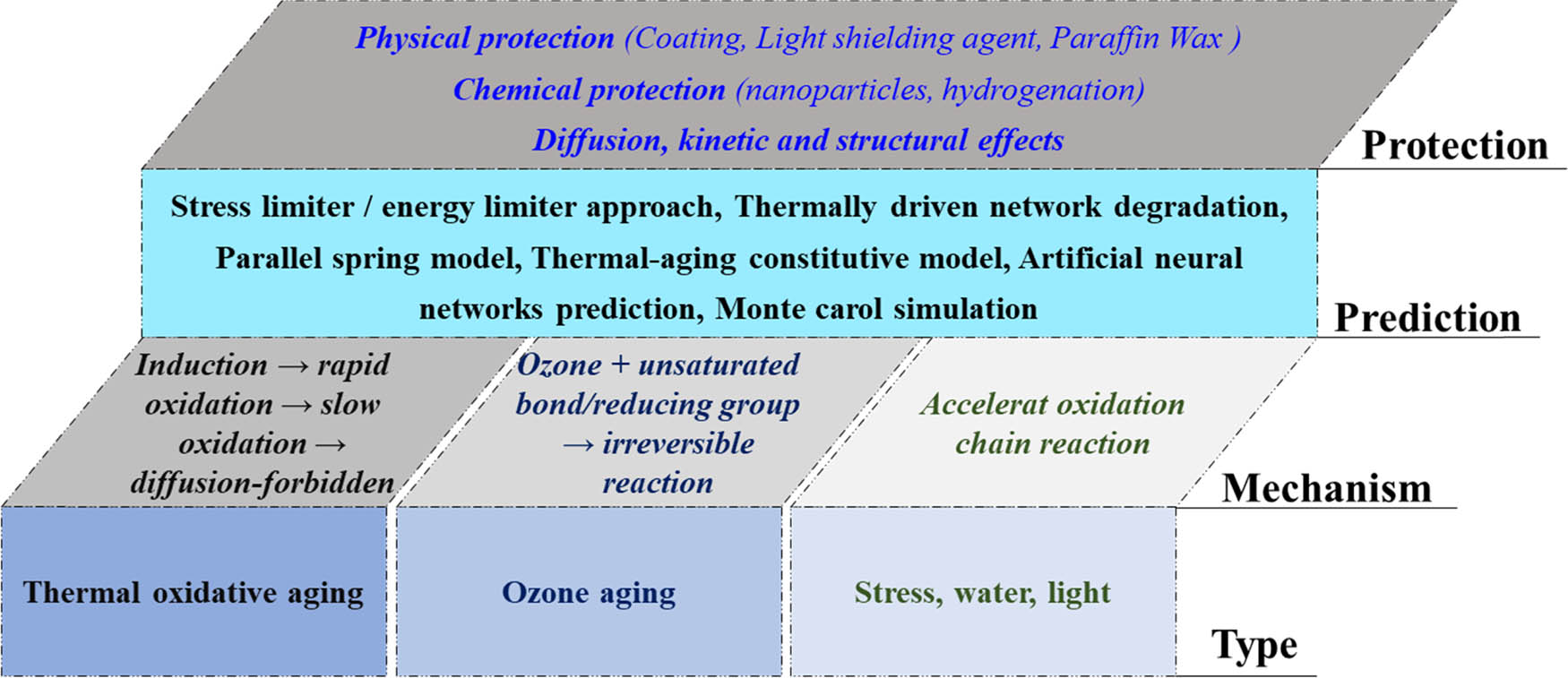
Research progress of rubber material aging.

4.2 The aging analysis model

Two new methods for predicting failure characteristics are proposed. The first one is the stress limiter method, which uses “damage” parameters to determine the failure stress and strain of the aged material. Meanwhile, it also acquires the mechanical properties and polymer network characteristics of the receiving material [85]. The second method is an extension of the energy limiter method, which captures the stress drop at failure by replacing the SED function of the receiving elastic material with a function expressed by the energy limiter [86].

By considering a series of chemical and physical changes in the rubber filling material system, a network change theory of thermal-driven network degradation was proposed. The decomposition of the network considered the break-back mechanism of links (between filler aggregates and elastically active cross-linked chains), as well as changes in free chain motion superimposed on chemical linked networks (nascent and original networks) [87].

Some scholars had carried out swelling tests to analyze the relationship between the SED obtained by mechanical experiments and the cross-linking density obtained by chemical experiments. The results of the swelling test were substituted into the Flory-Reihner equation to obtain the cross-linking density, and an equation assuming that the cross-linking structure was a spring model was proposed. The relationship between SED and cross-linking density was summarized, and a method to predict the aging behavior of NR/BR blends using cross-linking density was proposed [88].

Besides, there are also many life prediction models based on experimental methods [89,90,91,92,93], artificial neural networks [94], Monte Carlo methods [95], and so on.

4.3 Protection strategies against ageing

Given that the rubber aging is a complex comprehensive chemical reaction process and it is impossible to absolutely prevent rubber aging, physical or chemical measures can be taken to delay the aging rate of rubber and achieve the purpose of extending the service life of the rubber [96,97].

Physical protection means avoiding the interaction between rubber and various aging factors as far as possible, such as using a surface layer or treatment, adding a light-blocking agent, adding paraffin, etc., [98]. Chemical protection refers to the addition of certain substances to prevent or delay rubber aging [99]. The results showed that the tensile strength, tear strength, and modulus of NR are increased after the aging test, while the elongation at break was decreased due to introduction of Al₂O₃ nanoparticles into NR. These were attributed to cross-linking maturation reactions that result in the conversion of poly sulfur bonds to disulfide and monoculture bonds [100]. The physical, chemical, and thermal properties of diene polymer were improved by hydrogenated degreasing NR. The thermal aging and ozone resistance of hydrogenated defatted NR blends were also improved [101]. The diffusion, kinetics, and structural effects were used to prevent rubber aging. The aging process of rubber under different dynamic modes was studied, including the mathematical model of the aging and destruction process under extreme conditions. The aging process of rubber as a thermodynamic open nonlinear system was also considered. The results showed that the aging process can be controlled by the organization of internal physical and chemical processes as well as by the organization of external influences (through thermodynamic forces and flows). According to the Onsager principle, conjugation of thermodynamic forces and flows is possible under certain aging conditions. The diffusion and structure aspects of aging of elastomer compositions and their products were considered [102].

5 Fatigue of rubber materials

In analogy with the fatigue damage process of metal materials, the fatigue damage process of rubber materials can usually be divided into two stages as follows. In the first stage, microscopic defects gradually sprout and accumulate to form cracks in the regions within the material where there are no visible cracks originally; in the second stage, cracks continue to expand in the core area where tiny cracks are formed in the first stage until the material produces local or overall fracture [103]. Initially, the prediction model of fatigue life of rubber materials was based on these two stages separately. And with the in-depth study of the microscopic crack formation mechanism and the continuous expansion of the continuous medium mechanics method, Gent et al. [104] first pointed out that the macroscopically visible cracks in rubber materials during fatigue loading ascribe to the continuous expansion of microscopic initial defects, and the above two physical processes can be unified in terms of the intrinsic mechanism, i.e., the two processes of microscopic fatigue crack nucleation and expansion in rubber materials should be combined. The formation of macroscopic fatigue cracks should be studied by combining the two processes of nucleation and expansion of microscopic fatigue cracks in rubber materials.

5.1 Crack initiation approaches

The life prediction methods for the fatigue crack initiation stage of rubber materials include two types of methods: continuous medium mechanics method and continuous damage mechanics method. Since the fatigue life is related to the magnitude of the local load on the material, the continuum mechanics approach generally assumes that the material remains internally homogeneous and continuous throughout the stage from initial loading to crack initiation. Therefore, a fatigue predictor related to the local force or deformation state of the material is usually used as a physical quantity to describe the magnitude of the load, and based on the theory of continuum mechanics, a power series function is established between this predictor and the fatigue crack sprouting life on account of the results of simple material or component fatigue tests. The commonly used fatigue predictors are strain-, stress- and energy-related physical quantities and other parameters.

5.1.1 Strain-related physical quantities

In 1940, Cadwell et al. [105] investigated the fatigue life of filled vulcanizates and found that the fatigue life of NR grew with increasing cyclic minimum strain at constant amplitude and used experimental data to obtain empirical relationships between strain and fatigue life under uniaxial and shear deformation conditions, respectively. Based on the experimental data of Roberts and Benzies [106], an analysis by Ro [107], which used strain-based physical quantities such as octahedral shear strain and maximum shear strain as fatigue life assessment parameters, showed that none of these strain parameters could well unify the test results of uniaxial tension with biaxial tension.

Luo [108] proposed an effective strain criterion, which unified multimodal and multiaxial loading into a single parameter and expressed it in an analytical form without rotating the plane to search for the maximum damage parameter, for fatigue design of vibration-resistant members. Luo [109] also presented a new method for fatigue damage prediction based on the shear modulus and effective tensile strain of rubber materials put forward and validated in three independent fatigue programs. Shangguan et al. [110] raised seven fatigue life prediction models using different damage parameters to predict the fatigue life of rubber isolators via the measurement of the fatigue life of dumbbell cylindrical specimens. It is also pointed out that the model with Luo stress or Saintier stress as the damage parameter can predict fatigue life up to two times better than the other models. In addition, criteria based on effective tensile strain [111] were developed and validated on published experimental data of 30 positive R and negative R-ratio fatigue cases [112]. Li et al. [113] utilized a combination of material property tests and finite element analysis to predict the fatigue life of NR materials employing the maximum total principal strains as the fatigue parameter. Gehrmann et al. [114] introduced a method to convert strain variations into constant equivalent strains conforming to the Wöhler curve. The finite element simulation results showed that the method can be applied to specimens with other geometries or components. Luo et al. [115] conducted fatigue failure tests using hourglass-type rubber specimens and experimentally determined the conventional S–N curve adopting the maximum principal strain as the fatigue parameter to establish the relationship between steady state temperature rise and maximum principal strain. Shangguan et al. [116] investigated the relationship between the tensile fatigue life of rubber specimens with three different geometries and various commonly used damage parameters, as well as the dependence of the geometries for the fatigue life prediction model. Kim et al. [117] concluded that Green – Lagrange should be more suitable as a damage parameter for estimating the fatigue life of rubber compared to the SED method.

5.1.2 Stress-related physical quantities

Saintier et al. [118] pointed out that the direction given by the maximum first principal stress during a cycle can correctly predict the direction of cracking under non-proportional multiaxial fatigue loading if the plane rotation of the material was considered. Saintier et al. [119] also investigated the sprouting of cracks for NR under the abovementioned loads and came up with two fatigue cracking criteria based on the first and second invariants of the Cauchy stress tensor, and pointed out that the latter was a better predictor. Gosar et al. [120] put forward a new multi-axial energy-based method introducing mean stress corrections to combine elastic strain and complementary energy changes to form an energy damage parameter, which was used for fatigue life prediction of air springs in commercial vehicles. Chung and Kim [121] proposed a rain flow counting method with multiple stress components for variable amplitude loading and found the plane with the maximum damage parameter taking the critical surface method.

5.1.3 Energy-related physical quantities

A study by Ro [107] showed that utilizing strain energy as a fatigue damage covariate to predict fatigue life of rubber materials was superior to other strain-based damage covariates, but the stress–strain relationship was assumed to be linear in that study, which was not consistent with reality. Li and Xin [122] proposed a simple bending fatigue life prediction method for toothed v-belts by combining material property tests with finite element analysis and regarding the maximum SED as the damage parameter. Wang et al. [123] performed fatigue tests on rubber beads to determine the cycle number and the finite element method was employed to analyze the steady state rolling of several bead compounds to obtain their maximum SED range. Kim et al. [124] used the finite element method for steady state rolling analysis to acquire the SED range in the strip edge region to gain the tire strip edge failure life due to high-speed conditioning tests. Shangguan et al. [116] pointed out that different strain and energy bases can be used as effective damage parameters for predicting uniaxial tensile fatigue life of filled NR, and the relationship between tensile fatigue life and damage parameters can be considered independent of geometry. Shangguan et al. [125] established fatigue life prediction models at three different temperatures using engineering strain as the damage parameter, but the relationship model between temperature and fatigue life prediction was not constructed. Thereafter, Zhang et al. [126] chose strain energy as the fatigue damage parameter and investigated the effect of thermal aging and fatigue damage on the fatigue life of rubber based on data from specimens of uniaxially stretched dumbbell rubber at different temperatures. Moon et al. [127] indicated that the predicted life of the hollow bamboo specimens was underestimated due to shear deformation and suggested that both positive and shear strains be included to improve the accuracy. Liao and Zhu [128] presented a new energy field intensity (EFI) concept and established an EFI-based framework for fatigue analysis of notched engineering components under multi-axial stress states.

The fatigue life of rubber can be well predicted using SED under simple uniaxial loading conditions, but it is much more difficult under complex loading conditions. In this regard, the critical surface method is proposed to predict the fatigue crack sprouting of rubber materials under multi-axial loading conditions. The fatigue prediction factor is associated with a certain material plane, and the crack emergence parameters in this plane can be calculated by the critical surface method [119], by which good results are achieved.

Moon et al. [127] pointed out that the energy driving the expansion of microcracks within a rubber material is a fraction of the SED, which was defined as the cracking energy density (CED) (Figure 4). By defining the direction of the cracking surface, the method is extended from the macrostrain range to the finite strain range, enabling it to be applied to the fatigue life calculation of rubber materials in the finite deformation range, which greatly improves the practical value of the method. Following this, he investigated the property and evolution of cracks in naturally filled rubber by direct observation, comparing the damaged surface behavior with predictions based on CED [129]. Xu et al. [130] proposed a fatigue life prediction method for rubber bushing stud shear connectors based on the critical surface and finite element method. Nyaaba et al. [131] used assumed intrinsic defects, fatigue crack expansion laws, and rubber intrinsic structure laws to calculate local crack driving forces for a type of tire component based on past strain loading. Saintier and his team [119] found that the critical plane method could predict fatigue life and determine the site and direction of crack emergence, with the major drawback that it could not take size or gradient effects into consideration. Harbour et al. [132] investigated the effect of variable amplitude loading conditions on the fatigue life of multi-axial rubber specimens by searching the critical surface through normal strain. Luo [108] applied the effective strain criterion in combination with the critical surface method for fatigue life prediction under non-proportional loading. Zine et al. [133] determined parameters based on SED and predicted the occurrence and possible directions of primary cracks, confirming the superiority of the CED criterion over the SED criterion.

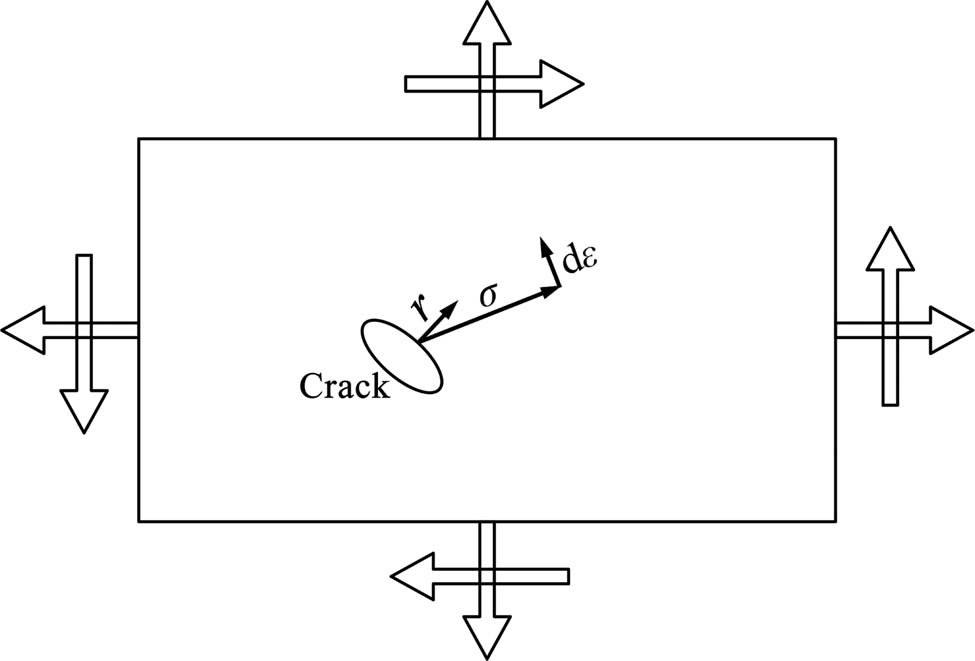
$Figure 4 Schematic diagram of CED of rubber materials. ( r r is the normal to the crack plane; σ \sigma is the vector of tensile stress; d ε {\rm{d}}\varepsilon is the vector of strain increments.)$

Figure 4

Schematic diagram of CED of rubber materials. ( r is the normal to the crack plane; σ is the vector of tensile stress; d ε is the vector of strain increments.)

For scenarios of different rubber materials and usage, each of the above fatigue predictors has its own merits and defects. Liu et al. [134] evaluated the relative performance of the models which consist of different damage indices using rubber stents as the study object. Ayoub et al. [135] found that the prediction methods based on stress and cracking energy showed the best predictive validity for isometric tests after comparison. Shangguan et al. [136] also established three fatigue life prediction models based on SED, maximum principal Green–Lagrange strain, and effective stress [137], and compared their respective predicted fatigue lives with the test life using a typical powertrain rubber vibration isolator as an example. Wang et al. [138] compared and evaluated the existing major fatigue life prediction methods using the life data obtained from the tests to investigate the multi-axial fatigue performance of vulcanized NR.

5.1.4 Damage rule

The above methods for studying the fatigue life of rubber materials are based on the continuous medium mechanics theory, which have great limitations and are only suitable for predicting the test results of the fatigue life of rubber components under uniaxial or extra multi-axial loading methods and simple amplitude cyclic loading conditions [139]. Another approach for fatigue crack sprouting life prediction is based on the continuum damage mechanics (CDM) theory [140], which generally constructs the relationship between load and damage fatigue life by defining the damage stress (or effective stress) and the damage kinetic function.

Wang et al. [141] defined the damage strain energy function and damage evolution equation using a CDM approach and described the SED of the damaged part using the Ogden intrinsic model. Ayoub et al. [140] came up with a fatigue criterion based on the CDM theory to predict the fatigue life of rubber-like materials. Subsequently, for the multi-axial fatigue damage parameter for rubber, the equivalent force was proposed, a three-dimensional model was derived, and the fatigue life of styrene–butadiene rubber (SBR) was predicted by introducing the CED criterion [142]. Ayoub et al. [143] also used the Ogden strain energy function and the CED function to describe the damage strain energy release rate, deriving a general expression for the damage parameter. Harbour et al. [132] explained the difference in crack development in materials that produced many cracks in NR compared to SBR by predicting the linear damage law. Rangarajan and Ramarathnam [144] designed and implemented an experimental procedure binding fatigue life measurements and characterization of the intrinsic response of rubber. Tao et al. [145] and Pan et al. [146] tried some methods to improve on the CDM concept.

5.1.5 Other predictors

With the development of technology, artificial intelligence-based life expectancy prediction methods are maturing. Liu et al. [147] developed a support vector machine (SVM) model with empirical reliability and rubber fatigue life as input and output variables, respectively, which is a probability distribution model. Xiang et al. [148] established a back propagation artificial neural network model for predicting the fatigue performance of NR composites. Marco et al. [149] constructed a nonlinear correlation between the input and output variables of the model based on machine learning (ML). Liu et al. [150] raised a rubber fatigue life prediction model based on random forest algorithm with strain amplitude, which regarded average strain and strain ratio as input variables and fatigue life of NR under equal amplitude load as output variable. Neuhaus et al. [151] proposed a new model considering various effects of high temperature on fatigue life. Choi et al. [152] used six ML models for fatigue life prediction and the comparison concluded that deep neural network exhibited the highest accuracy Liu et al. [153] developed a back propagation neural network model for predicting fatigue life and brought forward an improved sine cosine algorithm to optimize its parameters. Liu et al. [154] developed a fatigue life prediction model for vibration isolated rubber materials using an SVM model and optimized the parameters by an improved gravity search algorithm.

5.2 Crack propagation approaches

The fatigue crack propagation approach of rubber is based on Griffith’s fracture mechanics theory [155], which focuses on individual preexisting cracks or flaws. The crack growth criteria were proposed based on the energy balance hypothesis, which hold that crack growth is a process of converting potential energy stored in elastic bodies into new crack surface energy. The energy release rate and the CED are two essential components to predict fatigue lifetime of rubber materials.

In the crack propagation fatigue test of rubber material, the energy release rate (or CED) at the crack tip can be calculated from the stress–strain field obtained from the material test. Noted that all the specimens are specially designed and with preexisting cracks. Besides, the crack growth rate can be calculated by monitoring the crack growth size and loading times. Therefore, the fatigue crack propagation rate and fatigue life of rubber materials can be predicted under other loading cycle conditions.

In 1953, Rivlin and Thomas [156] first applied Griffith’s theory to study the tensile strength of rubber material with local cracks. He found that when the energy release rate exceeded a certain critical value, cracks will propagate continuously in rubbers, and the critical value is independent of the geometrical size of specimens. Thomas [157,158] extended the Griffith’s approach to analyze the growth of cracks under cyclic loads in NR. He discovered a square-law relationship between peak energy release rate and crack growth rate for NR. Gent et al. [104] verified Thomas’s finding through experiments. He proposed that the relationship between the crack growth rate and energy release rate was a rubber material property independent of the structure and load form. After analyzing many test data of unfilled NR and SBR, Lake and Lindley [159,160] divided the crack growth behavior of rubber materials into four stages based on the maximum energy release rate per cycle, T . As shown in equation (13), He provided approximate expressions of crack growth rate for each stage for unfilled NR and SBR. The full range of behavior is shown in Figure 5.

(13) d a d N = r z , T < T 0 , d a d N = A 0 ( T − T 0 ) + r z , T 0 ⩽ T < T t , d a d N = B 0 T p , T t ⩽ T < T c , d a d N = ∞ , T ⩾ T c ,

where d a / d N ( a is crack tip position; and N is the number of cycles) is the crack growth rate; T is the energy release rate of crack tips, and T 0 , T t , and T c are the critical energy release rate thresholds at different stages, which can be measured by experiments. The crack growth rate is different with different energy release rates at different stages. r z represents the uniform crack growth rate caused by temperature and aging under small cyclic load, and A 0 , B 0 , and T p are material constants.

Figure 5

Lake–Lindley’s crack growth model of rubber materials. Adapted with permission from ref. [160].

Paris et al. [161] and Paris and Erdogan [162] found a similar power-law between the peak energy release rate and fatigue crack growth rate in metallic alloys. Without considering the internal strain crystallization effect, Paris’s model based on equivalent tearing energy could be combined with the calculation method of crack growth rate to predict the fatigue crack growth life of rubber materials under cyclic loading with incomplete relaxation. Experiments showed that considering the internal strain crystallization effect, the fatigue crack growth rate of the rubber material was not only related to cyclic maximum energy release rate, it was also affected by the minimum energy release rate within the cycle [107]. Mars et al. [163], Mars and Fatemi [164,165], and Mars [166] summarized the above work and proposed that rubber crack propagation was caused by internal microcrack propagation driven by cracking energy. Specifically, they combined the CED theory with fracture mechanics method to calculate the fatigue life of rubber material under finite deformation to achieve better prediction. Different from the previous use of maximum energy release rate as the driving force of crack growth, they assumed that the intrinsic microcrack of rubber material has the possibility to expand in all directions, and the crack growth in each direction is driven by the crack energy in that direction, and the actual crack direction should be the fastest crack growth direction. This method can not only predict the fatigue crack initiation life of rubber material, but also predict the potential crack direction. Meanwhile, the critical plane method was recently innovatively applied to the calculation of rubber crack growth in engineering fatigue life assessment [167,168].

Moreover, Aït-Bachir et al. [170] focused on the steady state crack growth with the condition that the damage zone did not reach the boundary of the domain, and derived the energy release rate of a center cracked region with Configurational Mechanics. Based on arbitrary far-field homogeneous multiaxial loading conditions. their approach demonstrated that the energy release rate of a small crack is proportional to the size of the crack, irrespective of the state of loading or the orientation of the crack. Using the strain energy release rate as the variable, Papadopoulos et al. [169] proposed an efficient mathematical equation to characterize the transitions of fatigue crack growth rate in NR and SBR.

Fukahori et al. [171] proposed a new elastic-viscous transition diagram to explain the transition in the relationship between critical strain energy release rate and critical crack growth rate. The diagram consists of three zones: elastic-brittle fracture zone, a viscous-ductile fracture zone and an intermediate transition zone between the elastic and viscous zones. The transition zone, characterized by stick-slip motion, is the result of unstable fluctuations of crack growth rate due to the energy dissipation near the glass transition temperature. Netzker et al. [172] analyzed the fracture behavior of rubber materials based on a global energy balance. They claimed that the measured fracture sensitivity values and the energy losses were mainly related to the development and increase of a dissipative zone. Saintier et al. [118] investigated that the crack orientation was dependent not only on the type of loading (tension, torsion, etc.) but also on the maximum level of loading. The condition was more complex when strain crystallization induces reinforcement in rubbers. Their fatigue model showed that if large strain conditions were correctly considered, cracks were found to propagate systematically in the direction given by the maximal first principal stress reached during a cycle, even under non-proportional loading. By relating the crack surface density to the ratio between the global energy dissipated and the fatigue-related energy, Marco et al. [173] built a new fatigue criterion for carbon black filled NR.

Asare and Busfield [174] validated the fracture mechanics approach when they successfully predicted the fatigue crack growth behavior at both room temperature and high temperature. In fact, the cyclic stress softening associated with fatigue of filled rubber was quantitatively accounted for the first time. The fatigue behavior at different temperature was assessed through the crack growth approach and a lower crack growth resistance was found at higher temperatures. A very recent work by Schieppati et al. [175] proposed a new procedure for building fatigue master curves of a non-crystallizing rubber.

6 Reinforcement of rubber materials

Unlike plastics with high crystallinity or high vitrification temperature, rubber has a large free volume, low intermolecular force, and lack of crystallinity. Therefore, in terms of strength and elongation, hardness, wear resistance, fatigue, and other compressive performance, most rubbers cannot be applied without reinforcement. Pure rubber products are also difficult to process due to the high elasticity of the rubber. Generally, it can only be manufactured by liquid forming or limited to simple products. Since the rubber began to be applied in industry, people have been committed to the study of rubber reinforcement mode and mechanism and the development of related technology (Figure 6). The development process ranges from the use of zinc oxide to the carbon black [176,177,178], and further to the development and application of various filling reinforcing agents and reinforcing technologies [179,180,181]. It can be said that the search for efficient, simple, and economical reinforcing methods and strengthening agents has always been the focus and hotspot of rubber science research. Rubber strengthening research is an important subject of the rubber industry, technology, and science [182,183,184,185,186,187,188,189,190].

Particle size is the first factor to affect the rubber reinforcement [191]. According to the study, the free volume of rubber, namely, the void size, is about 0.6 nm. The high matching of the particle size to the cavity size of the rubber leads to the smaller impurity effect of the reinforcing agent in the rubber matrix, and the stronger ability to hinder the growth of rubber microcracks. The particle size element also includes some surface activity factors [192,193]. The smaller particle size causes a larger specific surface area, contributing to the larger proportion of atoms on the particle surface to the total atomic number. Since the surface effect significantly improves the interaction force between particles and rubber macromolecules, the ability to restrict the movement of rubber macromolecules is enhanced. To some extent, it makes up for the deficiency of weak interfacial interactions and the lack of “conventional chemical forces.”

For graphitized carbon black and fluorinated carbon black rubber hard phase [194], some scholars proposed that the smaller enough size can still strengthen the rubber well even though the interface adhesion between them and rubber is poor. Therefore, nanoscale reinforcement of rubber is an alternative and promising choice. Scholars dispersed C₆₀ into ethylene–propylene rubber, which increased the tensile strength of ethylene–propylene rubber by 3.83 times, proving the importance of nanoparticle size. Therefore, to prepare high reinforced rubber filler, the filler should be equipped with nanoscale particle size distribution. The research of inorganic reinforced materials with nanometer-size has once been a research focus. The common preparation methods of nano-inorganic materials mainly include blending, in-situ generation, sol–gel, and intercalation.

Surface activity is the second factor in the three factors of rubber reinforcer [195,196,197,198]. The enhancement advantages of nano enhancers come from various nano effects. Due to the large surface free energy of nanoparticles, nanoparticles are easy to form aggregates and uneven dispersion in the rubber matrix, which hinders the surface effect of nanoparticles in rubber. Therefore, the increasing surface activity of nanoparticles can enhance the dispersion of nanoparticles in rubber and the interfacial force [199]. It is necessary to maximize the reinforcing effect of reinforcing particles and prepare high-performance rubber with good dynamic mechanical properties.

Most of the enhanced phases of thermoplastic elastomers exhibit uniform dispersion [200,201,202]. Researchers found that a uniform "mixing" of hard and soft regions of the microphase was formed in the molecular chain of the block polymer. The dispersion of the nanoscale regions derived from the thermodynamic phase separation is uniform and plays a role in cross-linking and strengthening the whole system. The “self-strengthening” property of block thermoplastic elastomers also proves the importance of uniform dispersion.

If the dispersion of rubber reinforcement in rubber realizes the uniform distribution effect of hard and soft phases in thermoplastic elastomer [203], the enhancement effect of rubber reinforcement will be brought to the extreme. This can achieve rolling resistance and internal lag heat reduction, and further achieve the greatest advantage of rubber material performance.

The organic modification was carried out from the surface activity of the reinforcer to reduce the surface free energy of inorganic particles and reduce the hysteresis effect [204]. Research shows that every 10% reduction in the lag loss will reduce the fuel consumption of tire drive by 5%.

The structure was the last factor [205,206]. Researchers worked on nano-preparation technology and surface activity improvement of inorganic enhancers. The molecular design was thought to get better compatibility with the rubber matrix of organic reinforcement and expected to solve the friction between the reinforcement and rubber endogenous heat problem. There were two main methods for the design and synthesis of nano-polymer reinforced fillers [207]: in-situ polymerization technology and cross-linking technology. The in-situ polymerization technology has better processing performance and nano-enhancement after cross-linking. However, the high price and inconvenient demolding limit its application in rubber reinforcement. The cross-linking technology was used to design polymer materials and prepare nano-sized hard phases as rubber reinforcement filler. The advantages were that the structure can be designed from the molecule, and further modified and surface treated. Under the surface functional effect, the organic combination of filler and rubber can be realized, and the lag loss caused by inorganic particles such as carbon black can be greatly reduced.

Figure 6

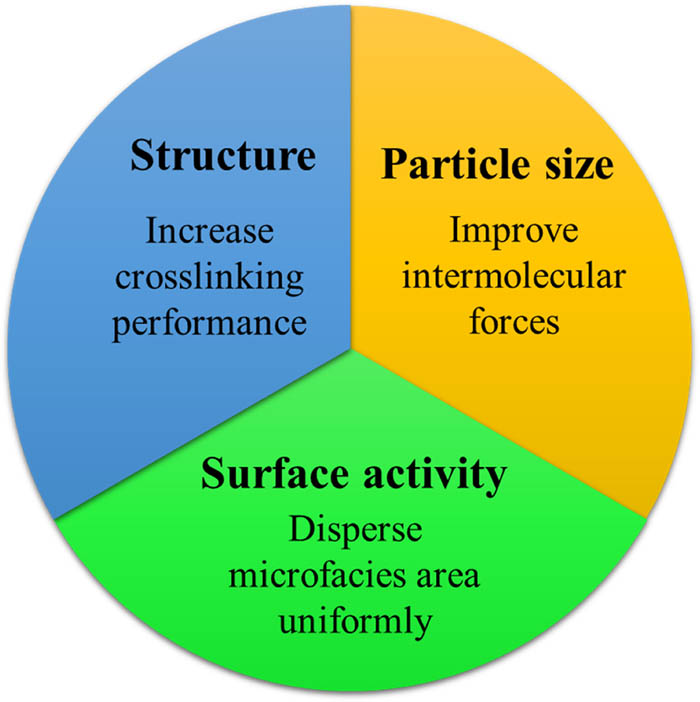
The reinforcement mechanism of rubber materials and structures.

Carbon black is another important reinforcing agent and filler for rubber, and its consumption is about 40–50% of that of rubber. The filling of carbon black can reduce the amount of rubber, and increase the wear resistance and life of rubber products [208]. Rubber reinforcement theory was widely used in the following theoretical models: molecular chain sliding theory, binder theory, filler network theory, carbon black surface structure theory, and van der Waals network theory. The molecular chain sliding theory and binding glue theory confirmed that the molecular chains formed by carbon black particles and rubber particles slide on the surface of particles under stress and explain the Mullins phenomenon. But black carbon particles were rigid particles, which ignored the interactions between nanoparticles [209,210]. Filler network theory, carbon black surface structure theory, and van der Waals network theory considered the existence of network structure and deformation of network structure under stress. However, these theories were limited due to many parameters and the lack of definite methods.

In addition to carbon black and silica [211,212,213,214], clay [16,215,216,217], montmorillonite [218,219,220], calcium carbonate [221,222,223,224], and staple fiber [225,226,227] were all commonly used in rubber reinforced fillers. Clay rubber nanocomposites had good processing properties, physical properties, and barrier properties. Calcium carbonate rubber composite material had good performance and price advantage. Short fiber reinforced rubber composite had both the elasticity of rubber and the strength and stiffness of fiber. Its products have high strength, high modulus, tear resistance, swelling resistance, and other excellent properties.

7 Rubber components for railway vehicles

With the development of finite element analysis, rubber material tests and analysis methods are more accurate. Because of the excellent elastic properties, rubber elastic components are widely used in railway vehicles. Many scholars have conducted in-depth research on the stiffness, damping, fatigue, and so on.

Sjöberg and Kari [228] experimentally studied the influence of nonlinear excitation on dynamic stiffness and damping of filled rubber isolator. Experimental results showed that the maximum excitation amplitude on the isolator was usually determined by the stiffness at the reference frequency, and the influence of envelope amplitude increases with the frequency of the approaching component. Yang et al. [229] proposed the concepts of fragment elastic modulus and fragment stiffness factor, and determined the solution equation. The methods for evaluating nonlinear tensile stiffness of bearings and the concepts of initial tensile stiffness were developed and offset initial tensile stiffness for stiffness characteristics of rubber isolators was described. Fredette and Singh [230] developed an analytical spectral element method to characterize the dynamic characteristics of viscoelastic isolators at ultrahigh frequencies. It extended the stiffness spectrum based on fractional calculus damping mechanisms to capture all 6% of freedom including coupling terms. This approach provided physical insights and a compact way to describe viscoelastic isolators.

To establish the hyperplastic material constants of bushings, Javořík et al. tested the elastomer material of bushings under uniaxial tensile, equiaxial tensile, and pure shear deformation modes [231]. The numerical model was in good agreement with the actual performance of the bushing, and the key point of the casing was found through the numerical analysis of the finite element model.

Li et al. [232] tested the mechanical properties of the high-damping rubber bearing model and studied the relationships among shear strain, equivalent stiffness, yield stiffness, force, and equivalent damping. The bearing remains stable even when the model was damaged, while the vertical and circumferential residual compression deformation existed. Kong et al. [233] introduced evidence theory to deal with uncertainty in air springs. The polynomial chaotic method based on evidence theory, was proposed to solve the problem of efficiently calculating the response of air spring system with evidence variables.

Mirza et al. [234] took spherical bearings as an example to introduce a method for modeling and durability evaluation of elastomers for rail vehicles. This approach enabled the assessment of various components of fatigue loads and the identification of the most damaging contributions and failure modes. In addition, the approach enabled component redesign and validation, significantly increasing the working life. Luo [235] analyzed Metacone springs for rail vehicles using the effective stress method. The analytic functions were used to determine the magnitude and direction of effective stresses, and three-dimensional tensors of all principal stress ranges were considered to estimate fatigue damage.

The synthesis, property, processing, and application of elastomers have become hot topics at the moment. More and more researchers are devoting to the research of theory, test methods, and the simulation technology of rubber elastic components, which provide an essential security blanket to the railway vehicle and passenger line.

8 Challenge and future work

Considering the literature study presented in the previous sections, the fatigue and aging of rubber materials were the biggest challenges in the application of rubber components in railway vehicles. Future research can focus on the following aspects. First, the advantages of different types of rubber need to be further studied to meet specific engineering requirements. In previous studies, NR and SBR appeared to be popular options in the research works and industry. Benefiting from industrial demand, a variety of rubbers with excellent cost effective and mechanical properties are studied in the lab, such as hydrogenated nitrile butadiene rubber which can withstand hostile environment [236]. Magnetorheological elastomer shows good application prospect in vibration absorber, base isolator, and sensing device [237]. Second, there is an emerging trend in using nanofillers to achieve better reinforcement in fatigue lifetime, such as carbon black [238] and carbon nanotubes [239]. Third, the effect of temperature on the fatigue and degradation of rubber materials is not clear. Due to non-availability of standard procedure in the study of heat on rubber specimen, the experimental approach varies for each researcher. Besides, more attention is focused on built models to quantitate the effects of aging on the fatigue life of rubbers. For the design of rubber components in railway vehicles, there is an urgent need for standardizing the related research following an acceptable guideline.

9 Conclusion

Mechanical properties of rubber materials include static mechanical properties and dynamic mechanical properties. To obtain the static mechanical properties, different from metal materials, rubber materials need to carry out more than three basic tests, including uniaxial, biaxial, planar and volumetric tests under the condition of tensile and compression, to describe its complex mechanical behavior based on the material constitutive model. Dynamic mechanical properties are the characteristics of rubber components and often determine their function. The structural response under static load is largely determined by the stiffness characteristics, while the structural response under dynamic load is largely determined by the damping characteristics. Due to the complex service environment of train elastic elements, it is necessary to improve the constitutive model applicable to both large and small deformation. As there is no standard procedure and geometric description of rubber specimen in the study, the experimental approach varies from research to research. Additional works need to be done before the results are comparable. Potential future trends in the study of rubber materials and components are identified, such as coupling thermo-mechanical in cyclic loading analysis and exploring alternative fillers to improve the durability of rubbers
Protection against aging and fatigue are the biggest challenges in the application of rubber materials. The mechanisms of thermal oxygen aging and ozone aging, as two main factors causing aging, are discussed. The crack nucleation and crack propagation approaches, as two popular approaches to evaluate the fatigue failure in rubber, are discussed. In crack nucleation approach, several predictors were used but none appears to be robustly successful in multiaxial fatigue prediction. The crack propagation approach unified the microcosmic crack initiation process and macroscopic fatigue crack propagation process of rubber material. The main challenge remains on the computation of the energy release rate associated with the crack in question.
By means of finite element simulation software, the fatigue life of rubber materials and rubber products is predicted under different loads and service conditions. Accurate fatigue simulation analysis of rubber material also depends on the study of fatigue durability mechanism of rubber material and reliable material fatigue test. On this basis, an effective mathematical model to describe the fatigue characteristics of rubber material is needed. In the fatigue life simulation of rubber products, different definitions of fatigue life under different service conditions should be considered. Therefore, corresponding fatigue criteria and life simulation methods should be selected according to the actual fatigue failure index of rubber products.

Funding information: This work was financially supported by The National Key R&D Program of China (2020YFE0204900-02). The authors would like to express their thanks.
Author contributions: Wei Kang: investigation and writing – original draft; Jiefu Liu: writing – review and editing and supervision; Wei Xiong: writing – review and editing; Tianyu You: writing – review and editing; Xinxin Wang: writing – review and editing; Kexing Zeng: writing – review and editing; Yingao Deng: writing – review and editing; Zichao Guo: writing – review and editing; Ke Yuan: conceptualization, supervision, and writing – review and editing.
Conflict of interest: Authors state no conflict of interest.

References

[1] Ikeda, Y., A. Kato, S. Kohjiya, and Y. Nakajima. Rubber science, Springer, Singapore, 2018.10.1007/978-981-10-2938-7Search in Google Scholar

[2] Tchemodanova, S. P., K. Tatsis, M. Sanayei, E. Chatzi, and V. Dertimanis. State estimation for prediction of fatigue life for a rollercoaster connection subjected to operational multiaxial nonproportional loading. Journal of Structural Engineering, Vol. 147, 2021, id. 04021041.10.1061/(ASCE)ST.1943-541X.0002961Search in Google Scholar

[3] Carleo, F., E. Barbieri, R. Wheal, and J. C. Busfield. Limitations of viscoelastic constitutive models for carbon-black reinforced rubber in medium dynamic strains and medium strain rates. Polymers, Vol. 10, 2018, pp. 988–988.10.3390/polym10090988Search in Google Scholar PubMed PubMed Central

[4] Wang, Y., P. Zhao, H. Liu, F. Zhang, Z. Li, T. Xu, et al. Structure and temperature induced crystallization of natural rubber with different milling times. Polymer Science, Series A, Vol. 63, 2021, pp. 228–237.10.1134/S0965545X21030135Search in Google Scholar

[5] Huang, Y., Z. Liu, H. Xu, and R. Hong. Conductive thermoplastic vulcanizates based on carbon black-filled bromo-isobutylene-isoprene rubber (BIIR)/polypropylene (PP). Reviews on Advanced Materials Science, Vol. 60, 2021, pp. 303–312.10.1515/rams-2021-0013Search in Google Scholar

[6] Tharasana, C., A. Wongaunjai, P. Sornsanee, V. Jitprarop, and N. Tangboriboon. Alternative of bone china and porcelain as ceramic hand molds for rubber latex glove films formation via dipping process. Reviews on Advanced Materials Science, Vol. 59, 2020, pp. 523–537.10.1515/rams-2020-0042Search in Google Scholar

[7] Barot, T., D. Rawtani, and P. Kulkarni. Nanotechnology-based materials as emerging trends for dental applications. Reviews on Advanced Materials Science, Vol. 60, 2021, pp. 173–189.10.1515/rams-2020-0052Search in Google Scholar

[8] Thompson, L., J. Azadmanjiri, M. Nikzad, I. Sbarski, J. Wang, and A. Yu. Cellulose nanocrystals: Production, functionalization and advanced applications. Reviews on Advanced Materials Science, Vol. 58, 2019, pp. 1–16.10.1515/rams-2019-0001Search in Google Scholar

[9] Chanda, S. and D. Bajwa. A review of current physical techniques for dispersion of cellulose nanomaterials in polymer matrices. Reviews on Advanced Materials Science, Vol. 60, 2021, pp. 325–341.10.1515/rams-2021-0023Search in Google Scholar

[10] Ahmed, A., X. Wang, and M. Yang. Biocompatible materials of pulsatile and rotary blood pumps: A brief review. Reviews on Advanced Materials Science, Vol. 59, 2020, pp. 322–339.10.1515/rams-2020-0009Search in Google Scholar

[11] Bhaska, S., M. Kumar, and A. Patnaik. Mechanical and Tribological overview of ceramic particulates reinforced aluminium alloy composites. Reviews on Advanced Materials Science, Vol. 58, 2019, pp. 280–294.10.1515/rams-2019-0033Search in Google Scholar

[12] Meng, T., S. Ahmed, D. Dai, and Y. Yu. Effects of load types and critical molar ratios on strength properties and geopolymerization mechanism. Reviews on Advanced Materials Science, Vol. 60, 2021, pp. 216–222.10.1515/rams-2021-0019Search in Google Scholar

[13] Xu, Z., Z. Huang, C. Liu, X. Deng, D. Hui, and S. Deng. Research progress on mechanical properties of geopolymer recycled aggregate concrete. Reviews on Advanced Materials Science, Vol. 60, 2021, pp. 158–172.10.1515/rams-2021-0021Search in Google Scholar

[14] Ali, Md. A. M., M. Z. Omar, H. Hashim, M. S. Salleh, and I. F. Mohamed. Recent development in graphene-reinforced aluminium matrix composite: A review. Reviews on Advanced Materials Science, Vol. 60, 2021, pp. 801–817.10.1515/rams-2021-0062Search in Google Scholar

[15] Figiela, B., H. Šimonová, and K. Korniejenko. State of the art, challenges, and emerging trends: Geopolymer composite reinforced by dispersed steel fibers. Reviews on Advanced Materials Science, Vol. 61, 2022, pp. 1–15.10.1515/rams-2021-0067Search in Google Scholar

[16] Luo, Y., K. Yuan, L. Shen, and J. Liu. Sandwich panel with in-plane honeycombs in different Poisson’s ratio under low to medium impact loads. Reviews on Advanced Materials Science, Vol. 60, 2021, pp. 145–157.10.1515/rams-2021-0020Search in Google Scholar

[17] Selyutina, N. S. and Y. V. Petrov. Comparative analysis of dynamic plasticity models. Reviews on Advanced Materials Science, Vol. 57, 2018, pp. 199–211.10.1515/rams-2018-0065Search in Google Scholar

[18] Zhang, P., X. Han, Y. Zheng, J. Wan, and D. Hui. Effect of PVA fiber on mechanical properties of fly ash-based geopolymer concrete. Reviews on Advanced Materials Science, Vol. 60, 2021, pp. 418–437.10.1515/rams-2021-0039Search in Google Scholar

[19] Lou, W., W. Zhang, T. Jin, X. Liu, and W. Dai. Synergistic effects of multiple environmental factors on degradation of hydrogenated nitrile rubber seals. Polymers, Vol. 10, 2018, pp. 897–897.10.3390/polym10080897Search in Google Scholar PubMed PubMed Central

[20] Zisan, M. B. and A. Igarashi. Lateral load performance and seismic demand of unbonded scrap tire rubber pad base isolators. Earthquake Engineering and Engineering Vibration, Vol. 20, 2021, pp. 803–821.10.1007/s11803-021-2053-4Search in Google Scholar

[21] Li, X. and Y. Wei. Classic strain energy functions and constitutive tests of rubber-like materials. Rubber Chemistry and Technology, Vol. 88, 2015, pp. 604–627.10.5254/rct.15.84879Search in Google Scholar

[22] Wu, Y., H. Wang, and A. Li. Parameter identification methods for hyperelastic and hyper-viscoelastic models. Applied Sciences, Vol. 6, 2016, id. 386.10.3390/app6120386Search in Google Scholar

[23] Íñiguez-Macedo, S., R. Lostado-Lorza, R. Escribano-García, and M. Martinez-Calvo. Finite element model updating combined with multi-response optimization for hyper-elastic materials characterization. Materials, Vol. 12, 2019, id. 1019.10.3390/ma12071019Search in Google Scholar

[24] Bergström, J. S. and L. B. Hilbert Jr. A constitutive model for predicting the large deformation thermomechanical behavior of fluoropolymers. Mechanics of Materials, Vol. 37, 2005, pp. 899–913.10.1016/j.mechmat.2004.09.002Search in Google Scholar

[25] Marckmann, G., E. Verron, L. Gornet, L. Chagnon, P. Charrier, and P. Fort. A theory of network alteration for the Mullins effect. Journal of the Mechanics and Physics of Solids, Vol. 50, 2002, pp. 2011–2028.10.1016/S0022-5096(01)00136-3Search in Google Scholar

[26] Boyce, M. C. and E. M. Arruda. Constitutive models of rubber elasticity: a review. Rubber Chemistry and Technology, Vol. 73, 2000, pp. 504–523.10.5254/1.3547602Search in Google Scholar

[27] Yeoh, O. H. Characterization of elastic properties of carbon-black-filled rubber vulcanizates. Rubber Chemistry and Technology, Vol. 63, 1990, pp. 792–805.10.5254/1.3538289Search in Google Scholar

[28] Rivlin, R. S. Large elastic deformations of isotropic materials. I. Fundamental concepts. Collected Papers of RS Rivlin, Springer, New York, 1997, pp. 23–54.10.1007/978-1-4612-2416-7_5Search in Google Scholar

[29] Ogden, R. W. Large deformation isotropic elasticity-On the correlation of theory and experiment for incompressible rubber like solids. Rubber Chemistry and Technology, Vol. 46, 1973, pp. 398–416.10.5254/1.3542910Search in Google Scholar

[30] Adeel, Y. J., A. I. Muhammad, and A. Zeeshan. Characterization of hyperelastic (Rubber) material using uniaxial and biaxial tension tests. Advanced Materials Research, Trans Tech Publications Ltd, Vol. 570, 2012, pp. 1–7.10.4028/www.scientific.net/AMR.570.1Search in Google Scholar

[31] Kim, B., S. B. Lee, J. Lee, S. Cho, H. Park, S. Yeom, et al. A comparison among Neo-Hookean model, Mooney-Rivlin model, and Ogden model for chloroprene rubber. International Journal of Precision Engineering and Manufacturing, Vol. 13, 2012, pp. 759–764.10.1007/s12541-012-0099-ySearch in Google Scholar

[32] Woo, C. S. and W. D. Kim. Design of mechanical testing specimens for rubber material using finite element analysis. Multidiscipline Modeling in Materials and Structures, Vol. 3, 2007, pp. 325–336.10.1163/157361107781389535Search in Google Scholar

[33] Eberlein, R. and S. Holenstein. Efficient material parameter calibration of elastomer specimen in uniaxial tension, planar shear and equibiaxial tension. Kautschuk, Gummi, Kunststoffe, Vol. 7–8, 2018, pp. 36–40.Search in Google Scholar

[34] Montella, G., A. Calabrese, and G. Serino. Mechanical characterization of a Tire Derived Material: Experiments, hyperelastic modeling and numerical validation. Construction and Building Materials, Vol. 66, 2014, pp. 336–347.10.1016/j.conbuildmat.2014.05.078Search in Google Scholar

[35] Liu, C., C. M. Cady, M. L. Lovato, and E. B. Oeler. Uniaxial tension of thin rubber liner sheets and hyperelastic model investigation. Journal of Materials Science, Vol. 50, 2015, pp. 1401–1411.10.1007/s10853-014-8700-7Search in Google Scholar

[36] Starkova, O. and A. Aniskevich. Poisson’s ratio and the incompressibility relation for various strain measures with the example of a silica-filled SBR rubber in uniaxial tension tests. Polymer Testing, Vol. 29, 2010, pp. 310–318.10.1016/j.polymertesting.2009.12.005Search in Google Scholar

[37] Kody, R. S. and A. J. Lesser. Yield behavior and energy absorbing characteristics of rubber-modified epoxies subjected to biaxial stress states. Polymer Composites, Vol. 20, 1999, pp. 250–259.10.1002/pc.10352Search in Google Scholar

[38] Fujikawa, M., N. Maeda, J. Yamabe, Y. Kodama, and M. Koishi. Determining stress–strain in rubber with in-plane biaxial tensile tester. Experimental Mechanics, Vol. 54, 2014, pp. 1639–1649.10.1007/s11340-014-9942-7Search in Google Scholar

[39] Brieu, M., J. Diani, and N. Bhatnagar. A new biaxial tension test fixture for uniaxial testing machine-A validation for hyperelastic behavior of rubber-like materials. Journal of Testing and Evaluation, Vol. 35, 2007, id. 364.10.1520/JTE100688Search in Google Scholar

[40] Sasso, M., G. Palmieri, G. Chiappini, and D. Amodio. Characterization of hyperelastic rubber-like materials by biaxial and uniaxial stretching tests based on optical methods. Polymer Testing, Vol. 27, 2008, pp. 995–1004.10.1016/j.polymertesting.2008.09.001Search in Google Scholar

[41] Ru, M., X. Q. Lei, X. M. Liu, and Y. J. Wei. An equal-biaxial test device for large deformation in cruciform specimens. Experimental Mechanics, Vol. 62, 2022, pp. 1–7.10.1007/s11340-021-00810-wSearch in Google Scholar

[42] Garishin, O., V. Shadrin, and Y. Kornev. Mechanical studies of rubber micro-and nanocomposites promising for the tire industry. uniaxial and biaxial tests. Materials Physics & Mechanics, Vol. 42, 2019, pp. 445–454.Search in Google Scholar

[43] Hamdi, A., M. Abdelaziz, N. Hocine, P. Heuillet, and N. Benseddiq. A fracture criterion of rubber-like materials under plane stress conditions. Polymer Testing, Vol. 25, 2006, pp. 994–1005.10.1016/j.polymertesting.2006.06.005Search in Google Scholar

[44] Xia, Y., Y. Dong, Y. Xia, and W. Li. A novel planar tension test of rubber for evaluating the prediction ability of the modified eight-chain model under moderate finite deformation. Rubber Chemistry and Technology, Vol. 78, 2005, pp. 879–892.10.5254/1.3547920Search in Google Scholar

[45] Radek, K., K. Jiøí, H. Jan, and K. Jan. Investigation of the mechanical properties of a cork/rubber composite. Materiali in Tehnologije, Vol. 50, 2016, pp. 579–583.10.17222/mit.2015.172Search in Google Scholar

[46] Cui, K., J. Qin, C. Di, and Y. Yang. Finite element analysis and simulation of the sealing performance of y-ring rubber seal. Applied Mechanics and Materials, Trans Tech Publications Ltd, Vol. 444, 2014, pp. 1379–1383.10.4028/www.scientific.net/AMM.444-445.1379Search in Google Scholar

[47] Liu, J., K. Deng, S. Liu, X. Yan, D. Zou, and Y. Lin. Mechanical behavior and structure optimization of compressed PHP packer rubber. Journal of Materials Engineering and Performance, Vol. 30, 2021, pp. 3691–3704.10.1007/s11665-021-05686-4Search in Google Scholar

[48] Lee, Y., J. Kim, K. Kim, T. Ahn, B. Choi, H. Lee, et al. Prediction of dynamic stiffness on rubber components considering preloads. Materialwissenschaft und Werkstofftechnik, Vol. 44, 2013, pp. 372–379.10.1002/mawe.201300139Search in Google Scholar

[49] Horton, J. and G. Tupholme. Stiffness of annular bonded rubber flanged bushes. Rubber Chemistry and Technology, Vol. 79, 2006, pp. 233–248.10.5254/1.3547935Search in Google Scholar

[50] Yu, W., L. Zhijun, L. Baolin, and G. Mingshuai. Stiffness characteristic comparison between metal-rubber and rubber isolator under sonic vibration. Journal of Vibroengineering, Vol. 16, 2014, pp. 645–655.Search in Google Scholar

[51] Zhang, R. and A. Li. Probability distribution characteristics and statistical parameters of the horizontal stiffness of rubber isolation bearings. Journal of Earthquake Engineering, Vol. 26, 2022, pp. 2437–2449.10.1080/13632469.2020.1762806Search in Google Scholar

[52] Zhou, G., X. Mi, H. Zhang, D. Liao, and K. Wu. Nonlinear finite element analysis and experimental study on the stiffness of rubber joint. Journal of the Chinese Institute of Engineers, Vol. 43, 2020, pp. 603–612.10.1080/02533839.2020.1719898Search in Google Scholar

[53] Persson, B. N. J., O. Albohr, G. Heinrich, and H. Ueba. Crack propagation in rubber-like materials. Journal of Physics: Condensed Matter, Vol. 17, 2005, id. R1071.10.1088/0953-8984/17/44/R01Search in Google Scholar

[54] Yu, F., A. Lu, J. Lu, Z. Wang, Q. Zhang, C. Geng, et al. Effect of phenyl content, sample thickness and compression on damping performances of silicone rubber: A study by dynamic mechanical analysis and impact damping test. Polymer Testing, Vol. 80, 2019, id. 106101.10.1016/j.polymertesting.2019.106101Search in Google Scholar

[55] Yu, W., L. Baolin, and L. Yuru. Effect of loading speed on the damping performance of metal rubber material. Rare Metal Materials and Engineering, Vol. 41, 2012, pp. 381–383.10.1016/S1875-5372(12)60032-0Search in Google Scholar

[56] Burgoa, A., R. Hernandez, and J. L. Vilas. New ways to improve the damping properties in high-performance thermoplastic vulcanizates. Polymer International, Vol. 69, 2020, pp. 467–475.10.1002/pi.5977Search in Google Scholar

[57] Shengbo, L., Y. Hui, J. Hongyuan, and C. Liang. Analysis of dynamic performance of metal rubber damping ring applied in high-speed rotor system. Acta Physica Sinica, Vol. 61, 2012, pp. 10702–10702.10.7498/aps.61.010702Search in Google Scholar

[58] Zheng, X., Z. Ren, L. Shen, B. Zhang, and H. Bai. Dynamic performance of laminated high-damping and high-stiffness composite structure composed of metal rubber and silicone rubber. Materials, Vol. 14, 2021, id. 187.10.3390/ma14010187Search in Google Scholar PubMed PubMed Central

[59] Zhang, Y. Study on seismic behaviour for high damping rubber bearings of continuous beam bridges. IOP Conference Series: Earth and Environmental Science, IOP Publishing, Vol. 153, 2018, id. 052049.10.1088/1755-1315/153/5/052049Search in Google Scholar

[60] Qin, R., R. Huang, and X. Lu. Use of gradient laminating to prepare NR/ENR composites with excellent damping performance. Materials & Design, Vol. 149, 2018, pp. 43–50.10.1016/j.matdes.2018.03.063Search in Google Scholar

[61] Lie, L., B. Sun, M. He, and H. Hua. Analysis of the radial stiffness of rubber bush used in dynamic vibration absorber based on artificial neural network. Neuro Quantology, Vol. 16, 2018, pp. 737–744.10.14704/nq.2018.16.6.1643Search in Google Scholar

[62] Lee, H., J. K. Shin, S. Msolli, and H. S. Kim. Prediction of the dynamic equivalent stiffness for a rubber bushing using the finite element method and empirical modeling. International Journal of Mechanics and Materials in Design, Vol. 15, 2019, pp. 77–91.10.1007/s10999-017-9400-7Search in Google Scholar

[63] Luo, Y., Y. Liu, and H. P. Yin. Numerical investigation of nonlinear properties of a rubber absorber in rail fastening systems. International Journal of Mechanical Sciences, Vol. 69, 2013, pp. 107–113.10.1016/j.ijmecsci.2013.01.034Search in Google Scholar

[64] Payungwong, N., S. Tuampoemsab, P. Rojruthai, and J. Sakdapipanich. The role of model fatty acid and protein on thermal aging and ozone resistance of peroxide vulcanized natural rubber. Journal of Rubber Research, Vol. 24, 2021, pp. 1–11.10.1007/s42464-021-00100-zSearch in Google Scholar

[65] McDonel, E. T. and J. R. Shelton. Effect of curing system on rubber oxidation and physical degradation. Journal of Chemical and Engineering Data, Vol. 4, 1959, pp. 360–366.10.1021/je60004a021Search in Google Scholar

[66] Han, R., Y. Wu, X. Quan, and K. Niu. Effects of crosslinking densities on mechanical properties of nitrile rubber composites in thermal oxidative aging environment. Journal of Applied Polymer Science, Vol. 137, 2020, id. 49076.10.1002/app.49076Search in Google Scholar

[67] Xiang, L., J. Cheng, and S. Kang. Thermal oxidative aging mechanism of crumb rubber/SBS composite modified asphalt. Construction and Building Materials, Vol. 75, 2015, pp. 169–175.10.1016/j.conbuildmat.2014.08.035Search in Google Scholar

[68] He, H., K. Liu, X. Fu, and K. Ye. Development of rubber aging life prediction software. International Conference on Intelligent Robotics and Applications, Springer, Cham, 2017, pp. 831–842.10.1007/978-3-319-65298-6_74Search in Google Scholar

[69] Liu, Q., W. Shi, K. Li, Z. Chen, and H. Liu. Performance degradation prediction and reliability evaluation of rubber aging in natural environment under alternating cyclic thermal load. IEEE Access, Vol. 7, 2019, pp. 63027–63035.10.1109/ACCESS.2019.2917008Search in Google Scholar

[70] Yuan, K., K. Liu, M. Zhao, K. Wei, and Z. Wang. The in-situ matrix cracking behavior in cross-ply laminates under out-of-plane shear loading. Composite Structures, Vol. 290, 2022, id. 115563.10.1016/j.compstruct.2022.115563Search in Google Scholar

[71] Wang, X., K. Yang, C. Zong, and P. Zhang. The evolution of microstructure of Styrene-Isoprene-Butadiene Rubber during the thermal-oxidative aging process using in-situ FTIR way. Polymer Degradation and Stability, Vol. 188, 2021, id. 109573.10.1016/j.polymdegradstab.2021.109573Search in Google Scholar

[72] Chang, T., X. Zhang, and H. Cui. Thermal aging analysis of carbon black and silica filled natural rubber based on terahertz dielectric spectroscopy. Infrared Physics and Technology, Vol. 105, 2020, id. 103195.10.1016/j.infrared.2020.103195Search in Google Scholar

[73] Zhi, J., Q. Wang, M. Zhang, M. Li, and Y. Jia. Coupled analysis on heterogeneous oxidative aging and viscoelastic performance of rubber based on multi-scale simulation. Journal of Applied Polymer Science, Vol. 136, 2019, id. 47452.10.1002/app.47452Search in Google Scholar

[74] Kratina, O., R. Stoček, B. Musil, M. Johlitz, and A. Lion. The study of fatigue behavior of thermally aged rubber based on natural rubber and butadiene rubber. Constitutive models for rubber X, CRC Press, Los Angeles, 2017, pp. 365–370.10.1201/9781315223278-58Search in Google Scholar

[75] Kim, D., J. Oh, J. Do, and J. Park. Effects of thermal aging on mechanical properties of laminated lead and natural rubber bearing. Earthquakes and Structures, Vol. 6, 2014, pp. 127–140.10.12989/eas.2014.6.2.127Search in Google Scholar

[76] Sun, H. C., Y. Y. Hao, and L. N. Wang. Macroscopical contact pressure and microscopic leakage performance analysis of rubber seal considering thermal oxygen aging effect. Proceedings of the Institution of Mechanical Engineers, Part G: Journal of Aerospace Engineering, 2022, id. 09544100221080504.10.1177/09544100221080504Search in Google Scholar

[77] Baer, N. S. Accelerated aging: Photochemical and thermal aspects. Getty, Google Scholar, Los Angeles, CA, 1996.10.2307/3179994Search in Google Scholar

[78] Fubao, J. I., Z. H. Yuanxiang, B. Liang, X. Liang, Z. H. Zhongliu, and L. Zhang. Effect of UV radiation aging on creepage discharge characteristics of high temperature vulcanized silicon rubber at high altitude. Plasma Science and Technology, Vol. 21, 2019, id. 054003.10.1088/2058-6272/aaff0cSearch in Google Scholar

[79] Zheng, T., X. Zheng, S. Zhan, J. Zhou, and S. Liao. Study on the ozone aging mechanism of natural rubber. Polymer Degradation and Stability, Vol. 186, 2021, id. 109514.10.1016/j.polymdegradstab.2021.109514Search in Google Scholar

[80] Mazurkiewicz, D. Problems of identification of strength properties of rubber materials for purposes of numerical analysis: a review. Archives of Civil and Mechanical Engineering, Vol. 10, 2010, pp. 69–84.10.1016/S1644-9665(12)60131-9Search in Google Scholar

[81] Wang, X., H. Pan, K. Yang, and P. Zhang. Cracking, structural, and mechanical property changes of SIBR and related elastomers during the ozone aging process. Polymer Degradation and Stability, Vol. 195, 2022, id. 109774.10.1016/j.polymdegradstab.2021.109774Search in Google Scholar

[82] Ning, N. Y., Z. P. Zheng, L. Zhang, and M. Tian. An excellent ozone-resistant polymethylvinylsiloxane coating on natural rubber by thiol-ene click chemistry. Express Polymer Letters, Vol. 9, 2015, pp. 490–495.10.3144/expresspolymlett.2015.47Search in Google Scholar

[83] Botros, S. H., F. F. El-Mohsen, and E. A. Meinecke. Effect of brown vulcanized vegetable oil on ozone resistance, aging, and flow properties of rubber compounds. Rubber Chemistry and Technology, Vol. 60, 1987, pp. 159–175.10.5254/1.3536116Search in Google Scholar

[84] Yang, T., C. Yang, H. Wei, Z. Zhang, J. Jiang, C. Xu, et al. Study on Aging Evaluation Method of Silicone Rubber in Dongguan. International Conference on Power System Technology (POWERCON), IEEE, Singapore, 2018, pp. 3740–3747.10.1109/POWERCON.2018.8602035Search in Google Scholar

[85] Abdelaziz, M. N., G. Ayoub, X. Colin, M. Benhassine, and M. Mouwakeh. New developments in fracture of rubbers: Predictive tools and influence of thermal aging. International Journal of Solids and Structures, Vol. 165, 2019, pp. 127–136.10.1016/j.ijsolstr.2019.02.001Search in Google Scholar

[86] Chaabane, M., N. Ding, and F. Zaïri. An approach to assess the thermal aging effects on the coupling between inelasticity and network alteration in filled rubbers. International Journal of Non-Linear Mechanics, Vol. 136, 2021, id. 103783.10.1016/j.ijnonlinmec.2021.103783Search in Google Scholar

[87] Moon, B., J. Lee, S. Park, and C. S. Seok. Study on the aging behavior of natural rubber/butadiene rubber (NR/BR) blends using a parallel spring model. Polymers, Vol. 10, 2018, id. 658.10.3390/polym10060658Search in Google Scholar

[88] Rodionova, O. Y. and A. L. Pomerantsev. Prediction of rubber stability by accelerated aging test modeling. Journal of Applied Polymer Science, Vol. 95, 2005, pp. 1275–1284.10.1002/app.21347Search in Google Scholar

[89] Woo, C. S., S. S. Choi, S. B. Lee, and H. Kim. Useful lifetime prediction of rubber components using accelerated testing. IEEE Transactions on Reliability, Vol. Vol. 59, 2010, pp. 11–17.10.1109/TR.2010.2042103Search in Google Scholar

[90] Itoh, Y. and H. Gu. Prediction of aging characteristics in natural rubber bearings used in bridges. Journal of Bridge Engineering, Vol. 14, 2009, pp. 122–128.10.1061/(ASCE)1084-0702(2009)14:2(122)Search in Google Scholar

[91] Lou, W., C. Xie, and X. Guan. Thermal-aging constitutive model for a silicone rubber foam under compression. Polymer Degradation and Stability, Vol. 198, 2022, id. 109873.10.1016/j.polymdegradstab.2022.109873Search in Google Scholar

[92] Zhou, J., J. Yao, H. H. Hu, and Y. Song. Accelerated aging life evaluation method of silicone rubber based on segmented nonlinear. Arrhenius Model Materials Research Innovations, Vol. 19, 2015, pp. 5–855.10.1179/1432891714Z.0000000001207Search in Google Scholar

[93] Ružiak, I., P. Koštial, Z. Jančíková, M. Gajtanska, Ľ. Krišťák, I. Kopal, et al. Artificial neural networks prediction of rubber mechanical properties in aged and nonaged state. Improved performance of materials, Springer, Cham, 2018, pp. 27–35.10.1007/978-3-319-59590-0_3Search in Google Scholar

[94] Mark, J. E. and J. G. Curro. Monte Carlo simulations relevant to the upturns in modulus observed for natural rubber at high elongations. Journal of Polymer Science: Polymer Physics Edition, Vol. 23, 1985, pp. 2629–2632.10.1002/pol.1985.180231218Search in Google Scholar

[95] Cataldo, F. Protection mechanism of rubbers from ozone attack. Ozone: Science & Engineering, Vol. 41, 2019, pp. 358–368.10.1080/01919512.2018.1542518Search in Google Scholar

[96] Mao, Z., W. Wang, and G. Mao. Improving the thermal aging resistance of γ-vulcanized polybutadiene rubber (BR)/Nature Rubber (NR) blends with sulfur added. Advances in Materials Science and Engineering, 2021, id. 5782539.10.1155/2021/5782539Search in Google Scholar

[97] Fang, Y., Y. Deng, and Y. Li. The Research of Silicone Rubber Aging Factors by Attenuated Total Reflection Infrared Spectroscopy. International Electrical and Energy Conference (CIEEC), IEEE, Dalian, 2019, pp. 1444–1449.10.1109/CIEEC47146.2019.CIEEC-2019526Search in Google Scholar

[98] Liu, K., P. Li, and Z. Wang. Statistical modeling of random hail impact. Extreme Mechanics Letters, Vol. 48, 2021, id. 101374.10.1016/j.eml.2021.101374Search in Google Scholar

[99] Choi, S. S. Influence of rubber composition on change of crosslink density of rubber vulcanizates with EV cure system by thermal aging. Journal of Applied Polymer Science, Vol. 75, 2000, pp. 1378–1384.10.1002/(SICI)1097-4628(20000314)75:11<1378::AID-APP9>3.0.CO;2-ISearch in Google Scholar

[100] Fu, J. F., L. Y. Chen, H. Yang, Q. D. Zhong, L. Y. Shi, W. Deng, et al. Mechanical properties, chemical and aging resistance of natural rubber filled with nano-Al2O3. Polymer Composites, Vol. 33, 2012, pp. 404–411.10.1002/pc.22162Search in Google Scholar

[101] Simma, K., G. L. Rempel, and P. Prasassarakich. Improving thermal and ozone stability of skim natural rubber by diimide reduction. Polymer Degradation and Stability, Vol. 94, 2009, pp. 1914–1923.10.1016/j.polymdegradstab.2009.08.005Search in Google Scholar

[102] Kablov, V. F. and G. E. Zaikov. Protection of rubbers against ageing using diffusion, kinetic and structural effects. Elastomery, Vol. 18, 2014, pp. 31–36.Search in Google Scholar

[103] Mars, W. V. and A. Fatemi. A literature survey on fatigue analysis approaches for rubber. International Journal of Fatigue, Vol. 24, 2002, pp. 949–961.10.1016/S0142-1123(02)00008-7Search in Google Scholar

[104] Gent, A. N., P. B. Lindley, and A. G. Thomas. Cut growth and fatigue of rubbers. I. The relationship between cut growth and fatigue. Journal of Applied Polymer Science, Vol. 8, 1964, pp. 455–466.10.1002/app.1964.070080129Search in Google Scholar

[105] Cadwell, S. M., R. A. Merrill, C. M. Sloman, and F. L. Yost. Dynamic fatigue life of rubber. Rubber Chemistry and Technology, Vol. 13, 1940, pp. 304–315.10.4271/390023Search in Google Scholar

[106] Roberts, B. J. and J. B. Benzies. Relationship between uniaxial and equi-biaxial fatigue in gum and cabon-black-filled vulcanizates. Plastics and Rubber: Materials and Applications, Vol. 3, 1978, pp. 49–54.Search in Google Scholar

[107] Ro, H. S. Modeling and interpretation of fatigue failure initiation in rubber related to pneumatic tires, Doctoral dissertation. Purdue University, West Lafayette, 1989.Search in Google Scholar

[108] Luo, R. K. Effective strain criterion under multimode and multiaxial loadings-A rubber SN curve with the scatter-band factor of 1.6 from 90 fatigue cases. Express Polymer Letters, Vol. 6, 2022, pp. 130–141.10.3144/expresspolymlett.2022.11Search in Google Scholar

[109] Luo, R. K. Shear modulus-based prediction of the fatigue life of antivibration rubber components. International Journal of Fatigue, Vol. 162, 2022, id. 107010.10.1016/j.ijfatigue.2022.107010Search in Google Scholar

[110] Shuangguan, W. B., X. Duan, and T. Liu. Study on the effect of different damage parameters on the predicting fatigue life of rubber isolators. Journal of Mechanical Engineering, Vol. 52, 2016, pp. 116–126.10.3901/JME.2016.02.116Search in Google Scholar

[111] Luo, R. K. Rubber fatigue prediction for filled natural rubber under positive and negative R ratios. International Journal of Fatigue, Vol. 158, 2022, id. 106769.10.1016/j.ijfatigue.2022.106769Search in Google Scholar

[112] Wang, X. L., W. B. Shangguan, S. Rakheja, W. C. Li, and B. Yu. A method to develop a unified fatigue life prediction model for filled natural rubbers under uniaxial loads. Fatigue & Fracture of Engineering Materials & Structures, Vol. 37, 2014, pp. 50–61.10.1111/ffe.12081Search in Google Scholar

[113] Li, Q., J. Zhao, and B. Zhao. Fatigue life prediction of a rubber mount based on test of material properties and finite element analysis. Engineering Failure Analysis, Vol. 16, 2009, pp. 2304–2310.10.1016/j.engfailanal.2009.03.008Search in Google Scholar

[114] Gehrmann, O., N. H. Kröger, and A. Muhr. Displacement-controlled fatigue testing of rubber is not strain-controlled. International Journal of Fatigue, Vol. 145, 2021, id. 106083.10.1016/j.ijfatigue.2020.106083Search in Google Scholar

[115] Luo, W., Y. Huang, B. Yin, X. Jiang, and X. Hu. Fatigue life assessment of filled rubber by hysteresis induced self-heating temperature. Polymers, Vol. 12, 2020, id. 846.10.3390/polym12040846Search in Google Scholar PubMed PubMed Central

[116] Shangguan, W. B., X. L. Wang, J. X. Deng, S. Rakheja, X. Y. Pan, and B. Yu. Experiment and modeling of uniaxial tension fatigue performances for filled natural rubbers. Materials & Design, Vol. 58, 2014, pp. 65–73.10.1016/j.matdes.2014.01.035Search in Google Scholar

[117] Kim, W. D., H. J. Lee, J. Y. Kim, and S. K. Koh. Fatigue life estimation of an engine rubber mount. International Journal of Fatigue, Vol. 26, 2004, pp. 553–560.10.1016/j.ijfatigue.2003.08.025Search in Google Scholar

[118] Saintier, N., G. Cailletaud, and R. Piques. Crack initiation and propagation under multiaxial fatigue in a natural rubber. International Journal of Fatigue, Vol. 28, 2006, pp. 61–72.10.1016/j.ijfatigue.2005.03.006Search in Google Scholar

[119] Saintier, N., G. Cailletaud, and R. Piques. Multiaxial fatigue life prediction for a natural rubber. International Journal of Fatigue, Vol. 28, 2006, pp. 530–539.10.1016/j.ijfatigue.2005.05.011Search in Google Scholar

[120] Gosar, A., M. Nagode, and S. Oman. Continuous fatigue damage prediction of a rubber fibre composite structure using multiaxial energy-based approach. Fatigue & Fracture of Engineering Materials & Structures, Vol. 42, 2019, pp. 307–320.10.1111/ffe.12908Search in Google Scholar

[121] Chung, J. and N. H. Kim. Numerical methods of multiaxial fatigue life prediction for elastomers under variable amplitude loadings. Fatigue & Fracture of Engineering Materials & Structures, Vol. 39, 2016, pp. 866–876.10.1111/ffe.12401Search in Google Scholar

[122] Li, W. and Z. Xin. Flexural fatigue life prediction of a tooth V-belt made of fiber reinforced rubber. International Journal of Fatigue, Vol. 111, 2018, pp. 269–277.10.1016/j.ijfatigue.2018.02.025Search in Google Scholar

[123] Wang, G., W. Wang, C. Liang, and L. Cao. Fatigue life prediction of radial tire bead using a maximum strain energy density range method. Applied Sciences, Vol. 11, 2021, id. 5477.10.3390/app11125477Search in Google Scholar

[124] Kim, S., H. Park, B. Moon, K. Sung, J. M. Koo, and C. S. Seok. The prediction methodology for tire’s high speed durability regulation test using a finite element method. International Journal of Fatigue, Vol. 118, 2019, pp. 77–86.10.1016/j.ijfatigue.2018.08.036Search in Google Scholar

[125] Shangguan, W. B., M. M. Li, and X. C. Duan. Fatigue life prediction and tests for rubber mounts under high temperature. Journal of Vibration and Shock, Vol. 34, 2015, pp. 66–71.Search in Google Scholar

[126] Zhang, J., F. Xue, Y. Wang, X. Zhang, and S. Han. Strain energy-based rubber fatigue life prediction under the influence of temperature. Royal Society Open Science, Vol. 5, 2018, id. 180951.10.1098/rsos.180951Search in Google Scholar PubMed PubMed Central

[127] Moon, S. I., I. J. Cho, C. S. Woo, and W. Kim. Study on determination of durability analysis process and fatigue damage parameter for rubber component. Journal of Mechanical Science and Technology, Vol. 25, 2011, pp. 1159–1165.10.1007/s12206-011-0221-6Search in Google Scholar

[128] Liao, D. and S. P. Zhu. Energy field intensity approach for notch fatigue analysis. International Journal of Fatigue, Vol. 127, 2019, pp. 190–202.10.1016/j.ijfatigue.2019.06.010Search in Google Scholar

[129] Mars, W. V. and A. Fatemi. Nucleation and growth of small fatigue cracks in filled natural rubber under multiaxial loading. Journal of Materials Science, Vol. 41, 2006, pp. 7324–7332.10.1007/s10853-006-0962-2Search in Google Scholar

[130] Xu, X., X. Zhou, and Y. Liu. Fatigue life prediction of rubber-sleeved stud shear connectors under shear load based on finite element simulation. Engineering Structures, Vol. 227, 2021, id. 111449.10.1016/j.engstruct.2020.111449Search in Google Scholar

[131] Nyaaba, W., S. Frimpong, and A. Anani. Fatigue damage investigation of ultra-large tire components. International Journal of Fatigue, Vol. 119, 2019, pp. 247–260.10.1016/j.ijfatigue.2018.07.009Search in Google Scholar

[132] Harbour, R. J., A. Fatemi, and W. V. Mars. Fatigue life analysis and predictions for NR and SBR under variable amplitude and multiaxial loading conditions. International Journal of Fatigue, Vol. 30, 2008, pp. 1231–1247.10.1016/j.ijfatigue.2007.08.015Search in Google Scholar

[133] Zine, A., N. Benseddiq, and M. N. Abdelaziz. Rubber fatigue life under multiaxial loading: Numerical and experimental investigations. International Journal of Fatigue, Vol. 33, 2011, pp. 1360–1368.10.1016/j.ijfatigue.2011.05.005Search in Google Scholar

[134] Liu, K., J. Liu, and Z. Wang. A damage threshold prediction model of CFRP panel by hail impact based on delamination mechanism. Engineering Fracture, Vol. 239, 2020, id. 107282.10.1016/j.engfracmech.2020.107282Search in Google Scholar

[135] Ayoub, G., M. Naït-Abdelaziz, and F. Zaïri. Multiaxial fatigue life predictors for rubbers: Application of recent developments to a carbon-filled SBR. International Journal of Fatigue, Vol. 66, 2014, pp. 168–176.10.1016/j.ijfatigue.2014.03.026Search in Google Scholar

[136] Shangguan, W. B., T. K. Liu, X. L. Wang, C. Xu, and B. Yu. A method for modelling of fatigue life for rubbers and rubber isolators. Fatigue & Fracture of Engineering Materials & Structures, Vol. 37, 2014, pp. 623–636.10.1111/ffe.12145Search in Google Scholar

[137] Luo, R. K., W. J. Mortel, and X. P. Wu. Fatigue failure investigation on anti-vibration springs. Engineering Failure Analysis, Vol. 16, 2009, pp. 1366–1378.10.1016/j.engfailanal.2008.09.005Search in Google Scholar

[138] Wang, Y., W. Yu, X. Chen, and L. Yan. Fatigue life prediction of vulcanized natural rubber under proportional and non-proportional loading. Fatigue & Fracture of Engineering Materials & Structures, Vol. 31, 2008, pp. 38–48.10.1111/j.1460-2695.2007.01199.xSearch in Google Scholar

[139] Mars, W. V. Multiaxial fatigue of rubber. Doctoral dissertation. The University of Toledo, Toledo, 2001.Search in Google Scholar

[140] Ayoub, G., M. Nait-Abdelaziz, F. Zaïri, and J. M. Gloaguen. Multiaxial fatigue life prediction of rubber-like materials using the continuum damage mechanics approach. Procedia Engineering, Vol. 2, 2010, pp. 985–993.10.1016/j.proeng.2010.03.107Search in Google Scholar

[141] Wang, B., H. Lu, and G. Kim. A damage model for the fatigue life of elastomeric materials. Mechanics of Materials, Vol. 34, 2002, pp. 475–483.10.1016/S0167-6636(02)00175-8Search in Google Scholar

[142] Ayoub, G., M. Nait-Abdelaziz, F. Zaïri, J. M. Gloaguen, and P. Charrier. A continuum damage model for the high-cycle fatigue life prediction of styrene-butadiene rubber under multiaxial loading. International Journal of Solids and Structures, Vol. 48, 2011, pp. 2458–2466.10.1016/j.ijsolstr.2011.04.003Search in Google Scholar

[143] Ayoub, G., M. Nait-Abdelaziz, F. Zaïri, J. M. Gloaguen, and P. Charrier. Fatigue life prediction of rubber-like materials under multiaxial loading using a continuum damage mechanics approach: Effects of two-blocks loading and R ratio. Mechanics of Materials, Vol. 52, 2012, pp. 87–102.10.1016/j.mechmat.2012.03.012Search in Google Scholar

[144] Rangarajan, S. E. and K. K. Ramarathnam. Viscoelastic properties of natural rubber with fatigue damage. International Journal of Fatigue, Vol. 150, 2021, id. 106344.10.1016/j.ijfatigue.2021.106344Search in Google Scholar

[145] Tao, Y., C. A. Stevens, E. Bilotti, T. Peijs, and J. J. Busfield. Fatigue of carbon cord-rubber composites: Effect of frequency, R ratio and life prediction using constant life models. International Journal of Fatigue, Vol. 135, 2020, id. 105558.10.1016/j.ijfatigue.2020.105558Search in Google Scholar

[146] Pan, Z., Y. Lai, Y. Wang, W. Duan, Y. Qiao, Y. Liu, et al. Fatigue life prediction and effects of cerium oxide-filled vulcanized natural rubber on fatigue life under multiaxial loading. Fatigue & Fracture of Engineering Materials & Structures, Vol. 44, 2021, pp. 3349–3362.10.1111/ffe.13561Search in Google Scholar

[147] Liu, X., X. Zhao, and W. B. Shangguan. Probabilistic fatigue life prediction model of natural rubber components based on the expanded sample data. International Journal of Fatigue, Vol. 163, 2022, id. 107034.10.1016/j.ijfatigue.2022.107034Search in Google Scholar

[148] Xiang, K. L., P. Y. Xiang, and Y. P. Wu. Prediction of the fatigue life of natural rubber composites by artificial neural network approaches. Materials & Design, Vol. 57, 2014, pp. 180–185.10.1016/j.matdes.2013.12.044Search in Google Scholar

[149] Marco, Y., B. Huneau, I. Masquelier, V. Le Saux, and P. Charrier. Prediction of fatigue properties of natural rubber based on the descriptions of the cracks population and of the dissipated energy. Polymer Testing, Vol. 59, 2017, pp. 67–74.10.1016/j.polymertesting.2017.01.015Search in Google Scholar

[150] Liu, Q., W. Shi, and Z. Chen. Rubber fatigue life prediction using a random forest method and nonlinear cumulative fatigue damage model. Journal of Applied Polymer Science, Vol. 137, 2020, id. 48519.10.1002/app.48519Search in Google Scholar

[151] Neuhaus, C., A. Lion, M. Johlitz, P. Heuler, M. Barkhoff, and F. Duisen. Fatigue behaviour of an elastomer under consideration of ageing effects. International Journal of Fatigue, Vol. 104, 2017, pp. 72–80.10.1016/j.ijfatigue.2017.07.010Search in Google Scholar

[152] Choi, J., L. Quagliato, S. Lee, J. Shin, and N. Kim. Multiaxial fatigue life prediction of polychloroprene rubber (CR) reinforced with tungsten nano-particles based on semi-empirical and machine learning models. International Journal of Fatigue, Vol. 145, 2021, id. 106136.10.1016/j.ijfatigue.2020.106136Search in Google Scholar

[153] Liu, X., X. Zhao, and W. B. Shangguan. Fatigue life prediction of natural rubber components using an artificial neural network. Fatigue & Fracture of Engineering Materials & Structures, Vol. 45, 2022, pp. 1678–1689.10.1111/ffe.13690Search in Google Scholar

[154] Liu, Q., W. Shi, and Z. Chen. Fatigue life prediction for vibration isolation rubber based on parameter‐optimized support vector machine model. Fatigue & Fracture of Engineering Materials & Structures, Vol. 42, 2019, pp. 710–718.10.1111/ffe.12945Search in Google Scholar

[155] Griffith, A. A. The phenomena of rupture and flow in solids. Philosophical Transactions of the Royal Society of London, Vol. 221, 1920, pp. 163–198.10.1098/rsta.1921.0006Search in Google Scholar

[156] Rivlin, R. S. and A. G. Thomas. Rupture of rubber. I. Characteristic energy for tearing. Journal of Polymer Science, Vol. 10, 1953, pp. 291–318.10.1007/978-1-4612-2416-7_180Search in Google Scholar

[157] Thomas, A. G. Rupture of rubber. V. Cut growth in natural rubber vulcanizates. Journal of Polymer Science, Vol. 31, 1958, pp. 467–480.10.1002/pol.1958.1203112324Search in Google Scholar

[158] Thomas, A. G. Rupture of rubber. II. The strain concentration at an incision. Journal of Polymer Science, Vol. 18, 1955, pp. 177–188.10.1002/pol.1955.120188802Search in Google Scholar

[159] Lake, G. J. and P. B. Lindley. Cut growth and fatigue of rubbers. II. Experiments on a noncrystallizing rubber. Rubber Chemistry and Technology, Vol. 38, 1965, pp. 301–313.10.5254/1.3535649Search in Google Scholar

[160] Lake, G. J. and P. B. Lindley. The mechanical fatigue limit for rubber. Journal of Applied Polymer Science, Vol. 9, 1965, pp. 1233–1251.10.1002/app.1965.070090405Search in Google Scholar

[161] Paris, P. C., M. P. Gomez, and W. P. Anderson. A rational analytic theory of fatigue, Trends Engin, Vol. 13, 1997, pp. 9–14.Search in Google Scholar

[162] Paris, P. and F. A. Erdogan. Critical analysis of crack propagation laws. Journal of Basic Engineering, Vol. 85, 1963, pp. 528–534.10.1115/1.3656900Search in Google Scholar

[163] Mars, W. V. Cracking energy density as a predictor of fatigue life under multiaxial conditions. Rubber Chemistry and Technology, Vol. 75, 2002, pp. 1–17.10.5254/1.3547670Search in Google Scholar

[164] Mars, W. V. and A. Fatemi. A phenomenological model for the effect of R ratio on fatigue of strain crystallizing rubbers. Rubber Chemistry and Technology, Vol. 76, 2003, pp. 1241–1258.10.5254/1.3547800Search in Google Scholar

[165] Mars, W .V. and A. Fatemi. Analysis of fatigue life under complex loading: revisiting Cadwell, Merrill, Sloman, and Yost. Rubber Chemistry and Technology, 79, 2006, pp. 589–601.10.5254/1.3547953Search in Google Scholar

[166] Mars, W. V. Computed dependence of rubber’s fatigue behavior on strain crystallization. Rubber Chemistry and Technology, Vol. 82, 2009, pp. 51–61.10.5254/1.3557006Search in Google Scholar

[167] Mars, W. V., Y. Wei, W. Hao, and M. A. Bauman. Computing tire component durability via critical plane analysis. Tire Science and Technology, Vol. 47, 2019, pp. 31–54.10.2346/tire.19.150090Search in Google Scholar

[168] Robertson, C. G., J. D. Suter, M. A. Bauman, R. Stoček, and W. V. Mars. Finite element modeling and critical plane analysis of a cut-and-chip experiment for rubber. Tire Science and Technology, Vol. 49, 2021, pp. 128–145.10.2346/tire.20.190221Search in Google Scholar

[169] Papadopoulos, I., A. Thomas, and J. Busfield. Rate transitions in the fatigue crack growth of elastomers. Journal of Applied Polymer Science, Vol. 109, 2008, pp. 1900–1910.10.1002/app.28086Search in Google Scholar

[170] Aït-Bachir, M., W. Mars, and E. Verron. Energy release rate of small cracks in hyperelastic materials. International Journal of Non-Linear Mechanics, Vol. 47, 2012, pp. 22–29.10.1016/j.ijnonlinmec.2012.03.001Search in Google Scholar

[171] Fukahori, Y., K. Sakulkaew, and J. J. C. Busfield. Elastic-viscous transition in tear fracture of rubbers. Polymer, Vol. 54, 2013, pp. 1905–1915.10.1016/j.polymer.2013.01.019Search in Google Scholar

[172] Netzker, C., T. Horst, K. Reincke, R. Behnke, M. Kaliske, G. Heinrich, et al. Analysis of stable crack propagation in filled rubber based on a global energy balance. International Journal of Fracture, Vol. 181, 2013, pp. 13–23.10.1007/s10704-013-9816-5Search in Google Scholar

[173] Marco, Y., B. Huneau, I. Masquelier, V. Le Saux, and P. Charrier. Prediction of fatigue properties of natural rubber based on the descriptions of the cracks population and of the dissipated energy. Polymer Testing, Vol. 59, 2017, pp. 67–74.10.1016/j.polymertesting.2017.01.015Search in Google Scholar

[174] Asare, S. and J. Busfield. Fatigue life prediction of bonded rubber components at elevated temperature. Plast Rubber Compos, Vol. 40, 2011, pp. 194–200.10.1179/1743289810Y.0000000044Search in Google Scholar

[175] Schieppati, J., B. Schrittesser, A. Wondracek, S. Robin, A. Holzner, and G. Pinter. Temperature impact on the mechanical and fatigue behavior of a non-crystallizing rubber. International Journal of Fatigue, Vol. 144, 2021, id. 106050.10.1016/j.ijfatigue.2020.106050Search in Google Scholar

[176] Shahapurkar, K. Compressive behavior of crump rubber reinforced epoxy composites. Polymer Composites, Vol. 42, 2021, pp. 329–341.10.1002/pc.25828Search in Google Scholar

[177] Karim, A. A., E. E. Kader, A. A. Hamod, and A. J. Abdulrahman. Mechanical properties of a hybrid composite material (epoxy-polysulfide rubber) reinforced with fibres. IOP Conference Series: Materials Science and Engineering, IOP Publishing, Vol. 433, 2018, id. 012050.10.1088/1757-899X/433/1/012050Search in Google Scholar

[178] Wang, S., M. Cao, H. Xue, F. Cong, X. Li, C. Zhao, et al. Nano-silica reinforced epoxy resin/nano-rubber composite material with a balance of stiffness and toughness. High Performance Polymers, Vol. 33, 2021, pp. 685–694.10.1177/0954008320988752Search in Google Scholar

[179] Cui, J., L. Zhang, W. Wu, Z. Cheng, Y. Sun, H. Jiang, et al. Zinc oxide with dominant (1 0 0) facets boosts vulcanization activity. European Polymer Journal, Vol. 113, 2019, pp. 148–154.10.1016/j.eurpolymj.2019.01.032Search in Google Scholar

[180] Panampilly, B. and S. Thomas. Nano ZnO as cure activator and reinforcing filler in natural rubber. Polymer Engineering & Science, Vol. 53, 2013, pp. 1337–1346.10.1002/pen.23383Search in Google Scholar

[181] Zhang, C., Z. Tang, B. Guo, and L. Zhang. Significantly improved rubber-silica interface via subtly controlling surface chemistry of silica. Composites Science and Technology, Vol. 156, 2018, pp. 70–77.10.1016/j.compscitech.2017.12.020Search in Google Scholar

[182] Zhong, B., Z. Jia, D. Hu, Y. Luo, D. Jia, and F. Liu. Enhancing interfacial interaction and mechanical properties of styrene-butadiene rubber composites via silica-supported vulcanization accelerator. Composites Part A: Applied Science and Manufacturing, Vol. 96, 2017, pp. 129–136.10.1016/j.compositesa.2017.02.016Search in Google Scholar

[183] Khanra, S., A. Kumar, S. K. Ghorai, D. Ganguly, and S. Chattopadhyay. Influence of partial substitution of carbon black with silica on mechanical, thermal, and aging properties of super specialty elastomer based composites. Polymer Composites, Vol. 41, 2020, pp. 4379–4396.10.1002/pc.25720Search in Google Scholar

[184] Chollakup, R., S. Suethao, P. Suwanruji, J. Boonyarit, and W. Smitthipong. Mechanical properties and dissipation energy of carbon black/rubber composites. Composites and Advanced Materials, Vol. 30, 2021, id. 26349833211005476.10.1177/26349833211005476Search in Google Scholar

[185] Cha, J. H., G. J. Shin, M. J. Kang, H. I. Lee, K. Y. Rhee, and S. J. Park. A study on the effect of electron acceptor-donor interactions on the mechanical and interfacial properties of carbon black/natural rubber composites. Composites Part B: Engineering, Vol. 136, 2018, pp. 143–148.10.1016/j.compositesb.2017.10.003Search in Google Scholar

[186] Alkhazraji, A. N. Enhancement of mechanical properties and handling characteristic of tire rubber using different percentage of nano aluminum oxide and carbon black. SMR, Vol. 20, 2018, id. 100.Search in Google Scholar

[187] Kaliyappan, P., M. Dhananchezian, and K. Rajkumar. Utilization of waste tyre rubber and carbon black to develop a neoprene rubber hybrid composite. Materials Today: Proceedings, Vol. 27, 2020, pp. 724–728.10.1016/j.matpr.2019.11.307Search in Google Scholar

[188] Boukfessa, H. and B. Bezzazi. The effect of carbon black on the curing and mechanical properties of natural rubber/acrylonitrile-butadiene rubber composites. Journal of Applied Research and Technology, Vol. 19, 2021, pp. 194–201.10.22201/icat.24486736e.2021.19.3.1686Search in Google Scholar

[189] Wang, X., L. Wu, H. Yu, T. Xiao, H. Li, and J. Yang. Analysis of effect of modification of silica and carbon black co-filled rubber composite on mechanical properties. E-Polymers, Vol. 21, 2021, pp. 279–288.10.1515/epoly-2021-0034Search in Google Scholar

[190] Fan, Y., G. D. Fowler, and M. Zhao. The past, present and future of carbon black as a rubber reinforcing filler-A review. Journal of Cleaner Production, Vol. 247, 2020, id. 119115.10.1016/j.jclepro.2019.119115Search in Google Scholar

[191] Ain, Z. N. and A. R. Azura. Effect of different types of filler and filler loadings on the properties of carboxylated acrylonitrile-butadiene rubber latex films. Journal of Applied Polymer Science, Vol. 119, 2011, pp. 2815–2823.10.1002/app.32984Search in Google Scholar

[192] Chuayjuljit, S., A. Imvittaya, N. Na-ranong, and P. Potiyaraj. Effects of particle size and amount of carbon black and calcium carbonate on curing characteristics and dynamic mechanical properties of natural rubber. Journal of Metals, Materials and Minerals, Vol. 12, 2002, pp. 51–57.Search in Google Scholar

[193] Peterson, S. C. and S. Kim. Reducing biochar particle size with nanosilica and its effect on rubber composite reinforcement. Journal of Polymers and the Environment, Vol. 28, 2020, pp. 317–322.10.1007/s10924-019-01604-xSearch in Google Scholar

[194] Niedermeier, W., J. Frohlich, and H. D. Luginsland. Reinforcement mechanism in the rubber matrix by active fillers. Kautschuk Gummi Kunststoffe, Vol. 55, 2002, pp. 356–356.Search in Google Scholar

[195] Zhang, S., R. Zhong, R. Hong, and D. Hui. On factors affecting surface free energy of carbon black for reinforcing rubber. Nanotechnology Reviews, Vol. 9, 2020, pp. 170–181.10.1515/ntrev-2020-0015Search in Google Scholar

[196] Sittiphan, T., P. Prasassarakich, and S. Poompradub. Styrene grafted natural rubber reinforced by in situ silica generated via sol–gel technique. Materials Science and Engineering: B, Vol. 181, 2014, pp. 39–45.10.1016/j.mseb.2013.11.018Search in Google Scholar

[197] Kong, L., F. Li, F. Wang, Y. Miao, X. Huang, and H. Zhu. In situ assembly of SiO2 nanodots/layered double hydroxide nanocomposite for the reinforcement of solution-polymerized butadiene styrene rubber/butadiene rubber. Composites Science and Technology, Vol. 158, 2018, pp. 9–18.10.1016/j.compscitech.2018.01.036Search in Google Scholar

[198] Oboh, J. O., J. O. Okafor, A. S. Kovo, and A. S. Abdulrahman. Dynamic mechanical properties of crosslinked natural rubber composites reinforced with cellulosic nanoparticles. Nigerian Journal of Technology, Vol. 37, 2018, pp. 668–673.10.4314/njt.v37i3.16Search in Google Scholar

[199] Xu, P., X. Zhao, P. Ma, M. Q. Chen, W. F. Dong, M. Hoch, et al. Design of nano-starch-reinforced ethyl-co-vinyl acetate elastomers by simultaneously constructing interfacial bonding and novel reversible matrix crosslinking. Chemical Engineering Journal, Vol. 346, 2018, pp. 497–505.10.1016/j.cej.2018.03.189Search in Google Scholar

[200] Wang, G., A. Li, W. Zhao, Z. Xu, Y. Ma, F. Zhang, et al. A review on fabrication methods and research progress of superhydrophobic silicone rubber materials. Advanced Materials Interfaces, Vol. 8, 2021, id. 2001460.10.1002/admi.202001460Search in Google Scholar

[201] Shinde, A., I. Siva, Y. Munde, V. Deore, M. T. H. Suitan, A. U. M. Shah, et al. Testing of silicon rubber/montmorillonite nanocomposite for mechanical and tribological performance. Nanomaterials, Vol. 11, 2021, id. 3050.10.3390/nano11113050Search in Google Scholar PubMed PubMed Central

[202] Bakar, M., M. Przybyłek, A. Białkowska, W. Żurowski, B. Hanulikova, and R. Stoček. Effect of mixing conditions and montmorillonite content on the mechanical properties of a chloroprene rubber. Mechanics of Composite Materials, Vol. 57, 2021, pp. 387–400.10.1007/s11029-021-09962-1Search in Google Scholar

[203] Norazlina, H., A. R. M. Fahmi, and W. M. Hafizuddin. CaCO3 from seashells as a reinforcing filler for natural rubber. Journal of Mechanical Engineering and Sciences, Vol. 8, 2015, pp. 1481–1488.10.15282/jmes.8.2015.22.0144Search in Google Scholar

[204] Krishna, A., S. B. Sabarinath, P. S. Abhishek, G. U. Chandran, S. Hema, and S. Sambhudevan. Influence of wood husk and CaCO3 on the mechanical properties of nitrile butadiene rubber. Macromolecular Symposia, Vol. 402, 2022, id. 2100430.10.1002/masy.202100430Search in Google Scholar

[205] Sinclair, A., X. Zhou, S. Tangpong, D. S. Bajwa, M. Quadir, and L. Jiang. High-Performance styrene-butadiene rubber nanocomposites reinforced by surface-modified cellulose nanofibers. ACS Omega, Vol. 4, 2019, pp. 13189–13199.10.1021/acsomega.9b01313Search in Google Scholar PubMed PubMed Central

[206] Zheng, X., Y. Jin, J. Chen, B. H. Li, Q. S. Fu, and G. He. Mechanical properties and microstructure characterization of natural rubber reinforced by helical carbon nanofibers. Journal of Materials Science, Vol. 54, 2019, pp. 12962–12971.10.1007/s10853-019-03771-7Search in Google Scholar

[207] Roy, K., S. K. Mandal, M. Alam, and S. C. Debnath. A comparison between polyethylene glycol (PEG) and polypropylene glycol (PPG) treatment on the properties of nano-titanium dioxide (TiO2) based natural rubber (NR) nanocomposites. Polymer Bulletin, Vol. 73, 2016, pp. 3065–3079.10.1007/s00289-016-1641-3Search in Google Scholar

[208] Paderni, K., D. Morselli, F. Bondioli, S. L. Adriaan, T. H. Mokhothu, and M. Massimo. EPDM rubber reinforced with titania generated by nonhydrolytic sol-gel process. Polymer Engineering & Science, Vol. 54, 2014, pp. 2544–2552.10.1002/pen.23805Search in Google Scholar

[209] Viet, C. X., H. Ismail, A. A. Rashid, T. Takeichhi, and V. H. Thao. Organoclay filled natural rubber nanocomposites: the effects of filler loading. Polymer-Plastics Technology and Engineering, Vol. 47, 2008, pp. 1090–1096.10.1080/03602550802355800Search in Google Scholar

[210] Sookyung, U., C. Nakason, W. Thaijaroen, and V. Norbert. Influence of modifying agents of organoclay on properties of nanocomposites based on natural rubber. Polymer Testing, Vol. 33, 2014, pp. 48–56.10.1016/j.polymertesting.2013.11.006Search in Google Scholar

[211] Roy, K., S. C. Debnath, A. Das, H. Gert, and P. Pranut. Exploring the synergistic effect of short jute fiber and nanoclay on the mechanical, dynamic mechanical and thermal properties of natural rubber composites. Polymer Testing, Vol. 67, 2018, pp. 487–493.10.1016/j.polymertesting.2018.03.032Search in Google Scholar

[212] Taherzadeh, F. A., A. Khodadadi, G. Liaghat, X. F. Yao, and M. A. Z. Mehrizia. Mechanical properties and energy absorption capacity of chopped fiber reinforced natural rubber. Composites Part C: Open Access, Vol. 7, 2022, id. 100237.10.1016/j.jcomc.2022.100237Search in Google Scholar

[213] Chen, L. and B. Gu. Predicting fatigue damage in interphase of short fiber reinforced rubber composites under transverse load. Polymer Composites, Vol. 39, 2018, pp. 1455–1467.10.1002/pc.24086Search in Google Scholar

[214] Abraham, F., T. Alshuth, and S. Jerrams. The effect of minimum stress and stress amplitude on the fatigue life of non strain crystallising elastomers. Materials and Design, Vol. 26, 2004, pp. 239–245.10.1016/j.matdes.2004.02.020Search in Google Scholar

[215] Mars, W. V. and A. Fatemi. Observations of the constitutive response and characterization of filled natural rubber under monotonic and cyclic multiaxial stress states. Journal of Engineering Materials and Technology, Vol. 126, 2004, pp. 19–28.10.1115/1.1631432Search in Google Scholar

[216] Liu, J. F., W. S. Chen, H. Hong, and Z. G. Wang. In-plane crushing behaviors of hexagonal honeycombs with different Poisson’s ratio induced by topological diversity. Thin-Walled Structures, Vol. 159, 2021, id. 107223.10.1016/j.tws.2020.107223Search in Google Scholar

[217] Liu, Y., H. Kim, Q. M. Pan, and L. R. Grray. Hydrogenation of acrylonitrile-butadiene copolymer latex using water-soluble rhodium catalysts. Catalysis Science & Technology, Vol. 3, 2013, pp. 2689–2698.10.1039/c3cy00257hSearch in Google Scholar

[218] Karsten, B., K. Schneidera, S. V. Rothc, and G. Heinrichab. Strain-induced crystallization around a crack tip in natural rubber under dynamic load. Polymer, Vol. 54, 2013, pp. 6200–6205.10.1016/j.polymer.2013.08.045Search in Google Scholar

[219] Dominik, P. and D. M. Bieliński. Application of multi-capillary column – ion mobility spectrometry (MCC-IMS) in rubber chemistry and technology. International Journal for Ion Mobility Spectrometry, Vol. 21, 2018, pp. 1–9.10.1007/s12127-018-0229-zSearch in Google Scholar

[220] Arpan, D. S., C. E. Federicoa, M. Staropolia, F. Nzulub, M. Weydertb, P. Vergea, et al. Properties of silica-filled rubber compounds vs epoxidized oil content and degree of epoxidation. Industrial Crops & Products, Vol. 168, 2021, id. 113600.10.1016/j.indcrop.2021.113600Search in Google Scholar

[221] Cindy, S. B. and K. Cornish. Characterization of agricultural and food processing residues for potential rubber filler applications. Journal of Composites Science, Vol. 3, 2019, pp. 102–102.10.3390/jcs3040102Search in Google Scholar

[222] Wang, Z. G., X. X. Wang, K. Liu, J. Zhang, and Z. J. Lu. Crashworthiness index of honeycomb sandwich structures under low-speed oblique impact. International Journal of Mechanical Sciences, Vol. 208, 2021, id. 106683.10.1016/j.ijmecsci.2021.106683Search in Google Scholar

[223] Liu, P. Z., X. M. Zhang, H. B. Jia, Q. Yin, J. Y. Wang, B. Yin, et al. High mechanical properties, thermal conductivity and solvent resistance in graphene oxide/styrene-butadiene rubber nanocomposites by engineering carbonylated acrylonitrile-butadiene rubber. Composites Part B, Vol. 130, 2017, pp. 257–266.10.1016/j.compositesb.2017.07.048Search in Google Scholar

[224] Korn, T., T. Tulyapong, P. Pranee, R. Polphat, R. Jareerat, L. Fabienne, et al. The effect of percent hydrogenation and vulcanization system on ozone stability of hydrogenated natural rubber vulcanizates using Raman spectroscopy. Polymer Degradation and Stability, Vol. 141, 2017, pp. 58–68.10.1016/j.polymdegradstab.2017.04.006Search in Google Scholar

[225] Yuan, K., K. Liu, Z. G. Wang, and M. Z. Yang. An investigation on the perforation resistance of laminated CFRP beam and square plate. International Journal of Impact Engineering, Vol. 157, 2021, id. 103967.10.1016/j.ijimpeng.2021.103967Search in Google Scholar

[226] Li, J., A. I. Isayev, Q. Wang, and D. S. Mark. Sustainable plasticizer for butyl rubber cured by phenolic resin. Journal of Applied Polymer Science, Vol. 135, 2017, id. 45500.10.1002/app.45500Search in Google Scholar

[227] Nisrine, S., C. Thierry, P. Serge, L. Frédéric, A. Ali, J. G. García, et al. Technical and economic feasibility of a guayule commodity chain in Mediterranean Europe. Industrial Crops & Products, Vol. 59, 2014, pp. 55–62.10.1016/j.indcrop.2014.04.043Search in Google Scholar

[228] Sjöberg, M. and L. Kari. Testing of nonlinear interaction effects of sinusoidal and noise excitation on rubber isolator stiffness. Polymer Testing, Vol. 22, 2003, pp. 343–351.10.1016/S0142-9418(02)00110-1Search in Google Scholar

[229] Yang, Q. R., W. G. Liu, W. F. He, and D. M. Feng. Tensile stiffness and deformation model of rubber isolators in tension and tension-shear states. Journal of Engineering Mechanics, Vol. 136, 2010, pp. 429–437.10.1061/(ASCE)EM.1943-7889.0000007Search in Google Scholar

[230] Fredette, L. and R. Singh. High frequency, multi-axis dynamic stiffness analysis of a fractionally damped elastomeric isolator using continuous system theory. Journal of Sound and Vibration, Vol. 389, 2017, pp. 468–483.10.1016/j.jsv.2016.11.025Search in Google Scholar

[231] Javořík, J., J. Kledrowetz, R. Keerthiwansa, and P. Nekoksa. The numerical analysis of axially loaded elastomeric bushing. Materials Science Forum. , 919, Trans Tech Publications Ltd, 2018, pp. 315–324.10.4028/www.scientific.net/MSF.919.315Search in Google Scholar

[232] Li, Y. L., Z. H. Zong, X. Y. Huang, J. Xia, and L. Liu. Experimental study on mechanical properties of high damping rubber bearing model. IOP Conference Series: Earth and Environmental Science, IOP Publishing, Vol. 61, 2017, id. 012105.10.1088/1755-1315/61/1/012105Search in Google Scholar

[233] Kong, F., Y. Bai, X. F. Liang, Z. J. Lu, and S. W. Yin. Response analysis and optimization of the air spring with epistemic uncertainties. Reviews on Advanced Materials Science, Vol. 61, No. 1, 2022, pp. 79–89.10.1515/rams-2022-0008Search in Google Scholar

[234] Mirza, S., P. Hansen, and J. Harris. Modelling and durability assessment for rubber components in rail vehicles. Plastics, Rubber and Composites, Vol. 40, No. 4, 2011, pp. 185–193.10.1179/1743289810Y.0000000041Search in Google Scholar

[235] Luo, R. K. Multiaxial fatigue prediction on crack initiation for rubber antivibration design–location and orientation with stress ranges. Proceedings of the Institution of Mechanical Engineers, Part L: Journal of Materials: Design and Applications, Vol. 235, No. 3, 2021, pp. 460–480.10.1177/1464420720969857Search in Google Scholar

[236] Wu, Y. P., W. Zhao, and L. Q. Zhang. Improvement of flex-fatigue life of carbon-black filled styrene-butadiene rubber by addition of nanodispersed clay. Macromolecular Materials and Engineering, Vol. 291, No. 8, 2006, pp. 944–949.10.1002/mame.200600114Search in Google Scholar

[237] Chen, S., H. Yu, W. Ren, and Y. Zhang. Thermal degradation behavior of hydrogenated nitrile-butadiene rubber (HNBR)/clay nanocomposite and HNBR/clay/carbon nanotubes nanocomposites. Thermochimica Acta, Vol. 491, No. 1, 2009, pp. 103–108.10.1016/j.tca.2009.03.010Search in Google Scholar

[238] Rausch, S., M. Ruderer, W. Enke, A. Narváez, M. Ludwig, and T. Alshuth. Lifetime prediction of elastomer components within gasoline engines. Constitutive Models Rubber IX, Los Angeles, 2015, id. 363.Search in Google Scholar

[239] Li, Y., J. Li, W. Li, and H. Du. A state-of-the-art review on magnetorheological elastomer devices. Smart Materials and Structures, Vol. 23, No. 12, 2014, id. 123001.10.1088/0964-1726/23/12/123001Search in Google Scholar

Received: 2022-06-02

Revised: 2022-06-29

Accepted: 2022-07-02

Published Online: 2022-09-26

This work is licensed under the Creative Commons Attribution 4.0 International License.

Articles in the same Issue

https://doi.org/10.1515/rams-2022-0054

Keywords for this article

rubber; railway vehicle; test method; fatigue; aging; life prediction

Creative Commons

BY 4.0