Home Application research of acoustic black hole in floating raft vibration isolation system
Article Open Access

Application research of acoustic black hole in floating raft vibration isolation system

  • Shengyao Gao , Zhou Tao , Yuhui Li EMAIL logo and Fuzhen Pang EMAIL logo
Published/Copyright: December 21, 2022
Download Article (PDF)
Become an author with De Gruyter Brill
Submit Manuscript Author Information
REVIEWS ON ADVANCED MATERIALS SCIENCE
From the journal REVIEWS ON ADVANCED MATERIALS SCIENCE Volume 61 Issue 1

Abstract

Acoustic black holes have good application prospects in the field of vibration and noise reduction. Based on engineering practice, this study proposes a systematic process method for the application of acoustic black hole structure in raft structure, which provides new ideas and references for improving the vibration isolation performance of floating raft system and reducing the level of ship vibration and noise. The influence law of each parameter on structural vibration and the recommended value range of each parameter are given, which provides support for the systematic method and process of the application of acoustic black holes in the raft structure. Then, the acoustic black hole process is applied to a floating raft system. According to the characteristics of the raft structure, an application scheme of the acoustic black hole in the raft structure is formed, and the vibration level drop of the floating raft vibration isolation system before and after the acoustic black hole is embedded, calculated, and analyzed. The changes further improve the vibration reduction and isolation performance of the raft system and effectively reduced the mechanical noise level of the ship’s cabin.

Graphical abstract

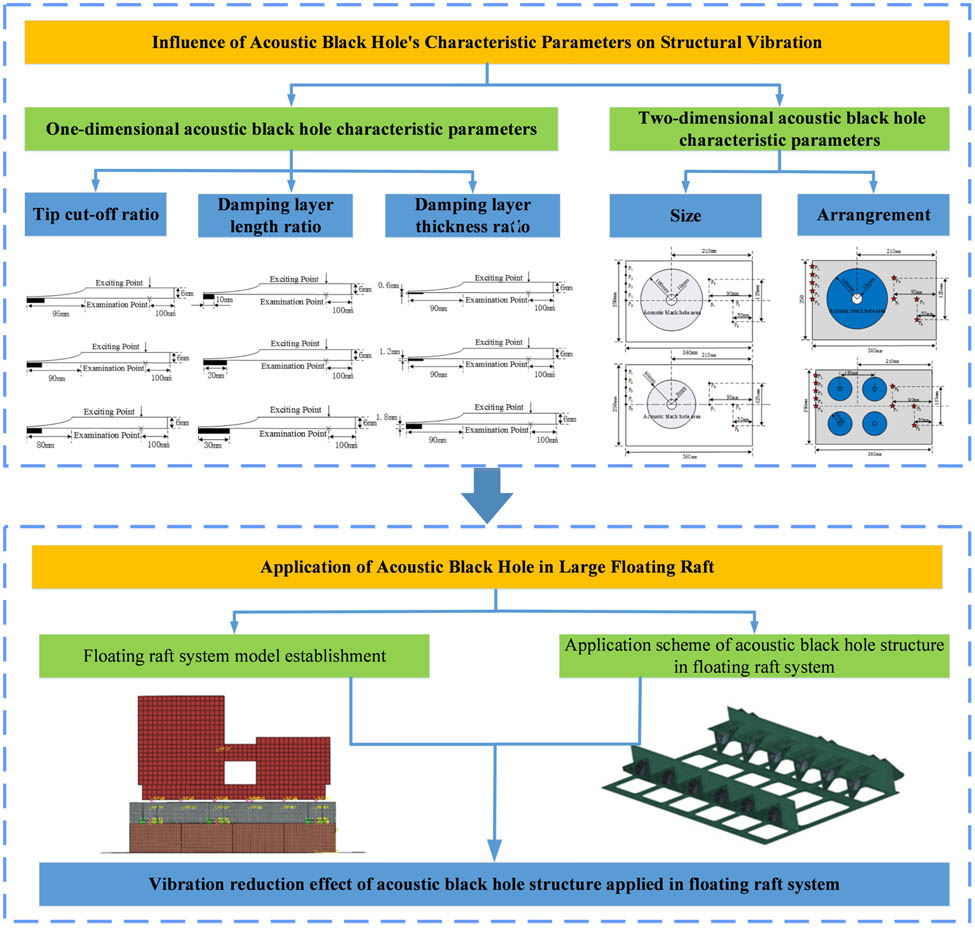
Keywords: acoustic black hole; floating raft vibration isolation system; vibration level drop; mechanical noise

1 Introduction

The United States took the lead in applying floating raft vibration isolation technology to submarines, which reduced its underwater radiated noise by about 35 dB; the former Soviet Union proposed to place multiple devices on a single raft structure to achieve centralized vibration isolation of the equipment. The technology has reduced the underwater radiation noise of multiple warships to 125–130 dB [1]. In Italy, the raft structure was changed to a slender longitudinal raft, and multiple devices were installed on the longitudinal raft [2]. In terms of using new materials to improve the vibration isolation performance of floating rafts, Zhang et al. designed a carbon fiber raft structure. Research shows that carbon fiber materials can not only improve the vibration reduction and isolation performance of the floating raft vibration isolation system but also reduce the structural quality to achieve a lightweight design of the structure [3].

In summary, it can be seen that the floating raft vibration isolation system is widely used in the field of ship and ocean engineering, has good vibration reduction and isolation performance, and can effectively reduce the vibration and noise level of ships; research in the field of improving the vibration isolation performance of the floating raft system is also relatively large. The emerging vibration reduction and isolation technology is developed and being constantly applied to the floating raft system. It is of great significance to further develop the research on improving the vibration isolation performance of the floating raft system.

The acoustic black hole effect usually includes a local reduction in the thickness profile of the structure, associated with a thin viscoelastic coating placed in the area of minimum thickness [4]. For the structure of acoustic black holes, the current theoretical analysis theories mainly include: geometric acoustics theory, impedance matrix theory, and wavelet decomposition energy principle. The above theory can be used to explain the principle of one-dimensional acoustic black hole structure effect, but for two-dimensional acoustic black holes, the theoretical research content is relatively small. Based on the geometric acoustic theory, the propagation trajectory of bending waves in the two-dimensional acoustic black hole structure can be solved. In addition, Krylov et al. [5,6,7] also conducted theoretical modeling of acoustic black hole structures with damping layers. Based on the Ross–unar–kerwin theory [8], Georgiev et al. proposed a method that will not be affected by the assumptions in the geometric acoustic theory, that is, based on the impedance transfer matrix method [9,10]. And the space is numerically calculated and solved, and the expression of the reflection coefficient matrix is given [9,10]. In terms of theoretical research on the two-dimensional acoustic black hole structure, Krylov analyzed and discussed the propagation trajectory of bending waves in the two-dimensional acoustic black hole structure based on the approximation method of geometric acoustic theory [11]. At different rates, the trajectory of the bending wave will be deflected to the center of the acoustic black hole [11]. A typical two-dimensional acoustic black hole structure is composed of a constant thickness area, an acoustic black hole area, [12] and the circular plate [13] embedded with a two-dimensional acoustic black hole. Analysis and research results show that the embedded two-dimensional acoustic black hole structure can effectively reduce the structure’s mid- and high-frequency vibration response. Lian et al. [14] studied the low-frequency sound insulation characteristics of thin acoustic black holes by numerical and experimental methods. Yan [15] derived the phonon metric and effective action using displacement transformation and functional integration methods to describe the fluctuations of phonon field in quantum fluids. Chakraborty and Majumdar [16] derived the precise precession frequency of a free precession test gyroscope for a (2 + 1) dimensional rotating acoustic black hole simulation of space-time. Chakraborty and Majumdar [16] designed a new structure that approximates the acoustic black hole effect of curved waves. The structure has a rod/plate with grooves, the depth of the grooves increases gradually, and the flexural stiffness decreases gradually as a certain bulk density is maintained. In order to facilitate machining and engineering applications, Mironov [17] designed acoustic black hole wedge plate superstructures and found that these acoustic black hole superstructures had an average sound insulation strength of 30 dB in the frequency range of 50–1,600 Hz. Zhou et al. [18], Yu et al. [19], Liu et al. [20], and Yu et al. [21] used the transfer matrix method to study the vibration and noise transfer characteristics of the structure, and passed it. In terms of vibration and acoustic analysis, Li et al. [22], Pang et al. [23], and Li et al. [24,25,26] used semi-analytical methods to analyze the vibration characteristics of various structures.

Based on the acoustic black hole theory and experimental research status, acoustic black hole structure has been initially applied in engineering practice. The test structure shows that after the introduction of the acoustic black hole composite structure, the vibration response and internal stress of the engine fan blades are significantly reduced [27]. In the automotive field, Browyer embedded a two-dimensional acoustic black hole structure in the engine shell. Experiments have proved that the two-dimensional acoustic black hole can significantly reduce the noise level in the car [28]. In the field of energy recovery, Zhou and Semperlotti combined the acoustic black hole structure with the Helmholtz resonator, and successfully improved the energy absorption efficiency and operating frequency range of the Helmholtz resonator through experiments [29]. In addition, Zhao et al.’s piezoelectric transducer is connected to the central area of the acoustic black hole by pasting. Experiments have shown that the energy recovery efficiency is higher when the two-dimensional acoustic black hole is added compared with the ordinary flat plate structure [30].

In summary, it can be seen that there are relatively many studies on floating raft vibration isolation systems. In terms of improving the vibration isolation performance of floating raft systems, the research on raft structure design and parameter optimization is relatively mature, based on new composite materials, phononic crystals, and acoustics. The research on the vibration reduction and isolation performance of metamaterials of floating rafts mostly relies on the development of new materials, which is more difficult, and the acoustic black hole structure only needs to change its own structural thickness, which has a good application prospect in the field of improving the vibration reduction and isolation performance of the floating raft system. At present, the vibration and noise reduction characteristics of acoustic black hole structures have been well applied in some fields, but there are relatively few applications in the shipping field, and few research on how to select acoustic black hole parameters in engineering practice and the systematic application process of acoustic black holes. It has not been solved well yet.

2 Acoustic black hole effect based on geometric acoustic theory

2.1 Propagation characteristics of one-dimensional acoustic black holes

The structure of acoustic black holes means that the concept of acoustic black holes is based on the concept of black holes in astronomy. Taking the end of the acoustic black hole structure as the origin of the coordinates, the thickness of the black hole structure h(x) satisfies the relationship h(x) = εx m (m ≥ 2), and ε is a constant. The bending wave propagates to the origin along the negative direction of the x-axis. According to the geometric acoustics theory, the overall wave phase from any point of the acoustic black hole’s cross section to the origin of the coordinate is shown in the following equation.

(1.1) ϕ = ∫ 0 x k ( x ) d x ,

where k(x) is the local beam of the bending wave on the structure, and its specific value is

(1.2) k ( x ) = 12 1 / 4 k p 1 / 2 ( ε x m ) − 1 / 2 ,

where k p = ω/c p is the wave number of the symmetrical plate wave. c p is the wave number, and c p = 2 c t ( 1 − c t 2 / c l 2 ) 1 / 2 , where c t and c l are the wave speeds of longitudinal and transverse waves propagating in the structure, respectively. Among them, at a given frequency, k p is a constant, and under the condition that m is greater than or equal to 2, when x tends to 0, k(x) tends to infinity. At this time, the overall wave phase φ is infinite, indicating that at the tip of the structure, the local wave number tends to infinity, and the wavelength tends to zero. That is, bending waves can never reach the tip of the structure, and reflections will not occur, thereby realizing the vibration reduction effect of the acoustic black hole structure.

Figure 1 Diagram of polar coordinates of two-dimensional acoustic black hole structure.
Figure 1

Diagram of polar coordinates of two-dimensional acoustic black hole structure.

2.2 Propagation characteristics of two-dimensional acoustic black holes

For a rectangular plate with a two-dimensional acoustic black hole structure, as shown in Figure 1, the polar coordinate system is established with the center of the acoustic black hole as the coordinate origin, and the propagation path of the bending wave in the structure can be expressed in the following form:

(1.3) d r d θ = r 1 tan α ,

(1.4) n ( r ) sin α = const .

where α is the angle between the flexural wave propagation vector and the coordinate axis r in the polar coordinate system, n(r) is the refractive index of the flexural wave in the acoustic black hole region, and its value is equal to C 0/C r , and C 0 is the phase velocity of the bending wave outside the acoustic black hole region and C(r) is the phase velocity of the bending wave in the acoustic black hole region. Since the thickness of the acoustic black hole structure conforms to a specific power exponential function, its refractive index n(r) can be expressed as n ( r ) = h 0 1 / 2 / h ( r ) 1 / 2 , h (r) is the power exponential function that the acoustic black hole thickness conforms to. For bending waves whose starting point is outside the area of an acoustic black hole, equation (1.4) can be rewritten as follows:

(1.5) n ( r ) sin α = r 0 sin α 0 = p ,

where p describes the trajectory of bending waves with different incident angles. The physical meaning of this parameter is the straight line distance between the flexural wave trajectory and the polar coordinate center. For a rectangular plate without black hole structure, given the parameters r 0 and α 0, the flexural wave propagation trajectory is a straight line. But for a rectangular plate with a two-dimensional acoustic black hole structure, the existence of the acoustic black hole will have an impact on the trajectory of the bending wave, and its trajectory is no longer a straight line. The analysis of the above equations (1.3)–(1.5) shows that when the black hole structure is thick when m is greater than or equal to 2 in the power exponential function satisfied by the change, |p| of all flexural waves will be less than a certain critical value. At this time, the flexural waves will be deflected toward the center of the black hole, resulting in a phenomenon of flexural energy accumulation at the center of the black hole, as shown in Figure 2. For a perfect acoustic black hole structure, the thickness of its central area will be close to 0. At this time, the bending wave will converge at its central position and will not continue to propagate, and its energy will gradually dissipate and disappear, achieving the purpose of vibration reduction and noise reduction. And a certain damping material can be added at the center position to achieve efficient energy absorption and dissipation, to improve the efficiency of structural vibration suppression, and at the same time simulate structural damage caused during the model processing.

Figure 2 Propagation trajectory of bending wave in perfect acoustic black hole structure.
Figure 2

Propagation trajectory of bending wave in perfect acoustic black hole structure.

3 Research on the influence of acoustic black hole’s characteristic parameters on structural vibration

The acoustic black hole structure has the effect of gathering and dissipating flexural waves, and achieves the suppression of structural vibration, but the vibration suppression effect is affected by the combination of multiple parameters such as the cut-off length, the selection of damping materials, and the number and location of acoustic black holes. In order to better apply the acoustic black hole structure to engineering practice, this section will carry out the analysis of the influence of the above parameter changes on the structural vibration, and point out the law of the influence of the parameter changes on the structural vibration and the recommended value range of the parameters, thereby provide support for the application of the acoustic black hole in the raft structure later.

3.1 Analysis of the influence of one-dimensional acoustic black hole characteristic parameters on structural vibration

3.1.1 Analysis of the influence of one-dimensional acoustic black hole tip cut-off ratio on structural vibration

Acoustic black hole tip cut-off ratio λ = L 0/L, where L is the length of the perfect acoustic black hole structure, and L 0 is the acoustic black hole tip cut-off length. In this article, three acoustic black hole calculation conditions with different cutoff ratios are designed in combination with actual engineering. The vibration acceleration transfer function of the model origin is used as an assessment index to study the influence of one-dimensional acoustic black hole tip cutoff ratio, and those with different tip cutoff ratios. The schematic diagram of the one-dimensional acoustic black hole model is shown in Figure 3. The material parameters are shown in Table 1.

Figure 3 The calculation conditions of acoustic black holes under cut-off lengths. (a) Condition 1 λ = 5%. (b) Condition 2 λ = 10%. (c) Condition 3 λ = 20%.
Figure 3

The calculation conditions of acoustic black holes under cut-off lengths. (a) Condition 1 λ = 5%. (b) Condition 2 λ = 10%. (c) Condition 3 λ = 20%.

Table 1

Material parameter table

Structural material (steel) Damping material
Density t·mm−3 7.85 × 10−9 1.1 × 10−9
Poisson’s ratio 0.3 0.46
Young’s modulus N·mm−2 2.1 × 105 250
Structural damping 0.005 0.3

The calculation frequency domain is 4 Hz to 8 kHz, the calculation step is 4 Hz, and the above three models with no tip cut-off length and the origin vibration transfer function of the ordinary plate are obtained as shown in Figure 4.

Figure 4 Vibration transfer function of the assessment point under various conditions.
Figure 4

Vibration transfer function of the assessment point under various conditions.

It can be seen from the origin transfer function curve in Figure 4 that the model tip cutoff ratio has a greater influence on the origin transfer function peak value and the peak corresponding frequency, but all the three acoustic black hole models with cutoff ratios of 5, 10, and 20% can effectively reduce the peak value of the origin vibration transfer function. Among the three groups of acoustic black hole models, when the model cut-off ratio is 5%, the acoustic black hole has the best vibration reduction effect, and the vibration reduction effect of each peak is generally more than 35 dB. As the model cut-off ratio increases, the corresponding frequency of the origin transfer function peak increases, the peak position shifts to the right, and the peak size increases, indicating that the larger the acoustic black hole structure cut-off ratio, the worse the vibration reduction effect. However, when the tip cut-off ratio is 5 and 10%, the effect of the acoustic black hole structure’s vibration reduction system is relatively small, and the difference in peak size is about 3–5 dB. It can be seen that under the premise, a perfect acoustic black hole structure cannot be achieved, the acoustic black hole tip comparison is excessively reduced and the improvement of its damping effect is small.

In summary, when designing the acoustic black hole structure, the cutoff ratio of the model should be minimized to achieve the best vibration reduction effect. However, considering the difficulty of model processing, model strength, and other factors, it is recommended that the cutoff ratio be about 10%.

3.1.2 Analysis of the influence of damping layer length ratio on structural vibration

The acoustic black hole structure has an elastic wave reflectivity of 0 in theory. Since the tip thickness is close to 0, the tip of the acoustic black hole needs to be truncated when the acoustic black hole is used in engineering to reduce the processing difficulty of the acoustic black hole model, and the acoustic black hole’s vibration damping performance will be greatly reduced. Therefore, an acoustic damping material needs to be added to the tip junction to absorb and consume energy to achieve the vibration and noise reduction characteristics of the acoustic black hole. Acoustic black hole damping length ratio φ = L n /L, where L n is the length of the damping layer material.

In order to explore the length of the additional damping material in the acoustic black hole structure, three sets of calculation conditions were designed for the length ratio of the damping layer, namely, 5, 15, and 25%, respectively. The cut-off ratio of the acoustic black hole structure is all 10%. The other parameters are as shown in Table 1, and the schematic diagram of the calculation conditions is shown in Figure 5.

Figure 5 Calculation conditions with different damping layer length ratios: (a) Condition 1 φ = 10%. (b) Condition 2 φ = 20%. (c) Condition 3 φ = 30%.
Figure 5

Calculation conditions with different damping layer length ratios: (a) Condition 1 φ = 10%. (b) Condition 2 φ = 20%. (c) Condition 3 φ = 30%.

Using the steady-state dynamics analysis module in the finite element software, the vibration transfer function curves at the origin of the assessment point are calculated as shown in Figure 6.

Figure 6 The origin vibration transfer function under different damping length ratios in the full frequency range.
Figure 6

The origin vibration transfer function under different damping length ratios in the full frequency range.

It can be seen from Figure 7 that the length ratio of the damping layer has a great impact on the peak value of the origin transfer function and the corresponding frequency of the peak values, and the three acoustic black hole models can effectively reduce the peak value of the vibration transfer function. In the three acoustic black hole models, when the length ratio of the damping layer is 30%, the acoustic black hole has the best vibration reduction effect, with each peak vibration reduction generally reaching more than 30 dB. As the length ratio of the damping material increases, the peak value of the origin vibration transfer function decreases, and the vibration damping effect of the acoustic black hole structure increases. In the frequency domain below 2,000 Hz, the vibration reduction effect of the damping layer length ratio of 30% is about 5–10 dB higher than that of the damping length ratio of 20%. The damping effect of the three models above 2,000 Hz is similar, and the peak difference is about 1–2 dB, indicating that as the length of the damping material increases, the increase in the damping effect gradually decreases.

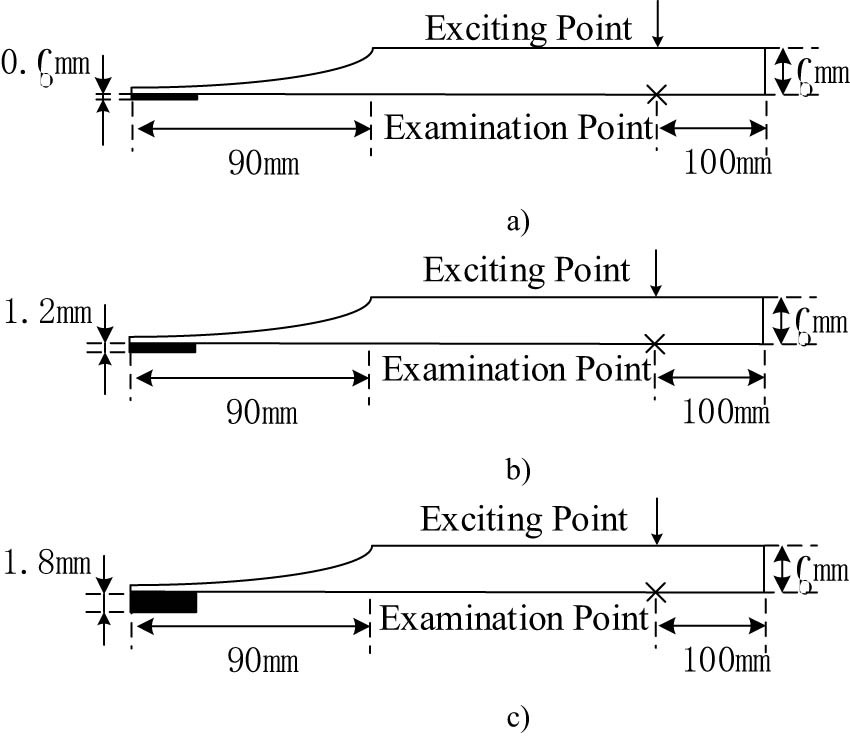
Figure 7 Calculation conditions of acoustic black holes with different damping layer thicknesses. (a) Condition 1 μ = 10%, (b) condition 2 μ = 20%, and (c) condition 3 μ = 30%.
Figure 7

Calculation conditions of acoustic black holes with different damping layer thicknesses. (a) Condition 1 μ = 10%, (b) condition 2 μ = 20%, and (c) condition 3 μ = 30%.

In summary, when designing the acoustic black hole structure, the length of the damping material should be increased as much as possible to achieve the best vibration reduction effect. An excessively large damping length ratio will lead to higher material cost, increased structural weight, and other negative effects. At the same time, the improvement in the medium- and high-frequency vibration damping effect is small. It is recommended that the damping layer length ratio is about 20%. If attention is paid to the damping effect in the low frequency range, a larger damping layer length ratio should be used.

3.2 Research of the influence of two-dimensional acoustic black hole characteristic parameters on structural vibration

3.2.1 Analysis of the influence of the size of the two-dimensional acoustic black hole on structural vibration

Two-dimensional acoustic black holes are based on one-dimensional acoustic black holes. Two-dimensional acoustic black holes are more complex in terms of structure. In addition to parameters such as cut-off length, damping layer material thickness, and length, there are also factors such as the size, the number, and arrangement of acoustic black holes. For this reason, based on the above research, the unique parameters of two-dimensional acoustic black holes are further studied. First the following dimensionless parameters are defined. In Figure 8, R is the radius of the largest circle that can be embedded in the area, R 0 is the radius of the acoustic black hole, and the dimensionless parameter γ is defined as the ratio of the radius of the acoustic black hole, γ = R 0 /R.

Figure 8 Diagram of the definition of two-dimensional acoustic black hole parameters.
Figure 8

Diagram of the definition of two-dimensional acoustic black hole parameters.

There are three calculation models as shown in Figure 9. The acoustic black hole radius ratios are 80, 64, and 40%, respectively. The cut-off length of the model is 10% of the radius of the black hole region. The damping layer covering radius is 20% of the black hole region radius. The main scale of the model, the size of the excitation load, the location of the excitation point, and the location of the assessment point are consistent with the previous article. At the same time, in order to improve the calculation efficiency, the step simplification method is used to model the acoustic black hole models of different sizes, and the acoustic black hole area is equally divided into 45 parts.

Figure 9 Acoustic black hole plate models with different sizes: (a) γ = 80% model diagram, (b) γ = 80% model diagram, (c) γ = 64% model diagram, (d) γ = 64% model diagram, (e) γ = 40% model diagram, and (f) γ = 40% model diagram.
Figure 9

Acoustic black hole plate models with different sizes: (a) γ = 80% model diagram, (b) γ = 80% model diagram, (c) γ = 64% model diagram, (d) γ = 64% model diagram, (e) γ = 40% model diagram, and (f) γ = 40% model diagram.

The calculated results are shown in Figure 10. The vibration response of the assessment points P1–P5 is averaged to represent the average vibration response at the edge of the structure, as shown in Figure 10(a). The vibration response of the assessment points P6–P8 is energy-averaged to represent the average vibration response of the area near the excitation force, as shown in Figure 10(b).

Figure 10 Vibration response curve of each working condition assessment point: (a) average vibration response of P1–P5 and (b) average vibration response of P6–P8.
Figure 10

Vibration response curve of each working condition assessment point: (a) average vibration response of P1–P5 and (b) average vibration response of P6–P8.

From Figure 10, it can be seen that there are many peaks in the vibration response curve of the acoustic black hole plate with a radius of 50 mm, and the peak size is significantly higher than that of the 80 mm radius. The vibration damping effect is relatively poor under 80 mm conditions and 100 mm radius conditions. The vibration response of the acoustic black hole plate with a radius of 80 mm and the acoustic black hole plate with a radius of 100 mm are relatively close, and the peak size is relatively close. Among them, the acoustic black hole plate with a radius of 100 mm has a slightly lower vibration response peak, and the vibration reduction effect is slightly better than that of the operating condition with a radius of 80 mm.

From the above calculation results, it can be seen that when the radius is 50 mm, the size of the acoustic black hole is smaller, resulting in a smaller area that can effectively absorb and converge flexural waves. Some flexural waves are less affected by the acoustic black hole effect during the propagation process, so the vibration response of the acoustic black hole plate with a radius of 50 mm is the largest among the three working conditions. When the radius is 100 mm, the acoustic black hole area is larger, and the ability to capture and dissipate medium and high frequency bending waves is strong, although it is generated at about 500 Hz, a new and larger peak is achieved, but the acoustic black hole plate with a radius of 100 mm has the best damping effect in the full frequency range.

In summary, when using the embedded two-dimensional acoustic black hole to control the vibration response of the structure, the selection of the acoustic black hole radius will affect its vibration reduction effect, and increasing the acoustic black hole structure radius too large will improve the vibration reduction effect. And by reducing the radius too small will bring about negative effects such as structural strength reduction. It is recommended that the acoustic black hole radius ratio should not exceed 80%.

3.2.2 Analysis of the influence of two-dimensional acoustic black hole layout on structural vibration

Different from the one-dimensional acoustic black hole, the one-dimensional acoustic black hole structure can only be applied to the edge of the structure and will form a sharp tip. In the application process of the two-dimensional acoustic black hole, the position of the acoustic black hole can be anywhere in the structure, so it involves turning to the problem of the layout of two-dimensional acoustic black holes. This article explores the layout of two-dimensional acoustic black holes. Five calculation conditions are designed, as shown in Figure 11, and the finite element model is shown in Figure 12.

Figure 11 Acoustic black hole plates with different arrangements. (a) Condition 1. (b) Condition 2. (c) Condition 3. (d) Condition 4. (e) Condition 5.
Figure 11

Acoustic black hole plates with different arrangements. (a) Condition 1. (b) Condition 2. (c) Condition 3. (d) Condition 4. (e) Condition 5.

Figure 12 Finite element model.
Figure 12

Finite element model.

Using the finite element steady-state dynamics frequency domain analysis, the calculation results of the above working conditions are obtained as follows. Among them, the vibration response of the assessment points P1–P5 is energy-averaged to represent the average vibration response at the edge of the structure, as shown in Figure 13. The vibration response of the assessment points P6–P8 is averaged to represent the average vibration response of the area near the excitation force, as shown in Figure 14.

Figure 13 Vibration response of test points P1–P5 for conditions 1 and 2.
Figure 13

Vibration response of test points P1–P5 for conditions 1 and 2.

Figure 14 Vibration response of test points P6–P8 for conditions 1 and 2.
Figure 14

Vibration response of test points P6–P8 for conditions 1 and 2.

Condition 1 is a single large-size acoustic black hole, Condition 2 is 4 small-size acoustic black holes, but the area of the acoustic black hole area of Conditions 1 2 is the same, and the quality of the damping material is the same. It can be seen from Figures 13 and 14 that the overall response curve of a single large-size acoustic black hole is smoother and has fewer peaks, while the introduction of four small-size acoustic black holes results in a rich natural frequency of the structure as a whole, and an increase in the peak value of the response curve of each test point. In the low frequency range below 1,000 Hz, the peak value of working Condition 2 is less than that of working Condition 1 by about 3–7 dB, indicating that the design of multiple acoustic black holes will improve the low frequency. The ability to capture bending waves improves the damping effect in the low-frequency range of acoustic black holes; in the frequency range above 1,000 Hz, the response curve of each test point in the second working condition has multiple prominent peaks, and the damping effect is not as good as the first working condition. In summary, the number of acoustic black holes can be determined according to requirements such as the frequency range, processing difficulty, area size, and other factors. A single large-size acoustic black hole design is preferred. If the design requirements of floating raft vibration reduction and isolation requirements cannot be met, a single large dimensional black hole is replaced with multiple small-sized acoustic black holes to further improve the vibration isolation performance of the raft.

Conditions 3, 4, and 5 are all two small-sized acoustic black hole designs. The difference lies in the position of the acoustic black hole. The position of the acoustic black hole in Condition 3 is the farthest from the excitation point, and Condition 5 is the closest. From Figures 15 and 16, it can be seen that the vibration response curve trends of the assessment points of the three sets of test conditions are basically the same, and the peak position deviation is not obvious, but there are certain differences in the peak size. Except for the peak near 3,000 Hz, the peak value of working condition five is lower than that of working conditions three and four, and the peak size is reduced by about 5–10 dB. The reason for the large peak near 3,000 Hz is due to the different positions of the acoustic black hole structure, so that the structure produces a new vibration mode, but on the whole, the vibration response of the condition 5 is lower than the condition 3 and condition 4, indicating that the acoustic black hole is arranged on the right side, that is, when the acoustic black hole structure is arranged near the excitation point, the acoustic black hole will have a certain improvement in the vibration reduction and noise reduction effect of the structure, so when applying the two-dimensional acoustic black hole structure for the vibration reduction and noise reduction design of the structure, acoustic black holes should be placed as close to the excitation point as possible.

Figure 15 Vibration response of test points P1–P5 for conditions 3–5.
Figure 15

Vibration response of test points P1–P5 for conditions 3–5.

Figure 16 Vibration response of test points P6–P8 for conditions 3–5.
Figure 16

Vibration response of test points P6–P8 for conditions 3–5.

4 Application of acoustic black hole in large floating raft

4.1 Floating raft system model establishment

Based on a large-scale floating raft vibration isolation system of a ship, a distributed acoustic black hole floating raft system was designed. When modeling the floating raft system, a rigid body is used to model the carried equipment, and its mass is 2.1 t. Four-node shell elements are used to model the raft structure and the base structure. The main dimension of the raft is 3,500 mm × 2,000 mm × 400 mm. The spring damping system is used to model the vibration isolator unit. There are 12 upper vibration isolators and 6 absorption vibration isolators. The final finite element analysis model of the floating raft vibration isolation system is shown in Figure 17.

Figure 17 Floating raft system model.
Figure 17

Floating raft system model.

4.2 Application scheme of acoustic black hole structure in floating raft system

According to the influence law of the acoustic black hole structure position on the vibration reduction effect, the acoustic black hole structure should be embedded in the upper vibration isolator panel or bracket to obtain a better vibration reduction effect. Because the panel needs to be installed with vibration isolation devices, it is difficult to embed the acoustic black hole structure, and it is finally determined to embed the two-dimensional acoustic black hole structure at the bracket position.

Multiple large-size acoustic black holes will further improve the damping effect of acoustic black holes in the low frequency range, but at the same time it will greatly increase the difficulty of the actual engineering application. Therefore, when the acoustic black hole structure is applied this time, a single acoustic black hole is used. This will reduce the difficulty and cost of engineering application.

The shape of this area is approximately triangular, and the size of the acoustic black hole is about 80% of the radius of the inscribed circle. After approximate rounding, the radius of the acoustic black hole structure is determined to be 90 mm, and the tip cut length is 10% of the radius, that is, the tip cut length is 9 mm, The truncated area is filled with a constant thickness plate to ensure that the thickness of the acoustic black hole structure changes. Considering the difficulty in processing, the power exponent parameter of the acoustic black hole is 2, and the length of the damping layer is 20% of the radius. That is, a damping layer with a radius of 18 mm is attached to the center of the acoustic black hole structure, and the thickness of the damping layer is 2 mm (Figure 18).

Figure 18 Raft model embedded with two-dimensional acoustic black hole.
Figure 18

Raft model embedded with two-dimensional acoustic black hole.

4.3 Vibration reduction effect of acoustic black hole structure applied in floating raft system

In general, the evaluation methods for the vibration isolation effect of the raft include: force transmission rate, vibration level drop, vibration intensity, and power flow. Among them, the vibration level drop evaluation method is relatively simple and convenient, and it is widely used in the field of evaluation of the vibration reduction and isolation performance of the floating raft system in engineering practice. At the same time, considering that the floating raft vibration isolation system has multiple vibration isolation devices, the vibration level drop at one location cannot fully reflect the vibration reduction and isolation performance of the floating raft vibration isolation system. Therefore, this article averages the energy of multiple vibration acceleration levels to obtain the average vibration acceleration level of the machine foot and the average vibration acceleration level at the base panel. The energy average formula is as follows:

(1.6) L e = 10 lg 1 n ∑ i = 1 n 10 0.1 L i ,

where L i is the vibration acceleration level of the i-th evaluation point. The average vibration acceleration level L e1 of the 12 equipment foot vibration evaluation points and the average vibration acceleration level L e2 of the 6 base panel evaluation points are calculated, respectively, and the difference is L e1−L e2. Thus, the vibration level drop of the floating raft vibration isolation system is obtained.

After determining the application scheme of the abovementioned acoustic black hole in the floating raft system, based on the finite element analysis software ABAQUS, the calculation of the vibration reduction and isolation performance of the floating raft before and after the application of the acoustic black hole is carried out. The calculation frequency range is 5–1,000 Hz, the calculation step length is 5 Hz, and the applied excitation load is the unit force directly above the device. The final vibration response curve of vibration isolation is shown in Figure 19.

Figure 19 1/3 octave curve of the vibration level drop.
Figure 19

1/3 octave curve of the vibration level drop.

It can be seen from Figure 19 that whether or not an acoustic black hole is embedded, the raft frame under unit force has good vibration isolation performance in the range of 5–1,000 Hz, and the vibration isolation performance shows an upward trend with the increase in frequency. The vibration level drop in the low frequency range (0–250 Hz) is about 20–40 dB, and the vibration level drop in the range of 250–1,000 Hz can reach about 70 dB. After being embedded in the acoustic black hole structure, the trend of the vibration level drop curve in the frequency range of 5–1,000 Hz has basically not changed, but the peak value of the low-frequency line spectrum of the multiple vibration level drop has increased. The lowest frequency with obvious effect of vibration reduction is 80 Hz, and the effect of vibration reduction is increased by 2.5 dB. In addition, the effect of vibration reduction is also increased by 3–7 dB at frequency points of 140 Hz, 280 Hz, 315 Hz, 625 Hz, 670 Hz and et al. It can be seen that the embedding of acoustic black holes can effectively improve the mid- and low-frequency vibration isolation performance of the floating raft vibration isolation system.

5 Conclusion

Based on the simplification method of acoustic black hole modeling, this article has carried out the research of one-dimensional and two-dimensional acoustic black hole vibration reduction effect with the change in parameters. First, taking a one-dimensional acoustic black hole as the research object, the vibration response of different structural parameter models were compared and analyzed at the same assessment position under the action of unit force, to verify the vibration damping effect of the acoustic black hole structure. Second, taking the two-dimensional acoustic black hole as the research object, the influence law of the size, quantity, and location of the two-dimensional acoustic black hole on the vibration reduction effect is explored. Finally, the acoustic black hole was applied to the raft structure, and the vibration reduction effect was verified. The specific conclusions are as follows.

  1. As acoustic black hole tip cutoff ratio decreases, damping layer length ratio increases, and damping layer thickness ratio increases, the damping effect of acoustic black holes improves, but the improvement of the acoustic black hole structure damping effect by continuously optimizing the above parameters will gradually decrease. The recommended values are as follows: tip cut-off ratio λ = 10%, damping length ratio φ = 20%, and damping thickness ratio μ = 20%. When using the recommended values of the above parameters, the peaks of the vibration response curve of the one-dimensional acoustic black hole flat panel test point drop by more than 30 dB

  2. As the size of the radius of the acoustic black hole structure increases, the number of acoustic black hole structures increases, the distance from the excitation point decreases, and the vibration reduction effect of the two-dimensional acoustic black hole improves. However, an excessively large acoustic black hole radius will bring about negative effects such as insufficient structural strength. It is recommended that the value not exceed 80% of the radius of the largest inscribed circle in the area. Replacing a single large-size acoustic black hole with multiple small-size acoustic black holes will increase the damping effect of the acoustic black hole structure in the low-frequency range and increase the difficulty of construction. In engineering practice, one large acoustic black hole or several small acoustic black holes should be selected according to the actual engineering requirements.

  3. Based on the systematic process method of the application of acoustic black holes in the raft structure, an application scheme of embedding a single large-size acoustic black hole in the bracket of the raft structure is formed. This solution increases the level drop of the floating raft vibration isolation at multiple frequencies by 2–7 dB, the lowest operating frequency is 80 Hz, and the level drop of this frequency is increased by 2.5 dB.

Acknowledgments

This study was funded by National Natural Science Foundation of China (U2006229).

  1. Funding information: This study was funded by National Natural Science Foundation of China (U2006229).

  2. Author contributions: Shengyao Gao: Conceptualization Methodology; Yuhui Li: Formal analysis Writing – review & editing (equal); Zhou Tao: Conceptualization; Fuzhen Pang: Formal analysis Funding acquisition.

  3. Conflict of interest: The authors state no conflict of interest.

References

[1] Sciully, D. and D.J. Inman. Isolation design for a flexible system. Journal of Sound and Vibration, Vol. 212, No. 2, 1995, pp. 251–267.10.1006/jsvi.1998.1667Search in Google Scholar

[2] Qu, Z.-Q. and R. P. Selvam. Hybrid expansion method for frequency responses and their sensitivities, Part 2: viscously damped systems. Journal of Sound and Vibration, Vol. 238, No. 3, 2000, pp. 175–193.10.1006/jsvi.2000.3085Search in Google Scholar

[3] Zhang, J., H. Yang, G. Chen, and Z. Zhang. Structure and modal analysis of carbon fiber reinforced polymer raft frame. Journal of Low Frequency Noise Vibration & Active Control, 2017, id. 146134841772596.Search in Google Scholar

[4] Li, H., C. Touzé, A. Pelat, and F. Gautier. Combining nonlinear vibration absorbers and the Acoustic Black Hole for passive broadband flexural vibration mitigation. International Journal of Non-Linear Mechanics, Vol. 129, 2021, id. 103558.1–103558.13.10.1016/j.ijnonlinmec.2020.103558Search in Google Scholar

[5] Krylov, V. V. and F. J. B. S. Tilman. Acoustic ‘black holes’ for flexural waves as effective vibration dampers. Journal of Sound Vibration, Vol. 274, No. 3, 2004, pp. 605–619.10.1016/j.jsv.2003.05.010Search in Google Scholar

[6] Krylov, V. V. New type of vibration dampers utilising the effect of acoustic ‘black holes.’ Acta Acustica United with Acustica, Vol. 90, No. 5, 2004, pp. 830–837.Search in Google Scholar

[7] Krylov, V. V. and R. E. T. B. Winward. Experimental investigation of the acoustic black hole effect for flexural waves in tapered plates. Journal of Sound & Vibration, Vol. 300, No. 1, 2007, pp. 43–49.10.1016/j.jsv.2006.07.035Search in Google Scholar

[8] Ross, D. Damping of plate flexural vibrations by means of viscoelastic laminate. Structual Damping ASME, 1960, pp. 49–97.Search in Google Scholar

[9] Georgiev, V. B., J. Cuenca, F. Gautier, L. Simon, and V. V. Krylov. Damping of structural vibrations in beams and elliptical plates using the acoustic black hole effect. Journal of Sound & Vibration, Vol. 330, No. 11, 2011, pp. 2497–2508.10.1016/j.jsv.2010.12.001Search in Google Scholar

[10] Georgiev, V. B., J. Cuenca, M. A. Moleron Bermudez, and F. Gautier. Numerical and experimental investigation of the acoustic black hole effect for vibration damping in beams and elliptical plates. Euronoise, 2009, p. 3318.10.1121/1.2933786Search in Google Scholar

[11] Krylov, V. V. Propagation of plate bending waves in the vicinity of one- and two-dimensional acoustic black hole. Proceedings of the First International ECCOMAS Thematic Conference on Computational Methods in Structural Dynamics and Earthquake Engineering, Greece, 2007.Search in Google Scholar

[12] O’Boy, D. J. and V. V. Krylov. Vibration of a rectangular plate with a central power-law profiled groove by the Rayleigh-Ritz method. Applied Acoustics, Vol. 104, 2016, pp. 24–32.10.1016/j.apacoust.2015.10.018Search in Google Scholar

[13] O’Boy, D. J. and V. V. Krylov. Damping of flexural vibrations in circular plates with tapered central holes. Journal of Sound and Vibration, Vol. 330, 2011, pp. 2220–2236.10.1016/j.jsv.2010.11.017Search in Google Scholar

[14] Lian, X., S. Wang, M. Liu, S. Nie, J. Peng, Z. Zhou, et al. Study on low frequency sound insulation characteristic of thin acoustic black hole. Modern Physics Letters B, Vol. 35, 2021, id. 2150198.10.1142/S0217984921501980Search in Google Scholar

[15] Yan, J. The phonon mass and the Hawking temperature in the two-dimensional acoustic black hole model – ScienceDirect. Physics Letters B, 2021, id. 818.10.1016/j.physletb.2021.136359Search in Google Scholar

[16] Chakraborty, C. and P. Majumdar. Spinning gyroscope in an acoustic black hole: precession effects and observational aspects. European Physical Journal C, Vol. 80, No. 6, 2020, id. 2280.10.1140/epjc/s10052-020-8060-1Search in Google Scholar

[17] Mironov, M. A. A notched bar as a vibrational black hole. Acoustical Physics, Vol. 65, No. 6, 2019, pp. 634–636.10.1134/S1063771019060095Search in Google Scholar

[18] Zhou, Z., X. Liang, J. H. Wu, P. Shang, and J. Niu. Investigation on low-frequency broadband characteristics of three-dimensional acoustic black hole superstructures. International Journal of Modern Physics B, Vol. 34, 2020, id. 2050151.10.1142/S0217979220501519Search in Google Scholar

[19] Yu, D. L., H. J. Shen, J. W. Liu, J. F. Yin, Z. F. Zhang, and J. H. Wen. Propagation of acoustic waves in a fluid-filled pipe with periodic elastic Helmholtz resonators. Chinese Physics B, Vol. 27, No. 6, 2019, pp. 7.10.1088/1674-1056/27/6/064301Search in Google Scholar

[20] Liu, J. W., D. L. Yu, H. B. Yang, H. J. Shen, and J. H. Wen. Effect of mean flow on acoustic wave propagation in a duct with a periodic array of helmholtz resonators. Chinese Physics Letters, Vol. 37, No. 3, 2020, id. 034301.10.1088/0256-307X/37/3/034301Search in Google Scholar

[21] Yu, D. L., C. Y. Du, H. J. Shen, J. W. Liu, and J. H. Wen. An analysis of structural-acoustic coupling band gaps in a fluid-filled periodic pipe. Chinese Physics Letters, Vol. 34, No. 7, 2017, pp. 190–194.10.1088/0256-307X/34/7/076202Search in Google Scholar

[22] Li, H., F. Pang, X. Miao, and Y. Li. Jacobi–Ritz method for free vibration analysis of uniform and stepped circular cylindrical shells with arbitrary boundary conditions: A unified formulation. Computers & Mathematics with Applications, Vol. 77, No. 2, 2019, pp. 427–440.10.1016/j.camwa.2018.09.046Search in Google Scholar

[23] Pang, F., H. Li, X. Wang, X. Miao, and S. Li. A semi analytical method for the free vibration of doubly-curved shells of revolution. Computers & Mathematics with Applications, Vol. 75, No. 9, 2018, pp. 3249–3268.10.1016/j.camwa.2018.01.045Search in Google Scholar

[24] Li, H., F. Pang, H. Chen, and Y. Du. Vibration analysis of functionally graded porous cylindrical shell with arbitrary boundary restraints by using a semi analytical method. Composites Part B: Engineering, Vol. 164, 2019, pp. 249–264.10.1016/j.compositesb.2018.11.046Search in Google Scholar

[25] Li, H., F. Pang, X. Miao, S. Gao, and F. Liu. A semi analytical method for free vibration analysis of composite laminated cylindrical and spherical shells with complex boundary conditions. Thin-Walled Structures, Vol. 136, 2019, pp. 200–220.10.1016/j.tws.2018.12.009Search in Google Scholar

[26] Li, H., F. Pang, and H. Chen. A semi-analytical approach to analyze vibration characteristics of uniform and stepped annular-spherical shells with general boundary conditions. European Journal of Mechanics-A/Solids, Vol. 74, 2019, pp. 48–65.10.1016/j.euromechsol.2018.10.017Search in Google Scholar

[27] Bowyer, E. P. and V. V. Krylov. Damping of flexural vibrations in turbofan blades using the acoustic black hole effect. Applied Acoustics, Vol. 76, 2014, pp. 359–365.10.1016/j.apacoust.2013.09.009Search in Google Scholar

[28] Prill, O., C. Roos, and R. Busch. Finite element simulations of acoustic black holes as lightweight damping treatments for automotive body panels with application to full vehicle interior wind noise predictions. Proceedings of the 45th International Congress and Exposition on Noise Control Engineering, Institute of Noise Control Engineering, Hamburg, Germany, 2016, pp. 2445–2451.Search in Google Scholar

[29] Zhou, X. and F. Semperlotti. The energy absorption properties of Helmholtz resonators enhanced by acoustic black holes. Proceedings of the 45th International Congress and Exposition on Noise Control Engineering. The German Acoustical Society, Hamburg, Germany, 2016, pp. 2422–2430.Search in Google Scholar

[30] Zhao, L., S. C. Conlon, and F. Semperlotti. Experimental verification of energy harvesting performance in plate-like structures with embedded acoustic black holes. Inter-Noise and Nosie-Con Congress and Conference Proceedings, 2015.10.1088/0964-1726/24/6/065039Search in Google Scholar
Received: 2021-12-15
Revised: 2022-02-22
Accepted: 2022-03-17
Published Online: 2022-12-21

© 2022 Shengyao Gao et al., published by De Gruyter

This work is licensed under the Creative Commons Attribution 4.0 International License.

Articles in the same Issue

  1. Review Articles
  2. State of the art, challenges, and emerging trends: Geopolymer composite reinforced by dispersed steel fibers
  3. A review on the properties of concrete reinforced with recycled steel fiber from waste tires
  4. Copper ternary oxides as photocathodes for solar-driven CO2 reduction
  5. Properties of fresh and hardened self-compacting concrete incorporating rice husk ash: A review
  6. Basic mechanical and fatigue properties of rubber materials and components for railway vehicles: A literature survey
  7. Research progress on durability of marine concrete under the combined action of Cl− erosion, carbonation, and dry–wet cycles
  8. Delivery systems in nanocosmeceuticals
  9. Study on the preparation process and sintering performance of doped nano-silver paste
  10. Analysis of the interactions between nonoxide reinforcements and Al–Si–Cu–Mg matrices
  11. Research Articles
  12. Study on the influence of structural form and parameters on vibration characteristics of typical ship structures
  13. Deterioration characteristics of recycled aggregate concrete subjected to coupling effect with salt and frost
  14. Novel approach to improve shale stability using super-amphiphobic nanoscale materials in water-based drilling fluids and its field application
  15. Research on the low-frequency multiline spectrum vibration control of offshore platforms
  16. Multiple wide band gaps in a convex-like holey phononic crystal strip
  17. Response analysis and optimization of the air spring with epistemic uncertainties
  18. Molecular dynamics of C–S–H production in graphene oxide environment
  19. Residual stress relief mechanisms of 2219 Al–Cu alloy by thermal stress relief method
  20. Characteristics and microstructures of the GFRP waste powder/GGBS-based geopolymer paste and concrete
  21. Development and performance evaluation of a novel environmentally friendly adsorbent for waste water-based drilling fluids
  22. Determination of shear stresses in the measurement area of a modified wood sample
  23. Influence of ettringite on the crack self-repairing of cement-based materials in a hydraulic environment
  24. Multiple load recognition and fatigue assessment on longitudinal stop of railway freight car
  25. Synthesis and characterization of nano-SiO2@octadecylbisimidazoline quaternary ammonium salt used as acidizing corrosion inhibitor
  26. Perforated steel for realizing extraordinary ductility under compression: Testing and finite element modeling
  27. The influence of oiled fiber, freeze-thawing cycle, and sulfate attack on strain hardening cement-based composites
  28. Perforated steel block of realizing large ductility under compression: Parametric study and stress–strain modeling
  29. Study on dynamic viscoelastic constitutive model of nonwater reacted polyurethane grouting materials based on DMA
  30. Mechanical behavior and mechanism investigation on the optimized and novel bio-inspired nonpneumatic composite tires
  31. Effect of cooling rate on the microstructure and thermal expansion properties of Al–Mn–Fe alloy
  32. Research on process optimization and rapid prediction method of thermal vibration stress relief for 2219 aluminum alloy rings
  33. Failure prevention of seafloor composite pipelines using enhanced strain-based design
  34. Deterioration of concrete under the coupling action of freeze–thaw cycles and salt solution erosion
  35. Creep rupture behavior of 2.25Cr1Mo0.25V steel and weld for hydrogenation reactors under different stress levels
  36. Statistical damage constitutive model for the two-component foaming polymer grouting material
  37. Nano-structural and nano-constraint behavior of mortar containing silica aggregates
  38. Influence of recycled clay brick aggregate on the mechanical properties of concrete
  39. Effect of LDH on the dissolution and adsorption behaviors of sulfate in Portland cement early hydration process
  40. Comparison of properties of colorless and transparent polyimide films using various diamine monomers
  41. Study in the parameter influence on underwater acoustic radiation characteristics of cylindrical shells
  42. Experimental study on basic mechanical properties of recycled steel fiber reinforced concrete
  43. Dynamic characteristic analysis of acoustic black hole in typical raft structure
  44. A semi-analytical method for dynamic analysis of a rectangular plate with general boundary conditions based on FSDT
  45. Research on modification of mechanical properties of recycled aggregate concrete by replacing sand with graphite tailings
  46. Dynamic response of Voronoi structures with gradient perpendicular to the impact direction
  47. Deposition mechanisms and characteristics of nano-modified multimodal Cr3C2–NiCr coatings sprayed by HVOF
  48. Effect of excitation type on vibration characteristics of typical ship grillage structure
  49. Study on the nanoscale mechanical properties of graphene oxide–enhanced shear resisting cement
  50. Experimental investigation on static compressive toughness of steel fiber rubber concrete
  51. Study on the stress field concentration at the tip of elliptical cracks
  52. Corrosion resistance of 6061-T6 aluminium alloy and its feasibility of near-surface reinforcements in concrete structure
  53. Effect of the synthesis method on the MnCo2O4 towards the photocatalytic production of H2
  54. Experimental study of the shear strength criterion of rock structural plane based on three-dimensional surface description
  55. Evaluation of wear and corrosion properties of FSWed aluminum alloy plates of AA2020-T4 with heat treatment under different aging periods
  56. Thermal–mechanical coupling deformation difference analysis for the flexspline of a harmonic drive
  57. Frost resistance of fiber-reinforced self-compacting recycled concrete
  58. High-temperature treated TiO2 modified with 3-aminopropyltriethoxysilane as photoactive nanomaterials
  59. Effect of nano Al2O3 particles on the mechanical and wear properties of Al/Al2O3 composites manufactured via ARB
  60. Co3O4 nanoparticles embedded in electrospun carbon nanofibers as free-standing nanocomposite electrodes as highly sensitive enzyme-free glucose biosensors
  61. Effect of freeze–thaw cycles on deformation properties of deep foundation pit supported by pile-anchor in Harbin
  62. Temperature-porosity-dependent elastic modulus model for metallic materials
  63. Effect of diffusion on interfacial properties of polyurethane-modified asphalt–aggregate using molecular dynamic simulation
  64. Experimental study on comprehensive improvement of shear strength and erosion resistance of yellow mud in Qiang Village
  65. A novel method for low-cost and rapid preparation of nanoporous phenolic aerogels and its performance regulation mechanism
  66. In situ bow reduction during sublimation growth of cubic silicon carbide
  67. Adhesion behaviour of 3D printed polyamide–carbon fibre composite filament
  68. An experimental investigation and machine learning-based prediction for seismic performance of steel tubular column filled with recycled aggregate concrete
  69. Effects of rare earth metals on microstructure, mechanical properties, and pitting corrosion of 27% Cr hyper duplex stainless steel
  70. Application research of acoustic black hole in floating raft vibration isolation system
  71. Multi-objective parametric optimization on the EDM machining of hybrid SiCp/Grp/aluminum nanocomposites using Non-dominating Sorting Genetic Algorithm (NSGA-II): Fabrication and microstructural characterizations
  72. Estimating of cutting force and surface roughness in turning of GFRP composites with different orientation angles using artificial neural network
  73. Displacement recovery and energy dissipation of crimped NiTi SMA fibers during cyclic pullout tests
https://doi.org/10.1515/rams-2022-0235
Keywords for this article
acoustic black hole; floating raft vibration isolation system; vibration level drop; mechanical noise
Creative Commons
BY 4.0

Articles in the same Issue

  1. Review Articles
  2. State of the art, challenges, and emerging trends: Geopolymer composite reinforced by dispersed steel fibers
  3. A review on the properties of concrete reinforced with recycled steel fiber from waste tires
  4. Copper ternary oxides as photocathodes for solar-driven CO2 reduction
  5. Properties of fresh and hardened self-compacting concrete incorporating rice husk ash: A review
  6. Basic mechanical and fatigue properties of rubber materials and components for railway vehicles: A literature survey
  7. Research progress on durability of marine concrete under the combined action of Cl− erosion, carbonation, and dry–wet cycles
  8. Delivery systems in nanocosmeceuticals
  9. Study on the preparation process and sintering performance of doped nano-silver paste
  10. Analysis of the interactions between nonoxide reinforcements and Al–Si–Cu–Mg matrices
  11. Research Articles
  12. Study on the influence of structural form and parameters on vibration characteristics of typical ship structures
  13. Deterioration characteristics of recycled aggregate concrete subjected to coupling effect with salt and frost
  14. Novel approach to improve shale stability using super-amphiphobic nanoscale materials in water-based drilling fluids and its field application
  15. Research on the low-frequency multiline spectrum vibration control of offshore platforms
  16. Multiple wide band gaps in a convex-like holey phononic crystal strip
  17. Response analysis and optimization of the air spring with epistemic uncertainties
  18. Molecular dynamics of C–S–H production in graphene oxide environment
  19. Residual stress relief mechanisms of 2219 Al–Cu alloy by thermal stress relief method
  20. Characteristics and microstructures of the GFRP waste powder/GGBS-based geopolymer paste and concrete
  21. Development and performance evaluation of a novel environmentally friendly adsorbent for waste water-based drilling fluids
  22. Determination of shear stresses in the measurement area of a modified wood sample
  23. Influence of ettringite on the crack self-repairing of cement-based materials in a hydraulic environment
  24. Multiple load recognition and fatigue assessment on longitudinal stop of railway freight car
  25. Synthesis and characterization of nano-SiO2@octadecylbisimidazoline quaternary ammonium salt used as acidizing corrosion inhibitor
  26. Perforated steel for realizing extraordinary ductility under compression: Testing and finite element modeling
  27. The influence of oiled fiber, freeze-thawing cycle, and sulfate attack on strain hardening cement-based composites
  28. Perforated steel block of realizing large ductility under compression: Parametric study and stress–strain modeling
  29. Study on dynamic viscoelastic constitutive model of nonwater reacted polyurethane grouting materials based on DMA
  30. Mechanical behavior and mechanism investigation on the optimized and novel bio-inspired nonpneumatic composite tires
  31. Effect of cooling rate on the microstructure and thermal expansion properties of Al–Mn–Fe alloy
  32. Research on process optimization and rapid prediction method of thermal vibration stress relief for 2219 aluminum alloy rings
  33. Failure prevention of seafloor composite pipelines using enhanced strain-based design
  34. Deterioration of concrete under the coupling action of freeze–thaw cycles and salt solution erosion
  35. Creep rupture behavior of 2.25Cr1Mo0.25V steel and weld for hydrogenation reactors under different stress levels
  36. Statistical damage constitutive model for the two-component foaming polymer grouting material
  37. Nano-structural and nano-constraint behavior of mortar containing silica aggregates
  38. Influence of recycled clay brick aggregate on the mechanical properties of concrete
  39. Effect of LDH on the dissolution and adsorption behaviors of sulfate in Portland cement early hydration process
  40. Comparison of properties of colorless and transparent polyimide films using various diamine monomers
  41. Study in the parameter influence on underwater acoustic radiation characteristics of cylindrical shells
  42. Experimental study on basic mechanical properties of recycled steel fiber reinforced concrete
  43. Dynamic characteristic analysis of acoustic black hole in typical raft structure
  44. A semi-analytical method for dynamic analysis of a rectangular plate with general boundary conditions based on FSDT
  45. Research on modification of mechanical properties of recycled aggregate concrete by replacing sand with graphite tailings
  46. Dynamic response of Voronoi structures with gradient perpendicular to the impact direction
  47. Deposition mechanisms and characteristics of nano-modified multimodal Cr3C2–NiCr coatings sprayed by HVOF
  48. Effect of excitation type on vibration characteristics of typical ship grillage structure
  49. Study on the nanoscale mechanical properties of graphene oxide–enhanced shear resisting cement
  50. Experimental investigation on static compressive toughness of steel fiber rubber concrete
  51. Study on the stress field concentration at the tip of elliptical cracks
  52. Corrosion resistance of 6061-T6 aluminium alloy and its feasibility of near-surface reinforcements in concrete structure
  53. Effect of the synthesis method on the MnCo2O4 towards the photocatalytic production of H2
  54. Experimental study of the shear strength criterion of rock structural plane based on three-dimensional surface description
  55. Evaluation of wear and corrosion properties of FSWed aluminum alloy plates of AA2020-T4 with heat treatment under different aging periods
  56. Thermal–mechanical coupling deformation difference analysis for the flexspline of a harmonic drive
  57. Frost resistance of fiber-reinforced self-compacting recycled concrete
  58. High-temperature treated TiO2 modified with 3-aminopropyltriethoxysilane as photoactive nanomaterials
  59. Effect of nano Al2O3 particles on the mechanical and wear properties of Al/Al2O3 composites manufactured via ARB
  60. Co3O4 nanoparticles embedded in electrospun carbon nanofibers as free-standing nanocomposite electrodes as highly sensitive enzyme-free glucose biosensors
  61. Effect of freeze–thaw cycles on deformation properties of deep foundation pit supported by pile-anchor in Harbin
  62. Temperature-porosity-dependent elastic modulus model for metallic materials
  63. Effect of diffusion on interfacial properties of polyurethane-modified asphalt–aggregate using molecular dynamic simulation
  64. Experimental study on comprehensive improvement of shear strength and erosion resistance of yellow mud in Qiang Village
  65. A novel method for low-cost and rapid preparation of nanoporous phenolic aerogels and its performance regulation mechanism
  66. In situ bow reduction during sublimation growth of cubic silicon carbide
  67. Adhesion behaviour of 3D printed polyamide–carbon fibre composite filament
  68. An experimental investigation and machine learning-based prediction for seismic performance of steel tubular column filled with recycled aggregate concrete
  69. Effects of rare earth metals on microstructure, mechanical properties, and pitting corrosion of 27% Cr hyper duplex stainless steel
  70. Application research of acoustic black hole in floating raft vibration isolation system
  71. Multi-objective parametric optimization on the EDM machining of hybrid SiCp/Grp/aluminum nanocomposites using Non-dominating Sorting Genetic Algorithm (NSGA-II): Fabrication and microstructural characterizations
  72. Estimating of cutting force and surface roughness in turning of GFRP composites with different orientation angles using artificial neural network
  73. Displacement recovery and energy dissipation of crimped NiTi SMA fibers during cyclic pullout tests
Sign up now to receive a 20% welcome discount
Institutional Access
How does access work?
Have an idea on how to improve our website?
Please write us.
© 2025 De Gruyter Brill
Downloaded on 10.9.2025 from https://www.degruyterbrill.com/document/doi/10.1515/rams-2022-0235/html
Scroll to top button