Home Study in the parameter influence on underwater acoustic radiation characteristics of cylindrical shells
Article Open Access

Study in the parameter influence on underwater acoustic radiation characteristics of cylindrical shells

  • Yuhang Tang , Fuxin Jia , Di Jia EMAIL logo , Xueren Wang EMAIL logo and Yong liu
Published/Copyright: July 13, 2022
Download Article (PDF)
Become an author with De Gruyter Brill
Submit Manuscript Author Information
REVIEWS ON ADVANCED MATERIALS SCIENCE
From the journal REVIEWS ON ADVANCED MATERIALS SCIENCE Volume 61 Issue 1

Abstract

At present, the cylindrical shell was regarded as the dominating structure in underwater vehicles, which raised the crucial significance to research underwater vehicles’ vibration and acoustic radiation features. In this study, the analytical expression of vibration–acoustic theory had been given according to the derivation with the vibration–acoustic theory of ribless cylindrical shell structure. Meanwhile, the effects of key parameters on vibration–acoustic characteristics are investigated including modulus, density, thickness, loss factor, etc. The research shows that the stiffness and damping of the shell directly affected the vibration of the structure. Furthermore, the performance of vibration attenuation and noise reduction of the shell had been enhanced by increasing the modulus, thickness, and loss factor in materials.

Keywords: cylindrical shell; vibration; acoustic radiation; influence parameters

1 Introduction

Research shows that when the underwater navigator sails, the mechanical equipment, propeller, water flow impact, and other external loads will cause a vibration response [1,2,3], which greatly affects the concealment of the underwater navigator. The cylindrical shell structure, which is the main form of the underwater navigation body, is crucial to study its underwater vibration and acoustic radiation properties [4].

In the earlier study, Junger [5] found that the presence of attached water reduces the natural frequency of the shell and significantly affects the structural low-frequency vibration, by analyzing the influence of fluid load on the vibration properties of the cylindrical shell. In the literature [6], Junger derives the systematic Lagrange equation and studies the acoustic radiation induced by shell vibration in an external acoustic medium, pointing out that the fluid loading on the shell reaction force is equivalent to the additional mass and damping forces. Bleich and Baron [7] introduced the modal superposition method into the investigation of underwater shell vibration to emphasize the necessity of solving the equation of shell and acoustic field simultaneously under the given object surface and far-field conditions, which promoted the research in coupled vibration problem. Williams et al. [8] expanded the velocity potential and boundary conditions into an infinite series of their respective characteristic functions with the semi-analytic method employed and converted those infinite series into terms of finite series with deducible coefficients based on the principle of minimum mean error. Then, the acoustic radiation in cylindrical shells with infinite and finite in length had been compared and analyzed by a semi-analytical method. Junger and Feit [9] analyzed the acoustic vibration problem of the beam, plate, spherical shell, and cylindrical shell and summarized the work and results of shell stimulated vibration and acoustic radiation.

Overall, early studies have established theoretical computational methods, and subsequent scholars carried out further studies on the problems of limited application scope and low computational accuracy. Ji et al. [10] and Zou et al. [11] presented an element group method and a mixed analytical-numerical substructure method separately to improve the computational efficiency of the hull-substructure coupled and fluid-structure interacted vibration and acoustic radiation of a submerged cylindrical shell-type vehicle. Ning [12] Researched the influence of ring rib arrangement on vibration and acoustic radiation of cylindrical shells and shows that the ring rib structure can suppress the transmission of medium and high-frequency vibration. Sun et al. [13] and Tong et al. [14,15] proved that the calculation precision for natural frequency and radiation efficiency of thick shells is inferior to thin shells by studying the modal of cylindrical shells and investigating the effects of layer angle on natural frequencies. Guo et al. [16] studied the effects of tensile and compressive stresses, stress direction, value size, and distribution on vibration and sound radiation of cylindrical shells for the problem of Vibration and sound radiation of submerged finite cylindrical shells with pre-stress.

In 2019, Wang et al. [17,18,19,20] carried out a vibro-acoustic behavior study of cylindrical shells in ice-covered water and analyzed the vibro-acoustic behavior of submerged double-walled cylindrical shells with general boundary conditions and the free vibration of stiffened cylindrical shells with variable thickness by a precise transfer matrix method (PTMM). Multiple experiments have shown that the PTMM is reliable and the result from PTMM is credible. Chai and Wang [21], Wang et al. [22], and Ye and Wang [23] established cylindrical shell and plate models for nonlinear vibration analysis by Donnel theory and discussed the influence of material, porosity distribution, and size on vibration characteristics. Li et al. [24,25,26] proposed a semi-analytical method to analyze the vibration response of cylindrical shells with arbitrary boundary restraints. Zhang et al. [27] adopted FEM/BEM algorithm and, via the virtual source chain model to calculate the modal source strengths and modal coordinate responses of cylindrical shell, analyzed the influence of the seabed parameters on the acoustic radiation of the cylindrical shell. Guo et al. [28] proposed a new method that has a wide application scope and good accuracy in the solution of the vibro-acoustic behaviors of an elastic cylindrical shell partially coupled with fluids theoretically. Tang et al. [29] proposed a new method to simplify the calculation process of radiated sound power by simplifying the cylindrical shell to a beam and adding mass to approximate fluid-structure coupling. Zhang et al. [30] proposed a sound radiation calculation method by using dominant modes to predict the sound radiation from a cylindrical shell that can reduce the number of displacement monitoring points as possible on the structure surface. Du et al. [31] and Du et al. [32] propose efficient calculation methods for analyzing the vibration characteristics of the Spherical Cap and stiffened plate.

To effectively control the acoustic radiation of the cylindrical shell structure, scholars have launched research in materials [33,34] and structure [35,36,37]. The acoustic characteristics of cylindrical shells with additional materials and noise reduction measures are the focus of attention. Ding et al. [38] and Dai et al. [39] studied the radiation characteristic and active control of the cylindrical shell and provided theoretical support for the effective control of the acoustic vibration response of the submerged structure. Zou et al. [40] and Liu et al. [41] established an analytical formulation theoretically for the shell-coating-fluid system to calculate underwater acoustic radiation for the cylindrical shell structure covering the acoustic cover layer.

Based on the previous studies mentioned above, the vibration–acoustic theory of single-layer cylindrical shells had been deduced. Considering the case of underwater single-layer cylindrical shells, the influence of parameters, such as modulus, density, thickness, and loss on the vibration and acoustic performance with finite-length cylindrical shells, had been calculated, while the acoustic radiation characteristics of underwater cylindrical shells had been analyzed in this work. Results provided the guidelines for the acoustic stealth design for underwater vehicles.

2 Vibration–acoustic theory of cylindrical shells with isotropic materials

With the purpose to reveal the vibration mechanism of a finite-length cylindrical shell shown in Figure 1, the governing equations in cylindrical coordinates based on elasticity theory had been first established, which are presented as follows.

(1) L 11 L 12 L 13 L 21 L 22 L 23 L 31 L 32 L 33 u v w = β 2 u ̈ β 2 v ̈ β 2 w ̈ ,

where β 2 = 2 ρ / E ( 1 + μ ) ( 1 − 2 μ ) , in which ρ, E, and μ are the density, Young’s modulus, and Poisson’s ratio of the elastomer, respectively. L mn represent the partial differential operators.

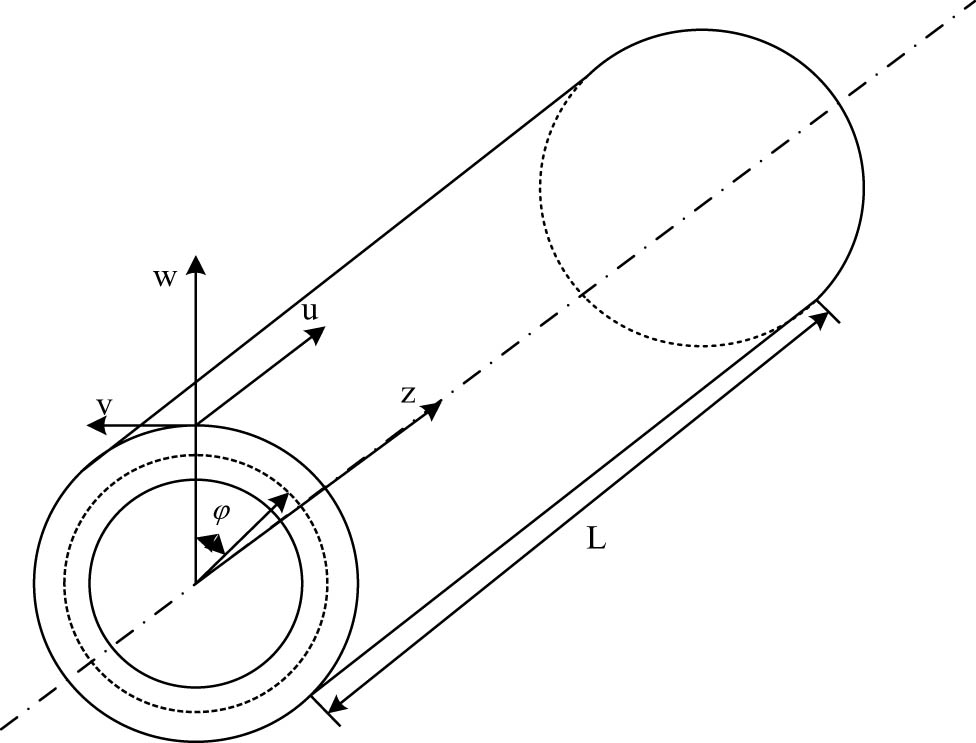
Figure 1 Schematic diagram of the cylindrical shell.
Figure 1

Schematic diagram of the cylindrical shell.

According to Donnell’s theory [42,43], the kinetics equation of a free-vibration cylindrical thin shell was written as

(2) ∂ 2 u ∂ z 2 + 1 − μ 2 a 2 ∂ 2 u ∂ ϕ 2 + 1 + μ 2 a ∂ 2 v ∂ z ∂ ϕ + μ a ∂ w ∂ z − ρ 1 − μ 2 E ∂ 2 u ∂ t 2 = 0 1 + μ 2 a ∂ 2 u ∂ z ∂ ϕ + 1 − μ 2 ∂ 2 v ∂ z 2 + 1 a 2 ∂ 2 v ∂ ϕ 2 + 1 a 2 ∂ w ∂ ϕ − ρ 1 − μ 2 E ∂ 2 v ∂ t 2 = 0 μ a ∂ u ∂ z + 1 a 2 ∂ v ∂ ϕ + w a 2 + β 2 a 2 ∂ 4 w ∂ z 4 + 2 ∂ 4 w ∂ z 2 ∂ ϕ 2 + 1 a 2 ∂ 4 w ∂ ϕ 4 − ρ 1 − μ 2 E ∂ 2 w ∂ t 2 = 1 − μ 2 E h ( f ( a , ϕ , z ) − p ( a , ϕ , z ) ) ,

which can be rewritten into the matrix as

(3) E h 1 − μ 2 [ L D ] u v w + ρ h ω 2 u v w = 0 0 f ( a , ϕ , z ) − p ( a , ϕ , z ) ,

where a denote the radius of the cylinder, h denote the shell thickness, β 2 = h 2 / 12 a 2 , and [L D ] denote the Donnell operator.

The harmonic field in a cylindrical shell resulting from a small perturbation within the ideal fluid medium can be described by the Helmholtz equation with Neumann boundary conditions and Somerfield radiation conditions [44,45,46]. The continuity condition of normal velocity on the coupling surface was

(4) ∂ p ( r , φ , z ) ∂ r r = a = ρ 0 ω 2 w ( a , φ , z ) , 0 ≤ z ≤ L , 0 , z < 0 and z > L ,

where L denote the length of the cylindrical shell, ρ 0 denote media density, k = ω/c 0, and ω and c 0 are a number of acoustic waves, angular frequency of acoustic waves, and the speed of sound in a certain medium.

The wave propagation within a cylindrical shell with finite length was reflected by the end faces, and the vibration of the shell was presented as the form of the stationary wave, which relied on the boundary conditions of the shell. As to simplify the theoretical analysis, the transverse bulkhead support of submarine pressure shell had been generally regarded as simply supported at both ends. Hence, the boundary conditions of simply supported at both ends of the cylindrical shell had to be satisfied [47,48,49].

(5) v = w = N z = M z , z = 0 and z = L ,

in which N z is the force and M z is the moment.

Whereafter, the kinetics equation of the shell was solved through the modal expansion method. In the investigation of the acoustic and vibration under the symmetric excitation, the displacement solution in the following form had been applied[32,50].

(6) u ( φ , z ) = ∑ m = 1 + ∞ ∑ n = 0 + ∞ U m n cos ( n φ ) cos ( k m z ) , v ( φ , z ) = ∑ m = 1 + ∞ ∑ n = 0 + ∞ V m n sin ( n φ ) sin ( k m z ) , w ( φ , z ) = ∑ m = 1 + ∞ ∑ n = 0 + ∞ W m n cos ( n φ ) sin ( k m z ) .

Thereafter, the radial excitation force and surface sound pressure were expanded into the series of the (m, n) order modal namely { cos ( n φ ) sin ( k m z ) } of radial displacement; thus,

(7) f ( a , φ , z ) p ( a , φ , z ) = ∑ m ∑ n f m n p m n cos ( n φ ) sin ( k m z ) ,

the expansion coefficient was determined by the following equation:

(8) f m n p m n = ε n π L ∫ − π π ∫ 0 L f ( a , φ , z ) p ( a , φ , z ) cos ( n φ ) sin ( k m z ) d φ d z ,

where ε n was the Neumann factor. ε n = 1 while n = 0 and ε n = 2 when n ≥1. The modal equation was obtained by substitution of equations (6) and (7) into the kinetics equation of the cylindrical thin shell,

(9) a 11 a 12 a 13 a 21 a 22 a 23 a 31 a 32 a 33 U m n V m n W m n = a 2 ρ p c p 2 h 0 0 f m n − p m n .

In which each element a ij in the eigenmatrix depended on the governing equation forms corresponding to different thin shell theories. Considering that the frequency band was lower than the critical frequency of the shell, the kinetics equation based on Donnell’s shell theory mentioned in the above section had been selected; thus,

(10) a 11 = − Ω 2 + k m 2 a 2 + 1 2 ( 1 − μ ) n 2 , a 22 = − Ω 2 + 1 2 ( 1 − μ ) k m 2 a + n 2 , a 12 = a 21 = 1 2 ( 1 + μ ) n k m a , a 23 = a 32 = n , a 13 = a 31 = μ k m a , a 33 = 1 − Ω 2 + β 2 ( k m 2 a + n 2 ) 2 ,

where c p = E / ρ p ( 1 − μ 2 ) , which represented the longitudinal wave velocity while the shell was extended into a flat plate. Ω = ω a / c p , which represented the longitudinal wave velocity while the shell was extended into a flat plate. Ω = ω a / c p , n, and k m a were marked as dimensionless quantities.

As revealed from equation (3), the normal mode velocity satisfied the following equation:

(11) W ̇ m n Z m n M = f m n − p m n .

Assuming p mn = 0, the mechanical impedance in the (m,n) order normal mode of the cylindrical shell surface with finite length had to be obtained as

(12) Z m n M = i ρ p h ω ∣ a i j ∣ / Ω 2 a 11 a 12 a 21 a 22 .

Moreover, according to the Green’s function G, a fundamental solution of the wave equation, sound pressure at the arbitrary point of A ( r , ϕ , z ) in the acoustics field was expressed as

(13) p ( A ) = ∬ s G ( A ∣ A 0 ) w ̇ ( A 0 ) d s ,

where A 0 ( a , φ 0 , z 0 ) represented the arbitrary point on the surface of the shell while w ̇ ( A 0 ) was the radial velocity of shell surface. Hence, Green’s function satisfied with

(14) G ( A ∣ A 0 ) = ρ 0 ω 4 π 2 ⋅ ∑ n = 0 ∞ ε n cos ( n ( φ − φ 0 ) ) × ∫ − ∞ ∞ i H n ( 1 ) ( k 2 − k z 2 r ) k r a H n ( 1 ) ' ( k 2 − k z 2 a ) e i k z ∣ z − z 0 ∣ d k z ,

where k 2 = k r 2 + k z 2 , k r and k z denote the radial and axial components of a wave vector.

By substituting the radial modal velocity into the above equation, the sound pressure at the arbitrary point within acoustic field was able to be deduced as

(15) p ( r , φ , z ) = − i ρ 0 ω 2 4 π 2 ∑ n = 0 ∞ ∑ m = 1 ∞ W m n cos n φ ⋅ × ∫ − ∞ ∞ i H n ( 1 ) ( k 2 − k z 2 r ) k 2 − k z 2 H n ( 1 ) ' ( k 2 − k z 2 a ) × k m [ 1 − ( − 1 ) m e − i k z L ] k m 2 − k z 2 e i k z z d k z ,

Which expressed in the following form:

(16) p m n = ∑ q Z n m q W ̇ q n .

As β = k z / k , α = k a 1 − β 2 , Z n ( α ) = i H n ( 1 ) ( α ) / H n ( 1 ) ′ ( α ) , and the dimensionless radiation impedance Z nmq was written as

(17) z n m q = Z n m q ρ 0 c 0 S = R n m q − i χ n m q = 8 m q π ε n ( k L ) 3 ∫ 0 ∞ Z n ( α ) N m q ( β ) d β ( 1 − β 2 ) 1 / 2 [ β 2 − ( k m / k ) 2 ] [ β 2 − ( k q / k ) 2 ] ,

where

(18) N m q ( β ) = cos 2 ( k L β / 2 ) , m , q = 1 , 3 , 5 … ∓ i sin ( k L β / 2 ) cos ( k L β / 2 ) , m ( q ) = 1 , 3 , 5 … ; q ( m ) = 2 , 4 , 6 … sin 2 ( k L β / 2 ) , m , q = 2 , 4 , 6 … .

The acoustic radiation impedance reflected the interaction between the medium and the sound source, which was considered the fundamental of structural-acoustic radiation analysis. As introduced in the equation above, non-zero axial half-wave numbers (m and q) are exhibited only when both of them are odd or even numbers.

Therefore, in combination with equations (11) and (17), the coupling kinetics equation of excitation source-cylindrical shell-external flow field was yielded,

(19) Z n m M W ̇ m n + Z n m m W ̇ m n = f m n − ∑ q = 1 , q ≠ m ∞ Z n m q W ̇ q n ,

Once the modal vibration velocity was obtained, the sound pressure, intensity, radiated power, radiation efficiency, and other associated acoustic quantities were able to be deduced as consequence.

Wherein, the acoustic radiation power of the shell surface was

(20) W ( ω ) = 1 2 Re ∬ s p ( a , φ , z ) w ̇ ( φ , z ) d s = S 4 Re ∑ q ∑ m ∑ n 1 ε n W ̇ q n Z n m q W ̇ q n ⁎ .

The radial mean square velocity on the shell surface was

(21) 〈 v r 2 〉 = 1 2 S ∬ s w ̇ ( φ , z ) w ̇ ( φ , z ) ⁎ d s = 1 4 ∑ m ∑ n 1 ε n W ̇ m n W ̇ m n ⁎ .

And the radiation efficiency was

(22) σ ( ω ) = W ( ω ) ρ 0 c 0 S < v r 2 > = Re ∑ q ∑ m ∑ n 1 ε n W ̇ q n Z n m q W ̇ q n ⁎ ρ 0 c 0 ∑ m ∑ n 1 ε n W ̇ m n W ̇ m n ⁎ .

3 Theoretical model of calculation conditions

In this paper, a cylindrical shell with a radius of 0.5 m and a length of 1.2 m is taken as an example to study the parameter influence on underwater acoustic radiation characteristics of cylindrical shells. The density ρ, modulus E, thickness h, loss factor η and Poisson’s ratio v were valued of the cylindrical shell as the controlling variables，specific inputs are shown in Tables 1–5.

Table 1

Total level of vibration and radiation power of shell under different density materials

Groups Density (kg·m−3) Cylindrical shell
Overall mean square vibration velocity level (dB) Overall acoustic radiation power level (dB)
1-1 0.1 121.74 101.23
1-2 0.05 125.31 101.41
1-3 0.01 130.86 103.86
1-4 0.001 137.60 103.96
Table 2

The overall vibration level and the overall sound power level of the shell with different elastic moduli of materials

Groups Elastic modulus (GPa) Cylindrical shell
Overall mean square vibration velocity level (dB) Overall acoustic radiation power level (dB)
2-1 200 121.15 99.68
2-2 100 124.05 99.04
2-3 50 130.86 102.09
2-4 25 138.22 106.63
Table 3

The overall vibration level and the overall sound power level of the shell with different shell thicknesses of materials

Groups Shell thickness (mm) Cylindrical shell
Overall mean square vibration velocity level (dB) Overall acoustic radiation power level (dB)
3-1 20 126.25 88.73
3-2 15 129.17 91.16
3-3 10 132.84 88.29
3-4 5 140.75 88.61
Table 4

The overall vibration level and the overall sound power level of the shell with different material losses

Groups Material loss factor Cylindrical shell
Overall mean square vibration velocity level (dB) Overall acoustic radiation power level (dB)
4-1 0.1 121.74 101.23
4-2 0.05 125.31 101.41
4-3 0.01 130.86 103.86
4-4 0.001 137.60 103.96
Table 5

The overall vibration level and the overall sound power level of the shell with different Poisson’s ratios of materials

Groups Poisson’s ratio Cylindrical shell
Overall mean square vibration velocity level (dB) Overall acoustic radiation power (dB)
5–1 0.4 128.51 101.37
5–2 0.3 128.80 101.30
5–3 0.2 130.86 102.09
5–4 0.1 130.59 102.75

According to the above theory, the vibration–acoustic calculation theory of the cylindrical shell had been programmed, and the vibration and acoustic radiation response curves of the ideal homogeneous shell plate under the influence of different parameters were calculated by Matlab to understand the influence introduced by parameters setting. For cylindrical shells, the radial exciting force acted at (L/2, 0) of the shell with the amplitude of 1 N. Fluid density ρ f = 1.025 × 103 kg·m−3, sound velocity cf = 1,500 m·s−1, reference velocity ν ref = 10−9 m·s−1, and reference sound power W ref = 10−12 W were set. Respected to the value presented in Tables 1–5, step size was 2 Hz per step, a total of 750 steps.

4 Analysis of underwater acoustic radiation parameters of cylindrical shell

4.1 Influence of material density on vibro-acoustic characteristics of cylindrical shell

The vibration and acoustic performance of the theoretical model of the cylindrical shell had been calculated according to the structural model described in Section 1. The differences in vibration and acoustic performance of structures under different densities had been compared. Results are revealed in Figure 2. In addition, overall vibration levels and the overall acoustic power levels within the 0–1,500 Hz frequency band are shown in Table 1.

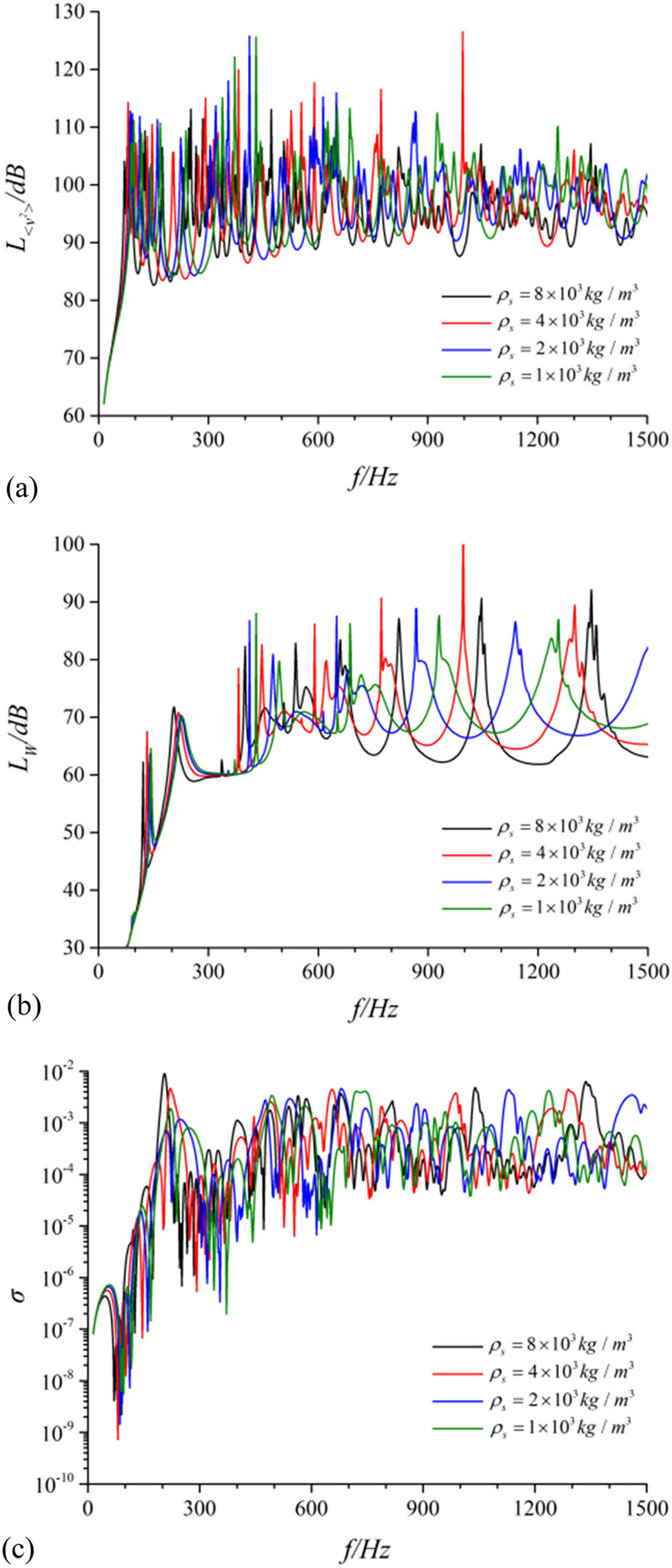
Figure 2 Contrast of vibration and noise performance for the cylindrical shell under different densities. (a) Radial quadratic velocity level, (b) sound radiation power level, and (c) sound radiation efficiency.
Figure 2

Contrast of vibration and noise performance for the cylindrical shell under different densities. (a) Radial quadratic velocity level, (b) sound radiation power level, and (c) sound radiation efficiency.

Figure 2 and Table 1 reveal that with the increase in material density, the mean square velocity of structure and the acoustics radiation power in the vibro-acoustic performance of the simply supported cylindrical shell deceased. However, within the designed variation range of density in the calculation conditions, theoretical calculation models exhibited their characteristics. With the decreasing of density, the peak of vibration of the structure shifted toward a higher frequency with a lower modal density in the same frequency band.

For the cylindrical shell, two independent domains existed in and outside of the shell, which lead to a certain analogousness to the case with the baffle in radiation performance. The mean vibration velocity level and acoustics radiation power level were barely affected by the density. In comparison under the same radiation mode, the peak value of acoustic vibration response increased slightly with the decrease in density. Nevertheless, limited to the extremely dense radiation modes and the calculation accuracy, position, and amplitude of peaks were failed to detective in some frequency bands, which occurred with errors in certain levels. However, in general, the acoustics power level of the underwater cylindrical shell was hardly disturbed by the density. The variation in density mainly affected the modal distribution, and the magnitude of the radiation energy was similar. Whereas, the surface velocity increased with the decrease in the density, which was significantly related. Compared with the 1–4 working condition, the overall mean square vibration velocity and the overall acoustic radiation power in the frequency band of 0–1,500 Hz decreased by 4.57 and −0.6 dB, respectively, under the 1–1 working condition.

4.2 Influence of elasticity modulus in materials on vibro-acoustic characteristics of cylindrical shell

The vibration and acoustic performance of the theoretical model of the cylindrical shell had been calculated according to the structural model described in Section 1. The differences in performance of the structure with the influence of different elasticity modulus in materials had been compared. Results are revealed in Figure 3. In addition, the overall vibration levels and the overall acoustics power levels within the 0–1,500 Hz frequency band are shown in Table 2.

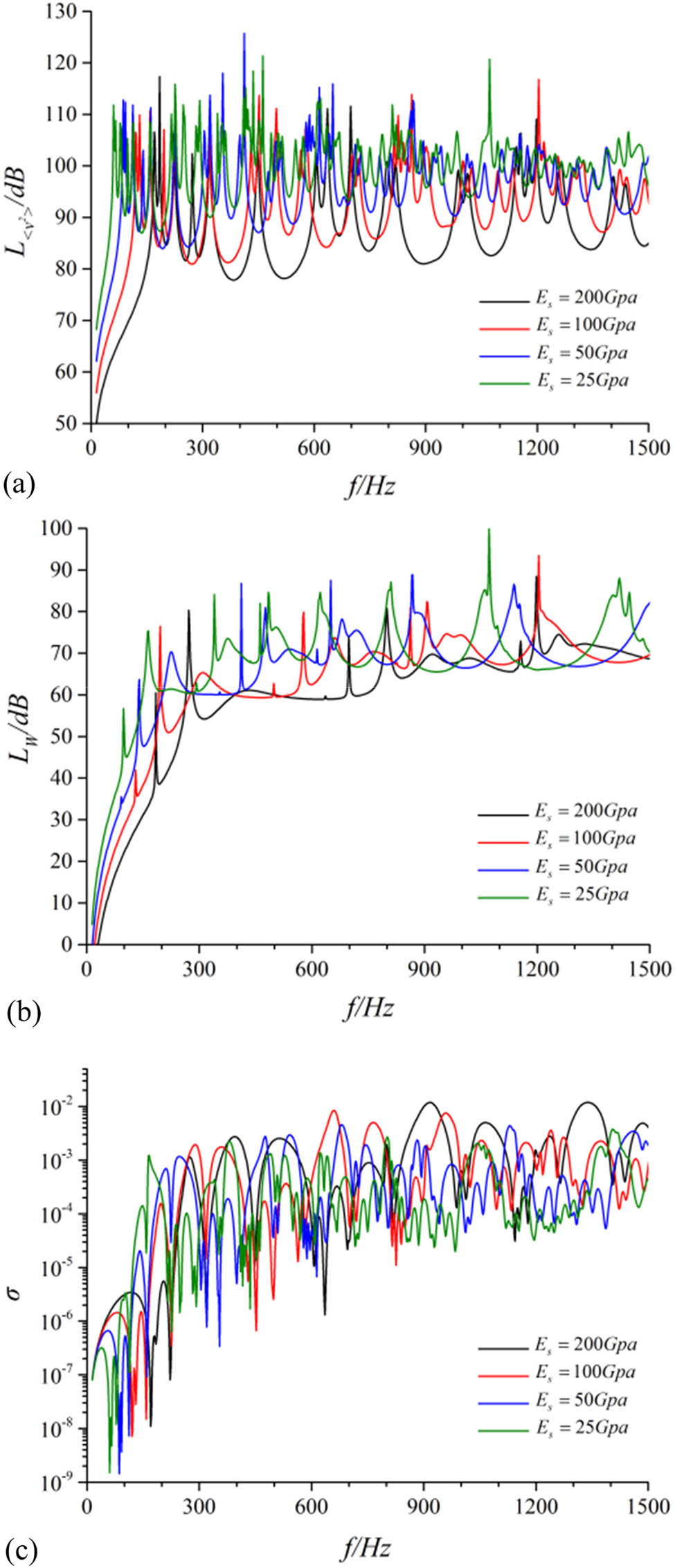
Figure 3 Contrast of vibration and noise performance for the cylindrical shell under different elasticity moduli. (a) Radial quadratic velocity level, (b) sound radiation power level, and (c) sound radiation efficiency.
Figure 3

Contrast of vibration and noise performance for the cylindrical shell under different elasticity moduli. (a) Radial quadratic velocity level, (b) sound radiation power level, and (c) sound radiation efficiency.

Variation in the elasticity modulus of materials would significantly influence the vibration and acoustic performance of cylindrical shell structures. Concretely, with the consideration of simply supported cylindrical shells, the vibration level and the acoustic radiation level of the cylindrical shells remarkably increased with the decrease in the elastic modulus. On the contrary, as the increment of elastic modulus, the acoustic radiation efficiency of the theoretical model increased consequently, which offsets the negative effect of reducing the acoustic radiation power resulting from the decrement of vibration level.

For the cylindrical shell, the level of mean vibration velocity and acoustics radiation power were greatly impacted by the elastic modulus of the material in evidence by the comparison of spectral peak size in the same order. The level of mean square velocity and acoustics radiation power increased with the decrease in the modulus. Compared with the 2–4 working condition, the overall mean square vibration velocity and the overall acoustic radiation power in the frequency band of 0–1,500 Hz decreased by 8.19 and 8.31 dB, respectively, under the 2–1 working condition, which is revealed in Table 2. Therefore, the performance of vibration and acoustic radiation of cylindrical shells was significantly affected by the elastic modulus of materials. And the composite materials with relatively large elastic modulus were a better choice for non-pressure shell design.

4.3 Influence of shell thickness on vibro-acoustic characteristics of cylindrical shell

The vibration and acoustic performance of the theoretical model of the cylindrical shell had been calculated according to the structural model described in Section 1. The differences in performance of the structure with the influence of different thicknesses in materials had been compared. Results are revealed in Figure 4. In addition, the overall vibration levels and the overall acoustics power levels within the 0–1,500 Hz frequency band are shown in Table 3.

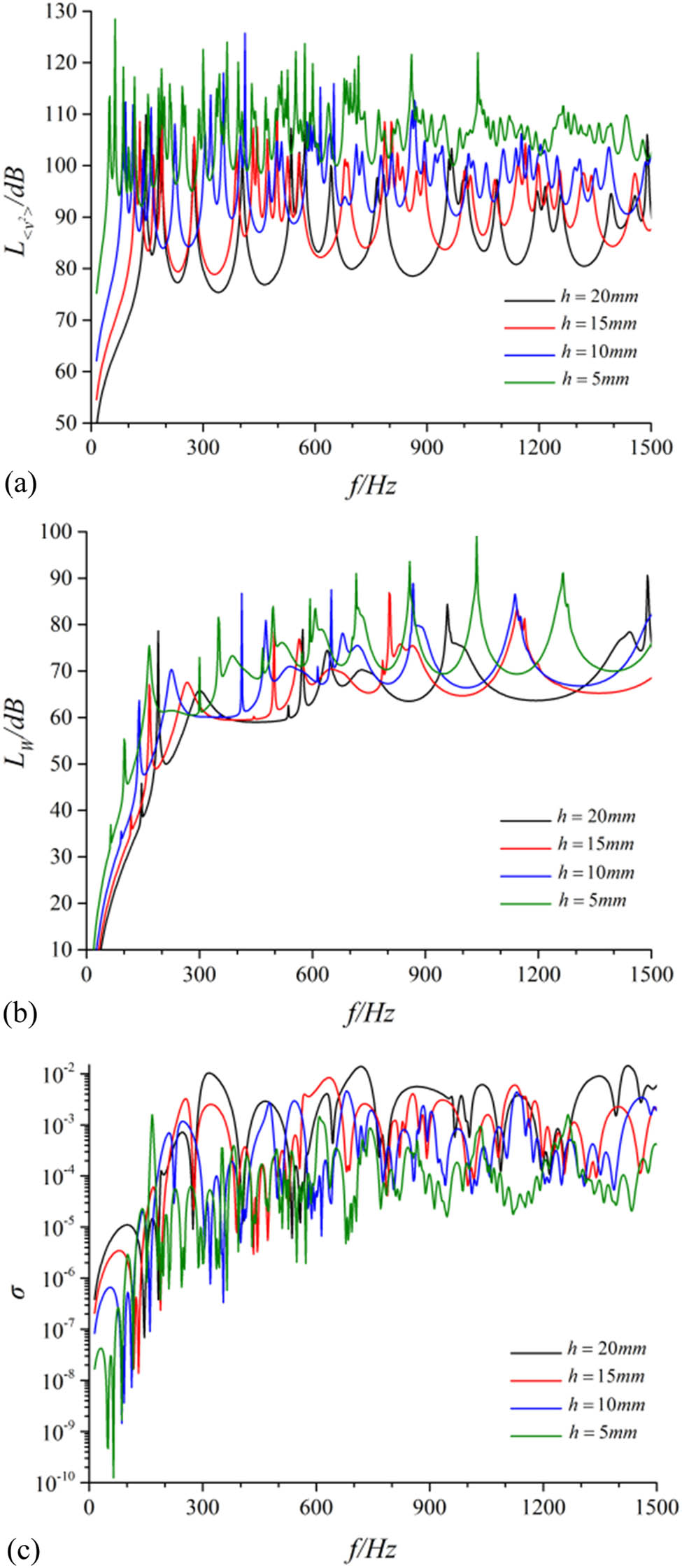
Figure 4 Contrast of vibration and noise performance for the cylindrical shell under different shell thicknesses. (a) Radial quadratic velocity level, (b) sound radiation power level, and (c) sound radiation efficiency.
Figure 4

Contrast of vibration and noise performance for the cylindrical shell under different shell thicknesses. (a) Radial quadratic velocity level, (b) sound radiation power level, and (c) sound radiation efficiency.

Analogous to the elastic modulus of materials, the thickness of shell h was also one of the crucial parameters that affected the structural stiffness, which was proportion to h 3. In addition, in comparison of different thicknesses, the underwater mean vibration velocity level of the cylindrical shell calculation model decreased overtly with the increase in shell thickness; however, the acoustic radiation efficiency increased and the acoustic power level decreased consecutively.

For the cylindrical shell, the mean vibration velocity level and the acoustic radiated power level were significantly affected by the thickness and the mean square vibration velocity level and the acoustic radiated power level of the cylindrical shell decreased dramatically with the increasing of the shell thickness. Compared with the 3–4 working conditions, the overall mean square vibration velocity and the overall acoustic radiation power in the frequency band of 0–1,500 Hz decreased by 17.07 and 6.95 dB, respectively, under the 3–1 working condition. Hence, the vibration and acoustic radiation properties of cylindrical shells were greatly affected by the shell thickness. The employment of composite materials in the shell was capable to maximize the thickness (stiffness) of the shell while satisfying the index of weight.

4.4 Influence of loss factors in materials on vibro-acoustic characteristics of cylindrical shell

The vibration and acoustic performance of the theoretical model of the cylindrical shell had been calculated according to the structural model described in Section 1. Results are illustrated in Figure 5. The differences in the performance of the structure with the influence of different loss factors in materials had been compared. The overall vibration levels and the overall acoustic power levels within the 0–1,500 Hz frequency band are shown in Table 4.

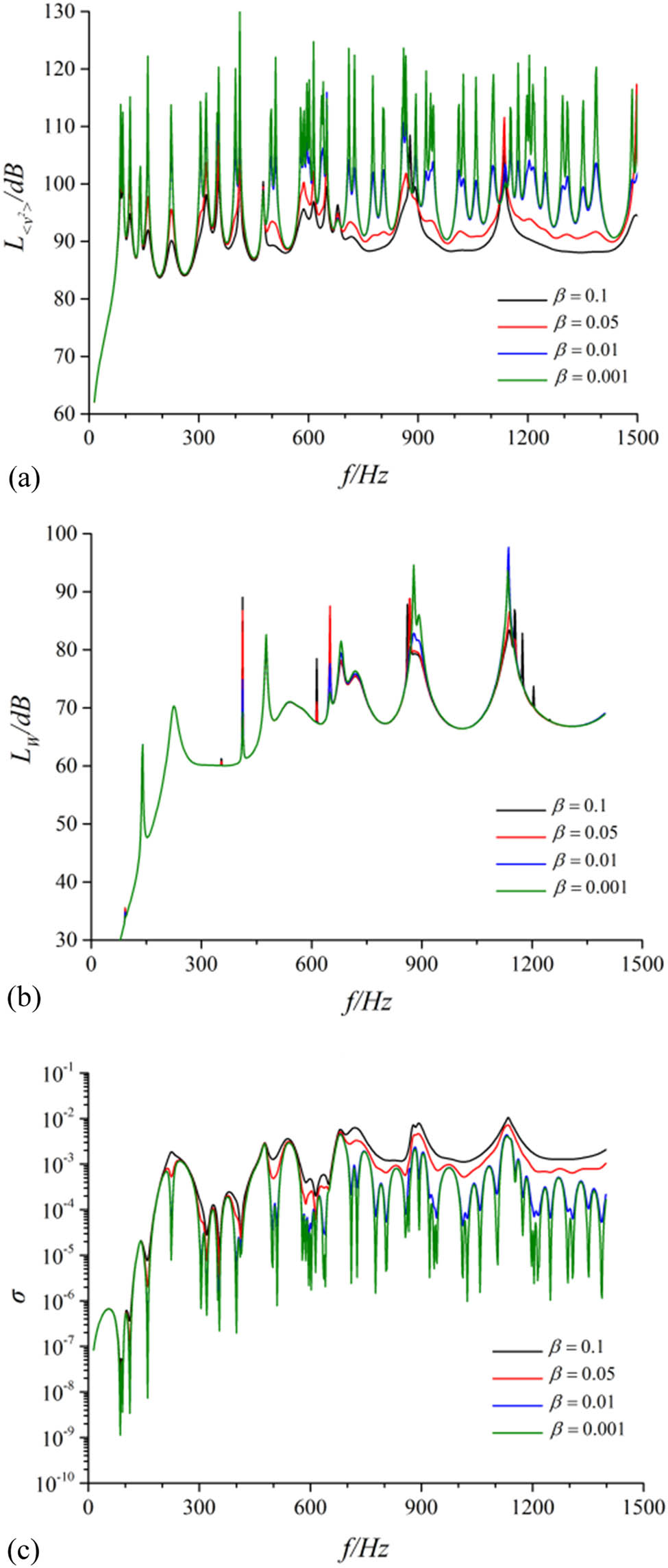
Figure 5 Contrast of vibration and noise performance for the cylindrical shell under different dissipation factors. (a) Radial quadratic velocity level, (b) sound radiation power level, and (c) sound radiation efficiency.
Figure 5

Contrast of vibration and noise performance for the cylindrical shell under different dissipation factors. (a) Radial quadratic velocity level, (b) sound radiation power level, and (c) sound radiation efficiency.

With different losses in materials, the underwater mean vibration velocity level and the acoustic radiation power level of the cylindrical shell calculation model with simply supported boundary decreased obviously with the increasing of loss factor. Despite the acoustic radiation efficiency increasing simultaneously, one was not enough to introduce higher acoustic radiation in the structure with large damping than that of the structure with small damping.

For the cylindrical shell, the increase in the loss leads to a significant increase in the radiation efficiency. The variation in the acoustic radiation within the frequency band was faint except for a conspicuous drop in the peak value. Compared with the 4–4 working condition, the overall mean square vibration velocity and the overall acoustic radiation power in the frequency band of 0–1,500 Hz decreased by 15.86 and 2.73 dB, respectively, under the 4–1 working condition. Therefore, the vibration and acoustic radiation performance of the cylindrical shell were remarkably affected by the loss in materials, which suggested that the damping performance should be improved as possible while maintaining the stiffness and strength of the shell to reduce the radiation spectrum significantly.

4.5 Influence of Poisson’s ratio in materials on vibro-acoustic characteristics of cylindrical shell

The vibration and acoustic performance of the theoretical model of the cylindrical shell had been calculated according to the structural model described in Section 1. Results are illustrated in Figure 6. The differences in performance of the structure with the influence of different Poisson ratios in materials had been compared. The overall vibration levels and the overall acoustic power levels within the 0–1,500 Hz frequency band are shown in Table 5.

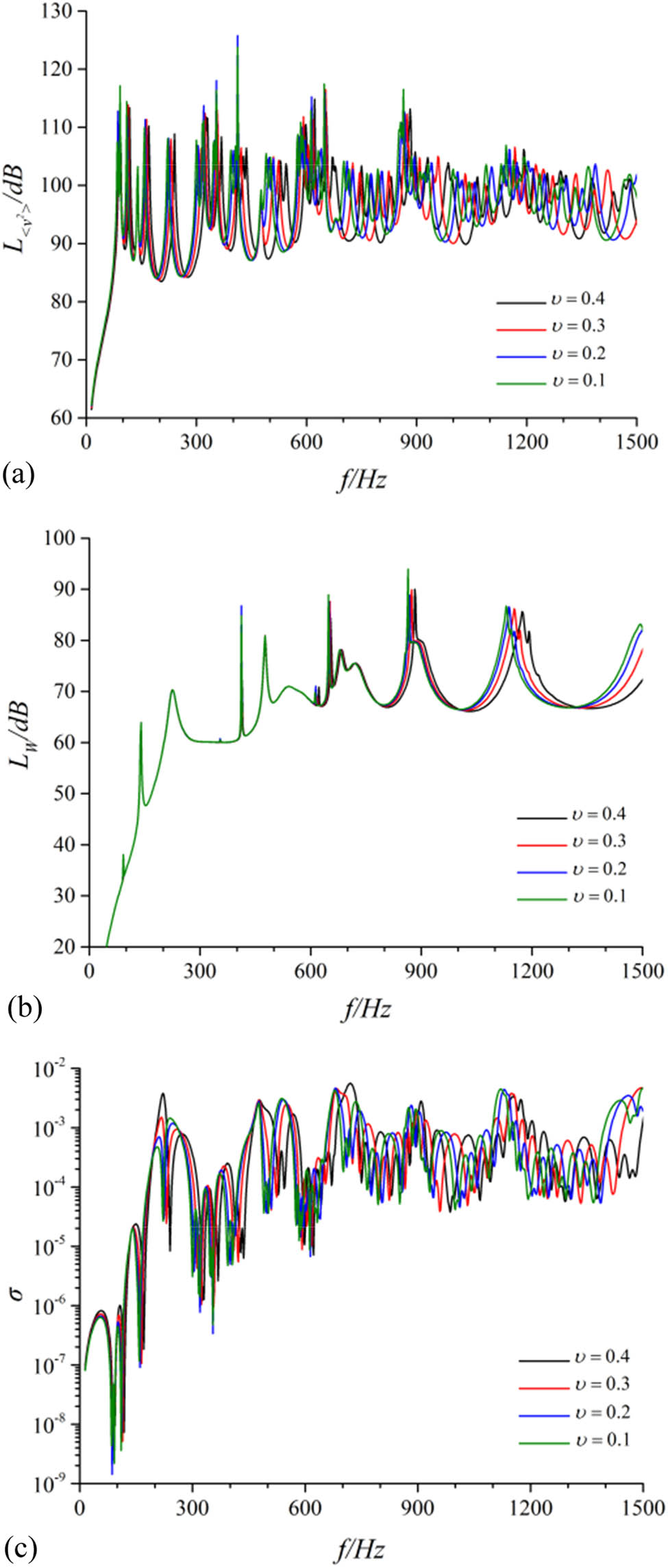
Figure 6 Contrast of vibration and noise performance for the cylindrical shell under different Poisson ratios. (a) Radial quadratic velocity level, (b) sound radiation power level, and (c) sound radiation efficiency.
Figure 6

Contrast of vibration and noise performance for the cylindrical shell under different Poisson ratios. (a) Radial quadratic velocity level, (b) sound radiation power level, and (c) sound radiation efficiency.

With different Poisson’s ratio parameters, the vibration and acoustic performance of the cylindrical shell with simply supported boundary are analogical. The mean square vibration velocity level and the acoustic radiation power level slightly decreased with the increase in Poisson’s ratio in materials. For the cylindrical shell, compared with the 5-4 working conditions, the overall mean square vibration velocity and the overall acoustic radiation power in the frequency band of 0–1,500 Hz decreased by 2.08 and 1.38 dB, respectively, under the 5–1 working condition.

5 Conclusion

Based on the Donnel shell theory and modal expansion method, the article constructs the parameterized by the theoretical model of free vibrating cylindrical thin shells. This theory model has the advantages of fast convergence, easy parametric analysis, no repeated modeling, and high computational efficiency. In this work, the acoustic radiation characteristics of cylindrical shells had been analyzed. With consideration of the underwater simply supported cylindrical shells, the structural vibration and acoustic performance under different structural parameters had been calculated and compared. The influence of the parameters, such as modulus, density, thickness, and loss on the vibration and acoustic performance, had been revealed. The main conclusions were summarized as follows:

  1. With the increase in the cylindrical shell density, the mean square vibration velocity of the structure, and the acoustic radiation power were decreased.

  2. As the elastic modulus of materials decreased, the vibration and the acoustic radiation level of the cylindrical shell increased remarkably. With the higher the modulus, the acoustic radiation efficiency of the model was getting higher.

  3. The underwater mean square vibration velocity level and the sound power level of the cylindrical shell calculation model decreased significantly with the increase in the shell thickness, while the acoustic radiation efficiency increased.

  4. The underwater mean square vibration velocity level and the acoustic radiation power level of the cylindrical shell decreased markedly with the increase in the loss factor in the material. In spite of the increase in acoustic radiation efficiency, one was not enough to introduce a higher acoustic radiation in the structure with large damping than that of the structure with small damping.

  5. The mean square vibration velocity level and the acoustic radiation power level slightly decreased with the increase in Poisson’s ratio in materials.

With the increase in the above parameters, the mean square vibration velocity level and the acoustic radiation power level of the cylindrical shell gradually decrease. Therefore, in structural design and material selection, it is necessary to ensure the maximum value of these parameters, which is expected to achieve the reduction of the surface vibration velocity and acoustic radiation power of the cylindrical shell. The research provided the theoretical guidelines in the acoustic stealth design for underwater vehicles, and the specific engineering application needs further study.

Acknowledgment

This research was supported by Naval Research Institute and Harbin Engineering University.

  1. Funding information: This study was funded by the Key Research and Development Program of Shandong Province (2019JZZY010125, 2020CXGC010701, and 2020CXGC010702).

  2. Author contributions: Yuhang Tang provided theoretical support and research ideas. Fuxin Jia analyzed the data and complete the corresponding chapter. Di Jia modified and improved the manuscript. Xueren Wang provided necessary guidance. Yong liu performed the simulation.

  3. Conflict of interest: Authors state no conflict of interest.

References

[1] Chen, F., Y. Chen, and H. Hua. Coupled vibration characteristics of a submarine propeller-shaft-hull system at low frequency. Journal of Low Frequency Noise, Vibration and Active Control, Vol. 39, No. 2, 2020, pp. 258–279.10.1177/1461348419846722Search in Google Scholar

[2] Huang, J., Y. Tang, H. Li, F. Pang, and Y. Qin. Vibration characteristics analysis of composite floating rafts for marine structure based on modal superposition theory. Reviews on Advanced Materials Science, Vol. 60, No. 1, 2021, pp. 719–730.10.1515/rams-2021-0043Search in Google Scholar

[3] Yeo, S.-J., S. Y. Hong, J. H. Song, H. W. Kwon, and H. S. Seol. Integrated analysis of flow-induced noise from submarine under snorkel condition. Proceedings of the Institution of Mechanical Engineers, Part M: Journal of Engineering for the Maritime Environment, Vol. 234, No. 4, 2020, pp. 771–784.10.1177/1475090220916594Search in Google Scholar

[4] Rex, P. Future submarine stealth secret revealed. Asia-Pacific Defence Reporter (2002), Vol. 40, No. 5, 2014, pp. 52–57.Search in Google Scholar

[5] Junger, M. C. Vibrations of elastic shells in a fluid medium and the associated radiation of sound. Journal of Applied Mechanics, Vol. 19, No. 4, 1952, pp. 439–445.10.1115/1.4010540Search in Google Scholar

[6] Junger, M. C. The physical interpretation of the expression for an outgoing wave in cylindrical coordinates. The Journal of the Acoustical Society of America, Vol. 25, No. 1, 1953, pp. 40–47.10.1121/1.1907005Search in Google Scholar

[7] Bleich, H. H. and M. L. Baron. Free and forced vibrations of an infinitely long cylindrical shell in an infinite acoustic medium. Journal of Applied Mechanics, Vol. 21, No. 1, 1954, pp. 167–177.10.21236/AD0002661Search in Google Scholar

[8] Williams, W., N. G. Parke, D. A. Moran, and C. H. Sherman. Acoustic radiation from a finite cylinder. The Journal of the Acoustical Society of America, Vol. 36, No. 12, 1964, pp. 2316–2322.10.1121/1.1919357Search in Google Scholar

[9] Junger, M. C. and D. Feit. Sound, structures, and their interaction, Vol. 225, MIT Press, Cambridge, MA, 1986.Search in Google Scholar

[10] Ji, G., Q. D. Zhou, and C. W. Huang. Element grouping method for the calculation of dynamic response and acoustic radiation from an underwater structure. Applied Mechanics and Materials, Vol. 105–107, 2011, pp. 189–195.10.4028/www.scientific.net/AMM.105-107.189Search in Google Scholar

[11] Zou, M.-S., Y. S. Wu, J. D. Liu, and S. X. Liu. A mixed analytical-numerical method for the vibro-acoustic analysis of an underwater ring-stiffened cylindrical shell containing substructures. Acoustical Physics, Vol. 64, No. 5, 2018, pp. 596–604.10.1134/S1063771018050111Search in Google Scholar

[12] Ning, R. and Z. Zhang. Research on the influence of ring rib arrangement on vibration and acoustic radiation of cylindrical shell. Vibroengineering Procedia, Vol. 21, 2018, pp. 172–177.10.21595/vp.2018.20394Search in Google Scholar

[13] Sun, Y., T. Yang, and Y. Chen. Sound radiation modes of cylindrical surfaces and their application to vibro-acoustics analysis of cylindrical shells. Journal of Sound and Vibration, Vol. 424, 2018, pp. 64–77.10.1016/j.jsv.2018.03.004Search in Google Scholar

[14] Tong, B., Y. Li, X. Zhu, and Y. Zhang. Three-dimensional vibration analysis of arbitrary angle-ply laminated cylindrical shells using differential quadrature method. Applied Acoustics, Vol. 146, 2019, pp. 390–397.10.1016/j.apacoust.2018.11.031Search in Google Scholar

[15] Tong, B., Y. Zhu, X. Zhang, and B. Yan Three-dimensional elastic exact solution for free vibration of composite cylindrical shells considering ply angle. Journal of Acoustics, Vol. 38, No. 4, 2019, id. 16.Search in Google Scholar

[16] Guo, Y., H. Wang, and H. Yi. Vibration and sound radiation of submerged finite cylindrical shells with pre-stress. Scientific Reports, Vol. 9, No. 1, 2019, pp. 1–11.10.1038/s41598-019-47809-xSearch in Google Scholar PubMed PubMed Central

[17] Wang, X., E. Xu, C. Jiang, and W. Wu. Vibro-acoustic behavior of double-walled cylindrical shells with general boundary conditions. Ocean Engineering, Vol. 192, 2019, id. 106529.10.1016/j.oceaneng.2019.106529Search in Google Scholar

[18] Wang, X., H. Lin, Y. Zhu, and W. Wu. Vibro-acoustic modelling of immersed cylindrical shells with variable thickness. International Journal of Naval Architecture and Ocean Engineering, Vol. 12, 2020, pp. 343–353.10.1016/j.ijnaoe.2019.12.003Search in Google Scholar

[19] Wang, X., D. Chen, Y. Xiong, Q. Jiang, and Y. Zuo. Experiment and modeling of vibro-acoustic response of a stiffened submerged cylindrical shell with force and acoustic excitation. Results in Physics, Vol. 11, 2018, pp. 315–324.10.1016/j.rinp.2018.09.017Search in Google Scholar

[20] Wang, X., D. Chen, Y. Xiong, and W. Wu. Simulation and investigations on the vibro-acoustic behavior of cylindrical shells in ice-covered water. Results in Physics, Vol. 15, 2019, id. 102764.10.1016/j.rinp.2019.102764Search in Google Scholar

[21] Chai, Q. and Y. Q. Wang. Traveling wave vibration of graphene platelet reinforced porous joined conical-cylindrical shells in a spinning motion. Engineering Structures, Vol. 252, 2022, id. 113718.10.1016/j.engstruct.2021.113718Search in Google Scholar

[22] Wang, Y. Q., C. Ye, and J. W. Zu. Nonlinear vibration of metal foam cylindrical shells reinforced with graphene platelets. Aerospace Science and Technology, Vol. 85, 2019, pp. 359–370.10.1016/j.ast.2018.12.022Search in Google Scholar

[23] Ye, C. and Y. Q. Wang. Nonlinear forced vibration of functionally graded graphene platelet-reinforced metal foam cylindrical shells: internal resonances. Nonlinear Dynamics, Vol. 104, No. 3, 2021, pp. 2051–2069.10.1007/s11071-021-06401-7Search in Google Scholar

[24] Li, H., F. Pang, H. Chen and Y. Du. Vibration analysis of functionally graded porous cylindrical shell with arbitrary boundary restraints by using a semi analytical method. Composites Part B: Engineering, Vol. 164, 2019, pp. 249–264.10.1016/j.compositesb.2018.11.046Search in Google Scholar

[25] Li, H., F. Pang, X. Miao, and Y. Li. Jacobi–Ritz method for free vibration analysis of uniform and stepped circular cylindrical shells with arbitrary boundary conditions: A unified formulation. Computers & Mathematics with Applications, Vol. 77, No. 2, 2019, pp. 427–440.10.1016/j.camwa.2018.09.046Search in Google Scholar

[26] Li, H., F. Pang, X. Miao, and Y. Li. Jacobi–Ritz method for free vibration analysis of uniform and stepped circular cylindrical shells with arbitrary boundary conditions: A unified formulation. Computers & Mathematics with Applications, Vol. 77, No. 2, 2019, pp. 427–440.10.1016/j.camwa.2018.09.046Search in Google Scholar

[27] Zhang, L., J. Duan, L. Da, G. Xu, and X. Sun. Vibroacoustic radiation and propagation properties of slender cylindrical shell in uniform shallow sea. Ocean Engineering, Vol. 195, 2020, id. 106659.10.1016/j.oceaneng.2019.106659Search in Google Scholar

[28] Guo, W., Q. Feng, T. Li, X. Zhu, and Y. Miao. A new solution for vibroacoustic analysis of two-dimensional cylindrical shells partially liquid-filled or partially submerged in fluid. Mechanical Systems and Signal Processing, Vol. 140, 2020, id. 106685.10.1016/j.ymssp.2020.106685Search in Google Scholar

[29] Tang, R., H. Tian, and D. Shang. Faster calculation of the low-frequency radiated sound power of underwater slender cylindrical shells. Mathematical Problems in Engineering, Vol. 2020, 2020, pp. 2020–2110.10.1155/2020/3939160Search in Google Scholar

[30] Zhang, C., S. Li, D. Shang, Y. Han, and Y. Shang. Prediction of sound radiation from submerged cylindrical shell based on dominant modes. Applied Sciences, Vol. 10, No. 9, 2020, id. 3073.10.3390/app10093073Search in Google Scholar

[31] Du, Y., F. Pang, L. Sun, and H. Li. A unified formulation for dynamic behavior analysis of spherical cap with uniform and stepped thickness distribution under different edge constraints. Thin-Walled Structures, Vol. 146, No. C, 2020, id. 106445.10.1016/j.tws.2019.106445Search in Google Scholar

[32] Du, Y., D. Jia, H. Li, C. Gao, and H. Wang A unified method to analyze free and forced vibration of stiffened plates under various edge conditions. European Journal of Mechanics – A/Solids, Vol. 94, 2022, id. 104573.10.1016/j.euromechsol.2022.104573Search in Google Scholar

[33] Bhaskar, S., M. Kumar, and A. Patnaik. Mechanical and tribological overview of ceramic particulates reinforced aluminium alloy composites. Reviews on Advanced Materials Science, Vol. 58, No. 1, 2019, pp. 280–294.10.1515/rams-2019-0033Search in Google Scholar

[34] Sun, Y., Y. Peng, T. Zhou, H. Liu, and P. Gao. Study of the mechanical-electrical-magnetic properties and the microstructure of three-layered cement-based absorbing boards. Reviews on Advanced Materials Science, Vol. 59, No. 1, 2020, pp. 160–169.10.1515/rams-2020-0014Search in Google Scholar

[35] Deng, J., O. Guasch, L. Maxit, and L. Zheng. Annular acoustic black holes to reduce sound radiation from cylindrical shells. Mechanical Systems and Signal Processing, Vol. 158, 2021, id. 107722.10.1016/j.ymssp.2021.107722Search in Google Scholar

[36] Pang, F., Y. Qin, H. Li, Y. Teng, Q. Gong, and S. Wang. Study on impact resistance of composite rocket launcher. Reviews on Advanced Materials Science, Vol. 60, No. 1, 2021, pp. 615–630.10.1515/rams-2021-0045Search in Google Scholar

[37] Xiuchang, H., Z. Zhiyi, Z. Zhenhua, and H. Hongxing. Multi-channel active vibration isolation for the control of underwater sound radiation from a stiffened cylindrical structure: A numerical study. Journal of Vibration and Acoustics, Vol. 134, 2012, id. 1.10.1115/1.4004684Search in Google Scholar

[38] Ding, S., C. Mu, Y. Gao, H. Liu, and M. Li. Investigation of low-frequency sound radiation characteristics and active control mechanism of a finite cylindrical shell. Shock and Vibration, Vol. 2021, 2021, pp. 2021–2116.10.1155/2021/6669284Search in Google Scholar

[39] Dai, L., T. J. Yang, Y. Sun, and J. X. Liu. Influence of boundary conditions on the active control of vibration and sound radiation for a circular cylindrical shell. Applied Mechanics and Materials, Vol. 66–68, 2011, pp. 1270–1277.10.4028/www.scientific.net/AMM.66-68.1270Search in Google Scholar

[40] Zou, M.-S., L.-W. Jiang, and S.-X. Liu. Underwater acoustic radiation by structures arbitrarily covered with acoustic coatings. Journal of Sound and Vibration, Vol. 443, 2019, pp. 748–763.10.1016/j.jsv.2018.12.017Search in Google Scholar

[41] Liu, S.-X., M. S. Zou, L. W. Jiang, and X. Y. Zhao. Vibratory response and acoustic radiation of a finite cylindrical shell partially covered with circumferential compliant layers. Applied Acoustics, Vol. 141, 2018, pp. 188–197.10.1016/j.apacoust.2018.07.012Search in Google Scholar

[42] Wang, Y. Q., C. Ye, and J. Zhu. Chebyshev collocation technique for vibration analysis of sandwich cylindrical shells with metal foam core. ZAMM – Journal of Applied Mathematics and Mechanics/Zeitschrift für Angewandte Mathematik und Mechanik, Vol. 100, No. 5, 2020, id. e201900199.10.1002/zamm.201900199Search in Google Scholar

[43] Chai, Q. and Y. Q. Wang. A general approach for free vibration analysis of spinning joined conical–cylindrical shells with arbitrary boundary conditions. Thin-Walled Structures, Vol. 168, 2021, id. 108243.10.1016/j.tws.2021.108243Search in Google Scholar

[44] Mercan, K., Ç. Demir, and Ö. Civalek. Vibration analysis of FG cylindrical shells with power-law index using discrete singular convolution technique. Curved and Layered Structures, Vol. 3, 2016, id. 1.10.1515/cls-2016-0007Search in Google Scholar

[45] Arefi, M., S. Firouzeh, E. Mohammad-Rezaei Bidgoli, and Ö. Civalek. Analysis of porous micro-plates reinforced with FG-GNPs based on Reddy plate theory. Composite Structures, Vol. 247, 2020, id. 112391.10.1016/j.compstruct.2020.112391Search in Google Scholar

[46] Kim, S. Application of a complete radiation boundary condition for the Helmholtz equation in locally perturbed waveguides. Journal of Computational and Applied Mathematics, Vol. 367, 2020, id. 112458.10.1016/j.cam.2019.112458Search in Google Scholar

[47] Gao, C., H. Zhang, H. Li, F. Pang, and H. Wang. Numerical and experimental investigation of vibro-acoustic characteristics of a submerged stiffened cylindrical shell excited by a mechanical force. Ocean Engineering, Vol. 249, 2022, id. 110913.10.1016/j.oceaneng.2022.110913Search in Google Scholar

[48] Pang, F., H. Li, X. Wang, X. Miao, and S. Li. A semi analytical method for the free vibration of doubly-curved shells of revolution. Computers & Mathematics with Applications, Vol. 75, No. 9, 2018, pp. 3249–3268.10.1016/j.camwa.2018.01.045Search in Google Scholar

[49] Pang, F., H. Li, H. Chen, and Y. Shan. Free vibration analysis of combined composite laminated cylindrical and spherical shells with arbitrary boundary conditions. Mechanics of Advanced Materials and Structures, Vol. 28, No. 2, 2021, pp. 182–199.10.1080/15376494.2018.1553258Search in Google Scholar

[50] Du, Y., L. Sun, S. Li, and Y. Li. Vibration analysis of truncated spherical shells under various edge constraints. Thin-Walled Structures, Vol. 147, No. C, 2020, id. 106544.10.1016/j.tws.2019.106544Search in Google Scholar
Received: 2021-12-19
Revised: 2022-03-31
Accepted: 2022-04-12
Published Online: 2022-07-13

© 2022 Yuhang Tang et al., published by De Gruyter

This work is licensed under the Creative Commons Attribution 4.0 International License.

Articles in the same Issue

  1. Review Articles
  2. State of the art, challenges, and emerging trends: Geopolymer composite reinforced by dispersed steel fibers
  3. A review on the properties of concrete reinforced with recycled steel fiber from waste tires
  4. Copper ternary oxides as photocathodes for solar-driven CO2 reduction
  5. Properties of fresh and hardened self-compacting concrete incorporating rice husk ash: A review
  6. Basic mechanical and fatigue properties of rubber materials and components for railway vehicles: A literature survey
  7. Research progress on durability of marine concrete under the combined action of Cl− erosion, carbonation, and dry–wet cycles
  8. Delivery systems in nanocosmeceuticals
  9. Study on the preparation process and sintering performance of doped nano-silver paste
  10. Analysis of the interactions between nonoxide reinforcements and Al–Si–Cu–Mg matrices
  11. Research Articles
  12. Study on the influence of structural form and parameters on vibration characteristics of typical ship structures
  13. Deterioration characteristics of recycled aggregate concrete subjected to coupling effect with salt and frost
  14. Novel approach to improve shale stability using super-amphiphobic nanoscale materials in water-based drilling fluids and its field application
  15. Research on the low-frequency multiline spectrum vibration control of offshore platforms
  16. Multiple wide band gaps in a convex-like holey phononic crystal strip
  17. Response analysis and optimization of the air spring with epistemic uncertainties
  18. Molecular dynamics of C–S–H production in graphene oxide environment
  19. Residual stress relief mechanisms of 2219 Al–Cu alloy by thermal stress relief method
  20. Characteristics and microstructures of the GFRP waste powder/GGBS-based geopolymer paste and concrete
  21. Development and performance evaluation of a novel environmentally friendly adsorbent for waste water-based drilling fluids
  22. Determination of shear stresses in the measurement area of a modified wood sample
  23. Influence of ettringite on the crack self-repairing of cement-based materials in a hydraulic environment
  24. Multiple load recognition and fatigue assessment on longitudinal stop of railway freight car
  25. Synthesis and characterization of nano-SiO2@octadecylbisimidazoline quaternary ammonium salt used as acidizing corrosion inhibitor
  26. Perforated steel for realizing extraordinary ductility under compression: Testing and finite element modeling
  27. The influence of oiled fiber, freeze-thawing cycle, and sulfate attack on strain hardening cement-based composites
  28. Perforated steel block of realizing large ductility under compression: Parametric study and stress–strain modeling
  29. Study on dynamic viscoelastic constitutive model of nonwater reacted polyurethane grouting materials based on DMA
  30. Mechanical behavior and mechanism investigation on the optimized and novel bio-inspired nonpneumatic composite tires
  31. Effect of cooling rate on the microstructure and thermal expansion properties of Al–Mn–Fe alloy
  32. Research on process optimization and rapid prediction method of thermal vibration stress relief for 2219 aluminum alloy rings
  33. Failure prevention of seafloor composite pipelines using enhanced strain-based design
  34. Deterioration of concrete under the coupling action of freeze–thaw cycles and salt solution erosion
  35. Creep rupture behavior of 2.25Cr1Mo0.25V steel and weld for hydrogenation reactors under different stress levels
  36. Statistical damage constitutive model for the two-component foaming polymer grouting material
  37. Nano-structural and nano-constraint behavior of mortar containing silica aggregates
  38. Influence of recycled clay brick aggregate on the mechanical properties of concrete
  39. Effect of LDH on the dissolution and adsorption behaviors of sulfate in Portland cement early hydration process
  40. Comparison of properties of colorless and transparent polyimide films using various diamine monomers
  41. Study in the parameter influence on underwater acoustic radiation characteristics of cylindrical shells
  42. Experimental study on basic mechanical properties of recycled steel fiber reinforced concrete
  43. Dynamic characteristic analysis of acoustic black hole in typical raft structure
  44. A semi-analytical method for dynamic analysis of a rectangular plate with general boundary conditions based on FSDT
  45. Research on modification of mechanical properties of recycled aggregate concrete by replacing sand with graphite tailings
  46. Dynamic response of Voronoi structures with gradient perpendicular to the impact direction
  47. Deposition mechanisms and characteristics of nano-modified multimodal Cr3C2–NiCr coatings sprayed by HVOF
  48. Effect of excitation type on vibration characteristics of typical ship grillage structure
  49. Study on the nanoscale mechanical properties of graphene oxide–enhanced shear resisting cement
  50. Experimental investigation on static compressive toughness of steel fiber rubber concrete
  51. Study on the stress field concentration at the tip of elliptical cracks
  52. Corrosion resistance of 6061-T6 aluminium alloy and its feasibility of near-surface reinforcements in concrete structure
  53. Effect of the synthesis method on the MnCo2O4 towards the photocatalytic production of H2
  54. Experimental study of the shear strength criterion of rock structural plane based on three-dimensional surface description
  55. Evaluation of wear and corrosion properties of FSWed aluminum alloy plates of AA2020-T4 with heat treatment under different aging periods
  56. Thermal–mechanical coupling deformation difference analysis for the flexspline of a harmonic drive
  57. Frost resistance of fiber-reinforced self-compacting recycled concrete
  58. High-temperature treated TiO2 modified with 3-aminopropyltriethoxysilane as photoactive nanomaterials
  59. Effect of nano Al2O3 particles on the mechanical and wear properties of Al/Al2O3 composites manufactured via ARB
  60. Co3O4 nanoparticles embedded in electrospun carbon nanofibers as free-standing nanocomposite electrodes as highly sensitive enzyme-free glucose biosensors
  61. Effect of freeze–thaw cycles on deformation properties of deep foundation pit supported by pile-anchor in Harbin
  62. Temperature-porosity-dependent elastic modulus model for metallic materials
  63. Effect of diffusion on interfacial properties of polyurethane-modified asphalt–aggregate using molecular dynamic simulation
  64. Experimental study on comprehensive improvement of shear strength and erosion resistance of yellow mud in Qiang Village
  65. A novel method for low-cost and rapid preparation of nanoporous phenolic aerogels and its performance regulation mechanism
  66. In situ bow reduction during sublimation growth of cubic silicon carbide
  67. Adhesion behaviour of 3D printed polyamide–carbon fibre composite filament
  68. An experimental investigation and machine learning-based prediction for seismic performance of steel tubular column filled with recycled aggregate concrete
  69. Effects of rare earth metals on microstructure, mechanical properties, and pitting corrosion of 27% Cr hyper duplex stainless steel
  70. Application research of acoustic black hole in floating raft vibration isolation system
  71. Multi-objective parametric optimization on the EDM machining of hybrid SiCp/Grp/aluminum nanocomposites using Non-dominating Sorting Genetic Algorithm (NSGA-II): Fabrication and microstructural characterizations
  72. Estimating of cutting force and surface roughness in turning of GFRP composites with different orientation angles using artificial neural network
  73. Displacement recovery and energy dissipation of crimped NiTi SMA fibers during cyclic pullout tests
https://doi.org/10.1515/rams-2022-0036
Keywords for this article
cylindrical shell; vibration; acoustic radiation; influence parameters
Creative Commons
BY 4.0

Articles in the same Issue

  1. Review Articles
  2. State of the art, challenges, and emerging trends: Geopolymer composite reinforced by dispersed steel fibers
  3. A review on the properties of concrete reinforced with recycled steel fiber from waste tires
  4. Copper ternary oxides as photocathodes for solar-driven CO2 reduction
  5. Properties of fresh and hardened self-compacting concrete incorporating rice husk ash: A review
  6. Basic mechanical and fatigue properties of rubber materials and components for railway vehicles: A literature survey
  7. Research progress on durability of marine concrete under the combined action of Cl− erosion, carbonation, and dry–wet cycles
  8. Delivery systems in nanocosmeceuticals
  9. Study on the preparation process and sintering performance of doped nano-silver paste
  10. Analysis of the interactions between nonoxide reinforcements and Al–Si–Cu–Mg matrices
  11. Research Articles
  12. Study on the influence of structural form and parameters on vibration characteristics of typical ship structures
  13. Deterioration characteristics of recycled aggregate concrete subjected to coupling effect with salt and frost
  14. Novel approach to improve shale stability using super-amphiphobic nanoscale materials in water-based drilling fluids and its field application
  15. Research on the low-frequency multiline spectrum vibration control of offshore platforms
  16. Multiple wide band gaps in a convex-like holey phononic crystal strip
  17. Response analysis and optimization of the air spring with epistemic uncertainties
  18. Molecular dynamics of C–S–H production in graphene oxide environment
  19. Residual stress relief mechanisms of 2219 Al–Cu alloy by thermal stress relief method
  20. Characteristics and microstructures of the GFRP waste powder/GGBS-based geopolymer paste and concrete
  21. Development and performance evaluation of a novel environmentally friendly adsorbent for waste water-based drilling fluids
  22. Determination of shear stresses in the measurement area of a modified wood sample
  23. Influence of ettringite on the crack self-repairing of cement-based materials in a hydraulic environment
  24. Multiple load recognition and fatigue assessment on longitudinal stop of railway freight car
  25. Synthesis and characterization of nano-SiO2@octadecylbisimidazoline quaternary ammonium salt used as acidizing corrosion inhibitor
  26. Perforated steel for realizing extraordinary ductility under compression: Testing and finite element modeling
  27. The influence of oiled fiber, freeze-thawing cycle, and sulfate attack on strain hardening cement-based composites
  28. Perforated steel block of realizing large ductility under compression: Parametric study and stress–strain modeling
  29. Study on dynamic viscoelastic constitutive model of nonwater reacted polyurethane grouting materials based on DMA
  30. Mechanical behavior and mechanism investigation on the optimized and novel bio-inspired nonpneumatic composite tires
  31. Effect of cooling rate on the microstructure and thermal expansion properties of Al–Mn–Fe alloy
  32. Research on process optimization and rapid prediction method of thermal vibration stress relief for 2219 aluminum alloy rings
  33. Failure prevention of seafloor composite pipelines using enhanced strain-based design
  34. Deterioration of concrete under the coupling action of freeze–thaw cycles and salt solution erosion
  35. Creep rupture behavior of 2.25Cr1Mo0.25V steel and weld for hydrogenation reactors under different stress levels
  36. Statistical damage constitutive model for the two-component foaming polymer grouting material
  37. Nano-structural and nano-constraint behavior of mortar containing silica aggregates
  38. Influence of recycled clay brick aggregate on the mechanical properties of concrete
  39. Effect of LDH on the dissolution and adsorption behaviors of sulfate in Portland cement early hydration process
  40. Comparison of properties of colorless and transparent polyimide films using various diamine monomers
  41. Study in the parameter influence on underwater acoustic radiation characteristics of cylindrical shells
  42. Experimental study on basic mechanical properties of recycled steel fiber reinforced concrete
  43. Dynamic characteristic analysis of acoustic black hole in typical raft structure
  44. A semi-analytical method for dynamic analysis of a rectangular plate with general boundary conditions based on FSDT
  45. Research on modification of mechanical properties of recycled aggregate concrete by replacing sand with graphite tailings
  46. Dynamic response of Voronoi structures with gradient perpendicular to the impact direction
  47. Deposition mechanisms and characteristics of nano-modified multimodal Cr3C2–NiCr coatings sprayed by HVOF
  48. Effect of excitation type on vibration characteristics of typical ship grillage structure
  49. Study on the nanoscale mechanical properties of graphene oxide–enhanced shear resisting cement
  50. Experimental investigation on static compressive toughness of steel fiber rubber concrete
  51. Study on the stress field concentration at the tip of elliptical cracks
  52. Corrosion resistance of 6061-T6 aluminium alloy and its feasibility of near-surface reinforcements in concrete structure
  53. Effect of the synthesis method on the MnCo2O4 towards the photocatalytic production of H2
  54. Experimental study of the shear strength criterion of rock structural plane based on three-dimensional surface description
  55. Evaluation of wear and corrosion properties of FSWed aluminum alloy plates of AA2020-T4 with heat treatment under different aging periods
  56. Thermal–mechanical coupling deformation difference analysis for the flexspline of a harmonic drive
  57. Frost resistance of fiber-reinforced self-compacting recycled concrete
  58. High-temperature treated TiO2 modified with 3-aminopropyltriethoxysilane as photoactive nanomaterials
  59. Effect of nano Al2O3 particles on the mechanical and wear properties of Al/Al2O3 composites manufactured via ARB
  60. Co3O4 nanoparticles embedded in electrospun carbon nanofibers as free-standing nanocomposite electrodes as highly sensitive enzyme-free glucose biosensors
  61. Effect of freeze–thaw cycles on deformation properties of deep foundation pit supported by pile-anchor in Harbin
  62. Temperature-porosity-dependent elastic modulus model for metallic materials
  63. Effect of diffusion on interfacial properties of polyurethane-modified asphalt–aggregate using molecular dynamic simulation
  64. Experimental study on comprehensive improvement of shear strength and erosion resistance of yellow mud in Qiang Village
  65. A novel method for low-cost and rapid preparation of nanoporous phenolic aerogels and its performance regulation mechanism
  66. In situ bow reduction during sublimation growth of cubic silicon carbide
  67. Adhesion behaviour of 3D printed polyamide–carbon fibre composite filament
  68. An experimental investigation and machine learning-based prediction for seismic performance of steel tubular column filled with recycled aggregate concrete
  69. Effects of rare earth metals on microstructure, mechanical properties, and pitting corrosion of 27% Cr hyper duplex stainless steel
  70. Application research of acoustic black hole in floating raft vibration isolation system
  71. Multi-objective parametric optimization on the EDM machining of hybrid SiCp/Grp/aluminum nanocomposites using Non-dominating Sorting Genetic Algorithm (NSGA-II): Fabrication and microstructural characterizations
  72. Estimating of cutting force and surface roughness in turning of GFRP composites with different orientation angles using artificial neural network
  73. Displacement recovery and energy dissipation of crimped NiTi SMA fibers during cyclic pullout tests
Sign up now to receive a 20% welcome discount
Institutional Access
How does access work?
Have an idea on how to improve our website?
Please write us.
© 2025 De Gruyter Brill
Downloaded on 31.10.2025 from https://www.degruyterbrill.com/document/doi/10.1515/rams-2022-0036/html
Scroll to top button