Home Technology Study on dynamic viscoelastic constitutive model of nonwater reacted polyurethane grouting materials based on DMA
Article Open Access

Study on dynamic viscoelastic constitutive model of nonwater reacted polyurethane grouting materials based on DMA

  • Zhang Jingwei , Li Jia EMAIL logo , Huang Chuhao and Chen Shuo
Published/Copyright: April 19, 2022
Download Article (PDF)
Become an author with De Gruyter Brill
Submit Manuscript Author Information
REVIEWS ON ADVANCED MATERIALS SCIENCE
From the journal REVIEWS ON ADVANCED MATERIALS SCIENCE Volume 61 Issue 1

Abstract

Nonwater reacted polyurethane grouting materials are new materials developed to make up for the shortcomings of water-reactive materials in emergency rescue. However, its viscoelastic properties and constitutive model under dynamic loads have not been systematically studied. Based on dynamic thermal mechanical analysis (DMA), the dynamic viscoelastic indexes such as storage modulus, loss modulus, and loss factor of nonwater reacted polymer grouting material were obtained, and the frequency spectrum of polymer with different densities were analyzed. In addition, comparing and analyzing the classical viscoelastic constitutive models such as Maxewell model, Kelvin model, and Fractional model, the fourth-order generalized Maxwell model (GMM) was selected to construct the viscoelastic constitutive model of polyurethane grounding materials. Then, the parameters of the viscoelastic constitutive model of polyurethane grounding materials were obtained by using multi-objective shared parameter fitting method, and dynamic viscoelastic constitutive model of nonwater reacted polyurethane grouting materials was established. Furthermore, the viscoelastic constitutive model with different densities was verified by the DMA test. The results show that the dynamic viscoelastic constitutive model of nonwater reacted polyurethane grouting materials in the article can accurately and efficiently describe the dynamic viscoelastic properties of polyurethane grounding materials, which lays a foundation for the dynamic response analysis of polymer structures.

Keywords: non-water reacted polymer material; dynamic thermomechanical analysis; dynamic viscoelastic constitutive model; generalized Maxwell model

1 Introduction

In recent years, many materials have been studied for the repair and improvement of engineering structures. Their mechanical properties, service life, and engineering properties have also been analyzed and verified [1,2,3,4]. As a new material, nonwater reacted polyurethane grouting materials (hereinafter referred to as polyurethane grounding materials) are new repairing and impermeable materials developed for the shortage of water reacted materials with significantly changing volume and mechanical properties in the water environment. The materials are made of polyisocyanate and polyether polyols or polyester polyols, whose shape and properties can be changed by changing the type and composition of raw materials, so as to obtain the final product from soft to hard. Polyurethane grounding materials have been applied in a number of infrastructure water disaster prevention and repair projects, such as crack treatment of highway, track slab lifting of high-speed railway, and emergency reinforcement of water conservancy projects [5,6,7,8,9,10,11,12,13] (Figure 1). In fact, the polyurethane grounding materials are often under dynamic loads such as vehicles and trains, so the study of dynamic viscoelastic properties of polyurethane grounding materials can actually reflect the mechanical properties of materials [14,15]. This article aims to obtain the constitutive model of polyurethane grounding materials under dynamic conditions for dynamic response analysis and finite element simulation.

Figure 1 Engineering application of nonwater reacted polyurethane grouting materials.
Figure 1

Engineering application of nonwater reacted polyurethane grouting materials.

As an effective method for studying the viscoelastic properties of polyurethane materials, the dynamic mechanical analysis (DMA) method has been widely used to study the dynamic viscoelastic properties of materials. Shamsi et al. [16] studied the viscoelastic properties of polyurethane materials at different temperatures and frequencies based on the DMA method. Hartman et al. [17] constructed the master curves of shear modulus and the loss factor over a wide range of reduced frequencies by using the DMA method. Dadbin et al. [18] used the DMA method to accurately test the glass transition temperature of polyurethane materials with different densities. It can be seen from the previous studies that the viscoelastic energy parameters obtained by the DMA test are an important basis for establishing a viscoelastic constitutive model [19,20,21,22].

Christensen and Freund [23] have made a great contribution to the study of the constitutive model of viscoelastic materials by discussing the theory and the application of the viscoelastic constitutive model based on continuum mechanics. Yang et al. [24] also studied the constitutive relation of viscoelastic materials by analyzing the structural characteristics, mechanical behavior, energy loss, and so on. In the study by Sun et al. [25], a fractional plasticity model for geomaterials is proposed by using the fractional derivative. Among existing constitutive models [26,27,28,29,30,31], the generalized Maxwell model (GMM), as a classical viscoelastic constitutive model, can describe the stress–strain relation of viscoelastic materials accurately and be directly used in the finite element method (FEM), so it is widely applied in the structure analysis. Jalocha et al. [32] used the GMM to fit the DMA test results and obtained the model parameters. Wan et al. [33] used the GMM to describe the relationship between dynamic viscoelastic modulus and frequency of polyurethane grounding materials at different temperatures.

In this article, the dynamic viscoelastic frequency spectra of polyurethane grounding materials are obtained based on the DMA test analysis. By analyzing and comparing various viscoelastic constitutive models, the fourth-order GMM is selected to construct the viscoelastic constitutive model of polyurethane grounding materials. Furthermore, the validity and rationality of the model were verified with DMA test data. The results provide a theoretical reference for the study of the dynamic response of a polymer compound structure.

2 DMA test

2.1 Test method

DMA test can obtain storage modulus, loss modulus, and loss factor of testing materials, which are important to characterize the dynamic viscoelastic properties of materials. Storage modulus E ′ is the energy storage capacity of viscoelastic materials under a cyclic alternating load. The larger the storage modulus is, the greater the stiffness of the material will be. Loss modulus E ″ represents the ability to dissipate energy within a period of changing and reflects the viscosity of the material. Loss factor reflects the damping performance of viscoelastic materials, which is the ratio of loss modulus and storage modulus, represented as tan δ = E ″ / E ′ .

DMAQ800 dynamic thermal-mechanical analysis instrument (Figure 2) is used in this test with the three-point bending method. The dynamic viscoelastic parameters of polyurethane grounding materials with different densities (Figure 3) at different frequencies are measured at −50, −25, 0, 25, and 50°C. Besides, test data are recorded every 2 Hz interval in the frequency spectra scanning test. The test scheme is as presented in Table 1. For more details, one can refer to ref. [34].

Figure 2 Dynamic thermo-mechanical analysis instrument.
Figure 2

Dynamic thermo-mechanical analysis instrument.

Figure 3 Polymer grouting materials sample.
Figure 3

Polymer grouting materials sample.

Table 1

DMA test scheme

Test method Test temperature (°C) Test frequency (Hz) Density (g·cm−3)
Three-point bending method −50, −25, 0, 25, 50 1–40 0–0.6

2.2 Test results

The curves of storage modulus and loss factor of polyurethane grounding materials with different densities (0–0.6 g·cm−3) at room temperature (25°C) are plotted in Figure 3. As can be seen from Figure 4, at room temperature, the storage modulus of polymer material with each density increases at first and then decreases with the increase of frequency, while the loss factor first decreases slightly and then increases greatly with the increase of frequency.

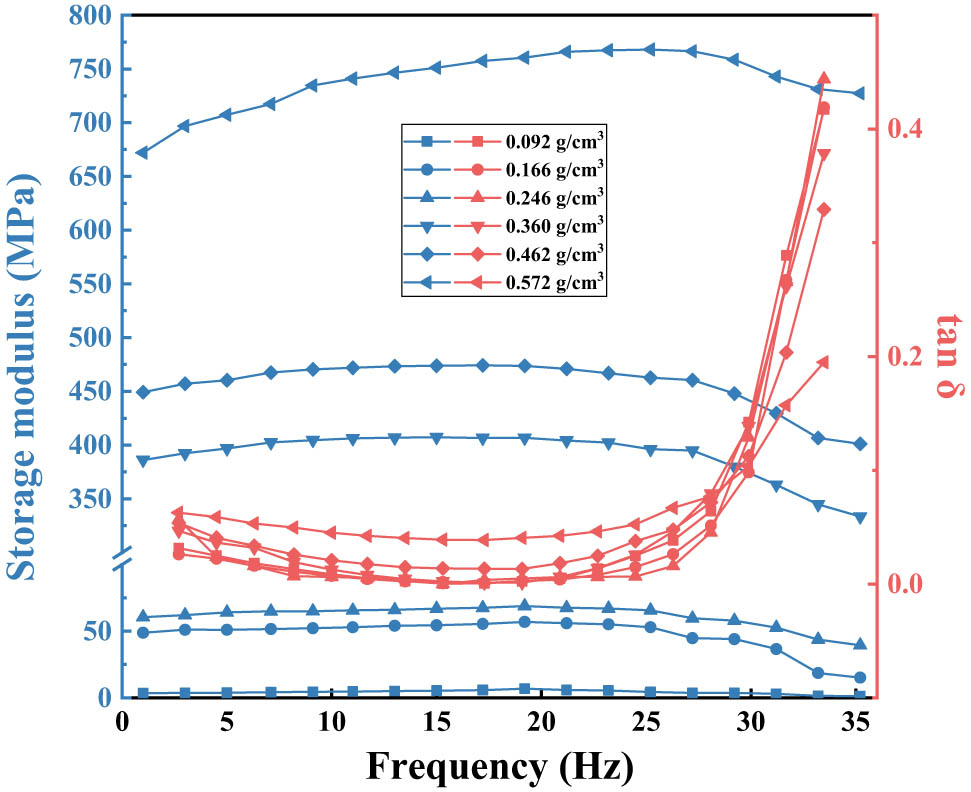
Figure 4 Frequency spectra of storage modulus and loss factor at different densities.
Figure 4

Frequency spectra of storage modulus and loss factor at different densities.

3 Study on viscoelastic constitutive model

3.1 Maxwell model

Maxwell model is composed with a Hooke spring and a Newton dashpot in series, as shown in Figure 5.

Figure 5 Maxwell model.
Figure 5

Maxwell model.

According to the characteristics of series connection, the stress on each element is equal to the total stress, and the total strain is the sum of the strains of each element. Thus, the constitutive relation of the Maxwell model can be deduced as follows:

(1) σ ( t ) + η E ∂ σ ∂ t = η ∂ ε ∂ t ,

where σ ( t ) is the stress of material at time t, E is Young’s modulus, and η is the viscosity coefficient.

When the sinusoidal alternating stress is applied to the Maxwell model, expressions of storage modulus E ′ , loss modulus E ″ , and loss factor tan θ can be obtained as follows:

(2) E ′ = E η 2 ω 2 E + η 2 ω 2 ,

(3) E ″ = E 2 η ω E 2 + η 2 ω 2 ,

(4) tan θ = E η ω .

It can be seen from equations (2) and (4) that the storage modulus of this model increases with the increase of frequency, and the loss factor decreases linearly as the frequency increased. However, the loss factor first decreases and then increases with the increase of frequency in the DMA test of polyurethane grounding materials. Therefore, this model is not suitable for describing the dynamic viscoelastic characteristics of polyurethane grounding materials.

3.2 Kelvin model

Kelvin model is formed by a Hooke spring and a Newton dashpot in parallel, as shown in Figure 6.

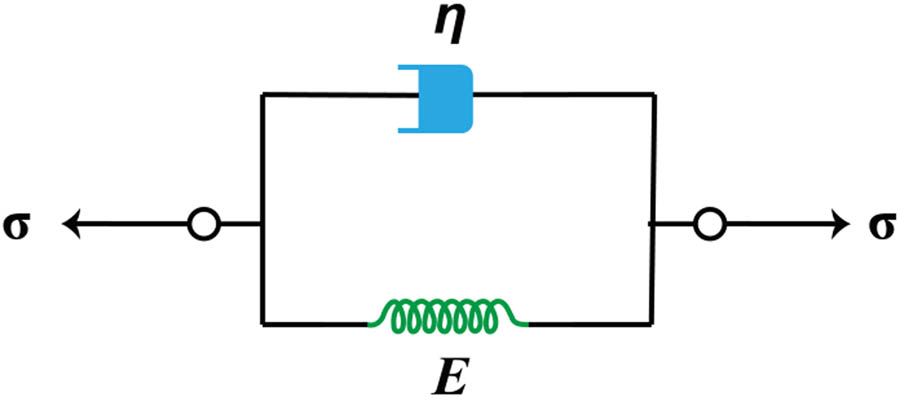
Figure 6 Kelvin model.
Figure 6

Kelvin model.

According to the nature of the parallel connection, the strain of each element in this model is equal, while the total stress is the sum of the stresses of each element. Its constitutive model can be expressed as follows:

(5) σ ( t ) = E ε ( t ) + η ∂ ε ( t ) ∂ t ,

where ε(t) is the strain of material at time t.

When applying sinusoidal alternating stress on the Kelvin model, the expressions of storage modulus, loss modulus, and loss factor can be derived as following equations:

(6) E ′ = E ,

(7) E ″ = η ω ,

(8) tan θ = η ω E .

Equations (6) and (8) describe that storage modulus is constant and independent of frequency, and the loss factor increases linearly with the increase of frequency. However, the storage modulus of polyurethane grounding materials increases and then decreases with the increase of frequency in the DMA test of polyurethane grounding materials. It indicates that this model may not accurately describe the dynamic viscoelastic properties of polyurethane grounding materials.

3.3 Fractional viscoelastic model

3.3.1 Fractional Maxwell model

The fractional Maxwell model is composed of a Hooke spring in series with an Abel dashpot, as shown in Figure 7.

Figure 7 Fractional Maxwell model.
Figure 7

Fractional Maxwell model.

According to the series characteristics, the constitutive relation of the fractional Maxwell model can be described as follows:

(9) σ ( t ) = E 1 E τ α D α E 1 + E τ α D α ε ( t ) ,

where E 1 is the young’s modulus of Hooke spring, E is the young’s modulus of Abel dashpot, τ is the relaxation time, and D α is the fractional calculus operator.

The expressions of storage modulus, loss modulus, and loss factor can be deduced as follows:

(10) E ′ = E 1 E τ α ω α E 1 cos α π 2 + E τ α ω α E 1 2 + 2 E 1 E τ α ω α cos α π 2 + E 2 τ 2 α ω 2 α ,

(11) E ″ = E 1 2 E τ α ω α sin α π 2 E 1 2 + 2 E 1 E τ α ω α cos α π 2 + E 2 τ 2 α ω 2 α ,

(12) tan θ = E 1 2 E τ α ω α sin α π 2 E 1 E τ α ω α E 1 cos α π 2 + E τ α ω α .

3.3.2 Fractional Kelvin model

The fractional Kelvin model is composed of a Hooke spring and an Abel dashpot in parallel, as shown in Figure 8.

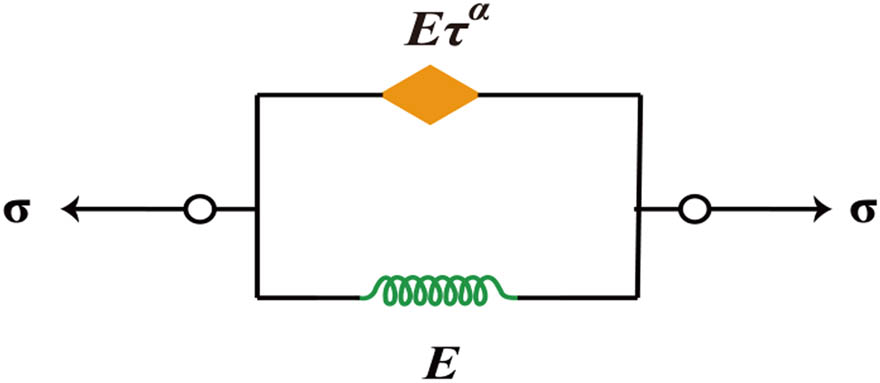
Figure 8 Fractional Kelvin model.
Figure 8

Fractional Kelvin model.

From the characteristics of parallel connection, the constitutive relation of the fractional Kelvin model is obtained as follows:

(13) σ ( t ) = ( E 1 + E τ α D α ) ε ( t ) .

The expressions of storage modulus, loss modulus, and loss factor are as follows:

(14) E ′ = E 1 + E τ α ω α cos α π 2 ,

(15) E ″ = E τ α ω α sin α π 2 ,

(16) tan θ = E τ α ω α sin α π 2 E 1 + E τ α ω α cos α π 2 .

From equations (10), (12), (14), and (16), it is seen that the storage modulus of the aforementioned two models first increases and then decreases with the increase of frequency, the loss factor first decreases and then increases with the increase of frequency, which can accurately describe the dynamic viscoelastic properties of polyurethane grounding materials. However, it also indicates that these models have a large amount of calculation, and it is relatively difficult to obtain the parameters.

3.4 GMM

GMM is composed of any number of Maxwell models in parallel, and each Maxwell model is different. Its modulus is E i , viscosity is η i , and relaxation time τ i = η i / E i , as shown in Figure 9.

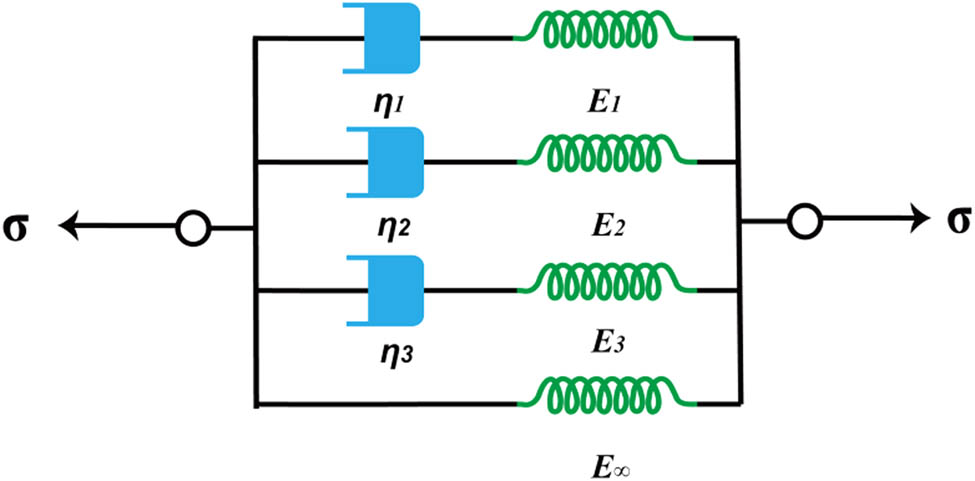
Figure 9 GMM.
Figure 9

GMM.

The relaxation modulus of the GMM can be expressed as follows:

(17) E ( t ) = E ∞ + ∑ i = 1 n E i e − t τ i ,

where E ∞ is quasi static modulus.

The expressions of storage modulus and loss modulus of each Maxwell model can be known from equations (2) and (3). Through Fourier transform and inverse transform, the storage modulus and loss modulus of the GMM can be expressed as follows:

(18) E ′ = E ∞ + ∑ i = 1 n E i ω 2 τ i 2 1 + ω 2 τ i 2 ,

(19) E ″ = ∑ i = 1 n E i ω τ i 1 + ω 2 τ i 2 ,

(20) tan θ = E ∞ + ∑ i = 1 n E i w 2 τ i 2 1 + w 2 τ i 2 ∑ i = 1 n E i w τ i 1 + w 2 τ i 2 .

According to equations (18) and (20), the storage modulus first increases and then decreases with the increase of frequency, while the loss factor first decreases and then increases with the increase of frequency. Therefore, this kind of model can exactly describe viscoelastic characteristics under dynamic load. Moreover, the GMM is composed of several units, corresponding to several relaxation times. So it is relatively easy to obtain the model parameters, which can be calculated directly by fitting the DMA test data.

In conclusion, Maxwell and Kelvin models can describe the creep and stress relaxation of viscoelastic materials, but they are not applicable to describe the dynamic viscoelastic properties of materials. The fractional constitutive model is comparatively difficult to obtain the model parameters although it can precisely represent dynamic viscoelastic properties of materials. GMM can accurately describe the dynamic viscoelastic properties of materials, and the model parameters can be easily obtained as well. Furthermore, it can also describe the frequency dependence of viscoelastic materials under dynamic alternating loads. As a result, the GMM is used to establish the dynamic viscoelastic constitutive model of polyurethane grounding materials [35,36,37,38].

4 Dynamic viscoelastic constitutive model of polyurethane grounding materials

4.1 Relationship between density and dynamic viscoelastic modulus

In engineering applications, polymer structures with different densities meet different demands of actual projects. For example, 0–0.2 g·cm−3 polyurethane grounding materials are usually used for seepage control and reinforcement of water conservancy projects, while the materials with densities of 0.5–0.6 g·cm−3 are usually used for pavement lifting. Therefore, it is very important to research the relationship between density and dynamic viscoelastic modulus.

4.1.1 Relationship between density and storage modulus

As the common frequency range of dynamic loads on polymer material is mostly from 1 to 19 Hz, the frequency of the scope in this study is set from 1 to 19 Hz. As the scanning interval of testing frequency is 2 Hz, the data are extracted every 2 Hz. As is shown in Figure 10, the fitting curves of DMA testing data of storage modulus under different densities at 25°C are obtained, where the points are test values and the curves are the fitting curve.

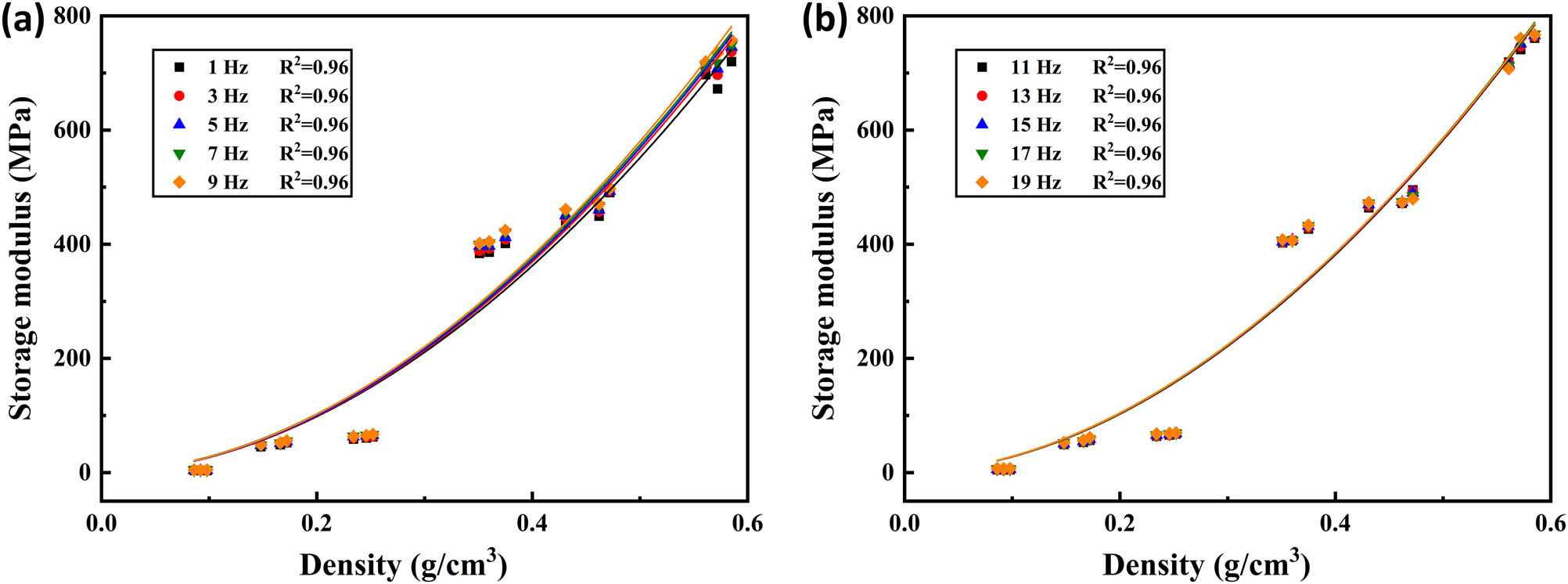
Figure 10 Relationship between density and storage modulus of polyurethane grounding materials (25°C): (a) fitting results (1–9 Hz) and (b) fitting results (11–13 Hz).
Figure 10

Relationship between density and storage modulus of polyurethane grounding materials (25°C): (a) fitting results (1–9 Hz) and (b) fitting results (11–13 Hz).

From Figure 9, the relationship between density and storage modulus could be approximately expressed by the following equation, and the correlation coefficients R 2 are all greater than 0.96.

(21) E ′ = a ρ b ,

where E ′ is storage modulus, ρ is the density of polyurethane grounding materials, and a and b are fitting parameters.

The fitting parameters at each frequency are presented in Table 2.

Table 2

Fitting parameters of storage modulus

Frequency (Hz) a b
1 2048.08 1.87
3 2109.37 1.88
5 2124.78 1.88
7 2127.84 1.87
9 2168.19 1.88
11 2176.63 1.88
13 2180.64 1.88
15 2181.53 1.88
17 2184.69 1.88
19 2173.54 1.87

4.1.2 Relationship between density and loss modulus

Similarly, the relationship curve between density and loss modulus at 25°C is fitted, and fitting results are shown in Figure 11.

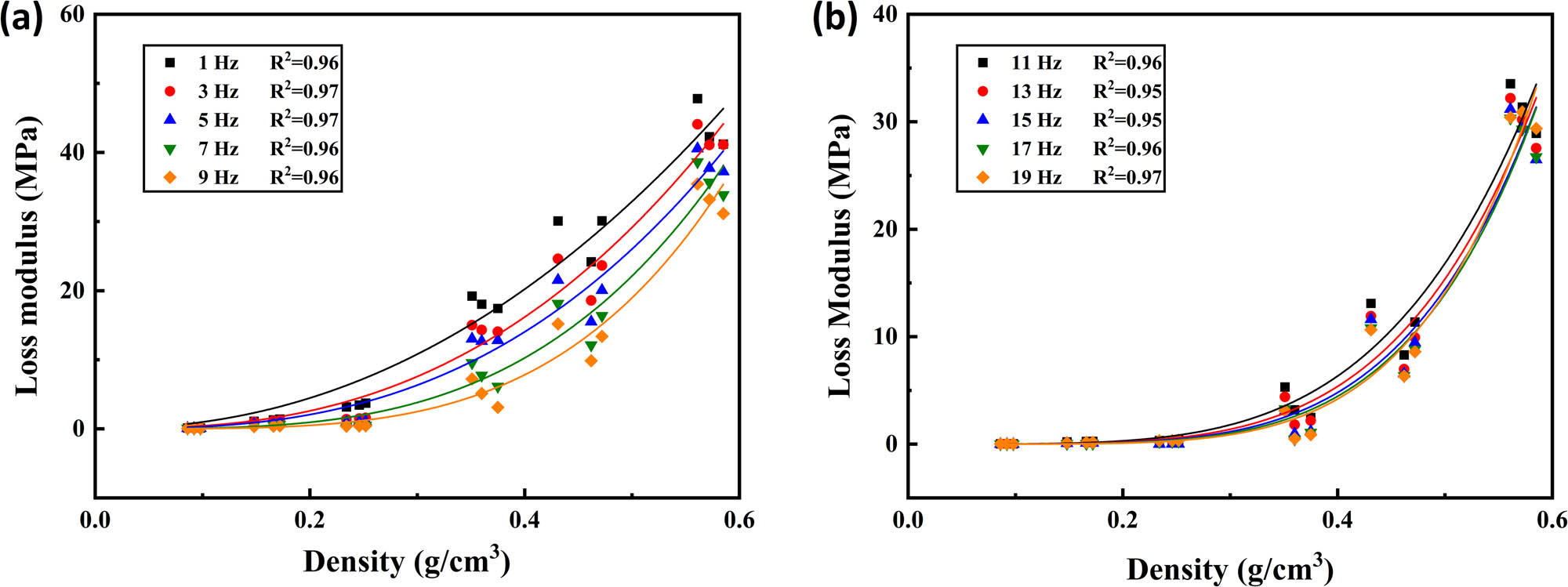
Figure 11 Relationship between density and loss modulus of polyurethane grounding materials (25°C): (a) fitting results (1–9 Hz) and (b) fitting results (11–13 Hz).
Figure 11

Relationship between density and loss modulus of polyurethane grounding materials (25°C): (a) fitting results (1–9 Hz) and (b) fitting results (11–13 Hz).

The relationship between density and loss modulus can be approximately shown by the following equation, and the correlation coefficients R 2 are all greater than 0.95.

(22) E ″ = a ρ b ,

where E ″ is loss modulus, ρ is densities of polyurethane grounding materials, and a and b are fitting parameters.

The fitting parameters at each frequency are presented in Table 3.

Table 3

Fitting parameters of loss modulus

Frequency (Hz) a b
1 185.74 2.36
3 187.17 2.59
5 186.52 2.75
7 215.61 3.12
9 236.22 3.43
11 271.88 3.78
13 320.07 4.13
15 330.66 4.25
17 355.52 4.40
19 370.81 4.50

Based on equations (21) and (22), the storage modulus and loss modulus of polyurethane grounding materials with different densities of 0–0.6 g·cm−3 in the frequency range of 1–19 Hz at room temperature (25°C) can be calculated. Then, the model parameters of polyurethane grounding materials with a certain density can be obtained.

4.2 Viscoelastic constitutive model of polyurethane grounding materials

The steps for establishing the viscoelastic model are as follows:

4.2.1 Constitutive equations

First, equations (18) and (19) need to be transformed into expressions in the form of the Prony series before fitting model parameters:

(23) E ′ = E ∞ + E 0 ∑ i = 1 n g i τ i 2 ω 2 1 + τ i 2 ω 2 ,

(24) E ″ = E 0 ∑ i = 1 n g i τ i ω 1 + τ i 2 ω 2 ,

where E 0 = E ∞ / 1 − ∑ i = 1 n g i is instantaneous modulus, and g i = E i / E 0 is dimensionless modulus parameters, τ i = η i / E i is relaxation time, ω is frequency, and n is the model order.

In addition, the order of the GMM also has to be determined. Related studies [39] show that the fourth-order model (i.e., n = 4) has high efficiency, small error, and convenient parameter acquisition. Therefore, the fourth order of GMM is used in this article for establishing the viscoelastic constitutive model, and its constitutive equations after expansion are as follows:

(25) E ′ = E ∞ + E ∞ ( g 1 + g 2 + g 3 + g 4 ) g 1 τ 1 2 ω 2 1 + τ 1 2 ω 2 + g 2 τ 2 2 ω 2 1 + τ 2 2 ω 2 + g 3 τ 3 2 ω 2 1 + τ 3 2 ω 2 + g 4 τ 4 2 ω 2 1 + τ 4 2 ω 2 ,

(26) E ″ = E ∞ ( g 1 + g 2 + g 3 + g 4 ) g 1 τ 1 ω 1 + τ 1 2 ω 2 + g 2 τ 2 ω 1 + τ 2 2 ω 2 + g 3 τ 3 ω 1 + τ 3 2 ω 2 + g 4 τ 4 ω 1 + τ 4 2 ω 2 ,

where E ′ is storage modulus, E ″ is loss modulus, E ∞ is quasi-static modulus, g i is dimensionless modulus parameters, τ i is relaxation time, and ω is frequency.

4.2.2 Model parameters

To obtain optimal model parameters [40,41], the Lsqcurvefit function was used in the fitting program based on the least square method, and by fitting the experimental data and the GMM, the model parameters are obtained under the condition of minimum error sum of squares.

As storage modulus and loss modulus shared the same parameter, the multiconstraint sharing parameter method is adopted, which ensures that the constraints forced parameters to be equal, so that they were regarded as a group of shared parameters. Moreover, to narrow the search range and improve the computational efficiency, the relaxation time of parameters should be constrained as follows:

(27) τ 1 > τ 2 > … > τ n .

As g i = E i / E 0 , the parameters gi and ∑gi should satisfy the constraints as shown in equation (28) to avoid large values.

(28) 0 < g i < 1 , ∑ g i < 1 .

In addition, it is necessary to determine the value of the parameters E ∞ , which usually corresponds to the storage modulus of polyurethane grounding materials at 0 Hz. Ref. [36] points out that its value is approximately 80% of the energy storage modulus at 1 Hz, which can be referred in the fitting process.

After the aforementioned steps, the lsqcurvefit function is used to fit the fourth-order generalized Maxwell constitutive equation and the test data. Subsequently, the model parameters are obtained and the correlation coefficient of the fitting curve is analyzed. If the correlation coefficient meets the requirements, g i and τ i can be substituted into equations (25) and (26), and the dynamic viscoelastic constitutive model of polyurethane grounding materials at the particular density is obtained. Furthermore, model parameters g i and τ i are also input parameters for the finite element analysis.

4.3 Verification of viscoelastic constitutive model of polyurethane grounding materials

For the validity of the new viscoelastic constitutive model, taking 0.375, 0.430, and 0.506 g·cm−3 polyurethane grounding materials as examples, the dynamic viscoelastic modulus of different densities are calculated, respectively, based on the aforementioned derivation. Then, the viscoelastic constitutive model of the polymer material is fitted and the fitting results are compared with DMA test data to verify the correctness of the viscoelastic constitutive model.

4.3.1 Model fitting

The first step of fitting the viscoelastic constitutive parameters is to calculate the dynamic viscoelastic modulus, and calculation data are used as DMA test data in the fitting program. The storage modulus and loss modulus within 0–19 Hz of 0.375, 0.430, and 0.506 g·cm−3 polyurethane grounding materials were calculated by equations (21) and (22), respectively, as shown in Table 4.

Table 4

Calculation of dynamic viscoelastic modulus

Frequency (Hz) 1 3 5 7 9 11 13 15 17 19
ρ = 0.375 g·cm−3 E′ (MPa) 327.1 333.1 336.5 341.0 343.4 344.6 345.8 346.6 347.1 347.6
E″ (MPa) 18.3 14.8 12.6 10.1 8.1 6.7 5.6 5.1 4.7 4.5
ρ = 0.430 g·cm−3 E′ (MPa) 422.5 430.9 435.2 440.3 444.1 445.7 447.1 448.0 448.7 448.9
E″ (MPa) 25.3 21.0 18.4 15.5 13.0 11.2 9.8 9.2 8.6 8.3
ρ = 0.506 g·cm−3 E′ (MPa) 572.9 585.4 590.9 596.6 602.9 605.1 606.9 607.9 608.9 608.5
E″ (MPa) 37.2 32.1 28.7 25.8 22.8 20.7 19.2 18.3 17.7 17.3

To obtain fitting parameters of the constitutive model, these data are input into the lsqcurvefit function, which is simulated by GMM. The calculation criterion of the lsqcurvefit function is that the sum of square error between the fitting value and the calculated value is the minimum. The expression is expressed as follows:

(29) R = ∑ i = 1 n [ ( E i − E ¯ i ) 2 + ( G i − G ¯ i ) 2 ] ,

where E i is fitted value of storage modulus, E ¯ i is the test value of storage modulus, G i is fitted value of loss modulus, and G ¯ i is test value of loss modulus.

4.3.2 Results and discussion

To determine the GMM viscoelastic constitutive parameters, curve fitting is done on the data points of E′ and E″ of the polyurethane grounding materials obtained from the calculation results (Table 4). The fitting parameters of the viscoelastic constitutive model (Table 5) and the fitting results of dynamic viscoelastic modulus (Figure 12) are obtained.

Table 5

Fitting parameters of constitutive model

Fitting parameters 1 2 3 4
ρ = 0.375 g·cm−3 g i 0.1068 0.1180 0.0742 0.6571
τ i (s) 0.7695 0.7262 0.0457 0.0001
ρ = 0.430 g·cm−3 g i 0.1025 0.0788 0.0622 0.4951
τ i (s) 0.7046 0.6563 0.0400 0.0001
ρ = 0.506 g·cm−3 g i 0.1040 0.1217 0.0791 0.6057
τ i (s) 0.6043 0.5979 0.0362 0.0002
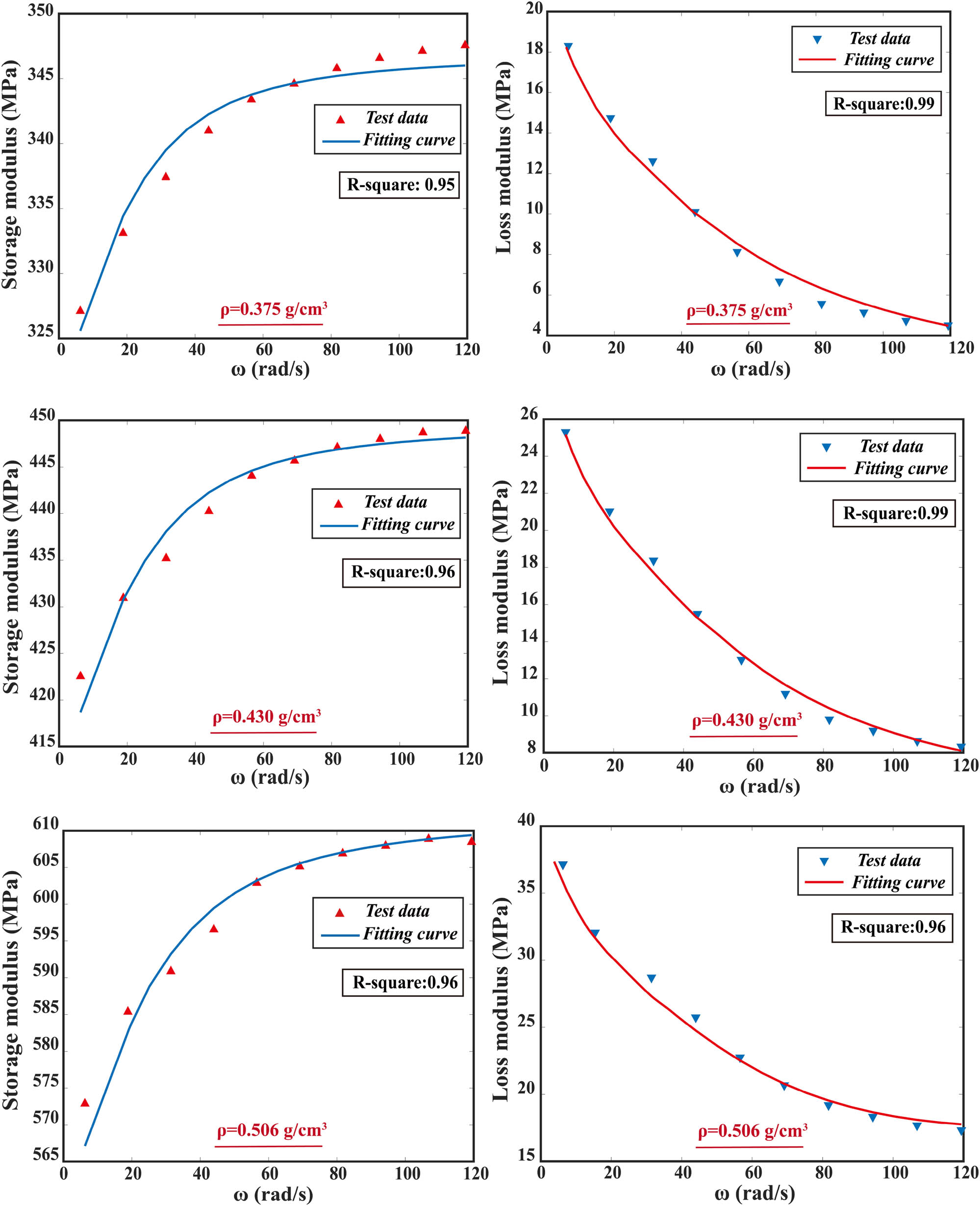
Figure 12 Fitting results of dynamic viscoelastic modulus at different densities.
Figure 12

Fitting results of dynamic viscoelastic modulus at different densities.

As can be seen from Figure 12, the calculated data of the viscoelastic constitutive model and DMA test data have a high degree of fitting, and the correlation coefficients are all greater than 0.95. Therefore, this constitutive model can accurately and efficiently characterize the dynamic viscoelastic properties of polyurethane grounding materials and can be directly used in the finite element simulation, which lays a foundation for the dynamic response analysis of polymer structures.

5 Conclusions

In this article, based on the DMA test of polyurethane grounding materials, the dynamic viscoelastic properties and constitutive models were systematically studied. Then, the dynamic viscoelastic constitutive model of polyurethane grounding materials based on generalized Maxwell was proposed, and the correctness and rationality of the constitutive model were verified. The main conclusions are as follows:

(1) Different viscoelastic constitutive models are compared based on frequency spectra of E′ and tan δ at different densities from the DMA test. The test results show that Maxwell and Kelvin models are not applicable in describing dynamic viscoelastic properties, and fractional viscoelastic models are not suitable for establishing the constitutive model of polyurethane grounding materials because the parameters are difficult to obtain. Owing to the feasibility of parameter acquisition and direct application in the structure analysis, the fourth-order GMM was adopted to construct the viscoelastic constitutive model of polyurethane grounding materials.

(2) To obtain the dynamic viscoelastic constitutive model of polyurethane grounding materials with different density. The multi-constraint sharing parameter method is adopted in fitting program. Based on the relationship between density and dynamic viscoelastic modulus, the fitting parameters were obtained. Then, the dynamic viscoelastic constitutive model of polyurethane grounding materials at particular density is obtained. The results of comparison show that the dynamic viscoelastic constitutive model constructed in this article is a more accurate and efficient model for polyurethane grounding materials that can serve as a reference for dynamic response analysis of structures.

Acknowledgements

The authors wish to thank the supports from National Natural Science Foundation of China (No. 51909243) and Key Scientific and Technological Project of Henan Province (202102310293).

  1. Funding information: National Natural Science Foundation of China (No. 51909243) and Key Scientific and Technological Q89 Q7 Project of Henan Province (202102310293)

  2. Author contributions: Zhang Jingwei: formal analysis, writing – original draft, and project administration; Li Jia: methodology, project administration, supervision, resources, and writing – original draft; Huang Chuhao: writing – review & editing, methodology. Chen Shuo: formal analysis. All authors have accepted responsibility for the entire content of this manuscript and approved its submission.

  3. Conflict of interest: Authors state no conflict of interest.

  4. Data availability statement: The raw data related to this article will be made available on request.

References

[1] Ding, H., A. Rahman, Q. Li, and Y. Qiu. Advanced mechanical characterization of asphalt mastics containing tourmaline modifier. Construction and Building Materials, Vol. 150, 2017, pp. 520–528.10.1016/j.conbuildmat.2017.05.203Search in Google Scholar

[2] Ling, M., Y. Zhang, F. Kaseer, A. E. Martin, and R. L. Lytton. Investigation of fracture behavior of asphalt mixture composite using energy-based approach. Composites Part B: Engineering, Vol. 181, 2020, id. 107324.10.1016/j.compositesb.2019.107324Search in Google Scholar

[3] Hesp, S. A. M., S. Iliuta, and J. W. Shirokoff. Reversible aging in asphalt binders. Energy & Fuels, Vol. 21, No. 2, 2007, pp. 1112–1121.10.1021/ef060463bSearch in Google Scholar

[4] Wang, X., S. Sadati, P. Taylor, C. Li, X. Wang, and A. Sha. Material characterization to assess effectiveness of surface treatment to prevent joint deterioration from oxychloride formation mechanism. Cement and Concrete Composites, Vol. 104, 2019, id. 103394.10.1016/j.cemconcomp.2019.103394Search in Google Scholar

[5] Wang, F., J. Li, M. Shi, and C. Guo. New seepage-proof and reinforcing technologies for dikes and dams and their applications. Journal of Hydroelectric Engineering, Vol. 35, 2016, pp. 1–11.Search in Google Scholar

[6] Fang, H., B. Li, F. Wang, Y. Wang, and C. Cui. The mechanical behaviour of drainage pipeline under traffic load before and after polymer grouting trenchless repairing. Tunnelling and Underground Space Technology, Vol. 74, 2018, pp. 185–194.10.1016/j.tust.2018.01.018Search in Google Scholar

[7] Guo, C., X. Chu, and F. Wang. Research on feasibility of non-water reaction polymer grouting technology application in seepage prevention of tailings reservoir. Water Science and Technology: Water Supply, Vol. 18, No. 1, 2017, pp. 203–213.10.2166/ws.2017.096Search in Google Scholar

[8] Li, L., S. Li, Q. Zhang, J. Cui, Z. H. Xu, and Z. Li. Experimental Study of a new polymer grouting material. Chinese Journal of Rock Mechanics and Engineering, Vol. 29, 2010, pp. 3150–3156.Search in Google Scholar

[9] Li, J., B. Wang, J. Zhang, and H. Hu. Experimental research on dynamic property of polymer grouting materials. Chinese Journal of Building Materials, Vol. 20, 2017, pp. 198–203.Search in Google Scholar

[10] Zhang, B., X. Zhang, Y. Zhong, X. Li, M. Hao, X. Sang, et al. Research on fatigue model of semi-rigid base asphalt pavement before and after polymer grouting. Advances in Civil Engineering, Vol. 2021, 2021, pp. 1–16.10.1155/2021/6658943Search in Google Scholar

[11] Shi, M., F. Wang, and J. Luo. Compressive strength of polymer grouting material at different temperatures. Journal of Wuhan University of Technology-Mater Sci Ed, Vol. 25, 2010, pp. 962–965.10.1007/s11595-010-0129-5Search in Google Scholar

[12] Li, J., J. Zhang, J. Xu, F. Wang, B. Wang, and Q. Li. Dynamic behavior of polymer antiseepage wall for earth dam by centrifuge test. International Journal of Geomechanics, Vol. 18, No. 12, 2018, pp. 04018179.1–04018179.17.10.1061/(ASCE)GM.1943-5622.0001294Search in Google Scholar

[13] Li, B., F. Wang, H. Fang, K. Yang, X. Zhang, and Y. Ji. Experimental and numerical study on polymer grouting pretreatment technology in void and corroded concrete pipes. Tunnelling and Underground Space Technology, Vol. 113, 2021, id. 103842.10.1016/j.tust.2021.103842Search in Google Scholar

[14] Ferry, J. D. Viscoelastic properties of polymer. Journal of Research of the National Bureau of Standards, Vol. 41, 1980, pp. 53–61.10.6028/jres.041.008Search in Google Scholar

[15] Seymour, R. and S. Cooper. Viscoelastic properties of polyurethane block polymers. Journal of Polymer Science: Polymer Symposia, Vol. 46, 2009, pp. 69–81.10.1002/polc.5070460107Search in Google Scholar

[16] Shamsi, R., G. Mir Mohamad Sadeghi, and G. Asghari. Dynamic mechanical analysis of polyurethanes and carbon nanotube based composites obtained from PET waste. Polymer Composites, Vol. 39, No. S2, 2018, pp. E754–E764.10.1002/pc.24155Search in Google Scholar

[17] Hartmann, B., J. Duffy, G. Lee, and E. Balizer. Thermal and dynamic mechanical properties of polyurethaneureas. Journal of Applied Polymer Science, Vol. 35, No. 7, 1988, pp. 1829–1852.10.1002/app.1988.070350710Search in Google Scholar

[18] Dadbin, S., R. Burford, and R. Chaplin. Interpenetrating polymer networks of Poly(allyl diglycol carbonate) and polyurethane: effect of composition and crosslink density on morphology and mechanical properties. Polymer, Vol. 37, 1996, pp. 785–792.10.1016/0032-3861(96)87254-5Search in Google Scholar

[19] He, Z., Q. Li, J. Wang, N. Yin, S. Jiang, and M. Kang. Effect of silane treatment on the mechanical properties of polyurethane/water glass grouting materials. Construction and Building Materials, Vol. 116, 2016, pp. 110–120.10.1016/j.conbuildmat.2016.04.112Search in Google Scholar

[20] Ahmad, M. A. A., M. S. Abdul Majid, M. R. Mohd Jamir, M. Mohd Noor, and A. G. Gibson. Dynamic mechanical analysis and effects of moisture on mechanical properties of interwoven hemp/polyethylene terephthalate (PET) hybrid composites. Construction and Building Materials, Vol. 179, 2018, pp. 265–276.10.1016/j.conbuildmat.2018.05.227Search in Google Scholar

[21] Faria, R., J. Duncan, and R. Brereton. Dynamic mechanical analysis and chemometrics for polymer identification. Polymer Testing, Vol. 26, 2007, pp. 402–412.10.1016/j.polymertesting.2006.12.012Search in Google Scholar

[22] Satapathy, S. and R. V. Kothapalli. Mechanical, dynamic mechanical and thermal properties of banana fiber/recycled high density polyethylene biocomposites filled with flyash cenospheres. Journal of Polymers and the Environment, Vol. 26, No. 1, 2018, pp. 200–213.10.1007/s10924-017-0938-0Search in Google Scholar

[23] Christensen, R. and L. Freund. Theory of viscoelasticity, Academic Press, Inc., New York, NY, 1982.10.1016/B978-0-12-174252-2.50012-0Search in Google Scholar

[24] Yang, T., W. Luo and P. Xu. Viscoelastic theory and application, Science Press, Inc., Beijing, China, 2004.Search in Google Scholar

[25] Sun, Y., Y. Gao, and S. Song. Effect of integrating memory on the performance of the fractional plasticity model for geomaterials. Acta Mechanica Sinica, Vol. 34, No. 5, 2018, pp. 896–901.10.1007/s10409-018-0777-9Search in Google Scholar

[26] Cheng, H., J. Wang, and Z. Huang. A thermo-viscoelastic constitutive model for compressible amorphous polymers. Mechanics of Time-Dependent Materials, Vol. 14, 2010, pp. 261–275.10.1007/s11043-010-9111-zSearch in Google Scholar

[27] Bagley, R. and P. Torvik. Fractional calculus in the transient analysis of viscoelastically damped structures. Aiaa Journal, Vol. 23, 1985, pp. 918–925.10.2514/6.1983-901Search in Google Scholar

[28] Bagley, R. L. and P. Torvik. On the fractional calculus model of viscoelastic behavior. Journal of Rheology, Vol. 30, No. 1, 1986, pp. 133–155.10.1122/1.549887Search in Google Scholar

[29] Pritz, T. Loss factor peak of viscoelastic materials: magnitude to width relations. Journal of Sound and Vibration, Vol. 246, 2001, pp. 265–280.10.1006/jsvi.2001.3636Search in Google Scholar

[30] Pritz, T. Five-parameter fractional derivative model for polymeric damping materials. Journal of Sound and Vibration, Vol. 265, 2003, pp. 935–952.10.1016/S0022-460X(02)01530-4Search in Google Scholar

[31] Nguyen, T., J. Li, L. Sun, D. Tran, and F. Xuan. Viscoelasticity modeling of dielectric elastomers by kelvin voigt-generalized maxwell model. Polymers, Vol. 13, 2021, id. 2203.10.3390/polym13132203Search in Google Scholar PubMed PubMed Central

[32] Jalocha, D., A. Constantinescu, and R. Nevière. Revisiting the identification of generalized maxwell models from experimental results. International Journal of Solids and Structures, Vol. Complete, No. 67–68, 2015, pp. 169–181.10.1016/j.ijsolstr.2015.04.018Search in Google Scholar

[33] Wan, Y., Y.-P. Xiong, and S. Zhang. Temperature dependent dynamic mechanical properties of magnetorheological elastomers: experiment and modeling. Composite Structures, Vol. 202, 2018, pp. 768–773.10.1016/j.compstruct.2018.04.010Search in Google Scholar

[34] Li, J., J. Zhang, and S. Chen. Study on dynamic viscoelastic properties and constitutive model of non-water reacted polyurethane grouting materials. Measurement, Vol. 176, 2021, id. 109115.10.1016/j.measurement.2021.109115Search in Google Scholar

[35] Hao, D., D. Li, and Y. Liao. A finite Viscoelastic Constitutive model for filled rubber-like materials. International Journal of Solids and Structures, Vol. 64–65, 2015, pp. 232–245.10.1016/j.ijsolstr.2015.04.002Search in Google Scholar

[36] Junior, P., J. Soares, A. Holanda, E. Parente Junior, and F. Junior. Dynamic viscoelastic analysis of asphalt pavements using a finite element formulation. Road Materials and Pavement Design, Vol. 11, 2010, pp. 409–433.10.3166/rmpd.11.409-433Search in Google Scholar

[37] Rameshkhah, S., M. Malakooti, P. Malekzadeh, and S. H. Meraji. Dynamic response analysis of viscoelastic pavement using differential quadrature element method. International Journal of Pavement Engineering, Vol. 21, 2018, pp. 1–15.10.1080/10298436.2018.1545091Search in Google Scholar

[38] Zhang, W. Power∼train rubber mounting constitutive relation and optimization. Master’s thesis, Tsinghua University, Beijing, China, 2012.Search in Google Scholar

[39] lv, H., H. Liu, Y. Tan, A. Meng, A. Cyriaque, and S. Xiao. An extended search method for identifying optimal parameters of the generalized maxwell model. Construction and Building Materials, Vol. 266, 2021, id. 120796.10.1016/j.conbuildmat.2020.120796Search in Google Scholar

[40] Shuai, C., J. Duan, and J. Wang. Method of establishing generalized maxwell model for viscoelastic material. Chinese Journal of Theoretical and Applied Mechanics, Vol. 38, 2006, pp. 565–569.Search in Google Scholar

[41] Diani, J., P. Gilormini, C. Fredy, and I. Rousseau. Predicting thermal shape memory of crosslinked polymer networks from linear viscoelasticity. International Journal of Solids and Structures, Vol. 49, 2012, pp. 793–799.10.1016/j.ijsolstr.2011.11.019Search in Google Scholar
Received: 2021-08-25
Revised: 2021-10-18
Accepted: 2021-10-28
Published Online: 2022-04-19

© 2022 Zhang Jingwei et al., published by De Gruyter

This work is licensed under the Creative Commons Attribution 4.0 International License.

Articles in the same Issue

  1. Review Articles
  2. State of the art, challenges, and emerging trends: Geopolymer composite reinforced by dispersed steel fibers
  3. A review on the properties of concrete reinforced with recycled steel fiber from waste tires
  4. Copper ternary oxides as photocathodes for solar-driven CO2 reduction
  5. Properties of fresh and hardened self-compacting concrete incorporating rice husk ash: A review
  6. Basic mechanical and fatigue properties of rubber materials and components for railway vehicles: A literature survey
  7. Research progress on durability of marine concrete under the combined action of Cl− erosion, carbonation, and dry–wet cycles
  8. Delivery systems in nanocosmeceuticals
  9. Study on the preparation process and sintering performance of doped nano-silver paste
  10. Analysis of the interactions between nonoxide reinforcements and Al–Si–Cu–Mg matrices
  11. Research Articles
  12. Study on the influence of structural form and parameters on vibration characteristics of typical ship structures
  13. Deterioration characteristics of recycled aggregate concrete subjected to coupling effect with salt and frost
  14. Novel approach to improve shale stability using super-amphiphobic nanoscale materials in water-based drilling fluids and its field application
  15. Research on the low-frequency multiline spectrum vibration control of offshore platforms
  16. Multiple wide band gaps in a convex-like holey phononic crystal strip
  17. Response analysis and optimization of the air spring with epistemic uncertainties
  18. Molecular dynamics of C–S–H production in graphene oxide environment
  19. Residual stress relief mechanisms of 2219 Al–Cu alloy by thermal stress relief method
  20. Characteristics and microstructures of the GFRP waste powder/GGBS-based geopolymer paste and concrete
  21. Development and performance evaluation of a novel environmentally friendly adsorbent for waste water-based drilling fluids
  22. Determination of shear stresses in the measurement area of a modified wood sample
  23. Influence of ettringite on the crack self-repairing of cement-based materials in a hydraulic environment
  24. Multiple load recognition and fatigue assessment on longitudinal stop of railway freight car
  25. Synthesis and characterization of nano-SiO2@octadecylbisimidazoline quaternary ammonium salt used as acidizing corrosion inhibitor
  26. Perforated steel for realizing extraordinary ductility under compression: Testing and finite element modeling
  27. The influence of oiled fiber, freeze-thawing cycle, and sulfate attack on strain hardening cement-based composites
  28. Perforated steel block of realizing large ductility under compression: Parametric study and stress–strain modeling
  29. Study on dynamic viscoelastic constitutive model of nonwater reacted polyurethane grouting materials based on DMA
  30. Mechanical behavior and mechanism investigation on the optimized and novel bio-inspired nonpneumatic composite tires
  31. Effect of cooling rate on the microstructure and thermal expansion properties of Al–Mn–Fe alloy
  32. Research on process optimization and rapid prediction method of thermal vibration stress relief for 2219 aluminum alloy rings
  33. Failure prevention of seafloor composite pipelines using enhanced strain-based design
  34. Deterioration of concrete under the coupling action of freeze–thaw cycles and salt solution erosion
  35. Creep rupture behavior of 2.25Cr1Mo0.25V steel and weld for hydrogenation reactors under different stress levels
  36. Statistical damage constitutive model for the two-component foaming polymer grouting material
  37. Nano-structural and nano-constraint behavior of mortar containing silica aggregates
  38. Influence of recycled clay brick aggregate on the mechanical properties of concrete
  39. Effect of LDH on the dissolution and adsorption behaviors of sulfate in Portland cement early hydration process
  40. Comparison of properties of colorless and transparent polyimide films using various diamine monomers
  41. Study in the parameter influence on underwater acoustic radiation characteristics of cylindrical shells
  42. Experimental study on basic mechanical properties of recycled steel fiber reinforced concrete
  43. Dynamic characteristic analysis of acoustic black hole in typical raft structure
  44. A semi-analytical method for dynamic analysis of a rectangular plate with general boundary conditions based on FSDT
  45. Research on modification of mechanical properties of recycled aggregate concrete by replacing sand with graphite tailings
  46. Dynamic response of Voronoi structures with gradient perpendicular to the impact direction
  47. Deposition mechanisms and characteristics of nano-modified multimodal Cr3C2–NiCr coatings sprayed by HVOF
  48. Effect of excitation type on vibration characteristics of typical ship grillage structure
  49. Study on the nanoscale mechanical properties of graphene oxide–enhanced shear resisting cement
  50. Experimental investigation on static compressive toughness of steel fiber rubber concrete
  51. Study on the stress field concentration at the tip of elliptical cracks
  52. Corrosion resistance of 6061-T6 aluminium alloy and its feasibility of near-surface reinforcements in concrete structure
  53. Effect of the synthesis method on the MnCo2O4 towards the photocatalytic production of H2
  54. Experimental study of the shear strength criterion of rock structural plane based on three-dimensional surface description
  55. Evaluation of wear and corrosion properties of FSWed aluminum alloy plates of AA2020-T4 with heat treatment under different aging periods
  56. Thermal–mechanical coupling deformation difference analysis for the flexspline of a harmonic drive
  57. Frost resistance of fiber-reinforced self-compacting recycled concrete
  58. High-temperature treated TiO2 modified with 3-aminopropyltriethoxysilane as photoactive nanomaterials
  59. Effect of nano Al2O3 particles on the mechanical and wear properties of Al/Al2O3 composites manufactured via ARB
  60. Co3O4 nanoparticles embedded in electrospun carbon nanofibers as free-standing nanocomposite electrodes as highly sensitive enzyme-free glucose biosensors
  61. Effect of freeze–thaw cycles on deformation properties of deep foundation pit supported by pile-anchor in Harbin
  62. Temperature-porosity-dependent elastic modulus model for metallic materials
  63. Effect of diffusion on interfacial properties of polyurethane-modified asphalt–aggregate using molecular dynamic simulation
  64. Experimental study on comprehensive improvement of shear strength and erosion resistance of yellow mud in Qiang Village
  65. A novel method for low-cost and rapid preparation of nanoporous phenolic aerogels and its performance regulation mechanism
  66. In situ bow reduction during sublimation growth of cubic silicon carbide
  67. Adhesion behaviour of 3D printed polyamide–carbon fibre composite filament
  68. An experimental investigation and machine learning-based prediction for seismic performance of steel tubular column filled with recycled aggregate concrete
  69. Effects of rare earth metals on microstructure, mechanical properties, and pitting corrosion of 27% Cr hyper duplex stainless steel
  70. Application research of acoustic black hole in floating raft vibration isolation system
  71. Multi-objective parametric optimization on the EDM machining of hybrid SiCp/Grp/aluminum nanocomposites using Non-dominating Sorting Genetic Algorithm (NSGA-II): Fabrication and microstructural characterizations
  72. Estimating of cutting force and surface roughness in turning of GFRP composites with different orientation angles using artificial neural network
  73. Displacement recovery and energy dissipation of crimped NiTi SMA fibers during cyclic pullout tests
https://doi.org/10.1515/rams-2022-0004
Keywords for this article
non-water reacted polymer material; dynamic thermomechanical analysis; dynamic viscoelastic constitutive model; generalized Maxwell model
Creative Commons
BY 4.0

Articles in the same Issue

  1. Review Articles
  2. State of the art, challenges, and emerging trends: Geopolymer composite reinforced by dispersed steel fibers
  3. A review on the properties of concrete reinforced with recycled steel fiber from waste tires
  4. Copper ternary oxides as photocathodes for solar-driven CO2 reduction
  5. Properties of fresh and hardened self-compacting concrete incorporating rice husk ash: A review
  6. Basic mechanical and fatigue properties of rubber materials and components for railway vehicles: A literature survey
  7. Research progress on durability of marine concrete under the combined action of Cl− erosion, carbonation, and dry–wet cycles
  8. Delivery systems in nanocosmeceuticals
  9. Study on the preparation process and sintering performance of doped nano-silver paste
  10. Analysis of the interactions between nonoxide reinforcements and Al–Si–Cu–Mg matrices
  11. Research Articles
  12. Study on the influence of structural form and parameters on vibration characteristics of typical ship structures
  13. Deterioration characteristics of recycled aggregate concrete subjected to coupling effect with salt and frost
  14. Novel approach to improve shale stability using super-amphiphobic nanoscale materials in water-based drilling fluids and its field application
  15. Research on the low-frequency multiline spectrum vibration control of offshore platforms
  16. Multiple wide band gaps in a convex-like holey phononic crystal strip
  17. Response analysis and optimization of the air spring with epistemic uncertainties
  18. Molecular dynamics of C–S–H production in graphene oxide environment
  19. Residual stress relief mechanisms of 2219 Al–Cu alloy by thermal stress relief method
  20. Characteristics and microstructures of the GFRP waste powder/GGBS-based geopolymer paste and concrete
  21. Development and performance evaluation of a novel environmentally friendly adsorbent for waste water-based drilling fluids
  22. Determination of shear stresses in the measurement area of a modified wood sample
  23. Influence of ettringite on the crack self-repairing of cement-based materials in a hydraulic environment
  24. Multiple load recognition and fatigue assessment on longitudinal stop of railway freight car
  25. Synthesis and characterization of nano-SiO2@octadecylbisimidazoline quaternary ammonium salt used as acidizing corrosion inhibitor
  26. Perforated steel for realizing extraordinary ductility under compression: Testing and finite element modeling
  27. The influence of oiled fiber, freeze-thawing cycle, and sulfate attack on strain hardening cement-based composites
  28. Perforated steel block of realizing large ductility under compression: Parametric study and stress–strain modeling
  29. Study on dynamic viscoelastic constitutive model of nonwater reacted polyurethane grouting materials based on DMA
  30. Mechanical behavior and mechanism investigation on the optimized and novel bio-inspired nonpneumatic composite tires
  31. Effect of cooling rate on the microstructure and thermal expansion properties of Al–Mn–Fe alloy
  32. Research on process optimization and rapid prediction method of thermal vibration stress relief for 2219 aluminum alloy rings
  33. Failure prevention of seafloor composite pipelines using enhanced strain-based design
  34. Deterioration of concrete under the coupling action of freeze–thaw cycles and salt solution erosion
  35. Creep rupture behavior of 2.25Cr1Mo0.25V steel and weld for hydrogenation reactors under different stress levels
  36. Statistical damage constitutive model for the two-component foaming polymer grouting material
  37. Nano-structural and nano-constraint behavior of mortar containing silica aggregates
  38. Influence of recycled clay brick aggregate on the mechanical properties of concrete
  39. Effect of LDH on the dissolution and adsorption behaviors of sulfate in Portland cement early hydration process
  40. Comparison of properties of colorless and transparent polyimide films using various diamine monomers
  41. Study in the parameter influence on underwater acoustic radiation characteristics of cylindrical shells
  42. Experimental study on basic mechanical properties of recycled steel fiber reinforced concrete
  43. Dynamic characteristic analysis of acoustic black hole in typical raft structure
  44. A semi-analytical method for dynamic analysis of a rectangular plate with general boundary conditions based on FSDT
  45. Research on modification of mechanical properties of recycled aggregate concrete by replacing sand with graphite tailings
  46. Dynamic response of Voronoi structures with gradient perpendicular to the impact direction
  47. Deposition mechanisms and characteristics of nano-modified multimodal Cr3C2–NiCr coatings sprayed by HVOF
  48. Effect of excitation type on vibration characteristics of typical ship grillage structure
  49. Study on the nanoscale mechanical properties of graphene oxide–enhanced shear resisting cement
  50. Experimental investigation on static compressive toughness of steel fiber rubber concrete
  51. Study on the stress field concentration at the tip of elliptical cracks
  52. Corrosion resistance of 6061-T6 aluminium alloy and its feasibility of near-surface reinforcements in concrete structure
  53. Effect of the synthesis method on the MnCo2O4 towards the photocatalytic production of H2
  54. Experimental study of the shear strength criterion of rock structural plane based on three-dimensional surface description
  55. Evaluation of wear and corrosion properties of FSWed aluminum alloy plates of AA2020-T4 with heat treatment under different aging periods
  56. Thermal–mechanical coupling deformation difference analysis for the flexspline of a harmonic drive
  57. Frost resistance of fiber-reinforced self-compacting recycled concrete
  58. High-temperature treated TiO2 modified with 3-aminopropyltriethoxysilane as photoactive nanomaterials
  59. Effect of nano Al2O3 particles on the mechanical and wear properties of Al/Al2O3 composites manufactured via ARB
  60. Co3O4 nanoparticles embedded in electrospun carbon nanofibers as free-standing nanocomposite electrodes as highly sensitive enzyme-free glucose biosensors
  61. Effect of freeze–thaw cycles on deformation properties of deep foundation pit supported by pile-anchor in Harbin
  62. Temperature-porosity-dependent elastic modulus model for metallic materials
  63. Effect of diffusion on interfacial properties of polyurethane-modified asphalt–aggregate using molecular dynamic simulation
  64. Experimental study on comprehensive improvement of shear strength and erosion resistance of yellow mud in Qiang Village
  65. A novel method for low-cost and rapid preparation of nanoporous phenolic aerogels and its performance regulation mechanism
  66. In situ bow reduction during sublimation growth of cubic silicon carbide
  67. Adhesion behaviour of 3D printed polyamide–carbon fibre composite filament
  68. An experimental investigation and machine learning-based prediction for seismic performance of steel tubular column filled with recycled aggregate concrete
  69. Effects of rare earth metals on microstructure, mechanical properties, and pitting corrosion of 27% Cr hyper duplex stainless steel
  70. Application research of acoustic black hole in floating raft vibration isolation system
  71. Multi-objective parametric optimization on the EDM machining of hybrid SiCp/Grp/aluminum nanocomposites using Non-dominating Sorting Genetic Algorithm (NSGA-II): Fabrication and microstructural characterizations
  72. Estimating of cutting force and surface roughness in turning of GFRP composites with different orientation angles using artificial neural network
  73. Displacement recovery and energy dissipation of crimped NiTi SMA fibers during cyclic pullout tests
Sign up now to receive a 20% welcome discount
Institutional Access
How does access work?
Have an idea on how to improve our website?
Please write us.
© 2025 De Gruyter Brill
Downloaded on 18.12.2025 from https://www.degruyterbrill.com/document/doi/10.1515/rams-2022-0004/html
Scroll to top button