Abstract
Two novel nonpneumatic tires named Tweel-2, designed based on the commercial Tweel model, and Saddle with hyperbolic paraboloid spokes are proposed in this study. Four nonpneumatic tire samples were successfully prepared with the 3D printing technology to measure and analyze and compare their properties. The results of quasi-static compression experiments showed that with the same relative density, the vertical bearing capacity of Tweel-2 tire was 1.4 times that of Tweel tire, while the vertical bearing capacity of the saddle tire was 4 times and 2.4 times that of Tweel and honeycomb tires, respectively. The finite element simulation method was used to explore the mechanism of improvement in vertical bearing capacity and energy absorption of the Tweel-2 and saddle design. The so-called circumferential unit in Tweel-2 and honeycomb tires enhances the deformation coordination between the spokes of Tweel-2 and increases the critical bearing capacity of the spokes by shortening the length of the deformation zone, so that more external work can be consumed under the same vertical deformation. The spatial configuration of the hyperbolic paraboloid can optimize the spatial stress distribution of the saddle tire and makes sure that a bigger amount of material deforms and participates in energy absorption, thus improving the overall strain energy level of the spokes.
1 Introduction
Tires are the only medium between a vehicle’s body and the ground. Its basic function, besides driving the vehicle, is to bear the weight of the vehicle’s body, and at the same time, it can absorb the impact of rough roads on the vehicle through its own deformation, so as to achieve buffering and damping [1,2,3]. Pneumatic tires have the advantages of lightweight, low energy loss, and so on, and it has dominated the world tire market for more than 100 years [4]. However, due to the structural form of the inner pneumatic tube, air leakage or tire burst is an insurmountable challenge for the safe service of the pneumatic tires. In recent years, researchers have replaced the inner pneumatic tube with elastic materials or deformable elastic structures and proposed nonpneumatic tires with the resistance of puncture and blowout [5,6,7]. Currently, vertical load, vertical stiffness, absorbed energy, and the like are used as main evaluation indexes of mechanical properties of the tire [8,9,10,11,12]. In the initial stage of quasi-static vertical compression, with the increase of vertical deformation, the vertical load on the tire increases nearly linearly, and the slope of the load–displacement curve is the vertical stiffness. The greater the vertical stiffness in this stage is, the greater the vertical load for the same vertical deformation is, which means the vertical bearing capacity of the tire is higher [8,9,10]. Meanwhile, the greater the integral area under the load–displacement curve is, the higher the energy absorbed through the deformation of the tire during the bearing process is, which means better buffering and damping performance [11].
Researchers have applied honeycomb structures with lightweight, high strength, and excellent energy absorption properties [13,14,15,16,17,18] to the deformable structure layers of nonpneumatic tires (Figure 1(a)) and have developed a lot of lightweight and topology optimization designs to improve the vertical bearing capacity of nonpneumatic tires.
Ju et al. [4] and Kim et al. [19] designed a honeycomb tire with an average cell expanding angle of 15.76°, which had the same geometric dimension and similar vertical stiffness as those of the conventional pneumatic tire, but more compliant, being the vertical load born by the honeycomb tire about 88% that of pneumatic tires at the same vertical strain.
Jin et al. [1] used the same average cell expanding angle and slightly increased hub and tread radiuses of the pneumatic tire, while the vertical load born by the honeycomb tire under the same vertical strain was 103% that of conventional pneumatic tires. Further research has shown that the vertical stiffness of the approximately linear stage of the honeycomb tire can be improved by reducing the average cell expanding angle or increasing the cell wall thickness [4,11,19] and by reducing the cell side length or in-creasing the cell density [11,20], but the greater the vertical stiffness is, the lower the energy absorbed by the structure at this stage is, for a specific practical strain range.
On the commercial side, with the gradual maturity of polyurethane hyperelastic materials in commercial fields, Jang et al. [21] and Kucewicz et al. [22] have successively launched two commercial nonpneumatic tires, Tweel (Figure 1(b)) and AirFree Concept (AC) (Figure 1(c)), respectively. Aboul-Yazid et al. [23] numerically analyzed the vertical stiffness of the honeycomb tire, the Tweel tire, and the AC tire with the same spoke thickness, and the results showed that the total mass of the latter two kinds of tires was slightly higher than that of the honeycomb tire, and the vertical stiffness of the Tweel tire was the highest, about 2.3 times that of the honeycomb tire and 3.8 times that of the AC tire, respectively. Rugsaj and Suvanjumrat [9] experimentally measured the vertical stiffness of the Tweel tire with a spoke thickness of 5 mm, which was 109% of the upper limit of the vertical stiffness of the pneumatic tire. Rugsaj and Suvanjumrat [10] proposed an interconnected mesh spoke tire (Figure 1(d)) and compared it with the honeycomb tire and Tweel tire with the same relative density. It is found that under the same vertical deformation, the vertical load born by the interconnected mesh spoke tire was 1.2 and 1.4 times that of the honeycomb tire and the Tweel tire, respectively. Kucewicz et al. [22] proposed a Kucwheel (Figure 1(e)) and compared it with the honeycomb tire, the Tweel tire, and AC tire with the same relative density. The numerical results showed that for the same vertical deformation, the vertical load born by the Kuc tire was similar to that of the honeycomb design, 1.4 times that of the Tweel tire, and much higher than that of the AC tire. Referring to the geometric dimensions of the 195/50R16 pneumatic tire, Zhang et al. [24] proposed a grid type tire (Figure 1(f)) and compared it with the honeycomb tire, the Tweel tire, and the AC tire with the same relative density and the same spoke thickness of 5 mm. It is found that under the same vertical deformation, the vertical load born by the grid type tire was similar to that of the honeycomb tire and 1.7 and 1.2 times that of the Tweel tire and pneumatic tire, respectively.
Among the relatively mature commercial nonpneumatic tires, with the same relative density, the vertical bearing capacity of the honeycomb tire is higher than that of the Tweel tire, and both are higher than that of the AC tire. However, nonpneumatic tires with novel structural designs, such as the Kucwheel, interconnected mesh, spoke and grid type tires, only have a very limited improvement in vertical bearing capacity, compared to the honeycomb tire.
Surprisingly, nature provides us with another example of an exquisite structure with excellent energy absorption. It was observed by Patek et al. [27], Devries et al. [28], and Tadayon et al. [29] that there is a saddle structure in the forelimb of a mantis shrimp, which is equivalent to a flexible biological spring, and in which a large amount of deformation energy can be stored. The mantis shrimp can release this energy instantaneously to achieve a fatal attack on its prey. Further research by Tadayon et al. [30] showed that the stress distribution on the surface of the saddle structure is relatively uniform in a pressure bearing process, which can effectively reduce stress concentration.
Two new nonpneumatic tire designs are proposed in this article. Combined with the 3D printing technology, static compression experiment, and finite element simulation, the quasi-static compression processes of the honeycomb, Tweel, Tweel-2, and saddle tire samples were studied and the quantitative characterization of the vertical bearing performance and the deformation energy absorption of the four types of samples were given. Furthermore, the mechanism of significant improvement in the static mechanical properties of tires with the Tweel-2 and saddle designs were discussed, which provides an idea for the novel structural design of nonpneumatic tires.
2 Experimental details and results
2.1 Nonpneumatic tire models
Four nonpneumatic tire samples of Tweel, Tweel-2, honeycomb, and saddle were designed. The Tweel and honeycomb samples were referred to as prototypes of nonpneumatic tires available in the market, while the Tweel-2 sample was an optimized one based on Tweel, and the saddle sample was a novel nonpneumatic tire structure in which bionic elements were introduced. The design parameters are described in Figure 2(a). The tire samples were printed by Object260 Connex3 (Stratasys Ltd USA) with a print precision of 16 µm in the layer deposition direction with high-quality mode and standard resolution of 600DPI (dots per inch) in the print plane [31], and the printing material was T8430. T8430 is a composite material with mixed properties created by combining Verowhite and Tangoplus [32], two basic photopolymers for the 3D printer, at a specific concentration. All of these possible combinations are preconfigured and selectable by using the production software Objet Studio (Stratasys Ltd USA) to ensure predictable, repeatable results, and these materials are called digital materials by Straysis. The relative density of the tire sample is defined as the actual material volume divided by the volume, which is π(R + t 1)2 b of cylindrical space occupied by the tire, where R and t 1 are the inner radius and wall thickness of tire outer ring, respectively, and b is the axial thickness of tires. The relative density of the four-tire samples was 22.3%, the axial thickness was b = 15 mm, the wall thickness of the inner and outer rings was t 1 = 1.20 mm, and the radiuses of inner and outer rings were r = 27.15 mm and R = 50.00 mm, respectively. The structural layer was between the inner and outer rings and was divided by 24 groups of structural units with equal central angles of 15°, see Figure 2(b)–(e). The sample center o was the origin of coordinates (0, 0, 0).
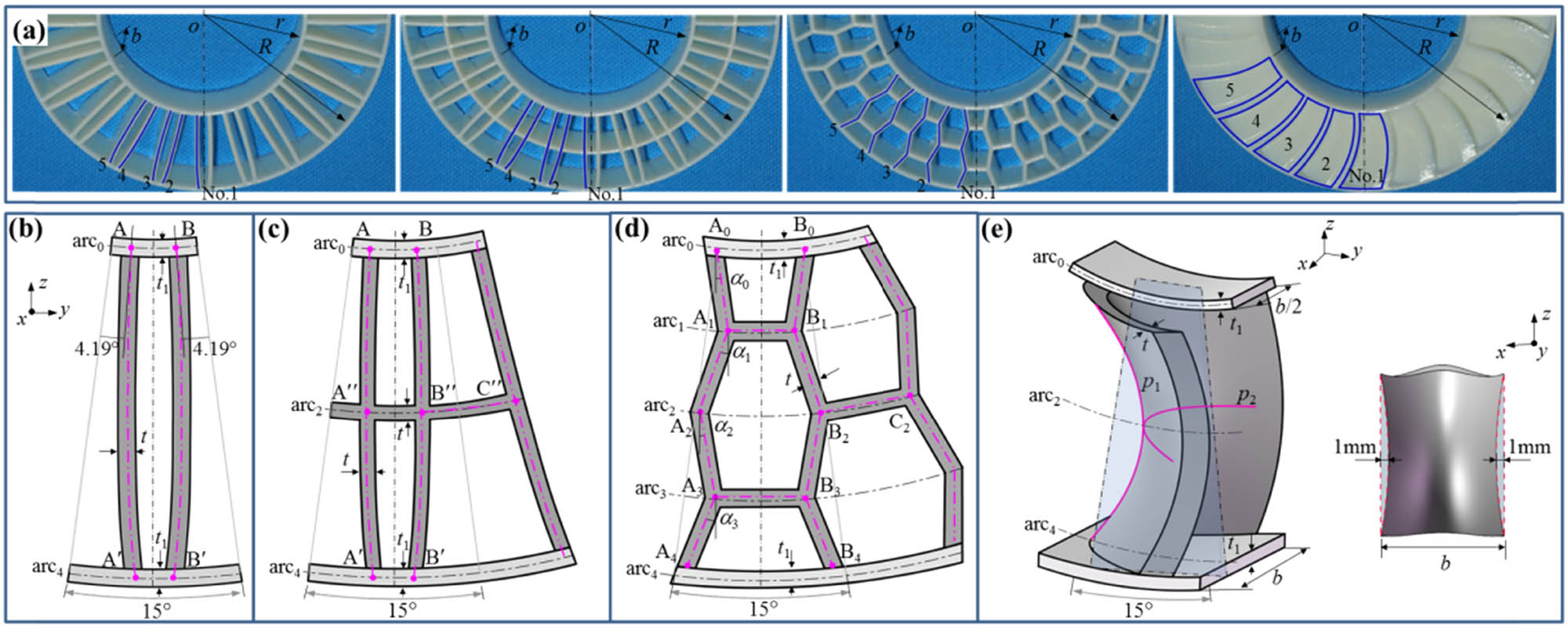
(a) Nonpneumatic tire samples and corresponding structure units: (b) Tweel tire; (c) Tweel-2 tire; (d) honeycomb tire; and (e) saddle tire.
First, for the Tweel, Tweel-2, and honeycomb samples, the centerlines of the wall sections of the structural units were generated; second, the unit wall thicknesses t were set as 1.19, 1.00, and 1.24 mm, respectively; and finally, the thickness b along the x direction was set as 15 mm, and thus, a three-dimensional geometrical model was obtained. The specific process of generating the centerlines of the wall sections of the structural units is as follows. For the Tweel sample (Figure 2(b)), referring to the photo of Michelin’s Tweel tire, two radii were drawn, which form an angle of 4.19°, respectively, with the left and right boundaries of the sector with a central angle of 15°; the two radii intersect with the inner ring centerline arc0 at points A and B, respectively; and with A and B as the starting points, two spline curves that fit with the Tweel picture and intersect with the outer ring centerline at points A′ and B′ were, respectively, drawn. The radial curves AA′ and BB′ are the centerlines of the wall sections of a Tweel structural unit. For the Tweel-2 sample (Figure 2(c)), a middle ring centerline arc2 was added between the inner and outer rings of the Tweel sample, which intersects with the curves AA′ and BB′ at points A″ and B″, respectively. The two radial curves AA′ and BB′ were connected by a circumferential arc A″B″ to form the centerlines of the wall sections of a Tweel-2 structural unit. In addition, the adjacent Tweel-2 structural units were connected by a circumferential arc B″C″. For the honeycomb sample (Figure 2(d)), the inner ring section centerline arc0 intersects with the left and right boundaries of the sector with a central angle of 15° at A0 and B0, respectively. Concentric arcs arc1, arc2, and arc3 were, respectively, drawn, connecting quarter points of the radial distance between arc0 and the outer ring section centerline arc4. With A
i
and B
i
as the starting points, straight lines forming included angle α
i
with the vertical direction were drawn, intersecting with arc
i+1 at A
i+1 and B
i+1, respectively, where
Compared with the aforementioned three structures, the projection plane of the structural unit of the saddle sample on the yoz plane is different (Figure 2(e)). A saddle surface p
1
p
2 was generated, with a control equation of
Obviously, the structural units of Tweel-2 and saddle samples are composed of radial spokes, while those of Tweel-2 and honeycomb samples are composed of radial spokes and circumferential elements. All these aforementioned geometric design parameters are tuned to make the four nonpneumatic tire samples have constant total mass. The subsequent stress analysis showed that the spoke was the main force bearing member when the sample bears the vertical load. For the convenience of description, spokes were numbered as No. 1, No. 2, and No. 5, as shown in Figure 2(a). The spokes of the Tweel and Tweel-2 tires were curved panels with small curvatures, while the spokes of the honeycomb and saddle tires were corrugated plates and hyperbolic parabolic plates, respectively. In addition, the spokes of the Tweel-2 and honeycomb tires were connected by the circumferential elements, and the spokes were interrelated with each other.
2.2 Experimental details
A self-designed and processed rigid fixture was used to simulate a rigid hub to apply vertical pressure to the structural layer of the tire (Figure 3). The rigid cylinder of the fixture was closely jointed with the inner ring of the tire sample; the upper end of the fixture was connected with the force sensor by bolts to ensure that the central axis of the force sensor is overlapped with that of the sample and passes through the center of the bottom plate of the testing machine. Uniaxial compression tests were carried out on the samples using an MTS testing machine (MTS Systems, Minnesota, USA), and the rising speed of the bottom plate was 1 mm·min−1. The bottom plate of the testing machine was adjusted to be nearly in contact with the bottom face of the sample, and displacement and force sensors were reset to zero. At the same time, the height and the angle of the camera were adjusted so that the central axis of the lens is perpendicular to the surface of the sample and is located at the same height as the center o of the sample at the same time.
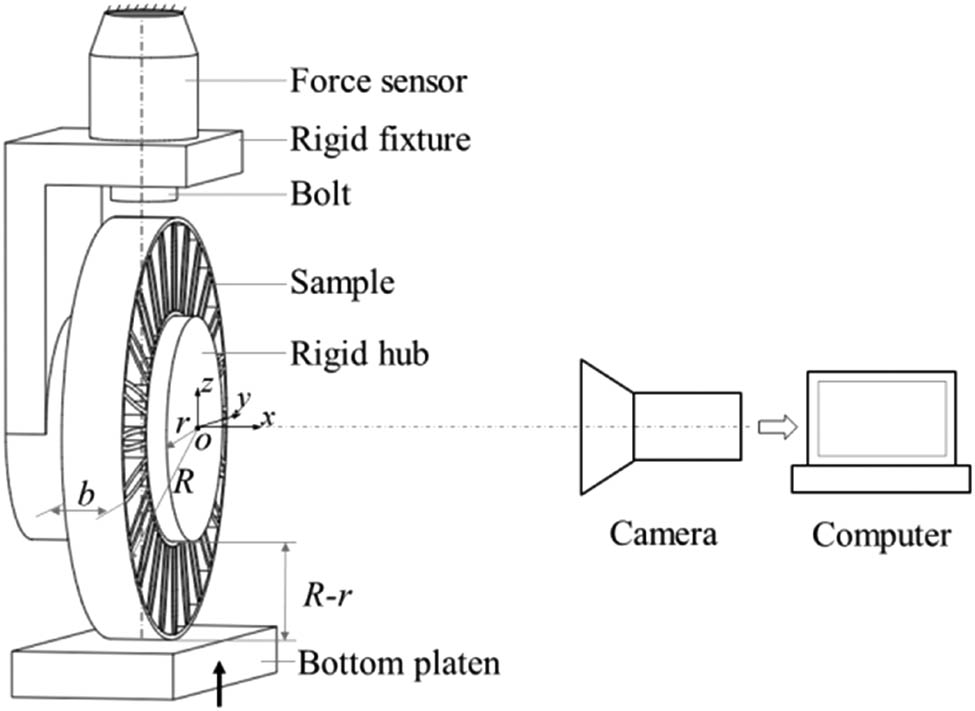
Diagram of quasi-static uniaxial compression experiment.
During loading, the displacement sensor’s reading of the testing machine is the deformation amount of the tire sample, and the nominal strain of the tire sample can be obtained by dividing the measured displacement by the tire section height R–r–t 1, as per GB/T 2977-2008. The force sensor’s reading is the vertical load born by the tire sample, and the nominal stress of the tire sample can be obtained by dividing the measured force by 2br [33]. The solid lines in Figure 4 are nominal stress–strain curves of the four nonpneumatic tire samples under quasi-static uniaxial compression. At the same time, the evolution process of the tire sample configuration was recorded by the camera synchronously, and the sampling frame frequency was 1 fps. The images show the strain situation during the test and the corresponding simulation results, as shown in Figure 5 for each tire at six different time points. Stress–strain points 1 to 6 in the experiment (solid symbols) and simulation (hollow symbols) are also marked in Figure 4 according to the time points labeled in Figure 5.
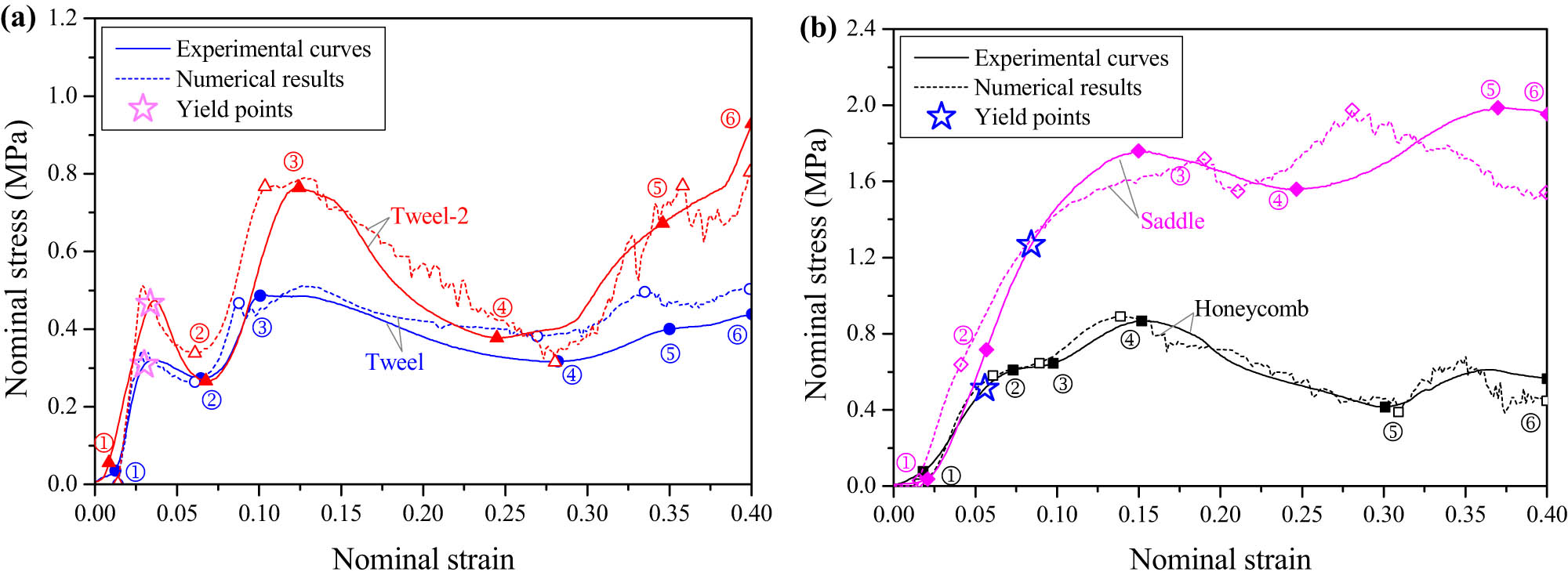
Nominal stress–strain curves of nonpneumatic (a) Tweel and Tweel-2; (b) honeycomb and saddle tire samples under quasi-static uniaxial compression.
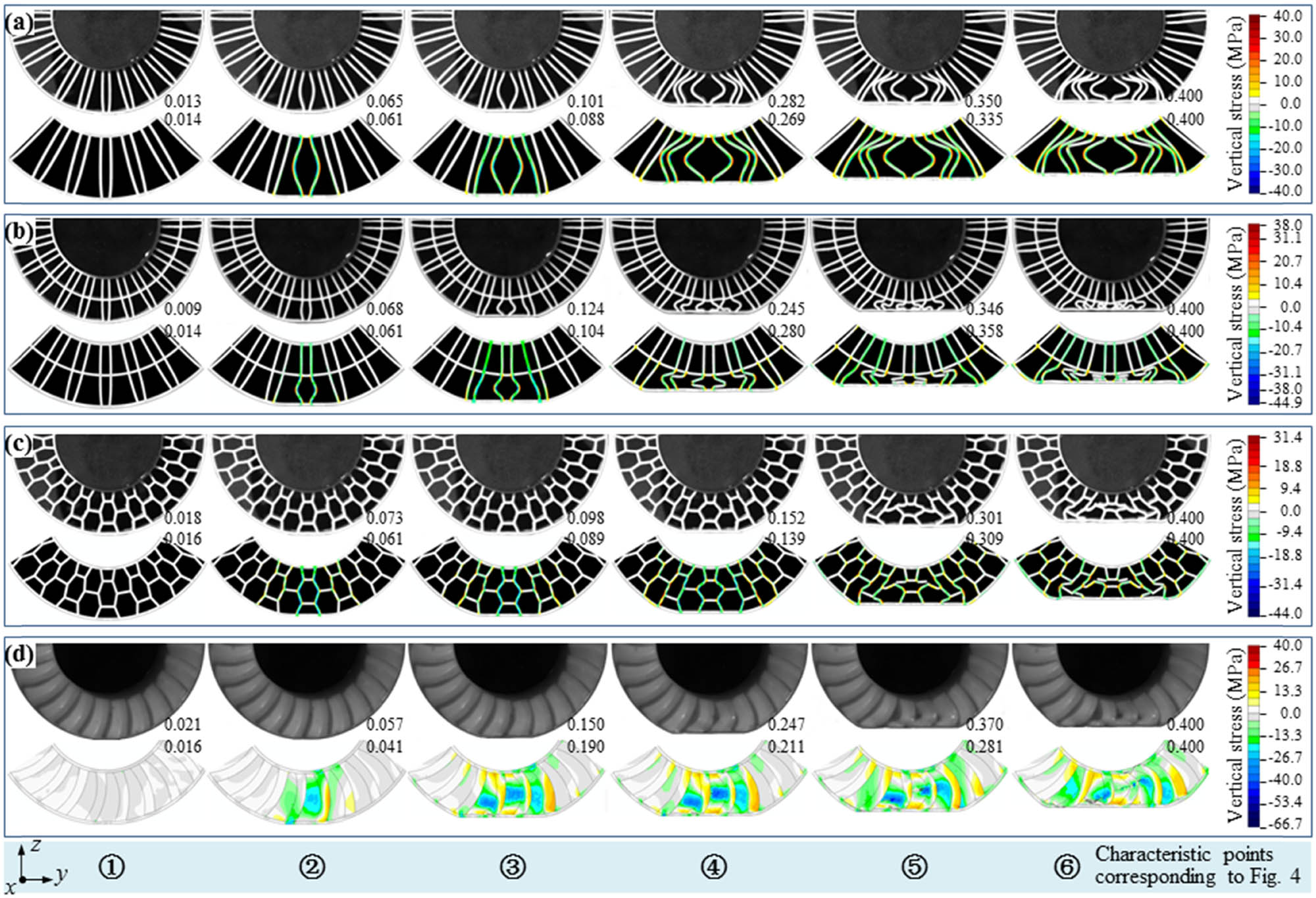
Evolution of the tire shape as obtained from the camera images and FEM simulation results, for six strain points and each tire: (a) Tweel; (b) Tweel-2; (c) honeycomb; and (d) saddle. The stress levels, in color scale, were evaluated with FEM models. (a)–(d) The first rows are the camera images, while the second rows are the FE results.
3 Numerical modeling and analysis
3.1 Material properties
According to the ASTM D638 standard, dumbbell-shaped tensile samples with a thickness of 3 mm, width of 19 mm, distance between grips of 65 mm, and gauge section length and width of 25 mm and 6 mm, respectively, of stiff T8430, which has similar properties to Verowhite, were prepared with the 3D printing technology, and uniaxial tensile tests were performed using Instron 5848 MicroTester (Instron, Massachusetts, USA) with the load accuracy of ±0.4%. The previous study has shown that the strain rate effect of stiff materials like Verowhite can be ignored when the strain rate is less than 10−1 s−1. Therefore, the material parameters of T8430 measured at the loading rate of 5 mm·min−1, i.e., the strain rate of about 10−3 × s−1, can be used for quasi-static compression simulation of the tire at the strain rate of about 10−4 × s−1 [34]. The experimental nominal stress–strain curve and transformed true stress–strain curve of the T8430 are shown in Figure 6. Three tests were repeated for the T8430 specimens. The nominal stress
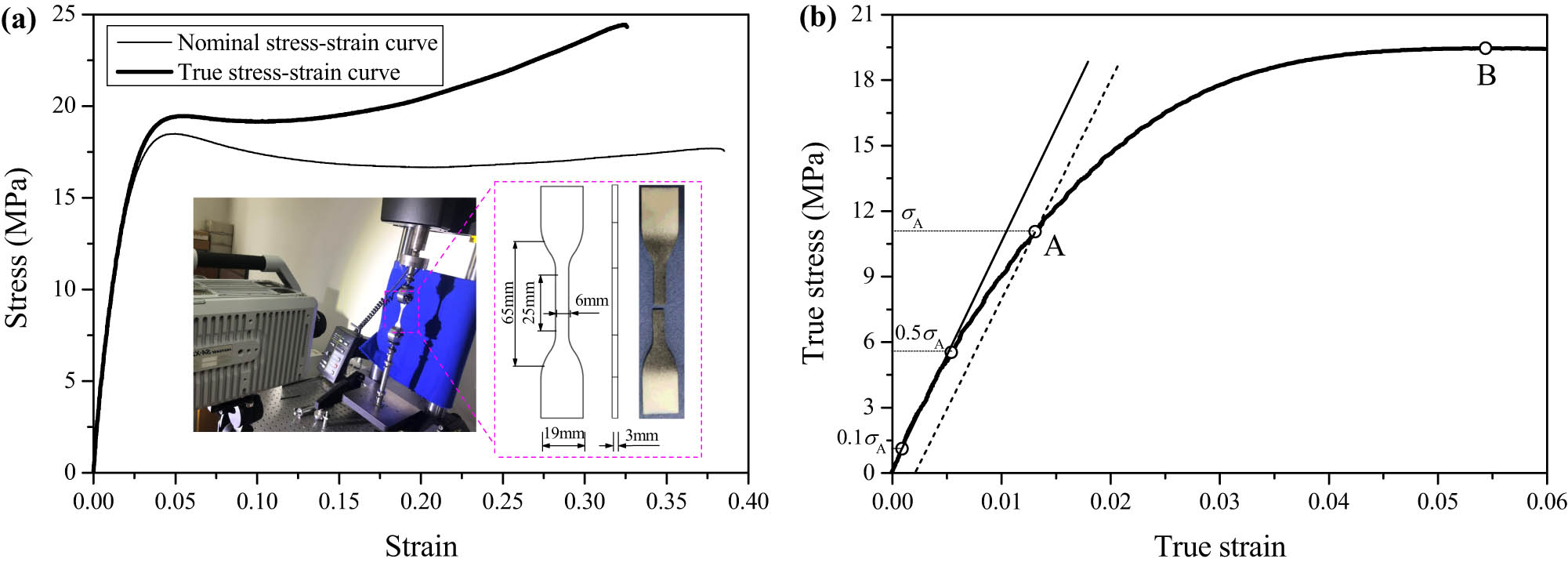
Nominal and true stress–strain curves of T8430 under quasi-static uniaxial tension (a) and schematic diagram of determining elastic modulus and yield strength (b).
3.2 Finite element simulation and experimental verification
The quasi-static uniaxial compression processes of the nonpneumatic tire samples were simulated using finite element software ABAQUS. Rigid body models were adopted for the hub and the bottom plate of the testing machine, and three-dimensional deformable solid models were adopted for the inner ring, the outer ring, and the structural layer of the tire. For the Tweel, Tweel-2, and honeycomb FE model, the model meshes were based on eight-node linear brick elements (C3D8R type) generated by sweeping techniques with the element size of 0.2 mm, and the element numbers of the three tire samples were 1,565,550, 1,656,000, and 1,647,750, respectively. For the saddle FE model, the model mesh was based on four-node linear tetrahedron elements (C3D4 type), generated by free mesh technique with the element size of 0.45 mm and element number of 1,521,443.
An elastic–plastic model was adopted, and the density, elastic modulus, Poisson’s ratio, and the true stress–strain curve of T8430 in the plastic stage were input according to the values presented in the previous section. For the model, it was considered, as usually accepted, to delete the failing elements, defining the failure condition according to the ductile fracture failure criterion, that is, based on the yield strength value and the strain measured. The equivalent plastic strain, consistent with the definition of the von Mises stress equation, was defined as
In accordance with the experimental conditions, all degrees of freedom of the bottom plate except the z direction were constrained, and the translational and rotational degrees of freedom of the hub in three directions were constrained. Surface-to-surface contact was adopted between the bottom plate and the outer surface of the tire outer ring, a tie constraint was adopted between the outer surface of the wheel hub and the inner surface of the tire inner ring, and self-contact was adopted between the components of the structural layer of the tire, to consider the case of contact after material plying. Details of the contact definitions can be found in the help files of Abaqus software.
Similarly, by dividing the vertical load of the center point o of the hub and the vertical displacement of the bottom plate by 2br and R–r–t 1, respectively, the numerical simulation results of the nominal stress–strain curves of the tire samples under quasi-static compression can be obtained (dashed lines in Figure 4). According to the nominal stress–strain curves and configuration evolution diagrams (Figure 5), the finite element simulation results in this article were in good agreement with the experimental results. The simulation curves reproducing the experimental profiles, such as fluctuation characteristics and maximum value, and the relative errors are mainly between ±10%, except for some local strain regions, such as the initial stage and the region of the nominal strain close to 0.4. The mechanical properties of the nonpneumatic tire samples within the range of 0–0.40 of the nominal strain are focused in this article.
4 Results and discussion
4.1 Vertical bearing capacity
As shown in Figure 4, the stress–strain curves of nonpneumatic tires show a nearly linear increase with the vertical deformation in the initial loading stage, which was similar to that presented in refs [4,20,22]. As described in the study by Gibson and Ashby [38] for cell structures, the stress–strain curve of the nonpneumatic tires measured in this work, after the initial loading stage, fluctuates as the deformation increases. That is visible in Figure 4 for honeycomb, Tweel, and Tweel-2 tires beyond point 2, and for saddle tire beyond point 3.
Referring to the performance evaluation indexes of the cell structure, in this article, elastic modulus, yield strength, and absorbed energy are used as the quantitative characterization parameters of the vertical bearing capacity and the energy absorption and damping performance of the nonpneumatic tire samples (Figure 7(a)). At the initial near-linear stage of the nominal stress–strain curve, a tangent line to the initial near-linear segment of the test curve is drawn, and it intersects with the coordinate axis at a point (ε
a, 0). With (ε
a + 0.2%, 0) as the starting point, a straight line parallel to the tangent line is drawn and intersects with the σ–ε curve at the point (ε
s,σ
s). σ
s represents the yield strength of the sample. The slope of a cord of two points where the stresses are 0.1σ
s and 0.5σ
s on the σ–ε curve is taken as the elastic modulus E of the sample according to National Standards GBT 22315-2008. When σ > σ
s, the strain stage where the stress oscillates is entered. If friction loss or the like is neglected, the work done by an external force under a quasi-static loading condition will be completely transformed into the energy absorbed by the structure and stored in the form of strain energy. The integral area under the nominal stress–strain curve is the energy absorbed by per unit volume of the material. When the nominal strain is
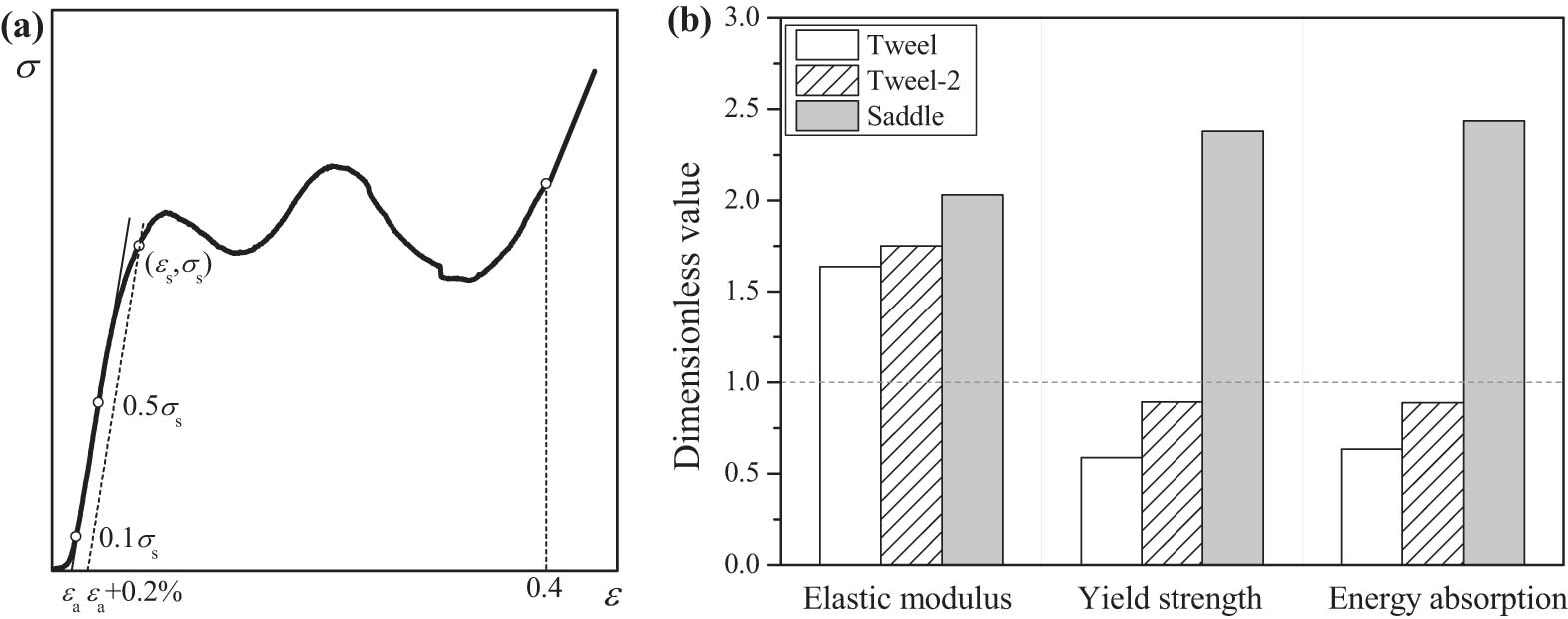
Characterization parameters of the vertical bearing capacity and energy absorption performance of the nonpneumatic tire samples. (a) Schematic diagram of parameter calculation and (b) experimental results normalized to the values of the honeycomb tire.
Based on the nominal stress–strain curves obtained from the experiments (solid lines in Figure 4), the characterization parameters of the vertical bearing performance of the four nonpneumatic tire samples are calculated as listed in Table 1, and the performance parameters of the Tweel, Tweel-2, and saddle samples were normalized with the vertical bearing performance parameters of the honeycomb sample as shown in Figure 7(b). Among the four samples, the honeycomb sample had the lowest elastic modulus. The elastic modulus of the Tweel sample was about 1.6 times that of the honeycomb sample, but the yield strength and absorbed energy were lower than those of the honeycomb sample, only about 0.6 times those of the latter. Two newly designed nonpneumatic tires, Tweel-2 and saddle, achieved the original design intention that effectively improve the vertical bearing capacity and the energy-absorbing capacity of the nonpneumatic tires, without increasing the relative density of the samples. Compared with the Tweel sample, the elastic modulus of the Tweel-2 sample increases slightly due to the increase of the circumferential element in the middle of the spoke, and the yield strength and absorbed energy were increased by more than 40%. The elastic modulus of the saddle sample with the hyperbolic paraboloid design on the spoke was 2.0 times that of the honeycomb sample, approximately that of the Tweel sample, and the yield strength and energy absorbed of the saddle sample were significantly improved, 2.4 times that of the honeycomb sample and 4 times that of the Tweel sample, respectively.
Vertical bearing performance parameters of the four nonpneumatic tire samples
| Characterization parameters | Honeycomb | Tweel | Tweel-2 | Saddle |
|---|---|---|---|---|
| Elastic modulus (MPa) | 10.15 | 16.34 | 17.76 | 20.60 |
| Yield strength (MPa) | 0.51 | 0.30 | 0.45 | 1.21 |
| Energy absorption (J) | 3.80 | 2.43 | 3.38 | 9.27 |
4.2 Evolution of deformable structural layers
The analysis of the deformation process of the four nonpneumatic tire samples was obtained from the FE models, and the corresponding stress in the spokes is shown in Figure 5. The spokes of the nonpneumatic tire are the main bearing components under vertical compression. The spokes on the central axis first participate in the bearing, then the spokes on both sides. The difference is that the spokes of Tweel, Tweel-2, and honeycomb tires mainly bend and fold in the yoz plane, while the spokes of the saddle show necking in the xoy plane of the middle section.
As the nominal strain reaches 0.014, 0.061, 0.088, 0.269, and 0.335 at strain points ① to ⑤ of Tweel in Figure 4(a), respectively, the spokes No. 1, No. 2, No. 3, No. 4, and No. 5 of the Tweel tire participate in the bearing in turn (Figure 5(a)). During compression, these spokes generate different degrees of bending deformation in the yoz plane, and there are significant stress concentrations at both ends and centers of the spokes. As the nominal strain reaches 0.014, 0.061, 0.104, 0.280, and 0.358 at strain points ① to ⑤ of Tweel-2 in Figure 4(a), respectively, the spokes No. 1, No. 2, No. 3, No. 4, and No. 5 of the Tweel-2 tire participate in the bearing in turn (Figure 5(b)). For Tweel-2 tire, during compression, the outer rings of these spokes generate different degrees of bending deformation in the yoz plane until they are compacted, and there are significant stress concentrations at both ends and centers of the outer rings, while the inner rings basically maintain the initial configuration, and the stress distribution is relatively uniform. As the nominal strain reaches 0.016, 0.089, and 0.309 at strain points ①, ③, and ⑤ of honeycomb in Figure 4(b), respectively, the spokes No. 1, No. 2, and No. 3 of the honeycomb tire participate in bearing in turn (Figure 5(c)). During compression, the corrugated plate spokes are folded and buckled in the plane, and stress concentrations occur at the corners, and the deformation of the bearing spokes is restrained by the adjacent spokes due to the connection of the circumferential elements. As the nominal strain reaches 0.016, 0.041, and 0.211 at strain points ①, ②, and ④ in Figure 4(b), respectively, the spokes No. 1, No. 2, and No. 3 of the saddle tire participate in the bearing in turn. During compression, necking occurs in the middle of the spoke in the xoy plane, and stress concentration occurs in the necking area and the lower end part.
During the bearing process, the bending deformation of the spoke increases. The bent spoke can bear less vertical load than its initial state, which leads to the decrease of the vertical load that the whole tire sample can bear. As the adjacent spokes participate in the bearing, the vertical load that the sample can bear is improved. This is the main reason for the oscillation in the nominal stress–strain curve of the tire sample (Figure 4). In addition, there is an overlap between the spokes of the saddle tire. When the bearing capacity of the spoke that plays the dominant role in the vertical bearing is slightly reduced, the adjacent spokes have participated in the bearing, which is one of the reasons why the yield stress and the plateau stress of the saddle tire are much higher than those of the other three kinds of tires.
4.3 Strain energy analysis
Figure 8 shows the percentage of the strain energy stored in each component of the tire sample (spokes, treads, and circumferential units) to the total strain energy during the bearing process. With the increase of the nominal strain, the percentages of the strain energy stored in spokes No. 1 to No. 3 decrease slowly, but are always higher than 70% (Figure 8(a)), and the percentages of the strain energy stored in the other spokes, the circumferential elements, or the outer tread are always lower than 15%. In other words, most of the energy transformed from the work done by the external force is absorbed by spokes No. 1 to No. 3.
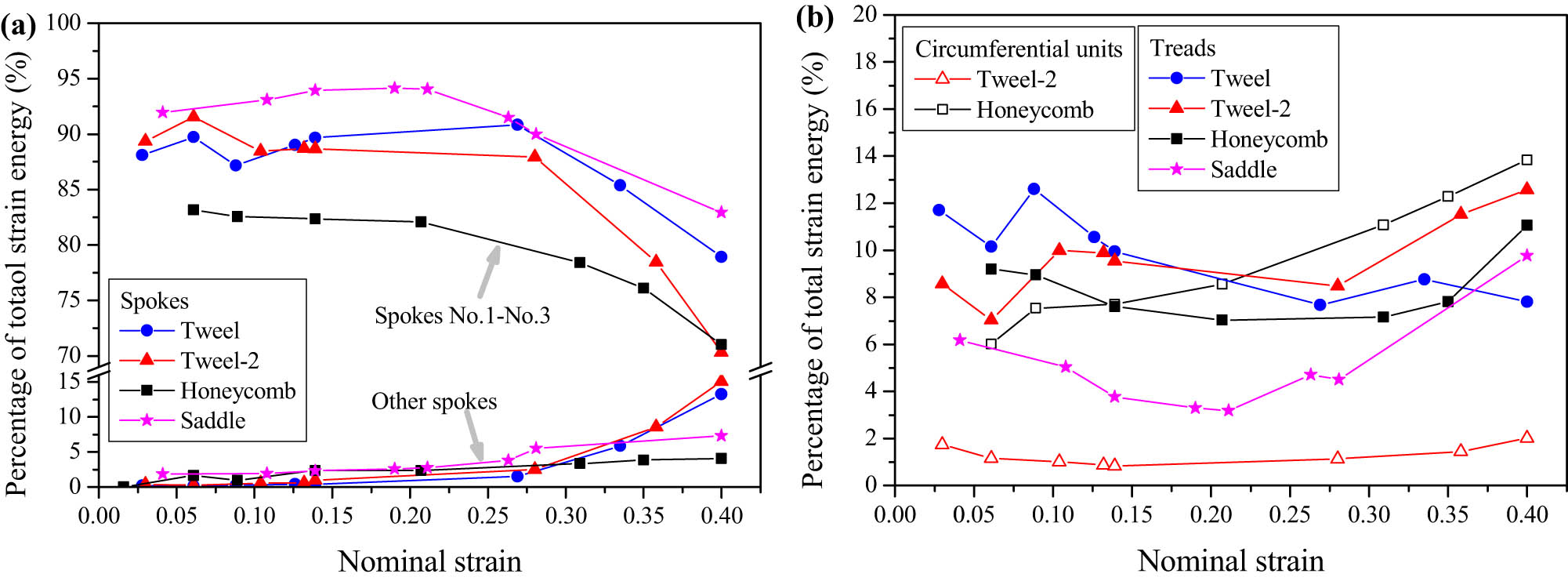
Percentage of the stored strain energy relative to the total strain energy under quasi-static uniaxial compression for (a) spokes, divided into two groups: spokes 1–3 and the rest; (b) circumferential units and treads of tire samples.
The evolution of the strain energy stored in spokes No. 1, No. 2, and No. 3 are shown in Figure 9(a)–(c), respectively. The strain energy stored in each spoke increases monotonously with the increase of the deformation of the sample. The distances between spokes No. 1, No. 2, and No. 3 and the central axis increase, while the deformation degrees of the spokes after participating in the bearing decrease in turn, and the stored strain energy also decreases. The strain energy stored in each spoke of the Tweel-2 tire is higher than that of the Tweel tire. The strain energy stored in the circumferential element itself is less, which accounts for less than 2% of the total strain energy of the Tweel-2 tire (hollow triangles in Figure 8(b)). However, the circumferential elements strengthen the deformation coordination among the spokes and increase the critical bearing capacity of the spokes by shortening the length of the deformation zone, so that more external force work is consumed under the same vertical deformation condition, thus improving the energy absorption performance of single spoke and the whole tire. Therefore, the energy absorption performance of the Tweel-2 tire is better than that of the Tweel tire. The strain energy stored in each spoke of the honeycomb tire is slightly higher than that of the two Tweel tires. In addition to strengthening the deformation coordination among the spokes, the circumferential element of the honeycomb tire also has a certain degree of deformation, which accounts for 14% of the total strain energy of the honeycomb tire (hollow squares in Figure 8(b)). This makes the energy absorption property of honeycomb tire better than the Tweel and Tweel-2 tires. The strain energy stored in spokes No. 1 or No. 2 of saddle tire is much higher than that of other spokes. When the nominal strain is 0.4, the strain energy stored in spokes No. 1 and No. 2 of the saddle tire is about 2.4 J, which is six times that of the other spokes. This fully demonstrates the high energy absorption performance of the hyperbolic parabolic panel.
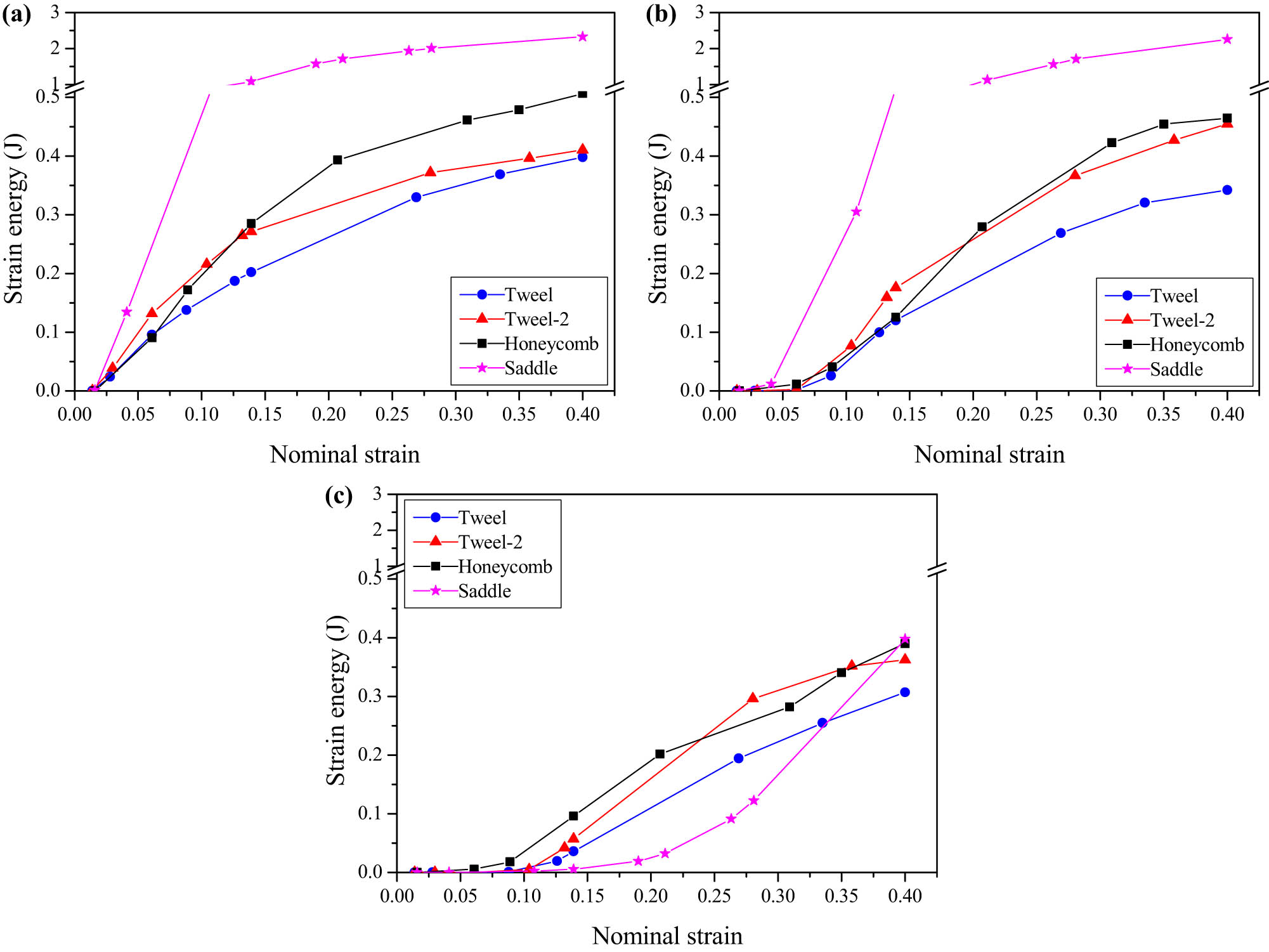
Strain energy stored in spoke, obtained from the FE models: (a) No. 1, (b) No. 2, and (c) No. 3.
Based on the strain energy fields of spokes No. 1 to No. 3 of the tire obtained from numerical simulation (Figure 10), the strain energy distribution of the spokes along the radial direction (Figure 11) was counted. Specifically, the initial configuration of the spoke was equally divided into 20 parts along the radial direction, and the sum of the strain energy of all elements in each equally divided area was calculated, and the abscissa was the distance between the midpoint of each area and the outer wall of the inner ring, divided by R–r–t 1 for normalization. During the bearing process, the Tweel, Tweel-2, and honeycomb tires have obvious strain energy concentration areas, which are located at the ends and centers of the spokes (Figure 10(a)), the end and centers of the outer rings of the spokes (Figure 10(b)), and the corrugation corners of the spokes (Figure 10(c)), respectively. With the increase of the nominal strain of the sample, the bending or folding degree of the spokes increases, while the position of strain energy concentration remains unchanged, and the value increases greatly (Figure 11(a)–(c)). Different from the former three kinds of tires, when the nominal strain is smaller, such as 0.156, the strain energy of the saddle tire is almost uniformly distributed along the radial direction, and there is no obvious strain energy concentration area. With the increase of the nominal strain, strain energy concentration occurs at the center of spoke No. 1, the center and lower part of spoke No. 2, and the lower part of spoke No. 3, and the strain energy level of each point in the spoke increases at the same time (Figures 10(d) and 11(d)). Accordingly, due to the structural design of the saddle, more material in the sample deforms and participates in the energy absorption, and thus, the saddle tire achieves the optimal deformation energy absorption performance.
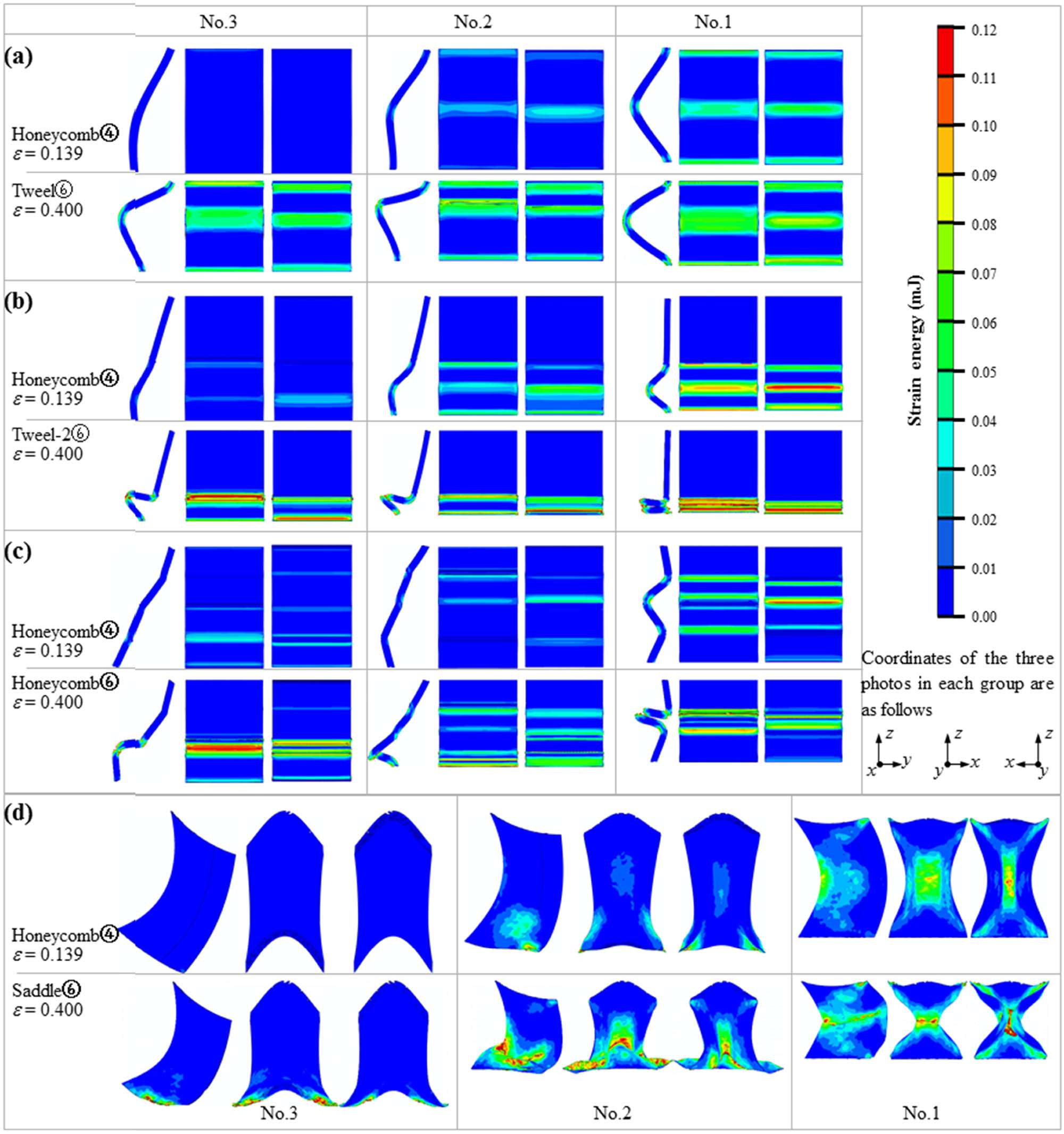
Strain energy field of spokes No. 1, No. 2, and No. 3 at different time points for (a) Tweel; (b) Tweel-2; (c) honeycomb; and (d) saddle tire FE models. The honeycomb ④ corresponds to the nominal strain of 0.139, which is chosen as the first time point, and there is no element failure in the four tire samples.
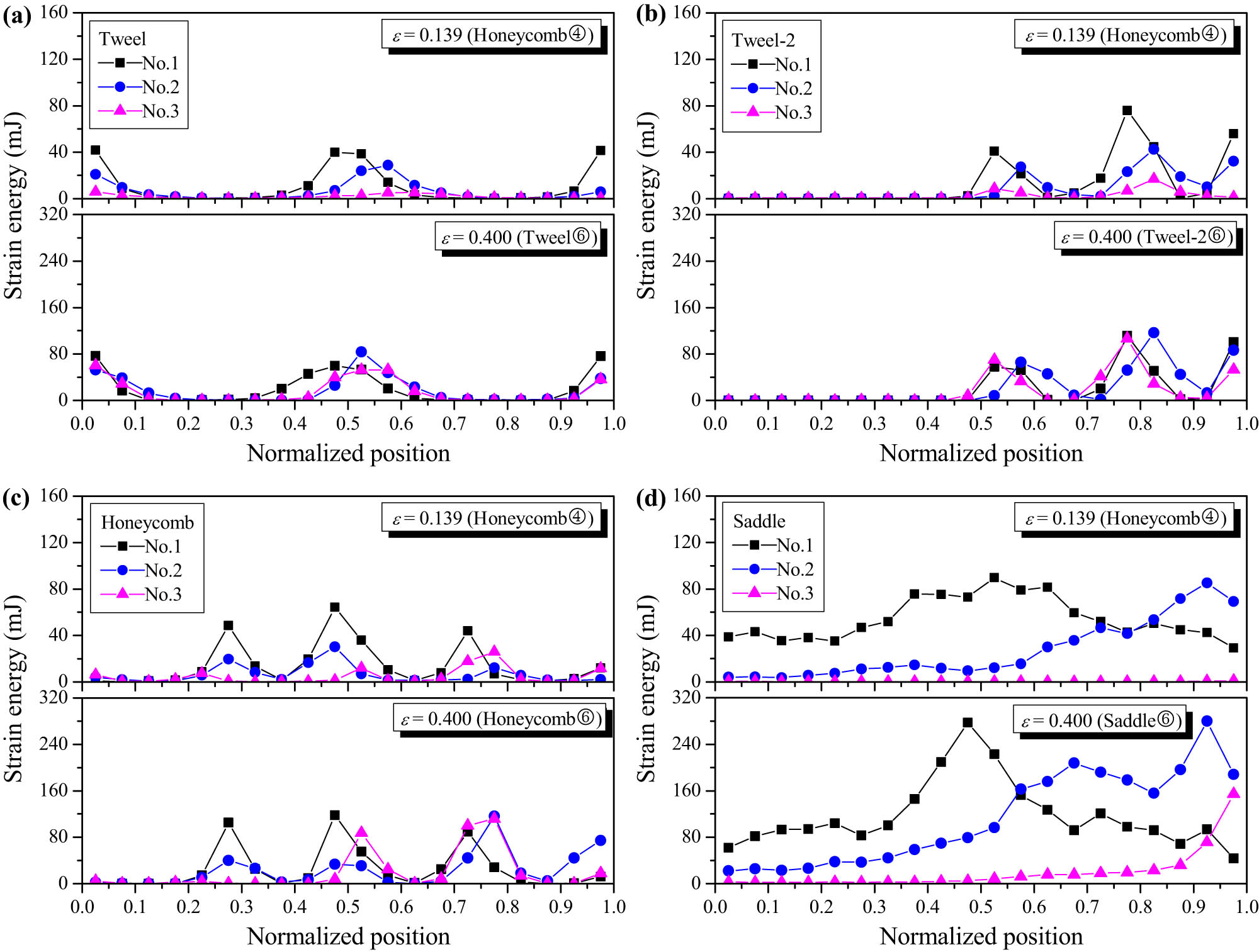
Radial distribution curves of strain energy of (a) Tweel; (b) Tweel-2; (c) honeycomb; and (d) saddle tire samples.
4.4 Quasi-static load performance improvement mechanism
Based on the vertical stress fields of spoke No. 1 at the moment before and after failure (Figure 12), the maximum vertical compressive stress, referring to the maximum absolute value, along the radial direction of the tire spoke was calculated (Figure 13). Similarly, the initial configuration of the spokes was divided into 20 radial parts, the maximum vertical compressive stress of all elements in each equal region was calculated, and the abscissa was the distance between the midpoint of each area and the outer wall of the inner ring, divided by R–r–t 1 for normalization.
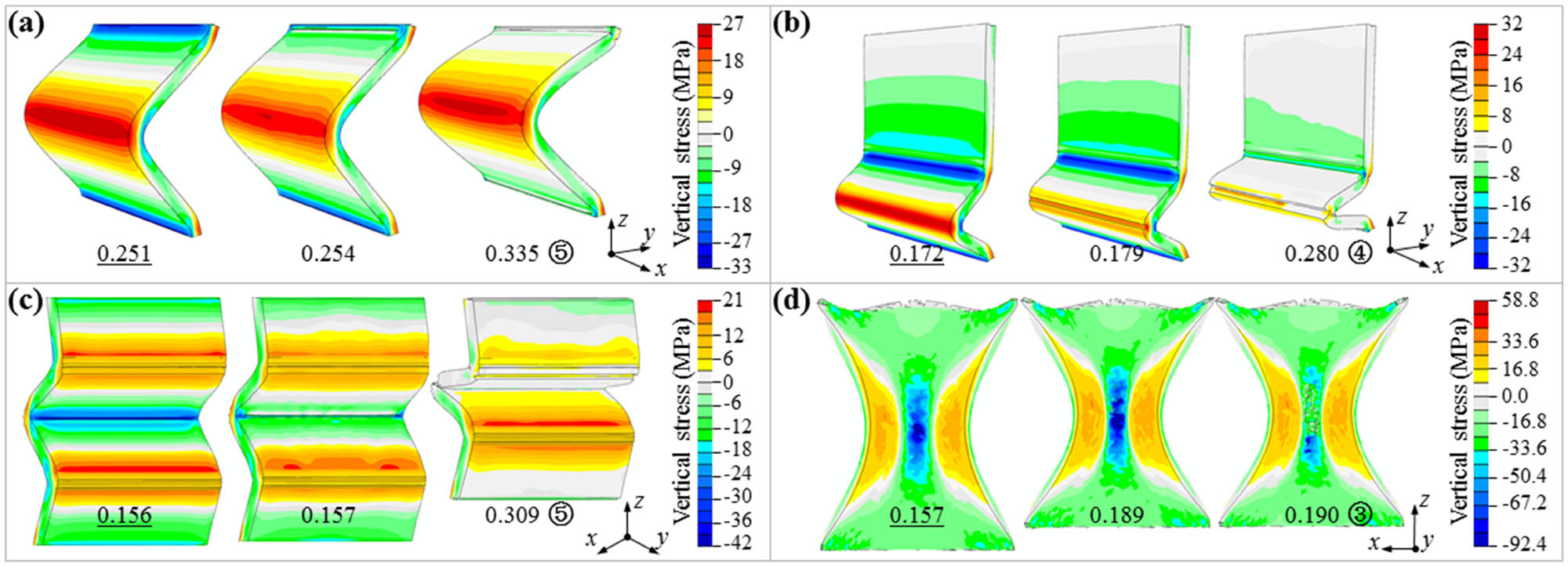
Vertical stress field of spoke No. 1 of (a) Tweel; (b) Tweel-2; (c) honeycomb; and (d) saddle tire samples. The underlined values represent the nominal strain at the moment before failure.
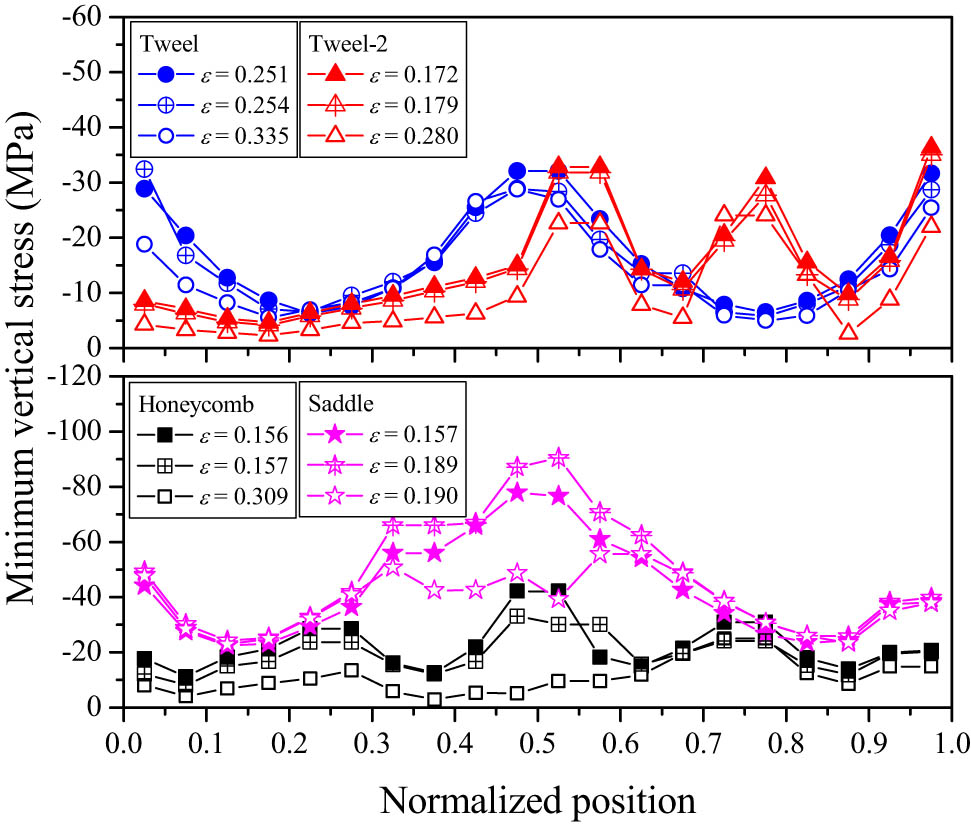
Radial distribution curves of the maximum compressive stress of spoke No. 1.
The common characteristics of the deformable structural layers of honeycomb, Tweel, and Tweel-2 tires are that the projection of different cross sections on the yoz plane is the same, and the stress field distribution of each spoke at different yoz cross sections is similar. When the equivalent strain of a certain element in the stress concentration zone reaches the fracture strain, a cascade failure of the element along the x-axis will occur subsequently (Figure 12(a)–(c)), leading to a decrease in the overall vertical compressive stress of the spoke (Figure 13).
Different from the former three kinds of tires, the saddle tire has different projections on the yoz plane with different cross sections of the deformable structure layer, and the stress field distribution of each spoke with different yoz cross sections varies greatly. When an element in the middle neck region of the spoke fails, no x-direction cascade failure occurs, and the failure elements are only distributed in a small amount along the direction of the main parabolic p 1 in the neck compression region (Figure 12(d)). When the element fails, the vertical compressive stress in the vicinity of the element continues to increase until the nominal strain reaches 0.189, and the vertical compressive stress reaches the maximum. Subsequently, the failure elements in the necking area were further increased, and the vertical compressive stress levels in each area decreased (Figure 13). In addition, at the moment before the failure of spoke No. 1, the maximum vertical compressive stress of the spoke of the saddle tire was much higher than that of the other three structures. In other words, the spatial configuration of the hyperbolic paraboloid can optimize the spatial stress distribution and effectively improve the yield strength and energy absorption properties of the saddle tire in the bearing process.
5 Conclusions
Two new nonpneumatic tires, Tweel-2 and saddle, were designed and 3D printed for study in this article. Based on the static compression experiment and finite element numerical simulation, the mechanism of improvement in vertical bearing capacity and energy absorption performance of nonpneumatic tire was studied.
Based on Michelin Tweel tire, the design of the circumferential unit was introduced in Tweel-2 tire. It was found that the circumferential unit can strengthen the deformation compatibility between the spokes by shortening the length of the deformation area. This leads to the improvement in the critical bearing capacity of the spokes and more external work consumed under the same vertical deformation. Therefore, the energy absorption of a single spoke and the whole tire is improved, and the energy absorption performance of Tweel-2 is better than Tweel tire. The yield strength and absorbed energy of the Tweel-2 tire are 1.4 times higher than those of Tweel tire with similar elastic modulus.
By using the bionic design concept of flexible biological spring for reference, the spoke was designed as a hyperbolic paraboloid, and the saddle tire was proposed for the first time. The spatial configuration of the hyperbolic paraboloid can optimize the spatial distribution of stress and make more materials deform and participate in energy absorption. The strain energy distribution of spokes is more uniform under compression, and the overall strain energy level of spokes is improved, thus effectively improving the yield strength and energy absorption of the tire. Under the same relative density, the elastic modulus of saddle tire is about twice that of honeycomb tire and similar to that of Tweel tire. The yield strength and absorbed energy are approximately 2.4 times and 4 times those of the honeycomb and Tweel tires, respectively.
Acknowledgements
The authors gratefully acknowledge the support provided by the National Natural Science Foundation of China (No. 11672297) and the Strategic Priority Research Program of the Chinese Academy of Sciences (No. XDB22020200).
-
Funding information: This study was funded by the National Natural Science Foundation of China (No. 11672297), the Strategic Priority Research Program of the Chinese Academy of Sciences (No. XDB22020200).
-
Author contributions: Xianghong Xu provided guidance on data processing and analysis, and helped drafted and revised it for the whole content. Bing Liu conducted all simulations and experiments, and performed the analysis of data.
-
Conflict of interest: The authors declare that they have no conflict of interest.
-
Data availability statement:The data of these findings cannot be shared at this time as the data also forms part of an ongoing study.
References
[1] Jin, X., C. Hou, X. Fan, Y. Sun, J. Lv, and C. Lu. Investigation on the static and dynamic behaviors of non-pneumatic tires with honeycomb spokes. Composite Structures, Vol. 187, 2018, pp. 27–35.10.1016/j.compstruct.2017.12.044Search in Google Scholar
[2] Baranowski, P., J. Malachowski, and L. Mazurkiewicz. Numerical and experimental testing of vehicle tyre under impulse loading conditions. International Journal of Mechanical Sciences, Vol. 106, 2016, pp. 346–356.10.1016/j.ijmecsci.2015.12.028Search in Google Scholar
[3] Gent, A. N. and J. D. Walter. The Pneumatic Tire; National Highway Traffic Safety Administration, Washington, D.C, U.S., U.S. Department of Transportation, 2006.Search in Google Scholar
[4] Ju, J., D.-M. Kim, and K. Kim. Flexible cellular solid spokes of a non-pneumatic tire. Composite Structures, Vol. 94, 2012, pp. 2285–2295.10.1016/j.compstruct.2011.12.022Search in Google Scholar
[5] Ju, J., B. Ananthasayanam, J. D. Summers, and P. Joseph. Design of cellular shear bands of a non-pneumatic tire – investigation of contact pressure. SAE International Journal of Passenger Cars - Mechanical Systems, Vol. 3, 2010, pp. 598–606.10.4271/2010-01-0768Search in Google Scholar
[6] Wu, T., M. Li, X. Zhu, and X. Lu. Research on non-pneumatic tire with gradient anti-tetrachiral structures. Mechanics of Advanced Materials and Structures, Vol. 28, No. 22, 2021, pp. 2351–2359.10.1080/15376494.2020.1734888Search in Google Scholar
[7] Lu, H. B., F. Liang, and J. H. Gou. Nanopaper enabled shape-memory nanocomposite with vertically aligned nickel nanostrand: controlled synthesis and electrical actuation. Soft Matter, Vol. 7, No. 16, 2011, pp. 7416–7423.10.1039/c1sm05765kSearch in Google Scholar
[8] Kim, K. and D. M. Kim. Contact pressure of non-pneumatic tires with hexagonal lattice spokes. SAE 2011 World Congress and Exhibition, 2011. 10.4271/2011-01-0099.Search in Google Scholar
[9] Rugsaj, R. and C. Suvanjumrat. Proper radial spokes of non-pneumatic tire for vertical load supporting by finite element analysis. International Journal of Automotive Technology, Vol. 20, 2019, pp. 801–812.10.1007/s12239-019-0075-ySearch in Google Scholar
[10] Rugsaj, R. and C. Suvanjumrat. Study of geometric effects on nonpneumatic tire spoke structures using finite element method. Mechanics Based Design of Structures and Machines, 2020, pp. 1–21. 10.1080/15397734.2020.1777875.Search in Google Scholar
[11] Ganniari-Papageorgiou, E., P. Chatzistergos, and X. Wang. The influence of the honeycomb design parameters on the mechanical behavior of non-pneumatic tires. International Journal of Applied Mechanics, Vol. 12, 2020, id. 2050024.10.1142/S1758825120500246Search in Google Scholar
[12] Li, Y., X. Sun, J. Song, S. Zhang, and S. Han. Topological structure and experimental investigation of a novel whole tire bead. Materials & Design, Vol. 203, 2021, id. 109592.10.1016/j.matdes.2021.109592Search in Google Scholar
[13] Zhang, Q., X. Yang, P. Li, G. Huang, S. Feng, C. Shen, et al. Bioinspired engineering of honeycomb structure – Using nature to inspire human innovation. Progress in Materials Science, Vol. 74, 2015, pp. 332–400.10.1016/j.pmatsci.2015.05.001Search in Google Scholar
[14] Xue, R., X. Cui, P. Zhang, K. Liu, Y. Li, W. Wu, et al. Mechanical design and energy absorption performances of novel dual scale hybrid plate-lattice mechanical metamaterials. Extreme Mechanics Letters, Vol. 40, 2020, id. 100918.10.1016/j.eml.2020.100918Search in Google Scholar
[15] Li, X., F. Lu, Y. Zhang, Y. Lin, and Y. Meng. Experimental study on out-of-plane mechanical and energy absorption properties of combined hexagonal aluminum honeycombs under dynamic impact. Materials & Design, Vol. 194, 2020, id. 108900.10.1016/j.matdes.2020.108900Search in Google Scholar
[16] Heo, H., J. Ju, and D.-M. Kim. Compliant cellular structures: application to a passive morphing airfoil. Composite Structures, Vol. 106, 2013, pp. 560–569.10.1016/j.compstruct.2013.07.013Search in Google Scholar
[17] Lu, H. B. and W. M. Huang. On the origin of the Vogel-Fulcher-Tammann law in the thermo-responsive shape memory effect of amorphous polymers. Smart Materials and Structures, Vol. 22, No. 10, 2013, id. 105021.10.1088/0964-1726/22/10/105021Search in Google Scholar
[18] Lu, H. B. and S. Y. Du. A phenomenological thermodynamic model for the chemo-responsive shape memory effect in polymers based on Flory-Huggins solution theory. Polymer Chemistry-UK, Vol. 5, No. 4, 2014, pp. 1155–1162.10.1039/C3PY01256ESearch in Google Scholar
[19] Kim, K., J. Ju, and D. M. Kim. Static contact behaviors of a non-pneumatic tire with hexagonal lattice spokes. SAE International Journal of Passenger Cars - Mechanical Systems, Vol. 6, 2013, pp. 1518–1527.10.4271/2013-01-9117Search in Google Scholar
[20] Zang, L., X. Wang, P. Yan, and Z. Zhao. Structural design and characteristics of a non-pneumatic tire with honeycomb structure. Mechanics of Advanced Materials and Structures, 2021, pp. 1–8. 10.1080/15376494.2021.1919800.Search in Google Scholar
[21] Jang, I. G., Y. H. Sung, E. J. Yoo, and B. M. Kwak. Pattern design of a non-pneumatic tyre for stiffness using topology optimization. Engineering Optimization, Vol. 44, 2012, pp. 119–131.10.1080/0305215X.2011.569546Search in Google Scholar
[22] Kucewicz, M., P. Baranowski, and J. Malachowski. Airless tire conceptions modeling and simulations. Preceedings of the 13th International Scientific Conference: Computer Aided Engineering, Polanica Zdroj, Poland, June 22–25, 2016, pp. 293–301.10.1007/978-3-319-50938-9_30Search in Google Scholar
[23] Aboul-Yazid, A., M. Emam, S. Shaaban, and M. El-Nashar. Effect of spokes structures on characteristics performance of non-pneumatic tires. International Journal of Automotive and Mechanical Engineering, Vol. 11, 2015, pp. 2212–2223.10.15282/ijame.11.2015.4.0185Search in Google Scholar
[24] Zhang, Z., H. Fu, X. Liang, X. Chen, and D. Tan. Comparative analysis of static and dynamic performance of non-pneumatic tire with flexible spoke. Structure, Vol. 66, 2020, pp. 458–466.10.5545/sv-jme.2020.6676Search in Google Scholar
[25] URL: https://www.michelin.com.cn/ (JULY 10, 2021).Search in Google Scholar
[26] URL: https://www.bridgestone.com/technology_innovation/air_free_concept/ (JULY 10, 2021).Search in Google Scholar
[27] Patek, S. N., W. Korff, and R. L. Caldwell. Deadly strike mechanism of a mantis shrimp – This shrimp packs a punch powerful enough to smash its prey’s shell underwater. Nature, Vol. 428, 2004, pp. 819–820.10.1038/428819aSearch in Google Scholar PubMed
[28] Devries, M. S., E. A. K. Murphy, and S. N. Patek. Strike mechanics of an ambush predator: The spearing mantis shrimp. Journal of Experimental Biology, Vol. 215, 2012, pp. 4374–4384.10.1242/jeb.075317Search in Google Scholar PubMed
[29] Tadayon, M., S. Amini, A. Masic, and A. Miserez. The mantis shrimp saddle: a biological spring combining stiffness and flexibility. Advanced Functional Materials, Vol. 25, 2015, pp. 6437–6447.10.1002/adfm.201502987Search in Google Scholar
[30] Tadayon, M., S. Amini, Z. Wang, and A. Miserez. Biomechanical design of the mantis shrimp saddle: a biomineralized spring used for rapid raptorial strikes. iScience, Vol. 8, 2018, pp. 271–282.10.1016/j.isci.2018.08.022Search in Google Scholar PubMed PubMed Central
[31] Stratasys. Available from: http://www.stratasys.com.Search in Google Scholar
[32] Wu, X., X. Meng, and H. Zhang. An experimental investigation of the dynamic fracture behavior of 3D printed nacre-like composites. Journal of the Mechanical Behavior of Biomedical Materials, Vol. 112, 2020, id. 104068.10.1016/j.jmbbm.2020.104068Search in Google Scholar PubMed
[33] Sun, X., X. Fang, L. Guan. Mechanics of materials, Higher Education Press, Beijing, China, 2002.Search in Google Scholar
[34] Gu, G. X., M. Takaffoli, and M. J. Buehler. Hierarchically enhanced impact resistance of bioinspired composites. Advanced Materials, Vol. 29, 2017, id. 1700060.10.1002/adma.201700060Search in Google Scholar PubMed
[35] Milosevic, N., B. Younise, A. Sedmak, M. Travica, and A. Mitrovic. Evaluation of true stress–strain diagrams for welded joints by application of digital image correlation. Engineering failure analysis, Vol. 128, 2021, id. 105609.10.1016/j.engfailanal.2021.105609Search in Google Scholar
[36] Gu, G. X., S. Wettermark, and M. J. Buehler. Algorithm-driven design of fracture resistant composite materials realized through additive manufacturing. Additive manufacturing, Vol. 17, 2017, pp. 47–54.10.1016/j.addma.2017.07.002Search in Google Scholar
[37] Mendelson, A. Plasticity: Theory and application, The Macmillan, New York, NY, USA, 1968.Search in Google Scholar
[38] Gibson, L. J. and M. F. Ashby. Cellular solids: Structure and properties, Cambridge University Press, Cambridge, 1999.Search in Google Scholar
© 2022 Bing Liu and Xianghong Xu, published by De Gruyter
This work is licensed under the Creative Commons Attribution 4.0 International License.
Articles in the same Issue
- Review Articles
- State of the art, challenges, and emerging trends: Geopolymer composite reinforced by dispersed steel fibers
- A review on the properties of concrete reinforced with recycled steel fiber from waste tires
- Copper ternary oxides as photocathodes for solar-driven CO2 reduction
- Properties of fresh and hardened self-compacting concrete incorporating rice husk ash: A review
- Basic mechanical and fatigue properties of rubber materials and components for railway vehicles: A literature survey
- Research progress on durability of marine concrete under the combined action of Cl− erosion, carbonation, and dry–wet cycles
- Delivery systems in nanocosmeceuticals
- Study on the preparation process and sintering performance of doped nano-silver paste
- Analysis of the interactions between nonoxide reinforcements and Al–Si–Cu–Mg matrices
- Research Articles
- Study on the influence of structural form and parameters on vibration characteristics of typical ship structures
- Deterioration characteristics of recycled aggregate concrete subjected to coupling effect with salt and frost
- Novel approach to improve shale stability using super-amphiphobic nanoscale materials in water-based drilling fluids and its field application
- Research on the low-frequency multiline spectrum vibration control of offshore platforms
- Multiple wide band gaps in a convex-like holey phononic crystal strip
- Response analysis and optimization of the air spring with epistemic uncertainties
- Molecular dynamics of C–S–H production in graphene oxide environment
- Residual stress relief mechanisms of 2219 Al–Cu alloy by thermal stress relief method
- Characteristics and microstructures of the GFRP waste powder/GGBS-based geopolymer paste and concrete
- Development and performance evaluation of a novel environmentally friendly adsorbent for waste water-based drilling fluids
- Determination of shear stresses in the measurement area of a modified wood sample
- Influence of ettringite on the crack self-repairing of cement-based materials in a hydraulic environment
- Multiple load recognition and fatigue assessment on longitudinal stop of railway freight car
- Synthesis and characterization of nano-SiO2@octadecylbisimidazoline quaternary ammonium salt used as acidizing corrosion inhibitor
- Perforated steel for realizing extraordinary ductility under compression: Testing and finite element modeling
- The influence of oiled fiber, freeze-thawing cycle, and sulfate attack on strain hardening cement-based composites
- Perforated steel block of realizing large ductility under compression: Parametric study and stress–strain modeling
- Study on dynamic viscoelastic constitutive model of nonwater reacted polyurethane grouting materials based on DMA
- Mechanical behavior and mechanism investigation on the optimized and novel bio-inspired nonpneumatic composite tires
- Effect of cooling rate on the microstructure and thermal expansion properties of Al–Mn–Fe alloy
- Research on process optimization and rapid prediction method of thermal vibration stress relief for 2219 aluminum alloy rings
- Failure prevention of seafloor composite pipelines using enhanced strain-based design
- Deterioration of concrete under the coupling action of freeze–thaw cycles and salt solution erosion
- Creep rupture behavior of 2.25Cr1Mo0.25V steel and weld for hydrogenation reactors under different stress levels
- Statistical damage constitutive model for the two-component foaming polymer grouting material
- Nano-structural and nano-constraint behavior of mortar containing silica aggregates
- Influence of recycled clay brick aggregate on the mechanical properties of concrete
- Effect of LDH on the dissolution and adsorption behaviors of sulfate in Portland cement early hydration process
- Comparison of properties of colorless and transparent polyimide films using various diamine monomers
- Study in the parameter influence on underwater acoustic radiation characteristics of cylindrical shells
- Experimental study on basic mechanical properties of recycled steel fiber reinforced concrete
- Dynamic characteristic analysis of acoustic black hole in typical raft structure
- A semi-analytical method for dynamic analysis of a rectangular plate with general boundary conditions based on FSDT
- Research on modification of mechanical properties of recycled aggregate concrete by replacing sand with graphite tailings
- Dynamic response of Voronoi structures with gradient perpendicular to the impact direction
- Deposition mechanisms and characteristics of nano-modified multimodal Cr3C2–NiCr coatings sprayed by HVOF
- Effect of excitation type on vibration characteristics of typical ship grillage structure
- Study on the nanoscale mechanical properties of graphene oxide–enhanced shear resisting cement
- Experimental investigation on static compressive toughness of steel fiber rubber concrete
- Study on the stress field concentration at the tip of elliptical cracks
- Corrosion resistance of 6061-T6 aluminium alloy and its feasibility of near-surface reinforcements in concrete structure
- Effect of the synthesis method on the MnCo2O4 towards the photocatalytic production of H2
- Experimental study of the shear strength criterion of rock structural plane based on three-dimensional surface description
- Evaluation of wear and corrosion properties of FSWed aluminum alloy plates of AA2020-T4 with heat treatment under different aging periods
- Thermal–mechanical coupling deformation difference analysis for the flexspline of a harmonic drive
- Frost resistance of fiber-reinforced self-compacting recycled concrete
- High-temperature treated TiO2 modified with 3-aminopropyltriethoxysilane as photoactive nanomaterials
- Effect of nano Al2O3 particles on the mechanical and wear properties of Al/Al2O3 composites manufactured via ARB
- Co3O4 nanoparticles embedded in electrospun carbon nanofibers as free-standing nanocomposite electrodes as highly sensitive enzyme-free glucose biosensors
- Effect of freeze–thaw cycles on deformation properties of deep foundation pit supported by pile-anchor in Harbin
- Temperature-porosity-dependent elastic modulus model for metallic materials
- Effect of diffusion on interfacial properties of polyurethane-modified asphalt–aggregate using molecular dynamic simulation
- Experimental study on comprehensive improvement of shear strength and erosion resistance of yellow mud in Qiang Village
- A novel method for low-cost and rapid preparation of nanoporous phenolic aerogels and its performance regulation mechanism
- In situ bow reduction during sublimation growth of cubic silicon carbide
- Adhesion behaviour of 3D printed polyamide–carbon fibre composite filament
- An experimental investigation and machine learning-based prediction for seismic performance of steel tubular column filled with recycled aggregate concrete
- Effects of rare earth metals on microstructure, mechanical properties, and pitting corrosion of 27% Cr hyper duplex stainless steel
- Application research of acoustic black hole in floating raft vibration isolation system
- Multi-objective parametric optimization on the EDM machining of hybrid SiCp/Grp/aluminum nanocomposites using Non-dominating Sorting Genetic Algorithm (NSGA-II): Fabrication and microstructural characterizations
- Estimating of cutting force and surface roughness in turning of GFRP composites with different orientation angles using artificial neural network
- Displacement recovery and energy dissipation of crimped NiTi SMA fibers during cyclic pullout tests
Articles in the same Issue
- Review Articles
- State of the art, challenges, and emerging trends: Geopolymer composite reinforced by dispersed steel fibers
- A review on the properties of concrete reinforced with recycled steel fiber from waste tires
- Copper ternary oxides as photocathodes for solar-driven CO2 reduction
- Properties of fresh and hardened self-compacting concrete incorporating rice husk ash: A review
- Basic mechanical and fatigue properties of rubber materials and components for railway vehicles: A literature survey
- Research progress on durability of marine concrete under the combined action of Cl− erosion, carbonation, and dry–wet cycles
- Delivery systems in nanocosmeceuticals
- Study on the preparation process and sintering performance of doped nano-silver paste
- Analysis of the interactions between nonoxide reinforcements and Al–Si–Cu–Mg matrices
- Research Articles
- Study on the influence of structural form and parameters on vibration characteristics of typical ship structures
- Deterioration characteristics of recycled aggregate concrete subjected to coupling effect with salt and frost
- Novel approach to improve shale stability using super-amphiphobic nanoscale materials in water-based drilling fluids and its field application
- Research on the low-frequency multiline spectrum vibration control of offshore platforms
- Multiple wide band gaps in a convex-like holey phononic crystal strip
- Response analysis and optimization of the air spring with epistemic uncertainties
- Molecular dynamics of C–S–H production in graphene oxide environment
- Residual stress relief mechanisms of 2219 Al–Cu alloy by thermal stress relief method
- Characteristics and microstructures of the GFRP waste powder/GGBS-based geopolymer paste and concrete
- Development and performance evaluation of a novel environmentally friendly adsorbent for waste water-based drilling fluids
- Determination of shear stresses in the measurement area of a modified wood sample
- Influence of ettringite on the crack self-repairing of cement-based materials in a hydraulic environment
- Multiple load recognition and fatigue assessment on longitudinal stop of railway freight car
- Synthesis and characterization of nano-SiO2@octadecylbisimidazoline quaternary ammonium salt used as acidizing corrosion inhibitor
- Perforated steel for realizing extraordinary ductility under compression: Testing and finite element modeling
- The influence of oiled fiber, freeze-thawing cycle, and sulfate attack on strain hardening cement-based composites
- Perforated steel block of realizing large ductility under compression: Parametric study and stress–strain modeling
- Study on dynamic viscoelastic constitutive model of nonwater reacted polyurethane grouting materials based on DMA
- Mechanical behavior and mechanism investigation on the optimized and novel bio-inspired nonpneumatic composite tires
- Effect of cooling rate on the microstructure and thermal expansion properties of Al–Mn–Fe alloy
- Research on process optimization and rapid prediction method of thermal vibration stress relief for 2219 aluminum alloy rings
- Failure prevention of seafloor composite pipelines using enhanced strain-based design
- Deterioration of concrete under the coupling action of freeze–thaw cycles and salt solution erosion
- Creep rupture behavior of 2.25Cr1Mo0.25V steel and weld for hydrogenation reactors under different stress levels
- Statistical damage constitutive model for the two-component foaming polymer grouting material
- Nano-structural and nano-constraint behavior of mortar containing silica aggregates
- Influence of recycled clay brick aggregate on the mechanical properties of concrete
- Effect of LDH on the dissolution and adsorption behaviors of sulfate in Portland cement early hydration process
- Comparison of properties of colorless and transparent polyimide films using various diamine monomers
- Study in the parameter influence on underwater acoustic radiation characteristics of cylindrical shells
- Experimental study on basic mechanical properties of recycled steel fiber reinforced concrete
- Dynamic characteristic analysis of acoustic black hole in typical raft structure
- A semi-analytical method for dynamic analysis of a rectangular plate with general boundary conditions based on FSDT
- Research on modification of mechanical properties of recycled aggregate concrete by replacing sand with graphite tailings
- Dynamic response of Voronoi structures with gradient perpendicular to the impact direction
- Deposition mechanisms and characteristics of nano-modified multimodal Cr3C2–NiCr coatings sprayed by HVOF
- Effect of excitation type on vibration characteristics of typical ship grillage structure
- Study on the nanoscale mechanical properties of graphene oxide–enhanced shear resisting cement
- Experimental investigation on static compressive toughness of steel fiber rubber concrete
- Study on the stress field concentration at the tip of elliptical cracks
- Corrosion resistance of 6061-T6 aluminium alloy and its feasibility of near-surface reinforcements in concrete structure
- Effect of the synthesis method on the MnCo2O4 towards the photocatalytic production of H2
- Experimental study of the shear strength criterion of rock structural plane based on three-dimensional surface description
- Evaluation of wear and corrosion properties of FSWed aluminum alloy plates of AA2020-T4 with heat treatment under different aging periods
- Thermal–mechanical coupling deformation difference analysis for the flexspline of a harmonic drive
- Frost resistance of fiber-reinforced self-compacting recycled concrete
- High-temperature treated TiO2 modified with 3-aminopropyltriethoxysilane as photoactive nanomaterials
- Effect of nano Al2O3 particles on the mechanical and wear properties of Al/Al2O3 composites manufactured via ARB
- Co3O4 nanoparticles embedded in electrospun carbon nanofibers as free-standing nanocomposite electrodes as highly sensitive enzyme-free glucose biosensors
- Effect of freeze–thaw cycles on deformation properties of deep foundation pit supported by pile-anchor in Harbin
- Temperature-porosity-dependent elastic modulus model for metallic materials
- Effect of diffusion on interfacial properties of polyurethane-modified asphalt–aggregate using molecular dynamic simulation
- Experimental study on comprehensive improvement of shear strength and erosion resistance of yellow mud in Qiang Village
- A novel method for low-cost and rapid preparation of nanoporous phenolic aerogels and its performance regulation mechanism
- In situ bow reduction during sublimation growth of cubic silicon carbide
- Adhesion behaviour of 3D printed polyamide–carbon fibre composite filament
- An experimental investigation and machine learning-based prediction for seismic performance of steel tubular column filled with recycled aggregate concrete
- Effects of rare earth metals on microstructure, mechanical properties, and pitting corrosion of 27% Cr hyper duplex stainless steel
- Application research of acoustic black hole in floating raft vibration isolation system
- Multi-objective parametric optimization on the EDM machining of hybrid SiCp/Grp/aluminum nanocomposites using Non-dominating Sorting Genetic Algorithm (NSGA-II): Fabrication and microstructural characterizations
- Estimating of cutting force and surface roughness in turning of GFRP composites with different orientation angles using artificial neural network
- Displacement recovery and energy dissipation of crimped NiTi SMA fibers during cyclic pullout tests

![Figure 1
Nonpneumatic tires. (a) Honeycomb tire [6]; (b) Tweel tire [25]; (c) AC tire [26]; (d) interconnected mesh tire [10]; (e) Kucwheel [22]; and (f) grid type tire [24].](/document/doi/10.1515/rams-2022-0002/asset/graphic/j_rams-2022-0002_fig_001.jpg)
