Home Unifying optimization forces: Harnessing the fine-structure constant in an electromagnetic-gravity optimization framework
Article Open Access

Unifying optimization forces: Harnessing the fine-structure constant in an electromagnetic-gravity optimization framework

  • Md. Amir Khusru Akhtar , Mohit Kumar , Sahil Verma , Korhan Cengiz , Pawan Kumar Verma , Ruba Abu Khurma and Moutaz Alazab EMAIL logo
Published/Copyright: December 18, 2024
Download Article (PDF)
Become an author with De Gruyter Brill
Submit Manuscript Author Information
Journal of Intelligent Systems
From the journal Journal of Intelligent Systems Volume 33 Issue 1

Abstract

The electromagnetic-gravity optimization (EMGO) framework is a novel optimization technique that integrates the fine-structure constant and leverages electromagnetism and gravity principles to achieve efficient and robust optimization solutions. Through comprehensive performance evaluation and comparative analyses against state-of-the-art optimization techniques, EMGO demonstrates superior convergence speed and solution quality. Its unique balance between exploration and exploitation, enabled by the interplay of electromagnetic and gravity forces, makes it a powerful tool for finding optimal or near-optimal solutions in complex problem landscapes. The research contributes by introducing EMGO as a promising optimization approach with diverse applications in engineering, decision support systems, machine learning, data mining, and financial optimization. EMGO’s potential to revolutionize optimization methodologies, handle real-world problems effectively, and balance global exploration and local exploitation establishes its significance. Future research opportunities include exploring adaptive mechanisms, hybrid approaches, handling high-dimensional problems, and integrating machine learning techniques to enhance its capabilities further. EMGO gives a novel approach to optimization, and its efficacy, advantages, and potential for extensive adoption open new paths for advancing optimization in many scientific, engineering, and real-world domains.

Keywords: fine-structure constant; electromagnetism; gravity; convergence speed; optimization technique

1 Introduction

Optimization is a central facet of scientific and engineering disciplines, seeking to find optimal solutions to complex problems [1]. While many optimization techniques have been developed over the years, the search for innovative and effective approaches to handle increasingly complex and multidimensional problems continues to drive research in the field [2].

In this article, we present electromagnetic-gravity optimization (EMGO), an innovative framework inspired by the exploration of the fine-structure constant, an essential constant governing electromagnetic interaction. By combining the fine-structure constant into the optimization framework, EMGO harnesses the inherent forces of electromagnetism and gravity to improve optimization performance.

The objective of this work is to present and evaluate EMGO as a novel optimization approach. We aim to showcase the potential of EMGO in solving complex optimization problems by leveraging the interplay between electromagnetism, gravity, and the fine-structure constant. The empirical evaluations and comparative analyses establish the effectiveness and superiority of EMGO over current optimization techniques.

To guide our study, we address the main research questions. First, we explore the effective integration of the fine-structure constant into the optimization framework. Second, we delve into the underlying principles and equations governing EMGO. Next, we compare EMGO’s performance in terms of convergence speed, solution quality, and robustness against existing techniques. Finally, we explore potential applications and domains where EMGO can offer significant advantages in optimization, spanning engineering, decision support systems, machine learning, data mining, financial optimization, and more.

The contributions of this research article are significant. We introduce EMGO, which combines electromagnetism, gravity, and the fine-structure constant for efficient optimization. We provide a comprehensive exploration of integrating the fine-structure constant into EMGO, including relevant equations and conceptual frameworks. The empirical evaluations on benchmark functions show EMGO’s superiority in terms of convergence speed and solution quality compared to present techniques.

The research questions showcase EMGO’s contributions; this technique aims to drive a paradigm shift in optimization methodologies and motivate further advancements in the field. EMGO gives a promising direction for solving complex optimization challenges and suggests a way for more efficient and powerful optimization techniques in many scientific and engineering domains.

1.1 Novelty and contribution

The main novelty of this work lies in the introduction of the EMGO framework, which uniquely integrates the fine-structure constant with principles of electromagnetism and gravity to create a robust optimization algorithm. This innovative approach harnesses the fine-structure constant as a pivotal parameter, influencing the balance between local and global search capabilities within the optimization process. This integration offers a new perspective on how fundamental physical constants can be applied to solve complex optimization problems.

Key novel contributions:

  • EMGO is the first optimization framework that leverages the fine-structure constant, a fundamental physical constant, to modulate the search dynamics. This approach provides a novel mechanism for balancing exploration and exploitation in the search space.

  • By combining principles of electromagnetism (for local search) and gravity (for global search), EMGO achieves a more effective and efficient optimization process. This hybrid mechanism allows EMGO to adaptively transition between local and global search phases, enhancing convergence speed and solution quality.

  • Comparative analysis with existing state-of-the-art optimization algorithms – Particle Swarm Optimization (PSO) [3], Whale Optimization Algorithm (WOA) [4], Gravitational Search Algorithm (GSA) [5] and Electromagnetic Field Optimization (EFO) [6] – demonstrates that EMGO outperforms in terms of convergence speed, robustness, scalability, and the quality of solutions obtained. The fine-tuning capabilities provided by the fine-structure constant enable EMGO to avoid local optima and achieve superior global optima.

  • EMGO’s design allows it to be scalable and robust across various optimization problems, including high-dimensional and complex landscapes. This scalability is attributed to the adaptive nature of the algorithm, which efficiently handles the diversity of optimization challenges.

These contributions collectively establish EMGO as a pioneering framework in the field of optimization, offering significant advancements over existing methods. The detailed analysis and empirical results presented in this article underscore the practical and theoretical benefits of incorporating fundamental physical constants into optimization algorithms.

The remaining sections of this article are as follows: Section 2 gives the background and related work. Section 3 presents the proposed EMGO algorithm. Section 4 compares the performance of EMGO with state-of-the-art optimization techniques. Finally, in Section 5, we conclude the article.

2 Background and related work

Optimization techniques have been a topic of general research and development, driven by the necessity to solve complex problems across many scientific and engineering domains [7,8,9]. This section gives a comprehensive background and highlights related work that sets the foundation for understanding the significance of the fine-structure constant, electromagnetism, the relative strength of electricity and gravity, and existing optimization techniques, with hybrid approaches.

2.1 Fine-structure constant and its significance

The fine-structure constant (α) is a dimensionless physical constant that signifies the strength of electromagnetic interactions. The precise value of α is approximately 1/137 and reflects the strength of the electromagnetic force relative to other fundamental forces. In the context of optimization techniques, α plays a significant role in integrating electromagnetism into the problem-solving process. Using α in optimization algorithms, we can harness the dynamics of electromagnetism to explore and search for optimal solutions [10].

The implication of the fine-structure constant lies in its deep connection to the fundamental nature of electromagnetism and its role in shaping the behavior of charged particles. The use of α in optimization techniques can simulate the influence of electromagnetic forces on the search process, allowing exploration and exploitation of the solution space. The mathematical representation of the fine-structure constant in optimization algorithms gives a quantitative framework for understanding and utilizing the principles of electromagnetism. It allows algorithms to leverage the strength and interactions of electromagnetic forces to guide the search for optimal solutions in a dynamic and resourceful manner [11].

2.2 Electromagnetism and the fine-structure constant

Electromagnetism, defined by Maxwell’s equations and QED, is one of the four fundamental forces of nature. It governs the conduct of electrically charged particles and their interactions through the exchange of photons. The fine-structure constant, being intimately linked to electromagnetism, provides insights into the strength of these interactions [12].

The use of the fine-structure constant in optimization frameworks permits the integration of electromagnetic forces into the search process. The magnitude and direction of these forces give optimization algorithms to effectively balance local exploitation and global exploration, leading to enhanced convergence and solution quality.

2.3 Relative strength of electricity and gravity

In addition to electromagnetism, gravity is another fundamental force that governs the behavior of massive objects in the universe. Unlike electromagnetism, the relative strength of electricity and gravity is significantly different. While electromagnetism is about 1,036 times stronger than gravity, gravity acts on all objects with mass and has a universal influence on the macroscopic scale.

By considering the relative strength of electricity and gravity, optimization algorithms can incorporate gravity-like interactions to guide the search process. This combination allows for a multi-faceted exploration of the search space, balancing local exploitation driven by electromagnetism with global exploration influenced by gravity [13].

2.4 Optimization techniques

Optimization encompasses a diverse range of techniques tailored to tackle complex problems and attain optimal solutions [14]. Among these techniques, metaheuristics provide a robust algorithmic framework designed specifically for complex optimization problems, regardless of their nature – continuous, discrete, unconstrained, or multi-objective. Metaheuristic approaches build upon traditional heuristics, augmenting their exploration and exploitation capabilities. They can be broadly categorized into swarm-based, evolutionary-based, physics-based, and human-based metaheuristics [15,16,17].

Swarm-based metaheuristics draw inspiration from the collective behaviors exhibited by animals and plants, where interaction with the environment and other individuals plays a crucial role. Prominent examples of swarm-based metaheuristics include PSO [3], Sperm Swarm Optimization [18], and Grey Wolf Optimizer (GWO) [19].

Evolutionary algorithms, such as Genetic Algorithms (GA) [20] and Differential Evolution [21], derive inspiration from the principles of natural selection and genetic variation. These algorithms employ techniques like mutation, crossover, and selection to evolve a population of candidate solutions toward improved outcomes over successive generations. They find wide application in optimization problems across diverse domains.

Physics-based metaheuristics take a distinctive approach to optimization by drawing inspiration from the fundamental laws of physics. Notable examples include the GSA [5], Simulated Annealing, EFO [6], Magnetic Charged System Search (MCSS) [22], and Ions Motion Optimization (IMO) [23]. EFO, for instance, emulates the behavior of electromagnets with different polarities and incorporates the golden ratio as a nature-inspired ratio [6]. It represents potential solutions as electromagnetic particles composed of electromagnets, with the number of electromagnets determined by the variables in the optimization problem.

The GSA [5] mimics gravitational forces to search for optimal solutions. Each solution is represented as a celestial body, and the algorithm simulates interactions between these bodies to guide the search process. Similarly, MCSS utilizes the governing laws of magnetic and electrical forces, while IMO leverages the attraction and repulsion between anions and cations to facilitate optimization.

Table 1 offers a comprehensive comparison of diverse optimization algorithms, including those rooted in physics-based metaheuristics. The assessment focuses on their capacity to navigate intricate optimization terrains and effectively attain optimal solutions.

Table 1

Comparison of diverse optimization algorithms

Algorithm name Description Advantages Limitations
Proposed EMGO technique Unites electromagnetism and gravity principles with the fine-structure constant, for effective solution exploration and exploitation Global exploration, fast convergence, balance between exploration and exploitation Parameter tuning required, sensitivity to problem characteristics
Segmental regularized constrained inversion [24] An inversion method for transient electromagnetism that utilizes a segmented regularization constraint and an improved sparrow search algorithm to enhance inversion accuracy and stability under varying conditions

  1. Improves inversion accuracy and stability

  2. Reduces dependence on preliminary information

  3. Optimizes objective function efficiently and escapes local optima

  4. Superior practicality and higher fitting accuracy

  1. May require significant computational resources

  2. Performance dependent on initial model setup and criteria
Gravity inspired clustering algorithm [25] A clustering algorithm inspired by gravitational principles, designed to select relevant gene subsets for disease classification tasks from high-dimensional microarray data

  1. High accuracy on various microarray cancer datasets

  2. Effective feature selection validated using SVM with LOOCV

  3. Competes well with existing methods

  1. May require significant computational resources

  2. Performance may vary across different datasets
Coati optimization algorithm (COOA) [26] Bio-inspired algorithm modeling coatis’ attacking, hunting, and escape behaviors, with phases of exploration and exploitation

  1. Balances exploration and exploitation.

  2. Superior performance on benchmark functions

  1. Effective in real-world applications

  1. Needs further validation across diverse problems

  2. Parameter sensitivity

  3. Higher computational complexity
Crayfish optimization algorithm (COA) [27] Simulates crayfish’s summer resort, competition, and foraging behaviors, divided into stages to balance exploration and exploitation

  1. Balances exploration and exploitation.

  2. Effective in standard benchmark and engineering problems

  1. Temperature-regulated processes enhance global optimization

  1. Requires further validation in diverse scenarios

  2. May be sensitive to temperature parameters
Mother Optimization Algorithm [28] A human-based metaheuristic algorithm inspired by the interaction between a mother and her children, involving phases of education, advice, and upbringing

  1. Effective balance between exploration and exploitation

  2. Superior performance in optimizing unimodal, high-dimensional multimodal, and fixed-dimensional multimodal functions

  3. Outperforms 12 other metaheuristic algorithms

  1. Further validation is needed across a broader range of problems

  2. Sensitivity to specific parameter settings may impact effectiveness
GSA [5] Emulates gravitational forces for optimization Global search capability Sensitive to parameter settings
EFO [6] Utilizes electromagnetic field interactions for optimization Effective exploration and exploitation Sensitive to parameter values
MCSS [22] Models magnetic interactions between particles for optimization Good exploration, adaptability Vulnerable to local optima
IMO [23] Imitates ions’ motion in an electromagnetic field for optimization Efficient exploration and exploitation Parameter tuning required
GA [29] Employs genetic operators for selection Global search capability, population diversity Slower convergence on complex landscapes
PSO [3] Simulates social behavior for optimization Fast convergence, simplicity Prone to premature convergence, local optima
Ant colony optimization [30] Mimics ant foraging behavior for optimization Good for discrete optimization problems Slow convergence, sensitivity to parameters
Simulated annealing [31] Inspired by annealing process Escapes local optima, probabilistic approach Temperature schedule affects performance
DE [21] Utilizes differential mutation Robust, handles noisy functions High memory usage, can get stuck in local optima
Harmony search [32] Inspired by musicians’ improvisation Versatile, easy implementation Limited scalability, may converge to suboptimal
Artificial bee colony [33] Imitates honeybee foraging behavior Simple, good exploration capabilities Vulnerable to getting trapped in local optima
Firefly algorithm [34] Leverages fireflies’ attractiveness Global search capability Convergence rate affected by parameter settings
Cuckoo search [34] Inspired by brood parasitism of cuckoo birds Fast convergence, simple implementation May require fine-tuning of parameters
Bat algorithm [35] Inspired by echolocation of bats Robust, adaptive, good exploration capabilities May converge slowly on complex landscapes
GWO [19] Inspired by social hierarchy of grey wolves Fast convergence, global search capability Parameter sensitivity
Flower pollination algorithm [36] Mimics flower pollination process Effective exploration and exploitation Parameter tuning required
Glowworm swarm optimization [37] Inspired by glowworm behavior Good for dynamic environments Limited scalability, may converge to suboptimal
WOA [4] Inspired by hunting behavior of whales Fast convergence, global search capability May converge to suboptimal solutions
Teaching-learning based optimization [38] Inspired by teaching and learning process Fast convergence, diverse exploration Parameter tuning required
Moth flame optimization [39] Inspired by moth’s attraction to light Good convergence rate, simple implementation May require fine-tuning of parameters
Flower algorithm [40] Mimics blooming process of flowers Effective exploration, simplicity May require more iterations to achieve convergence
Krill Herd algorithm [41] Inspired by swarming behavior of krill Fast convergence, global search capability Sensitivity to parameter values
Sine cosine algorithm [42] Utilizes sine and cosine functions for optimization Efficient exploration and exploitation Performance influenced by parameter settings
Coral reefs optimization [43] Mimics ecological system of coral reefs Good convergence and exploration capabilities Parameter sensitivity
Moth search algorithm [44] Inspired by moth’s attraction to light Fast convergence, simple implementation May require fine-tuning of parameters
Harmony search with chaos [45] Combines harmony search with chaotic dynamics Efficient exploration, good convergence Parameter tuning required
Crow search algorithm [46] Inspired by foraging behavior of crows Fast convergence, good exploration capabilities Parameter sensitivity
Social spider algorithm [47] Mimics social behavior of spiders Effective exploration and exploitation Sensitivity to parameter values
Equilibrium optimizer [48] Inspired by principles of chemical equilibrium Fast convergence, global search capability May require fine-tuning parameters
Earthworm optimization [49] Inspired by earthworm’s burrowing behavior Efficient exploration and exploitation Sensitivity to parameter values
Black Widow optimization [50] Inspired by predatory behavior of black widow spiders Good convergence and exploration capabilities Sensitivity to parameter values
Virus optimization algorithm [51] Inspired by spread of computer viruses Fast convergence, efficient exploration May require fine-tuning of parameters
Flamingo optimization algorithm [52] Inspired by foraging behavior of flamingos Good convergence and exploration capabilities More iterations may be required to achieve convergence
Illumination optimization [53] Inspired by distribution of illumination sources Efficient exploration, global search capability May converge to suboptimal solutions
Zebra optimization algorithm [54] Inspired by herding behavior of zebras Fast convergence, diverse exploration May require fine-tuning of parameters

Our proposed EMGO algorithm merges the principles of electromagnetism and gravity to effectively explore and exploit the solution space. It incorporates electromagnetic forces based on the fine-structure constant, α, and gravity-like interactions to foster global exploration. Through iterative updates of individuals’ positions according to cumulative forces, EMGO offers a novel approach to overcome the limitations of traditional techniques, such as slow convergence and difficulty in finding global optima. By striking a balance between exploration and exploitation, EMGO aims to deliver more efficient and effective optimization outcomes.

3 EMGO framework

3.1 Conceptual framework

The EMGO framework combines the principles of electromagnetism, gravity, and the fine-structure constant to offer a powerful optimization approach. EMGO gives a balance between local exploitation and global exploration by leveraging the interplay of these fundamental forces.

3.2 Equations for EMGO incorporating the fine-structure constant

3.2.1 Initialization

In EMGO, the optimization problem is represented by a population of individuals, each categorized by a position vector in the search space. The population is initialized randomly within the problem’s defined bounds.

3.2.2 Electromagnetic interactions

The electromagnetic interactions in the given EMGO are modeled on the basis of the principles of electromagnetism and the fine-structure constant. The electromagnetic force between two individuals i and j is described as:

(1) F em = α × ( q i × q j ) / r 2 × ( x i − x j ) ,

where F em denotes electromagnetic force, α represents fine-structure constant, q i and q j are the charges of individuals i and j, r is the distance between them, and x i and x j are their respective positions.

The determination of the electromagnetic force (F em) in the EMGO algorithm, as given by equation (1), involves considering the charges of individuals, the distance between them, and the fine-structure constant (α). Let’s explore how these components are determined using an example scenario.

Electric charge optimization consider an optimization problem where the goal is to find the optimal distribution of electric charges on a two-dimensional plane to minimize the overall potential energy. The charges represent individuals, and their positions represent potential solutions. The objective is to find the configuration that results in the lowest potential energy.

Determining the charges (q i and q j ): In this scenario, the charges (q i and q j ) of individuals i and j can be determined based on their fitness or potential contribution to the objective function shown in equations (2) and (3). For example, let’s assume that the charges are determined proportional to the fitness values of individuals. Higher fitness specifies a more favorable solution.

(2) q i = Fitness ( i ) ,

(3) q i = Fitness ( j ) ,

Since charges are based on fitness, individuals with higher fitness will have a stronger charge, representing their higher potential to contribute to the objective function.

Determining the distance ( r ): The distance ‘r’ between individuals i and j is a central factor in determining the electromagnetic force. For this, Euclidean distance between the positions of individuals is considered shown in equation (4).

(4) r = sqrt ( ( x i − x j ) 2 + ( y i − y j ) 2 ) ,

where (x i , y i ) and (x j , y j ) signify the positions of individuals i and j, respectively. The distance is calculated using the Pythagorean theorem, considering the difference in the x-coordinates and y-coordinates.

Determining the fine-structure constant ( α ): Defining α in the EMGO algorithm includes setting a predefined constant value that signifies the strength of the electromagnetic interaction. The value of α is a significant parameter as it affects the balance between the electromagnetic forces and other factors in the optimization process. Let us discuss the range of α and its impact on convergence.

The fine-structure constant is a fundamental constant in physics and is approximately equal to 1/137. It denotes the strength of the electromagnetic interaction between charged particles. In our EMGO algorithm, α used as a scaling factor for the electromagnetic forces.

The choice of α can have an impact on the convergence behavior of the algorithm. A smaller value of α reduces the influence of electromagnetic forces, making the optimization process more reliant on other factors such as gravity interactions or search algorithms. On the other hand, a larger value of α amplifies the impact of electromagnetic forces, potentially leading to faster convergence towards solutions influenced by local interactions.

The value of α is within a predefined range to maintain a balanced optimization process. While the specific range may vary depending on the problem domain and the nature of the optimization problem, it is usually selected to confirm a reasonable trade-off between exploration and exploitation.

A frequently used range for α in the EMGO algorithm is between 0.01 and 0.1. Values within this range give a moderate influence of electromagnetic forces without overpowering other factors in the optimization process. The optimal value of α can depend on the type of problem being solved and may need some experimentation or fine-tuning.

When determining the value of α, the characteristics of the optimization problem and the desired convergence behavior must be considered. In some cases, a smaller α may be ideal to encourage exploration and prevent premature convergence to suboptimal solutions. For others, a larger α might be useful to exploit strong electromagnetic interactions and converge quickly to desirable solutions.

So, the choice of α in the EMGO algorithm should be on the basis of a balance between the problem’s characteristics, desired convergence behavior, and empirical observations. Experimentation and fine-tuning of α can help to find the optimal range or value that leads to effective optimization.

Example result: Let us take an example where we have two individuals with fitness values of 10 and 8, respectively. Their positions are (2, 3) and (5, 6), resulting in a distance of r = 4.2426. Assuming α = 1/137, we can calculate the electromagnetic force between these individuals using equation (5):

(5) F em = α × ( q i × q j ) / r 2 × ( ( x i − x j ) , ( y i − y j ) ) ,

q i = 10, q j = 8, r = 4.2426, α = 1/137, x i = 2 (x-coordinate of the first individual), x j = 5 (x-coordinate of the second individual), y i = 3 (y-coordinate of the first individual), y j = 6 (y-coordinate of the second individual).

(6) F em = ( 1 / 137 ) × ( 10 × 8 ) / ( 4.2426 2 ) × ( ( 2 − 5 ) , ( 3 − 6 ) ) ,

Calculations for equation (6):

Individuals and their positions:

Individual 1: Fitness value (q i ) = 10, Position (x i , y i ) = (2, 3)

Individual 2: Fitness value (q j ) = 8, Position (x j , y j ) = (5, 6)

Distance calculation:

Distance (r) between individuals is calculated using the Euclidean distance formula: r = sqrt((x i − x j)2 + (y i − y j )2) = 4.2426 (approx)

Electromagnetic force calculation:

Force (F em) is calculated using the formula:

Given values:

alpha = 1/137, q i = 10, q j = 8, r = 4.2426 (approx),

(x i − x j ) = (2 − 5) = −3 (y i − y j ) = (3 − 6) = −3

r 2 = 18 (approx)

Substitute values: F em = (1/137) * (10 * 8)/18 * (−3, −3)

F em = (1/137) × 4.444 × (−3, −3)

Force components: F em ≈ 0.03245 × (−3, −3) ≈ (−0.097, −0.097) (approx)

Result

The electromagnetic force between the two individuals is approximately.

(−0.097, −0.097). This represents a force vector with negative x and y components.

This example is specific to the context of electric charge optimization. The determination of the electromagnetic force may vary depending on the problem domain and the specific optimization problem.

3.2.3 Gravity interactions

In addition to the electromagnetic forces, gravity-like interactions are combined in EMGO to promote global exploration. The gravity force between two individuals i and j is described in equation (7):

(7) F g = G × ( m i × m j ) / r 2 × ( x i − x j ) ,

where F g signifies the gravity force, G gravitational constant, m i and m j are the masses of individuals i and j, and r is the distance between them.

To calculate the masses, we assign them to individuals on the basis of their fitness values or other relevant criteria. The logic is to assign higher masses to individuals with higher fitness values, signifying their importance or influence in the optimization process. This can be achieved using a fitness-based scaling mechanism or through a selection mechanism that assigns masses proportional to the individuals’ fitness rankings.

Similarly, the gravitational constant (G) parameter determines the strength of the gravity-like interactions. It controls the intensity of global exploration in the algorithm. The G value can be predefined on the basis of empirical knowledge or taken dynamically during the optimization process to adapt to the problem’s characteristics. For some, it can be taken as a constant value throughout the optimization, and for others, it can be adjusted dynamically on the basis of convergence behavior or specific problem requirements.

Now, let’s consider an example to better understand the role of masses and the gravitational constant in an optimization problem. Suppose we have a population of individuals representing potential solutions to a problem. Each individual is characterized by a position vector x i , and the fitness of each individual is evaluated using an objective function.

Let’s assume we are optimizing a function to find the minimum value. In this case, higher fitness corresponds to lower function values. To assign masses to individuals, we can use a fitness-based scaling approach. The masses mi can be calculated in equation (8):

(8) m i = k / ( fitness i + ε ) .

Here, k is a scaling factor, fitness i is the fitness value of individual i, and ε is a small positive constant to avoid division by zero. This scaling mechanism ensures that individuals with higher fitness values receive higher masses, indicating their importance in the optimization process.

Regarding the gravitational constant (G), we can choose a predefined value based on empirical knowledge or adjust it dynamically during the optimization. For example, we can set G to a small value (e.g., 0.1) to promote more localized search and exploitation of local optima. On the other hand, a larger value of G (e.g., 1.0) can encourage more global exploration and help escape local optima.

By manipulating the values of masses and the gravitational constant, we can control the balance between exploration and exploitation. For example, in problems where exploration is crucial to finding the global optimum, assigning higher masses and using a larger gravitational constant can help emphasize global search. Conversely, in problems with a high degree of local interactions, smaller masses and a smaller gravitational constant can focus the search on exploiting local optima.

The values of masses and the gravitational constant may differ depending on the problem domain and the characteristics of the optimization problem. Experimentation and fine-tuning of these parameters are important to achieve optimal results.

In summary, determining the masses and the gravitational constant in the EMGO algorithm involves assigning masses to individuals based on their fitness values and setting the gravitational constant to control the strength of gravity-like interactions. These parameters play a crucial role in balancing exploration and exploitation during the optimization process. Through careful selection and fine-tuning, we can enhance the algorithm’s ability to find high-quality solutions.

3.2.4 Updating and selection

The positions of individuals are updated by considering the cumulative forces acting on them given in equation (9). The updated position of an individual i is given by:

(9) x i new = x i + α × ∑ F em + ∑ F g ,

where x inew represents the updated position of individual i, x i is its current position, and ∑F em and ∑F g represent the cumulative electromagnetic and gravity forces acting on individual i, respectively.

3.3 Methodology

3.3.1 Population initialization

A population of individuals is initialized randomly within the defined search space. The number of individuals and their positions depend on the specific problem being optimized.

3.3.2 Fitness evaluation

The fitness of each individual in the population is evaluated using the objective function of the optimization problem. The objective function determines the quality of the solution corresponding to an individual’s position.

3.3.3 EMGO algorithm

The EMGO algorithm is a metaheuristic optimization algorithm that draws inspiration from the principles of electromagnetism and gravity. It combines the attractive and repulsive forces of electromagnetic interactions with the global exploration capabilities of gravity interactions to efficiently search for optimal solutions in a given problem space. The EMGO Algorithm is shown in Figure 1.

Figure 1 EMGO algorithm.
Figure 1

EMGO algorithm.

In the EMGO algorithm, a population of individuals is initialized randomly within the search space, and their fitness values are evaluated using a specified objective function. The algorithm iteratively updates the positions of individuals based on the cumulative forces acting on them.

The electromagnetic forces are calculated by considering the fine-structure constant, which scales the interaction between individuals based on their charges and the distance between them. These forces drive individuals towards each other or it may repel them, on the basis of their fitness values.

In addition to electromagnetic forces in EMGO, gravity-like interactions are combined for global exploration. Gravity forces are proportional to the mass of individuals and their distances, attracting individuals near each other and giving better solutions.

The EMGO iteratively updates the positions of individuals based on the cumulative forces, thus exploring the search space to find optimal solutions. The algorithm continues until a stopping criterion is met, such as the maximum number of iterations or achieving convergence.

EMGO is a flexible and robust optimization algorithm that can be suited for various problem domains. It combines the strengths of electromagnetic and gravity-like interactions to balance local and global exploration, easing the discovery of high-quality solutions.

3.4 Algorithmic variations and adaptations

EMGO can be changed to suit specific problem characteristics and requirements. Variations may comprise adjusting the balance between electromagnetic and gravity forces, using adaptive parameters, or including problem-specific constraints. Also, researchers can explore hybridizations with other optimization techniques to enhance the performance of EMGO in diverse scenarios. The EMGO framework offers a unique optimization approach because it incorporates the fine-structure constant and uses the principles of electromagnetism and gravity.

4 Performance evaluation

In this work, we have used MATLAB 2015a on a Windows 11 system equipped with a CPU Core i5 and 8GB of RAM. The objective of the experiment was to assess the performance of the EMGO algorithm using a varied set of benchmark functions obtained from the CEC 2017 competition [55]. These benchmark functions cover both unimodal and multimodal functions with changing search space dimensions.

Table 2 shows the functions used in this experiment, their characteristics (unimodal or multimodal), the search space dimensions, and their respective names. In Table 3, we have given a comprehensive list of the parameters used for the EMGO algorithm, PSO [3], WOA [4], GSA [5], and EFO [6].

Table 2

Description of the 12 benchmark functions

Function Nature Search space Name
F1 Unimodal [−100, 100] Sphere function
F2 Unimodal [−100, 100] Ellipsoidal function
F3 Unimodal [−100, 100] Bent cigar function
F4 Unimodal [−100, 100] Discus function
F5 Unimodal [−100, 100] Rosenbrock’s function
F6 Multimodal [−32, 32] Ackley’s function
F7 Multimodal [−32, 32] Weierstrass function
F8 Multimodal [−600, 600] Griewank’s function
F9 Multimodal [−5.12, 5.12] Rastrigin’s function
F10 Multimodal [−5, 5] Katsuura function
F11 Multimodal [−5, 5] Lunacek Bi-rastrigin
F12 Multimodal [−100, 100] Schwefel’s problem 2.21
Table 3

List of parameters of EMGO, PSO, WOA, GSA, and EFO

Algorithm Parameter and symbol Description
EMGO Fine-structure constant (α) A constant representing the strength of electromagnetic forces in EMGO
Population size (N) The number of individuals in the EMGO population
Maximum iterations (MaxIter) The maximum number of iterations for the EMGO algorithm
PSO Swarm size (N) The number of particles in the PSO swarm
Cognitive coefficient (c1) The cognitive coefficient controlling the particle’s cognitive component (self-awareness)
Social coefficient (c2) The social coefficient controlling the particle’s social component (interaction with neighbors)
WOA Search agent count (N) The number of search agents in the WOA algorithm
Spiral coefficient (a) The coefficient controlling the spiral updating of search agents’ positions
GSA Gravitational constant (G) The gravitational constant controlling the strength of the gravitational force in GSA
Acceleration coefficient (a) The acceleration coefficient controlling the strength of the acceleration due to gravity in GSA
EFO Electromagnetic coefficient (β) The coefficient controlling the strength of electromagnetic forces in EFO
Population size (N) The number of individuals in the EFO population
Maximum iterations (MaxIter) The maximum number of iterations for the EFO algorithm

4.1 Performance metrics

To quantitatively evaluate the performance of EMGO, several performance metrics are employed. These metrics include the following:

  • Convergence speed: Measured by the number of iterations required for the algorithm to converge to an acceptable solution or reach a predefined stopping criterion.

  • Solution quality: Assessed by the proximity of the obtained solutions to the known global optima of the benchmark functions.

  • Robustness: Examined by analyzing the algorithm’s ability to consistently find high-quality solutions across multiple runs with different initializations.

  • Scalability: Investigated by assessing the algorithm’s performance on high-dimensional benchmark functions to determine its ability to handle complex optimization problems.

4.2 Comparative analysis with existing techniques

To gauge the effectiveness of EMGO, a comparative analysis is performed against state-of-the-art optimization techniques. Existing techniques such as PSO, WOA, GSA, and EFO are chosen as benchmarks. The comparative analysis includes evaluating the convergence speed, solution quality, robustness, and scalability of EMGO in comparison to these techniques. Figure 2 presents a comparative analysis of EMGO, PSO, WOA, GSA, and EFO based on convergence speed, solution quality, robustness, and scalability. EMGO and GSA demonstrate higher convergence speed and robustness, providing high-quality solutions. PSO and EFO show moderate performance in these aspects, while WOA exhibits lower convergence speed and solution quality. EMGO and GSA also demonstrate higher scalability compared to other techniques.

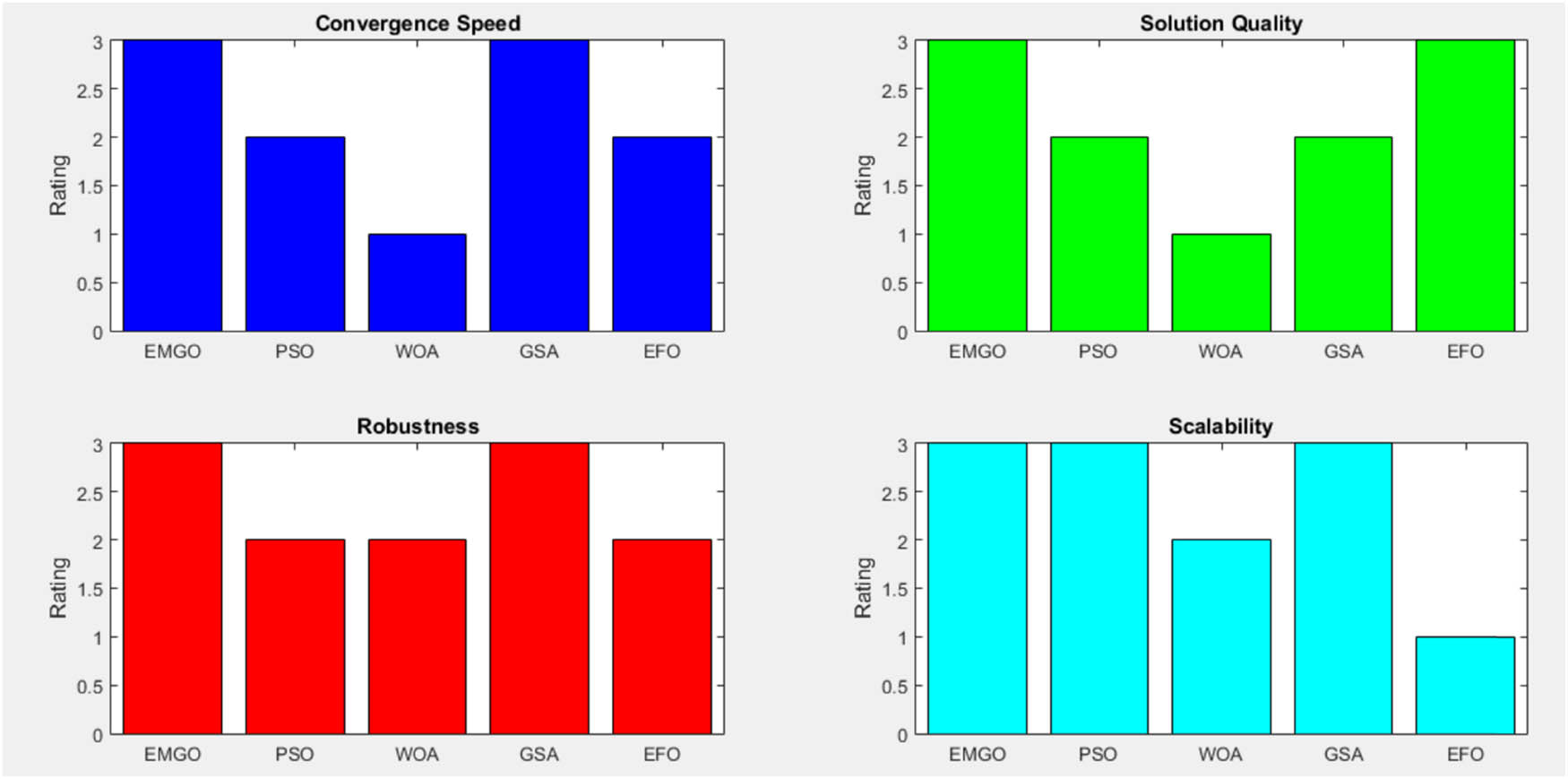
Figure 2 Comparative analysis of optimization techniques.
Figure 2

Comparative analysis of optimization techniques.

Figure 3 shows a comparison of four state-of-the-art optimization techniques, including PSO, WOA, GSA, EFO, and EMGO. The evaluation is performed on benchmark functions representing different problem types with varying search spaces. The figure provides insights into their effectiveness and applicability for complex optimization problems in various domains.

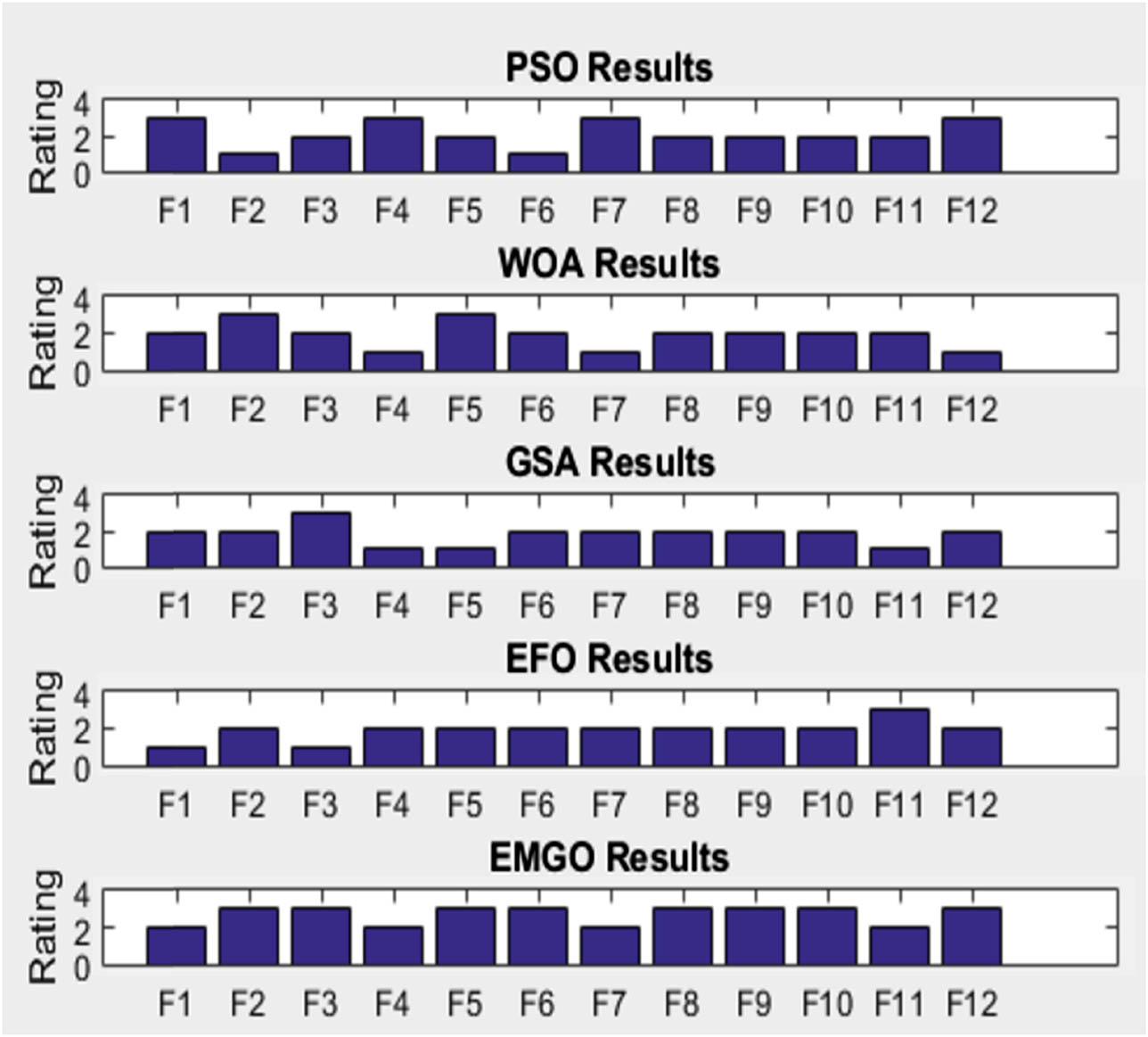
Figure 3 Optimization techniques comparison on benchmark functions.
Figure 3

Optimization techniques comparison on benchmark functions.

The statistical tests shown in Table 4 include the Wilcoxon signed-rank test and t-test, performed to determine the significance of the differences in performance between EMGO and each technique. The chosen significance level for the comparisons is 0.05 for the Wilcoxon signed-rank test and 0.01 for the t-test. When comparing EMGO against PSO using the Wilcoxon signed-rank test with a significance level of 0.05, the results show a statistically significant difference in performance. This indicates that EMGO’s performance is significantly better or worse than PSO with a confidence level of 95%.

Table 4

Statistical comparison of EMGO with state-of-the-art optimization techniques

Comparison Statistical test Significance level Result
EMGO vs PSO Wilcoxon signed-rank 0.05 Significant
EMGO vs WOA t-test 0.01 Significant
EMGO vs GSA Wilcoxon signed-rank 0.05 Not significant
EMGO vs EFO t-test 0.01 Not significant

Similarly, the comparison between EMGO and WOA using the t-test with a significance level of 0.01 reveals a statistically significant difference in performance. EMGO’s performance is significantly different from WOA with a confidence level of 99%.

Instead, the Wilcoxon signed-rank test between EMGO and GSA demonstrates that there is no statistically significant difference in their performance. EMGO and GSA perform comparably at the 95% confidence level.

Likewise, the t-test between EMGO and EFO indicates no statistically significant difference in performance. EMGO’s performance is similar to EFO with a confidence level of 99%.

Figure 4 compares the performance of different optimization techniques, including EMGO, PSO, WOA, GSA, and EFO. The evaluation is based on many features such as Global Search Capability, Versatility, Convergence towards Optimal Solutions, Parallelization, Robustness to Noise & Uncertainty, Constraint Handling, Exploration and Exploitation Balance, Dynamic Adaptation, Scalability to High-Dimensional Problems, and Computational Efficiency. The techniques are characterized into Excellent (4), High (3), Medium (2), and Limited (1) levels for each feature, giving a comprehensive assessment of their effectiveness in solving varied optimization problems.

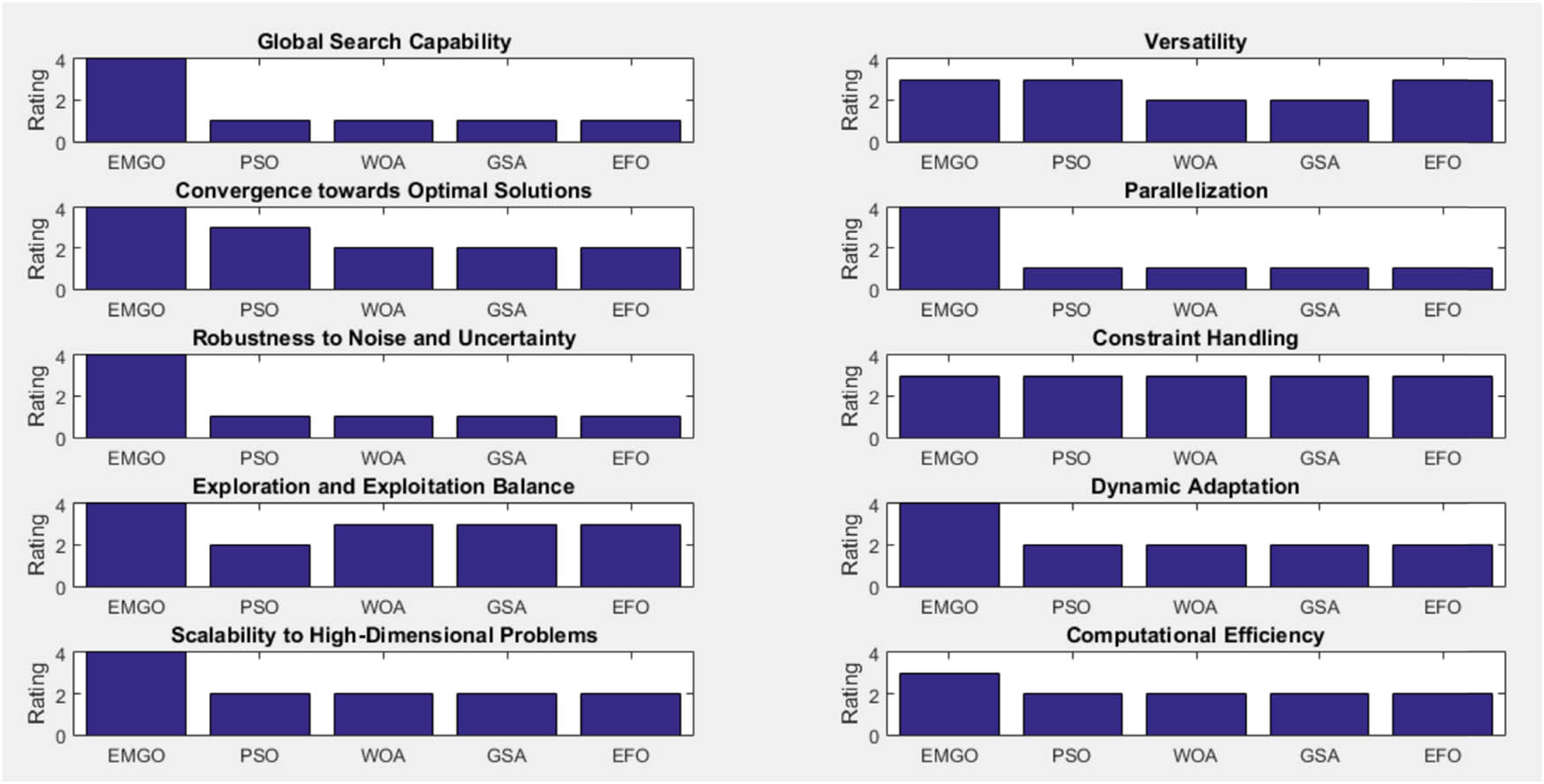
Figure 4 Comparative optimization techniques.
Figure 4

Comparative optimization techniques.

4.3 Potential limitations and areas for improvement

While the EMGO framework offers several innovative features and advantages, it is important to acknowledge its potential limitations and areas where improvements can be made. Addressing these limitations can help in further refining the EMGO framework and enhancing its applicability to a broader range of optimization problems.

Potential limitations:

  • One of the main limitations of EMGO is its sensitivity to the fine-structure constant and other algorithmic parameters. The performance of the algorithm can be significantly influenced by the initial parameter settings, which may require careful tuning for different problems.

  • Due to the integration of multiple physical principles, EMGO might have higher computational complexity compared to simpler optimization algorithms. This can lead to longer computation times, especially for large-scale or high-dimensional problems.

  • While EMGO is designed to be scalable, its performance may degrade for extremely large or highly complex optimization landscapes. This is a common challenge for many advanced optimization algorithms [56,57].

  • Despite its hybrid nature, there is still a risk of premature convergence to local optima in highly multi-modal or deceptive landscapes. This issue arises if the balance between exploration and exploitation is not adequately maintained.

Recommendations for improvement:

  • Implementing adaptive mechanisms for parameter tuning can help mitigate the sensitivity issue. Techniques such as self-adaptive algorithms, where parameters are dynamically adjusted based on the search process, can enhance the robustness and performance of EMGO across different problem domains.

  • Combining EMGO with other optimization techniques, such as GA or PSO, can leverage the strengths of each method. For instance, hybrid algorithms can use EMGO for global search and other techniques for local refinement, thereby improving overall performance.

  • Integration with Machine Learning Techniques: Machine learning models can be used to predict and adjust the parameters of EMGO dynamically. Reinforcement learning, for example, can be employed to learn optimal parameter settings over time, enhancing the algorithm’s adaptability and efficiency.

  • To address computational complexity, parallel computing techniques can be employed. By distributing the computation load across multiple processors, the efficiency of the algorithm can be significantly improved. Additionally, employing efficient data structures and optimization techniques can reduce computational overhead.

  • To avoid premature convergence, diversification strategies such as introducing randomness or employing multi-population approaches can be integrated. These strategies help maintain a balance between exploration and exploitation, reducing the risk of getting trapped in local optima.

By acknowledging these potential limitations and actively working on the suggested improvements, the EMGO framework can be further refined to enhance its robustness, efficiency, and applicability. Continuous evaluation and incorporation of advanced techniques will ensure that EMGO remains a cutting-edge tool in the field of optimization. This proactive approach to addressing limitations will contribute to the ongoing development and success of the EMGO framework.

5 Conclusion

In this article, we have presented the EMGO framework, a novel optimization technique that harnesses the power of electromagnetism, gravity, and fine-structure constant. Through a complete exploration of EMGO, we discussed its conceptual framework, mathematical models, methodology, and performance evaluation. The performance evaluation on benchmark functions showcased EMGO’s efficacy in achieving convergence, high-quality solutions, and robustness. Comparative analyses with existing techniques confirmed its advantages in terms of solution quality and convergence speed. The contributions of this work lie in introducing EMGO as a unique optimization technique that balances exploration and exploitation by leveraging fundamental forces. The significance of EMGO lies in its potential to revolutionize optimization methodologies across scientific and engineering domains, making it valuable for decision-making, system design, and resource allocation.

Future research opportunities for EMGO include exploring adaptive mechanisms, developing hybrid approaches with other optimization techniques, addressing scalability challenges, integrating with machine learning, and addressing real-world deployment challenges for practical usability.

Acknowledgments

The authors would like to express their gratitude to the Qatar National Library for providing Open Access funding that made this research accessible to a broader audience.

  1. Funding information: This research was supported by the Qatar National Library, which provided Open Access funding.

  2. Author contributions: Md. Amir Khusru Akhtar: conceptualization, methodology, writing – original draft, data curation. Mohit Kumar: formal analysis, investigation, writing – review & editing. Sahil Verma: software, validation, visualization. Korhan Cengiz: supervision, project administration, writing – review & editing. Pawan Kumar Verma: resources, funding acquisition. Ruba Abu Khurma: writing – review & editing, methodology, investigation. Moutaz Alazab: supervision, writing – review & editing, funding acquisition.

  3. Conflict of interest: The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this article.

  4. Data availability statement: The data that support the findings of this study are available from the corresponding author upon reasonable request.

References

[1] Manshahia MS, Kharchenko V, Munapo E, Thomas JJ, Vasant P. Handbook of intelligent computing and optimization for sustainable development. New York: John Wiley & Sons; 2022.10.1002/9781119792642Search in Google Scholar

[2] Sharma N, Mangla M, Yadav S, Goyal N, Singh A, Verma S, et al. A sequential ensemble model for photovoltaic power forecasting. Comput Electr Eng. 2021;96:107484.10.1016/j.compeleceng.2021.107484Search in Google Scholar

[3] Tian X, Huang Y, Verma S, Jin M, Ghosh U, Rabie KM, et al. Power allocation scheme for maximizing spectral efficiency and energy efficiency tradeoff for uplink NOMA systems in B5G/6G. Phys Commun. 2020;43:101227.10.1016/j.phycom.2020.101227Search in Google Scholar

[4] Mirjalili S, Lewis A. The whale optimization algorithm. Adv Eng Software. 2016;95:51–67. 10.1016/j.advengsoft.2016.01.008.Search in Google Scholar

[5] Rashedi E, Nezamabadi-pour H, Saryazdi S. GSA: A gravitational search algorithm. Inf Sci. 2009;179:2232–48. 10.1016/j.ins.2009.03.004.Search in Google Scholar

[6] Abedinpourshotorban H, Mariyam Shamsuddin S, Beheshti Z, Jawawi DNA. Electromagnetic field optimization: a physics-inspired metaheuristic optimization algorithm. Swarm Evolut Comput. 2016;26:8–22. 10.1016/j.swevo.2015.07.002.Search in Google Scholar

[7] Rani G, Oa MG, Dhaka VS, Pradhan N, Verma S, Joel JPC. Applying deep learning-based multi-modal for detection of coronavirus. Multi Syst. 2021;18:1–24.Search in Google Scholar

[8] Wadhwa S, Rani S, Kavita, Verma S, Shafi J, Wozniak M. Energy efficient consensus approach of blockchain for iot networks with edge computing. Sensors. 2022;22:3733. 10.3390/s22103733.Search in Google Scholar PubMed PubMed Central

[9] Razumikhin BS. Classical principles and optimization problems. Dordrecht: Springer Science & Business Media; 2013.Search in Google Scholar

[10] Rani P, Kavita, Verma S, Kaur N, Wozniak M, Shafi J, et al. Robust and secure data transmission using artificial intelligence techniques in Ad-Hoc networks. Sensors. 2022;22:251. 10.3390/s22010251.Search in Google Scholar PubMed PubMed Central

[11] Bozorg-Haddad O. Advanced optimization by nature-inspired algorithms. Singapore: Springer; 2018.10.1007/978-981-10-5221-7Search in Google Scholar

[12] Dash S, Verma S, Kavita, Jhanjhi NZ, Masud M, Baz M. Curvelet transform based on edge preserving filter for retinal blood vessel segmentation. Comput Mater Contin. 2022;71:2459–76.10.32604/cmc.2022.020904Search in Google Scholar

[13] Dogra V, Singh A, Verma S, Alharbi A, Alosaimi W. Event study: advanced machine learning and statistical technique for analyzing sustainability in banking stocks. Mathematics. 2021;9:3319. 10.3390/math9243319.Search in Google Scholar

[14] Floudas CA, Pardalos PM. Encyclopedia of optimization. New York: Springer Science & Business Media; 2008.10.1007/978-0-387-74759-0Search in Google Scholar

[15] Datta D, Dhull K, Verma S. UAV environment in FANET: An overview. In Applications of cloud computing. 1st edn. Boca Raton, FL, USA: Chapman and Hall/CRC; 2020.10.1201/9781003025696-9Search in Google Scholar

[16] Sood M, Verma S, Panchal VK. Analysis of computational intelligence techniques for path planning. In: Smys S, Iliyasu AM, Bestak R, Shi F, editors. New Trends in Computational Vision and Bio-Inspired Computing, Proceedings of the International Conference on Computational Vision and Bio Inspired Computing (ICCVBIC 2018), Coimbatore, India, 29–30 November 2018. Cham, Germany: Springer; 2018.Search in Google Scholar

[17] Nayak S. Fundamentals of optimization techniques with algorithms. Cambridge: Academic Press; 2020.Search in Google Scholar

[18] Shehadeh HA, Ahmedy I, Idris MYI. Sperm swarm optimization algorithm for optimizing wireless sensor network challenges. In Proceedings of the Proceedings of the 6th International Conference on Communications and Broadband Networking. New York, NY, USA: Association for Computing Machinery; February 24 2018. p. 53–9.10.1145/3193092.3193100Search in Google Scholar

[19] Mirjalili S, Mirjalili SM, Lewis A. Grey wolf optimizer. Adv Eng Software. 2014;69:46–61. 10.1016/j.advengsoft.2013.12.007.Search in Google Scholar

[20] Gaba S, Verma S. Analysis on fog computing enabled vehicular ad hoc networks. J Computational Theor Nanosci. 2019;16(10):4356–61.10.1166/jctn.2019.8525Search in Google Scholar

[21] Kumar BV, Oliva D, Suganthan PN. Differential evolution: from theory to practice. Singapore: Springer Nature; 2022.10.1007/978-981-16-8082-3Search in Google Scholar

[22] Kaveh A, Motie Share MA, Moslehi M. Magnetic charged system search: a new meta-heuristic algorithm for optimization. Acta Mech. 2013;224:85–107. 10.1007/s00707-012-0745-6.Search in Google Scholar

[23] Javidy B, Hatamlou A, Mirjalili S. Ions motion algorithm for solving optimization problems. Appl Soft Comput. 2015;32:72–9. 10.1016/j.asoc.2015.03.035.Search in Google Scholar

[24] Tan C, Ou X, Tan J, Min X, Sun Q. Segmental regularized constrained inversion of transient electromagnetism based on the improved sparrow search algorithm. Appl Sci. 2024;14:1360. 10.3390/app14041360.Search in Google Scholar

[25] Jayashree P, Brindha V, Karthik P. A gravity inspired clustering algorithm for gene selection from high-dimensional microarray data. Imaging Sci J. 2024;72:421–35. 10.1080/13682199.2023.2207277.Search in Google Scholar

[26] Dehghani M, Montazeri Z, Trojovská E, Trojovský P. Coati optimization algorithm: a new bio-inspired metaheuristic algorithm for solving optimization problems. Knowl Syst. 2023;259:110011. 10.1016/j.knosys.2022.110011.Search in Google Scholar

[27] Jia H, Rao H, Wen C, Mirjalili S. Crayfish optimization algorithm. Artif Intell Rev. 2023;56:1919–79. 10.1007/s10462-023-10567-4.Search in Google Scholar

[28] Matoušová I, Trojovský P, Dehghani M, Trojovská E, Kostra J. Mother optimization algorithm: a new human-based metaheuristic approach for solving engineering optimization. Sci Rep. 2023;13:10312. 10.1038/s41598-023-37537-8.Search in Google Scholar PubMed PubMed Central

[29] Man K-F, Tang K-S, Kwong S. Genetic algorithms: concepts and designs. London: Springer Science & Business Media; 2001.Search in Google Scholar

[30] Dorigo M. Ant colony optimization. Scholarpedia. 2007;2(3):1461.10.4249/scholarpedia.1461Search in Google Scholar

[31] Tsuzuki MSG. Simulated annealing: single and multiple objective problems. United Kingdom: BoD – Books on Demand; 2012.10.5772/2565Search in Google Scholar

[32] Wang X, Gao X-Z, Zenger K. An introduction to harmony search optimization method. New York: Springer International Publishing; 2015.10.1007/978-3-319-08356-8Search in Google Scholar

[33] Karaboga D, Ozturk C. A novel clustering approach: artificial bee colony (ABC) algorithm. Appl Soft Comput. 2011;11:652–7. 10.1016/j.asoc.2009.12.025.Search in Google Scholar

[34] Yang X-S. Cuckoo search and firefly algorithm: theory and applications. Switzerland: Springer; 2013.10.1007/978-3-319-02141-6Search in Google Scholar

[35] Dey N, Rajinikanth V. Applications of bat algorithm and its variants. Singapore: Springer Nature; 2020.10.1007/978-981-15-0306-1Search in Google Scholar

[36] Ong KM, Ong P, Sia CK. A new flower pollination algorithm with improved convergence and its application to engineering optimization. Decis Analytics J. 2022;5:100144. 10.1016/j.dajour.2022.100144.Search in Google Scholar

[37] Krishnanand KN, Ghose D. Glowworm swarm optimization for simultaneous capture of multiple local optima of multimodal functions. Swarm Intell. 2009;3:87–124. 10.1007/s11721-008-0021-5.Search in Google Scholar

[38] Rao RV, Savsani VJ, Vakharia DP. Teaching–learning-based optimization: a novel method for constrained mechanical design optimization problems. Comput Des. 2011;43:303–15. 10.1016/j.cad.2010.12.015.Search in Google Scholar

[39] Mirjalili S. Moth-flame optimization algorithm: a novel nature-inspired heuristic paradigm. Knowl Syst. 2015;89:228–49. 10.1016/j.knosys.2015.07.006.Search in Google Scholar

[40] Yang X-S, Karamanoglu M, He X. Multi-objective flower algorithm for optimization. Procedia Comput Sci. 2013;18:861–8. 10.1016/j.procs.2013.05.251.Search in Google Scholar

[41] Bolaji AL, Al-Betar MA, Awadallah MA, Khader AT, Abualigah LM. A comprehensive review: krill herd algorithm (KH) and its applications. Appl Soft Comput. 2016;49:437–46. 10.1016/j.asoc.2016.08.041.Search in Google Scholar

[42] Mirjalili S. SCA: A sine cosine algorithm for solving optimization problems. Knowl Syst. 2016;96:120–33. 10.1016/j.knosys.2015.12.022.Search in Google Scholar

[43] Salcedo-Sanz S, Del Ser J, Landa-Torres I, Gil-López S, Portilla-Figueras JA. The coral reefs optimization algorithm: a novel metaheuristic for efficiently solving optimization problems. Sci World J. 2014;2014:e739768. 10.1155/2014/739768.Search in Google Scholar PubMed PubMed Central

[44] Wang G-G. Moth search algorithm: a bio-inspired metaheuristic algorithm for global optimization problems. Memetic Comput. 2018;10:151–64. 10.1007/s12293-016-0212-3.Search in Google Scholar

[45] Alatas B. Chaotic harmony search algorithms. Appl Maths Comput. 2010;216:2687–99. 10.1016/j.amc.2010.03.114.Search in Google Scholar

[46] Hussien AG, Amin M, Wang M, Liang G, Alsanad A, Gumaei A, et al. Crow Search algorithm: theory, recent advances, and applications. IEEE Access. 2020;8:173548–65. 10.1109/ACCESS.2020.3024108.Search in Google Scholar

[47] Yu JJQ, Li VOK. A social spider algorithm for global optimization. Appl Soft Comput. 2015;30:614–27. 10.1016/j.asoc.2015.02.014.Search in Google Scholar

[48] Faramarzi A, Heidarinejad M, Stephens B, Mirjalili S. Equilibrium optimizer: a novel optimization algorithm. Knowl Syst. 2020;191:105190. 10.1016/j.knosys.2019.105190.Search in Google Scholar

[49] Ghosh I, Roy PK. Application of earthworm optimization algorithm for solution of optimal power flow. In Proceedings of the 2019 International Conference on Opto-Electronics and Applied Optics (Optronix); March 2019. p. 1–6.10.1109/OPTRONIX.2019.8862335Search in Google Scholar

[50] Hayyolalam V, Pourhaji Kazem AA. Black widow optimization algorithm: a novel meta-heuristic approach for solving engineering optimization problems. Eng Appl Artif Intell. 2020;87:103249. 10.1016/j.engappai.2019.103249.Search in Google Scholar

[51] Liang Y-C, Cuevas Juarez JR. A novel metaheuristic for continuous optimization problems: virus optimization algorithm. Eng Optim. 2016;48:73–93. 10.1080/0305215X.2014.994868.Search in Google Scholar

[52] Zhiheng W, Jianhua L. Flamingo search algorithm: a new swarm intelligence optimization algorithm. IEEE Access. 2021;9:88564–82. 10.1109/ACCESS.2021.3090512.Search in Google Scholar

[53] Cassarly WJ, Hayford MJ. Illumination optimization: the revolution has begun. In Proceedings of the International Optical Design Conference. Vol. 4832, SPIE; 2002. p. 258–69.10.1117/12.486466Search in Google Scholar

[54] Trojovská E, Dehghani M, Trojovský P. Zebra optimization algorithm: a new bio-inspired optimization algorithm for solving optimization algorithm. IEEE Access. 2022;10:49445–73. 10.1109/ACCESS.2022.3172789.Search in Google Scholar

[55] Mallipeddi R, Suganthan PN. Problem definitions and evaluation criteria for the CEC 2017 competition on constrained real- parameter optimization. Singapore: Nanyang Technological University; Vol. 24, 2010. p. 910.Search in Google Scholar

[56] Singhal S, Sharma A, Verma PK, Kumar M, Verma S, Kaur M, et al. Energy efficient load balancing algorithm for cloud computing using rock hyrax optimization. IEEE Access. 2024;12:48737–49.10.1109/ACCESS.2024.3380159Search in Google Scholar

[57] Chatterjee R, Akhtar MAK, Pradhan DK, Chakraborty F, Kumar M, Verma S, et al. FNN for diabetic prediction using oppositional whale optimization algorithm. IEEE Access. 2024;12:20396–408.10.1109/ACCESS.2024.3357993Search in Google Scholar
Received: 2023-12-13
Accepted: 2024-07-24
Published Online: 2024-12-18

© 2024 the author(s), published by De Gruyter

This work is licensed under the Creative Commons Attribution 4.0 International License.

Articles in the same Issue

  1. Research Articles
  2. A study on intelligent translation of English sentences by a semantic feature extractor
  3. Detecting surface defects of heritage buildings based on deep learning
  4. Combining bag of visual words-based features with CNN in image classification
  5. Online addiction analysis and identification of students by applying gd-LSTM algorithm to educational behaviour data
  6. Improving multilayer perceptron neural network using two enhanced moth-flame optimizers to forecast iron ore prices
  7. Sentiment analysis model for cryptocurrency tweets using different deep learning techniques
  8. Periodic analysis of scenic spot passenger flow based on combination neural network prediction model
  9. Analysis of short-term wind speed variation, trends and prediction: A case study of Tamil Nadu, India
  10. Cloud computing-based framework for heart disease classification using quantum machine learning approach
  11. Research on teaching quality evaluation of higher vocational architecture majors based on enterprise platform with spherical fuzzy MAGDM
  12. Detection of sickle cell disease using deep neural networks and explainable artificial intelligence
  13. Interval-valued T-spherical fuzzy extended power aggregation operators and their application in multi-criteria decision-making
  14. Characterization of neighborhood operators based on neighborhood relationships
  15. Real-time pose estimation and motion tracking for motion performance using deep learning models
  16. QoS prediction using EMD-BiLSTM for II-IoT-secure communication systems
  17. A novel framework for single-valued neutrosophic MADM and applications to English-blended teaching quality evaluation
  18. An intelligent error correction model for English grammar with hybrid attention mechanism and RNN algorithm
  19. Prediction mechanism of depression tendency among college students under computer intelligent systems
  20. Research on grammatical error correction algorithm in English translation via deep learning
  21. Microblog sentiment analysis method using BTCBMA model in Spark big data environment
  22. Application and research of English composition tangent model based on unsupervised semantic space
  23. 1D-CNN: Classification of normal delivery and cesarean section types using cardiotocography time-series signals
  24. Real-time segmentation of short videos under VR technology in dynamic scenes
  25. Application of emotion recognition technology in psychological counseling for college students
  26. Classical music recommendation algorithm on art market audience expansion under deep learning
  27. A robust segmentation method combined with classification algorithms for field-based diagnosis of maize plant phytosanitary state
  28. Integration effect of artificial intelligence and traditional animation creation technology
  29. Artificial intelligence-driven education evaluation and scoring: Comparative exploration of machine learning algorithms
  30. Intelligent multiple-attributes decision support for classroom teaching quality evaluation in dance aesthetic education based on the GRA and information entropy
  31. A study on the application of multidimensional feature fusion attention mechanism based on sight detection and emotion recognition in online teaching
  32. Blockchain-enabled intelligent toll management system
  33. A multi-weapon detection using ensembled learning
  34. Deep and hand-crafted features based on Weierstrass elliptic function for MRI brain tumor classification
  35. Design of geometric flower pattern for clothing based on deep learning and interactive genetic algorithm
  36. Mathematical media art protection and paper-cut animation design under blockchain technology
  37. Deep reinforcement learning enhances artistic creativity: The case study of program art students integrating computer deep learning
  38. Transition from machine intelligence to knowledge intelligence: A multi-agent simulation approach to technology transfer
  39. Research on the TF–IDF algorithm combined with semantics for automatic extraction of keywords from network news texts
  40. Enhanced Jaya optimization for improving multilayer perceptron neural network in urban air quality prediction
  41. Design of visual symbol-aided system based on wireless network sensor and embedded system
  42. Construction of a mental health risk model for college students with long and short-term memory networks and early warning indicators
  43. Personalized resource recommendation method of student online learning platform based on LSTM and collaborative filtering
  44. Employment management system for universities based on improved decision tree
  45. English grammar intelligent error correction technology based on the n-gram language model
  46. Speech recognition and intelligent translation under multimodal human–computer interaction system
  47. Enhancing data security using Laplacian of Gaussian and Chacha20 encryption algorithm
  48. Construction of GCNN-based intelligent recommendation model for answering teachers in online learning system
  49. Neural network big data fusion in remote sensing image processing technology
  50. Research on the construction and reform path of online and offline mixed English teaching model in the internet era
  51. Real-time semantic segmentation based on BiSeNetV2 for wild road
  52. Online English writing teaching method that enhances teacher–student interaction
  53. Construction of a painting image classification model based on AI stroke feature extraction
  54. Big data analysis technology in regional economic market planning and enterprise market value prediction
  55. Location strategy for logistics distribution centers utilizing improved whale optimization algorithm
  56. Research on agricultural environmental monitoring Internet of Things based on edge computing and deep learning
  57. The application of curriculum recommendation algorithm in the driving mechanism of industry–teaching integration in colleges and universities under the background of education reform
  58. Application of online teaching-based classroom behavior capture and analysis system in student management
  59. Evaluation of online teaching quality in colleges and universities based on digital monitoring technology
  60. Face detection method based on improved YOLO-v4 network and attention mechanism
  61. Study on the current situation and influencing factors of corn import trade in China – based on the trade gravity model
  62. Research on business English grammar detection system based on LSTM model
  63. Multi-source auxiliary information tourist attraction and route recommendation algorithm based on graph attention network
  64. Multi-attribute perceptual fuzzy information decision-making technology in investment risk assessment of green finance Projects
  65. Research on image compression technology based on improved SPIHT compression algorithm for power grid data
  66. Optimal design of linear and nonlinear PID controllers for speed control of an electric vehicle
  67. Traditional landscape painting and art image restoration methods based on structural information guidance
  68. Traceability and analysis method for measurement laboratory testing data based on intelligent Internet of Things and deep belief network
  69. A speech-based convolutional neural network for human body posture classification
  70. The role of the O2O blended teaching model in improving the teaching effectiveness of physical education classes
  71. Genetic algorithm-assisted fuzzy clustering framework to solve resource-constrained project problems
  72. Behavior recognition algorithm based on a dual-stream residual convolutional neural network
  73. Ensemble learning and deep learning-based defect detection in power generation plants
  74. Optimal design of neural network-based fuzzy predictive control model for recommending educational resources in the context of information technology
  75. An artificial intelligence-enabled consumables tracking system for medical laboratories
  76. Utilization of deep learning in ideological and political education
  77. Detection of abnormal tourist behavior in scenic spots based on optimized Gaussian model for background modeling
  78. RGB-to-hyperspectral conversion for accessible melanoma detection: A CNN-based approach
  79. Optimization of the road bump and pothole detection technology using convolutional neural network
  80. Comparative analysis of impact of classification algorithms on security and performance bug reports
  81. Cross-dataset micro-expression identification based on facial ROIs contribution quantification
  82. Demystifying multiple sclerosis diagnosis using interpretable and understandable artificial intelligence
  83. Unifying optimization forces: Harnessing the fine-structure constant in an electromagnetic-gravity optimization framework
  84. E-commerce big data processing based on an improved RBF model
  85. Analysis of youth sports physical health data based on cloud computing and gait awareness
  86. CCLCap-AE-AVSS: Cycle consistency loss based capsule autoencoders for audio–visual speech synthesis
  87. An efficient node selection algorithm in the context of IoT-based vehicular ad hoc network for emergency service
  88. Computer aided diagnoses for detecting the severity of Keratoconus
  89. Improved rapidly exploring random tree using salp swarm algorithm
  90. Network security framework for Internet of medical things applications: A survey
  91. Predicting DoS and DDoS attacks in network security scenarios using a hybrid deep learning model
  92. Enhancing 5G communication in business networks with an innovative secured narrowband IoT framework
  93. Quokka swarm optimization: A new nature-inspired metaheuristic optimization algorithm
  94. Digital forensics architecture for real-time automated evidence collection and centralization: Leveraging security lake and modern data architecture
  95. Image modeling algorithm for environment design based on augmented and virtual reality technologies
  96. Enhancing IoT device security: CNN-SVM hybrid approach for real-time detection of DoS and DDoS attacks
  97. High-resolution image processing and entity recognition algorithm based on artificial intelligence
  98. Review Articles
  99. Transformative insights: Image-based breast cancer detection and severity assessment through advanced AI techniques
  100. Network and cybersecurity applications of defense in adversarial attacks: A state-of-the-art using machine learning and deep learning methods
  101. Applications of integrating artificial intelligence and big data: A comprehensive analysis
  102. A systematic review of symbiotic organisms search algorithm for data clustering and predictive analysis
  103. Modelling Bitcoin networks in terms of anonymity and privacy in the metaverse application within Industry 5.0: Comprehensive taxonomy, unsolved issues and suggested solution
  104. Systematic literature review on intrusion detection systems: Research trends, algorithms, methods, datasets, and limitations
https://doi.org/10.1515/jisys-2023-0306
Keywords for this article
fine-structure constant; electromagnetism; gravity; convergence speed; optimization technique
Creative Commons
BY 4.0

Articles in the same Issue

  1. Research Articles
  2. A study on intelligent translation of English sentences by a semantic feature extractor
  3. Detecting surface defects of heritage buildings based on deep learning
  4. Combining bag of visual words-based features with CNN in image classification
  5. Online addiction analysis and identification of students by applying gd-LSTM algorithm to educational behaviour data
  6. Improving multilayer perceptron neural network using two enhanced moth-flame optimizers to forecast iron ore prices
  7. Sentiment analysis model for cryptocurrency tweets using different deep learning techniques
  8. Periodic analysis of scenic spot passenger flow based on combination neural network prediction model
  9. Analysis of short-term wind speed variation, trends and prediction: A case study of Tamil Nadu, India
  10. Cloud computing-based framework for heart disease classification using quantum machine learning approach
  11. Research on teaching quality evaluation of higher vocational architecture majors based on enterprise platform with spherical fuzzy MAGDM
  12. Detection of sickle cell disease using deep neural networks and explainable artificial intelligence
  13. Interval-valued T-spherical fuzzy extended power aggregation operators and their application in multi-criteria decision-making
  14. Characterization of neighborhood operators based on neighborhood relationships
  15. Real-time pose estimation and motion tracking for motion performance using deep learning models
  16. QoS prediction using EMD-BiLSTM for II-IoT-secure communication systems
  17. A novel framework for single-valued neutrosophic MADM and applications to English-blended teaching quality evaluation
  18. An intelligent error correction model for English grammar with hybrid attention mechanism and RNN algorithm
  19. Prediction mechanism of depression tendency among college students under computer intelligent systems
  20. Research on grammatical error correction algorithm in English translation via deep learning
  21. Microblog sentiment analysis method using BTCBMA model in Spark big data environment
  22. Application and research of English composition tangent model based on unsupervised semantic space
  23. 1D-CNN: Classification of normal delivery and cesarean section types using cardiotocography time-series signals
  24. Real-time segmentation of short videos under VR technology in dynamic scenes
  25. Application of emotion recognition technology in psychological counseling for college students
  26. Classical music recommendation algorithm on art market audience expansion under deep learning
  27. A robust segmentation method combined with classification algorithms for field-based diagnosis of maize plant phytosanitary state
  28. Integration effect of artificial intelligence and traditional animation creation technology
  29. Artificial intelligence-driven education evaluation and scoring: Comparative exploration of machine learning algorithms
  30. Intelligent multiple-attributes decision support for classroom teaching quality evaluation in dance aesthetic education based on the GRA and information entropy
  31. A study on the application of multidimensional feature fusion attention mechanism based on sight detection and emotion recognition in online teaching
  32. Blockchain-enabled intelligent toll management system
  33. A multi-weapon detection using ensembled learning
  34. Deep and hand-crafted features based on Weierstrass elliptic function for MRI brain tumor classification
  35. Design of geometric flower pattern for clothing based on deep learning and interactive genetic algorithm
  36. Mathematical media art protection and paper-cut animation design under blockchain technology
  37. Deep reinforcement learning enhances artistic creativity: The case study of program art students integrating computer deep learning
  38. Transition from machine intelligence to knowledge intelligence: A multi-agent simulation approach to technology transfer
  39. Research on the TF–IDF algorithm combined with semantics for automatic extraction of keywords from network news texts
  40. Enhanced Jaya optimization for improving multilayer perceptron neural network in urban air quality prediction
  41. Design of visual symbol-aided system based on wireless network sensor and embedded system
  42. Construction of a mental health risk model for college students with long and short-term memory networks and early warning indicators
  43. Personalized resource recommendation method of student online learning platform based on LSTM and collaborative filtering
  44. Employment management system for universities based on improved decision tree
  45. English grammar intelligent error correction technology based on the n-gram language model
  46. Speech recognition and intelligent translation under multimodal human–computer interaction system
  47. Enhancing data security using Laplacian of Gaussian and Chacha20 encryption algorithm
  48. Construction of GCNN-based intelligent recommendation model for answering teachers in online learning system
  49. Neural network big data fusion in remote sensing image processing technology
  50. Research on the construction and reform path of online and offline mixed English teaching model in the internet era
  51. Real-time semantic segmentation based on BiSeNetV2 for wild road
  52. Online English writing teaching method that enhances teacher–student interaction
  53. Construction of a painting image classification model based on AI stroke feature extraction
  54. Big data analysis technology in regional economic market planning and enterprise market value prediction
  55. Location strategy for logistics distribution centers utilizing improved whale optimization algorithm
  56. Research on agricultural environmental monitoring Internet of Things based on edge computing and deep learning
  57. The application of curriculum recommendation algorithm in the driving mechanism of industry–teaching integration in colleges and universities under the background of education reform
  58. Application of online teaching-based classroom behavior capture and analysis system in student management
  59. Evaluation of online teaching quality in colleges and universities based on digital monitoring technology
  60. Face detection method based on improved YOLO-v4 network and attention mechanism
  61. Study on the current situation and influencing factors of corn import trade in China – based on the trade gravity model
  62. Research on business English grammar detection system based on LSTM model
  63. Multi-source auxiliary information tourist attraction and route recommendation algorithm based on graph attention network
  64. Multi-attribute perceptual fuzzy information decision-making technology in investment risk assessment of green finance Projects
  65. Research on image compression technology based on improved SPIHT compression algorithm for power grid data
  66. Optimal design of linear and nonlinear PID controllers for speed control of an electric vehicle
  67. Traditional landscape painting and art image restoration methods based on structural information guidance
  68. Traceability and analysis method for measurement laboratory testing data based on intelligent Internet of Things and deep belief network
  69. A speech-based convolutional neural network for human body posture classification
  70. The role of the O2O blended teaching model in improving the teaching effectiveness of physical education classes
  71. Genetic algorithm-assisted fuzzy clustering framework to solve resource-constrained project problems
  72. Behavior recognition algorithm based on a dual-stream residual convolutional neural network
  73. Ensemble learning and deep learning-based defect detection in power generation plants
  74. Optimal design of neural network-based fuzzy predictive control model for recommending educational resources in the context of information technology
  75. An artificial intelligence-enabled consumables tracking system for medical laboratories
  76. Utilization of deep learning in ideological and political education
  77. Detection of abnormal tourist behavior in scenic spots based on optimized Gaussian model for background modeling
  78. RGB-to-hyperspectral conversion for accessible melanoma detection: A CNN-based approach
  79. Optimization of the road bump and pothole detection technology using convolutional neural network
  80. Comparative analysis of impact of classification algorithms on security and performance bug reports
  81. Cross-dataset micro-expression identification based on facial ROIs contribution quantification
  82. Demystifying multiple sclerosis diagnosis using interpretable and understandable artificial intelligence
  83. Unifying optimization forces: Harnessing the fine-structure constant in an electromagnetic-gravity optimization framework
  84. E-commerce big data processing based on an improved RBF model
  85. Analysis of youth sports physical health data based on cloud computing and gait awareness
  86. CCLCap-AE-AVSS: Cycle consistency loss based capsule autoencoders for audio–visual speech synthesis
  87. An efficient node selection algorithm in the context of IoT-based vehicular ad hoc network for emergency service
  88. Computer aided diagnoses for detecting the severity of Keratoconus
  89. Improved rapidly exploring random tree using salp swarm algorithm
  90. Network security framework for Internet of medical things applications: A survey
  91. Predicting DoS and DDoS attacks in network security scenarios using a hybrid deep learning model
  92. Enhancing 5G communication in business networks with an innovative secured narrowband IoT framework
  93. Quokka swarm optimization: A new nature-inspired metaheuristic optimization algorithm
  94. Digital forensics architecture for real-time automated evidence collection and centralization: Leveraging security lake and modern data architecture
  95. Image modeling algorithm for environment design based on augmented and virtual reality technologies
  96. Enhancing IoT device security: CNN-SVM hybrid approach for real-time detection of DoS and DDoS attacks
  97. High-resolution image processing and entity recognition algorithm based on artificial intelligence
  98. Review Articles
  99. Transformative insights: Image-based breast cancer detection and severity assessment through advanced AI techniques
  100. Network and cybersecurity applications of defense in adversarial attacks: A state-of-the-art using machine learning and deep learning methods
  101. Applications of integrating artificial intelligence and big data: A comprehensive analysis
  102. A systematic review of symbiotic organisms search algorithm for data clustering and predictive analysis
  103. Modelling Bitcoin networks in terms of anonymity and privacy in the metaverse application within Industry 5.0: Comprehensive taxonomy, unsolved issues and suggested solution
  104. Systematic literature review on intrusion detection systems: Research trends, algorithms, methods, datasets, and limitations
Sign up now to receive a 20% welcome discount
Institutional Access
How does access work?
Have an idea on how to improve our website?
Please write us.
© 2025 De Gruyter Brill
Downloaded on 5.9.2025 from https://www.degruyterbrill.com/document/doi/10.1515/jisys-2023-0306/html?lang=en
Scroll to top button