Home Expertise and Uncertainty Processing with Nonlinear Scaling and Fuzzy Systems for Automation
Article Open Access

Expertise and Uncertainty Processing with Nonlinear Scaling and Fuzzy Systems for Automation

  • Esko K. Juuso EMAIL logo
Published/Copyright: August 7, 2020
Download Article (PDF)
Become an author with De Gruyter Brill
Submit Manuscript Author Information
Open Engineering
From the journal Open Engineering Volume 10 Issue 1

Abstract

Integration of domain expertise and uncertainty processing is increasingly important in automation solutions which rely on data analytics and artificial intelligence. We need a level to assess what is approximately correct. Uncertainties of the inputs are taken into account by using fuzzy numbers as the inputs of different fuzzy and parametric systems. Nonlinear scaling functions (NSFs) integrate these solutions and make them easier to tune. Fuzzy rule-based systems are represented with scaled fuzzy inputs. Membership functions (MFs) can be developed from NSFs and existing MFs can be used in developing NSFs. Fuzzy set systems and linguistic equation (LE) systems become consistent within the limits of detail. In recursive analysis, both meanings and interactions on all levels can be tuned together with genetic algorithms. In applications, the modular overall system consists of similar subsystems, which are normally used, with extensions to fuzzy. The compact fuzzy modules can be developed for specific tasks which are combined within Cyber Physical Systems (CPS). Uncertainty processing is embedded in the recursive analysis. The fuzzy extensions provide a feasible way for the sensitivity analysis of the solution.

Keywords: fuzzy set systems; fuzzy arithmetics; domain expertise; uncertainty

1 Introduction

Domain expertise and uncertainty processing are increasingly important in automation solutions which rely on data analytics and artificial intelligence. Keeping the appropriate operating conditions and assessing the approximate correctness are needed to avoid faulty decisions. Fuzzy systems provide tools where the uncertainties of the inputs are taken into account by using fuzzy numbers, labels and rules. Fuzzy set systems use degrees of membership for calculating firing the rules [1, 2]. Fuzzy inputs can introduce additional active labels and thus more conditions for the firing of rules. Additional alternatives of outputs with different degrees of membership increase the uncertainty of the response. Fuzzy relations are based on the intensities of interactions [3]. These methodologies are closely related.

Alternatively, fuzzy inputs can be processed with fuzzy arithmetic where the calculations use the fuzzy extensions of the interval analysis [4]. Equations and models include functions which can be handled with the extension principle [5]. The fuzzy result can be sufficient, e.g. in diagnostics, but it can be defuzzified in a normal way. The fuzzy mathematics has tools for handling in-equalitieswhich provide additional fuzzy facts for the rule-based fuzzy systems. Any fuzzy response can be further processed with the fuzzy arithmetic instead of going to the defuzzification.

Adaptation, which is essential in varying operating conditions, is an important part of fuzzy systems: scaling, modifying membership functions and updating rules are supported in many ways. There are many mechanisms for self-organising [6] and self-tuning [7] fuzzy controllers. Powering modifiers can be used for the fuzzy numbers and labels [8].

More or less automatic modelling possibilities have increased the popularity of artificial neural networks (ANNs) in building nonlinear transformation layers for complicated interactions within different sources of varying data [9]. Self-organising maps (SOM), which have many alternatives for calculating distances in the competitive layer [10], are suitable for clustering and shaping fuzzy rule-based systems. SOMis a feasible solution for adaptive filtering [11]. The fuzzy Kohonen clustering network integrates the fuzzy c-means (FCM) model into the Kohonen network [12].

Linguistic equation (LE) systems originate from fuzzy systems [13]: nonlinear scaling makes the solutions compact by facilitating the use of linear methodologies for analysing interactions [14]. The systems are parametric and can be tuned with genetic algorithms [15], also recursively [16]. The compact solution makes them suitable for big data analysis and Cyber Physical Systems (CPS) [17].

This paper analyses alternatives of the fuzzy extensions of parametric systems. Meanings of variables, different types fuzzy and parametric systems are building blocks of these systems (Section 2). Feasible adaptation solutions are presented in Section 3 and application requirements for modelling, control and diagnostics in Section 4. The compact systems for varying operating conditions are discussed in Section 5. Conclusions and future work are presented in Section 6.

2 Methodologies

Statistical models are in various ways used in data-driven modelling and rule-based systems form the basis for handling expertise. Both lines of modelling can be efficiently extended to nonlinear applications by modifying the variables to correspond better with the meanings of the variable levels. Then the linear models and rulebases can focus on the directions of interactions.

2.1 Meanings

In fuzzy systems, the labels are represented by membership functions (MFs) which provide the link to the numeric values. Scaling and modifying the parameters of the membership functions are efficient in the adaptation of the fuzzy systems. Nonlinear scaling functions (NSFs) make the sets of MFs consistent [14].

2.1.1 Membership functions

In fuzzy set theory, a fuzzy subset A on universe (domain) E is defined by representing the characteristic function cA by a membership function μ(x) ∈ [0, 1].

In the vertical representation, a fuzzy set A = {(u, μA(u) | u ∈ U} can be defined by a sum of ordered pairs: membership degree/set element:

(1)A=μA(u1)/u1+⋯+μA(un)/un=∑i=1nμA(ui)/ui,

where + means a/u + b/u = max(a, b)/u. This can be extended to discrete and continuous. A fuzzy set can be presented in the form of two related vectors:

(2)x=[x1,x2,…,xn]T,
(3)μ=[μA(x1),μA(x2),…μA(xn)]T.

Vertical MFs are used together with rule-based systems (Section 2.2.1) and relation-based systems (Section 2.2.2).

Horisontal MFs are represented by α-cuts Aα:

(4)Aα={x∣x∈E and μA≥α},

where α ∈ (0, 1]. The α-cut operator is also denoted by α-cut (A, α). The α-cuts of higher membership degrees are always subsets of the α-cuts of lower membership degrees:

(5)α≥α′⇒Aα⊆Aα′andAα=limβ↑αAβ.

Horisontal MFs are used in fuzzy arithmetic (Section 2.2.3).

A fuzzy number A is a fuzzy set of the real line with a normal, (fuzzy) convex and continuous membership function of bounded support. Fuzzy numbers are defined by support and core: supp(A) = {x | μA(x) > 0}, and core(A) = {x | μA(x) = 1}. The height is defined by supremum: the smallest degree of membership that is greater than or equal to each of the set. The representation can be either vertical or horisontal.

MFs are normally presented with mathematical functions, e.g. triangular, trapezoidal and bell-shaped functions. Also piece-wise linear functions are used. Fuzzy rule-based systems use sets of MFs. In developing MFs, probability distributions can be used by interpreting MFs on the basis of possibilistic extension.

Fuzzy modifiers provide intensifying or weakening adverbs to obtain new terms:

(6)A1⊆A2⊆A3⊆A4⊆A5,

which correspond to the powers of the membership in the powering modifiers (Table 1). Using modifiers for α values of the α-cuts can be a feasible alternative. Memberships can be further processed with the conjunction (and), disjunction (or) and negation (not), see more examples in [8].

Table 1

Modifiers of fuzzy numbers [18]

Fuzzy numberFuzzy labelDegree of membership
A1extremely Aμ4
A2very Aμ2
A3Aμ
A4more or less Aμ12
A5roughly Aμ14

Modifiers can be used for introducing additional membership functions or fuzzy numbers which take better the domain expertise into account. Modifiers can be used for both MFs by changing μ(x) vectors in vertical and α-cuts in horisontal representation, respectively.

2.1.2 Nonlinear scaling

The nonlinear scaling was presented already in 1991 [13, 19] as a methodology for improving membership functions of fuzzy set systems. Nonlinear scaling functions (NSFs) are monotonously increasing functions xj = f(Xj) where xj is the variable and Xj the corresponding scaled variable in the range [-2, 2]. The function f() consist of two second order polynomials, one for the negative values of Xj ∈ [−2, 0] and one for the positive values Xj ∈ [0, 2], respectively. Five parameters are needed to define these functions since the overall functions are continuous (Figure 1). [14]

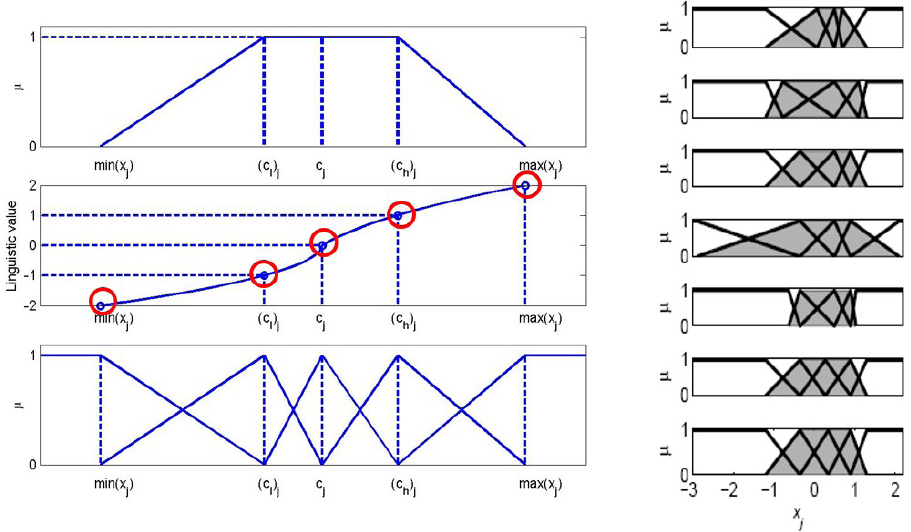
Figure 1 Nonlinear scaling and membership functions.
Figure 1

Nonlinear scaling and membership functions.

The core area [(cl)j,(ch)j], corresponding [-1, 1], is within the support area defined by the minimum and maximum values. The shapes are defined by

(7)αj−=(cl)j−min(xj)cj−(cl)j,αj+=max(xj)−(ch)j(ch)j−cj,

where cj is the central tendency value, corresponding 0. The scaling functions are monotonous and increasing if these ratios are both in the range [13,3],see [15]. The parameters of the scaling functions can be defined manually or by data-based methodologies [20]. In genetic tuning, the shape requirements are taken into account. In manual tuning, the parameters are modified to achieve monotonously increasing functions.

The corresponding inverse functions xj = f−1(Xj) based on square root functions are used for scaling to the scaled range.

Monotonously increasing nonlinear scaling functions, xj = f(Xj) and xj = f−1(Xj), are suitable for inductive mappings in the extension principle. This can be used in transforming fuzzy numbers and membership functions to both directions between the real and scaled values.

The NSFs, also called membership definitions, originate from MFs [14]. A set of MFs can be generated by selecting the locations for the functions (Figure 2). Natural language interpretation provides a basis for the transformation. The integer numbers {-2, -1, 0, 1, 2} correspond labels {very low, low, normal, high, very high} or {high negative, negative, zero, positive, high positive} or {accelerating decrease, decrease, constant, increase, accelerating increase}. The vocabulary can also be chosen in a different way, e.g. by using modifiers highly, fairly or quite [21]. Only the sequence of the labels is important.

Figure 2 Fuzzy set systems and linguistic equations [14].
Figure 2

Fuzzy set systems and linguistic equations [14].

The set of MFs depends strongly on the shape of the NSFs as can be seen in the examples shown in Figure 1. The number of MFs is not limited to five.Modifiers of the labels can introduce domain expertise for defining corresponding membership locations in the scaled range (Figure 2).

The scaling can be extended to the temporal analysis: increasing and decreasing changes can be quantified, trend and fluctuation indices are calculated by using scaled values. Resulting values are within the range [-2, 2] and can be interpreted with MFs as in Figure 1 and explained with natural language.

Uncertainties are embedded in the nonlinear scaling approach: feasible ranges and labels are presented with MFs (Figure 1). The data-based computation of the NSFs is done by using equal-sized sub-blocks, i.e. the norm for several samples can be obtained as the norm for the norms of individual samples [20, 22]. The parameters can have differences between the sub-blocks, which introduces uncertainties to the NSFs and MFs.

2.2 Fuzzy systems

Fuzzy systems are based on rules, relations and local models, including fuzzy numbers and labels represented by MFs. The uncertainties of the facts are processed by the calculations with the degrees of membership. Fuzzy systems may include versatile facts, including labels, equalities and inequalities. The nonlinear scaling improves the numerical calculations in these systems.

2.2.1 Rule-based fuzzy set systems

Fuzzy set systems focus on the linguistic meanings of the variables, which suit very well to qualitative descriptions of the process. In linguistic fuzzy systems, both the antecedents and consequents are fuzzy propositions, which can be interpreted by using natural language, heuristics and common sense knowledge. The rules can have several consequents. Fuzzy rule-based systems maintain clear connections with expert systems [23]. Fuzzy set theory first presented by Zadeh [1] form a conceptual framework for linguistically represented knowledge.

Local models based on crisp functions of the antecedent variables are used in Takagi-Sugeno (TS) fuzzy models [24]. The consequent is a parameterized function, whose structure remains constant and only the parameters vary. For linear models, smoothing techniques are needed to avoid erroneous hedges and valleys on the response surfaces [25]. The freedom of parameters needs to be reduced to improve system development [26].

Type-2 fuzzy models introduced by Zadeh in 1975 take into account uncertainty about the membership function [27]. Most systems based on interval type-2 fuzzy sets are reduced to an interval-valued type-1 fuzzy set. However, the level 2 is important for the uncertainty processing. The nonlinear scaling can introduce Type-2 MFs, see Section 2.1.2.

Rule-based fuzzy set systems are highly flexible: facts can be based on fuzzification of crisp or fuzzy input values, manually provided domain expertise or calculations by using changes, trends, fluctuations, equalities and inequalities. Each fact has a degree of membership.The systems can handle contradictory data, i.e. some consequents may define forbidden areas for the outputs [28, 29].

The operating area of different types of rule-based fuzzy set systems can be extended by selecting membership locations (Figure 2) for inputs and/or outputs together with the LE models are needed to tune the sets of MFs, see Section 2.3.3. The rulebase can focus on the directions of interactions. For example, all the alternative MFs shown in Figure 1 could be handled with the same rule-based system with an appropriate set of MFs.

2.2.2 Fuzzy relational systems

Fuzzy relational models [3] allow one particular antecedent proposition to be associated with several different consequent propositions. Each element of the relation represents the degree of association between the individual reference fuzzy sets defined in the input and output domains. The relations can be represented by fuzzy rule-based systems where the rules have weight values. In these models, the membership functions can be chosen in a fairly mechanistic way since the association intensities take care of the interactions.

These systems suit well for higher levels of abstraction where the labels are objects which do not necessarily have any connections with numeric values. NSFs could be useful in translating the intensities [0, 1] to the range [-2, 2] and natural language.

2.2.3 Fuzzy arithmetic

Fuzzy arithmetic provides methods for including uncertainty processing within equations and models. The extension principle is the basic generalization of the arithmetic operations if the inductive mapping F(xj) is a monotonously increasing function of the input. The interval arithmetic presented by Moore [4] is used together with the extension principle on several membership α-cuts of the fuzzy number xj for evaluating fuzzy expressions [5, 30, 31]. The fuzzy sets can be modified by intensifying or weakening modifiers [8].

Membership degree for fuzzy equality of two fuzzy sets can obtained by

(8)μA=B=supxmin[μA(x),μB(x)].

The calculation of inequalities is based on comparing modified identities. Fuzzy equalities and inequalities <, ≤, =, ≥ and > produce new facts for rule-based fuzzy set systems.

Calculations with fuzzy numbers expand step by step the uncertainty of the results. Therefore, associations are important in reducing the uncertainty of calculations. LE models are used for representing various types of associations, see Section 2.3.3. For example, high flow is associated with short time delay.

2.3 Parametric models

Case-based systems can be built by integrating local parametric models. Linear parameter varying models (LPV) and fuzzy set systems are alternatives for working point models.

2.3.1 Statistical models

Statistical modelling in its basic form uses linear regression for solving coefficients for linear functions F(⃗x). Interactions between variables become important in the multiple regression. Principal component analysis (PCA) reduces the number of dimensions [32]. Latent structures and collinear variables are important in avoiding overfitting [33].

In the response surface methodology (RSM), the relationships are represented with multiple input, single output (MISO) models, which contain linear, quadratic and interactive terms [34]. Model selection algorithms are important in finding efficient predictions with less parameters [35]. Expert knowledge and robust fitting techniques can improve these models [36].

LPV models extend application areas of the linear modelling. Semi-physical models bring appropriate calculated variables as inputs, see [37]. Fuzzy inputs move the analysis to several α-levels. The interval arithmetic can be used within models and also the coefficients can be fuzzy numbers.

Various advanced methodologies are available for extending the statistical model approach. However, the high complexity makes the adaptation of the system difficult.

2.3.2 Neural and neurofuzzy systems

Artificial neural networks (ANN) are used as behavioural input-output models consisting of neurons. The response of each neuron i is obtained by an activation function, Fi:

(9)yi=Fi(∑j=1mwijNNpj+biNN),

whose input is calculated from a weighted sum of the normalised variables and a bias term: wijNNis the weight factor of the element pj in the input vector of the neuron i, and biNNa scalar bias. For the input layer, the elements pj are usually normalised values of the variables xj, j = 1, 2, ..., m. Network architectures differ from each other in their way of forming the net input, use of activation functions Fi and number of layers.

Neurofuzzy systems use fuzzy neurons to combine the weight factors wij and the inputs pj in (9). The activation function is handled with the extension principle from the fuzzy input, which is obtained by the fuzzy arithmetics. Different combinations with fuzzy and crisp weight factors and elements can be used in these models [38]. Cascade architectures of fuzzy set systems and neural networks are often called neurofuzzy systems. Neural computation is used for tuning fuzzy set systems which can be represented by neural networks, see [39].

Overfitting is a real risk in neural computation, especially in deep learning. Although the weights could be fuzzy, it is difficult to introduce this idea in the learning algorithms. However, fuzzy inputs are possible and then the responses would be fuzzy. The solutions can be extended with the NSFs in the same way as in the rule-based fuzzy set systems, see Section 2.2.1.

2.3.3 Linguistic equations

Linguistic equation (LE) approach originates from fuzzy set systems [13]. The main idea is to make compact systems which take into account nonlinearities by using the nonlinear scaling (Section 2.1.2) together with linear equations [14]. Extensions to more complex statistical models could be used but considerable improvements are not achieved if the NSFs are on a reasonable level.

The LE systems can be extended to fuzzy systems by using the NSFs for transforming fuzzy numbers to both directions between the real and scaled values (Section 2.1.2). The linear equations are processed by the fuzzy interval analysis and finally the resulting fuzzy numbers are scaled back to the real scale.

Associations are simple interactions, e.g. a positive association leads to extending fuzziness for a sum of two fuzzy numbers. This is the normal way used in fuzzy arithmetic. On the other hand, a negative association means that the same sum has much less uncertainty.

Locations for all membership functions or singletons can be defined for one variable in each equation of a LE model (Figure 2). Pruning is used for combining membership functions which are close to each other.

Fuzzy set systems can be changed into LE models by replacing linguistic labels with real numbers (Figure 2). Slight adjusting of these locations is usually needed, and NSFs are generated from adjusted locations and the center points of the corresponding MFs. The model surface is directly used for very small fuzzy set systems as there are too few relations for the parameter-based approach. [14] Linguistic Takagi-Sugeno (LTS) models were developed for improving the operation of TS models in the border areas of local models [40]. The linear models are replaced by LE models by using the NSFs. The LTS models are robust solutions for applications where the same variables can be used for defining operating areas and in the submodels. No special smoothing algorithms are needed.

The nonlinear scaling is the key part of the LE models: compact basic models can be extended with the statistical, fuzzy and neural methodologies.

3 Adaptation

Uncertainty processing and temporal analysis are essential in assessing the need for adaptation. Recursive data analysis provides material for the detection of changes and finally, consistent systems facilitate the efficient adaptation. The recursive part focuses on the scaling and the interactions are updated only if needed (Table 2).

Table 2

Adaptation

Adaptation levelFuzzy set systemsLinguistic equationsApplication
Scaling1. All the MFs1. All the NSFsWorking point adaptation
Shape2. Modify individual MFs2.1 Parameters of NSFs from generalised normsSmooth changes
2.2 Update generalised normsDrastic changes
Interactions3. The rules3. New interaction coefficientsNew model

3.1 Recursive data analysis

The parameters of the NSFs can be recursively updated by using generalised norms with the defined orders. This can be done real-time: the norm values are updated by including new equal sized sub-blocks in the calculations [41]. The norm for several samples is obtained as the norm of the norms of the individual samples [22, 42]. Outliers should be excluded, but the suspicious values may mean that the operating conditions are changing, i.e. the identity of the short long term NSFs is not sufficient [41]. The new set of parameters is checked and corrected if the monotonous increase is not achieved.

The new orders are obtained by using the generalised skewness for the data extended with the data collected from the new situation [20]. The same check of monotonocity is performed in this analysis.

The uncertainties can be analysed since the calculations are based on several sub-blocks which can have different data distributions. Levels, changes, trends and fluctuations can be followed for all five parameters of each scaling function (Figure 1). IndividualMFs can be analysed by using only the corner points of the trapezoidal MFs.

3.2 Detection of changes

The temporal analysis of levels and features representing the increase, decrease, trends and fluctuations introduces information for detecting changes in operating conditions. An increasing number of correction requirements can be an indication of changing operating conditions. The parameters obtained from the recent data need to be compared with the active parameters. The comparison, which is based on fuzzy inequalities <, ≤, =, ≥ and >, provides uncertain facts for the fuzzy decision making.

The generalised statistical process control (GSPC) is an additional tool for detecting changes, anomalies and novelties in connection with the operation [43].Warnings and alarms are generated by the control charts.

The detection focuses on the NSFs since the sets of the MFs can be built from the NSFs. The analysis of the individual MFs is a special case of this.

3.3 System adaptation

Fuzzy set systems can be adapted on three levels: (1) scaling the sets of MFs, (2) adapting the shapes of the MFs and (3) adapting the rulebase. The scaling is easy and well understood, but the importance to understand correctly the meanings of the MFs is not so well shared. Adapting the rulebase should really be the last in the sequence (Table 2).

In the adapting of the NSFs, the first level is also the scaling: the functions become sharper or wider. Adapting the shape of the functions is the key and there are two levels of the operation: (2.1) new parameters are obtained by the generalised norms with active orders, and (2.2) the orders of the norms are re-analysed. The directions of interactions handled with linear equations provide results for the rules as well.

The interactions are re-analysed if the adaptation of the NSFs does not lead to sufficient improvements.

Genetic algorithms are well suitable for adapting the LE systems with a very high number of parameters. Efficient calculations can be achieved since the acceptable range [13,3]of the shape factors αj−andαj+accept only the solutions which are monotonously increasing. All the parameters can be handled simultaneously.

4 Application areas

The nonlinear scaling functions provide compact links between the applications and uncertainty processing. Uncertainty processing brings the data-driven development and solutions available to the assessment based on domain expertise.

4.1 Modelling

Case-based models can be combined as multimodel LE systems, where a fuzzy decision module is used for proving the degree of membership for each active model. The decisions can be based on fuzzy working point models. Since the interactions are presented by linear equations, these models extend the linear parameter varying (LPV) models. The submodels can also have totally different structures and variables. The LTS models are special cases of these models. [44]

4.2 Intelligent control

Intelligent methods are widely used for nonlinear multi-variable control systems, e.g. a large number of highly successful fuzzy logic control (FLC) applications are implemented in process industry. The system structures are similar to the fuzzy models: crisp responses are obtained by defuzzification.

In feedback control, the LE controllers use similar structures enhanced with the NSFs. Intelligent analysers are increasingly important in these systems [45]. Model-based control is widely applied to industrial applications [46]. The LE control systems use predefined model-based techniques and activate special features when needed, since the adaptation needs to be fast [47].

Fuzzy adaptation of em LE controllers opens additional possibilities to the decision making by extending the smart working point control. The operation is kept smooth by limiting the allowed temperature range in difficult situations. [48]

4.3 Diagnostics

Rule-based fuzzy set systems result fuzzy sets which include alternative faults with degrees of membership. Efficient solutions can be developed integrating condition monitoring data in the form of intelligent indices into the operation and maintenance. The NSFs methodologies are also used for handling performance measures used in the same scale as intelligent condition and stress indices. Performance indicators are responses of the process, machine or system to the stress contributions analyzed from process and condition monitoring data. The systems are adapted to the changing operation conditions by the recursive tuning of the NSFs. [49]

Fuzzy relational systems are based on intensities of interactions between symptoms and faults. Symptoms are facts, including labels, inequalities and trends. As the labels do not need to any links with numerical values, the relations can be the first or highest level in the diagnostics.

5 Discussion

In applications, the systems need to use both crisp and fuzzy numbers as well as additional facts. The domain expertise can be introduced by fuzzy labels and understanding of variable meanings. Fuzzy relations are used within higher level systems. Neural models are numeric models in the same way as the statistical and LE models.

Nonlinear scaling and LE systems with fuzzy arithmetic make the systems more compact. Rule-based fuzzy systems and neural networks can be simplified by including layers which use NSFs. The coefficients of the LE systems are based on linear regression. Therefore, feedforward LE models can be transformed to feedforward controllers. Adaptation can be done even recursively with the NSFs. The overall solution forms a feasible basis for building tunable large-scale systems.

The NSFs and LE models are compact and easy to adapt but the structural limitations need to be kept in mind. The basic systems are feasible for monotonously increasing subsystems where the LE models and fuzzy systems can be transformed to both directions. Higher levels need fuzzy systems for utilizing contradictory data, non-numeric information and balancing different operating conditions.

6 Conclusions

Meanings of variables are the key to handling expertise and uncertainty processing in automation applications. Nonlinear scaling provides additional calculation levels which simplify statistical, fuzzy and neural solutions. Large-scale applications can be built and tuned as modular parametric systems. The embedded uncertainty processing in the recursive analysis form a basis for the adaptation. Fuzzy systems are needed for balancing contradictory information, non-numeric expertise and operating areas.

References

[1] Zadeh LA. Fuzzy sets. Inf Control. 1965;8(June):338–53.10.1016/S0019-9958(65)90241-XSearch in Google Scholar

[2] Zimmermann HJ. Fuzzy set theory and its applications. Kluwer Academic Publishers; 1992.10.1007/978-94-015-7949-0Search in Google Scholar

[3] Pedrycz W. An identification algorithm in fuzzy relational systems. Fuzzy Sets Syst. 1984;13(2):153–67.10.1016/0165-0114(84)90015-0Search in Google Scholar

[4] Moore RE. Interval Analysis. Englewood Cliffs (NJ): Prentice Hall; 1966.Search in Google Scholar

[5] Buckley JJ, Feuring T. Universal approximators for fuzzy functions. Fuzzy Sets Syst. 2000;113(3):411–5.10.1016/S0165-0114(98)00069-4Search in Google Scholar

[6] Jantzen J, Poulsen NK. Adaptation in the Fuzzy Self-Organizing Controller. In: Proceedings of Eunite 2003 - European Symposium on Intelligent Technologies, Hybrid Systems and their implementation on Smart Adaptive Systems, July 10-11, 2003, Oulu, Finland. Aachen: Wissenschaftsverlag Mainz; 2003. p. 49–57.Search in Google Scholar

[7] Pirrello L, Yliniemi L, Leiviskä K, Galluzzo M. Self-tuning fuzzy control of a rotary dryer. In: Basanez L, de la Puente JA, editors. Proceedings of the 15th Triennial World Congress, Barcelona, Spain, July 21-26, 2011. IFAC; 2002. p. 125–130. http://www.ifac-papersonline.net/10.3182/20020721-6-ES-1901.01172Search in Google Scholar

[8] De Cock M, Kerre EE. Fuzzy modifiers based on fuzzy relations. Inf Sci. 2004;160(1-4):173–99.10.1016/j.ins.2003.09.002Search in Google Scholar

[9] Schmidhuber J. Deep learning in neural networks: an overview. Neural Netw. 2015 Jan;61 Supplement C:85–117. Available from: http://www.sciencedirect.com/science/article/pii/S08936080110.1016/j.neunet.2014.09.003Search in Google Scholar PubMed

[10] Kohonen T. Self-Organizing Maps. Berlin: Springer; 1995. https://doi.org/10.1007/978-3-642-97610-010.1007/978-3-642-97610-0Search in Google Scholar

[11] Barreto GA. Lime kiln hybrid control system. In: Proceedings of Dynamic Modeling Control Applications for Industry Workshop, Vancouver. IEEE Industry Applications Society; 1997. p. 44–50.10.1109/DMCA.1997.603488Search in Google Scholar

[12] Bezdek JC, Tsao EC, Pal NR. Fuzzy Kohonen clustering networks. In: [1992 Proceedings] IEEE International Conference on Fuzzy Systems; 1992. p. 1035–1043.10.1109/FUZZY.1992.258797Search in Google Scholar

[13] Juuso EK, Leiviskä K. Adaptive Expert Systems for Metallurgical Processes. IFAC Proceedings Volumes. 1992;25(17):119–124. https://doi.org/10.1016/B978-0-08-041704-2.50027-3.https://doi.org/10.1016/B978-0-08-041704-2.50027-3Search in Google Scholar

[14] Juuso EK. Integration of Intelligent Systems in Development of Smart Adaptive Systems. Int J Approx Reason. 2004;35(3):307–37.10.1016/j.ijar.2003.08.008Search in Google Scholar

[15] Juuso EK. Tuning of Large-Scale Linguistic Equation (LE) Models with Genetic Algorithms. In: Kolehmainen M, editor. Revised selected papers of the International Conference on Adaptive and Natural Computing Algorithms - ICANNGA 2009, Kuopio, Finland, Lecture Notes in Computer Science. vol. LNCS 5495. Heidelberg: Springer-Verlag; 2009. p. 161–170.10.1007/978-3-642-04921-7_17Search in Google Scholar

[16] Juuso EK. Recursive Tuning of Intelligent Controllers of Solar Collector Fields in Changing Operating Conditions. IFAC Proceedings Volumes. 2011;44(1):12282–12288. https://doi.org/10.3182/20110828-6-IT-1002.03621.https://doi.org/10.3182/20110828-6-IT-1002.03621Search in Google Scholar

[17] Juuso EK. Smart Adaptive Big Data Analysis with Advanced Deep Learning. Open Eng. 2018;8(1):403–16. Available from: www.scopus.com10.1515/eng-2018-0043Search in Google Scholar

[18] Juuso EK. Informative process monitoring with a natural language interface. In: 2016 UKSim-AMSS 18th International Conference on Modelling and Simulation, 6-8 April, 2016, Cambridge, UK. IEEE Computer Society; 2016. p. 105–110.10.1109/UKSim.2016.37Search in Google Scholar

[19] Juuso EK. Linguistic Equation Framework for Adaptive Expert Systems. In: Stephenson J, editor. Modelling and Simulation 1992, Proceedings of the 1992 European Simulation Multiconference, York, UK, June 1-3, 1992. San Diego, USA: SCS International; 1992. p. 99–103.Search in Google Scholar

[20] Juuso E, Lahdelma S. Intelligent scaling of features in fault diagnosis. In: 7th International Conference on Condition Monitoring and Machinery Failure Prevention Technologies, CM 2010 – MFPT 2010, 22-24 June 2010. Volume 2. Stratford-upon-Avon, UK; 2010. pp. 1358–72. Available from www.scopus.comSearch in Google Scholar

[21] Juuso EK. Integration of Knowledge-based Information in Intelligent Condition Monitoring. In: 9th International Conference on Condition Monitoring and Machinery Failure Prevention Technologies, 12-14 June 2012, London, UK. Volume 1. NY, USA: Curran Associates; 2012. pp. 217–28., Available from www.scopus.comSearch in Google Scholar

[22] Lahdelma S, Juuso E. Signal processing and feature extraction by using real order derivatives and generalised norms. Part 1: methodology. International Journal of Condition Monitoring. 2011;1(2):46–53.10.1784/204764211798303805Search in Google Scholar

[23] Dubois D, Prade H, Ughetto L. Fuzzy Logic, Control Engineering and Artificial Intelligence. In: Verbruggen HB, Zimmermann HJ, Babuska R, editors. Fuzzy Algorithms for Control, International Series in Intelligent Technologies. Boston: Kluwer; 1999. pp. 17–57.10.1007/978-94-011-4405-6_2Search in Google Scholar

[24] Takagi T, Sugeno M. Fuzzy identification of systems and its applications to modeling and control. IEEE Trans Syst Man Cybern. 1985;15(1):116–32.10.1016/B978-1-4832-1450-4.50045-6Search in Google Scholar

[25] Babuška R. Fuzzy Modeling and Identification. Boston: Kluwer Academic Publisher; 1998. p. 100.10.1007/978-94-011-4868-9_2Search in Google Scholar

[26] Johansen TA, Babuška R. Multiobjective identification of Takagi-Sugeno fuzzy models. IEEE Trans Fuzzy Syst. 2003;11(6):847–60.10.1109/TFUZZ.2003.819824Search in Google Scholar

[27] Mendel JM. Advances in type-2 fuzzy sets and systems. Information Sciences. 2007;177(1):84–110. 105 https://doi.org/10.1016/j.ins.2006.05.00310.1016/j.ins.2006.05.003Search in Google Scholar

[28] Krone A, Kiendl H. Automatic Generation of Positive and Negative Rules for Two-Way Fuzzy Controllers. In: Zimmermann HJ, editor. Proceedings of the Second European Congress on Intelligent Technologies and Soft Computing -EUFIT’94, Aachen, September 21 - 23, 1994. vol. 1. Aachen: Augustinus Buchhandlung; 1994. p. 438–447.Search in Google Scholar

[29] Krone A, Schwane U. Generating Fuzzy Rules from Contradictory Data of Different Control Strategies and Control Performances. In: Proceedings of the Fuzz-IEEE’96, New Orleans, USA; 1996. p. 492–497.10.1109/FUZZY.1996.551790Search in Google Scholar

[30] Buckley JJ, Qu Y. On using α-cuts to evaluate fuzzy equations. Fuzzy Sets Syst. 1990;38(3):309–12.10.1016/0165-0114(90)90204-JSearch in Google Scholar

[31] Buckley JJ, Hayashi Y. Can neural nets be universal approximators for fuzzy functions? Fuzzy Sets Syst. 1999;101(3):323–30.10.1016/S0165-0114(97)00069-9Search in Google Scholar

[32] Jolliffe IT. Principal Component Analysis. 2nd ed. New York: Springer; 2002. 487 pp.Search in Google Scholar

[33] Gerlach RW, Kowalski BR, Wold HO. Partial least squares modelling with latent variables. Anal Chim Acta. 1979;112(4):417–21.10.1016/S0003-2670(01)85039-XSearch in Google Scholar

[34] Box GE, Wilson KB. On the experimental attainment of optimum conditions. JR Stat Soc B. 1951;13(1):1–45.10.1007/978-1-4612-4380-9_23Search in Google Scholar

[35] Efron B, Hastie T, Johnstone I, Tibshirani R. Least angle regression. Ann Stat. 2004;32(2):407–99.10.1214/009053604000000067Search in Google Scholar

[36] Morgenthaler S, Schumacher MM. Robust analysis of a response surface design. Chemom Intell Lab Syst. 1999;47(1):127–41.10.1016/S0169-7439(98)00199-3Search in Google Scholar

[37] Ljung L. System Identification - Theory for the User. 2nd ed. Upper Saddle River (N.J.): Prentice Hall; 1999.Search in Google Scholar

[38] Fullér R. Introduction to Neuro-Fuzzy Systems. Advances in Soft Computing. Springer; 2000. 289 pp. https://doi.org/10 1007/978-3-7908-1852-9.10.1007/978-3-7908-1852-9Search in Google Scholar

[39] Jang JS. ANFIS: Adaptive-Network-based Fuzzy Inference Systems. IEEE Trans Syst Man Cybern. 1993;23(3):665–85.10.1109/21.256541Search in Google Scholar

[40] Juuso EK. Development of Multiple Linguistic Equation Models with Takagi-Sugeno Type Fuzzy Models. In: Carvalho JP, Dubois D, Kaymak U, Sousa JC, editors. Proceedings of 2009 IFSA World 35 Congress / 2009 EUSFLAT Conference. Lisboa, Portugal: IFSA-EUSFLAT; July 20-24, 2009. pp. 1779–84. http://www.eusflat.org/publications_proceedings_IFSA-EUSFLAT_2009.phpSearch in Google Scholar

[41] Juuso EK. Recursive Data Analysis in Large Scale Complex Systems. In: Juuso E, Dahlquist E, Leiviskä, editors. Proceedings of The 9th EUROSIM Congress on Modelling and Simulation, EUROSIM 2016, The 57th SIMS Conference on Simulation and Modelling SIMS 2016. No. 142 in Linköping Electronic Conference Proceedings. Linköping University Electronic Press; 2018. p. 1053–1059. https://doi.org/10.3384/ecp171421053.10.3384/ecp171421053Search in Google Scholar

[42] Lahdelma S, Juuso E. Signal processing and feature extraction by using real order derivatives and generalised norms. Part 2: applications. International Journal of Condition Monitoring. 2011;1(2):54–66.10.1784/204764211798303814Search in Google Scholar

[43] Juuso EK. Generalised statistical process control GSPC in stress monitoring. IFAC-PapersOnLine. 2015;48(17):207–12. Available from: www.scopus.com10.1016/j.ifacol.2015.10.104Search in Google Scholar

[44] Juuso EK. Intelligent Multimodel Simulation in Decomposed Systems. In: Øi LE, Komulainen T, Bye RT, Nord LO, editors. Proceedings of The 59th Conference on Simulation and Modelling (SIMS 59), 26-28 September 2018, Oslo Metropolitan University, Norway. No. 153 in Linköping Electronic Conference Proceedings. Linköping University Electronic Press; 2018. p. 308–315.Search in Google Scholar

[45] Juuso EK. Intelligent trend analysis for a solar thermal energy collector field. IOP Conf Ser Earth Environ Sci. 2018;136:1–8.10.1088/1755-1315/136/1/012007Search in Google Scholar

[46] Camacho EF, Bordons C. Model Predictive Control in the Process Industry. Berlin, Germany: Springer; 1995. https://doi.org/10.1007/978-1-4471-3008-610.1007/978-1-4471-3008-6Search in Google Scholar

[47] Juuso EK, Yebra LJ. Model-based intelligent control of a solar energy collector field. In: Proceedings - 8th EUROSIM Congress on Modelling and Simulation, EUROSIM 2013, 10-13 September, 2013, Cardiff, UK; 2013. p. 513–518. Available from: www.scopus.comhttps://doi.org/10.1109/EUROSIM.2013.9210.1109/EUROSIM.2013.92Search in Google Scholar

[48] Juuso EK. Fuzzy adaptation of intelligent control for solar thermal power plants. In: 30th European Modeling and Simulation Symposium. EMSS; 2018. pp. 343–8., Available from www.scopus.comSearch in Google Scholar

[49] Juuso EK. Intelligent Performance Analysis with a Natural Language Interface. Management Systems in Production Engineering. 2017;25(3):168–75.10.1515/mspe-2017-0025Search in Google Scholar

Received: 2019-10-06
Accepted: 2020-04-29
Published Online: 2020-08-07

© 2020 E. K. Juuso, published by De Gruyter

This work is licensed under the Creative Commons Attribution 4.0 International License.

Articles in the same Issue

  1. Regular Articles
  2. Fabrication of aluminium covetic casts under different voltages and amperages of direct current
  3. Inhibition effect of the synergistic properties of 4-methyl-norvalin and 2-methoxy-4-formylphenol on the electrochemical deterioration of P4 low carbon mold steel
  4. Logistic regression in modeling and assessment of transport services
  5. Design and development of ultra-light front and rear axle of experimental vehicle
  6. Enhancement of cured cement using environmental waste: particleboards incorporating nano slag
  7. Evaluating ERP System Merging Success In Chemical Companies: System Quality, Information Quality, And Service Quality
  8. Accuracy of boundary layer treatments at different Reynolds scales
  9. Evaluation of stabiliser material using a waste additive mixture
  10. Optimisation of stress distribution in a highly loaded radial-axial gas microturbine using FEM
  11. Analysis of modern approaches for the prediction of electric energy consumption
  12. Surface Hardening of Aluminium Alloy with Addition of Zinc Particles by Friction Stir Processing
  13. Development and refinement of the Variational Method based on Polynomial Solutions of Schrödinger Equation
  14. Comparison of two methods for determining Q95 reference flow in the mouth of the surface catchment basin of the Meia Ponte river, state of Goiás, Brazil
  15. Applying Intelligent Portfolio Management to the Evaluation of Stalled Construction Projects
  16. Disjoint Sum of Products by Orthogonalizing Difference-Building ⴱ
  17. The Development of Information System with Strategic Planning for Integrated System in the Indonesian Pharmaceutical Company
  18. Simulation for Design and Material Selection of a Deep Placement Fertilizer Applicator for Soybean Cultivation
  19. Modeling transportation routes of the pick-up system using location problem: a case study
  20. Pinless friction stir spot welding of aluminium alloy with copper interlayer
  21. Roof Geometry in Building Design
  22. Review Articles
  23. Silicon-Germanium Dioxide and Aluminum Indium Gallium Arsenide-Based Acoustic Optic Modulators
  24. RZ Line Coding Scheme With Direct Laser Modulation for Upgrading Optical Transmission Systems
  25. LOGI Conference 2019
  26. Autonomous vans - the planning process of transport tasks
  27. Drivers ’reaction time research in the conditions in the real traffic
  28. Design and evaluation of a new intersection model to minimize congestions using VISSIM software
  29. Mathematical approaches for improving the efficiency of railway transport
  30. An experimental analysis of the driver’s attention during train driving
  31. Risks associated with Logistics 4.0 and their minimization using Blockchain
  32. Service quality of the urban public transport companies and sustainable city logistics
  33. Charging electric cars as a way to increase the use of energy produced from RES
  34. The impact of the truck loads on the braking efficiency assessment
  35. Application of virtual and augmented reality in automotive
  36. Dispatching policy evaluation for transport of ready mixed concrete
  37. Use of mathematical models and computer software for analysis of traffic noise
  38. New developments on EDR (Event Data Recorder) for automated vehicles
  39. General Application of Multiple Criteria Decision Making Methods for Finding the Optimal Solution in City Logistics
  40. The influence of the cargo weight and its position on the braking characteristics of light commercial vehicles
  41. Modeling the Delivery Routes Carried out by Automated Guided Vehicles when Using the Specific Mathematical Optimization Method
  42. Modelling of the system “driver - automation - autonomous vehicle - road”
  43. Limitations of the effectiveness of Weigh in Motion systems
  44. Long-term urban traffic monitoring based on wireless multi-sensor network
  45. The issue of addressing the lack of parking spaces for road freight transport in cities - a case study
  46. Simulation of the Use of the Material Handling Equipment in the Operation Process
  47. The use of simulation modelling for determining the capacity of railway lines in the Czech conditions
  48. Proposals for Using the NFC Technology in Regional Passenger Transport in the Slovak Republic
  49. Optimisation of Transport Capacity of a Railway Siding Through Construction-Reconstruction Measures
  50. Proposal of Methodology to Calculate Necessary Number of Autonomous Trucks for Trolleys and Efficiency Evaluation
  51. Special Issue: Automation in Finland
  52. 5G Based Machine Remote Operation Development Utilizing Digital Twin
  53. On-line moisture content estimation of saw dust via machine vision
  54. Data analysis of a paste thickener
  55. Programming and control for skill-based robots
  56. Using Digital Twin Technology in Engineering Education – Course Concept to Explore Benefits and Barriers
  57. Intelligent methods for root cause analysis behind the center line deviation of the steel strip
  58. Engaging Building Automation Data Visualisation Using Building Information Modelling and Progressive Web Application
  59. Real-time measurement system for determining metal concentrations in water-intensive processes
  60. A tool for finding inclusion clusters in steel SEM specimens
  61. An overview of current safety requirements for autonomous machines – review of standards
  62. Expertise and Uncertainty Processing with Nonlinear Scaling and Fuzzy Systems for Automation
  63. Towards online adaptation of digital twins
  64. Special Issue: ICE-SEAM 2019
  65. Fatigue Strength Analysis of S34MnV Steel by Accelerated Staircase Test
  66. The Effect of Discharge Current and Pulse-On Time on Biocompatible Zr-based BMG Sinking-EDM
  67. Dynamic characteristic of partially debonded sandwich of ferry ro-ro’s car deck: a numerical modeling
  68. Vibration-based damage identification for ship sandwich plate using finite element method
  69. Investigation of post-weld heat treatment (T6) and welding orientation on the strength of TIG-welded AL6061
  70. The effect of nozzle hole diameter of 3D printing on porosity and tensile strength parts using polylactic acid material
  71. Investigation of Meshing Strategy on Mechanical Behaviour of Hip Stem Implant Design Using FEA
  72. The effect of multi-stage modification on the performance of Savonius water turbines under the horizontal axis condition
  73. Special Issue: Recent Advances in Civil Engineering
  74. The effects of various parameters on the strengths of adhesives layer in a lightweight floor system
  75. Analysis of reliability of compressed masonry structures
  76. Estimation of Sport Facilities by Means of Technical-Economic Indicator
  77. Integral bridge and culvert design, Designer’s experience
  78. A FEM analysis of the settlement of a tall building situated on loess subsoil
  79. Behaviour of steel sheeting connections with self-drilling screws under variable loading
  80. Resistance of plug & play N type RHS truss connections
  81. Comparison of strength and stiffness parameters of purlins with different cross-sections of profiles
  82. Bearing capacity of floating geosynthetic encased columns (GEC) determined on the basis of CPTU penetration tests
  83. The effect of the stress distribution of anchorage and stress in the textured layer on the durability of new anchorages
  84. Analysis of tender procedure phases parameters for railroad construction works
  85. Special Issue: Terotechnology 2019
  86. The Use of Statistical Functions for the Selection of Laser Texturing Parameters
  87. Properties of Laser Additive Deposited Metallic Powder of Inconel 625
  88. Numerical Simulation of Laser Welding Dissimilar Low Carbon and Austenitic Steel Joint
  89. Assessment of Mechanical and Tribological Properties of Diamond-Like Carbon Coatings on the Ti13Nb13Zr Alloy
  90. Characteristics of selected measures of stress triaxiality near the crack tip for 145Cr6 steel - 3D issues for stationary cracks
  91. Assessment of technical risk in maintenance and improvement of a manufacturing process
  92. Experimental studies on the possibility of using a pulsed laser for spot welding of thin metallic foils
  93. Angular position control system of pneumatic artificial muscles
  94. The properties of lubricated friction pairs with diamond-like carbon coatings
  95. Effect of laser beam trajectory on pocket geometry in laser micromachining
  96. Special Issue: Annual Engineering and Vocational Education Conference
  97. The Employability Skills Needed To Face the Demands of Work in the Future: Systematic Literature Reviews
  98. Enhancing Higher-Order Thinking Skills in Vocational Education through Scaffolding-Problem Based Learning
  99. Technology-Integrated Project-Based Learning for Pre-Service Teacher Education: A Systematic Literature Review
  100. A Study on Water Absorption and Mechanical Properties in Epoxy-Bamboo Laminate Composite with Varying Immersion Temperatures
  101. Enhancing Students’ Ability in Learning Process of Programming Language using Adaptive Learning Systems: A Literature Review
  102. Topical Issue on Mathematical Modelling in Applied Sciences, III
  103. An innovative learning approach for solar power forecasting using genetic algorithm and artificial neural network
  104. Hands-on Learning In STEM: Revisiting Educational Robotics as a Learning Style Precursor
https://doi.org/10.1515/eng-2020-0080
Keywords for this article
fuzzy set systems; fuzzy arithmetics; domain expertise; uncertainty
Creative Commons
BY 4.0

Articles in the same Issue

  1. Regular Articles
  2. Fabrication of aluminium covetic casts under different voltages and amperages of direct current
  3. Inhibition effect of the synergistic properties of 4-methyl-norvalin and 2-methoxy-4-formylphenol on the electrochemical deterioration of P4 low carbon mold steel
  4. Logistic regression in modeling and assessment of transport services
  5. Design and development of ultra-light front and rear axle of experimental vehicle
  6. Enhancement of cured cement using environmental waste: particleboards incorporating nano slag
  7. Evaluating ERP System Merging Success In Chemical Companies: System Quality, Information Quality, And Service Quality
  8. Accuracy of boundary layer treatments at different Reynolds scales
  9. Evaluation of stabiliser material using a waste additive mixture
  10. Optimisation of stress distribution in a highly loaded radial-axial gas microturbine using FEM
  11. Analysis of modern approaches for the prediction of electric energy consumption
  12. Surface Hardening of Aluminium Alloy with Addition of Zinc Particles by Friction Stir Processing
  13. Development and refinement of the Variational Method based on Polynomial Solutions of Schrödinger Equation
  14. Comparison of two methods for determining Q95 reference flow in the mouth of the surface catchment basin of the Meia Ponte river, state of Goiás, Brazil
  15. Applying Intelligent Portfolio Management to the Evaluation of Stalled Construction Projects
  16. Disjoint Sum of Products by Orthogonalizing Difference-Building ⴱ
  17. The Development of Information System with Strategic Planning for Integrated System in the Indonesian Pharmaceutical Company
  18. Simulation for Design and Material Selection of a Deep Placement Fertilizer Applicator for Soybean Cultivation
  19. Modeling transportation routes of the pick-up system using location problem: a case study
  20. Pinless friction stir spot welding of aluminium alloy with copper interlayer
  21. Roof Geometry in Building Design
  22. Review Articles
  23. Silicon-Germanium Dioxide and Aluminum Indium Gallium Arsenide-Based Acoustic Optic Modulators
  24. RZ Line Coding Scheme With Direct Laser Modulation for Upgrading Optical Transmission Systems
  25. LOGI Conference 2019
  26. Autonomous vans - the planning process of transport tasks
  27. Drivers ’reaction time research in the conditions in the real traffic
  28. Design and evaluation of a new intersection model to minimize congestions using VISSIM software
  29. Mathematical approaches for improving the efficiency of railway transport
  30. An experimental analysis of the driver’s attention during train driving
  31. Risks associated with Logistics 4.0 and their minimization using Blockchain
  32. Service quality of the urban public transport companies and sustainable city logistics
  33. Charging electric cars as a way to increase the use of energy produced from RES
  34. The impact of the truck loads on the braking efficiency assessment
  35. Application of virtual and augmented reality in automotive
  36. Dispatching policy evaluation for transport of ready mixed concrete
  37. Use of mathematical models and computer software for analysis of traffic noise
  38. New developments on EDR (Event Data Recorder) for automated vehicles
  39. General Application of Multiple Criteria Decision Making Methods for Finding the Optimal Solution in City Logistics
  40. The influence of the cargo weight and its position on the braking characteristics of light commercial vehicles
  41. Modeling the Delivery Routes Carried out by Automated Guided Vehicles when Using the Specific Mathematical Optimization Method
  42. Modelling of the system “driver - automation - autonomous vehicle - road”
  43. Limitations of the effectiveness of Weigh in Motion systems
  44. Long-term urban traffic monitoring based on wireless multi-sensor network
  45. The issue of addressing the lack of parking spaces for road freight transport in cities - a case study
  46. Simulation of the Use of the Material Handling Equipment in the Operation Process
  47. The use of simulation modelling for determining the capacity of railway lines in the Czech conditions
  48. Proposals for Using the NFC Technology in Regional Passenger Transport in the Slovak Republic
  49. Optimisation of Transport Capacity of a Railway Siding Through Construction-Reconstruction Measures
  50. Proposal of Methodology to Calculate Necessary Number of Autonomous Trucks for Trolleys and Efficiency Evaluation
  51. Special Issue: Automation in Finland
  52. 5G Based Machine Remote Operation Development Utilizing Digital Twin
  53. On-line moisture content estimation of saw dust via machine vision
  54. Data analysis of a paste thickener
  55. Programming and control for skill-based robots
  56. Using Digital Twin Technology in Engineering Education – Course Concept to Explore Benefits and Barriers
  57. Intelligent methods for root cause analysis behind the center line deviation of the steel strip
  58. Engaging Building Automation Data Visualisation Using Building Information Modelling and Progressive Web Application
  59. Real-time measurement system for determining metal concentrations in water-intensive processes
  60. A tool for finding inclusion clusters in steel SEM specimens
  61. An overview of current safety requirements for autonomous machines – review of standards
  62. Expertise and Uncertainty Processing with Nonlinear Scaling and Fuzzy Systems for Automation
  63. Towards online adaptation of digital twins
  64. Special Issue: ICE-SEAM 2019
  65. Fatigue Strength Analysis of S34MnV Steel by Accelerated Staircase Test
  66. The Effect of Discharge Current and Pulse-On Time on Biocompatible Zr-based BMG Sinking-EDM
  67. Dynamic characteristic of partially debonded sandwich of ferry ro-ro’s car deck: a numerical modeling
  68. Vibration-based damage identification for ship sandwich plate using finite element method
  69. Investigation of post-weld heat treatment (T6) and welding orientation on the strength of TIG-welded AL6061
  70. The effect of nozzle hole diameter of 3D printing on porosity and tensile strength parts using polylactic acid material
  71. Investigation of Meshing Strategy on Mechanical Behaviour of Hip Stem Implant Design Using FEA
  72. The effect of multi-stage modification on the performance of Savonius water turbines under the horizontal axis condition
  73. Special Issue: Recent Advances in Civil Engineering
  74. The effects of various parameters on the strengths of adhesives layer in a lightweight floor system
  75. Analysis of reliability of compressed masonry structures
  76. Estimation of Sport Facilities by Means of Technical-Economic Indicator
  77. Integral bridge and culvert design, Designer’s experience
  78. A FEM analysis of the settlement of a tall building situated on loess subsoil
  79. Behaviour of steel sheeting connections with self-drilling screws under variable loading
  80. Resistance of plug & play N type RHS truss connections
  81. Comparison of strength and stiffness parameters of purlins with different cross-sections of profiles
  82. Bearing capacity of floating geosynthetic encased columns (GEC) determined on the basis of CPTU penetration tests
  83. The effect of the stress distribution of anchorage and stress in the textured layer on the durability of new anchorages
  84. Analysis of tender procedure phases parameters for railroad construction works
  85. Special Issue: Terotechnology 2019
  86. The Use of Statistical Functions for the Selection of Laser Texturing Parameters
  87. Properties of Laser Additive Deposited Metallic Powder of Inconel 625
  88. Numerical Simulation of Laser Welding Dissimilar Low Carbon and Austenitic Steel Joint
  89. Assessment of Mechanical and Tribological Properties of Diamond-Like Carbon Coatings on the Ti13Nb13Zr Alloy
  90. Characteristics of selected measures of stress triaxiality near the crack tip for 145Cr6 steel - 3D issues for stationary cracks
  91. Assessment of technical risk in maintenance and improvement of a manufacturing process
  92. Experimental studies on the possibility of using a pulsed laser for spot welding of thin metallic foils
  93. Angular position control system of pneumatic artificial muscles
  94. The properties of lubricated friction pairs with diamond-like carbon coatings
  95. Effect of laser beam trajectory on pocket geometry in laser micromachining
  96. Special Issue: Annual Engineering and Vocational Education Conference
  97. The Employability Skills Needed To Face the Demands of Work in the Future: Systematic Literature Reviews
  98. Enhancing Higher-Order Thinking Skills in Vocational Education through Scaffolding-Problem Based Learning
  99. Technology-Integrated Project-Based Learning for Pre-Service Teacher Education: A Systematic Literature Review
  100. A Study on Water Absorption and Mechanical Properties in Epoxy-Bamboo Laminate Composite with Varying Immersion Temperatures
  101. Enhancing Students’ Ability in Learning Process of Programming Language using Adaptive Learning Systems: A Literature Review
  102. Topical Issue on Mathematical Modelling in Applied Sciences, III
  103. An innovative learning approach for solar power forecasting using genetic algorithm and artificial neural network
  104. Hands-on Learning In STEM: Revisiting Educational Robotics as a Learning Style Precursor
Sign up now to receive a 20% welcome discount
Institutional Access
How does access work?
Have an idea on how to improve our website?
Please write us.
© 2025 De Gruyter Brill
Downloaded on 6.9.2025 from https://www.degruyterbrill.com/document/doi/10.1515/eng-2020-0080/html
Scroll to top button