Artificial intelligence-driven education evaluation and scoring: Comparative exploration of machine learning algorithms

2.1 Experimental dataset

This article used the Predict students’ dropout and academic success dataset from the UC Irvine ML Repository dataset. There were a total of 36 attributes and 4,424 instances, with each instance corresponding to a student. Now, using the stratified sampling method [15], the grades were divided into four levels: 0–60, 60–70, 70–80, and 80–100. This helps to ensure representativeness at all levels of the sample, reflecting the overall characteristics of the population. Finally, the dataset was divided into 80% for training and 20% for testing. In addition, the Turkiye Student Evaluation dataset was used, including students’ evaluation scores for teachers. There were a total of 33 attributes, including 28 course-specific questions and an additional five attributes (teacher identifier, course code, number of students participating in this course, attendance rate, and course difficulty) and 5,820 instances, each corresponding to an evaluation record. The same classification method was used to divide the test set and training set into two levels: positive evaluation and negative evaluation.

2.2 Dataset preprocessing

2.2.1 Data encoding and data normalization

To improve the visualization of the data, the student performance data were now split. Then, the course name, student information, and other information are encoded and normalized [16]. The grade ratio was uniformly retained to two decimal places for the convenience of model training. The specific display results are shown in Figures 1 and 2. Figure 1 shows the partial data display after splitting and encoding the teaching quality data, and Figure 2 shows the partial data display after normalizing the student grade data. In Figure 1, the data include teacher ID, class, repetition rate, attendance rate, course difficulty level, and evaluation data for Q1–Q28 questions.

Figure 1

Partial data display after encoding teaching quality data.

Figure 2

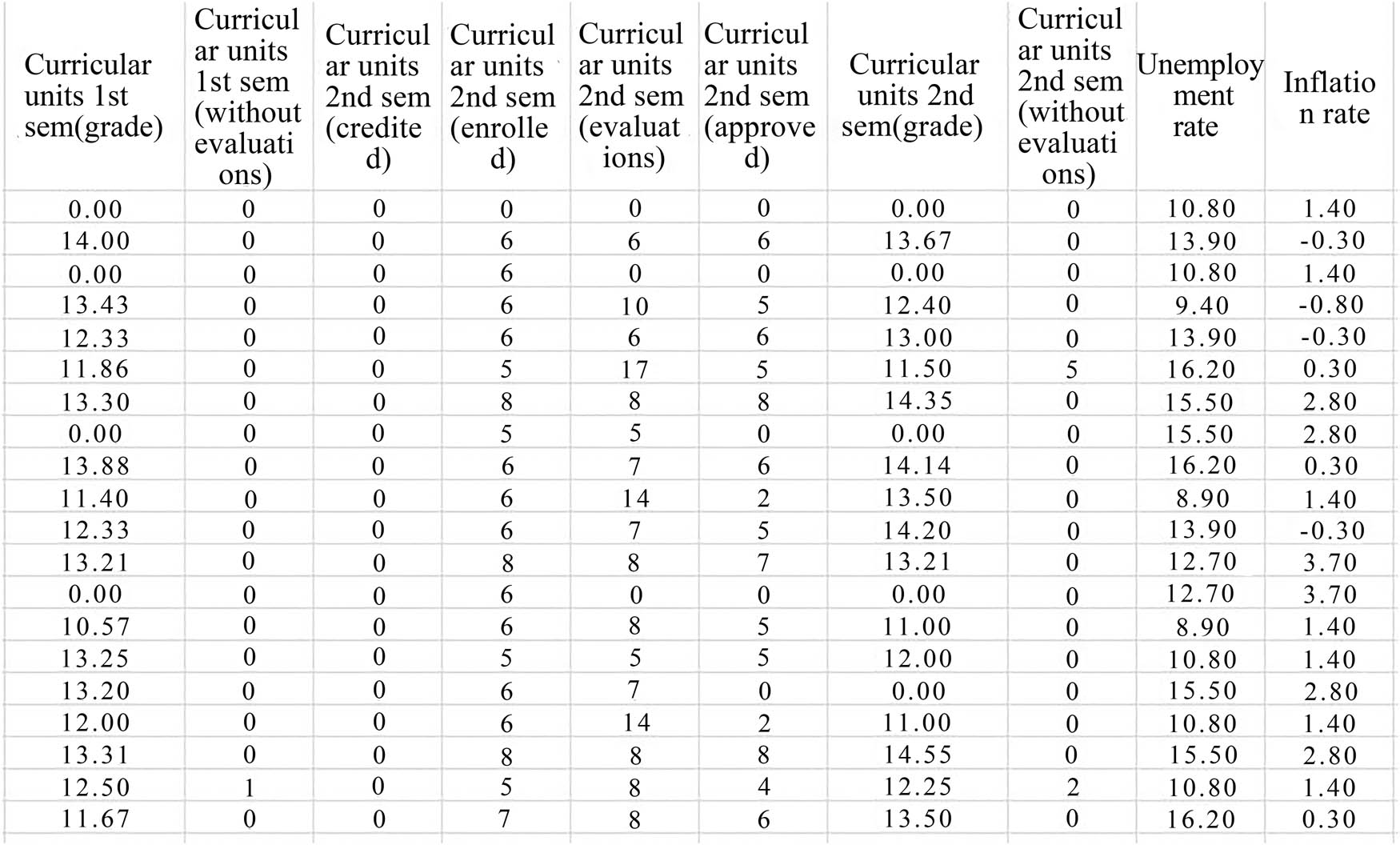
Partial data display after normalization encoding of student performance data.

2.2.2 Feature selection

For the teaching quality evaluation dataset, there are 28 specific questions and five additional attributes. PCA [17,18] was used to select the proportion of six questions with higher contribution rates, which were Q1, Q2, Q3, Q4, Q5, and Q6. The specific proportion is shown in Figure 3(a) and Figure 3(b). In Figure 3(a), the main components were mainly concentrated in PC1 and PC2, corresponding to Q1 and Q2, with the largest proportion. Correspondingly, in Figure 3(b), it can be seen that the total of Q1 and Q2 reached 86.76%. To further balance various component factors, the top six components were now extracted, totaling 91.41%, which could represent the typical performance of most data.

Figure 3

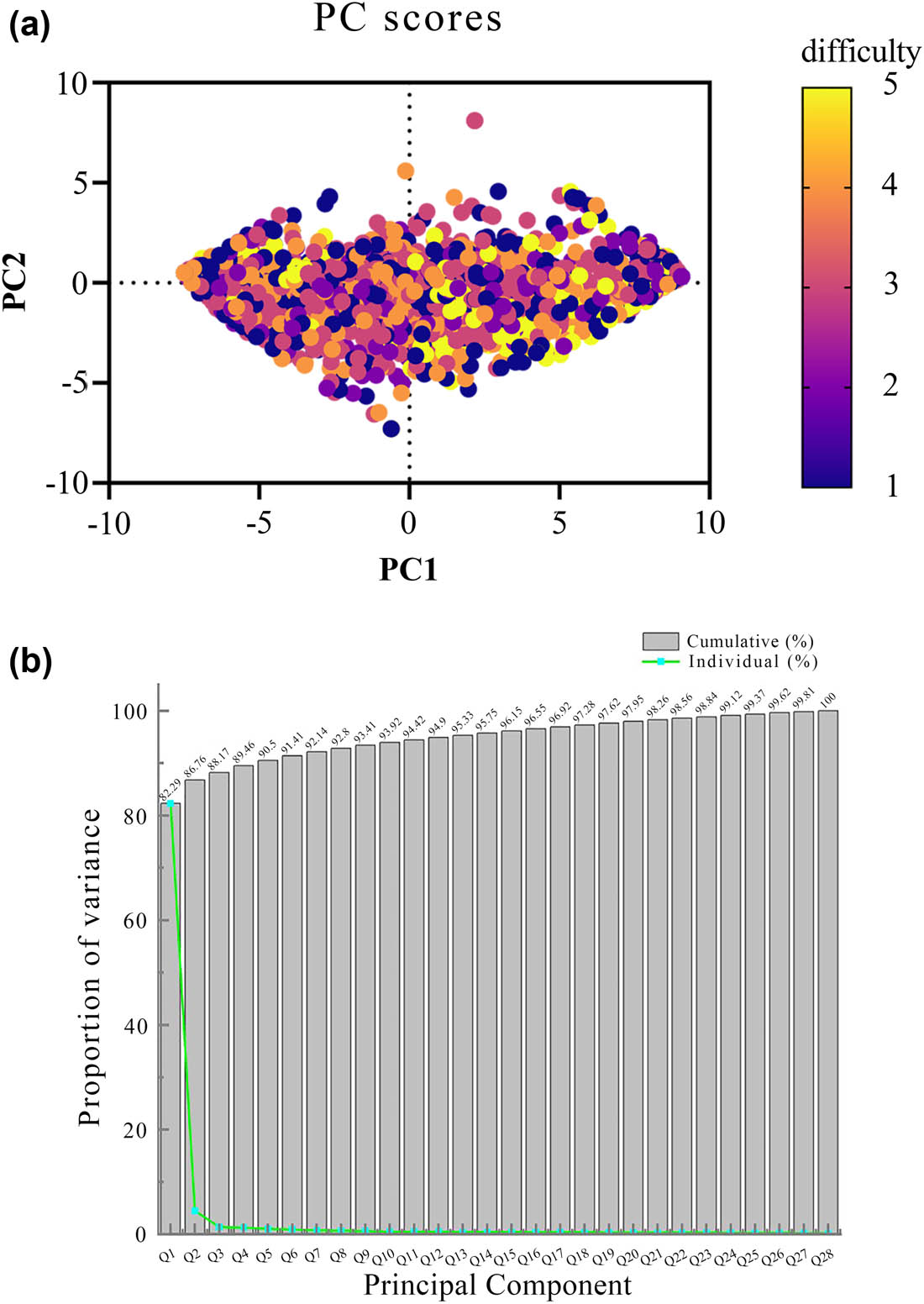
(a) Principal component analysis. (b) Principal component contribution rate.

3.1 RF

RF [19,20] is a classifier composed of multiple DTs, each of which is independent of each other. The sample set N of the trained DT corresponds to the number of samples, and the test sample feature vector is X. The training program for a single DT mainly involves the following process: first, randomly sampling N times in N samples according to the bagging sampling rule as the root node training samples. The DT randomly selects m dimensions from the feature attribute M dimensions of nodes, where m is less than M. Next, their Gini impurity indices are calculated separately. The feature with the smallest index selected according to the minimum criterion is set as a node splitting attribute, and the splitting function is used to split the node into two subtrees until it reaches the leaf node.

The implementation steps of the RF classification process are as follows: the number of DTs n is determined as needed, and n training sets of the same size are obtained through random sampling. Second, by randomly rotating k attributes to obtain n attribute subsets in the attribute set, k = log2v, and using the DT algorithm to correspond the training set to the attribute subset, a DT is obtained. Finally, the DT is summarized and optimized to form an RF model. Based on the voting mechanism, the DT is selected to classify the predicted samples with the highest number of times, and the classification results are determined. The accuracy of the five models in evaluating student grades and teaching quality is shown in Figure 4. The RF model had an accuracy of 85.6% in evaluating student grades and 84.2% in evaluating teaching quality. In Figure 5, the RF model achieved an F1 score of 85.5% in the evaluation of student performance and 84.0% in the evaluation of teaching quality.

Figure 4

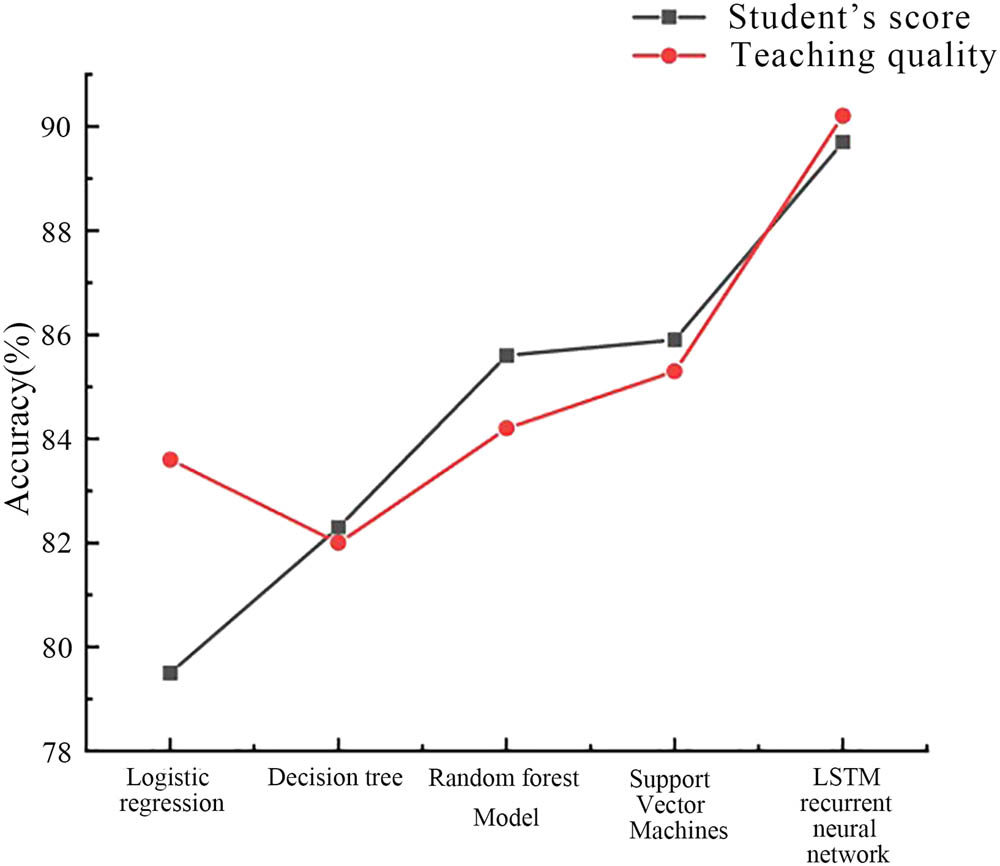
Estimated accuracy of the model in terms of student grades and student quality.

Figure 5

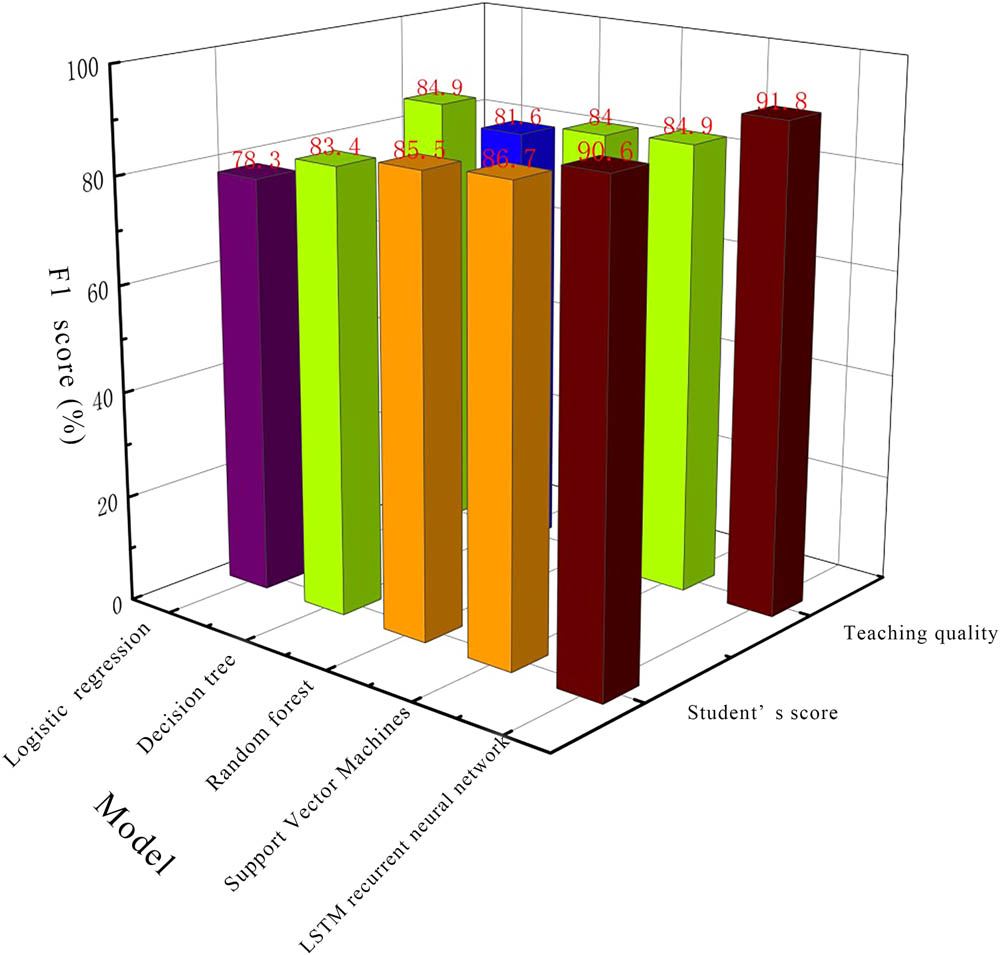
Estimated F1 score of the model in terms of student grades and student quality.

3.2 Decision tree

DT is a modeling method from tree roots, branches to branches. The DT algorithm [21] is a decision algorithm that adopts a tree structure, where each node corresponds to a judgment of an attribute; the branch corresponds to the judgment result, and the leaf corresponds to the final judgment result. The DT algorithm is a recursive process.

The training set is D, and the attribute set a = { a 1 , a 2 , . . . . . . an } . The recursive function is set to TreeF(D, a). First, the root node is determined, and samples of the same type are labeled as leaf nodes. Then, for the empty attribute a, the node is labeled as the leaf node with the most frequent occurrence of class labels. Finally, the optimal partitioning attribute a* is selected in the attribute set, and a recursive loop is used to first generate a branch of the node. The sample subset of D at a* and an* values is represented as Dn. The DT model in Figure 4 had an accuracy of 82.3% in evaluating student grades and 82.0% in evaluating teaching quality. In Figure 5, the DT model achieved an F1 score of 83.4% in the evaluation of student grades and 81.6% in the evaluation of teaching quality.

3.3 SVM

SVM is an effective classification method based on statistical learning theory, which transforms the sample space into another feature space through nonlinear transformation and constructs a regression estimation function, where a suitable kernel function K(X _i , Y _i ) is defined for nonlinear transformation [22]. Given a training dataset on the feature space, the sample is set as x, and n is the vector; the calculation of m samples and output values is shown in formula (1).

x _i ∈ R _n , y _i ∈ {+1, −1}, i = 1, 2, 3,… N. X _i is the i-th feature vector, labeled as y _i . When y _i is equal to +1, it is a positive example, and a negative example is −1.

For the case where the training set is linearly separable, the learning process of the SVM is a quadratic programming process, and the regression function calculation is shown in formula (2).

The SVM model had an accuracy of 85.9% in evaluating student grades and 85.3% in evaluating teaching quality. In Figure 5, the SVM model achieved an F1 score of 86.7% in the evaluation of student grades and 84.9% in the evaluation of teaching quality.

3.4 Logistic regression

Logistic regression is a supervised learning algorithm used to solve binary classification problems and can also be used for multi-classification problems. Its basic idea is to linearly combine input features and transform the linear output into probability values within the (0,1) interval through a special activation function. Logical regression is suitable for cases where label values are discrete, and its functional representation is shown in formula (3).

Among them, θ represents the parameter vector of the logistic regression model, and x is the eigenvalue vector of the data sample. h θ ( x ) is a threshold set, and when the number exceeds this threshold, the sample is evaluated as belonging to a specific classification.

The logistic regression classification model [23] uses a cost function to measure the precision of the model, and the regularized cost function is shown in formula (4).

Among them, the feature vector of the i-th data sample is represented as x ( i ) . y ( i ) represents the classification annotation of the i-th sample in the training set. A value of 1 indicates that the sample belongs to a certain category, while a value of 0 indicates that the sample does not belong to that category. λ is a regularization parameter that controls the equilibrium relationship between two different objectives. After regularization, the cost function can maintain a relatively simple form and low fit, which is equivalent to the logistic regression model parameter θ vector corresponding to J ( θ ) taking the minimum value, which can be applied to predict new samples.

The gradient descent algorithm [24] can be used to solve the parameter A vector. The minimization regularization cost function is upgraded, as shown in formulas (5) and (6).

Among them, j = 1,2,…n. α represents the learning rate, mainly used to control the gradient descent of step size values. In Figure 4, the accuracy of the logistic regression model in evaluating student performance reached 79.5%, and the accuracy in evaluating teaching quality reached 83.6%. In Figure 5, the logistic regression model achieved an F1 score of 78.3% in the evaluation of student performance and 84.9% in the evaluation of teaching quality.

3.5 RNN

LSTM is a special recurrent network model that uses LSTM to capture time series information during the student learning process for predicting student grades. The model can fully consider the historical learning behavior of students to predict future trends in student performance. This helps to provide more accurate academic advice and intervention measures. LSTM is also used to analyze time series data during the teaching process, including the use of teaching resources, student participation, and teaching effectiveness. By modeling these sequence data, it can evaluate the quality of teaching and provide improvement suggestions to optimize the educational process. LSTM can also be used to analyze student learning behavior, including learning duration, learning activities, and the use of online learning platforms. It can provide a deeper understanding of student learning habits, thereby improving personalized teaching and providing personalized feedback.

LSTM is a special cyclic network model that uses special implicit units and is mainly used to process long time series data. This model mainly consists of forgetting threshold, input threshold, output threshold, and neural unit state. The forgetting threshold, as shown in formula (7), determines the information that needs to be discarded [25,26].

Among them, f t represents the activation vector of the forgetting threshold, σ represents the sigmoid function, h _t represents the output vector of LSTM neurons, x _t represents LSTM neurons, the subscript t represents different times, and b _f represents the bias term.

The input threshold formula [27], as shown in formulas (8) and (9), can determine which new information is stored in the unit state.

Among them, i t represents the activation function of the input threshold, and C t ∼ represents the current input unit state.

The unit state runs through the entire chain, and only small linear interactions make it easy to flow downward in a constant manner. The specific expression formula is shown in formula (10).

Among them, C t represents the neuron cell state vector.

The output threshold is the current value used to control how much unit state is output to the LSTM model, as shown in formulas (11) and (12).

Among them, o t represents the activation vector of the output threshold.

The LSTM model had an accuracy of 89.7% in evaluating student grades and 90.2% in evaluating teaching quality. In Figure 5, the LSTM model achieved an F1 score of 90.6% in student performance evaluation and 91.8% in teaching quality evaluation.

The specific process of the LSTM model is as follows: first, the output values of each neuron are calculated forward according to formulas (7)–(12), corresponding to five vector values, namely f t , i t , C t , o t , and h t . Then, the error term values of each neuron are calculated in reverse. A certain optimization algorithm is used based on the error term, and the model parameters are adjusted by calculating the gradient of each weight so that the evaluation results are close to the optimization target parameters. Finally, using the above iterative process to train the model until the optimization objectives that meet the requirements are achieved, an LSTM RNN model with low error is established to evaluate and grade students’ grades [28].

3.6 Multi-classifier fusion

This study adopts a multi-classifier fusion strategy to fully leverage the advantages of different machine learning algorithms and improve the overall performance of the model. Different machine learning algorithms may exhibit different advantages in different data distributions and scenarios. In this article, by combining multiple algorithms, the robustness of the model can be improved, and it can perform well in all situations. Moreover, a single model may overfit a specific dataset, resulting in poor generalization ability for other data. Multi-classifier fusion can reduce the risk of overfitting and improve the generalization ability of models by integrating the opinions of multiple models. In addition, in practical applications, there may be a class imbalance in the data, and adopting a multi-classifier fusion strategy can better handle this imbalance. By adjusting the weight of each classifier, greater attention can be paid to its performance in minority categories, resulting in superior results in educational evaluation and rating scenarios.

4.1 Experimental environment

This experiment was based on a Windows 10 system and implemented using the TensorFlow framework in Python, using the Intel Core i7-6800k Central Processing Unit with 16GB of memory.

4.2 Model comparison experiment process in different scenarios

To verify the adaptability of the model, its performance was tested in different scenarios. The scenario was divided into two: student performance and teaching quality evaluation and grading. The model includes a single model, which is followed by logical regression, DT, RF, SVM, and LSTM RNN. The multiple classification models are sequentially combined into six types: logistic regression + DT, SVM + DT, LSTM RNN + RF, logistic regression + SVM, logistic regression + LSTM RNN, and DT + LSTM neural network. First, the data in the dataset were encoded and normalized, and feature selection was performed using PCA to evaluate the teaching quality of the data. Next, pre-normalized student performance data were used as input to a single model in sequence. In the pre-training phase of the entire experiment, all samples in the training set were first trained 30 times (epoch = 30). When adjusting the parameters, the number of training sessions was dynamically expanded to a multiple of 10 and stacked to 300 times (epoch = 300), and each training session took size = 50 data. By reducing the number of samples used in each iteration and taking size = 50 data for each training, the training process is accelerated and, to some extent, adapted to data diversity. The loss function and accuracy curve under the student performance scenario are shown in Figures 6–9. To prevent overfitting, in the logistic regression model, L1 regularization [29] was used to limit the weight size, reduce complexity, and avoid fitting phenomena. In the DT model, pruning techniques were used to delete some branches in the DT and reduce the depth of the tree. In the model of RF, the overfitting risk of a single model was reduced by combining multiple models through integrated methods. In the SVM model, different weights were assigned to each sample to balance the impact between different samples. This study has achieved the best results by setting the following parameters through multiple experiments. In the LSTM RNN model, this study set the dropout layer loss rate of the time network to 0.7 and the initial learning rate to 0.001. In addition, the weight attenuation coefficient for training was set to 0.0004 and the momentum was 0.9. Next, the effectiveness of a single model was tested on the validation set of student grades and teaching quality in sequence. Finally, six multi-classification models were trained and validated separately, and the performance of the model was verified by comparing parameters such as accuracy, precision, recall value, F1 score, and training duration in different scenarios.

Figure 6

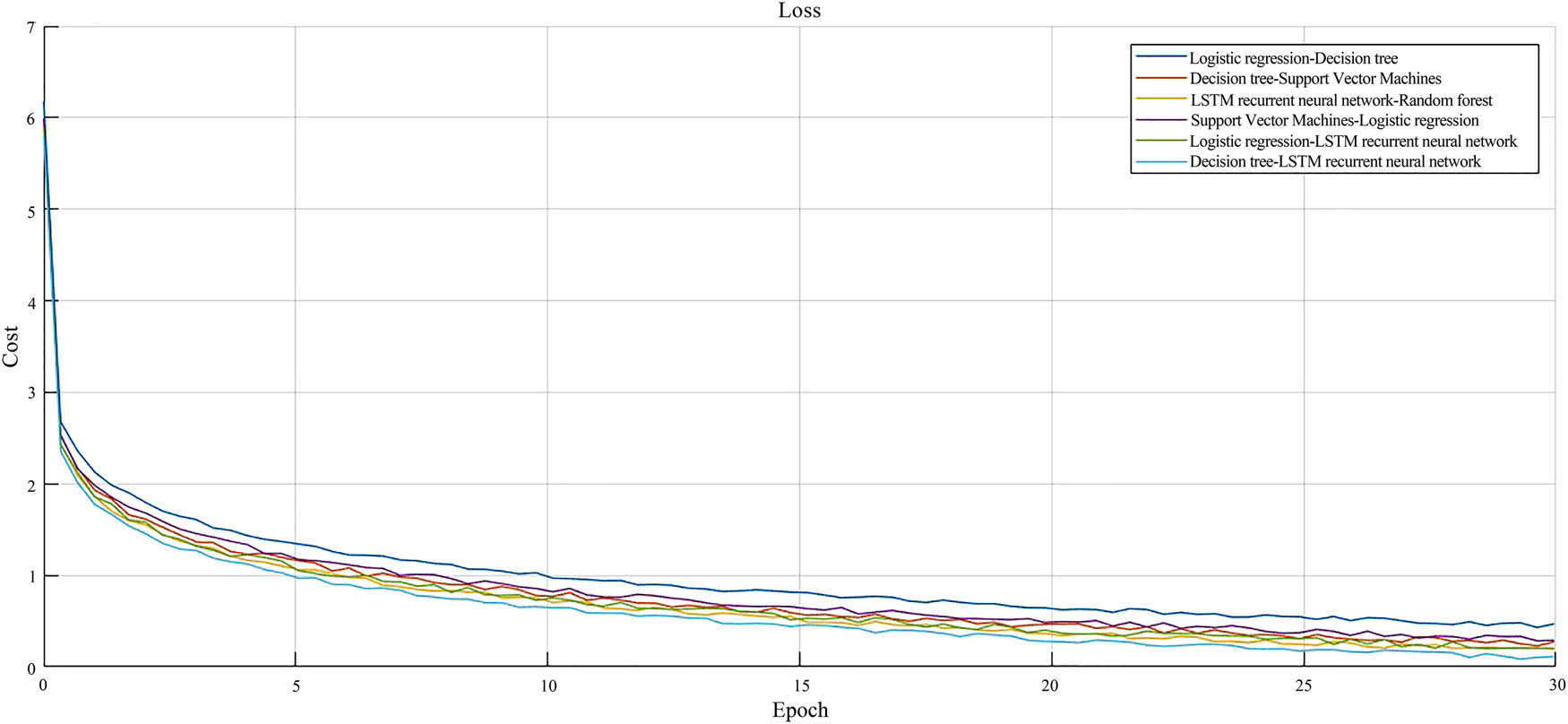
30 epochs loss function curve of the model.

Figure 7

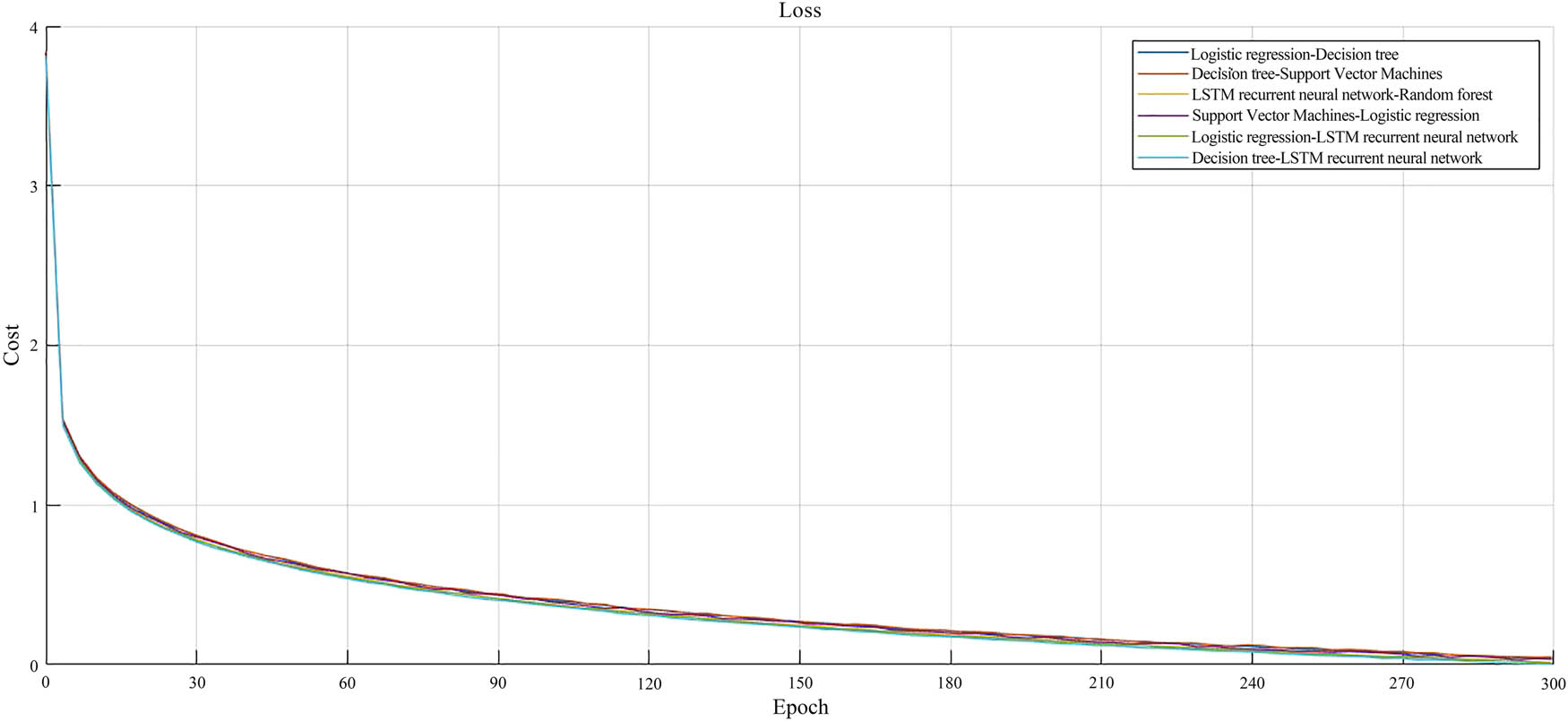
Model 300 epochs loss function curve.

Figure 8

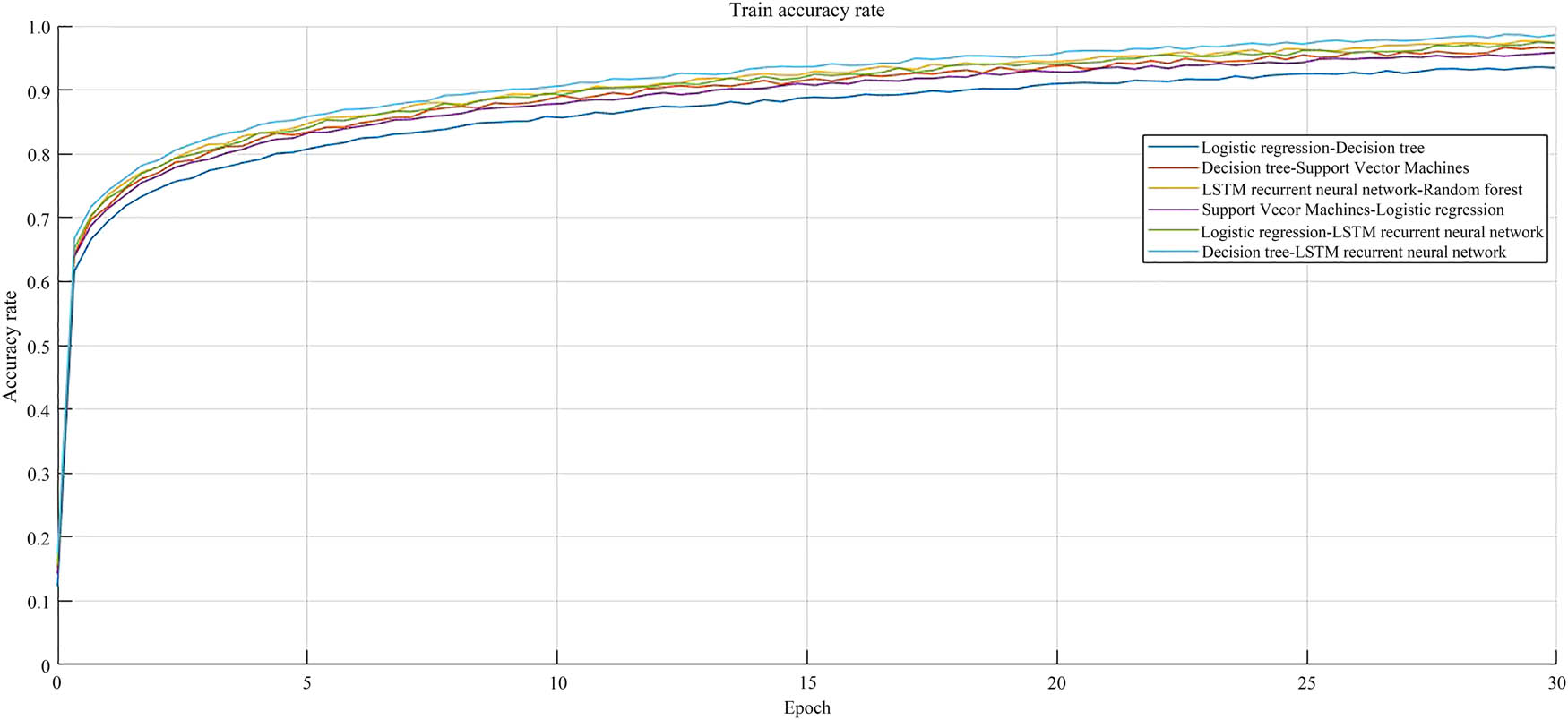
Accuracy curve of model 30 epochs.

Figure 9

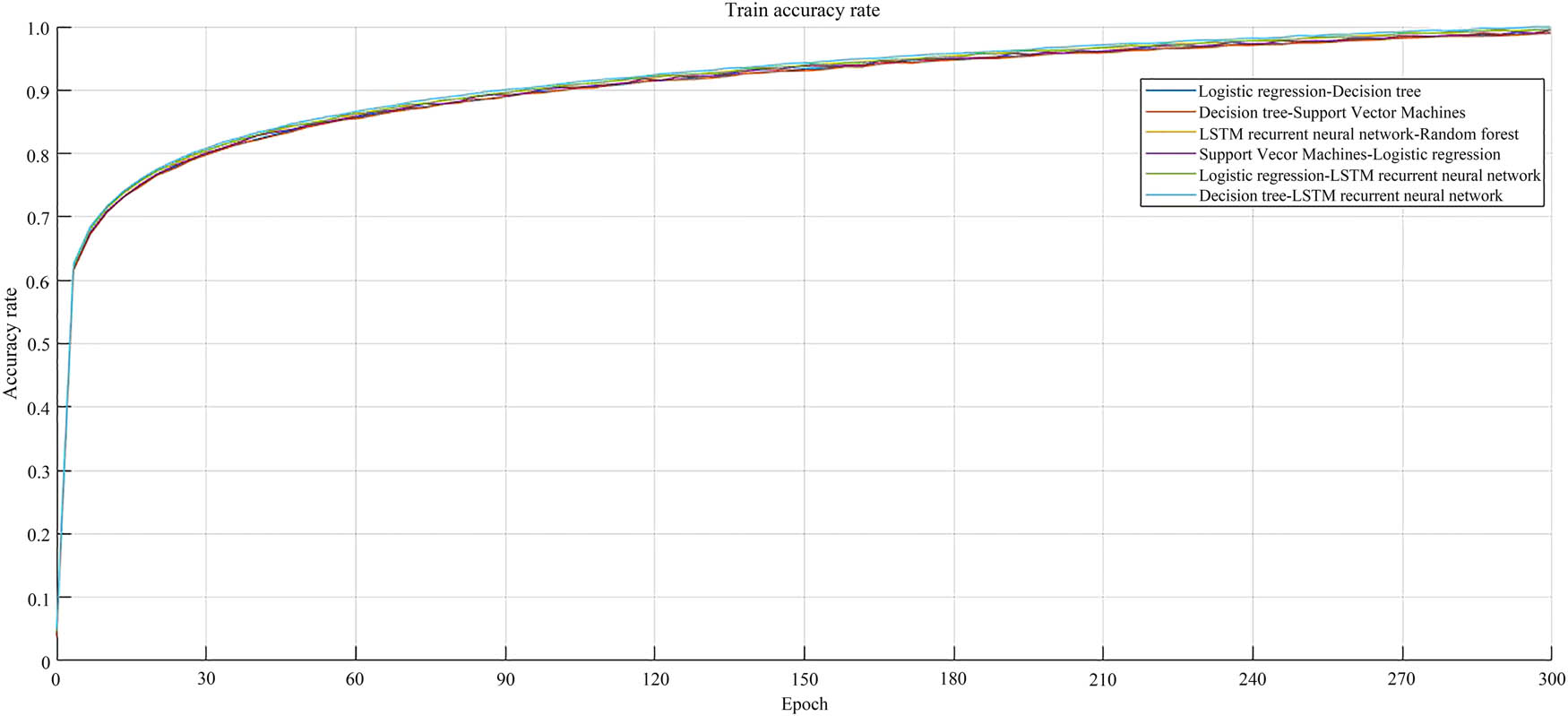
Accuracy curve of model 300 epochs.

In Figure 6, the horizontal axis represents the number of epochs, and the vertical axis represents the loss. Overall, after 30 epochs, the loss tended to range from 0 to 0.5, with the DT–LSTM RNN model having the smoothest loss function and the lowest loss; it was easier to converge, approaching 0.1, achieving ideal expectations. The loss of the LSTM RNN–RF model decreased from 6.0 to 0.3, with a decrease of 95% from the initial level, and the effect was quite impressive. The loss of the logistic regression–LSTM RNN model decreased from 6.0 to 0.4, a decrease of 5.6. The overall curve was similar to that of the LSTM RNN–RF model, but the LSTM RNN–RF model had less loss and better performance. In addition, the overall curves of the three curves were higher than the three combination models mentioned above, with a convergence range of 0.45–0.56. In summary, the LSTM RNN model had a better contribution to the combination model and had a good effect.

Figure 7 shows the loss function curve of the model for 300 epochs. Overall, after 300 epochs, the losses can converge between 0.01 and 0.05, with a maximum loss of only 3.8. Compared to the curve of 30 epochs, it can be analyzed that the minimum loss value decreased from 0.1 to 0.01, with a significant decrease, reaching the initial 90%. The DT–LSTM RNN model had the best performance, with a convergence value of 0.01 and the overall amplitude being the smoothest. The LSTM RNN–RF model had a slightly weaker performance, with a convergence value of 0.02. Compared to the curve with 30 epochs, the convergence value decreased by an initial 93%. For the logistic regression–LSTM RNN model, the curve was more jittery compared to the two combination models mentioned above, with a convergence value of 0.04. Compared to the DT–LSTM RNN model, the convergence value had increased by 0.03, resulting in poorer performance. In summary, the DT–LSTM RNN model and LSTM RNN–RF model showed good performance and were feasible for application in this experiment.

Figure 8 shows the accuracy curve of the model for 30 epochs. Overall, after 30 epochs, the evaluation accuracy of the six combined models reached 94.0–98.2%, with an average of 96.1%. In addition, the DT–LSTM RNN model was relatively flat and more stable overall. For the DT–LSTM RNN model, the estimation accuracy reached 98.2%, but it did not converge well. The LSTM RNN–RF model achieved an estimation accuracy of 97.1%, with a decrease of 1.2% compared to the DT–LSTM RNN model. The prediction accuracy of the logistic regression–LSTM RNN model reached 96.9%, which was closer to the curve of the LSTM RNN–RF model. However, the curve of the LSTM RNN–RF model was more stable, and the prediction accuracy of the logistic regression–LSTM RNN model was improved by 0.2%, resulting in better results. The other three models had lower estimation accuracy, ranging from 94.0 to 96.3%, and failed to converge well, resulting in worse results. In summary, the first two models had better performance and were more prone to convergence after multiple trainings.

In Figure 9, the horizontal axis represents 300 epochs, and the vertical axis represents the estimated accuracy. Overall, the overall curve was relatively stable with no significant differences, and the estimation accuracy tended to be between 99.2 and 9.9%. The prediction accuracy of the DT–LSTM RNN model reached 99.9%, and the curve was relatively stable, approaching convergence at 1.0. Compared with 30 epochs, the prediction accuracy improved by 1.7%, achieving the expected training effect. For the LSTM RNN–RF model, its estimation accuracy reached 99.8%, which was a significant decrease of 0.1% compared to the DT–LSTM RNN model. In addition, compared to 30 epochs, the estimation accuracy was improved by 2.7%, a significant improvement. The accuracy of logistic regression–LSTM RNN estimation reached 99.6%, which decreased by 0.3% compared to the DT–LSTM RNN model. However, both models converged well, and the results met the experimental requirements. In summary, the DT–LSTM RNN model and LSTM RNN–RF model had the best performance in predicting accuracy among the six combined models and could achieve good results in experiments.

5.1 Evaluation criteria

When evaluating the results of the study, accuracy, precision, recall, and comprehensive evaluation index F1 score were used [30]. This article evaluated the evaluation and grading of student grades and teaching quality scenarios based on a multi-classification model.

Accuracy: it refers to the proportion of all correct judgments in the classification model to the total.

Precision: it refers to the proportion of truly correct predictions that are positive for all predictions.

Recall: it refers to the proportion of what is truly correct to what is actually positive.

F1 score: the f1 value is the arithmetic mean divided by the geometric mean, and the larger the result, the better the score. The f1 value is weighted for both precision and recall, and the f1 score belongs to 0–1. In this model, 1 represents the best recognition and classification results of the model, while 0 represents the worst.

In this study, multiple classifications were used as a whole. Taking teaching quality as an example, the actual positive class prediction is True Positive (TP), which means that 90 points of teaching quality are predicted as 90 points of teaching quality. The actual positive class prediction is False Negative (FN), which means that 90 points of teaching quality are predicted to be 60 points of teaching quality. The actual negative class is predicted to be False Positive (FP), which means that 60 points of teaching quality are predicted to be 90 points of teaching quality. The actual negative class prediction is True Negative (TN), which means that 60 points of teaching quality are predicted as 60 points of teaching quality.

5.2 Comparison of experimental results of multi-classifier models in student achievement and teaching quality scenarios

The evaluation results of LSTM RNN–RF in the scenario of student performance estimation and DT–LSTM RNN in the teaching quality evaluation are shown in Table 1.

5.3 Comparative experimental discussion of multi-classifier models in student achievement and teaching quality scenarios

5.3.1 Error estimation and confusion matrix

From Table 1 analysis, it can be seen that the actual score of student 77 with course number 9254 was 72.92, located in the range of 70–80, but the predicted score was 69.70, located in the range of 60–70, which was one level lower than the estimated classification. According to the analysis of the student’s admission score and learning time, the admission score was not high and the learning time was short, so this model had errors in predicting student grades. The actual score of the student with course number 9,500 and course number 280 was 89.44, which belonged to the range of 80–90. However, the predicted score was 92.70, which belonged to the range of 90–100, and was one level higher overall. The reason for the opposite was the same. In the future, the prediction results will be more refined and integrated with various factors during training. For teaching quality, the teacher with teacher number 2 and class number 11 had an actual quality score of 92.30, which was between 90 and 100, but the predicted score was 88.80, which was between 80 and 90. The analysis of the data showed that the teacher’s teaching quality was very good, but the attendance was very low. Therefore, when analyzing the data, the model showed a slight decrease compared to the actual estimated results, and the overall effect was good.

For different score segment types, the LSTM RNN–RF model was used for predicting student performance scenarios, and the DT–LSTM RNN model was used for predicting teaching quality. The confusion matrix is shown in Figure 10. The horizontal axis represents the predicted type score segment, which is 0–60, 60–70, 70–80, 80–90, and 90–100 from left to right. The vertical axis represents the actual score segment, which is the same as the horizontal axis from top to bottom. For the confusion matrix of student performance estimation (left figure in Figure 10), the proportion of samples actually belonging to the corresponding actual category predicted to be the corresponding predicted category was highest in the 90–100 and 80–90 score ranges, and the proportion of correctly predicted samples reached 98%; the classification effect was very impressive, with a minimum concentration of 60–70, and the proportion of correctly predicted samples reaching 95%. In contrast, there were more classification errors, with 1% being incorrectly predicted as 0–60, 3% being incorrectly predicted as 70–80, and 1% being predicted as 80–90. The 70–80 score range was difficult to classify, only 96%, with 1% predicted as 80–90 and 3% predicted as 60–70. Other categories had good classification results and could meet practical application needs.

Figure 10

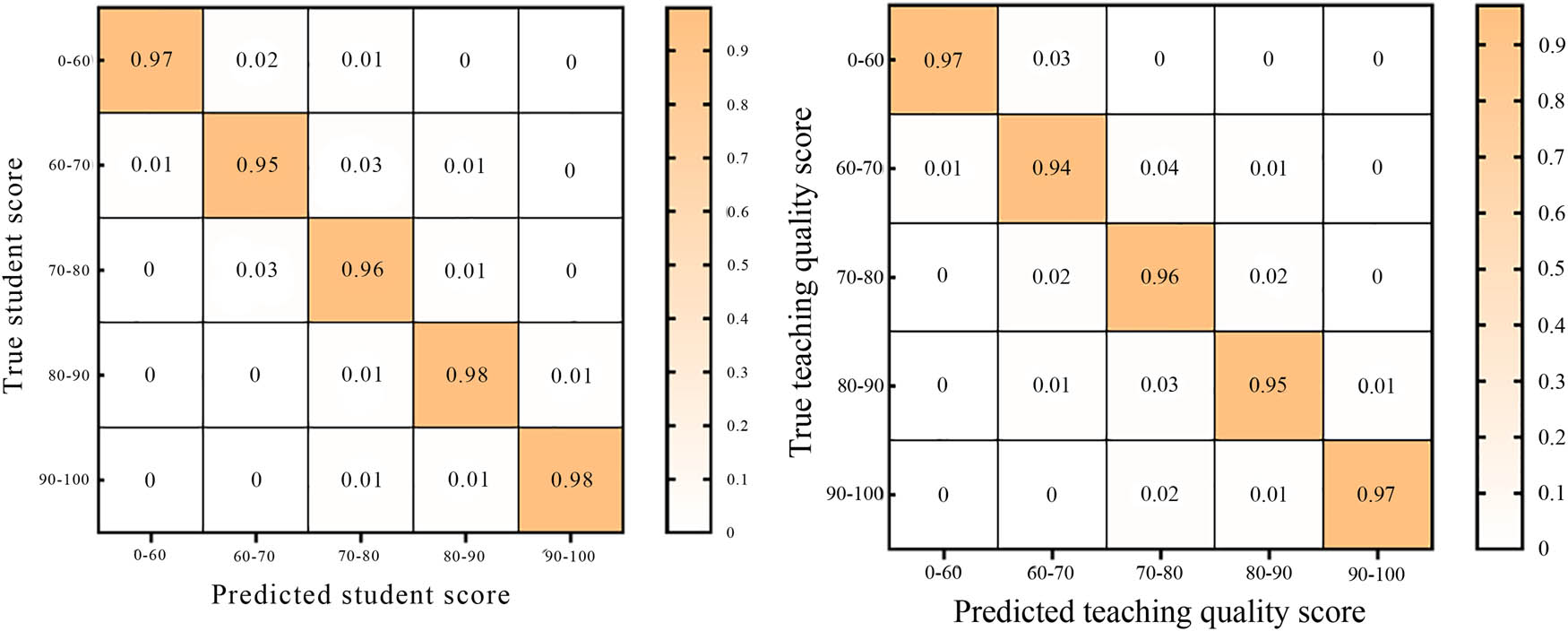
Confusion matrix between student performance and teaching quality estimation.

For the confusion matrix of teaching quality evaluation (shown in the right figure of Figure 10), the proportion of samples actually belonging to the corresponding actual category being predicted as the corresponding predicted category was highest in the 0–60 and 90–100 score ranges, and the proportion of correctly predicted samples reached 97%; the classification achieved ideal results, with a minimum concentration of 60–70, and the proportion of correctly predicted samples reached 94%. In contrast, there were more classification errors, with 1% being incorrectly predicted as 0–60, 4% being incorrectly predicted as 70–80, and 1% being predicted as 80–90. The 80–90 score range was difficult to classify, with only 95% predicted, with 1% predicted as 60–70, 3% predicted as 70–80, and 1% predicted as 90–100. Other categories were relatively low but had also achieved good practical results.

5.3.2 Comparison of the accuracy of different models in different scenarios

The comparison of estimation accuracy for different models in different scenarios is shown in Figure 11. In the scenario of predicting student grades, the logistic regression–DT model had the worst prediction performance, only 91.2%. The LSTM RNN–RF model achieved the best estimation performance, with an accuracy of 98.5%, which was 7.3% higher than logistic regression–DT. The logistic regression–LSTM RNN model achieved 97.3% improvement, which was 6.1% higher than the logistic regression–DT model, and the estimation accuracy was significantly improved. The DT–LSTM RNN model achieved 96.9% improvement, which was 5.7% higher than logistic regression–DT.

Figure 11

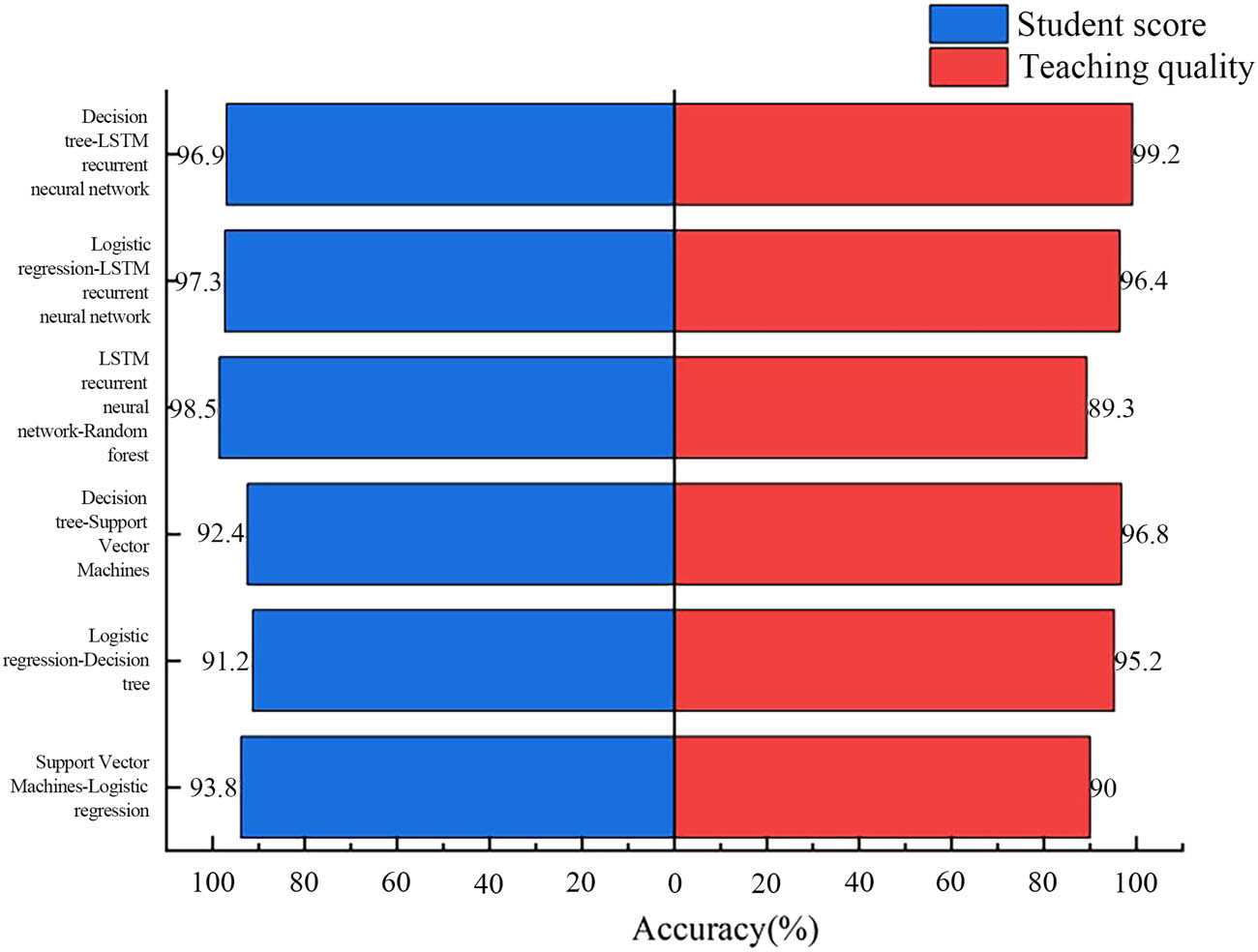
Comparison of the accuracy of different models in different scenarios.

In the scenario of predicting teaching quality, the DT–LSTM RNN model had the best prediction performance, reaching 99.2%, while the LSTM RNN–RF model had the worst prediction performance, only 89.3%. Compared with the estimation effect under the scenario of predicting student grades, the LSTM RNN–RF model achieved the best effect under the scenario of predicting student grades, but the effect on predicting teaching quality was not ideal. The effect of DT–LSTM RNN on student performance prediction was not the best, which showed that the same model had different adaptability to different scenarios. Analysis showed that DT–LSTM RNN is more suitable for evaluating teaching quality, precisely because DT is more suitable for interpretability and rule extraction of teaching quality. At the same time, LSTM RNN can capture long-term time dependencies and is suitable for analyzing changes in teaching quality over time. The LSTM RNN–RF model is more suitable for evaluating students’ grades, precisely because using LSTM RNN to capture students’ time series information, such as historical exam scores or learning behaviors, is more convenient and applicable. RF can be used to process other non-time series features, such as students’ background information and attendance rate, with stronger practicality.

5.3.3 Comparison of precision, recall, and F1 score in student performance evaluation and grading scenarios

The comparison of prediction, recall, and F1 score of different models under student grades is shown in Figure 12. The horizontal axis represents the classification of the model, and the vertical axis represents the proportion of parameters. Overall, the LSTM RNN–RF histogram had the highest precision of 97.4%, recall of 94.4%, and F1 score of 98.1%, achieving the best performance. Compared to the DT–LSTM RNN model, the distribution of the above three parameters increased by 1.8, 0.9, and 2.2%. The logistic regression–LSTM RNN histogram was second, with a precision of 96.2%, recall of 93.9%, and F1 score of 96.5%. Compared to the DT–LSTM RNN model, it increased by 0.6, 0.4, and 0.6%, respectively. In summary, analyzing the above parameters showed that the LSTM RNN–RF model achieved the best performance and stronger adaptability in student performance scenarios (Figure 13).

Figure 12

Comparison of precision, recall, and F1 score in student performance scenarios.

Figure 13

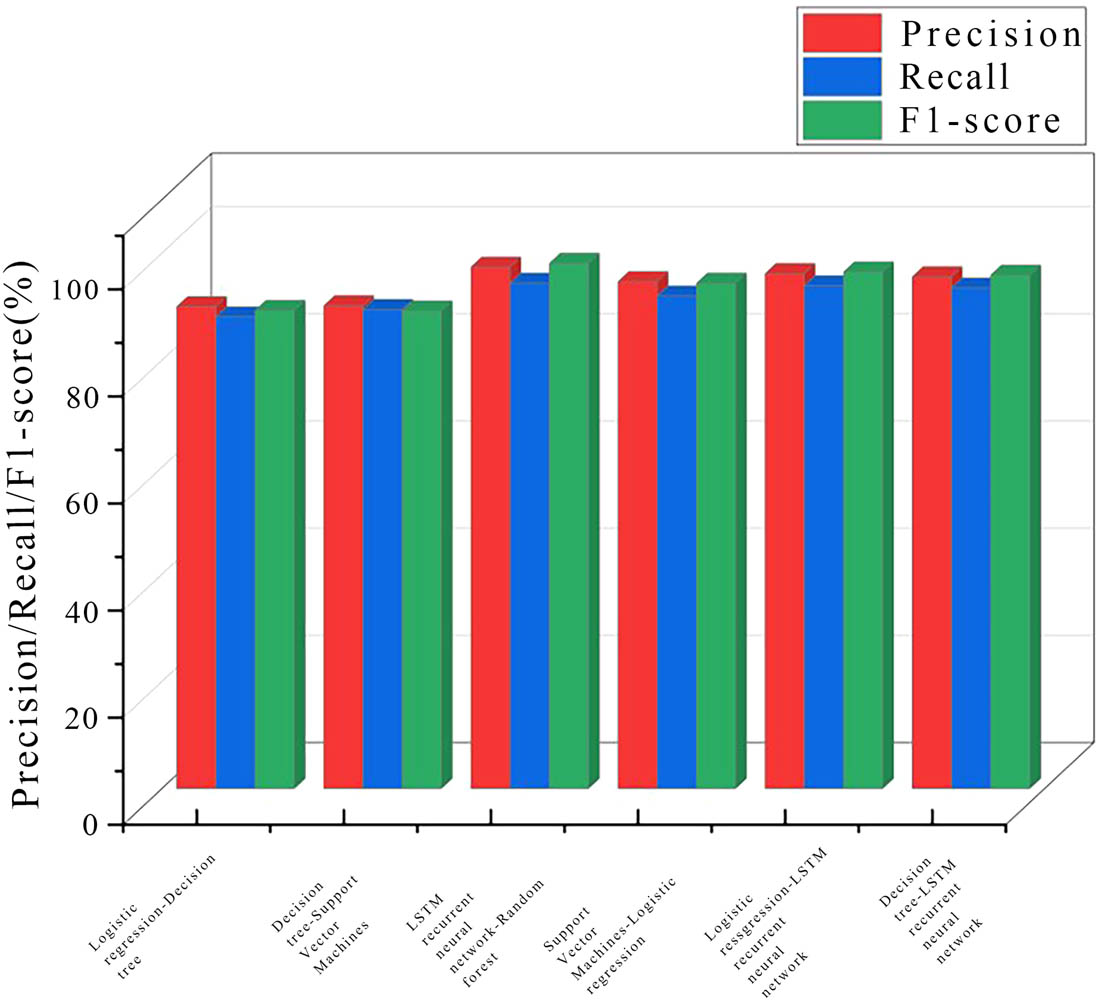
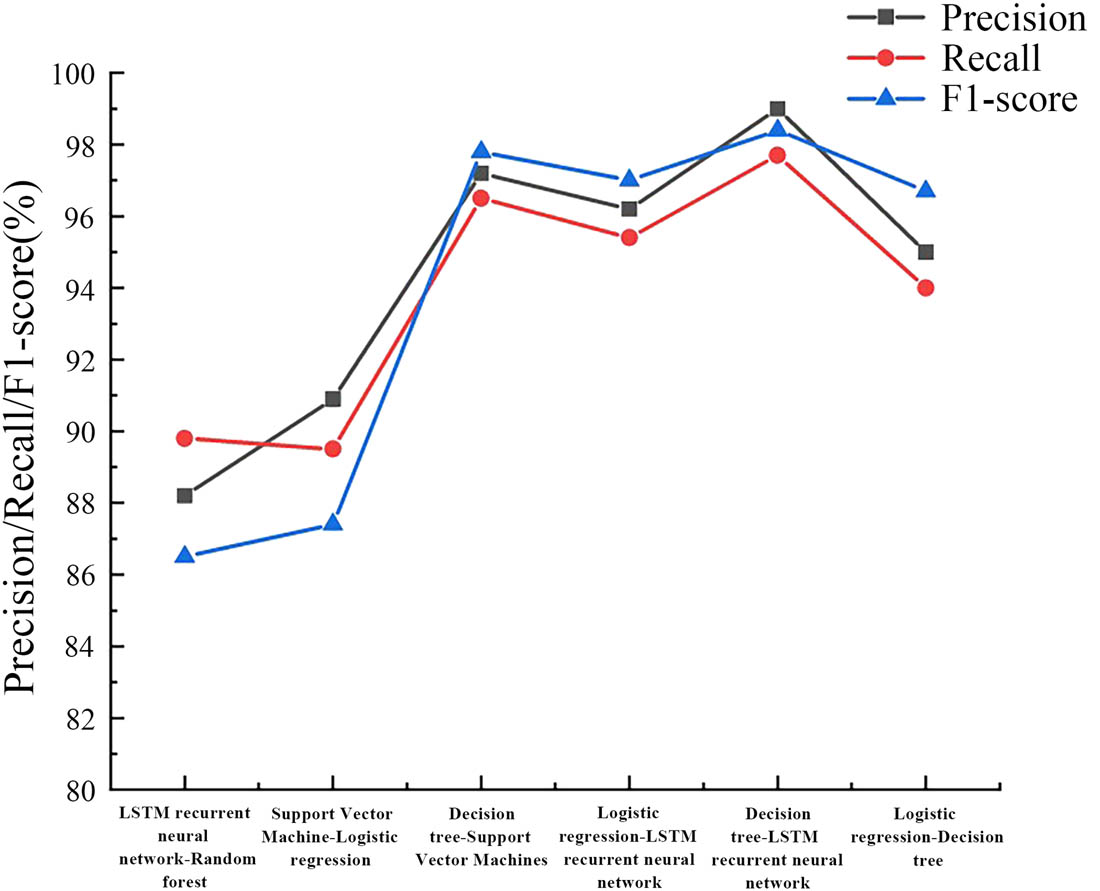
Comparison of precision, recall, and F1 score in teaching quality scenarios.