A modified Hoek–Brown model considering softening effects and its applications

Lei Zhang; Shaofei Li; Zhihua Tan; Bingxu Wang; Yuting Xu; Yanglun Fu; Jian Mi; Yang Yang; Dongyuan Su; Yi Tian

doi:10.1515/geo-2025-0787

Article Open Access

A modified Hoek–Brown model considering softening effects and its applications

Lei Zhang , Shaofei Li , Zhihua Tan , Bingxu Wang , Yuting Xu , Yanglun Fu , Jian Mi , Yang Yang , Dongyuan Su and Yi Tian

Published/Copyright: May 23, 2025

Published by

Become an author with De Gruyter Brill

Submit Manuscript Author Information

From the journal Open Geosciences Volume 17 Issue 1

Abstract

Considering that the traditional Hoek–Brown model only accounts for strain hardening effects in rock materials, while many rock materials exhibit strain softening effects under large deformation, a modified Hoek–Brown model has been developed to simultaneously describe both material hardening and softening characteristics. This enhancement builds upon the traditional Hoek–Brown model by introducing plastic internal variables that characterize material damage or degradation. To address numerical singularities and convergence difficulties encountered during the implementation of the modified Hoek–Brown model, a function smoothing method is employed. The physical significance of model parameters in the modified model is clarified through theoretical analysis and single-factor variable analysis methods. Finally, the modified Hoek–Brown model is applied to practical engineering calculations. The study results demonstrate that the modified Hoek–Brown model can effectively account for both strain hardening and strain softening effects in materials. The function smoothing method proves to be effective in mitigating numerical singularities and convergence issues encountered in the implementation of the modified Hoek–Brown model. For soft rock tunnels, when significant displacements occur in the surrounding rock, both displacements and stresses around the tunnel calculated using the modified Hoek–Brown model are more consistent with engineering reality than those obtained using the traditional Hoek–Brown model. It is recommended to consider applying the modified Hoek–Brown model in practical engineering calculations.

Keywords: softening effects; Hoek–Brown model; numerical implementation; engineering applications

1 Introduction

In practical construction, such as during excavation of underground shafts, tunnels, and similar structures, the stress conditions of adjacent or nearby rock masses continue to change after excavation [1]. The stress field within the rock mass also undergoes continual alteration. Studying the mechanical properties and failure mechanisms of rock materials under stress is crucially significant. Strength criteria determine the stress and strain conditions under which rock specimens or rock engineering structures are likely to fail. Current failure theories can explain certain aspects of rock behavior well but often fail to generalize to complex stress conditions, particularly where many rock constitutive models cannot account for strain softening effects, posing significant challenges for engineering applications [2,3].

Many scholars have conducted extensive research on rock damage constitutive models from various perspectives and approaches based on various rock strength theories and failure theories to consider the strain softening effects of rocks. Currently, there are two main research methods for mechanical constitutive models of rock types: first, assuming that rocks follow certain mathematical or physical models, conducting loading and unloading tests to obtain experimental data, and then deriving the constitutive model of rocks; second, combining relevant theories of probability theory in mathematics, introducing the Weibull formula, and assuming that the micro unit destruction of rocks follows this formula, deducing the rock’s constitutive model. Gao et al. [4], based on statistical theory and damage mechanics, defined a rock fracture intensity variable from a mechanical perspective, where the work done by friction between fracture surfaces equals the strain energy released upon material fracture. They assumed that the strength distribution of rock micro-cubes follows a Weibull distribution and the stress levels satisfy the Hoek–Brown criterion. They derived a constitutive model for fractured rock masses and validated it using experimental data and discrete element methods. Wang et al. [5] developed a thermo-hydro-mechanical constitutive model based on an internal variable theory to simulate the damage and failure of rocks under freeze–thaw cycles. Zhang et al. [6] simplified cold-region rocks under geostress into three forms: complete failure, weak failure, and non-failure units. They represented the degree of unit damage by changing the elastic modulus and established a constitutive model for freeze-thawing rocks that considers softening effects. Yang et al. [7] summarized the stress–strain relationships of rocks under conventional triaxial compression test conditions, exploring the underlying mechanisms and improving classical plastic statistical damage models. They derived a constitutive model for rocks under conventional triaxial compression test conditions and preliminarily validated it using results from such tests. The results indicate that the modified constitutive model effectively and comprehensively reflects rock strain softening and expansion, capturing the transition from brittle flow to plastic flow characteristics with increasing confining pressure. Wei et al. [8] developed an elasto-plastic constitutive model that considers both fracture and plastic deformation for deep rock masses experiencing high stress conditions. Assuming that the strength of rock micro-elements follows a Weibull random distribution, Chen and Qiao [9], based on the Drucker–Prager criterion, energy principles, and fracture damage theory, derived a constitutive model that accounts for the effects of crack propagation length and joint closure friction in rock masses. The theoretical constitutive model curve of the model fits well with experimental constitutive curves of discontinuous jointed rock masses. A comparison between the effects considering and not considering the crack propagation length and joint friction effects showed superiority in the former case, validating the model’s rationality and effectiveness. Li et al. [10], through an analysis of rock damage mechanisms, identified correlations between damaged and undamaged specimens. Using the Mohr–Coulomb criterion as a basis, they established a constitutive model for rock materials considering damage under triaxial compression conditions and conducted simulation analysis validation. The results indicate that the established model effectively reflects the stress–strain relationship throughout the rock failure process. Xie et al. [11], based on modified Harris functions and analysis of indoor shear test results, proposed a new serrated rock constitutive model. Validation results demonstrate that the model accurately reflects the variation trend of peak shear curves, with straightforward parameter estimation and physically meaningful parameters. In order to elucidate the complete shear deformation evolution of rock materials, Xin et al. [12] established a macroscopic constitutive relationship for rock shear deformation by calculating micro-pore shear deformations and solid skeleton deformations. Validation results show that the established constitutive model can characterize the entire process of shear deformation and failure evolution in rocks, including stages such as compaction deformation, linear elastic deformation, shear hardening deformation, shear softening deformation, bimodal phenomena, and residual deformation stages. Within the framework of existing shear constitutive models, Xie et al. [13,14] assumed rock materials composed of relatively intact elements and damaged elements, establishing a rock constitutive model that considers softening effects. Based on the strain equivalence hypothesis and assuming the statistical distribution of micro-element strength follows a Weibull distribution, with micro-element failure governed by the Hoek–Brown criterion, Chen et al. [15] derived the relationship between rock micro-element strength and damage variables. They developed a new statistical damage constitutive model based on the Hoek–Brown criterion. Validation confirmed that the new model effectively describes the entire stress–strain relationship during the rock failure process. Bian et al. [16] estimated the mechanical properties of shale specimens over immersion time through laboratory tests. They subsequently investigated the degradation mechanisms of shale parameters under immersion conditions using X-ray diffraction and scanning electron microscopy at the microscopic level. They established a rock constitutive model considering the effects of pore compression under uniaxial loading conditions. Based on the assumption that the elastic modulus of rock microstructural units approximately follows a Weibull distribution and integrating strain energy density theory, Wen et al. [17] developed a damage constitutive model for rocks. A comparison of the simulation results from the new model with theoretical curves from existing models and experimental curves under uniaxial loading demonstrated that the new model effectively characterizes the stress–strain relationship of rocks. Based on the principles of statistical strength theory and damage mechanics and incorporating the Lemaitre strain equivalence hypothesis with consideration of acidic environments, Qu et al. [18] studied the freeze–thaw damage evolution mechanisms of sandstone specimens. They developed damage evolution equations and a constitutive model for rocks. Considering freeze–thaw and loading conditions, Fang et al. [19] utilized statistical methods to establish a damage constitutive model for rocks and validated its rationality. Based on triaxial compression creep tests under high confining pressure and high water pressure conditions for sandstone, Jiang et al. [20] concatenated a nonlinear viscoplastic model reflecting accelerated creep characteristics of rocks and a Burgers model. They constructed a new six-element nonlinear viscoelastic–plastic creep model and identified model parameters, verifying its correctness and rationality using experimental results. To more accurately quantify the mechanical properties of rocks after freeze–thaw cycles from a damage perspective, Lin et al. [21], based on the coupling damage hypothesis of rocks and utilizing the lognormal distribution commonly used in engineering reliability analysis and strain strength theory, established a statistical damage constitutive model for rocks under freeze–thaw cycles. Combining the Mohr–Coulomb criterion with energy dissipation theory and considering the hardening and softening characteristics of rocks during loading, Ma et al. [22] employed a non-associated plastic flow rule to describe the plastic deformation of rocks. They established a damage-plasticity constitutive model for rocks by dividing dissipated energy during the damage process by the rate of damage energy consumption. Meng et al. [23], through conventional triaxial compression tests, obtained stress–strain curves of red sandstone after freeze–thaw cycles. They then used logistic equations to reduce the ultimate stress and elastic modulus based on the number of freeze–thaw cycles. The study results indicated that with an increasing number of freeze–thaw cycles, the extent of rock damage intensified, leading to greater reductions in ultimate stress and elastic modulus, decreased compressive strength, enhanced plastic properties, and confining pressure mitigated rock damage.

In summary, numerous scholars have developed constitutive models that account for rock damage to address the softening effects of rocks. However, many of these models are quite complex, which directly limits their practical application in engineering. Considering that the Hoek–Brown strength criterion can be applied to rocks under various complex stress conditions and compared to several other classic strength criteria, it reflects the inherent nonlinear failure characteristics of rocks, including the effects of various factors such as minimum principal stress regions, low stress areas, and tensile stress regions on strength [24,25]. The Hoek–Brown criterion has become one of the most widely used and influential rock strength criteria to date [26,27,28,29], having a significant impact on engineering practice. Therefore, this article attempts to introduce internal variables based on the Hoek–Brown strength criterion to develop a modified Hoek–Brown model that accounts for rock softening effects.

2 Modified Hoek–Brown model considering softening effects

Building upon the traditional Hoek–Brown model, a modified version is proposed by introducing internal variables that characterize material degradation, thus enabling the description of material softening effects. This modified model is outlined as follows.

2.1 Elasticity relationship

(1) σ ̇ = ( λ δ δ + 2 G I ) : ε ̇ e ,

where σ ̇ denotes the stress increment; λ and G represent the elastic Lamé constants and shear modulus, respectively; δ denotes the second-order equivalent tensor; I denotes the fourth-order equivalent tensor; ε ̇ e denotes the increment of elastic strain.

2.2 Plastic potential function and yield function

The yield criterion of the traditional Hoek–Brown model is given by

(2) ϕ ( σ 1 , σ 3 ) = σ 1 − σ 3 − σ c m σ 3 σ c + s α ,

where σ 1 represents the maximum principal stress, σ 3 is the minimum principal stress, σ c is the uniaxial compressive strength of the rock, m is an empirical parameter with dimensional consistency for rocks, s is a parameter that indicates the intactness of the rock, and α is the rock strength exponent.

Considering a specific rock material, the model parameters σ c , m, s, and α in equation (2) are predetermined. The yield function described by equation (2) clearly falls within the scope of an ideal plasticity model. However, real-world rock materials typically exhibit strain softening characteristics, indicating that the yield function given by equation (2) cannot adequately capture the strain softening effect of rock materials.

Equation (2) can been considered as it comprises two terms, σ 1 − σ 3 and σ c m σ 3 σ c + s α . Clearly, the first term represents the shear stress experienced by the rock material, while the second term represents the shear strength of the rock material. According to the representation of the second term, the shear strength of the rock material is primarily influenced by the uniaxial compressive strength σ c , the ratio of the minimum principal stress to the uniaxial compressive strength σ 3 σ c , and the intactness parameter s of the rock. Considering that both the intactness and shear strength of rock materials should gradually decrease with ongoing damage, an internal variable D representing rock damage is introduced and equation (2) is reformulated as follows:

(3) ϕ ( σ 1 , σ 3 , D ) = σ 1 − σ 3 − σ c ( 1 − n D ) m σ 3 σ c + ( 1 − n ′ D ) s α .

Here, the internal variable D represents the degree of damage to the rock material as deformation progresses. Model parameters n and n ′ , respectively, denote the residual strength coefficients associated with m and s, with n ranging between (0, 1) and n ′ between (0, 1).

The modified model employs a non-associated flow rule, where the plastic potential function used is similar to equation (3), with the difference that m in equation (3) is replaced by m ′ .

2.3 Hardening rule

In the modified yield function in equation (3), which includes the plastic internal variable D, it is essential for a complete constitutive model to specify the evolution rule of D. Upon initial yielding of the rock material, the internal variable D, which characterizes rock damage, should be 0.0. As deformation of the rock progresses, the damage to the rock gradually intensifies, and D increases from 0.0 to 1.0, indicating that the rock material reaches residual strength. Considering that once damage occurs in the rock, its rate of damage development accelerates with continued deformation, an exponential function is employed to describe the evolution rule of the internal variable D.

(4) D = 1 − exp ( − k ε d p ) ,

where k represents the parameter governing the evolution rate of the internal variable D; ε d p denotes the equivalent plastic strain influencing the evolution of D, which incorporates both the plastic shear strain e p and the plastic volumetric strain ε v p , expressed specifically as ε d p = ( 1 − A ) ( ε v p ) 2 + 2 / 3 A e p : e p . Here, A signifies the proportion of plastic shear strain in the equivalent plastic strain ε d p .

3 Numerical implementation of the modified model

Before conducting in-depth analysis and engineering applications of the modified model, it is essential to first implement it numerically. For the modified model, numerical implementation necessitates addressing the issues of three-dimensional formulation of the yield function and the presence of corner points in the principal stress space of the yield function.

3.1 Three-dimensional formulation of the yield function

Considering the satisfaction between principal stresses and stress invariants,

(5) σ 1 σ 2 σ 3 = 2 3 − J 2 cos θ σ + 1 3 I 1 − 2 3 − J 2 cos θ σ + π 3 + 1 3 I 1 − 2 3 − J 2 cos θ σ − π 3 + 1 3 I 1 .

Substituting this equation into the yield function, equation (3), the following equation can be easily obtained:

(6) ϕ ( σ , D ) = K ( θ σ ) − J 2 − σ c Θ α ,

where

(7) K ( θ σ ) = 2 sin θ σ + π 3 ,

(8) Θ = ( 1 − n D ) m − 2 3 − J 2 cos θ σ − π 3 + 1 3 I 1 σ c + ( 1 − n ′ D ) s ,

where J 2 and I 1 represent the second invariant associated with the deviatoric stress tensor and the first invariant associated with the stress tensor, respectively. The stress rod angle θ σ satisfies tan ( θ σ − π / 6 ) = ( 2 σ 2 − ( σ 1 + σ 3 ) ) / ( 3 ( σ 1 − σ 3 ) ) , where θ σ ranges between 0 and π / 3 .

3.2 Smoothing treatment of yield functions and plastic potential functions

By differentiating the plastic potential function with respect to stress σ , the plastic flow direction r = ∂ ϕ / ∂ σ can be determined. However, in the principal stress space, the plastic potential function of the modified model exhibits multi-solution characteristics for the plastic flow direction at corner points. To address this issue, a smoothing method is employed to transition at the corner points.

The stress rod angle θ σ corresponds to approximately 0 or π / 3 at the corner points. When the stress rod angle θ σ is near 0, according to equation (5), it can be observed that σ 2 ≈ σ 3 . Substituting σ 3 with σ 2 in equation (3) and then substituting equation (5) in the modified equation straightforwardly yield the following:

(9) ϕ ′ ( σ , D ) = K ′ ( θ σ ) − J 2 − σ c Θ ′ α ,

where

(10) K ′ ( θ σ ) = 2 cos θ σ + π 6 ,

(11) Θ ′ = ( 1 − n D ) m − 2 3 − J 2 cos θ σ + π 3 + 1 3 I 1 σ c + ( 1 − n ′ D ) s .

When the stress rod angle θ σ is slightly greater than 0, the stress point lies on the yield surface corresponding to yield functions in equation (6) or (9). Efforts are made to smooth the transition using the following equation:

(12) ϕ 1 ( σ , D ) = ϕ else 1 2 ( ϕ + ϕ ′ ) + 1 2 a − a π cos π ( ϕ − ϕ ′ ) 2 a if ( ϕ − ϕ ′ ) < a ,

where a is a parameter representing the degree of smoothness. Clearly, as a increases, the transition segment from ϕ ′ to ϕ is longer, resulting in a smoother yield surface at the corners. However, this smoother surface introduces greater deviation from the true yield surface, as depicted by equation (3). To ensure smoothness and minimize error, a is set to 1.0 × 10⁻³.

When the stress rod angle θ σ is around π / 3 , as indicated by equation (5), it can be observed that σ 1 ≈ σ 2 . Substituting σ 1 in equation (3) with σ 2 and then substituting equation (5) in the modified equation yield

(13) ϕ ″ ( σ , D ) = K ″ ( θ σ ) − J 2 − σ c Θ α ,

where

(14) K ″ ( θ σ ) = 2 s in θ σ .

When the stress rod angle θ σ is slightly less than π / 3 , the stress point lies on the yield surface corresponding to yield functions in equation (6) or (13). Smooth transition is achieved by employing the following equation:

(15) ϕ 2 ( σ , D ) = ϕ else 1 2 ( ϕ + ϕ ″ ) + 1 2 a − a π cos π ( ϕ − ϕ ″ ) 2 a if ( ϕ − ϕ ″ ) < a .

Combining the two smoothing transition equations, equations (12) and (15) yield the following smoothed yield function:

(16) ϕ 3 ( σ , D ) = 1 2 ( ϕ + ϕ ′ ) + 1 2 a − a π cos π ( ϕ − ϕ ′ ) 2 a if ( ϕ − ϕ ′ ) < a 1 2 ( ϕ + ϕ ″ ) + 1 2 a − a π cos π ( ϕ − ϕ ″ ) 2 a if ( ϕ − ϕ ″ ) < a ϕ else .

Clearly, the piecewise function corresponding to equation (16) satisfies continuity of zeroth and first-order derivatives, effectively avoiding numerical singularity issues during the numerical implementation process.

3.3 Numerical implementation of the model

The fundamental equations to be solved for the numerical implementation of the modified model using implicit algorithms are as follows:

(17) σ n + 1 − σ n − C n + 1 : Δ ε n + 1 + Δ λ C n + 1 : r n + 1 D n + 1 − D n − Δ λ D ¯ n + 1 ϕ n + 1 = 0 0 0 ,

where the physical quantities indexed with n + 1 represent the corresponding quantities updated after the ( n + 1 )th incremental step; C , Δ ε , Δ λ , r , and D ¯ denote the elastic stiffness, strain increment, plastic consistency parameter, plastic flow direction, and hardening direction, respectively. The key to updating the state variables using implicit algorithms lies in solving the nonlinear system of equation (17) with σ n + 1 , D n + 1 , and Δ λ as unknowns, typically solved using the Newton–Raphson iteration method [1]. It should be noted that the finite element software used in this study is the open-source finite element analysis tool FreeFEM.

4 Analysis of model parameters for the modified model

4.1 Physical meanings of model parameters

Before applying the modified model in engineering practice, it is essential to determine the model parameters. Clarifying the physical meanings of each model parameter is often necessary prior to their determination. As shown in Table 1, the model parameters of the modified model can be categorized into three classes. The first class includes parameters related to elasticity, such as elastic modulus E and Poisson’s ratio μ . The second class encompasses parameters associated with the yield function and plastic potential function, including uniaxial compressive strength of rock σ c , intact rock parameter s, rock strength index α , parameters m and m ′ , which represent the influence of ratio σ 3 σ c on the shear strength, and residual strength coefficients n and n ′ corresponding to m and s, respectively. The third class comprises parameters related to internal variables, such as the evolution rate parameter k and the proportion A of plastic shear strain in the equivalent plastic strain that causes material degradation. From Table 1, it is evident that each model parameter in the modified model has a distinct physical significance.

Table 1

Physical meaning of model parameters

Categories	Parameters	Physical meaning
Related to the elastic relationship	E	The slope of the stress–strain relationship during the elastic deformation stage of the material
Related to the elastic relationship	μ	The ratio of lateral strain to axial strain during the elastic deformation stage of the material
Related to the yield function and plastic potential function	σ c	Uniaxial compressive strength of rocks
	s	Rock integrity parameter
	α	Rock strength index
	m	Degree of influence of the ratio σ 3 σ c on shear strength in the yield function
	m ′	Degree of influence of the ratio σ 3 σ c on shear strength in the plastic potential function
	n	Residual strength coefficient corresponding to m
	n ′	Residual strength coefficient corresponding to s
Related to plastic internal variable	k	Evolution speed of internal variables
Related to plastic internal variable	A	Proportion of plastic shear strain in the equivalent plastic strain that causes material degradation or damage

4.2 Multivariate analysis of model parameters

For a new constitutive model, conducting multivariate analysis of model parameters can visually illustrate the influence of each parameter on the stress–strain relationship. Therefore, multivariate analysis of model parameters for the modified model is conducted. Specifically, the initial stress state used for analysis is 400.0, 115.0, 115.0, 0.0, 0.0, and 0.0 MPa, and the strain increments are 0.10, −0.05, −0.05, 0.00, 0.00, and 0.00. The initial value of internal variable D is set to 0.10, and the elastic modulus E and Poisson’s ratio μ are taken as 2000.0 MPa and 0.30, respectively. The single-factor variable method is employed to calculate the effects of each parameter. During calculation, apart from the varying model parameter, all other model parameters are taken as the corresponding third values in Table 2. The calculation results are shown in Figures 1 and 2 and Table 3.

Table 2

Single-factor variable values

Parameter	Values
σ c (MPa)	64.00, 72.00, 80.00, 88.00, 96.00
s	0.40, 0.45, 0.50, 0.55, 0.60
α	0.40, 0.45, 0.50, 0.55, 0.60
m	8.0, 9.0, 10.0, 11.0, 12.0
n	0.64, 0.72, 0.80, 0.88, 0.96
n ′	0.64, 0.72, 0.80, 0.88, 0.96
k	16.0, 18.0, 20.0, 22.0, 24.0
A	0.40, 0.45, 0.50, 0.55, 0.60

Figure 1

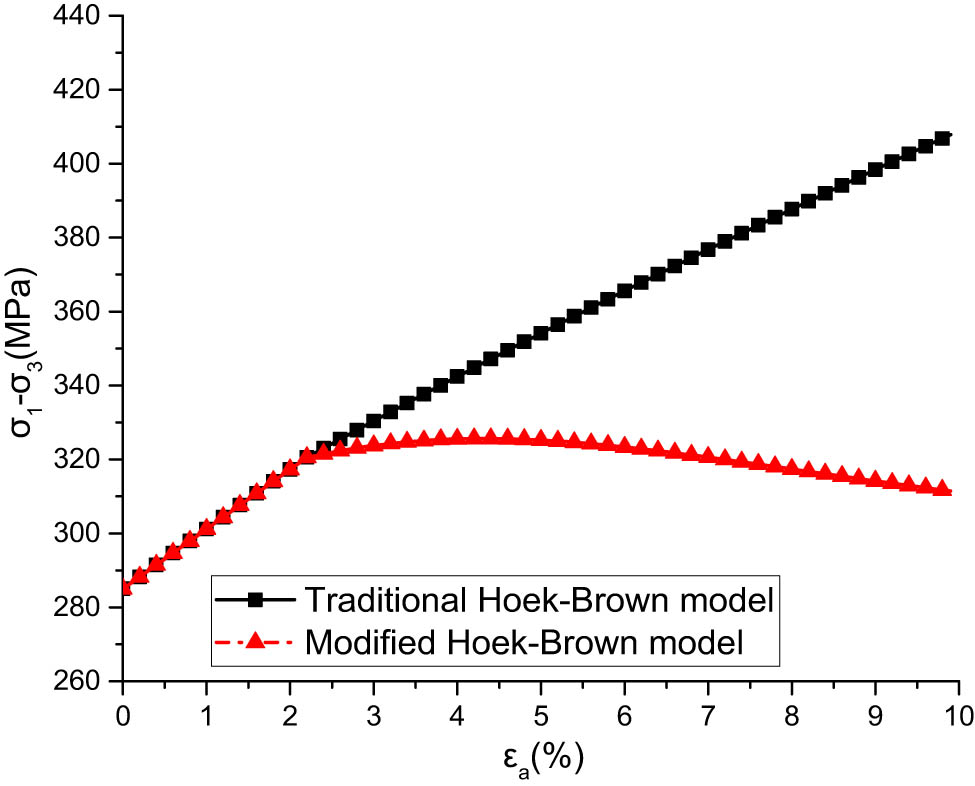
Comparison between the improved model and the traditional model.

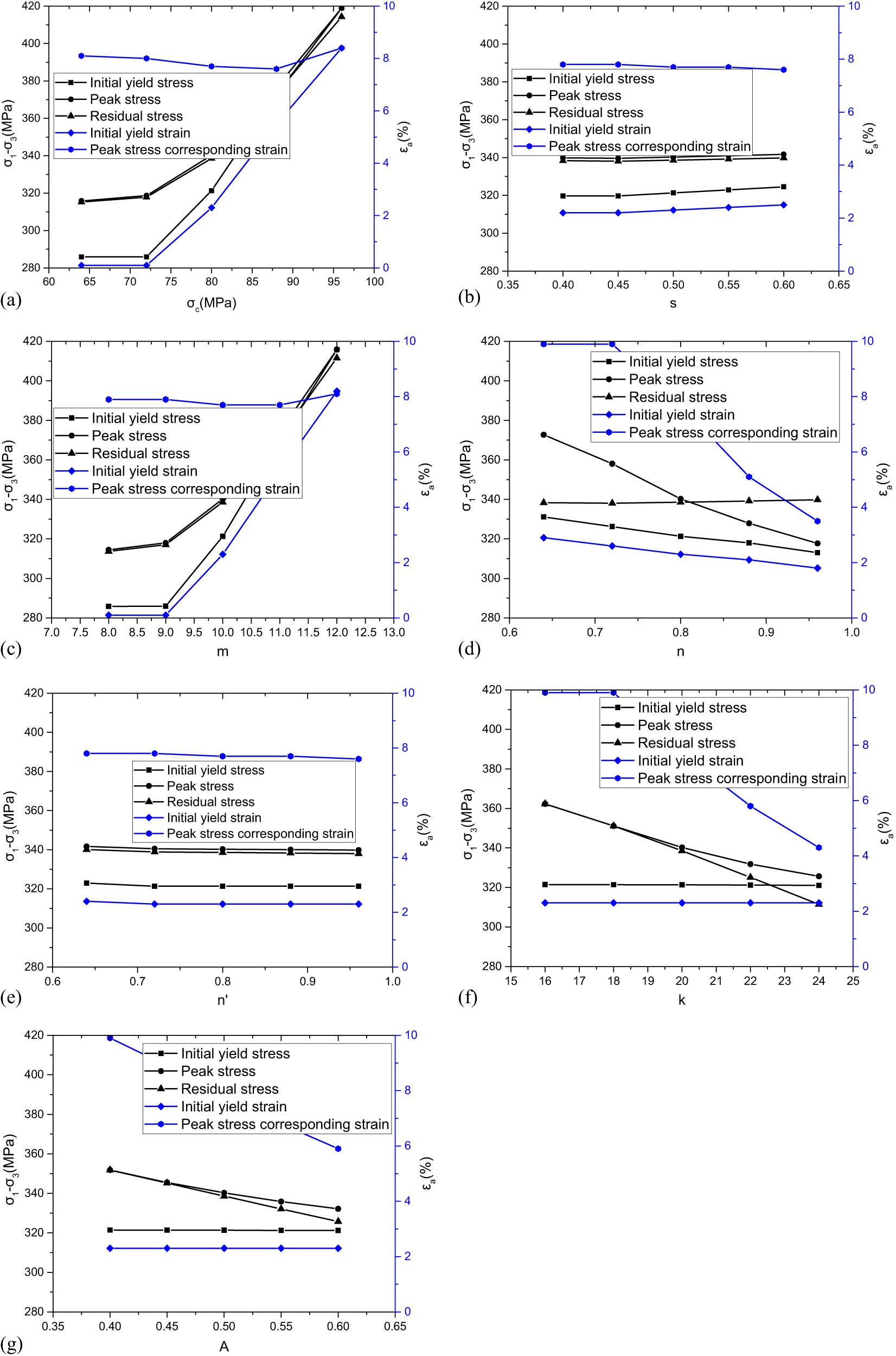
$Figure 2 Multivariate calculation results. (a) Calculation results when σ c {\sigma }_{\text{c}} changes. (b) Calculation results when s s changes. (c) Calculation results when m changes. (d) Calculation results when n changes. (e) Calculation results when n ′ n^{\prime} changes. (f) Calculation results when k changes. (g) Calculation results when A changes.$

Figure 2

Multivariate calculation results. (a) Calculation results when σ c changes. (b) Calculation results when s changes. (c) Calculation results when m changes. (d) Calculation results when n changes. (e) Calculation results when n ′ changes. (f) Calculation results when k changes. (g) Calculation results when A changes.

Table 3

Calculation results when α changes

Value of α	Initial yield		Peak value		Residual stress (MPa)
Value of α	Stress (MPa)	Strain (%)	Stress (MPa)	Strain (%)	Residual stress (MPa)
0.40	285.54	0.1	302.37	8.4	302.15
0.45	285.74	0.1	309.73	8.2	309.29
0.50	321.31	2.3	340.25	7.7	338.59
0.55	—	—	444.92	10.0	444.92
0.60	—	—	444.92	10.0	444.92

The comparison of calculation results between the modified model and the traditional model is shown in Figure 1. From the figure, it is evident that the traditional Hoek–Brown model fails to account for the strain softening effect of the material, whereas the modified Hoek–Brown model proposed in this article can describe the mechanical behavior of materials, including initial elastic deformation, subsequent hardening, and eventual softening. This clearly aligns more closely with the actual mechanical properties of rock-like materials.

When the model parameters change, the modified model calculates the initial yield stress, peak stress, and residual stress, as shown in Figure 2. As depicted in Figure 2(a), the parameter σ c significantly influences both the initial yield stress and the corresponding strain. With increasing σ c , both the initial yield stress and strain increase, consistent with the pattern described by equation (3). When comparing the calculation results with varying parameter s, as shown in Figure 2(b), it is evident from the comparison between Figure 2(a) and (b) that the influence of parameter s is relatively small. When comparing the calculation results with varying parameter α , as shown in Table 3, it can be observed from the table that as the parameter α increases, the corresponding strain at initial yielding increases, along with the yielding stress, peak stress, and residual stress. This is because the parameter α corresponds to the exponent in the yielding function, equation (3). Clearly, as this parameter increases, the material becomes less prone to yielding, resulting in a rapid increase in stress and strain at yielding. In some cases, yielding may not occur at all as this parameter increases. When varying m, as shown in Figure 2(c), it is evident that its influence on strength follows a pattern similar to that of σ c 's influence on strength. As shown in Figure 2(d), the initial yield stress and the corresponding strain decrease with increasing n, and similarly the peak stress and its corresponding strain also decrease with increasing n. When n = 0.64, the peak stress exceeds the residual stress, indicating strain softening in the material. When n = 0.96, the peak stress is less than the residual stress, indicating strain hardening in the material. This demonstrates that parameter n significantly influences whether and to what degree strain softening occurs in the material. When varying the parameter n ′ , as depicted in Figure 2(e), it is evident from the comparison with Figure 2(d) and (e) that the influence of parameter n ′ is significantly reduced.

As shown in Figure 2(f), parameter k has no effect on the initial yield stress and its corresponding strain. When k = 16, the peak stress equals the residual stress, both of which are greater than the initial yield stress, indicating no strain softening in the material. When k = 20, the peak stress is slightly greater than the residual stress, with the residual stress still greater than the initial yield stress, indicating mild strain softening in the material. When k = 22, the peak stress exceeds the initial yield stress, and the initial yield stress exceeds the residual stress, indicating significant strain softening in the material. It is evident that the parameter k effectively controls the rate of strain softening. As shown in Figure 2(g), the parameter A has no effect on the initial yield stress and its corresponding strain. With increasing A, the softening effect becomes more pronounced, which is determined by the physical meaning of A. As shown in Table 1, A represents the proportion of plastic shear strain in the equivalent plastic strain causing material degradation or damage. The multivariate calculations adopt a model where volumetric strain is zero; hence, a larger A indicates faster material damage development, resulting in a more pronounced softening effect accordingly.

5 Engineering applications of the modified model

The Dianzhong Diversion Project, a pivotal water diversion initiative undertaken by the state, addresses the pressing water scarcity in the central region of Yunnan Province [30]. As shown in Figure 3, this monumental engineering endeavor encompasses a water receiving area spanning 3.69 × 10⁴ km², with an annual average diversion volume reaching 34.03 × 10⁹ m³. Within the tunnel which extends over a length of 102.74 km, particularly in the Dali city segment, the project encounters the challenges posed by red bed soft rocks. The construction of tunnels through these geological formations has been fraught with varying degrees of soft rock deformation, with the deformation near the exit section of the tunnel emerging as a particularly exemplary case. The project’s complexity is further amplified by the intricate topography and geological conditions. This study focuses on a segment of a tunnel exit in the Dianzhong Diversion Project, analyzing deformation characteristics of the tunnel and the surrounding rocks using the modified Hoek–Brown model, combined with field monitoring data. The findings provide valuable insights for the construction of subsequent soft rock tunnels.

Figure 3

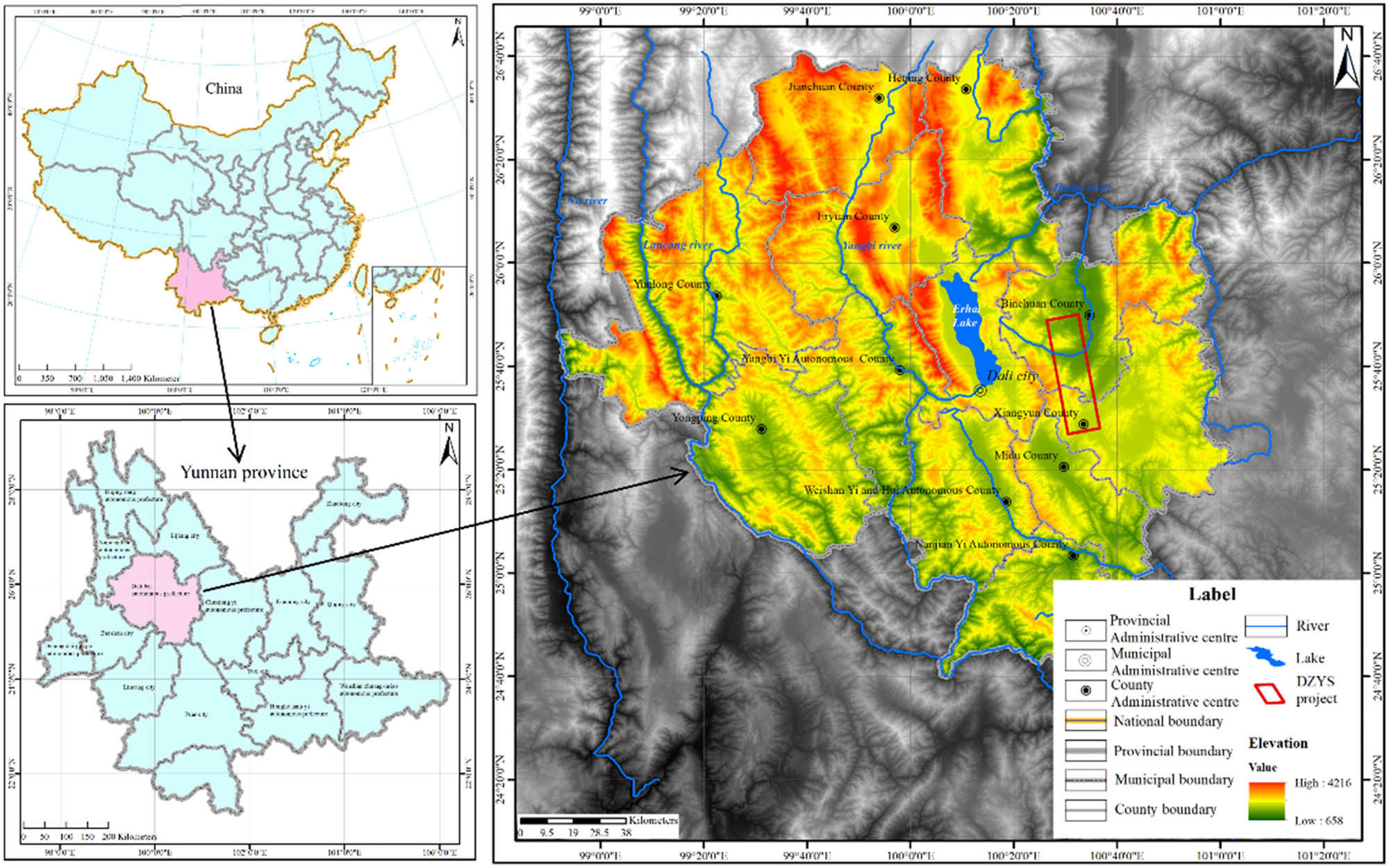
Location map of background engineering.

During tunnel excavation, stress redistributes in the surrounding rock mass. As stress conditions change, rock masses within a certain range around the tunnel may exceed their ultimate strength. Additionally, due to the weakening of rock strength on the tunnel’s inner side, its load-bearing capacity decreases. This results in increased loads on adjacent rock masses, causing deformation and plastic zones to expand outward until the rock masses within the load-bearing zone reach their ultimate stress state. Considering the softening effect of rock masses, the mechanical properties of the surrounding rock decrease, making it easier for the rock masses to reach their ultimate stress state, thereby further expanding the plastic zone outward from the tunnel and affecting the stability of the tunnel surrounding the rock mass.

The tunnel is located in a red soft rock region where significant surrounding rock deformations can occur. Considering that the tunnel depth is much greater than its diameter, and surface topography has minimal impact, the computational model adopts a quasi-three-dimensional approach. To minimize boundary effects, the model ensures that boundaries are more than five times the tunnel diameter away from the tunnel. The computational model, constructed using hexahedral elements, as shown in Figure 4(a), comprises over 60,000 elements. Initial support measures are designed for Class V surrounding rock conditions, with the specific support structure depicted in Figure 4(b).

Figure 4

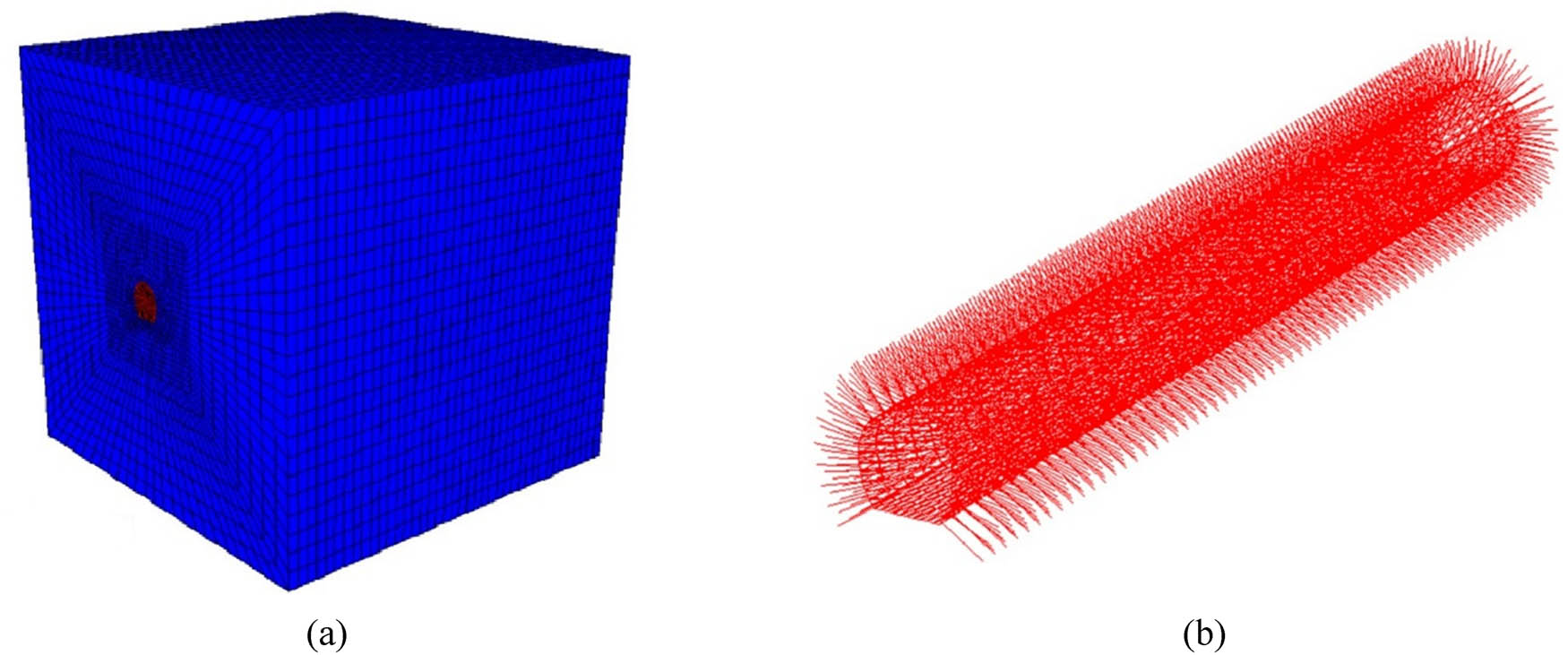
Computation model. (a) Tunnel and surrounding rock model. (b) Tunnel support model.

The total displacements and maximum principal stresses calculated using both the traditional Hoek–Brown model and the modified Hoek–Brown model proposed in this article are shown in Figure 5(a)–(d), and the comparison with field measurements is presented in Table 4. According to the calculations using the traditional Hoek–Brown model, which does not account for rock softening, the most significant displacements occur at the bottom of the tunnel, reaching up to 6.16 cm. When considering rock softening effects using the modified Hoek–Brown model, the maximum displacement calculated is 15.13 cm, still located at the tunnel bottom. Compared to the scenario without considering rock softening, this represents an increase of nearly 9 cm, a percentage increase of 146%. This clearly indicates a substantial difference in displacements between considering rock softening and not considering it. Furthermore, when using the traditional Hoek–Brown model, the maximum principal stress around the tunnel ranges from 0.98 to 21.63 MPa, whereas with the modified Hoek–Brown model considering rock softening effects, the maximum principal stress ranges from 1.14 to 18 MPa. This directly illustrates that considering rock softening reduces the range of principal stress distribution around the tunnel, thereby improving the stress conditions and promoting the stability of the surrounding rock mass.

Figure 5

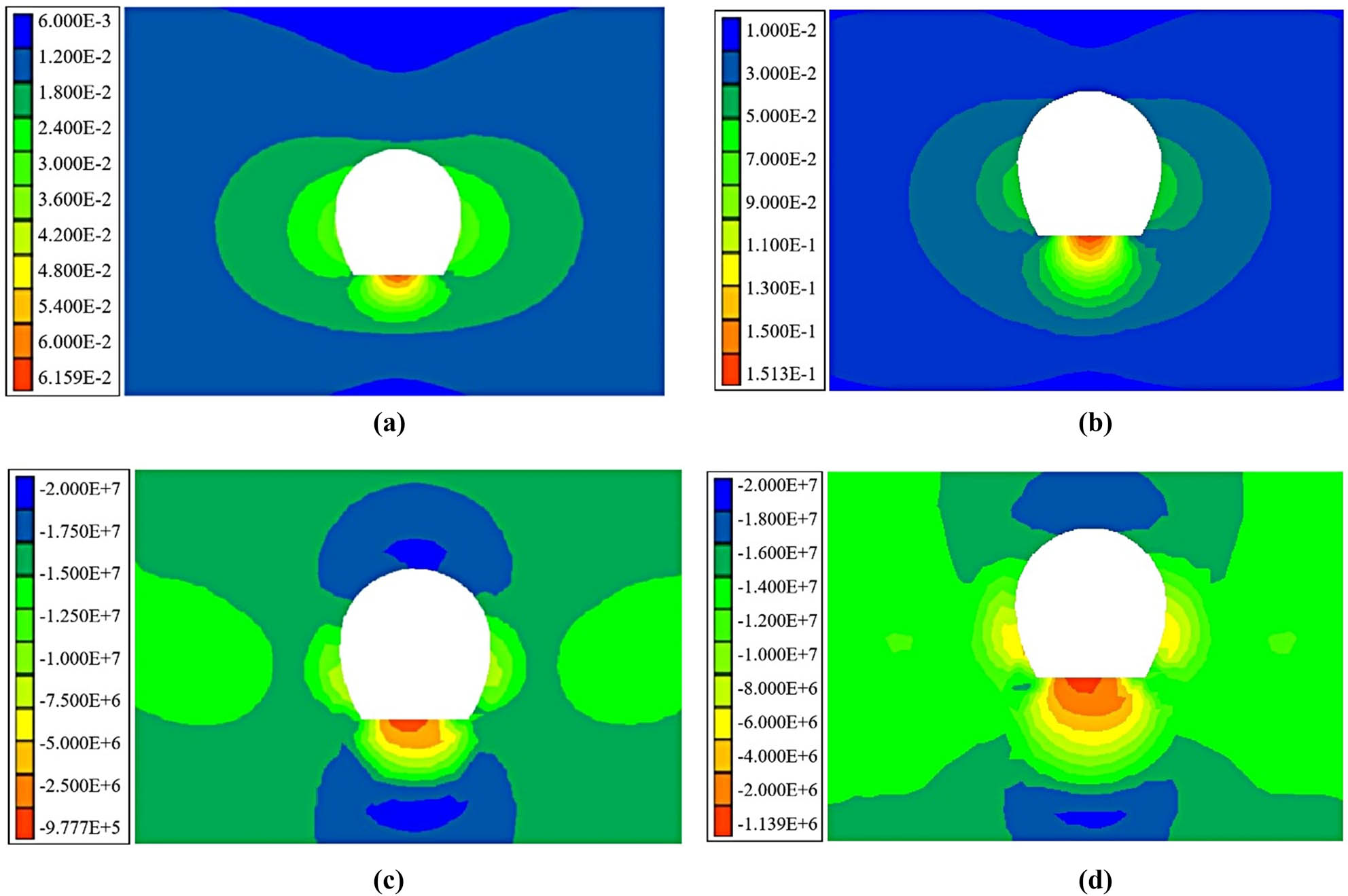
Comparison of results between the traditional Hoek–Brown model and the modified Hoek–Brown model. (a) Total displacement calculated by the traditional model (m). (b) Total displacement calculated by the modified model (m). (c) Maximum principal stress calculated by the traditional model (Pa). (d) Maximum principal stress calculated by the modified model (Pa).

Table 4

Comparison between calculation results and monitoring results

Position	Displacement at the bottom of the tunnel (mm)	Stress at the bottom of the tunnel (MPa)	Stress at the top of the tunnel (MPa)
Monitor value	138.47	1.28	14.32
Traditional model calculation values	61.6	0.98	21.63
Modified model calculation values	151.3	1.14	18.00

The displacements and stresses obtained from the traditional Hoek–Brown model, the modified Hoek–Brown model, and on-site monitoring results are compared in Table 4. As shown in the table, for soft rock tunnels, both the displacements around the tunnel perimeter and the stresses obtained from the modified Hoek–Brown model are much more consistent with engineering practice compared to those from the traditional Hoek–Brown model. This discrepancy primarily arises because the surrounding rock mass undergoes significant deformation in the case studies, triggering strain softening effects. The traditional Hoek–Brown model, which only considers strain hardening effects and neglects strain softening of the rock mass, therefore produces results that diverge significantly from reality.

6 Conclusions

In order to simultaneously consider strain hardening and softening effects, this study proposes a modified Hoek–Brown model based on the traditional Hoek–Brown model. The modified model addresses numerical singularity and convergence challenges encountered during its implementation and applies the modified model to engineering practice. The main conclusions are as follows:

The traditional Hoek Brown model can only consider strain hardening effects. Improving the traditional Hoek–Brown model by introducing internal variables is feasible, enabling the modified Hoek–Brown model to simultaneously account for strain hardening and strain softening effects of materials.
The function smoothing method proposed in this article effectively resolves numerical singularity and convergence issues in the implementation of the modified Hoek–Brown model. It is suggested that this method can be applied to similar cases where the yield function has corner points in the stress space in the future.
For soft rock tunnels, when significant displacements occur in the surrounding rock mass, both perimeter displacements and stresses predicted by the modified Hoek–Brown model are much closer to engineering reality compared to those predicted by the traditional Hoek–Brown model, which exhibits an error as high as 146%.

Acknowledgments

The Major Science and Technology Special Plan of Yunnan Province Science and Technology Department (Grant No. 202002AF080003) is greatly appreciated for providing financial support to this work. This work was completed on the basis of the open-source finite element software FreeFEM, and the work done by the developers is greatly appreciated.

Funding information: This work was financially supported by The Major Science and Technology Special Plan of Yunnan Province Science and Technology Department (Grant No. 202002AF080003).
Author contributions: LZ and SFL developed the research frameworks. LZ and ZHT proposed the modified model. YTX and YLF wrote the corresponding program for the modified model. JM and YY validated the effectiveness of the modified model. DYS and YT applied the modified model for practical engineering. LZ and BXW wrote the initial draft. ZHT and YTX revised the manuscript. The authors applied the SDC approach for the sequence of authors.
Conflict of interest: The authors state no conflict of interest.

References

[1] Geng D, Dai N, Guo P, Zhou S, Di H. Implicit numerical integration of highly nonlinear plasticity models. Comput Geotech. 2021;132:103961. 10.1016/j.compgeo.2020.103961.Search in Google Scholar

[2] Sun Z, Zhang D, Fang Q, Dui G, Chu Z. Analytical solutions for deep tunnels in strain-softening rocks modeled by different elastic strain definitions with the unified strength theory. Sci China Technol Sci. 2022;65(10):2503–19. 10.1007/s11431-022-2158-9.Search in Google Scholar

[3] Li J, Shen C, He X, Zheng X, Yuan J. Numerical solution for circular tunnel excavated in strain-softening rock masses considering damaged zone. Sci Rep. 2022;12(1):4465. 10.1038/s41598-022-08531-3.Search in Google Scholar PubMed PubMed Central

[4] Gao W, Hu C, He T, Chen X, Zhou C, Cui S. Study on constitutive model of fractured rock mass based on statistical strength theory. Rock Soil Mech. 2020;41(7):2179–88. 10.16285/j.rsm.2019.1673 (in Chinese).Search in Google Scholar

[5] Wang Z, Zhu Z, Zhu S. Thermo-mechanical-water migration coupled plastic constitutive model of rock subjected to freeze-thaw. Cold Reg Sci Technol. 2019;161:71–80. 10.1016/j.coldregions.2019.03.001.Search in Google Scholar

[6] Zhang H, Meng X, Liu X. Establishment of constitutive model and analysis of damage characteristics of frozen-thawed rock under load. Arab J Geosci. 2021;14:1–13. 10.1007/s12517-021-07598-y.Search in Google Scholar

[7] Yang P, Wu X, Chen J. Elastic and plastic-flow damage constitutive model of rock based on conventional triaxial compression test. Int J Heat Technol. 2018;36(3):627–35. 10.18280/ijht.360320.Search in Google Scholar

[8] Wei X, Zhao B, Ji C, Liu Z, Zhang Z. Elastoplastic augmented virtual internal bond modeling for rock: A fracture‐plasticity combined constitutive model. Int J Numer Anal Methods Geomech. 2023;47(8):1331–48. 10.1002/nag.3516.Search in Google Scholar

[9] Chen S, Qiao C. Composite damage constitutive model of jointed rock mass considering crack propagation length and joint friction effect. Arab J Geosci. 2018;11:1–11. 10.1007/s12517-018-3643-y.Search in Google Scholar

[10] Li T, Lyu L, Zhang S, Sun J. Development and application of a statistical constitutive model of damaged rock affected by the load-bearing capacity of damaged elements. J Zhejiang Univ-Sci A (Appl Phys Eng). 2015;8:644–55. 10.1631/jzus.A1500034.Search in Google Scholar

[11] Xie S, Lin H, Wang Y, Cao R, Yong R, Du S, et al. Nonlinear shear constitutive model for peak shear-type joints based on improved Harris damage function. Arch Civ Mech Eng. 2020;20:1–14. 10.1007/s43452-020-00097-z.Search in Google Scholar

[12] Xin J, Jiang Q, Liu Q, Zheng H, Li S. A shear constitutive model and experimental demonstration considering dual void portion and solid skeleton portion of rock. Eng Fract Mech. 2023;281:109066. 10.1016/j.engfracmech.2023.109066.Search in Google Scholar

[13] Xie S, Han Z, Hu H, Lin H. Application of a novel constitutive model to evaluate the shear deformation of discontinuity. Eng Geol. 2022;304:106693. 10.1016/j.enggeo.2022.106693.Search in Google Scholar

[14] Xie S, Lin H, Chen Y. New constitutive model based on disturbed state concept for shear deformation of rock joints. Arch Civ Mech Eng. 2022;23(1):26. 10.1007/s43452-022-00560-z.Search in Google Scholar

[15] Chen Y, Lin H, Wang Y, Xie S, Zhao Y, Yong W. Statistical damage constitutive model based on the Hoek–Brown criterion. Arch Civ Mech Eng. 2021;21:1–9. 10.1007/s43452-021-00270-y.Search in Google Scholar

[16] Bian K, Liu J, Zhang W, Zheng X, Ni S, Liu Z. Mechanical behavior and damage constitutive model of rock subjected to water-weakening effect and uniaxial loading. Rock Mech Rock Eng. 2019;52:97–106. 10.1007/s00603-018-1580-4.Search in Google Scholar

[17] Wen Z, Tian L, Jiang Y, Zuo Y, Meng F, Dong Y, et al. Research on damage constitutive model of inhomogeneous rocks based on strain energy density. Chin J Rock Mech Eng. 2019;7:1332–43. 10.13722/j.cnki.jrme.2018.1125 (in Chinese).Search in Google Scholar

[18] Qu D, Li D, Li X, Yi L, Xu K. Damage evolution mechanism and constitutive model of freeze-thaw yellow sandstone in acidic environment. Cold Reg Sci Technol. 2018;155:174–83. 10.1016/j.coldregions.2018.07.012.Search in Google Scholar

[19] Fang W, Jiang N, Luo X. Establishment of damage statistical constitutive model of loaded rock and method for determining its parameters under freeze-thaw condition. Cold Reg Sci Technol. 2019;160:31–8. 10.1016/j.coldregions.2019.01.004.Search in Google Scholar

[20] Jiang H, Liu D, Zhao B, Li D. Nonlinear creep constitutive model of rock under high confining pressure and high water pressure. J Min Saf Eng. 2014;31(2):284–91 (in Chinese).Search in Google Scholar

[21] Lin H, Liang L, Chen Y, Cao R. A damage constitutive model of rock subjected to freeze-thaw cycles based on lognormal distribution. Adv Civ Eng. 2021;2021:1–8. 10.1155/2021/6658915.Search in Google Scholar

[22] Ma Q, Liu Z, Qin Y, Tian J, Wang J. Rock plastic-damage constitutive model based on energy dissipation. Rock Soil Mech. 2021;42(05):1210–20. 10.16285/j.rsm.2020.1091 (in Chinese).Search in Google Scholar

[23] Meng X, Zhang H, Liu X. Rock damage constitutive model based on the modified logistic equation under freeze–thaw and load conditions. J Cold Reg Eng. 2021;35(4):04021016. 10.1061/(ASCE)CR.1943-5495.0000268.Search in Google Scholar

[24] Leng D, Shi W, Liang F, Li H, Yan L. Stability and deformation evolution analysis of karstified slope subjected to underground mining based on Hoek–Brown failure criterion. Bull Eng Geol Environ. 2023;82(5):174. 10.1007/s10064-023-03211-6.Search in Google Scholar

[25] Wang J, Wu S, Cheng H, Sun J, Wang X, Shen Y. A generalized nonlinear three-dimensional Hoek-Brown failure criterion. J Rock Mech Geotech Eng. 2024;16(8):3149–64. 10.1016/j.jrmge.2023.10.022.Search in Google Scholar

[26] He L, Zhao Y, Yin L, Zhong D, Xiong H, Chen S, et al. Research on a non-synchronous coordinated reduction method for slopes based on the Hoek–Brown criterion and acoustic testing technology. Sustainability. 2023;15(21):15516. 10.3390/su152115516.Search in Google Scholar

[27] Liu J, Jiang Q, Dias D, Tao C. Probability quantification of GSI and D in Hoek–Brown criterion using Bayesian inversion and ultrasonic test in rock mass. Rock Mech Rock Eng. 2023;56(10):7701–19. 10.1016/j.jrmge.2023.06.004.Search in Google Scholar

[28] Cai W, Su C, Zhu H, Liang W, Ma Y, Xu J, et al. Elastic–plastic response of a deep tunnel excavated in 3D Hoek–Brown rock mass considering different approaches for obtaining the out-of-plane stress. Int J Rock Mech Min Sci. 2023;169:105425. 10.1016/j.ijrmms.2023.105425.Search in Google Scholar

[29] Zhong J, Hou C, Yang X. Three-dimensional face stability analysis of rock tunnels excavated in Hoek-Brown media with a novel multi-cone mechanism. Comput Geotech. 2023;154:105158. 10.1016/j.compgeo.2022.105158.Search in Google Scholar

[30] Yuan F, Bao C, Wang M, Su W, Zhou J. Study on large deformation characteristics and control measures of red-bed soft rock tunnel. Chin J Undergr Space Eng. 2022;18(S1):332–40 + 349 (in Chinese).Search in Google Scholar

Received: 2024-07-23

Revised: 2024-11-25

Accepted: 2024-12-18

Published Online: 2025-05-23

This work is licensed under the Creative Commons Attribution 4.0 International License.

Articles in the same Issue

https://doi.org/10.1515/geo-2025-0787

Keywords for this article

softening effects; Hoek–Brown model; numerical implementation; engineering applications

Creative Commons

BY 4.0