Abstract
China has one of the highest rates of natural disasters in the world. In recent years, the Chinese government has placed a high value on improving emergency natural disaster relief. The goal of this research was to resolve a key issue for emergency natural disaster relief: the emergency vehicle routing problem (EmVRP) with relief materials in sudden disasters. First, we provided a description of the EmVRP, and defined the boundary conditions. On this basis, we constructed an optimization model of EmVRP with relief materials in sudden disasters. To reach the best solution in the least amount of time, we proposed an enhanced monarch butterfly optimization (EMBO) algorithm, incorporating two modifications to the basic MBO: a self-adaptive strategy and a crossover operator. Finally, the EMBO algorithm was used to solve the EmVRP. Our experiments using two examples EmVRP with relief materials in a sudden-onset disaster proved the suitability of EMBO. In addition, an array of comparative studies showed that the proposed EMBO algorithm can achieve satisfactory solutions in less time than the basic MBO algorithm and seven other intelligent algorithms.
1 Introduction
When natural disasters occur, an efficient logistics system is vital for emergency relief work. Although rapid advances in science and technology have improved our ability to predict some natural disasters with increasing certainty, sudden natural disasters are still a major threat to the survival of regional populations and to the maintenance of social and economic development. Even when a disaster can be predicted in advance, obstacles such as short warning times and long transport distances make it difficult to protect threatened populations in the interval between the forecast and the event. Therefore, an efficient emergency natural disaster relief logistics system is key to providing rescue and post-disaster relief for many people.
Studies of emergent natural disaster relief logistics systems have concentrated primarily on two areas of concern [75]. First, researchers have explored methods for evaluating the degree of impact of a natural disaster. The evaluation results determine the level of demand for emergency relief, and the logistics of distribution. Second, studies have examined the topologies of emergency logistics distribution networks, including the emergency vehicle routing problem (EmVRP). This paper focuses on finding the most efficient way to assign vehicles to bring relief materials and goods to disaster sites from various storage areas such as depots, railway stations, airports, and docks.
One of the most representative studies on emergency logistics was the LP (linear programming) model proposed by Rathi et al. [41]. In that study, the authors assigned each vehicle to each route to obtain the optimal network. A traditional optimization algorithm was adopted in this model, but the process fell easily into the local optimum. Equi et al. [8] studied the optimal number of trips and the number of vehicles needed to complete each travel route in the context of a given number of supply centers. While it may be feasible to target those receiving relief after a natural disaster, it is difficult to differentiate the amount of relief provided among beneficiaries. This is because much of the relief consists of food, clothing, and medicine, all goods for which the absorptive capacity of households is limited. Empirical tests using data from Honduras following Hurricane Mitch confirm this hypothesis. The probability of receiving relief was negatively correlated with wealth and positively correlated with assets losses (with a higher weight placed on losses than pre-disaster wealth) and the fact that households suffered damage to their dwelling. By contrast, controlling for whether households suffered damage to their dwelling, the amount of relief received was related neither to pre-Mitch wealth, nor to assets losses [36].
Current studies of the EmVRP have provided greater depth by considering changes of various factors in the models, and by using more advanced algorithms. However, studies that consider a combination of the EmVRP and the logistics of emergency materials distribution are still relatively scarce. Moreover, the models that have been produced to date for the mechanisms and optimization of emergency distribution have not been able to meet real-world demands in terms of objective function and boundary conditions [75].
In contrast, the monarch butterfly optimization (MBO) algorithm proposed by Wang et al. in 2015 [55] is a novel and promising swarm-based intelligent method [48]. Although the MBO algorithm was proposed only two years prior to the writing of this paper, some researchers have implemented several in-depth studies from algorithm improvements and engineering application [12, 13, 14].
In fact, the EmVRP with relief materials in sudden disasters is an NP-hard problem [75] that is difficult to solve using traditional methods. In this paper, we proposed an enhanced monarch butterfly optimization (EMBO) algorithm to tackle the EmVRP problem. In the EMBO algorithm, the crossover operator used in evolutionary algorithms (EAs) is incorporated into the basic MBO algorithm to generate a new offspring population for the next generation. In addition, the self-adaptive scheme is used to establish the butterfly adjusting rate. We used the proposed EMBO algorithm to solve the EmVRP with relief materials in sudden disasters, and we provided comparative studies between the basic MBO algorithm and seven other intelligent algorithms to demonstrate the superiority of EMBO in terms of accuracy.
The remainder of this paper is structured as follows. The next section reviews the related preliminaries, including the EmVRP and MBO algorithm. Section 3 provides the description of the EmVRP with relief materials in sudden disasters, followed by the main framework of MBO and the proposed EMBO algorithm, as shown in Section 4. Subsequently, Section 5 details how to use EMBO to solve the EmVRP with relief materials in sudden disasters. Then, in Section 6, an array of experiments on EmVRP are carried out. The final section summarizes our current work, and provides our future work orientation.
2 Preliminaries
2.1 EmVRP
In the Introduction above, we described briefly some of the prior work focused on EmVRP. In this section, we review examples of other significant contributions to the field.
Hale and Mober [23] studied the selection of emergency logistics supply nodes, with particular attention to the number of nodes (sites) for storage of emergency supplies. Their research proposed a quantitative model. For vehicle routing within a time window (VRPTW) involving a limited number of vehicles, Lau et al. [30] constructed a model and put forward the related solutions. In addition, they implemented a substantial number of fundamental studies on the variants of the traditional VRP problem.
Based on the features of multi-resource and multipoint rescue, Dai et al. [6] constructed a mathematical model to solve the multi-resource emergency problem. Fu et al. [15] divided emergency logistics distribution issues into three categories: road conditions, vehicle conditions, and the state of materials. They proposed a static, dynamic, and functional model in accordance with each emergency issue category. To address actual challenges of VRP with time windows, Li [32] put forward a method based on affinity group match, and further proved that the immune algorithm can provide an effective solution for routing vehicle within a time frame.
Özdamar et al. [38] studied distribution decision support systems after natural disasters. A model was established by considering disaster relief materials comprehensively, regarding vehicles as both relief materials and transportation resources. In addition, Ghiani [21], Ikou [24], and Özyurt [39] proposed several different algorithms to solve the EmVRP problem.
Though many scholars have carried out several in-depth studies regarding emergency relief, few of them has used swarm intelligence algorithm to solve emergency vehicle routing problem with relief materials in sudden disasters. In this paper, one of the most representative swarm intelligence algorithms, called monarch butterfly optimization (MBO), is introduced to solve emergency vehicle routing problem with relief materials in sudden disasters. Next, the mainframe of MBO algorithm will be provided.
2.2 MBO algorithm
Since MBO [55] was proposed, many scholars have explored this approach. In this section, some of the most representative work regarding MBO is summarized and reviewed.
Yi et al. [70] combined quantum computation theory into MBO algorithm, and proposed a novel quantum-inspired MBO methodology, called QMBO, by incorporating quantum computation into the basic MBO algorithm. In QMBO, a certain number of the worst butterflies were updated by quantum operators. The path planning navigation problem for Unmanned Combat Air Vehicles (UCAVs) was modeled into an optimization problem, and then its optimal path could be obtained by the proposed QMBO algorithm. Furthermore, B-Spline curves were utilized to refine the obtained path, making it more suitable for UCAVs. The UCAV path obtained by QMBO was studied and analyzed in comparison with the basic MBO. The experimental results showed that QMBO can find a much shorter path than MBO.
Ghetas et al. [20] incorporated the harmony search (HS) algorithm into the basic MBO algorithm, and proposed a variant of MBO, called MBHS, to deal with the standard benchmark problems. In MBHS, the HS algorithm was considered as a mutation operator to improve the butterfly adjusting operator, with the aim of accelerating the convergence rate of MBO.
Feng et al. [10] presented a novel binary MBO (BMBO) method used to address the 0-1 knapsack problem (0-1 KP). In BMBO, each butterfly individual was represented as a two-tuple string. Several individual allocation techniques were used to improve BMBO’s performance. In order to keep the number of infeasible solutions to a minimum, a novel repair operator was applied. The comparative study of BMBO with other optimization techniques showed the superiority of the former in solving the 0-1 KP.
Wang et al. [62] put forward another variant of the MBO method in combination with GCMBO. In GCMBO, two modification strategies, including a self-adaptive crossover (SAC) operator and a greedy strategy, were utilized to improve its search ability.
Feng et al. [14] combined chaos theory [50] with the basic MBO algorithm, and then proposed a novel chaotic MBO (CMBO) algorithm. The proposed CMBO algorithm enhanced the search effectiveness significantly. In CMBO, in order to tune two main operators, the best chaotic map was selected from 12 maps. Meanwhile, some of the worst individuals were improved by using a Gaussian mutation operator to avoid premature convergence.
Ghanem and Jantan [19] combined ABC with elements from MBO to proposed a new hybrid metaheuristic algorithm named Hybrid ABC/MBO (HAM). The combined method used an updated butterfly adjusting operator, considered to be a mutation operator, with the aim of sharing the information with the employee bees in ABC.
Wang et al. [59] proposed a discrete version of MBO (DMBO) that was applied successfully to tackle the Chinese TSP (CTSP). They also studied and analyzed the parameter butterfly adjusting rate (BAR). The chosen BAR was used to find the best solution for the CTSP.
Feng et al. [12] proposed a type of multi-strategy MBO (MMBO) technique for the discounted 0-1 knapsack problem (DKP). In MMBO, two modifications, including neighborhood mutation and Gaussian perturbation, were utilized to retain the diversity of the population. An array of experimental results showed that the neighborhood mutation and Gaussian perturbation were quite capable of providing significant improvement in the exploration and exploitation of the MMBO approach, respectively. Accordingly, two kinds of NMBO were proposed: NCMBO and GMMBO, respectively.
Feng et al. [13] combined MBO with seven kinds of DE mutation strategies, using the intrinsic mechanism of the search process of MBO and the character of the differential mutation operator. They presented a novel DEMBO based on MBO and an improved DE mutation strategy. In this work, the migration operator was replaced by a differential mutation operator with the aim of improving its global optimization ability. The overall performance of DEMBO was fully assessed using thirty typical discounted 0-1 knapsack problem instances. The experimental results demonstrated that DEMBO could enhance the search ability while not increasing the time complexity. Meanwhile, the approximation ratio of all the 0-1 KP instances obtained by DEMBO was close to 1.0.
Wang et al. [49] proposed a new population initialization strategy in order to improve MBO’s performance. Firstly, the whole search space is equally divided into N P (population size) parts at each dimension. Subsequently, two random distributions (T and F distribution) are used to mutate the equally divided population. Accordingly, five variants of MBOs are proposed with a new initialization strategy.
Feng et al. [11] presented OMBO, a generalized opposition-based learning (OBL) [56] MBO with Gaussian perturbation. The authors used the OBL strategy on the portion of the individuals in the late stage of evolution, and used Gaussian perturbation on the individuals with poor fitness in each evolution. OBL guaranteed the higher convergence speed of OMBO, and Gaussian perturbation avoided the possibility of falling into a local optimum. For the sake of testing and verifying the effectiveness of OMBO, three categories of 15 large-scale 0-1 KP cases from 800 to 2,000 dimensions were used. The experimental results indicated that OMBO could find high-quality solutions.
Chen et al. [4] proposed a new variant of MBO by introducing a greedy strategy to solve dynamic vehicle routing problems (DVRPs). In contrast to the basic MBO algorithm, the proposed algorithm accepted only butterfly individuals that had better fitness than before implementation of the migration and butterfly adjusting operator. Also, a later perturbation procedure was introduced to make a trade-off between global and local search.
Meng et al. [34] proposed an improved MBO (IMBO) for the sake of enhancing the optimization ability of MBO. In IMBO, the authors divided the two subpopulations in a dynamic and random fashion at each generation, instead of using the fixed strategy applied in the original MBO approach. Also, the butterfly individuals were updated in two different ways for the sake of maintaining the diversity of the population.
Faris et al. [9] modified the position updating strategy used in the basic MBO algorithm by utilizing both the previous solutions and the butterfly individuals with the best fitness at the time. For the sake of fully exploring the search behavior of the Improved MBO (IMBO), it was benchmarked by 23 functions. Furthermore, the IMBO was applied to train neural networks. The IMBO-based trainer was verified on 15 machine learning datasets from the UCI repository. The experimental results showed that the IMBO algorithm could enhance the learning ability of neural networks significantly.
Ehteram et al. [7] used the MBO algorithm to address the utilization of a multi-reservoir system for the sake of improving production of hydroelectric energy. They studied three periods of dry (1963-64), wet (1951-52), and normal (1985-86) conditions in a 4-reservoir system. The experiments indicated that MBO can generate more energy when compared with particle swarm optimization (PSO) and a genetic algorithm (GA).
Xue et al. [67] added a self-adaptive strategy to the basic ABC algorithm in accordance with the global optimal solution, so a new variant of ABC named SABC-GB was proposed. SABC-GB has shown its superiority to other meta-heuristic algorithms when dealing the complicated optimization problems.
In addition to the MBO algorithm studied in this paper, many other intelligent algorithms [65] have been proposed, such as elephant herding optimization (EHO) [33, 57], simulated annealing (SA) [27], evolutionary strategy (ES) [2], particle swarm optimization (PSO) [26, 44], moth search (MS) algorithm [47], bat algorithm (BA) [35, 68], differential evolution (DE) [43, 53], biogeography-based optimization (BBO) [42, 52], krill herd (KH) [16, 51, 54], cuckoo search (CS) [5, 69], artificial bee colony (ABC) [25, 64], genetic algorithm (GA) [22], fireworks algorithm (FWA) [46], earthworm optimization algorithm (EWA) [61], and harmony search (HS) [18, 63]. These algorithms are used widely in various engineering applications [73, 74].
In this paper, the model of emergency vehicle routing problem with relief materials in sudden disasters is provided. Also, we will further improve the performance of the basic MBO algorithm by introducing the self-adaptive strategy and crossover operator to form a novel enhanced MBO (EMBO) algorithm. The proposed EMBO algorithm is then used to tackle EmVRP problem in comparison with the basic MBO algorithm and seven other intelligent algorithms.
3 EmVRP with relief materials in sudden disasters
3.1 Problem description
If the scale of a sudden natural disaster is large, the distribution of emergency materials may require a variety of transport modes as well as the conversion of various transportation modes. In our current work, we focused on one mode of transportation only, assuming that relief supplies brought by rail, air, and water had already arrived at train stations, airports, and docks in the general disaster area. Therefore, those terminals (depots, railway stations, airports, and docks) were also seen as material storage facilities. Our goal was to determine how to assign vehicles from parking areas (such as garages) to transport relief materials and goods from the various storage sites (depots, railway stations, airports, and docks) to the primary disaster points. An overview of the whole system involved in the emergency VRP with materials in sudden disasters is shown in Fig. 1 [75].
As shown in Fig. 1, the emergency relief material distribution system is a three-layer structure. Transporting the materials is essentially a vehicle routing problem involving movement from multiple parking areas (garages) to multiple storage sites, and then to multiple disaster points. Layer 1 includes the parking areas; all the vehicles assigned to carrying relief materials start from the parking lots. The number of vehicle types may vary, but the number is known.
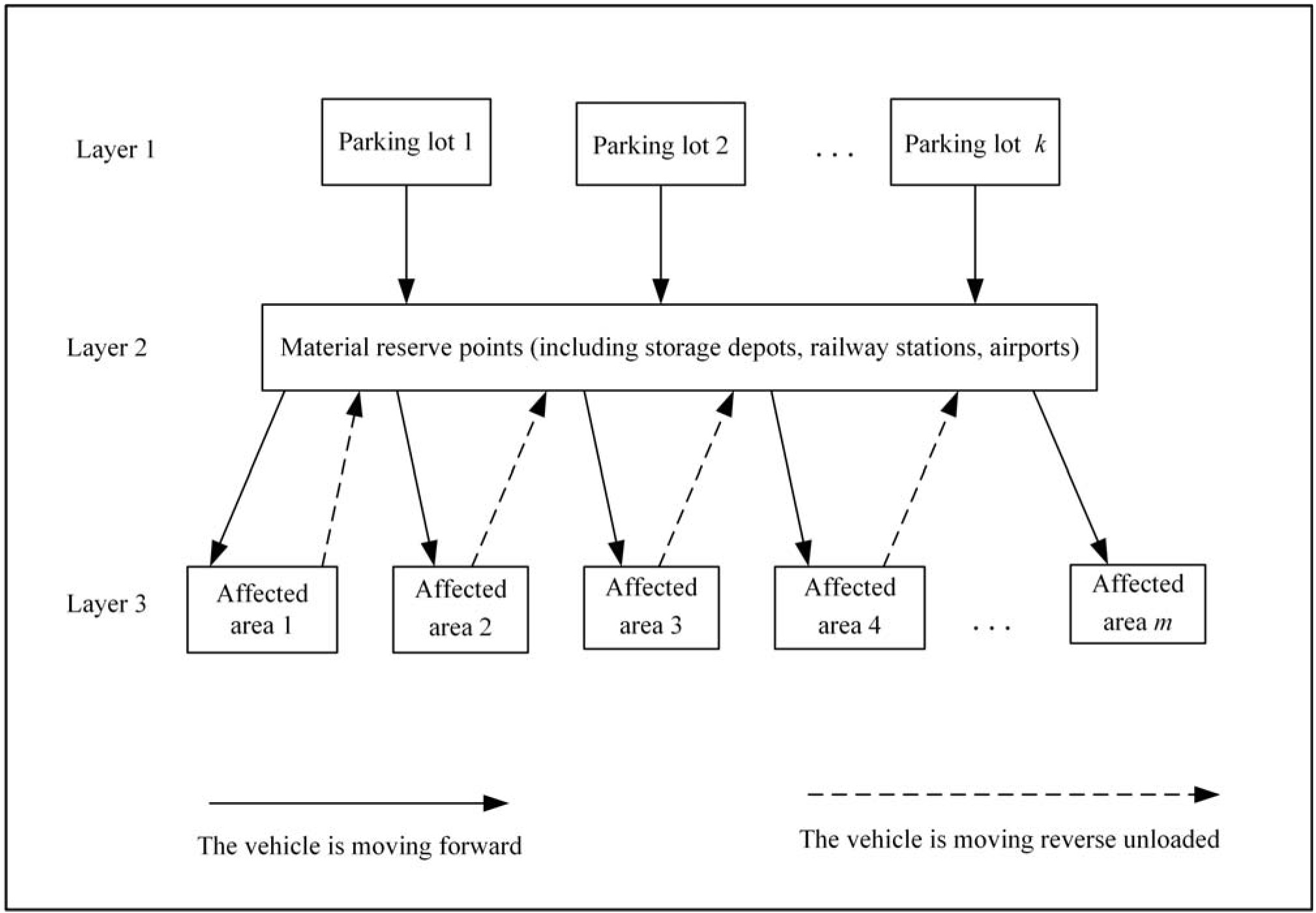
The structure of three hierarchy of vehicle scheduling for emergency relief goods.
Layer 2 is made up of the material reserve storage sites, including all wharfs, train stations, airports, and similar facilities. We assume that the relief supplies at each reserve point are varied, and that the number of certain types of materials is unchanged during the emergency period. The bottom layer, Layer 3, comprises the affected areas that are the destinations for relief distribution. After a disaster, demand for all kinds of emergency supplies will be generated at all the impact points according to the disaster assessment. This demand will determine the need to move reserves at all levels and locations, which in turn will call for a certain number of vehicles to begin distribution of aid materials.
From Layer 1 to Layer 2, there is vehicle flow only, with no material flow, i.e., the vehicles run from Layer 1 to Layer 2, but they are not loaded. Moreover, this flow is one-way, with the vehicles moving only from the parking areas to the various material reserve sites. They do not return to the parking areas during the emergency period. However, both vehicle flow and material flow occur between Layer 2 and Layer 3. Materials move in a one-way unidirectional flow from Layer 2 to Layer 3, while the vehicles form a two-way flow between these two layers. After a vehicle arrives at a disaster point, it does not immediately return to the parking areas, but instead remains in the arrival spot on standby. Once a new distribution task is ordered, the vehicle will go back to the appropriate material storage site to be loaded and start a new distribution.
Therefore, after a vehicle arrives at an affected area from a reserve area, there are two possible states for the vehicle. Either it remains in the impacted area waiting for new orders, or it may be given a new task immediately, in which case it returns right way to the reserve to begin the next round of distribution, as shown by the dotted line in Fig. 1. In our current work, we assumed that the vehicle is running along the unloaded reverse flow. In this process, the flow of vehicles is significantly different from that of common commercial logistics.
Both materials and vehicles flow between Layers 2 and 3. However, there is no connection between each point of the same layer because the demand for supplies after a sudden disasters is much greater than the normal customer demand for small batches commonly encountered in business logistics. This difference also is reflected by the characteristics of the emergency relief supplies demanded by the affected points. The primary goal of post-disaster distribution is to meet the needs of all the disaster sites as much as possible while shortening the running time of the entire distribution system. In this way, losses are reduced at each disaster point, and the cost of vehicle operations is reduced as well.Vehicles can be reused throughout the distribution system, i.e., the vehicle flow is repeated between the second and the third layers until all the needs of the disaster sites are met.
3.2 Definition and explanation of boundary conditions of model
Under the guidance of the distribution system model of the EmVRP with relief materials in sudden disasters, the boundary conditions of the vehicle distribution system are defined as follows:
There are multiple supply points and demand points in the network. The supply and demand of emergency materials are known at each point, and the total supply can meet the needs of the affected areas.
There are many parking areas, and each parking area may have a variety of vehicles. The number of parked vehicles is sufficient to meet the need for materials distribution, and each vehicle has a number.
There are a variety of emergency supplies to be delivered. Each is different in weight and volume, and each has different loading efficiency. It is assumed that the loading efficiency of the material at the supply site is the same as the unloading efficiency at the disaster site.
Each disaster site can be served by multiple vehicles.
Each delivery task carries only one kind of material.
After the completion of a distribution task, if the vehicle still has supplies, then it will continue to complete the delivery task; otherwise, it will return to the starting point at the parking area to wait for the next dispatch.
There is neither vehicle flow nor material flow between the points of each layer.
3.3 The model of the EmVRP with relief materials in sudden disasters
The model of the emergency VRP with relief materials in sudden disasters consists mainly of four parts: the symbol definition, objective function, constraint condition, and the model description.
(1) Symbol definition
The model of the EmVRP with relief materials in sudden disasters includes the definition of five kinds of symbols: set, parameters related to transportation, parameters related to relief materials, parameters related to distance, and decision variables.
1) Set
The set of materials/goods:
The set of supply sites (i.e., relief materials reserve sites/points, material storage sites/ points):
The set of disaster sites (affected areas/points):
The set of parking areas (garages, parking lots):
The set of vehicles:
The set of edges:
2) Parameters related to transportation
Vl: the maximum volume of the vehicle l;
capl: the maximum dead weight tonnage of the vehicle l;
vl: the speed of the vehicle l.
3) Parameters related to relief materials
wg: the unit weight of material type g;
cg: the unit volume of material type g;
tg: the time needed for loading and unloading material g.
4) Parameters related to distance
d ki: the distance from the parking area to the material supply site;
dij: the distance between the supply site and the demand point.
5) Decision variables
xlijg: the quantity of material g that is conveyed from the supply site i to j by vehicle l;
(2) Objective function
(3) Constraint condition
(4) Model description
For the model of the EmVRP with relief materials in sudden disasters, the goal is to meet the needs of the affected points in the shortest total running time possible. The total running time of a vehicle includes the travel time from the parking areas to material reserve sites, travel time from material reserve areas to the affected areas, loading time at reserve sites, and unloading time at the affected areas.
For the objective function in the model of the EmVRP with relief materials in sudden disasters, Eq. 1 represents the time from the parking area to the reserve site; Eq. 2 represents the loading time at the reserve site; Eq. 3 represents the time from the material reserve site to the affected site; and Eq. 4 represents the unloading time of the material at the affected area. In our current work, we suppose the vehicles will take the same time moving from the affected point to reserve point.
For the constraint conditions, Eq. 5 means that the goods transported by each vehicle cannot exceed the maximum load capacity of the vehicle; Eq. 6 means that the goods delivered by each vehicle should not exceed the maximum volume of the vehicle; Eq. 7 means that each vehicle carries only one material at a time from the material reserve site to the affected area; Eq. 8 means that the vehicles starting from the garage can only reach a material reserve site, which is a one-way non-circular flow between the first and second layers; and Eqs. 9-10 indicate that the variables of this problem satisfy the 0-1 integer constraint. Eq. 11 represents the range of the indexes in constraints. |·| represents the number of elements contained in a set.
To solve the problem of the model constructed in this paper, it is necessary to construct a heuristic algorithm with simple operation and excellent search performance. At present, the heuristic algorithms used to solve the vehicle scheduling problem include primarily the genetic algorithm (GA), neural network method, ant colony algorithm (ACO), tabu search (TS), and simulated annealing algorithm (SA). Among them, the most popular strategies involve the application of modern intelligent algorithms to vehicle scheduling. Many scholars have proven that the performance achieved using intelligent algorithms is better than the results from other traditional optimization algorithms. Therefore, this paper employed a new intelligent algorithm, monarch butterfly optimization (MBO), to solve the above-established EmVRP model. The required solutions can be represented by a butterfly individual, while a butterfly individual can be represented by different parking areas, reserve sites, and the affected areas.
3.4 Difference between emergency VRP and regular VRP
Emergency VRP is a special vehicle routing activity caused by outbreak of emergencies. Due to its suddenness and lack of information, it is quite different from that of regular VRP (RVRP) [29].
The goal of RVRP is to minimize costs or maximize profits [75]. The distribution network is permanent, and its network structure is designed by the needs of the customer [75]. Participants are mainly all kinds of economic entities closely related to each other, such as manufacturers, distributors and transport companies [75]. The driving force of logistics is demand, and facilities planning, fleet size and vehicle routing need to be planned in the long, medium and short term, respectively [75]. The quantity and variety of materials are limited, the means of transportation are used for a long time, and the information in the external environment is full and not easy to change [75].
The goal of emergency VRP is to meet the requirements of minimizing the delay time (primary goal) and minimizing the cost (secondary goal) [75]. The distribution network of logistics facilities is temporary, the network structure is simple and the functions are simplified [75]. The main participants are not closely linked to the interests of institutions or organizations, such as government departments, non-governmental organizations, donors and institutions that are temporarily established [75]. The driving force of logistics is divided into two kinds, the reflection stage is system propelling, and the recovery stage is demand promotion [75]. Usually, resource reserve planning is made [75]. In wartime or emergency, material transportation and vehicle scheduling plan are urgent, making the best possible decisions under shorter term and limited information, and the plan scheme will often change greatly in the implementation process [75]. There are the quantity and variety of material stock, the means of transportation are temporarily collected, the information in the external environment is inadequate and easy to change [75].
4 Enhanced MBO algorithm
In this part of our research, we proposed a new variant of the basic MBO approach, called the enhanced MBO (EMBO), that includes a crossover operator and self-adaptive strategy. First, we will describe the main framework of the original MBO approach, and then we will give a full description of the proposed EMBO approach.
Here, t is the current generation. rand is a random number. NP is the number of butterflies in the population, and p is the ratio of butterflies in Subpopulation 1. BAR is the butterfly adjusting rate. Cr is the crossover rate.
4.1 MBO algorithm
4.1.1 Migration operator
The number of butterflies located at Land 1 and Land 2 can be calculated as ceil(p * NP) (NP1, Subpopulation 1) and NP−NP1 (NP2, Subpopulation 2), respectively. We can use SP1 and SP2 to denote Subpopulation 1 and Subpopulation 2, respectively. Here, ceil(x) rounds x to the nearest integer not less than x. Therefore, when r ≤ p, then
where
where peri is the migration period [55]. In comparison, when r > p, then
where
4.1.2 Butterfly adjusting operator
For butterfly j, if rand is not more than p, the kth element k can be given as [55]
where
where
In this case, when rand is bigger than BAR, it can be calculated in another form [55]:
where dx is the walk step of butterfly j.
According to the above description, the structure of MBO can be provided in Algorithm 1.
4.2 EMBO algorithm
MBO has been shown to have its own advantages over other intelligent algorithms for benchmarking and other application engineering problems [55]. However, as mentioned before, sometimes MBO may be stuck at local optima on certain problems [55]. In this paper, a self-adaptive strategy and crossover operators were combined with the basic MBO approach for the sake of enhancing the searchability of MBO. This enhanced MBO (EMBO) algorithm will be described in detail later in this paper.
Initialization. Set the generation counter t = 1, and set the maximum generation tmax, NP1, NP2, BAR, peri, and p;
Population evaluation. Calculate the fitness according to the objective function;

Monarch Butterfly Optimization
4.2.1 Self-adaptive butterfly adjusting operator
One of the most important parameters in the basic MBO algorithm is the butterfly adjusting rate (BAR). In MBO, the value of BAR is the same as for p, which is unchanged during the whole optimization process. Here, a self-adaptive scheme is introduced first to adjust the parameter BAR. The value of BAR changes self-adaptively as the optimization process continues between the initial value BAR0 and the maximum 1, as given mathematically below:
where BAR0 is the initial butterfly adjusting rate; t and tmax are the current and maximum generation, respectively.
From Eq. 18, we can see, though BAR is always changing during the whole MBO process, its value remains in the range (BAR0, 1].
4.2.2 Crossover operator
As we are aware, for EAs, two of the most important operators are the crossover operator and mutation operator [37], both of which have a great influence on the behavior and performance of EAs [3, 58, 60]. In the present work, we introduced the crossover operator originally used in EAs to the butterfly adjusting operator of the basic MBO algorithm. The introduced crossover operator fully explores the information of the butterfly individual, which can be given as shown:
where
At the same time, the crossover rate (Cr) is a critical factor for how the crossover operator behaves, which determines the performance of the EAs to some extent. A substantial number of strategies have been designed to adjust the crossover rate, with the goal of improving the EAs’ search effectiveness. In the present work, a self-adaptive scheme was used to adjust the crossover rate. Therefore, according to the fitness of butterfly j in SP2
where xbest and xworst are the best and the worst butterfly with the fitness of f (xbest) and (xworst), respectively. In addition, from Eq. 20, the minimum and maximum of the crossover rate Cr are 0.2 and 0.8, respectively.
Up to now, two butterfly individuals
where
After incorporating the crossover operator and self-adaptive scheme into the butterfly adjusting operator, an updated butterfly adjusting operator, called the self-adaptive butterfly adjusting (SABA) operator, was then proposed, as shown in Algorithm 2.
According to the previous description, the main step of the EMBO algorithm is given in Algorithm 3.
5 The EMBO for emergency VRP with relief materials in sudden disasters
The original MBO approach was designed for continuous optimization problems [55], while the EmVRP studied in this paper is a classical discrete optimization problem. Therefore, the main framework of EMBO must be adjusted in many aspects to tackle the EmVRP, including individual encoding and decoding. Next, we demonstrate how to use EMBO to solve the EmVRP.
5.1 Individual coding and initial solutions construction
In our work, we utilize an improved natural number coding strategy [75]. A butterfly individual is a string representing an emergency relief material transportation scheme. In general, a butterfly individual is also called a chromosome in EAs.
A butterfly individual is made up of two substrings. The first substring has an element that represents the vehicle number. If there are K vehicles, the first element is an integer selected from 1 to K. The second substring has 3n elements, and n represents the number of tasks completed by the vehicle. For example, vehicle 2 at parking area 1 arrives at material storage site I3 to transport material G1 to the affected area J2. Then vehicle 2 goes to material storage site I1 to transport material G2 to the affected area J4. This process can be represented as K1 − I3 − G1 − J2 − I1 − G2 − J4, and its corresponding butterfly individual can be expressed as 2-3-1-2-1-2-4. The (3n − 1)th element represents the number of the material reserve site, the (3n)th element represents the material type number, and the (3n + 1)th element represents the number of the disaster site (affected area). The element segments of all vehicles are arranged in parallel from small to large in order to form a single butterfly individual.
Suppose there are 3 vehicles that are numbered 1, 2, 3, located in the parking lot K2, K1, and K3, respectively; there are 2 materials that are numbered G1 and G2 ; there are 2 reserve sites that are numbered I1 and I2 ; and there are 3 disaster sites that are numbered J1, J2, and J3. The following butterfly individuals can be generated:
Butterfly individual 1:
Its corresponding solution is:
Butterfly individual 2:
Its corresponding solution is:
Butterfly individual 1 represents vehicle 1 from parking lot K2, which arrives at material storage site I2 to transport material G1 to the affected area J1. Then vehicle 1 goes to material storage site I1 to transport material G2 to the affected area J2. Vehicle 2 from parking lot K1 arrives at material storage site I1 to transport material G2 to the affected area J3. Vehicle 3 from parking lot K3 arrives at material storage site I2 to transport material G1 to the affected area J2, and then vehicle 3 goes to material storage site I1 to transport material G2 to the affected area J2. When the above transportation tasks have been completed, all requirements of all the affected areas will have been met. Butterfly individual 2 can be explained in the same way.
Calculate the butterfly adjusting rate BAR by using Eq. 18.

SABA operator
Initialization. Set the generation counter t = 1, and set the maximum generation tmax, NP1, NP2, BAR0, peri, and p.
Population evaluation. Evaluate the butterfly individuals with their objective functions.

EMBO approach
Now, we will describe how to generate the initial solutions. First, vehicle l is selected randomly from the parking areas. This selection will be considered the starting point. Second, the reserve site Si (i = 1, 2, ..., n) is selected randomly from reserve site set S. Finally, the affected area Dj (j = 1, 2, ..., m) is selected randomly from the affected area set D. This selection process is repeated until a whole butterfly individual is constructed, so the initial solution of the EmVRP is obtained. After all the butterfly individuals have been generated, the initial butterfly population is formed.
5.2 The EMBO for emergency VRP with relief materials in sudden disasters
In this section, we discuss how to use EMBO to solve the EmVRP with relief materials in sudden disasters. First, the initialization process is implemented, including the parameters and initial population, as described previously. Next, the optimization process is implemented to update butterfly individuals in the population. Then the newly generated butterfly individuals are evaluated according to the objective functions. The implementation of the EMBO algorithm is repeated until the given requirements are met. Finally, the optimal butterfly individual is decoded in order to get the final solution scheme for the EmVRP with relief materials in sudden disasters as given in Algorithm 4.
In Algorithm 4, Line 4 encoding is essentially the population initialization process needed so that the EMBO algorithm can solve the EmVRP. Through this encoding, the initial population is generated. Line 4 describes the decoding process that transforms the butterfly individual into the actual solution scheme for the EmVRP. Encoding and decoding are opposite processes.
6 Simulation results
In this portion of our work, we used the proposed EMBO algorithm to solve the EmVRP with relief materials in sudden disasters. In addition, to show the advantages of the EMBO algorithm, we performed several studies comparing the basic MBO algorithm with seven other intelligent algorithms. Finally, to show the robustness of the proposed EMBO algorithm, we reviewed the effects of parametric settings on the performance of EMBO.
6.1 An EmVRP with relief materials in sudden disasters (case 1)
To test our approach, we solved a hypothetical EmVRP with relief materials in a sudden-onset disaster [75] that can be described as follows. Suppose a sudden natural disaster occurred. There are 4 disaster spots in need of emergency materials. These locations can be identified as J1, J2, J3, and J4, respectively. The relief materials have been transported to the local airport and railway station by aircraft and railway. There are a total of 3 reserve sites, denoted by I1, I2, and I3, respectively, including the airport and railway station together with the local relief supply reserve area. A total of 20 vehicles are collected, and they are located randomly in 3 parking locations numbered K1, K2, and K3. There are 4 kinds of materials to be delivered: tents, quilts, clothing, and food, represented as G1, G2, G3, and G4, respectively. The number of tasks to be completed by each vehicle is not more than 5. Tables 1-3 provide the related information for the above EmVRP example.
Related parameters of vehicles.
| Vehicle number | Parking lot | Speed (km/h) | Load capacity (ton) | Volume (m3) |
|---|---|---|---|---|
| 1 | K2 | 50 | 4 | 30 |
| 2 | K1 | 45 | 5 | 34 |
| 3 | K2 | 55 | 3 | 27 |
| 4 | K3 | 40 | 6 | 40 |
| 5 | K1 | 50 | 4 | 30 |
| 6 | K2 | 55 | 3 | 27 |
| 7 | K3 | 35 | 7 | 45 |
| 8 | K2 | 50 | 4 | 30 |
| 9 | K1 | 45 | 5 | 34 |
| 10 | K2 | 45 | 5 | 34 |
| 11 | K3 | 40 | 6 | 40 |
| 12 | K1 | 45 | 5 | 34 |
| 13 | K2 | 55 | 3 | 27 |
| 14 | K3 | 40 | 6 | 40 |
| 15 | K1 | 50 | 4 | 30 |
| 16 | K2 | 55 | 3 | 27 |
| 17 | K3 | 35 | 7 | 45 |
| 18 | K2 | 50 | 4 | 30 |
| 19 | K1 | 45 | 5 | 34 |
| 20 | K2 | 45 | 5 | 34 |
Related parameters of emergency supplies.
| Materials | Tent | Quilt | Clothes | Food |
|---|---|---|---|---|
| Weight (kg) | 30 | 6 | 5 | 10 |
| Volume (m3) | 1.1 | 0.15 | 0.3 | 0.5 |
| Unit materialloading (unloading)time (min) | 0.2 | 0.2 | 0.1 | 0.1 |
The demand of emergency supplies in every affected point.
| Affected point | Tent | Quilt | Clothes | Food |
|---|---|---|---|---|
| J1 | 2000 | 10000 | 6000 | 3000 |
| J2 | 5000 | 20000 | 6000 | 8000 |
| J3 | 3000 | 10000 | 8000 | 4000 |
| J4 | 4000 | 10000 | 6000 | 5000 |
Reserves of emergency supplies in every reserve point.
| Reserve point | Tent | Quilt | Clothes | Food |
|---|---|---|---|---|
| I1 | 4000 | 200000 | 8000 | 8000 |
| I2 | 3000 | 10000 | 6000 | 4000 |
| I2 | 8000 | 20000 | 12000 | 9000 |
The distance between every point.
| Distance (km) | I1 | I2 | I3 | J1 | J2 | J3 | J4 |
|---|---|---|---|---|---|---|---|
| K1 | 45 | 60 | 70 | ||||
| K2 | 60 | 50 | 80 | ||||
| K3 | 70 | 80 | 60 | ||||
| I1 | 60 | 50 | 70 | 80 | |||
| I2 | 70 | 60 | 55 | 65 | |||
| I3 | 100 | 80 | 50 | 60 |
6.2 The shortest time used by nine algorithms on the EmVRP with relief materials in sudden disasters
For the sake of carrying out a fair comparison, all the approaches were compiled using MATLAB R2017a (9.2) running under the Windows 10 Enterprise operating system on a PC with an Intel(R) Core(TM) i5-4590 CPU operating at 3.30 GHz, 8.00GB of RAM, and a hard drive of 1024 GB.
In all experiments for MBO and EMBO, we used the same parameter settings: probability p = 5/12, elitism number Keep = 2,
In this paper, the proposed EMBO algorithm will be compared with seven intelligent algorithms when dealing with emergency vehicle routing problem with relief materials in sudden disasters. The seven comparative algorithms
Initialization. Set the generation counter t = 1, and set the maximum generation tmax, NP1, NP2, BAR0, peri, and p.
Encoding. Initialize the population according to the encoding method in Section 5.1.
Population evaluation. Calculate the shortest time used by each butterfly individual.

EMBO algorithm for emergency VRP with relief materials in sudden disasters
can be described below. ABC (artificial bee colony) [25] is an intelligent optimization algorithm based on the smart behavior of honey bee swarm. BA (bat algorithm) [17] is a new powerful and efficient meta-heuristic optimization algorithm inspired by the echolocation behavior of bats with varying pulse rates of emission and loudness. BBO (biogeography-based optimization) [42] is a new evolution algorithm developed for the global optimization inspired by the immigration and emigration of species between islands (or habitats) in search of more compatible islands. CS (cuckoo search) [69] is a meta-heuristic optimization algorithm inspired by the obligate brood parasitism of some
cuckoo species by laying their eggs in the nests of other host birds (of other species). DE (differential evolution) [43] is a simple but excellent optimization method that uses the difference between two solutions to probabilistically adapt a third solution. An ES (evolutionary strategy) [2] is an algorithm that generally distributes equal importance to mutation and recombination, and that allows two or more parents to reproduce an offspring. PSO (particle swarm optimization) [26, 71, 72] is also a swarm intelligence algorithm which is based on the swarm behavior of fish, and bird schooling in nature.
The parameters for the other seven algorithms were set as follows.
For ABC, the population size N P = 50, the number of food sources FoodNumber = N P/2, maximum search times limit = 100.
For BA, loudness A = 0.5, pulse rate r = 0.5, and scaling factor ε = 0.001.
For BBO, habitat modification probability = 1, immigration probability bounds per gene = [0, 1], step size for numerical integration of probabilities =1, maximum migration rate for each island = 1, and mutation probability = 0.005.
For CS, the discovery rate pa = 0.25.
For DE, the weighting factor F = 0.5, and crossover constant CR = 0.5.
For ES, the number of offspring produced in each generation λ = 10, and the standard deviation for changing solutions is σ = 1 .
For PSO, the inertial constant = 0.3, the cognitive constant = 1, and the social constant for swarm interaction = 1.
For one implementation of EMBO, the convergent trend of the best and average time of the EMBO approach is shown in Fig. 2. In Fig. 2, the best and mean time after 100 generations were 109.4341 and 109.489, respectively. Furthermore, the EMBO algorithm converged to the least time after about 20 generations. These findings indicated that the EMBO algorithm could solve the emergency VRP problem well.
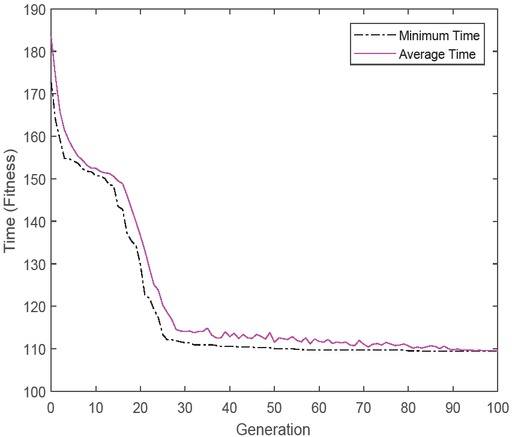
The convergent trend of the best and average time for EMBO algorithm.
In addition, the shortest time over 30 independent runs was obtained by EMBO and the eight other intelligent algorithms, and the results are displayed in Table 6. From Table 6, although EMBO had the biggest std value, it is clear that EMBO was able to complete the task with the least time among the nine intelligent algorithms for the average, best, and worst performance. For the other eight intelligent algorithms, BBO, CS, and DE had similar performances that were inferior only to the EMBO algorithm. Also, MBO performed similarly to PSO, which was better than ABC, BA, and ES.
The least time used by nine intelligent algorithms for the emergency VRP with relief materials in sudden disasters.
| ABC | BA | BBO | CS | DE | EMBO | ES | MBO | PSO | |
|---|---|---|---|---|---|---|---|---|---|
| Best | 158.31 | 154.10 | 142.64 | 143.43 | 142.52 | 109.06 | 163.93 | 152.08 | 157.19 |
| Mean | 162.96 | 161.27 | 145.69 | 145.26 | 144.68 | 118.18 | 165.89 | 154.51 | 159.03 |
| Worst | 167.35 | 167.86 | 148.29 | 150.21 | 146.10 | 140.77 | 167.25 | 158.24 | 162.23 |
| Std | 2.2516 | 3.1246 | 1.6231 | 1.3777 | 0.8202 | 13.2842 | 0.8953 | 1.5353 | 1.4138 |
The convergent trend of the average time obtained by the nine algorithms is shown in Fig. 3. From Fig. 3, it is clear that EMBO converged in the fastest fashion among the nine intelligent algorithms. This convergent trend was consistent with the results provided in Table 6.
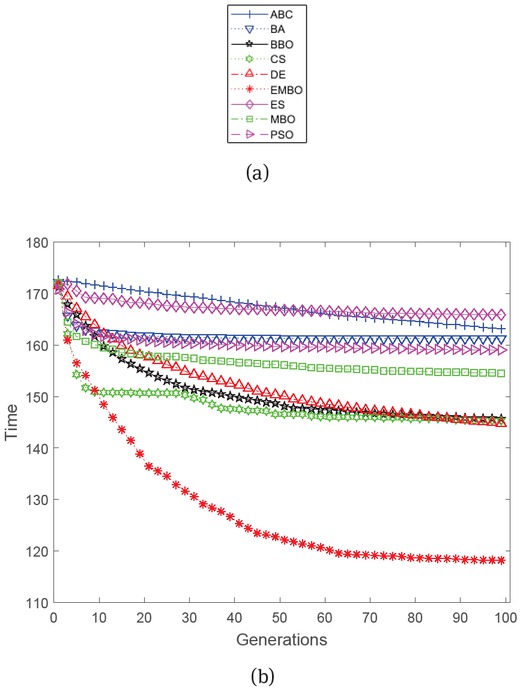
Results obtained by nine algorithms.
6.3 Another EmVRP with relief materials in sudden disasters (case 2)
Like case 1 studied in Section 6.1, another emergency VRP problem is further used to verify our proposed EMBO algorithm. In case 2, there are 5 disaster spots in need of emergency materials. These locations can be identified as J1, J2, J3, J4, and J5, respectively. The relief materials have been transported to the local airport and railway station by aircraft and railway. There are a total of 4 reserve sites, denoted by I1, I2, I3, and I4, respectively. A total of 25 vehicles are collected, and they are located randomly in 3 parking locations numbered K1, K2, and K3. There are 4 kinds of materials to be delivered: tents, quilts, clothing, and food, represented as G1, G2, G3, and G4, respectively. The number of tasks to be completed by each vehicle is not more than 5. The parameters of emergency supplies used in case 2 is the same with case 1, as shown in Table 2. Tables 7-10 provide the other related information for case 2.
Related parameters of vehicles for case 2.
| Vehicle number | Parking lot | Speed (km/h) | Load capacity (ton) | Volume (m3) |
|---|---|---|---|---|
| 1 | K1 | 45 | 5 | 34 |
| 2 | K2 | 45 | 5 | 34 |
| 3 | K3 | 50 | 4 | 30 |
| 4 | K2 | 35 | 7 | 45 |
| 5 | K1 | 55 | 3 | 27 |
| 6 | K3 | 50 | 4 | 30 |
| 7 | K2 | 40 | 6 | 40 |
| 8 | K1 | 55 | 3 | 27 |
| 9 | K3 | 45 | 5 | 34 |
| 10 | K2 | 40 | 6 | 40 |
| 11 | K1 | 45 | 5 | 34 |
| 12 | K2 | 45 | 5 | 34 |
| 13 | K3 | 50 | 4 | 45 |
| 14 | K2 | 35 | 7 | 27 |
| 15 | K1 | 55 | 3 | 30 |
| 16 | K3 | 50 | 4 | 40 |
| 17 | K2 | 40 | 6 | 27 |
| 18 | K1 | 55 | 3 | 34 |
| 19 | K2 | 45 | 5 | 30 |
| 20 | K2 | 50 | 4 | 28 |
| 21 | K1 | 45 | 5 | 29 |
| 22 | K2 | 55 | 3 | 38 |
| 23 | K3 | 50 | 6 | 43 |
| 24 | K2 | 40 | 3 | 31 |
| 25 | K1 | 55 | 5 | 37 |
The demand of emergency supplies in every affected point for case 2.
| Affected point | Tent | Quilt | Clothes | Food |
|---|---|---|---|---|
| J1 | 3000 | 9000 | 7000 | 4000 |
| J2 | 6000 | 19000 | 7000 | 7000 |
| J3 | 4000 | 9000 | 9000 | 5000 |
| J4 | 5000 | 9000 | 7000 | 4000 |
| J5 | 4000 | 11000 | 6500 | 5000 |
Reserves of emergency supplies in every reserve point for case 2.
| Reserve point | Tent | Quilt | Clothes | Food |
|---|---|---|---|---|
| I1 | 5000 | 19000 | 9000 | 9000 |
| I2 | 4000 | 11000 | 7000 | 5000 |
| I3 | 9000 | 21000 | 11000 | 10000 |
| I4 | 7000 | 20000 | 10000 | 9000 |
The distance between every point for case 2.
| Distance (km) | I1 | I2 | I3 | I4 | J1 | J2 | J3 | J4 | J5 |
|---|---|---|---|---|---|---|---|---|---|
| K1 | 50 | 65 | 70 | 75 | |||||
| K2 | 65 | 55 | 50 | 85 | |||||
| K3 | 75 | 85 | 65 | 65 | |||||
| I1 | 55 | 55 | 70 | 75 | 60 | ||||
| I2 | 65 | 65 | 60 | 60 | 55 | ||||
| I3 | 95 | 85 | 55 | 55 | 80 | ||||
| I4 | 65 | 55 | 60 | 70 | 90 |
For the software, hardware environments and parameter settings used in nine intelligent algorithms, they are the same with case 1.
In addition, the shortest time over 30 independent runs was obtained by EMBO and the eight other intelligent algorithms, and the results are displayed in Table 11. From Table 11, it is clear that EMBO was able to complete the task with the least time among the nine intelligent algorithms for the average, best, and worst performance. Also, EMBO had the smallest Std value for this case. For the other eight intelligent algorithms, BBO, BA, and MBO had similar performances that were inferior only to the EMBO algorithm. Comparing with case 1, EMBO algorithm takes less time to complete the task, and the reason is that five more vehicles are added to case 2.
The least time used by nine intelligent algorithms for case 2.
| ABC | BA | BBO | CS | DE | EMBO | ES | MBO | PSO | |
|---|---|---|---|---|---|---|---|---|---|
| Best | 137.03 | 96.13 | 91.00 | 102.65 | 104.84 | 85.66 | 114.38 | 93.72 | 119.67 |
| Mean | 148.29 | 113.33 | 95.38 | 108.85 | 113.96 | 86.39 | 119.28 | 99.19 | 140.33 |
| Worst | 164.45 | 126.22 | 100.37 | 110.78 | 125.30 | 87.97 | 122.79 | 104.32 | 155.02 |
| Std | 6.6743 | 6.9830 | 2.0991 | 1.5518 | 5.4081 | 0.5022 | 2.1377 | 2.6460 | 7.4307 |
6.4 Parameter study
As we are aware, for all the intelligent algorithms, the parameter setting is of significant importance to their performance. In this section, the effectiveness of the initial butterfly adjusting rate BAR0, probability p, elitism Keep, population size NP, and maximum generation tmax are analyzed for the proposed EMBO algorithm on case 1.
6.4.1 Influence of the initial butterfly adjusting rate BAR0 for EMBO
First, we examined the initial butterfly adjusting rate BAR0. The other parameters were set as follows: elitism number Keep = 2, probability p = 5/12, population size NP = 50, and maximum generation tmax = 100. The final times required by EMBO with different values of BAR0 were recorded as shown in Table 12 and Fig. 4. From Table 12, when BAR0 was equal to 0.6 or 0.7, EMBO could find the optimal scheduling scheme with the least time. Looking carefully at Fig. 4, we can observe that the performance of EMBO was significantly improved with the increment of BAR0. However, EMBO had a similar performance when BAR0 was between 0.6 and 1.0. Considering matters overall, we set the initial butterfly adjusting rate
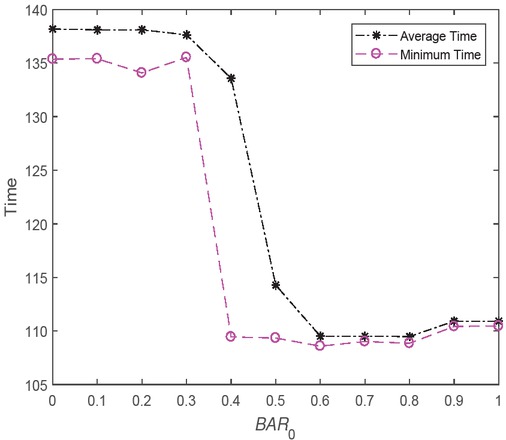
Results obtained by EMBO with different BAR0.
The least time used by the proposed EMBO algorithm for the EmVRP with relief materials in sudden disasters with different BAR0.
| 0 | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | 1.0 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Best | 135.36 | 135.39 | 134.07 | 135.52 | 109.44 | 109.34 | 108.58 | 109.02 | 108.85 | 110.42 | 110.46 |
| Mean | 138.17 | 138.09 | 138.10 | 137.63 | 133.57 | 114.28 | 109.51 | 109.51 | 109.47 | 110.91 | 110.91 |
| Worst | 140.69 | 140.84 | 140.55 | 139.91 | 140.86 | 137.88 | 110.14 | 109.94 | 109.94 | 111.03 | 111.03 |
| Std | 1.5266 | 1.3504 | 1.3326 | 0.8532 | 9.7697 | 10.3059 | 0.3526 | 0.2779 | 0.3323 | 0.1675 | 0.1856 |
It should be mentioned that the initial butterfly adjusting rate BAR0 was between 0 and 1.0. When the initial butterfly adjusting rate BAR0 = 0, the updating Eq. 18 would degenerate into the following equation:
In this case, the butterfly adjusting rate BAR is changing in a linear fashion. On the other hand, when the initial butterfly adjusting rate BAR0 = 1.0, the butterfly adjusting rate BAR is equal to the initial butterfly adjusting rate BAR0. The butterfly adjusting rate BAR will not change during the whole optimization process. Essentially, this description fits a basic MBO algorithm.
6.4.2 Influence of the probability p for EMBO
In EMBO, there is another probability p that decides the number of NP1 and NP2. In other words, there are NP1 and NP2 butterflies that implement the migration operator and butterfly adjusting operator, respectively. Here, we studied the probability p. The other parameters were set as follows: population size NP = 50, the initial butterfly adjusting rate

Results obtained by EMBO with different p.
The least time used by the proposed EMBO algorithm for the emergency VRP with relief materials in sudden disasters with different p.
| 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | |
|---|---|---|---|---|---|---|---|---|---|
| Best | 136.05 | 109.57 | 109.43 | 109.16 | 108.89 | 108.92 | 108.62 | 108.81 | 109.33 |
| Mean | 137.97 | 136.86 | 127.41 | 117.89 | 111.30 | 109.73 | 109.58 | 108.58 | 110.08 |
| Worst | 140.56 | 141.69 | 139.68 | 139.36 | 138.08 | 116.14 | 110.47 | 110.54 | 110.67 |
| Std | 1.0755 | 7.4311 | 13.6690 | 12.6734 | 6.4444 | 1.2843 | 0.3514 | 0.4003 | 0.3664 |
It should be mentioned that the probability p was between 0.1 and 0.9. For MBO, when probability p = 0, all the individuals will be updated only by the butterfly adjusting operator. When probability p = 1.0, all the individuals will be updated only by the migration operator.
No special attention was paid to these two extreme cases of p = 0 and p = 1.0.
6.4.3 Influence of the elitism Keep for EMBO
As we can see, most intelligent algorithms involve an elitism strategy that has a great influence on the performance. Here, the elitism Keep was studied in the range of [0, 10]. The other parameters were set as follows: probability p = 5/12, initial butterfly adjusting rate
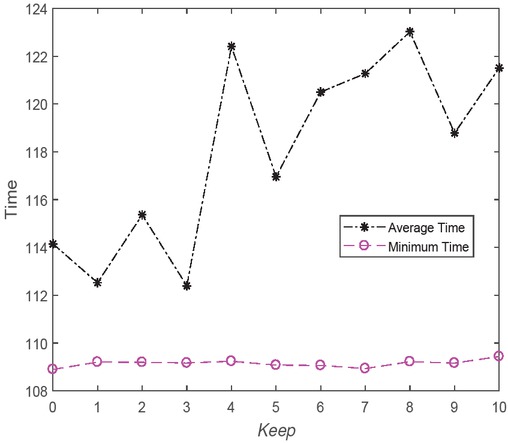
Results obtained by EMBO with different Keep.
The least time used by the proposed EMBO algorithm for the emergency VRP with relief materials in sudden disasters with different Keep.
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Best | 108.89 | 109.19 | 109.19 | 109.16 | 109.23 | 109.07 | 109.06 | 108.92 | 109.21 | 109.15 | 109.43 |
| Mean | 114.14 | 112.52 | 115.36 | 112.39 | 112.40 | 126.95 | 120.49 | 121.27 | 123.02 | 118.78 | 121.51 |
| Worst | 137.74 | 137.92 | 139.75 | 137.83 | 138.34 | 138.35 | 138.55 | 138.79 | 137.49 | 137.94 | 139.17 |
| Std | 10.2456 | 8.4974 | 11.5944 | 8.4129 | 13.8968 | 12.2843 | 13.5096 | 13.5515 | 13.6949 | 13.0870 | 13.5949 |
6.4.4 Influence of the population size NP for EMBO
Subsequently, we studied the population size NP in the range of [10, 100] with interval 10. The other parameters were set as follows: the initial butterfly adjusting rate
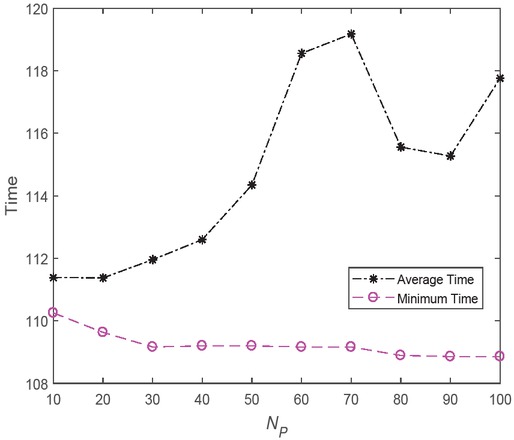
Results obtained by EMBO with different NP.
The least time used by the proposed EMBO algorithm for the emergency VRP with relief materials in sudden disasters with different NP.
| 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Best | 110.25 | 109.63 | 109.16 | 109.19 | 109.20 | 109.16 | 109.16 | 108.89 | 108.85 | 108.85 |
| Mean | 111.38 | 111.37 | 111.95 | 112.60 | 114.34 | 118.55 | 119.17 | 115.55 | 115.27 | 117.76 |
| Worst | 116.17 | 139.58 | 139.23 | 137.49 | 139.86 | 138.85 | 137.51 | 136.82 | 135.96 | 135.97 |
| Std | 1.8294 | 5.4166 | 7.2907 | 8.3299 | 10.4997 | 12.9187 | 13.0635 | 11.3207 | 10.9097 | 12.2106 |
6.4.5 Influence of the maximum generation tmax for EMBO
Last, we studied the maximum generation tmax in the range of [20, 200] with interval 20. The other parameters were set as follows: the initial butterfly adjusting rate
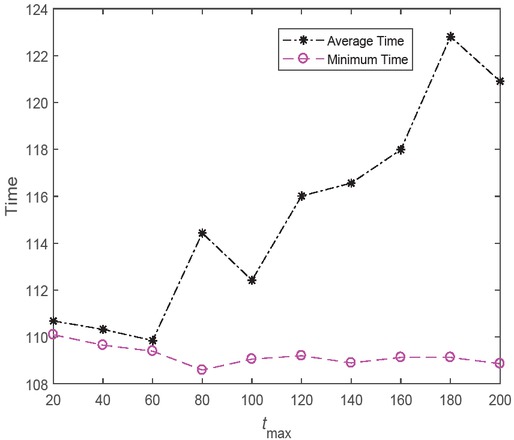
Results obtained by EMBO with different tmax.
The least time used by the proposed EMBO algorithm for the emergency VRP with relief materials in sudden disasters with different tmax.
| 20 | 40 | 60 | 80 | 100 | 120 | 140 | 160 | 180 | 200 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Best | 110.09 | 109.65 | 109.39 | 108.59 | 109.06 | 109.20 | 108.89 | 109.12 | 109.12 | 108.85 |
| Mean | 110.68 | 110.32 | 109.85 | 114.43 | 112.41 | 116.01 | 116.56 | 117.99 | 122.81 | 120.91 |
| Worst | 111.03 | 114.64 | 110.30 | 141.23 | 139.51 | 137.50 | 138.50 | 136.32 | 135.83 | 136.52 |
| Std | 0.2450 | 0.8589 | 0.2236 | 10.8763 | 8.7851 | 11.6742 | 11.7442 | 12.2216 | 12.6813 | 12.3809 |
7 Conclusions
In this paper, we constructed a model of the EmVRP ( emergency vehicle routing problem) with relief materials in sudden disasters, and then solved the problem using the intelligent EMBO algorithm. For EMBO, we incorporated two modifications into the basic MBO algorithm: a self-adaptive strategy and a crossover operator. Our experiments using two examples EmVRP with relief materials in a sudden-onset disaster proved the suitability of EMBO. In addition, an array of comparative studies showed that the proposed EMBO algorithm can achieve satisfactory solutions in less time than the basic MBO algorithm and seven other intelligent algorithms.
Consistent with on our interest in the EmVRP with relief materials in sudden disasters, we look toward the following future work. First, more efficient optimization strategies, such as a self-adaptive strategy, should be incorporated into our original approach, thereby allowing the method to solve the EmVRP more efficiently and accurately. Second, new methods should be designed to solve the EmVRP with relief materials in sudden disasters. Third, the performance of EMBO should be studied and analyzed further for cases where the probability p is equal to 0 and 1.00. Fourthly, the performance of the basic MBO algorithm should be studied and analyzed more extensively with regard to the probability p and other parameters. Fifthly, in the current work, though the crossover rate is changed during the search process, it does not take into account the state of the search process. In our future research, the state of the search process should be taken into account and a more intelligent crossover operator should be developed. Sixthly, in our current work, the emergency VRP is just solved by our proposed MBO algorithm. That is to say, in this version of the paper there is no an equilibrium between methods and decision making processes. In our future work, we will build the equilibrium between methods and decision making processes. Seventhly, in our current work, all the parameters fall into the small range, therefore, try-and-error method can well solve it. In our future work, if there are more complicated parameters to be adjusted, irace and other parametric techniques will be used. At last, in our currentwork, we just use our proposed MBO algorithm to solve the relatively idealized mathematical model. So, other factors is canceled in our current work. In our future work, we will reconsider these factors to our mathematical model (such as congestion or unreliable road network [28, 40, 45]), which is much closer to real world problems. Eighth, for other road network, like grid of streets [31, 66], we will study them in our future studies. Ninth, we will learn from other models (like [1]) to improve the model used in our current work. These studies will contribute to the best implementation of MBO and EMBO.
References
[1] Ofer Amram, Nadine Schuurman, and Syed M Hameed. Mass casualty modelling: a spatial tool to support triage decision making. International Journal of Health Geographics 10(1):40, 2011. ISSN 1476-072X.10.1186/1476-072X-10-40Suche in Google Scholar
[2] H. Beyer. The theory of evolution strategies Springer, New York, 2001.10.1007/978-3-662-04378-3Suche in Google Scholar
[3] Xingjuan Cai, Xiao-zhi Gao, and Yu Xue. Improved bat algorithm with optimal forage strategy and random disturbance strategy. International Journal of Bio-Inspired Computation 8(4):205–214, 2016. 10.1504/IJBIC.2016.078666Suche in Google Scholar
[4] Shifeng Chen, Rong Chen, and Jian Gao. A monarch butterfly optimization for the dynamic vehicle routing problem. Algorithms 10(3):107, 2017. ISSN 1999-4893. 10.3390/a10030107Suche in Google Scholar
[5] Zhihua Cui, Bin Sun, Gai-Ge Wang, Yu Xue, and Jinjun Chen. A novel oriented cuckoo search algorithm to improve dv-hop performance for cyber-physical systems. Journal of Parallel and Distributed Computing 103:42–52, 2017. ISSN 07437315. 10.1016/j.jpdc.2016.10.011Suche in Google Scholar
[6] Geng-Xin Dai and Qing-Li Da. The study of combinatorial scheduling problem in emergency systems. System Engineering - Theory & Practice 20(9):52–55, 2000. ISSN 1000-6788.Suche in Google Scholar
[7] Mohammad Ehteram, Hojat Karami, Sayed-Farhad Mousavi, Saeed Farzin, and Ozgur Kisi. Optimization of energy management and conversion in the multi-reservoir systems based on evolutionary algorithms. Journal of Cleaner Production 168:1132–1142, 2017. ISSN 09596526. 10.1016/j.jclepro.2017.09.099Suche in Google Scholar
[8] Luisa Equi, Giorgio Gallo, Silvia Marziale, and Andres Weintraub. A combined transportation and scheduling problem. European Journal of Operational Research 97(1):94–104, 1997. ISSN 0377-2217.10.1016/S0377-2217(96)00085-9Suche in Google Scholar
[9] Hossam Faris, Ibrahim Aljarah, and Seyedali Mirjalili. Improved monarch butterfly optimization for unconstrained global search and neural network training. Applied Intelligence 48(2):445–464, 2018. ISSN 0924-669X 1573-7497. 10.1007/s10489-017-0967-3Suche in Google Scholar
[10] Yanhong Feng, Gai-Ge Wang, Suash Deb, Mei Lu, and Xiangjun Zhao. Solving 0-1 knapsack problem by a novel binary monarch butterfly optimization. Neural Computing and Applications 28(7):1619–1634, 2017. ISSN 0941-0643 1433-3058. 10.1007/s00521-015-2135-1Suche in Google Scholar
[11] Yanhong Feng, Gai-Ge Wang, Junyu Dong, and Ling Wang. Opposition-based learning monarch butterfly optimization with gaussian perturbation for large-scale 0-1 knapsack problem. Computers & Electrical Engineering 67:454–468, 2018. ISSN 00457906. 10.1016/j.compeleceng.2017.12.01410.1016/j.compeleceng.2017.12.014Suche in Google Scholar
[12] Yanhong Feng, Gai-Ge Wang, Wenbin Li, and Ning Li. Multi-strategy monarch butterfly optimization algorithm for discounted 0-1 knapsack problem. Neural Computing and Applications 30(10):3019–3036, 2018. ISSN 0941-0643 1433-3058. 10.1007/s00521-017-2903-1Suche in Google Scholar
[13] Yanhong Feng, Juan Yang, Yichao He, and Gai-Ge Wang. Monarch butterfly optimization algorithm with differential evolution for the discounted 0-1 knapsack problem. Acta Electronica Sinica 46(6):1343–1350, 2018. 10.3969/j.issn.0372-2112.2018.06.010.10.3969/j.issn.0372-2112.2018.06.010Suche in Google Scholar
[14] Yanhong Feng, Juan Yang, Congcong Wu, Mei Lu, and Xiang-Jun Zhao. Solving 0-1 knapsack problems by chaotic monarch butterfly optimization algorithm. Memetic Computing 10(2):135–150, 2018. ISSN 1865-9284 1865-9292. 10.1007/s12293-016-0211-4Suche in Google Scholar
[15] Ke-Jun Fu, Xu-Ping Wang, and Xiang-Pei HU. Modeling of logistics distribution process based on emergency event. Logistics Technology (10):263–266, 2005.Suche in Google Scholar
[16] Amir Hossein Gandomi and Amir Hossein Alavi. Krill herd: a new bio-inspired optimization algorithm. Communications in Nonlinear Science and Numerical Simulation 17(12):4831–4845, 2012. ISSN 1007-5704. 10.1016/j.cnsns.2012.05.010Suche in Google Scholar
[17] Amir Hossein Gandomi, Xin-She Yang, Amir Hossein Alavi, and Siamak Talatahari. Bat algorithm for constrained optimization tasks. Neural Computing & Applications 22(6):1239–1255, 2013. ISSN 0941-0643. 10.1007/s00521-012-1028-9Suche in Google Scholar
[18] Z.W. Geem, J.H. Kim, and G.V. Loganathan. A new heuristic optimization algorithm: harmony search. Simulation 76(2):60–68, 2001. ISSN 0037-5497. 10.1177/003754970107600201Suche in Google Scholar
[19] Waheed A. H. M. Ghanem and Aman Jantan. Hybridizing artificial bee colony with monarch butterfly optimization for numerical optimization problems. Neural Computing and Applications 2016. ISSN 0941-0643 1433-3058. 10.1007/s00521-016-2665-1Suche in Google Scholar
[20] Mohamed Ghetas, Chan Huah Yong, and Putra Sumari. Harmony-based monarch butterfly optimization algorithm. In 2015 IEEE International Conference on Control System, Computing and Engineering (ICCSCE) pages 156–161. IEEE. ISBN 978-1-4799-8251-6. 10.1109/ICCSCE.2015.7482176Suche in Google Scholar
[21] Gianpaolo Ghiani, Francesca Guerriero, Gilbert Laporte, and Roberto Musmanno. Real-time vehicle routing: Solution concepts, algorithms and parallel computing strategies. European Journal of Operational Research 151(1):1–11, 2003. ISSN 0377-2217.10.1016/S0377-2217(02)00915-3Suche in Google Scholar
[22] D.E. Goldberg. Genetic Algorithms in Search, Optimization and Machine learning Addison-Wesley, New York, 1998.Suche in Google Scholar
[23] Trevor Hale and Christopher R Moberg. Improving supply chain disaster preparedness: A decision process for secure site location. International Journal of Physical Distribution & Logistics Management 35(3):195–207, 2005. ISSN 0960-0035.10.1108/09600030510594576Suche in Google Scholar
[24] Ikou Kaku, Yiyong Xiao, and Guoping Xia. The deterministic annealing algorithms for vehicle routing problems. International Journal of Smart Engineering System Design 5(4):327–339, 2003. ISSN 1025-5818.10.1080/10255810390224080Suche in Google Scholar
[25] Dervis Karaboga and Bahriye Basturk. A powerful and efficient algorithm for numerical function optimization: artificial bee colony (abc) algorithm. Journal of Global Optimization 39(3):459–471, 2007. ISSN 0925-5001. 10.1007/s10898-007-9149-x.10.1007/s10898-007-9149-xSuche in Google Scholar
[26] J. Kennedy and R. Eberhart. Particle swarm optimization. In Proceeding of the IEEE International Conference on Neural Networks volume 4, pages 1942–1948. IEEE. ISBN 0780327683.10.1109/ICNN.1995.488968Suche in Google Scholar
[27] S. Kirkpatrick, C.D. Gelatt Jr, and M.P. Vecchi. Optimization by simulated annealing. Science 220(4598):671–680, 1983. ISSN 0036-8075.10.1126/science.220.4598.671Suche in Google Scholar
[28] V. A. Knight, P. R. Harper, and L. Smith. Ambulance allocation for maximal survival with heterogeneous outcome measures. Omega 40(6):918–926, 2012. ISSN 03050483. 10.1016/j.omega.2012.02.003.10.1016/j.omega.2012.02.003Suche in Google Scholar
[29] Gilbert Laporte. The vehicle routing problem: An overview of exact and approximate algorithms. European Journal of Operational Research 59(3):345–358, 1992. ISSN 0377-2217. 10.1016/0377-2217(92)90192-C.10.1016/0377-2217(92)90192-CSuche in Google Scholar
[30] Hoong Chuin Lau, Melvyn Sim, and Kwong Meng Teo. Vehicle routing problem with time windows and a limited number of vehicles. European Journal of Operational Research 148(3): 559–569, 2003. ISSN 0377-2217.10.1016/S0377-2217(02)00363-6Suche in Google Scholar
[31] Marcin Lewandowski, Bartłomiej Płaczek, and Marcin Bernas. Decentralized control of traffic signals with priority for ambulances. Journal of Medical Informatics & Technologies 26:9–17, 2017. ISSN 1642-6037.Suche in Google Scholar
[32] Quan-Liang Li. Immune algorithm for vehicle routing problem with time windows. System Engineering - Theory & Practice 26 (10):119–124, 2006.Suche in Google Scholar
[33] Nand K. Meena, Sonam Parashar, Anil Swarnkar, Nikhil Gupta, and K. R. Niazi. Improved elephant herding optimization for multiobjective der accommodation in distribution systems. IEEE Transactions on Industrial Informatics 14(3):1029–1039, 2018. ISSN 1551-3203 1941-0050. 10.1109/tii.2017.2748220.10.1109/tii.2017.2748220Suche in Google Scholar
[34] Liping Meng, Yong Wang, and Huajuan Huang. Improved monarch butterfly optimization by using strategy of dynamic-dividing population. Computer Engineering and Applications 53(18):149–156, 2017.Suche in Google Scholar
[35] Seyedali Mirjalili, Seyed Mohammad Mirjalili, and Xin-She Yang. Binary bat algorithm. Neural Computing and Applications 25(3-4):663–681, 2013. ISSN 0941-0643 1433-3058. 10.1007/s00521-013-1525-5.10.1007/s00521-013-1525-5Suche in Google Scholar
[36] Saul S Morris and Quentin Wodon. The allocation of natural disaster relief funds: Hurricane mitch in honduras. World Development 31(7):1279–1289, 2003. ISSN 0305-750X.10.1016/S0305-750X(03)00072-XSuche in Google Scholar
[37] Nadia Nedjah and Luiza De Macedo Mourelle. Encodings and genetic operators for efficient evolutionary design of digital circuits. International Journal of Bio-Inspired Computation 9(4): 197–210, 2017. 10.1504/ijbic.2017.084319. URL https://www.inderscienceonline.com/doi/abs/10.1504/IJBIC.2017.08431910.1504/IJBIC.2017.084319Suche in Google Scholar
[38] Linet Ozdamar, Ediz Ekinci, and Beste Kucukyazici. Emergency logistics planning in natural disasters. Annals of Operations Research 129(1):217–245, 2004. ISSN 0254-5330.10.1023/B:ANOR.0000030690.27939.39Suche in Google Scholar
[39] Zeynep Ozyurt, Deniz Aksen, and Necati Aras. Open Vehicle Routing Problem with Time Deadlines: Solution Methods and an Application pages 73–78. Springer Berlin Heidelberg, Berlin, Heidelberg, 2006. ISBN 978-3-540-32539-0. 10.1007/3-54032539-5_12.10.1007/3-54032539-5_12Suche in Google Scholar
[40] Adam Piórkowski. Construction of a dynamic arrival time coverage map for emergency medical services. Open Geosciences 10(1):167–173, 2018. ISSN 2391-5447. 10.1515/geo-2018-0013.10.1515/geo-2018-0013Suche in Google Scholar
[41] Ajay K Rathi, Richard L Church, and Rajendra S Solanki. Allocating resources to support a multicommodity flow with time windows. Logistics and Transportation Review 28(2):167–188, 1992. ISSN 0047-4991.Suche in Google Scholar
[42] Dan Simon. Biogeography-based optimization. IEEE Transactions on Evolutionary Computation 12(6):702–713, 2008. ISSN 1089-778X. 10.1109/TEVC.2008.919004.10.1109/TEVC.2008.919004Suche in Google Scholar
[43] Rainer Storn and Kenneth Price. Differential evolution-a simple and efficient heuristic for global optimization over continuous spaces. Journal of Global Optimization 11(4):341–359, 1997. ISSN 0925-5001. 10.1023/a:1008202821328.10.1023/a:1008202821328Suche in Google Scholar
[44] Yifei Sun, Licheng Jiao, Xiaozheng Deng, and Rongfang Wang. Dynamic network structured immune particle swarm optimisation with small-world topology. International Journal of Bio-Inspired Computation 9(2):93–105, 2017. 10.1504/ijbic.2017.083100. URL https://www.inderscienceonline.com/doi/abs/10.1504/IJBIC.2017.08310010.1504/ijbic.2017.083100Suche in Google Scholar
[45] Rajeshwari Sundar, Santhoshs Hebbar, and Varaprasad Golla. Implementing intelligent traffic control system for congestion control, ambulance clearance, and stolen vehicle detection. IEEE Sensors Journal 15(2):1109–1113, 2015. ISSN 1530-437X 1558-1748 2379-9153. 10.1109/jsen.2014.2360288.10.1109/jsen.2014.2360288Suche in Google Scholar
[46] Ying Tan. Fireworks Algorithm-A Novel Swarm Intelligence Optimization Method Springer-Verlag Berlin Heidelberg, Berlin, 2015. ISBN Hardcover ISBN 978-3-662-46352-9 eBook ISBN 978-3-662-46353-6. 10.1007/978-3-662-46353-6.10.1007/978-3-662-46353-6Suche in Google Scholar
[47] Gai-Ge Wang. Moth search algorithm: a bio-inspired metaheuristic algorithm for global optimization problems. Memetic Computing 10(2):151–164, 2018. 10.1007/s12293-016-0212-3.10.1007/s12293-016-0212-3Suche in Google Scholar
[48] Gai-Ge Wang and Ying Tan. Improving metaheuristic algorithms with information feedback models. IEEE Transactions on Cybernetics 49(2):542–555, 2019. ISSN Print ISSN: 2168-2267 Online ISSN: 2168-2275. 10.1109/TCYB.2017.2780274.10.1109/TCYB.2017.2780274Suche in Google Scholar PubMed
[49] Gai-Ge Wang, Guo-Sheng Hao, Shi Cheng, and Zhihua Cui. An improved monarch butterfly optimization with equal partition and f/t mutation. In Eight International Conference on Swarm Intelligence (ICSI 2017) Springer.10.1007/978-3-319-61824-1_12Suche in Google Scholar
[50] Gai-Ge Wang, Amir Hossein Gandomi, and Amir Hossein Alavi. A chaotic particle-swarm krill herd algorithm for global numerical optimization. Kybernetes 42(6):962–978, 2013. ISSN 0368-492X. 10.1108/K-11-2012-0108.10.1108/K-11-2012-0108Suche in Google Scholar
[51] Gai-Ge Wang, Amir H. Gandomi, and Amir H. Alavi. Stud krill herd algorithm. Neurocomputing 128:363–370, 2014. ISSN 09252312. 10.1016/j.neucom.2013.08.031.10.1016/j.neucom.2013.08.031Suche in Google Scholar
[52] Gai-Ge Wang, Amir Hossein Gandomi, and Amir Hossein Alavi. An effective krill herd algorithm with migration operator in biogeography-based optimization. Applied Mathematical Modelling 38(9-10):2454–2462, 2014. ISSN 0307-904X. 10.1016/j.apm.2013.10.052. URL http://www.sciencedirect.com/science/article/pii/S0307904X1300675610.1016/j.apm.2013.10.052Suche in Google Scholar
[53] Gai-Ge Wang, Amir Hossein Gandomi, Amir Hossein Alavi, and Guo-Sheng Hao. Hybrid krill herd algorithm with differential evolution for global numerical optimization. Neural Computing and Applications 25(2):297–308, 2014. ISSN 0941-0643 1433-3058. 10.1007/s00521-013-1485-9.10.1007/s00521-013-1485-9Suche in Google Scholar
[54] Gai-Ge Wang, Lihong Guo, Amir Hossein Gandomi, Guo-Sheng Hao, and Heqi Wang. Chaotic krill herd algorithm. Information Sciences 274:17–34, 2014. ISSN 00200255. 10.1016/j.ins.2014.02.123.10.1016/j.ins.2014.02.123Suche in Google Scholar
[55] Gai-Ge Wang, Suash Deb, and Zhihua Cui. Monarch butterfly optimization. Neural Computing and Applications 2015. ISSN 0941-0643 1433-3058. 10.1007/s00521-015-1923-ySuche in Google Scholar
[56] Gai-Ge Wang, Suash Deb, Amir H. Gandomi, and Amir H. Alavi. Opposition-based krill herd algorithm with cauchy mutation and position clamping. Neurocomputing 177:147–157, 2016. ISSN 09252312. 10.1016/j.neucom.2015.11.018.10.1016/j.neucom.2015.11.018Suche in Google Scholar
[57] Gai-Ge Wang, Suash Deb, Xiao-Zhi Gao, and Leandro dos Santos Coelho. A new metaheuristic optimization algorithm motivated by elephant herding behavior. International Journal of Bio-Inspired Computation 8(6):394–409, 2016. 10.1504/IJBIC.2016.10002274.10.1504/IJBIC.2016.10002274Suche in Google Scholar
[58] Gai-Ge Wang, Amir Hossein Gandomi, Xin-She Yang, and Amir Hossein Alavi. A new hybrid method based on krill herd and cuckoo search for global optimization tasks. International Journal of Bio-Inspired Computation 8(5):286–299, 2016. ISSN 1758-0366. 10.1504/IJBIC.2016.10000414.10.1504/IJBIC.2016.10000414Suche in Google Scholar
[59] Gai-Ge Wang, Guo-Sheng Hao, Shi Cheng, and Quande Qin. A discrete monarch butterfly optimization for Chinese TSP problem volume 9712 of Lecture Notes in Computer Science pages 165–173. Springer International Publishing, Cham, 2016. ISBN 978-3-319-41000-5. 10.1007/978-3-319-41000-5_16.10.1007/978-3-319-41000-5_16Suche in Google Scholar
[60] Gai-Ge Wang, Xingjuan Cai, Zhihua Cui, Geyong Min, and Jin-jun Chen. High performance computing for cyber physical social systems by using evolutionary multi-objective optimization algorithm. IEEE Transactions on Emerging Topics in Computing 2017. ISSN Print ISSN: 2168-6750 Online ISSN: 2168-6750. 10.1109/TETC.2017.2703784.10.1109/TETC.2017.2703784Suche in Google Scholar
[61] Gai-Ge Wang, Suash Deb, and Leandro dos Santos Coelho. Earthworm optimization algorithm: a bio-inspired metaheuristic algorithm for global optimization problems. International Journal of Bio-Inspired Computation 12(1):1–22, 2018. 10.1504/IJBIC.2015.10004283.10.1504/IJBIC.2015.10004283Suche in Google Scholar
[62] Gai-Ge Wang, Suash Deb, Xinchao Zhao, and Zhihua Cui. A new monarch butterfly optimization with an improved crossover operator. Operational Research: An International Journal 18(3): 731–755, 2018. ISSN 1109-2858 1866-1505. 10.1007/s12351-016-0251-z.10.1007/s12351-016-0251-zSuche in Google Scholar
[63] Gaige Wang, Lihong Guo, Heqi Wang, Hong Duan, Luo Liu, and Jiang Li. Incorporating mutation scheme into krill herd algorithm for global numerical optimization. Neural Computing and Applications 24(3-4):853–871, 2014. ISSN 0941-0643 1433-3058. 10.1007/s00521-012-1304-8.10.1007/s00521-012-1304-8Suche in Google Scholar
[64] Heqi Wang and Jiao-Hong Yi. An improved optimization method based on krill herd and artificial bee colony with information exchange. Memetic Computing 10(2):177–198, 2018. 10.1007/s12293-017-0241-6.10.1007/s12293-017-0241-6Suche in Google Scholar
[65] Rui Wang, Robin C. Purshouse, and Peter J. Fleming. Preference-inspired coevolutionary algorithms for many-objective optimization. IEEE Transactions on Evolutionary Computation 17 (4):474–494, 2013. ISSN 1089-778X 1089-778X 1941-0026. 10.1109/tevc.2012.2204264.10.1109/tevc.2012.2204264Suche in Google Scholar
[66] Bradford S. Westgate, Dawn B. Woodard, David S. Matteson, and Shane G. Henderson. Travel time estimation for ambulances using bayesian data augmentation. The Annals of Applied Statistics 7(2):1139–1161, 2013. ISSN 1932-6157. 10.1214/13-aoas626.10.1214/13-aoas626Suche in Google Scholar
[67] Yu Xue, Jiongming Jiang, Binping Zhao, and Tinghuai Ma. A self-adaptive artificial bee colony algorithm based on global best for global optimization. Soft Computing 2017. ISSN 1432-7643 1433-7479. 10.1007/s00500-017-2547-1.10.1007/s00500-017-2547-1Suche in Google Scholar
[68] Xin-She Yang. Nature-inspired metaheuristic algorithms Luniver Press, Frome, 2nd edition, 2010. ISBN 1905986106.Suche in Google Scholar
[69] X.S. Yang and S. Deb. Engineering optimisation by cuckoo search. International Journal of Mathematical Modelling and Numerical Optimisation 1(4):330–343, 2010. ISSN 2040-3607. 10.1504/IJMMNO.2010.03543.10.1504/IJMMNO.2010.03543Suche in Google Scholar
[70] Jiao-Hong Yi, Mei Lu, and Xiang-Jun Zhao. Quantum inspired monarch butterfly optimization for ucav path planning navigation problem. International Journal of Bio-Inspired Computation 2017.Suche in Google Scholar
[71] Yong Zhang, Dunwei Gong, Ying Hu, and Wanqiu Zhang. Feature selection algorithm based on bare bones particle swarm optimization. Neurocomputing 148:150–157, 2015. ISSN 09252312. 10.1016/j.neucom.2012.09.049.10.1016/j.neucom.2012.09.049Suche in Google Scholar
[72] Yong Zhang, D. W. Gong, and J. Cheng. Multi-objective particle swarm optimization approach for cost-based feature selection in classification. IEEE/ACM Trans Comput Biol Bioinform 14(1): 64–75, 2017. ISSN 1557-9964 (Electronic) 1545-5963 (Linking). 10.1109/TCBB.2015.2476796.10.1109/TCBB.2015.2476796Suche in Google Scholar PubMed
[73] Yong Zhang, Xian-fang Song, and Dun-wei Gong. A return-cost-based binary firefly algorithm for feature selection. Information Sciences 418-419:561–574, 2017. ISSN 00200255. 10.1016/j.ins.2017.08.047.10.1016/j.ins.2017.08.047Suche in Google Scholar
[74] Yong Zhang, Dun-wei Gong, Jian-yong Sun, and Bo-yang Qu. A decomposition-based archiving approach for multi-objective evolutionary optimization. Information Sciences 430-431:397–413, 2018. ISSN 00200255. 10.1016/j.ins.2017.11.052.10.1016/j.ins.2017.11.052Suche in Google Scholar
[75] Tong Zhao. The study on optimized emergency logistics distribution system of burst natural disasters recuing in China Ph.d, 2011.Suche in Google Scholar
© 2019 Jiao-Hong Yi et al., published by De Gruyter
This work is licensed under the Creative Commons Attribution 4.0 Public License.
Artikel in diesem Heft
- Regular Articles
- 2D Seismic Interpretation of the Meyal Area, Northern Potwar Deform Zone, Potwar Basin, Pakistan
- A new method of lithologic identification and distribution characteristics of fine - grained sediments: A case study in southwest of Ordos Basin, China
- Modified Gompertz sigmoidal model removing fine-ending of grain-size distribution
- Diagenesis and its influence on reservoir quality and oil-water relative permeability: A case study in the Yanchang Formation Chang 8 tight sandstone oil reservoir, Ordos Basin, China
- Evaluation of AHRS algorithms for Foot-Mounted Inertial-based Indoor Navigation Systems
- Identification and evaluation of land use vulnerability in a coal mining area under the coupled human-environment
- Hydrocarbon Generation Potential of Chia Gara Formation in Three Selected Wells, Northern Iraq
- Source Analysis of Silicon and Uranium in uranium-rich shale in the Xiuwu Basin, Southern China
- Lithologic heterogeneity of lacustrine shale and its geological significance for shale hydrocarbon-a case study of Zhangjiatan Shale
- Characterization of soil permeability in the former Lake Texcoco, Mexico
- Detrital zircon trace elements from the Mesozoic Jiyuan Basin, central China and its implication on tectonic transition of the Qinling Orogenic Belt
- Turkey OpenStreetMap Dataset - Spatial Analysis of Development and Growth Proxies
- Morphological Changes of the Lower Ping and Chao Phraya Rivers, North and Central Thailand: Flood and Coastal Equilibrium Analyses
- Landscape Transformations in Rapidly Developing Peri-urban Areas of Accra, Ghana: Results of 30 years
- Division of shale sequences and prediction of the favorable shale gas intervals: an example of the Lower Cambrian of Yangtze Region in Xiuwu Basin
- Fractal characteristics of nanopores in lacustrine shales of the Triassic Yanchang Formation, Ordos Basin, NW China
- Selected components of geological structures and numerical modelling of slope stability
- Spatial data quality and uncertainty publication patterns and trends by bibliometric analysis
- Application of microstructure classification for the assessment of the variability of geological-engineering and pore space properties in clay soils
- Shear failure modes and AE characteristics of sandstone and marble fractures
- Ice Age theory: a correspondence between Milutin Milanković and Vojislav Mišković
- Are Serbian tourists worried? The effect of psychological factors on tourists’ behavior based on the perceived risk
- Real-Time Map Matching: A New Algorithm Integrating Spatio-Temporal Proximity and Improved Weighted Circle
- Characteristics and hysteresis of saturated-unsaturated seepage of soil landslides in the Three Gorges Reservoir Area, China
- Petrographical and geophysical investigation of the Ecca Group between Fort Beaufort and Grahamstown, in the Eastern Cape Province, South Africa
- Ecological risk assessment of geohazards in Natural World Heritage Sites: an empirical analysis of Bogda, Tianshan
- Integrated Subsurface Temperature Modeling beneath Mt. Lawu and Mt. Muriah in The Northeast Java Basin, Indonesia
- Go social for your own safety! Review of social networks use on natural disasters – case studies from worldwide
- Forestry Aridity Index in Vojvodina, North Serbia
- Natural Disasters vs Hotel Industry Resilience: An Exploratory Study among Hotel Managers from Europe
- Using Monarch Butterfly Optimization to Solve the Emergency Vehicle Routing Problem with Relief Materials in Sudden Disasters
- Potential influence of meteorological variables on forest fire risk in Serbia during the period 2000-2017
- Controlling factors on the geochemistry of Al-Shuaiba and Al-Mejarma coastal lagoons, Red Sea, Saudi Arabia
- The Influence of Kaolinite - Illite toward mechanical properties of Claystone
- Two critical books in the history of loess investigation: ‘Charakteristik der Felsarten’ by Karl Caesar von Leonhard and ‘Principles of Geology’ by Charles Lyell
- The Mechanism and Control Technology of Strong Strata Behavior in Extra-Thick Coal Seam Mining Influenced by Overlying Coal Pillar
- Shared Aerial Drone Videos — Prospects and Problems for Volunteered Geographic Information Research
- Stable isotopes of C and H in methane fermentation of agriculture substrates at different temperature conditions
- Prediction of Compression and Swelling Index Parameters of Quaternary Sediments from Index Tests at Mersin District
- Detection of old scattered windthrow using low cost resources. The case of Storm Xynthia in the Vosges Mountains, 28 February 2010
- Remediation of Copper and Zinc from wastewater by modified clay in Asir region southwest of Saudi Arabia
- Sedimentary facies of Paleogene lacustrine dolomicrite and implications for petroleum reservoirs in the southern Qianjiang Depression, China
- Correlation between ore particle flow pattern and velocity field through multiple drawpoints under the influence of a flexible barrier
- Atmospheric refractivity estimation from AIS signal power using the quantum-behaved particle swarm optimization algorithm
- A geophysical and hydro physico-chemical study of the contaminant impact of a solid waste landfill (swl) in King Williams’ Town, Eastern Cape, South Africa
- Landscape characterization using photographs from crowdsourced platforms: content analysis of social media photographs
- A Study on Transient Electromagnetic Interpretation Method Based on the Seismic Wave Impedance Inversion Model
- Stratigraphy of Architectural Elements of a Buried Monogenetic Volcanic System
- Variable secondary porosity modeling of carbonate rocks based on μ-CT images
- Traditional versus modern settlement on torrential alluvial fans considering the danger of debris flows: a case study of the Upper Sava Valley (NW Slovenia)
- The Influence of Gangue Particle size and Gangue Feeding Rate on Safety and Service Life of the Suspended Buffer’s Spring
- Research on the Transition Section Length of the Mixed Workface Using Gangue Backfilling Method and Caving Method
- Rainfall erosivity and extreme precipitation in the Pannonian basin
- Structure of the Sediment and Crust in the Northeast North China Craton from Improved Sequential H-k Stacking Method
- Planning Activities Improvements Responding Local Interests Change through Participatory Approach
- GIS-based landslide susceptibility mapping using bivariate statistical methods in North-western Tunisia
- Uncertainty based multi-step seismic analysis for near-surface imaging
- Deformation monitoring and prediction for residential areas in the Panji mining area based on an InSAR time series analysis and the GM-SVR model
- Statistical and expert-based landslide susceptibility modeling on a national scale applied to North Macedonia
- Natural hazards and their impact on rural settlements in NE Romania – A cartographical approach
- Rock fracture initiation and propagation by mechanical and hydraulic impact
- Influence of Rapid Transit on Accessibility Pattern and Economic Linkage at Urban Agglomeration Scale in China
- Near Infrared Spectroscopic Study of Trioctahedral Chlorites and Its Remote Sensing Application
- Problems with collapsible soils: Particle types and inter-particle bonding
- Unification of data from various seismic catalogues to study seismic activity in the Carpathians Mountain arc
- Quality assessment of DEM derived from topographic maps for geomorphometric purposes
- Remote Sensing Monitoring of Soil Moisture in the Daliuta Coal Mine Based on SPOT 5/6 and Worldview-2
- Utilizing Maximum Entropy Spectral Analysis (MESA) to identify Milankovitch cycles in Lower Member of Miocene Zhujiang Formation in north slope of Baiyun Sag, Pearl River Mouth Basin, South China Sea
- Stability Analysis of a Slurry Trench in Cohesive-Frictional Soils
- Integrating Landsat 7 and 8 data to improve basalt formation classification: A case study at Buon Ma Thuot region, Central Highland, Vietnam
- Assessment of the hydrocarbon potentiality of the Late Jurassic formations of NW Iraq: A case study based on TOC and Rock-Eval pyrolysis in selected oil-wells
- Rare earth element geochemistry of sediments from the southern Okinawa Trough since 3 ka: Implications for river-sea processes and sediment source
- Effect of gas adsorption-induced pore radius and effective stress on shale gas permeability in slip flow: New Insights
- Development of the Narva-Jõesuu beach, mineral composition of beach deposits and destruction of the pier, southeastern coast of the Gulf of Finland
- Selecting fracturing interval for the exploitation of tight oil reservoirs from logs: a case study
- A comprehensive scheme for lithological mapping using Sentinel-2A and ASTER GDEM in weathered and vegetated coastal zone, Southern China
- Sedimentary model of K-Successions Sandstones in H21 Area of Huizhou Depression, Pearl River Mouth Basin, South China Sea
- A non-uniform dip slip formula to calculate the coseismic deformation: Case study of Tohoku Mw9.0 Earthquake
- Decision trees in environmental justice research — a case study on the floods of 2001 and 2010 in Hungary
- The Impacts of Climate Change on Maximum Daily Discharge in the Payab Jamash Watershed, Iran
- Mass tourism in protected areas – underestimated threat? Polish National Parks case study
- Decadal variations of total organic carbon production in the inner-shelf of the South China Sea and East China Sea
- Hydrogeothermal potentials of Rogozna mountain and possibility of their valorization
- Postglacial talus slope development imaged by the ERT method: comparison of slopes from SW Spitsbergen, Norway and Tatra Mountains, Poland
- Seismotectonics of Malatya Fault, Eastern Turkey
- Investigating of soil features and landslide risk in Western-Atakent (İstanbul) using resistivity, MASW, Microtremor and boreholes methods
- Assessment of Aquifer Vulnerability Using Integrated Geophysical Approach in Weathered Terrains of South China
- An integrated analysis of mineralogical and microstructural characteristics and petrophysical properties of carbonate rocks in the lower Indus Basin, Pakistan
- Applicability of Hydrological Models for Flash Flood Simulation in Small Catchments of Hilly Area in China
- Heterogeneity analysis of shale reservoir based on multi-stage pumping data
Artikel in diesem Heft
- Regular Articles
- 2D Seismic Interpretation of the Meyal Area, Northern Potwar Deform Zone, Potwar Basin, Pakistan
- A new method of lithologic identification and distribution characteristics of fine - grained sediments: A case study in southwest of Ordos Basin, China
- Modified Gompertz sigmoidal model removing fine-ending of grain-size distribution
- Diagenesis and its influence on reservoir quality and oil-water relative permeability: A case study in the Yanchang Formation Chang 8 tight sandstone oil reservoir, Ordos Basin, China
- Evaluation of AHRS algorithms for Foot-Mounted Inertial-based Indoor Navigation Systems
- Identification and evaluation of land use vulnerability in a coal mining area under the coupled human-environment
- Hydrocarbon Generation Potential of Chia Gara Formation in Three Selected Wells, Northern Iraq
- Source Analysis of Silicon and Uranium in uranium-rich shale in the Xiuwu Basin, Southern China
- Lithologic heterogeneity of lacustrine shale and its geological significance for shale hydrocarbon-a case study of Zhangjiatan Shale
- Characterization of soil permeability in the former Lake Texcoco, Mexico
- Detrital zircon trace elements from the Mesozoic Jiyuan Basin, central China and its implication on tectonic transition of the Qinling Orogenic Belt
- Turkey OpenStreetMap Dataset - Spatial Analysis of Development and Growth Proxies
- Morphological Changes of the Lower Ping and Chao Phraya Rivers, North and Central Thailand: Flood and Coastal Equilibrium Analyses
- Landscape Transformations in Rapidly Developing Peri-urban Areas of Accra, Ghana: Results of 30 years
- Division of shale sequences and prediction of the favorable shale gas intervals: an example of the Lower Cambrian of Yangtze Region in Xiuwu Basin
- Fractal characteristics of nanopores in lacustrine shales of the Triassic Yanchang Formation, Ordos Basin, NW China
- Selected components of geological structures and numerical modelling of slope stability
- Spatial data quality and uncertainty publication patterns and trends by bibliometric analysis
- Application of microstructure classification for the assessment of the variability of geological-engineering and pore space properties in clay soils
- Shear failure modes and AE characteristics of sandstone and marble fractures
- Ice Age theory: a correspondence between Milutin Milanković and Vojislav Mišković
- Are Serbian tourists worried? The effect of psychological factors on tourists’ behavior based on the perceived risk
- Real-Time Map Matching: A New Algorithm Integrating Spatio-Temporal Proximity and Improved Weighted Circle
- Characteristics and hysteresis of saturated-unsaturated seepage of soil landslides in the Three Gorges Reservoir Area, China
- Petrographical and geophysical investigation of the Ecca Group between Fort Beaufort and Grahamstown, in the Eastern Cape Province, South Africa
- Ecological risk assessment of geohazards in Natural World Heritage Sites: an empirical analysis of Bogda, Tianshan
- Integrated Subsurface Temperature Modeling beneath Mt. Lawu and Mt. Muriah in The Northeast Java Basin, Indonesia
- Go social for your own safety! Review of social networks use on natural disasters – case studies from worldwide
- Forestry Aridity Index in Vojvodina, North Serbia
- Natural Disasters vs Hotel Industry Resilience: An Exploratory Study among Hotel Managers from Europe
- Using Monarch Butterfly Optimization to Solve the Emergency Vehicle Routing Problem with Relief Materials in Sudden Disasters
- Potential influence of meteorological variables on forest fire risk in Serbia during the period 2000-2017
- Controlling factors on the geochemistry of Al-Shuaiba and Al-Mejarma coastal lagoons, Red Sea, Saudi Arabia
- The Influence of Kaolinite - Illite toward mechanical properties of Claystone
- Two critical books in the history of loess investigation: ‘Charakteristik der Felsarten’ by Karl Caesar von Leonhard and ‘Principles of Geology’ by Charles Lyell
- The Mechanism and Control Technology of Strong Strata Behavior in Extra-Thick Coal Seam Mining Influenced by Overlying Coal Pillar
- Shared Aerial Drone Videos — Prospects and Problems for Volunteered Geographic Information Research
- Stable isotopes of C and H in methane fermentation of agriculture substrates at different temperature conditions
- Prediction of Compression and Swelling Index Parameters of Quaternary Sediments from Index Tests at Mersin District
- Detection of old scattered windthrow using low cost resources. The case of Storm Xynthia in the Vosges Mountains, 28 February 2010
- Remediation of Copper and Zinc from wastewater by modified clay in Asir region southwest of Saudi Arabia
- Sedimentary facies of Paleogene lacustrine dolomicrite and implications for petroleum reservoirs in the southern Qianjiang Depression, China
- Correlation between ore particle flow pattern and velocity field through multiple drawpoints under the influence of a flexible barrier
- Atmospheric refractivity estimation from AIS signal power using the quantum-behaved particle swarm optimization algorithm
- A geophysical and hydro physico-chemical study of the contaminant impact of a solid waste landfill (swl) in King Williams’ Town, Eastern Cape, South Africa
- Landscape characterization using photographs from crowdsourced platforms: content analysis of social media photographs
- A Study on Transient Electromagnetic Interpretation Method Based on the Seismic Wave Impedance Inversion Model
- Stratigraphy of Architectural Elements of a Buried Monogenetic Volcanic System
- Variable secondary porosity modeling of carbonate rocks based on μ-CT images
- Traditional versus modern settlement on torrential alluvial fans considering the danger of debris flows: a case study of the Upper Sava Valley (NW Slovenia)
- The Influence of Gangue Particle size and Gangue Feeding Rate on Safety and Service Life of the Suspended Buffer’s Spring
- Research on the Transition Section Length of the Mixed Workface Using Gangue Backfilling Method and Caving Method
- Rainfall erosivity and extreme precipitation in the Pannonian basin
- Structure of the Sediment and Crust in the Northeast North China Craton from Improved Sequential H-k Stacking Method
- Planning Activities Improvements Responding Local Interests Change through Participatory Approach
- GIS-based landslide susceptibility mapping using bivariate statistical methods in North-western Tunisia
- Uncertainty based multi-step seismic analysis for near-surface imaging
- Deformation monitoring and prediction for residential areas in the Panji mining area based on an InSAR time series analysis and the GM-SVR model
- Statistical and expert-based landslide susceptibility modeling on a national scale applied to North Macedonia
- Natural hazards and their impact on rural settlements in NE Romania – A cartographical approach
- Rock fracture initiation and propagation by mechanical and hydraulic impact
- Influence of Rapid Transit on Accessibility Pattern and Economic Linkage at Urban Agglomeration Scale in China
- Near Infrared Spectroscopic Study of Trioctahedral Chlorites and Its Remote Sensing Application
- Problems with collapsible soils: Particle types and inter-particle bonding
- Unification of data from various seismic catalogues to study seismic activity in the Carpathians Mountain arc
- Quality assessment of DEM derived from topographic maps for geomorphometric purposes
- Remote Sensing Monitoring of Soil Moisture in the Daliuta Coal Mine Based on SPOT 5/6 and Worldview-2
- Utilizing Maximum Entropy Spectral Analysis (MESA) to identify Milankovitch cycles in Lower Member of Miocene Zhujiang Formation in north slope of Baiyun Sag, Pearl River Mouth Basin, South China Sea
- Stability Analysis of a Slurry Trench in Cohesive-Frictional Soils
- Integrating Landsat 7 and 8 data to improve basalt formation classification: A case study at Buon Ma Thuot region, Central Highland, Vietnam
- Assessment of the hydrocarbon potentiality of the Late Jurassic formations of NW Iraq: A case study based on TOC and Rock-Eval pyrolysis in selected oil-wells
- Rare earth element geochemistry of sediments from the southern Okinawa Trough since 3 ka: Implications for river-sea processes and sediment source
- Effect of gas adsorption-induced pore radius and effective stress on shale gas permeability in slip flow: New Insights
- Development of the Narva-Jõesuu beach, mineral composition of beach deposits and destruction of the pier, southeastern coast of the Gulf of Finland
- Selecting fracturing interval for the exploitation of tight oil reservoirs from logs: a case study
- A comprehensive scheme for lithological mapping using Sentinel-2A and ASTER GDEM in weathered and vegetated coastal zone, Southern China
- Sedimentary model of K-Successions Sandstones in H21 Area of Huizhou Depression, Pearl River Mouth Basin, South China Sea
- A non-uniform dip slip formula to calculate the coseismic deformation: Case study of Tohoku Mw9.0 Earthquake
- Decision trees in environmental justice research — a case study on the floods of 2001 and 2010 in Hungary
- The Impacts of Climate Change on Maximum Daily Discharge in the Payab Jamash Watershed, Iran
- Mass tourism in protected areas – underestimated threat? Polish National Parks case study
- Decadal variations of total organic carbon production in the inner-shelf of the South China Sea and East China Sea
- Hydrogeothermal potentials of Rogozna mountain and possibility of their valorization
- Postglacial talus slope development imaged by the ERT method: comparison of slopes from SW Spitsbergen, Norway and Tatra Mountains, Poland
- Seismotectonics of Malatya Fault, Eastern Turkey
- Investigating of soil features and landslide risk in Western-Atakent (İstanbul) using resistivity, MASW, Microtremor and boreholes methods
- Assessment of Aquifer Vulnerability Using Integrated Geophysical Approach in Weathered Terrains of South China
- An integrated analysis of mineralogical and microstructural characteristics and petrophysical properties of carbonate rocks in the lower Indus Basin, Pakistan
- Applicability of Hydrological Models for Flash Flood Simulation in Small Catchments of Hilly Area in China
- Heterogeneity analysis of shale reservoir based on multi-stage pumping data

