Equipping the integral approach with generalized least squares to reconstruct relict channel profile and its usage in the Shanxi Rift, northern China

Yarong Zhang; Yizhou Wang; Hao Xie; Chaopeng Li; Huiping Zhang

doi:10.1515/geo-2025-0900

Article Open Access

Equipping the integral approach with generalized least squares to reconstruct relict channel profile and its usage in the Shanxi Rift, northern China

Yarong Zhang , Yizhou Wang , Hao Xie , Chaopeng Li and Huiping Zhang

Published/Copyright: October 21, 2025

Published by

Become an author with De Gruyter Brill

Submit Manuscript Author Information

From the journal Open Geosciences Volume 17 Issue 1

Abstract

Transient river profiles with slope-break knickpoints record past and present tectonic information. The channel upstream of a knickpoint represents a relict profile in equilibrium with previous tectonic forcing, while the downstream segment reflects current uplift rates. Relict profile reconstruction projects the paleo-channel across the knickpoint to estimate the minimum incision depth. Traditional methods, such as slope-area analysis and the integral approach, can introduce errors due to data smoothing, resampling, and residual autocorrelation in chi-elevation regressions. To address these limitations, we propose an improved integral approach equipped with generalized least squares to eliminate autocorrelated residuals and provide accurate estimates of channel concavity and steepness indices. These indices are then used to reconstruct the relict profile and estimate incision depth. We validate our method using a synthetic transient river profile generated by 1D numerical modeling and further apply it to rivers crossing the mountain ranges bounding the Taiyuan Basin in northern China. Our results identify slope-break knickpoints, reconstruct relict profiles, and estimate incision depths, which provide lower limits of fault throw since the late Miocene to early Pliocene. This improved method offers a robust approach to analyzing transient river profiles and quantifying tectonic deformation.

Keywords: slope-break knickpoint; concavity index; relict channel profile reconstruction; the integral approach; generalized least squares; Shanxi Rift

1 Introduction

In the field of tectonic geomorphology, one of the primary goals is to decode the coupling mechanisms between tectonic uplift, river incision, and landscape evolution over geological time scales [1,2,3]. As river network draining through active orogens sets the erosional baselevel for hillslope processes, changes in the shape and elevation of river long profile define the landscape evolution of mountain ranges [4,5,6]. For regions that are under steady-state (i.e. a balance between tectonic uplift and erosion) and uniform climatic and tectonic settings, a growing body of studies show that the river longitudinal profiles usually exhibit smooth, concave-up shape [7,8,9]. Along the river profile, local channel gradient decreases as drainage area increases, which can be expressed by a power-law scaling [10,11]:

(1) d z d x = k s A − θ ,

(2) k s = ( E / K ) 1 / n θ = m n ,

where z is the elevation, x is the upstream distance, t is the time, k s and θ are channel steepness and concavity indices, respectively, K is the channel erodibility (affected by lithology, climate, etc.), E is the channel erosion rate, A is the drainage area (a simple proxy for river discharge and channel width), and m and n are constants. The slope-area scaling has long been applied for river profile analysis [6,12,13,14]. However, estimating channel slope requires smoothing and resampling noisy elevation data, which causes large scatters in the log-transformed slope-area plot and high uncertainties in the derived stream power parameters [15,16]. Alternatively, the integral approach was proposed, i.e., an analytical solution to equation (1) [15,17,18]:

(3) z ( x ) = z b + U K 1 n χ ,

(4) χ = ∫ x b x A 0 A ( x ) m n d x ,

where z b is the base-level elevation, and A 0 is an arbitrary drainage area to simplify the unit of χ to be the same as the river length. When setting A ₀ = 1 m², the slope of the χ – z plot is the steepness index (k _s). Following the transformation of equations (3) and (4), the steady-state channel profile will become a straight line in the χ -domain. And, any departure from a linear trend can be found with noise in a χ – z plot [15].

A sudden increase in the tectonic uplift rate drives the steepening of local channel segment at the river outlet, i.e. a knickpoint occurs [4,19]. The knickpoint is not stable but migrates upstream gradually, reshaping its downstream channel profile [20,21]. The positive coupling between tectonic uplift and knickpoint migration drives the river profile evolution to meet a balance between erosion and tectonic uplift at a new stage (Figure 1). Along the channel long profile, upstream and downstream reaches of the knickpoint are under steady-state with the previous and current tectonic forcing, respectively. The upstream reach, which contains information of the previous tectonic uplift rate, is called the relict (or paleo) channel profile [22,23,24]. Using equation (1), the shape of the relict profile can be modeled. If projecting this scaling formula out to the river outlet (mountain front, or the cross between river and active fault that sets the tectonic uplift boundary condition), the former shape of the river long profile can be re-constructed [9,25]. If assuming no significant long-wavelength tilting effects on the upstream channel segment, the difference between the current elevation at the river outlet and the reconstructed elevation represents the incision depth of the knickpoint and provides a minimum constraint on the magnitude of differential rock uplift or river incision [26,27]. Using the χ – z plot to reconstruct relict profile can also estimate the uncertainty of incision magnitude (Figure 1b). However, the integral approach requires a uniform concavity along the whole river profile. And, across the landscape, calculating χ value calls for a reference concavity index (θ _ref). In fact, equation (1) was changed to be

(5) d z d x = k s A − θ + θ ref A − θ ref = k sn A − θ ref ,

where k sn = k s A − θ + θ ref is the normalized channel steepness index. Thus, even for the steady-state channel, we still can find departures from a linear χ – z plot. Because the χ transform accumulates contributions from upstream drainage areas, neighboring χ values are not independent; consequently, χ – z regression residuals are often positively autocorrelated. This serial correlation inflates errors and causes ordinary least squares (OLS) uncertainty estimates for the steepness index (k _s) to be underestimated, particularly when the relict concavity differs from the reference concavity θ _ref (see details in our numerical case).

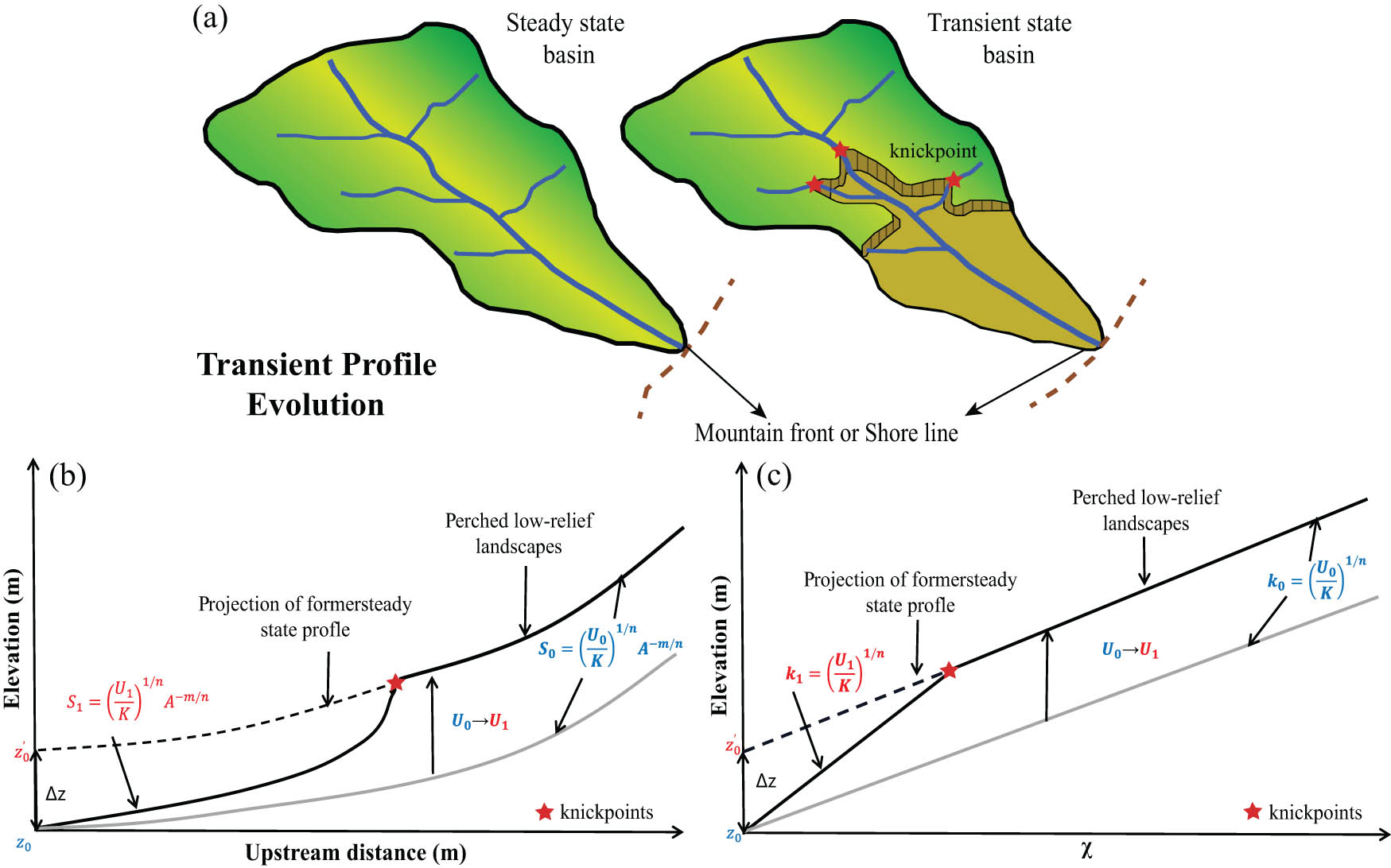
$Figure 1 (a) Conceptual model for the evolution of a transient basin from a steady state basin(b) and (c). Schematic diagram of knickpoint trace migration. The present-day river outlet elevation is z 0 , elevation of the projected paleochannel at the outlet is z 0 ′ , ∆ z = z 0 ′ − z 0 {z}_{0}^{^{\prime} },\triangle z={z}_{0}^{^{\prime} }-{z}_{0} is the minimum knickpoint incision depth from the time of its formation to the present day. (adapted from (Kirby and Whipple, 2012)).$

Figure 1

(a) Conceptual model for the evolution of a transient basin from a steady state basin(b) and (c). Schematic diagram of knickpoint trace migration. The present-day river outlet elevation is z ₀, elevation of the projected paleochannel at the outlet is z 0 ′ , ∆ z = z 0 ′ − z 0 is the minimum knickpoint incision depth from the time of its formation to the present day. (adapted from (Kirby and Whipple, 2012)).

In this study, we proposed to equip the integral approach with the generalized least squares (GLS) to eliminate residual auto-correlation in the χ – z plot. Using this method, we calculate the concavity of the relict channel profile and reconstruct the relict χ – z plot with this concavity value. A synthetic case is first used to show the validity of our approach. Then, this method is applied to analyze the rivers draining through the mountain ranges bounding the Taiyuan Basin in the Shanxi Rift, northern China.

2 Theoretical background

2.1 Equipping the integral approach with GLSs

We use the GLS method to perform χ – z regression, aiming to eliminate serially correlated residuals

(6) z i = z b + k s χ i + ε i ( i = 1 , 2 , … , p ) ,

where p is the number of elevation data points and ε i is the residual. Then, we calculate the self-correlation coefficient (ρ) of residuals:

(7) ρ = ∑ 2 p ε i ε i − 1 ∑ 1 p ε i 2 .

Multiplying equation (6) with ρ and replacing the subscript i with i − 1:

(8) ρ z i − 1 = ρ z b + ρ k s χ i − 1 + ρ ε i − 1 .

Equations (6)–(8):

(9) ( z i − ρ z i − 1 ) = z b ( 1 − ρ ) + k s ( χ i − ρ χ i − 1 ) + ε i − ρ ε i − 1 .

We defined z b * = z b ( 1 − ρ ) , z i * = z i − ρ z i − 1 , χ i * = χ i − ρ χ i − 1 , and ε i * = ε i − ρ ε i − 1 . Equation (9) can be further written as

(10) z i * = z b * + k s χ i * + ε i * .

Compared with equation (6), we find that the slope of the linear fit of χ i * and z i * corresponds to the steepness index, and the intercept represents a correction that must be modified by z b = ( 1 − ρ ) / z b * before it can be considered the base-level elevation.

Equation (10) is called the generalized difference equation. It is not in its original form, but rather regresses z on χ in a quasi-differenced form. This form is obtained by subtracting a proportion ( ρ ) of the previous period’s value from the current period’s value of the variable. However, in the process of taking the difference, an observation is lost because the first observation does not have the previous value. So we can set the first observation of the loss to be

(11) z 1 * = 1 − ρ 2 z 1 χ 1 * = 1 − ρ 2 χ 1 ′ .

This transformation is known as the Prais–Winsten transformation [28,29]. After the transformation, ε 1 * are no longer autocorrelated and the data pair ( χ 1 * – z 1 * ) meets the requirement of linear regression. The GLS procedure removes the predictable lagged component of the residuals, thereby restoring the OLS assumption of independent errors and yielding valid standard errors and confidence intervals. Therefore, k _s and z _b derived from the linear regression on the transformed variables z i * and χ i * are regression parameters without residual autocorrelation. To distinguish with the χ – z plot method, we refer to the integral approach equipped with GLS as the χ * – z * plot method.

3 Relict channel projection

Knickpoints along a channel profile can be distinguished into two end-member morphologies, i.e. vertical-step and slope-break types ([30]; Figure 2). The former type is defined by a local, discrete increase in channel gradients, which is recognized as a steep elevation drop in river long profile and spikes in slope-area plots (Figure 2a–c). Slope-break knickpoints, on the contrary, are recognized as markers that divide the river long profile into a series of reaches with different channel steepness (Figure 2d–f) [31].

Figure 2

Classification of knickpoints based on channel profile, slope-area scaling, and Chi-z plot. (a)–(c) illustrate the characteristics of vertical-step knickpoints, while (d)–(f) illustrate the characteristics of slope-break knickpoints (adapted from [30].

Paleochannel reconstruction deals with the mobile slope-break knickpoint, above which the channel segment is still under steady-state with the previous tectonic uplift rate [26]. We followed the integral approach by Perron and Royden [15], in which the θ that corresponds to the maximum R ² (correlation coefficient) of the χ * – z * plot is chosen as the relict channel concavity.

Using the relict channel concavity ( θ ), the χ * – z * plot of the paleochannel is calculated. The intercept with the Y-axis, z _b, represents the projected elevation of the paleochannel at the mountain front. And the difference between z _b and the present-day mountain front elevation corresponds to the minimum incision depth of the knickpoint. The reconstructed paleochannel elevation will help in estimating the net surface uplift ( ∆ z = U − E ) and the paleo-relief (Figure 3).

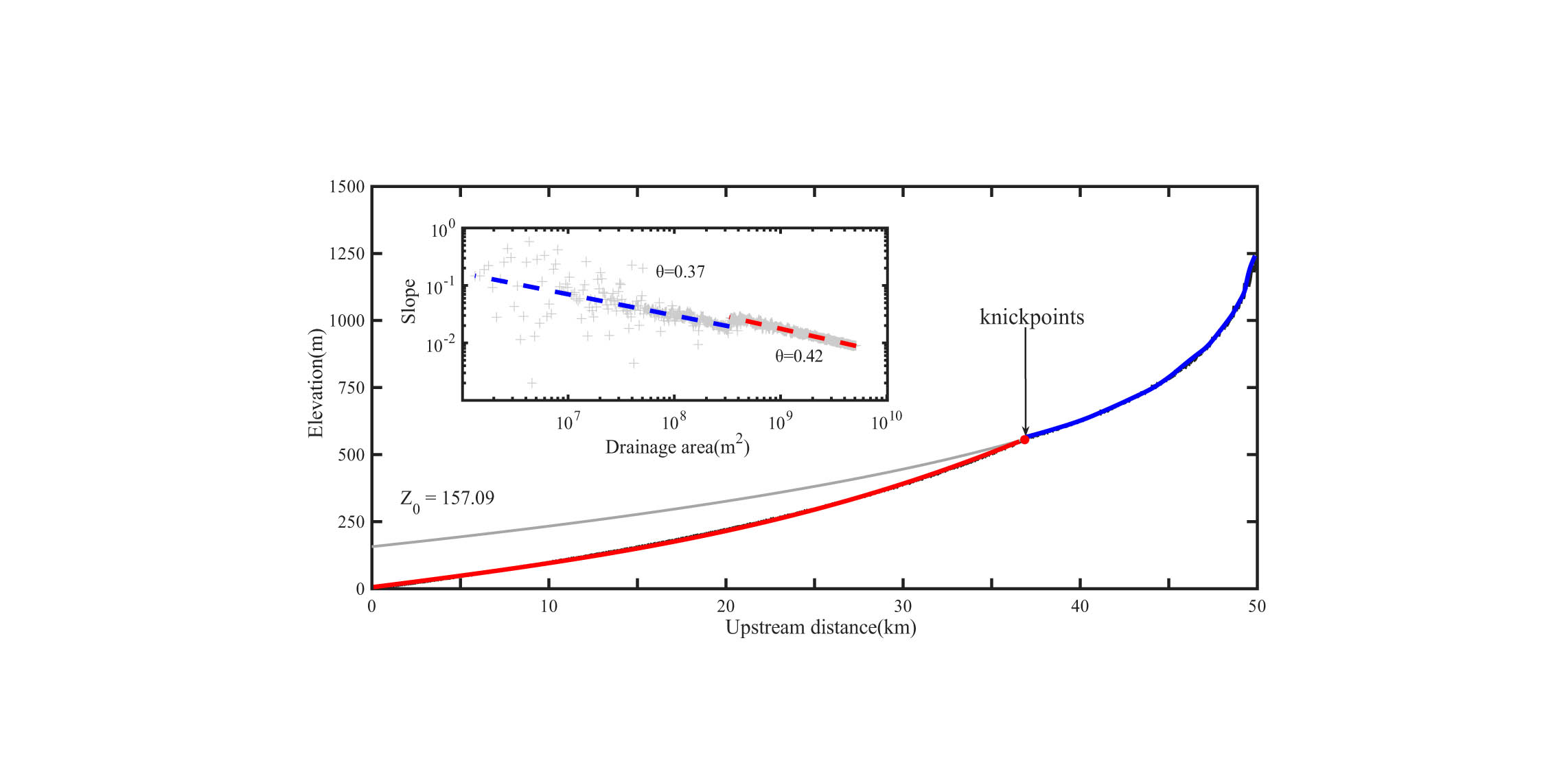
$Figure 3 Numerical profile and slope-area data (inset). Parameters: set θ = 0.45 ; A 0 \theta =0.45{\rm{;}}{A}_{0} = 1 m2; Initial bedrock uplift rate U 0 = 0.1 m m a − 1 {U}_{0}=0.1{\rm{m}}{\rm{m}}{a}^{-1} ; tectonic uplift rate U 1 = 0.3 mm a − 1 {{U}}_{1}=0.3\hspace{0.25em}{\rm{mm}}{a}^{-1} ; erosion coefficient K = 5 × 10 − 7 m m − 0.1 a − 1 K=5\times {10}^{-7}{{\rm{m}}{\rm{m}}}^{-0.1}{a}^{-1} ; h = 2.1; k a = 2/3.$

Figure 3

Numerical profile and slope-area data (inset). Parameters: set θ = 0.45 ; A 0 = 1 m²; Initial bedrock uplift rate U 0 = 0.1 m m a − 1 ; tectonic uplift rate U 1 = 0.3 mm a − 1 ; erosion coefficient K = 5 × 10 − 7 m m − 0.1 a − 1 ; h = 2.1; k _a = 2/3.

4 Case studies

4.1 Numerical cases

We applied the new method to a numerical case to show the importance of using relict channel concavity rather than the reference concavity for re-constructing paleo channel profiles. We first generated a transient profile using the stream-power parameters of channel erodibility K = 5 × 10 − 7 mm − 0.1 a − 1 , n = 2.5, m = 1.125 and hack parameters of h = 2.1 and k _a = 2/3. The Hack’s law is

(12) A = k a ( L − x ) h ,

where L is the river total length, x is the upstream distance, and k _a and h are constants related to river morphology [32,33]. We assumed a steady-state river profile with E 0 = U 0 = 0.1 mm a − 1 . We added random errors via z i ˆ = z i + ( z i + 1 − z i − 1 ) × rand [ 0 , 2 ] , where rand [ 0 , 2 ] is denoted as a random number between 0 and 2.

Then, we imported an uplift history with an increase in the uplift rates to be U 1 = 0.3 mm a − 1 at 1 Ma. Accordingly, the minimum depth of knickpoint incision derived from relict profile reconstruction should be ( U 1 − U 0 ) × t = 200 m.

We used both the slope-area analysis method and the integral approach to reconstruct the relict channel profile. The former method, via the smoothing window = 5 and sampling interval = 10 m, resulted in a concavity value of 0.37 and a knickpoint incision depth of about 157.1 m. However, for the noisy elevation data, the integral approach produced relict channel concavity of 0.46 (Figure 4a). Thus, the differences between the estimated and real parameter values may be more attributed to resampling and differentiating elevation data than to elevation noise itself.

Figure 4

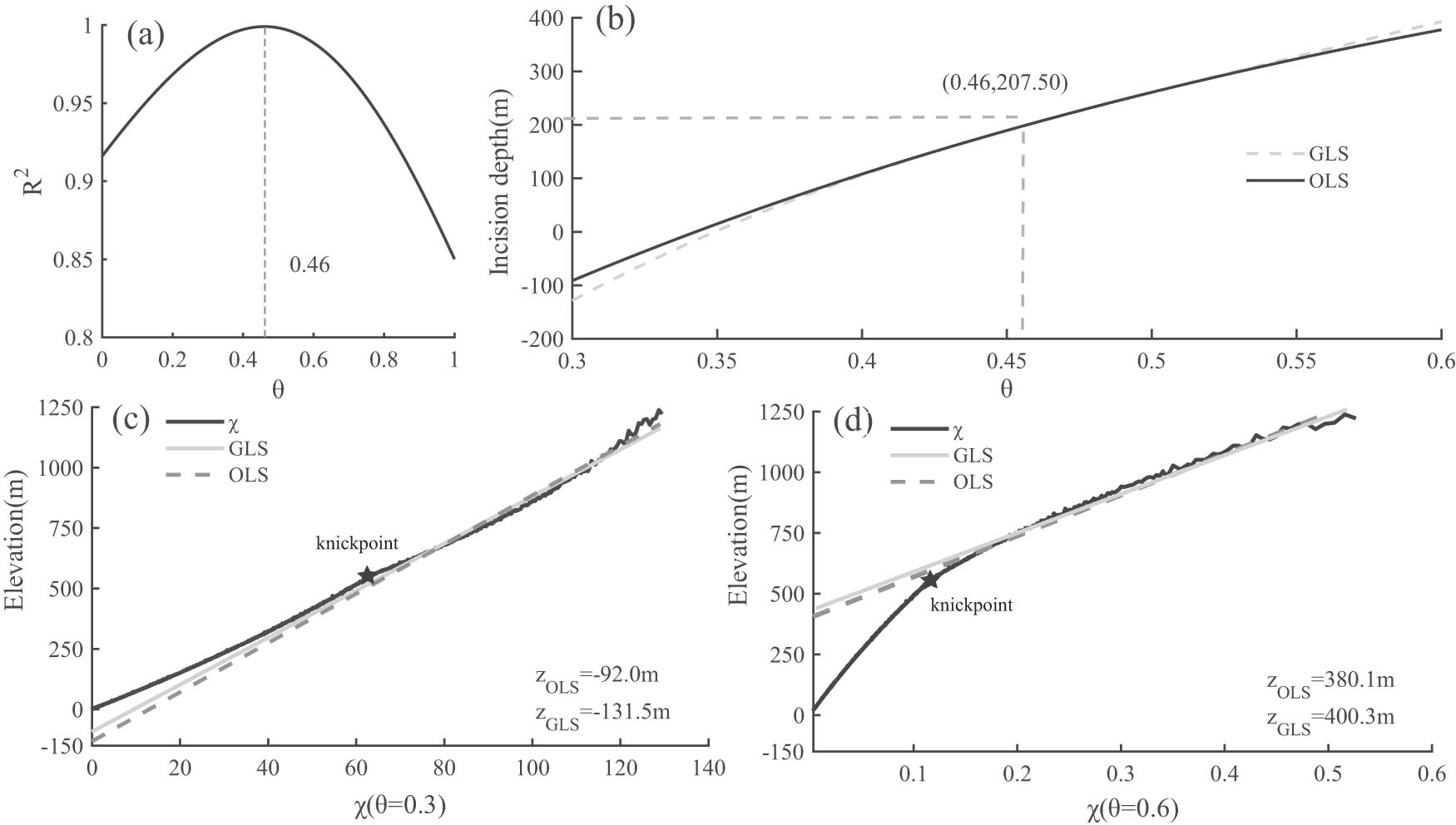
(a) Coefficient of determination (R ²) as a function of concavity, where the peak R² indicates the actual concavity of the river; (b) incision depths calculated by GLS and OLS as the reference concavity varies from 0.3 to 0.6; (c) comparison of chi-z projections of relict channels and calculated incision depths using OLS and GLS for a reference concavity of 0.3 and (d) of 0.6.

Then, based on the integral approach, we utilized a series of reference concavity indices (0.3 and 0.6) to reconstruct the relict profile. We utilized both χ – z (OLS) and χ * – z * (GLS) regression. The results are shown in Figure 4. The estimated incision depth increases as θ _ref increases from 0.3 to 0.6. And, the closer the θ _ref to 0.45, the lower is the difference between the incision amounts derived from the OLS and GLS methods. When θ _ref = 0.3, OLS and GLS produced incision depths of −131.5 and −92.0 m, respectively. θ _ref = 0.6 produced an incision depth of 380.1 m (OLS) and 400.3 m (GLS). When using the concavity (θ = 0.46) derived from the integral approach, the incision depth values calculated by OLS and GLS remain constant at about 207.5 m. Thus, as long as channel concavity is used, both OLS and GLS can nearly produce the real relict channel concavity index and incision depth. However, in many studies, calculating the k _sn -map requires the use of a reference concavity (θ _ref). The autocorrelation of residuals will significantly affect the χ – z fitting. In Section 4.1, we present a detailed discussion on the influences of residual auto-correlation on the χ – z correlation coefficient and channel steepness.

4.2 Natural case – mountains bounding the Taiyuan Basin

The Shanxi Rift, well known as the continental rift system, is located in the eastern margin of the Ordos Plateau and is adjacent to the N-S trending Taihang Mountains [34,35,36]. The Taiyuan Basin is situated in the central region of the Shanxi Rift, with the NNE-oriented Taiyue Shan in the east side and Taiyuanxi Shan in the west [37,38,39]. The Taiyuan basin is constrained by two high-angle normal faults, the Jiaocheng Fault in the west side and the Taigu Fault in the east (Figure 5b). The paleomagnetic chronology of the bottom sediment strata in Taiyuan Basin was dated to be about 8.1 Ma, indicating that the basin formed at the late Miocene [40,41]. Wang et al. extracted two transient river channels in the northern tip of the Taiyuanxi Shan and inferred a tectonic history with increases in the uplift rates since the late Miocene [42]. This previous work indicate that the profiles of rivers draining through the mountains bounding the Taiyuan basin can record a history of mountain growth or fault throw at the time scale of more than 10⁶ year and even provide insights into the basin subsidence if considering the case of basin–mountain coupling mechanism. To minimize the influence of the Fenhe River formation and evolution on incision-depth estimates, we used the Fenhe River elevation as the reference base level for its tributaries. In this study, we analyzed 14 rivers in the Taiyuanxi Shan, 6 rivers in the Taiyue Shan, and 17 rivers in the Fenhe River drainage catchment (locations shown in Figure 5b). We analyzed 34 rivers, of which 20 are under steady-state and 14 are characterized by convex-up knickpoints (this analysis is based on the ALOS-12.5 m DEM data). The locations of the knickpoints and the river profiles are shown in Figure 5c. The concavity of the river channels was calculated using both slope-area method and the integral approach equipped with GLS (results are presented in Figure 6).

Figure 5

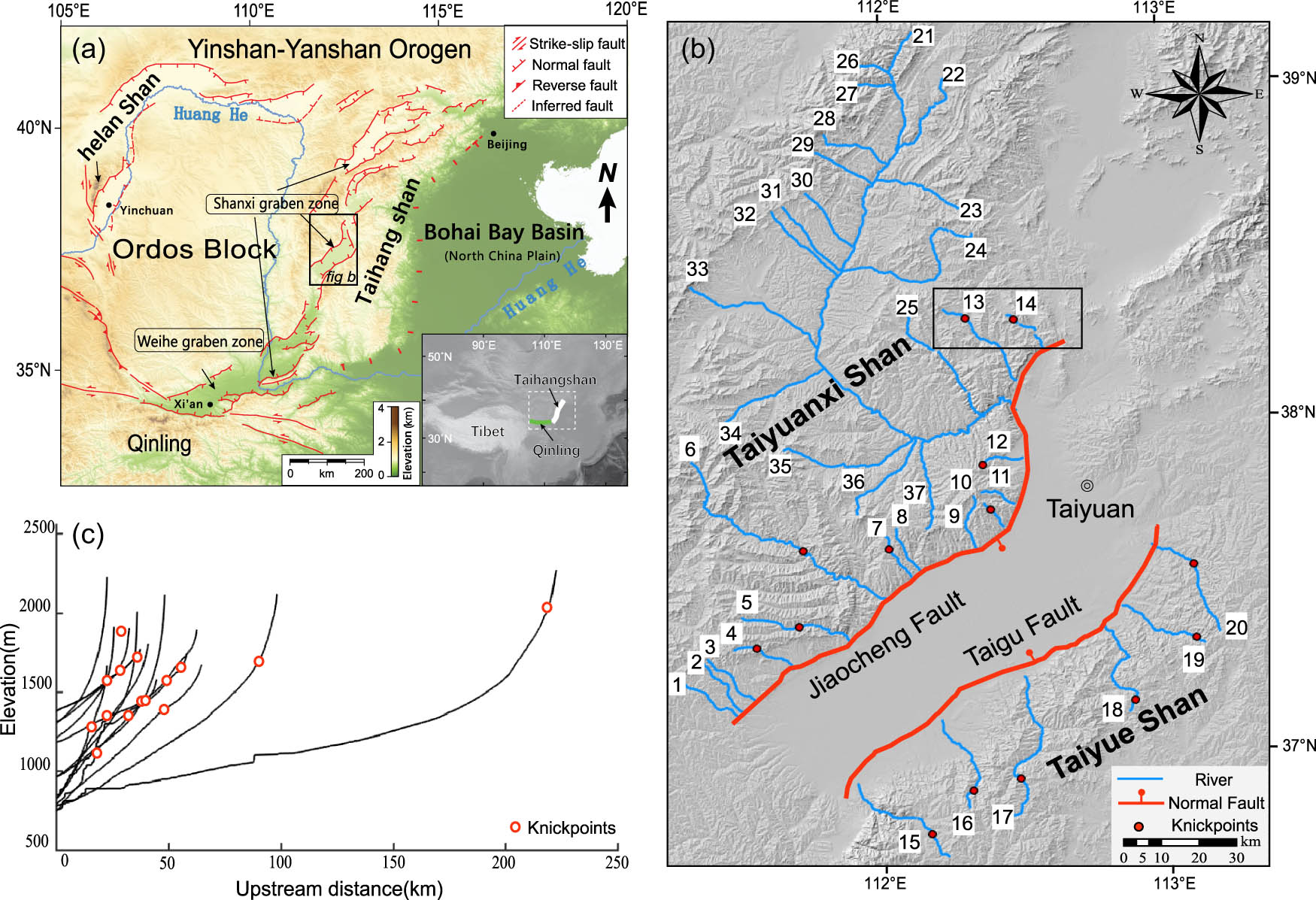
(a) Regional topographic and neotectonic map of North China. Black boxes show the location of the study areas; (b) landforms and rivers around Taiyuan Basin; and (c) river longitudinal profile and location of knickpoints.

Figure 6

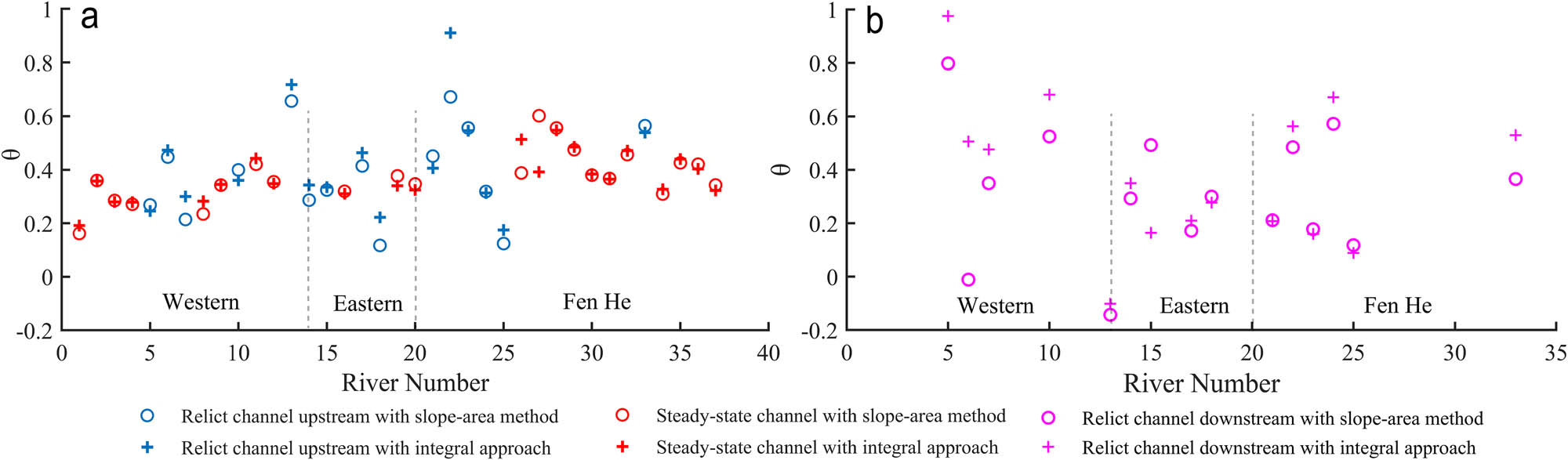
Comparison of results between slope-area analysis and integral approach. (a) Concavity of the steady state channel and the channel upstream of the knickpoint; and (b) the calculated results for the channel below the knickpoints.

Although both methods yield similar concavity index values for steady-state and relict channel profiles, differences are observed for some segments (Figures 6 and 7). Figure 7(a)–(c) shows that, for River 7 on the western side, slope-area analysis produces a concavity of 0.39 and an incision depth of 247.6 m, while our method presents a concavity of 0.3 and an incision depth of 130.5 m. Similarly, for River 17, the slope-area method yields a concavity of 0.42 and an incision depth of 377.4 m, while our method yields a concavity of 0.47 and an incision depth of 367.5 m (Figure 7(d)–(f)). In Figure 7(g)–(i), slope-area analysis on River No. 22 produces a concavity of 0.67 and an incision depth of 92.8 m, while the concavity and incision depth estimated by our method are 0.91 and 136.9 m, respectively.

Figure 7

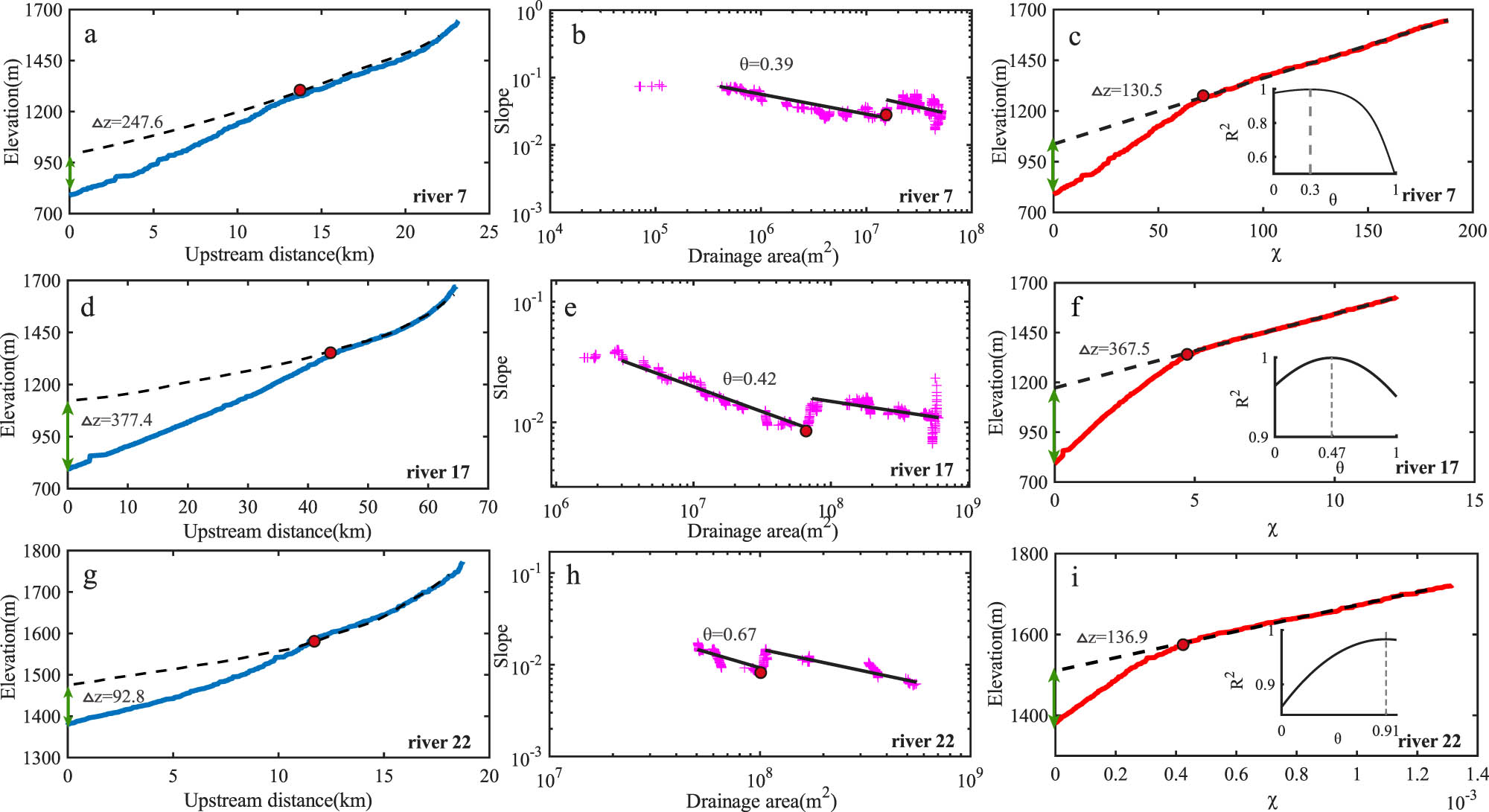
River elevation profile analysis. (a)–(c) Elevation profiles, log-transformed slope–area plot, Chi-plot plots with paleochannel projection for River 7, respectively, and concavity-determination coefficient R ² plots for calculating the true concavity in the middle and lower panels of (c); (d)–(f) for River 17; (g)–(i) for river 22.

Figure 7 shows that knickpoints on river profiles can cause large scatters in the estimated channel gradients, leading to high uncertainties in the calculated concavity indices. When the slope values are with less scatters (Figure 7(d)–(f)), the slope-area method and the integral approach yield similar results. The integral approach is less influenced by noises in topographic data, which can bring results with higher accuracy relative to the slope-area method.

In addition to slope-break knickpoints, vertical-step types can also affect the concavity calculation when using the slope-area method. As shown in Figure 8a (River No. 27), vertical-step knickpoints cause spikes in the slope-area logarithmic plot. This also demonstrates the impact of DEM quality on concavity calculation, as low-precision DEMs tend to contain numerous similar knickpoints resulting from insufficient accuracy. In Figure 8b and c, we changed the elevation smoothing window and sampling interval to test this effect. The results indicate that the concavities derived from the slope-area method vary a lot as the smoothing window and sampling interval change.

Figure 8

Concavity estimation for River 27, which contains vertical step-like knickpoints. (a) Elevation profile and slope-area logarithmic plot of the river; (b) effect of smoothing window size on concavity calculations using the slope-area method and the integral approach with a fixed resampling interval; and (c) effect of resampling interval on concavity calculations with a fixed smoothing window.

Via both the slope-area method and our χ * – z * regression approach, we projected the paleo channels onto river outlet to estimate knickpoint incision depths (Figure 9). The upper part of Figure 9 illustrates significant differences in outlet elevations among rivers at the mountain front. However, the incision depths show limited variation, clustering around two distinct values. This suggests that river location has minimal impact on incision depth, despite the variability in outlet elevations (River Nos. 7 and 22, presented in Figure 7, are specific cases). The lower part of Figure 9 displays the knickpoint incision depths. The incision depth calculated by the two methods are nearly identical, with the slope-area method yielding values of about 180.13 ± 90.04 m (Nos. 13, 14, 15, and 17) and 330.58 ± 87.56 m (other rivers), and the χ * – z * approach yielding values of about 128.29 ± 24.79 m (Nos. 13, 14, 15, and 17) and 339.50 ± 53.56 m (other rivers). However, some rivers, such as River Nos. 7 and 22, exhibit significant differences due to differences in concavity values estimated via the slope-area method. As shown in Figure 9, the χ * – z * approach produces results with less variability than that derived from slope-area method, suggesting that the former method may provide more stable estimates.

Figure 9

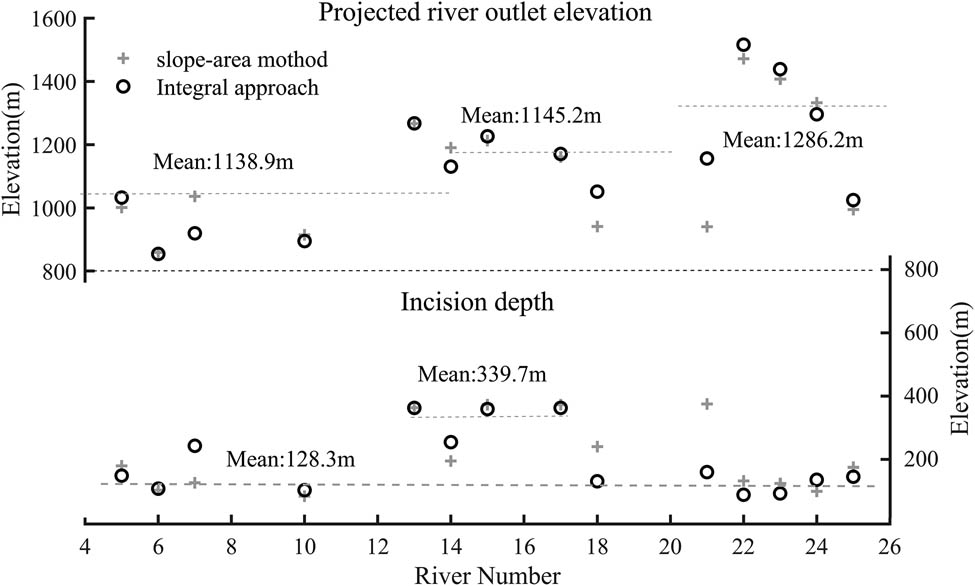
Knickpoint outlet elevation and incision depth in Taiyuan Basin.

5 Discussion

5.1 Influences of smoothing window and re-sampling elevation interval on slope-area analysis

Despite large scatters in the slope dots, the slope-area plot was emphasized for its unique usage in detecting the variations in channel concavity [16]. Theoretical predictions indicate that: (1) a steady-state river should exhibit a smooth concave shape; (2) in the absence of long-wavelength tilting, the concavity of river segments upstream and downstream of a knickpoint should be consistent. However, along real river channels, variations in lithology or landslides and debris flows can lead to departure from theoretical predictions. This is considered to be the reason of large scatters in slope-area plots. However, according to Section 3.1, even for very small elevation noise, resampling and smoothing elevation data can also cause large errors in calculating stream-power parameters. And, there is yet no standard window sizes for smooth and resampling river long profile.

Since in the theistic case, all the parameters can be preset, we used this case to discuss the influences of smoothing and re-sampling windows on calculating slope-area plots and concavity values. First, we fixed the resampling elevation interval at 20 m and changes the smoothing window. Subsequently, we fixed the smoothing window at 10 and varied the resampling interval, with concavity set at 0.46.

The results in Figure 10(a)–(d) show that smaller smoothing windows and resampling intervals lead to greater scatter in slope calculation values. Figure 10e and f further illustrate that parameter changes have a random effect on the concavity calculations, making it difficult to identify an optimal setting. Our conclusions are as follows: (1) resampling interval variations have a greater impact on θ than smoothing windows; and (2) both resampling interval and smoothing window adjustments produce random effects on the results, with no single optimal standard. Consequently, the slope-area method is inherently limited by its calculation approach, resulting in θ values that deviate from the true concavity.

Figure 10

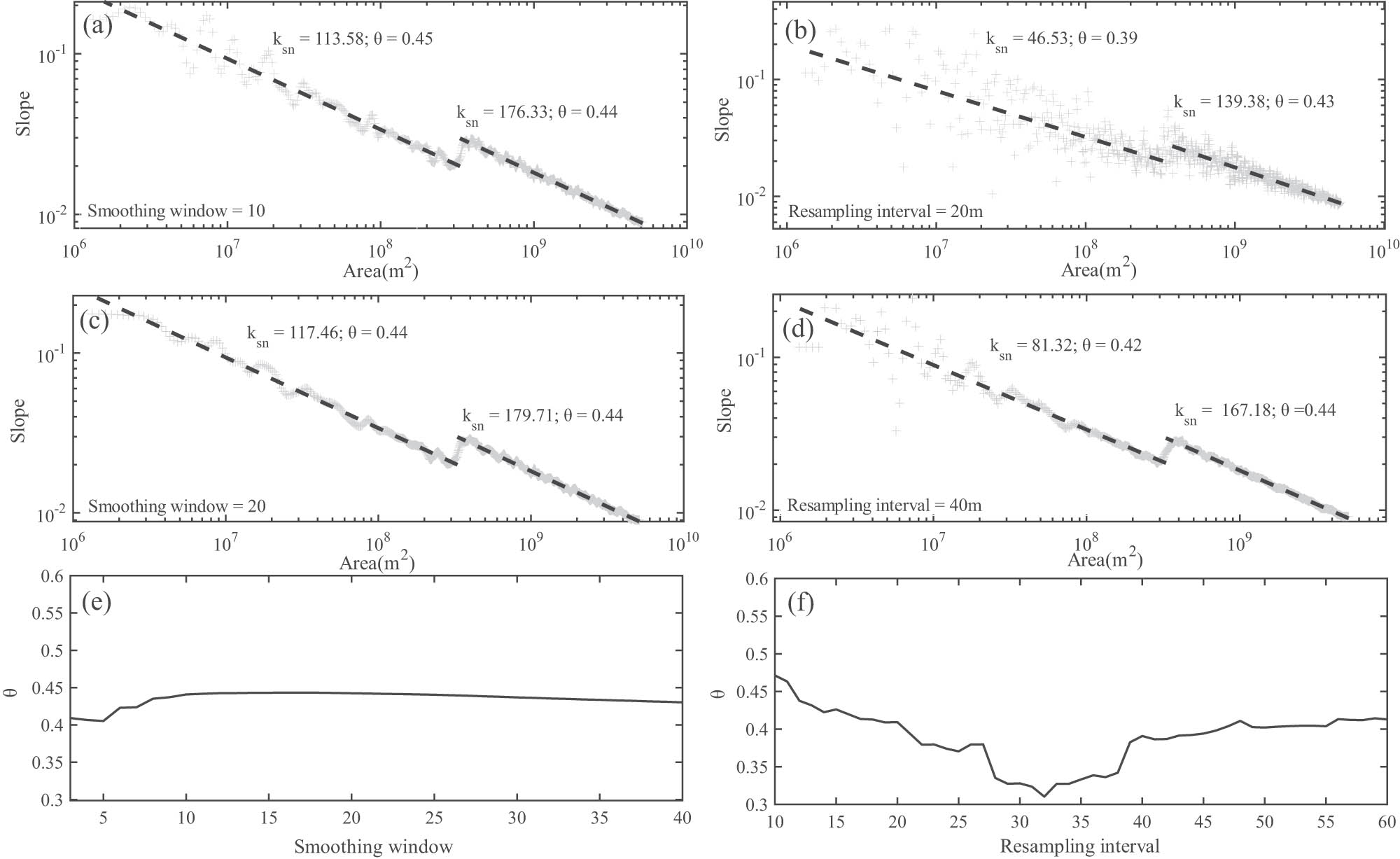
Comparison of results of the slope-area approach. (a) and (c) with no resampling in the plot and smoothing window of 10 and 20; (b) and (d) with no smoothing and resampling intervals of 20 and 40 m, respectively; (e) effect of the smoothing window on the results of concavity calculations; and (f) effect of the results of resampling intervals.

5.2 Residual autocorrelation of χ – z regression

The χ – z profile is a continuous curve, resulting in the serial correlation of the residuals of the linear χ – z regression. Since in previous studies, a reference concavity has always been used to calculate χ and then to fit the χ – z plot, here we present a detailed analysis on how the residual autocorrelation affects the estimated values of channel steepness and knickpoint incision depth. We labeled the correlation coefficient, channel steepness, and incision depth that are derived from the χ – z fit as R ², k _s, and z _b, respectively. Those parameters derived from χ ′ – z ′ fit are labeled as R 2 ′ , k s ′ and z b ′ .

To compare the shape of the χ – z plot under different concavity values, we normalized χ values as shown in Figure 11(a). We found that when the reference concavity is lower than the actual concavity, the χ – z curve bends upward. Conversely, when the reference concavity is higher, the curve bends downward. When the reference concavity is equal to the actual concavity, the χ – z plot is a straight line. This tells us that we may have misunderstood some information encoded in river long profiles when using reference concavity.

Figure 11

(a) Trend of chi values for the reference concavity, where chi values for all concavities are homogenized to [0, 1]; (b)–(e) effect of OLS versus GLS methods on the computed results, with (b) representing the difference in knickpoint incision depths; (c) the k _sn ratio, and (e) the effect of the confidence intervals.

The integral approach chooses theta that best fits χ – z as river concavity. Figure 11(b) shows that both χ – z and χ ′ –z ′ methods produce the same concavity. However, the correlation coefficients differ a lot. As pointed out by Perron and Royden (2013), the R ² of χ – z is overestimated due to residual auto-correlation. We also calculated z _b– z b ′ and k _s/ k s ′ , based on a series of theta values (Figure 11c and d). Only when theta falls into a very narrow range of 0.4 to 0.5, z _b is nearly equal to z b ′ and k _s ∼ k s ′ . This shows that, when the difference between reference concavity and channel actual concavity is no more than 0.05, the k _sn values derived from θ _ref can well map details of spatial patterns of regional incision and/or uplift.

Figure 11(e) shows concavity probability distributions with 95% confidence intervals, [0.18, 0.74] for OLS, and [0.27, 0.65] for GLS, indicating that GLS reduces the uncertainty and improves the accuracy of the estimated incision depth. By addressing serial autocorrelation inherent in the integral approach, GLS mitigates accuracy overestimation, resulting in narrower error intervals. Therefore, applying the GLS approach is essential for obtaining accurate estimates of channel concavity and knickpoint incision depth.

5.3 Implications for the subsidence of the Taiyuan Basin

Based on sediment dating from boreholes in the Taiyuan Basin, during the Pliocene (5.8 Ma), the Lvliang Mountains experienced rapid uplift, while the northern section of the Jiaocheng Fault began to activate [43,44]. The faults within the basin controlled much of the subsidence process, leading to a rapid expansion phase of the Taiyuan Basin. In the Early Pleistocene (2.2 Ma), a tectonic stress field transformation occurred, causing the basin’s extension direction to shift from NW-SE to NE-SW [45,46]. This change led to the rapid activity of the NW-SE-trending faults at the front of the Lingshi Uplift, resulting in renewed uplift of the underlying Lingshi Uplift.

We propose that basin subsidence led to the formation of river knickpoints, all of which occurred during the Pliocene. The results of paleochannel reconstruction indicate that the knickpoint incision depths of rivers surrounding the Taiyuan Basin range from 128.3 to 339.7 m, with rivers 13, 14, 15, and 17 having incision depths around 339.7 m. Rivers 13 and 14 are located in the northern Shilingguan Uplift, while rivers 15 and 17 are situated in the southern Lingshi Uplift. The knickpoint incision depth represents a minimum estimate of net surface uplift. Since these knickpoints formed in the early stages of basin formation during the Pliocene, and given that the overall erosion rate of the basin is likely uniform, it suggests that the uplift rate in the uplifted areas is significantly greater than in other regions. Importantly, the high-incision clusters do not coincide systematically with particular lithologic boundaries, implying that lithology exerts only a secondary, local influence on incision [44]. Instead, this finding aligns with structural analysis results, indicating that the Shilingguan and Lingshi uplifts are the areas with the highest regional uplift rates.

6 Conclusions

In this article, we equipped the integral approach with GLSs for relict channel profile re-construction. Via synthetic river profiles generated by numerical modeling, we demonstrate that (1) the difference between channel concavity and reference concavity, and the residual auto-correlation of the χ – z plot can cause significant errors in the estimated river incision depth, and (2) despite noise in topographic elevation data, our method can produce proper estimates on channel concavity and incision magnitude. By analyzing rivers around the Taiyuan Basin, we find that the uplift rates of the Shilingguan Uplift and Lingshi Uplift since the Pliocene have been higher than those in the surrounding regions.

Acknowledgments

We appreciated the Topographic Analysis Kit (TAK) for providing valuable references in analyzing river profiles.

Funding information: This study was supported by the National Natural Science Foundation of China (Grant No. 42361144839).
Author contributions: Yarong Zhang: writing – original draft, methodology, formal analysis. Yizhou Wang: writing – original draft, project administration, funding acquisition. Hao Xie: writing – original draft, investigation. Chaopeng Li: writing – review & editing, investigation. Huiping Zhang: writing – review & editing.
Conflict of interest: The authors declare no conflict of interest.
Data availability statement: The data used in this study are available upon reasonable request from the corresponding author. The manuscript has not been submitted to this or any other journal previously.

References

[1] Snyder NP, Whipple KX, Tucker GE, Merritts DJ. Landscape response to tectonic forcing: Digital elevation model analysis of stream profiles in the Mendocino triple junction region, northern California. GSA Bull. 2000;112(8):1250–63.10.1130/0016-7606(2000)112<1250:LRTTFD>2.3.CO;2Search in Google Scholar

[2] Burbank DW, Anderson RS. Tectonic geomorphology. 2nd edn. Environ Eng Geosci. 2013;19(2):198–200.10.2113/gseegeosci.19.2.198Search in Google Scholar

[3] Whipple KX. Bedrock rivers and the geomorphology of active orogens. Annu Rev Earth Planet Sci. 2004;32(1):151–85.10.1146/annurev.earth.32.101802.120356Search in Google Scholar

[4] Crosby BT, Whipple KX. Knickpoint initiation and distribution within fluvial networks: 236 waterfalls in the Waipaoa River, North Island, New Zealand. Geomorphology. 2006;82(1–2):16–38.10.1016/j.geomorph.2005.08.023Search in Google Scholar

[5] Berlin MM, Anderson RS. Modeling of knickpoint retreat on the Roan Plateau, western Colorado. J Geophys Res: Earth Surf. 2007;112(F3):F03S06.10.1029/2006JF000553Search in Google Scholar

[6] Willett SD, McCoy SW, Perron JT, Goren L, Chen C-Y. Dynamic reorganization of river basins. Science. 2014;343(6175):1248765.10.1126/science.1248765Search in Google Scholar

[7] Tarboton DG, Bras RL, Rodriguez-Iturbe I. Scaling and elevation in river networks. Water Resour Res. 1989;25(9):2037–51.10.1029/WR025i009p02037Search in Google Scholar

[8] Whipple KX, Hancock GS, Anderson RS. River incision into bedrock: Mechanics and relative efficacy of plucking, abrasion, and cavitation. GSA Bull. 2000;112(3):490–503.10.1130/0016-7606(2000)112<0490:RIIBMA>2.3.CO;2Search in Google Scholar

[9] Wobus C, Whipple KX, Kirby E, Snyder N, Johnson J, Spyropolou K, et al. Tectonics from topography: Procedures, promise, and pitfalls. Tectonics, climate, and landscape evolution. Vol. 398. Boulder, CO, USA: Geological Society of America; 2006.10.1130/2006.2398(04)Search in Google Scholar

[10] Flint JJ. Stream gradient as a function of order, magnitude, and discharge. Water Resour Res. 1974;10(5):969–73.10.1029/WR010i005p00969Search in Google Scholar

[11] Howard AD, Kerby G. Channel changes in badlands. GSA Bull. 1983;94(6):739–52.10.1130/0016-7606(1983)94<739:CCIB>2.0.CO;2Search in Google Scholar

[12] Howard AD, Dietrich WE, Seidl MA. Modeling fluvial erosion on regional to continental scales. J Geophys Res: Solid Earth. 1994;99(B7):13971–86.10.1029/94JB00744Search in Google Scholar

[13] Kirby E, Whipple K. Quantifying differential rock-uplift rates via stream profile analysis. Geology. 2001;29(5):415–8.10.1130/0091-7613(2001)029<0415:QDRURV>2.0.CO;2Search in Google Scholar

[14] Zhang H, Kirby E, Pitlick J, Anderson RS, Zhang P. Characterizing the transient geomorphic response to base‐level fall in the northeastern Tibetan Plateau. J Geophys Res: Earth Surf. 2017;122(2):546–72.10.1002/2015JF003715Search in Google Scholar

[15] Perron JT, Royden L. An integral approach to bedrock river profile analysis. Earth Surf Process Landf. 2013;38(6):570–6.10.1002/esp.3302Search in Google Scholar

[16] Wang Y, Zhang H, Zheng D, Yu J, Pang J, Ma Y. Coupling slope–area analysis, integral approach and statistic tests to steady-state bedrock river profile analysis. Earth Surf Dyn. 2017;5(1):145–60.10.5194/esurf-5-145-2017Search in Google Scholar

[17] Royden L, Clark M, Whipple K. Evolution of river elevation profiles by bedrock incision: Analytical solutions for transient river profiles related to changing uplift and precipitation rates. Eos Trans Am Geophys Union. 2000;81(48):T62F–09.Search in Google Scholar

[18] Sorby A, England P. Critical assessment of quantitative geomorphology in the footwall of active normal faults, Basin and Range province, western USA. EOS Trans Am Geophys Union. 2004;85:7866219.Search in Google Scholar

[19] Kirby E, Whipple KX. Expression of active tectonics in erosional landscapes. J Struct Geol. 2012;44:54–75.10.1016/j.jsg.2012.07.009Search in Google Scholar

[20] Korup O. Rock-slope failure and the river long profile. Geology. 2006;34(1):45–8.10.1130/G21959.1Search in Google Scholar

[21] Gallen SF, Wegmann KW, Bohnenstieh DR. Miocene rejuvenation of topographic relief in the southern Appalachians. GSA Today. 2013;23(2):4–10.10.1130/GSATG163A.1Search in Google Scholar

[22] Schoenbohm LM, Whipple KX, Burchfiel BC, Chen L. Geomorphic constraints on surface uplift, exhumation, and plateau growth in the Red River region, Yunnan Province, China. GSA Bull. 2004;116(7–8):895–909.10.1130/B25364.1Search in Google Scholar

[23] Clark MK, Mahéo G, Saleeby JB, Farley KA. The non-equilibrium landscape of the southern Sierra Nevada, California. GSA Today. 2005;15:4.10.1130/1052-5173(2005)15[4:TNLOTS]2.0.CO;2Search in Google Scholar

[24] Harkins N, Kirby E, Heimsath A, Robinson R, Reiser U. Transient fluvial incision in the headwaters of the Yellow River, northeastern Tibet, China. J Geophys Res: Earth Surf. 2007;112(F3):F03S04.10.1029/2006JF000570Search in Google Scholar

[25] Duvall A, Kirby E, Burbank D. Tectonic and lithologic controls on bedrock channel profiles and processes in coastal California. J Geophys Res: Earth Surf. 2004;109(F3):F03002.10.1029/2003JF000086Search in Google Scholar

[26] Niemann JD, Gasparini NM, Tucker GE, Bras R. Landforms. A quantitative evaluation of Playfair’s law and its use in testing long‐term stream erosion models. Earth Surf Process Landf. 2001;26(12)1317–32.10.1002/esp.272Search in Google Scholar

[27] Kirby E, Whipple KX, Tang W, Chen Z. Distribution of active rock uplift along the eastern margin of the Tibetan Plateau: Inferences from bedrock channel longitudinal profiles. J Geophys Res: Solid Earth. 2003;108(B4):2217.10.1029/2001JB000861Search in Google Scholar

[28] Prais SJ, Winsten CB. Trend estimators and serial correlation. Chicago, IL: Cowles Commission (Discussion Paper No. 383); 1954.Search in Google Scholar

[29] Hamilton JD. Chapter 50 State-space models. Handbook of econometrics. Vol. 4. Amsterdam, Netherlands: Elsevier; 1994. p. 3039–80.10.1016/S1573-4412(05)80019-4Search in Google Scholar

[30] Haviv I, Enzel Y, Whipple KX, Zilberman E, Matmon A, Stone J, et al. Evolution of vertical knickpoints (waterfalls) with resistant caprock: Insights from numerical modeling. J Geophys Res: Earth Surf. 2010;115(F3):F03028.10.1029/2008JF001187Search in Google Scholar

[31] Whipple KX. The influence of climate on the tectonic evolution of mountain belts. Nat Geosci. 2009;2(2):97–104.10.1038/ngeo413Search in Google Scholar

[32] Hack JT. Studies of longitudinal stream profiles in Virginia and Maryland. Washington, D.C.: U.S. Government Printing Office; Report. 1957. Report No.: 294B.10.3133/pp294BSearch in Google Scholar

[33] Sassolas-Serrayet T, Cattin R, Ferry M. The shape of watersheds. Nat Commun. 2018;9(1):3791.10.1038/s41467-018-06210-4Search in Google Scholar

[34] Chen G. On the geotectonic nature of the Fen-Wei rift system. Tectonophysics. 1987;143(1):217–23.10.1016/0040-1951(87)90091-6Search in Google Scholar

[35] Xu X, Ma X, Deng Q. Neotectonic activity along the Shanxi rift system, China. Tectonophysics. 1993;219(4):305–25.10.1016/0040-1951(93)90180-RSearch in Google Scholar

[36] Clinkscales C, Kapp PA, Wang H. Exhumation history of the north-central Shanxi Rift, North China, revealed by low-temperature thermochronology. Earth Planet Sci Lett. 2020;536:116146.10.1016/j.epsl.2020.116146Search in Google Scholar

[37] Xu Y, Yue L, Yue L, Li J, Li J, Sun L, et al. An 11-Ma-old red clay sequence on the Eastern Chinese Loess Plateau. Palaeogeogr, Palaeoclimatol, Palaeoecol. 2009;284:383–91.10.1016/j.palaeo.2009.10.023Search in Google Scholar

[38] Shi W, Dong S, Hu J. Neotectonics around the Ordos Block, North China: A review and new insights. Earth-Sci Rev. 2020;200:102969.10.1016/j.earscirev.2019.102969Search in Google Scholar

[39] Chen X, Dong S, Shi W, Zuza AV, Li Z, Chen P, et al. Magnetostratigraphic ages of the Cenozoic Weihe and Shanxi Grabens in North China and their tectonic implications. Tectonophysics. 2021;813:228914.10.1016/j.tecto.2021.228914Search in Google Scholar

[40] Yin A. Cenozoic tectonic evolution of Asia: A preliminary synthesis. Tectonophysics. 2010;488(1–4):293–325.10.1016/j.tecto.2009.06.002Search in Google Scholar

[41] Wei R, Zhuang Q, Yan J, Wei Y, Du Y, Fan J. Late Cenozoic stratigraphic division and sedimentary environment of Jinzhong Basin in Shanxi Province, with the climate and lake evolution since the pre-Qin period (2500 years ago). Geol China. 2022;49(3):912–28.Search in Google Scholar

[42] Wang Y, Zheng D, Zhang H. The methods and program implementation for river longitudinal profile analysis—RiverProAnalysis, a set of open-source functions based on the Matlab platform. Sci China Earth Sci. 2022;65(9):1788–809.10.1007/s11430-021-9938-xSearch in Google Scholar

[43] Pan F, Li J, Xu Y, Wingate MTD, Yue L, Li Y, et al. Uplift of the lüliang mountains at ca. 5.7 Ma: Insights from provenance of the Neogene eolian red clay of the eastern Chinese Loess Plateau. Palaeogeogr Palaeoclimatol Palaeoecol. 2018;502:63–73.10.1016/j.palaeo.2018.04.024Search in Google Scholar

[44] Zhuang Q, Wei R, He H. Depositional record and geochemistry constraints on the late miocene–quaternary evolution of the taiyuan basin in shanxi rift system, China. Front Earth Sci. 2022;10:833585.10.3389/feart.2022.833585Search in Google Scholar

[45] Wang M, Shen Z-K. Present-day crustal deformation of continental china derived from GPS and its tectonic implications. J Geophys Res: Solid Earth. 2020;125(2):e2019JB018774.10.1029/2019JB018774Search in Google Scholar

[46] Ao H, Rohling EJ, Zhang R, Roberts AP, Holbourn AE, Ladant J-B, et al. Global warming-induced Asian hydrological climate transition across the Miocene–Pliocene boundary. Nat Commun. 2021;12(1):6935.10.1038/s41467-021-27054-5Search in Google Scholar PubMed PubMed Central

Received: 2024-12-09

Revised: 2025-08-20

Accepted: 2025-09-17

Published Online: 2025-10-21

This work is licensed under the Creative Commons Attribution 4.0 International License.

Articles in the same Issue

https://doi.org/10.1515/geo-2025-0900

Keywords for this article

slope-break knickpoint; concavity index; relict channel profile reconstruction; the integral approach; generalized least squares; Shanxi Rift

Creative Commons

BY 4.0