Home Compressive forces influence on the vibrations of double beams
Article Open Access

Compressive forces influence on the vibrations of double beams

  • Qasim Abbas Atiyah EMAIL logo and Imad Abdulhussein Abdulsahib
Published/Copyright: May 9, 2023
Download Article (PDF)
Become an author with De Gruyter Brill
Submit Manuscript Author Information
Open Engineering
From the journal Open Engineering Volume 13 Issue 1

Abstract

The influence of compressive forces on the lower and upper natural frequencies of the double beams has been studied in this article. Euler–Bernoulli’s hypotheses have been used to derive the natural frequency equations. Two asymmetric beams were assumed in this work, and four different boundary conditions were applied in these equations: Pinned–Pinned, Clamped–Clamped, Clamped–Free, and Clamped–Pinned. When the axial compressive force is increased about 18 times, it is observed that the lower natural frequencies decreased by 19% for PP beam, 8% for CC beam, 81% for CF beam, and 12% for CP beam. However, the greatest effect of the axial force on the higher frequencies is by reducing it in the CC beam by a ratio that does not exceed 2%. A rise in the values of axial compressive force causes a reduction in the lower natural frequencies, mostly for the CF beam, while it has a little effect on the higher natural frequencies. Similarly, when the compressive forces on the upper and lower beams fluctuate simultaneously, their effect is doubled on the frequencies when the axial compressive force on one of the two beams changes only.

Keywords: double beam; vibration of beam; compressive force

1 Introduction

The double beam is considered one of the relatively recent developments in the field of creating materials that have unique properties of high resistance to stress and shock through the two outer layers and high flexibility with the light weight of the inner layer connecting between these two layers, which gave it a high resistance to bear the stresses of buckling and bending and gave these materials a wide space for engineering applications in aerospace fields such as aircraft structures, marine applications, the automotive industry, and structural applications. The vibration of beam constructions is essential in mechanical, civil, and aeronautical engineering. A double beam is a type of composite beam construction that is linked together to form a single beam. For different purposes, the beam’s thickness and material qualities may vary. Zhang et al. [1,2] evaluated the vibrations of a coupled S.S double-beam system under compressive load using Bernoulli–Euler beam theory. A Winkler elastic layer is supposed to connect the two beams of the system indefinitely. The system’s dynamic reactions to arbitrarily disperse continuous loads were determined, for two situations with specific excitation loadings. Zhao et al. [3,4,5] investigated the closed-form solutions of a Timoshenko double-beam forced transverse vibration under compressive axial stress. The two beams are represented by the Timoshenko model. The steady-state of the linked double-beam system was derived from the Laplace transform. Mao and Wattanasakulpong [6,7] evaluated the free vibration of a cantilever double-beam system that is constantly linked. The differential equations for the double beam were expressed as a recursive algebraic equation based on the AMDM. Fei et al. [8,9,10] investigated the vibration properties of inclined double-beam. Two elastic beams make up the double-beam system of varying mass which are connected by elastic springs. A tensile axial force was used on the beam with the higher rigidity mass. The dynamic equations of the double beam were developed by concurrently taking into account the effects of stiffness, sag, and other parameters. The element and stiffness matrix was generated from the governing equations to get the dynamic balance equations of the system. Sari et al. [11] studied the free vibration and stability assessments of single and double composite beams. A constant axially compressive or tensile force was applied to the closed-section beams. A layer of rotational and translational springs is supposed to link the twin beams. The discretization process was utilized to find the partial differential equations. On the mode forms, the critical loads, natural frequencies, impacts of elastic layer characteristics, axial forces, and boundary conditions have been examined. Stojanović et al. [12,13] investigated the effects of rotating inertia on the vibration and buckling of a double beam. The starting value and boundary value difficulties have been solved. An elastically coupled double-beam complex system’s natural frequencies and amplitude ratios were determined. The influence of physical characteristics describing the vibrating system on the natural frequency, critical buckling load, and amplitude ratios was examined in the theoretical analysis. Kozić et al. [14] prepossessed an analytical method for defining the properties of coupled parallel beams subjected to axial force. For a complicated system, the amplitude ratio, natural frequencies, and critical buckling stress were calculated. Abdulsahib and Abbas Atiyah [15,16] investigated the influence of nonlinear elasticity on the frequency of sandwich beams with arbitrary boundary conditions. The energy balancing technique was used to calculate the effect of the inner layer’s non-linearity stiffness on those frequencies. The behavior of the higher and lower natural frequencies of the asymmetric doubled beams will be studied under various boundary conditions, with the influence of a number of properties, such as the difference in thickness of the two beams, their mass densities, their elasticity modulus, the properties of the connected layer between them, or the length of beams. Milenković et al. [17] studied the natural frequencies of a Rayleigh double-beam system with a Keer layer in-between and the influence of axial stress. It was considered that the system’s two beams being continually linked by a Keer layer. The system’s equations of motion were defined by a number of differential equations. The standard Bernoulli–Fourier approach was employed to resolve these equations, and the Rayleigh theory was applied to derive the natural frequency and amplitude ratio of the examined model. Abbas Atiyah and Abdulsahib [18,19] examined the effect of four geometric and material properties on the twin beam vibration. The intermediate layer’s properties, as well as the mass density, thickness, and modulus of elasticity of the two beams, were investigated. The Bernoulli–Euler beam equation was used to calculate the frequencies of the twin beams. In this article, the influence of the axial compressive forces on the lower and higher natural frequencies of the double beams was studied. Euler–Bernoulli’s hypotheses have been used to derive the natural frequency equations. Two asymmetric beams were assumed in this work, and four different boundary conditions were applied in these equations: Pinned–Pinned, Clamped–Clamped, Clamped–Free, and Clamped–Pinned.

2 Theoretical work

Assuming two asymmetric beams joined by an elastic layer. Compressive axial loads are applied to both ends of each beam (F 1) and (F 2), respectively. Each beam has a different thickness (h), mass density (ρ), and modulus of elasticity (E), as shown in Figure 1. The two beams have the same length (L) and width (b). The Bernoulli–Euler beam theory was used to find the equations of motion as follows:

(1) ∂ 2 ∂ x 2 E 1 I 1 ∂ 2 W 1 ∂ x 2 + K ( W 1 − W 2 ) + ρ 1 A 1 ∂ 2 W 1 ∂ t 2 + F 1 ∂ 2 W 1 ∂ x 2 = 0 ,

(2) ∂ 2 ∂ x 2 E 2 I 2 ∂ 2 W 2 ∂ x 2 − K ( W 1 − W 2 ) + ρ 2 A 2 ∂ 2 W 2 ∂ t 2 + F 2 ∂ 2 W 2 ∂ x 2 = 0 ,

where, A 1 , A 2 , E , I 1 , I 2 , W 1 , and W 2 are the cross-sectional areas, modulus of elasticity, moments of area, and the deflection for the upper and lower beam, respectively.

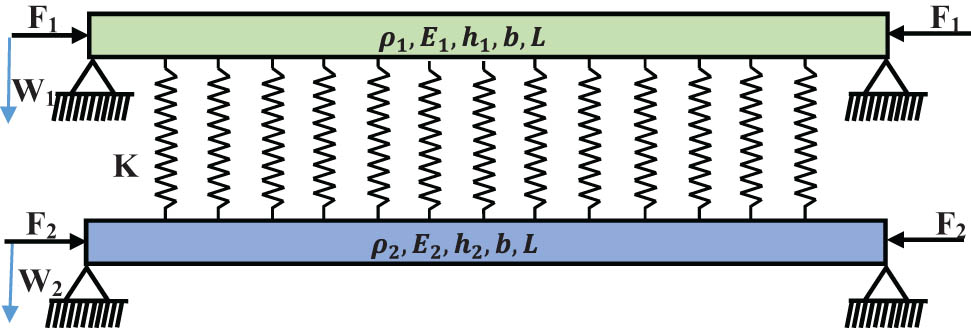
Figure 1 Asymmetric double beam with compressive loads on ends.
Figure 1

Asymmetric double beam with compressive loads on ends.

The following Boundary conditions were used in this work:

For Cantilever (Pinned–Free) beam:

(3) W 1 ( 0 , t ) = W 1 ́ ( 0 , t ) = W 1 ́ ́ ( L , t ) = W 1 ́ ́ ́ ( L , t ) = 0 ,

(4) W 2 ( 0 , t ) = W 2 ́ ( 0 , t ) = W 2 ́ ́ ( L , t ) = W 2 ́ ́ ́ ( L , t ) = 0 ,

For Pinned–Pinned beam:

(5) W 1 ( 0 , t ) = W 1 ́ ( 0 , t ) = W 1 ( L , t ) = W 1 ́ ( L , t ) = 0

(6) W 2 ( 0 , t ) = W 2 ́ ( 0 , t ) = W 2 ( L , t ) = W 2 ́ ( L , t ) = 0

For Simply supported-Simply supported beam:

(7) W 1 ( 0 , t ) = W 1 ́ ́ ( 0 , t ) = W 1 ( L , t ) = W 1 ́ ́ ( L , t ) = 0 ,

(8) W 2 ( 0 , t ) = W 2 ́ ́ ( 0 , t ) = W 2 ( L , t ) = W 2 ́ ́ ( L , t ) = 0 .

For Free–Free beam:

(9) W 1 ́ ́ ( 0 , t ) = W 1 ́ ́ ́ ( 0 , t ) = W 1 ́ ́ ( L , t ) = W 1 ́ ́ ́ ( L , t ) = 0 ,

(10) W 1 ́ ́ ( 0 , t ) = W 1 ́ ́ ́ ( 0 , t ) = W 1 ́ ́ ( L , t ) = W 1 ́ ́ ́ ( L , t ) = 0 .

For Pinned-simply Supported beam:

(11) W 1 ( 0 , t ) = W 1 ́ ( 0 , t ) = W 1 ( L , t ) = W ́ ́ 1 ( L , t ) = 0 ,

(12) W 2 ( 0 , t ) = W 2 ́ ( 0 , t ) = W 2 ( L , t ) = W 2 ́ ́ ( L , t ) = 0 .

In order to solve equations (1) and (2), the following functions are assumed:

(13) W 1 ( x , t ) = ∑ n = 1 ∞ X n 1 ( x ) · T n 1 ( t ) ,

(14) W 2 ( x , t ) = ∑ n = 1 ∞ X n 2 ( x ) · T n 2 ( t ) .

here:

(15) T n 1 = D 1 e j ω n t ,

(16) T n 2 = D 2 e j ω n t ,

(17a) X n 1 ( x ) = C 1 sin β n 1 x + C 2 cos β n 1 x + C 3 sinh β n 1 x + C 4 cosh β n 1 x ,

(17b) X n 2 ( x ) = C 5 sin β n 2 x + C 6 cos β n 2 x + C 7 sinh β n 2 x + C 8 cosh β n 2 x ,

(18) β ni = ω ni 2 ρ i A i E i I i , i = 1 , 2 .

When substituting equations (15)–(17) into equations (1) and (2), one gets:

(19) ∑ n = 1 ∞ { [ ( E 1 I 1 β n 1 4 + K − F 1 β n 1 2 ) − ρ 1 A 1 ω n 2 ] T n 1 − K T n 2 } X n ,

(20) ∑ n = 1 ∞ { − K T n 1 + [ ( E 2 I 2 β n 2 4 + K − F 2 β n 2 2 ) − ρ 2 A 2 ω n 2 ] T n 2 } X n .

The differential equations (19) and (20) can be expressed as follows:

(21) E 1 I 1 β n 1 4 + K ρ 1 A 1 − β n 1 2 ρ 1 A 1 F 1 − ω n 2 D 1 − K ρ 1 A 1 D 2 = 0 ,

(22) − K ρ 2 A 2 D 1 + E 2 I 2 β n 2 4 + K ρ 2 A 2 − β n 2 2 ρ 2 A 2 F 2 − ω n 2 D 2 = 0 .

Equations (20) and (21) can be expressed in matrix form as follows:

(23) E 1 I 1 β n 1 4 + K ρ 1 A 1 − β n 1 2 ρ 1 A 1 F 1 − ω n 2 − K ρ 1 A 1 − K ρ 2 A 2 E 2 I 2 β n 2 4 + K ρ 2 A 2 − β n 2 2 ρ 2 A 2 F 2 − ω n 2 D 1 D 2 = 0 0 .

The non-trivial solution of equation (23) is as follows:

(24) ω n 4 − E 1 I 1 β n 1 4 + K ρ 1 A 1 − β n 1 2 ρ 1 A 1 F 1 + E 2 I 2 β n 2 4 + K ρ 2 A 2 − β n 2 2 ρ 2 A 2 F 2 2 + ω n 2 + E 1 I 1 β n 1 4 + K ρ 1 A 1 − β n 1 2 ρ 1 A 1 F 1 E 2 I 2 β n 2 4 + K ρ 2 A 2 − β n 2 2 ρ 2 A 2 F 2 − K 2 ρ 1 A 1 ρ 2 A 2 = 0 .

From equation (24), the lower natural frequency is:

(25) ω n 1 = 1 2 E 1 I 1 β n 1 4 + K ρ 1 A 1 − β n 1 2 ρ 1 A 1 F 1 + E 2 I 2 β n 2 4 + K ρ 2 A 2 − β n 2 2 ρ 2 A 2 F 2 − E 1 I 1 β n 1 4 + K ρ 1 A 1 − β n 1 2 ρ 1 A 1 F 1 + E 2 I 2 β n 2 4 + K ρ 2 A 2 − β n 2 2 ρ 2 A 2 F 2 2 − 4 E 1 I 1 β n 1 4 + K ρ 1 A 1 − β n 1 2 ρ 1 A 1 F 1 E 2 I 2 β n 2 4 + K ρ 2 A 2 − β n 2 2 ρ 2 A 2 F 2 − K 2 ρ 1 A 1 ρ 2 A 2 .

And, the higher natural frequency is:

(26) ω n 2 = 1 2 E 1 I 1 β n 1 4 + K ρ 1 A 1 − β n 1 2 ρ 1 A 1 F 1 + E 2 I 2 β n 2 4 + K ρ 2 A 2 − β n 2 2 ρ 2 A 2 F 2 + E 1 I 1 β n 1 4 + K ρ 1 A 1 − β n 1 2 ρ 1 A 1 F 1 + E 2 I 2 β n 2 4 + K ρ 2 A 2 − β n 2 2 ρ 2 A 2 F 2 2 − 4 E 1 I 1 β n 1 4 + K ρ 1 A 1 − β n 1 2 ρ 1 A 1 F 1 E 2 I 2 β n 2 4 + K ρ 2 A 2 − β n 2 2 ρ 2 A 2 F 2 − K 2 ρ 1 A 1 ρ 2 A 2 .

When applying the boundary conditions in equations (7)–(14), the following shape functions can be obtained [33]:

(27) X n ( x ) = cos h ( β n x ) − cos ( β n x ) − σ n [ sin h ( β n x ) − sin ( β n x ) ] , β n = π ( 2 n + 1 ) 2 , n = 1 , 2 , 3 , … , σ n ≅ 1 for Clamped beams ,

(28) X n ( x ) = sin ( β n x ) , β n = n π , n = 1 , 2 , 3 , … for Pinned beams ,

(29) X n ( x ) = cos h ( β n x ) + cos ( β n x ) − σ n [ sin h ( β n x ) + sin ( β n x ) ] , β n = π ( 2 n + 1 ) 2 , n = 1 , 2 , 3 , … , σ n ≅ 1 for Free beams ,

(30) X n ( x ) = cos h ( β n x ) − cos ( β n x ) − σ n [ sin h ( β n x ) − sin ( β n x ) ] , β n = π ( 2 n − 1 ) 2 , n = 1,2,3 , … , σ n ≅ 1 for Cantilever beam ,

(31) X n ( x ) = cos h ( β n x ) − cos ( β n x ) − σ n [ sin h ( β n x ) − sin ( β n x ) ] , β n = π ( 4 n + 1 ) 4 , n = 1,2,3 , … , σ n ≅ 1 for Clamped − Pinned beams .

3 Results and discussions

Table 1 shows the first lower and higher eight natural frequency values for a double beam under compressive axial load for PP, CC, CF, and CP boundary conditions.

Table 1

First six lower and higher natural frequencies for double beam

No.of mode PP Beam CC Beam CF Beam CP Beam
L H L H L H L H
1 27.734 103.774 63.184 118.288 9.720 100.471 43.465 109.038
2 111.678 149.906 174.600 201.210 62.223 117.778 141.407 173.194
3 251.583 270.728 342.523 356.822 174.669 201.269 295.302 311.774
4 447.449 458.487 566.368 575.128 342.518 356.817 505.157 514.960
5 699.277 706.391 846.177 852.065 566.366 575.126 770.972 777.430

ρ 1 = ρ 2 = 2 , 000 kg / m 3 , E 1 = E 2 = 1 × 10 11 N / m 2 , K = 10 5 N / m 2 , F 1 = F 2 = 1 , 000 N , L = 6 m , b = 0 . 2 m , h = 0 . 05 m .

The influence of the axial compressive force on the natural frequencies can be seen in Figures 2 and 3, and Table 2. When the axial compressive force is increased from 2,000 to 38,000 N, it is noticed that the lower natural frequencies decreased by 19% for the PP beam, 8% for the CC beam, 81% for the CF beam, and by 12% for the CP beam. While the greatest effect of the compressive force on the higher frequencies is by reducing it in the CC beam by a ratio that does not exceed 2%. Therefore, it can be concluded that the axial compressive force has a clear effect by reducing the lower natural frequencies, especially for the CF beam, and its effect is almost marginal on the higher frequencies. The same effect and behavior of the frequencies were observed when the axial compressive force on the upper beam of the double beam changed with the stability of the force value on the lower beam or when the effect was reversed by changing the compressive force on the lower beam and fixing it on the upper beam.

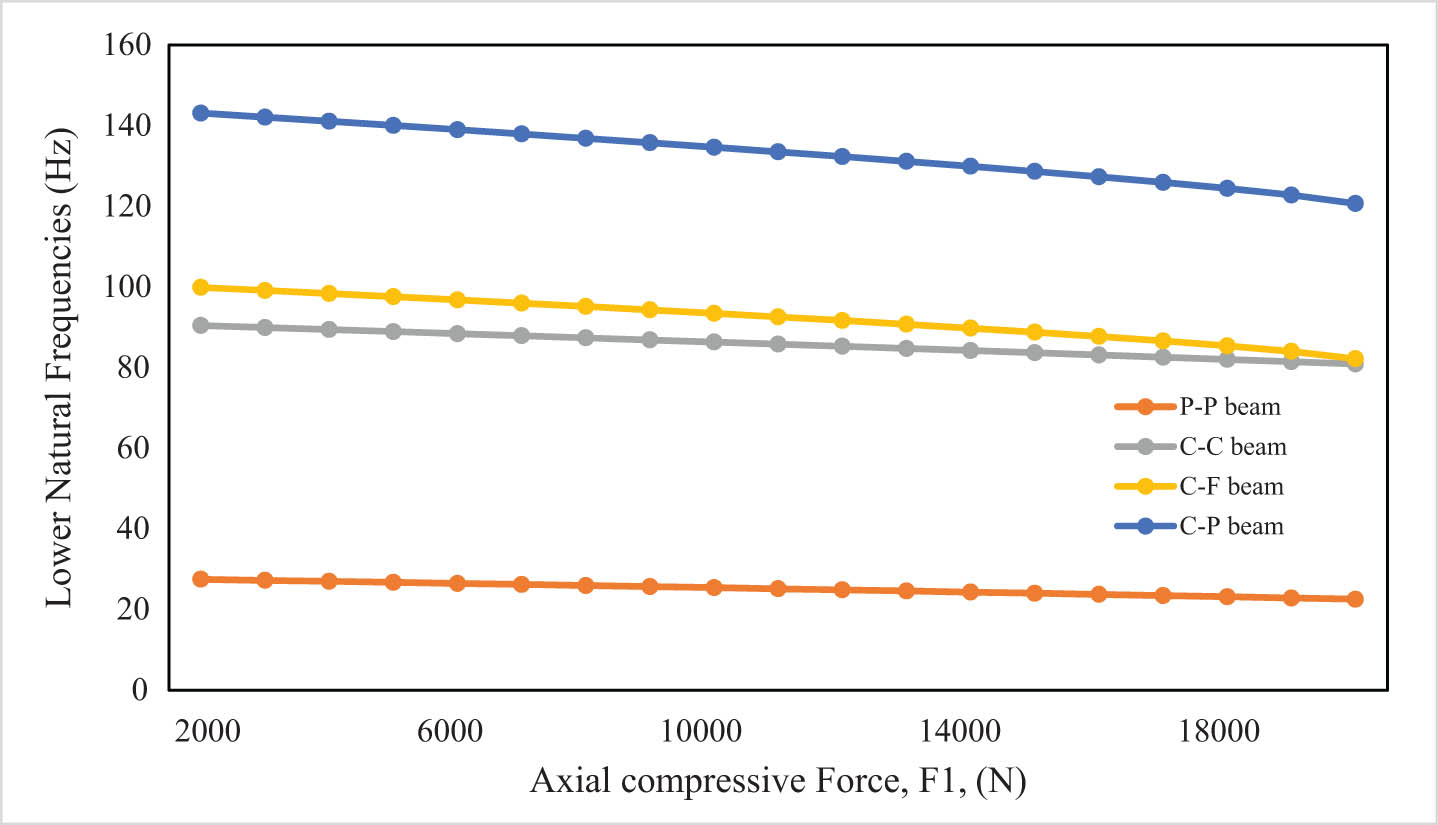
Figure 2 Lower natural frequency vs the axial compressive force (F 1).
Figure 2

Lower natural frequency vs the axial compressive force (F 1).

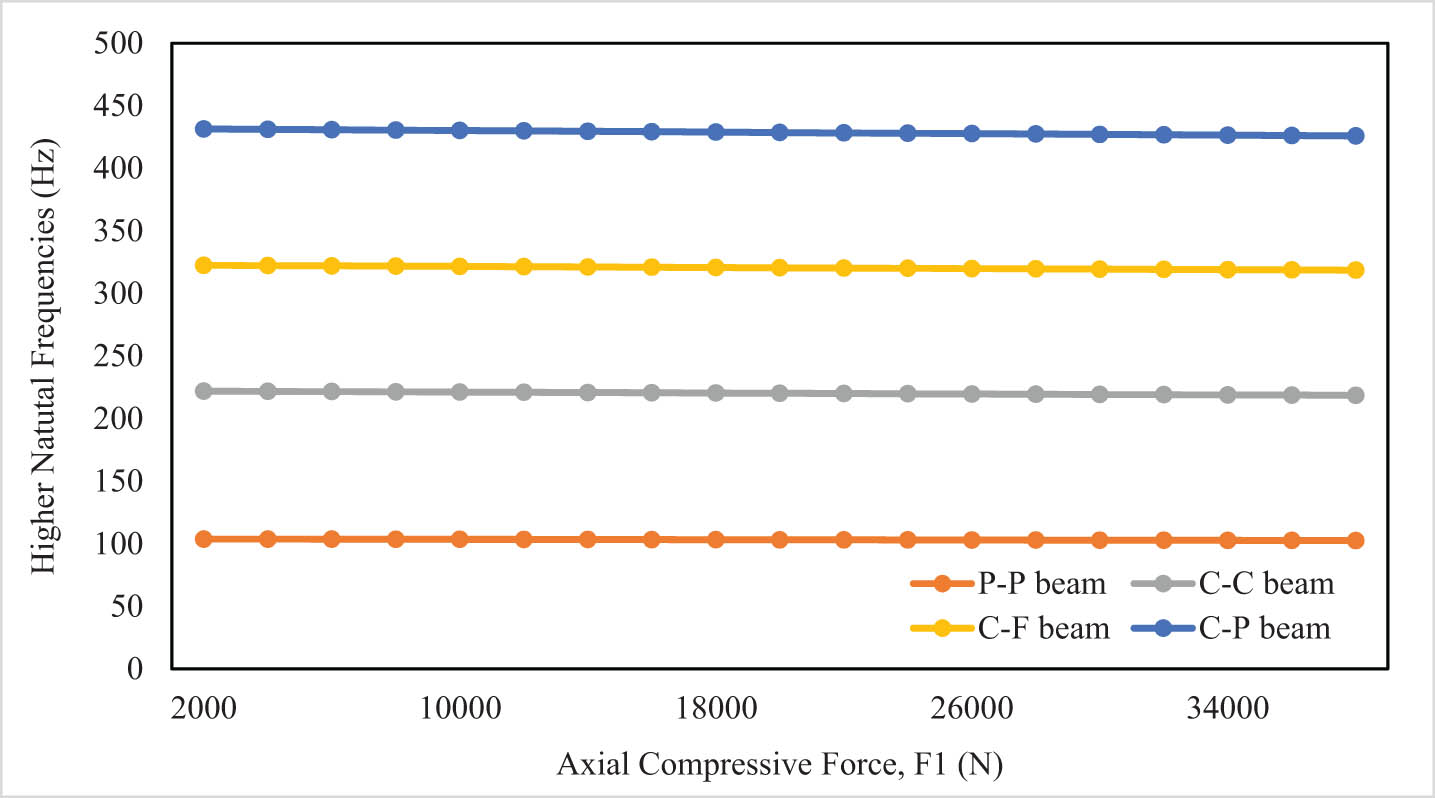
Figure 3 Higher natural frequency vs the axial compressive force (F 1).
Figure 3

Higher natural frequency vs the axial compressive force (F 1).

Table 2

The natural frequencies vs the axial compressive force

F 1 (N) PP Beam CC Beam CF Beam CP beam
L H L H L H L H
2,000 27.61095 103.7419 63.0608 118.2232 9.59361 100.4591 43.34236 108.9889
4,000 27.36091 103.6760 62.8124 118.0925 9.33538 100.4349 43.09355 108.8910
6,000 27.10786 103.6102 62.5615 117.9625 9.06953 100.4106 42.84223 108.7935
8,000 26.85174 103.5446 62.3080 117.8332 8.79538 100.3863 42.58835 108.6963
10,000 26.59244 103.4791 62.05197 117.7045 8.51213 100.3621 42.33186 108.5995
12,000 26.32987 103.4137 61.79327 117.5766 8.21883 100.3379 42.07272 108.5029
14,000 26.06393 103.3485 61.53191 117.4493 7.91436 100.3137 41.81088 108.4068
16,000 25.79453 103.2835 61.26787 117.3227 7.59739 100.2895 41.54628 108.3109
18,000 25.52155 103.2185 61.0011 117.1967 7.26628 100.2654 41.27888 108.2154
20,000 25.24487 103.1537 60.73158 117.0715 6.91900 100.2412 41.00862 108.1202
22,000 24.96438 103.0891 60.45927 116.947 6.55298 100.2171 40.73545 108.0254
24,000 24.67993 103.0246 60.18414 116.8231 6.16488 100.1930 40.4593 107.9309
26,000 24.39141 102.9602 59.90614 116.6999 5.75023 100.1689 40.18011 107.8367
28,000 24.09864 102.896 59.62524 116.5775 5.30281 100.1448 39.89783 107.7429
30,000 23.80149 102.8319 59.3414 116.4557 4.81349 100.1208 39.61239 107.6495
32,000 23.49979 102.7680 59.05458 116.3346 4.26788 100.0968 39.32371 107.5563
34,000 23.19335 102.7042 58.76474 116.2142 3.64077 100.0727 39.03173 107.4635
36,000 22.88199 102.6406 58.47183 116.0945 2.87937 100.0487 38.73638 107.3711
38,000 22.56551 102.5771 58.17583 115.9754 1.82252 100.0248 38.43757 107.2790

ρ 1 = ρ 2 = 2 , 000 kg / m 3 , E 1 = E 2 = 1 × 10 11 N / m 2 , K = 10 5 N / m 2 , F 2 = 1 , 000 N , L = 6 m , b = 0 . 2 m , h = 0 . 05 m .

Figures 4 and 5, and Table 3 depict the behavior of the changing in natural frequencies when changing the values of the axial compressive forces on the upper and lower beams with the same values.

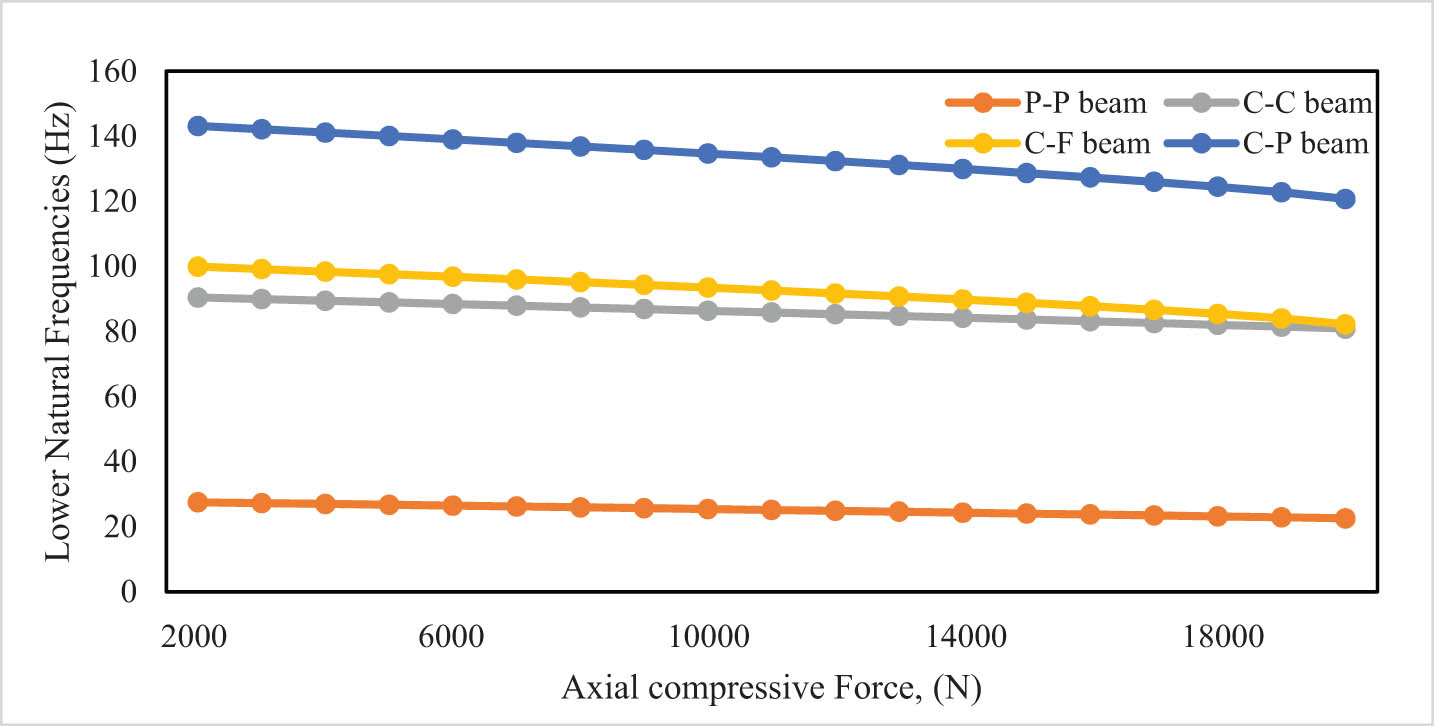
Figure 4 Lower natural frequency vs the axial compressive forces (F 1 and F 2).
Figure 4

Lower natural frequency vs the axial compressive forces (F 1 and F 2).

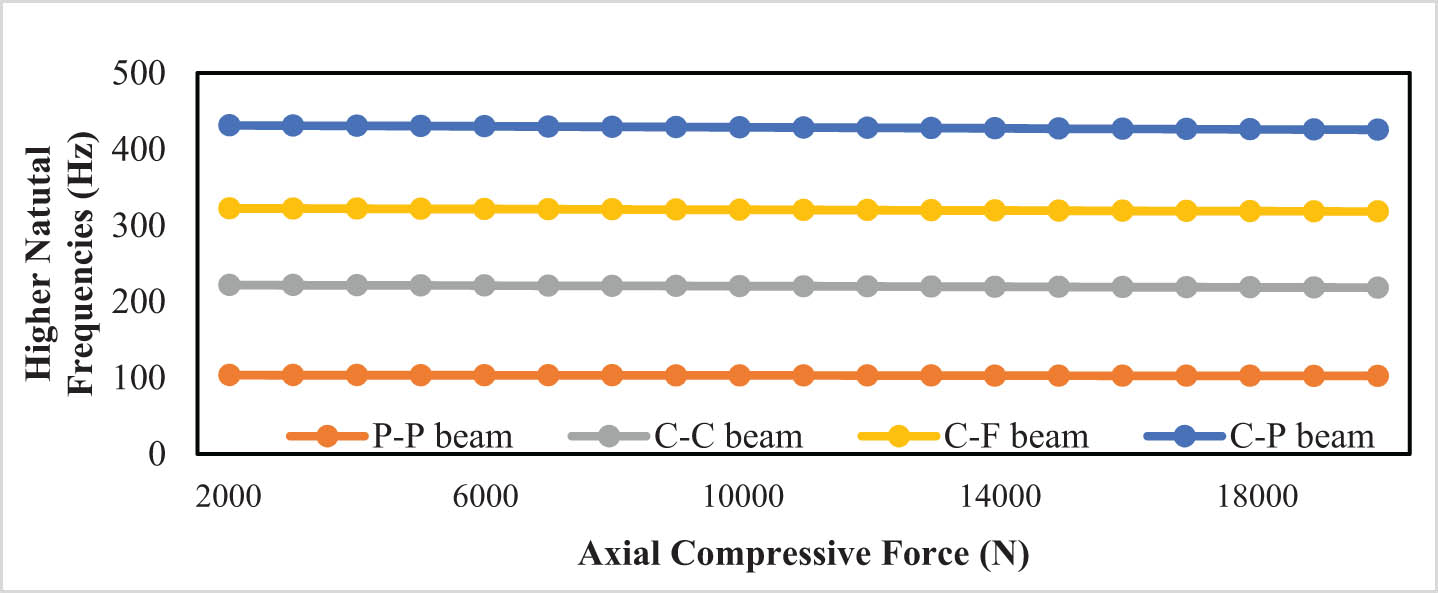
Figure 5 Higher natural frequency vs the axial compressive forces (F 1 and F 2).
Figure 5

Higher natural frequency vs the axial compressive forces (F 1 and F 2).

Table 3

The natural frequencies vs the axial compressive forces (F 1 and F 2)

Axial compressive force (N) PP Beam CC Beam CF Beam CP Beam
L H L H L H L H
2,000 27.4866 103.7088 62.93775 118.1574 9.4655 100.4470 43.2188 108.9397
3,000 27.2361 103.6427 62.69041 118.0258 9.2039 100.4227 42.9703 108.8414
4,000 26.9833 103.5765 62.44208 117.8941 8.9347 100.3984 42.7204 108.7430
5,000 26.7281 103.5103 62.19276 117.7622 8.6571 100.3740 42.4690 108.6445
6,000 26.4704 103.4441 61.94243 117.6302 8.3703 100.3497 42.2162 108.5459
7,000 26.2102 103.3778 61.69109 117.498 8.0733 100.3254 41.9618 108.4472
8,000 25.9474 103.3115 61.43872 117.3657 7.7650 100.3010 41.7058 108.3484
9,000 25.6819 103.2451 61.18532 117.2333 7.4439 100.2767 41.4483 108.2496
10,000 25.4136 103.1787 60.93085 117.1007 7.1084 100.2523 41.1892 108.1506
11,000 25.1425 103.1123 60.67532 116.9679 6.7561 100.2280 40.9284 108.0515
12,000 24.8684 103.0458 60.41871 116.835 6.3845 100.2036 40.6659 107.9524
13,000 24.5912 102.9793 60.16101 116.702 5.9899 100.1792 40.4018 107.8532
14,000 24.3109 102.9127 59.90219 116.5687 5.5674 100.1549 40.1359 107.7539
15,000 24.0273 102.8461 59.64226 116.4354 5.1100 100.1305 39.8682 107.6544
16,000 23.7403 102.7794 59.38118 116.3019 4.6075 100.1061 39.5988 107.5549
17,000 23.4499 102.7127 59.11895 116.1682 4.0430 100.0817 39.3275 107.4553
18,000 23.1557 102.6459 58.85556 116.0344 3.3856 100.0573 39.0542 107.3557
19,000 22.8578 102.5792 58.59098 115.9004 2.5650 100.0329 38.7791 107.2559
20,000 22.5560 102.5123 58.3252 115.7663 1.3023 100.0085 38.5020 107.1560

ρ 1 = ρ 2 = 2 , 000 kg / m 3 , E 1 = E 2 = 1 × 10 11 N / m 2 , K = 10 5 N / m 2 , L = 6 m , b = 0 . 2 m , and h = 0 . 05 m .

When the values of the axial forces are increased from 2,000 to 20,000, a decrease in the values of low natural frequencies is observed by 18% for the PP beam, 8% for the CC beam, 86% for the CF beam, and 11% for the CP beam. The greatest effect of changing the values of the axial compressive force on the higher natural frequencies when its values change symmetrically from 2,000 to 20,000 N for the CC beam causes it to decrease by less than 2%. A rise in the axial compressive force causes a lessening in the lower natural frequencies, particularly for the CF beam, while it has so little influence on the higher natural frequencies. Likewise, when the compressive forces on the upper and lower beams fluctuate at the same time, their effect is doubled on the frequencies when the axial compressive force on one of the two beams changes only.

The behavior of natural frequencies when the axial compressive force on the upper beam changes and no force acts on the lower beam are shown in Figures 6 and 7 and Table 4. When the axial force is increased from 2,000 to 38,000, the lower natural frequencies decreased by 18% for the PP beam, 9% for the CC beam, 86% for the CF beam, and by 11% for the CP beam. Also, the effect of changing the value of the axial force in this case is so little on the higher natural frequencies and is almost imperceptible. In general, the natural frequencies change in the same proportion when the axial compressive force on one of the two beams changes, whether it is the upper or lower, and the value of the axial force remains constant on the other beam. This change is doubled when the two axial forces applied to the two beams change with the same value.

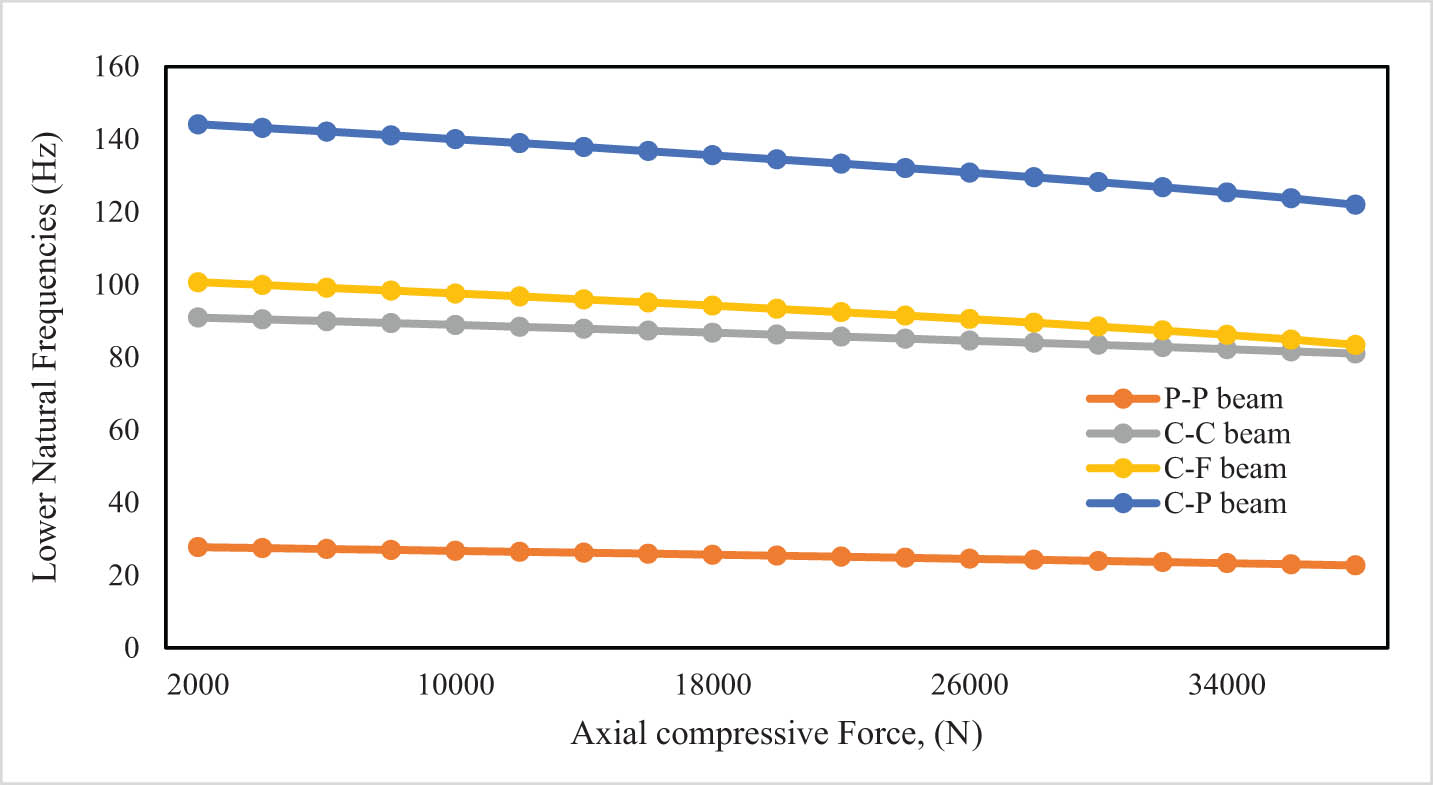
Figure 6 Lower natural frequency vs the axial compressive forces (F 2 = 0).
Figure 6

Lower natural frequency vs the axial compressive forces (F 2 = 0).

Figure 7 Lower natural frequency vs the axial compressive forces.
Figure 7

Lower natural frequency vs the axial compressive forces.

Table 4

The natural frequencies vs the axial compressive force (F 2 = 0)

F 1 (N) PP Beam CC Beam CF Beam CP Beam
L H L H L H L H
2,000 27.73453 103.775 63.18337 118.2892 9.719947 100.4713 43.4653 109.0382
4,000 27.48527 103.7092 62.93469 118.159 9.465034 100.447 43.21668 108.9406
6,000 27.23304 103.6435 62.68347 118.0295 9.202803 100.4228 42.96554 108.8433
8,000 26.97775 103.578 62.42971 117.9006 8.932611 100.3985 42.71185 108.7464
1,0000 26.71932 103.5126 62.17335 117.7725 8.653712 100.3743 42.45557 108.6498
1,2000 26.45766 103.4474 61.91438 117.645 8.365234 100.3501 42.19665 108.5535
14,000 26.19267 103.3823 61.65275 117.5182 8.066151 100.326 41.93504 108.4575
16,000 25.92424 103.3173 61.38844 117.392 7.755235 100.3018 41.67068 108.362
18,000 25.65227 103.2525 61.12142 117.2666 7.431001 100.2776 41.40353 108.2667
20,000 25.37665 103.1878 60.85164 117.1419 7.091622 100.2535 41.13353 108.1718
22,000 25.09725 103.1233 60.57908 117.0178 6.734811 100.2294 40.86063 108.0772
24,000 24.81396 103.0589 60.30369 116.8944 6.357632 100.2053 40.58477 107.983
26,000 24.52662 102.9947 60.02545 116.7717 5.956216 100.1812 40.30589 107.8891
28,000 24.23511 102.9306 59.74431 116.6497 5.525285 100.1572 40.02393 107.7955
30,000 23.93926 102.8666 59.46024 116.5284 5.057299 100.1332 39.73881 107.7023
32,000 23.63892 102.8028 59.17319 116.4078 4.540815 100.1091 39.45048 107.6094
34,000 23.3339 102.7391 58.88313 116.2879 3.956888 100.0851 39.15887 107.5169
36,000 23.02404 102.6756 58.59001 116.1687 3.26958 100.0612 38.86389 107.4247
38,000 22.70912 102.6122 58.29379 116.0502 2.391355 100.0372 38.56549 107.3329

ρ 1 = ρ 2 = 2 , 000 kg / m 3 , E 1 = E 2 = 1 × 10 11 N / m 2 , K = 10 5 N / m 2 , L = 6 m , b = 0 . 2 m , and h = 0 . 05 m .

From the foregoing, it can be concluded that the effect of the axial force on the natural frequencies is clear when one end of the beam is free, and this effect is negligible if the two ends are fixed, especially if both are clamped. This may be due to the buckling effect of the compressive axial force, so the more serious effect of the axial force is expected on natural frequencies when both ends are free. It was also noticed that the change in compressive force affects the lower natural frequencies (synchronous), while its effect is almost non-existent on the higher natural frequencies (asynchronous).

4 Conclusions

When the axial compressive force is increased from 2,000 to 38,000 N, it is noted that the lower natural frequencies decreased by 19% for the PP beam, 8% for the CC beam, 81% for the CF beam, and by 12% for the CP beam. While it is noticed that the greatest effect of the axial force on the higher natural frequencies is by reducing it in the CC beam by a ratio that does not exceed 2%. A rise in the axial force causes a lessening in the lower natural frequencies, especially for the CF beam, while it has a small influence on the higher natural frequencies. Similarly, when the compressive forces on the upper and lower beams fluctuate at the same time, their effect is doubled on the frequencies when the axial compressive force on one of the two beams changes only. The natural frequencies change in the same proportion when the axial compressive force on one of the two beams changes, whether it is the upper or lower, and the value of the axial force remains constant on the other beam.

In this study, when both the upper and lower layers of the double beam are fixed symmetrically, it was found that the axial force has a significant effect on the lower natural frequencies (synchronous) and its effect is minimal on the higher natural frequencies (asynchronous), especially when one or both ends of the beam are free. In the future, it is important to study the change in the boundary conditions for the connection of the upper and lower layers to be asymmetrical by stabilization and the effect of this on the natural frequencies.

  1. Conflict of interest: Authors state no conflict of interest.

References

[1] Zhang YQ, Lu Y, Ma GW. Effect of compressive axial load on forced transverse vibrations of a double-beam system. Int J Mech Sci. 2008;50(2):299–305. 10.1016/j.ijmecsci.2007.06.003.Search in Google Scholar

[2] Zhang YQ, Lu Y, Wang SL, Liu X. Vibration and buckling of a double-beam system under compressive axial loading. J Sound Vib. 2008;318(1–2):341–52. 10.1016/j.jsv.2008.03.055.Search in Google Scholar

[3] Zhao X, Chen B, Li YH, Zhu WD, Nkiegaing FJ, Shao YB. Forced vibration analysis of Timoshenko double-beam system under compressive axial load by means of Green’s functions. J Sound Vib. 2019;464:115001. 10.1016/j.jsv.2019.115001.Search in Google Scholar

[4] Zhao X. Solution to vibrations of double-beam systems under general boundary conditions. J Eng Mech. 2021;147(10):04021073. 10.1061/(ASCE)EM.1943-7889.0001953.Search in Google Scholar

[5] Zhao X, Chang P. Free and forced vibration of double beam with arbitrary end conditions connected with a viscoelastic layer and discrete points. Int J Mech Sci. 2021;209:106707. 10.1016/j.ijmecsci.2021.106707.Search in Google Scholar

[6] Mao Q, Wattanasakulpong N. Vibration and stability of a double-beam system interconnected by an elastic foundation under conservative and nonconservative axial forces. Int J Mech Sci. 2015;93:1–7. 10.1016/j.ijmecsci.2014.12.019.Search in Google Scholar

[7] Mao Q. Free vibration analysis of elastically connected multiple-beams by using the Adomian modified decomposition method. J Sound Vib. 2012;331(11):2532–42. 10.1016/j.jsv.2012.01.028.Search in Google Scholar

[8] Fei H, Danhui D, Cheng W, Jia P. Analysis on the dynamic characteristic of a tensioned double-beam system with a semi theoretical semi numerical method. Compos Struct. 2017;185:S0263822317304968. 10.1016/j.compstruct.2017.11.010.Search in Google Scholar

[9] Fei H, Danhui D, Wei C, Jubao Z. A novel analysis method for damping characteristic of a type of double-beam systems with viscoelastic layer. Appl Math Model. 2020;80:911–28. 10.1016/j.apm.2019.11.008.Search in Google Scholar

[10] Fei H, Danhui D, Zichen D. A dynamic stiffness-based modal analysis method for a double-beam system with elastic supports. Mech Syst Signal Process. 2021;146:106978. 10.1016/j.ymssp.2020.106978.Search in Google Scholar

[11] Sari ME, Al-Kouz WG, Al-Waked R. Bending–torsional-coupled vibrations and buckling characteristics of single and double composite Timoshenko beams. Adv Mech Eng. 2019;11(3):168781401983445. 10.1177/1687814019834452.Search in Google Scholar

[12] Stojanović V, Kozić P, Pavlović R, Janevski G. Effect of rotary inertia and shear on vibration and buckling of a double beam system under compressive axial loading. 2011;81(12):1993–2005. 10.1007/s00419-011-0532-1.Search in Google Scholar

[13] Stojanović V, Kozić P. Forced transverse vibration of Rayleigh and Timoshenko double-beam system with effect of compressive axial load. Int J Mech Sci. 2012;60(1):59–71. 10.1016/j.ijmecsci.2012.04.009.Search in Google Scholar

[14] Kozić P, Pavlović R, Karličić D. The flexural vibration and buckling of the elastically connected parallel-beams with a Kerr-type layer in between. Mech Res Commun. 2014;56:83–9. 10.1016/j.mechrescom.2013.12.003.Search in Google Scholar

[15] Abdulsahib IA, abbas Atiyah Q. Effects of internal connecting layer properties on the vibrations of double beams at different boundary conditions. J Mech Eng Res Dev. 2020;43:289–96.Search in Google Scholar

[16] Abdulsahib IA, abbas Atiyah Q. Vibration analysis of a symmetric double-beam with an elastic middle layer at arbitrary boundary conditions. Math Model Eng Probl. 2022;9(4):1136–42. 10.18280/mmep.090433.Search in Google Scholar

[17] Milenković B, Karličić D, Jovanović Đ. Determination of natural frequency and amplitude ratio of a Rayleigh double beam system with a Keer middle layer subjected to compressive axial load; XI International Conference Industrial Engineering and Environmental Protection; 2021. (IIZS 2021).10.5937/str2102036MSearch in Google Scholar

[18] Abbas Atiyah Q, Abdulsahib IA. Effects of geometrical and material properties on vibrations of double beams at different boundary conditions. J Mech Eng Res Dev. 2020;43(7):310–25.Search in Google Scholar

[19] Abbas Atiyah Q, Abdulsahib IA. The behavior of the synchronous and asynchronous natural frequencies for asymmetric double beams. Math Model Eng Probl. 2022;9(5):1243–50. 10.18280/mmep.090511 Search in Google Scholar
Received: 2022-07-22
Revised: 2023-01-08
Accepted: 2023-01-25
Published Online: 2023-05-09

© 2023 the author(s), published by De Gruyter

This work is licensed under the Creative Commons Attribution 4.0 International License.

Articles in the same Issue

  1. Regular Articles
  2. Design optimization of a 4-bar exoskeleton with natural trajectories using unique gait-based synthesis approach
  3. Technical review of supervised machine learning studies and potential implementation to identify herbal plant dataset
  4. Effect of ECAP die angle and route type on the experimental evolution, crystallographic texture, and mechanical properties of pure magnesium
  5. Design and characteristics of two-dimensional piezoelectric nanogenerators
  6. Hybrid and cognitive digital twins for the process industry
  7. Discharge predicted in compound channels using adaptive neuro-fuzzy inference system (ANFIS)
  8. Human factors in aviation: Fatigue management in ramp workers
  9. LLDPE matrix with LDPE and UV stabilizer additive to evaluate the interface adhesion impact on the thermal and mechanical degradation
  10. Dislocated time sequences – deep neural network for broken bearing diagnosis
  11. Estimation method of corrosion current density of RC elements
  12. A computational iterative design method for bend-twist deformation in composite ship propeller blades for thrusters
  13. Compressive forces influence on the vibrations of double beams
  14. Research on dynamical properties of a three-wheeled electric vehicle from the point of view of driving safety
  15. Risk management based on the best value approach and its application in conditions of the Czech Republic
  16. Effect of openings on simply supported reinforced concrete skew slabs using finite element method
  17. Experimental and simulation study on a rooftop vertical-axis wind turbine
  18. Rehabilitation of overload-damaged reinforced concrete columns using ultra-high-performance fiber-reinforced concrete
  19. Performance of a horizontal well in a bounded anisotropic reservoir: Part II: Performance analysis of well length and reservoir geometry
  20. Effect of chloride concentration on the corrosion resistance of pure Zn metal in a 0.0626 M H2SO4 solution
  21. Numerical and experimental analysis of the heat transfer process in a railway disc brake tested on a dynamometer stand
  22. Design parameters and mechanical efficiency of jet wind turbine under high wind speed conditions
  23. Architectural modeling of data warehouse and analytic business intelligence for Bedstead manufacturers
  24. Influence of nano chromium addition on the corrosion and erosion–corrosion behavior of cupronickel 70/30 alloy in seawater
  25. Evaluating hydraulic parameters in clays based on in situ tests
  26. Optimization of railway entry and exit transition curves
  27. Daily load curve prediction for Jordan based on statistical techniques
  28. Review Articles
  29. A review of rutting in asphalt concrete pavement
  30. Powered education based on Metaverse: Pre- and post-COVID comprehensive review
  31. A review of safety test methods for new car assessment program in Southeast Asian countries
  32. Communication
  33. StarCrete: A starch-based biocomposite for off-world construction
  34. Special Issue: Transport 2022 - Part I
  35. Analysis and assessment of the human factor as a cause of occurrence of selected railway accidents and incidents
  36. Testing the way of driving a vehicle in real road conditions
  37. Research of dynamic phenomena in a model engine stand
  38. Testing the relationship between the technical condition of motorcycle shock absorbers determined on the diagnostic line and their characteristics
  39. Retrospective analysis of the data concerning inspections of vehicles with adaptive devices
  40. Analysis of the operating parameters of electric, hybrid, and conventional vehicles on different types of roads
  41. Special Issue: 49th KKBN - Part II
  42. Influence of a thin dielectric layer on resonance frequencies of square SRR metasurface operating in THz band
  43. Influence of the presence of a nitrided layer on changes in the ultrasonic wave parameters
  44. Special Issue: ICRTEEC - 2021 - Part III
  45. Reverse droop control strategy with virtual resistance for low-voltage microgrid with multiple distributed generation sources
  46. Special Issue: AESMT-2 - Part II
  47. Waste ceramic as partial replacement for sand in integral waterproof concrete: The durability against sulfate attack of certain properties
  48. Assessment of Manning coefficient for Dujila Canal, Wasit/-Iraq
  49. Special Issue: AESMT-3 - Part I
  50. Modulation and performance of synchronous demodulation for speech signal detection and dialect intelligibility
  51. Seismic evaluation cylindrical concrete shells
  52. Investigating the role of different stabilizers of PVCs by using a torque rheometer
  53. Investigation of high-turbidity tap water problem in Najaf governorate/middle of Iraq
  54. Experimental and numerical evaluation of tire rubber powder effectiveness for reducing seepage rate in earth dams
  55. Enhancement of air conditioning system using direct evaporative cooling: Experimental and theoretical investigation
  56. Assessment for behavior of axially loaded reinforced concrete columns strengthened by different patterns of steel-framed jacket
  57. Novel graph for an appropriate cross section and length for cantilever RC beams
  58. Discharge coefficient and energy dissipation on stepped weir
  59. Numerical study of the fluid flow and heat transfer in a finned heat sink using Ansys Icepak
  60. Integration of numerical models to simulate 2D hydrodynamic/water quality model of contaminant concentration in Shatt Al-Arab River with WRDB calibration tools
  61. Study of the behavior of reactive powder concrete RC deep beams by strengthening shear using near-surface mounted CFRP bars
  62. The nonlinear analysis of reactive powder concrete effectiveness in shear for reinforced concrete deep beams
  63. Activated carbon from sugarcane as an efficient adsorbent for phenol from petroleum refinery wastewater: Equilibrium, kinetic, and thermodynamic study
  64. Structural behavior of concrete filled double-skin PVC tubular columns confined by plain PVC sockets
  65. Probabilistic derivation of droplet velocity using quadrature method of moments
  66. A study of characteristics of man-made lightweight aggregate and lightweight concrete made from expanded polystyrene (eps) and cement mortar
  67. Effect of waste materials on soil properties
  68. Experimental investigation of electrode wear assessment in the EDM process using image processing technique
  69. Punching shear of reinforced concrete slabs bonded with reactive powder after exposure to fire
  70. Deep learning model for intrusion detection system utilizing convolution neural network
  71. Improvement of CBR of gypsum subgrade soil by cement kiln dust and granulated blast-furnace slag
  72. Investigation of effect lengths and angles of the control devices below the hydraulic structure
  73. Finite element analysis for built-up steel beam with extended plate connected by bolts
  74. Finite element analysis and retrofit of the existing reinforced concrete columns in Iraqi schools by using CFRP as confining technique
  75. Performing laboratory study of the behavior of reactive powder concrete on the shear of RC deep beams by the drilling core test
  76. Special Issue: AESMT-4 - Part I
  77. Depletion zones of groundwater resources in the Southwest Desert of Iraq
  78. A case study of T-beams with hybrid section shear characteristics of reactive powder concrete
  79. Feasibility studies and their effects on the success or failure of investment projects. “Najaf governorate as a model”
  80. Optimizing and coordinating the location of raw material suitable for cement manufacturing in Wasit Governorate, Iraq
  81. Effect of the 40-PPI copper foam layer height on the solar cooker performance
  82. Identification and investigation of corrosion behavior of electroless composite coating on steel substrate
  83. Improvement in the California bearing ratio of subbase soil by recycled asphalt pavement and cement
  84. Some properties of thermal insulating cement mortar using Ponza aggregate
  85. Assessment of the impacts of land use/land cover change on water resources in the Diyala River, Iraq
  86. Effect of varied waste concrete ratios on the mechanical properties of polymer concrete
  87. Effect of adverse slope on performance of USBR II stilling basin
  88. Shear capacity of reinforced concrete beams with recycled steel fibers
  89. Extracting oil from oil shale using internal distillation (in situ retorting)
  90. Influence of recycling waste hardened mortar and ceramic rubbish on the properties of flowable fill material
  91. Rehabilitation of reinforced concrete deep beams by near-surface-mounted steel reinforcement
  92. Impact of waste materials (glass powder and silica fume) on features of high-strength concrete
  93. Studying pandemic effects and mitigation measures on management of construction projects: Najaf City as a case study
  94. Design and implementation of a frequency reconfigurable antenna using PIN switch for sub-6 GHz applications
  95. Average monthly recharge, surface runoff, and actual evapotranspiration estimation using WetSpass-M model in Low Folded Zone, Iraq
  96. Simple function to find base pressure under triangular and trapezoidal footing with two eccentric loads
  97. Assessment of ALINEA method performance at different loop detector locations using field data and micro-simulation modeling via AIMSUN
  98. Special Issue: AESMT-5 - Part I
  99. Experimental and theoretical investigation of the structural behavior of reinforced glulam wooden members by NSM steel bars and shear reinforcement CFRP sheet
  100. Improving the fatigue life of composite by using multiwall carbon nanotubes
  101. A comparative study to solve fractional initial value problems in discrete domain
  102. Assessing strength properties of stabilized soils using dynamic cone penetrometer test
  103. Investigating traffic characteristics for merging sections in Iraq
  104. Enhancement of flexural behavior of hybrid flat slab by using SIFCON
  105. The main impacts of a managed aquifer recharge using AHP-weighted overlay analysis based on GIS in the eastern Wasit province, Iraq
https://doi.org/10.1515/eng-2022-0408
Keywords for this article
double beam; vibration of beam; compressive force
Creative Commons
BY 4.0

Articles in the same Issue

  1. Regular Articles
  2. Design optimization of a 4-bar exoskeleton with natural trajectories using unique gait-based synthesis approach
  3. Technical review of supervised machine learning studies and potential implementation to identify herbal plant dataset
  4. Effect of ECAP die angle and route type on the experimental evolution, crystallographic texture, and mechanical properties of pure magnesium
  5. Design and characteristics of two-dimensional piezoelectric nanogenerators
  6. Hybrid and cognitive digital twins for the process industry
  7. Discharge predicted in compound channels using adaptive neuro-fuzzy inference system (ANFIS)
  8. Human factors in aviation: Fatigue management in ramp workers
  9. LLDPE matrix with LDPE and UV stabilizer additive to evaluate the interface adhesion impact on the thermal and mechanical degradation
  10. Dislocated time sequences – deep neural network for broken bearing diagnosis
  11. Estimation method of corrosion current density of RC elements
  12. A computational iterative design method for bend-twist deformation in composite ship propeller blades for thrusters
  13. Compressive forces influence on the vibrations of double beams
  14. Research on dynamical properties of a three-wheeled electric vehicle from the point of view of driving safety
  15. Risk management based on the best value approach and its application in conditions of the Czech Republic
  16. Effect of openings on simply supported reinforced concrete skew slabs using finite element method
  17. Experimental and simulation study on a rooftop vertical-axis wind turbine
  18. Rehabilitation of overload-damaged reinforced concrete columns using ultra-high-performance fiber-reinforced concrete
  19. Performance of a horizontal well in a bounded anisotropic reservoir: Part II: Performance analysis of well length and reservoir geometry
  20. Effect of chloride concentration on the corrosion resistance of pure Zn metal in a 0.0626 M H2SO4 solution
  21. Numerical and experimental analysis of the heat transfer process in a railway disc brake tested on a dynamometer stand
  22. Design parameters and mechanical efficiency of jet wind turbine under high wind speed conditions
  23. Architectural modeling of data warehouse and analytic business intelligence for Bedstead manufacturers
  24. Influence of nano chromium addition on the corrosion and erosion–corrosion behavior of cupronickel 70/30 alloy in seawater
  25. Evaluating hydraulic parameters in clays based on in situ tests
  26. Optimization of railway entry and exit transition curves
  27. Daily load curve prediction for Jordan based on statistical techniques
  28. Review Articles
  29. A review of rutting in asphalt concrete pavement
  30. Powered education based on Metaverse: Pre- and post-COVID comprehensive review
  31. A review of safety test methods for new car assessment program in Southeast Asian countries
  32. Communication
  33. StarCrete: A starch-based biocomposite for off-world construction
  34. Special Issue: Transport 2022 - Part I
  35. Analysis and assessment of the human factor as a cause of occurrence of selected railway accidents and incidents
  36. Testing the way of driving a vehicle in real road conditions
  37. Research of dynamic phenomena in a model engine stand
  38. Testing the relationship between the technical condition of motorcycle shock absorbers determined on the diagnostic line and their characteristics
  39. Retrospective analysis of the data concerning inspections of vehicles with adaptive devices
  40. Analysis of the operating parameters of electric, hybrid, and conventional vehicles on different types of roads
  41. Special Issue: 49th KKBN - Part II
  42. Influence of a thin dielectric layer on resonance frequencies of square SRR metasurface operating in THz band
  43. Influence of the presence of a nitrided layer on changes in the ultrasonic wave parameters
  44. Special Issue: ICRTEEC - 2021 - Part III
  45. Reverse droop control strategy with virtual resistance for low-voltage microgrid with multiple distributed generation sources
  46. Special Issue: AESMT-2 - Part II
  47. Waste ceramic as partial replacement for sand in integral waterproof concrete: The durability against sulfate attack of certain properties
  48. Assessment of Manning coefficient for Dujila Canal, Wasit/-Iraq
  49. Special Issue: AESMT-3 - Part I
  50. Modulation and performance of synchronous demodulation for speech signal detection and dialect intelligibility
  51. Seismic evaluation cylindrical concrete shells
  52. Investigating the role of different stabilizers of PVCs by using a torque rheometer
  53. Investigation of high-turbidity tap water problem in Najaf governorate/middle of Iraq
  54. Experimental and numerical evaluation of tire rubber powder effectiveness for reducing seepage rate in earth dams
  55. Enhancement of air conditioning system using direct evaporative cooling: Experimental and theoretical investigation
  56. Assessment for behavior of axially loaded reinforced concrete columns strengthened by different patterns of steel-framed jacket
  57. Novel graph for an appropriate cross section and length for cantilever RC beams
  58. Discharge coefficient and energy dissipation on stepped weir
  59. Numerical study of the fluid flow and heat transfer in a finned heat sink using Ansys Icepak
  60. Integration of numerical models to simulate 2D hydrodynamic/water quality model of contaminant concentration in Shatt Al-Arab River with WRDB calibration tools
  61. Study of the behavior of reactive powder concrete RC deep beams by strengthening shear using near-surface mounted CFRP bars
  62. The nonlinear analysis of reactive powder concrete effectiveness in shear for reinforced concrete deep beams
  63. Activated carbon from sugarcane as an efficient adsorbent for phenol from petroleum refinery wastewater: Equilibrium, kinetic, and thermodynamic study
  64. Structural behavior of concrete filled double-skin PVC tubular columns confined by plain PVC sockets
  65. Probabilistic derivation of droplet velocity using quadrature method of moments
  66. A study of characteristics of man-made lightweight aggregate and lightweight concrete made from expanded polystyrene (eps) and cement mortar
  67. Effect of waste materials on soil properties
  68. Experimental investigation of electrode wear assessment in the EDM process using image processing technique
  69. Punching shear of reinforced concrete slabs bonded with reactive powder after exposure to fire
  70. Deep learning model for intrusion detection system utilizing convolution neural network
  71. Improvement of CBR of gypsum subgrade soil by cement kiln dust and granulated blast-furnace slag
  72. Investigation of effect lengths and angles of the control devices below the hydraulic structure
  73. Finite element analysis for built-up steel beam with extended plate connected by bolts
  74. Finite element analysis and retrofit of the existing reinforced concrete columns in Iraqi schools by using CFRP as confining technique
  75. Performing laboratory study of the behavior of reactive powder concrete on the shear of RC deep beams by the drilling core test
  76. Special Issue: AESMT-4 - Part I
  77. Depletion zones of groundwater resources in the Southwest Desert of Iraq
  78. A case study of T-beams with hybrid section shear characteristics of reactive powder concrete
  79. Feasibility studies and their effects on the success or failure of investment projects. “Najaf governorate as a model”
  80. Optimizing and coordinating the location of raw material suitable for cement manufacturing in Wasit Governorate, Iraq
  81. Effect of the 40-PPI copper foam layer height on the solar cooker performance
  82. Identification and investigation of corrosion behavior of electroless composite coating on steel substrate
  83. Improvement in the California bearing ratio of subbase soil by recycled asphalt pavement and cement
  84. Some properties of thermal insulating cement mortar using Ponza aggregate
  85. Assessment of the impacts of land use/land cover change on water resources in the Diyala River, Iraq
  86. Effect of varied waste concrete ratios on the mechanical properties of polymer concrete
  87. Effect of adverse slope on performance of USBR II stilling basin
  88. Shear capacity of reinforced concrete beams with recycled steel fibers
  89. Extracting oil from oil shale using internal distillation (in situ retorting)
  90. Influence of recycling waste hardened mortar and ceramic rubbish on the properties of flowable fill material
  91. Rehabilitation of reinforced concrete deep beams by near-surface-mounted steel reinforcement
  92. Impact of waste materials (glass powder and silica fume) on features of high-strength concrete
  93. Studying pandemic effects and mitigation measures on management of construction projects: Najaf City as a case study
  94. Design and implementation of a frequency reconfigurable antenna using PIN switch for sub-6 GHz applications
  95. Average monthly recharge, surface runoff, and actual evapotranspiration estimation using WetSpass-M model in Low Folded Zone, Iraq
  96. Simple function to find base pressure under triangular and trapezoidal footing with two eccentric loads
  97. Assessment of ALINEA method performance at different loop detector locations using field data and micro-simulation modeling via AIMSUN
  98. Special Issue: AESMT-5 - Part I
  99. Experimental and theoretical investigation of the structural behavior of reinforced glulam wooden members by NSM steel bars and shear reinforcement CFRP sheet
  100. Improving the fatigue life of composite by using multiwall carbon nanotubes
  101. A comparative study to solve fractional initial value problems in discrete domain
  102. Assessing strength properties of stabilized soils using dynamic cone penetrometer test
  103. Investigating traffic characteristics for merging sections in Iraq
  104. Enhancement of flexural behavior of hybrid flat slab by using SIFCON
  105. The main impacts of a managed aquifer recharge using AHP-weighted overlay analysis based on GIS in the eastern Wasit province, Iraq
Sign up now to receive a 20% welcome discount
Institutional Access
How does access work?
Have an idea on how to improve our website?
Please write us.
© 2025 De Gruyter Brill
Downloaded on 6.9.2025 from https://www.degruyterbrill.com/document/doi/10.1515/eng-2022-0408/html
Scroll to top button