Abstract
The iterative Shehu transform homotopy perturbation method (HPM) is used in the present research to address fractional telegraph equations in different dimensions, respectively. Considered equations particularly stand out in the field of material science and certain other significant fields. A graphic comparison of estimated and actual results is used to assess the validity and efficacy of the suggested technique. Graphs show a match of approximate to exact findings. Without any linearization or discretization, the iterative Shehu HPM offers a reliable and efficient way to deliver approximations and accurate outcomes that is also error-free. The development of numerical regimes based on discretization is difficult and expensive computationally. Additionally, discretization error is produced as a result of discretization in purely numerical regimes. The present regime has produced robust results and is time-efficient. Also, no discretization error was produced.
1 Introduction
Numerous areas of the physical sciences, including diffusion, control processes, elasticity, relaxation processes, and many others, use fractional calculus extensively [1,2,3]. The telegraph equation is employed in the reaction–diffusion process, as well as in signal observation for the transmission and propagation of electrical signals [4,5]. Many researchers have offered various types of solutions for fractional telegraph equations. Momani utilized Adomian decomposition method (ADM) [6]. Yildrim [7] put homotopy perturbation method (HPM) into the application. The variable separable technique was incorporated by Chen et al. [8]. Variation iteration method (VIM) was implemented by Sevimlican [9]. For the fractional hyperbolic telegraph (HT) equation, Khan et al. [10] adopted natural ADM, combining natural transform and ADM to produce a fusion. Fractional VIM was utilized by Jassim and Shahab [11] to solve the HT equation. The Shehu transform was used for the fractional HT equation in one dimension (1D), two dimension (2D), and three dimension (3D) by Kapoor et al. [12]. The concept of Laplace ADM in the Caputo sense was applied by Khan et al. [13] to cope with the fractional-order telegraph equation. The ECB-spline technique was utilized by Akram et al. [14] to solve the fractional telegraph problem. Regarding the pseudo HT equation, Modanli [15] provided compatibility between Caputo and Atangana–Baleanu fractional derivatives. The Legendre collocation method was applied to the fractional telegraph equation by Mishra et al. [16]. To obtain the precise analytical solution of fractional-order telegraph equations, Khan et al. [17] employed the triple Laplace transform.
1.1 Shehu transform
Integral transformation is necessary to effectively answer mathematical issues. Dealing with several partial differential equations (PDEs) is also made easier via an integral transform that has been proven to work. The integral transform is a straightforward method for managing numerous complex PDEs. Many studies on integral transformations have been conducted in recent years. Sumudu transformation, Elzaki transformation, natural transformation, Pourreza transformation, G transformation, Sawi transformation, Shehu transform, etc., are a few examples of integral transformations. Some integral equations, ordinary differential equations, PDEs, and fractional PDEs (FPDEs) can be solved using transformations described in literature [18–23].
Result 1
Iterative Shehu transform of fractional derivative in Caputo sense:
Result 2
The iterative Shehu transformation has been notified as follows:
Laplace transform would be converted from iterative Shehu transform via considering
Iterative Shehu transformation will lead to Yang transformation via considering
Result 3
Considered
where
Result 4
Result 5
Result 6 Linearity property of Shehu transform.
Proof
Proved.
Result 7 Shehu transform of single derivative of
Proof
Proved.
Result 8 Shehu transform of double derivative of
Proof
Proved.
Result 9 Shehu transform of triple derivative of
Proof
Proved.
Result 10 Shehu transform of
Proof similarly,
In Tables 1 and 2, charts are provided regarding Shehu transform and iterative Shehu transform.
Iterative Shehu transform of diversified functions
| S. No. |
|
|
|---|---|---|
| 1 |
|
|
| 2 |
|
|
| 3 |
|
|
| 4 |
|
|
| 6 |
|
|
| 7 |
|
|
| 8 |
|
|
| 9 |
|
|
| 10 |
|
|
| 11 |
|
|
| 12 |
|
|
| 13 |
|
|
| 14 |
|
|
| 15 |
|
|
| 16 |
|
|
| 17 |
|
|
| 18 |
|
|
| 19 |
|
|
| 20 |
|
|
| 21 |
|
|
| 23 |
|
|
| 26 |
|
|
| 27 |
|
|
| 28 |
|
|
| 29 |
|
|
| 30 |
|
|
| 31 |
|
|
Inverse Shehu transform of diversified functions [19]
|
|
|
|
|---|---|---|
| 1 |
|
|
| 2 |
|
|
| 3 |
|
|
| 4 |
|
|
| 5 |
|
|
| 6 |
|
|
| 7 |
|
|
| 8 |
|
|
| 9 |
|
|
1.2 HPM
He [18] first proposed the idea of HPM and then combined the conventional perturbation regime with the Homotopy regarding topology by producing a Homotopy (convex in nature). He then found the solution to the problem, which was then presented in series form and converged to the precise solution. He [24–26] used HPM to address non-linear issues in applied sciences, such as the Duffing equation and the Ear Drum equation, among others.
A Chinese scholar named He [27] launched HPM. He combined the conventional perturbation regime with topological Homotopy, which is used to resolve several crucial equations. Fundamentally, Homotopy is a concept borrowed from topology and differential geometry [28]. The French mathematician Poincare referred to the idea of Homotopy [29].
For HPM, the following equation is considered:
Any convex homotopy deformation
where
In such a method, the equation's solution is given as a power series and embedding parameter
1.3 Time-fractional HT equation
Due to their relevance in numerous engineering and scientific sectors, FPDEs have recently become most crucial topic from the viewpoint of researchers and scientists. The fractional derivatives have a very high degree of flexibility, which results in an outstanding tool for expressing the varied past and inherited traits of the numerous prototypes. For the development of analytical and numeric outcomes of linear and non-linear FPDEs, large-scale research is conducted.
Fractional hyperbolic telegraph equation in 1D [10]. Some more references relevant to fractional calculus are provided in previous literature [30–37].
For
For
In signal processing for transmission of electrical impulses and wave theory processes, the telegraph equation model is primarily and most frequently utilized. The biomedical sciences and aerospace have seen a number of these models implemented. Problems involving fractional derivatives are attracting the attention of researchers. Fractional-order PDEs are modelled specifically by linear PDEs of integer order. For outcomes of integer-order techniques, fractional-order schemes converge. Some latest references are provided in previous literature [38–48].
Fractional HT equation in 2D [10].
I.C.:
Fractional HT equation in 3D [10].
I.C.:
1.3.1 Motivation of the study
There are many literary solutions to fractional telegraph equation in 1D, 2D, or 3D , but there are very few approaches that address the fractional telegraph equation in all three dimensions. The development of a method that can demonstrate the reliability of the estimated analytical solutions to the aforementioned equations in one, two, and three dimensions is therefore the main goal. In the present study, an iterative approach to tackle fractional HT equation in 1D, 2D, and 3D is presented. The present approach is simple to use and does not require intricate numerical discretization programming. It is difficult to create numerical programs for FPDEs, hence creating such iterative techniques is necessary to obtain approximate analytical solutions. Numerous transforms are offered in literature; however, from the perspective of calculation, some transforms are simple to use and others are not. Among all the available integral transforms, Shehu transform HPM is regarded as one of the simplest to use. Due to the significance of these equations, this research concentrates on their solution, maintaining the study's uniqueness. Additionally, the article includes assessments of convergence and error.
1.3.2 Research questions
1Q. What is the novelty of this work?
Reply – In the present study, a numerical convergence aspect is discussed in detail regarding the proposed regime. Moreover, graphical and tabular compatibility of results are also validated.
2Q. Why only Shehu transform is used in this study?
Reply – Some integral transforms are simple to use from a calculation standpoint, whereas others are more difficult. The Shehu transform is one of the simplest integral transforms, hence it is being used.
3Q. Why is any discretization-based technique not implemented?
Reply – The development of numerical regimes based on discretization is difficult and expensive computationally. Additionally, discretization error is produced as a result of discretization.
1.3.3 Outline of the research work
The present study is framed into diversified sections to create a better notion regarding the work done. In Section 2, general formulas are developed for fractional Telegraph equation in 1D. In Section 3, five examples are evaluated regarding fractional HT equations in different dimensions. In Section 4, graphical and tabular analyses of the work are provided along with numerical convergence. Section 5 is related to the concluding remarks.
2 Implementation of the regime
Implementation upon
Applying Shehu transform
Applying HPM
where
Comparing
Comparing
Comparing
Comparing
and so on.
In Figure 1, steps regarding the solution of the proposed regime are provided.

Steps regarding the solution of the proposed regime.
Uniqueness and convergence theorems
Theorem 1
Let
Proof provided.
The aim is to prove that
It is provided that for
Let us find
Considered
Theorem 2
Let
Proof
Let
3 Examples and discussion
Example 1
Considered fractional
I.C.:
Applying Shehu transform upon Eq. (9)
Applying HPM
Comparing
Considered
Comparing
where
Comparing
Comparing
Comparing
where
Comparing
where
Considered
Example 2 Considered fractional
I.C.:
Applying Shehu transform upon Eq. (10)
Applying HPM
Comparing
Considered
Comparing
Comparing
Comparing
Comparing
Comparing
Considered
Example 3
Considered fractional
I.C.:
Applying Shehu transform upon Eq. (11)
Applying HPM
Comparing
Comparing
where
Considered
Where
Comparing
where
where
Comparing
where
Comparing
where
Comparing
where
Considered
Example 4. Considered fractional
I.C.:
Applying Shehu transform upon Eq. (12)
Applying HPM
Comparing
Considered
Comparing
where
where
Comparing
where
where
Comparing
where
where
Comparing
where
where
Comparing
where
where
Considered
Example 5. Considered
I.C.:
Applying Shehu transform upon Eq. (13)
Applying HPM upon Eq. (14)
Comparing
Considered
Comparing
where
Considered
where
Comparing
where
where
Comparing
where
where
Comparing
where
where
Comparing
where
where
Considered
4 Graphs and error analysis
In the present section, graphical and tabular analyses of the present regime is proposed for several examples. Along with it, the error analysis via
In Figure 2, comparison of approximate and exact outcomes is notified at

Comparison of approximate and exact outcomes at

Comparison of approximate and exact outcomes at
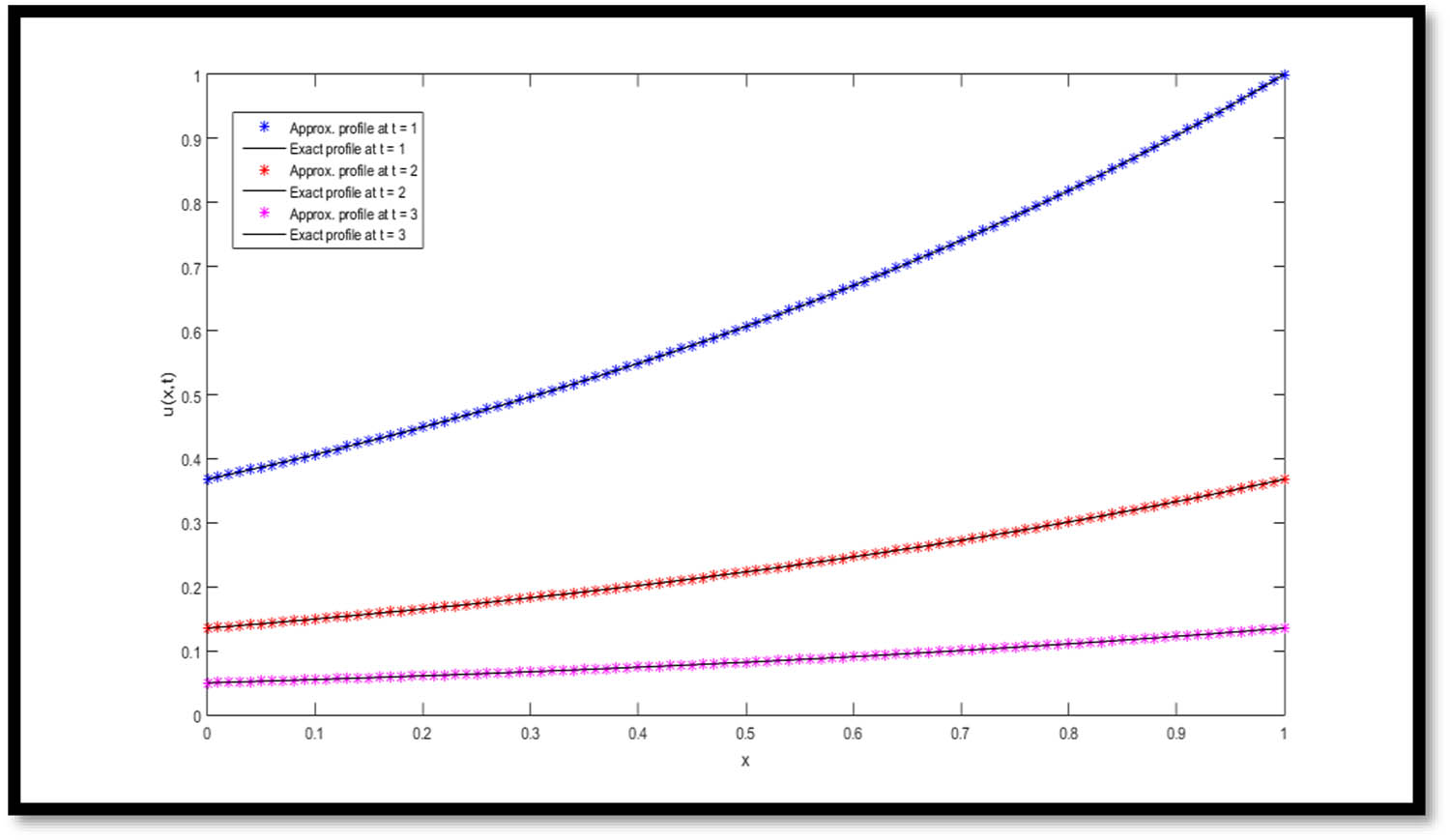
Comparison of approximate and exact outcomes at

Comparison of approximate and exact outcomes at

Comparison of approximate and exact outcomes at

Comparison of approximate and exact outcomes at
Analysis of errors for Example 1
|
|
|
||
|---|---|---|---|
|
|
|
|
|
| 21 | −3.1042 × 10−13 | −6.0062 × 10−7 | −2.7791 × 10−3 |
| 31 | −4.4409 × 10−16 | −9.3814 × 10−15 | −1.3578 × 10−9 |
| 41 | −4.4409 × 10−16 | −4.2744 × 10−15 | 3.0923 × 10−14 |
| ↓ | ↓ | ↓ | |
|
Converging up to
|
Converging up to
|
Converging up to
|
|
Approximate and exact outcomes match for Example 1
|
|
Approx. | Exact | Approx. | Exact |
|---|---|---|---|---|
|
|
|
|||
| 1.00 × 10−1 | 1.50 × 10−1 | 1.50 × 10−1 | 2.02 × 10−2 | 2.02 × 10−2 |
| 1.50 × 10−1 | 1.57 × 10−1 | 1.57 × 10−1 | 2.13 × 10−2 | 2.13 × 10−2 |
| 2.00 × 10−1 | 1.65 × 10−1 | 1.65 × 10−1 | 2.24 × 10−2 | 2.24 × 10−2 |
Analysis of errors for Example 2
|
|
|
||
|---|---|---|---|
|
|
|
|
|
| 11 | −1.3916 × 10−7 | −2.6433 × 10−4 | −2.1305 × 10−2 |
| 21 | 8.8818 × 10−16 | −3.1042 × 10−13 | −1.4863 × 10−9 |
| 31 | −4.4409 × 10−16 | −4.4409 × 10−16 | −1.6653 × 10−16 |
| ↓ | ↓ | ↓ | |
|
Converging up to
|
Converging up to
|
Converging up to
|
|
Approximate and exact outcomes match for Example 2
|
|
Approx. | Exact | Approx. | Exact |
|---|---|---|---|---|
|
|
|
|||
| 1.00 × 10−1 | 4.07 × 10−1 | 4.07 × 10−1 | 1.50 × 10−1 | 1.50 × 10−1 |
| 1.50 × 10−1 | 4.27 × 10−1 | 4.27 × 10−1 | 1.57 × 10−1 | 1.57 × 10−1 |
| 2.00 × 10−1 | 4.49 × 10−1 | 4.49 × 10−1 | 1.65 × 10−1 | 1.65 × 10−1 |
Approximate and exact outcomes match for Example 3
|
|
Approx. | Exact | Approx. | Exact |
|---|---|---|---|---|
|
|
|
|||
| 1.00 × 10−1 | 0.4066 | 0.4066 | 0.1496 | 0.1496 |
| 1.50 × 10−1 | 0.4274 | 0.4274 | 0.1572 | 0.1572 |
| 2.00 × 10−1 | 0.4493 | 0.4493 | 0.1653 | 0.1653 |
Error analysis for Example 4
|
|
|
||
|---|---|---|---|
|
|
|
|
|
| 20 | 2.3873 × 10−3 | 1.3436 × 10−2 | 6.5796 × 10−2 |
| 30 | 2.5102 × 10−10 | 4.3929 × 10−10 | 1.1569 × 10−9 |
| 40 | 1.7462 × 10−10 | 1.9918 × 10−10 | 6.2482 × 10−10 |
| ↓ | ↓ | ↓ | |
|
Converging up to
|
Converging up to
|
Converging up to
|
|
Approximate and exact outcomes match regarding Example 4
|
|
Approx. | Exact | Approx. | Exact |
|---|---|---|---|---|
|
|
|
|||
| (3.14 × 10 −1 , 3.14 × 10 −1 ) | 6.91 × 10−2 | 0.069136 | 5.12 × 10−2 | 0.051217 |
| (6.28 × 10 −1 , 6.28 × 10 −1 ) | 1.30 × 10−1 | 0.129592 | 9.60 × 10−2 | 0.096004 |
| (9.42 × 10 −1 , 9.42 × 10 −1 ) | 2.43 × 10−1 | 0.242915 | 1.80 × 10−1 | 0.179956 |
(x, y) are points in the spatial domain. t is the time level.
4.1 Observation regarding numerical convergence of the proposed regime
Through Table 3, numerical convergence of the proposed regime is provided. It is notified that on increasing the value of
4.2 Application of the proposed regime
4.2.1 Telegraph transmission line with leakage
Any system that transmits telegraph signals over a long distance – usually by a wire or cable – is referred to as a telegraph transmission line with leakage. In this context, "leakage" refers to the weakening of the signal down the transmission line, which can be caused by a number of different things, including capacitance, inductance, and resistance.
Some main elements and traits of a leaky telegraph transmission line:
Transmitter: A telegraph transmitter is located at one end of the wire. This device produces electrical signals that must be transferred in order to represent telegraph codes, such as Morse code.
Transmission line: An electrical signal travels from the transmitter to the receiver via a physical conductor, typically a wire or cable. When it comes to telegraphy, this connection can link offices or telegraph stations over great distances.
Leakage: Losses in electrical impulses along the transmission line result in leakage. This may be caused by elements such as the line's inductance, capacitance between the conductors, and wire resistance. The signal gradually weakens as a result of these losses.
Receiver: A telegraph receiver at the other end of the wire deciphers the weaker signals and transforms them back into legible telegraph code. Despite any communication losses, the recipient bears the responsibility of deriving the provided data.
Plotting the transmission line: A straightforward line representing the physical link between the transmitter and the receiver would be used to depict the telegraph transmission line visually. In keeping with this, you might incorporate components that depict leakage, like arrows that show the signal intensity decreasing at different spots.
Consider an infinitesimal piece of the telegraph cable wire as an electrical circuit (Figure 9), and consider that the cable has the perfect insulation, so that the capacitor and leakage to the floor are present.

Telegraph transmission line with leakage.
4.2.2 Fractional derivative model equations are as follows [10]:
and
and where
4.2.3 Study of effect of changed values of “
α
” on the numerical solution
The effect of different values of fractional order derivative is claimed via
Figures 9–14. For Example 1,
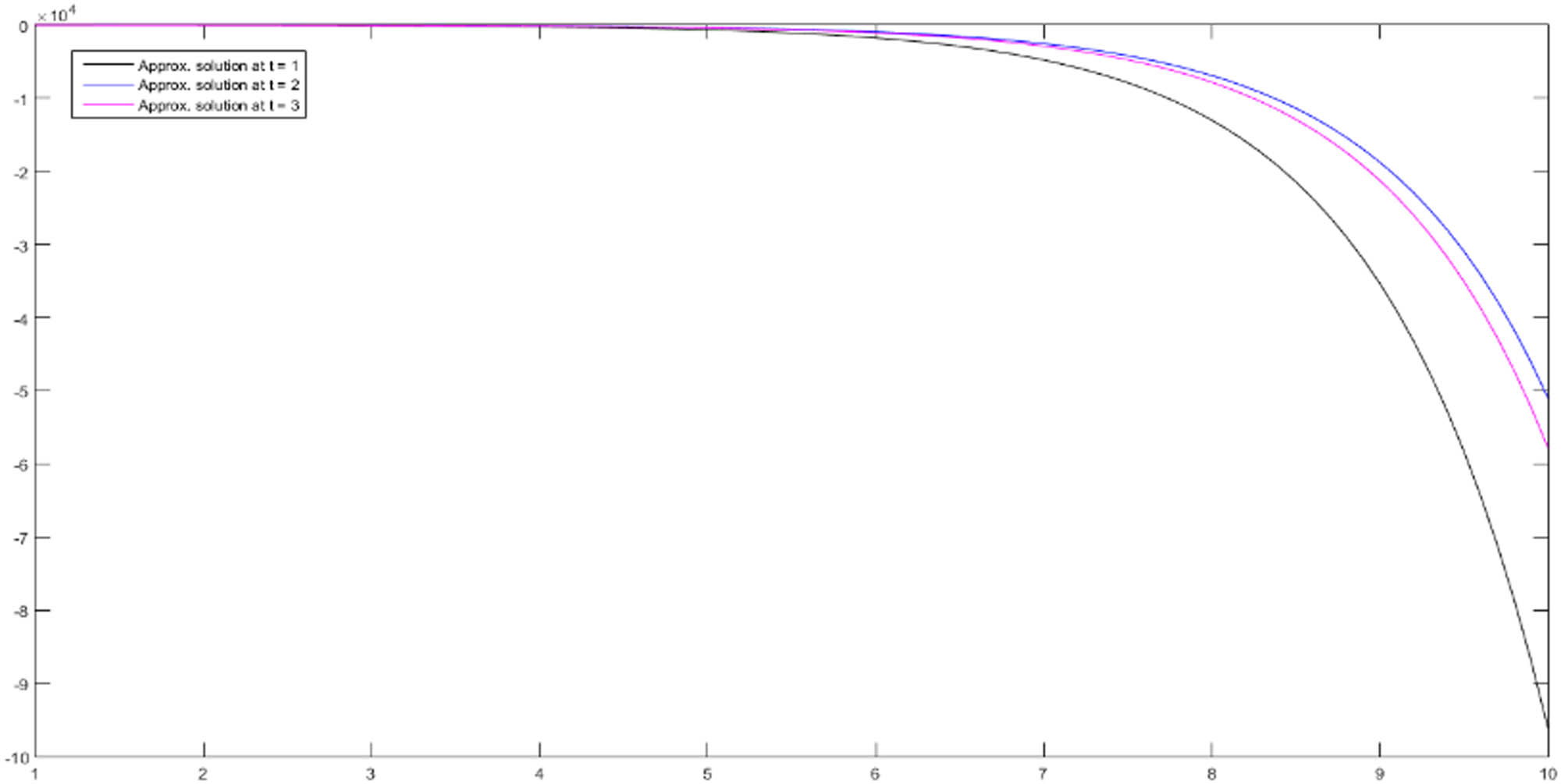
Approximated solution up to fourth term for

Approximated solution up to fourth term for

Approximated solution up to fourth term for

Approximated solution up to fourth term for

Approximated solution up to

Approximated solution up to fourth term for
5 Concluding remarks
This article presents the integration of the Shehu transform with the homotopy perturbation method. The series and accurate approximation of the fractional HT equation in various dimensions are the subjects of this research. There are five instances of fractional HT equations in
Acknowledgments
This project was supported by the Researchers Supporting Project number (RSP2024R413), King Saud University, Riyadh, Saudi Arabia.
-
Funding information: This project was supported by the Researchers Supporting Project number (RSP2024R413), King Saud University, Riyadh, Saudi Arabia.
-
Author contributions: All authors have accepted responsibility for the entire content of this manuscript and approved its submission.
-
Conflict of interest: The authors state no conflict of interest.
-
Data availability statement: All data generated or analysed during this study are included in this published article (and its supplementary information files).
References
[1] Oldham K, Spanier J. The fractional calculus theory and applications of differentiation and integration to arbitrary order. Elsevier; 1974.Search in Google Scholar
[2] Miller KS, Ross B. An introduction to the fractional integrals and derivatives-theory and applications. New York: John Willey and Sons; 1993.Search in Google Scholar
[3] Kilbas AA, Marichev OI, Samko SG. Fractional integrals and derivatives (theory and applications); 1993.Search in Google Scholar
[4] Debnath L. Nonlinear diffusion-reaction phenomena, burgers’ and fisher’s equations. In Nonlinear Partial Differential Equations for Scientists and Engineers. Boston, MA: Birkhäuser; 1997. p. 283–329.10.1007/978-1-4899-2846-7_8Search in Google Scholar
[5] Metaxas AA, Meredith RJ. Industrial microwave heating. IET. No. 4; 1983.Search in Google Scholar
[6] Momani S. Analytic and approximate solutions of the space-and time-fractional telegraph equations. Appl Math Comput. 2005;170(2):1126–34.10.1016/j.amc.2005.01.009Search in Google Scholar
[7] Yıldırım A. He's homotopy perturbation method for solving the space-and time-fractional telegraph equations. Int J Computer Math. 2010;87(13):2998–3006.10.1080/00207160902874653Search in Google Scholar
[8] Chen J, Liu F, Anh V. Analytical solution for the time-fractional telegraph equation by the method of separating variables. J Math Anal Appl. 2008;338(2):1364–77.10.1016/j.jmaa.2007.06.023Search in Google Scholar
[9] Sevimlican A. An approximation to solution of space and time fractional telegraph equations by He's variational iteration method. Math Probl Eng. 2010;2010.10.1155/2010/290631Search in Google Scholar
[10] Khan H, Shah R, Baleanu D, Kumam P, Arif M. Analytical solution of fractional-order hyperbolic telegraph equation, using natural transform decomposition method. Electronics. 2019;8(9):1015.10.3390/electronics8091015Search in Google Scholar
[11] Jassim HK, Shahab WA. Fractional variational iteration method for solving the hyperbolic telegraph equation. In Journal of Physics: Conference Series. Vol. 1032. Issue. 1. IOP Publishing; 2018. p. 012015.10.1088/1742-6596/1032/1/012015Search in Google Scholar
[12] Kapoor M, Shah NA, Saleem S, Weera W. An analytical approach for fractional hyperbolic telegraph equation using Shehu transform in one, two and three dimensions. Mathematics. 2022;10(12):1961.10.3390/math10121961Search in Google Scholar
[13] Khan H, Shah R, Kumam P, Baleanu D, Arif M. An efficient analytical technique, for the solution of fractional-order telegraph equations. Mathematics. 2019;7(5):426.10.3390/math7050426Search in Google Scholar
[14] Akram T, Abbas M, Ismail AI, Ali NHM, Baleanu D. Extended cubic B-splines in the numerical solution of time fractional telegraph equation. Adv Differ Equ. 2019;2019(1):1–20.10.1186/s13662-019-2296-9Search in Google Scholar
[15] Modanli M. Comparison of Caputo and Atangana–Baleanu fractional derivatives for the pseudohyperbolic telegraph differential equations. Pramana. 2022;96(1):1–8.10.1007/s12043-021-02250-6Search in Google Scholar
[16] Mishra AK, Kumar S, Shukla AK. Numerical approximation of fractional telegraph equation via Legendre collocation technique. Int J Appl Comput Math. 2021;7(5):1–27.10.1007/s40819-021-01133-zSearch in Google Scholar
[17] Khan RA, Li Y, Jarad F. Exact analytical solutions of fractional order telegraph equations via triple Laplace transform; 2021.10.3934/dcdss.2020427Search in Google Scholar
[18] Kapoor M. Exact solution of coupled 1D non-linear Burgers’ equation by using Homotopy Perturbation Method (HPM): A review. J Phys Commun. 2020;4(9):095017.10.1088/2399-6528/abb218Search in Google Scholar
[19] He W, Chen N, Dassios I, Chung JD. Fractional system of Korteweg-De Vries equations via Elzaki transform. Mathematics. 2021;9:673.10.3390/math9060673Search in Google Scholar
[20] Chu YM, Agarwal P, Chung JD. Analysis of fractional multi-dimensional Navier–Stokes equation. Adv Differ Equ. 2021;2021:91.10.1186/s13662-021-03250-xSearch in Google Scholar
[21] Shah NA, Agarwal P, Chung JD, El-Zahar ER, Hamed YS. Analysis of optical solitons for nonlinear Schrödinger equation with Detuning term by iterative transform method. Symmetry. 2020;12:1850. 10.3390/sym12111850.Search in Google Scholar
[22] Shah NA, El-Zahar ER, Akgül A, Khan A, Kafle J. Analysis of fractional-order regularized long-wave models via a novel transform. J Funct Spaces. 2022;2022:Article ID 2754507. 10.1155/2022/2754507.Search in Google Scholar
[23] Chu Y-M, Hani EHB, El-Zahar ER, Ebaid A. Combination of Shehu decomposition and variational iteration transform methods for solving fractional third order dispersive partial differential equations. Numer Methods Partial Differ Equ. 2024;40:e22755. 10.1002/num.22755.Search in Google Scholar
[24] He JH. Homotopy perturbation method: a new nonlinear analytical technique. Appl Math Comput. 2003;135(1):73–9.10.1016/S0096-3003(01)00312-5Search in Google Scholar
[25] He JH. Application of homotopy perturbation method to nonlinear wave equations. Chaos Solitons Fractals. 2005;26(3):695–700.10.1016/j.chaos.2005.03.006Search in Google Scholar
[26] Vickers NJ. Animal communication: when I’m calling you, will you answer too? Curr Biol. 2017;27(14):R713–5.10.1016/j.cub.2017.05.064Search in Google Scholar PubMed
[27] He JH. Homotopy perturbation technique. Comput Methods Appl Mech Eng. 1999;178:257.10.1016/S0045-7825(99)00018-3Search in Google Scholar
[28] Armstrong MA. Basic topology. Berlin: Springer Science & Business Media; 2013.Search in Google Scholar
[29] Poincaré H. Sur les intégrales irrégulières. Acta Math. 1886;8(1):295–344.10.1007/BF02417092Search in Google Scholar
[30] Ali HM, Ahmad H, Askar S, Ameen IG. Efficient approaches for solving systems of nonlinear time-fractional partial differential equations. Fractal Fract. 2022;6(1):32.10.3390/fractalfract6010032Search in Google Scholar
[31] Baleanu D, Jassim HK, Al Qurashi M. Solving Helmholtz equation with local fractional derivative operators. Fractal Fract. 2019;3(3):43.10.3390/fractalfract3030043Search in Google Scholar
[32] Zhang M, Shen M, Chen H. An implicit numerical method for the Riemann–Liouville distributed-order space fractional diffusion equation. Fractal Fract. 2023;7(5):382.10.3390/fractalfract7050382Search in Google Scholar
[33] Shah R, Mofarreh F, Tag EM, Ghamry NA. Implementation of analytical techniques for the solution of nonlinear fractional order Sawada–Kotera–Ito equation. Fractal Fract. 2023;7(4):299.10.3390/fractalfract7040299Search in Google Scholar
[34] Alyousef HA, Shah R, Shah NA, Chung JD, Ismaeel SM, El-Tantawy SA. The fractional analysis of a nonlinear mKdV equation with Caputo operator. Fractal Fract. 2023;7(3):259.10.3390/fractalfract7030259Search in Google Scholar
[35] Alaroud M, Alomari AK, Tahat N, Ishak A. Analytical computational scheme for multivariate nonlinear time-fractional generalized biological population model. Fractal Fract. 2023;7(2):176.10.3390/fractalfract7020176Search in Google Scholar
[36] Areshi M, Seadawy AR, Ali A, Alharbi AF, Aljohani AF. Analytical solutions of the Predator–Prey model with fractional derivative order via applications of three modified mathematical methods. Fractal Fract. 2023;7(2):128.10.3390/fractalfract7020128Search in Google Scholar
[37] Iqbal N, Chughtai MT, Ullah R. Fractional study of the non-linear Burgers’ equations via a semi-analytical technique. Fractal Fract. 2023;7(2):103.10.3390/fractalfract7020103Search in Google Scholar
[38] Arqub OA, Maayah B. Adaptive the Dirichlet model of mobile/immobile advection/dispersion in a time-fractional sense with the reproducing kernel computational approach: Formulations and approximations. Int J Mod Phys B. 2023;37(18):2350179.10.1142/S0217979223501795Search in Google Scholar
[39] Arqub OA. Numerical solutions for the Robin time-fractional partial differential equations of heat and fluid flows based on the reproducing kernel algorithm. Int J Numer Methods Heat Fluid Flow. 2018;28(4):828–56.10.1108/HFF-07-2016-0278Search in Google Scholar
[40] Abu Arqub O. Numerical simulation of time-fractional partial differential equations arising in fluid flows via reproducing Kernel method. Int J Numer Methods Heat Fluid Flow. 2020;30(11):4711–33.10.1108/HFF-10-2017-0394Search in Google Scholar
[41] Abu Arqub O, Alsulami H, Alhodaly M. Numerical Hilbert space solution of fractional Sobolev equation in 1+ 1-dimensional space. Math Sci. 2022;2022:1–12.10.1007/s40096-022-00495-9Search in Google Scholar
[42] Ahmed S, Jahan S, Ansari KJ, Shah K, Abdeljawad T. Wavelets collocation method for singularly perturbed differential–difference equations arising in control system. Results Appl Math. 2024;21:100415.10.1016/j.rinam.2023.100415Search in Google Scholar
[43] Yadav P, Jahan S, Nisar KS. Fibonacci wavelet method for time fractional convection–diffusion equations. Math Methods Appl Sci. 2024;47(4):2639–55.10.1002/mma.9770Search in Google Scholar
[44] Yadav P, Jahan S, Nisar KS. Fractional order mathematical model of Ebola virus under Atangana–Baleanu–Caputo operator. Results Control Optim. 2023;13:100332.10.1016/j.rico.2023.100332Search in Google Scholar
[45] Yadav P, Jahan S, Shah K, Peter OJ, Abdeljawad T. Fractional-order modelling and analysis of diabetes mellitus: Utilizing the Atangana-Baleanu Caputo (ABC) operator. Alex Eng J. 2023;81:200–9.10.1016/j.aej.2023.09.006Search in Google Scholar
[46] Ahmed S, Shah K, Jahan S, Abdeljawad T. An efficient method for the fractional electric circuits based on Fibonacci wavelet. Results Phys. 2023;52:106753.10.1016/j.rinp.2023.106753Search in Google Scholar
[47] Jahan S, Ahmed S, Yadav P, Nisar KS. Fibonacci wavelet method for the numerical solution of a fractional relaxation–oscillation model. Partial Differ Equ Appl Math. 2023;8:100568.10.1016/j.padiff.2023.100568Search in Google Scholar
[48] Yadav P, Jahan S, Nisar KS. Solving fractional Bagley-Torvik equation by fractional order Fibonacci wavelet arising in fluid mechanics. Ain Shams Eng J. 2024;15(1):102299.10.1016/j.asej.2023.102299Search in Google Scholar
© 2024 the author(s), published by De Gruyter
This work is licensed under the Creative Commons Attribution 4.0 International License.
Articles in the same Issue
- Regular Articles
- Numerical study of flow and heat transfer in the channel of panel-type radiator with semi-detached inclined trapezoidal wing vortex generators
- Homogeneous–heterogeneous reactions in the colloidal investigation of Casson fluid
- High-speed mid-infrared Mach–Zehnder electro-optical modulators in lithium niobate thin film on sapphire
- Numerical analysis of dengue transmission model using Caputo–Fabrizio fractional derivative
- Mononuclear nanofluids undergoing convective heating across a stretching sheet and undergoing MHD flow in three dimensions: Potential industrial applications
- Heat transfer characteristics of cobalt ferrite nanoparticles scattered in sodium alginate-based non-Newtonian nanofluid over a stretching/shrinking horizontal plane surface
- The electrically conducting water-based nanofluid flow containing titanium and aluminum alloys over a rotating disk surface with nonlinear thermal radiation: A numerical analysis
- Growth, characterization, and anti-bacterial activity of l-methionine supplemented with sulphamic acid single crystals
- A numerical analysis of the blood-based Casson hybrid nanofluid flow past a convectively heated surface embedded in a porous medium
- Optoelectronic–thermomagnetic effect of a microelongated non-local rotating semiconductor heated by pulsed laser with varying thermal conductivity
- Thermal proficiency of magnetized and radiative cross-ternary hybrid nanofluid flow induced by a vertical cylinder
- Enhanced heat transfer and fluid motion in 3D nanofluid with anisotropic slip and magnetic field
- Numerical analysis of thermophoretic particle deposition on 3D Casson nanofluid: Artificial neural networks-based Levenberg–Marquardt algorithm
- Analyzing fuzzy fractional Degasperis–Procesi and Camassa–Holm equations with the Atangana–Baleanu operator
- Bayesian estimation of equipment reliability with normal-type life distribution based on multiple batch tests
- Chaotic control problem of BEC system based on Hartree–Fock mean field theory
- Optimized framework numerical solution for swirling hybrid nanofluid flow with silver/gold nanoparticles on a stretching cylinder with heat source/sink and reactive agents
- Stability analysis and numerical results for some schemes discretising 2D nonconstant coefficient advection–diffusion equations
- Convective flow of a magnetohydrodynamic second-grade fluid past a stretching surface with Cattaneo–Christov heat and mass flux model
- Analysis of the heat transfer enhancement in water-based micropolar hybrid nanofluid flow over a vertical flat surface
- Microscopic seepage simulation of gas and water in shale pores and slits based on VOF
- Model of conversion of flow from confined to unconfined aquifers with stochastic approach
- Study of fractional variable-order lymphatic filariasis infection model
- Soliton, quasi-soliton, and their interaction solutions of a nonlinear (2 + 1)-dimensional ZK–mZK–BBM equation for gravity waves
- Application of conserved quantities using the formal Lagrangian of a nonlinear integro partial differential equation through optimal system of one-dimensional subalgebras in physics and engineering
- Nonlinear fractional-order differential equations: New closed-form traveling-wave solutions
- Sixth-kind Chebyshev polynomials technique to numerically treat the dissipative viscoelastic fluid flow in the rheology of Cattaneo–Christov model
- Some transforms, Riemann–Liouville fractional operators, and applications of newly extended M–L (p, s, k) function
- Magnetohydrodynamic water-based hybrid nanofluid flow comprising diamond and copper nanoparticles on a stretching sheet with slips constraints
- Super-resolution reconstruction method of the optical synthetic aperture image using generative adversarial network
- A two-stage framework for predicting the remaining useful life of bearings
- Influence of variable fluid properties on mixed convective Darcy–Forchheimer flow relation over a surface with Soret and Dufour spectacle
- Inclined surface mixed convection flow of viscous fluid with porous medium and Soret effects
- Exact solutions to vorticity of the fractional nonuniform Poiseuille flows
- In silico modified UV spectrophotometric approaches to resolve overlapped spectra for quality control of rosuvastatin and teneligliptin formulation
- Numerical simulations for fractional Hirota–Satsuma coupled Korteweg–de Vries systems
- Substituent effect on the electronic and optical properties of newly designed pyrrole derivatives using density functional theory
- A comparative analysis of shielding effectiveness in glass and concrete containers
- Numerical analysis of the MHD Williamson nanofluid flow over a nonlinear stretching sheet through a Darcy porous medium: Modeling and simulation
- Analytical and numerical investigation for viscoelastic fluid with heat transfer analysis during rollover-web coating phenomena
- Influence of variable viscosity on existing sheet thickness in the calendering of non-isothermal viscoelastic materials
- Analysis of nonlinear fractional-order Fisher equation using two reliable techniques
- Comparison of plan quality and robustness using VMAT and IMRT for breast cancer
- Radiative nanofluid flow over a slender stretching Riga plate under the impact of exponential heat source/sink
- Numerical investigation of acoustic streaming vortices in cylindrical tube arrays
- Numerical study of blood-based MHD tangent hyperbolic hybrid nanofluid flow over a permeable stretching sheet with variable thermal conductivity and cross-diffusion
- Fractional view analytical analysis of generalized regularized long wave equation
- Dynamic simulation of non-Newtonian boundary layer flow: An enhanced exponential time integrator approach with spatially and temporally variable heat sources
- Inclined magnetized infinite shear rate viscosity of non-Newtonian tetra hybrid nanofluid in stenosed artery with non-uniform heat sink/source
- Estimation of monotone α-quantile of past lifetime function with application
- Numerical simulation for the slip impacts on the radiative nanofluid flow over a stretched surface with nonuniform heat generation and viscous dissipation
- Study of fractional telegraph equation via Shehu homotopy perturbation method
- An investigation into the impact of thermal radiation and chemical reactions on the flow through porous media of a Casson hybrid nanofluid including unstable mixed convection with stretched sheet in the presence of thermophoresis and Brownian motion
- Establishing breather and N-soliton solutions for conformable Klein–Gordon equation
- An electro-optic half subtractor from a silicon-based hybrid surface plasmon polariton waveguide
- CFD analysis of particle shape and Reynolds number on heat transfer characteristics of nanofluid in heated tube
- Abundant exact traveling wave solutions and modulation instability analysis to the generalized Hirota–Satsuma–Ito equation
- A short report on a probability-based interpretation of quantum mechanics
- Study on cavitation and pulsation characteristics of a novel rotor-radial groove hydrodynamic cavitation reactor
- Optimizing heat transport in a permeable cavity with an isothermal solid block: Influence of nanoparticles volume fraction and wall velocity ratio
- Linear instability of the vertical throughflow in a porous layer saturated by a power-law fluid with variable gravity effect
- Thermal analysis of generalized Cattaneo–Christov theories in Burgers nanofluid in the presence of thermo-diffusion effects and variable thermal conductivity
- A new benchmark for camouflaged object detection: RGB-D camouflaged object detection dataset
- Effect of electron temperature and concentration on production of hydroxyl radical and nitric oxide in atmospheric pressure low-temperature helium plasma jet: Swarm analysis and global model investigation
- Double diffusion convection of Maxwell–Cattaneo fluids in a vertical slot
- Thermal analysis of extended surfaces using deep neural networks
- Steady-state thermodynamic process in multilayered heterogeneous cylinder
- Multiresponse optimisation and process capability analysis of chemical vapour jet machining for the acrylonitrile butadiene styrene polymer: Unveiling the morphology
- Modeling monkeypox virus transmission: Stability analysis and comparison of analytical techniques
- Fourier spectral method for the fractional-in-space coupled Whitham–Broer–Kaup equations on unbounded domain
- The chaotic behavior and traveling wave solutions of the conformable extended Korteweg–de-Vries model
- Research on optimization of combustor liner structure based on arc-shaped slot hole
- Construction of M-shaped solitons for a modified regularized long-wave equation via Hirota's bilinear method
- Effectiveness of microwave ablation using two simultaneous antennas for liver malignancy treatment
- Discussion on optical solitons, sensitivity and qualitative analysis to a fractional model of ion sound and Langmuir waves with Atangana Baleanu derivatives
- Reliability of two-dimensional steady magnetized Jeffery fluid over shrinking sheet with chemical effect
- Generalized model of thermoelasticity associated with fractional time-derivative operators and its applications to non-simple elastic materials
- Migration of two rigid spheres translating within an infinite couple stress fluid under the impact of magnetic field
- A comparative investigation of neutron and gamma radiation interaction properties of zircaloy-2 and zircaloy-4 with consideration of mechanical properties
- New optical stochastic solutions for the Schrödinger equation with multiplicative Wiener process/random variable coefficients using two different methods
- Physical aspects of quantile residual lifetime sequence
- Synthesis, structure, I–V characteristics, and optical properties of chromium oxide thin films for optoelectronic applications
- Smart mathematically filtered UV spectroscopic methods for quality assurance of rosuvastatin and valsartan from formulation
- A novel investigation into time-fractional multi-dimensional Navier–Stokes equations within Aboodh transform
- Homotopic dynamic solution of hydrodynamic nonlinear natural convection containing superhydrophobicity and isothermally heated parallel plate with hybrid nanoparticles
- A novel tetra hybrid bio-nanofluid model with stenosed artery
- Propagation of traveling wave solution of the strain wave equation in microcrystalline materials
- Innovative analysis to the time-fractional q-deformed tanh-Gordon equation via modified double Laplace transform method
- A new investigation of the extended Sakovich equation for abundant soliton solution in industrial engineering via two efficient techniques
- New soliton solutions of the conformable time fractional Drinfel'd–Sokolov–Wilson equation based on the complete discriminant system method
- Irradiation of hydrophilic acrylic intraocular lenses by a 365 nm UV lamp
- Inflation and the principle of equivalence
- The use of a supercontinuum light source for the characterization of passive fiber optic components
- Optical solitons to the fractional Kundu–Mukherjee–Naskar equation with time-dependent coefficients
- A promising photocathode for green hydrogen generation from sanitation water without external sacrificing agent: silver-silver oxide/poly(1H-pyrrole) dendritic nanocomposite seeded on poly-1H pyrrole film
- Photon balance in the fiber laser model
- Propagation of optical spatial solitons in nematic liquid crystals with quadruple power law of nonlinearity appears in fluid mechanics
- Theoretical investigation and sensitivity analysis of non-Newtonian fluid during roll coating process by response surface methodology
- Utilizing slip conditions on transport phenomena of heat energy with dust and tiny nanoparticles over a wedge
- Bismuthyl chloride/poly(m-toluidine) nanocomposite seeded on poly-1H pyrrole: Photocathode for green hydrogen generation
- Infrared thermography based fault diagnosis of diesel engines using convolutional neural network and image enhancement
- On some solitary wave solutions of the Estevez--Mansfield--Clarkson equation with conformable fractional derivatives in time
- Impact of permeability and fluid parameters in couple stress media on rotating eccentric spheres
- Review Article
- Transformer-based intelligent fault diagnosis methods of mechanical equipment: A survey
- Special Issue on Predicting pattern alterations in nature - Part II
- A comparative study of Bagley–Torvik equation under nonsingular kernel derivatives using Weeks method
- On the existence and numerical simulation of Cholera epidemic model
- Numerical solutions of generalized Atangana–Baleanu time-fractional FitzHugh–Nagumo equation using cubic B-spline functions
- Dynamic properties of the multimalware attacks in wireless sensor networks: Fractional derivative analysis of wireless sensor networks
- Prediction of COVID-19 spread with models in different patterns: A case study of Russia
- Study of chronic myeloid leukemia with T-cell under fractal-fractional order model
- Accumulation process in the environment for a generalized mass transport system
- Analysis of a generalized proportional fractional stochastic differential equation incorporating Carathéodory's approximation and applications
- Special Issue on Nanomaterial utilization and structural optimization - Part II
- Numerical study on flow and heat transfer performance of a spiral-wound heat exchanger for natural gas
- Study of ultrasonic influence on heat transfer and resistance performance of round tube with twisted belt
- Numerical study on bionic airfoil fins used in printed circuit plate heat exchanger
- Improving heat transfer efficiency via optimization and sensitivity assessment in hybrid nanofluid flow with variable magnetism using the Yamada–Ota model
- Special Issue on Nanofluids: Synthesis, Characterization, and Applications
- Exact solutions of a class of generalized nanofluidic models
- Stability enhancement of Al2O3, ZnO, and TiO2 binary nanofluids for heat transfer applications
- Thermal transport energy performance on tangent hyperbolic hybrid nanofluids and their implementation in concentrated solar aircraft wings
- Studying nonlinear vibration analysis of nanoelectro-mechanical resonators via analytical computational method
- Numerical analysis of non-linear radiative Casson fluids containing CNTs having length and radius over permeable moving plate
- Two-phase numerical simulation of thermal and solutal transport exploration of a non-Newtonian nanomaterial flow past a stretching surface with chemical reaction
- Natural convection and flow patterns of Cu–water nanofluids in hexagonal cavity: A novel thermal case study
- Solitonic solutions and study of nonlinear wave dynamics in a Murnaghan hyperelastic circular pipe
- Comparative study of couple stress fluid flow using OHAM and NIM
- Utilization of OHAM to investigate entropy generation with a temperature-dependent thermal conductivity model in hybrid nanofluid using the radiation phenomenon
- Slip effects on magnetized radiatively hybridized ferrofluid flow with acute magnetic force over shrinking/stretching surface
- Significance of 3D rectangular closed domain filled with charged particles and nanoparticles engaging finite element methodology
- Robustness and dynamical features of fractional difference spacecraft model with Mittag–Leffler stability
- Characterizing magnetohydrodynamic effects on developed nanofluid flow in an obstructed vertical duct under constant pressure gradient
- Study on dynamic and static tensile and puncture-resistant mechanical properties of impregnated STF multi-dimensional structure Kevlar fiber reinforced composites
- Thermosolutal Marangoni convective flow of MHD tangent hyperbolic hybrid nanofluids with elastic deformation and heat source
- Investigation of convective heat transport in a Carreau hybrid nanofluid between two stretchable rotatory disks
- Single-channel cooling system design by using perforated porous insert and modeling with POD for double conductive panel
- Special Issue on Fundamental Physics from Atoms to Cosmos - Part I
- Pulsed excitation of a quantum oscillator: A model accounting for damping
- Review of recent analytical advances in the spectroscopy of hydrogenic lines in plasmas
- Heavy mesons mass spectroscopy under a spin-dependent Cornell potential within the framework of the spinless Salpeter equation
- Coherent manipulation of bright and dark solitons of reflection and transmission pulses through sodium atomic medium
- Effect of the gravitational field strength on the rate of chemical reactions
- The kinetic relativity theory – hiding in plain sight
- Special Issue on Advanced Energy Materials - Part III
- Eco-friendly graphitic carbon nitride–poly(1H pyrrole) nanocomposite: A photocathode for green hydrogen production, paving the way for commercial applications
Articles in the same Issue
- Regular Articles
- Numerical study of flow and heat transfer in the channel of panel-type radiator with semi-detached inclined trapezoidal wing vortex generators
- Homogeneous–heterogeneous reactions in the colloidal investigation of Casson fluid
- High-speed mid-infrared Mach–Zehnder electro-optical modulators in lithium niobate thin film on sapphire
- Numerical analysis of dengue transmission model using Caputo–Fabrizio fractional derivative
- Mononuclear nanofluids undergoing convective heating across a stretching sheet and undergoing MHD flow in three dimensions: Potential industrial applications
- Heat transfer characteristics of cobalt ferrite nanoparticles scattered in sodium alginate-based non-Newtonian nanofluid over a stretching/shrinking horizontal plane surface
- The electrically conducting water-based nanofluid flow containing titanium and aluminum alloys over a rotating disk surface with nonlinear thermal radiation: A numerical analysis
- Growth, characterization, and anti-bacterial activity of l-methionine supplemented with sulphamic acid single crystals
- A numerical analysis of the blood-based Casson hybrid nanofluid flow past a convectively heated surface embedded in a porous medium
- Optoelectronic–thermomagnetic effect of a microelongated non-local rotating semiconductor heated by pulsed laser with varying thermal conductivity
- Thermal proficiency of magnetized and radiative cross-ternary hybrid nanofluid flow induced by a vertical cylinder
- Enhanced heat transfer and fluid motion in 3D nanofluid with anisotropic slip and magnetic field
- Numerical analysis of thermophoretic particle deposition on 3D Casson nanofluid: Artificial neural networks-based Levenberg–Marquardt algorithm
- Analyzing fuzzy fractional Degasperis–Procesi and Camassa–Holm equations with the Atangana–Baleanu operator
- Bayesian estimation of equipment reliability with normal-type life distribution based on multiple batch tests
- Chaotic control problem of BEC system based on Hartree–Fock mean field theory
- Optimized framework numerical solution for swirling hybrid nanofluid flow with silver/gold nanoparticles on a stretching cylinder with heat source/sink and reactive agents
- Stability analysis and numerical results for some schemes discretising 2D nonconstant coefficient advection–diffusion equations
- Convective flow of a magnetohydrodynamic second-grade fluid past a stretching surface with Cattaneo–Christov heat and mass flux model
- Analysis of the heat transfer enhancement in water-based micropolar hybrid nanofluid flow over a vertical flat surface
- Microscopic seepage simulation of gas and water in shale pores and slits based on VOF
- Model of conversion of flow from confined to unconfined aquifers with stochastic approach
- Study of fractional variable-order lymphatic filariasis infection model
- Soliton, quasi-soliton, and their interaction solutions of a nonlinear (2 + 1)-dimensional ZK–mZK–BBM equation for gravity waves
- Application of conserved quantities using the formal Lagrangian of a nonlinear integro partial differential equation through optimal system of one-dimensional subalgebras in physics and engineering
- Nonlinear fractional-order differential equations: New closed-form traveling-wave solutions
- Sixth-kind Chebyshev polynomials technique to numerically treat the dissipative viscoelastic fluid flow in the rheology of Cattaneo–Christov model
- Some transforms, Riemann–Liouville fractional operators, and applications of newly extended M–L (p, s, k) function
- Magnetohydrodynamic water-based hybrid nanofluid flow comprising diamond and copper nanoparticles on a stretching sheet with slips constraints
- Super-resolution reconstruction method of the optical synthetic aperture image using generative adversarial network
- A two-stage framework for predicting the remaining useful life of bearings
- Influence of variable fluid properties on mixed convective Darcy–Forchheimer flow relation over a surface with Soret and Dufour spectacle
- Inclined surface mixed convection flow of viscous fluid with porous medium and Soret effects
- Exact solutions to vorticity of the fractional nonuniform Poiseuille flows
- In silico modified UV spectrophotometric approaches to resolve overlapped spectra for quality control of rosuvastatin and teneligliptin formulation
- Numerical simulations for fractional Hirota–Satsuma coupled Korteweg–de Vries systems
- Substituent effect on the electronic and optical properties of newly designed pyrrole derivatives using density functional theory
- A comparative analysis of shielding effectiveness in glass and concrete containers
- Numerical analysis of the MHD Williamson nanofluid flow over a nonlinear stretching sheet through a Darcy porous medium: Modeling and simulation
- Analytical and numerical investigation for viscoelastic fluid with heat transfer analysis during rollover-web coating phenomena
- Influence of variable viscosity on existing sheet thickness in the calendering of non-isothermal viscoelastic materials
- Analysis of nonlinear fractional-order Fisher equation using two reliable techniques
- Comparison of plan quality and robustness using VMAT and IMRT for breast cancer
- Radiative nanofluid flow over a slender stretching Riga plate under the impact of exponential heat source/sink
- Numerical investigation of acoustic streaming vortices in cylindrical tube arrays
- Numerical study of blood-based MHD tangent hyperbolic hybrid nanofluid flow over a permeable stretching sheet with variable thermal conductivity and cross-diffusion
- Fractional view analytical analysis of generalized regularized long wave equation
- Dynamic simulation of non-Newtonian boundary layer flow: An enhanced exponential time integrator approach with spatially and temporally variable heat sources
- Inclined magnetized infinite shear rate viscosity of non-Newtonian tetra hybrid nanofluid in stenosed artery with non-uniform heat sink/source
- Estimation of monotone α-quantile of past lifetime function with application
- Numerical simulation for the slip impacts on the radiative nanofluid flow over a stretched surface with nonuniform heat generation and viscous dissipation
- Study of fractional telegraph equation via Shehu homotopy perturbation method
- An investigation into the impact of thermal radiation and chemical reactions on the flow through porous media of a Casson hybrid nanofluid including unstable mixed convection with stretched sheet in the presence of thermophoresis and Brownian motion
- Establishing breather and N-soliton solutions for conformable Klein–Gordon equation
- An electro-optic half subtractor from a silicon-based hybrid surface plasmon polariton waveguide
- CFD analysis of particle shape and Reynolds number on heat transfer characteristics of nanofluid in heated tube
- Abundant exact traveling wave solutions and modulation instability analysis to the generalized Hirota–Satsuma–Ito equation
- A short report on a probability-based interpretation of quantum mechanics
- Study on cavitation and pulsation characteristics of a novel rotor-radial groove hydrodynamic cavitation reactor
- Optimizing heat transport in a permeable cavity with an isothermal solid block: Influence of nanoparticles volume fraction and wall velocity ratio
- Linear instability of the vertical throughflow in a porous layer saturated by a power-law fluid with variable gravity effect
- Thermal analysis of generalized Cattaneo–Christov theories in Burgers nanofluid in the presence of thermo-diffusion effects and variable thermal conductivity
- A new benchmark for camouflaged object detection: RGB-D camouflaged object detection dataset
- Effect of electron temperature and concentration on production of hydroxyl radical and nitric oxide in atmospheric pressure low-temperature helium plasma jet: Swarm analysis and global model investigation
- Double diffusion convection of Maxwell–Cattaneo fluids in a vertical slot
- Thermal analysis of extended surfaces using deep neural networks
- Steady-state thermodynamic process in multilayered heterogeneous cylinder
- Multiresponse optimisation and process capability analysis of chemical vapour jet machining for the acrylonitrile butadiene styrene polymer: Unveiling the morphology
- Modeling monkeypox virus transmission: Stability analysis and comparison of analytical techniques
- Fourier spectral method for the fractional-in-space coupled Whitham–Broer–Kaup equations on unbounded domain
- The chaotic behavior and traveling wave solutions of the conformable extended Korteweg–de-Vries model
- Research on optimization of combustor liner structure based on arc-shaped slot hole
- Construction of M-shaped solitons for a modified regularized long-wave equation via Hirota's bilinear method
- Effectiveness of microwave ablation using two simultaneous antennas for liver malignancy treatment
- Discussion on optical solitons, sensitivity and qualitative analysis to a fractional model of ion sound and Langmuir waves with Atangana Baleanu derivatives
- Reliability of two-dimensional steady magnetized Jeffery fluid over shrinking sheet with chemical effect
- Generalized model of thermoelasticity associated with fractional time-derivative operators and its applications to non-simple elastic materials
- Migration of two rigid spheres translating within an infinite couple stress fluid under the impact of magnetic field
- A comparative investigation of neutron and gamma radiation interaction properties of zircaloy-2 and zircaloy-4 with consideration of mechanical properties
- New optical stochastic solutions for the Schrödinger equation with multiplicative Wiener process/random variable coefficients using two different methods
- Physical aspects of quantile residual lifetime sequence
- Synthesis, structure, I–V characteristics, and optical properties of chromium oxide thin films for optoelectronic applications
- Smart mathematically filtered UV spectroscopic methods for quality assurance of rosuvastatin and valsartan from formulation
- A novel investigation into time-fractional multi-dimensional Navier–Stokes equations within Aboodh transform
- Homotopic dynamic solution of hydrodynamic nonlinear natural convection containing superhydrophobicity and isothermally heated parallel plate with hybrid nanoparticles
- A novel tetra hybrid bio-nanofluid model with stenosed artery
- Propagation of traveling wave solution of the strain wave equation in microcrystalline materials
- Innovative analysis to the time-fractional q-deformed tanh-Gordon equation via modified double Laplace transform method
- A new investigation of the extended Sakovich equation for abundant soliton solution in industrial engineering via two efficient techniques
- New soliton solutions of the conformable time fractional Drinfel'd–Sokolov–Wilson equation based on the complete discriminant system method
- Irradiation of hydrophilic acrylic intraocular lenses by a 365 nm UV lamp
- Inflation and the principle of equivalence
- The use of a supercontinuum light source for the characterization of passive fiber optic components
- Optical solitons to the fractional Kundu–Mukherjee–Naskar equation with time-dependent coefficients
- A promising photocathode for green hydrogen generation from sanitation water without external sacrificing agent: silver-silver oxide/poly(1H-pyrrole) dendritic nanocomposite seeded on poly-1H pyrrole film
- Photon balance in the fiber laser model
- Propagation of optical spatial solitons in nematic liquid crystals with quadruple power law of nonlinearity appears in fluid mechanics
- Theoretical investigation and sensitivity analysis of non-Newtonian fluid during roll coating process by response surface methodology
- Utilizing slip conditions on transport phenomena of heat energy with dust and tiny nanoparticles over a wedge
- Bismuthyl chloride/poly(m-toluidine) nanocomposite seeded on poly-1H pyrrole: Photocathode for green hydrogen generation
- Infrared thermography based fault diagnosis of diesel engines using convolutional neural network and image enhancement
- On some solitary wave solutions of the Estevez--Mansfield--Clarkson equation with conformable fractional derivatives in time
- Impact of permeability and fluid parameters in couple stress media on rotating eccentric spheres
- Review Article
- Transformer-based intelligent fault diagnosis methods of mechanical equipment: A survey
- Special Issue on Predicting pattern alterations in nature - Part II
- A comparative study of Bagley–Torvik equation under nonsingular kernel derivatives using Weeks method
- On the existence and numerical simulation of Cholera epidemic model
- Numerical solutions of generalized Atangana–Baleanu time-fractional FitzHugh–Nagumo equation using cubic B-spline functions
- Dynamic properties of the multimalware attacks in wireless sensor networks: Fractional derivative analysis of wireless sensor networks
- Prediction of COVID-19 spread with models in different patterns: A case study of Russia
- Study of chronic myeloid leukemia with T-cell under fractal-fractional order model
- Accumulation process in the environment for a generalized mass transport system
- Analysis of a generalized proportional fractional stochastic differential equation incorporating Carathéodory's approximation and applications
- Special Issue on Nanomaterial utilization and structural optimization - Part II
- Numerical study on flow and heat transfer performance of a spiral-wound heat exchanger for natural gas
- Study of ultrasonic influence on heat transfer and resistance performance of round tube with twisted belt
- Numerical study on bionic airfoil fins used in printed circuit plate heat exchanger
- Improving heat transfer efficiency via optimization and sensitivity assessment in hybrid nanofluid flow with variable magnetism using the Yamada–Ota model
- Special Issue on Nanofluids: Synthesis, Characterization, and Applications
- Exact solutions of a class of generalized nanofluidic models
- Stability enhancement of Al2O3, ZnO, and TiO2 binary nanofluids for heat transfer applications
- Thermal transport energy performance on tangent hyperbolic hybrid nanofluids and their implementation in concentrated solar aircraft wings
- Studying nonlinear vibration analysis of nanoelectro-mechanical resonators via analytical computational method
- Numerical analysis of non-linear radiative Casson fluids containing CNTs having length and radius over permeable moving plate
- Two-phase numerical simulation of thermal and solutal transport exploration of a non-Newtonian nanomaterial flow past a stretching surface with chemical reaction
- Natural convection and flow patterns of Cu–water nanofluids in hexagonal cavity: A novel thermal case study
- Solitonic solutions and study of nonlinear wave dynamics in a Murnaghan hyperelastic circular pipe
- Comparative study of couple stress fluid flow using OHAM and NIM
- Utilization of OHAM to investigate entropy generation with a temperature-dependent thermal conductivity model in hybrid nanofluid using the radiation phenomenon
- Slip effects on magnetized radiatively hybridized ferrofluid flow with acute magnetic force over shrinking/stretching surface
- Significance of 3D rectangular closed domain filled with charged particles and nanoparticles engaging finite element methodology
- Robustness and dynamical features of fractional difference spacecraft model with Mittag–Leffler stability
- Characterizing magnetohydrodynamic effects on developed nanofluid flow in an obstructed vertical duct under constant pressure gradient
- Study on dynamic and static tensile and puncture-resistant mechanical properties of impregnated STF multi-dimensional structure Kevlar fiber reinforced composites
- Thermosolutal Marangoni convective flow of MHD tangent hyperbolic hybrid nanofluids with elastic deformation and heat source
- Investigation of convective heat transport in a Carreau hybrid nanofluid between two stretchable rotatory disks
- Single-channel cooling system design by using perforated porous insert and modeling with POD for double conductive panel
- Special Issue on Fundamental Physics from Atoms to Cosmos - Part I
- Pulsed excitation of a quantum oscillator: A model accounting for damping
- Review of recent analytical advances in the spectroscopy of hydrogenic lines in plasmas
- Heavy mesons mass spectroscopy under a spin-dependent Cornell potential within the framework of the spinless Salpeter equation
- Coherent manipulation of bright and dark solitons of reflection and transmission pulses through sodium atomic medium
- Effect of the gravitational field strength on the rate of chemical reactions
- The kinetic relativity theory – hiding in plain sight
- Special Issue on Advanced Energy Materials - Part III
- Eco-friendly graphitic carbon nitride–poly(1H pyrrole) nanocomposite: A photocathode for green hydrogen production, paving the way for commercial applications

