Abstract
The present study formulates and further examines a steady-state heat diffusion process in a generalized multilayered heterogeneous circular composite. Sufficient boundary and interfacial data are assumed at the endpoints of the circumferential length, and the interfaces, cutting across the respective perfectly welded cylinders. A well-known classical method for solving linear partial differential equations has been sought to derive a compacted solution for the diffusion process in governing heterogeneous cylinders. Certainly, among the significant novel findings of the current study is the acquisition of a generalized series solution for
1 Introduction
The heat diffusion processes arise in a variety of thermodynamical-related processes and have been comprehensively analyzed in both the past and present literature [1–3]. Certainly, these processes occur in different forms and materials, including, in particular, their occurrence in single-layered and multilayered shapes [4,5]. Further, “diffusion processes through a multilayered material are of interest for a wide range of applications, including industrial, biological, electrical, and environmental areas,” see Hickson et al. [6]. Moreover, there have been various studies with regard to the interaction of heat and wave processes in dissimilar elastic media, see the recent findings reported by Mubaraki et al. [7] and Althobaiti et al. [8] to mention a few. In light of the importance of the phenomena at hand, various methods have been devised to study the diffusional field relevance in several media. For instance, Akel et al. [9] employed the Laplace-typed transform to acquire a closed-form solution for diffusion problems in multilayer structures. Abro et al. [10] utilized the statistical method to solve the conductance and thermal resistance in conducting convection flow, while Al-Khaled and Momani [11] and Bokhari et al. [12] made use of the Adomian decomposition method (ADM) to treat wave-diffusion and nonlinear diffusion problems, respectively. Finally we make mention of the Wiener-Hopf method, which was used by Nuruddeen and Zaman [13] to solve a diffusion mixed problem in a cylindrical media, and on the other hand, a mixture of ADM with integral transform to tackle the class of fractional heat diffusion model [14]; see also the application of the method of separation of variables [15] in solving diverse mathematical physics problems. Besides, the study of heat transfer or diffusion in multilayered bodies has been comprehensively examined in the literature concerning its vast relevance in contemporary science and engineering applications. As the steady-state condition is attained upon reaching the equilibrium stage where time variation is immaterial, various researchers have profoundly scrutinized such a condition with the help of various analytical and approximation methods. Indeed, it is relevant to recall here that both Fourier’s equation of heat transfer and that of the Cattaneo, which is popularly called the hyperbolic heat equation, have been used in the open literature to model a variety of heat conduction processes. Thus, for more on these studies as well as various analytical and approximation techniques, below is an up-to-date collection of various relevant methods in thermoelasticity and dynamical systems. To begin with, Eltayeb et al. [16] made use of the Laplace decomposition method, a famous semi-analytical method to obtain approximate closed-form solution for closed systems of Emden-Fowler equation. In addition, Islam et al. [17] equally deployed the same Laplace decomposition method to computationally examine the class of logistic differential equations. Yan et al. [18] proposed a novel series technique for diffusion equations gifted with fractional-order derivatives, while Ray and Bera [19] solved the same diffusion equations via the use of Adomian decomposition approach in the presence of fractional-order derivative in Caputo’s sense. Accordingly, Bokhari et al. [12,20] deployed the same Adomian’s approach to thermodynamic equations with local and nonlocal boundary conditions, respectively; besides, the consideration in the study by Bokhari et al. [12] was moved by nonlinearity and temperature-dependent material thermal property. Further, Nuruddeen and Garba [21] model the diffusion of heat amidst fractional derivative with nonlocal boundary data, while Anwar et al. [22] employed the double Laplace transform method on fractional heating models. In fact, double Laplace method is a sort of integral transform method, through the application of Laplace transform method twice to solve the partial differential equation under scrutiny. In addition, interested reader(s) can consult the recent work of Alotaibi and Althobaiti [23] and Althobaiti et al. [24] that examined some nonlinear evolution equations with the help of numerical and analytical methods, respectively, which are promising and portray agreeing solutions with the corresponding exact solutions.
Furthermore, with an emphasis on the diffusional heating transfers in multilayered, various research studies have examined the scenario extensively due to its vast application in contemporary thermodynamics. In this regard, we recall some of these studies: to start with, we make mention of the good work of Negi and Singh [25] that theoretically describes the heating process in a horizontally stratified spherical shell and slab presided over by temperature-depending heating sources with emerging application in the earth’s crust. Noor and Burton [26] similarly examined the state-of-the-art of heating process in composite multilayer shells and plates; read also the study by Zhou [27] that analytically examined the transfer of heat in multilayered hollow cylindrical tubes containing stirred fluid with uniform heat sink. In addition, Yu et al. [28] made use of the Laplace transform method, to analytically derive the resulting diffusional fields in a multilayered conducting porous media that governs the transfer of chloride concentration fields in multiple layered systems. In the end, a comparative analysis was established between the derived analytical solution and the simulated corresponding numerical results. Further, Yuan et al. [29] analyzed the effect of the interfacial thermal resistance (ITR) on the diffusion of heat in multilayered materials; some application problems have been considered, where the effect of ITR was examined concerning the materials of a multiply coated substrate. Yang et al. [30] made use of integral (Laplace and Henkel) transform method, with a particular quadrature method to study the heat-emitting process in an axisymmetric cylindrical multilayer thermoelastic medium; moreover, an interesting real-life application was presented in geological science – see the work of Akbarzadeh and Pasini [31] that equally deployed the application of Laplace transform in the determination of the resulting temperature in phase-lag heat transfer associated with a multilayered media with sliding contact interfaces. Moreover, certain numerical procedures were equally used in the literature to determine the approximate fields for the transfer, In light of this, Kalis and Kangro [32] numerically deployed the finite difference method (FDM) and the finite element method to examine the transfer of two-dimensional (2D) heat in multilayer body, while Alaa et al. [33] coupled the analytical eigen-function method with the FDM to examine a 2D heating process in an inhomogeneous multilayered cylinder; read also the semi-analytical perspective of Ramadan [34] on dual-phase lag heating in perfectly conducting multilayered bodies, and the previous studies by Abbas et al. and Al Owidh et al. [35–37] for the recent findings and mathematical methods on the flow of thermodynamical and thermoelectric fluids in different settings.
However, motivated by the findings of the submissions in previous studies [25–35] concerning the heat transfer process in diverse multilayered structural shapes, the present study thus formulates and analytically examines a steady-state heat diffusion process in a highly heterogeneous multilayered circular cylinder via the application of the method of separation of variables [15]. The method of separation of variables is surely among the oldest methods for the study of linear partial differential equations that is frequently used in modern times due to its efficiency. Besides, the choice of separation of variables is associated with its easy implementation process, yet efficient against many sophisticated numerical methods or integral transform methods where their inversion procedures are computationally expensive. Another unique feature of this research is the inventive utilization of the variable separable approach, which provides a comprehensive and efficient technique for solving linear differential equations in multilayered thermodynamics. Two advantages of the current work are the construction of a generalized compact system to address a wide range of multi-heat equations and the capability to precisely characterize multiple physical processes. In addition, the successful resolution of prototype difficulties demonstrates the practical relevance and versatility of the proposed approach. To sum up, this work seeks to address the limitations of existing methods for solving numerous models in multilayered settings; its novelty stems from the inventive method proposed, which may contribute to advances in the study of thermodynamics in modern applications. Further, sufficient boundary and interfacial conditions will be imposed at the end-points of the circumferential length and in between the respective bounded layers, sequentially; this assumption or rather the imposition of perfect contact conditions between the respect layers does away with imperfection conditions, which “invalidates the continuity condition of temperature at the interface, so that a special treatment is required” [29]. What is more, the study will deeply examine certain prototype cases of the structure graphically – by numerically simulating the resulting diffusional fields – to validate the formulated generalized model. Finally, the communication is organized as follows: Section 2 portrays the model formulation. Section 3 analytically tackles the formulated model. Sections 4 and 5 give the application and the numerical results and discussion, respectively; while Section 6 outlines the concluding remarks.
2 Problem formulation
We make consideration to a multilayered heterogeneous circular cylinder, with constant thermal properties in all the layers and no heating source (Figure 1). Thus, the governing thermodynamic equations, featuring heat diffusion in the respective layers of the multilayered heterogeneous circular composite, are presided over by the following steady-state equations:
where
where
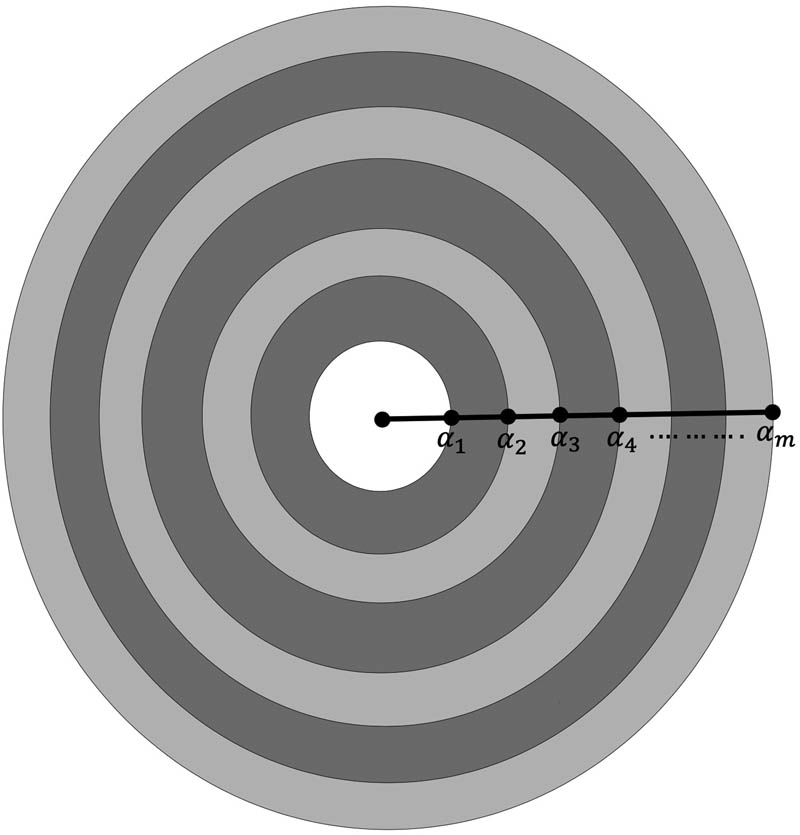
Multilayered heterogeneous circular cylinder.
Further, the imposition of appropriate endpoint boundary conditions is carried out on the structure. In fact, the related boundary conditions at
which characterize equal boundary data on the two end-points in the azimuthal direction,
where
In the same vein, the respective layers of the governing multilayered heterogeneous circular cylinder are presumed to be perfectly welded. That is, perfect interfacial conditions hold among the related diffusional fields
where
Above and beyond, such types of perfect continuity conditions at the respective interfaces, as imposed in (5), are typical to thermodynamic and elasticity problems in multilayered and composite bodies, refer to [2,3,7,8,39] for more on perfect continuity conditions in multilayered bodies, while [40,41] examined the parallel imperfect interfacial conditions.
3 Problem solution
To solve the governing problem, an analytical approach through the application of the method of separation of variables [15] is employed. Thus, the solution of Eq. (1) is considered to admit the following solution pattern:
where
or equally,
which subsequently separated to the following boundary-value problem (BVP):
and the following associated differential equation:
More so, the azimuthal solution
where
In addition, the radial solutions
where
Hence, the overall solution without the involvement of the interfacial and boundary conditions, which was earlier expressed in Eq. (6) is now rewritten using Eqs. (11) and (12) as follows:
where
all for
where
Certainly, one might unambiguously express the aforementioned compacted solution in each layer of the multilayer body in a more comprehending form as follows:
Moreover, to determine the explicit solution of the governing model, we now employ the prescribed boundary condition in Eq.
at
while at
for
In addition, on utilizing the second boundary condition expressed in Eq. (4)2 when
which upon employing the application of Fourier’s series [15] then yields the explict expressions for the involving coefficients as follows:
Finally, the overall general solution is explicitly determined while solving the
Remarkably, when the examining multilayered heterogeneous cylinder is considered to be a hollow one, that is, the inner most cylinder is vacuum layer, where fluid can be flowed in; then, the acquired solution in Eq. (13) take the following general form:
where
4 Application
The present section makes consideration of three prototypical multilayered cylinders as an application of the governing generalized multilayered heterogeneous cylinder that was successfully examined in the aforementioned section. More precisely, we will determine the diffusional fields in the following prototypes: a single-layered cylinder, a two-layered heterogeneous cylinder, and a three-layered heterogeneous cylinder. Indeed, all the related unknown coefficients – in each of the three cases – will be explicitly determined by solving the posed system of algebraic equations (see Figure 2 for the schema of the prototype multilayered cylinders of concern).

Prototype schema for: (a) a single-layered cylinder, (b) a two-layered heterogeneous cylinder, and (c) a three-layered heterogeneous cylinder.
4.1 Single-layered cylinder
Explicit solution for the resulting diffusional field with regard to a single-layered cylinder for
where the coefficients
4.2 Two-layered heterogeneous cylinder
Equally, the explicit expressions for the resulting diffusional fields with regard to a two-layered cylinder for
where the involving coefficients
where
with
4.3 Three-layered heterogeneous cylinder
As proceed, the explicit expressions for the resulting diffusional fields in this regard for
where the involving coefficients
where
while
with
5 Results and discussion
This section discusses the obtained results in the above section numerically, by graphically portraying the resulting diffusional fields in the three prototype heterogeneous cylinders under consideration. Certainly, these prototypes include a single-layered cylinder, a two-layered heterogeneous cylinder, and a three-layered heterogeneous cylinder. In addition, perfect interfacial conditions were imposed in their respective interfaces, while the outer boundary face was assumed to be at a fixed decaying temperature. Such consideration of perfect interfacial condition is industrially practical as an imperfection on boundary causes a lot of drawbacks in thermodynamical systems. More so, the two-dimensional (2D) and three-dimensional (3D) illustrations are used in depicting the obtained diffusional Âăsolutions while fixing the infinite summation
Comparatively, the acquired general solution for the transfer of heat in a steady-state multilayered heterogeneous circular composite is very complicated to be established numerically, as rightly asserted by Haberman [38], where the single-layered was examined – this assertion has equally been affirmed by deploying several scheme by the study. In fact, Haberman [38] made use of the effective Green’s function method to acquire the solution of single-layered problem, which admits the following closed-integral solution form:
where
The latter integral, realized in Eq. (32), is the known as the Poisson’s formula. Moreover, the method of Green’s function is equally not that straightforward method concerning the determination of perfect Green’s function of the given problem. Therefore, with the consideration of
which is, indeed, a complex-valued function amidst the presence of hypergeometric function
Thus, back to the acquired solution in Section 4, without much delay, we depict in Figures 3 and 4 the graphical view of the diffusional field for a single-layered cylinder determined in Eq. (22) when
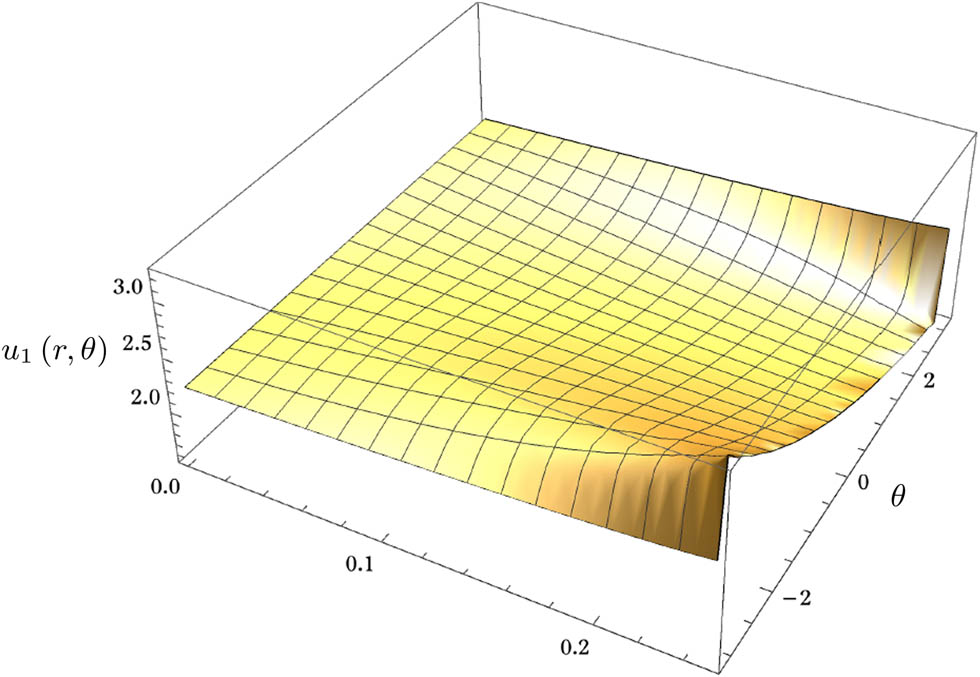
Graphical view of the diffusional field for a single-layered cylinder Eq. (22) portrayed using a 3D plot when

Graphical view of the diffusional field for a single-layered cylinder Eq. (22) portrayed using a 2D plot when
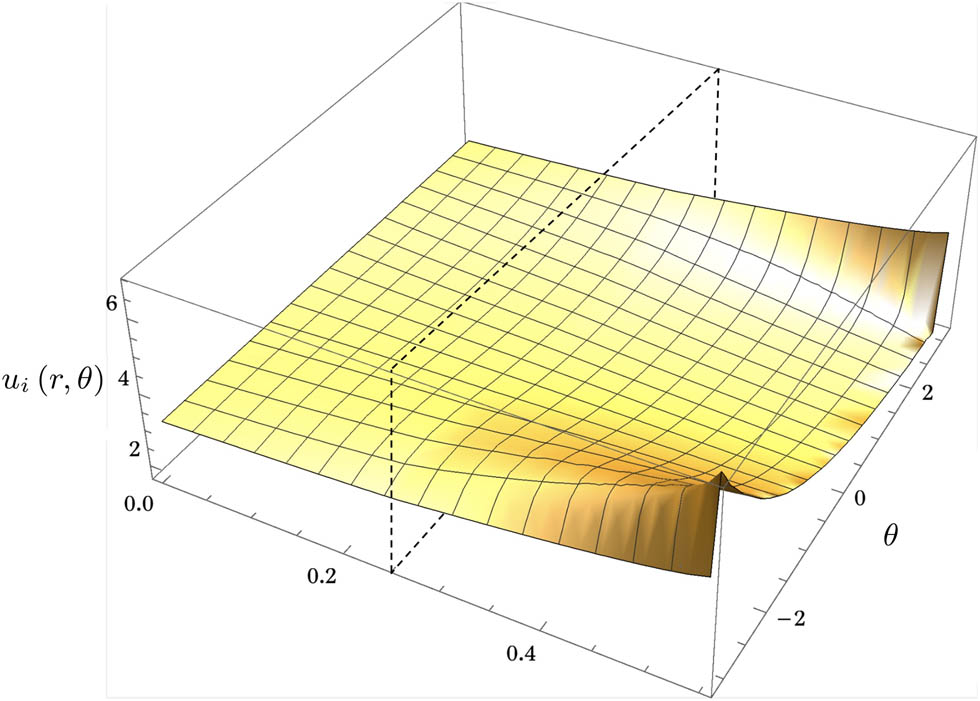
Graphical view of the diffusional fields for a two-layered cylinder Eq. (24) portrayed using a 3D plot when
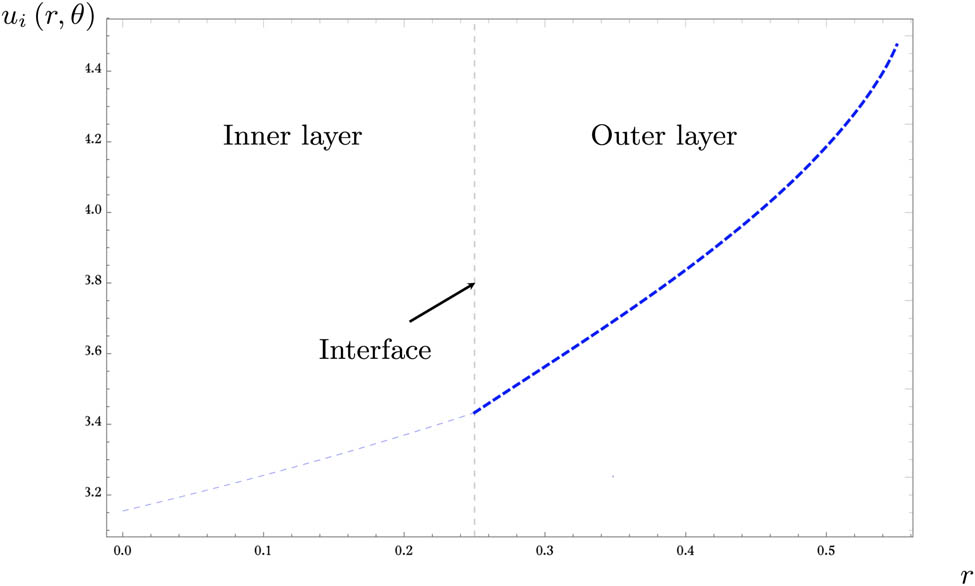
Graphical view of the diffusional fields for a two-layered cylinder Eq. (24) portrayed using a 2D plot when
Finally, Figures 7 and 8 depict the graphical view of the diffusional fields for a three-layered cylinder as determined in Eq. (27) when

Graphical view of the diffusional fields for a three-layered cylinder Eq. (27) portrayed using a 3D plot when
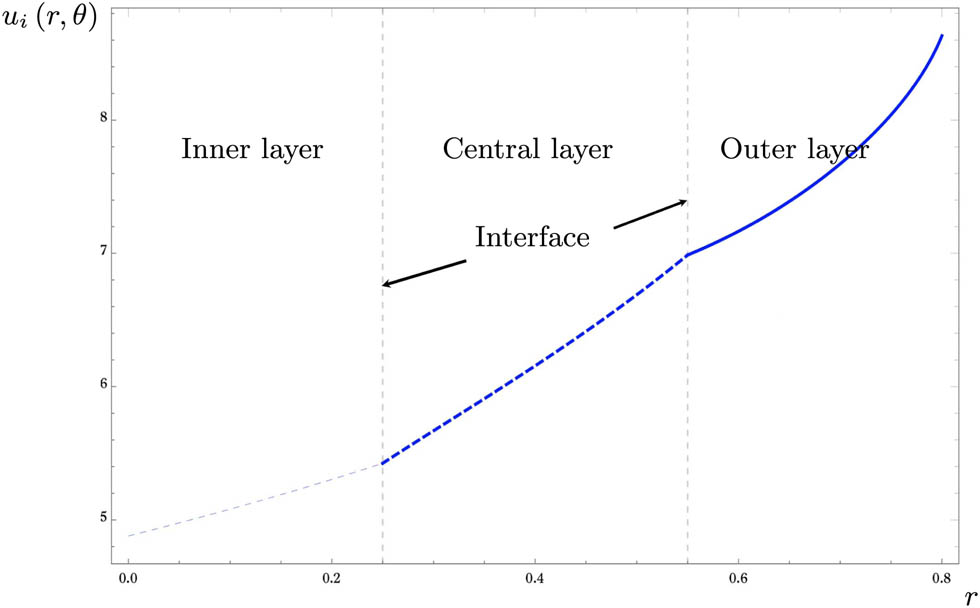
Graphical view of the diffusional fields for a three-layered cylinder Eq. (27) portrayed using a 2D plot when
6 Concluding remarks
The present communication formulated and analytically examined a steady-state heat diffusion process in a multilayered heterogeneous cylinder. Indeed, such structural configurations arise in many real-world applications, most especially, with the current advancement in contemporary science and engineering applications. Moreover, sufficient boundary and interfacial conditions were imposed at the endpoints of the circumferential length and in between the respective bounded layers, respectively. The promising method of separation of variables was adopted as the focal approach for the solution, which then revealed a compacted solution for the governing model for
Acknowledgments
The authors extend their appreciation to Taif University, Saudi Arabia, for supporting this work through project number (TU-DSPP-2024-231).
-
Funding information: This research was funded by Taif University, Saudi Arabia, Project No. (TU-DSPP-2024-231).
-
Author contributions: Basic idea of the paper was conceived by Ali M. Mubaraki and Rahmatullah Ibrahim Nuruddeen. Rahmatullah Ibrahim Nuruddeen implemented these ideas. Ali M. Mubaraki identified major issues with correctness of the paper and Rahmatullah Ibrahim Nuruddeen rectified these in consultation with Ali M. Mubaraki. The manuscript was written through the contribution of all authors. All authors have accepted responsibility for the entire content of this manuscript and approved its submission.
-
Conflict of interest: The authors state no conflict of interest.
-
Data availability statement: All data generated or analyzed during this study are included in this published article.
References
[1] Souayeh B, Abro KA, Alnaim N, Al Nuwairan M, Hdhiri N, Yasin E. Heat transfer characteristics of fractionalized hydromagnetic fluid with chemical reaction in permeable media. Energies. 2022;15(6):2196. 10.3390/en15062196Suche in Google Scholar
[2] Masood K, Zaman FD. Initial inverse problem in a two-layer heat conduction model. Arabian J Sci Eng. 2004;29(1B):1–12. Suche in Google Scholar
[3] Kukla S, Siedlecka U. Time-fractional heat conduction in a finite composite cylinder with heat source. J Appl Math Comput Mech. 2020;19(2):85–94. 10.17512/jamcm.2020.2.07Suche in Google Scholar
[4] Al-Duhaim HR, Yilbas BS, Zaman FD. Hyperbolic nature of heat conduction for short pulse laser irradiation of solid surfaces: analytical solution for the thermal stress field. Lasers Eng. 2017;36:331–53. Suche in Google Scholar
[5] Nuruddeen RI, Zaman FD. Heat conduction of a circular hollow cylinder amidst mixed boundary conditions. Int J Sci Eng Tech. 2016;5(1):18–22. Suche in Google Scholar
[6] Hickson RI, Barry SI, Mercer GN, Sidhu HS. Finite difference schemes for multilayer diffusion. Math Comp Model. 2011;1–2(54):210–20. 10.1016/j.mcm.2011.02.003Suche in Google Scholar
[7] Mubaraki AM, Althobaiti S, Nuruddeen RI. Heat and wave interactions in a thermoelastic coaxial solid cylinder driven by laser heating sources. Case Stud Thermal Eng. 2022;38:102338. 10.1016/j.csite.2022.102338Suche in Google Scholar
[8] Althobaiti S, Mubaraki A, Nuruddeen RI, Gomez-Aguilar JF. Wave propagation in an elastic coaxial hollow cylinder when exposed to thermal heating and external load. Results Phys. 2022;38:105582. 10.1016/j.rinp.2022.105582Suche in Google Scholar
[9] Akel M, Elshehabey H, Ahmaed R. Generalized Laplace-type transform method for solving multilayer diffusion problems. J Function Spaces. 2022;2022:7–8. 10.1155/2022/2304219Suche in Google Scholar
[10] Abro KA, Siyal A, Souayeh B, Atangana A. Application of statistical method on thermal resistance and conductance during magnetization of fractionalized free convection flow. Int Comm Heat Mass Transf. 2020;119:104971. 10.1016/j.icheatmasstransfer.2020.104971Suche in Google Scholar
[11] Al-Khaled K, Momani S. An approximate solution for a fractional diffusion-wave equation using the decomposition method. Appl Math Comput. 2005;2(15):473–83. 10.1016/j.amc.2004.06.026Suche in Google Scholar
[12] Bokhari AH, Mohammad G, Mustafa MT, Zaman FD. Adomian decomposition method for a nonlinear heat equation with temperature dependent thermal properties. Math Problems Eng. 2009;2009:926086. Suche in Google Scholar
[13] Nuruddeen RI, Zaman FD. Temperature distribution in a circular cylinder with general mixed boundary conditions. J Multidiscipl Eng Sci Tech. 2016;3(1):3653–8. Suche in Google Scholar
[14] Nuruddeen RI, Zaman FD, Zakariya YF. Analysing the fractional heat diffusion equation solution in comparison with the new fractional derivative by decomposition method. Malaya J Matematik 2019;7(2):213–22. 10.26637/MJM0702/0012Suche in Google Scholar
[15] Haberman R. Elementary Applied Differential Equations. Englewood Cliffs, New Jersey, USA: A Paramaout Communication Company; 1987. Suche in Google Scholar
[16] Eltayeb H, Adem K, Said M. Modified Laplace decomposition method for solving system of equations Emden-Fowler type. J Comp Theor Nanosci. 2015;12:5297–301. 10.1166/jctn.2015.4518Suche in Google Scholar
[17] Islam S, Khan Y, Faraz N, Austin F. Numerical solution of logistic differential equations by using the Laplace decomposition method. World Appl Sci J. 2010;8:1100–5. Suche in Google Scholar
[18] Yan SP, Zhong WP, Yang XJ. A novel series method for fractional diffusion equation within Caputo fractional derivative. Thermal Sci 2016;20(3):S695–9. 10.2298/TSCI16S3695YSuche in Google Scholar
[19] Ray SS, Bera RK. Analytical solution of a fractional diffusion equation by Adomian decomposition method. Appl Math Comp. 2006;174:329–36. 10.1016/j.amc.2005.04.082Suche in Google Scholar
[20] Bokhari AH, Mohammad G, Mustafa MT, Zaman FD. Solution of heat equation with nonlocal boundary conditions. Int J Math Comp. 2009;3(J09):100–13. 10.1155/2009/926086Suche in Google Scholar
[21] Nuruddeen RI, Garba BD. Analytical technique for (2+1) fractional diffusion equation with nonlocal boundary conditions. Open J Math Sci. 2018;2(1):287–300. 10.30538/oms2018.0035Suche in Google Scholar
[22] Anwar AMO, Jarad F, Baleanu D, Ayaz F. Fractional Caputo heat equation within the double Laplace transform. Rom J Phys. 2013;58:15–22. Suche in Google Scholar
[23] Alotaibi T, Althobaiti A. Exact wave solutions of the nonlinear Rosenau equation using an analytical method. Open Phys. 2021;19:889–96. 10.1515/phys-2021-0103Suche in Google Scholar
[24] Althobaiti A, Althobaiti S, El-Rashidy K, Seadawy AR. Exact solutions for the nonlinear extended KdV equation in a stratified shear flow using modified exponential rational method. Results Phys. 2021;29:104723. 10.1016/j.rinp.2021.104723Suche in Google Scholar
[25] Negi JG, Singh RN. Heat transfer in multi-layered media with temperature dependent sources. PAGEOPH. 1968; 69:110–8. 10.1007/BF00874909. Suche in Google Scholar
[26] Noor AK, Burton WS. Steady-state heat conduction in multilayered composite plates and shells. Comput Struct. 1991;39(1–2):185–93. 10.1016/0045-7949(91)90086-2Suche in Google Scholar
[27] Zhou ZW. Analytical solution for transient heat conduction in hollow cylinders containing well-stirred fluid with uniform heat sink. Int J Heat Mass Transf. 2002;45(7):1571–82. Suche in Google Scholar
[28] Yu B, Harajli A, Yunping X. Analytical solutions of ionic diffusion and heat conduction in multilayered porous media. J Appl Math. 2015;208914:1–11. 10.1155/2015/208914. Suche in Google Scholar
[29] Yuan W-b, Nanting Y, Li L, Fang Y. Heat transfer analysis in multi-layered materials with interfacial thermal resistance. Composite Struct. 2022;293(1):115728. 10.1016/j.compstruct.2022.115728Suche in Google Scholar
[30] Yang Y, Datcheva M, Schanz T. Axisymmetric analysis of multilayered thermoelastic media with application to a repository for heat-emitting high-level nuclear waste in a geological formation. Geophys J Int. 2016;206:1144–61. 10.1093/gji/ggw194Suche in Google Scholar
[31] Akbarzadeh AH, Pasini D. Phase-lag heat conduction in multilayered cellular media with imperfect bonds. Int J Heat Mass Transfer. 2014;75:656–67. 10.1016/j.ijheatmasstransfer.2014.03.090Suche in Google Scholar
[32] Kalis H, Kangro I. Simple methods of engineering calculation for solving stationary 2D heat transfer problems in multilayer media. Envir Techn Resour. 2006;1:359–66. 10.17770/etr2003vol1.1991. Suche in Google Scholar
[33] Alaa S, Irwansyah, Kurniawidi DW, Rahayu S. The analytical and numerical solutions of two dimensional heat transfer equation in a multilayered composite cylinder. Conf Ser Mater Sci Eng. 2020;858:012038. 10.1088/1757-899X/858/1/012038. Suche in Google Scholar
[34] Ramadan K. Semi-analytical solutions for the dual phase lag heat conduction in multilayered media. Int J Thermal Sci. 2009;48(1):14–25. 10.1016/j.ijthermalsci.2008.03.004Suche in Google Scholar
[35] Abbas N, Ali M, Shatanawi W. Chemical reactive second-grade nanofluid flow past an exponential curved stretching surface: Numerically. Int J Modern Phys. 2024;38(2):2450026. 10.1142/S0217979224500267Suche in Google Scholar
[36] Abbas N, Shaheen A, Shatanawi W. Simulation of mixed convection flow for a physiological breakdown of Jeffrey six-constant fluid model with convective boundary condition. Int J Modern Phys. 2023;37(6):2350058. 10.1142/S0217979223500583Suche in Google Scholar
[37] Al Owidh M, Souayeh B, Memon IQ, Abro KA, Alfannakh H. Heat transfer and fluid circulation of thermoelectric fluid through the fractional approach based on local kernel. Energies. 2022;15(22):8473. 10.3390/en15228473Suche in Google Scholar
[38] Haberman R. Elementary applied partial differential equations: with Fourier series and boundary value problems. Englewood Cliffs, New Jersey, USA: Prentice Hall; 1987. Suche in Google Scholar
[39] Manna S, Pramanik D, Althobaiti SN. Love-type surface wave propagation due to interior impulsive point source in a homogenous-coated anisotropic poroelastic layer over a non-homogenous extended substance. Waves Random Complex Media. 2022;1–37. 10.1080/17455030.2022.2081737. Suche in Google Scholar
[40] Benveniste Y. The effective mechanical behaviour of composite materials with imperfect contact between the constituents. Mech Materials. 1985;4(2):197–208. 10.1016/0167-6636(85)90016-XSuche in Google Scholar
[41] Abo-Dahab SM, Lotfy K, Gohaly A. Rotation and magnetic field effect on surface waves propagation in an elastic layer lying over a generalized thermoelastic diffusive half-space with imperfect boundary. Math Probl Eng. 2015;2015(3):1–15. 10.1155/2015/671783Suche in Google Scholar
[42] Sollund HA, Vedeld K, Hellesland J. Efficient analytical solutions for heated and pressurized multi-layer cylinders. Ocean Eng. 2014;92:285–95. 10.1016/j.oceaneng.2014.10.003Suche in Google Scholar
[43] Sim LC, Yeo WH, Purbolaksono J, Saw LH, Tey JY. Analytical solution of thermo-mechanical stresses of multi-layered hollow spherical pressure vessel. Int J Pressure Vessels Piping. 2021;191:104355. 10.1016/j.ijpvp.2021.104355Suche in Google Scholar
© 2024 the author(s), published by De Gruyter
This work is licensed under the Creative Commons Attribution 4.0 International License.
Artikel in diesem Heft
- Regular Articles
- Numerical study of flow and heat transfer in the channel of panel-type radiator with semi-detached inclined trapezoidal wing vortex generators
- Homogeneous–heterogeneous reactions in the colloidal investigation of Casson fluid
- High-speed mid-infrared Mach–Zehnder electro-optical modulators in lithium niobate thin film on sapphire
- Numerical analysis of dengue transmission model using Caputo–Fabrizio fractional derivative
- Mononuclear nanofluids undergoing convective heating across a stretching sheet and undergoing MHD flow in three dimensions: Potential industrial applications
- Heat transfer characteristics of cobalt ferrite nanoparticles scattered in sodium alginate-based non-Newtonian nanofluid over a stretching/shrinking horizontal plane surface
- The electrically conducting water-based nanofluid flow containing titanium and aluminum alloys over a rotating disk surface with nonlinear thermal radiation: A numerical analysis
- Growth, characterization, and anti-bacterial activity of l-methionine supplemented with sulphamic acid single crystals
- A numerical analysis of the blood-based Casson hybrid nanofluid flow past a convectively heated surface embedded in a porous medium
- Optoelectronic–thermomagnetic effect of a microelongated non-local rotating semiconductor heated by pulsed laser with varying thermal conductivity
- Thermal proficiency of magnetized and radiative cross-ternary hybrid nanofluid flow induced by a vertical cylinder
- Enhanced heat transfer and fluid motion in 3D nanofluid with anisotropic slip and magnetic field
- Numerical analysis of thermophoretic particle deposition on 3D Casson nanofluid: Artificial neural networks-based Levenberg–Marquardt algorithm
- Analyzing fuzzy fractional Degasperis–Procesi and Camassa–Holm equations with the Atangana–Baleanu operator
- Bayesian estimation of equipment reliability with normal-type life distribution based on multiple batch tests
- Chaotic control problem of BEC system based on Hartree–Fock mean field theory
- Optimized framework numerical solution for swirling hybrid nanofluid flow with silver/gold nanoparticles on a stretching cylinder with heat source/sink and reactive agents
- Stability analysis and numerical results for some schemes discretising 2D nonconstant coefficient advection–diffusion equations
- Convective flow of a magnetohydrodynamic second-grade fluid past a stretching surface with Cattaneo–Christov heat and mass flux model
- Analysis of the heat transfer enhancement in water-based micropolar hybrid nanofluid flow over a vertical flat surface
- Microscopic seepage simulation of gas and water in shale pores and slits based on VOF
- Model of conversion of flow from confined to unconfined aquifers with stochastic approach
- Study of fractional variable-order lymphatic filariasis infection model
- Soliton, quasi-soliton, and their interaction solutions of a nonlinear (2 + 1)-dimensional ZK–mZK–BBM equation for gravity waves
- Application of conserved quantities using the formal Lagrangian of a nonlinear integro partial differential equation through optimal system of one-dimensional subalgebras in physics and engineering
- Nonlinear fractional-order differential equations: New closed-form traveling-wave solutions
- Sixth-kind Chebyshev polynomials technique to numerically treat the dissipative viscoelastic fluid flow in the rheology of Cattaneo–Christov model
- Some transforms, Riemann–Liouville fractional operators, and applications of newly extended M–L (p, s, k) function
- Magnetohydrodynamic water-based hybrid nanofluid flow comprising diamond and copper nanoparticles on a stretching sheet with slips constraints
- Super-resolution reconstruction method of the optical synthetic aperture image using generative adversarial network
- A two-stage framework for predicting the remaining useful life of bearings
- Influence of variable fluid properties on mixed convective Darcy–Forchheimer flow relation over a surface with Soret and Dufour spectacle
- Inclined surface mixed convection flow of viscous fluid with porous medium and Soret effects
- Exact solutions to vorticity of the fractional nonuniform Poiseuille flows
- In silico modified UV spectrophotometric approaches to resolve overlapped spectra for quality control of rosuvastatin and teneligliptin formulation
- Numerical simulations for fractional Hirota–Satsuma coupled Korteweg–de Vries systems
- Substituent effect on the electronic and optical properties of newly designed pyrrole derivatives using density functional theory
- A comparative analysis of shielding effectiveness in glass and concrete containers
- Numerical analysis of the MHD Williamson nanofluid flow over a nonlinear stretching sheet through a Darcy porous medium: Modeling and simulation
- Analytical and numerical investigation for viscoelastic fluid with heat transfer analysis during rollover-web coating phenomena
- Influence of variable viscosity on existing sheet thickness in the calendering of non-isothermal viscoelastic materials
- Analysis of nonlinear fractional-order Fisher equation using two reliable techniques
- Comparison of plan quality and robustness using VMAT and IMRT for breast cancer
- Radiative nanofluid flow over a slender stretching Riga plate under the impact of exponential heat source/sink
- Numerical investigation of acoustic streaming vortices in cylindrical tube arrays
- Numerical study of blood-based MHD tangent hyperbolic hybrid nanofluid flow over a permeable stretching sheet with variable thermal conductivity and cross-diffusion
- Fractional view analytical analysis of generalized regularized long wave equation
- Dynamic simulation of non-Newtonian boundary layer flow: An enhanced exponential time integrator approach with spatially and temporally variable heat sources
- Inclined magnetized infinite shear rate viscosity of non-Newtonian tetra hybrid nanofluid in stenosed artery with non-uniform heat sink/source
- Estimation of monotone α-quantile of past lifetime function with application
- Numerical simulation for the slip impacts on the radiative nanofluid flow over a stretched surface with nonuniform heat generation and viscous dissipation
- Study of fractional telegraph equation via Shehu homotopy perturbation method
- An investigation into the impact of thermal radiation and chemical reactions on the flow through porous media of a Casson hybrid nanofluid including unstable mixed convection with stretched sheet in the presence of thermophoresis and Brownian motion
- Establishing breather and N-soliton solutions for conformable Klein–Gordon equation
- An electro-optic half subtractor from a silicon-based hybrid surface plasmon polariton waveguide
- CFD analysis of particle shape and Reynolds number on heat transfer characteristics of nanofluid in heated tube
- Abundant exact traveling wave solutions and modulation instability analysis to the generalized Hirota–Satsuma–Ito equation
- A short report on a probability-based interpretation of quantum mechanics
- Study on cavitation and pulsation characteristics of a novel rotor-radial groove hydrodynamic cavitation reactor
- Optimizing heat transport in a permeable cavity with an isothermal solid block: Influence of nanoparticles volume fraction and wall velocity ratio
- Linear instability of the vertical throughflow in a porous layer saturated by a power-law fluid with variable gravity effect
- Thermal analysis of generalized Cattaneo–Christov theories in Burgers nanofluid in the presence of thermo-diffusion effects and variable thermal conductivity
- A new benchmark for camouflaged object detection: RGB-D camouflaged object detection dataset
- Effect of electron temperature and concentration on production of hydroxyl radical and nitric oxide in atmospheric pressure low-temperature helium plasma jet: Swarm analysis and global model investigation
- Double diffusion convection of Maxwell–Cattaneo fluids in a vertical slot
- Thermal analysis of extended surfaces using deep neural networks
- Steady-state thermodynamic process in multilayered heterogeneous cylinder
- Multiresponse optimisation and process capability analysis of chemical vapour jet machining for the acrylonitrile butadiene styrene polymer: Unveiling the morphology
- Modeling monkeypox virus transmission: Stability analysis and comparison of analytical techniques
- Fourier spectral method for the fractional-in-space coupled Whitham–Broer–Kaup equations on unbounded domain
- The chaotic behavior and traveling wave solutions of the conformable extended Korteweg–de-Vries model
- Research on optimization of combustor liner structure based on arc-shaped slot hole
- Construction of M-shaped solitons for a modified regularized long-wave equation via Hirota's bilinear method
- Effectiveness of microwave ablation using two simultaneous antennas for liver malignancy treatment
- Discussion on optical solitons, sensitivity and qualitative analysis to a fractional model of ion sound and Langmuir waves with Atangana Baleanu derivatives
- Reliability of two-dimensional steady magnetized Jeffery fluid over shrinking sheet with chemical effect
- Generalized model of thermoelasticity associated with fractional time-derivative operators and its applications to non-simple elastic materials
- Migration of two rigid spheres translating within an infinite couple stress fluid under the impact of magnetic field
- A comparative investigation of neutron and gamma radiation interaction properties of zircaloy-2 and zircaloy-4 with consideration of mechanical properties
- New optical stochastic solutions for the Schrödinger equation with multiplicative Wiener process/random variable coefficients using two different methods
- Physical aspects of quantile residual lifetime sequence
- Synthesis, structure, I–V characteristics, and optical properties of chromium oxide thin films for optoelectronic applications
- Smart mathematically filtered UV spectroscopic methods for quality assurance of rosuvastatin and valsartan from formulation
- A novel investigation into time-fractional multi-dimensional Navier–Stokes equations within Aboodh transform
- Homotopic dynamic solution of hydrodynamic nonlinear natural convection containing superhydrophobicity and isothermally heated parallel plate with hybrid nanoparticles
- A novel tetra hybrid bio-nanofluid model with stenosed artery
- Propagation of traveling wave solution of the strain wave equation in microcrystalline materials
- Innovative analysis to the time-fractional q-deformed tanh-Gordon equation via modified double Laplace transform method
- A new investigation of the extended Sakovich equation for abundant soliton solution in industrial engineering via two efficient techniques
- New soliton solutions of the conformable time fractional Drinfel'd–Sokolov–Wilson equation based on the complete discriminant system method
- Irradiation of hydrophilic acrylic intraocular lenses by a 365 nm UV lamp
- Inflation and the principle of equivalence
- The use of a supercontinuum light source for the characterization of passive fiber optic components
- Optical solitons to the fractional Kundu–Mukherjee–Naskar equation with time-dependent coefficients
- A promising photocathode for green hydrogen generation from sanitation water without external sacrificing agent: silver-silver oxide/poly(1H-pyrrole) dendritic nanocomposite seeded on poly-1H pyrrole film
- Photon balance in the fiber laser model
- Propagation of optical spatial solitons in nematic liquid crystals with quadruple power law of nonlinearity appears in fluid mechanics
- Theoretical investigation and sensitivity analysis of non-Newtonian fluid during roll coating process by response surface methodology
- Utilizing slip conditions on transport phenomena of heat energy with dust and tiny nanoparticles over a wedge
- Bismuthyl chloride/poly(m-toluidine) nanocomposite seeded on poly-1H pyrrole: Photocathode for green hydrogen generation
- Infrared thermography based fault diagnosis of diesel engines using convolutional neural network and image enhancement
- On some solitary wave solutions of the Estevez--Mansfield--Clarkson equation with conformable fractional derivatives in time
- Impact of permeability and fluid parameters in couple stress media on rotating eccentric spheres
- Review Article
- Transformer-based intelligent fault diagnosis methods of mechanical equipment: A survey
- Special Issue on Predicting pattern alterations in nature - Part II
- A comparative study of Bagley–Torvik equation under nonsingular kernel derivatives using Weeks method
- On the existence and numerical simulation of Cholera epidemic model
- Numerical solutions of generalized Atangana–Baleanu time-fractional FitzHugh–Nagumo equation using cubic B-spline functions
- Dynamic properties of the multimalware attacks in wireless sensor networks: Fractional derivative analysis of wireless sensor networks
- Prediction of COVID-19 spread with models in different patterns: A case study of Russia
- Study of chronic myeloid leukemia with T-cell under fractal-fractional order model
- Accumulation process in the environment for a generalized mass transport system
- Analysis of a generalized proportional fractional stochastic differential equation incorporating Carathéodory's approximation and applications
- Special Issue on Nanomaterial utilization and structural optimization - Part II
- Numerical study on flow and heat transfer performance of a spiral-wound heat exchanger for natural gas
- Study of ultrasonic influence on heat transfer and resistance performance of round tube with twisted belt
- Numerical study on bionic airfoil fins used in printed circuit plate heat exchanger
- Improving heat transfer efficiency via optimization and sensitivity assessment in hybrid nanofluid flow with variable magnetism using the Yamada–Ota model
- Special Issue on Nanofluids: Synthesis, Characterization, and Applications
- Exact solutions of a class of generalized nanofluidic models
- Stability enhancement of Al2O3, ZnO, and TiO2 binary nanofluids for heat transfer applications
- Thermal transport energy performance on tangent hyperbolic hybrid nanofluids and their implementation in concentrated solar aircraft wings
- Studying nonlinear vibration analysis of nanoelectro-mechanical resonators via analytical computational method
- Numerical analysis of non-linear radiative Casson fluids containing CNTs having length and radius over permeable moving plate
- Two-phase numerical simulation of thermal and solutal transport exploration of a non-Newtonian nanomaterial flow past a stretching surface with chemical reaction
- Natural convection and flow patterns of Cu–water nanofluids in hexagonal cavity: A novel thermal case study
- Solitonic solutions and study of nonlinear wave dynamics in a Murnaghan hyperelastic circular pipe
- Comparative study of couple stress fluid flow using OHAM and NIM
- Utilization of OHAM to investigate entropy generation with a temperature-dependent thermal conductivity model in hybrid nanofluid using the radiation phenomenon
- Slip effects on magnetized radiatively hybridized ferrofluid flow with acute magnetic force over shrinking/stretching surface
- Significance of 3D rectangular closed domain filled with charged particles and nanoparticles engaging finite element methodology
- Robustness and dynamical features of fractional difference spacecraft model with Mittag–Leffler stability
- Characterizing magnetohydrodynamic effects on developed nanofluid flow in an obstructed vertical duct under constant pressure gradient
- Study on dynamic and static tensile and puncture-resistant mechanical properties of impregnated STF multi-dimensional structure Kevlar fiber reinforced composites
- Thermosolutal Marangoni convective flow of MHD tangent hyperbolic hybrid nanofluids with elastic deformation and heat source
- Investigation of convective heat transport in a Carreau hybrid nanofluid between two stretchable rotatory disks
- Single-channel cooling system design by using perforated porous insert and modeling with POD for double conductive panel
- Special Issue on Fundamental Physics from Atoms to Cosmos - Part I
- Pulsed excitation of a quantum oscillator: A model accounting for damping
- Review of recent analytical advances in the spectroscopy of hydrogenic lines in plasmas
- Heavy mesons mass spectroscopy under a spin-dependent Cornell potential within the framework of the spinless Salpeter equation
- Coherent manipulation of bright and dark solitons of reflection and transmission pulses through sodium atomic medium
- Effect of the gravitational field strength on the rate of chemical reactions
- The kinetic relativity theory – hiding in plain sight
- Special Issue on Advanced Energy Materials - Part III
- Eco-friendly graphitic carbon nitride–poly(1H pyrrole) nanocomposite: A photocathode for green hydrogen production, paving the way for commercial applications
Artikel in diesem Heft
- Regular Articles
- Numerical study of flow and heat transfer in the channel of panel-type radiator with semi-detached inclined trapezoidal wing vortex generators
- Homogeneous–heterogeneous reactions in the colloidal investigation of Casson fluid
- High-speed mid-infrared Mach–Zehnder electro-optical modulators in lithium niobate thin film on sapphire
- Numerical analysis of dengue transmission model using Caputo–Fabrizio fractional derivative
- Mononuclear nanofluids undergoing convective heating across a stretching sheet and undergoing MHD flow in three dimensions: Potential industrial applications
- Heat transfer characteristics of cobalt ferrite nanoparticles scattered in sodium alginate-based non-Newtonian nanofluid over a stretching/shrinking horizontal plane surface
- The electrically conducting water-based nanofluid flow containing titanium and aluminum alloys over a rotating disk surface with nonlinear thermal radiation: A numerical analysis
- Growth, characterization, and anti-bacterial activity of l-methionine supplemented with sulphamic acid single crystals
- A numerical analysis of the blood-based Casson hybrid nanofluid flow past a convectively heated surface embedded in a porous medium
- Optoelectronic–thermomagnetic effect of a microelongated non-local rotating semiconductor heated by pulsed laser with varying thermal conductivity
- Thermal proficiency of magnetized and radiative cross-ternary hybrid nanofluid flow induced by a vertical cylinder
- Enhanced heat transfer and fluid motion in 3D nanofluid with anisotropic slip and magnetic field
- Numerical analysis of thermophoretic particle deposition on 3D Casson nanofluid: Artificial neural networks-based Levenberg–Marquardt algorithm
- Analyzing fuzzy fractional Degasperis–Procesi and Camassa–Holm equations with the Atangana–Baleanu operator
- Bayesian estimation of equipment reliability with normal-type life distribution based on multiple batch tests
- Chaotic control problem of BEC system based on Hartree–Fock mean field theory
- Optimized framework numerical solution for swirling hybrid nanofluid flow with silver/gold nanoparticles on a stretching cylinder with heat source/sink and reactive agents
- Stability analysis and numerical results for some schemes discretising 2D nonconstant coefficient advection–diffusion equations
- Convective flow of a magnetohydrodynamic second-grade fluid past a stretching surface with Cattaneo–Christov heat and mass flux model
- Analysis of the heat transfer enhancement in water-based micropolar hybrid nanofluid flow over a vertical flat surface
- Microscopic seepage simulation of gas and water in shale pores and slits based on VOF
- Model of conversion of flow from confined to unconfined aquifers with stochastic approach
- Study of fractional variable-order lymphatic filariasis infection model
- Soliton, quasi-soliton, and their interaction solutions of a nonlinear (2 + 1)-dimensional ZK–mZK–BBM equation for gravity waves
- Application of conserved quantities using the formal Lagrangian of a nonlinear integro partial differential equation through optimal system of one-dimensional subalgebras in physics and engineering
- Nonlinear fractional-order differential equations: New closed-form traveling-wave solutions
- Sixth-kind Chebyshev polynomials technique to numerically treat the dissipative viscoelastic fluid flow in the rheology of Cattaneo–Christov model
- Some transforms, Riemann–Liouville fractional operators, and applications of newly extended M–L (p, s, k) function
- Magnetohydrodynamic water-based hybrid nanofluid flow comprising diamond and copper nanoparticles on a stretching sheet with slips constraints
- Super-resolution reconstruction method of the optical synthetic aperture image using generative adversarial network
- A two-stage framework for predicting the remaining useful life of bearings
- Influence of variable fluid properties on mixed convective Darcy–Forchheimer flow relation over a surface with Soret and Dufour spectacle
- Inclined surface mixed convection flow of viscous fluid with porous medium and Soret effects
- Exact solutions to vorticity of the fractional nonuniform Poiseuille flows
- In silico modified UV spectrophotometric approaches to resolve overlapped spectra for quality control of rosuvastatin and teneligliptin formulation
- Numerical simulations for fractional Hirota–Satsuma coupled Korteweg–de Vries systems
- Substituent effect on the electronic and optical properties of newly designed pyrrole derivatives using density functional theory
- A comparative analysis of shielding effectiveness in glass and concrete containers
- Numerical analysis of the MHD Williamson nanofluid flow over a nonlinear stretching sheet through a Darcy porous medium: Modeling and simulation
- Analytical and numerical investigation for viscoelastic fluid with heat transfer analysis during rollover-web coating phenomena
- Influence of variable viscosity on existing sheet thickness in the calendering of non-isothermal viscoelastic materials
- Analysis of nonlinear fractional-order Fisher equation using two reliable techniques
- Comparison of plan quality and robustness using VMAT and IMRT for breast cancer
- Radiative nanofluid flow over a slender stretching Riga plate under the impact of exponential heat source/sink
- Numerical investigation of acoustic streaming vortices in cylindrical tube arrays
- Numerical study of blood-based MHD tangent hyperbolic hybrid nanofluid flow over a permeable stretching sheet with variable thermal conductivity and cross-diffusion
- Fractional view analytical analysis of generalized regularized long wave equation
- Dynamic simulation of non-Newtonian boundary layer flow: An enhanced exponential time integrator approach with spatially and temporally variable heat sources
- Inclined magnetized infinite shear rate viscosity of non-Newtonian tetra hybrid nanofluid in stenosed artery with non-uniform heat sink/source
- Estimation of monotone α-quantile of past lifetime function with application
- Numerical simulation for the slip impacts on the radiative nanofluid flow over a stretched surface with nonuniform heat generation and viscous dissipation
- Study of fractional telegraph equation via Shehu homotopy perturbation method
- An investigation into the impact of thermal radiation and chemical reactions on the flow through porous media of a Casson hybrid nanofluid including unstable mixed convection with stretched sheet in the presence of thermophoresis and Brownian motion
- Establishing breather and N-soliton solutions for conformable Klein–Gordon equation
- An electro-optic half subtractor from a silicon-based hybrid surface plasmon polariton waveguide
- CFD analysis of particle shape and Reynolds number on heat transfer characteristics of nanofluid in heated tube
- Abundant exact traveling wave solutions and modulation instability analysis to the generalized Hirota–Satsuma–Ito equation
- A short report on a probability-based interpretation of quantum mechanics
- Study on cavitation and pulsation characteristics of a novel rotor-radial groove hydrodynamic cavitation reactor
- Optimizing heat transport in a permeable cavity with an isothermal solid block: Influence of nanoparticles volume fraction and wall velocity ratio
- Linear instability of the vertical throughflow in a porous layer saturated by a power-law fluid with variable gravity effect
- Thermal analysis of generalized Cattaneo–Christov theories in Burgers nanofluid in the presence of thermo-diffusion effects and variable thermal conductivity
- A new benchmark for camouflaged object detection: RGB-D camouflaged object detection dataset
- Effect of electron temperature and concentration on production of hydroxyl radical and nitric oxide in atmospheric pressure low-temperature helium plasma jet: Swarm analysis and global model investigation
- Double diffusion convection of Maxwell–Cattaneo fluids in a vertical slot
- Thermal analysis of extended surfaces using deep neural networks
- Steady-state thermodynamic process in multilayered heterogeneous cylinder
- Multiresponse optimisation and process capability analysis of chemical vapour jet machining for the acrylonitrile butadiene styrene polymer: Unveiling the morphology
- Modeling monkeypox virus transmission: Stability analysis and comparison of analytical techniques
- Fourier spectral method for the fractional-in-space coupled Whitham–Broer–Kaup equations on unbounded domain
- The chaotic behavior and traveling wave solutions of the conformable extended Korteweg–de-Vries model
- Research on optimization of combustor liner structure based on arc-shaped slot hole
- Construction of M-shaped solitons for a modified regularized long-wave equation via Hirota's bilinear method
- Effectiveness of microwave ablation using two simultaneous antennas for liver malignancy treatment
- Discussion on optical solitons, sensitivity and qualitative analysis to a fractional model of ion sound and Langmuir waves with Atangana Baleanu derivatives
- Reliability of two-dimensional steady magnetized Jeffery fluid over shrinking sheet with chemical effect
- Generalized model of thermoelasticity associated with fractional time-derivative operators and its applications to non-simple elastic materials
- Migration of two rigid spheres translating within an infinite couple stress fluid under the impact of magnetic field
- A comparative investigation of neutron and gamma radiation interaction properties of zircaloy-2 and zircaloy-4 with consideration of mechanical properties
- New optical stochastic solutions for the Schrödinger equation with multiplicative Wiener process/random variable coefficients using two different methods
- Physical aspects of quantile residual lifetime sequence
- Synthesis, structure, I–V characteristics, and optical properties of chromium oxide thin films for optoelectronic applications
- Smart mathematically filtered UV spectroscopic methods for quality assurance of rosuvastatin and valsartan from formulation
- A novel investigation into time-fractional multi-dimensional Navier–Stokes equations within Aboodh transform
- Homotopic dynamic solution of hydrodynamic nonlinear natural convection containing superhydrophobicity and isothermally heated parallel plate with hybrid nanoparticles
- A novel tetra hybrid bio-nanofluid model with stenosed artery
- Propagation of traveling wave solution of the strain wave equation in microcrystalline materials
- Innovative analysis to the time-fractional q-deformed tanh-Gordon equation via modified double Laplace transform method
- A new investigation of the extended Sakovich equation for abundant soliton solution in industrial engineering via two efficient techniques
- New soliton solutions of the conformable time fractional Drinfel'd–Sokolov–Wilson equation based on the complete discriminant system method
- Irradiation of hydrophilic acrylic intraocular lenses by a 365 nm UV lamp
- Inflation and the principle of equivalence
- The use of a supercontinuum light source for the characterization of passive fiber optic components
- Optical solitons to the fractional Kundu–Mukherjee–Naskar equation with time-dependent coefficients
- A promising photocathode for green hydrogen generation from sanitation water without external sacrificing agent: silver-silver oxide/poly(1H-pyrrole) dendritic nanocomposite seeded on poly-1H pyrrole film
- Photon balance in the fiber laser model
- Propagation of optical spatial solitons in nematic liquid crystals with quadruple power law of nonlinearity appears in fluid mechanics
- Theoretical investigation and sensitivity analysis of non-Newtonian fluid during roll coating process by response surface methodology
- Utilizing slip conditions on transport phenomena of heat energy with dust and tiny nanoparticles over a wedge
- Bismuthyl chloride/poly(m-toluidine) nanocomposite seeded on poly-1H pyrrole: Photocathode for green hydrogen generation
- Infrared thermography based fault diagnosis of diesel engines using convolutional neural network and image enhancement
- On some solitary wave solutions of the Estevez--Mansfield--Clarkson equation with conformable fractional derivatives in time
- Impact of permeability and fluid parameters in couple stress media on rotating eccentric spheres
- Review Article
- Transformer-based intelligent fault diagnosis methods of mechanical equipment: A survey
- Special Issue on Predicting pattern alterations in nature - Part II
- A comparative study of Bagley–Torvik equation under nonsingular kernel derivatives using Weeks method
- On the existence and numerical simulation of Cholera epidemic model
- Numerical solutions of generalized Atangana–Baleanu time-fractional FitzHugh–Nagumo equation using cubic B-spline functions
- Dynamic properties of the multimalware attacks in wireless sensor networks: Fractional derivative analysis of wireless sensor networks
- Prediction of COVID-19 spread with models in different patterns: A case study of Russia
- Study of chronic myeloid leukemia with T-cell under fractal-fractional order model
- Accumulation process in the environment for a generalized mass transport system
- Analysis of a generalized proportional fractional stochastic differential equation incorporating Carathéodory's approximation and applications
- Special Issue on Nanomaterial utilization and structural optimization - Part II
- Numerical study on flow and heat transfer performance of a spiral-wound heat exchanger for natural gas
- Study of ultrasonic influence on heat transfer and resistance performance of round tube with twisted belt
- Numerical study on bionic airfoil fins used in printed circuit plate heat exchanger
- Improving heat transfer efficiency via optimization and sensitivity assessment in hybrid nanofluid flow with variable magnetism using the Yamada–Ota model
- Special Issue on Nanofluids: Synthesis, Characterization, and Applications
- Exact solutions of a class of generalized nanofluidic models
- Stability enhancement of Al2O3, ZnO, and TiO2 binary nanofluids for heat transfer applications
- Thermal transport energy performance on tangent hyperbolic hybrid nanofluids and their implementation in concentrated solar aircraft wings
- Studying nonlinear vibration analysis of nanoelectro-mechanical resonators via analytical computational method
- Numerical analysis of non-linear radiative Casson fluids containing CNTs having length and radius over permeable moving plate
- Two-phase numerical simulation of thermal and solutal transport exploration of a non-Newtonian nanomaterial flow past a stretching surface with chemical reaction
- Natural convection and flow patterns of Cu–water nanofluids in hexagonal cavity: A novel thermal case study
- Solitonic solutions and study of nonlinear wave dynamics in a Murnaghan hyperelastic circular pipe
- Comparative study of couple stress fluid flow using OHAM and NIM
- Utilization of OHAM to investigate entropy generation with a temperature-dependent thermal conductivity model in hybrid nanofluid using the radiation phenomenon
- Slip effects on magnetized radiatively hybridized ferrofluid flow with acute magnetic force over shrinking/stretching surface
- Significance of 3D rectangular closed domain filled with charged particles and nanoparticles engaging finite element methodology
- Robustness and dynamical features of fractional difference spacecraft model with Mittag–Leffler stability
- Characterizing magnetohydrodynamic effects on developed nanofluid flow in an obstructed vertical duct under constant pressure gradient
- Study on dynamic and static tensile and puncture-resistant mechanical properties of impregnated STF multi-dimensional structure Kevlar fiber reinforced composites
- Thermosolutal Marangoni convective flow of MHD tangent hyperbolic hybrid nanofluids with elastic deformation and heat source
- Investigation of convective heat transport in a Carreau hybrid nanofluid between two stretchable rotatory disks
- Single-channel cooling system design by using perforated porous insert and modeling with POD for double conductive panel
- Special Issue on Fundamental Physics from Atoms to Cosmos - Part I
- Pulsed excitation of a quantum oscillator: A model accounting for damping
- Review of recent analytical advances in the spectroscopy of hydrogenic lines in plasmas
- Heavy mesons mass spectroscopy under a spin-dependent Cornell potential within the framework of the spinless Salpeter equation
- Coherent manipulation of bright and dark solitons of reflection and transmission pulses through sodium atomic medium
- Effect of the gravitational field strength on the rate of chemical reactions
- The kinetic relativity theory – hiding in plain sight
- Special Issue on Advanced Energy Materials - Part III
- Eco-friendly graphitic carbon nitride–poly(1H pyrrole) nanocomposite: A photocathode for green hydrogen production, paving the way for commercial applications

