Characterizing magnetohydrodynamic effects on developed nanofluid flow in an obstructed vertical duct under constant pressure gradient

Syed M. Hussain; Kashif Ali; Sohail Ahmad; Muhammad Amer Qureshi; Assmaa Abd-Elmonem; Wasim Jamshed; Ibrahim Alraddadi

doi:10.1515/phys-2024-0070

Article Open Access

Characterizing magnetohydrodynamic effects on developed nanofluid flow in an obstructed vertical duct under constant pressure gradient

Syed M. Hussain , Kashif Ali , Sohail Ahmad , Muhammad Amer Qureshi , Assmaa Abd-Elmonem , Wasim Jamshed and Ibrahim Alraddadi

Published/Copyright: September 3, 2024

Published by

Become an author with De Gruyter Brill

Submit Manuscript Author Information Explore this Subject

From the journal Open Physics Volume 22 Issue 1

Abstract

This research endeavors to conduct an examination of the thermal characteristics within the duct filled with the copper nanoparticles and water as base fluid. In exhaust systems, like car exhausts, chimneys, and kitchen hoods, duct flows are crucial. These systems safely discharge odors, smoke, and contaminants into the atmosphere after removing them from enclosed places. The study focuses on a laminar flow regime that is both hydrodynamically and thermally developed, with a specified constraints at any cross-sectional plane. To address this, we employ the finite volume method as it stands as a judicious choice, offering a balance between computational efficiency and solution accuracy. Notably, we have observed that the deceleration of flow induced by elevated Rayleigh numbers can be effectively regulated by the application of an appropriately calibrated external magnetic field. The prime parameters of the problem with ranges are: pressure gradient ( 1 ≤ p 0 ≤ 100 ) , Hartmann number ( 0 ≤ Ha ≤ 50 ) , Rayleigh number ( 1 , 000 ≤ Ra ≤ 40 , 000 ) , and magnetic parameter ( 0 ≤ M ≤ 50 ) . Furthermore, our analysis reveals that the Nusselt number exhibits a nearly linear correlation with the nanoparticle volume fraction parameter, a trend observed across a range of Rayleigh numbers and magnetic parameter values. We have noted that a mere 20% nanoparticle volume fraction can result in up to 62% rise in the Nusselt number while causing an almost 50% decrease in the factor f _Re. This research framework serves as a robust foundation for understanding the intricate interplay between magnetic influences and thermal-hydraulic behavior within the delineated system.

Keywords: fully developed flow; obstructed vertical duct; constant pressure gradient; magnetohydrodynamics; constant heat flux

1 Introduction

Numerous technical and industrial applications highlight the importance of duct flows, which can be summed up in a number of applications. Heating, ventilation, and air conditioning systems depend heavily on duct flows. Maintaining comfortable interior spaces and energy efficiency depends on the effective distribution of conditioned air, which is ensured by well-designed and maintained ductwork. Duct flows are essential in industrial environments for regulating and eliminating airborne pollutants such as dust, odor, and dangerous gases. This is essential for upholding employee health and safety as well as adhering to environmental laws. Many items, including bulk solids, liquids, and gases, are transported using ducts. Ducts in industrial processes make it easier for waste, products, and raw materials to move around, which is essential for manufacturing and production processes. Duct flows are significant for many different sectors and applications since they affect system and process operation as well as comfort, safety, efficiency, and environmental concerns. Duct flows must be properly designed, maintained, and controlled in order to maximize their effectiveness and produce the intended results in a variety of settings.

Some recent work explores the new features of duct flows. A numerical analysis was presented by Ali et al. [1] for featuring the thermal characteristics of water-copper based nanofluid inside the duct. The unique conclusion of the study was that the wires’ mass flux balanced the flow reversal because of the high Rayleigh number. Ortloff [2] studied analytically the problem regarding the nanoparticles flow within a duct taking into account the impacts of static pressure and high Froude number. The static pressure profiles exhibited the characteristic wave solutions of the problem. Dolon et al. [3] reported a dynamical study of nanofluid through a duct via a computational modeling taking a large aspect ratio. Some numerical techniques were elaborated to achieve the computational procedure. The governing system was then solved iteratively. The primary goal of the article was to examine the flow features involving the thermal jump conditions and heat transfer characteristics. The flow in the divergent and convergent ducts was interpreted by Su and Lin [4]. It was discovered that when the Reynolds number rises, the thermal characteristics increase but the pressure dropped in the flow regime at a given divergent angle.

Riaz et al. [5] discussed the movement of fluid in a duct containing an obstacle, and whose cross-section was rectangular. They proposed that such geometries can be used increasingly in various medical and industrial applications. The current analysis took into account the limitations of lubrication theory and solved the Navier-Stokes partial differential equations using a perturbation technique. In a study reported by Garud et al. [6], the thermal and flow properties of diverging ducts for the cooling system of electric vehicles with different rib forms were examined. The computational domains were modeled as divergent ducts, which are composed of ribs with various rectangular forms. Tokgoz and Sahin [7] conducted an experimental investigation of the flow structures in a corrugated obstacle duct using particle image velocimetry. For the accessible ribbed channel, two different Reynolds Numbers and two distinct phase shifts, such as φ = 0° and 90°, have been studied. Sutevski et al. [8], Krasnov et al. [9], and Ting and Hou [10] numerically investigated the duct flows taking magnetohydrodynamic (MHD) effect, high Hartmann numbers, and constant heat flux, respectively.

Fully developed flows in the magnetic field environment have been studied by various researchers. Fonseca et al. [11] conducted a 3D numerical investigation of the MHD flow in a circular duct using the finite volume method (FVM). The under-consideration flow was laminar and completely developed. Magnets were positioned around the duct to create magnetic fields in a radial direction along the first segment of the duct. A few mathematical calculations regarding the developed flow of a Bingham fluid in a vertical channel were made by Borrelli et al. [12]. Analysis was done on the state of affairs as a result of both external magnetic field and natural convection. In a channel having vertical parallel plates, Saleh and Hashim [13] studied the phenomena of reversal fully-developed flow involving MHD and forced and mixed convections. Parameter zones were provided where reversed flow could occur. The hydromagnetic natural convection flow, which was fully developed and caused by asymmetric heating in a vertical microporous channel, was investigated by Jha et al. [14]. The dimensionless form of energy and momentum equations was derived, and the method of unknown coefficients was used to solve them analytically. Ghosh et al. [15] found asymptotic solutions and closed-form for the fully-developed MHD flow with forced and free convection in a rotating horizontal parallel plate channel when there is an inclined magnetic field and a constant pressure gradient acting on the channel’s longitudinal axis. Previous literature [16,17,18,19,20,21,22,23,24,25] comprise further relevant work.

The application of MHDs to fluid flow in a blocked or obstructed vertical duct is distinctive. The interaction of magnetic fields with electrically conductive fluids, which can result in intricate and unusual behaviors in fluid flow, is the focus of this research. Perhaps the present work is a first effort to investigate the effects of MHD on flow patterns, heat transmission, or other features in an obstructed duct. The study focuses on the particular geometry and properties of the obstruction as well as fluid flow through a blocked vertical duct. Studying these impacts can be a novel contribution because different impediments can result in different flow patterns and phenomena depending on their size and shape. The majority of research on fluid flow in ducts takes into account various driving factors; yet, employing a constant pressure gradient may offer novel perspectives on fluid behavior.

2 Mathematical formulation

An examination is conducted for the developed flow in a vertical duct whose side length is L. The conducting liquid under consideration is a nanofluid composed of water with dispersed copper particles. The system is subjected to fixed constraints and a consistently maintained temperature at any given cross-sectional plane. For analysis, we assume that the duct wall thickness can be neglected, allowing for the assumption of infinite wall conductivity in the outward direction. This assumption aligns with a more realistic scenario, whereas the temperature is presumed to be uniform at the duct outer surface and fluid–solid interface. Furthermore, we consider the fluid to possess electrical conductivity and applied Lorentz force. Moreover, the externally imposed field is higher, in the current study, as compared to the induced magnetic field that is considered as negligible. This framework provides a setup to examine the interaction between hydraulic as well as magnetic forces within the specified system. Figure 1 depicts the problem geometry.

Figure 1

Geometry of the problem.

Governing equations for the present problem [26,27]

(1) ∂ u 1 ∂ η 1 + ∂ u 2 ∂ η 2 + ∂ u 3 ∂ η 3 = 0 ,

(2) ρ nf u 1 ∂ u 1 ∂ η 1 + u 2 ∂ u 1 ∂ η 2 + u 3 ∂ u 1 ∂ η 3 = − ∂ p ∂ η 1 + μ nf ∂ 2 u 1 ∂ η 1 2 + ∂ 2 u 1 ∂ η 2 2 + ∂ 2 u 1 ∂ η 3 2 ,

(3) ρ nf u 1 ∂ u 2 ∂ η 1 + u 2 ∂ u 2 ∂ η 2 + u 3 ∂ u 2 ∂ η 3 = − ∂ p ∂ η 2 + μ nf ∂ 2 u 2 ∂ η 1 2 + ∂ 2 u 2 ∂ η 2 2 + ∂ 2 u 2 ∂ η 3 2 ,

(4) ρ nf u 1 ∂ u 3 ∂ η 1 + u 2 ∂ u 3 ∂ η 2 + u 3 ∂ u 3 ∂ η 3 = − ∂ p ∂ η 3 + μ nf ∂ 2 u 3 ∂ η 1 2 + ∂ 2 u 3 ∂ η 2 2 + ∂ 2 u 3 ∂ η 3 2 + β g ( T − T ∞ ) g − σ nf B 0 2 u 3 ,

(5) u 1 ∂ T ∂ η 1 + u 2 ∂ T ∂ η 2 + u 3 ∂ T ∂ η 3 = ( k nf / ( ρ c p ) nf ) ∂ 2 T ∂ η 1 2 + ∂ 2 T ∂ η 2 2 + ∂ 2 T ∂ η 3 2 ,

where η 1 , η 2 and η 3 are the usual coordinates in the Cartesian coordinate system and u 1 , u 2 and u 3 are the, respective, velocity components, with the rest of the physical quantities bearing their usual meanings. It is to point out that the terms on the left-hand side of the Eqs (1)–(4) represent the inertial forces, whereas the pressure and viscous forces are represented by the first and second terms on the right-hand side of the above system. Further, the last two terms in Eq. (4) stand for the body forces due to convection and external magnetic field effects. Finally, the left- and right-hand sides of Eq. (5) represent, respectively, the heat gain and the heat transfer due to conduction. Moreover, the subscript nf stands for the physical quantities related to the nanofluids.

Now, considering the one-dimensional flow ( 0 , 0 , u 3 ( η 1 , η 2 ) ) and incorporating the transformation:

(6) x = η 1 L , y = η 2 L , v 3 = u 3 u 0 , θ = T − T w T 0 ,

where u 0 = − L 2 p 0 μ f and T 0 = q ′ k f v 3 ( m ) are the reference velocity and temperature, respectively, with v 3 ( m ) = 1 A 0 ∬ Ω v 3 d x d y is taken over domain Ω having area A 0 and represents the mean velocity.

The above system acquires the shape

(7) ( 1 − ϕ ) 2.5 p 0 + ∂ 2 T ∂ x 2 + ∂ 2 T ∂ y 2 + ( 1 − ϕ ) 2.5 1 − ϕ + ϕ ( ρ C p ) s ( ρ C p ) f 1 − ϕ + ϕ ( ρ β ) s ( ρ β ) f Ra θ − ( 1 − ϕ ) 2.5 Δ 0 M 2 v 3 = 0 ,

(8) ( k s + 2 k f ) − 2 ϕ ( k f − k s ) ( k s + 2 k f ) + ϕ ( k f − k s ) ∂ 2 θ ∂ x 2 + ∂ 2 θ ∂ y 2 = v 3 ,

With p 0 = Dimensionless pressure gradient , Ra = Rayleigh number, and M = Magnetic parameter.

The uniform temperature and the no slip boundary conditions at the solid boundaries and the obstacle (located at the region defined by 0.4 ≤ x ≤ 0.6 and 0.4 ≤ y ≤ 0.6 ) are translated in terms of the dimensionless velocity and temperature as

(9) v 3 ( x , 0 ) = v 3 ( x , 1 ) = θ ( x , 0 ) = θ ( x , 1 ) = 0 , 0 ≤ x ≤ 1 v 3 ( 0 , y ) = v 3 ( 1 , y ) = θ ( 0 , y ) = θ ( 1 , y ) = 0 , 0 ≤ y ≤ 1 v 3 ( x , 0.4 ) = v 3 ( x , 0.6 ) = θ ( x , 0.4 ) = θ ( x , 0.6 ) = 0 , 0.4 ≤ x ≤ 0.6 v 3 ( 0.4 , y ) = v 3 ( 0.6 , y ) = θ ( 0.4 , y ) = θ ( 0.6 , y ) = 0 . 0.4 ≤ y ≤ 0.6 ,

3 Numerical solution

We use the FVM which is based on the fundamental principle of discretizing the computational domain into a finite number of control volumes. These control volumes are small subregions over which the partial differential equations (PDEs) are integrated, effectively dividing the domain into discrete cells. Within each control volume, the governing PDE is approximated by an algebraic equation, representing the engineering interest quantities behavior. The method is conservative in nature, ensuring that the total flux of the conserved quantity in and out of each control volume remains balanced. This is achieved through the evaluation of fluxes at the faces of the control volumes, which are computed based on gradients of the conserved quantity. For the iterative solution, the mechanism (about any general point P ) of rectangular-shaped control volume is portrayed in Figure 2.

Figure 2

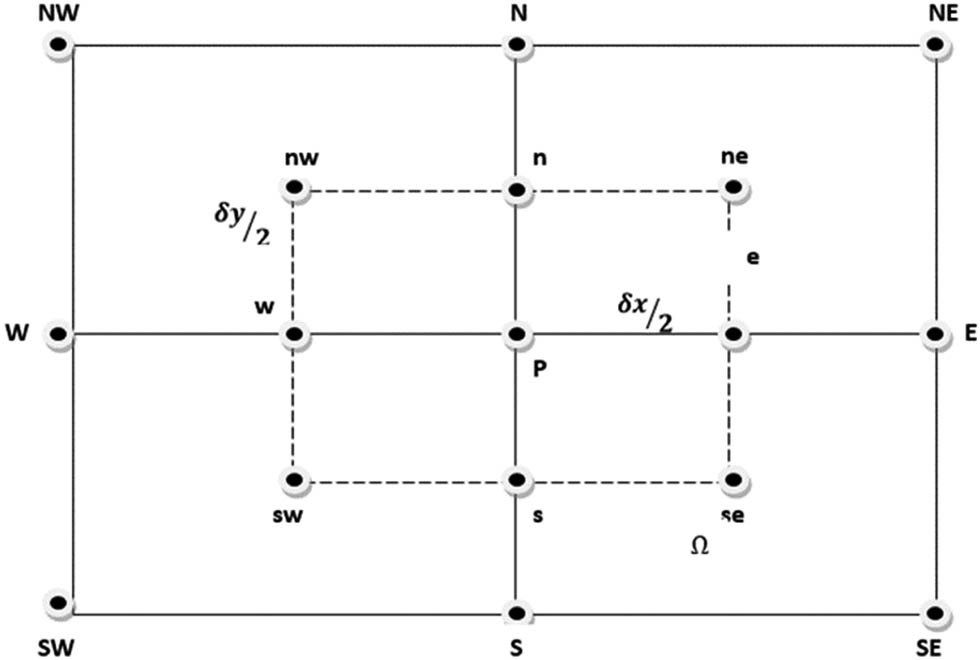
Rectangular-shaped control volume around a grid point P.

The mathematical expressions for the FVM are given below:

(10) ∬ Ω ∂ 2 f ∂ x 2 + ∂ 2 f ∂ y 2 + c f d A = ∬ Ω g ( x , y ) d A ,

(11) ∬ Ω ∂ 2 f ∂ x 2 d A + ∬ Ω ∂ 2 f ∂ y 2 d A + c ∬ Ω f d A = ∬ Ω g ( x , y ) d A .

As the domain Ω is taken to be rectangular, so it can be stated as

(12) x w ≤ x ≤ x e , y s ≤ y ≤ y n ,

Here the relations mentioned above take the form

(13) ∫ x w x e ∫ y s y n ∂ 2 f ∂ x 2 d y d x + ∫ x w x e ∫ y s y n ∂ 2 f ∂ y 2 d y d x + c ∫ x w x e ∫ y s y n f d y d x = ∫ x w x e ∫ y s y n g ( x , y ) d y d x .

One by one the evaluation of integrals yields the following expressions:

(14) ∫ x w x e ∫ y s y n ∂ 2 f ∂ x 2 d y d x = ∫ y s y n ∫ x w x e ∂ 2 f ∂ x 2 d x d y ,

(15) = ∫ y s y n ∂ f ∂ x x e − ∂ f ∂ x x w d y ,

(16) = ∫ y s y n f E − f P Δ x d y − ∫ y s y n f P − f W Δ x d y ,

(17) = f E − f P Δ x ( y n − y s ) − f P − f W Δ x ( y n − y s ) ,

= Δ y Δ x { f E − f P − f P + f W } ,

(18) = Δ y Δ x { f E − 2 f P + f W } .

The mathematical expression for the second term is given below:

∫ x w x e ∫ y s y n ∂ 2 f ∂ y 2 d y d x = ∫ x w x e ∂ f ∂ y y n − ∂ f ∂ y y s d x ,

(19) = ∫ x w x e f N − f P Δ y − f P − f S Δ y d x ,

(20) = ∫ x w x e f N − 2 f P + f s Δ y d x ,

(21) = f N − 2 f P + f s Δ y ( x e − x w ) ,

(22) = Δ x Δ y { f N − 2 f P + f S } .

Moreover,

∫ x w x e ∫ y s y n f d y d x = f P Δ x Δ y

(23) = ∫ x w x e f ne − f nw Δ x − f se − f sw Δ x d x ,

(24) = 1 Δ x 1 4 f NE − 1 4 f NW − 1 4 f SE + 1 4 f SW Δ x ,

(25) = 1 4 ( f NE − f NW − f SE + f SW ) .

At the end, we obtain

(26) f E − 2 f P + f W Δ x 2 + f N − 2 f P + f S Δ y 2 + c f P = g P .

This method is a widely employed numerical technique for solving PDEs arising in various fields of science and engineering. It is particularly well-suited for problems involving the conservation of physical quantities, such as mass, energy, or momentum. The FVM offers several advantages, including its ability to handle complex geometries and its inherent conservation properties.

For the case when no obstruction is present in the cavity, we compare our numerical results (in Table 1) with those presented by Ali et al. [28] based on the spectral method and a finite difference scheme over a stretched grid.

Table 1

Comparison of our numerical results with the literature in the absence of any obstruction for ϕ = 0.1 , Ra = 30 , 000 and M = 5

	f _Re			Nu
Grid	Finite difference method Ali et al. [28]	Spectral method Ali et al. [28]	FVM (present study)	FDM Ali et al. [28]	Spectral method Ali et al. [28]	FVM (present study)
31 × 31	862.5459	863.1074	863.0055	37.9579	37.8454	37.8251
51 × 51	863.5687	863.8322	863.2211	37.9283	37.8977	37.8734
61 × 61	863.7380	863.9398	863.3166	37.9234	37.9088	37.8910
81 × 81	863.9108	864.0353	863.9985	37.9183	37.9107	37.9087
101 × 101	863.9833	864.0735	864.0214	37.9162	37.9113	37.9095

Table 2 provides the analysis of numerical uncertainty analysis in the study.

Table 2

Numerical solution for W (x, y) along the line y = 0.2 for different step-sizes δ x

	W ( x , 0.2 )
x	δ x = 0.02	δ x = 0.01	Uncertainty	δ x = 0.005	Uncertainty	δ x = 0.0025	Uncertainty
0	0	0	0	0	0	0	0
0.1	4.8965	4.9437	0.0472	4.9632	0.0195	4.9719	0.0087
0.2	7.0253	7.1353	0.1100	7.1823	0.0470	7.2038	0.0215
0.3	7.5583	7.7474	0.1891	7.8303	0.0829	7.8688	0.0385
0.4	7.4196	7.6558	0.2362	7.7622	0.1064	7.8124	0.0502
0.5	7.3650	7.5707	0.2057	7.6658	0.0951	7.7113	0.0455
0.6	7.6255	7.7479	0.1224	7.8057	0.0578	7.8335	0.0278
0.7	7.8206	7.8647	0.0441	7.8857	0.0210	7.8957	0.0100
0.8	7.2065	7.2171	0.0106	7.2211	0.0040	7.2227	0.0016
0.9	4.9777	4.9805	0.0028	4.9807	0.0002	4.9804	0.0003
1.0	0	0	0	0	0	0	0

4 Results and discussion

This section is devoted to study the impact of the governing parameters not only on the velocity and temperature fields but also on the product of the fanning factor f, Nusselt number Nu, and the Reynolds number Re, which are given below:

(27) f Re = 1 − ϕ + ϕ ρ s ρ f − 1 2 v 3 ( m ) ,

(28) Nu = ( k s + 2 k f ) − 2 ϕ ( k E − k s ) ( k s + 2 k f ) + ϕ ( k f − k s ) ( v 3 ( m ) ) 2 ∬ Ω v 3 θ d x d y .

The thermos-physical properties of nanofluid are mentioned in Tables 3 and 4.

Table 3

Fixed values of copper and water

Nanofluid properties	Copper (Cu)	H₂O
ρ ( kg/m 3 )	8,933	997
C p ( J/kg K )	385	4,180
k ( W / mK )	400	0.6071

Table 4

Physical properties of nanofluid

Nanofluid properties	Mathematical formula
Heat capacitance ( ρ c p ) nf	( ρ c p ) nf = ϕ ( ρ c p ) s ( ρ c p ) f + ( 1 ‒ ϕ ) ( ρ c p ) f
Dynamic viscosity ( μ nf )	μ nf = 1 ( 1 ‒ ϕ ) 2.5 μ f
Thermal conductivity ( k nf )	k nf k f = ( ( s ‒ 1 ) k f + k s ) ‒ ( s ‒ 1 ) ϕ ( k f ‒ k s ) ( ( s ‒ 1 ) k f + k s ) + ϕ ( k f ‒ k s )
Density ( ρ nf )	ρ nf = ρ f ϕ ρ s ρ f + ( 1 ‒ ϕ )

Figures 3–9 show that the pressure gradient causes a significant rise in the flow velocity. The relationship between pressure gradients and flow velocity is a fundamental principle in fluid dynamics that is both fascinating and practical. When we talk about a pressure gradient, we are essentially describing how pressure changes within a fluid system. As the fluid moves from an area of higher pressure to an area of lower pressure, it is essentially responding to this pressure difference. Due to this phenomenon, there is an increase in the flow velocity. This is due to the conservation of energy principle and controlled by the Bernoulli’s equation, i.e., as liquid passes from high pressure region to low-pressure region, its kinetic energy increases. practical applications. In many practical cases, this relationship is crucial. For example, aircrafts use pressure gradients in this way to generate lift: by increasing the flow velocity over the curved upper surface of a wing.

$Figure 3 Velocity distribution for p 0 = 1 {p}_{0}=1 .$

Figure 3

Velocity distribution for p 0 = 1 .

$Figure 4 Velocity distribution for p 0 = 10 {p}_{0}=10 .$

Figure 4

Velocity distribution for p 0 = 10 .

$Figure 5 Velocity distribution for p 0 = 50 {p}_{0}=50 .$

Figure 5

Velocity distribution for p 0 = 50 .

$Figure 6 Velocity distribution for p 0 = 100 {p}_{0}=100 .$

Figure 6

Velocity distribution for p 0 = 100 .

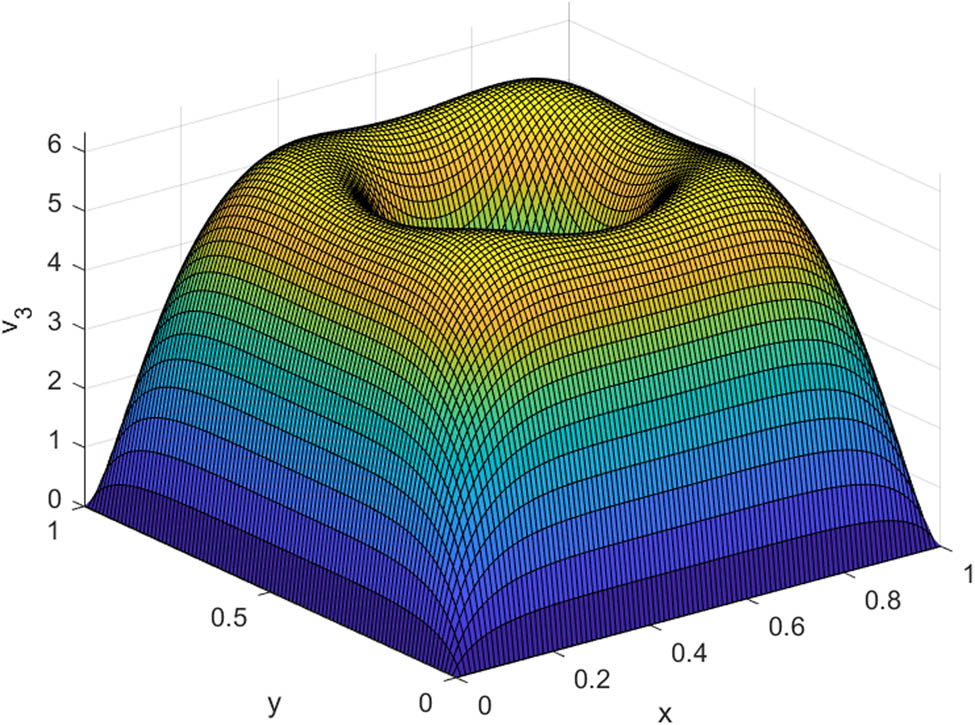
$Figure 7 Velocity distribution for p 0 = 500 {p}_{0}=500 .$

Figure 7

Velocity distribution for p 0 = 500 .

$Figure 8 Velocity distribution for p 0 = 1 , 000 {p}_{0}=1,000 .$

Figure 8

Velocity distribution for p 0 = 1 , 000 .

Figure 9

Change in velocity in the middle of the duct with the pressure gradient.

A remarkable rise in the dimensionless temperature is noted with the pressure gradient (Figures 10–16). The interaction between pressure gradients and flow temperature provides the link to other domains where fluid flows are encountered. When a fluid undergoes a transition in its thermodynamics due to change in pressure along its path, this pressure increase in the fluid causes an increased energy density within the fluid. This increased energy level results an increase in the temperature, a phenomenon that is explained by adiabatic heating. But in simple terms, the molecules contained inside a fluid interact more strongly with each other as it is forced through an area of higher pressure, and these interactions lead to a gain in energy known as kinetic energy – or heat. This has major consequences for applications in industrial processes up to geophysical phenomena.

$Figure 10 Temperature distribution for p 0 = 1 {p}_{0}=1 .$

Figure 10

Temperature distribution for p 0 = 1 .

$Figure 11 Temperature distribution for p 0 = 10 {p}_{0}=10 .$

Figure 11

Temperature distribution for p 0 = 10 .

$Figure 12 Temperature distribution for p 0 = 50 {p}_{0}=50 .$

Figure 12

Temperature distribution for p 0 = 50 .

$Figure 13 Temperature distribution for p 0 = 100 {p}_{0}=100 .$

Figure 13

Temperature distribution for p 0 = 100 .

$Figure 14 Temperature distribution for p 0 = 500 {p}_{0}=500 .$

Figure 14

Temperature distribution for p 0 = 500 .

$Figure 15 Temperature distribution for p 0 = 1 , 000 {p}_{0}=1,000 .$

Figure 15

Temperature distribution for p 0 = 1 , 000 .

Figure 16

Change in temperature in the middle of the duct with the pressure gradient.

Now, from Figures 17–22, it is seen that the external magnetic field decelerates the flow in the present geometry. Relations between pressure gradients and flow temperature in free-standing fluids are fundamental to fluid dynamics of wide scope. Within the range of a fluid, changing pressure as it flows over a perfect level surface and there is no statement that how this change occurs or what its thermodynamic qualities are alluded to as compressible streams. The greater the pressure, the higher the energy contained in the fluid. This high energy state results in a temperature rise, which describes adiabatic heating. In simplest form, fluid molecules are urged through the higher-pressure area, those interactions accelerate their rate of energy exchange (aka kinetic energy) meaning they will then show an increased temperature. Such an effect has important impacts in applications from industrial processes to geophysical phenomena.

$Figure 17 Velocity distribution for Ha = 0 \text{Ha}=0 .$

Figure 17

Velocity distribution for Ha = 0 .

$Figure 18 Velocity distribution for Ha = 10 \text{Ha}=10 .$

Figure 18

Velocity distribution for Ha = 10 .

$Figure 19 Velocity distribution for Ha = 20 \text{Ha}=20 .$

Figure 19

Velocity distribution for Ha = 20 .

$Figure 20 Velocity distribution for Ha = 30 \text{Ha}=30 .$

Figure 20

Velocity distribution for Ha = 30 .

$Figure 21 Velocity distribution for Ha = 50 \text{Ha}=50 .$

Figure 21

Velocity distribution for Ha = 50 .

Figure 22

Change in velocity in the middle of the duct with the magnetic field intensity.

Figures 23–28 show that the external magnetic field decelerates the flow in the present geometry. From a physical point of view, when a fluid medium is exposed to an external magnetic field, it initiates a cascade of effects that lead to alterations in thermal behavior. This arises from the magneto-thermodynamic properties inherent to the fluid. The presence of a magnetic field influences the motion and energy states of the fluid’s constituent particles, which in turn impacts their kinetic behavior. As a consequence, the fluid experiences a reduction in temperature, a phenomenon referred to as magnetocaloric cooling.

$Figure 23 Temperature distribution for Ha = 0 \text{Ha}=0 .$

Figure 23

Temperature distribution for Ha = 0 .

$Figure 24 Temperature distribution for Ha = 10 \text{Ha}=10 .$

Figure 24

Temperature distribution for Ha = 10 .

$Figure 25 Temperature distribution for Ha = 20 \text{Ha}=20 .$

Figure 25

Temperature distribution for Ha = 20 .

$Figure 26 Temperature distribution for Ha = 30 \text{Ha}=30 .$

Figure 26

Temperature distribution for Ha = 30 .

$Figure 27 Temperature distribution for Ha = 50 \text{Ha}=50 .$

Figure 27

Temperature distribution for Ha = 50 .

Figure 28

Change in temperature in the middle of the duct with the magnetic field intensity.

Tables 5–7 describe the results for the numerical data of the problem. The impact of the main problem parameters on the shear stress f _Re and the Nusselt number Nu can be examined from these Tables.

Table 5

Variation in f _Re and Nu with M and Ra, for the fixed p 0 = 100 and ϕ = 0.10

	f _Re			Nu
M	Ra = 1,000	Ra = 10,000	Ra = 50,000	Ra = 1,000	Ra = 10,000	Ra = 50,000
0	0.2666	0.7492	2.5003	40.2846	44.9223	59.0917
10	0.6580	1.1197	2.8627	42.8179	46.3360	58.3918
20	1.7732	2.2042	3.9264	46.6720	48.8617	57.3482
30	3.5616	3.9708	5.6673	49.6202	51.0300	56.8467
40	6.0112	6.4057	8.0778	51.7104	52.6764	56.7874
50	9.1194	9.5038	11.1548	53.2228	53.9209	56.9427

Table 6

Variation in f _Re and Nu with M and ϕ , for the fixed p 0 = 100 and Ra = 10 , 000

	f _Re			Nu
ϕ	M = 0	M = 10	M = 20	M = 0	M = 10	M = 20
0	2.0122	2.4684	3.8204	51.7777	51.9860	52.6572
0.05	1.2353	1.5955	2.6617	56.9036	57.6244	59.1979
0.10	0.8562	1.1733	2.1082	62.6713	64.0042	66.5844
0.15	0.6397	0.9359	1.8046	69.2449	71.2689	74.9400
0.20	0.5056	0.7926	1.6299	76.8088	79.5824	84.4152

Table 7

Variation in f _Re and Nu with ϕ and Ra, for the fixed p 0 = 100 and M = 10

	f _Re			Nu
ϕ	Ra = 1,000	Ra = 10,000	Ra = 20,000	Ra = 1,000	Ra = 10,000	Ra = 20,000
0	0.8695	1.6649	2.4684	42.9275	47.5622	51.9860
0.05	0.6580	1.1197	1.5955	49.5482	53.6193	57.6244
0.10	0.5594	0.8592	1.1733	56.8934	60.4345	64.0042
0.15	0.5087	0.7159	0.9359	65.0810	68.1319	71.2689
0.20	0.4837	0.6327	0.7926	74.2587	76.8620	79.5824

The impact of the Rayleigh number on the flow is to cause a remarkable reduction in the flow velocity (Figures 29–33). In fluid dynamics, the Rayleigh number serves as a critical dimensionless parameter that plays a pivotal role in dictating the behavior of fluid flows. Essentially, it acts as a barometer of the relative significance of buoyancy forces in comparison to viscous forces within a fluid medium. A higher Rayleigh number signifies a scenario where buoyancy forces take precedence, potentially instigating convective motion. Conversely, a lower Rayleigh number indicates a situation where viscous forces dominate, resulting in a more ordered and laminar flow. Hence, as the Rayleigh number increases, it indicates an environment where buoyancy forces are exerting greater influence compared to viscous forces. Consequently, the flow velocity tends to decrease, as the fluid is more prone to convective motion (Figure 34). From Figures 35–40, it is noted that the Rayleigh number increases the flow temperature. However, the impact of the parameter is not very pronounced. From a physical point of view, the increased convective motion (due to the high Rayleigh number) causes regions of differing temperatures to mix more vigorously, resulting in an overall rise in temperature. In simpler terms, an increase in the Rayleigh number intensifies the heat transfer process within the fluid, leading to an elevation in flow temperature.

$Figure 29 Velocity distribution for Ra = 1 , 000 \text{Ra}=1,000 .$

Figure 29

Velocity distribution for Ra = 1 , 000 .

$Figure 30 Velocity distribution for Ra = 10 , 000 \text{Ra}=10,000 .$

Figure 30

Velocity distribution for Ra = 10 , 000 .

$Figure 31 Velocity distribution for Ra = 20 , 000 \text{Ra}=20,000 .$

Figure 31

Velocity distribution for Ra = 20 , 000 .

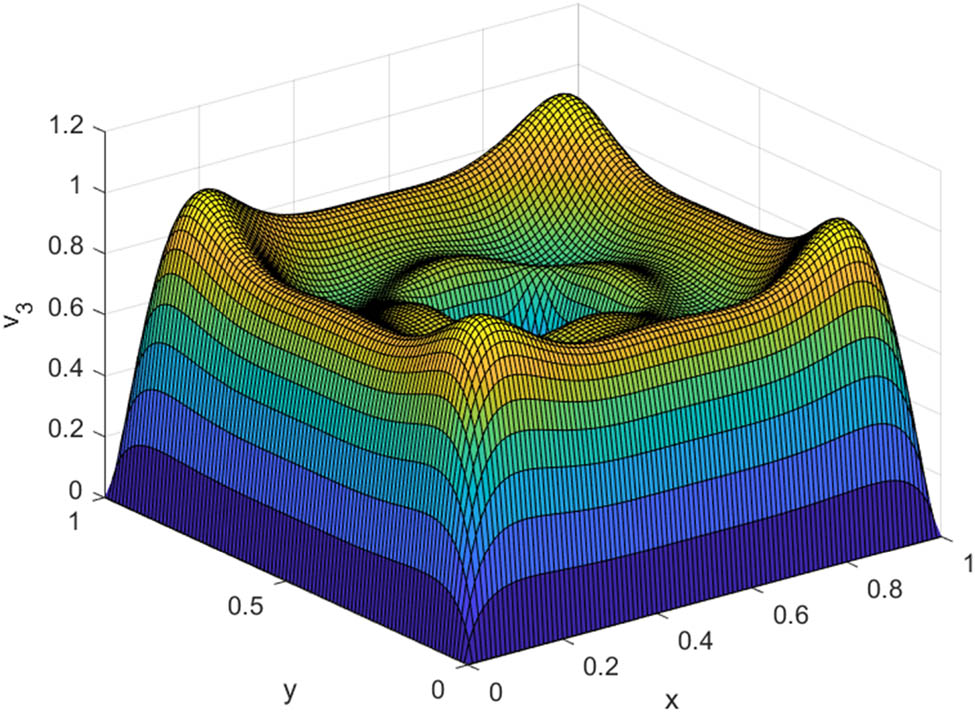
$Figure 32 Velocity distribution for Ra = 30 , 000 \text{Ra}=30,000 .$

Figure 32

Velocity distribution for Ra = 30 , 000 .

$Figure 33 Velocity distribution for Ra = 4 , 000 \text{Ra}=4,000 .$

Figure 33

Velocity distribution for Ra = 4 , 000 .

Figure 34

Velocity change in the middle of the duct with the Rayleigh number.

$Figure 35 Thermal distribution for Ra = 1 , 000 \text{Ra}=1,000 .$

Figure 35

Thermal distribution for Ra = 1 , 000 .

$Figure 36 Thermal distribution for Ra = 10 , 000 \text{Ra}=10,000 .$

Figure 36

Thermal distribution for Ra = 10 , 000 .

$Figure 37 Thermal distribution for Ra = 20 , 000 \text{Ra}=20,000 .$

Figure 37

Thermal distribution for Ra = 20 , 000 .

$Figure 38 Thermal distribution for Ra = 30 , 000 \text{Ra}=30,000 .$

Figure 38

Thermal distribution for Ra = 30 , 000 .

$Figure 39 Thermal distribution for Ra = 50 , 000 \text{Ra}=50,000 .$

Figure 39

Thermal distribution for Ra = 50 , 000 .

Figure 40

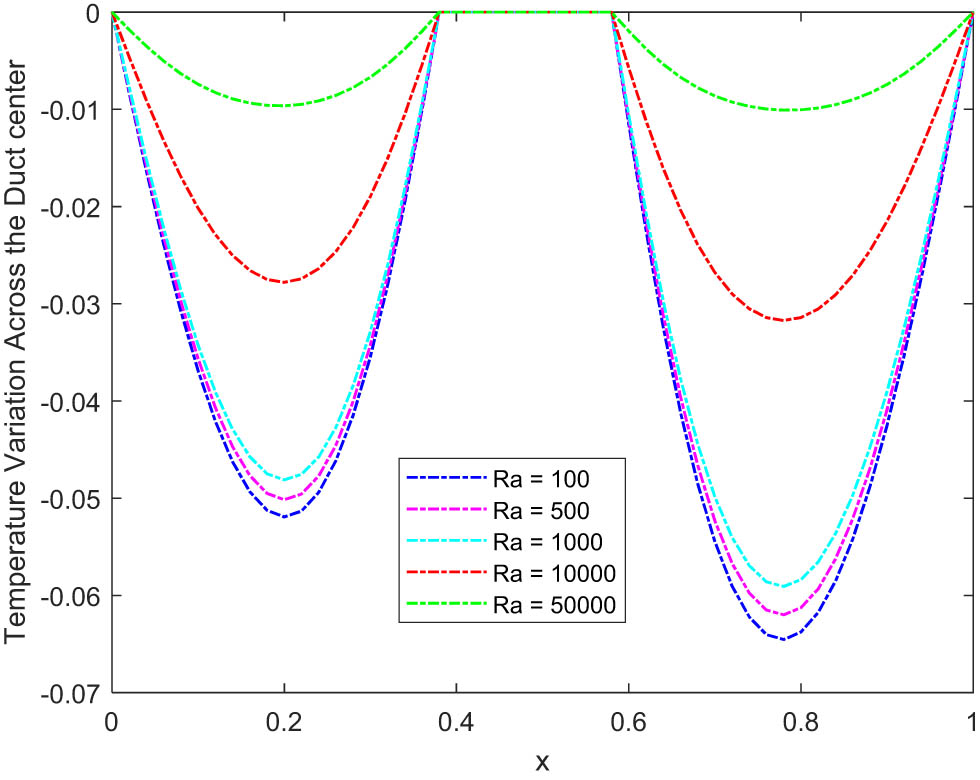
Temperature change in the middle of the duct with the Rayleigh number.

Figure 41 shows that the Nusselt number increases with both the magnetic parameter and the Rayleigh number. In the realm of heat transfer, the Nusselt number stands as a critical dimensionless parameter that plays a pivotal role in characterizing convective heat transfer processes. It quantifies the enhancement of heat transfer due to convection over that of pure conduction. The Nusselt number is paramount and positively-associated with both the magnetic parameter and the Rayleigh number. The convection heat transfer process is highly dependent on the magneto parameter. Increase in the magnetic parameter leads to an increase in the fluid accelerations force and hence high convective heat transfer is obtained. Similarly, the Rayleigh number (a non-dimensional number) describes the importance of buoyancy forces for the viscous flows and, it affects the Nusselt number directly inside the vertical duct. A higher Rayleigh number induces a more vigorous convective flow inside the fluid yielding better heat transfer process.

Figure 41

Nusselt number variation with the magnetic field intensity and the Rayleigh number.

Therefore, it can be deduced that both an elevated magnetic parameter and Rayleigh number contribute to an increase in the Nusselt number, indicating a more pronounced enhancement of heat transfer due to convection.

It is obvious from Figure 42 that the product of the fanning factor and the Reynolds number increases with both the magnetic parameter and the Rayleigh number. The relationship between the fanning factor and the Reynolds number is a crucial aspect to the present problem. It has been observed that the product of these two parameters exhibits a notable increase with variations in both the magnetic parameter and the Rayleigh number. This phenomenon underscores the significant influence of magnetic fields and thermal buoyancy on the flow characteristics of the system under investigation. The concurrent influence of these factors highlights the intricate interplay between magnetic effects and thermal gradients. Figure 43 shows that the product of the fanning factor and the Reynolds number decreases with both pressure gradients. This observation underscores the significant influence of pressure differentials on the flow characteristics. A heightened pressure gradient exerts a notable effect on the flow regime, influencing factors such as flow velocity and boundary layer development. Consequently, this alteration in pressure conditions manifests itself in the product of the fanning factor and the Reynolds number, leading to a reduction in its magnitude (Figure 44). The Nusselt number first increases and then decreases with the nanoparticle volume fraction with an optimum for a 10% concentration of the solid particles (Figure 45) whereas f _Re is noted to be always decreasing with the increase in the nanostructure in the fluid (Figure 46).

Figure 42

f _Re variation with the magnetic field intensity and the Rayleigh number.

Figure 43

f _Re variation with the magnetic field intensity and pressure gradient.

Figure 44

Nusselt number variation with the magnetic field intensity and pressure gradient.

Figure 45

Nusselt number variation with the nanoparticle concentration and the Rayleigh number.

Figure 46

f _Re variation with the nanoparticle concentration and the pressure gradient.

5 Conclusion

The purpose of the study is to present the numerical study of external magnetic field effects on the developed laminar flow and thermal characteristics of nanofluid within a vertical square duct containing an obstacle in the middle of the duct, by employing a finite volume approach. We have noted that

A 20% nanoparticle volume fraction resulted in up to 62% rise in the Nusselt number while causing an almost 50% decrease in the factor f _Re.
The pressure gradient causes a significant rise in the flow velocity and temperature distribution.
When a flow encounters a magnetic field, the magnetic forces exerted on its charged particles can induce changes in the flow behavior; consequently, the Lorentz force comes into play which acts perpendicular to both the direction of the magnetic field and the fluid flow, leading to a resistance against the flow motion.
Due to the presence of the external magnetic field, the fluid experiences a reduction in temperature, a phenomenon referred to as magnetocaloric cooling.
When the buoyancy forces are exerting greater influence compared to viscous forces, the flow velocity tends to decrease, as the fluid is more prone to convective motion.
An increase in the Rayleigh number intensifies the heat transfer process within the fluid, leading to an elevation in flow temperature.
As the magnetic parameter increases, it enhances the magnetic forces acting on the fluid, consequently intensifying the convective heat transfer.
An increase in the Rayleigh number leads to heightened convective motion within the fluid, resulting in a more efficient heat transfer process. Therefore, it can be deduced that both an elevated magnetic parameter and Rayleigh number contribute to an increase in the Nusselt number, indicating a more pronounced enhancement of heat transfer due to convection.

The Nusselt number first increases and then decreases with the nanoparticle volume fraction with an optimum for a 10% concentration of the solid particles whereas f _Re is noted to be always decreasing with the increase in the nanostructure in the fluid.

Acknowledgments

The authors extend their appreciation to the Deanship of Research and Graduate Studies at King Khalid University for funding this work through Large Research Project under grant number RGP2/354/45.

Funding information: The authors extend their appreciation to the Deanship of Research and Graduate Studies at King Khalid University for funding this work through Large Research Project under grant number RGP2/354/45.
Author contributions: All authors have accepted responsibility for the entire content of this manuscript and approved its submission.
Conflict of interest: The authors state no conflict of interest.

References

[1] Ali K, Jamshed W, Suriya Uma Devi S, Ibrahim RW, Ahmad S, Tag El Din ESM. A study of pressure-driven flow in a vertical duct near two current-carrying wires using finite volume technique. Sci Rep. 2022;12:21273. 10.1038/s41598-022-25756-4.Search in Google Scholar

[2] Ortloff CR. Supercritical Froude number flow through ducts with statistically roughened walls. Water. 2023;15:2849. 10.3390/w15152849.Search in Google Scholar

[3] Dolon SN, Hasan MS, Lorenzini G, Mondal RN. A computational modeling on transient heat and fluid flow through a curved duct of large aspect ratio with centrifugal instability. Eur Phys J Plus. 2021;136:382. 10.1140/epjp/s13360-021-01331-0.Search in Google Scholar

[4] Su CC, Lin RH. Experimental studies on flow in convergent and divergent ducts of rectangular cross section. Int J Energy Res. 1997;21(1):77–86.10.1002/(SICI)1099-114X(199701)21:1<77::AID-ER257>3.0.CO;2-GSearch in Google Scholar

[5] Riaz A, Ahammad NA, Alqarni MM, Hejazi HA, Tag-ElDin EM. Peristaltic flow of a viscous fluid in a curved duct with a rectangular cross section. Front Phys. 2022;10:961201. 10.3389/fphy.2022.961201.Search in Google Scholar

[6] Garud KS, Kudriavskyi Y, Lee MS, Kang EH, Lee MY. Numerical study on thermal and flow characteristics of divergent duct with different rib shapes for electric-vehicle cooling system. Symmetry. 2022;14:1696. 10.3390/sym14081696.Search in Google Scholar

[7] Tokgoz N, Sahin B. Experimental studies of flow characteristics in corrugated ducts. Int Commun Heat Mass Transf. 2019;104:41–50. 10.1016/j.icheatmasstransfer.2019.03.003.Search in Google Scholar

[8] Sutevski D, Smolentsev S, Morley N, Abdou M. 3D numerical study of MHD flow in a rectangular duct with a flow channel insert. Fusion Sci Technol. 2011;60(2):513–7. 10.13182/FST11-A12433.Search in Google Scholar

[9] Krasnov D, Zikanov O, Boeck T. Numerical study of magnetohydrodynamic duct flow at high Reynolds and Hartmann numbers. J Fluid Mech. 2012;704:421–46. 10.1017/jfm.2012.256.Search in Google Scholar

[10] Ting HH, Hou SS. Numerical Study of laminar flow and convective heat transfer utilizing nanofluids in equilateral triangular ducts with constant heat flux. Materials. 2016;9:576. 10.3390/ma9070576.Search in Google Scholar

[11] Fonseca WDS, Araujo RCF, Silva MDOE, Cruz DODA. Analysis of the magnetohydrodynamic behavior of the fully developed flow of conducting fluid. Energies. 2021;14:2463. 10.3390/en14092463.Search in Google Scholar

[12] Borrelli A, Giantesio G, Patria MC. Exact solutions in MHD natural convection of a Bingham fluid: fully developed flow in a vertical channel. J Therm Anal Calorim. 2022;147:5825–38. 10.1007/s10973-021-10882-4.Search in Google Scholar

[13] Saleh H, Hashim I. Flow reversal of fully-developed mixed MHD convection in vertical channels. Chin Phys Lett. 2010;27(2):024401. 10.1088/0256-307X/27/2/024401.Search in Google Scholar

[14] Jha BK, Malgwi PB, Aina B. Fully developed magnetohydrodynamics natural convection flow in a vertical micro-porous-channel with Hall effects. Proc Inst Mech Eng, Part N: J Nanomater, Nanoeng Nanosyst. 2019;233(2–4): 73–85. 10.1177/2397791419863596.Search in Google Scholar

[15] Ghosh S, Bég O, Aziz A. A mathematical model for magnetohydrodynamic convection flow in a rotating horizontal channel with inclined magnetic field, magnetic induction and Hall current effects. World J Mech. 2011;1(3):137–54. 10.4236/wjm.2011.13019.Search in Google Scholar

[16] Singh JK, Seth GS, Hussain SM. Thermal performance of hydromagnetic nanofluid flow within an asymmetric channel with arbitrarily conductive walls filled with Darcy-Brinkmann porous medium. J Magn Magn Mater. 2023;582:171034. 10.1016/j.jmmm.2023.171034.Search in Google Scholar

[17] Hussain SM. Irreversibility analysis of time-dependent magnetically driven flow of Sutterby hybrid nanofluid: a thermal mathematical model. Waves Random Complex Media. 2022;1–33. 10.1080/17455030.2022.2089369.Search in Google Scholar

[18] Sajid T, Algarni S, Ahmad H, Alqahtani T, Jamshed W, Eid MR, et al. Exploration of irreversibility process and thermal energy of a tetra hybrid radiative binary nanofluid focusing on solar implementations. Nanotechnol Rev. 2024;13:20240040.10.1515/ntrev-2024-0040Search in Google Scholar

[19] Sankari MS, Rao ME, Shams ZE, Algarni S, Nadeem Sharif M, Alqahtani T, et al. Williamson MHD nanofluid flow via a porous exponentially stretching sheet with bioconvective fluxes. Case Stud Therm Eng. 2024;59:104453.10.1016/j.csite.2024.104453Search in Google Scholar

[20] Nazir U, Sohail M, Singh A, Muhsen S, Galal AM, Tag El Din ESM. Finite element analysis for thermal enhancement in power law hybrid nanofluid. Front Phys. 2022;10:996174. 10.3389/fphy.2022.996174.Search in Google Scholar

[21] Halder A, Bhattacharya A, Biswas N, Manna NK, Mandal DK. Convective heat transport and entropy generation in butterfly-shaped magneto-nanofluidic systems with bottom heating and top cooling. Int J Numer Methods Heat Fluid Flow. 2024;34:837–77. 10.1108/HFF-06-2023-0353.Search in Google Scholar

[22] Manna NK, Saha A, Biswas N, Ghosh K. Effects of enclosure shape on MHD nanofluid flow and irreversibility in different shaped systems under fluid volume constraint. Int J Numer Methods Heat Fluid Flow. 2024;34:666–708. 10.1108/HFF-06-2023-0348.Search in Google Scholar

[23] Biswas N, Mandal DK, Manna NK, Gorla RSR, Chamkha AJ. Hybridized nanofluidic convection in umbrella-shaped porous thermal systems with identical heating and cooling surfaces. Int J Numer Methods Heat Fluid Flow. 2023;33:3164–201. 10.1108/HFF-11-2022-0639.Search in Google Scholar

[24] Chatterjee D, Biswas N, Manna NK, Mandal DK, Chamkha AJ. Magneto-nanofluid flow in cylinder-embedded discretely heated-cooled annular thermal systems: Conjugate heat transfer and thermodynamic irreversibility. J Magn Magn Mater. 2023;569:170442. 10.1016/j.jmmm.2023.170442.Search in Google Scholar

[25] Chatterjee D, Biswas N, Manna NK, Sarkar S. Effect of discrete heating-cooling on magneto-thermal-hybrid nanofluidic convection in cylindrical system. Int J Mech Sci. 2023;238:107852. 10.1016/j.ijmecsci.2022.107852.Search in Google Scholar

[26] Li S, Leng Y, Ali K, Ahmad S, Jamshed W, Saddam EN. Machine learning based evaluation of thermal signature and slip flow dynamics in a lubricated vertical duct exposed to solar energy-induced heating. Int Commun Heat Mass Transf. 2024;152:107308.10.1016/j.icheatmasstransfer.2024.107308Search in Google Scholar

[27] Leng Y, Li S, Al Mesfer MK, Danish M, Ali K, Ahmad S, et al. A finite volume and machine learning based investigation of flow dynamics in a vertical duct heated by the sunlight. Int Commun Heat Mass Transf. 2024;153:107340.10.1016/j.icheatmasstransfer.2024.107340Search in Google Scholar

[28] Ali K, Ahmad S, Ahmad S, Ashraf M, Asif M. On the interaction between the external magnetic field and nanofluid inside a vertical square duct. AIP Adv. 2015;5:107120. 10.1063/1.4934484.Search in Google Scholar

Received: 2024-03-30

Revised: 2024-06-01

Accepted: 2024-07-17

Published Online: 2024-09-03

This work is licensed under the Creative Commons Attribution 4.0 International License.

Articles in the same Issue

https://doi.org/10.1515/phys-2024-0070

Keywords for this article

fully developed flow; obstructed vertical duct; constant pressure gradient; magnetohydrodynamics; constant heat flux

Creative Commons

BY 4.0