Thermal proficiency of magnetized and radiative cross-ternary hybrid nanofluid flow induced by a vertical cylinder

Wael Al-Kouz; Wahib Owhaib; Assad Ayub; Basma Souayeh; Montasir Hader; Raad Z. Homod; Taseer Muhammad; Anuar Ishak; Umair Khan

doi:10.1515/phys-2023-0197

Article Open Access

Thermal proficiency of magnetized and radiative cross-ternary hybrid nanofluid flow induced by a vertical cylinder

Wael Al-Kouz , Wahib Owhaib , Assad Ayub , Basma Souayeh , Montasir Hader , Raad Z. Homod , Taseer Muhammad , Anuar Ishak and Umair Khan

Published/Copyright: February 22, 2024

Published by

Become an author with De Gruyter Brill

Submit Manuscript Author Information Explore this Subject

From the journal Open Physics Volume 22 Issue 1

Abstract

The ternary hybrid nanofluid leads to a significant enhancement in thermal performance applications like heat transfer in automotive engines, solar thermal energy storage, aerospace, and electronic cooling. The present study investigates the thermal characteristics of a ternary hybrid magnetized and radiated cross nanofluid comprising Al₂O₃, TiO₂, and Ag nanoparticles in water subjected to combined convection flow around a vertical cylinder. Furthermore, innovative effects of the magnetic field, absorber surface of the cylinder, non-linear thermal radiations, and effective thermophysical characteristics of ternary nanofluid are taken, and a new model for heat transport is successfully achieved. The governing equations in the form of partial differential equations (PDEs) are obtained through Navier–Stokes and heat equations by applying current assumptions. The system of PDEs is converted into a set of ordinary differential equations (ODEs) via a similarity variable. The built-in code bvp4c in Matlab software further exercises the dimensionless ODE equations numerically. Adding multiple nanoparticles and the magnetic field effect enhances the heat transfer rate in the ternary hybrid cross nanofluid. The Weissenberg number reduces the velocity, the radiation parameter increases heat transport, and the increased volume friction of nanoparticles enhances thermal conductivity and rapid heat transport.

Keywords: ternary hybrid nanofluid; MHD; mixed convection flow; vertical cylinder; cross-fluid model

1 Introduction

Nanofluids are a promising class of heat transfer fluids that have gained significant attention recently due to their enhanced thermal properties. Among the various types of nanofluids, ternary hybrid nanofluids have emerged as a promising candidate due to their unique composition and superior thermal properties. In a recent study, ternary hybrid nanofluid comprises three different types of nanoparticles, namely, Al₂O₃, TiO₂, and Ag, dispersed in water. The study of ternary hybrid nanofluid and its thermal characteristics is significant for advancing the field of nanofluid technology and its potential applications. Many scholars [1–5] have worked on hybrid nanofluids and proved that bihybrid and trihybrid nanofluids enhance thermal performance and reduce energy consumption. The latest study regarding ternary hybrid nanofluid under the influence of thermal radiation and a nonuniform heat source (sink) was conducted by Pavithra et al. [6]. Ahmed et al. [7] investigated binary fluids and analysis related to heat transfer measurement and ultrasonic velocity. This study uses Al₂O₃–TiO₂–ZnO/DW ternary composite nanoparticles in a horizontal circular flow passage. Adnan et al. [8] discovered the thermal efficiency of a radiated tetra hybrid nanofluid associated with combined convection and magnetic fields attached to cylinder geometry.

Heat transfer over a cylindrical surface is an essential topic in thermal engineering. The transfer of heat from a cylindrical surface occurs due to the temperature difference between the surface and the surrounding fluid. The heat transfer coefficient, which measures heat transfer efficiency, is influenced by various parameters such as fluid properties, surface geometry, and flow conditions. Understanding heat transfer over a cylindrical surface is critical for designing and optimizing heat transfer systems in various industrial applications, such as cooling nuclear reactors, heat exchangers, and air conditioning systems. Furthermore, the study of heat transfer over cylindrical surfaces has led to the development of advanced heat transfer techniques, such as nanofluid-based heat transfer, which can significantly improve heat transfer efficiency in various industrial applications [9–15]. Souayeh et al. [16] discussed the role of copper and alumina in heat transfer in a hybrid nanofluid by using the Fourier sine transform. Ali et al. [17] analysed the heat transport analysis in a water-based cross-hybrid nanofluid with the attached effect of entropy generation. Arif et al. [18] proved that heat transfer can be enhanced by using differently shaped nanoparticles in water and making base fluid water as a ternary nanofluid. Gupta et al. [19–21] did work on heat transport incorporating different nanoparticles like GP-MoS₂/C₂H₆O₂-H₂O and (SWCNT-MWCNT/C₃H₈O₂) over a porous and permeable surface with different mathematical fluid models.

Magnetohydrodynamics (MHD) is an essential field of study in the context of nanofluids. Al₂O₃, TiO₂, and Ag nanofluids have been studied extensively under the influence of MHD due to their potential for various industrial applications. The presence of a magnetic field alters the behaviour of the nanofluid by inducing Lorentz forces that affect the fluid flow and heat transfer characteristics. The study of MHD in Al₂O₃, TiO₂, and Ag nanofluids is critical for developing efficient and sustainable heat transfer systems in various industrial applications. Most recent studies regarding MHD flow in hybrid nanofluid can be traced by refs [22–24] and found convenient advantages in heat transfer fluid. One of the primary advantages of MHD in heat transfer fluids is that it can significantly enhance the convective heat transfer coefficient. This is because the presence of a magnetic field can induce fluid motion and turbulence, increasing the heat transfer rate. Ishtiaq et al. [25] worked on scrutinizing MHD stagnation point flow in hybrid nanofluids. The use of MHD in stagnation point flow can provide several advantages. One of the primary advantages is that it can increase the heat transfer rate at the stagnation point. Kho et al. [26] discussed the MHD flow of a hybrid nanofluid associated with a permeable wedge with thermal radiation and viscous dissipation effect. Patel et al. [27] made their investigative study related to hybrid nanofluid and MHD flows with the effect of slip conditions and radiation with the geometry of stretching and shrinking sheets.

The cross-fluid model is an important concept in fluid mechanics and has gained significant attention in recent years. The cross-fluid model considers the interaction between two or more fluids, which can have different physical properties, such as density, viscosity, and thermal conductivity. Detailed investigations regarding cross-fluid models with various facts and geometries can be seen through [28–33]. Ali et al. [34] scrutinized the irreversibility process in cross-fluid, which passes through a stretchable vertical sheet. The cross-fluid flow contains a mixture of carboxymethyl cellulose and water-based hybrid nanofluid. Srinivas Reddy et al. [35] described the thermal analyses and entropy generation of cross-fluid flow through the geometry of an inclined microchannel. Khan et al. [36] investigated numerical analysis of the thermally radiative stagnation point flow of cross nanofluid due to shrinking surface.

The study of the thermal characteristics of nanofluids has gained significant attention in recent years due to their potential applications in various industrial and engineering fields. The investigation of the thermal behaviour of ternary hybrid magnetized and radiated cross nanofluid [(Al₂O₃–TiO₂–Ag)/water] with combined convection subjected to a vertical cylinder is of utmost importance as it provides insights into the heat transfer mechanism and the efficiency of such nanofluids in thermal applications.

This research investigates the combined effects of magnetization and radiation on the heat transfer characteristics of the nanofluid, which contains a mixture of four different nanoparticles. Furthermore, using a vertical cylinder as the study object is an innovative approach to understanding the complex behaviour of nanofluids under various thermal conditions.

2 Mathematical formulation of the flow problem

Ternary nanofluids are considered to research no transient heat transfer in stagnation point flow. The shape of a cylinder is used, and it is assumed that the surface of the cylinder acts as an absorber for both thermal radiation and magnetic fields. In addition, the flow is linear and uninterrupted by time. The nanoparticles in the base solution are evenly dispersed, with no slipping occurring between them. Figure 1 shows ternary and ternary nanofluids rising to a stagnation point inside a vertically permeable cylinder. Moreover, the x -axis is vertical. The approach was fine-tuned by including the impact of non-linear thermal radiation and magnetic fields. Near the surface of the cylinder T w and the free steam position T ∞ are where the temperatures are measured. Furthermore, let U w ( x ) and V w ( x ) be the free-stream and inward/outward velocities of the fluid, respectively.

Figure 1

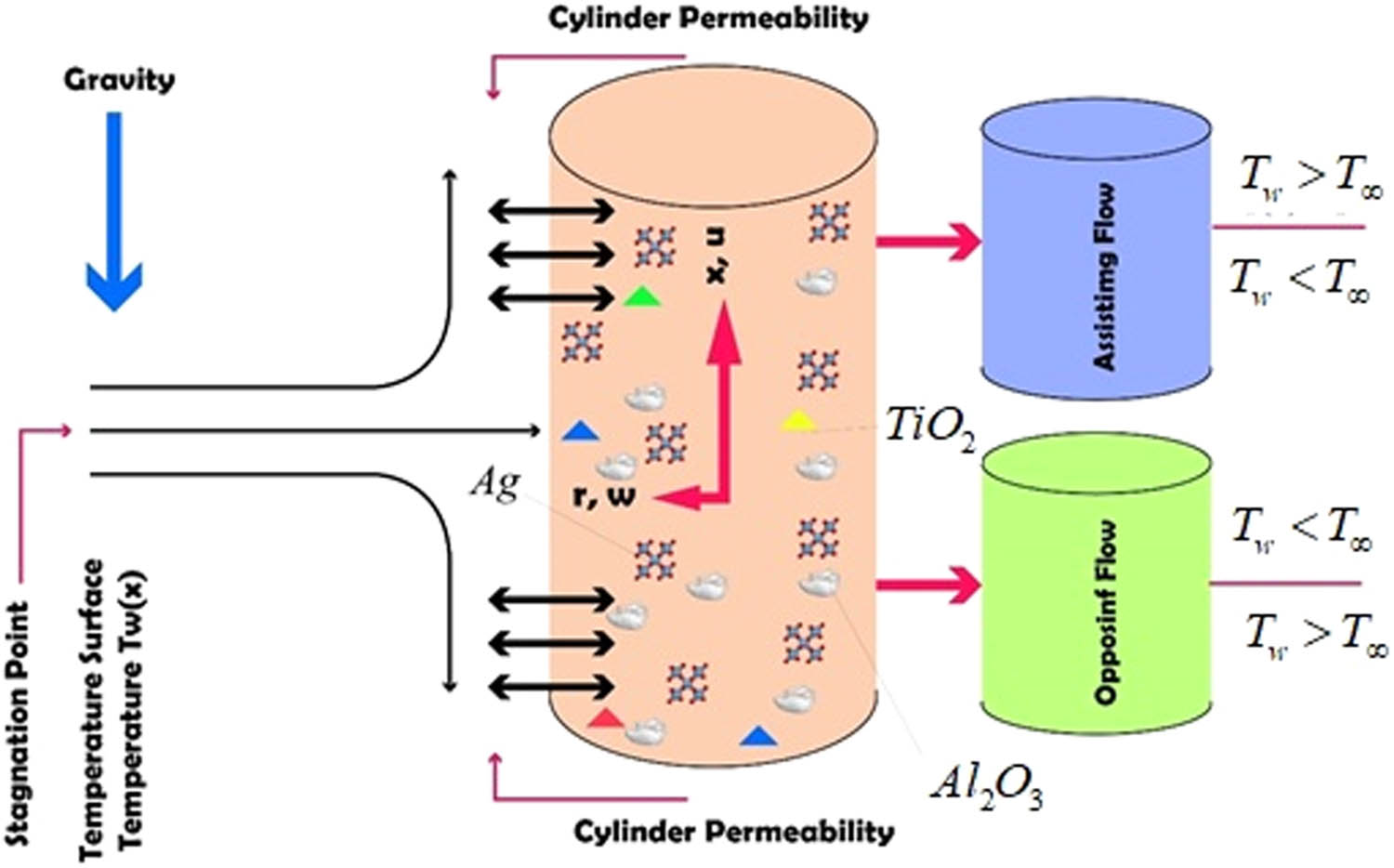
Flow configuration.

The governing equations for the assumed problem in cylindrical coordinates [37–40] are as follows:

(1) ∂ ( r u ) ∂ x + ∂ ( r w ) ∂ r = 0 ,

(2) w ∂ u ∂ r + u ∂ u ∂ x = U e d U e d x + μ ternary ρ ternary 1 r ∂ ∂ r ∂ u ∂ r 1 + Γ ∂ u ∂ r n − 1 + ( ρ β ) ternary ρ ternary g ( T − T ∞ ) − σ ternary B 2 ρ ternary ( u − U e ) ,

(3) ( ρ C p ) ternary w ∂ T ∂ r + u ∂ T ∂ x = k ternary 1 r ∂ ∂ r r ∂ T ∂ r + ∂ ∂ r 16 σ ⁎ ⁎ T ∞ 3 3 k ⁎ ∂ T ∂ r ,

with associated boundary conditions:

(4) u w T = 0 r = R V w r = R T w ( x ) r = R , u T = U w ( x ) r = ∞ T ∞ r = ∞ ,

(5) U w T w ( x ) = U 0 x l T ∞ + Δ T x l .

The following similarity transformations [41–43] are used to develop the alike expression:

(6) η = r 2 − R 2 2 R U 0 υ f l , u = x U 0 l F ′ ( η ) , w = R r υ f U 0 l F ( η ) ,

(7) β ( η ) = T − T m T ∞ − T m , Ψ ( η ) = R υ f U w F ( η ) .

In addition, Table 1 presents the thermophysical properties of the ternary hybrid nanofluid for the modification of the model, while the correlations of these ternary hybrid nanofluid models are given later in this section.

Table 1

Physical properties [44] of ternary hybrid nanofluid

Property	Water	Ag	TiO₂	Al₂O₃
ρ (kg/m³)	997.1	10,500	4,250	3,970
C p ( J / kg K )	4,179	235	690	765
k (W/m K)	0.613	429	8.953	40
σ ( Ω / m ) ‒ 1	0.05	62.1 × 10 6	2.6 × 10 6	3.5 × 10 7
β × 10 ‒ 5 (1/K)	21	1.89	0.90	0.85
Pr	6.2	—	—	—

Furthermore, the similarity variables are used in Eqs. (2) and (3) to form the following reduced form of ordinary differential equations (ODEs):

(8) μ ternary μ f ( 1 + 2 γ 1 η ) ( 1 + ( 1 − n ) ( We ( F ″ ) n ) ) F ‴ ρ ternary ρ f [ 1 + ( We F ″ ) n ] 2 γ 1 F ″ + F ′ F ″ − ( F ′ ) 2 + λ β + M σ ternary ρ ternary ( F ' − 1 ) = 0 ,

(9) k ternary k f + 4 3 R d ( ( 1 + 2 η γ 1 ) β ″ + 2 γ 1 β ′ ) + ( ρ C p ) ternary ( ρ C p ) f Pr ( F β ′ − F ′ β ) − ( 1 + 2 η γ 1 ) ( θ w − 1 ) + 2 γ 1 β ′ ( ( θ w − 1 ) + 1 ) = 0 .

Furthermore, the reduced boundary conditions are as follows:

(10) F ( 0 ) F ′ ( 0 ) β ( 0 ) = α 0 1 , F ′ ( ∞ ) β ( ∞ ) = 1 0 .

The correlations for the ternary hybrid nanofluids like viscosity, density, thermal conductivity, electrical conductivity, and heat capacitance are described in Eqs. (8)–(15), see [6,8]. Thus, the correlations are as follows:

(11) μ ternary = μ f [ ( 1 − ϑ 1 ) 2.5 ( 1 − ϑ 2 ) 2.5 ( 1 − ϑ 3 ) 2.5 ] − 1 ,

(12) ρ ternary = ( 1 − ϑ 3 ) ( 1 − ϑ 1 ) 1 − ϑ 1 + ϑ 1 ρ s 1 ρ f + ϑ 2 ρ s 2 ρ f + ϑ 3 ρ s 3 ρ f ,

(13) ( ρ C p ) ternary = ( 1 − ϑ 3 ) ( 1 − ϑ 1 ) 1 − ϑ 1 + ϑ 1 ( ρ C p ) s 1 ρ f + ϑ 2 ( ρ C p ) s 2 ρ f + ϑ 3 ( ρ C p ) s 3 ρ f ,

(14) ( ρ β ) ternary = ( 1 − ϑ 3 ) ( 1 − ϑ 1 ) 1 − ϑ 1 + ϑ 1 ( ρ β ) s 1 ρ f + ϑ 2 ( ρ β ) s 2 ρ f + ϑ 3 ( ρ β ) s 3 ρ f ,

(15) k ternary k hybrid = ( k s 3 + 2 k hybrid − 2 ϑ 3 ( k hybrid − k s 3 ) ) ( k s 3 + 2 k hybrid + ϑ 3 ( k hybrid − k s 3 ) ) k hybrid k nano = ( k s 2 + 2 k nano − 2 ϑ 2 ( k nano − k s 2 ) ) ( k s 2 + 2 k nano + ϑ 2 ( k nano − k s 2 ) ) k nano k f = ( k s 1 + 2 k f − 2 ϑ 1 ( k f − k s 1 ) ) ( k s 1 + 2 k f + ϑ 1 ( k f − k s 1 ) ) ,

and

(16) σ ternary σ hybrid = ( σ s 3 + 2 σ hybrid − 2 ϑ 3 ( σ hybrid − σ s 3 ) ) ( σ s 3 + 2 σ hybrid + ϑ 3 ( σ hybrid − σ s 3 ) ) σ hybrid σ nano = ( σ s 2 + 2 σ nano − 2 ϑ 2 ( σ nano − σ s 2 ) ) ( σ s 2 + 2 σ nano + ϑ 2 ( σ nano − σ s 2 ) ) σ nano σ f = ( σ s 1 + 2 σ f − 2 ϑ 1 ( σ f − σ s 1 ) ) ( σ s 1 + 2 σ f + ϑ 1 ( σ f − σ s 1 ) ) .

Furthermore,

(17) k ternary k f = ( k s 3 + 2 k hybrid − 2 ϑ 3 ( k hybrid − k s 3 ) ) ( k s 3 + 2 k hybrid + ϑ 3 ( k hybrid − k s 3 ) ) ( k s 2 + 2 k nano − 2 ϑ 2 ( k nano − k s 2 ) ) ( k s 2 + 2 k nano + ϑ 2 ( k nano − k s 2 ) ) × ( k s 1 + 2 k f − 2 ϑ 1 ( k f − k s 1 ) ) ( k s 1 + 2 k f + ϑ 1 ( k f − k s 1 ) ) ,

and

(18) σ ternary σ f = ( σ s 3 + 2 σ hybrid − 2 ϑ 3 ( σ hybrid − σ s 3 ) ) ( σ s 3 + 2 σ hybrid + ϑ 3 ( σ hybrid − σ s 3 ) ) ( σ s 2 + 2 σ nano − 2 ϑ 2 ( σ nano − σ s 2 ) ) ( σ s 2 + 2 σ nano + ϑ 2 ( σ nano − σ s 2 ) ) × ( σ s 1 + 2 σ f − 2 ϑ 1 ( σ f − σ s 1 ) ) ( σ s 1 + 2 σ f + ϑ 1 ( σ f − σ s 1 ) ) .

In addition, the involved parameters are defined as curvature impact γ 1 = v f l R 2 U ∞ and magnetic parameter M = σ f B o 2 U ∞ l ρ f , and We = Γ U 0 l ( Re x ) 1 / 2 and Re x = x U w υ f are Weissenberg number and local Reynold number, respectively. Also, the temperature ratio parameter θ w = T w T ∞ and the thermal radiation parameter R d = 16 σ ⁎ T ∞ 3 3 k f k ⁎ .

The engineering physical quantities of interest are the skin friction coefficient and the rate of heat transfer. For model specification, the engineering quantities [45–47] are described as follows:

(19) C F Nu x = 2 τ w ρ f U w 2 − x q w k f ( T w − T ∞ ) , τ w q w = μ ternary ∂ u ∂ r r = R k ternary 1 + 4 3 R d ∂ T ∂ r r = R .

Utilizing the similarity transformations in Eq. (19) yields the following form:

(20) Re x 1 / 2 C F = 1 [ ( 1 − ϑ 1 ) 2.5 ( 1 − ϑ 2 ) 2.5 ( 1 − ϑ 3 ) 2.5 ] × F ″ ( η ) η = 0 [ 1 + ( We F ″ ( η ) ) n ] η = 0 ,

(21) Re x − 1 / 2 Nu x = − k ternary k f + R d ( ( θ w − 1 ) + 1 ) β ′ ( η ) η = 0 .

3 Numerical procedure of the solution

There are several numerical methods [48–53] to fetch the numerical solution of the set of ODEs, like Keller box, spectral relaxation technique, and finite difference method. In this study, Runge Kutta fourth-order method [54,55] is utilized, which is based on bvp4c [56–60]. Furthermore, the bvp4c command was also used and compared to the result. The non-linearities of the ternary nanofluid model’s velocity and energy model equations are initially reduced to a set of coupled ordinary differential equations with only first-order non-linear terms. Adopt a workable transformation for this stage. The flowchart below describes the entire RK technique implementation process (Figure 2a and b).

Figure 2

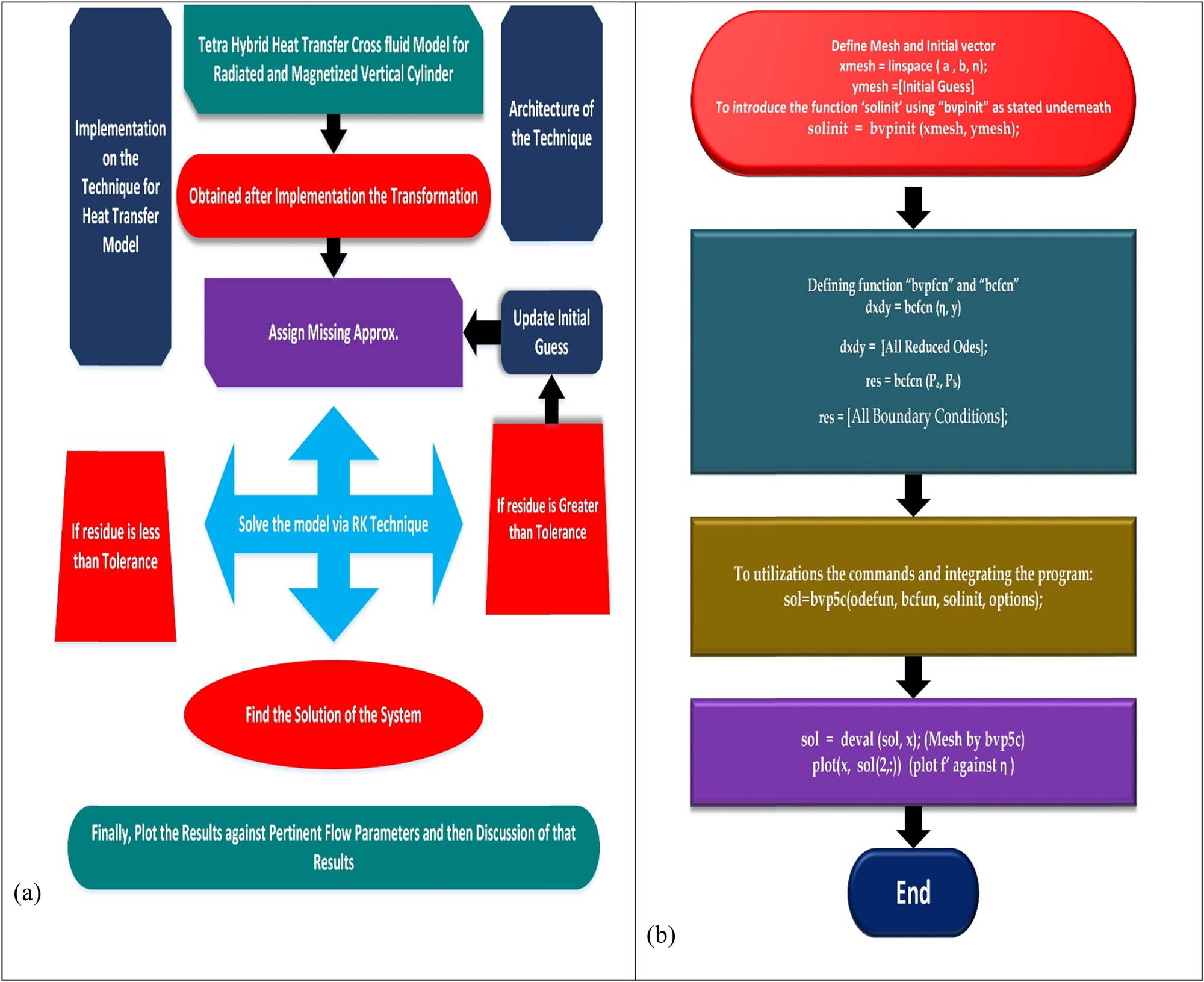
Flow chart of numerical scheme.

3.1 Validation of the scheme coefficient and the rate of heat transfer

This section of the work represents the validity of the code with variations in different values of the Prandtl number and found smooth agreement. Table 2 represents numerical agreement keeping fixed parameters like γ 1 = We = ϑ 1 = ϑ 2 = ϑ 3 = λ = R d = M = ρ s 1 = ρ s2 = ρ s3 = 0 .

Table 2

Numerical results of − β ' ( 0 ) old literature and the present study

Parameter	‒ β ' ( 0 )
Pr	Ref [61]	Present study
0.07	0.65526	0.65521272
0.2	0.164047	0.16404064
0.7	0.418299	0.41827666
2	0.826827	0.82687898
7	1.80433	1.80434569
20	3.25603	3.25602170
70	6.36662	6.36664989

4 Analysis of the results

This study focused on the investigation into the thermal proficiency of the magnetized and radiated ternary hybrid cross nanofluid, incorporating aluminium oxide (Al₂O₃), titanium dioxide (TiO₂), and silver (Ag) nanoparticles when subjected to a vertical cylinder. The influence of magnetic properties has a significant impact on its thermal performance. Incorporating Al₂O₃, TiO₂, and Ag nanoparticles has proven effective in enhancing thermal conductivity. The radiation exposure has potentially influenced the nanofluids’ thermal stability and heat absorption capacity. This whole interaction of several parameters with velocity and temperature of radiated ternary hybrid cross nanofluid with the vertical cylinder has been shown through promising results.

4.1 Impacts of a sundry parameter on velocity profiles

This section aims to research the kinetic properties of [(Al₂O₃–TiO₂–Ag)/water] at varying concentrations. Figure 3a shows the fluid’s movement in relation to the curvature number ( γ 1 ). Figure 3a shows that fluid mobility has increased over time. Physically, the larger flowing surface created by the cylinder’s greater curvature causes the fluid’s velocity to increase. At the surface of the cylinder, where η = 0, the speed is zero, and the speed of the ternary nanofluid layer next to the cylinder is the same as the speed of the surface of the cylinder when no-slip effects are considered. Moreover, the velocity changes are significantly faster at α = α 1 = 0.2 compared to α = α 1 = 0.8 , which is indicative of higher surface permeability. The real velocity changes due to coupled convection effects ( λ ) are shown in Figure 3b. Natural convection and forced convection are both components of mixed and combined convection. The physical phenomena of forced and natural convection are characterized by the Grashof and Reynolds numbers, respectively; the parameter is the quotient of these two numbers. As altitude increases, the buoyancy forces grow stronger, slowing the rate of acceleration. These physical repercussions for absorber cylinder surfaces with α = α 1 = 0.2 and α = α 1 = 0.8 are depicted in Figure 3b.

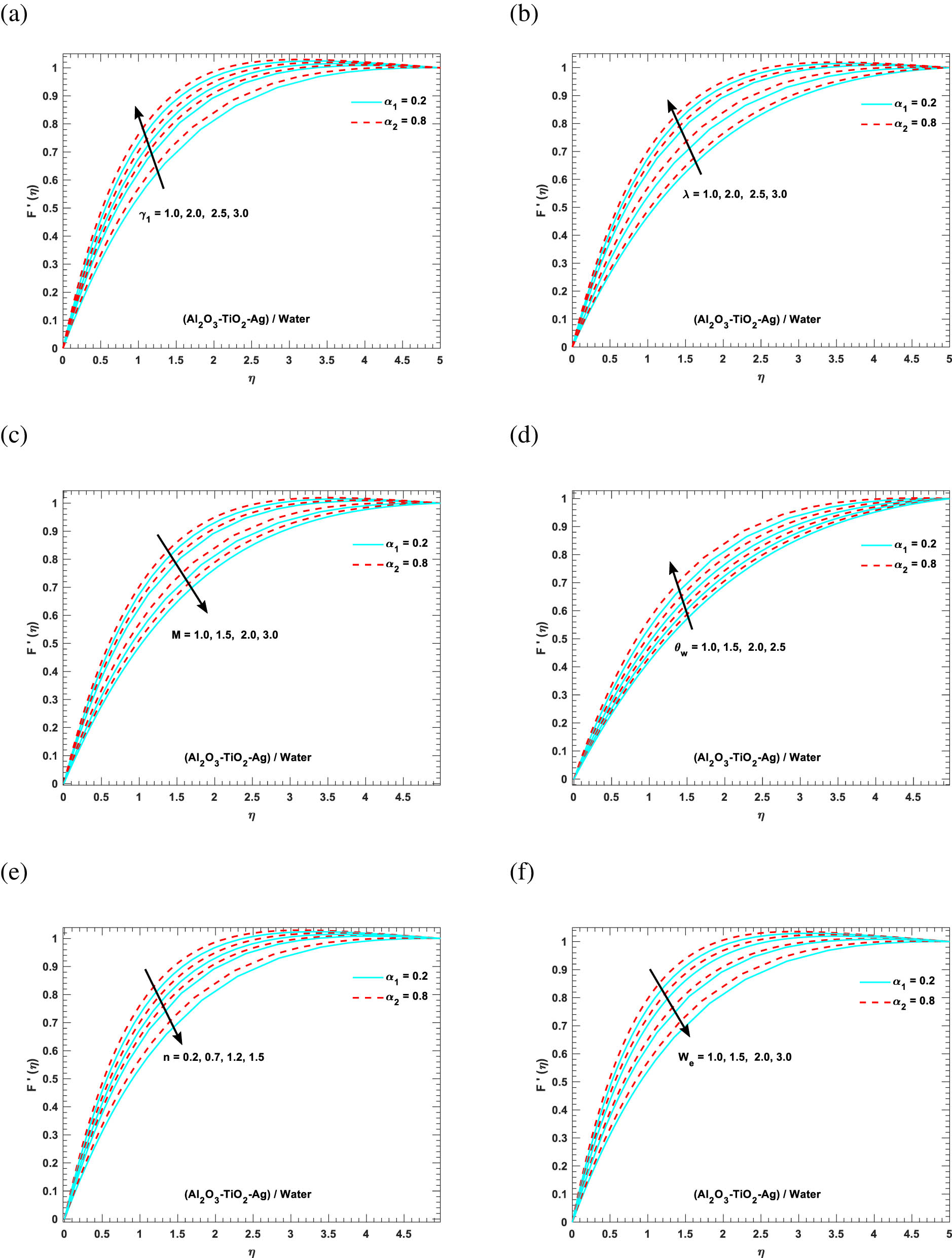
$Figure 3 The velocity F′ against the various values of parameters (a) γ 1 {\gamma }_{1} , (b) λ \lambda , (c) M, (d) θ w {\theta }_{\text{w}} , (e) n, and (f) We.$

Figure 3

The velocity F′ against the various values of parameters (a) γ 1 , (b) λ , (c) M, (d) θ w , (e) n, and (f) We.

In addition, many factors, including physical characteristics, fluid properties, and the proper shape, influence fluid velocity. Figure 3c shows the results of a velocity simulation subject to varying magnetic field influences. When the resistive Lorentz forces rise in a larger magnetic field and have a dissipative property, this resists the motion of the fluid particles over the surface of the cylinder. Figure 3d examples show similar, nearly non-existent fluid motion. To do this, Figure 3e investigates the impact of the Weissenberg number We on F′(η). We may deduce from the diagram that increasing We reduces the fluid’s velocity across the board. The parameter establishes the link between the elastic forces and the viscous forces. Owing to the higher impacts of the Weissenberg number, the kind of elastic forces are more powerful as compare to viscous forces.

Figure 3f shows how the power law index n alters the F′(η) function. The degree to which a liquid is dense is dependent on the value of n. If n is greater than one, water’s viscosity increases; if it is less than one, water splashes out; and if it is exactly one, the water’s viscosity is Newtonian. Since n is increasing, so is the water’s viscosity, to a far greater extent. As this occurs on a physical level, more resistance is produced, and the resistive forces eventually take command from the imaginary ones. Figure 3f demonstrates that the boundary layer’s relative thickness increases when the nanoparticles approach the vertical wall earlier for dihybrids than for ternary hybrids. Figure 3f indicates that as n and the mass of the ternary hybrid nanoparticles increase, fluid density increases and F′(η) drops.

4.2 Impacts of a sundry parameter on temperature profiles

Figure 4a–f provides a comparison of the effects of the parameters α = α 1 , γ 1 , θ w , R d , λ, and M on the heat conduction in binary and ternary hybrid nanofluids. The temperature behaviour for a range of α = α 1 values is shown in Figure 4a. The provided results show that the absorber surface heats up as expected due to the passage of fluid particles filling the surface gaps. In addition, the thermal enhancement properties of ternary hybrid nanofluid [(Al₂O₃–TiO₂–Ag)/water] were discovered. Ternary hybrid nanofluid was shown to be superior to hybrid nanofluid in its ability to regulate the thickness of the thermal boundary layer. Figure 4b–d similarly depicts the temperature under increasing curvature γ 1 , θ w , and R d . In all three instances, ternary hybrid nanofluid was found to insert non-linear thermal radiation and increase heat transmission.

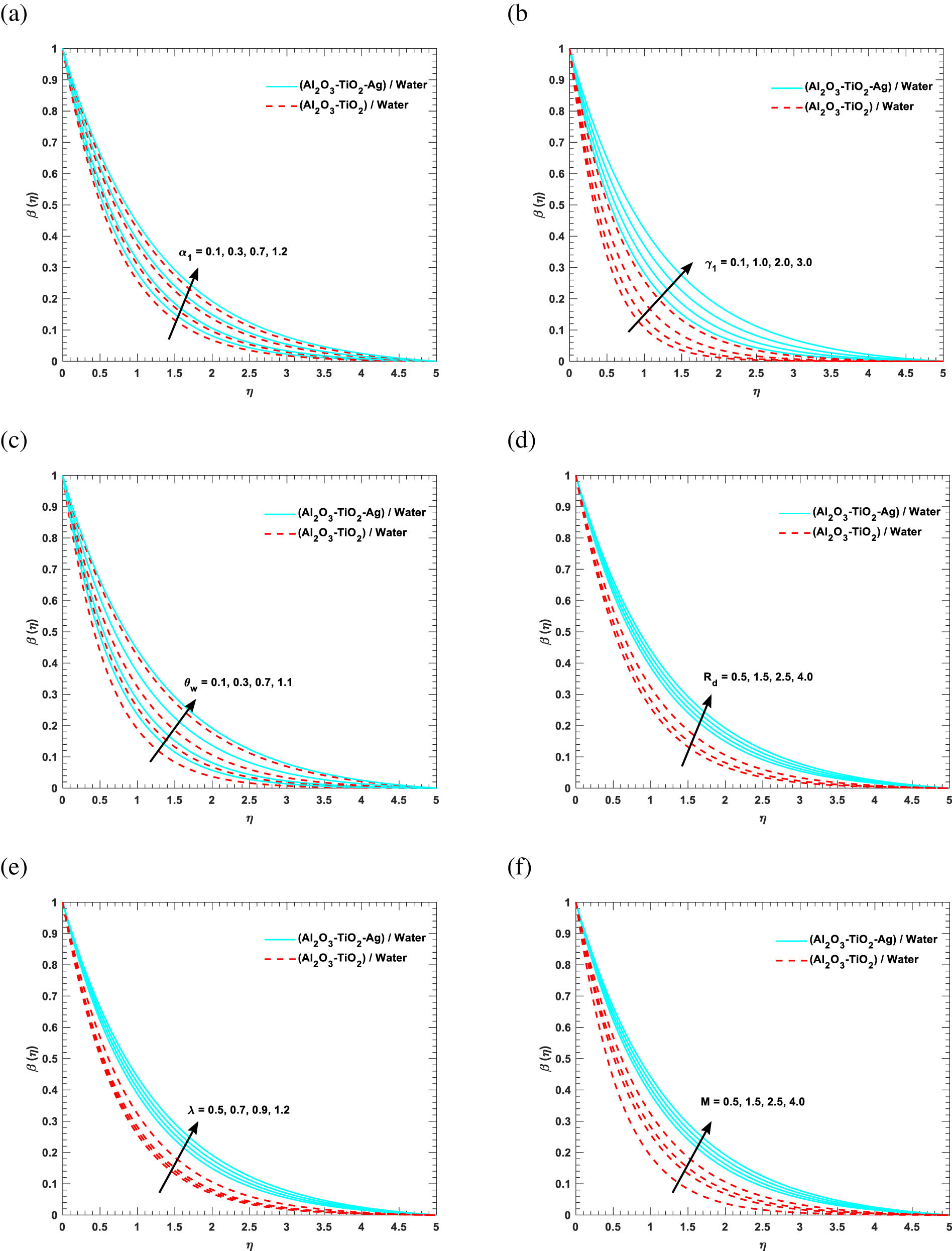
$Figure 4 The temperature β ( η ) \beta (\eta ) against the various values of parameters (a) α 1 {\alpha }_{1} , (b) γ 1 {\gamma }_{1} , (c) θ w {\theta }_{\text{w}} , (d) R d {R}_{\text{d}} (e) λ, and (f) M.$

Figure 4

The temperature β ( η ) against the various values of parameters (a) α 1 , (b) γ 1 , (c) θ w , (d) R d (e) λ, and (f) M.

Mixed convection is a form of heat conduction in which both spontaneous and forced convection contribute to the process. Figure 4e and f displays the results of our investigation into the temperature of ternary hybrid nanofluids and hybrid nanofluids under the most stringent of physical conditions, λ and M. It is proved that as λ and M are increased, so is the temperature of the particles in the fluid. Physically, the fluid velocity is increased by the predominance of buoyant forces and the resistance to motion introduced by the Lorentz forces of a coupled convection and magnetic field. These factors allow for fluid motion to be accepted and particle collisions to occur at high rates, both of which contribute to the phenomenon of heat transmission.

4.3 Impacts of a sundry parameter on gradients (shear stress and rate of heat transfer)

Figures 5–8 show the skin friction and Nusselt number trends for hybrid [(Al₂O₃–TiO₂)/water] and ternary hybrid [(Al₂O₃–TiO₂–Ag)/water] nanofluids instead of the magnetic field parameter M, the radiation parameter R d , the convection parameter λ, and the curvature parameter γ 1 . Figures 5–8 show that as the values of skin friction and Nusselt number for ternary hybrid nanofluids grow, they are more extreme than those for hybrid nanofluids. The physical properties of ternary hybrid nanofluid [(Al₂O₃–TiO₂–Ag)/water] are altered by the presence of ternary nanoparticles, increasing the viscosity factor and favouring skin friction across the absorber surface. In addition, ternary hybrid nanofluid has the highest local heat transmission at the surface. Table 3 also provides the quantitative numerical data of these gradients for a diverse value of several physical parameters.

Figure 5

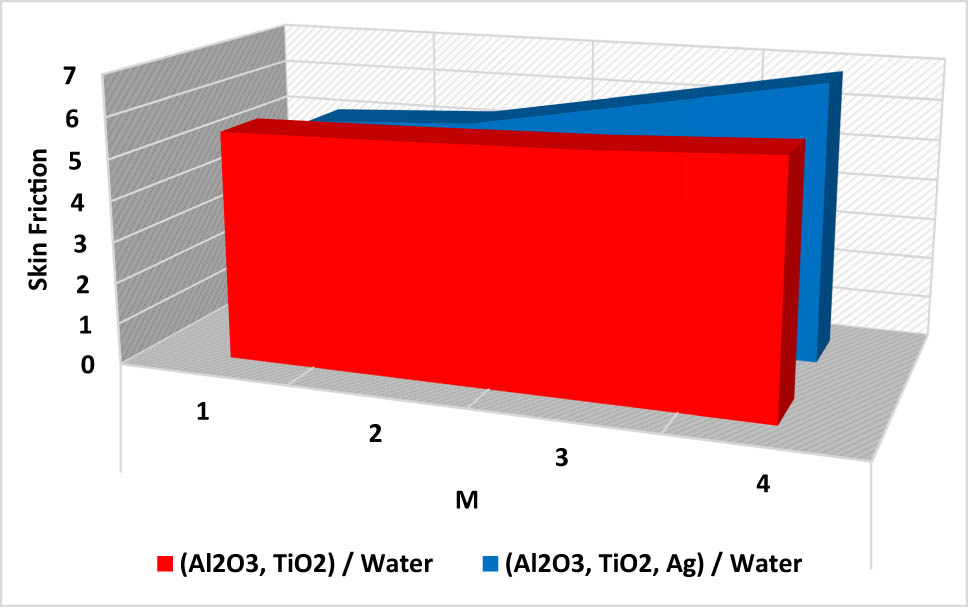
M vs the skin friction coefficient.

$Figure 6 R d {R}_{\text{d}} vs the skin friction coefficient.$

Figure 6

R d vs the skin friction coefficient.

Figure 7

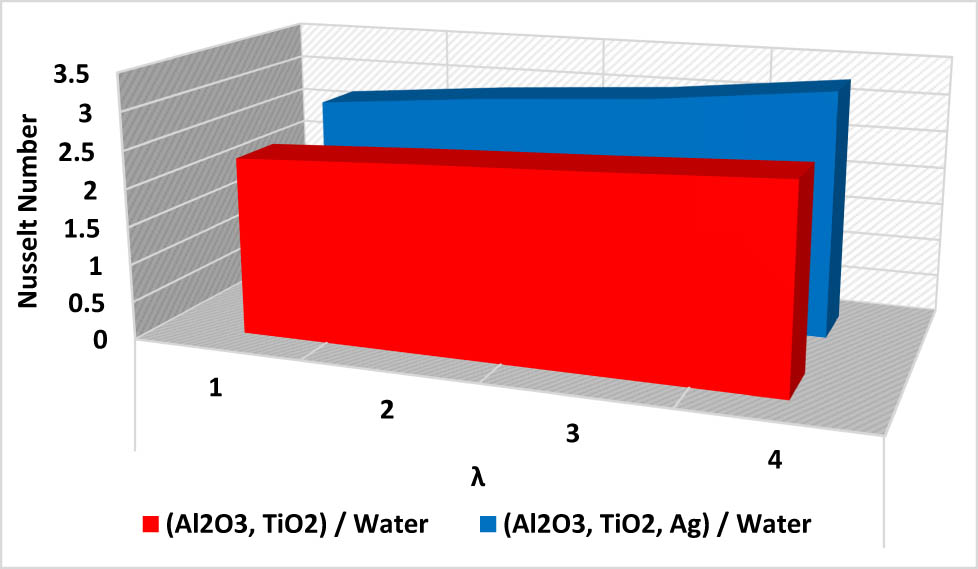
Effect of λ on the rate of heat delivery.

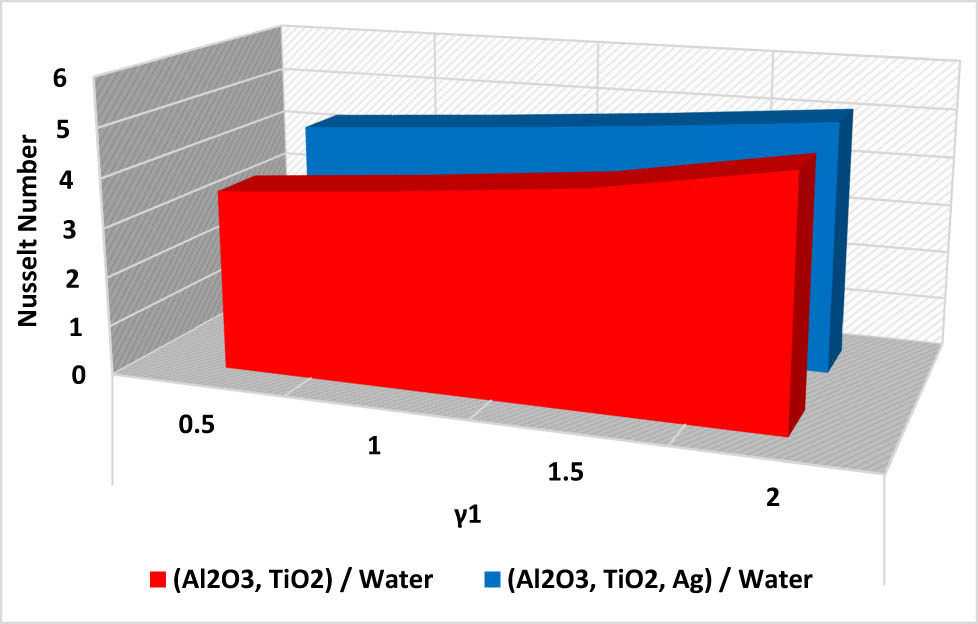
$Figure 8 Effect of γ 1 {\gamma }_{1} on the rate of heat delivery.$

Figure 8

Effect of γ 1 on the rate of heat delivery.

Table 3

Numerical outcomes of the gradients for several physical parameters

Physical quantity	Parameter	Value	(Al₂O₃, TiO₂)/Water	(Al₂O₃, TiO₂, Ag)/Water
Nusselt number	Λ	1.0	2.3476	2.6545
		2.0	2.4567	2.8567
		3.0	2.5467	3.0056
		4.0	2.6519	3.2529
	γ₁	0.5	3.6518	4.2376
		1.0	3.9567	4.4867
		1.5	4.3154	4.7692
		2.0	2.9478	5.0976
Skin friction	M	1.0	5.5643	5.0123
		2.0	5.6549	5.2398
		3.0	5.7754	6.0076
		4.0	5.9867	6.7865
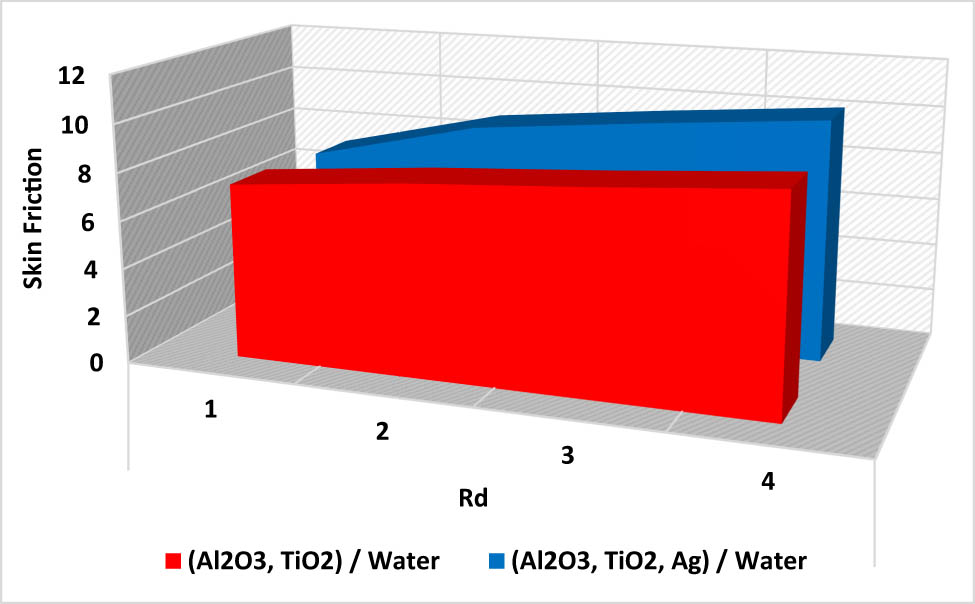
	R _d	1.0	7.3465	7.0967
		2.0	7.9976	8.7965
		3.0	8.4589	9.4987
		4.0	9.0035	10.1269

5 Conclusion

The study showed that increasing nanoparticle volume fraction (up to a certain limit) and magnetic field strength can improve the heat transfer rate. The combined convection effect was also significant in enhancing the heat transfer rate. In addition, using nanofluids can help improve the efficiency of heat exchangers and reduce energy consumption. A pointwise description of the outcome is given as follows:

Adding multiple nanoparticles and magnetic fields can enhance the heat transfer rate in the case of ternary hybrid nanofluids.
The Weissenberg number reduces the velocity of the ternary hybrid nanofluid due to the constant time relaxation.
The thermal enhancement over a vertically oriented cylinder is seen for the numerically greater value of the thermal radiation parameter, and it is also observed that the rate of heat transport is dominant in ternary hybrid nanofluid compared to binary hybrid nanofluid.
Thermal conductivity composed of ternary hybrid nanofluid plays a vital role in low heat transfer efficiency and thermal improvement.
Large cylindrical curvature and mixed convection effect reduce the velocity of ternary hybrid nanofluid.
Ternary hybrid nanofluid is strongly suggested for industrial applications requiring a huge amount of heat transfer.

6 Future direction

Future research directions in the field of ternary hybrid nanofluids with different facts could include investigating the effects of different types and concentrations of nanoparticles on heat transfer characteristics. It could be beneficial to study the behaviour of ternary hybrid nanofluids in different geometries and boundary conditions, as well as under different magnetic field strengths and radiation levels. In addition, the impact of other external factors, such as pressure and flow rate on heat transfer rates could also be explored. Moreover, future research could focus on developing models that can accurately predict the heat transfer performance of ternary hybrid nanofluids, which could be valuable in optimizing their use in practical applications.

umair.khan@lau.edu.lb

Acknowledgments

This work has been funded by the Universiti Kebangsaan Malaysia project number “DIP-2023-005.” In addition, the authors extend their appreciation to the Deanship of Scientific Research at King Khalid University, Abha, Saudi Arabia for funding this work through Small Groups Project under grant number RGP.1/370/44.

Funding information: This work has been funded by the Universiti Kebangsaan Malaysia project number “DIP-2023-005.” In addition, the authors extend their appreciation to the Deanship of Scientific Research at King Khalid University, Abha, Saudi Arabia for funding this work through Small Groups Project under grant number RGP.1/370/44.
Author contributions: W.Al-K., W.O., and A.A.: conceptualization, methodology, software, formal analysis, validation, and writing – original draft. M.H.: writing – original draft, data curation, investigation, visualization, and validation. B.S.: conceptualization, writing – review and editing, supervision, and resources. A.I., U.K., and T.M.: validation, writing review and editing, software, providing significant feedback, and assisting in revising the manuscript. Furthermore, they have also supported revising the manuscript critically for important intellectual content. All authors have accepted responsibility for the entire content of this manuscript and approved its submission.
Conflict of interest: The authors state no conflict of interest.
Data availability statement: The datasets used and/or analysed during the current study are available from the corresponding author on reasonable request.

References

[1] Rashidi MM, Sadri M, Sheremet MA. Numerical simulation of hybrid nanofluid mixed convection in a lid-driven square cavity with magnetic field using high-order compact scheme. Nanomaterials. 2021 Aug;11(9):2250.10.3390/nano11092250Search in Google Scholar PubMed PubMed Central

[2] Shah Z, Saeed A, Khan I, M, Selim M, Ikramullah, Kumam P. Numerical modeling on hybrid nanofluid (Fe3O4+ MWCNT/H2O) migration considering MHD effect over a porous cylinder. PLoS One. 2021 Jul;16(7):0251744.10.1371/journal.pone.0251744Search in Google Scholar PubMed PubMed Central

[3] Tian MW, Rostami S, Aghakhani S, Goldanlou AS, Qi C. A techno-economic investigation of 2D and 3D configurations of fins and their effects on heat sink efficiency of MHD hybrid nanofluid with slip and non-slip flow. Int J Mech Sci. 2021 Jan;189:105975.10.1016/j.ijmecsci.2020.105975Search in Google Scholar

[4] Abbas N, Nadeem S, Saleem A, Malik MY, Issakhov A, Alharbi FM. Models base study of inclined MHD of hybrid nanofluid flow over nonlinear stretching cylinder. Chin J Phys. 2021 Feb;69:109–17.10.1016/j.cjph.2020.11.019Search in Google Scholar

[5] Aziz A, Jamshed W, Aziz T, Bahaidarah HM, Ur Rehman K. Entropy analysis of Powell–Eyring hybrid nanofluid including effect of linear thermal radiation and viscous dissipation. J Therm Anal Calorim. 2021 Jan;143:1331–43.10.1007/s10973-020-10210-2Search in Google Scholar

[6] Pavithra KM, Srilatha P, Hanumagowda BN, Varma SV, Verma A, Alkarni S, et al. A free convective two-phase flow of optically thick radiative ternary hybrid nanofluid in an inclined symmetrical channel through a porous medium. Symmetry. 2023 Aug;15(8):1615.10.3390/sym15081615Search in Google Scholar

[7] Ahmed W, Kazi SN, Chowdhury ZZ, Johan MR, Soudagar ME, Mujtaba MA, et al. Ultrasonic assisted new Al2O3@ TiO2-ZnO/DW ternary composites nanofluids for enhanced energy transportation in a closed horizontal circular flow passage. Int Commun Heat Mass Transf. 2021 Jan;120:105018.10.1016/j.icheatmasstransfer.2020.105018Search in Google Scholar

[8] Adnan Abbas W, Bani-Fwaz ZM, Kenneth Asogwa K. Thermal efficiency of radiated tetra-hybrid nanofluid [(Al2O3-CuO-TiO2-Ag)/water] tetra under permeability effects over vertically aligned cylinder subject to magnetic field and combined convection. Sci Prog. 2023;106(1):00368504221149797.10.1177/00368504221149797Search in Google Scholar PubMed PubMed Central

[9] Singh SP, Upreti H, Kumar M. Flow and heat transfer assessment in magnetized Darcy-Forchheimer flow of Casson hybrid nanofluid through cone, wedge, and plate. BioNanoScience. 2023 Dec;1–4.10.1007/s12668-023-01253-4Search in Google Scholar

[10] Darvesh A, Altamirano GC, Salas SAH, Sánchez Chero M, Carrión Barco G, Bringas Salvador JL, et al. Infinite shear rate viscosity model of cross fluid flow containing nanoparticles and motile gyrotactic microorganisms over 3-D cylinder. J Nanofluids. 2023 May;12(4):930–41.10.1166/jon.2023.1968Search in Google Scholar

[11] Upreti H, Pandey AK, Gupta T, Upadhyay S. Exploring the nanoparticle’s shape effect on boundary layer flow of hybrid nanofluid over a thin needle with quadratic Boussinesq approximation: Legendre wavelet approach. J Therm Anal Calorim. 2023 Nov;148(22):12669–86.10.1007/s10973-023-12502-9Search in Google Scholar

[12] Wahab HA, Shah SZ, Ayub A, Sabir Z, Sadat R, Ali MR. Heterogeneous/homogeneous and inclined magnetic aspect of infinite shear rate viscosity model of Carreau fluid with nanoscale heat transport. Arab J Chem. 2023 May;16(5):104682.10.1016/j.arabjc.2023.104682Search in Google Scholar

[13] Khan U, Zaib A, Ishak A. Non-similarity solutions of radiative stagnation point flow of a hybrid nanofluid through a yawed cylinder with mixed convection. Alex Eng J. 2021 Dec;60(6):5297–309.10.1016/j.aej.2021.04.057Search in Google Scholar

[14] Waini I, Khan U, Zaib A, Ishak A, Pop I. Inspection of TiO2-CoFe2O4 nanoparticles on MHD flow toward a shrinking cylinder with radiative heat transfer. J Mol Liq. 2022 Sep;361:119615.10.1016/j.molliq.2022.119615Search in Google Scholar

[15] Jayavel P, Upreti H, Tripathi D, Pandey AK. Irreversibility and heat transfer analysis in MHD Darcy-Forchheimer flow of Casson hybrid nanofluid flow through cone and wedge. Numer Heat Transfer Part A: Appl. 2023 Sep;1–27.10.1080/10407782.2023.2260948Search in Google Scholar

[16] Souayeh B, Abro KA, Siyal A, Hdhiri N, Hammami F, Al-Shaeli M, et al. Role of copper and alumina for heat transfer in hybrid nanofluid by using Fourier sine transform. Sci Rep. 2022 Jul;12(1):11307.10.1038/s41598-022-14936-xSearch in Google Scholar PubMed PubMed Central

[17] Ali F, Loganathan K, Eswaramoorthi S, Prabu K, Zaib A, Chaudhary DK. Heat transfer analysis on carboxymethyl cellulose water-based cross hybrid nanofluid flow with entropy generation. J Nanomaterials. 2022 Jun;2022:2022.10.1155/2022/5252918Search in Google Scholar

[18] Arif M, Kumam P, Kumam W, Mostafa Z. Heat transfer analysis of radiator using different shaped nanoparticles water-based ternary hybrid nanofluid with applications: A fractional model. Case Stud Therm Eng. 2022 Mar;31:101837.10.1016/j.csite.2022.101837Search in Google Scholar

[19] Gupta T, Pandey AK, Kumar M. Numerical study for temperature-dependent viscosity based unsteady flow of GP-MoS2/C2H6O2-H2O over a porous stretching sheet. Numer Heat Transfer Part A: Appl. 2023 Mar;1–22.10.1080/10407782.2023.2195689Search in Google Scholar

[20] Gupta T, Kumar Pandey A, Kumar M. Effect of Thompson and Troian slip on CNT-Fe3O4/kerosene oil hybrid nanofluid flow over an exponential stretching sheet with Reynolds viscosity model. Mod Phys Lett B. 2024 Jan;38(2):2350209.10.1142/S0217984923502093Search in Google Scholar

[21] Gupta T, Kumar M, Yaseen M, Rawat SK. Heat transfer of MHD flow of hybrid nanofluid (SWCNT-MWCNT/C3H8O2) over a permeable surface with Cattaneo–Christov model. Numer Heat Transfer Part B: Fundam. 2023 Nov;1–6.10.1080/10407790.2023.2286250Search in Google Scholar

[22] Krishna MV, Chamkha AJ. Hall and ion slip impacts on unsteady MHD convective flow of Ag-TiO2/WEG hybrid nanofluid in a rotating frame. Curr Nanosci. 2023 Jan;19(1):15–32.10.2174/1573413717666211018113823Search in Google Scholar

[23] Ramzan M, Ali F, Akkurt N, Saeed A, Kumam P, Galal AM. Computational assessment of Carreau ternary hybrid nanofluid influenced by MHD flow for entropy generation. J Magn Magn Mater. 2023 Feb;567:170353.10.1016/j.jmmm.2023.170353Search in Google Scholar

[24] Farooq U, Waqas H, Aldhabani MS, Fatima N, Alhushaybari A, Ali MR, et al. Modeling and computational framework of radiative hybrid nanofluid configured by a stretching surface subject to entropy generation: Using Keller box scheme. Arab J Chem. 2023 Apr;16(4):104628.10.1016/j.arabjc.2023.104628Search in Google Scholar

[25] Ishtiaq B, Zidan AM, Nadeem S, Alaoui MK. Scrutinization of MHD stagnation point flow in hybrid nanofluid based on the extended version of Yamada-Ota and Xue models. Ain Shams Eng J. 2023 Apr;14(3):101905.10.1016/j.asej.2022.101905Search in Google Scholar

[26] Kho YB, Jusoh R, Salleh MZ, Ariff MH, Zainuddin N. Magnetohydrodynamics flow of Ag-TiO2 hybrid nanofluid over a permeable wedge with thermal radiation and viscous dissipation. J Magn Magn Mater. 2023 Jan;565:170284.10.1016/j.jmmm.2022.170284Search in Google Scholar

[27] Patel VK, Pandya JU, Patel MR. Testing the influence of TiO2− Ag/water on hybrid nanofluid MHD flow with effect of radiation and slip conditions over exponentially stretching & shrinking sheets. J Magn Magn Mater. 2023 Apr;572:170591.10.1016/j.jmmm.2023.170591Search in Google Scholar

[28] Ayub A, Shah SZ, Sabir Z, Rao NS, Sadat R, Ali MR. Spectral relaxation approach and velocity slip stagnation point flow of inclined magnetized cross-nanofluid with a quadratic multiple regression model. Waves Random Complex Media. 2022 Mar;1–25.10.1080/17455030.2022.2049923Search in Google Scholar

[29] Wahab HA, Hussain Shah SZ, Ayub A, Sabir Z, Bilal M, Altamirano GC. Multiple characteristics of three-dimensional radiative cross fluid with velocity slip and inclined magnetic field over a stretching sheet. Heat Transf. 2021 Jun;50(4):3325–41.10.1002/htj.22030Search in Google Scholar

[30] Ayub A, Sabir Z, Altamirano GC, Sadat R, Ali MR. Characteristics of melting heat transport of blood with time-dependent cross-nanofluid model using Keller–Box and BVP4C method. Eng Computers. 2022 Aug;38(4):3705–19.10.1007/s00366-021-01406-7Search in Google Scholar

[31] Shah SL, Ayub A, Dehraj S, Wahab HA, Sagayam KM, Ali MR, et al. Magnetic dipole aspect of binary chemical reactive cross nanofluid and heat transport over composite cylindrical panels. Waves Random Complex Media. 2022 Jan;1–24.10.1080/17455030.2021.2020373Search in Google Scholar

[32] Shah SZ, Ayub A, Sabir Z, Adel W, Shah NA, Yook SJ. Insight into the dynamics of time-dependent cross nanofluid on a melting surface subject to cubic autocatalysis. Case Stud Therm Eng. 2021 Oct;27:101227.10.1016/j.csite.2021.101227Search in Google Scholar

[33] Ayub A, Sabir Z, Wahab HA, Balubaid M, Mahmoud SR, Ali MR, et al. Analysis of the nanoscale heat transport and Lorentz force based on the time-dependent cross nanofluid. Eng Computers. 2022 Jan;39:1–20.10.1007/s00366-021-01579-1Search in Google Scholar

[34] Ali F, Kumar TA, Loganathan K, Reddy CS, Pasha AA, Rahman MM, et al. Irreversibility analysis of cross fluid past a stretchable vertical sheet with mixture of Carboxymethyl cellulose water based hybrid nanofluid. Alex Eng J. 2023 Feb;64:107–18.10.1016/j.aej.2022.08.037Search in Google Scholar

[35] Srinivas Reddy C, Mahanthesh B, Rana P, Muhammad T. Entropy generation and thermal analyses of a cross fluid flow through an inclined microchannel with non-linear mixed convection. ZAMM-J Appl Math Mech/Zeitschrift für Angewandte Mathematik und Mechanik. 2023;103:e202100364.10.1002/zamm.202100364Search in Google Scholar

[36] Khan M, Ahmad L, Yasir M, Ahmed J. Numerical analysis in thermally radiative stagnation point flow of cross nanofluid due to shrinking surface: dual solutions. Appl Nanosci. 2023 Jan;13(1):573–84.10.1007/s13204-021-01861-0Search in Google Scholar

[37] Alraddadi I, Ayub A, Hussain SM, Khan U, Shah SZ, Hassan AM. The significance of ternary hybrid cross bio-nanofluid model in expanding/contracting cylinder with inclined magnetic field. Front Mater. 2023 Sep;10:1242085.10.3389/fmats.2023.1242085Search in Google Scholar

[38] Mahmood R, Siddique I, Khan I, Badran M, Mehrez S, Majeed AH, et al. Numerical computation for modified cross model fluid flow around the circular cylinder with symmetric trapezoidal cavities. Front Phys. 2022;10:912213.10.3389/fphy.2022.912213Search in Google Scholar

[39] Sahu SK, Shaw S, Thatoi DN, Nayak MK. A thermal management of Darcy-Forchheimer SWCNT–MWCNT Cross hybrid nanofluid flow due to vertical stretched cylinder with and without inertia effects. Waves Random Complex Media. 2022 Jun;1–27.10.1080/17455030.2022.2088889Search in Google Scholar

[40] Alharbi SO, Khan U, Zaib A, Ishak A, Raizah Z, Eldin SM, et al. Heat transfer analysis of buoyancy opposing radiated flow of alumina nanoparticles scattered in water-based fluid past a vertical cylinder. Sci Rep. 2023 Jul;13(1):10725.10.1038/s41598-023-37973-6Search in Google Scholar PubMed PubMed Central

[41] Salahuddin T, Javed A, Khan M, Awais M, Bangali H. The impact of Soret and Dufour on permeable flow analysis of Carreau fluid near thermally radiated cylinder. Int Commun Heat Mass Transf. 2022 Nov;138:106378.10.1016/j.icheatmasstransfer.2022.106378Search in Google Scholar

[42] Rana P, Kumar A. Nonlinear buoyancy driven flow of hybrid nanoliquid past a spinning cylinder with quadratic thermal radiation. Int Commun Heat Mass Transf. 2022 Dec;139:106439.10.1016/j.icheatmasstransfer.2022.106439Search in Google Scholar

[43] Alam J, Murtaza MG, Tzirtzilakis EE, Ferdows M. Application of biomagnetic fluid dynamics modeling for simulation of flow with magnetic particles and variable fluid properties over a stretching cylinder. Math Computers Simul. 2022 Sep;199:438–62.10.1016/j.matcom.2022.04.008Search in Google Scholar

[44] Sajid T, Jamshed W, Algarni S, Alqahtani T, Eid MR, Irshad K, et al. Catalysis reaction influence on 3D tetra hybrid nanofluid flow via oil rig solar panel sheet: case study towards oil extraction. Case Stud Therm Eng. 2023 Sep;49:103261.10.1016/j.csite.2023.103261Search in Google Scholar

[45] Upadhyay S, Upreti H, Pandey AK. Three-dimensional flow of hybrid nanofluid through Darcy-Forchheimer porous surface: A Legendre wavelet collocation approach. Numer Heat Transfer Part A: Appl. 2023 Nov;1–25.10.1080/10407782.2023.2287543Search in Google Scholar

[46] Darvesh A, Altamirano GC, Sánchez-Chero M, Zamora WR, Campos FG, Sajid T, et al. Variable chemical process and radiative nonlinear impact on MHD Cross nanofluid: An approach towards controlling the global warming. Heat Transf. 2023;52(3):2559–75.10.1002/htj.22795Search in Google Scholar

[47] Darvesh A, Sánchez-Chero M, Sánchez-Chero JA, Hernández VD, Guachilema MD, Reyna-Gonzalez JE. Influence of motile gyrotactic microorganisms over cylindrical geometry attached Cross fluid flow mathematical model. Heat Transf. 2023 Sep;52(6):4293–316.10.1002/htj.22870Search in Google Scholar

[48] Darvesh A, Altamirano GC, Núñez RA, Gago DO, Fiestas RW, Hernán TC. Quadratic multiple regression and spectral relaxation approach for inclined magnetized Carreau nanofluid. Eur Phys J Plus. 2023 Mar;138(3):1–4.10.1140/epjp/s13360-023-03807-7Search in Google Scholar

[49] Darvesh A, Wahab HA, Sarakorn W, Sánchez-Chero M, Apaza OA, Villarreyes SS, et al. Infinite shear rate viscosity of cross model over Riga plate with entropy generation and melting process: A numerical Keller box approach. Results Eng. 2023 Mar;17:100942.10.1016/j.rineng.2023.100942Search in Google Scholar

[50] Darvesh A, Altamirano GC. Inclined magnetic dipole and nanoscale energy exchange with infinite shear rate viscosity of 3D radiative cross nanofluid. Heat Transf. 2022 Jun;51(4):3166–86.10.1002/htj.22442Search in Google Scholar

[51] El Din SM, Darvesh A, Ayub A, Sajid T, Jamshed W, Eid MR, et al. Quadratic multiple regression model and spectral relaxation approach for Carreau nanofluid inclined magnetized dipole along stagnation point geometry. Sci Rep. 2022 Oct;12(1):17337.10.1038/s41598-022-22308-8Search in Google Scholar PubMed PubMed Central

[52] Ayub A, Darvesh A, Altamirano GC, Sabir Z. Nanoscale energy transport of inclined magnetized 3D hybrid nanofluid with Lobatto IIIA scheme. Heat Transf. 2021 Nov;50(7):6465–90.10.1002/htj.22188Search in Google Scholar

[53] Botmart T, Shah SZ, Sabir Z, Weera W, Sadat R, Ali MR, et al. The inclination of magnetic dipole effect and nanoscale exchange of heat of the Cross nanofluid. Waves Random Complex Media. 2022 Sep;1–6.10.1080/17455030.2022.2128225Search in Google Scholar

[54] Rasool G, Shah SZ, Sajid T, Jamshed W, Cieza Altamirano G, Keswani B, et al. Spectral relaxation methodology for chemical and bioconvection processes for cross nanofluid flowing around an oblique cylinder with a slanted magnetic field effect. Coatings. 2022 Oct;12(10):1560.10.3390/coatings12101560Search in Google Scholar

[55] Ayub A, Wahab HA, Shah SZ, Shah SL, Darvesh A, Haider A, et al. Interpretation of infinite shear rate viscosity and a nonuniform heat sink/source on a 3D radiative cross nanofluid with buoyancy assisting/opposing flow. Heat Transf. 2021 Jul;50(5):4192–232.10.1002/htj.22071Search in Google Scholar

[56] Khan U, Zaib A, Pop I, Bakar SA, Ishak A. Unsteady micropolar hybrid nanofluid flow past a permeable stretching/shrinking vertical plate. Alex Eng J. 2022 Dec;61(12):11337–49.10.1016/j.aej.2022.05.011Search in Google Scholar

[57] Tag El Din ES, Sajid T, Jamshed W, Shah SZ, Eid MR, Ayub A, et al. Cross electromagnetic nanofluid flow examination with infinite shear rate viscosity and melting heat through Skan-Falkner wedge. Open Phys. 2022 Dec;20(1):1233–49.10.1515/phys-2022-0216Search in Google Scholar

[58] Khan U, Zaib A, Ishak A, Bakar SA. Time-dependent Blasius–Rayleigh–Stokes flow conveying hybrid nanofluid and heat transfer induced by non-Fourier heat flux and transitive magnetic field. Case Stud Therm Eng. 2021 Aug;26:101151.10.1016/j.csite.2021.101151Search in Google Scholar

[59] Khan U, Zaib A, Bakar SA, Roy NC, Ishak A. Buoyancy effect on the stagnation point flow of a hybrid nanofluid toward a vertical plate in a saturated porous medium. Case Stud Therm Eng. 2021 Oct;27:101342.10.1016/j.csite.2021.101342Search in Google Scholar

[60] Shah SH, Suleman M, Khan U. Dual solution of MHD mixed convection flow and heat transfer over a shrinking sheet subject to thermal radiation. Partial Differ Equ Appl Math. 2022 Dec;6:100412.10.1016/j.padiff.2022.100412Search in Google Scholar

[61] Khan M, Manzur M. Boundary layer flow and heat transfer of cross fluid over a stretching sheet. arXiv preprint arXiv:1609.01855. 2016 Sep 7.10.1016/j.rinp.2017.08.039Search in Google Scholar

Received: 2023-12-11

Revised: 2024-01-14

Accepted: 2024-01-21

Published Online: 2024-02-22

This work is licensed under the Creative Commons Attribution 4.0 International License.

Articles in the same Issue

https://doi.org/10.1515/phys-2023-0197

Keywords for this article

ternary hybrid nanofluid; MHD; mixed convection flow; vertical cylinder; cross-fluid model

Creative Commons

BY 4.0