Abstract
Dynamics of a dry-rebounding drop was studied experimentally, numerically, and theoretically. Experimental results were reproduced by our computational fluid dynamics simulations, from which time series of kinetic energy, potential energy, and surface energy were obtained. The time series of these energies quantitatively clarified the energy conversion and loss during the dry-rebound. These results were interpreted by using an imaginary spring model and a spherical harmonic analysis. The spring model explained the vertical deformation of the drop, however, could not completely explain the energy loss; the timings of the energy loss did not match. From a viewpoint of the spherical harmonic deformation of a drop, the deformation of the drop after the impact was found to be a combination of two vibrational motions. One of the two vibrational motions is an inertial motion derived from the free-fall and the another is a pressure-induced motion derived from a pressure surge due to the sudden stop of the bottom part of the drop at the impact. The existence of the pressure surge at the impact was confirmed in the simulated results. The pressure-induced motion resists the inertial motion and consequently dumps the kinetic energy of the drop.
1 Introduction
A drop on a superheated surface, of which the temperature is higher than a critical point, floats on a stable vapor film generated by evaporation of the drop. This is referred to as the Leidenfrost effect, named after the person who first discovered it [1, 2]. We will thus refer to such a drop as a Leidenfrost drop.
The drop can be regarded as completely floating and non-wetting on the surface [3] and the heat flux from the surface towards the drop is sufficiently small that changes in the fluid properties are negligible due to the heat insulating effect of the vapor [4, 5]. If the drop falls from a certain height towards the heated surface, it bounces on the surface similar to a bouncing ball, which is referred to as a dry rebound [5]. In a dry rebound, the drop falls while converting the initial potential energy to kinetic energy, then impacts on the surface while converting the kinetic energy to surface energy by deformation to a disk-like shape, and then shrinks while converting the surface energy to kinetic energy again. In these dynamics, the drop behaves similar to an elastic spring. As such, the spring model has helped to reveal interesting characteristics of the drop [4, 6].
A small amount (in the order of 100 ppm) of polymer additives in the drop is known to change the dynamic behavior and energy loss of the drop during the bounce [5, 7, 8, 9, 10]. However, the energy conversion and loss of a dry-rebounding drop, even without the polymer additive, have remained unclear [4].
An efficient approach to understand the drop characteristics is a numerical simulation of the drop under a completely non-wetting condition, which has successfully reproduced the experimental drop results [11]. Computational fluid dynamics (CFD) not only enables unknown phenomena to be expected, but also facilitates clarification of detailed physical information regarding complex fluidic phenomena. Previous studies [12, 13, 14] have shown that the volume of fluid (VOF) method provides reliable and reasonable results on two-phase flows. For example, an impacting mercury drop [12], a cavitation around a two-dimensional hydrofoil [13], and a drop impacting onto a liquid layer of finite thickness [14] have been simulated with the VOF method.
In the present study, dynamics of a dry-rebounding drop is observed by a high-speed camera, numerically simulated with a CFD solver, and theoretically modeled with a damped spring model. We focus on the first few bounces whose time span (∼ 0.1 s) is much shorter than the life time of a Leidenfrost drop on a hot plate at a temperature of 380 °C (∼ 100 s) [3], thus the volume change due to the evaporation is negligible. In the experiments (Section 2), drops falling from different heights were captured with a high-speed camera and the videos were analyzed to measure the geometrical properties of the drops. CFD simulations of the dry-rebounding drops were then performed using a two-phase solver under a completely non-wetting condition on a flat plate (Section 3). In Section 4, the numerical results were assessed by comparison with the experimental result, and then time evolutions of the kinetic energy, potential energy, and surface energy of the drop were calculated. An imaginary damped spring model and a spherical harmonic analysis were introduced to elucidate the mechanism for the energy loss of the drop. Final conclusions are described in Section 5.
2 Experiment
The experimental setup is shown in Figure 1. An aluminum plate (100 mm × 100 mm × 5 mm) was heated on a ceramic hot plate (As one, CHP-170DN) to 400 °C, which is sufficiently higher than the Leidenfrost temperature and the boiling point of water. A drop of distilled water was dropped from a pipette (inner diameter: 1 mm). Averaged diameter of the drop in all the experiments was 3.69 mm with the standard error of 0.10 mm. Experiments were conducted under the room conditions; the temperature was 23.9 ± 0.3 °C and the humidity was 80 ± 4%RH.
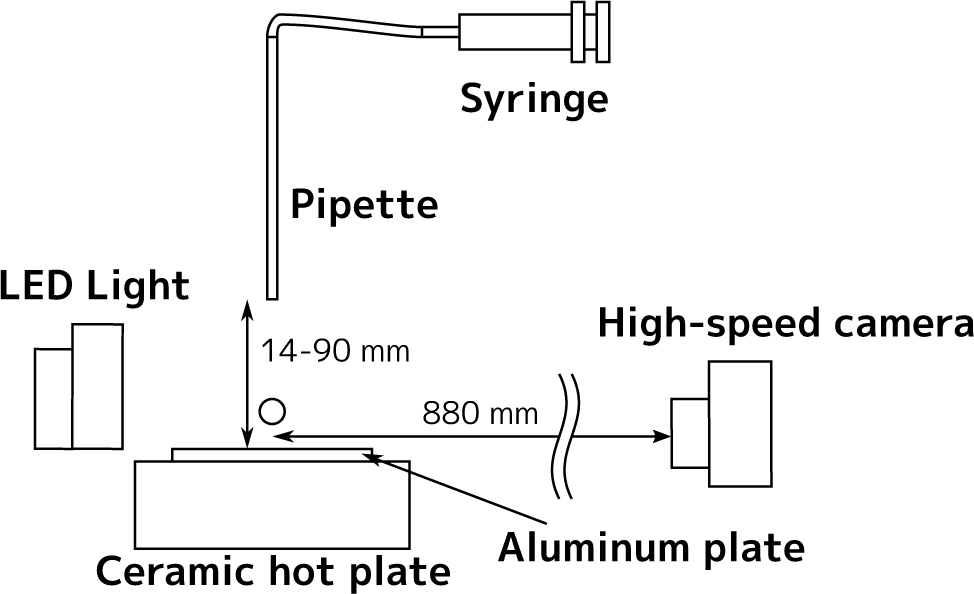
Experimental setup used to capture drop impact on a superheated flat surface. The drop was generated at the tip of a pipette and captured with a high-speed camera.
To characterize the drop, the Weber number We was used, which is a non-dimensional number that gives the ratio of kinetic energy to the surface energy of the drop and thus represents the stability of a drop. Weber number especially for a drop at impact is referred to as the dynamic Weber number, and can be expressed as
where ρ is the density of the drop, Uimpact is the velocity of the drop just before impact, D0 is the initial diameter of the drop, and σ is the surface tension coefficient between air and the internal fluid of the drop.
The height of the pipette tip above the plate was adjusted from 9 mm to 25 mm at 1 mm increments to change the impact velocity of the drop, Uimpact.
The drop impact on the plate was captured using a high-speed camera (Casio, EXILIM EX-F1) with a frame rate of 1200 fps and a resolution of 336×96 pixels. Experiments were performed three times for each initial height.
Captured videos were processed using an image processing pipeline that was written in Python [17] and using OpenCV [18], an open source computer vision library. The images were processed into binary images that indicate the interior or exterior of the drop, and from the binary images, contours for the drop edge were obtained. The geometric properties of the drop were obtained from the image processing pipeline (Figure 2): top height x1, bottom height x2, and width D.
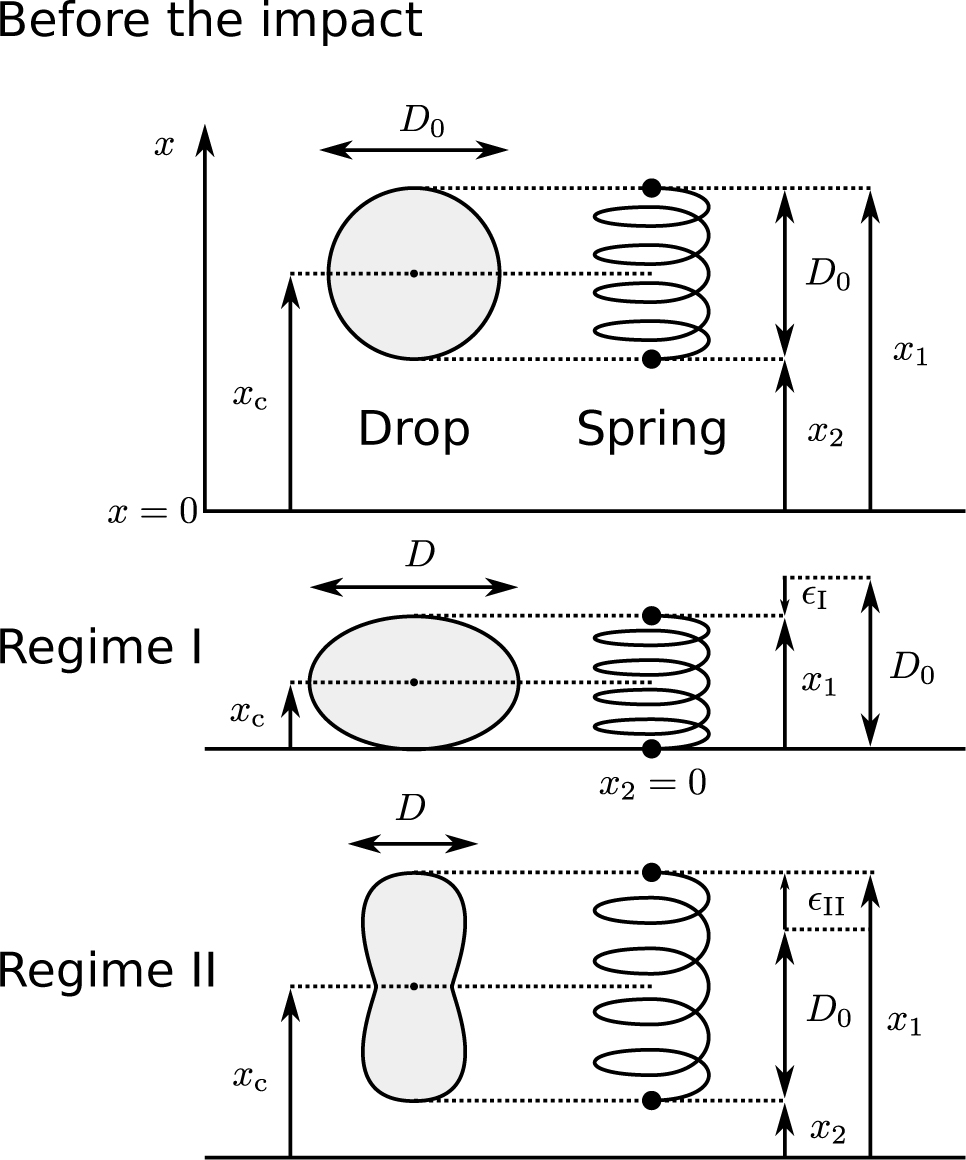
Schematic diagram of a drop and the imaginary damped spring model prior to impact, in regime I, and in regime II. The geometric properties of the drops were measured using an image-processing pipeline. The spring has two mass points (each one is half the weight of the drop) at both ends.
3 Numerical method
3.1 Finite volume method and volume of fluid method
The drop was simulated using a two-phase solver, interFoam [19] of OpenFOAM (version 3.0.x) [15, 20], a CFD toolkit software that can be used and exploited under the GNU General Public License (GPL) [16]. The interFoam solver is based on the finite volume method (FVM). In the FVM, the domain of calculation is divided into finite-volume cells which are referred to as control volumes, and physical values (e.g., velocity and pressure) are assigned to the centroid or faces of each cell.
A type of VOF method is used in interFoam to model two-phase flow and to track the free surface. In the present simulation, the two phases of water and air were considered. Note that in the two-phase flow, the volume fraction of liquid, αl = α, determines the volume fraction of gas, αg = 1 – α.
3.2 Interface capturing
An efficient method is required to simulate a multiphase flow and capture a sharp interface between the two immiscible phases. VOF methods have a problem with respect to the diffusive interface between two phases. In VOF methods, the volume fraction of each phase is tracked through every control volume. The volume fraction of each phase is expressed by a scalar function, which is referred to as a volume function or a color function. To reproduce the interface between immiscible phases, the volume function needs to keep a steep gradient at the interface. However, the steep gradient readily dissipates because VOF methods solve a momentum equation for a mixture of immiscible phases. Therefore, a special treatment is needed for the interface of volume functions. The relative velocity, Ur, is used to compress the interface between the two phases. Weller [21] proposed a relative velocity between two phases, Ur, as follows:
where U is the velocity field, and Cα is a coefficient set to 1 in the present simulation. This method has proven to be reliable in maintaining a sharp interface [21].
3.3 Surface tension force
Surface tension force is calculated using the continuum surface force (CSF) model [22]:
where σ is the surface tension coefficient and κ is the curvature of the interface between the liquid and gas. κ is given by
in which n̂ is the gradient vector at the face, which is given by
where δn is a stabilization factor depending on the volume of grid cells. The typical value of δn in our simulation is 1.0 × 10–5m–1.
3.4 Velocity-pressure coupling
The momentum equation is given by
where ρ is the mixture density, p is the pressure, g is the gravity vector, h is the position vector in the vertical direction, (g·h)∇ρ is the buoyancy force, and τ is the deviatoric stress. The interFoam solver uses the PIMPLE method, which is a combined velocity-pressure coupling algorithm of the SIMPLE (Semi-Implicit Method for Pressure-Linked Equations) and PISO (Pressure Implicit with Splitting of Operator) algorithm [23]. The PIMPLE algorithm is summarized as the following routine.
Momentum prediction: Predict the velocity field using the momentum equation.
Pressure solution: Solve the pressure equation and correct flux.
Explicit velocity correction: Correct the velocity field with the solved pressure field.
The routine is repeated for certain number of times, which was two times in the present simulation.
3.5 Computation and post-processing
A diameter given by the average diameter of 51 experimental drops was adopted as the initial diameter of the numerical drop, D0 = 3.7 mm. The initial velocity of the drop was determined using the conservation of mechanical energy:
where g is the gravitational acceleration, and xc,0 is the initial height of the centroid of the drop. The viscosities of water and air were set to 1.0 × 10–3 Pa · s and 1.84 × 10–5 Pa · s, respectively. The field of the initial volume fraction of water was set to α = 1.0 at the interior of the drop and α = 0.0 at the outside of the drop. The surface tension coefficient σ, between water and air was set to 0.07 N · m–1.
The boundary conditions used for the calculation are shown in Table 1. The contact angle between water and air on the bottom patch on which the drop impacted was set to 180° (a perfectly hydrophobic surface), which means that the gradient of α on the bottom boundary is determined as the negative normal vector of the boundary patch. The schematic diagram of the CFD setup is shown in Figure 3. The calculation domain was in the shape of a cube, 1.5 cm on a side (Figure 3(a)). A spherical drop of 3.8 mm diameter was placed at a height of 5 mm above the bottom boundary (Figure 3(a)). To improve efficiency of the calculation, the resolution of the mesh is uniform and finest at the interior of the central rectangular column covering the drop, while it becomes coarser toward the exterior, where the drop will never enter (Figures 3(b) and 3(c)). Number of grid cells above 1.0 cm from the bottom patch was reduced to 30 % of the finest region, and number of grid cells outside a square with a side length 1.0 cm and a center of the drop was reduced to 50 % of the finest region. From the finest grid cells towards boundaries except the bottom, the length of edge of grid cells are expanded with the expansion ratio of smallest length to largest length of the edge length of grid cells. The expansion ratios are 2.81 towards the left, the right, the front, the back patches of the drop and 6.26 towards the upper patch. Two resolutions of the mesh, 5 and 10 grid cells mm–1 at the finest part of the mesh, were used to validate the effect of the resolution.
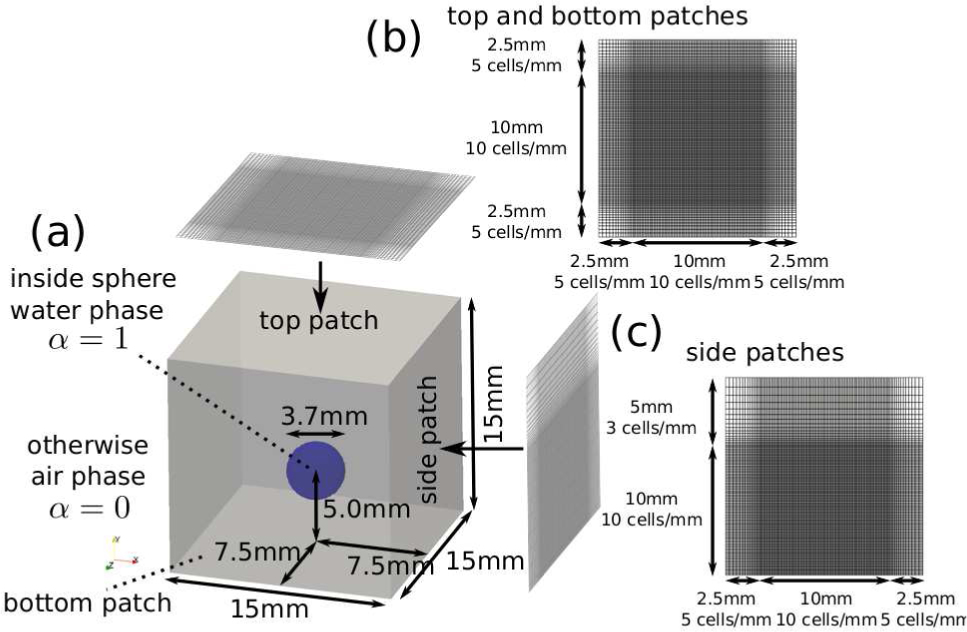
Schematic diagram of the CFD setup. (a) System size and initial setup of the volume fraction of water, α. The grid mesh from (b) top and bottom views, and (c) side views. The central cubic domain has the finest and unity resolution, otherwise domain has reduced resolution with expanding cell size outward.
Boundary conditions used in the calculation. “Bottom patch” is the patch on which the drop impacts and “Other patches” are placed at the left, the right, the back, the front, and the upper sides of the drop. Under condition #1, the gradient value of the boundary field is fixed to zero, except on the tangential component which is set to 0 for inflow. Under condition #2, the velocity field on the patch is evaluated from the flux, switching zero gradient, and the fixed value, depending on the direction of velocity with respect to the boundary. Under condition #3, the pressure gradient was adjusted depending on the flux.
| Variable | Bottom patch | Other patches |
|---|---|---|
| U | #1 | #1 |
| α | non-wetting condition | #2 |
| p - ρgh | #3 | fixed value (10 kPa) |
The simulations were performed on a computer equipped with an Intel® Core™ i7-3960X CPU and with 32GB RAM. The simulation results were rendered as movies using ParaView [24]. The interface between water and air was determined by thresholding the volume fraction of water at α = 0.5 to capture the center of transitional region between water and air. Rendered movies were processed using the image processing pipeline that was also used to process the experimental results.
4 Results and discussion
4.1 Assessment of the numerical result
Here, the numerical results are assessed by comparison with the experimental results.
Before assessment of the results from a physical perspective, the effect of the mesh design was validated by evaluating the dependency on the mesh resolution. No particular differences were observed in the results for the two different resolutions, which indicates that the mesh resolution has no significant effect on the result. To inspect the numerical result with the fine resolution, results calculated with the finer mesh (10 cells / mm) were used for further analysis.
Figure 4 shows sequential images of the experimental and simulated drops. The experimental and simulated drops were comparable in that each drop exhibited a stable rebound. The sequence of the deformation (spreading after first impact, forming a disk-shape, shrinking, making a head at the center of the disk, lift-off, shaking of the shape while in the air, and impacting again) was also reproduced in the calculation. For high Weber numbers (We ≥ 15), the experimental result fluctuated, possibly due to asymmetrical expansion and contraction, while the numerical result was stable and had symmetrical expansion and contraction. Deformation for the experimental drop was so sensitive that no symmetrical deformation could be achieved.

Sequential images of experimental drops (upper rows) and simulated drops (lower rows) captured every 5 ms for We = 7 (top), We = 15 (middle), and We = 23 (bottom).
Time evolutions of the height and width of the drop are expected to provide vibrational patterns of the deformation process. Time evolutions of relative diameter D/D0 for both experimental and simulated drops with different Weber numbers were compared (Figure 5), and the top, middle, and bottom heights of the drops, x1, xc, and x2, respectively (Figure 2 and Figure 6), show that both sets of results have the same vibrational patterns, although for high Weber numbers, the time spans between the first and second expansions and between the first and second impacts for the numerically simulated drops were slightly wider than those for the experimental drops. The time series for the horizontal diameter of the drop during the impact approximately represents how much kinetic energy is converted to surface energy (Figure 5). The time series for the middle height can be considered to represent approximately the potential energy of the drop. Thus, as shown in Figure 6, the time series for the potential energy of the drop for both the experiments and the simulations can be considered to be in agreement.
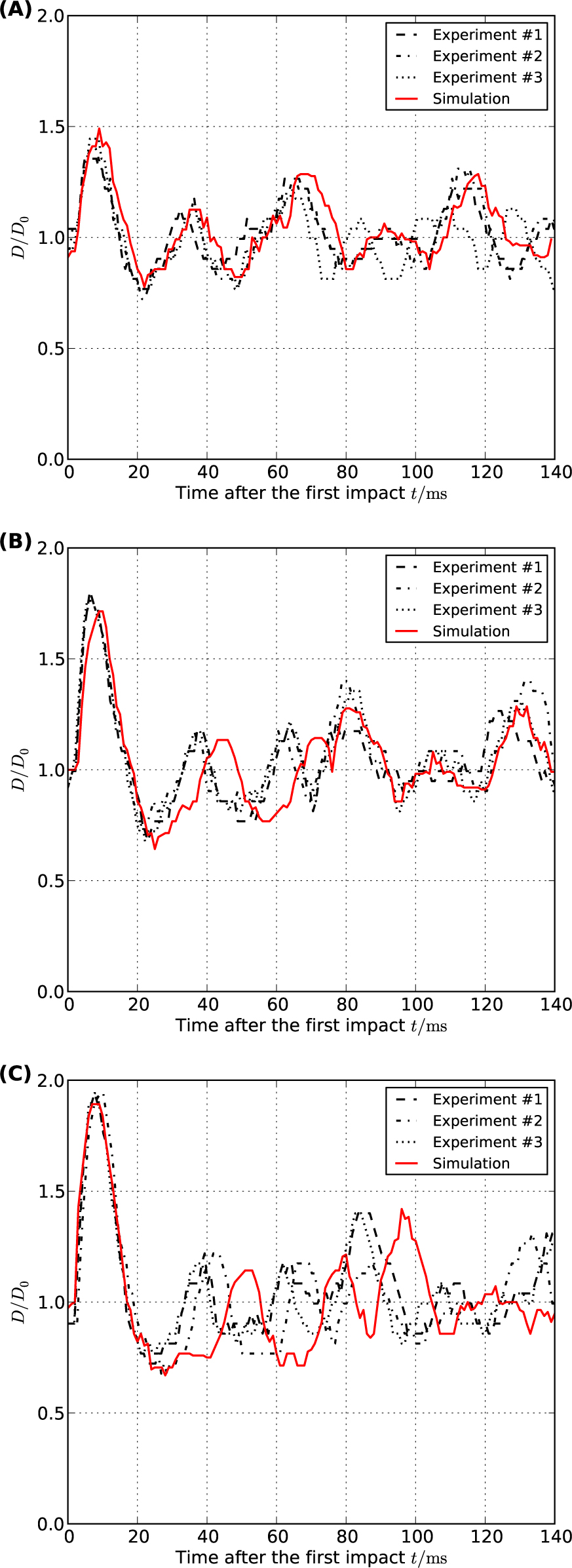
Time series of width for experimental and numerically simulated drops with (A) We = 7, (B) We = 15, and (C) We = 23. The first expansion and contraction (0-20 ms) have good agreement.
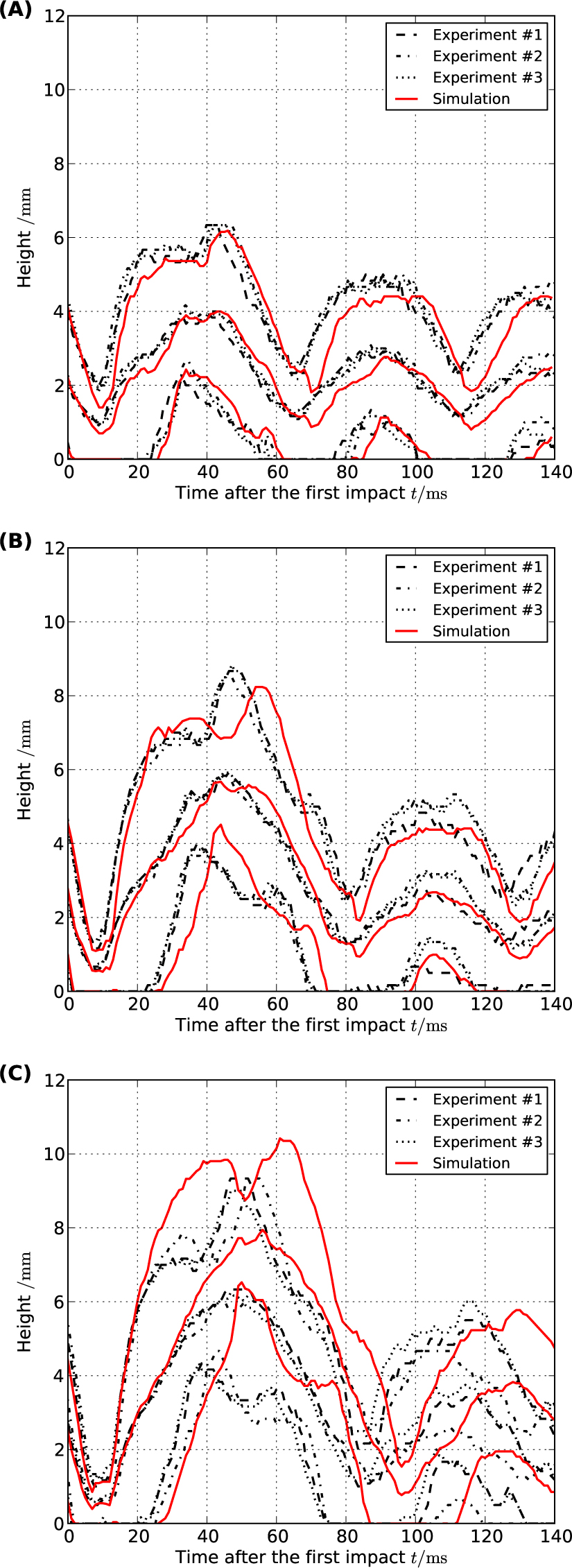
Time series of top height, middle height, and bottom height for experimental and numerically simulated drops with (A) We = 7, (B) We = 15, and (C) We = 23. The difference between the top and bottom heights represents deformation in the vertical direction and the middle height represents the approximate potential energy of the drop.
The dissipated energy during the rebound is very difficult to determine because both the velocity and the surface area of the drop are unknown [25]. One effective way to experimentally estimate the dissipated mechanical energy is to calculate the ratio of the maximum height after the first impact to the initial height, as a ratio of mechanical energy at the maximum height to the initial mechanical energy:
by assuming that the potential energy is equal to the mechanical energy when the drop is at the highest position.
The ratio of mechanical energy at the maximum height to the initial mechanical energy for each Weber number is shown in Figure 7. Both the numerical and experimental results showed a decrease with an increase of the Weber number. The energy loss for the experimental result with high Weber numbers is considered to fluctuate due to asymmetrical deformation during the rebound (Figure 4).
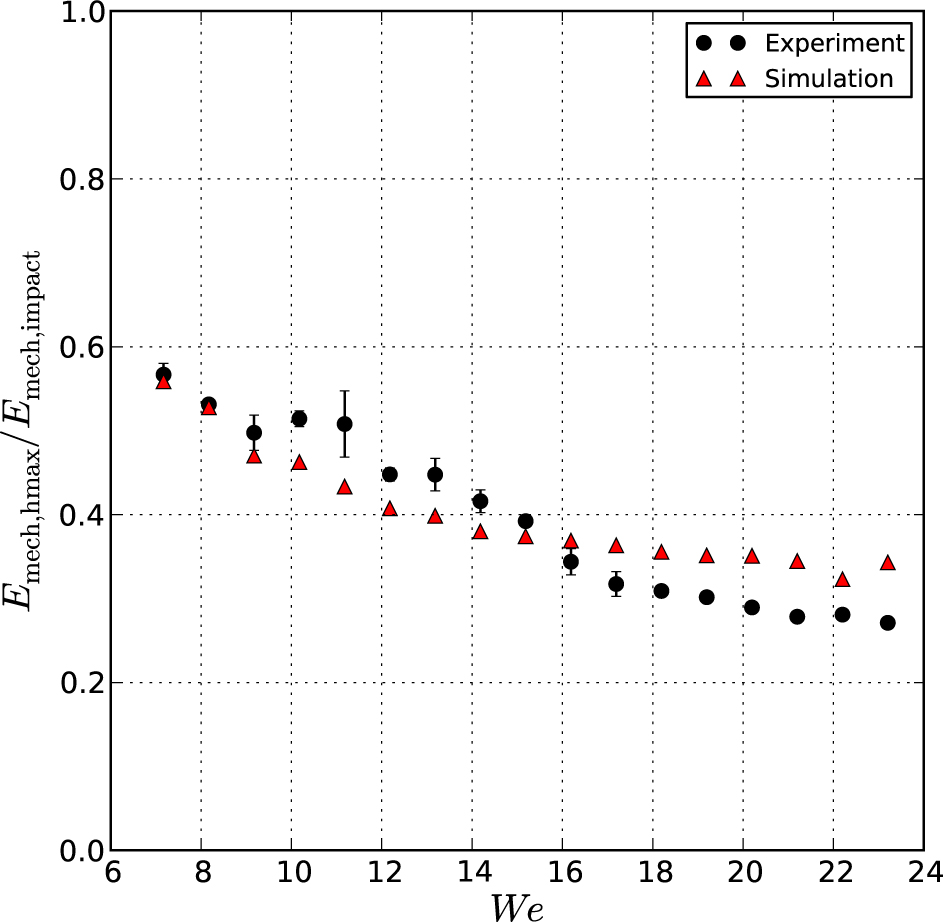
Weber number and the ratio of the mechanical energy of the drop at the maximum height after the impact to the initial mechanical energy. Both the numerical and experimental results showed a decrease in the ratio with an increase of the Weber number.
Through the assessment performed here, the numerical result is considered to be reasonably reliable with respect to the deformation and dissipated energy.
4.2 Quantitation of the energy conversion
Kinetic energy and potential energy were calculated using the following respective equations:
where V is the volume and Ω is the entire domain for the calculation. Under the condition that the width of the interface between water and air is asymptotically limited to zero, the integral over the interface can be reformulated by a volume with the gradient of the volume fraction, ∇α [22]. Thus, the surface energy can be calculated using
The sum of the kinetic and potential energies is the mechanical energy:
In this system, the pressure and volume are considered to be constant, and the energy of interest is the sum of the mechanical and surface energies:
Figure 8 shows the time evolution of the energies calculated from the numerical results. At the impact (t = 0 ms), the mechanical energy begins to decrease rapidly and the surface energy simultaneously begins to increase. When the surface energy reaches a maximum (t ≈ 8 ms), the kinetic energy has a local minimum. After reaching the maximum surface energy, the mechanical energy begins to increase while the surface energy decreases. After takeoff of the drop (t ≈ 15 ms), as evident for high Weber numbers, the conversion between the mechanical energy and surface energy still continues, which is considered to be caused by vibration of the drop in the air. Interestingly, the changes of these energies cancel each other out and are considered to be conserved in the form of the sum of the mechanical and surface energies.
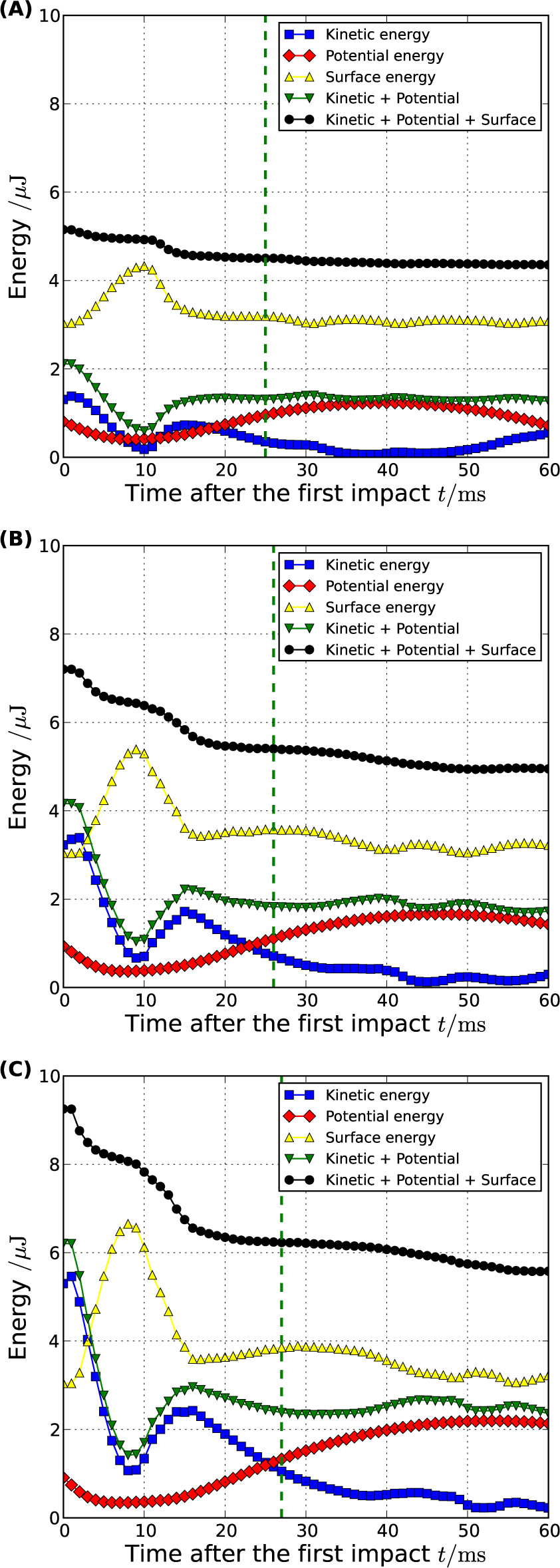
Kinetic, potential, and surface energies of drops as a function of t, the time after impact, with (A) We = 7, (B) We = 15, and (C) We = 23. The dashed line represents the transition point from regime I to regime II.
4.3 Imaginary damped spring model
A poorly elastic shock of a Leidenfrost drop has been modeled by an imaginary spring [4, 6], which is a linear spring model with two mass points that represent the mass of the drop at both ends of the spring. Here, we extend the imaginary spring model by adding a damping term:
where x1 and x2 are the heights of the bottom and top of the spring above the plate respectively, and
is the strain of the spring, m is the mass of the drop, D0 is the initial vertical length of the drop, k is the stiffness of the spring, c is the damping coefficient of the spring (c ≥ 0), and F is the external force loaded at the bottom of the spring. Figure 2 shows a schematic diagram of the imaginary damped spring model. Note that by combining Eqs. (14a) and (14b), the momentum equation for the centroid of the spring,
which plots the free-fall and bounce-back of the spring.
Let us define the regime in which the drop is in contact with the vapor film over the plate as regime I. In regime I, the height of the bottom of the spring is considered to be fixed (x2 = 0); therefore,
and
where ϵI is the strain in regime I. Equations (14a) and (14b) then become:
where
By solving Eq. (19a), we obtain
where tI is the time after the impact, AI is the initial amplitude of the oscillation,
The time span from the lift-up to the next impact of the drop is defined as regime II. In regime II, the bottom height of the spring is no longer fixed (x2 ≥ 0) and there is no external force loaded on the bottom mass point (F = 0). Differentiation of Eq. (15) gives
where ϵII is the strain in regime II. The combination of Eqs. (14a), (14b), and (22) gives
where
By solving Eq. (23), we obtain
where tII is the time after the lift-up, AII is the amplitude of the oscillation,
The coefficients were obtained according to the description given in Appendix A. The damping coefficient for regime I, cI, was determined to be 0.7 × 10–3 kgs–1 using Eq. (A.5) with the result for We = 7 and was reasonably assigned for all Weber numbers in this study, while that for regime II, cII, was determined to be half the value of cI. This difference of the damping coefficient indicates that the mechanism for energy loss is different between regimes I and II. The stiffness k, determined by Eq. (A.6), tends to decrease with an increase of the Weber number.
The sum of the kinetic, potential, and elastic energies as the surface energy of the spring model can be calculated for each regime:
where Ems,I and Ems,II are sums of the mechanical energy and the surface energy in regime I and regime II, respectively. These energies are shown in Figure 10 with We = 7, 15, 23.
The overall energy loss rate in regime I is expressed as
and the energy loss rate over 1 cycle of oscillation in regime II,
corresponds well for both the simulation and the spring model (Figure 11).
While the vertical strain and energy loss rates of the drop were well explained by the spring model (Figures 9 and 11), the second decrease of the spring model lagged that of the simulated drop (Figure 10). This time lag indicates that true damping factor has an other period than the damping term of the spring model.
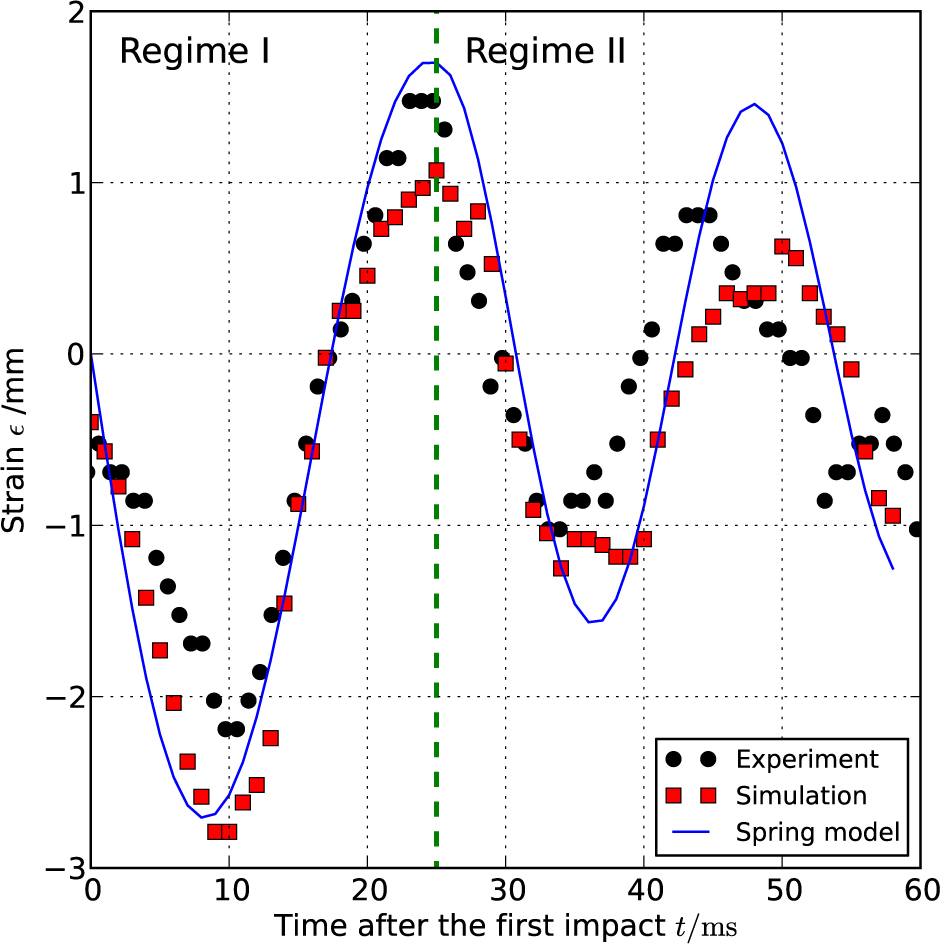
Time series of drop’s vertical strain for the experiment, simulation, and the spring model with We = 7.
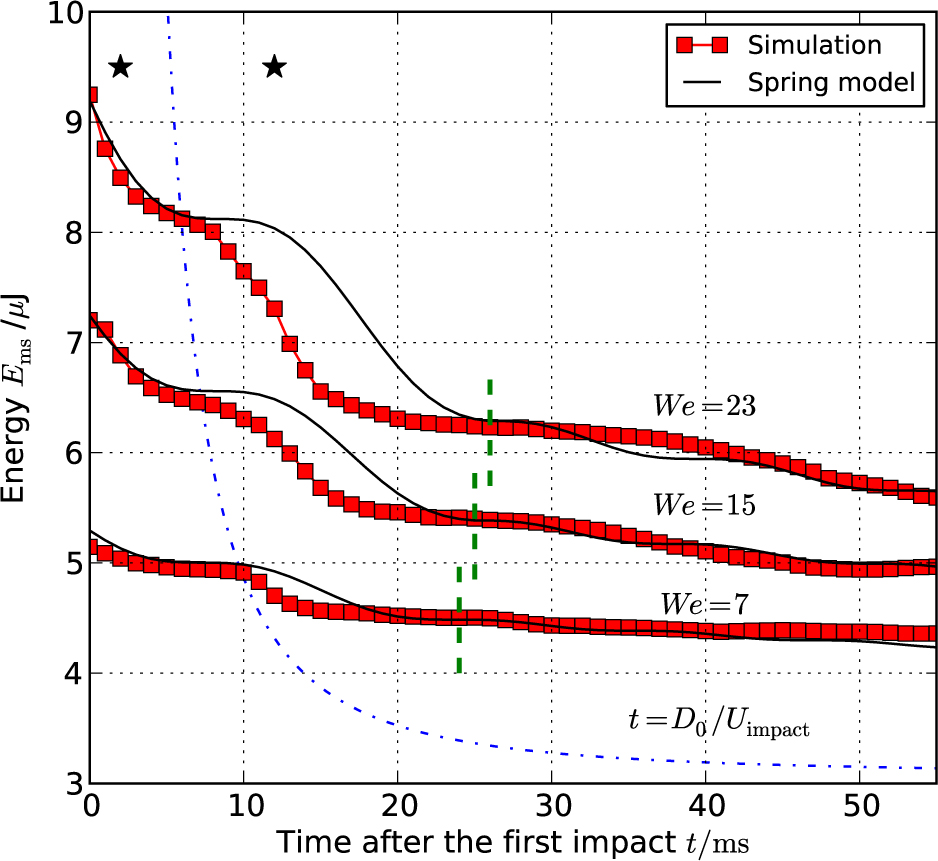
Time series for the sum of kinetic, potential, and surface energies from the simulation and spring model results. Each dashed line represents the transitional time from regime I to regime II. Major energy losses were observed at two moments, 2 ms and 12 ms after the impact as indicated by the “*” marks. The dash-dotted line shows t = D0/Uimpact, which predicts the start time of the second energy decay of the drop.
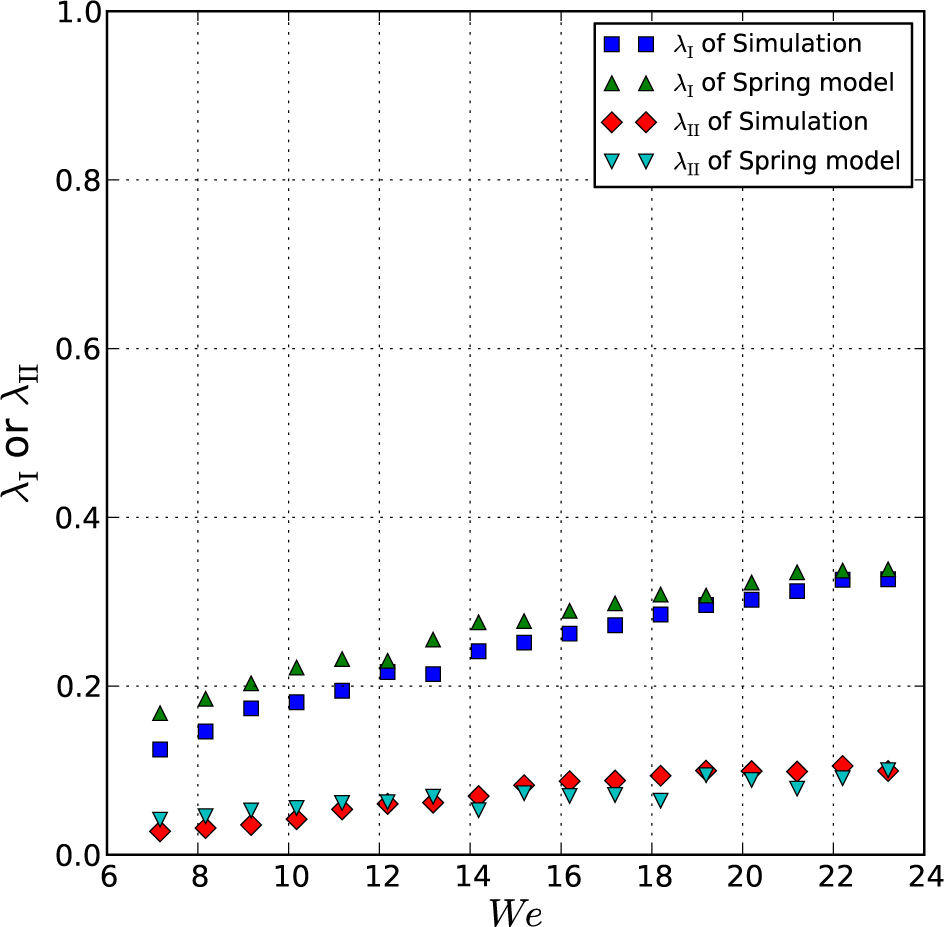
Energy loss rates over regime I λI, and the energy loss rate over 1 cycle of oscillation in regime II λII, with the simulated drop and the spring model.
4.4 Spherical harmonic analysis
A water drop on an oscillating plate [26, 27, 28] or on a superheated plate [29] is known to show spherical harmonic oscillation due to the surface tension force. We will compare the deformations of the drop on the impact with the spherical harmonic oscillation.
An oscillating drop can be represented as a linear combination of spherical harmonic functions as [30, 31, 32]
where R is the radius of an unperturbed sphere-shape drop, An (t) = an cos(ωnt + ψn) are intensities of the modes, and
The deformation of the drop in this study is radially symmetric, thus we only consider Laplace’s spherical harmonics with 0 degree,
Both of
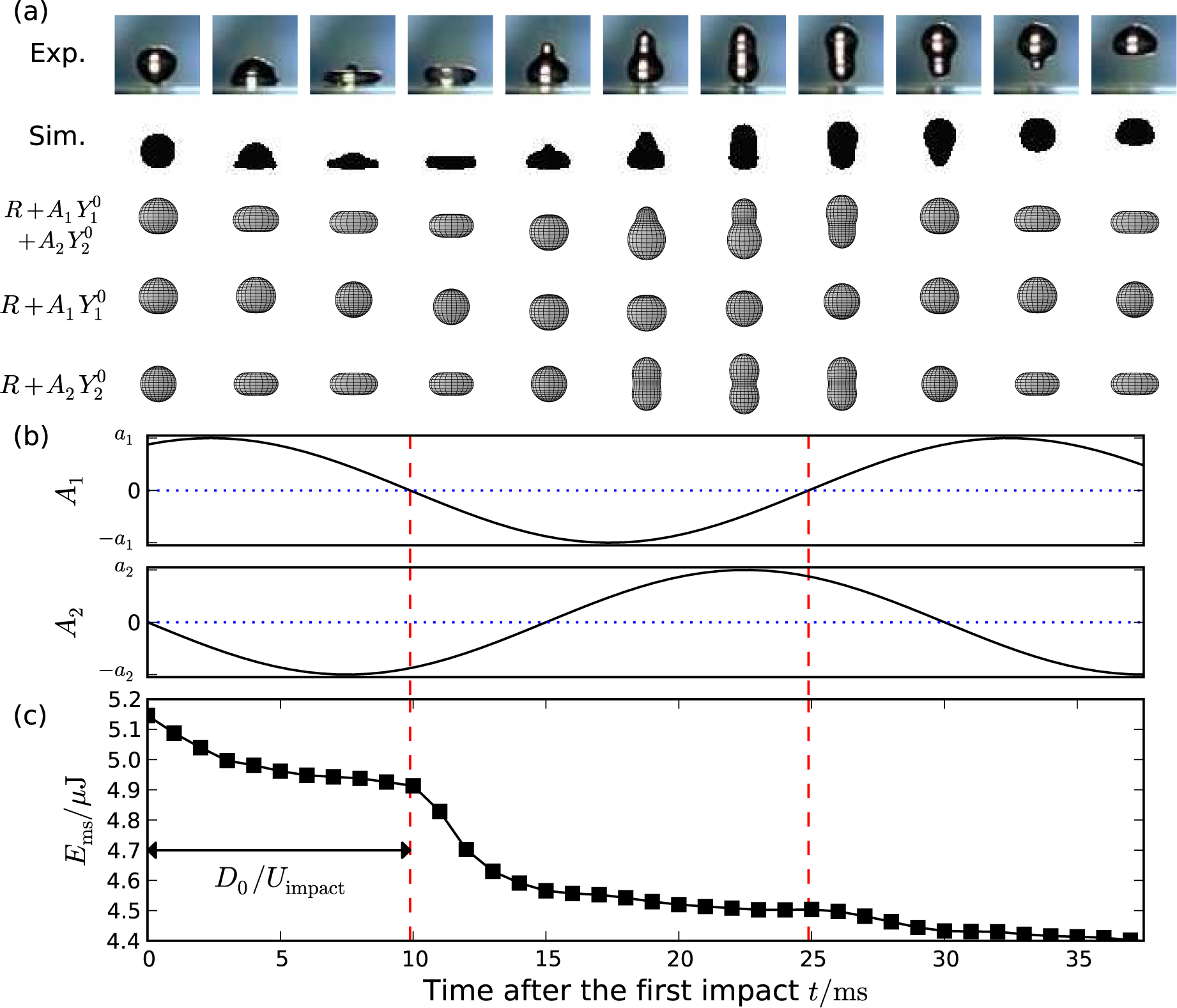
A sequential analysis of the deformation of the impacting drop with shared time axis, with We = 7. (a) Spherical harmonic deformations represented by
Immediately after the impact (t = 0 ms), the drop is in a spherical shape, thus the phase of mode n = 2 must be
The determination of the harmonic phase of the Y1 mode is more difficult than the Y2 mode. At the moment of the maximum width of spreading drop, the drop is in a disk-shape which is horizontally symmetric, therefore A1 = 0. From this moment to the lift-off, the drop forms an antisymmetric matryoshka-shape, which indicates A1 < 0. After the lift-off, the drop forms into a vertical peanut-shape (e.g. 25 ms) which is horizontally symmetric thus A1 = 0. By extrapolating from these conditions, A1 must be a positive value at t = 0. By looking carefully at energy decay curves in Figure 10, we found that the second energy decay starts slightly earlier at increasing Weber number. Let us consider a free end reflection of the drop as a pulse over the vertical axis on the bottom plate as a free end. We envisage that after the impact the drop receives the reflection of its impact velocity and induces a vertical uplift (i.e. A1 > 0), until the pulse passes over the end. Therefore, a length of the time during which the drop passes over its diameter with the impact velocity, D0/Uimpact, is considered to characterize the phase of the
The deformation of Eq. (31) with determined phases ψ1 and ψ2 together with experimental and simulated drops is shown in Figure 12(a). The deformation sequence of spherical shape, disk-shape, matrioshka-shape, and peanut-shape, is reproduced by Eq. (31).
A1 and A2 as functions of time after the impact are shown in Figure 12(b). Actually, the imaginary spring model represents the
One of the most important insights from the spherical harmonic analysis is the existence of an another vibrational mode,
4.5 Energy loss upon the impact
Time series of A1 and A2 were compared with that of the total energy Ems of the simulated drop with We = 7 (Figures 12(b) and (c)). We found that the cycle of the
When the drop impacts at the bottom plate, the bottom part of the drop is forced to stop and the vertical velocity is forced to be zero suddenly. This sudden change of the velocity induces the pressure surge (i.e., stagnation pressure). Figure 13(a) shows that a pressure surge occurs at the beginning of the impact. The amount of the pressure surge is roughly estimated as ρD0Uimpact/Δt ∼ 200 Pa, where Δt ≈ D0/Uimpact ∼ 10 ms is the time span to stop the free-fall motion of the drop. This phenomenon is similar to a water hammer with slow valve closure (slower than sound propagation), in which a pressure surge occurs when a fluid in motion is forced to stop. The pressure surge accompanies a pressure-gradient force, which is expressed by the term –∇p in the Eq. (6).
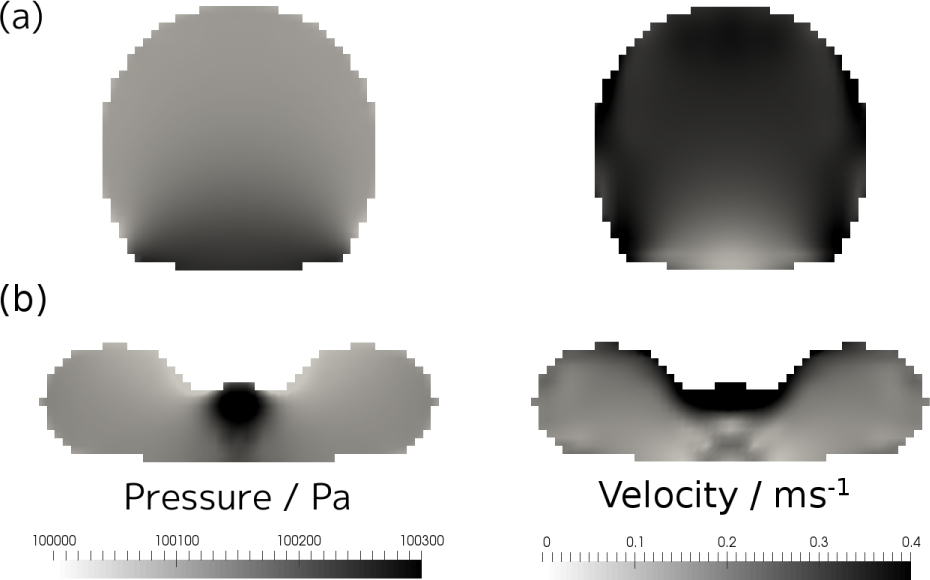
Pressure (left) and magnitude of the velocity (right) inside the drop, from a cross-sectional lateral view at the drop center (We = 7). (a) At the beginning of the impact (t = 2 ms), a pressure surge occurs at the bottom part of the drop, where magnitude of the velocity is nearly zero. and (b) At the retraction from the disk-shaped drop (t = 12 ms), the pressure-induced motion suppresses the retracting motion.
In many cases of fluid dynamics, a pressure-gradient force is a driving force of a flow (e.g., a channel flow). However, in this case, the pressure-gradient force consequently dumps the motion inside the drop. The pressure-induced force associated with the stagnation pressure is an important factor in the Drop Deformation and Breakup (DDB) model [33, 34] introduced by Ibrahim et al., which successfully predicts the deformation of spray drops.
The pressure-gradient force generated at the impact induces an upward flow inside the drop in the time span of D0/Uimpact from the impact. The upward flow is subsequently reflected at the end of the drop due to the surface tension. Therefore, the flow induced by the pressure-gradient force generates a vertical vibrational motion. The
Meanwhile after the impact, a major part of the free-fall motion of the drop is converted to radially spreading motion, which is also subsequently reflected at the end of the drop due to the surface tension. This motion forms a vibrational motion represented by the
To investigate the breakdown of the force acting to dump inside the drop, viscous force, pressure-gradient force, and total external force (viscous force, pressure-gradient force, surface tension force, and gravitational force) were summed inside the drop of the CFD simulation for each time step. Specifically, we calculated an α-weighted summation of each force over grid cells with a negative value of inner product of a force and velocity, as expressed in ∑i,fi·Ui<0αifi, where i is an index of grid cells, fi is a force at i-th cell, Ui is velocity at i-th cell, and αi is the volume fraction of water phase at i-th cell. Considering the deformation of the bounce of the 3D drop where spreading and shrinking in vertical and radial directions, these forces were split into vertical and radial components. The radial force component shows major forces within the drop in a disk-shape, while the vertical component shows ones within the drop in a cylinder-shape. Figure 14 shows that amongst the forces damping the motion of the drop, the pressure-gradient force dominates the external forces (right-hand side of Eq. (6)) and the viscosity effect is fairly small. The small impact of the viscosity on the drop deformation was also reported by Renardy et al. [11].
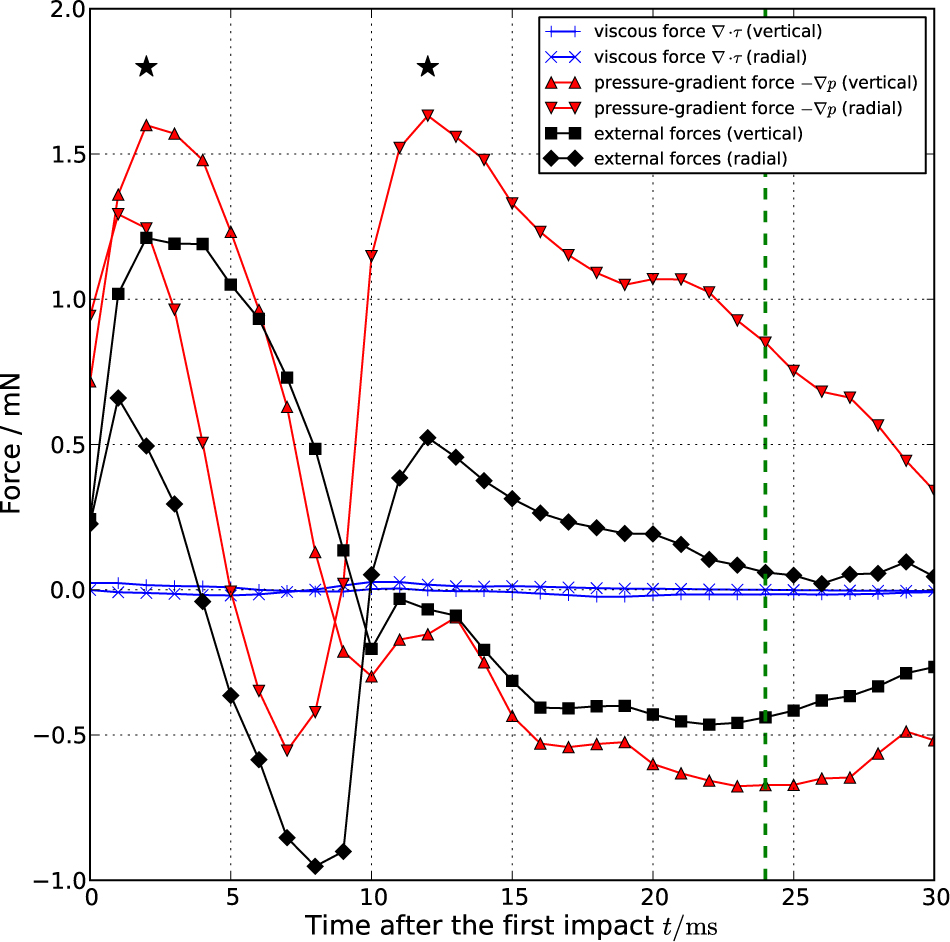
The viscous force ∇ · τ, pressure-gradient force –∇p, and the external forces (right-hand side of Eq. (6)) damping the motion of the drop for the vertical and radial directions were obtained from the simulated results (We = 7). The dashed line represents the transition point from regime I to regime II. The pressure-gradient force dominates the external force and the contribution of the viscous force is fairly small. At the two major energy losses (*), the external forces damp the velocity, the former against the vertical direction and the latter against the radial direction.
The pressure-induced motion resists the free-fall inertial motion at the beginning of the impact (t = 2 ms), and then resists the inertial motion when the drop is retracting from the disk-shape (t = 12 ms). Figure 14 shows that the pressure-gradient force dominantly resists the motion of the drop at these two timings. At the retraction of the drop, the direction of the pressure-induced motion is inherently downward, however, due to the disk-shaped drop as a flow field and the existence of the bottom plate, it is forced to advance radially (Figure 13(b)). As the result, the retracting inertial motion of the drop is dumped by this radially spreading pressure-induced motion.
Most part of the pressure-induced motion decays during the two resistances to the inertial motion, however, still remains with a small intensity after the lift-off, causing a small energy loss starting at t = 25 ms as shown in Figures 10 and 12(c).
Note that we have considered just the first dry-rebound. Biance et al. [4] have shown restitution coefficients of successive dry-rebounds of a drop with diameter of 1 mm. They reported that the restitution coefficient e is relatively low at the first impact (e ∼ We–1/2, called as poorly elastic shocks) but very close to 1 after multiple bounces (called as quasi-elastic shocks). With lower Weber number, the energy loss tends to be small as shown in Figure 7. Thus, one reason of the small energy loss after multiple bounce is the low Weber number. Biance et al. also reported that in the quasi-elastic shocks the vibration of drop’s diameter is in phase with the flight of the drop. The other reason of the small energy loss after multiple bounce is considered that the pressure surge disappears due to the inertial motion synchronized with the bounce of the drop. The synchronized
5 Conclusion
The dynamics of a dry-rebounding drop was quantitatively obtained from numerically simulated results that were assessed with respect to experimental results. The dynamics was quantitatively explained with an imaginary damped spring model, however, the second energy decay predicted by the spring model was lagged behind the simulated drop, which indicates that the true damping factor is other than the damping term of the spring model.
From the analysis of the spherical harmonic deformation, we found that the deformation is a combination of
At the beginning of the impact, the bottom part of the drop is forced to stop suddenly, which induces a pressure surge. From the simulated results, the pressure surge was actually found. The pressure-gradient force associated with the pressure surge induces a upward motion. At the same time, the free-fall motion is converted to the radially spreading motion. These two motions form two different vibrational modes due to the surface tension. The pressure-induced motion and inertial motion correspond to the
Analysis of the forces damping the motion of the drop suggested that the viscous impact on the drop is fairly small. Considering that the
Acknowledgement
A. Nishimura would like to thank Prof. Tsuguki Kinoshita for suggestions on the energy conversion. A. Nishimura would like to thank Dr. Chris Greenshields for training him in how to use OpenFOAM.
References
[1] Leidenfrost J., On the fixation of water in diverse fire, Int. J. Heat. Mass. Trans., 1966, 9, 1153-1166, 10.1016/0017-9310(66)90111-6Search in Google Scholar
[2] Quéré D., Leidenfrost Dynamics, Annu. Rev. Fluid. Mech., 2013, 45, 197-215, 10.1146/annurev-fluid-011212-140709Search in Google Scholar
[3] Biance A., Clanet C., Quéré D., Leidenfrost drops, Phys. Fluids, 2003, 15, 1632-1637, 10.1063/1.1572161Search in Google Scholar
[4] Biance A., Chevy F., Clanet C., Lagubeau G., Quéré D., On the elasticity of an inertial liquid shock, J. Fluid. Mech., 2006, 554, 47-66, 10.1017/S0022112006009189Search in Google Scholar
[5] Bertola V., Effect of polymer concentration on the dynamics of dilute polymer solution drops impacting on heated surfaces in the Leidenfrost regime, Exp. Therm. Fluid. Sci., 2014, 52, 259-269, 10.1016/j.expthermflusci.2013.09.019Search in Google Scholar
[6] Okumura K., Chevy F., Richard D., Quéré D., Clanet C., Water spring: A model for bouncing drops, EPL-Europhys. Lett., 2003, 62, 23710.1209/epl/i2003-00340-1Search in Google Scholar
[7] Bertola V., Drop impact on a hot surface: effect of a polymer additive, Exp. Fluids, 2004, 37, 653-664, 10.1007/s00348-004-0852-9Search in Google Scholar
[8] Bertola V., An experimental study of bouncing Leidenfrost drops: Comparison between Newtonian and viscoelastic liquids, Int. J. Heat. Mass. Tran., 2009, 52, 1786-1793, 10.1016/j.ijheatmasstransfer.2008.09.028Search in Google Scholar
[9] Smith M., Bertola V., Effect of Polymer Additives on the Wetting of Impacting Droplets, Phys. Rev. Lett., 2010, 104, 154502,10.1103/PhysRevLett.104.154502Search in Google Scholar PubMed
[10] Bertola V., Effect of polymer additives on the apparent dynamic contact angle of impacting drops, Colloid. Surface. A, 2010, 363, 135-140, 10.1016/j.colsurfa.2010.04.031Search in Google Scholar
[11] Renardy Y., Popinet S., Duchemin L., Renardy M., Zaleski S., Josserand C., Drumright-Clarke M.A., Richard D., Clanet C., Quéré D., Pyramidal and toroidal water drops after impact on a solid surface, J. Fluid Mech., 2003, 484, 69-83, 10.1017/S0022112003004142Search in Google Scholar
[12] Naoe T., Futakawa M., Kenny R., Otsuki M., Experimental and numerical investigations of liquid mercury droplet impacts, J. Fluid. Sci. Tech., 2014, 9, JFST0002-JFST0002, 10.1299/jfst.2014jfst0002Search in Google Scholar
[13] Roohi E., Zahiri A., Passandideh-Fard M., Numerical simulation of cavitation around a two-dimensional hydrofoil using VOF method and LES turbulence model, Appl. Math. Model., 2013, 37, 6469-6488, http://dx.doi.org/10.1016/j.apm.2012.09.002Search in Google Scholar
[14] Berberović E., van Hinsberg N., Jakirlić S., Roisman I., Tropea C., Drop impact onto a liquid layer of finite thickness: Dynamics of the cavity evolution, Phys. Rev. E, 2009, 79, 036306, 10.1103/PhysRevE.79.036306Search in Google Scholar
[15] OpenFOAM, http://www.openfoam.org/Search in Google Scholar
[16] Free Software Foundation, Inc., GNU General Public License Version 3, 2007, https://www.gnu.org/licenses/gpl.htmlSearch in Google Scholar
[17] Python, https://www.python.org/Search in Google Scholar
[18] OpenCV, http://opencv.org/Search in Google Scholar
[19] interFoam, https://github.com/OpenFOAM/OpenFOAM-3.0.x/tree/master/applications/solvers/multiphase/interFoamSearch in Google Scholar
[20] OpenFOAM-3.0, https://github.com/OpenFOAM/OpenFOAM-3.0.xSearch in Google Scholar
[21] Weller H., A new approach to VOF-based interface capturing methods for incompressible and compressible flow (Tech. Rep. No. TR/HGW/04), 2015Search in Google Scholar
[22] Brackbill J., Kothe D., Zemach C., A continuum method for modeling surface tension, J. Comput. Phys., 1992, 100, 335-354, 10.1016/0021-9991(92)90240-YSearch in Google Scholar
[23] Issa R., Solution of the implicitly discretised fluid flow equations by operator-splitting, J. Comput. Phys., 1986, 62, 40-65, 10.1016/0021-9991(86)90099-9Search in Google Scholar
[24] Ahrens J., Geveci B., Law C., ParaView: An End-User Tool for Large Data Visualization, In Visualization Handbook, Elsevier, 200510.1016/B978-012387582-2/50038-1Search in Google Scholar
[25] Mundo C., Sommerfeld M., Tropea C., Droplet-wall collisions: Experimental studies of the deformation and breakup process, Int. J. Multiphas. Flow, 1995, 21, 151-173, 10.1016/0301-9322(94)00069-VSearch in Google Scholar
[26] Okada M., Okada M., Observation of the shape of a water drop on an oscillating Teflon plate, Exp. Fluids, 2006, 41, 789–802, 10.1007/s00348-006-0203-0Search in Google Scholar
[27] Adachi K., Takaki R., Vibration of a Flattened Drop. I. Observation J. Phys. Soc. Jpn., 1984, 53, 4184-4191, 10.1143/JPSJ.53.4184Search in Google Scholar
[28] Takaki R., Adachi K., Vibration of a Flattened Drop. II. Normal Mode Analysis, J. Phys. Soc. Jpn., 1985, 54, 2462-2469, 10.1143/JPSJ.54.2462Search in Google Scholar
[29] Yoshiyasu N., Adachi K., Takaki R., Effect of Ambient Temperature on the Self-Induced Vibration of Boiling Drop, J. Phys. Soc. Jpn., 1993, 62, 2314-2323, 10.1143/JPSJ.62.2314Search in Google Scholar
[30] Lamb H., Hydrodynamics 6th ed., Dover Publications, 1945Search in Google Scholar
[31] Prosperetti A., Free oscillations of drops and bubbles: the initial-value problem, J. Fluid. Mech., 1980, 100, 333-347, 10.1017/S0022112080001188Search in Google Scholar
[32] Landau L., Lifshitz E., Fluid mechanics 2nd ed., Butterworth-Heinemann, 1987Search in Google Scholar
[33] Ibrahim E., Yang H., Przekwas A., Modeling of spray droplets deformation and breakup, J. Propul. Power., 1993, 9, 651-65410.2514/3.23672Search in Google Scholar
[34] Vargas M., Droplet Deformation Prediction with the Droplet Deformation and Breakup Model (DDB), In 4th AIAA Atmospheric and Space Environments Conference, 2012, pp. 313110.2514/6.2012-3131Search in Google Scholar
Coefficients of the imaginary damped spring model
To conserve the kinetic energy at impact, the impact speed of the spring,
Assuming that the strain of the spring has a maximal value at lift-off, the under-damped angular frequency, ωd,I, can be obtained by the period, Td,I, which is equal to twice the length of time from the minimum ϵ to the maximum ϵ:
The time derivative of the strain at impact is equal to the impact speed:
which leads, by assuming sin(ψI) ≈ 0 and cos(ψI) ≈ 1, to the amplitude
At the first moment of impact, assuming that mass point 1 continues to move at
The stiffness, kI, can be obtained from
At the start of contact of the bottom mass point of the spring (tI = 0), the strain is considered to be zero (ϵI = 0); therefore, the value of ψI can be obtained:
Assuming that the strain reaches a maximum at lift-off (tII = 0),
we obtain
The centroid of the spring in regime II, xc,II, is
and the velocity of the centroid of the spring is
where Ulift-off and xc, lift-off are respectively the velocity and the position of the centroid of the spring at lift-off. Ulift-off was obtained from
© 2018 A. Nishimura et al., published by De Gruyter
This work is licensed under the Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 License.
Articles in the same Issue
- Regular Articles
- A modified Fermi-Walker derivative for inextensible flows of binormal spherical image
- Algebraic aspects of evolution partial differential equation arising in the study of constant elasticity of variance model from financial mathematics
- Three-dimensional atom localization via probe absorption in a cascade four-level atomic system
- Determination of the energy transitions and half-lives of Rubidium nuclei
- Three phase heat and mass transfer model for unsaturated soil freezing process: Part 1 - model development
- Three phase heat and mass transfer model for unsaturated soil freezing process: Part 2 - model validation
- Mathematical model for thermal and entropy analysis of thermal solar collectors by using Maxwell nanofluids with slip conditions, thermal radiation and variable thermal conductivity
- Constructing analytic solutions on the Tricomi equation
- Feynman diagrams and rooted maps
- New type of chaos synchronization in discrete-time systems: the F-M synchronization
- Unsteady flow of fractional Oldroyd-B fluids through rotating annulus
- A note on the uniqueness of 2D elastostatic problems formulated by different types of potential functions
- On the conservation laws and solutions of a (2+1) dimensional KdV-mKdV equation of mathematical physics
- Computational methods and traveling wave solutions for the fourth-order nonlinear Ablowitz-Kaup-Newell-Segur water wave dynamical equation via two methods and its applications
- Siewert solutions of transcendental equations, generalized Lambert functions and physical applications
- Numerical solution of mixed convection flow of an MHD Jeffery fluid over an exponentially stretching sheet in the presence of thermal radiation and chemical reaction
- A new three-dimensional chaotic flow with one stable equilibrium: dynamical properties and complexity analysis
- Dynamics of a dry-rebounding drop: observations, simulations, and modeling
- Modeling the initial mechanical response and yielding behavior of gelled crude oil
- Lie symmetry analysis and conservation laws for the time fractional simplified modified Kawahara equation
- Solitary wave solutions of two KdV-type equations
- Applying industrial tomography to control and optimization flow systems
- Reconstructing time series into a complex network to assess the evolution dynamics of the correlations among energy prices
- An optimal solution for software testing case generation based on particle swarm optimization
- Optimal system, nonlinear self-adjointness and conservation laws for generalized shallow water wave equation
- Alternative methods for solving nonlinear two-point boundary value problems
- Global model simulation of OH production in pulsed-DC atmospheric pressure helium-air plasma jets
- Experimental investigation on optical vortex tweezers for microbubble trapping
- Joint measurements of optical parameters by irradiance scintillation and angle-of-arrival fluctuations
- M-polynomials and topological indices of hex-derived networks
- Generalized convergence analysis of the fractional order systems
- Porous flow characteristics of solution-gas drive in tight oil reservoirs
- Complementary wave solutions for the long-short wave resonance model via the extended trial equation method and the generalized Kudryashov method
- A Note on Koide’s Doubly Special Parametrization of Quark Masses
- On right-angled spherical Artin monoid of type Dn
- Gas flow regimes judgement in nanoporous media by digital core analysis
- 4 + n-dimensional water and waves on four and eleven-dimensional manifolds
- Stabilization and Analytic Approximate Solutions of an Optimal Control Problem
- On the equations of electrodynamics in a flat or curved spacetime and a possible interaction energy
- New prediction method for transient productivity of fractured five-spot patterns in low permeability reservoirs at high water cut stages
- The collinear equilibrium points in the restricted three body problem with triaxial primaries
- Detection of the damage threshold of fused silica components and morphologies of repaired damage sites based on the beam deflection method
- On the bivariate spectral quasi-linearization method for solving the two-dimensional Bratu problem
- Ion acoustic quasi-soliton in an electron-positron-ion plasma with superthermal electrons and positrons
- Analysis of projectile motion in view of conformable derivative
- Computing multiple ABC index and multiple GA index of some grid graphs
- Terahertz pulse imaging: A novel denoising method by combing the ant colony algorithm with the compressive sensing
- Characteristics of microscopic pore-throat structure of tight oil reservoirs in Sichuan Basin measured by rate-controlled mercury injection
- An activity window model for social interaction structure on Twitter
- Transient thermal regime trough the constitutive matrix applied to asynchronous electrical machine using the cell method
- On the zagreb polynomials of benzenoid systems
- Integrability analysis of the partial differential equation describing the classical bond-pricing model of mathematical finance
- The Greek parameters of a continuous arithmetic Asian option pricing model via Laplace Adomian decomposition method
- Quantifying the global solar radiation received in Pietermaritzburg, KwaZulu-Natal to motivate the consumption of solar technologies
- Sturm-Liouville difference equations having Bessel and hydrogen atom potential type
- Study on the response characteristics of oil wells after deep profile control in low permeability fractured reservoirs
- Depiction and analysis of a modified theta shaped double negative metamaterial for satellite application
- An attempt to geometrize electromagnetism
- Structure of traveling wave solutions for some nonlinear models via modified mathematical method
- Thermo-convective instability in a rotating ferromagnetic fluid layer with temperature modulation
- Construction of new solitary wave solutions of generalized Zakharov-Kuznetsov-Benjamin-Bona-Mahony and simplified modified form of Camassa-Holm equations
- Effect of magnetic field and heat source on Upper-convected-maxwell fluid in a porous channel
- Physical cues of biomaterials guide stem cell fate of differentiation: The effect of elasticity of cell culture biomaterials
- Shooting method analysis in wire coating withdrawing from a bath of Oldroyd 8-constant fluid with temperature dependent viscosity
- Rank correlation between centrality metrics in complex networks: an empirical study
- Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering
- Modeling of electric and heat processes in spot resistance welding of cross-wire steel bars
- Dynamic characteristics of triaxial active control magnetic bearing with asymmetric structure
- Design optimization of an axial-field eddy-current magnetic coupling based on magneto-thermal analytical model
- Thermal constitutive matrix applied to asynchronous electrical machine using the cell method
- Temperature distribution around thin electroconductive layers created on composite textile substrates
- Model of the multipolar engine with decreased cogging torque by asymmetrical distribution of the magnets
- Analysis of spatial thermal field in a magnetic bearing
- Use of the mathematical model of the ignition system to analyze the spark discharge, including the destruction of spark plug electrodes
- Assessment of short/long term electric field strength measurements for a pilot district
- Simulation study and experimental results for detection and classification of the transient capacitor inrush current using discrete wavelet transform and artificial intelligence
- Magnetic transmission gear finite element simulation with iron pole hysteresis
- Pulsed excitation terahertz tomography – multiparametric approach
- Low and high frequency model of three phase transformer by frequency response analysis measurement
- Multivariable polynomial fitting of controlled single-phase nonlinear load of input current total harmonic distortion
- Optimal design of a for middle-low-speed maglev trains
- Eddy current modeling in linear and nonlinear multifilamentary composite materials
- The visual attention saliency map for movie retrospection
- AC/DC current ratio in a current superimposition variable flux reluctance machine
- Influence of material uncertainties on the RLC parameters of wound inductors modeled using the finite element method
- Cogging force reduction in linear tubular flux switching permanent-magnet machines
- Modeling hysteresis curves of La(FeCoSi)13 compound near the transition point with the GRUCAD model
- Electro-magneto-hydrodynamic lubrication
- 3-D Electromagnetic field analysis of wireless power transfer system using K computer
- Simplified simulation technique of rotating, induction heated, calender rolls for study of temperature field control
- Design, fabrication and testing of electroadhesive interdigital electrodes
- A method to reduce partial discharges in motor windings fed by PWM inverter
- Reluctance network lumped mechanical & thermal models for the modeling and predesign of concentrated flux synchronous machine
- Special Issue Applications of Nonlinear Dynamics
- Study on dynamic characteristics of silo-stock-foundation interaction system under seismic load
- Microblog topic evolution computing based on LDA algorithm
- Modeling the creep damage effect on the creep crack growth behavior of rotor steel
- Neighborhood condition for all fractional (g, f, n′, m)-critical deleted graphs
- Chinese open information extraction based on DBMCSS in the field of national information resources
- 10.1515/phys-2018-0079
- CPW-fed circularly-polarized antenna array with high front-to-back ratio and low-profile
- Intelligent Monitoring Network Construction based on the utilization of the Internet of things (IoT) in the Metallurgical Coking Process
- Temperature detection technology of power equipment based on Fiber Bragg Grating
- Research on a rotational speed control strategy of the mandrel in a rotary steering system
- Dynamic load balancing algorithm for large data flow in distributed complex networks
- Super-structured photonic crystal fiber Bragg grating biosensor image model based on sparse matrix
- Fractal-based techniques for physiological time series: An updated approach
- Analysis of the Imaging Characteristics of the KB and KBA X-ray Microscopes at Non-coaxial Grazing Incidence
- Application of modified culture Kalman filter in bearing fault diagnosis
- Exact solutions and conservation laws for the modified equal width-Burgers equation
- On topological properties of block shift and hierarchical hypercube networks
- Elastic properties and plane acoustic velocity of cubic Sr2CaMoO6 and Sr2CaWO6 from first-principles calculations
- A note on the transmission feasibility problem in networks
- Ontology learning algorithm using weak functions
- Diagnosis of the power frequency vacuum arc shape based on 2D-PIV
- Parametric simulation analysis and reliability of escalator truss
- A new algorithm for real economy benefit evaluation based on big data analysis
- Synergy analysis of agricultural economic cycle fluctuation based on ant colony algorithm
- Multi-level encryption algorithm for user-related information across social networks
- Multi-target tracking algorithm in intelligent transportation based on wireless sensor network
- Fast recognition method of moving video images based on BP neural networks
- Compressed sensing image restoration algorithm based on improved SURF operator
- Design of load optimal control algorithm for smart grid based on demand response in different scenarios
- Face recognition method based on GA-BP neural network algorithm
- Optimal path selection algorithm for mobile beacons in sensor network under non-dense distribution
- Localization and recognition algorithm for fuzzy anomaly data in big data networks
- Urban road traffic flow control under incidental congestion as a function of accident duration
- Optimization design of reconfiguration algorithm for high voltage power distribution network based on ant colony algorithm
- Feasibility simulation of aseismic structure design for long-span bridges
- Construction of renewable energy supply chain model based on LCA
- The tribological properties study of carbon fabric/ epoxy composites reinforced by nano-TiO2 and MWNTs
- A text-Image feature mapping algorithm based on transfer learning
- Fast recognition algorithm for static traffic sign information
- Topical Issue: Clean Energy: Materials, Processes and Energy Generation
- An investigation of the melting process of RT-35 filled circular thermal energy storage system
- Numerical analysis on the dynamic response of a plate-and-frame membrane humidifier for PEMFC vehicles under various operating conditions
- Energy converting layers for thin-film flexible photovoltaic structures
- Effect of convection heat transfer on thermal energy storage unit
Articles in the same Issue
- Regular Articles
- A modified Fermi-Walker derivative for inextensible flows of binormal spherical image
- Algebraic aspects of evolution partial differential equation arising in the study of constant elasticity of variance model from financial mathematics
- Three-dimensional atom localization via probe absorption in a cascade four-level atomic system
- Determination of the energy transitions and half-lives of Rubidium nuclei
- Three phase heat and mass transfer model for unsaturated soil freezing process: Part 1 - model development
- Three phase heat and mass transfer model for unsaturated soil freezing process: Part 2 - model validation
- Mathematical model for thermal and entropy analysis of thermal solar collectors by using Maxwell nanofluids with slip conditions, thermal radiation and variable thermal conductivity
- Constructing analytic solutions on the Tricomi equation
- Feynman diagrams and rooted maps
- New type of chaos synchronization in discrete-time systems: the F-M synchronization
- Unsteady flow of fractional Oldroyd-B fluids through rotating annulus
- A note on the uniqueness of 2D elastostatic problems formulated by different types of potential functions
- On the conservation laws and solutions of a (2+1) dimensional KdV-mKdV equation of mathematical physics
- Computational methods and traveling wave solutions for the fourth-order nonlinear Ablowitz-Kaup-Newell-Segur water wave dynamical equation via two methods and its applications
- Siewert solutions of transcendental equations, generalized Lambert functions and physical applications
- Numerical solution of mixed convection flow of an MHD Jeffery fluid over an exponentially stretching sheet in the presence of thermal radiation and chemical reaction
- A new three-dimensional chaotic flow with one stable equilibrium: dynamical properties and complexity analysis
- Dynamics of a dry-rebounding drop: observations, simulations, and modeling
- Modeling the initial mechanical response and yielding behavior of gelled crude oil
- Lie symmetry analysis and conservation laws for the time fractional simplified modified Kawahara equation
- Solitary wave solutions of two KdV-type equations
- Applying industrial tomography to control and optimization flow systems
- Reconstructing time series into a complex network to assess the evolution dynamics of the correlations among energy prices
- An optimal solution for software testing case generation based on particle swarm optimization
- Optimal system, nonlinear self-adjointness and conservation laws for generalized shallow water wave equation
- Alternative methods for solving nonlinear two-point boundary value problems
- Global model simulation of OH production in pulsed-DC atmospheric pressure helium-air plasma jets
- Experimental investigation on optical vortex tweezers for microbubble trapping
- Joint measurements of optical parameters by irradiance scintillation and angle-of-arrival fluctuations
- M-polynomials and topological indices of hex-derived networks
- Generalized convergence analysis of the fractional order systems
- Porous flow characteristics of solution-gas drive in tight oil reservoirs
- Complementary wave solutions for the long-short wave resonance model via the extended trial equation method and the generalized Kudryashov method
- A Note on Koide’s Doubly Special Parametrization of Quark Masses
- On right-angled spherical Artin monoid of type Dn
- Gas flow regimes judgement in nanoporous media by digital core analysis
- 4 + n-dimensional water and waves on four and eleven-dimensional manifolds
- Stabilization and Analytic Approximate Solutions of an Optimal Control Problem
- On the equations of electrodynamics in a flat or curved spacetime and a possible interaction energy
- New prediction method for transient productivity of fractured five-spot patterns in low permeability reservoirs at high water cut stages
- The collinear equilibrium points in the restricted three body problem with triaxial primaries
- Detection of the damage threshold of fused silica components and morphologies of repaired damage sites based on the beam deflection method
- On the bivariate spectral quasi-linearization method for solving the two-dimensional Bratu problem
- Ion acoustic quasi-soliton in an electron-positron-ion plasma with superthermal electrons and positrons
- Analysis of projectile motion in view of conformable derivative
- Computing multiple ABC index and multiple GA index of some grid graphs
- Terahertz pulse imaging: A novel denoising method by combing the ant colony algorithm with the compressive sensing
- Characteristics of microscopic pore-throat structure of tight oil reservoirs in Sichuan Basin measured by rate-controlled mercury injection
- An activity window model for social interaction structure on Twitter
- Transient thermal regime trough the constitutive matrix applied to asynchronous electrical machine using the cell method
- On the zagreb polynomials of benzenoid systems
- Integrability analysis of the partial differential equation describing the classical bond-pricing model of mathematical finance
- The Greek parameters of a continuous arithmetic Asian option pricing model via Laplace Adomian decomposition method
- Quantifying the global solar radiation received in Pietermaritzburg, KwaZulu-Natal to motivate the consumption of solar technologies
- Sturm-Liouville difference equations having Bessel and hydrogen atom potential type
- Study on the response characteristics of oil wells after deep profile control in low permeability fractured reservoirs
- Depiction and analysis of a modified theta shaped double negative metamaterial for satellite application
- An attempt to geometrize electromagnetism
- Structure of traveling wave solutions for some nonlinear models via modified mathematical method
- Thermo-convective instability in a rotating ferromagnetic fluid layer with temperature modulation
- Construction of new solitary wave solutions of generalized Zakharov-Kuznetsov-Benjamin-Bona-Mahony and simplified modified form of Camassa-Holm equations
- Effect of magnetic field and heat source on Upper-convected-maxwell fluid in a porous channel
- Physical cues of biomaterials guide stem cell fate of differentiation: The effect of elasticity of cell culture biomaterials
- Shooting method analysis in wire coating withdrawing from a bath of Oldroyd 8-constant fluid with temperature dependent viscosity
- Rank correlation between centrality metrics in complex networks: an empirical study
- Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering
- Modeling of electric and heat processes in spot resistance welding of cross-wire steel bars
- Dynamic characteristics of triaxial active control magnetic bearing with asymmetric structure
- Design optimization of an axial-field eddy-current magnetic coupling based on magneto-thermal analytical model
- Thermal constitutive matrix applied to asynchronous electrical machine using the cell method
- Temperature distribution around thin electroconductive layers created on composite textile substrates
- Model of the multipolar engine with decreased cogging torque by asymmetrical distribution of the magnets
- Analysis of spatial thermal field in a magnetic bearing
- Use of the mathematical model of the ignition system to analyze the spark discharge, including the destruction of spark plug electrodes
- Assessment of short/long term electric field strength measurements for a pilot district
- Simulation study and experimental results for detection and classification of the transient capacitor inrush current using discrete wavelet transform and artificial intelligence
- Magnetic transmission gear finite element simulation with iron pole hysteresis
- Pulsed excitation terahertz tomography – multiparametric approach
- Low and high frequency model of three phase transformer by frequency response analysis measurement
- Multivariable polynomial fitting of controlled single-phase nonlinear load of input current total harmonic distortion
- Optimal design of a for middle-low-speed maglev trains
- Eddy current modeling in linear and nonlinear multifilamentary composite materials
- The visual attention saliency map for movie retrospection
- AC/DC current ratio in a current superimposition variable flux reluctance machine
- Influence of material uncertainties on the RLC parameters of wound inductors modeled using the finite element method
- Cogging force reduction in linear tubular flux switching permanent-magnet machines
- Modeling hysteresis curves of La(FeCoSi)13 compound near the transition point with the GRUCAD model
- Electro-magneto-hydrodynamic lubrication
- 3-D Electromagnetic field analysis of wireless power transfer system using K computer
- Simplified simulation technique of rotating, induction heated, calender rolls for study of temperature field control
- Design, fabrication and testing of electroadhesive interdigital electrodes
- A method to reduce partial discharges in motor windings fed by PWM inverter
- Reluctance network lumped mechanical & thermal models for the modeling and predesign of concentrated flux synchronous machine
- Special Issue Applications of Nonlinear Dynamics
- Study on dynamic characteristics of silo-stock-foundation interaction system under seismic load
- Microblog topic evolution computing based on LDA algorithm
- Modeling the creep damage effect on the creep crack growth behavior of rotor steel
- Neighborhood condition for all fractional (g, f, n′, m)-critical deleted graphs
- Chinese open information extraction based on DBMCSS in the field of national information resources
- 10.1515/phys-2018-0079
- CPW-fed circularly-polarized antenna array with high front-to-back ratio and low-profile
- Intelligent Monitoring Network Construction based on the utilization of the Internet of things (IoT) in the Metallurgical Coking Process
- Temperature detection technology of power equipment based on Fiber Bragg Grating
- Research on a rotational speed control strategy of the mandrel in a rotary steering system
- Dynamic load balancing algorithm for large data flow in distributed complex networks
- Super-structured photonic crystal fiber Bragg grating biosensor image model based on sparse matrix
- Fractal-based techniques for physiological time series: An updated approach
- Analysis of the Imaging Characteristics of the KB and KBA X-ray Microscopes at Non-coaxial Grazing Incidence
- Application of modified culture Kalman filter in bearing fault diagnosis
- Exact solutions and conservation laws for the modified equal width-Burgers equation
- On topological properties of block shift and hierarchical hypercube networks
- Elastic properties and plane acoustic velocity of cubic Sr2CaMoO6 and Sr2CaWO6 from first-principles calculations
- A note on the transmission feasibility problem in networks
- Ontology learning algorithm using weak functions
- Diagnosis of the power frequency vacuum arc shape based on 2D-PIV
- Parametric simulation analysis and reliability of escalator truss
- A new algorithm for real economy benefit evaluation based on big data analysis
- Synergy analysis of agricultural economic cycle fluctuation based on ant colony algorithm
- Multi-level encryption algorithm for user-related information across social networks
- Multi-target tracking algorithm in intelligent transportation based on wireless sensor network
- Fast recognition method of moving video images based on BP neural networks
- Compressed sensing image restoration algorithm based on improved SURF operator
- Design of load optimal control algorithm for smart grid based on demand response in different scenarios
- Face recognition method based on GA-BP neural network algorithm
- Optimal path selection algorithm for mobile beacons in sensor network under non-dense distribution
- Localization and recognition algorithm for fuzzy anomaly data in big data networks
- Urban road traffic flow control under incidental congestion as a function of accident duration
- Optimization design of reconfiguration algorithm for high voltage power distribution network based on ant colony algorithm
- Feasibility simulation of aseismic structure design for long-span bridges
- Construction of renewable energy supply chain model based on LCA
- The tribological properties study of carbon fabric/ epoxy composites reinforced by nano-TiO2 and MWNTs
- A text-Image feature mapping algorithm based on transfer learning
- Fast recognition algorithm for static traffic sign information
- Topical Issue: Clean Energy: Materials, Processes and Energy Generation
- An investigation of the melting process of RT-35 filled circular thermal energy storage system
- Numerical analysis on the dynamic response of a plate-and-frame membrane humidifier for PEMFC vehicles under various operating conditions
- Energy converting layers for thin-film flexible photovoltaic structures
- Effect of convection heat transfer on thermal energy storage unit

