Home Physical Sciences Exact solutions and conservation laws for the modified equal width-Burgers equation
Article Open Access

Exact solutions and conservation laws for the modified equal width-Burgers equation

  • Chaudry Masood Khalique EMAIL logo and Innocent Simbanefayi
Published/Copyright: December 26, 2018
Download Article (PDF)
Open Physics
From the journal Open Physics Volume 16 Issue 1

Abstract

In this paper we study the modified equal width-Burgers equation, which describes long wave propagation in nonlinear media with dispersion and dissipation. Using the Lie symmetry method in conjunction with the (G'/G)− expansion method we construct its travelling wave solutions. Also, we determine the conservation laws by invoking the new conservation theorem due to Ibragimov. As a result we obtain energy and linear momentum conservation laws.

Keywords: Modified equal width-Burgers equation; Lie point symmetries; exact solutions; conservation laws
PACS: 02.30.Jr; 04.20.Jb; 11.30.-j

1 Introduction

It is well-known that majority of the real-world physical phenomena are modeled by mathematical equations, especially nonlinear partial differential equations (NLPDEs). These phenomena include the problems from fluid mechanics, elasticity, plasma and optical fibers, relativity, gas dynamics, thermodynamics, and many more. In order to comprehend the understanding of such physical phenomena it is vital to look for exact solutions of the NLPDEs. During the last sixty years many scientists and mathematicians developed several effective and useful methods for obtaining exact solutions of NLPDEs. These include the simplified Hirota’s method [1, 2], the tanh-coth method [3], the sine-cosine method [4], the simplest equation method[5], the homogeneous balance method [6], the inverse scattering transform method [7], Hirota’s bilinear method [8], the (G'/G)−expansion method [9, 10], Riccati-Bernoulli sub-ordinary differential equation method [11], Jacobi elliptic function expansion method[12, 13], Kudryashov method [14, 15], the Lie symmetry method [16, 17, 18, 19, 20, 21], just to mention a few.

On the other hand conservation laws are very important in the study of NLPDEs and much research has been done on different methods of obtaining conservation laws. Conservation laws are essential in determining the extent of integrability of differential equations, development of numerical schemes, reduction and solutions of partial differential equations. See, for example [22, 23, 24, 25, 26, 27, 28, 29] and references therein.

The Burgers equation

(1.1)ut+uux−vuxx=0,

where v is a constant defining the kinematic viscosity models the turbulent flow in a channel and describes the effect of coupling between diffusion and convection processes on a fluid. It first appeared in academic circles in [30]. Over the years, various researchers have applied modifications to (1.1) and used many different methods to study the equation. For example, the equal width equation

(1.2)ut−uux−utxx=0

was first introduced in [31]. It describes amongst others, nonlinear dispersive waves such as shallow water waves and nonlinear waves in plasmas. Extensive work was done on Equation (1.2) in constructing numerical solutions [32, 33]. Arora et al. [34] performed the reduced differential transform method to find the numerical solution of the equal width wave equation and the exact analytical solution of the inviscid Burgers equation with initial conditions.

The modified equal width equation

(1.3)ut+au2ux−butxx=0

was studied in [35] and solitary wave solutions were obtained. Furthermore, using Quintic B-spline method the interactions through computer simulation were observed. In [36] the sine-cosine and the tanh methods were employed to obtain exact solutions of (1.3) and two of its variants, which included compactons, solitons, solitary patterns, and periodic solutions. Hasan [37] presented the numerical solution for (1.3) using Fourier spectral method that discretizes the space variable and Leap-frog method scheme for time dependence.

The generalised equal width equation

(1.4)ut+aumux−butxx=0

was studied in [38] and its solitary wave solutions were obtained by a collocation method using quadratic B-spline at the midpoints.

In [39] the author introduced the modified equal width-Burgers (MEW-Burgers) equation

(1.5)ut+αu2ux+ωuxx−βutxx=0,

which describes long wave propagation in nonlinear media with dispersion and dissipation. Here α, β are positive parameters and ω is a damping parameter. The bifurcation behaviour and an external periodic perturbation of the MEW-Burgers equation (1.5) was studied [39].

In this paper using the Lie symmetry method and the (G0/G)−expansion method we construct travelling wave solutions of (1.5). Furthermore, we derive the conservation laws by applying the new conservation theorem due to Ibragimov.

2 Travelling wave solutions of (1.5)

In this section we obtain travelling wave solutions of (1.5) by employing Lie symmetry analysis together with the (G'/G)−expansion method.

2.1 Lie point symmetries and reduction of (1.5)

We begin by determining the Lie point symmetries of (1.5). The vector field

(2.6)X=ξ1(t,u,x)∂∂t+ξ2(t,u,x)∂∂x+η(t,u,x)∂∂u

is a Lie point symmetry of (1.5) if and only if

(2.7)X[3](ut+αu2ux+ωuxx−βutxx)|(1.5)=0,

where

X[3]=X+ζ1∂∂ut+ζ2∂∂ux+ζ22∂∂uxx+ζ122∂∂utxx

is the third prolongation of X [18]. Expanding (2.7), we obtain

(2.8)ηt+2uxutξu2+2βuttxξt1−2μut,xξx1+2βutx2ξu1+βutxξxx2−μuxξxx2+βuttξxx1+2μuxηxu−μutξxx1−2βut,xηxu+αu2ηx+βξtxx1ut+βξtxx2ux+2βξtx1ut,x+2βuxxξtx2−βutηxxu−βηtuuux2−βηtuuxx+βξxxu1ut2+ux3βξtuu2+2βξtxu2ux2−2βuxηtxu−2μux2ξxu2−μux3ξuu2+μux2ηuu+μuxxξt1+βuxxxξt2+2ξx2ut−ξt2ux+ξu1ut2+μηxx−βηtxx+βutuxξuxx2+3βuxuxxξtu2+βutux2ξtuu1+2βutuxξtxu1−βutux2ηuuu+2αuuxη+βut2ux2ξuuu1+βuxxutξtu1+2uxutxβξtu1+4βututxξxu1+2βuxuttξxu1−2μutuxξxu1+2uxxutβξxu2+4uxβutxξxu2+3βux2utxξuu2−βuxxutηuu−2βutxηuu+βut2uxxξuu1+βux2uttξuu1−μutux2ξuu1+αu2uxξx2+αu2uxξt1+2ξu2αu2ux2+ξu2βutuxxx+3ξu2βutxuxx−αu2utξx1+2βuttxuxξu1+βuxxuttξu1+μuxxutξu1−2μuxutxξu1+utux3βξuuu2+2βut2uxξxuu1+2βutux2ξxuu2−2βutuxηxuu+3βutuxuxxξuu2+4βutuxutxξuu1+αu2utuxξu1=0.

Splitting the above equation with respect to derivatives of u yields the system of ten overdetermined linear partial differential equations

(2.9)ξx1=0,
(2.10)ξu1=0,
(2.11)ξt2=0,
(2.12)ξu2=0,
(2.13)ηuu=0,
(2.14)ξxx2−2ηxu=0,
(2.15)μξt1−βηtu=0,
(2.16)2ξx2−βηxxu=0,
(2.17)μηxx−βηtxx+ηt+αu2ηx=0,
(2.18)αu2ξx2+αu2ξt1+2αuη+2μηxu−μξxx2−2βηtxu=0.

Solving (2.9)–(2.18) for ξ1, ξ2 and η we obtain

ξ1=C1   ,ξ2=C2,   η=0,

which results in two translation symmetries

X1=∂∂t,  X2=∂∂x.

A linear combination of these Lie point symmetries, that is, X = X1 + cX2 produces the associated Lagrange equations

(2.19)dt1=dxc=du0,

which upon solving yields the two invariants z = x − ct and U = u, and hence the group-invariant solution u = U(z). Taking U and z as the new dependent and independent variables respectively, equation (1.5) is transformed into the third-order nonlinear ordinary differential equation (ODE)

(2.20)βcU′′′(z)−cU′(z)+ωU′′(z)+αU(z)2U′(z)=0.

2.2 Solution of (2.20) using (G'/G)−expansion method

In this subsection we use the (G'/G)−expansion method [9] to obtain solutions of (2.20). Firstly, we assume that

(2.21)U(z)=∑i=0mAi(G′(z)G(z))i

is the solution to (2.20), where A0, A1, · · · Am are to be determined. The balancing procedure is used to find the value of m, a positive integer. In our case the balancing procedure yields m = 1, thus (2.21) becomes

(2.22)U(z)=A0+A1(G′(z)G(z)).

Secondly, we substitute (2.22) into (2.20) and simultaneously use the second-order ODE

G′′+λG′(z)+μG(z)=0,

where λ and μ are arbitrary constants. This yields

(2.23)A1λμω+A1cμ−2A1βcμ2−αA02A1μ−A1βcλ2μ+(A1cλ−8A1βcλμ−A1βcλ3+2A1μω+A1λ2ω−αA02A1λ−2αA0A12μ)(G′(z)G(z))+(A1c−7A1βcλ2−8A1βcμ−αA02A1−2αA0A12λ−αA13μ+3A1λω)(G′(z)G(z))2+(2A1ω−2αA0A12−αA13λ−12A1βcλ)(G′(z)G(z))3−(6A1+βc+αA13)(G′(z)G(z))4=0.

Collecting terms with like powers of (G'/G) and equating them to zero gives the overdetermined system of five algebraic equations

(G′(z)G(z))4:αA13+6A1βc=0,
(G′(z)G(z))3:αA13λ+2αA0A12+12A1βcλ−2Α1ω=0,
(G′(z)G(z))2:2αA0A12λ + αΑ13μ+αA02A1+7A1βcλ2                        +8A1βcμ−A1c−3A1λω=0,
(G′(z)G(z))1:αA02Α1λ +2 αΑ0Α12μ+A1βcλ3+8A1βcλμ                        −A1cλ−A1λ2ω−2A1μω=0,
(G′(z)G(z))0:A1λμω+Α1cμ−αA02A1μ−A1βcλ2μ                         −2A1βcμ2=0.

Using Mathematica, two solutions of the above system of algebraic equations are

Solution set 1

A0−−2λω3α,    A1=−6ωλα,     c=23λ(3μ−λ2).

Solution set 2

A0=−2ωμα,    A1=32ωαμ,     c=−4ωμ3.

Thus corresponding to solution set 1 above, we have the following three types of solutions for the MEW-Burgers (1.5):

Case 1.1 For M = λ2 − 4μ > 0, we obtain the hyperbolic function solution

(2.24)u(t,x)=(1+3λ)−2λω3α                  (Δ1Acosh(Δ 1z)+Bsinh(Δ 1z)Asinh(Δ 1z)+Bcosh(Δ 1z)−λ2),

where Δ 1=M/2,z=x−2(3μ−λ2)t/(3λ)and A and B are constants.

Case 1.2 For M = λ2 − 4μ < 0, we obtain the trigonometric function solution

(2.25)u(t,x)=(1+3λ)−2λω3α                    (Δ 2Asinh(Δ 2z)+Bcosh(Δ 2z)Acos(Δ 2z)+Bsin(Δ 2z)−λ2),

where Δ2=−M/2,  z=x−2(3μ−λ2)t/(3λ)and A and B are constants.

Case 1.3 For M = λ2 − 4μ = 0, we obtain the rational function solution

(2.26)u(t,x)=(1+3λ)−2λω3α(BBz+A−λ2),

where z = x − 2(3μ − λ2)t/(3λ) and A and B are constants.

Similarly, considering the solution set 2 we obtain the following three types of solutions for the MEW-Burgers (1.5):

Case 2.1 For M = λ2 − 4μ > 0, we obtain the hyperbolic function solution

u(t,x)=(1+4βx)2μωα                   (λ2−Δ 1Acosh(Δ 1z)+Bsinh(Δ 1z)Asinh(Δ 1z)+Bcosh(Δ 1z)),

where Δ 1=M/2,z=x+4μ ωt/3and A and B are constants.

Case 2.2 For M = λ2 − 4μ < 0, we obtain the trigonometric function solution

u(t,x)=(1+4βλ)2μωα                (λ2−Δ 2Asin(Δ 2z)+Bcos(Δ 2z)Acos(Δ 2z)+Bsin(Δ 2z)),

where Δ 2=−M/2,  z=x+4μωt/3and A and B are constants.

Case 2.3 For M = λ2 − 4μ = 0, we obtain the rational function solution

u(t,x)=(1+4βλ)2μωα(BBz+A−λ2),

where z=x+4μ  ωt/3and A and B are constants.

The solution profile of (2.24) for λ = −0.09, A = 0, B = 1, μ = 0.01, ω = 0.03, α = 1 is presented in Figure 1, whereas the solution profile of (2.26) for λ = −0.8, A = 0.4, B = 3, μ = 0.2, ω = 0.01, α = 0.1 is given in Figure 2.

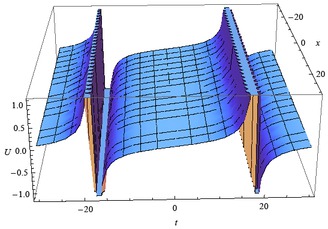
Figure 1 Profile of solution (2.24)
Figure 1

Profile of solution (2.24)

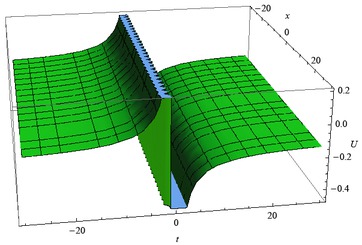
Figure 2 Profile of solution (2.26)
Figure 2

Profile of solution (2.26)

3 Conservation laws of (1.5)

In this section we derive conservation laws for the MEW-Burgers equation (1.5) using the new conservation theorem due to Ibragimov [40, 41].

We begin by determining the adjoint equation of (1.5), namely

F≡ut+αu2ux+ωuxx−βutxx=0,

using the formula

(3.27)F⋆≡δδu{v(ut+αu2ux+ωuxx−βutxx)}=0,

where δ/u is the Euler-Lagrange operator defined by

(3.28)δδu=∂∂u−Dt∂∂ut−Dx∂∂ux+Dx2∂∂uxx−DtDx2∂∂utxx

with the total differential operators Dt and D x given by

Dt=∂∂t+ut∂∂u+vt∂∂v+utt∂∂ut+vtt∂∂vt         +utx∂∂ux+vtx∂∂vx+⋯,Dt=∂∂x+ux∂∂u+vx∂∂v+uxx∂∂ux+vxx∂∂vx         +uxt∂∂ut+vxt∂∂vt+⋯.

Thus Equation (3.27) becomes

(3.29)F⋆≡vt+αu2vx−ωvxx−βvtxx=0.

The MEW-Burgers equation (1.5) together with its adjoint equation (3.29) have the Lagrangian

(3.30)L=v(ut+αu2ux+ωuxx−βutxx),

which is equivalent to the second-order Lagrangian

(3.31)L=vut+αvu2ux+ωvuxx+βvtuxx.

We recall that the MEW-Burgers equation (1.5) admits two translation symmetries X1 = ∂/∂t and X2 = ∂/∂x. To obtain the conserved vectors corresponding to these two infinitesimal generators we use [40]

(3.32)Ct=ξ1L+W1∂L∂ut+W2∂L∂vt,
(3.33)Cx=ξ2L+W1[∂L∂ux−Dx∂L∂uxx]+Dx(W1)∂L∂uxx,

where W1 and W2 are the Lie characteristic functions. Let us first consider the infinitesimal generator X1 = ∂/ ∂t. It can be easily shown that the prolongation of the generator X1 to the derivatives involved in the MEW-Burgers equation (1.5) has the form ∂/ ∂t. In order to determine the value

of λ we use equation X1[3](F)=λ(F),which yields λ = 0. Since Dt(ξ1) = 0, we obtain η* = 0 and hence the operator admitted by the adjoint equation (3.29) is

(3.34)Y=∂∂t.

We now use (3.34) to compute the Lie characteristic functions W1 and W2, which in this case are W1 = −ut and W2 = −vt. Thus by using (3.32) and (3.33) the conserved vector for the system (1.5) and (3.29) corresponding to X1 is

C1t=αvu2ux+ωvuxx,C1x=ωvxut+βvtxut−ωvuxt−αvu2ut−βuxtvt.

Similarly, we compute the conserved vector corresponding to X2. In this case W1 = −ux and W2 = −vx and the conserved vector thus rendered is

C2t=−vux−βvxuxx,Cx2=vut+ωvxux+βvtxux.

Remark: It should be noted that the time translation symmetry gives us the energy conservation law whereas the space translation symmetry provides us with the linear momentum conservation law.

4 Conclusion

In this paper we obtained travelling wave solutions of the MEW-Burgers equation (1.5) The two translation symmetries were used to reduce the MEW-Burgers equation to an ordinary differential equation. The (G'/G)−expansion method was applied to the ordinary differential equation to obtain its solutions. Consequently travelling wave solutions were obtained for the MEW-Burgers equation. These solutions were hyperbolic, trigonometric and rational functions. Furthermore we derived two conservation laws using the new conservation theorem due to Ibragimov. These were the energy and the linear momentum conservation laws.

References

[1] Wazwaz A.M., El-Tantawy S.A., A new integrable (3 + 1)- dimensional KdV-like model with its multiple-soliton solutions, Nonlin. Dyn., 2016, 83, 1529-1534.10.1007/s11071-015-2427-0Search in Google Scholar

[2] Wazwaz A.M., El-Tantawy S.A., Solving the (3+1)-dimensional KP-Boussinesq and BKP-Boussinesq equations by the simplified Hirota’s method, Nonlin. Dyn., 2017, 88, 3017-3021.10.1007/s11071-017-3429-xSearch in Google Scholar

[3] Wazwaz A.M., The tanh-coth method for solitons and kink solutions for nonlinear parabolic equations, Appl. Math. Comp., 2007, 188 , 1467-1475.10.1016/j.amc.2006.11.013Search in Google Scholar

[4] Wazwaz A.M., Exact solutions for the ZK-MEW equation by using the tanh and sine-cosine methods, J. Comp. Math., 2005, 82, 699-708.10.1080/00207160512331329069Search in Google Scholar

[5] Kudryashov N.A., Exact solitary waves of the Fisher equation, Phys. Lett. A., 2005, 342, 99-106.10.1016/j.physleta.2005.05.025Search in Google Scholar

[6] Wang M., Zhou Y., Li Z., Application of a homogeneous balance method to exact solutions of nonlinear equations in mathematical physics, Phys. Lett. A, 1996, 216, 67-75.10.1016/0375-9601(96)00283-6Search in Google Scholar

[7] Ablowitz M.J., Clarkson P.A., Solitons, Nonlinear evolution equations and inverse scattering, 1991, Cambridge University Press, Cambridge.10.1017/CBO9780511623998Search in Google Scholar

[8] Hirota R., The direct method in soliton theory, 2004, Cambridge University Press, Cambridge.10.1017/CBO9780511543043Search in Google Scholar

[9] Wang M., Li X., Zhang J., The G'/G− expansion method and travellingwave solutions for linear evolution equations inmathematical physics, Phys. Lett. A, 2005, 24, 1257-1268.10.1016/j.chaos.2004.09.044Search in Google Scholar

[10] Mhlanga I.E., Khalique C.M., A study of a generalized Benney-Luke equation with time-dependent coefficients, Nonlin. Dyn., 2017, 90, 1535-1544.10.1007/s11071-017-3745-1Search in Google Scholar

[11] Baleanu D., Inc M., Yusuf A., Aliyu A.I., Traveling wave solutions and conservation laws for nonlinear evolution equation, J.Math. Phys., 2018, 59, 023506.10.1063/1.5022964Search in Google Scholar

[12] Zhang Z., Jacobi elliptic function expansion method for the modi ed Korteweg-de Vries-Zakharov-Kuznetsov and the Hirota equations, Phys. Lett. A, 2001, 289, 69-74.10.1016/S0375-9601(01)00580-1Search in Google Scholar

[13] Simbanefayi I., Khalique C.M., Travelling wave solutions and conservation laws for the Korteweg-de Vries-Bejamin-Bona-Mahony equation, Results in Physics, 2018, 8, 57-6310.1016/j.rinp.2017.10.041Search in Google Scholar

[14] Kudryashov N.A., One method for finding exact solutions of nonlinear differential equations, Comm. Nonlin. Sci. Numer. Simulat., 2012, 17, 2248-2253.10.1016/j.cnsns.2011.10.016Search in Google Scholar

[15] Motsepa T., Khalique C.M., Conservation laws and solutions of a generalized coupled (2+1)-dimensional Burgers system, Comp. Math. Appl., 2017, 74, 1333-1339.10.1016/j.camwa.2017.06.015Search in Google Scholar

[16] Olver P.J., Applications of lie groups to differential equations, Springer-Verlag, New York, 1993.10.1007/978-1-4612-4350-2Search in Google Scholar

[17] Ibragimov N.H. (Ed.), CRC Handbook of Lie group analysis of differential equations, 1994-1996, vol. 1-3, CRC Press, Boca Raton.Search in Google Scholar

[18] Ibragimov N.H., Elementary Lie group analysis and ordinary differential equations, 1999, John Wiley and Sons, Chichester.Search in Google Scholar

[19] Hydon P.E., Symmetry methods for differential equations, 2000, Cambridge, Cambridge University Press.10.1017/CBO9780511623967Search in Google Scholar

[20] Motsepa T., Khalique C.M., Gandarias M.L., Symmetry analysis and conservation laws of the Zoomeron equation, Symmetry, 2017, 9, 27.10.3390/sym9020027Search in Google Scholar

[21] Motsepa T., Aziz T., Fatima A., Khalique C.M., Algebraic aspects of evolution partial differential equation arising in the study of constant elasticity of variance model from financial mathematics, Open Phys., 2018, 16, 31-36.10.1515/phys-2018-0006Search in Google Scholar

[22] Naz R., Mahomed F.M., Mason D.P., Comparison of different approaches to conservation laws for some partial differential equations in fluid mechanics, Appl. Math. Comp., 2008, 205, 212-230.10.1016/j.amc.2008.06.042Search in Google Scholar

[23] Anco S.C., Bluman G., Direct construction method for conservation laws of partial differential equations. Part I: Examples of conservation law classifications, Eur. J. Pure Appl. Math., 2002, 13, 545-566.10.1017/S095679250100465XSearch in Google Scholar

[24] Anco S.C., Bluman G., Direct construction method for conservation laws of partial differential equations. Part II: General treatment, Eur. J. Pure Appl. Math., 2002, 13, 567-585.10.1017/S0956792501004661Search in Google Scholar

[25] De la Rosa R., Bruzón M.S., On the classical and nonclassical symmetries of a generalized Gardner equation, Appl. Math. Nonlin. Sci., 2016, 1, 263-272.10.21042/AMNS.2016.1.00021Search in Google Scholar

[26] Rosa M., Gandarias M.L., Multiplier method and exact solutions for a density dependent reaction-diffusion equation, Appl. Math. Nonlin. Sci., 2016, 1, 311-320.10.21042/AMNS.2016.2.00026Search in Google Scholar

[27] Gandarias M.L., Bruzón M.S., Conservation laws for a Boussinesq equation, Appl. Math. Nonlin. Sci., 2017, 2, 465-472.10.21042/AMNS.2017.2.00037Search in Google Scholar

[28] Motsepa T., Khalique C.M., On the conservation laws and solutions of a (2+1) dimensional KdV-mKdV equation of mathematical physics, Open Phys., 2018, 16, 211-214.10.1515/phys-2018-0030Search in Google Scholar

[29] Leveque R.J., Numerical methods for conservation laws, 1992, Birkhäuser, Basel.10.1007/978-3-0348-8629-1Search in Google Scholar

[30] Burgers J.M., Application of a model system to illustrate some 20 points of statistical theory of free turbulence, Royal Netherlands Acad. Sci., XLIII 1940, 1, 2-12.Search in Google Scholar

[31] Morrison P.J., Meiss J.D., Cary J.R., Scattering of regularized long- wave solitary waves, Physica, 1984, 11D, 324-336.10.1016/0167-2789(84)90014-9Search in Google Scholar

[32] Zaki S.I., A least-squares finite element scheme for the EW equa tion, Comp. Meth. Appl. Mech. Eng., 2000, 189, 587-594.10.1016/S0045-7825(99)00312-6Search in Google Scholar

[33] Zaki S.I., Solitary waves induced by the boundary forced EW equation, Comp. Meth. Appl. Mech. Eng., 2001, 190, 4881-4887.10.1016/S0045-7825(99)00462-4Search in Google Scholar

[34] Arora R., Siddiqui Md.J., Singh V.P., Solutions of invscid Burgers’ and equal width wave equations by RDTM, International J. Appl. Phys. Math., 2012, 2, 212-214..10.7763/IJAPM.2012.V2.92Search in Google Scholar

[35] Zaki S.I., Solitarywave interactions for the modified equalwidth equation, Comp. Phys. Comm., 2000, 126, 219-231.10.1016/S0010-4655(99)00471-3Search in Google Scholar

[36] Wazwaz A.M., The tanh and sine-cosine methods for a reliable treatment of the modified equalwidth equation and its variants, Comm.. Nonlin. Sci. Numer. Simul., 2006, 11, 148-160.10.1016/j.cnsns.2004.07.001Search in Google Scholar

[37] Hassan H.N., An accurate numerical solution for the modified equal width wave equation using the Fourier pseudo-spectral method, J. Appl. Math. Phys., 2016, 4, 1054-1067.10.4236/jamp.2016.46110Search in Google Scholar

[38] Evans D.J., Raslan K.R., Solitary waves for the generalized equal width (GEW) equation, Int. J. Comp. Math., 20005, 82, 445-455.10.1080/0020716042000272539Search in Google Scholar

[39] Saha A., Bifurcation, periodic and chaotic motions of the modified equal width-Burgers (MEW-Burgers) equation with external periodic perturbation, Nonlin. Dyn., 2007, 87, 2193-2201.10.1007/s11071-016-3183-5Search in Google Scholar

[40] Ibragimov N.H., A new conservation theorem, J. Math. Anal. Appl., 2007, 333, 311-328.10.1016/j.jmaa.2006.10.078Search in Google Scholar

[41] Mothibi D.M., Khalique C.M., Conservation laws and exact solutions of a generalized Zakharov-Kuznetsov equation, Symmetry, 2015, 7, 949-961.10.3390/sym7020949Search in Google Scholar

Received: 2018-05-31
Accepted: 2018-07-02
Published Online: 2018-12-26

©2018 Chaudry Masood Khalique and Innocent Simbanefayi, published by De Gruyter

This work is licensed under the Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 License.

Articles in the same Issue

  1. Regular Articles
  2. A modified Fermi-Walker derivative for inextensible flows of binormal spherical image
  3. Algebraic aspects of evolution partial differential equation arising in the study of constant elasticity of variance model from financial mathematics
  4. Three-dimensional atom localization via probe absorption in a cascade four-level atomic system
  5. Determination of the energy transitions and half-lives of Rubidium nuclei
  6. Three phase heat and mass transfer model for unsaturated soil freezing process: Part 1 - model development
  7. Three phase heat and mass transfer model for unsaturated soil freezing process: Part 2 - model validation
  8. Mathematical model for thermal and entropy analysis of thermal solar collectors by using Maxwell nanofluids with slip conditions, thermal radiation and variable thermal conductivity
  9. Constructing analytic solutions on the Tricomi equation
  10. Feynman diagrams and rooted maps
  11. New type of chaos synchronization in discrete-time systems: the F-M synchronization
  12. Unsteady flow of fractional Oldroyd-B fluids through rotating annulus
  13. A note on the uniqueness of 2D elastostatic problems formulated by different types of potential functions
  14. On the conservation laws and solutions of a (2+1) dimensional KdV-mKdV equation of mathematical physics
  15. Computational methods and traveling wave solutions for the fourth-order nonlinear Ablowitz-Kaup-Newell-Segur water wave dynamical equation via two methods and its applications
  16. Siewert solutions of transcendental equations, generalized Lambert functions and physical applications
  17. Numerical solution of mixed convection flow of an MHD Jeffery fluid over an exponentially stretching sheet in the presence of thermal radiation and chemical reaction
  18. A new three-dimensional chaotic flow with one stable equilibrium: dynamical properties and complexity analysis
  19. Dynamics of a dry-rebounding drop: observations, simulations, and modeling
  20. Modeling the initial mechanical response and yielding behavior of gelled crude oil
  21. Lie symmetry analysis and conservation laws for the time fractional simplified modified Kawahara equation
  22. Solitary wave solutions of two KdV-type equations
  23. Applying industrial tomography to control and optimization flow systems
  24. Reconstructing time series into a complex network to assess the evolution dynamics of the correlations among energy prices
  25. An optimal solution for software testing case generation based on particle swarm optimization
  26. Optimal system, nonlinear self-adjointness and conservation laws for generalized shallow water wave equation
  27. Alternative methods for solving nonlinear two-point boundary value problems
  28. Global model simulation of OH production in pulsed-DC atmospheric pressure helium-air plasma jets
  29. Experimental investigation on optical vortex tweezers for microbubble trapping
  30. Joint measurements of optical parameters by irradiance scintillation and angle-of-arrival fluctuations
  31. M-polynomials and topological indices of hex-derived networks
  32. Generalized convergence analysis of the fractional order systems
  33. Porous flow characteristics of solution-gas drive in tight oil reservoirs
  34. Complementary wave solutions for the long-short wave resonance model via the extended trial equation method and the generalized Kudryashov method
  35. A Note on Koide’s Doubly Special Parametrization of Quark Masses
  36. On right-angled spherical Artin monoid of type Dn
  37. Gas flow regimes judgement in nanoporous media by digital core analysis
  38. 4 + n-dimensional water and waves on four and eleven-dimensional manifolds
  39. Stabilization and Analytic Approximate Solutions of an Optimal Control Problem
  40. On the equations of electrodynamics in a flat or curved spacetime and a possible interaction energy
  41. New prediction method for transient productivity of fractured five-spot patterns in low permeability reservoirs at high water cut stages
  42. The collinear equilibrium points in the restricted three body problem with triaxial primaries
  43. Detection of the damage threshold of fused silica components and morphologies of repaired damage sites based on the beam deflection method
  44. On the bivariate spectral quasi-linearization method for solving the two-dimensional Bratu problem
  45. Ion acoustic quasi-soliton in an electron-positron-ion plasma with superthermal electrons and positrons
  46. Analysis of projectile motion in view of conformable derivative
  47. Computing multiple ABC index and multiple GA index of some grid graphs
  48. Terahertz pulse imaging: A novel denoising method by combing the ant colony algorithm with the compressive sensing
  49. Characteristics of microscopic pore-throat structure of tight oil reservoirs in Sichuan Basin measured by rate-controlled mercury injection
  50. An activity window model for social interaction structure on Twitter
  51. Transient thermal regime trough the constitutive matrix applied to asynchronous electrical machine using the cell method
  52. On the zagreb polynomials of benzenoid systems
  53. Integrability analysis of the partial differential equation describing the classical bond-pricing model of mathematical finance
  54. The Greek parameters of a continuous arithmetic Asian option pricing model via Laplace Adomian decomposition method
  55. Quantifying the global solar radiation received in Pietermaritzburg, KwaZulu-Natal to motivate the consumption of solar technologies
  56. Sturm-Liouville difference equations having Bessel and hydrogen atom potential type
  57. Study on the response characteristics of oil wells after deep profile control in low permeability fractured reservoirs
  58. Depiction and analysis of a modified theta shaped double negative metamaterial for satellite application
  59. An attempt to geometrize electromagnetism
  60. Structure of traveling wave solutions for some nonlinear models via modified mathematical method
  61. Thermo-convective instability in a rotating ferromagnetic fluid layer with temperature modulation
  62. Construction of new solitary wave solutions of generalized Zakharov-Kuznetsov-Benjamin-Bona-Mahony and simplified modified form of Camassa-Holm equations
  63. Effect of magnetic field and heat source on Upper-convected-maxwell fluid in a porous channel
  64. Physical cues of biomaterials guide stem cell fate of differentiation: The effect of elasticity of cell culture biomaterials
  65. Shooting method analysis in wire coating withdrawing from a bath of Oldroyd 8-constant fluid with temperature dependent viscosity
  66. Rank correlation between centrality metrics in complex networks: an empirical study
  67. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering
  68. Modeling of electric and heat processes in spot resistance welding of cross-wire steel bars
  69. Dynamic characteristics of triaxial active control magnetic bearing with asymmetric structure
  70. Design optimization of an axial-field eddy-current magnetic coupling based on magneto-thermal analytical model
  71. Thermal constitutive matrix applied to asynchronous electrical machine using the cell method
  72. Temperature distribution around thin electroconductive layers created on composite textile substrates
  73. Model of the multipolar engine with decreased cogging torque by asymmetrical distribution of the magnets
  74. Analysis of spatial thermal field in a magnetic bearing
  75. Use of the mathematical model of the ignition system to analyze the spark discharge, including the destruction of spark plug electrodes
  76. Assessment of short/long term electric field strength measurements for a pilot district
  77. Simulation study and experimental results for detection and classification of the transient capacitor inrush current using discrete wavelet transform and artificial intelligence
  78. Magnetic transmission gear finite element simulation with iron pole hysteresis
  79. Pulsed excitation terahertz tomography – multiparametric approach
  80. Low and high frequency model of three phase transformer by frequency response analysis measurement
  81. Multivariable polynomial fitting of controlled single-phase nonlinear load of input current total harmonic distortion
  82. Optimal design of a for middle-low-speed maglev trains
  83. Eddy current modeling in linear and nonlinear multifilamentary composite materials
  84. The visual attention saliency map for movie retrospection
  85. AC/DC current ratio in a current superimposition variable flux reluctance machine
  86. Influence of material uncertainties on the RLC parameters of wound inductors modeled using the finite element method
  87. Cogging force reduction in linear tubular flux switching permanent-magnet machines
  88. Modeling hysteresis curves of La(FeCoSi)13 compound near the transition point with the GRUCAD model
  89. Electro-magneto-hydrodynamic lubrication
  90. 3-D Electromagnetic field analysis of wireless power transfer system using K computer
  91. Simplified simulation technique of rotating, induction heated, calender rolls for study of temperature field control
  92. Design, fabrication and testing of electroadhesive interdigital electrodes
  93. A method to reduce partial discharges in motor windings fed by PWM inverter
  94. Reluctance network lumped mechanical & thermal models for the modeling and predesign of concentrated flux synchronous machine
  95. Special Issue Applications of Nonlinear Dynamics
  96. Study on dynamic characteristics of silo-stock-foundation interaction system under seismic load
  97. Microblog topic evolution computing based on LDA algorithm
  98. Modeling the creep damage effect on the creep crack growth behavior of rotor steel
  99. Neighborhood condition for all fractional (g, f, n′, m)-critical deleted graphs
  100. Chinese open information extraction based on DBMCSS in the field of national information resources
  101. 10.1515/phys-2018-0079
  102. CPW-fed circularly-polarized antenna array with high front-to-back ratio and low-profile
  103. Intelligent Monitoring Network Construction based on the utilization of the Internet of things (IoT) in the Metallurgical Coking Process
  104. Temperature detection technology of power equipment based on Fiber Bragg Grating
  105. Research on a rotational speed control strategy of the mandrel in a rotary steering system
  106. Dynamic load balancing algorithm for large data flow in distributed complex networks
  107. Super-structured photonic crystal fiber Bragg grating biosensor image model based on sparse matrix
  108. Fractal-based techniques for physiological time series: An updated approach
  109. Analysis of the Imaging Characteristics of the KB and KBA X-ray Microscopes at Non-coaxial Grazing Incidence
  110. Application of modified culture Kalman filter in bearing fault diagnosis
  111. Exact solutions and conservation laws for the modified equal width-Burgers equation
  112. On topological properties of block shift and hierarchical hypercube networks
  113. Elastic properties and plane acoustic velocity of cubic Sr2CaMoO6 and Sr2CaWO6 from first-principles calculations
  114. A note on the transmission feasibility problem in networks
  115. Ontology learning algorithm using weak functions
  116. Diagnosis of the power frequency vacuum arc shape based on 2D-PIV
  117. Parametric simulation analysis and reliability of escalator truss
  118. A new algorithm for real economy benefit evaluation based on big data analysis
  119. Synergy analysis of agricultural economic cycle fluctuation based on ant colony algorithm
  120. Multi-level encryption algorithm for user-related information across social networks
  121. Multi-target tracking algorithm in intelligent transportation based on wireless sensor network
  122. Fast recognition method of moving video images based on BP neural networks
  123. Compressed sensing image restoration algorithm based on improved SURF operator
  124. Design of load optimal control algorithm for smart grid based on demand response in different scenarios
  125. Face recognition method based on GA-BP neural network algorithm
  126. Optimal path selection algorithm for mobile beacons in sensor network under non-dense distribution
  127. Localization and recognition algorithm for fuzzy anomaly data in big data networks
  128. Urban road traffic flow control under incidental congestion as a function of accident duration
  129. Optimization design of reconfiguration algorithm for high voltage power distribution network based on ant colony algorithm
  130. Feasibility simulation of aseismic structure design for long-span bridges
  131. Construction of renewable energy supply chain model based on LCA
  132. The tribological properties study of carbon fabric/ epoxy composites reinforced by nano-TiO2 and MWNTs
  133. A text-Image feature mapping algorithm based on transfer learning
  134. Fast recognition algorithm for static traffic sign information
  135. Topical Issue: Clean Energy: Materials, Processes and Energy Generation
  136. An investigation of the melting process of RT-35 filled circular thermal energy storage system
  137. Numerical analysis on the dynamic response of a plate-and-frame membrane humidifier for PEMFC vehicles under various operating conditions
  138. Energy converting layers for thin-film flexible photovoltaic structures
  139. Effect of convection heat transfer on thermal energy storage unit
https://doi.org/10.1515/phys-2018-0099
Keywords for this article
Modified equal width-Burgers equation; Lie point symmetries; exact solutions; conservation laws
Creative Commons
BY-NC-ND 4.0

Articles in the same Issue

  1. Regular Articles
  2. A modified Fermi-Walker derivative for inextensible flows of binormal spherical image
  3. Algebraic aspects of evolution partial differential equation arising in the study of constant elasticity of variance model from financial mathematics
  4. Three-dimensional atom localization via probe absorption in a cascade four-level atomic system
  5. Determination of the energy transitions and half-lives of Rubidium nuclei
  6. Three phase heat and mass transfer model for unsaturated soil freezing process: Part 1 - model development
  7. Three phase heat and mass transfer model for unsaturated soil freezing process: Part 2 - model validation
  8. Mathematical model for thermal and entropy analysis of thermal solar collectors by using Maxwell nanofluids with slip conditions, thermal radiation and variable thermal conductivity
  9. Constructing analytic solutions on the Tricomi equation
  10. Feynman diagrams and rooted maps
  11. New type of chaos synchronization in discrete-time systems: the F-M synchronization
  12. Unsteady flow of fractional Oldroyd-B fluids through rotating annulus
  13. A note on the uniqueness of 2D elastostatic problems formulated by different types of potential functions
  14. On the conservation laws and solutions of a (2+1) dimensional KdV-mKdV equation of mathematical physics
  15. Computational methods and traveling wave solutions for the fourth-order nonlinear Ablowitz-Kaup-Newell-Segur water wave dynamical equation via two methods and its applications
  16. Siewert solutions of transcendental equations, generalized Lambert functions and physical applications
  17. Numerical solution of mixed convection flow of an MHD Jeffery fluid over an exponentially stretching sheet in the presence of thermal radiation and chemical reaction
  18. A new three-dimensional chaotic flow with one stable equilibrium: dynamical properties and complexity analysis
  19. Dynamics of a dry-rebounding drop: observations, simulations, and modeling
  20. Modeling the initial mechanical response and yielding behavior of gelled crude oil
  21. Lie symmetry analysis and conservation laws for the time fractional simplified modified Kawahara equation
  22. Solitary wave solutions of two KdV-type equations
  23. Applying industrial tomography to control and optimization flow systems
  24. Reconstructing time series into a complex network to assess the evolution dynamics of the correlations among energy prices
  25. An optimal solution for software testing case generation based on particle swarm optimization
  26. Optimal system, nonlinear self-adjointness and conservation laws for generalized shallow water wave equation
  27. Alternative methods for solving nonlinear two-point boundary value problems
  28. Global model simulation of OH production in pulsed-DC atmospheric pressure helium-air plasma jets
  29. Experimental investigation on optical vortex tweezers for microbubble trapping
  30. Joint measurements of optical parameters by irradiance scintillation and angle-of-arrival fluctuations
  31. M-polynomials and topological indices of hex-derived networks
  32. Generalized convergence analysis of the fractional order systems
  33. Porous flow characteristics of solution-gas drive in tight oil reservoirs
  34. Complementary wave solutions for the long-short wave resonance model via the extended trial equation method and the generalized Kudryashov method
  35. A Note on Koide’s Doubly Special Parametrization of Quark Masses
  36. On right-angled spherical Artin monoid of type Dn
  37. Gas flow regimes judgement in nanoporous media by digital core analysis
  38. 4 + n-dimensional water and waves on four and eleven-dimensional manifolds
  39. Stabilization and Analytic Approximate Solutions of an Optimal Control Problem
  40. On the equations of electrodynamics in a flat or curved spacetime and a possible interaction energy
  41. New prediction method for transient productivity of fractured five-spot patterns in low permeability reservoirs at high water cut stages
  42. The collinear equilibrium points in the restricted three body problem with triaxial primaries
  43. Detection of the damage threshold of fused silica components and morphologies of repaired damage sites based on the beam deflection method
  44. On the bivariate spectral quasi-linearization method for solving the two-dimensional Bratu problem
  45. Ion acoustic quasi-soliton in an electron-positron-ion plasma with superthermal electrons and positrons
  46. Analysis of projectile motion in view of conformable derivative
  47. Computing multiple ABC index and multiple GA index of some grid graphs
  48. Terahertz pulse imaging: A novel denoising method by combing the ant colony algorithm with the compressive sensing
  49. Characteristics of microscopic pore-throat structure of tight oil reservoirs in Sichuan Basin measured by rate-controlled mercury injection
  50. An activity window model for social interaction structure on Twitter
  51. Transient thermal regime trough the constitutive matrix applied to asynchronous electrical machine using the cell method
  52. On the zagreb polynomials of benzenoid systems
  53. Integrability analysis of the partial differential equation describing the classical bond-pricing model of mathematical finance
  54. The Greek parameters of a continuous arithmetic Asian option pricing model via Laplace Adomian decomposition method
  55. Quantifying the global solar radiation received in Pietermaritzburg, KwaZulu-Natal to motivate the consumption of solar technologies
  56. Sturm-Liouville difference equations having Bessel and hydrogen atom potential type
  57. Study on the response characteristics of oil wells after deep profile control in low permeability fractured reservoirs
  58. Depiction and analysis of a modified theta shaped double negative metamaterial for satellite application
  59. An attempt to geometrize electromagnetism
  60. Structure of traveling wave solutions for some nonlinear models via modified mathematical method
  61. Thermo-convective instability in a rotating ferromagnetic fluid layer with temperature modulation
  62. Construction of new solitary wave solutions of generalized Zakharov-Kuznetsov-Benjamin-Bona-Mahony and simplified modified form of Camassa-Holm equations
  63. Effect of magnetic field and heat source on Upper-convected-maxwell fluid in a porous channel
  64. Physical cues of biomaterials guide stem cell fate of differentiation: The effect of elasticity of cell culture biomaterials
  65. Shooting method analysis in wire coating withdrawing from a bath of Oldroyd 8-constant fluid with temperature dependent viscosity
  66. Rank correlation between centrality metrics in complex networks: an empirical study
  67. Special Issue: The 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering
  68. Modeling of electric and heat processes in spot resistance welding of cross-wire steel bars
  69. Dynamic characteristics of triaxial active control magnetic bearing with asymmetric structure
  70. Design optimization of an axial-field eddy-current magnetic coupling based on magneto-thermal analytical model
  71. Thermal constitutive matrix applied to asynchronous electrical machine using the cell method
  72. Temperature distribution around thin electroconductive layers created on composite textile substrates
  73. Model of the multipolar engine with decreased cogging torque by asymmetrical distribution of the magnets
  74. Analysis of spatial thermal field in a magnetic bearing
  75. Use of the mathematical model of the ignition system to analyze the spark discharge, including the destruction of spark plug electrodes
  76. Assessment of short/long term electric field strength measurements for a pilot district
  77. Simulation study and experimental results for detection and classification of the transient capacitor inrush current using discrete wavelet transform and artificial intelligence
  78. Magnetic transmission gear finite element simulation with iron pole hysteresis
  79. Pulsed excitation terahertz tomography – multiparametric approach
  80. Low and high frequency model of three phase transformer by frequency response analysis measurement
  81. Multivariable polynomial fitting of controlled single-phase nonlinear load of input current total harmonic distortion
  82. Optimal design of a for middle-low-speed maglev trains
  83. Eddy current modeling in linear and nonlinear multifilamentary composite materials
  84. The visual attention saliency map for movie retrospection
  85. AC/DC current ratio in a current superimposition variable flux reluctance machine
  86. Influence of material uncertainties on the RLC parameters of wound inductors modeled using the finite element method
  87. Cogging force reduction in linear tubular flux switching permanent-magnet machines
  88. Modeling hysteresis curves of La(FeCoSi)13 compound near the transition point with the GRUCAD model
  89. Electro-magneto-hydrodynamic lubrication
  90. 3-D Electromagnetic field analysis of wireless power transfer system using K computer
  91. Simplified simulation technique of rotating, induction heated, calender rolls for study of temperature field control
  92. Design, fabrication and testing of electroadhesive interdigital electrodes
  93. A method to reduce partial discharges in motor windings fed by PWM inverter
  94. Reluctance network lumped mechanical & thermal models for the modeling and predesign of concentrated flux synchronous machine
  95. Special Issue Applications of Nonlinear Dynamics
  96. Study on dynamic characteristics of silo-stock-foundation interaction system under seismic load
  97. Microblog topic evolution computing based on LDA algorithm
  98. Modeling the creep damage effect on the creep crack growth behavior of rotor steel
  99. Neighborhood condition for all fractional (g, f, n′, m)-critical deleted graphs
  100. Chinese open information extraction based on DBMCSS in the field of national information resources
  101. 10.1515/phys-2018-0079
  102. CPW-fed circularly-polarized antenna array with high front-to-back ratio and low-profile
  103. Intelligent Monitoring Network Construction based on the utilization of the Internet of things (IoT) in the Metallurgical Coking Process
  104. Temperature detection technology of power equipment based on Fiber Bragg Grating
  105. Research on a rotational speed control strategy of the mandrel in a rotary steering system
  106. Dynamic load balancing algorithm for large data flow in distributed complex networks
  107. Super-structured photonic crystal fiber Bragg grating biosensor image model based on sparse matrix
  108. Fractal-based techniques for physiological time series: An updated approach
  109. Analysis of the Imaging Characteristics of the KB and KBA X-ray Microscopes at Non-coaxial Grazing Incidence
  110. Application of modified culture Kalman filter in bearing fault diagnosis
  111. Exact solutions and conservation laws for the modified equal width-Burgers equation
  112. On topological properties of block shift and hierarchical hypercube networks
  113. Elastic properties and plane acoustic velocity of cubic Sr2CaMoO6 and Sr2CaWO6 from first-principles calculations
  114. A note on the transmission feasibility problem in networks
  115. Ontology learning algorithm using weak functions
  116. Diagnosis of the power frequency vacuum arc shape based on 2D-PIV
  117. Parametric simulation analysis and reliability of escalator truss
  118. A new algorithm for real economy benefit evaluation based on big data analysis
  119. Synergy analysis of agricultural economic cycle fluctuation based on ant colony algorithm
  120. Multi-level encryption algorithm for user-related information across social networks
  121. Multi-target tracking algorithm in intelligent transportation based on wireless sensor network
  122. Fast recognition method of moving video images based on BP neural networks
  123. Compressed sensing image restoration algorithm based on improved SURF operator
  124. Design of load optimal control algorithm for smart grid based on demand response in different scenarios
  125. Face recognition method based on GA-BP neural network algorithm
  126. Optimal path selection algorithm for mobile beacons in sensor network under non-dense distribution
  127. Localization and recognition algorithm for fuzzy anomaly data in big data networks
  128. Urban road traffic flow control under incidental congestion as a function of accident duration
  129. Optimization design of reconfiguration algorithm for high voltage power distribution network based on ant colony algorithm
  130. Feasibility simulation of aseismic structure design for long-span bridges
  131. Construction of renewable energy supply chain model based on LCA
  132. The tribological properties study of carbon fabric/ epoxy composites reinforced by nano-TiO2 and MWNTs
  133. A text-Image feature mapping algorithm based on transfer learning
  134. Fast recognition algorithm for static traffic sign information
  135. Topical Issue: Clean Energy: Materials, Processes and Energy Generation
  136. An investigation of the melting process of RT-35 filled circular thermal energy storage system
  137. Numerical analysis on the dynamic response of a plate-and-frame membrane humidifier for PEMFC vehicles under various operating conditions
  138. Energy converting layers for thin-film flexible photovoltaic structures
  139. Effect of convection heat transfer on thermal energy storage unit
Sign up now to receive a 20% welcome discount
Institutional Access
How does access work?
Have an idea on how to improve our website?
Please write us.
© 2025 De Gruyter Brill
Downloaded on 7.12.2025 from https://www.degruyterbrill.com/document/doi/10.1515/phys-2018-0099/html
Scroll to top button