Characteristics of microscopic pore-throat structure of tight oil reservoirs in Sichuan Basin measured by rate-controlled mercury injection

Xinli Zhao; Zhengming Yang; Wei Lin; Shengchun Xiong; Yunyun Wei

doi:10.1515/phys-2018-0086

Enjoy 40% off

academic books on De Gruyter Brill *

Article Open Access

Characteristics of microscopic pore-throat structure of tight oil reservoirs in Sichuan Basin measured by rate-controlled mercury injection

Xinli Zhao , Zhengming Yang , Wei Lin , Shengchun Xiong and Yunyun Wei

Published/Copyright: November 19, 2018

Published by

Become an author with De Gruyter Brill

Submit Manuscript Author Information Explore this Subject

From the journal Open Physics Volume 16 Issue 1

Abstract

Based on the results of rate-controlled mercury-injection experiments, the microscopic pore-throat structure characteristics of tight sandstone in Sha-1 Section and tight limestone in Da’anzhai Section of Sichuan Basin were quantitatively characterized. The results show that the pore radius distribution characteristics of tight oil reservoirs are similar. The main distribution is between 100~190 μm, and the average pore radius is 160 μm. While the distribution of the throat radius of tight sandstone and limestone is quite different, the distribution of the throat of sandstone samples is relatively concentrated, and the distribution of the throat of limestone samples is relatively sparse. There is a good positive correlation between the average throat radius and permeability, but the correlation between fractal dimension and permeability is not obvious. This indicates that the permeability is mainly affected by the radius of the throat. The pore-throat ratio in tight oil reservoirs is relatively large, and the resistance to seepage is greater during development. Therefore, during the development of tight oil, measures should be taken to increase the radius of the throat, reduce the ratio of pore radius to pore-throat radius, and improve the seepage capacity of the reservoir, thereby improving the development of tight oil.

Keywords: Rate-controlled mercury injection; tight oil; pore-throat characteristics; fractal; Sichuan Basin

PACS: 91.25.Za; 91.60.-x; 91.65.-n; 93.85.-q; 93.90.+y

1 Introduction

Tight oil is new area for unconventional oil and gas exploration and development after shale gas [1, 2]. It is praised as "black gold" by the oil industry [3]. Tight oil refers to the accumulation of petroleum in the system of dark shale, argillaceous silt and sandstone intercalation that are rich in organic matter and have very poor permeability, which occurs in the form of adsorption or free state [4]. The boundary of the physical properties of the tight layer is determined. The surface air permeability is < 1.0×10⁻³ μm², the underground pressure permeability is < or equal to 0.1×10⁻³ μm², and the porosity is less than 10% [5]. The Jurassic unconventional oil in the Sichuan Basin is continuously distributed over a large area and has a large resource potential. The tight oil reservoirs in Sichuan Basin have poor pore-throat structure and strong heterogeneity. The tight reservoir pore-throat geometry (pore type, shape, size, and distribution) not only controls the physical properties of the reservoir, but also directly affects the production and recovery of tight oil. It has been a popular topic for scholars [6, 7, 8].

Xiao Qianhua [9] used cryogenic nitrogen adsorption technology to study the microscopic pore structure characteristics of reservoir rocks in typical tight oil regions. Li Bo [10] visualized the pore type of tight oil reservoirs in the Da’anzhai Section of the Middle Jurassic Ziliujing Formation using thin-slide observation and scanning electron microscopy techniques. CT scanning techniqueswere used to reconstruct the three-dimensional microscopic pore-throat model of reservoir-dense limestone. It was found that a large number of nano-sized pores exist within the reservoir matrix, and pore-throat connectivity was poor. Zhou Shangwen [11] applied the NMR technique to carry out movable fluid tests on the samples of the Jurassic tight oil reservoir in the Sichuan Basin. The results of the study showed that the fluid content of the tight oil reservoir is very low and mainly distributed in small pores; its fluid availability is poor and difficult to develop. The above studies mainly focused on pore-throat type analysis based on the experimental results, but the pore and throat radius distributions were not quantitatively characterized. The influence of pore-throat structure on seepage capacity was also not discussed. Due to capillary pressure, the conventional mercury-intrusion technique will exhibit a low numerical value when the microscopic pores and throats of tight oil reservoirs are characterized. High-pressure mercury intrusion has an extremely high mercury-inlet pressure, which can cause artificial cracks. Large errors persist in the testing of small pores [12]. The rate-controlled mercury-injection technology ensures the quasi-static process of mercury ingression at a very low mercury ingression rate. According to the rise and fall of the mercury ingression, the microscopic pore structure parameter information can be obtained and the number of pores and throats can be directly obtained. Capillary pressure curves of the pores and throats are provided and the microscopic pore structure parameters, including the pore-throat radius distribution, are given. It also provides information that reflects the development of pores, throats, and the degree of development (the ratio of pore-radius to pore-throat radius) between pores and throats [13]. Taking the tight reservoirs of the Sha-1 and Da’anzhai sections of the Shaxiamiao Formation in the middle-lower Jurassic in the Sichuan Basin as an example, the authors used the RMI test technique to analyze the porosity, throat, and throat ratios of tight reservoirs. The microscopic pore structure of these reservoirs was finely characterized and the pore structure was studied using fractal theory. To provide a theoretical basis for the efficient development of tight reservoirs in the research region, the influence of the pore-throat structure of tight reservoirs on the seepage capacity was explored.

2 Sample

The Jurassic in the Sichuan Basin is mainly a set of inland fluvial and lacustrine deposits. Oil and gas are mainly distributed in the Middle-Lower Jurassic. The middle section of the Shaximiao Formation in the Lower and Middle Jurassic, the Liangshang Section and the Da’anzhai Section of the Liangshan group are three main production zones. Over 90% of the crude oil in the Chuanzhong area is produced from these three sections [14, 15, 16]. The samples for this study were taken from the Sha-1 Section of the Shaximiao Formation and the Da’anzhai Section, and the constant velocity mercury intrusion data of the core (Table 1). The selected lithology of the sand sample from the first section was sandstone with a porosity of 3% to 6% and permeability between 0.082×10⁻³ μm² to 1.41×10⁻³ μm². The lithology of the reservoir in the Da’anzhai Section is in the form of shell limestone. Six of the samples were selected for study and the porosity is between 1.76% and 3.06%, the matrix permeability is between 0.014×10⁻³ μm² and 0.287×10⁻³ μm², and the Da’anzhai Section is the source of hydrocarbons. The type of rock organic matter is mainly type II, and the value of R_o is between 0.9% and 1.5%. The abundance of petroleum resources with a source rock thickness > 20m is (6~10)×104t/km² [17]. It can be seen from the above data that the main strata of the Shahemiao Formation and the Da’anzhai Section in the Sichuan Basin have extremely poor physical properties and are typical of tight oil reservoirs.

Table 1

Thecharacterization parameters of rate-controlled mercury injection

Sample	Lithology	Φ/%	K	R_t/ μm	R_p/ μm	η	S_f/%	S_p/%	S_t/%	P_d/MPa
H19	Sandstone	6.13	0.556	1.26	158.29	156.79	56.37	20.95	35.42	0.252
H21	Sandstone	5.65	0.283	0.91	156.12	194.94	50.35	16.62	33.73	0.523
52	Sandstone	3.47	0.082	0.80	152.91	186.48	39.53	4.31	35.22	0.516
58	Sandstone	3.96	0.415	1.33	136.69	114.63	45.08	5.89	39.20	0.171
60	Sandstone	3.95	1.41	1.43	135.49	106.03	56.79	10.72	46.07	0.130
89	Limestone	2.14	0.014	0.54	145.48	282.12	8.80	1.11	7.70	1.025
103	Limestone	3.06	0.265	0.92	151.44	187.79	17.84	5.08	12.76	0.442
108-2	Limestone	2.14	0.287	0.79	144.72	216.12	27.98	8.06	19.92	0.483
109A	Limestone	1.76	0.059	0.47	150.51	335.07	14.70	2.11	12.58	1.09
114A	Limestone	2.25	0.632	1.21	144.47	145.23	37.23	14.11	23.12	0.294
132-1	Limestone	2.24	0.241	0.85	147.13	188.11	13.61	2.24	11.38	0.565

Φ-porosity; K-permeability, 10⁻³ μ^m2; R_t-average throat radius; R_p - average pore radius; η-pore-throat radius ratio; S_f -final total mercury saturation; S_p-pore mercury saturation; S_t-throat mercury saturation; P_d-displacement pressure. (the porosity of the rock samples is the conventional gas measurement porosity using the nitrogen test, and the permeability is the Klinkenberg permeability measured when the net confining pressure is 2MPa [18, 19]).

3 Experimental method

During the experiment, when the injected mercury enters the main throat (Figure 1a), the pressure gradually rises. The pressure drops rapidly after breakthrough (Figure 1b). The first pressure drop can be seen at P₁. Then mercury gradually fills up the first pore and enters the next secondary throat, resulting in a second pressure fluctuation at P₂. Next, all the secondary pores controlled by the main throat are filled successively until the pressure rises to the pressure at the main throat, which is a complete pore unit. The radius of the throat is determined by the pressure value of the breakthrough point, and the size of the pores is determined by the volume of mercury ingress, thus separating the pores and the throat in the core [13]. The rate-controlled mercury-injection instrument used in this experiment was an ASPE 730 rate-controlled mercury analyzer, manufactured by the United States Coretest Corporation. The mercury feed pressure was 0-1000psi (about 7MPa), the mercury feed rate was 0.00005mL/min, and the contact angle was 140^∘. The interface tension coefficient was 485dyn/cm. The experimental sample was obtained by drilling a plug rock sample with a diameter of 2.5cm, drying it after washing oil and taking a small rock sample from the plug rock sample. The average volume of the sandstone sample was 3.7cm³ and the average volume of the limestone sample was 6.5cm³, and then a rate-controlled mercury injection experiment was performed after vacuuming.

Figure 1

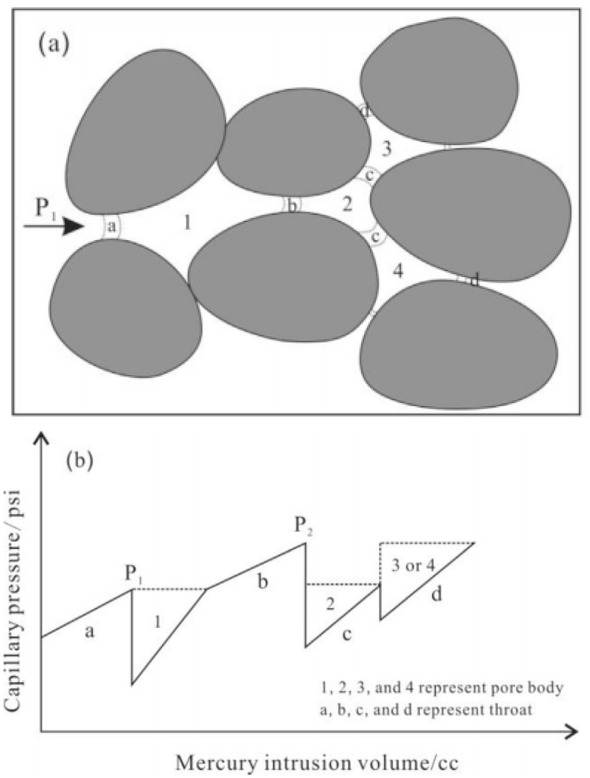
Rate-controlled mercury injection testing reservoir pore structure schematic. (a) Simplified schematic of pore body and throat configuration and (b) capillary pressure fluctuation and pore volume response

4 Results and discussion

4.1 Pore-throat distribution characteristics

4.1.1 Pore radius distribution characteristics

By analyzing the results of RMI experiments, we can see that the pore radius distribution of tight sandstones in the 5 sands (Figure 2a) is similar to the distribution of the pore radius of the tight limestones in the 6 Da’anzhai Sections (Figure 2b) Distribution in 100 μm~190 μm, the peak is about 160 μm. The predecessors found that their pore radius was distributed in the range of 100 μm~200 μm in the experiment of ultra-low permeability and tight permeability reservoirs. The peak value was about 140 μm [20, 21, 22]. Comparing the pore radius distribution characteristics of tight sandstones of Chang 6 and Chang 8 in the Ordos Basin, the main distribution is 100 μm~160 μm, and the peak is about 150 μm [23]. Thus, for ultra-low permeability [24] and tight reservoirs, the effect of pore radius distribution on reservoir permeability is not significant.

Figure 2

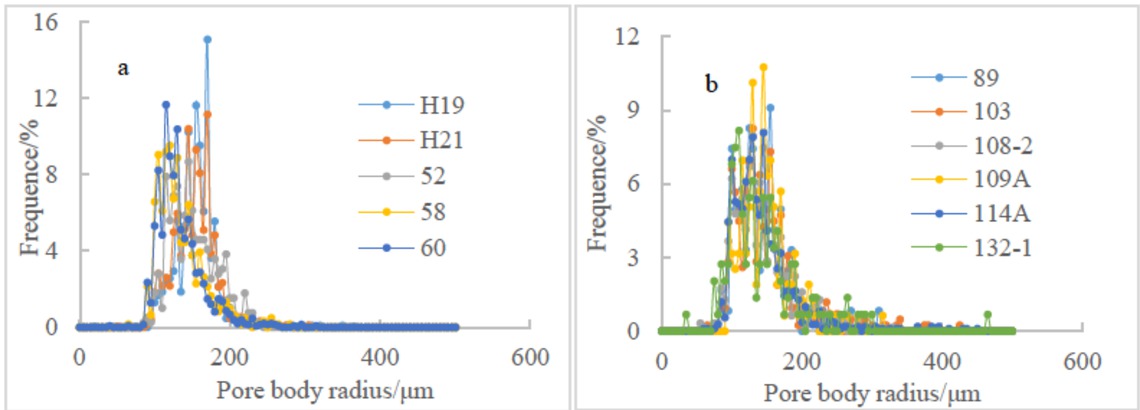
Pore size distribution by rate-controlled mercury injection of the samples

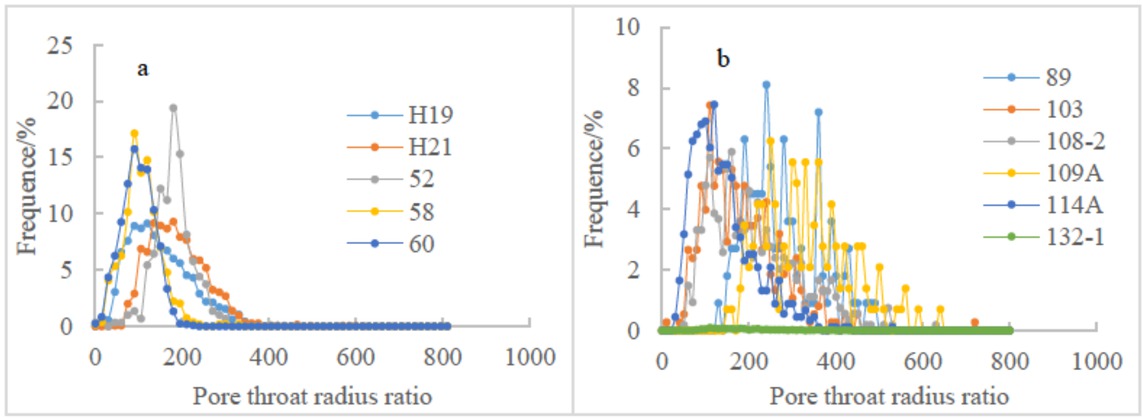
4.1.2 Throat radius distribution characteristics

The experimental results show that the characteristics of the distribution of the tight sandstone throat of the Sha-1

Section (Figure 3a) and the characteristics of the distribution of the limestone throat of the Da’anzhai Section (Figure 3b) are quite different. The distribution of throats in sandstone samples is relatively concentrated. The distribution of throats in limestone samples is relatively sparse. The radius of the throat of the sandstone is generally distributed between 0.2 μm and 1.8 μm with an average of approximately 0.5 μm. The main body radius of the limestone throat is 0.1 μm to 2.1 μm, with an average of 0.7 μm. As can be seen in Figure 3(b), the greater the permeability, the wider the distribution range and the more the peak distribution shifts to the right. Figure 4 shows the cumulative frequency distribution of five sandstone cores with different permeabilities. The cores with poor permeability and the small throats occupy a small part. When the value of permeability is 0.632×10⁻³ μm² and 0.014×10⁻³ μm², the throat with a radius < 1 μm occupies 40% and more than 90% respectively. There is a positive correlation between the average throat radius and permeability (Figure 5). The correlation coefficient is greater than 0.9 (R² = 0.918), indicating that the permeability of tight oil reservoirs is greatly affected by the throat, which is consistent with previous research results [25]. Waterflooding is an important technology for oilfield development [26]. However, with the decrease of permeability, the pore-throat of ultra-low permeability reservoir is smaller and the fluid-solid coupling is stronger [27, 28]. The higher the irreducible water saturation, the larger the starting pressure gradient. Therefore, the ability of porous media to allow fluid to flow through is becoming weaker [29]. At the same time, when the mainstream throat radius is < 1 μm, the actual permeability of waterflooding will be reduced exponentially; therefore, the likelihood of waterflooding will be increased [30]. Some studies also have suggested that a throat radius >1.0 μm has an important influence on core fluid flow. When the proportion of throats with a radius >1 μm is less than 40%, it is considered that the development of reservoir water injection is not feasible [31]. Theproportion of the total pore volume occupied by the throat with a radius > 1.0 μm in tight reservoirs in the central Sichuan region is between 3% and 35%. Therefore, it is difficult for the tight reservoirs in this area to be water-average throat radius and permeability injected and it is easy to cause various sensitive injuries, affecting single well productivity.

Figure 3

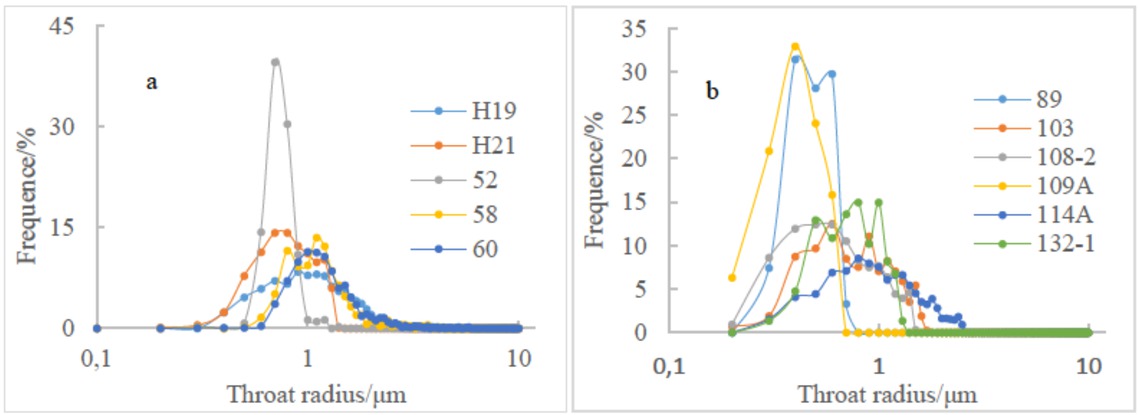
Throat size distribution by RMI of the samples

Figure 4

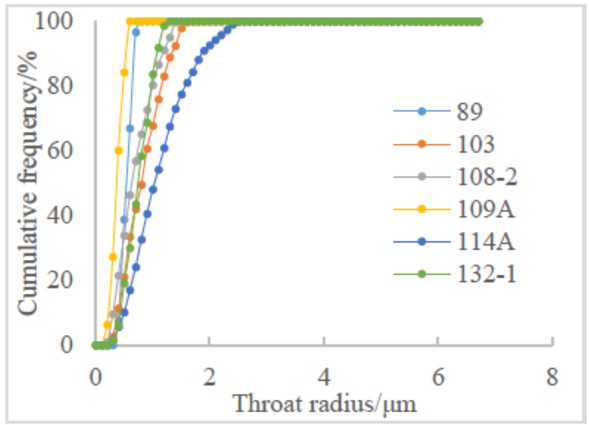
The cumulation frequency curves versus the throat radius of limestone

Figure 5

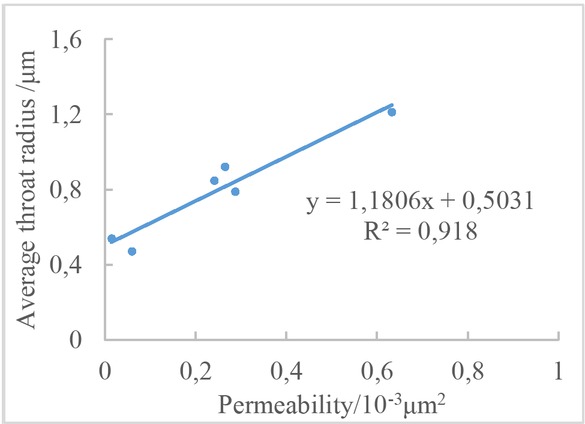
Correlationship between average throat radius and permeability

4.2 Capillary curve features

The pore and throat pressure and total capillary pressure curves, provided by the rate-controlled, mercury-injection test, can be used to visually reflect the relationship between mercury-inlet pressure, effective pore volume, effective throat volume, and total effective pore-throat volume [32, 33]. According to the tight rock sample, capillary pressure test results in the study area, there are 4 main types of pressure curves for rate-controlled mercury-intrusion capillary tubes, as shown in typical sandstone samples H19 and 52 (Figure 6a), and typical limestone samples 89 and 108-2 as shown in Figure 6b The detailed pore structure parameters are shown in Table 1. For the sandstone sample H19, the expulsion pressure is 0.252MPa, and the overall capillary drag-force curve in the early stage of mercury ingression is consistent with the pore capillary pressure curve. This indicates that mercury saturation is mainly controlled by pores in the early stage. As the pressure of incoming mercury increases, the pore capillary pressure curve becomes steep, and the overall mercury-influx curve is consistent with the capillary pressure curve of the throat. For sandstone sample 52, the expulsion pressure is 0.516MPa, which is higher than the expulsion pressure of sample H19. In the early stage of mercury ingression, the total mercury saturation is mainly controlled by the throat. The capillary pressure curve of 89 in the limestone sample is similar to that of the sandstone sample H19, and the capillary pressure curves of 108-2 and 52 are similar. However, the final mercury saturation of the limestone sample is lower than the final mercury saturation of the sandstone sample, which is related to its lithology. On the whole, for all rock samples in the study area, the pore mercury pressure curve gradually became steeper, parallel to the vertical axis, as the mercury-inlet pressure gradually increased (Figure 6).

Figure 6

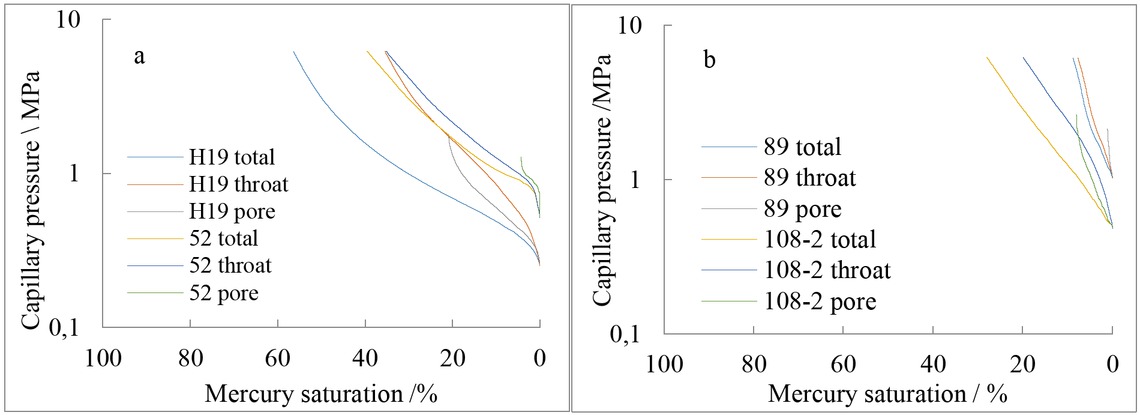
Capillary pressure curves of the representative samples

4.3 Pore structure fractal features

Fractal geometry is a branch of mathematics [34]. It can describe complex things in detail. The pore structure of reservoir rocks has fractal features [35, 36, 37, 38, 39, 40], which can be characterized quantitatively by fractal dimension. Based on the capillary beam model, the capillary pressure is calculated as follows:

(1)Pc=2σcos⁡θr

In the formula: P_c is the capillary pressure, MPa; σ is the interfacial tension, N/m; θ is the contact angle, (^∘); r is pore radius, μm.

The relationship between capillary force and wetting saturation can be written as [37]:

(2)log⁡S=(D−3)logPc+(3−D)logPmin

In the formula: S is the cumulative pore volume fraction in the rock, whose pore radius is smaller than a certain value. In the mercury-.injection test, saturation of the wetting phase corresponding to the capillary pressure, P_c, %;

D is the fractal dimension, dimensionless number; P_min is the capillary pressure corresponding to the largest pore-throat, MPa.

From formula (2), it can be seen that there is a linear relationship between the logarithm of the reservoir capillary pressure and the corresponding logarithm of the saturation of the wetting phase. Therefore, we can use the mercury-intrusion test results for linear regression analysis to obtain the pore fractal dimension D that reflects the pore structure characteristics. According to the fractal theory, the fractal dimension in the three-dimensional Euclidean space is between 2 and 3. The smaller the fractal dimension is, the more regular the pore shape, the smoother the pore surface, the better the reservoir pore permeability. However, the pore permeability of the reservoir is poor. A fractal dimension greater than 3 indicates that the corresponding pores do not have fractal features [41, 42].

For rocks with better porosity within the reservoir, there is a good linear relationship between the logarithm of capillary pressure and the logarithm of the saturation of the wetting phase (Equation 2). The pore structure has good statistical self-similarity. As the fractal dimension decreases, the pore structure becomes better. The fractal dimension of the sample is shown in Table 2. The fractal dimension of the five sandstone samples is 2.7066 to 2.8035, with an average of 2.7523. The fractal dimension of the six limestone samples is 2.8544 to 2.9530, with an average of 2.9077.Moreover, the fractal dimension of sandstone is smaller than that of limestone, so the pore structure of sandstone is more regular than limestone. Taking the two representative samples H19 (Figure 7a) and 58 (Figure 7b) in the target layer of the study area as examples, the porosity of the two samples was 6.13% and 3.96%, respectively. The relationship between the logarithm of the capillary pressure and the logarithm of the saturation of the wetting phase is:

Figure 7

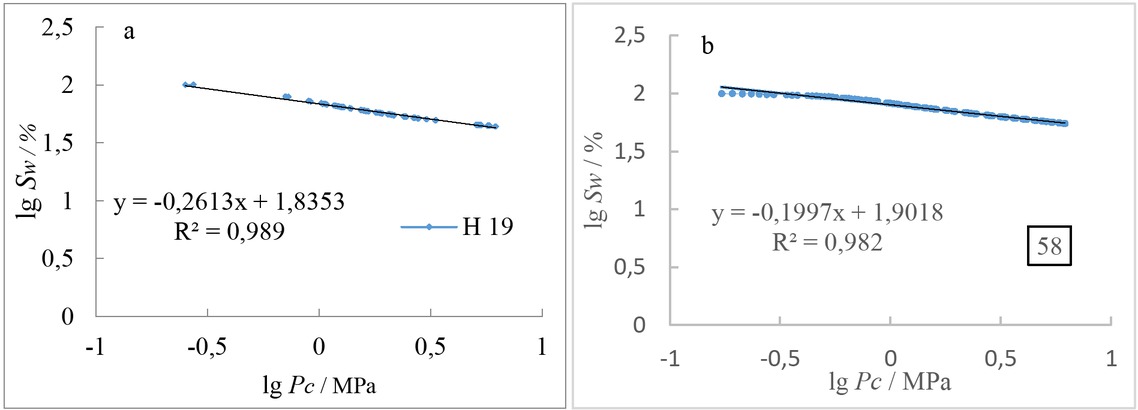
The relationship between capillary pressure and wetting phase saturation of H19 and 58 samples

Table 2

Fractal dimension of sandstone and limestone

Sample	Lithology	Φ/%	K	η	D	R²
H19	Sandstone	6.13	0.556	156.79	2.7393	0.989
H21	Sandstone	5.65	0.283	194.94	2.7066	0.994
52	Sandstone	3.47	0.082	186.48	2.7812	0.997
58	Sandstone	3.96	0.415	114.63	2.8035	0.986
60	Sandstone	3.95	1.41	106.03	2.7311	0.982
89	Limestone	2.14	0.014	282.12	2.9530	0.979
103	Limestone	3.06	0.265	187.79	2.9261	0.998
108-2	Limestone	2.14	0.287	216.12	2.8664	0.999
109A	Limestone	1.76	0.059	335.07	2.9051	0.999
114A	Limestone	2.25	0.632	145.23	2.8544	0.998
132-1	Limestone	2.24	0.241	188.11	2.9413	0.995

Φ-porosity; K -permeability,10⁻³ μm²; η-the ratio of pore radius to pore-throat radius;D-fractal dimension

H19 sample:

(3)log⁡Sw=−0.261log⁡Pc+1.835R2=0.989

58 samples:

(4)logSw=−0.199logPc+1.901R2=0.982

Using linear regression analysis, the fractal dimension of the pore structure of the two rock specimens is 2.7393 and 2.8035, respectively. Comparison shows that the fractal dimension of the H19 rock sample is smaller than the fractal dimension of the 58 rock sample. According to the foregoing rules, we can see that the pore structure of H19 is better, and the correlation between porosity and permeability is also better. The physical properties of the test of rock samples showed that the permeabilities of H19 and 58 samples were 0.556×10⁻³ μm² and 0.415×10⁻³ μm², respectively, confirming that the fractal dimension can reflect the quality of the rock pore structure. There is a good linear relationship between reservoir rock permeability and average throat radius (Figure 5), but the correlation between fractal dimension and rock reservoir permeability is not obvious (Figure 8). This is consistent with previous research [43]. It can be seen from Figure 9 that there is a certain correlation between the fractal dimension and the ratio of pore radius to pore-throat radius. As the fractal dimension increases, the ratio of pore radius to pore-throat radius increases.

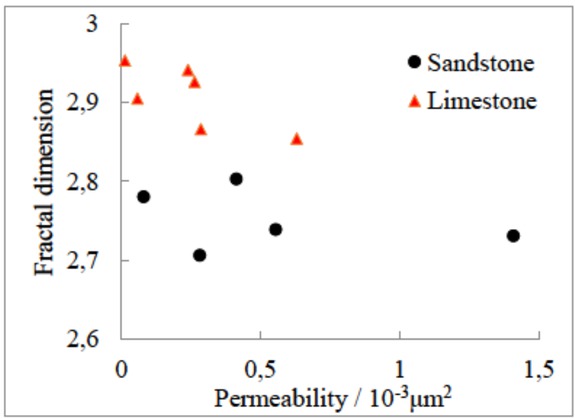
$Figure 8 The relationship between fractal dimension and permeability$

Figure 8

The relationship between fractal dimension and permeability

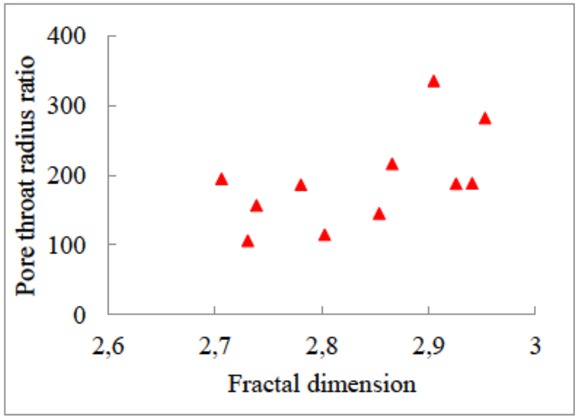
$Figure 9 The relationship between fractal dimension and the pore-throat radius ratio$

Figure 9

The relationship between fractal dimension and the pore-throat radius ratio

4.4 The ratio of pore radius to pore-throat radius distribution characteristics

The reservoir’s ratio of pore radius to pore-throat radius is one of the important parameters in the analysis of rock pore-throat characteristics. When the ratio between pore radius and throat radius is small, the throat’s ability to restrain oil (gas) is small. The connection of large throats is conducive to the recovery of oil and gas in pores. On the contrary, when the throat radius is relatively large, it indicates that the pores are connected by the smaller throats, and oil and gas must overcome relatively large capillary forces when passing through the narrow throats. This is not conducive to the recovery of oil and gas in pores [44, 45]. It can be seen from Figure 10 that the sandstone’s ratio of pore radius to pore-throat radius (Figure 10a) is mainly distributed between 30 and 300, and the limestone’s ratio of pore radius to pore-throat radius (Figure 10b) is mainly distributed between 40 and 480. Therefore, compared to the conventional reservoir ratio of pore radius to pore-throat radius, the ratio of pore radius to pore- throat radius of tight oil reservoirs is relatively large. Advanced technological transformation measures must be adopted to increase the radius of the throat and reduce the ratio of pore radius to pore-throat radius , so as to improve the development effect of the tight oil.

Figure 10

The ratio of pore radius to pore-throat radius size distribution by RMI of the samples

5 Conclusions

The oil reservoirs of the Sha-1 Section and Da’anzhai Section in the Shaxiamiao Formation of the Lower-Middle Jurassic in the Sichuan Basin are typical tight oil reservoirs. The permeability is < 0.1×10⁻³ μm². The distribution characteristics of the pore radius of sandstone and limestone are similar, and the main distribution is between 100 μm and 190 μm, the average pore radius is 160 μm.
The distribution of the throats of sandstone and limestone is quite different. The distribution of the throat of sandstone samples is relatively concentrated, and the distribution of the throat of limestone samples is relatively sparse. The throat radius of sandstone is generally between 0.2 μm and 1.8 μm, and the average throat radius is about 0.5 μm. The throat radius of limestone is mainly between 0.1 μm and 2.1 μm, and the average throat radius is about 0.7 μm. A good positive correlation exists between the average throat radius and permeability, indicating that the permeability is mainly controlled by the throat.
The pore structure of reservoir rocks has fractal features that can be characterized quantitatively by fractal dimensions. Studies show that the smaller the fractal dimension, the better the pore structure. The fractal dimension of sandstone is smaller than that of limestone, so the pore structure of sandstone is more regular than limestone. The correlation between the fractal dimension and the rock reservoir permeability is not obvious.
The ratio of pore-throat radii between sandstone in the first sand section and the Da’anzhai Section is relatively large, indicating that the pores are connected by the smaller throat, and oil and gas passing through the narrow throat need to overcome relatively large capillary forces, resulting in low oil displacement efficiency. For tight oil reservoirs, during the development process, emphasis was placed on increasing the radius of the throat and reducing the radius of the pores. Therefore, the pore-throat radius ratio can be reduced so that the development effect of tight oil can be improved.

ORCID ID: http://orcid.org/0000-0002-8643-594X

Acknowledgement

We gratefully acknowledge the financial support from the National Science and Technology Major Project (2017ZX05013-001).

References

[1] Zandong S., Unconventional oil and gas exploration and development, 2011, Beijing, Petrol. Industry Press.Search in Google Scholar

[2] Caineng Z., Shizhen T., et al., Unconventional petroleum geology, 2011, Beijing, Geological Publishing House.Search in Google Scholar

[3] Johnstone B., Bakklen black gold, Leader-Poster, 2007, 6.Search in Google Scholar

[4] Chengzao J., Caiceng Z., Jianzhong L., et al., Evaluation criteria, main types, basic characteristics and resource prospects of tight oil in China, Acta Petrolei- Sinica, 2012, 33(3), 343-350.Search in Google Scholar

[5] Caineng Z., Zhi Y., Rukai Z., et al., Unconventional oil and gas exploration, development and theoretical and technological advances in China, Geological J., 2015, 89(6), 979-1007.10.1111/1755-6724.12491Search in Google Scholar

[6] Behzad G., Allen G., Thomas E., et al., Saturation dependence of transport in porous media predicted by percolation and effective medium theories, Fractals, 2015, 23(1), 1540004.10.1142/S0218348X15400046Search in Google Scholar

[7] Huawei Z., Zhengfu N., Qing W. et al., Petrophysical characterization of tight oil reservoirs using pressure-controlled porosimetry combined with rate-controlled porosimetry, Fuel, 2015, 154, 233-242.10.1016/j.fuel.2015.03.085Search in Google Scholar

[8] Hao W., Chunlin Z., Youliang J. et al., An improved method of characterizing the pore structure in tight oil reservoirs: Integrated NMR and constant-rate-controlled porosimetry data, J. Petrol. Sci. Eng., 2018, DOI: 10.1016/j.petrol.2018.03.065.10.1016/j.petrol.2018.03.065Search in Google Scholar

[9] Qianhua X., Hao Z., Zhengming Y. et al., Low temperature nitrogen adsorption experiment in typical tight oil region in China, Special Oil and Gas Reservoirs, 2015, 22(4), 82-85.Search in Google Scholar

[10] Bo L., Hongsong L., YongjunW. et al., Micro-pore characteristics of tight oil reservoirs in the Da’anzhai Formation of the Ziliujing Formation in Central Sichuan Basin, J. Chengdu Univ. Techn. Sci. & Technol. Ed., 2018, 45(2), 211-220.Search in Google Scholar

[11] Shangwen Z., Huaqing X., Wei G., Experiments on the movable fluid of the Jurassic tight oil reservoir in the Middle Sichuan Basin, J. Liaoning Techn. Univ. (Natural Science Ed.), 2014(6), 768-772.Search in Google Scholar

[12] Kelai X., Yingchang G., Beyene G. et al., How does the pore-throat size control the reservoir quality and oiliness of tight sandstones? The case of the Lower Cretaceous Quantou Formation in the southern Songliao Basin, China, Marine Petrol. Geology, 2016, 76, 1-15.10.1016/j.marpetgeo.2016.05.001Search in Google Scholar

[13] Zhengming Y., Experimental technique for special low-ultra-low permeability reservoirs, 2012, Beijing, Petrol. Industry Press.Search in Google Scholar

[14] Shaoyong W., Jianzhong L., Denghua L. et al., The potential of tight oil resource in Jurassic Da’anzhai Formation of the Gongshanmiao oil field, central Sichuan Basin, Geology in China, 2013, 40(2), 477-486.Search in Google Scholar

[15] Xizhe L., Zhenhua G., Yujin W. et al., Geological characteristics and development strategies for Cambrian Longwangmiao Formation gas reservoir in Anyue gas field, Sichuan Basin, SW China, Petrol. Explor. Development, 2017, 44(3), 398-406.10.1016/S1876-3804(17)30049-6Search in Google Scholar

[16] Xizhe L., Zhenhua G.,Yong H. et al., Eflcient development strategies for large ultra-deep structural gas fields in China, Petrol. Explor. Development, 2018, 45(1), 111-118.10.1016/S1876-3804(18)30011-9Search in Google Scholar

[17] Bin Z., Jian H., Jiajing Y. et al., Control of tight source oil distribution by source rocks: A case study of Da’an Village in the Sichuan Basin, Bulletin of Mineralogy, Geochem., 2015, 34(1), 45-54.Search in Google Scholar

[18] Wei L., Zhengming Y., Xizhe L. et al., A method to select representative rock samples for digital core modeling, Fractals, 2017, 25(4),1740013.10.1142/S0218348X17400138Search in Google Scholar

[19] Wei L., Xizhe L., Zhengming Y. et al., Construction of dual pore 3-D digital cores with a hybrid method combined with physical experiment method and numerical reconstruction method, Transport in porous media, 2017, 120(1), 227-238.10.1007/s11242-017-0917-xSearch in Google Scholar

[20] Zhengming Y., Yingzhi Z., Mingqiang H. et al., Comprehensive reservoir evaluation method for low permeability oil fields, Acta PetroleiSinica, 2006, 27(2), 64-67.Search in Google Scholar

[21] Dianshi X., Zhengyuan L., Shu J. et al., Comparison and integration of experimental methods to characterize the full-range pore features of tight gas sandstone-A case study in Songliao Basin of China, Journal of Natural Gas Science & Engineering, 2016, 34,1412-1421.10.1016/j.jngse.2016.08.029Search in Google Scholar

[22] Hao W., Chunlin Z., Youliang J. et al., Size characterization of pore-throat in tight sandstone and control of reservoir properties: A case study of Yanchang Formation in Longdong area of Ordos Basin, Acta PetroleiSinica, 2017, 38(8), 876-887.Search in Google Scholar

[23] Weicheng L., Yanmei Z., Fang W. et al., Micropore-throat characteristics of tight oil reservoirs using constant-pressure mercury-intrusion technique: A case study of the Upper Triassic Yan-chang Formation in the Ordos Basin, Lithologic Reservoirs, 2012, 24(6), 60-65.Search in Google Scholar

[24] Daopin L., Development of low permeability sandstone oil-field,1997, Beijing, Petrol. Industry Press.Search in Google Scholar

[25] Qiang L., Study on the seepage mechanism of tight reservoirs in Sichuan Basin,2014, Beijing, Graduate University of Chinese Academy of Sciences (Institute of Fluid Dynamics).Search in Google Scholar

[26] Ganesh C., et al., Integratedmanagement of oilfield water injection development, 2001, Beijing, Petrol. Industry Press.Search in Google Scholar

[27] Ruifei W., Pingping S., Ziqi S. et al., Microscopic pore-throat characteristics of reservoirs in ultra-lowpermeability sandstone reservoirs, Editorial offlce of ACTA Petrolei Sinica, 2009, 30(4), 560-563.Search in Google Scholar

[28] Zhihai C., Microscopic pore-throat distribution and evaluation of movable oil in ultra-low permeability reservoirs: A case study of the Yingcheng Formation reservoir in Shiwu Oilfield, Petrol. Geology Sinica, 2011, 33(6), 657-661.Search in Google Scholar

[29] Wei X., Qun L., Xiangui L. et al., Proposed pressure gradient for low permeability reservoirs, Petrol. Explor. Development, 2009, 36(2), 232-236.10.1016/S1876-3804(09)60123-3Search in Google Scholar

[30] Yadong Q., Ailin J., Zhengming Y. et al., Feasibility evaluation method for water injection development in ultra-low permeability sandstone reservoirs, J. Centr. South Univ. Nat. Sci., 2014(11), 3886-3892.Search in Google Scholar

[31] Gavin L., Pre-Dancy flow: A missing piece of the improved oil recovery puzzle,SPE/DOE Symposium on Improved Oil Recovery, Soc. Petrol. Eng., 2004.10.2118/89433-MSSearch in Google Scholar

[32] Yuan H., Swanson B., Resolving pore-space characteristics by rate-controlled porosimetry, Spe Formation Evaluation, 1989, 4(1), 17-24.10.2118/14892-PASearch in Google Scholar

[33] Junchang S., Zhengming Y., Qianhua X., Development history of constant speed mercury injection technology and its application in oil and gas field development, Adv. Porous Flow, 2011, 1(1), 1-7.10.4236/apf.2011.11011Search in Google Scholar

[34] Mandelbrot B., The fractal geometry of nature,1982, New York, WH Freeman & Co.Search in Google Scholar

[35] Xinfang M., Shicheng Z., Zhaoxin L., Fractal dimension of pore structure calculated by piecewise regression method, J. China Univ. Petrol., 2004, 28(6), 54-56.Search in Google Scholar

[36] Xianguo Z., Tao Z., Chengyan L., Evaluation of pore structure of low permeability reservoir based on pore fractal feature, Litho-logic Reservoirs, 2013, 25(6), 40-45.Search in Google Scholar

[37] Naveen P., Asif M., Ojha K., Integrated fractal description of nanopore structure and its effect on CH4, adsorption on Jharia coals, India, Fuel, 2018, 232,190-204.10.1016/j.fuel.2018.05.124Search in Google Scholar

[38] Rui S., Mengmeng C., Jianjun L. et al., A pore-scale simulation on thermal-hydromechanical coupling mechanism of rock, Geofluids, 2017(21), 7510527.10.1155/2017/7510527Search in Google Scholar

[39] Rui S., Mengmeng C., Jianjun L., A correlation for heat transfer and flow friction characteristics of the offset strip fin heat exchanger, Int. J. Heat & Mass Transf., 2017, 115(PB), 695-705.10.1016/j.ijheatmasstransfer.2017.08.054Search in Google Scholar

[40] Rui S., Jianjun L., Mengmeng C., A new method to reconstruct structured mesh model from micro-computed tomography images of porous media and its application, Int. J. Heat & Mass Transf., 2017, 109, 705-715.10.1016/j.ijheatmasstransfer.2017.02.053Search in Google Scholar

[41] Liang Y., Ruicheng G., Qi’an M. et al., Sequence characteristics and control factors of the Lower Cretaceous in the Tanan Sag, Tamuztag Basin, China, Geological J., 2009, 83(6),827-835.Search in Google Scholar

[42] Wei L., Xizhe L., Zhengming Y. et al., A new improved threshold segmentation method for scanning images of reservoir rocks considering pore fractal characteristics, Fractals, 2018, 26(2),1840003.10.1142/S0218348X18400030Search in Google Scholar

[43] Yu S., Yadong Q., Zhengming Y. et al., Fractal study of low-permeability reservoirs based on constant rate mercury injection, Petrol. Geology Rec., 2009, 16(2), 88-90.Search in Google Scholar

[44] Rui S., Mengmeng C., Jianjun L., Single and multiple objective optimization of a natural gas liquefaction process, Energy, 2017, 124, 19-28.10.1016/j.energy.2017.02.073Search in Google Scholar

[45] Ruifei W., Pingping S., Ziqi S. et al., Micro pore-throat characteristics of ultra-low permeability sandstone reservoirs, Acta Petrolei Sinica, 2009, 30(4), 560-563.Search in Google Scholar

Received: 2018-05-16

Accepted: 2018-08-17

Published Online: 2018-11-19

This work is licensed under the Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 License.

Articles in the same Issue

https://doi.org/10.1515/phys-2018-0086

Keywords for this article

Rate-controlled mercury injection; tight oil; pore-throat characteristics; fractal; Sichuan Basin

Creative Commons

BY-NC-ND 4.0