A new operational matrix method to solve nonlinear fractional differential equations

Maryamsadat Hedayati; Reza Ezzati

doi:10.1515/nleng-2022-0364

Artikel Open Access

A new operational matrix method to solve nonlinear fractional differential equations

Maryamsadat Hedayati und Reza Ezzati

Veröffentlicht/Copyright: 28. März 2024

Veröffentlicht von

Veröffentlichen auch Sie bei De Gruyter Brill

Manuskript einreichen Informationen für Autor*innen

Aus der Zeitschrift Nonlinear Engineering Band 13 Heft 1

Abstract

This study aims to propose novel Zernike wavelets and a new method based on the operational matrices for solving nonlinear fractional differential equations. First, non-orthogonal Zernike wavelets are introduced using the Zernike polynomials. Then, a new technique based on combining these wavelets with the block pulse functions is presented to derive the operational matrix of fractional integration and to solve nonlinear fractional differential equations. Moreover, an error analysis is conducted by providing required theorems. Besides, the proposed method is employed to solve a nonlinear fractional competition model of breast cancer. Finally, a parametric study is performed to consider the effect of fractional order on the population of healthy, cancer stem, tumour, and immune cells, as well as the excess estrogen.

Keywords: Zernike wavelets; block pulse functions; operational matrix; nonlinear fractional differential equations; breast cancer model

1 Introduction

Bio-mathematical modelling of diseases has recently received significant attention from researchers to improve the process of treatments. Specifically, various types of cancer have been modelled using differential equations. Solving these equations enables researchers to predict the effect of drugs on the population of the immune system and tumour cells, as well as the interactions between them.

While integer-order time derivatives have been widely used in the aforementioned differential equations in primary studies, recently, fractional-order ones have been employed instead. To consider the memory of the biological systems and the history of their reactions, it has been frequently suggested that time fractional differential equations be employed [1,2]. In this article, a competition model of breast cancer, previously proposed and numerically analysed in [3], is investigated in which integer-order derivatives have been replaced with time-fractional ones. Fractional derivatives have also been used in several studies on the COVID-19 outbreak [4,5].

Moreover, several researches have been conducted on nonlinear fractional differential equations, e.g., solution of nonlinear fractional models using two kinds of fractional dual-function methods [6]. Furthermore, the nonlinear fractional partial differential Schrödinger equation was studied using fractional mapping and fractional bi-function methods [7]. Besides, conformable fractional derivative was used for solving the conformable fractional discrete complex cubic Ginzburg–Landau equation [8]. In addition, the wick-type stochastic nonlinear fractional Schrödinger equation was investigated employing the fractional F-expansion method in the study by Wang and Wang [9]. Additional bio-mathematical simulations have been presented in studies by Noeiaghdam et al. [10,11,12].

On the other hand, recently, breast cancer as a challenging area has drawn researchers’ attention. This issue has led to conducting numerous researches focusing on providing accurate mathematical models describing various aspects of the disease treatment. In the study by Bitsouni and Tsilidis [13], the intricate interactions among the tBregs, CD8⁺ T, CD4⁺ T, and B cells and the effect of concentration of rituximab as a monoclonal antibody were studied through a computational approach. In the study by Marino et al. [14], a numerical technique was developed to obtain a clear decision support system for breast carcinoma surgeries. Besides, the accuracy of predicting tumour size was improved by a new scheme of integrating a machine-learning algorithm with a mathematical model describing a chemotherapy treatment of breast cancer [15]. An experimental-mathematical basis, combining numerical magnetic resonance imaging data with a biophysical model, was employed in the study by Jarrett et al. [16] to simulate how locally advanced breast cancer responds to neoadjuvant therapy. A detailed mathematical modelling review can be found in the study by Simmons et al. [17] on the environmental factors in breast cancer invasion. In addition to the aforementioned research works on the mathematical modelling of breast cancer, numerous studies have been conducted to provide bio-mathematical simulations in other areas. The researchers interested in reading in this field might be referred to the previous studies [18,19,20,21].

In this research, radial Zernike polynomials are employed to create novel wavelets. The Zernike polynomials have been successfully used in various areas, including optical imaging. For instance, they have been employed as base functions of image moments as shape descriptors to classify benign and malignant breast masses [22]. In addition, they have been utilized in analysing the surface of vibrating disks [23]. Thus, using Zernike polynomials can enable researchers to model highly fluctuating phenomena.

This article examines a nonlinear time fractional model of breast cancer proposed in Solís-Pérez et al. [3]. First, the Zernike polynomials are employed to construct Zernike wavelets. Then, these wavelets are combined with block pulse functions to create a numerical method for solving nonlinear time fractional differential equations. Besides, error estimation is performed. Moreover, by employing this technique, an operational matrix of fractional integration is derived. Then, the mentioned breast cancer model is solved, and the effects of the fractional order on the response of the immune system, as well as the population of various cells, are investigated.

The article is organized as follows. In Section 2, some preliminaries and definitions regarding fractional calculus are presented. In Section 3, the properties of wavelets and block pulse functions are briefly reviewed. Moreover, Zernike wavelets are defined and proposed in Section 4. A novel scheme for solving fractional differential equations and the numerical solution of the breast cancer model are presented in Section 5. Section 6 presents the results, and a comprehensive discussion on the convergence, accuracy of the solution, computational costs, and the effects of the fractional orders on the field variables are provided. Finally, in Section 7, concluding clarifications are summarized.

2 Preliminaries

Definition 2.1

[24] The Riemann–Liouville fractional integral operator of order α is defined as follows:

(1) I α { u ( t ) } = 1 Γ ( α ) ∫ 0 t ( t − τ ) α − 1 u ( τ ) d τ , α > 0 u ( t ) = 0 , α = 0 .

Definition 2.2

[25] The Caputo fractional derivative operator of order Xα is defined as follows:

(2) D α { u ( t ) } = 1 Γ ( n − α ) ∫ 0 t ( t − τ ) n − α − 1 u ( n ) ( τ ) d τ , 0 ≤ n − 1 < α < n u ( n ) ( t ) , α = n ,

where t ≥ 0 and n ∈ N .

Definitions 2.1 and 2.2 demonstrate the following properties:

(3) D α { I α { u ( t ) } } = u ( t ) ,

(4) I α { D α { u ( t ) } } = u ( t ) − ∑ k = 0 n − 1 u ( k ) ( 0 + ) k ! t k , n − 1 < α < n , t ≥ 0 .

3 A brief review of wavelets and block pulse functions

3.1 Wavelets

Wavelets, as special functions, rapidly oscillate and then vanish. These properties have enabled researchers to extensively employ them as accurate tools for function approximation in recent studies.

Wavelets are constructed from a single function Ψ ( x ) called the mother wavelet [26]:

(5) ψ a , b ( t ) = | a | − 1 2 Ψ t − b a , a , b ∈ R , a ≠ 0 ,

where a and b are dilation and translation parameters, respectively. Continuously varying a and b creates a family of wavelets. Setting a = a 0 − k and b = n b 0 a 0 − k for real numbers a 0 > 1 and b 0 > 0 and integers n and k generate a family of discrete wavelets serving as an orthogonal basis of L 2 ( R ) :

(6) ψ k , n ( t ) = | a 0 | k 2 Ψ ( a 0 k t − n b 0 ) , k , n ∈ Z + .

Note that for a 0 = 2 and b 0 = 1 , ψ k , n ( t ) form an orthonormal basis.

3.2 Block pulse functions (BPFs)

The M -set of BPFs on [ 0 , 1 ) is defined as follows:

(7) b i ( t ) = 1 , i − 1 M ≤ t < i M 0 , Otherwise ,

where M is an integer and i = 1 , 2 , 3 , … , M . The vector of block pulse functions, B M ( t ) , is defined as follows:

(8) B M ( t ) = [ b 1 ( t ) , b 2 ( t ) , b 3 ( t ) , … , b M ( t ) ] T .

The following properties of b i ( t ) are considered:

(9) b i ( t ) b j ( t ) = 0 , i ≠ j b i ( t ) , i = j ,

(10) ∫ 0 1 b i ( t ) b j ( t ) dt = 0 , i ≠ j 1 M , i = j ,

(11) B M ( t ) ⨂ B M ( t ) = B M ( t ) ,

where ⨂ is the tensor product operator defined as follows:

For G M = [ g 1 , g 2 , g 3 , … , g M ] T , H M = [ h 1 , h 2 , h 3 , … , h M ] T , K M , M = [ k i , j ] M × M and L M , M = [ l i , j ] M × M :

G M ⨂ H M = ( g i × h i ) M = [ g 1 h 1 , g 2 h 2 , g 3 h 3 , … , g M h M ] T ,

(12) K M , M ⨂ L M , M = [ k i , j × l i , j ] M × M .

For the functions g ( t ) = G T B M ( t ) and h ( t ) = H T B M ( t ) , Eq. (11) directly leads to the following properties (2):

(13) g ( t ) h ( t ) = ( F T ⨂ G T ) B M ( t ) , g ( t ) n = ( G n ) T B M ( t ) .

Kilicman and Al Zhour [27] proposed the block pulse operational matrix of the fractional integration, F α , as follows:

(14) I α { B M ( t ) } ≅ F α B M ( t ) ,

where F α = [ F i , j α ] M × M and:

(15) F i , j α = 1 M α Γ ( α + 2 ) 0 , i > j 1 , i = j ξ j − i , i < j .

where

(16) ξ k = ( k + 1 ) α + 1 − 2 k α + 1 + ( k − 1 ) α + 1 .

4 Zernike wavelets

4.1 The Zernike polynomials

The Zernike polynomials form orthogonal basis functions on the continuous unit disk. These polynomials are two dimensional and constructed from a product of two separate angular and radial parts defined in polar coordinate system as follows [28].

(17) Z n m ( r , θ ) = 2 ( n + 1 ) 1 + δ m , 0 R n m ( r ) Θ ( m θ ) R n m ( r ) = ∑ s = 0 n − m 2 ( − 1 ) s ( n − s ) ! s ! n + m 2 − s ! n − m 2 − s ! r n − 2 s Θ ( m θ ) = cos ( m θ ) , m ≥ 0 − sin ( m θ ) , m < 0 ,

where Z n m ( r , θ ) is the Zernike polynomial of degree n and azimuthal order m . R n m ( r ) and Θ ( m θ ) are, respectively, radial and angular parts. In addition, δ represents Kronecker delta function. Moreover, n and m are integers in a way that ( n − m ) is an even element of N ∪ { 0 } . The following properties are considered for radial Zernike polynomials:

(18) R n m ( r ) = ( − 1 ) n − m 2 r m P n − m 2 ( m , 0 ) ( 1 − r 2 ) , ∫ 0 1 R n m ( r ) R k m ( r ) r d r = δ nk 2 ( n + 1 ) ,

where P is the Jacobi polynomial. Eq. (18) implies that for a certain order m , the set { R m + 2 i m ( r ) | i = 0 , 1 , 2 , … , N } is an orthogonal set of basis functions. For instance, { R 2 i 0 ( r ) | i = 0 , 1 , 2 , … , N } and { R 1 + 2 i 1 ( r ) | i = 0 , 1 , 2 , … , N } can be separately employed to approximate a function in L 2 [ 0, 1 ] , whereas the union of these sets does not form an orthogonal set.

4.2 Zernike wavelets

In this article, the following non-orthogonal wavelets are defined as follows. First, the domain [ 0, 1 ) is divided into 2 k ( k ∈ Z + ) equidistant subdomains. Then, the wavelet ψ i , j ( t ) on the (i + 1)th subdomain is defined as follows:

(19) ψ i , j ( t ) = Ψ j ( 2 k t − i ) , i 2 k ≤ t < i + 1 2 k 0 , Otherwise , i , j ∈ N ∪ { 0 }

where

(20) Ψ j ( t ) = R j 0 ( t ) , j = 2 s R j 1 ( t ) , j = 2 s + 1 , s ∈ N ∪ { 0 } .

Furthermore, the vector of all wavelets is defined as follows:

(21) Λ ( t ) = { ψ 0 , 0 ( t ) , ψ 0 , 1 ( t ) , ψ 0 , 2 ( t ) , … , ψ 0 , N − 1 ( t ) , … , ψ 2 k − 1 , N − 1 ( t ) } T , N ∈ N .

It is obvious from Eq. (21) that Λ ( t ) includes M = 2 k N wavelets whose polynomials’ degree varies from 0 to N − 1 .

4.3 Function approximation by Zernike wavelets

Since the proposed set of the Zernike wavelets, defined in Eq. (21), is non-orthogonal, a collocation scheme is employed to approximate a function f ( t ) as follows:

(22) f ( t ) ≅ C ̅ f T Λ ( t ) ,

where C ̅ f is the vector of constant coefficients, C ̅ f = { c 0,0 f , c 0, 1 f , c 0,2 f , … , c 0 , N − 1 f , … , c 2 k − 1 , N − 1 f } T , to be determined later. To calculate C ̅ f , both sides of Eq. (22) are collocated at points τ i = 2 i − 1 2 M for i = 1, 2, 3 , … , M :

(23) f ( τ i ) = C ̅ f T Λ ( τ i ) , i = 1 , 2 , 3 , … , M .

Solving Eq. (23) as a set of linear algebraic equations results in the approximation of the function f ( t ) using Eq. (22).

5 Hybrid Zernike-block pulse wavelets (HZBW) method

In this section, the proposed Zernike wavelets are combined with block pulse functions to develop a new technique for solving fractional differential equations. HZBW method is based on approximating a function using block pulse functions and Zernike wavelets, described in Section 5.1.

5.1 Function approximation by HZBW

First, the vector of Zernike wavelets is approximated by the vector of the block pulse function:

(24) Λ ( t ) ≅ ϕ B M ( t ) ,

where ϕ is an M × M unknown block pulse coefficient matrix to be determined by using collocation points τ i = 2 i − 1 2 M for i = 1, 2, 3 , … , M :

(25) Λ ( τ i ) ≅ ϕ B M ( τ i ) , i = 1 , 2 , 3 , … , M .

Applying Eq. (7) on the right-hand side of Eq. (25) leads to directly obtaining the block pulse coefficient matrix ϕ given as follows:

(26) ϕ = [ φ ij ] M × M , φ ij = Λ i ( τ j ) .

where Λ i is the ith element of the vector Λ , which can be expressed, according to Eq. (21), as follows:

(27) φ ij = ψ i N , i − 1 − N i − 1 N ( τ j ) .

Besides, according to Eq. (24), the vector of the block pulse function is approximated by the vector of Zernike wavelets as follows:

(28) B M ( t ) ≅ ϕ − 1 Λ ( t ) .

In a similar way, an arbitrary function f ( t ) can be approximated by block pulse functions via a collocation scheme:

(29) f ( t ) ≅ C f T B M ( t ) , C f = { f ( τ 1 ) , f ( τ 2 ) , f ( τ 3 ) , … , f ( τ M ) } T .

Hence, on the basis of Eqs. (28) and (29), the function f ( t ) can be approximated as follows:

(30) f ( t ) ≅ C f T ϕ − 1 Λ ( t ) .

Eq. (30) states that the function f ( t ) can be expressed and approximated in terms of Zernike wavelets Λ ( t ) using block pulse coefficient matrix ϕ . This proposed method is considered the HZBW approximation scheme.

This technique is used to derive the Zernike-block pulse operational matrix of fractional integration in Section 5.2.

5.2 Operational matrix of fractional integration by HZBW

Substituting B M ( t ) in Eq. (14) with ϕ − 1 Λ ( t ) (according to Eq. (28)) yields:

I α { ϕ − 1 Λ ( t ) } ≅ F α ϕ − 1 Λ ( t ) ⟹

ϕ − 1 I α { Λ ( t ) } ≅ F α ϕ − 1 Λ ( t ) ⟹

(31) I α { Λ ( t ) } ≅ ϕ F α ϕ − 1 Λ ( t ) .

Setting F ̅ α = ϕ F α ϕ − 1 in Eq. (31) rewrites this equation in terms of the HZBW fractional integration operational matrix, F ̅ α , as follows:

(32) I α { Λ ( t ) } ≅ F ̅ α Λ ( t ) .

5.3 HZBW method to solve set of nonlinear fractional differential equations (SNFDEs)

Consider the following SNFDEs:

(33) N i { D α i { K i ( U d ( t ) ) } , U d ( t ) } = 0 , i = 1 , 2 , 3 , … , d , t ∈ [ 0 , 1 ] ,

where d is the number of equations and N i is a nonlinear operator representing the ith fractional differential equation. Besides, U d ( t ) demonstrates the vector of unknown functions: U d ( t ) = { u s ( t ) | s = 1, 2, 3 , … , d } T . Moreover, K i is a nonlinear function to which the fractional derivative of the order α i is applied. It is defined as follows: K i ( U d ( t ) ) = K i ( u 1 ( t ) , u 2 ( t ) , u 3 ( t ) , … , u d ( t ) ) . To solve SNFDEs Eq. (33), unknown functions, u i ( t ) , their fractional derivatives, and nonlinear functions, K i , are approximated by Eq. (29):

(34) u i ( t ) ≅ C u i T B M ( t ) , i = 1 , 2 , 3 , … , d ,

(35) K i ( U d ( t ) ) − K i ( U d ( 0 ) ) ≅ C K i T B M ( t ) , i = 1 , 2 , 3 , … , d ,

(36) D α i { K i ( U d ( t ) ) } ≅ C D K i T B M ( t ) , i = 1 , 2 , 3 , … , d ,

where C u i T , C K i T , and C D K i T are unknown constants to be determined later. It should be mentioned that without loss of generality in Eq. (35), the function K i ( U d ( t ) ) − K i ( U d ( 0 ) ) is approximated instead of approximating K i ( U d ( t ) ) . This decision enables us to simplify the following relations.

Now, the mentioned constants C K i T and C D K i T can be calculated as follows. Applying I α to both sides of Eq. (36) and using Eqs. (4), (14), and (35) lead to:

K i ( U d ( t ) ) − K i ( U d ( 0 ) ) = C D K i T F α B M ( t ) ⟹

C K i T B M ( t ) = C D K i T F α B M ( t ) ⟹

C K i T = C D K i T F α ⟹

(37) C D K i T = C K i T ( F α ) − 1 , i = 1 , 2 , 3 , … , d .

Eq. (37) reveals how C D K i T is dependent on and can be substituted with C K i T ( F α ) − 1 . Besides, C K i can be obtained in terms of C u i as follows. According to Eq. (29),

(38) C K i = { K i ( U d ( τ 1 ) ) , K i ( U d ( τ 2 ) ) , K i ( U d ( τ 3 ) ) , … , K i ( U d ( τ M ) ) } T ,

(39) C D K i = { D α i { K i ( U d ( τ 1 ) ) } , D α i { K i ( U d ( τ 2 ) ) } , D α i { K i ( U d ( τ 3 ) ) } , … , D α i { K i ( U d ( τ M ) ) } } T .

On the other hand, U d ( τ j ) can be obtained as follows.

(40) U d ( τ j ) = { u 1 ( τ j ) , u 2 ( τ j ) , u 3 ( τ j ) , … , u d ( τ j ) } T .

According to Eqs. (29) and (34), u i ( τ j ) equals to the jth element of the vector C u i :

(41) u i ( τ j ) = ( C u i ) j .

where ( C u i ) j is the jth element of the vector C u i . Thus, Eq. (40) is changed to:

(42) U d ( τ j ) = { ( C u 1 ) j , ( C u 2 ) j , ( C u 3 ) j , … , ( C u d ) j } T .

Hence, Eq. (38) is simplified to:

(43) C K i = { K i ( ( C u 1 ) 1 , ( C u 2 ) 1 , … , ( C u d ) 1 ) , K i ( ( C u 1 ) 2 , ( C u 2 ) 2 , … , ( C u d ) 2 ) , … , K i ( ( C u 1 ) M , ( C u 2 ) M , … , ( C u d ) M ) } T .

By setting X = ⋃ i = 1 d C u i , Eq. (42) can be simply presented as follows:

(44) C K i = C K i ( X ) ,

where X is the vector of all unknowns. In addition, substituting Eq. (44) into Eq. (37) gives C D K i in terms of X :

(45) C D K i T = C K i ( X ) T ( F α ) − 1 , i = 1 , 2 , 3 , … , d .

Substituting Eqs. (34)–(36) as well as Eqs. (44) and (45) into Eq. (33) results in

(46) N i { C D K i T B M ( t ) , C u 1 T B M ( t ) , C u 2 T B M ( t ) , … , C u d T B M ( t ) } = 0 , i = 1 , 2 , 3 , … , d , t ∈ [ 0 , 1 ] .

Now, all arguments of N i in Eq. (46) have been rewritten in terms of the unknowns vector X and block pulse functions B M ( t ) . Then, the left-hand side of Eq. (46) is approximated using Eq. (29):

(47) N i ( t ) = C N i T B M ( t ) = 0 , i = 1 , 2 , 3 , … , d .

Similar to the procedure performed through Eqs. (38)–(44), C N i T can be proved to be in terms of X :

(48) C N i T = C N i T ( X ) = 0 , i = 1 , 2 , 3 , … , d .

Eq. (48) demonstrates a set of Md nonlinear algebraic equations to be solved using a proper numerical method to obtain unknowns C u i . After calculating C u i , a HZBW solution of Eq. (33) can be expressed as follows:

(49) u i ( t ) ≅ C u i T ϕ − 1 Λ ( t ) .

This method can be employed to solve numerous sets of nonlinear fractional differential equations arising in biomechanics, fluid dynamics, heat transfer, and more. Especially since fractional derivatives have been widely used in bio-mathematical modelling, this technique will definitely be utilized in future research in this area.

5.4 Error analysis of HZBW method

In this section, error bounds of approximating functions and fractional operational matrix are provided. Here, the absolute and L 2 norm of a function f ( x ) throughout its domain, [ a , b ] , are denoted, respectively, by Max | f ( x ) | [ a , b ] and ‖ f ( x ) ‖ L 2 [ a , b ] . The following theorem, rewritten for the functions of one variable using [29], constructs a basis for error analysis by calculating the error of interpolation of a function by ( n + 1 ) points.

Theorem 1

Suppose that f ( t ) ∈ C n + 1 [ a , b ] and p n ( t ) is a polynomial of degree at most n interpolating f ( t ) using n + 1 distinct points t i ∈ [ a , b ] ( i = 0 , 1 , 2 , … , n ). Then, for each t ∈ [ a , b ] , there exists ξ = ξ ( t ) ∈ [ a , b ] such that [29]:

(50) f ( t ) − p n ( t ) = 1 ( n + 1 ) ! f ( n + 1 ) ( ξ ) ∏ i = 0 n ( t − t i ) .

Lemma 1

Let n be a nonnegative integer, t ∈ [ a , b ] and H n ( t ) = ∏ i = 0 n | t − t i , n [ a , b ] | , where t i , n [ a , b ] = a + 2 i + 1 2 h n [ a , b ] and h n [ a , b ] = b − a n + 1 . Then, the absolute maximum of H n ( t ) occurs at t = a and

(51) Max | H n ( t ) | [ a , b ] = h n [ a , b ] 2 n + 1 ∏ i = 0 n ( 2 i + 1 ) .

Proof

Eq. (51) can be proved by employing mathematical induction on n as follows.

Base case: For n = 0 , H 0 ( t ) = t − h 0 [ a , b ] 2 . It is evident that Max | H 0 ( t ) | [ a , b ] = h 0 [ a , b ] 2 concedes that the proposition holds for n = 0 .

Induction step: Suppose that the proposition is true for n = k > 0 providing that for any real numbers a and b , Max | H k ( t ) | [ a , b ] = h k [ a , b ] 2 k + 1 ∏ i = 0 k ( 2 i + 1 ) . It should be noted that H n ( t ) is symmetric with respect to line x = a + b 2 . Thus:

(52) Max | H n ( t ) | [ a , b ] = Max | H n ( t ) | a , a + b 2 .

Since a + b 2 < b − h n [ a , b ] , Eq. (52) leads to:

(53) Max | H n ( t ) | [ a , b ] = Max | H n ( t ) | [ a , b − h n [ a , b ] ] .

In addition, it is obvious that

(54) h n + 1 [ a , b ] = h n [ a , b − h n + 1 [ a , b ] ] t i , n + 1 [ a , b ] = t i , n [ a , b − h n + 1 [ a , b ] ] .

By considering Eqs. (52)–(54), it can be written for n = k + 1 that

Max | H k + 1 ( t ) | [ a , b ] = Max ∏ i = 0 k + 1 | t − t i , k + 1 [ a , b ] | [ a , b ] ≤ Max ∏ i = 0 k | t − t i , k + 1 [ a , b ] | [ a , b ] ( Max | t − t k + 1 , k + 1 [ a , b ] | [ a , b ] ) = Max ∏ i = 0 k | t − t i , k + 1 [ a , b ] | a , a + b 2 2 k + 3 2 h k + 1 [ a , b ] = Max ∏ i = 0 k | t − t i , k [ a , b − h k + 1 [ a , b ] ] | a , a + b 2 × 2 k + 3 2 h k + 1 [ a , b ] = Max ∏ i = 0 k | t − t i , k [ a , b − h k + 1 [ a , b ] ] | [ a , b − h k + 1 [ a , b ] ] × 2 k + 3 2 h k + 1 [ a , b ] = Max | H k ( t ) | [ a , b − h k + 1 [ a , b ] ] 2 k + 3 2 h k + 1 [ a , b ] = 2 k + 3 2 h k + 1 [ a , b ] h k [ a , b − h k + 1 [ a , b ] ] 2 k + 1 ∏ i = 0 k ( 2 i + 1 ) = 2 k + 3 2 h k + 1 [ a , b ] h k + 1 [ a , b ] 2 k + 1 ∏ i = 0 k ( 2 i + 1 ) = h k + 1 [ a , b ] 2 k + 2 ∏ i = 0 k + 1 ( 2 i + 1 ) = H k + 1 ( a ) .

Therefore, the proposition holds for n = k + 1 .

Conclusion: As the base case and the induction step have been proved true, using mathematical induction, the proposition Eq. (51) holds for all nonnegative integer n .

Theorem 2

If f ( t ) is a function defined on [ 0 , 1 ] with bounded derivatives f ( i ) ( t ) ( i = 0 , 1 , 2 , … , N ), then there exists an approximation of f ( t ) by Zernike wavelets Λ ( t ) according to Eq. (22) with the following error upper bound:

(55) | f ( t ) − C ̅ f T Λ ( t ) | ≤ μ f Max | f ( N ) ( t ) | [ 0 , 1 ] ,

where μ f = 1 2 M N N ! ∏ i = 1 N ( 2 i − 1 ) .

Proof

Since Λ ( t ) includes polynomials of degree at most N − 1 , Eqs. (19)–(22) suggest that f ( t ) can be approximated on the interval i 2 k , i + 1 2 k as: p N − 1 ( t ) ≅ ∑ j = 1 N c ̅ f , j ψ i , j ( t ) . Thus, according to Theorem 1:

(56) E f i 2 k , i + 1 2 k ( t ) = f ( t ) − p N − 1 ( t ) = 1 N ! f ( N ) ( ξ ( t ) ) ∏ r = 0 N − 1 ( t − t r ) ,

where t r = i 2 k + 2 r + 1 2 M and E f i 2 k , i + 1 2 k is the error of f ( t ) throughout the interval i 2 k , i + 1 2 k . Hence, on the basis of Lemma 1, the upper bound of the error on this interval can be given as follows:

(57) Max E f i 2 k , i + 1 2 k = 1 N ! Max | f ( N ) ( t ) | i 2 k , i + 1 2 k × 1 2 M N ∏ r = 0 N − 1 ( 2 r + 1 ) = 1 N ! Max | f ( N ) ( t ) | i 2 k , i + 1 2 k × 1 2 M N ∏ r = 1 N ( 2 r − 1 ) .

Considering the maximum error over the whole interval [ 0, 1 ] results in

Max | E f [ 0, 1 ] | = Max E f i 2 k , i + 1 2 k i = 0, 1,2 , … , 2 k − 1 = 1 N ! Max | f ( N ) ( t ) | [ 0, 1 ] 1 2 M N ∏ r = 1 N ( 2 r − 1 ) = μ f Max | f ( N ) ( t ) | [ 0, 1 ] .

Since Max | f ( N ) ( t ) | [ 0, 1 ] is bounded, lim M → ∞ μ f Max | f ( N ) ( t ) | [ 0, 1 ] = 0 confirming that C ̅ f T Λ ( t ) converges to f ( t ) with the error upper bound given in Eq. (55).

Theorem 3

If f ( t ) is a function with conditions defined in Theorem 1, then there exists an approximation of f ( t ) by block pulse functions B M ( t ) according to Eq. (29) with the following error upper bound:

(58) | f ( t ) − C f T B M ( t ) | ≤ 1 2 M Max | f ′ ( t ) | [ 0 , 1 ] .

Proof

Since B M ( t ) includes polynomials of degree zero, the proof is simply obtained by considering a procedure similar to that in Theorem 1 for N = 1 .

Theorem 4

There exists an approximation of Λ ( t ) by block pulse functions B M ( t ) according to Eq. (24) with the following error upper bound:

(59) | Λ ( t ) − ϕ B M ( t ) | ≤ 1 2 M Max | Λ ′ ( t ) | [ 0 , 1 ] .

Proof

Λ ( t ) includes polynomials of degree at most N − 1 , each of which satisfies the required conditions of f ( t ) in Theorem (3), leading to the proof of the Eq. (59).

Theorem 5

There exists an approximation of I α { Λ ( t ) } by Zernike wavelets Λ ( t ) according to Eq. (32) with the order of O 1 M :

(60) ‖ I α { Λ ( t ) } − ϕ F α ϕ − 1 Λ ( t ) ‖ L 2 [ 0 , 1 ] = O 1 M .

Proof

According to Eq. (24), Λ i ( t ) can be approximated on the interval [ 0, 1 ] as follows: p i ( t ) ≅ ∑ j = 1 M φ i , j b j ( t ) = C Λ i T B M ( t ) , where C Λ i T = { Λ i ( τ 1 ) , Λ i ( τ 2 ) , Λ i ( τ 3 ) , … , Λ i ( τ M ) } . This states that Λ i ( t ) is approximated by a zero-degree polynomial on the interval i M , i + 1 M for i = 0, 1,2 , … , M − 1 . Therefore, considering Theorem (1) and Eq. (24) leads to:

(61) Λ i ( t ) − C Λ i T B M ( t ) = ∑ j = 1 M δ j ( t ) Λ i ′ ( ξ i , j ( t ) ) t − 2 j + 1 2 M ,

where

(62) δ j ( t ) = 1 , t ∈ j M , j + 1 M 0 , Otherwise .

Applying I α to both sides of Eq. (61) results in

(63) I α { Λ i ( t ) } − C Λ i T I α { B M ( t ) } = I α ∑ j = 1 M δ j ( t ) Λ i ′ ( ξ i , j ( t ) ) t − 2 j + 1 2 M .

Rewriting Eq. (14) gives

(64) I α { B M ( t ) } = F α B M ( t ) + E B [ 0 , 1 ] ( t ) .

Substituting Eq. (64) in Eq. (63) leads to

I α { Λ i ( t ) } − C Λ i T F α B M ( t ) = C Λ i T E B [ 0, 1 ] ( t ) + I α ∑ j = 1 M δ j ( t ) Λ i ′ ( ξ i , j ( t ) ) t − 2 j + 1 2 M ⟹

(65) ‖ I α { Λ i ( t ) } − C Λ i T F α ϕ − 1 Λ ( t ) ‖ L 2 [ 0 , 1 ] ≤ C Λ i T ‖ E B [ 0 , 1 ] ( t ) ‖ L 2 [ 0 , 1 ] + I α ∑ j = 1 M δ j ( t ) Λ i ′ ( ξ i , j ( t ) ) t − 2 j + 1 2 M L 2 [ 0 , 1 ] .

On the other hand,

(66) ∑ j = 1 M δ j ( t ) Λ i ′ ( ξ i , j ( t ) ) t − 2 j + 1 2 M ≤ 1 2 M Max | Λ i ′ ( t ) | [ 0 , 1 ] .

Thus,

(67) I α ∑ j = 1 M δ j ( t ) Λ i ′ ( ξ i , j ( t ) ) t − 2 j + 1 2 M ≤ 1 2 M Max | Λ i ′ ( t ) | [ 0 , 1 ] I α { 1 } = 1 2 M Max | Λ i ′ ( t ) | [ 0 , 1 ] t α Γ ( α + 1 ) .

Therefore,

(68) I α ∑ j = 1 M δ j ( t ) Λ i ′ ( ξ i , j ( t ) ) t − 2 j + 1 2 M L 2 [ 0 , 1 ] ≤ 1 2 M Γ ( α + 1 ) Max | Λ i ′ ( t ) | [ 0 , 1 ] ‖ t α ‖ L 2 [ 0 , 1 ] = 1 2 M Γ ( α + 1 ) ( 2 α + 1 ) Max | Λ i ′ ( t ) | [ 0 , 1 ] .

It can be deduced from [27,30] that ‖ E B [ 0, 1 ] ( t ) ‖ L 2 [ 0, 1 ] is of order O 1 M and can be expressed as follows:

(69) ‖ E B [ 0 , 1 ] ( t ) ‖ L 2 [ 0 , 1 ] ≤ C M .

Hence, substituting Eqs. (68) and (69) in Eq. (65) yields

(70) ‖ I α { Λ i ( t ) } − C Λ i T F α ϕ − 1 Λ ( t ) ‖ L 2 [ 0 , 1 ] ≤ C Λ i T C M + 1 2 M Γ ( α + 1 ) ( 2 α + 1 ) Max | Λ i ′ ( t ) | [ 0 , 1 ] .

Since C Λ i T , C and Max | Λ i ′ ( t ) | [ 0, 1 ] are bounded, ‖ I α { Λ i ( t ) } − C Λ i T F α ϕ − 1 Λ ( t ) ‖ L 2 [ 0, 1 ] and subsequently ‖ I α { Λ ( t ) } − ϕ F α ϕ − 1 Λ ( t ) ‖ L 2 [ 0, 1 ] tend to zero with the order of O 1 M when M → ∞ .

6 HZBW solution to the breast cancer competition model

The proposed method is now employed to study a fractional competition model of breast cancer, previously investigated in the study by Solís-Pérez et al. [3]. This model was first introduced by Abernathy et al. [31] as a system of five ordinary differential equations governing cancer stem cells ( C ), tumour cells ( T ), healthy cells ( H ), immune cells ( I ), and excess estrogen ( E ). Then, to include memory of the biological system, integer-order fractional derivatives were replaced with Caputo fractional derivatives in [3]. These SNFDEs were given as follows:

(71) D α 1 { C ( t ) } = k 1 C ( t ) 1 − C ( t ) M 1 − γ 1 I ( t ) C ( t ) + p 1 C ( t ) E ( t ) a 1 + C ( t ) , D α 2 { T ( t ) } = k 2 C ( t ) C ( t ) M 1 1 − T ( t ) M 2 − n 1 T ( t ) − γ 2 I ( t ) T ( t ) + p 2 T ( t ) E ( t ) a 2 + T ( t ) , D α 3 { H ( t ) } = qH ( t ) 1 − H ( t ) M 3 − δ H ( t ) T ( t ) − p 3 H ( t ) E ( t ) a 3 + H ( t ) t ∈ [ 0 , T ] , D α 4 { I ( t ) } = s + ρ I ( t ) T ( t ) ω + T ( t ) − n 2 I ( t ) − γ 3 I ( t ) T ( t ) − u I ( t ) E ( t ) ν + E ( t ) , D α 5 { E ( t ) } = τ − μ + d 1 C ( t ) a 1 + C ( t ) + d 2 T ( t ) a 2 + T ( t ) + d 3 H ( t ) a 3 + H ( t ) E ( t ) .

Under the following initial conditions:

(72) C ( 0 ) = C ̅ 0 , T ( 0 ) = T ̅ 0 , H ( 0 ) = H ̅ 0 , I ( 0 ) = I ̅ 0 , E ( 0 ) = E ̅ 0 .

The values of all parameters in Eq. (71) are presented in Table 1.

Table 1

The parameters in Eq. (71) and their values [3]

Parameter	Value	Parameter	Value
k 1	0.75 da y ‒ 1	a 3	1.25 × 10 6 cells
k 2	0.514 da y ‒ 1	n 1	0.01 da y ‒ 1
q	0.70 da y ‒ 1	n 2	0.29 da y ‒ 1
M 1	2.27 × 10 6 cells	δ	6 × 10 ‒ 8 ( day ) ‒ 1 ( cell ) ‒ 1
M 2	2.27 × 10 7 cells	s	1.3 × 10 4 ( cell ) ( day ) ‒ 1
M 3	2.5 × 10 7 cells	ρ	0.20 da y ‒ 1
γ 1	3 × 10 ‒ 7 ( day ) ‒ 1 ( cell ) ‒ 1	ω	3 × 10 5 cells
γ 2	3 × 10 ‒ 6 ( day ) ‒ 1 ( cell ) ‒ 1	u	0.2 da y ‒ 1
γ 3	1 × 10 ‒ 7 ( day ) ‒ 1 ( cell ) ‒ 1	ν	400 ( pgm ) L ‒ 1
p 1	600 ( cell ) ( day ) ‒ 1 pg mL ‒ 1	τ	2,000 ( pgm ) ( day ) ‒ 1 L ‒ 1
p 2	0 ( cell ) ( day ) ‒ 1 pg mL ‒ 1	μ	0.97 da y ‒ 1
p 3	100 ( cell ) ( day ) ‒ 1 pg mL ‒ 1	d 1	0.01 da y ‒ 1
a 1	1.135 × 10 6 cells	d 2	0.01 da y ‒ 1
a 2	1.135 × 10 7 cells	d 3 q	0.01 da y ‒ 1

To solve Eq. (71), the temporal domain must be changed from [ 0 , T ] to [ 0, 1 ] . Thus, the time domain is normalized by the total time, T . In other words, the non-dimensional time t * = t T is defined, and the time t must be replaced with T t * . It can be proved that:

(73) D α { u ( t ) } = 1 T α D α { u ( t * ) } .

Eq. (73) implies that to convert Eq. (71) into a non-dimensional form, it necessitates multiplying the fractional derivative terms by 1 T α i and rewriting all unknown functions in terms of t * . After applying these changes, for simplicity and without loss of generality, the superscript “ * ” is omitted. Moreover, to provide a unified notation and more simple presentation, unknown functions are renamed as follows: { C ( t ) , T ( t ) , H ( t ) , I ( t ) , E ( t ) } = { u 1 ( t ) , u 2 ( t ) , u 3 ( t ) , u 4 ( t ) , u 5 ( t ) } . Hence, Eq. (71) is changed to:

(74) 1 T α 1 D α 1 { u 1 ( t ) } = k 1 u 1 ( t ) 1 − u 1 ( t ) M 1 − γ 1 u 4 ( t ) u 1 ( t ) + p 1 u 1 ( t ) u 5 ( t ) a 1 + u 1 ( t ) , 1 T α 2 D α 2 { u 2 ( t ) } = k 2 u 1 ( t ) u 1 ( t ) M 1 1 − u 2 ( t ) M 2 − n 1 u 2 ( t ) − γ 2 u 4 ( t ) u 2 ( t ) + p 2 u 2 ( t ) u 5 ( t ) a 2 + u 2 ( t ) , 1 T α 3 D α 3 { u 3 ( t ) } = q u 3 ( t ) 1 − u 3 ( t ) M 3 − δ u 3 ( t ) u 2 ( t ) − p 3 u 3 ( t ) u 5 ( t ) a 3 + u 3 ( t ) t ∈ [ 0 , 1 ] , 1 T α 4 D α 4 { u 4 ( t ) } = s + ρ u 4 ( t ) u 2 ( t ) ω + u 2 ( t ) − n 2 u 4 ( t ) − γ 3 u 4 ( t ) u 2 ( t ) − u u 4 ( t ) u 5 ( t ) ν + u 5 ( t ) , 1 T α 5 D α 5 { u 5 ( t ) } = τ − μ + d 1 u 1 ( t ) a 1 + u 1 ( t ) + d 2 u 2 ( t ) a 2 + u 2 ( t ) + d 3 u 3 ( t ) a 3 + u 3 ( t ) u 5 ( t ) .

The solution procedure is the same as the one provided in Section 5.3. Note that the functions K i in this model are linear: K i ( u ) = u . Following the mentioned scheme, u i ( t ) and D α 1 { u i ( t ) } ( i = 1, 2, 3 , … , 5 ) are approximated as follows:

(75) u i ( t ) − u i ( 0 ) ≅ C u i T B M ( t ) , i = 1 , 2 , 3 , … , 5 ,

(76) D α i { u i ( t ) } ≅ C D i T B M ( t ) , i = 1 , 2 , 3 , … , 5 .

Applying I α in both sides of Eq. (76) and employing Eq. (14) yield:

(77) u i ( t ) − u i ( 0 ) = C D i T F α B M ( t ) .

Comparing Eq. (74) with Eq. (77) leads to:

C D i T F α B M ( t ) = C u i T B M ( t ) ⟹

C D i T F α = C u i T ⟹

(78) C D i T = C u i T ( F α ) − 1 .

Therefore, Eqs. (75) and (76) are changed to:

(79) u i ( t ) ≅ [ C u i T + u i ( 0 ) ] B M ( t ) , i = 1 , 2 , 3 , … , 5 ,

(80) D α i { u i ( t ) } ≅ C u i T ( F α ) − 1 B M ( t ) , i = 1 , 2 , 3 , … , 5 .

Now, after inserting u i ( t ) and D α i { u i ( t ) } from Eqs. (79) and (80) into Eq. (74) as well as employing the properties of Eq. (13), Eq. (74) is simplified to:

(81) 1 T α 1 C u 1 T ( F α ) − 1 B M ( t ) = k 1 [ C u 1 T + u 1 ( 0 ) ] 1 − C u 1 T + u 1 ( 0 ) M 1 B M ( t ) − γ 1 [ C u 4 T + u 4 ( 0 ) ] [ C u 1 T + u 1 ( 0 ) ] B M ( t ) + p 1 [ C u 1 T + u 1 ( 0 ) ] [ C u 5 T + u 5 ( 0 ) ] B M ( t ) [ a 1 + C u 1 T + u 1 ( 0 ) ] , 1 T α 2 C u 2 T ( F α ) − 1 B M ( t ) = k 2 [ C u 1 T + u 1 ( 0 ) ] [ C u 1 T + u 1 ( 0 ) ] M 1 1 − [ C u 2 T + u 2 ( 0 ) ] M 2 B M ( t ) − n 1 [ C u 2 T + u 2 ( 0 ) ] B M ( t ) − γ 2 [ C u 4 T + u 4 ( 0 ) ] [ C u 2 T + u 2 ( 0 ) ] B M ( t ) + p 2 [ C u 2 T + u 2 ( 0 ) ] [ C u 5 T + u 5 ( 0 ) ] B M ( t ) [ a 2 + C u 2 T + u 2 ( 0 ) ] , 1 T α 3 C u 3 T ( F α ) − 1 B M ( t ) = q [ C u 3 T + u 3 ( 0 ) ] 1 − [ C u 3 T + u 3 ( 0 ) ] M 3 B M ( t ) − δ [ C u 3 T + u 3 ( 0 ) ] [ C u 2 T + u 2 ( 0 ) ] B M ( t ) − p 3 [ C u 3 T + u 3 ( 0 ) ] [ C u 5 T + u 5 ( 0 ) ] B M ( t ) [ a 3 + C u 3 T + u 3 ( 0 ) ] , 1 T α 4 C u 4 T ( F α ) − 1 B M ( t ) = s B M ( t ) + ρ [ C u 4 T + u 4 ( 0 ) ] [ C u 2 T + u 2 ( 0 ) ] B M ( t ) [ ω + C u 2 T + u 2 ( 0 ) ] − n 2 [ C u 4 T + u 4 ( 0 ) ] B M ( t ) − γ 3 [ C u 4 T + u 4 ( 0 ) ] [ C u 2 T + u 2 ( 0 ) ] B M ( t ) − u [ C u 4 T + u 4 ( 0 ) ] [ C u 5 T + u 5 ( 0 ) ] B M ( t ) [ ν + C u 5 T + u 5 ( 0 ) ] , 1 T α 5 C u 5 T ( F α ) − 1 B M ( t ) = τ − [ C u 5 T + u 5 ( 0 ) ] × μ + d 1 [ C u 1 T + u 1 ( 0 ) ] [ a 1 + C u 1 T + u 1 ( 0 ) ] + d 2 [ C u 2 T + u 2 ( 0 ) ] [ a 2 + C u 2 T + u 2 ( 0 ) ] + d 3 [ C u 3 T + u 3 ( 0 ) ] [ a 3 + C u 3 T + u 3 ( 0 ) ] B M ( t ) .

Note that the initial values, u i ( 0 ) , are substituted from Eq. (72) in Eq. (81). Besides, in Eq. (81), the vector B M ( t ) can be cancelled out. Finally, the following set of 5 M nonlinear algebraic equations is obtained to be solved for the unknown constants C u i :

(82) 1 T α 1 C u 1 T ( F α ) − 1 = k 1 [ C u 1 T + u 1 ( 0 ) ] 1 − C u 1 T + u 1 ( 0 ) M 1 − γ 1 [ C u 4 T + u 4 ( 0 ) ] [ C u 1 T + u 1 ( 0 ) ] + p 1 [ C u 1 T + u 1 ( 0 ) ] [ C u 5 T + u 5 ( 0 ) ] [ a 1 + C u 1 T + u 1 ( 0 ) ] , 1 T α 2 C u 2 T ( F α ) − 1 = k 2 [ C u 1 T + u 1 ( 0 ) ] [ C u 1 T + u 1 ( 0 ) ] M 1 1 − [ C u 2 T + u 2 ( 0 ) ] M 2 − n 1 [ C u 2 T + u 2 ( 0 ) ] − γ 2 [ C u 4 T + u 4 ( 0 ) ] [ C u 2 T + u 2 ( 0 ) ] + p 2 [ C u 2 T + u 2 ( 0 ) ] [ C u 5 T + u 5 ( 0 ) ] [ a 2 + C u 2 T + u 2 ( 0 ) ] , 1 T α 3 C u 3 T ( F α ) − 1 = q [ C u 3 T + u 3 ( 0 ) ] 1 − [ C u 3 T + u 3 ( 0 ) ] M 3 − δ [ C u 3 T + u 3 ( 0 ) ] [ C u 2 T + u 2 ( 0 ) ] − p 3 [ C u 3 T + u 3 ( 0 ) ] [ C u 5 T + u 5 ( 0 ) ] [ a 3 + C u 3 T + u 3 ( 0 ) ] , 1 T α 4 C u 4 T ( F α ) − 1 = s + ρ [ C u 4 T + u 4 ( 0 ) ] [ C u 2 T + u 2 ( 0 ) ] [ ω + C u 2 T + u 2 ( 0 ) ] − n 2 [ C u 4 T + u 4 ( 0 ) ] − γ 3 [ C u 4 T + u 4 ( 0 ) ] [ C u 2 T + u 2 ( 0 ) ] − u [ C u 4 T + u 4 ( 0 ) ] [ C u 5 T + u 5 ( 0 ) ] [ ν + C u 5 T + u 5 ( 0 ) ] , 1 T α 5 C u 5 T ( F α ) − 1 = τ − [ C u 5 T + u 5 ( 0 ) ] × μ + d 1 [ C u 1 T + u 1 ( 0 ) ] [ a 1 + C u 1 T + u 1 ( 0 ) ] + d 2 [ C u 2 T + u 2 ( 0 ) ] [ a 2 + C u 2 T + u 2 ( 0 ) ] + d 3 [ C u 3 T + u 3 ( 0 ) ] [ a 3 + C u 3 T + u 3 ( 0 ) ] .

Now, an HZBW solution can be obtained using Eq. (49):

u i ( t ) ≅ C u i T ϕ − 1 Λ ( t ) .

7 Results and discussion

To demonstrate the capability of the proposed method for investigating a nonlinear fractional model of breast cancer, the set of equations in Eq. (82) is solved using Wolfram Mathematica software for T = 50 days. The initial values and fractional orders, respectively, arising in Eqs. (72) and (82), are given as follows [3]:

(83) u 1 ( 0 ) = C ̅ 0 = 7.3710 × 10 5 , u 2 ( 0 ) = T ̅ 0 = 7.6167 × 10 6 , u 3 ( 0 ) = H ̅ 0 = 2.5 × 10 7 , I ( 0 ) = I ̅ 0 = 0 , E ( 0 ) = E ̅ 0 = 0 , { α 1 , α 2 , α 3 , α 4 , α 5 } = { 0.95 , 0.94 , 0.97 , 0.98 , 0.99 } .

First, in this section, an experimental approach to considering the convergence of the solution is employed. As the exact solution is not available, the accuracy of the method is verified by comparing the results for the special case: α i = 1 ( i = 1 , 2 , 3 , … , 5 ) with the results obtained by the command “NDSolve” of the software Wolfram Mathematica using the Runge–Kutta (RK4) scheme. Then, the CPU running time, as the computational cost of the presented method, is reported. Finally, the effect of the fractional orders on the trend of breast cancer therapy is studied.

7.1 Convergence of the solution

In this section, Eq. (82) is solved for various values of k and N , and the results are tabulated to demonstrate the convergence trend.

Besides, to analyse the rate of convergence (ROC), it is calculated according to the following formula:

(84) ROC | m ˆ = m ˆ 4 = log f m ˆ 4 − f m ˆ 3 f m ˆ 3 − f m ˆ 2 log f m ˆ 3 − f m ˆ 2 f m ˆ 2 − f m ˆ 1 .

where f stands for each of the functions u i ( t ) ( i = 1 , 2 , 3 , … , 5 ) calculated at a certain time t = t j for four successive values of m ˆ : m ˆ 1 < m ˆ 2 < m ˆ 3 < m ˆ 4 . Moreover, m ˆ k ( k = 1 , 2 , 3 , 4 ) stands for different values of k or N for which the solution is obtained.

Tables 2–6 present C ( t ) , H ( t ) , T ( t ) , I ( t ) , and E ( t ) evaluated at t = 0.5 , 0.2 , 2 , 5 , 20 , and 50 for various values of k and N . To study the ROC with respect to k , the problem is solved for N = 7 and k = 3,4,5,6 . Then, the results are tabulated in columns 2–6 of the aforementioned tables. Similarly, columns 7–11 demonstrate the effect of N on the convergence of the solutions. It can be realized that by increasing the order of approximation, the solutions converge with higher precision. Besides, it is evident that ROC ≈ 1 with respect to k , while it is estimated as ROC ≈ 0.8 concerning N . Furthermore, it can be inferred that by increasing t , the solution demonstrates more rapid convergence due to the asymptotic behaviour of the functions C ( t ) , H ( t ) , T ( t ) , I ( t ) , and E ( t ) . These tables confirm that the solution is convergent with high accuracy and an acceptable convergence rate. Hence, for the next studies in this article, k = 5 and N = 6 have been considered as the proper values of k and N , respectively.

Table 2

The values of C ( t ) and ROC at various time

	N = 7					k = 6
t	C ( t )	C ( t )	C ( t )	C ( t )	ROC	C ( t )	C ( t )	C ( t )	C ( t )	ROC
t	k = 3	k = 4	k = 5	k = 6	k = 6	N = 4	N = 5	N = 6	N = 7	N = 7
0.2	915,195	845,577	836,043	833,752	0.71	835,246	834,478	834,031	833,752	0.87
0.5	1,046,786	1,019,888	1,012,614	1,010,839	1.07	1,012,047	1,011,398	1,011,054	1,010,839	0.73
2	2,161,037	2,173,559	2,176,700	2,177,468	1.01	2,176,923	2,177,223	2,177,376	2,177,468	0.74
5	3,035,799	3,030,602	3,029,474	3,029,196	0.91	3,029,388	3,029,285	3,029,229	3,029,196	0.82
20	3,121,885	3,121,873	3,121,870	3,121,869	1.01	3,121,870	3,121,869	3,121,869	3,121,869	0.82
50	3,127,251	3,127,250	3,127,250	3,127,250	1.01	3,127,250	3,127,250	3,127,250	3,127,250	0.83

Table 3

The values of H ( t ) and ROC at various time

	N = 7					k = 6
t	H ( t )	H ( t )	H ( t )	H ( t )	ROC	H ( t )	H ( t )	H ( t )	H ( t )	ROC
t	k = 3	k = 4	k = 5	k = 6	k = 6	N = 4	N = 5	N = 6	N = 7	N = 7
0.2	23,734,374	23,086,726	22,902,790	22,857,182	1.10	22,891,379	22,871,727	22,862,413	22,857,182	0.77
0.5	21,025,253	20,594,564	20,506,543	20,486,634	0.93	20,500,742	20,493,308	20,488,947	20,486,634	0.77
2	14,497,921	14,554,288	14,566,826	14,569,911	0.93	14,567,755	14,568,927	14,569,540	14,569,911	1.18
5	9,432,009	9,466,131	9,474,010	9,475,954	0.95	9,474,619	9,475,334	9,475,721	9,475,954	0.82
20	805,828	808,634	809,345	809,522	1.01	809,400	809,465	809,500	809,522	0.82
50	62,810	62,843	62,851	62,853	1.01	62,852	62,853	62,853	62,853	0.82

Table 4

The values of T ( t ) and ROC at various time

	N = 7					k = 6
t	T ( t )	T ( t )	T ( t )	T ( t )	ROC	T ( t )	T ( t )	T ( t )	T ( t )	ROC
t	k = 3	k = 4	k = 5	k = 6	k = 6	N = 4	N = 5	N = 6	N = 7	N = 7
0.2	7,589,301	7,611,697	7,613,242	7,613,584	0.56	7,613,331	7,613,478	7,613,545	7,613,584	0.73
0.5	7,612,520	7,604,421	7,602,227	7,601,638	1.00	7,602,040	7,601,825	7,601,709	7,601,638	0.78
2	7,826,293	7,800,672	7,794,362	7,792,808	0.99	7,793,885	7,793,304	7,792,995	7,792,808	0.80
5	9,738,601	9,737,352	9,736,917	9,736,808	1.32	9,736,882	9,736,842	9,736,821	9,736,808	0.83
20	15,269,829	15,267,517	15,266,924	15,266,777	1.02	15,266,878	15,266,824	15,266,795	15,266,777	0.82
50	17,075,106	17,074,775	17,074,691	17,074,670	1.01	17,074,685	17,074,677	17,074,673	17,074,670	0.82

Table 5

The values of I ( t ) and ROC at various time

	N = 7					k = 6
t	I ( t )	I ( t )	I ( t )	I ( t )	ROC	I ( t )	I ( t )	I ( t )	I ( t )	ROC
t	k = 3	k = 4	k = 5	k = 6	k = 6	N = 4	N = 5	N = 6	N = 7	N = 7
0.2	1,382	2,201	2,394	2,440	0.98	2,407	2,426	2,435	2,440	0.79
0.5	4,593	5,081	5,182	5,206	0.92	5,189	5,198	5,203	5,206	0.94
2	11,006	10,967	10,960	10,958	0.79	10,960	10,959	10,959	10,958	0.72
5	10,952	10,937	10,934	10,933	0.88	10,933	10,933	10,933	10,933	0.82
20	7,310	7,311	7,311	7,311	1.02	7,311	7,311	7,311	7,311	0.82
50	6,607	6,607	6,607	6,607	1.01	6,607	6,607	6,607	6,607	0.82

Table 6

The values of E ( t ) and ROC at various time

	N = 7					k = 6
t	E ( t )	E ( t )	E ( t )	E ( t )	ROC	E ( t )	E ( t )	E ( t )	E ( t )	ROC
t	k = 3	k = 4	k = 5	k = 6	k = 6	N = 4	N = 5	N = 6	N = 7	N = 7
0.2	212	331	360	367	0.98	362	364	366	367	0.79
0.5	701	774	789	793	0.93	790	792	793	793	0.94
2	1,747	1,739	1,737	1,737	0.89	1,737	1,737	1,737	1,737	0.72
5	2,009	2,006	2,005	2,005	0.94	2,005	2,005	2,005	2,005	0.82
20	2,031	2,031	2,031	2,031	1.00	2,031	2,031	2,031	2,031	0.82
50	2,033	2,033	2,033	2,033	1.10	2,033	2,033	2,033	2,033	0.82

7.2 Verification of the solution

Since this problem cannot be solved exactly, there is no absolute and definite criterion to ensure the level of accuracy. However, comparing the results of the HZBW method with a numerical method, e.g., RK4, may relatively verify the obtained results. In this section, the proposed solution procedure is verified by comparing the results of the problem with integer-order derivatives ( α 1 = α 2 = α 3 = α 4 = α 5 = 1 ) with those obtained by the RK4 method using the command “NDSolve” of the software “Wolfram Mathematica.”

Figures 1–5 depict the results of HZBW and RK4 methods. It is evident that these solutions are in great agreement, proving the trustworthiness of the HZBW method. To provide a more precise view of these results, they are listed in Table 7. It can be deduced that the results of these two methods are closely approximated as t increases. This table proves the high accuracy of the HZBW method as a promising scheme for solving similar nonlinear fractional differential equations in future works.

Figure 1

C ( t ) versus time for integer-order derivatives. Black line: HZBW method; red circles: RK4 method.

Figure 2

H ( t ) versus time for integer-order derivatives. Black line: HZBW method; red circles: RK4 method.

Figure 3

T ( t ) versus time for integer-order derivatives. Black line: HZBW method; red circles: RK4 method.

Figure 4

I ( t ) versus time for integer-order derivatives. Black line: HZBW method; red circles: RK4 method.

Figure 5

E ( t ) versus time for integer-order derivatives. Black line: HZBW method; red circles: RK4 method.

Table 7

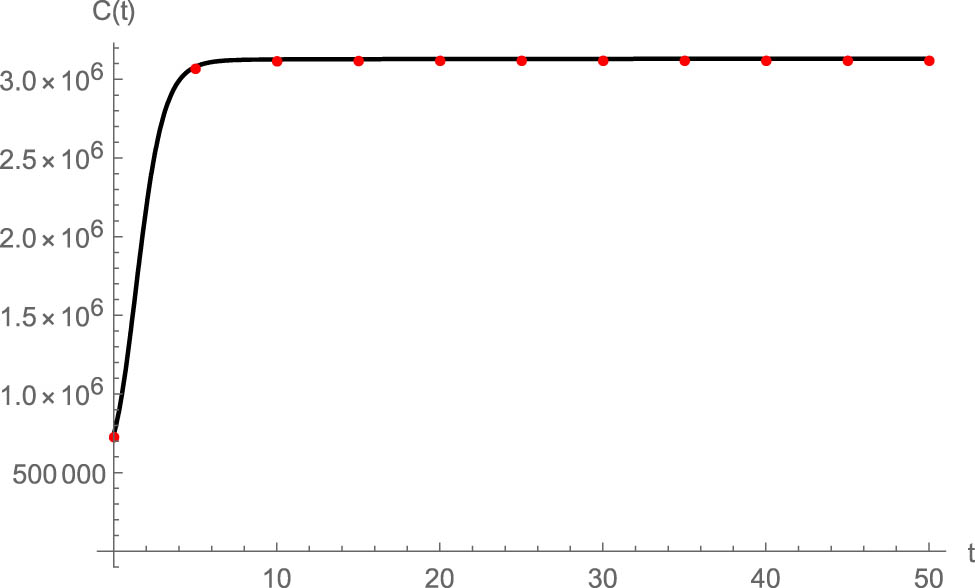
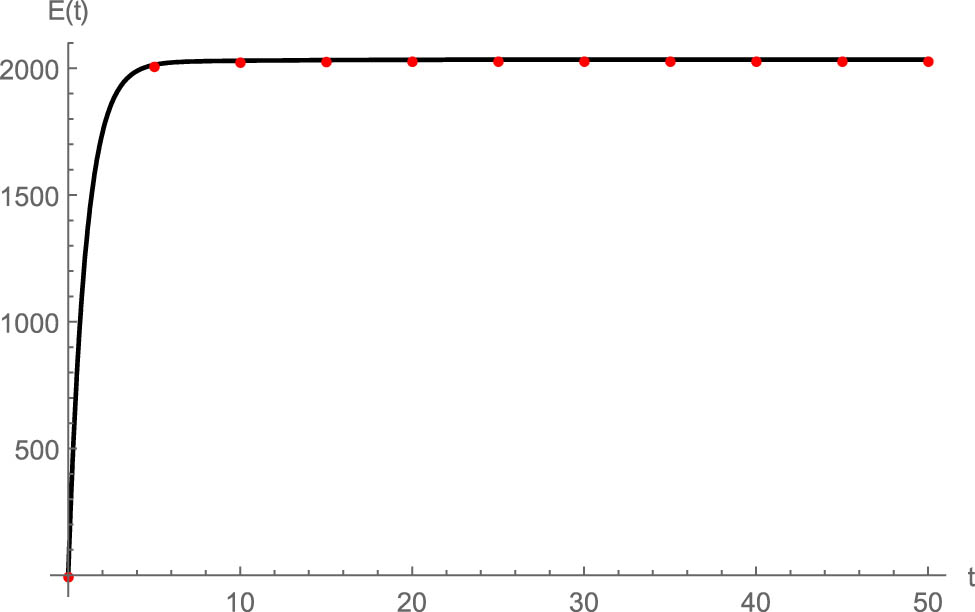
Comparison of the results obtained by HZBW and RK4

		t = 0.2	t = 0.5	t = 2	t = 5	t = 20	t = 50
C ( t )	HZBW	827,236	995,269	2,189,886	3,079,460	3,129,475	3,130,051
	RK4	822,958	991,868	2,191,348	3,078,877	3,129,475	3,130,051
H ( t )	HZBW	23,023,366	20,602,678	14,391,853	9,052,618	328,799	12.9698
	RK4	22,950,223	20,564,759	14,397,428	9,056,818	329,089	13.0636
T ( t )	HZBW	7,613,403	7,602,834	7,775,378	9,904,995	15,966,769	17,387,338
	RK4	7,614,117	7,602,043	7,772,045	9,904,757	15,966,481	17,387,315
I ( t )	HZBW	2,294	5,103	11,092	10,906	7,033	6,503
	RK4	2,371	5,147	11,090	10,905	7,034	6,503
E ( t )	HZBW	351	782	1,747	2,013	2,033	2,033
	RK4	363	789	1,746	2,013	2,033	2,033

7.3 Computational cost

The computational cost of numerical methods for solving algebraic equations can be generally estimated analytically by calculating the number of algebraic operations. For those methods, e.g., the HZBW scheme, in which the focus is only on converting differential equations into algebraic equations, computational cost can be analysed by measuring CPU running time.

The CPU running time depends upon the programming language, hardware configuration, and the algorithms used in the computer code. Thus, comparing CPU running time between two different methods requires these factors to be the same for both methods. In this section, CPU running time for solving the problem with fractional derivatives for various values of k and N are presented in Table 8 using “Wolfram Mathematica” to be compared with similar methods in future research works. However, this computed CPU running time cannot be compared with those presented in former studies by employing other programming languages. Table 8 indicates that this method imposes an acceptable computational cost and can be successfully employed to solve nonlinear fractional differential equations.

Table 8

CPU running time in seconds for various sets of { k , N }

	{ k , N } = { 4,5 }	{ k , N } = { 4,6 }	{ k , N } = { 5,5 }	{ k , N } = { 5,6 }
CPU running time	14.6	26.3	110.7	190.7

7.4 The effects of fractional orders

Since fractional derivatives are used to model the memory of a biological system, proper values for the fractional orders should be determined. In this section, the responses of the system to various values of the fractional orders are investigated for the case: α 1 = α 2 = α 3 = α 4 = α 5 = α . In this study, C ( t ) , H ( t ) , T ( t ) , I ( t ) , and E ( t ) are depicted versus time in Figures 6–10 for five different values of α , respectively. It can be inferred from these figures that increasing the fractional orders leads to more severe reactions in the response of the system. This implies larger values of fractional orders increase C ( t ) , T ( t ) , and E ( t ) , whereas increasing α results in a significant decrease in H ( t ) . On the other hand, changing the fractional orders totally alters I ( t ) . It is evident that for α = 0.2 , I ( t ) is an increasing function, whereas for α = 0.4 , 0.6 , 0.8 , 1 , it forms an absolute maximum, rising for greater values of fractional orders.

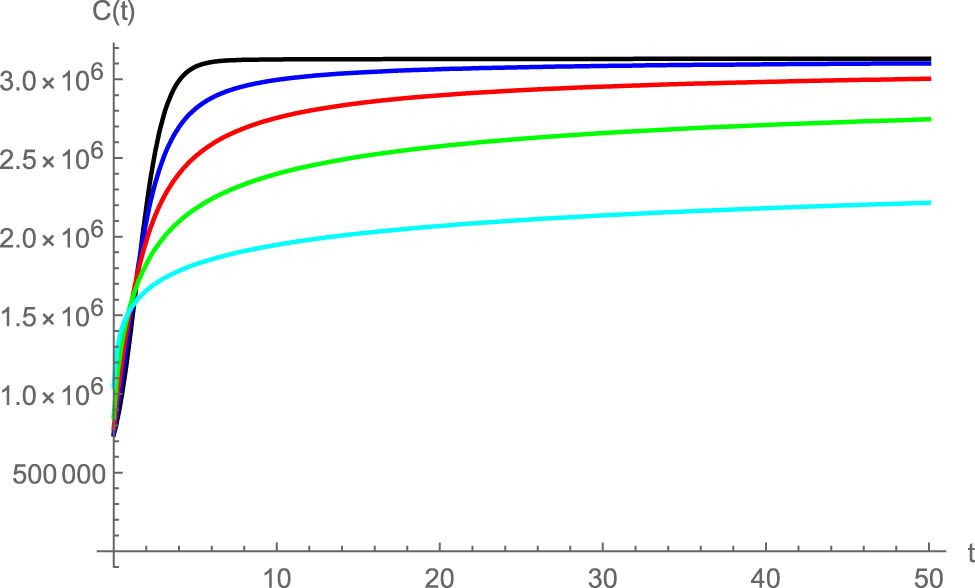
$Figure 6 The effect of fractional order on C ( t ) C(t) versus time. Black: α = 1 \alpha =1 , blue: α = 0.8 \alpha =0.8 , red: α = 0.6 \alpha =0.6 , green: α = 0.4 \alpha =0.4 , cyan: α = 0.2 \alpha =0.2 .$

Figure 6

The effect of fractional order on C ( t ) versus time. Black: α = 1 , blue: α = 0.8 , red: α = 0.6 , green: α = 0.4 , cyan: α = 0.2 .

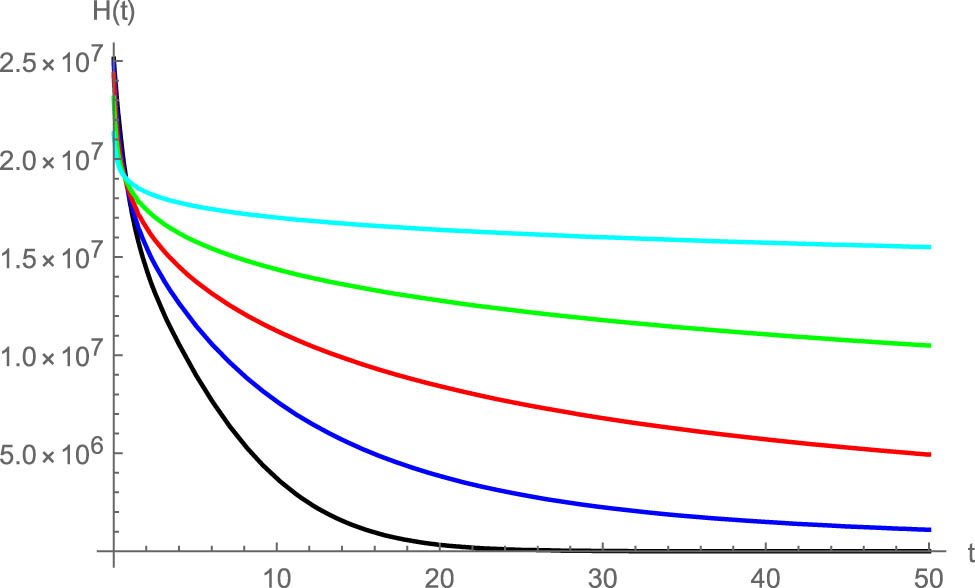
$Figure 7 The effect of fractional order on H ( t ) H(t) versus time. Black: α = 1 \alpha =1 , blue: α = 0.8 \alpha =0.8 , red: α = 0.6 \alpha =0.6 , green: α = 0.4 \alpha =0.4 , cyan: α = 0.2 \alpha =0.2 .$

Figure 7

The effect of fractional order on H ( t ) versus time. Black: α = 1 , blue: α = 0.8 , red: α = 0.6 , green: α = 0.4 , cyan: α = 0.2 .

$Figure 8 The effect of fractional order on T ( t ) T(t) versus time. Black: α = 1 \alpha =1 , blue: α = 0.8 \alpha =0.8 , red: α = 0.6 \alpha =0.6 , green: α = 0.4 \alpha =0.4 , cyan: α = 0.2 \alpha =0.2 .$

Figure 8

The effect of fractional order on T ( t ) versus time. Black: α = 1 , blue: α = 0.8 , red: α = 0.6 , green: α = 0.4 , cyan: α = 0.2 .

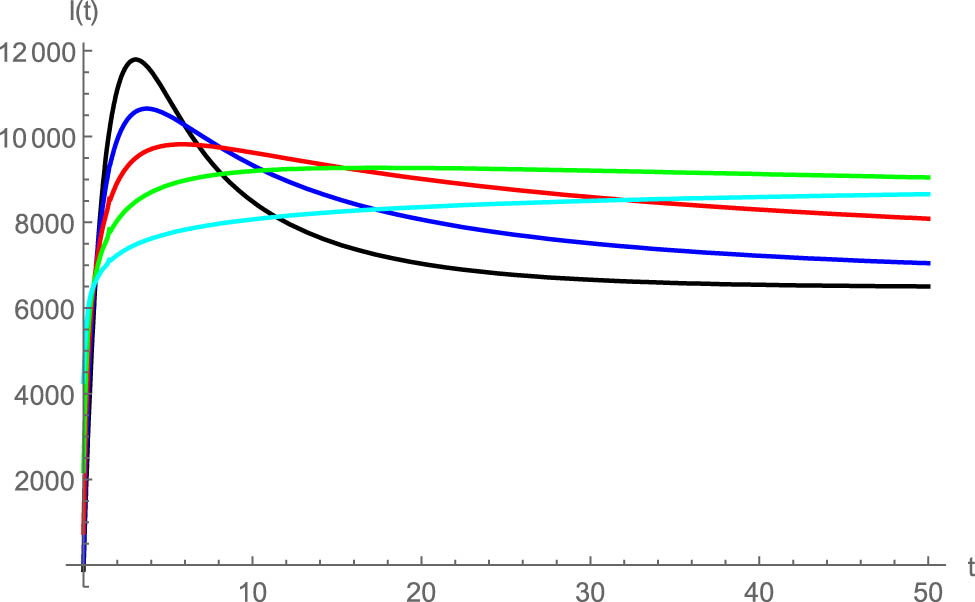
$Figure 9 The effect of fractional order on I ( t ) I(t) versus time. Black: α = 1 \alpha =1 , blue: α = 0.8 \alpha =0.8 , red: α = 0.6 \alpha =0.6 , green: α = 0.4 \alpha =0.4 , cyan: α = 0.2 \alpha =0.2 .$

Figure 9

The effect of fractional order on I ( t ) versus time. Black: α = 1 , blue: α = 0.8 , red: α = 0.6 , green: α = 0.4 , cyan: α = 0.2 .

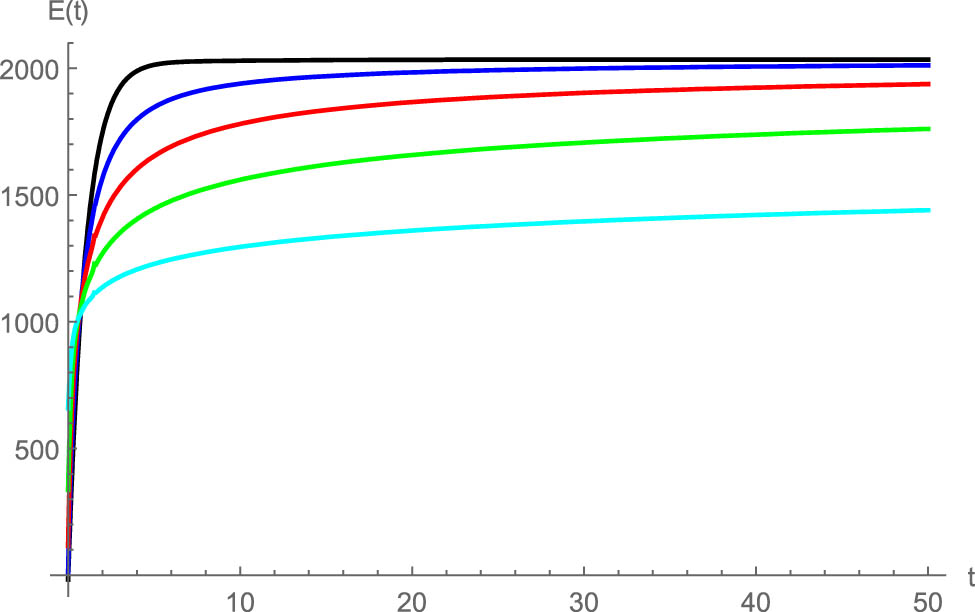
$Figure 10 The effect of fractional order on E ( t ) E(t) versus time. Black: α = 1 \alpha =1 , blue: α = 0.8 \alpha =0.8 , red: α = 0.6 \alpha =0.6 , green: α = 0.4 \alpha =0.4 , cyan: α = 0.2 \alpha =0.2 .$

Figure 10

The effect of fractional order on E ( t ) versus time. Black: α = 1 , blue: α = 0.8 , red: α = 0.6 , green: α = 0.4 , cyan: α = 0.2 .

This study reveals that selecting proper values of fractional derivatives may significantly change the trend of breast cancer treatment.

8 Conclusion

In this article, non-orthogonal Zernike wavelets were introduced based on Zernike polynomials. Since these polynomials have demonstrated their superiority over similar functions and capability in accurate approximations, they were utilized to construct novel wavelets in this research. Besides, a new hybrid method based on combining these wavelets with block pulse functions was proposed to solve nonlinear fractional differential equations. The limitation of the presented Zernike wavelets was that they were not orthogonal. Although this issue was resolved by combining them with block pulse functions, creating orthogonal Zernike wavelets might be the objective of future works.

Moreover, this technique was employed to investigate a fractional model of breast cancer treatment. Error analysis was also conducted. Furthermore, convergence analysis, verification, and computational cost of the results were provided. Finally, the effects of fractional orders on the population of healthy, cancer stem, tumour, and immune cells, as well as the excess estrogen, were studied. It was demonstrated that this method is a promising technique for obtaining an accurate solution of nonlinear fractional differential equations. Moreover, it was illustrated that considering appropriate values of fractional derivatives may remarkably affect the trend of breast cancer treatment.

Funding information: The authors state no funding involved.
Author contributions: All authors equally contributed to this article and read and approved the final manuscript.
Conflict of interest: The authors declare that they have no conflicts of interest.
Data availability statement: All data, generated or used during the study, is available within the article.

References

[1] Kisela T. Fractional differential equations and their applications [dissertation]. Brno: Brno University of Technology; 2008.Suche in Google Scholar

[2] Hedayati M, Ezzati R, Noeiaghdam S. New procedures of a fractional order model of novel coronavirus (COVID-19) outbreak via wavelets method. Axioms. 2021;10(2):122.10.3390/axioms10020122Suche in Google Scholar

[3] Solís-Pérez JE, Gómez-Aguilar JF, Atangana A. A fractional mathematical model of breast cancer competition model. Chaos Solitons Fractals. 2019;127:38–54.10.1016/j.chaos.2019.06.027Suche in Google Scholar

[4] Hussain A, Baleanu D, Adeel M. Existence of solution and stability for the fractional order novel coronavirus (nCoV-2019) model. Adv Differ Equ. 2020;2020(1):1–9.10.1186/s13662-020-02845-0Suche in Google Scholar PubMed PubMed Central

[5] Atangana A. Modelling the spread of COVID-19 with new fractal-fractional operators: Can the lockdown save mankind before vaccination? Chaos Solitons Fractals. 2020;136:109860.10.1016/j.chaos.2020.109860Suche in Google Scholar PubMed PubMed Central

[6] Wang B-H, Wang Y-Y, Dai C-Q, Chen Y-X. Dynamical characteristic of analytical fractional solitons for the space-time fractional Fokas-Lenells equation. Alex Eng J. 2020;59(6):4699–707.10.1016/j.aej.2020.08.027Suche in Google Scholar

[7] Yu L-J, Wu G-Z, Wang Y-Y, Chen Y-X. Traveling wave solutions constructed by Mittag–Leffler function of a (2 + 1)-dimensional space-time fractional NLS equation. Results Phys. 2020;17:103156.10.1016/j.rinp.2020.103156Suche in Google Scholar

[8] Fang J-J, Mou D-S, Wang Y-Y, Zhang H-C, Dai C-Q, Chen Y-X. Soliton dynamics based on exact solutions of conformable fractional discrete complex cubic Ginzburg–Landau equation. Results Phys. 2021;20:103710.10.1016/j.rinp.2020.103710Suche in Google Scholar

[9] Wang B-H, Wang Y-Y. Fractional white noise functional soliton solutions of a wick-type stochastic fractional NLSE. Appl Math Lett. 2020;110:106583.10.1016/j.aml.2020.106583Suche in Google Scholar

[10] Noeiaghdam S. A novel technique to solve the modified epidemiological model of computer viruses. SeMA J. 2019;76(1):97–108.10.1007/s40324-018-0163-3Suche in Google Scholar

[11] Noeiaghdam S, Micula S. Dynamical strategy to control the accuracy of the nonlinear bio-mathematical model of malaria infection. Mathematics. 2021;9(9):1031.10.3390/math9091031Suche in Google Scholar

[12] Noeiaghdam S, Suleman M, Budak H. Solving a modified nonlinear epidemiological model of computer viruses by homotopy analysis method. Math Sci. 2018;12(3):211–22.10.1007/s40096-018-0261-5Suche in Google Scholar

[13] Bitsouni V, Tsilidis V. Mathematical modeling of tumor-immune system interactions: the effect of rituximab on breast cancer immune response. J Theor Biol. 2022;539:111001.10.1016/j.jtbi.2021.111001Suche in Google Scholar PubMed

[14] Marino G, De Bonis MV, Lagonigro L, La Torre G, Prudente A, Sgambato A, et al. Towards a decisional support system in breast cancer surgery based on mass transfer modeling. Int Commun Heat Mass Transf. 2021;129:105733.10.1016/j.icheatmasstransfer.2021.105733Suche in Google Scholar

[15] Nave O, Elbaz M. Artificial immune system features added to breast cancer clinical data for machine learning (ML) applications. Biosystems. 2021;202:104341.10.1016/j.biosystems.2020.104341Suche in Google Scholar PubMed

[16] Jarrett AM, Hormuth DA, Wu C, Kazerouni AS, Ekrut DA, Virostko J, et al. Evaluating patient-specific neoadjuvant regimens for breast cancer via a mathematical model constrained by quantitative magnetic resonance imaging data. Neoplasia. 2020;22(12):820–30.10.1016/j.neo.2020.10.011Suche in Google Scholar PubMed PubMed Central

[17] Simmons A, Burrage PM, Nicolau DV, Lakhani SR, Burrage K. Environmental factors in breast cancer invasion: a mathematical modelling review. Pathology. 2017;49(2):172–80.10.1016/j.pathol.2016.11.004Suche in Google Scholar PubMed

[18] Abdelsalam SI, Zaher AZ. On behavioral response of ciliated cervical canal on the development of electroosmotic forces in spermatic fluid. Math Model Nat Phenom. 2022;17:27.10.1051/mmnp/2022030Suche in Google Scholar

[19] Bhatti MM, Abdelsalam SI. Scientific Breakdown of a Ferromagnetic Nanofluid in Hemodynamics: Enhanced Therapeutic Approach. Math Model Nat Phenom. 2022;17.10.1051/mmnp/2022045Suche in Google Scholar

[20] Abdelsalam SI, Bhatti MM. Unraveling the nature of nano-diamonds and silica in a catheterized tapered artery: highlights into hydrophilic traits. Sci Rep. 2023;13(1):5684.10.1038/s41598-023-32604-6Suche in Google Scholar PubMed PubMed Central

[21] Raza R, Naz R, Abdelsalam SI. Microorganisms swimming through radiative Sutterby nanofluid over stretchable cylinder: Hydrodynamic effect. Numer Methods Partial Differ Equ. 2023;39(2):975–94.10.1002/num.22913Suche in Google Scholar

[22] Tahmasbi A, Saki F, Shokouhi SB. Classification of benign and malignant masses based on Zernike moments. Comput Biol Med. 2011;41(8):726–35.10.1016/j.compbiomed.2011.06.009Suche in Google Scholar PubMed

[23] Rdzanek WP. Sound radiation of a vibrating elastically supported circular plate embedded into a flat screen revisited using the Zernike circle polynomials. J Sound Vib. 2018;434:92–125.10.1016/j.jsv.2018.07.035Suche in Google Scholar

[24] Yi M, Huang J. Wavelet operational matrix method for solving fractional differential equations with variable coefficients. Appl Math Comput. 2014;230:383–94.10.1016/j.amc.2013.06.102Suche in Google Scholar

[25] Yi M, Wang L, Huang J. Legendre wavelets method for the numerical solution of fractional integro-differential equations with weakly singular kernel. Appl Math Model. 2016;40(4):3422–37.10.1016/j.apm.2015.10.009Suche in Google Scholar

[26] Razzaghi M, Yousefi S. Sine-cosine wavelets operational matrix of integration and its applications in the calculus of variations. Int J Syst Sci. 2002;33(10):805–10.10.1080/00207720210161768Suche in Google Scholar

[27] Kilicman A, Al Zhour ZAA. Kronecker operational matrices for fractional calculus and some applications. Appl Math Comput. 2007;187(1):250–65.10.1016/j.amc.2006.08.122Suche in Google Scholar

[28] Ebadi MA, Hashemizadeh E. A new approach based on the Zernike radial polynomials for numerical solution of the fractional diffusion-wave and fractional Klein-Gordon equations. Phys Scr. 2018;93:125202.10.1088/1402-4896/aae726Suche in Google Scholar

[29] Gasca M, Sauer T. On the history of multivariate polynomial interpolation. J Comput Appl Mathematics. 2000;122(1):23–35.10.1016/S0377-0427(00)00353-8Suche in Google Scholar

[30] Yi M, Huang J, Wei J. Block pulse operational matrix method for solving fractional partial differential equation. Appl Math Comput. 2013;221:121–31.10.1016/j.amc.2013.06.016Suche in Google Scholar

[31] Abernathy K, Abernathy Z, Baxter A, Stevens M. Global dynamics of a breast cancer competition model. Differ Equ Dyn Syst. 2020;28(4):791–805.10.1007/s12591-017-0346-xSuche in Google Scholar PubMed PubMed Central

Received: 2023-09-01

Revised: 2023-09-22

Accepted: 2023-11-24

Published Online: 2024-03-28

This work is licensed under the Creative Commons Attribution 4.0 International License.

Artikel in diesem Heft

https://doi.org/10.1515/nleng-2022-0364

Schlagwörter für diesen Artikel

Zernike wavelets; block pulse functions; operational matrix; nonlinear fractional differential equations; breast cancer model

Creative Commons

BY 4.0