Modeling anomalous transport in fractal porous media: A study of fractional diffusion PDEs using numerical method

Imtiaz Ahmad; Ibrahim Mekawy; Muhammad Nawaz Khan; Rashid Jan; Salah Boulaaras

doi:10.1515/nleng-2022-0366

40% Rabatt

auf Fachbücher bei De Gruyter Brill *

Artikel Open Access

Modeling anomalous transport in fractal porous media: A study of fractional diffusion PDEs using numerical method

Imtiaz Ahmad , Ibrahim Mekawy , Muhammad Nawaz Khan , Rashid Jan und Salah Boulaaras

Veröffentlicht/Copyright: 12. März 2024

Veröffentlicht von

Veröffentlichen auch Sie bei De Gruyter Brill

Manuskript einreichen Informationen für Autor*innen

Aus der Zeitschrift Nonlinear Engineering Band 13 Heft 1

Abstract

Fractional diffusion partial differential equation (PDE) models are used to describe anomalous transport phenomena in fractal porous media, where traditional diffusion models may not be applicable due to the presence of long-range dependencies and non-local behaviors. This study presents an efficient hybrid meshless method to the compute numerical solution of a two-dimensional multiterm time-fractional convection-diffusion equation. The proposed meshless method employs multiquadric-cubic radial basis functions for the spatial derivatives, and the Liouville-Caputo derivative technique is used for the time derivative portion of the model equation. The accuracy of the method is evaluated using error norms, and a comparison is made with the exact solution. The numerical results demonstrate that the suggested approach achieves better accuracy and computationally efficient performance.

Keywords: meshless collocation method; hybrid multiquadric-cubic radial basis functions; mathematical model; fractional derivatives; multiterm time-fractional convection-diffusion model equation

1 Introduction

Numerous researchers have been exploring the application of fractional partial differential equations (FPDEs) in various scientific and technological domains in recent years. The versatility and efficacy of partial derivatives as a modeling tool have proven invaluable in capturing the historical behavior and inherent characteristics of diverse dynamic systems. Considerable efforts have been dedicated to developing numerical and analytical solutions for FPDEs [1–7]. However, many investigators have attempted to derive and simulate a variety of complicated phenomena using linear or nonlinear partial differential equations (PDEs) of integer order, but have been unsuccessful [8].

The FPDEs often encounter a diverse range of physical mechanisms. Despite the capability to represent numerous complicated phenomena in diverse fields, researchers have discovered that multiterm time-fractional PDEs, as compared to the results of a single term, enhance the modeling accuracy for characterizing diffusion processes. Nowadays, it catches the curiosity of active researchers. The objective of this work is to use a computationally appealing and trustworthy numerical technique to estimate the numerical solutions of the multiterm time-fractional convection-diffusion model equation.

The convection-diffusion PDE model holds significant physical significance and finds extensive applications in various scientific and mathematical domains. These PDEs are commonly employed in modeling biological phenomena, physical processes, and financial mathematics. Prominent examples include the Navier-Stokes equations [9], which describe fluid flow in various fields such as engineering, meteorology, and oceanography, and the well-known Burgers’ equation [10], which has applications in fluid mechanics and nonlinear waves. In addition to their relevance in physical and biological sciences, convection-diffusion models play a vital role in various environmental and energy-related studies [11–14]. For instance, these models are utilized to mathematically represent heat transport in buildings, contaminant transport in aquifers, air pollution dispersion, and groundwater flow [15]. Such applications are crucial for understanding environmental impacts, optimizing energy infrastructure, and implementing pollution control measures [16]. Moreover, many real-world phenomena involve species transportation and reaction processes that are coupled with flow processes. In the context of energy research, this is particularly significant when studying the transport and diffusion of energy-related substances or quantities [17]. Furthermore, in the field of financial mathematics and option pricing, convection-diffusion PDEs can be interpreted as probability distributions of one or more underlying stochastic processes [18–21]. This interpretation is essential for assessing and managing financial risks, especially in the context of option pricing and derivative securities.

Recent literature employs a wide range of meshless techniques to numerically address complicated PDE models in diverse fields of engineering, science, and technology. Among these methods, a prominent approach is the utilization of radial basis functions (RBFs). The meshless nature of these techniques, combined with their ability to overcome challenges associated with dimensionality, has made them increasingly popular among researchers. In addition, their versatility is enhanced by their capacity to compute solutions using uniform or non-uniform node distributions in regular and irregular domains. As a result, meshless techniques have proven to be both practical and effective in addressing various physical problems [22–28]. However, like any numerical method, meshless techniques have their limitations. Among the most significant challenges are determining the optimal shape-parameter value and handling dense, ill-conditioned matrices. To address these drawbacks, researchers have identified the local meshless technique as a favorable choice. This method exhibits accuracy and reliability in finding solutions for a wide range of integer and fractional PDE models [29,30]. Compared to the global version, the local approach yields sparse matrices that are well-conditioned and less sensitive to the choice of shape parameters. Consequently, the local meshless technique offers enhanced efficiency and benefits over its global counterpart. Due to these advantages, these methodologies are now being extensively explored and applied in various applications [31–36]. Researchers are actively utilizing meshless techniques to tackle challenging problems across different domains, demonstrating the versatility and potential of this numerical approach in advancing scientific understanding and technological innovation.

In the current research, a hybrid meshless method based on multiquadric-cubic RBF is suggested to compute the numerical solution of a two-dimensional multiterm time-fractional convection-diffusion equation, which is given as follows:

(1) ∑ k = 1 d ∂ β k U ( s ¯ , τ ) ∂ τ β k + α 1 ∇ 2 U ( s ¯ , τ ) + α 2 ∇ U ( s ¯ , τ ) = f ( s ¯ , τ ) , 0 < β k ≤ 1 , k = 1 , 2 , 3 , … , d , d ∈ N , s ¯ ∈ Ω ⊂ R n ,

with the conditions

(2) U ( s ¯ , 0 ) = U 0 ( s ¯ ) ,

(3) U ( s ¯ , τ ) = g 1 ( s ¯ , τ ) , s ¯ ∈ ∂ Ω ,

where the operators ∇ 2 and ∇ denote the Laplacian and Gradient operators, respectively, with α 1 and α 2 being known constants. In addition, ∂ β k ∂ τ β k represents the Caputo fractional derivative operator applied to the function U ( s ¯ , τ ) and is defined as follows [37]:

∂ β k U ( s ¯ , τ ) ∂ τ β k = 1 Γ ( 1 − β k ) ∫ 0 τ ( τ − ζ ) − β k U ζ ( s ¯ , ζ ) d ζ , 0 < β k < 1 , ∂ U ( s ¯ , τ ) ∂ τ , β k = 1 ,

where Γ ( ⋅ ) is the gamma function.

2 Motivation

The difficulty in obtaining analytical solutions for nonlinear PDEs motivates researchers to seek efficient numerical alternatives. PDEs play a fundamental role in various real-world applications, including engineering, physics, and finance, but exact analytical solutions are often infeasible due to their nonlinearity and complexity. In response, diverse numerical approaches have been developed and evaluated, customized for specific problem characteristics and computational demands. While traditional finite difference and finite element methods are widely used, they may encounter challenges in handling irregular geometries, complex domains, and moving boundaries. In contrast, meshless methods offer an appealing alternative as they do not require a predefined mesh and efficiently handle complex geometries and unstructured domains. This adaptability makes meshless methods well suited for problems encountered in fluid dynamics, structural mechanics, and data-driven modeling. This article introduces a meshless numerical scheme for PDE models, employing RBFs for spatial derivatives and enabling accurate representation of unknown functions in higher dimensions. In addition, the temporal direction is discretized using the Caputo derivative definition. The proposed meshless approach brings several key advantages over traditional methods, including eliminating the need for a structured grid, simplifying mesh generation for complex domains, and enabling seamless extension to multidimensional problems. Furthermore, the scheme demonstrates high accuracy and numerical stability, vital for reliable and robust simulations.

2.1 Fractional calculus

Fractional derivatives are essential in fractional calculus. The following are some fundamental definitions of fractional derivatives that are commonly utilized.

Definition 1

The Riemann-Liouville derivative [38,39]

(4) ∂ β k U ( s ¯ , τ ) ∂ τ β k = 1 Γ ( 1 − β k ) d d τ ∫ τ T × ( U ( s ¯ , ϑ ) − U ( s ¯ , T ) ) ( ϑ − τ ) β k d ϑ , 0 < β k < 1 .

Definition 2

The Caputo’s fractional derivative [37]

(5) ∂ β k U ( s ¯ , τ ) ∂ τ β k = 1 Γ ( 1 − β k ) × ∫ 0 τ ∂ U ( s ¯ , ζ ) ∂ ζ ( τ − ζ ) − β k d ζ , 0 < β k < 1 .

Definition 3

The Atangana and Baleanu fractional derivative [40]

(6) a A B C ∂ β k U ( s ¯ , τ ) ∂ τ β k = B ( β k ) 1 − β k ∫ a τ U ′ ( s ¯ ) E β k × − β k ( τ − s ¯ ) β k 1 − β k d s ¯ , 0 < β k < 1 .

Definition 4

He’s fractional derivative [41]

(7) ∂ β k U ( s ¯ , τ ) ∂ τ β k = 1 Γ ( 1 − β k ) d d s ¯ × ∫ τ 0 τ ( τ − ζ ) − β k [ U 0 ( ζ ) − U ( ζ ) ] , 0 < β k < 1 .

3 Analyzing the theoretical foundations of a time discrete scheme

Initially, we present the following preliminary concepts from functional analysis, which play a crucial role in discretizing the time variable.

3.1 Introduction to applied functional analysis: A preliminary overview

Consider a bounded and open domain Ω in R 2 , where d s ¯ denotes the Lebesgue measure on R 2 . For p < ∞ , we define the space L p ( Ω ) as the set of measurable functions U : Ω ⟶ R , satisfying ∫ Ω ∣ U ( s ¯ ) ∣ p d s ¯ ≤ ∞ . More generally, we can represent this Banach space by its norm as follows:

‖ U ‖ L p ( Ω ) = ∫ Ω ∣ U ( s ¯ ) ∣ p d s ¯ 1 p .

The Hilbert space L p ( Ω ) possesses an inner product given by

( U , W ) = ∫ Ω U ( s ¯ ) W ( s ¯ ) d s ¯ ,

using the prescribed norm in L 2

‖ U ‖ 2 = [ ( U , U ) ] 1 2 = ∫ Ω U ( s ¯ ) U ( s ¯ ) d s ¯ 1 2 .

In addition, we suppose that Ω is an open domain in R d , γ = ( γ 1 , … , γ d ) is a d -tuple of nonnegative integers, and ∣ γ ∣ = ∑ i = 1 p γ i . Accordingly, we put

D γ W = ∂ ∣ γ ∣ W ∂ s ¯ 1 γ ∂ s ¯ 2 γ ⋯ ∂ s ¯ d γ .

In this regard, one can obtain

(8) H 1 ( Ω ) = W ∈ L 2 ( Ω ) , d W d s ¯ ∈ L 2 ( Ω ) , H 0 1 ( Ω ) = { W ∈ H 1 ( Ω ) , W ∣ ∂ ( Ω ) = 0 } , H m ( Ω ) = W ∈ L 2 ( Ω ) , D γ W ∈ L 2 ( Ω ) for all positive integers ∣ γ ∣ ≤ m .

Next, we present the definition of the inner product within a Hilbert space.

( U , W ) m = ∑ ∣ γ ∣ ≤ m ∫ Ω D γ U ( s ¯ ) D γ W ( s ¯ ) d s ¯ ,

which induces the norm

‖ U ‖ H m ( Ω ) = ∑ ∣ γ ∣ ≤ m ∥ D γ U ∥ L 2 ( Ω ) 2 1 2 .

The Sobolev space X 1 , p ( I ) is said to be

X 1 , p ( I ) = U ∈ L p ( I ) ; ∃ g ∈ L P ( I ) : ∫ I U φ ′ = ∫ I g φ ′ , ∀ φ ∈ C 1 ( I ) .

In addition, in this article, we establish the following inner product and the corresponding energy norms in L 2 and H 1 :

‖ W ‖ = ( W , W ) 1 ∕ 2 , ‖ W ‖ 1 = ( W , W ) 1 1 ∕ 2 , ∣ W ∣ 1 = ∂ W ∂ s ¯ , ∂ W ∂ s ¯ 1 ∕ 2 ,

by inner products of L 2 ( Ω ) and H 1 ( Ω )

( U , W ) = ∫ U ( s ¯ ) W ( s ¯ ) d s ¯ , ( U , W ) 1 = ( U , W ) + ∂ U ∂ s ¯ , ∂ W ∂ s ¯ ,

respectively.

Let us define J = T M be the mesh size in time, and τ n = n J , n ∈ N + , are the total M temporal discretization points.

Lemma 1

Let us suppose η ( t ) ∈ C 2 [ 0 , T ] and 0 < β k < 1 , then it holds that

∫ 0 τ n η ′ ( s ¯ ) ( τ n − s ¯ ) − β k d s ¯ = ∑ j = 1 n η ( τ j ) − η ( τ j − 1 ) J , ∫ τ j − 1 τ j ( τ n − s ¯ ) − β k d s ¯ + R n , 1 ≤ n ≤ M ,

and ∣ R n ∣ ≤ 1 2 ( 1 − β k ) + 1 2 J 2 − β k max 0 ≤ τ ≤ τ n ∣ η ′ ′ ( t ) ∣ .

Proof

Sun and Wu [42].

Lemma 2

Let 0 < β k < 1 , a 0 = 1 J Γ ( 1 − β k ) , and b j = J 1 − β k ( 1 − β k ) [ ( j + 1 ) 1 − β k − ( j ) 1 − β k ] , then

1 Γ ( 1 − β k ) ∫ 0 τ n η ′ ( s ¯ ) ( τ n − s ¯ ) β k d s ¯ − a 0 b 0 η ( τ n ) − ∑ j = 1 n − 1 ( b n − j − 1 − b n − j ) η ( τ j ) − b n − 1 η ( 0 ) ≤ 1 2 Γ ( 1 − β k ) 1 + 1 ( 1 − β k ) J 2 − β k max 0 ≤ τ ≤ τ n ∣ η ′ ′ ( τ ) ∣ .

Proof

Directly follows from Lemma 1.

Lemma 3

Let b j = J 1 − β k ( 1 − β k ) [ ( j + 1 ) 1 − β k − ( j ) 1 − β k ] , where 0 < β k < 1 , j = 0 , 1 , 2 , … , then b 0 > b 1 > b 2 > ⋯ > b j → 0 , as j → ∞ .

Proof

Sun and Wu [42].

4 Spatial and temporal discretization techniques for derivatives

In this section, we present the main steps involved in computing the spatial and temporal derivatives. These steps are essential for the accurate numerical approximation.

4.1 Spatial discretization techniques for derivatives

The derivatives of U ( s ¯ , τ ) are approximated at the centers s ¯ i , { s ¯ i 1 , s ¯ i 2 , s ¯ i 3 , … , s ¯ i n i } ⊂ { s ¯ 1 , s ¯ 2 , … , s ¯ N n } , n i ≪ N n , i = 1 , 2 , … , N n . In case of one- and two-dimensional case, s ¯ = s and s ¯ = ( s , r ) , respectively.

Procedure for one-dimensional case is

(9) U ( s i ) ≈ ∑ j = 1 n i λ j ψ ( s i j ) + ∑ j = 1 n i γ k p ( s i j ) , i = 1 , 2 , … , N ,

where the hybrid RBF is defined as ψ ( ∣ s i j − s l ∣ ) = exp ( − ∣ s i j − s l ∣ 2 ∕ c 2 ) + ω ∣ s i j − s l ∣ 3 , l = i 1 , i 2 , … , i n i , where c represents the shape parameter. In addition, p ( s i j ) is a linear combination of polynomials on R n , subject to specific consistency conditions.

(10) ∑ j = 1 n i λ j U ( s i j ) = 0 , i = 1 , 2 , … , N .

The matrix representation of Eqs (9) and (10) is

(11) U 0 = A P P T 0 λ γ ,

where A = ψ ( ‖ s i j − s l ‖ ) , P = p ( s i j ) , λ = [ λ i 1 , … , λ i n i ] T , U = [ U i 1 , … , U i n i ] T , and γ = [ γ i 1 , … , γ i n i ] T .

Matrix notation of Eq. (11) is

(12) U = A Λ ,

where U = U 0 , A = A P P T 0 , and Λ = λ γ .

The matrix A is ensured to be invertible [43]. Utilizing Eq. (12), we obtain

(13) Λ = A − 1 U .

The derivative of U can be computed by taking the derivative of the expression given in Eq. (9).

(14) U ( m ) ( s i ) = ∑ j = 1 n i λ j ϕ ( m ) + ∑ j = 1 n i γ j p ( m ) , i = 1 , 2 , … , N .

Matrix notation of Eq. (14) is

(15) U ( m ) = A ( m ) Λ ,

(16) U ( m ) = A ( m ) A − 1 U .

The approximate semi-discretized form for model (1), using hybrid meshless method, along with the initial and boundary conditions, is

(17) ∑ k = 1 d d β k U d τ β k = D U + k ( τ ) , U ( 0 ) = b .

In this context, the matrix ( D ) corresponds to the sparse coefficient matrix resulting from the hybrid meshless method approximation. The initial and boundary conditions of the problem are denoted by vectors k and b , respectively, both of size N × 1 .

4.2 Numerical approaches for time derivatives discretization

The time derivative in the Caputo form, denoted as ∂ β k U ( s ¯ , τ ) ∂ τ β k , where 0 < β k ≤ 1 , is

(18) ∂ β k U ( s ¯ , τ ) ∂ τ β k = 1 Γ ( 1 − β k ) ∫ 0 τ ∂ U ( s ¯ , ζ ) ∂ ζ ( τ − ζ ) − β k d ζ , 0 < β k < 1 , ∂ U ( s ¯ , τ ) ∂ τ , β k = 1 .

Taking into account M + 1 equidistant time levels τ 0 , τ 1 , … , τ M within the interval [ 0 , τ ] , where the time step is denoted by J and τ n = n J for n = 0 , 1 , 2 , … , M , we employ a first-order finite difference scheme to approximate the time fractional derivative term as follows:

(19) ∂ β k U ( s ¯ , τ n + 1 ) ∂ τ β k = 1 Γ ( 1 − β k ) ∫ 0 τ n + 1 ∂ U ( s ¯ , ζ ) ∂ ζ ( τ n + 1 − ζ ) − β k d ζ , = 1 Γ ( 1 − β k ) ∑ j = 0 n ∫ j J ( j + 1 ) J ∂ U ( s ¯ , ζ j ) ∂ ζ ( τ j + 1 − ζ ) − β k d ζ ,

where ∂ U ( s ¯ , ζ j ) ∂ ζ , is approximated as follows:

∂ U ( s ¯ , ζ j ) ∂ ζ = U ( s ¯ , ζ j + 1 ) − U ( s ¯ , ζ j ) ζ + O ( J ) .

Then,

∂ β k U ( s ¯ , τ n + 1 ) ∂ τ β k = 1 Γ ( 1 − β k ) ∑ j = 0 n U ( s ¯ , τ j + 1 ) − U ( s ¯ , τ j ) J × ∫ j J ( j + 1 ) J ( τ j + 1 − ζ ) − β k d ζ , = 1 Γ ( 1 − β k ) ∑ j = 0 n U ( s ¯ , τ n + 1 − j ) − U ( s ¯ , τ n − j ) J × ∫ j J ( j + 1 ) J ( τ j + 1 − ζ ) − β k d ζ , = J − β k Γ ( 2 − β k ) ( U n + 1 − U n ) + J − β k Γ ( 2 − β k ) ∑ j = 1 n ( U n + 1 − j − U n − j ) [ ( j + 1 ) 1 − β k − j 1 − β k ] , n ≥ 1 J − β k Γ ( 2 − β k ) ( U 1 − U 0 ) , n = 0 .

Let a 0 = J − β k Γ ( 2 − β k ) and b j = ( j + 1 ) 1 − β k − j 1 − β k , j = 0 , 1 , … , n . The above equation in a more precise form can be written as follows:

(20) ∂ β k U ( s ¯ , τ n + 1 ) ∂ τ β k = a 0 ( U n + 1 − U n ) + a 0 ∑ j = 1 n b j ( U n + 1 − j − U n − j ) , n ≥ 1 a 0 ( U 1 − U 0 ) , n = 0 .

5 Results and discussion

The recommended hybrid meshless method is examined in this section for its application and accuracy in estimating the numerical solution of the two-dimensional multiterm time-fractional convection-diffusion model equation. Different time fractional orders, including two-term, three-term, and five-term, are taken into consideration. The method is coupled with multiquadric-cubic radial basis functions, and rectangular and nonrectangular domains have been taken into consideration. The temporal step size J = 0.001 and spatial domain [0, 1] are employed unless otherwise stated. The following is how accuracy is determined:

(21) Absolute-error = ∣ U ^ − U ∣ , Max E = max ( Absolute-error ) , RMS = ∑ i = 1 N n ( U ^ i − U i ) 2 N ,

where U ^ is the exact solution.

Problem 1

The exact solution for Eq. (1) with α 1 = α 2 = 1 , is

(22) U ( s ¯ , τ ) = e − τ sin ( π s ) sin ( π r ) , ( s , r ) ∈ Ω .

The required numerical results for Problem 1 are produced using the suggested hybrid meshless approach and are shown in Table 1. The nodes N and temporal step size J varied, and the fractional orders β 1 = β 2 = 0.5 , β 1 = β 2 = β 3 = 0.5 , and β 1 = β 2 = β 3 = β 4 = β 5 = 0.5 are considered for two-term, three-term, and five-term, respectively. The final time is set to 1, while the error norms MaxE and RMS are utilized. The recommended meshless approach is capable of producing better results, according to these data. The table makes it evident that accuracy improves as the number of time-fractional orders increases, as the number of nodes increases, and as the temporal step size decreases.

Table 1

Results of the hybrid meshless method for Problem 1

		N = 5		N = 10		N = 20
	J	RMS	MaxE	RMS	MaxE	RMS	MaxE
Two-term	0.1	2.0645 × 1 0 ‒ 2	4.2976 × 1 0 ‒ 2	1.8830 × 1 0 ‒ 2	5.8860 × 1 0 ‒ 2	4.2300 × 1 0 ‒ 2	2.3552 × 1 0 ‒ 1
	0.05	9.8545 × 1 0 ‒ 3	2.0585 × 1 0 ‒ 2	8.4668 × 1 0 ‒ 3	1.6698 × 1 0 ‒ 2	3.9218 × 1 0 ‒ 2	2.6484 × 1 0 ‒ 1
	0.01	6.7339 × 1 0 ‒ 4	1.5930 × 1 0 ‒ 3	8.8947 × 1 0 ‒ 4	3.8580 × 1 0 ‒ 3	1.5744 × 1 0 ‒ 3	1.3745 × 1 0 ‒ 2
	0.005	1.0034 × 1 0 ‒ 3	2.5963 × 1 0 ‒ 3	4.0744 × 1 0 ‒ 4	1.7415 × 1 0 ‒ 3	3.4312 × 1 0 ‒ 4	1.9687 × 1 0 ‒ 3
	0.001	1.1273 × 1 0 ‒ 3	2.7554 × 1 0 ‒ 3	4.5450 × 1 0 ‒ 4	1.0197 × 1 0 ‒ 3	2.2593 × 1 0 ‒ 4	5.0045 × 1 0 ‒ 4
Three-term	0.1	1.2273 × 1 0 ‒ 2	2.3872 × 1 0 ‒ 2	1.1571 × 1 0 ‒ 2	2.2576 × 1 0 ‒ 2	1.3246 × 1 0 ‒ 2	6.1633 × 1 0 ‒ 2
	0.05	5.0047 × 1 0 ‒ 3	1.0056 × 1 0 ‒ 2	5.2538 × 1 0 ‒ 3	1.0399 × 1 0 ‒ 2	6.4920 × 1 0 ‒ 3	3.7501 × 1 0 ‒ 2
	0.01	7.6508 × 1 0 ‒ 4	2.1338 × 1 0 ‒ 3	4.8450 × 1 0 ‒ 4	1.5991 × 1 0 ‒ 3	6.5136 × 1 0 ‒ 4	1.7731 × 1 0 ‒ 3
	0.005	1.0293 × 1 0 ‒ 3	2.6600 × 1 0 ‒ 3	3.4650 × 1 0 ‒ 4	1.0649 × 1 0 ‒ 3	2.4442 × 1 0 ‒ 4	8.9311 × 1 0 ‒ 4
	0.001	9.3642 × 1 0 ‒ 4	2.3562 × 1 0 ‒ 3	3.3295 × 1 0 ‒ 4	7.5659 × 1 0 ‒ 4	1.5284 × 1 0 ‒ 4	3.5259 × 1 0 ‒ 4
Five-term	0.1	7.5062 × 1 0 ‒ 3	1.6352 × 1 0 ‒ 2	8.3533 × 1 0 ‒ 3	1.7988 × 1 0 ‒ 2	8.7158 × 1 0 ‒ 3	1.7987 × 1 0 ‒ 2
	0.05	2.8803 × 1 0 ‒ 3	7.1647 × 1 0 ‒ 3	3.7202 × 1 0 ‒ 3	8.3322 × 1 0 ‒ 3	4.0825 × 1 0 ‒ 3	8.6422 × 1 0 ‒ 3
	0.01	7.3264 × 1 0 ‒ 4	2.0263 × 1 0 ‒ 3	4.3462 × 1 0 ‒ 4	1.1647 × 1 0 ‒ 3	5.9871 × 1 0 ‒ 4	1.4234 × 1 0 ‒ 3
	0.005	8.3438 × 1 0 ‒ 4	2.2149 × 1 0 ‒ 3	2.6260 × 1 0 ‒ 4	7.1538 × 1 0 ‒ 4	2.4476 × 1 0 ‒ 4	6.1235 × 1 0 ‒ 4
	0.001	7.4705 × 1 0 ‒ 4	1.9230 × 1 0 ‒ 3	2.2136 × 1 0 ‒ 4	5.0499 × 1 0 ‒ 4	8.6997 × 1 0 ‒ 5	2.1623 × 1 0 ‒ 4

In Table 2, the numerical results are obtained using a range of fractional-order and final time τ values. The number of nodes N = 10 and the fractional order β = β 1 = β 2 is used for two-term, β = β 1 = β 2 = β 3 for three-term, and β = β 1 = β 2 = β 3 = β 4 = β 5 for five-term. Reasonable better accuracy has been obtained in this scenario as well. Similarly, the results for τ = 0.5 are shown in Figure 1, in terms of RMS error norm for two-, three-, and five-term fractional orders. The figure shows that the accuracy of the five-term is higher than that of the two-term.

Table 2

Results of the hybrid meshless method for Problem 1

		Two-term		Three-term		Five-term
	τ	RMS	MaxE	RMS	MaxE	RMS	MaxE
β = 0.45	0.2	1.1317 × 1 0 ‒ 3	2.7069 × 1 0 ‒ 3	8.6422 × 1 0 ‒ 4	2.0603 × 1 0 ‒ 3	5.5294 × 1 0 ‒ 4	1.3532 × 1 0 ‒ 3
	0.5	8.7379 × 1 0 ‒ 4	2.0429 × 1 0 ‒ 3	6.7854 × 1 0 ‒ 4	1.5706 × 1 0 ‒ 3	4.4181 × 1 0 ‒ 4	1.0485 × 1 0 ‒ 3
	1	5.4753 × 1 0 ‒ 4	1.2573 × 1 0 ‒ 3	4.3109 × 1 0 ‒ 4	9.7438 × 1 0 ‒ 4	2.8514 × 1 0 ‒ 4	6.5925 × 1 0 ‒ 4
β = 0.5	0.2	9.3456 × 1 0 ‒ 4	2.1856 × 1 0 ‒ 3	6.6748 × 1 0 ‒ 4	1.5921 × 1 0 ‒ 3	4.3410 × 1 0 ‒ 4	1.0306 × 1 0 ‒ 3
	0.5	7.2439 × 1 0 ‒ 4	1.6544 × 1 0 ‒ 3	5.2471 × 1 0 ‒ 4	1.2178 × 1 0 ‒ 3	3.4537 × 1 0 ‒ 4	8.0161 × 1 0 ‒ 4
	1	4.5450 × 1 0 ‒ 4	1.0197 × 1 0 ‒ 3	3.3295 × 1 0 ‒ 4	7.5659 × 1 0 ‒ 4	2.2136 × 1 0 ‒ 4	5.0499 × 1 0 ‒ 4
β = 0.75	0.2	3.6045 × 1 0 ‒ 4	8.3755 × 1 0 ‒ 4	3.5415 × 1 0 ‒ 4	9.0635 × 1 0 ‒ 4	3.4052 × 1 0 ‒ 4	8.9625 × 1 0 ‒ 4
	0.5	2.7512 × 1 0 ‒ 4	6.4202 × 1 0 ‒ 4	2.7912 × 1 0 ‒ 4	7.2251 × 1 0 ‒ 4	2.8966 × 1 0 ‒ 4	7.7437 × 1 0 ‒ 4
	1	1.6960 × 1 0 ‒ 4	3.9662 × 1 0 ‒ 4	1.7477 × 1 0 ‒ 4	4.5473 × 1 0 ‒ 4	1.8891 × 1 0 ‒ 4	5.0807 × 1 0 ‒ 4

Figure 1

Results in terms of RMS error of the hybrid meshless method for Problem 1.

The ease of implementation in the irregular domain is one of the key benefits of meshless approaches over mesh-based techniques. The three non-rectangular domain types that are considered in this article are shown in Figures 2, 4, and 5. We have display the numerical results in Figure 3 for τ = 5 and N = 31 and for the domain given in Figure 2, using the suggested hybrid meshless technique. The value of β = 0.5 for the two-, three-, and five-term is used. The figure shows that in this domain, better accuracy has been attained. Figures 4 and 5, also display the outcome of the suggested effective approach for nonrectangular domains. In addition, better accuracy has been attained in this case as well.

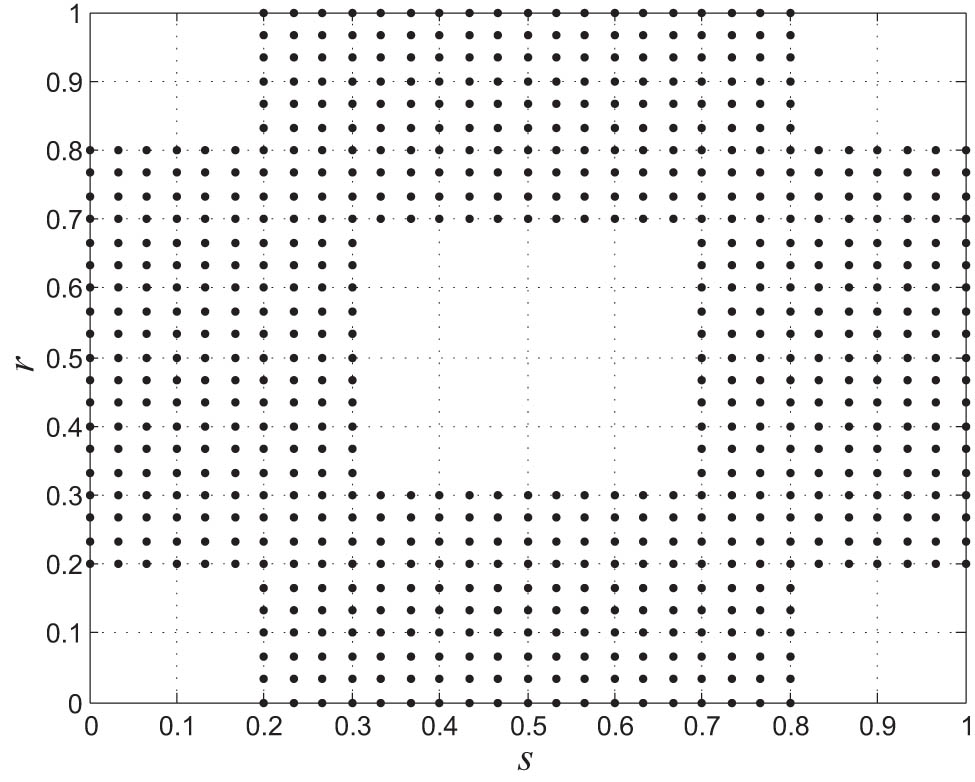
Figure 2

Computational domain.

Figure 3

Results for the computational domain given in Figure 2 of the hybrid meshless method for Problem 1.

Figure 4

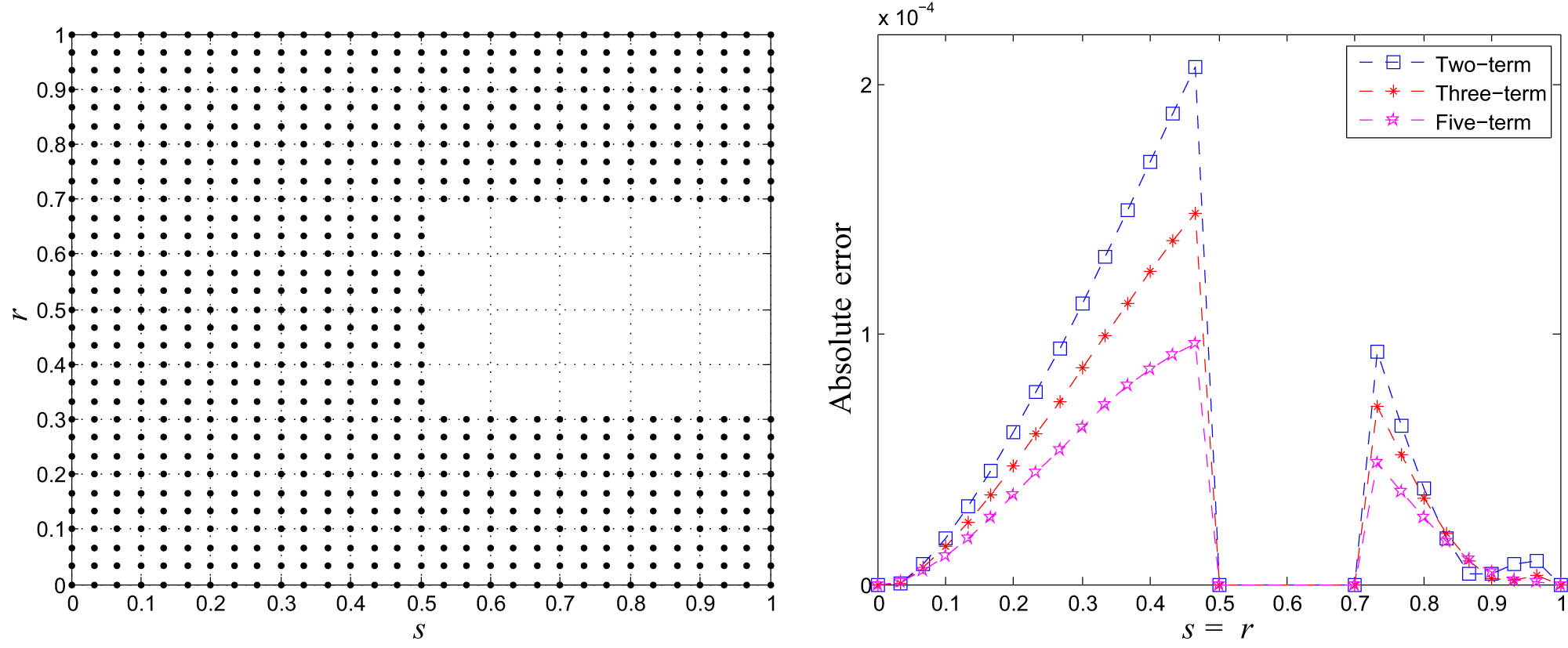
The computational domain and results of the hybrid meshless method for Problem 1.

Figure 5

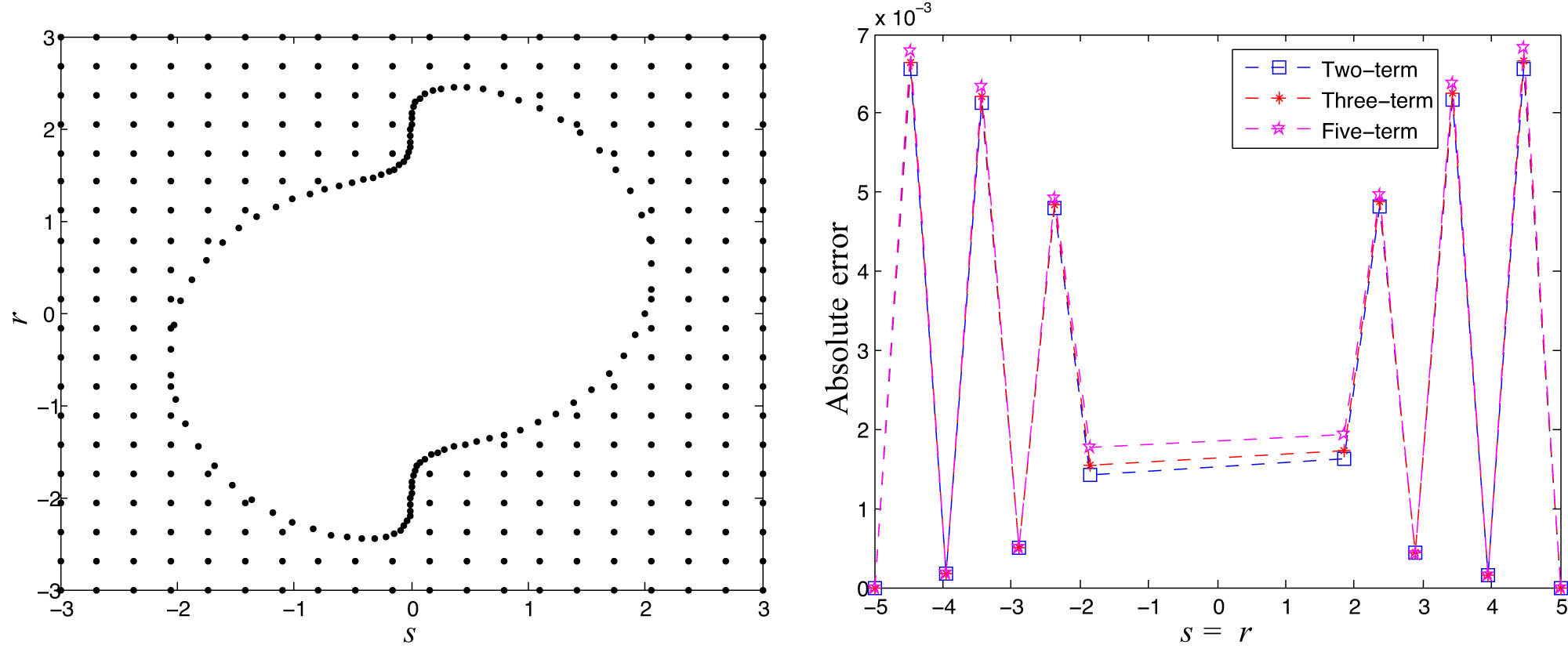
The computational domain and results of the hybrid meshless method for Problem 1.

Problem 2

As a second test problem, the exact solution for Eq. (1) with α 1 = α 2 = 1 , is

(23) U ( s ¯ , τ ) = e s − r − τ sin ( π s ) sin ( π r ) , ( s , r ) ∈ Ω .

The numerical results, the suggested hybrid meshless approach for Problem 2 are shown in Table 3. The nodes N and temporal step size J are varied, and the fractional orders β 1 = β 2 = 0.9 , β 1 = β 2 = β 3 = 0.9 and β 1 = β 2 = β 3 = β 4 = β 5 = 0.9 are considered for two-term, three-term, and five-term, respectively. The final time is set to 1, while the error norms MaxE and RMS are utilized. The recommended meshless approach is capable of producing better results, according to these data. The table makes it evident that accuracy improves as the number of time-fractional orders increases, as the number of nodes increases, and as the temporal step size decreases. In Table 4, the numerical results are obtained using range of fractional-order and final time τ values. The number of nodes N = 10 , and the fractional order β = β 1 = β 2 is used for two-term, β = β 1 = β 2 = β 3 for three-term and β = β 1 = β 2 = β 3 = β 4 = β 5 for five-term. Reasonable better accuracy has been obtained in this scenario as well.

Table 3

Results of the hybrid meshless method for Problem 2

		N = 5		N = 10		N = 20
	J	RMS	MaxE	RMS	MaxE	RMS	MaxE
Two-term	0.05	1.0068 × 1 0 ‒ 2	3.0095 × 1 0 ‒ 2	1.3810 × 1 0 ‒ 2	3.9711 × 1 0 ‒ 2	1.5683 × 1 0 ‒ 2	4.1649 × 1 0 ‒ 2
	0.01	3.2973 × 1 0 ‒ 3	9.7357 × 1 0 ‒ 3	4.2498 × 1 0 ‒ 3	1.1937 × 1 0 ‒ 2	4.9017 × 1 0 ‒ 3	1.3112 × 1 0 ‒ 2
	0.005	2.3063 × 1 0 ‒ 3	5.3171 × 1 0 ‒ 3	2.3336 × 1 0 ‒ 3	6.5874 × 1 0 ‒ 3	2.7170 × 1 0 ‒ 3	7.2470 × 1 0 ‒ 3
	0.001	2.1916 × 1 0 ‒ 3	5.5077 × 1 0 ‒ 3	7.5479 × 1 0 ‒ 4	1.5249 × 1 0 ‒ 3	6.4261 × 1 0 ‒ 4	1.7481 × 1 0 ‒ 3
Three-term	0.05	7.0554 × 1 0 ‒ 3	2.0852 × 1 0 ‒ 2	9.6667 × 1 0 ‒ 3	2.7994 × 1 0 ‒ 2	1.1139 × 1 0 ‒ 2	3.0671 × 1 0 ‒ 2
	0.01	2.6048 × 1 0 ‒ 3	6.2813 × 1 0 ‒ 3	2.7799 × 1 0 ‒ 3	7.8897 × 1 0 ‒ 3	3.2173 × 1 0 ‒ 3	8.8036 × 1 0 ‒ 3
	0.005	2.2486 × 1 0 ‒ 3	5.6483 × 1 0 ‒ 3	1.5563 × 1 0 ‒ 3	4.3004 × 1 0 ‒ 3	1.7677 × 1 0 ‒ 3	4.8286 × 1 0 ‒ 3
	0.001	2.3497 × 1 0 ‒ 3	5.8984 × 1 0 ‒ 3	7.2479 × 1 0 ‒ 4	1.6393 × 1 0 ‒ 3	4.2981 × 1 0 ‒ 4	1.1557 × 1 0 ‒ 3
Five-term	0.05	4.6404 × 1 0 ‒ 3	1.2415 × 1 0 ‒ 2	5.8721 × 1 0 ‒ 3	1.6845 × 1 0 ‒ 2	6.8030 × 1 0 ‒ 3	1.9726 × 1 0 ‒ 2
	0.01	2.5330 × 1 0 ‒ 3	6.4315 × 1 0 ‒ 3	1.6975 × 1 0 ‒ 3	4.5163 × 1 0 ‒ 3	1.8568 × 1 0 ‒ 3	5.2353 × 1 0 ‒ 3
	0.005	2.4648 × 1 0 ‒ 3	6.2632 × 1 0 ‒ 3	1.0817 × 1 0 ‒ 3	2.4276 × 1 0 ‒ 3	1.0232 × 1 0 ‒ 3	2.8558 × 1 0 ‒ 3
	0.001	2.5457 × 1 0 ‒ 3	6.3806 × 1 0 ‒ 3	7.7299 × 1 0 ‒ 4	1.8326 × 1 0 ‒ 3	2.9730 × 1 0 ‒ 4	6.7816 × 1 0 ‒ 4

Table 4

Results of the hybrid meshless method for Problem 2

		Two-term		Three-term		Five-term
	τ	RMS	MaxE	RMS	MaxE	RMS	MaxE
β = 0.55	1	6.0167 × 1 0 ‒ 3	1.6253 × 1 0 ‒ 2	4.0528 × 1 0 ‒ 3	1.1081 × 1 0 ‒ 2	2.4107 × 1 0 ‒ 3	6.7260 × 1 0 ‒ 3
	2	2.2883 × 1 0 ‒ 3	6.0982 × 1 0 ‒ 3	1.5622 × 1 0 ‒ 3	4.1962 × 1 0 ‒ 3	9.4889 × 1 0 ‒ 4	2.5894 × 1 0 ‒ 3
β = 0.65	1	3.0792 × 1 0 ‒ 3	8.4846 × 1 0 ‒ 3	2.0379 × 1 0 ‒ 3	5.6928 × 1 0 ‒ 3	1.2347 × 1 0 ‒ 3	3.3979 × 1 0 ‒ 3
	2	1.1635 × 1 0 ‒ 3	3.1752 × 1 0 ‒ 3	7.7690 × 1 0 ‒ 4	2.1462 × 1 0 ‒ 3	4.7799 × 1 0 ‒ 4	1.2955 × 1 0 ‒ 3
β = 0.75	1	1.5509 × 1 0 ‒ 3	4.3388 × 1 0 ‒ 3	1.0688 × 1 0 ‒ 3	2.8639 × 1 0 ‒ 3	7.8662 × 1 0 ‒ 4	1.6704 × 1 0 ‒ 3
	2	5.8034 × 1 0 ‒ 4	1.6157 × 1 0 ‒ 3	4.0297 × 1 0 ‒ 4	1.0703 × 1 0 ‒ 3	3.0897 × 1 0 ‒ 4	6.2538 × 1 0 ‒ 4

6 Conclusion

In this article, we have effectively solved the multiterm fractional-order convection-diffusion equation with the hybrid meshless method. Numerical studies were carried out for different values of time-fractional order β k to check positive contributions of the model. The calculated results demonstrate how impressively and precisely the proposed technique can handle these kinds of problems. The local meshless feature of the recommended method results in a sparse system of linear equations, which produced better accurate and efficient results. The hybrid approach uses both rectangular and nonrectangular domains to produce efficient and precise results. In light of recent research, the suggested method is a remarkably effective and strong tool for addressing numerical problems relating multiterm time-fractional PDEs that can be encountered in a variety of financial, scientific, and technological sectors.

Acknowledgments

Researchers would like to thank the Deanship of Scientific Research, Qassim University for funding publication of this project.

Author contributions: All authors have accepted responsibility for the entire content of this manuscript and approved its submission.
Conflict of interest: The authors declare no conflict of interest.
Ethics approval and consent to participate: All authors demonstrate adherence to accepted ethical standards for genuine research. As corresponding author, I have obtained consent from all authors for their participation in this study.
Consent to publish: All the authors are agreed to publish this research work.
Data availability statement: Data will be provided on request to the corresponding author.

References

[1] Ahmad H, Khan TA, Ahmad I, Stanimirović PS, Chu YM. A new analyzing technique for nonlinear time fractional Cauchy reaction-diffusion model equations. Results Phys. 2020;19:103462. 10.1016/j.rinp.2020.103462Suche in Google Scholar

[2] Inc M, Khan MN, Ahmad I, Yao SW, Ahmad H, Thounthong P. Analysing time-fractional exotic options via efficient local meshless method. Results Phys. 2020;19:103385. 10.1016/j.rinp.2020.103385Suche in Google Scholar

[3] Mahreen K, Ain QT, Rahman G, Abdalla B, Shah K, Abdeljawad T. Approximate solution for the nonlinear fractional order mathematical model. AIMS Math. 2022;7(10):19267–86. 10.3934/math.20221057Suche in Google Scholar

[4] Arfan M, Mahariq I, Shah K, Abdeljawad T, Laouini G, Mohammed PO. Numerical computations and theoretical investigations of a dynamical system with fractional order derivative. Alex Eng J. 2022;61(3):1982–94. 10.1016/j.aej.2021.07.014Suche in Google Scholar

[5] Rehman ZR, Boulaaras S, Jan R, Ahmad I, Bahramand S. Computational analysis of financial system through non-integer derivative. J Comput Sci. 2023;75:102204. 10.1016/j.jocs.2023.102204. Suche in Google Scholar

[6] Shah NNH, Jan R, Ahmad H, Razak NNA, Ahmad I, Ahmad H. Enhancing public health strategies for tungiasis: A mathematical approach with fractional derivative. AIMS Bioeng. 2023;10(4):384–405. 10.3934/bioeng.2023023Suche in Google Scholar

[7] Ain QT, Anjum N, Din A, Zeb A, Djilali S, Khan ZA. On the analysis of Caputo fractional order dynamics of middle east lungs coronavirus (MERS-CoV) model. Alex Eng J. 2022;61(7):5123–31. 10.1016/j.aej.2021.10.016Suche in Google Scholar

[8] Rizvi STR, Afzal I, Ali K. Chirped optical solitons for Triki-Biswas equation. Mod Phys Lett B. 2019;33(22):1950264. 10.1142/S0217984919502646Suche in Google Scholar

[9] McLean D. Understanding aerodynamics: Arguing from the real physics. Hoboken (NJ), USA: John Wiley and Sons; 2012. 10.1002/9781118454190Suche in Google Scholar

[10] Burgers JM. A mathematical model illustrating the theory of turbulence. Adv Appl Mech. 1948;1:171–99. 10.1016/S0065-2156(08)70100-5Suche in Google Scholar

[11] Ahmad I, Riaz M, Ayaz M, Arif M, Islam S, Kumam P. Numerical simulation of partial differential equations via local meshless method. Symmetry. 2019;11(2):257. 10.3390/sym11020257Suche in Google Scholar

[12] Ahmad I, Ahsan M, Din ZU, Masood A, Kumam P. An efficient local formulation for time-dependent PDEs. Mathematics. 2019;7(3):216. 10.3390/math7030216Suche in Google Scholar

[13] Ahmad I, Ahsan M, Hussain I, Kumam P, Kumam W. Numerical simulation of PDEs by local meshless differential quadrature collocation method. Symmetry. 2019 11(3):394. 10.3390/sym11030394Suche in Google Scholar

[14] Wang F, Zhang J, Ahmad I, Farooq A, Ahmad H. A novel meshfree strategy for a viscous wave equation with variable coefficients. Front Phys. 2021;9:701512. 10.3389/fphy.2021.701512Suche in Google Scholar

[15] Jalghaf HK, Kovács E, Bolló B. Comparison of old and new stable explicit methods for heat conduction, convection, and radiation in an insulated wall with thermal bridging. Buildings. 2022;12(9):1365. 10.3390/buildings12091365Suche in Google Scholar

[16] Li DS. Convection-diffusion modeling for chemical pollutant dispersion in the joint of artificial lake using finite element method. Bulg Chem Commun. 2015;47:949–58. Suche in Google Scholar

[17] Khan H, Mustafa S, Ali I, Kumam P, Baleanu D, Arif M. Approximate analytical fractional view of convection-diffusion equations. Open Phys. 2020;18(1):897–905. 10.1515/phys-2020-0184Suche in Google Scholar

[18] Safdari-Vaighani A, Heryudono A, Larsson E. A radial basis function partition of unity collocation method for convection-diffusion equations arising in financial applications. J Sci Comput. 2015;64(2):341–67. 10.1007/s10915-014-9935-9Suche in Google Scholar

[19] Ain QT, Wan J. A stochastic analysis of co-infection model in a finite carrying capacity population. Int J Biomath. 2023;2350083. 10.1142/S1793524523500833Suche in Google Scholar

[20] Mohammed PO, Alqudah MA, Hamed YS, Kashuri A, Abualnaja KM. Solving the modified regularized long wave equations via higher degree B-spline algorithm. J Funct Space. 2021;1–10. 10.1155/2021/5580687Suche in Google Scholar

[21] Ain QT, Nadeem M, Karim S, Akguuul A, Jarad F. Optimal variational iteration method for parametric boundary value problem. AIMS Math. 2022;7(9):16649–56. 10.3934/math.2022912Suche in Google Scholar

[22] Thounthong P, Khan MN, Hussain I, Ahmad I, Kumam P. Symmetric radial basis function method for simulation of elliptic partial differential equations. Mathematics. 2018;6(12):327. 10.3390/math6120327Suche in Google Scholar

[23] Wang F, Hou E, Ahmad I, Ahmad H, Gu Y. An efficient meshless method for hyperbolic telegraph equations in (1+1) dimensions. CMES-Comp. Model Eng Sci. 2021;128(2):687–98. 10.32604/cmes.2021.014739Suche in Google Scholar

[24] Mehnaz S, Khan MN, Ahmad I, Abdel-Khalek S, Alghamdi AM, Inc M. The generalized time fractional Gardner equation via numerical meshless collocation method. Therm Sci. 2022;26(1):469–74. 10.2298/TSCI22S1469MSuche in Google Scholar

[25] Ain QT, He JH, Anjum N, Ali M. The fractional complex transform: A novel approach to the time-fractional Schrödinger equation. Fractals. 2020;28(7):2050141. 10.1142/S0218348X20501418Suche in Google Scholar

[26] Khan Z, Srivastava HM, Mohammed PO, Jawad M, Jan R, Nonlaopon K. Thermal boundary layer analysis of MHD nanofluids across a thin needle using non-linear thermal radiation. Math Biosci Eng. 2022;19(12):14116–41. 10.3934/mbe.2022658Suche in Google Scholar PubMed

[27] Srivastava HM, Gusu DM, Mohammed PO, Wedajo G, Nonlaopon K, Hamed YS. Solutions of general fractional-order differential equations by using the spectral tau method. Fractal Fract. 2021;6(1):7. 10.3390/fractalfract6010007Suche in Google Scholar

[28] Jan A, Srivastava HM, Khan A, Mohammed PO, Jan R, Hamed YS. In vivo HIV dynamics, modeling the interaction of HIV and immune system via non-integer derivatives. Fractal Fract. 2023;7(5):361. 10.3390/fractalfract7050361Suche in Google Scholar

[29] Ahmad I, Ahmad H, Inc M, Yao SW, Almohsen B. Application of local meshless method for the solution of two term time fractional-order multi-dimensional PDE arising in heat and mass transfer. Therm Sci. 2020;24(1):95–105. 10.2298/TSCI20S1095ASuche in Google Scholar

[30] Ahmad I, Khan MN, Inc M, Ahmad H, Nisar KS. Numerical simulation of simulate an anomalous solute transport model via local meshless method. Alex Eng J. 2020;59(4):2827–38. 10.1016/j.aej.2020.06.029Suche in Google Scholar

[31] Wang F, Khan MN, Ahmad I, Ahmad H, Abu-Zinadah H, Chu YM. Numerical solution of traveling waves in chemical kinetics: time-fractional Fishers equations. Fractals. 2022;30(02):2240051. 10.1142/S0218348X22400515Suche in Google Scholar

[32] Ahmad I, Ali I, Jan R, Idris SA, Mousa M. Solutions of a three-dimensional multiterm fractional anomalous solute transport model for contamination in groundwater. PloS One. 2023;18(12):e0294348. 10.1371/journal.pone.0294348Suche in Google Scholar PubMed PubMed Central

[33] Ahmad I, Bakar AA, Ali I, Haq S, Yussof S, Ali AH. Computational analysis of time-fractional models in energy infrastructure applications. Alex Eng J. 2023;82:426–36. 10.1016/j.aej.2023.09.057Suche in Google Scholar

[34] Ahmad H, Khan MN, Ahmad I, Omri M, Alotaibi MF. A meshless method for numerical solutions of linear and nonlinear time-fractional Black-Scholes models. AIMS Math. 2023;8(8):19677–98. 10.3934/math.20231003Suche in Google Scholar

[35] Li JF, Ahmad I, Ahmad H, Shah D, Chu YM, Thounthong P, et al. Numerical solution of two-term time-fractional PDE models arising in mathematical physics using local meshless method. Open Phys. 2020;18(1):1063–72. 10.1515/phys-2020-0222Suche in Google Scholar

[36] Wang F, Ahmad I, Ahmad H, Alsulami MD, Alimgeer KS, Cesarano C, et al. Meshless method based on RBFs for solving three-dimensional multiterm time fractional PDEs arising in engineering phenomenons. J King Saud Univ Sci. 2021;33(8):101604. 10.1016/j.jksus.2021.101604Suche in Google Scholar

[37] Caputo M. Linear models of dissipation whose Q is almost frequency independent-II. Geophys J Int. 1967;13(5):529–39. 10.1111/j.1365-246X.1967.tb02303.xSuche in Google Scholar

[38] Jumarie G. Stock exchange fractional dynamics defined as fractional exponential growth driven by (usual) Gaussian white noise. Application to fractional Black-Scholes equations. Insur Math Econ. 2008;42(1):271–87. 10.1016/j.insmatheco.2007.03.001Suche in Google Scholar

[39] Jumarie G. Derivation and solutions of some fractional Black-Scholes equations in coarse-grained space and time. Application to Merton’s optimal portfolio. Comput Math Appl. 2010;59(3):1142–64. 10.1016/j.camwa.2009.05.015Suche in Google Scholar

[40] Atangana A, Baleanu D. New fractional derivatives with non-local and nonsingular kernel theory and application to heat transfer model. Therm Sci. 2016;20:763. 10.2298/TSCI160111018ASuche in Google Scholar

[41] He JH. A new fractal derivation. Therm Sci. 2011;15(1):145–7. 10.2298/TSCI11S1145HSuche in Google Scholar

[42] Sun ZZ, Wu X. A fully discrete difference scheme for a diffusion-wave system. Appl Numer Math. 2006;56(2):193–209. 10.1016/j.apnum.2005.03.003Suche in Google Scholar

[43] Sarra S. A local radial basis function method for advection-diffusion-reaction equations on complexly shaped domains. Appl Math Comput. 2012;218(19):9853–65. 10.1016/j.amc.2012.03.062Suche in Google Scholar

Received: 2023-10-17

Revised: 2023-12-05

Accepted: 2023-12-08

Published Online: 2024-03-12

This work is licensed under the Creative Commons Attribution 4.0 International License.

Artikel in diesem Heft

https://doi.org/10.1515/nleng-2022-0366

Schlagwörter für diesen Artikel

meshless collocation method; hybrid multiquadric-cubic radial basis functions; mathematical model; fractional derivatives; multiterm time-fractional convection-diffusion model equation

Creative Commons

BY 4.0