Abstract
With an emphasis on the combined degradation of railway track geometry and components, a new numerical-analytical method is proposed for predicting the track geometrical vertical levelling loss (VLL). In contrast to previous studies, this research unprecedentedly considers the influence of initial track irregularities (ITI) on VLL under cyclic loadings, elastic-plastic behaviour, and different operational dynamic conditions. The non-linear numerical models are simulated using an explicit finite element package known as LS-Dyna, and their results are validated by full-scale experimental and field measurement data. The outcomes are iteratively regressed by an analytical logarithmic function that cumulates permanent settlements, which innovatively extends the effect of ITI on VLL in a long-term behaviour. For a typical heavy-haul railway operating under 30 tons axle load and 60 km/h train velocity, the result indicates that the set of ITI with the highest standard deviation (SD) of vertical profile (VP) degrades faster (37% on average) than that with the lowest SD. Additionally, our new findings reveal that the worst scenario is related to a train running at 60 km/h and carrying a load of 20 tons/axle in an uneven track whose SD of VP evolves from 3.23 mm at N = 0 (ITI) to 7.20 mm, whereas the best one corresponds to a train at 60 km/h and 30 ton axle load in an uneven track whose SD of VP downgrades from 0.48 to 1.50 mm, both at 3 M cycles (or 60 million gross tons). These findings indicate the importance of considering the ITI for predicting track geometrical VLL under cyclic loadings. Therefore, based on this research, an acceptable condition (thresholds) of ITI can be redefined for a minimum effect on VLL, which can support the development of practical maintenance guidelines to extend the railway track service life.
1 Introduction
The track geometrical vertical levelling loss (VLL) is defined by Melo et al. [1 2 3 4 5] as a parameter of how much the rail loses its vertical position in the railway track physical space under cyclic loadings. In principle, it can be characterized to occur in two different phases before the first track maintenance or construction activities. In the first phase, straightaway after track intervention, there is a rapid consolidation of the railway ballast due to immediate particle rearrangements, whereas in the second one, there is a slower loss rate related mostly to further ballast particle rearrangements and particle breakdowns [3,6,7,8]. In this second phase, according to Indraratna et al. [9], the rate can be basically approximated by a linear degradation with the logarithm of the number of cyclic loadings or million gross tons (MGT) as the rate of ballast plastic deformation decreases gradually [2]. These two phases are also demonstrated in this study.
The dynamics forces caused by initial track irregularities (ITI) are responsible for expanding the VLL under dynamic cyclic loadings, e.g. due to compaction of ballast and fracture of ballast stones. Also, the natural wavelengths (or frequencies) of a railway track structures (and their components) influence on how much it vibrates under different train speeds [10 11,12,13,14 15 16] affecting negatively on rail vertical displacements and their reactions on the adjacent sleepers [2,17,18]. Therefore, our reasonable physical study about the effect of initial track roughness on VLL is of considerable interest for supporting the prediction of the long-term track geometrical degradation. Figures 1 and 2 illustrate, respectively, the track components on a typical heavy-haul railway and the concept of track geometrical vertical levelling (VL) parameter.

Typical ballasted railway track and its components.

The concept of the influence of initial track geometric irregularities on VLL in a ballasted railway track.
For the past three decades, many researchers have investigated the track settlements in a smooth track (without track geometry irregularities) and have proposed different approaches to predict the track geometrical VLL, mostly focusing on ballast settlement, as pointed out by Melo et al. [2,19]. Abadi et al. [20], Thom and Oakley [21], Dahlberg [22], and Grossoni et al. [23] carried out outstanding literature reviews revealing that there were no typical proceeds among investigation conditions and their outcomes. Also, most methods indicate dependency only on the number of cyclic loadings without taking into consideration any difference into railway dynamic conditions. Trying to address the investigations gaps, Melo et al. [2] suggested a new numerical-analytical approach considering operational, vehicle, and track conditions. However, the innovation proposed by Melo et al. [2] does not foresee the effect of ITI on VLL.
Based on a critical literature review, it has been indicated that no other studies have investigated the dynamic effect of ITI on VLL under cyclic loadings considering different operational conditions and elastic-plastic behaviour of track components. Generally, the research examines dynamic responses of track irregularities between maintenance interventions in a specific site and under a particular railway condition.
In the past, Partington [24] studied experimentally in laboratory that on ITI, the VLL is affected after 1,000 passes (or cyclic loadings) in the case of the high average lift (after tamping) for the low load tests. Suiker and Borst [25] performed a numerical modelling of railway track suggesting that dynamic effects of track irregularities can be taken into account by introducing the dynamic responses of instantaneous train axle load into one or more dynamic amplification factors, which may serve as multipliers for the quasi-static force applied in the performance of long-term track degradation. Augustin et al. [26] also studied the effect of ITI on VLL. They concluded that an initially strong deviation of track vertical levelling leads to large height differences among different track sections and left and/or right rails, as the discrepancies of loss are more extreme in the case of great initial height variance of vertical levelling along the segment of study. Takemiya and Bian [27] investigated different characteristics of layered subgrade and moving axle loads, which led to significantly dispersive response features, depending on the train velocity: (1) quasi-static for a low velocity, and (2) dynamic for a high-speed situation. Hawari and Murray [28] investigated experimentally in three sites the relationship between the standard deviation (SD) of roughness of a piece of railway track and the rate at which the vertical profile (VP) geometry of that track deteriorates indicating that there is a threshold of about 0.7 mm of roughness below which the rate of deterioration is relatively small. Chang et al. [29] performed field experiments and they considered that total passing tonnage was the main influential factor when predictions were made for the changes in VP irregularity level over a specific unit track section. Faiz [30] investigated the effect of univariate and multivariate correlation analysis of track irregularities on the track dynamic characteristics by analytical predictions indicating that since the track irregularity can be aligned it led to minimize the predictive error of track degradation problems.
In the beginning of last decade, some researchers carried out other investigations focused mostly on numerical analysis. Choi et al. [31] conducted a numerical simulation research to investigate the influence of track irregularities with various wavelengths and amplitudes modelled using the VAMPIRE program on the running behaviour of high-speed trains and to support the revision of the irregularity standards. They concluded that the vertical levelling irregularities, particularly at long wavelengths, had a strong influence on vertical vehicle acceleration as they increase with an increase in the wavelength (from 0.1 to 0.7 m/s2 vertical acceleration varying wavelength, respectively, from 2 to 20 m, both at 12 mm of amplitude). Berawi’s research [32] found that there was a strong positive relationship (95%) between the left and the right rails in a longitudinal profile as they were similar for wavelengths longer than 6 m. However, as the wavelengths get shorter, the coherence becomes lower and the relationship of two rails is more independent.
Guler [33] decided to study the effect of track roughness modelling the railway track geometrical degradation with Artificial neural network, which produced a reasonable R 2 value (0.742) for VP. Choi [34] evaluated theoretically and experimentally the dynamic features of a ballast track revealing that the track impact force for the service track appeared to increase with the track support stiffness. Naeimi et al. [35], employing a numerical modelling process, concluded that for the irregular rail cases, the dynamic responses of the consecutive sleepers appeared on a greater number of sleepers, while the static solution covered fewer sleepers. Moreover, Naeimi et al. [35] highlighted that the results of dynamic displacements for the consecutive sleepers in VP confirmed the effect of irregularities on dynamic responses and that the differences were even further meaningful when the severity of the longitudinal irregularity (difference between the left and right VPs) was increased. Shen et al. [36] investigated the effect of vertical track irregularities on ballast settlement under few cyclic loadings indicating that the amount of settlement increased: (1) three times when train velocity increased from 60 to 120 km/h, (2) rapidly when train velocity was more than 100 km/h, (3) by 38.6% as axle load increased from 25 to 30 tons, and (4) with increasing traffic as there was a linear relationship between amount of settlement and traffic.
For the last 10 years, some researchers have also worked on both numerical modelling and experiments to study the influence of track irregularities on VP; however, despite interesting findings, none of them presents findings related to the effect of ITI on VLL under both cyclic loadings and different track and operational conditions. The investigations mostly continue to focus on dynamic responses of track irregularities in a specific site and railway condition. Nguyen et al. [7] studied numerically based on an empirical ballast settlement law the effect of track geometry defects under railway traffic cyclic loadings finding significant influence of train velocity on the evaluation of VP loss. Soleimanmeigouni et al. [37] proposed a two-level framework to model the evolution of the track geometry degradation over a spatial and temporal space using a simple linear model finding that degradation parameters over the spatial interval may be generated by some Gaussian processes.
Nielsen and Li [3] carried out a numerical investigation to study the dynamic interaction between the wheel and the rail with longitudinal level and empirical settlement of ballast/subgrade. They demonstrated that the track geometrical degradation over time was caused by a prescribed initial rail irregularity; however, the settlement model did not explicitly account for the material properties and multiaxial stress-strain conditions in the track substructure or the interaction between different regions of the track substructure. Guo and Zhai [38] also carried out numerical simulation based on an empirical power model for settlement prediction to investigate the effect of track subgrade settlement with a regular operation pattern. They concluded that, during a long-term track degradation, the ITI induced dynamic responses of the vehicle–track coupled system in terms of the wheel-rail interactions.
De Miguel et al. [39] researched the response of track geometry irregularities by implementing an empirical settlement law and a multi-body simulation software at 80-km/h train velocity. They showed that it was possible to assess the development of both the dynamic interaction forces between the vehicle and the track and the vertical track irregularities with low computational time compared to Finite element method (FEM). Grossoni et al. [23] investigated analytically the role of track stiffness and its spatial variability through a set of computational experiments estimating the track geometry degradation rates. They suggested that the vertical track interactive model can calculate the evolution of the rail track irregularities under a particular cumulative empirical settlement law. Soleimanmeigouni et al. [40] developed a data-driven analytical approach considering the occurrence of shock events and showing that the linear model was an appropriate choice for modelling the degradation pattern of longitudinal level defects.
Bednarek [41] carried out a full-scale field experimental investigation and simulated the influence of short track geometry irregularities statically (no influence of train velocity) and with elastic parameters of the track components (no elastic-plastic deformation). They observed that the induced irregularity changed significantly the work of the loaded elements of the railway track structure, increasing the rail deflections. Grossoni et al. [42] suggested a semi-analytical approach based on the known behavior (empirical equation) of granular materials under cyclic loadings. It permits to capture the differences in the rate of development of permanent settlement as a result of the initial track bed stiffness.
Differently from others, Kosukegawa et al. [43] proposed recently a method to forecast the VP from track roughness taking into consideration exogenous factors and spatiotemporal correlations using a convolutional long short-term memory. They have found that linear regression may be enough if maintenance routine is lower; however, when maintenance operation is frequently required, spatial calculation and maintenance registries improve prediction significantly.
In general, as described above, the findings and insights from reviewed studies have demonstrated that the track geometrical degradation over time has also been caused and accelerated by a prescribed initial rail irregularity. Additionally, the previous investigations have identified a possible relationship between the SD of track vertical levelling and the rate at which it deteriorates. Furthermore, these studies have found that the main influential factor for the changes in VP irregularity level over a specific unit track section is the total passing tonnage. However, these studies have not provided an accurate and parametric investigation of the effect of ITI on railway track VLL considering the train-track interaction as a whole and: (1) long-term performance, (2) operational conditions (e.g. axle load, train velocity), (3) vehicle parameters (e.g. dynamic stiffness of one suspension), and (4) track parameters (e.g. dynamic elastic-plastic behavior of railway ballast). It means that despite the wealth of recent research on track irregularities, none have specifically explored the effect of ITI on VLL under cyclic loadings and different track and operational conditions. On this ground, to address the revealing knowledge gap related to predict properly the dynamic influence of initial geometric defects on VLL under cyclic loadings and elastic-plastic behavior of railway ballast tracks, this research proposes the development of an innovative non-linear numerical-analytical method to predict track geometrical VLL considering not only the transient dynamic conditions but also the long-term effect of ITI under repetitive loading cycles over the service life. This study examines the non-linearities of dynamic track irregularities in a heavy-haul railway engineering system to provide a more realistic mathematical modelling. Additionally, this study takes advantage of the non-linearities to discover the real-world behaviour of the railway geometrical track system by including non-linear interactions. This approach can support the development of an efficient practical maintenance guideline recommending ITI thresholds for a minimum effect on VLL over time.
2 Methodology
Based on a typical heavy-haul ballasted railway track, as illustrated in Figure 2 and its parameters described on Table 1, a 25 m straight track segment has been modelled in 3D on LS-Dyna, which is a commercial FE software package. Also, two adjacent bogies of a typical wagon are modelled considering the greatest load solicitation [2] as indicated in Figure 3.
Track and vehicle parameters (modified from Melo et al. [2])
| Track component(1) | Type of element | Constitutive material law | Type of finite element | Dynamic parameter(s) and contact type(s) |
|---|---|---|---|---|
| Rail(2) | 136RE | Elastic | Beam | Density: 7.85 × 10−9 ton/mm3 |
| Young’s modulus: 2 × 105 N/mm2 | ||||
| Poisson’s ratio: 0.3 | ||||
| Contact type: node-to-node | ||||
| Sleeper(3),(4) | Mono-block concrete | Elastic | Beam | Density: 2.5 × 10−9 ton/mm3 |
| Young’s modulus: 4.3 × 104 N/mm2 | ||||
| Poisson’s ratio: 0.15 | ||||
| Contact type: node-to-node | ||||
| Fastening system | E-clip and rail pad | Elastic | Spring | Elastic stiffness: 1.7 × 105 N/mm |
| Contact type: node-to-node | ||||
| Ballast(5) | Fresh crushed rock | Elastic-plastic | Spring and damper | Elastic stiffness: 45.43 kN/mm |
| Yield force: 250 N | ||||
| Tangent stiffness: 150 N/mm | ||||
| Damping constant: 3.2 N/mm | ||||
| Contact type: node-to-surface | ||||
| Sub-ballast | A-6 (TRB) | Elastic | Solid | Density: 1.7 × 10−9 ton/mm3 |
| Young’s modulus: 400 N/mm2 | ||||
| Poisson’s ratio: 0.33 | ||||
| Contact type: surface-to-surface | ||||
| Reinforcement of the subgrade | NA | Elastic | Solid | Density: 1.5 × 10−9 ton/mm3 |
| Young’s modulus: 160 N/mm2 | ||||
| Poisson’s ratio: 0.36 | ||||
| Contact type: surface-to-node | ||||
| Subgrade | NA | Elastic | Spring | Elastic stiffness: 1 kN/mm |
| Contact type: node-to-surface |
| Vehicle component(6) | Type | Constitutive material | Finite element | Dynamic parameter(s) |
|---|---|---|---|---|
| Wheel set | 6½″ × 9″, wheel diameter: 965 mm | Rigid | Beam | Density: 7.85 × 10−9 ton/mm3 |
| Young’s modulus: 2 × 105 N/mm2 | ||||
| Poisson’s ratio: 0.30 | ||||
| Contact type: node-to-node | ||||
| First suspension | NA | Elastic | Spring and damper | Elastic stiffness: 1.751 × 105 N/mm |
| Damping constant: 3.502 N s/mm | ||||
| Contact type: node-to-node | ||||
| Bogie | Ride control | Rigid | Shell | Density: 7.85 × 10−9 ton/mm3 |
| Young’s Modulus: 2 × 105 N/mm2 | ||||
| Poisson’s Ratio: 0.3 | ||||
| Contact type: node-to-node |
Note: (1) Track gauge: 1,600 mm; (2) ASTM 136RE rail weight: 68 kg/m; (3) mono-block concrete sleeper length, height, and width: 2,800 250, 265 mm, respectively; (4) spacing sleepers: 610 mm; (5) crushed rock ballast height and shoulder: 300 and 300 mm, respectively; (6) key railway vehicle: GDE wagon to transport iron ore.
![Figure 3
Typical railway vehicles (wagons): two iron ore wagons (right), and in detail (left), the two adjacent bogies (greatest load demand) configuration and their components (modified from Melo et al. [2]).](/document/doi/10.1515/nleng-2024-0011/asset/graphic/j_nleng-2024-0011_fig_003.jpg)
Typical railway vehicles (wagons): two iron ore wagons (right), and in detail (left), the two adjacent bogies (greatest load demand) configuration and their components (modified from Melo et al. [2]).
The track-vehicle model is simulated by applying both linear elastic and elastic-plastic constitutive law of the materials to investigate the effect of ITI on the VLL under cyclic loadings. This non-linear model employs moving mass loads to represent the vehicles, which travel in loop along both smooth tracks (perfect track geometry) and uneven tracks, the last ones with two different sets of ITI. The objective is to determine the effects of ITI on track geometrical VLL over time. To simulate the designed model, the BlueBEAR platform (BB) – a powerful and fast computing facility – has been used to accelerate performance as it supports to solve computationally intensive tasks. Additionally, the BB is composed of parallel computing technique that allows hundreds of processors to run calculations at the same time making it suitable for this study.
The wheel-rail contact algorithm considers the wheel nodes to represent the contact patch between wheel and rail. A penalty method is used to constrain the wheel nodes to slide along the track, which consists of two rails, each of which is defined by a set of beam elements. The “train” nodes to follow the line defined by the “rail” beam elements and transfers forces between them.
In turn, the vehicles are typically modeled using spring, damper, and rigid elements at each wheel position. Each node in the set referred represents the contact patch of one wheel. These nodes should be initially on the line defined by either of the two rails. LS-DYNA will move the train nodes initially onto the rails to achieve the correct initial wheel-rail forces. Wheel roughness input is available; however, it has not been considered in this study. The wheel-rail interface model is a simple penalty function designed to ensure that the train nodes follow the line of the track. It does not attempt to account for the shape of the rail profile (see Figure 4).
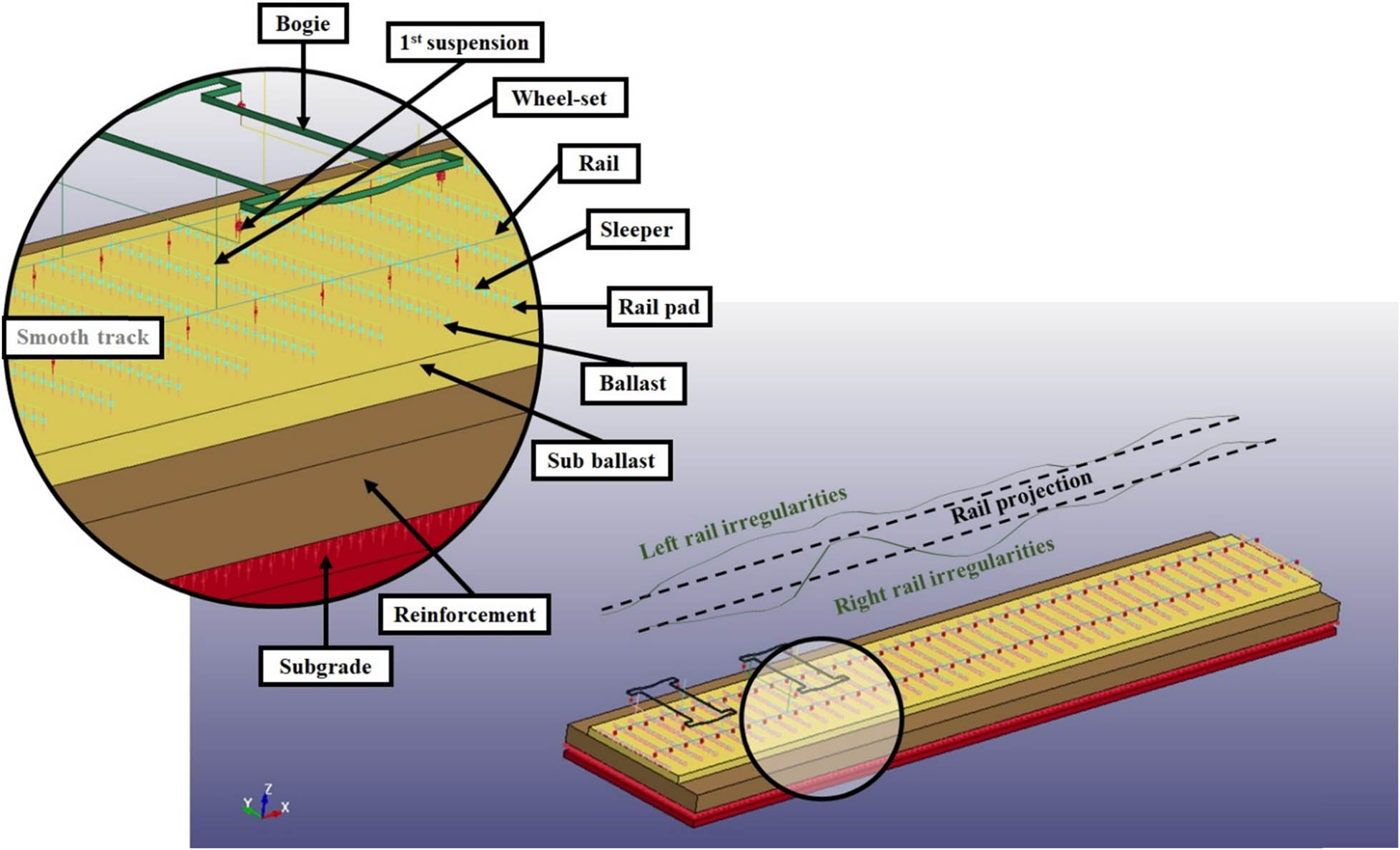
Railway track and vehicle model on LS-Dyna FE software (in detail, smooth track and left and right vertical rail irregularities).
Considering that the railway ballast settlement is the principal source of VLL [2], the track subgrade components are modelled with high elastic resilience modulus (Young’s modulus) including the reinforcement of subgrade [7]. Also, as the ballast is a granular layer subjected to an extreme stress under cyclic loadings, its accumulative deformation can be caused by compaction and breakage implying undoubtedly vertical settlements [44]. According to Melo et al. [2], this situation can be approximately characterized by FE models using an elastic-plastic discrete element with isotropic hardening, in which the applied load is split into a sequence of increments (cyclic loadings). Additionally, in a straight track section, the ITI (or initial roughness) is modelled innovatively as a non-linear function underpinned by displacement events and by a load curve of a given VP deviation (in mm) of the rail top from the theoretical centreline (smooth track) of the beam elements as a function of distance along the track from the origin node of the rail above each concrete sleeper [45]. The ITI curve profiles are measured from both rails of the same segment of track so that the relationship between bump and roll modes is correctly captured [46]. This robust approach can provide new findings related to actual dynamic forces on a ballasted railway track and better understandings from the previous studies about the effect of ITI on VLL over time. As soon as the sleeper is loaded and moves towards the ballast, a maximum vertical rail displacement (MaxVRD) is achieved [2] taking into consideration the effect of VP. The validation of this model is presented in Section 3. In this investigation, which focuses on low to medium frequencies and heavy-haul axle loads, the sleeper is modelled as a beam element due its higher computational efficiency and approachable results if compared to a solid element, as pointed out by Xu and Lu [47]. The non-linear characteristics of the model are shown in Figure 5. The force–displacement relationship during cyclic loading can be written as
where “n” is the number of cycles, “f n ” is the existing force considered as the impact force caused by the current rail top irregularity, “K e” is the elastic stiffness, “K t” is the tangent stiffness, “F y” is the yield force, and “Δl n ” is the increment of track settlement.
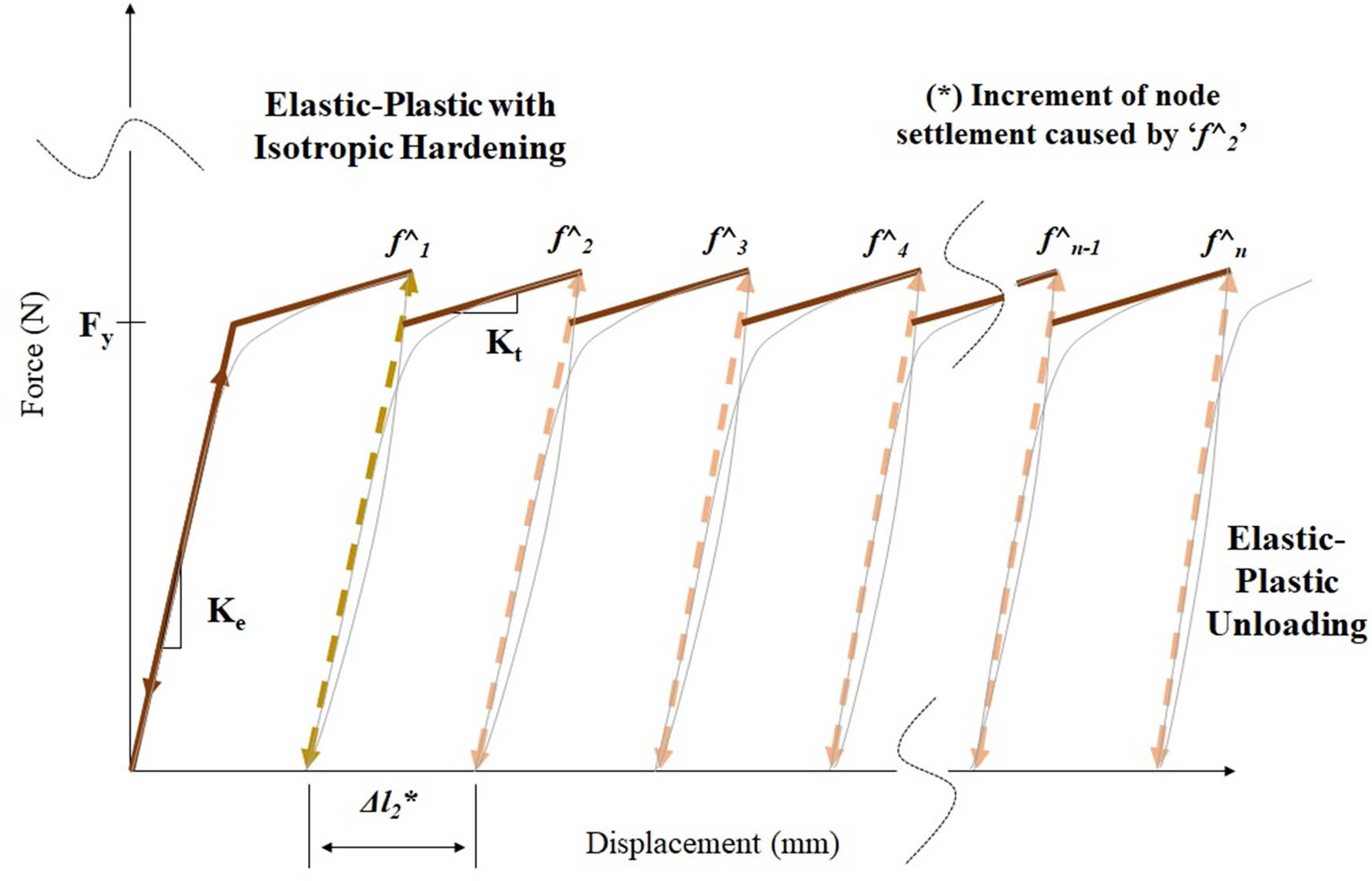
Loading and unloading force–displacement curves for considering the ballast elastic-plastic behaviour.
Initially, the MaxVRD is generated numerically by the non-linear FE model under repeated loadings; first, on a smooth track, afterward, on an uneven track. The outcomes of numerical simulation are later regressed by a Napierian logarithmic (LN) function to provide an analytical estimation of the “MaxVRD” for the real cyclic loadings of a smooth track (without track irregularities) as proposed by Melo et al. [2]. This equation may be written as
where “MaxVRD” is the maximum vertical rail displacement, “a” is the rate of “MaxVRD,” “N” is the number of repeated loadings, and “b” is the initial rail displacement for a smooth track.
Following this initial investigation, the differences between each four-cycle loads into the short-term performance of the MaxVRD regressed function (Eq. (2.2)) for smooth track are determined. The outcomes suggest the first term of Eq. (2.2) as the track geometrical VLL, which can also be written [2]:
where “VLL” is the vertical levelling loss, “a VLL” the rate of “VLL,” “N” is the number of repeated loadings, “T” is the MGT, and “W” is the axle load (in tons).
Eq. (2.3) provides an estimation of VLL for the real cyclic loadings in a smooth track [2]. In sequence, the MaxVRD values curve is also numerically generated taking into account the effect of two ITI on vertical rail displacement (VRD) in a short-term behaviour. Therefore, this study originally proposes to compare the response differences between low and medium SD of ITI over time on VLL in a ballasted railway track. The ratio curve indicates how much SD of ITI influences the VLL under repeated loadings.
In order to rigorously validate the effects of ITI on VLL, the wheel–rail contact force of the model as critical and usual parameter of assessment applied worldwide is also compared to the experiments carried out by Gadhave and Vyas [48] at the similar conditions, including 10 tons axle load and 72 km/h train velocity. This condition has been adopted for the model validation. The validation has been conducted using both time series and power spectral density (PSD) functions to create wavelength-based vertical rail irregularities that are identical to both studies defined in ERRI-B176 as [48,49]
where wavelengths of range 0.4–0.03 m−1 with 300 frequency components equidistant from one another are used for creating roughness in left and right rails [48] in 25 m railway track of this investigation (Figure 6).
![Figure 6
VP irregularities created by PSD in 25 m railway track (modified from [48]).](/document/doi/10.1515/nleng-2024-0011/asset/graphic/j_nleng-2024-0011_fig_006.jpg)
VP irregularities created by PSD in 25 m railway track (modified from [48]).
Examining that the ITI can affect the VLL over time, it is possible to assume that Eq. (2.2) also represents the new VLL (nVLL) taking into consideration the effect of ITI. It may be written as
where “nVLL” is the new “VLL” (considering the effect of ITI), “a nVLL” the rate of “nVLL” (uneven track), “N” is the number of repeated loadings, “T” is MGT, and “W” is the axle load (in tons).
From the validation steps, this study also presents the performance of numerical simulations considering three different parameters: ITI (low and medium SD of ITI registered by railway company recording car, RC, calculated as 0.48 and 3.23 mm, respectively), train velocity (60, 70, and 80 km/h), and axle load (20, 30, and 40 tons), other track, vehicle, and operational parameters are kept constant. The rates of SD of VPs are identified and the performance and analysis of long-term behaviour of the model are presented. The methodology to develop this investigation is indicated in Figure 7.

Methodology flowchart.
3 Results and discussion
The effect of ITI on VLL over time under cyclic loadings and elastic-plastic behaviour of material (e.g. railway ballast plastic deformation) has never been evaluated in the past. As the experimental data on uneven tracks under cyclic loadings are also extremely limited, a typical heavy-haul ballasted railway track with monoblock concrete sleepers and artificial track irregularities is first considered for validation of the model. It is important to acknowledge that the material properties of track and vehicle components do not change with the number of load cycles, which is a limitation of this model. Additionally, as this study focuses on low to medium frequencies and heavy-haul axle loads, the authors assume that the sleeper can be modelled as a beam element due its higher computational efficiency and approachable results if compared to a solid element. This assumption is also discussed in the study by Xu and Lu [47]. The results of wheel-rail contact forces from FEM are validated against a previous experimental study carried out by Gadhave and Vyas [48] under similar vehicle, track, and operational conditions. Wheel has a radius of 0.46 m with S1002 profile. Rails have UIC 60 profile with 1:40 cant. The modulus of elasticity of rails is 210 GPa and Poisson’s ratio is 0.3. The wheelset, bogie, and half of the body masses are, respectively, 1,200, 2,615, and 16,000 kg. Vertical stiffness of primary spring (first suspension) is 544.57 kN/m. The train runs over tracks at constant velocity of 72 km/h [48].
The dynamic forces are investigated considering monotonic loading, elastic behaviour of vehicle, and track components, and artificial track irregularities set by the PSD following ERRI-B176 [49] methodology. When contrasted to the experiments carried out by Gadhave and Vyas [48], the FEM model outcomes present acceptable matches with those measured data, in which the maximum differences related to the minimum and maximum vertical contact forces are approximately 3 and 2%, respectively. Table 2 presents a comparison between the values of wheel-rail contact forces from previous study (the Gadhave and Vyas’s experiment) and the current investigation. It is possible to conclude that these differences are too small, and it does not impact the overall validity of the FEM model.
Comparison between wheel-rail contact forces provided by the numerical investigation (FEM) and the Gadhave and Vyas’s experiment
| Study | Contact force (kN) | |
|---|---|---|
| Minimum | Maximum | |
| Gadhave and Vyas [48] | 48.00 | 57.00 |
| FEM | 46.50 | 56.00 |
| Difference (%) | 3.23 | 1.79 |
In this study, the railway track model has been developed based on Melo et al.’s study (smooth track) [2] considering different operational conditions such as axle load (20, 30, and 40 tons), train velocity (60, 70, and 80 km/h), and ITI (two sets of track irregularity SD: 0.48 and 3.23 mm). Figure 8 illustrates the two typical sets of ITI registered by RC, which are input to the track model performance on LS-Dyna to calculate the dynamic forces and the track cumulative displacement under cyclic loadings. This permits us to evaluate the influence of ITI on VLL.
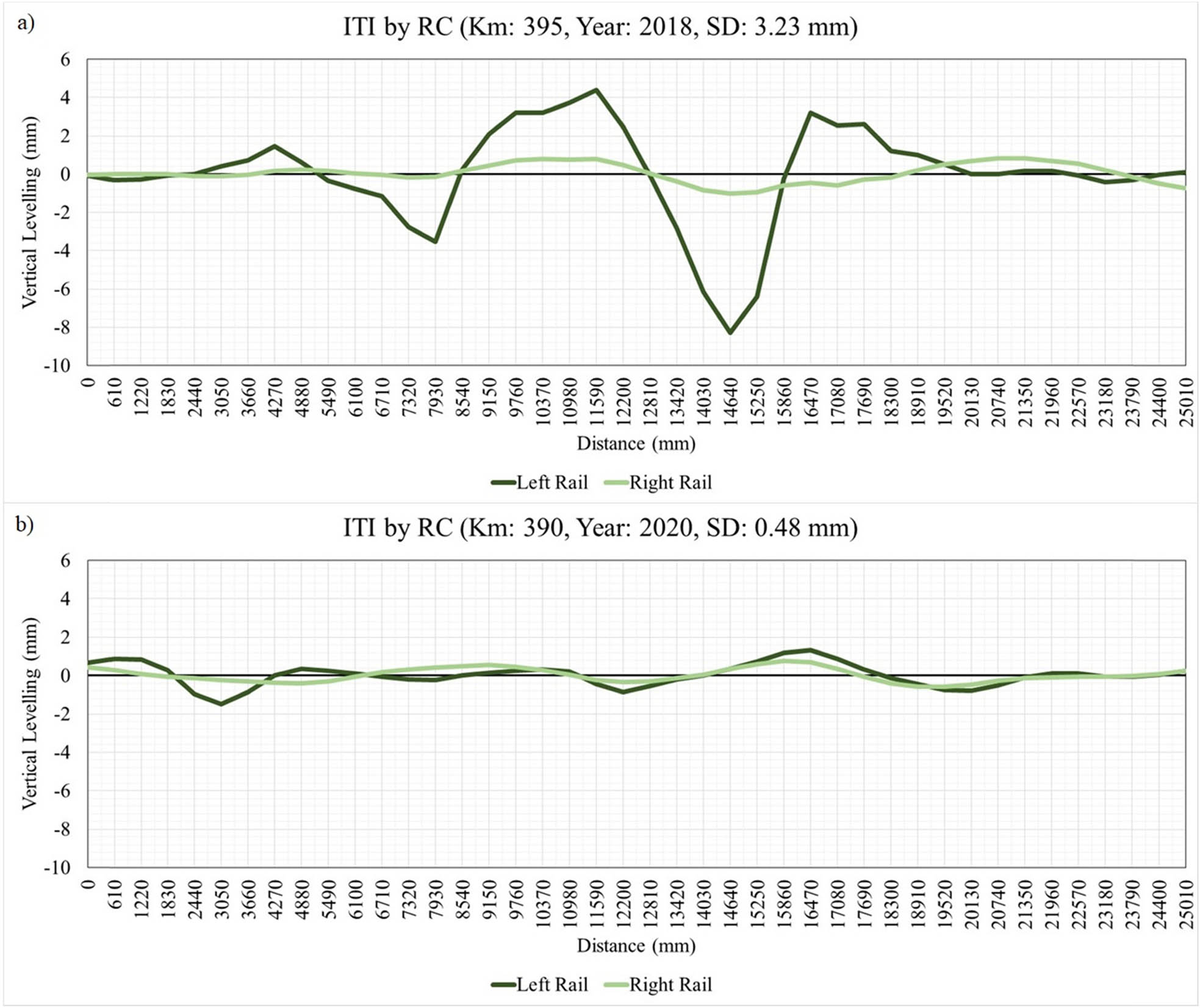
Vertical track irregularities registered by RC in 25 m railway track: (a) Km 395 in 2018 (SD: 0.48 mm), and (b) at Km 390 in 2020 (SD: 3.23 mm). Note: Km refers to kilometrage.
The VRDs are numerically calculated in vertical direction (“Z-Displacement”) on the top of each rail node for each repeated load. The slope of those displacements indicates the track longitudinal level loss over time [2]. The MaxVRD after every four repeated loads are identified for both track conditions: smooth and uneven tracks. During that stage, the maximum vertical rail displacement (MaxVRD) values, under repeated loadings (short-term), are regressed innovatively by a LN function to better estimate the MaxVRD regression function for a smooth track. This finding provides new insights about capturing numerically on FE analysis the elastic-plastic behaviour of a railway ballast, and consequently, the VP geometrical degradation of a ballasted railway track under cyclic loadings. The coefficient of determination, denoted as R 2, of the LN expression under regular operation of a heavy-haul railway (30 ton axle load and 60 km/h train velocity) is 0.9368 in the smooth track, which indicates a good accuracy. The results for this step can be written as follows:
where “MaxVRD” is the maximum VRD, “a = 3.3300” is the rate of “MaxVRD,” “N” is the number of repeated loadings, and “b = 14.7691” is the initial rail displacement for a smooth track.
As previously suggested by Melo et al. [2], the differences between every four repeated loads for a long-term performance of the MaxVRD LN function are also calculated. The outcome indicates that the first term of Eq. (3.1) is related to the VLL. Thus, the track geometrical VLL for those railway operation conditions, and smooth track may be written as
where “VLL” is the vertical levelling loss, “a VLL = 3.3300” the rate of “VLL,” “N” is the number of repeated loadings, “T” is MGT and “W = 30 tons” is the axle load.
Following on the proposed methodology, the ITI are modelled in an uneven track as non-linear features and, similar to that smooth track Eq. (3.1), the MaxVRD curves are identified for two types of ITI sets and regressed by LN function. It is important to note that the forces that act on each rail node above the sleepers exceed the usual dynamic forces (from smooth track) due to those irregularities. The coefficients of determination (R 2) of the LN equation for each MaxVRD node curve on the top of both left and right rails in the uneven track segments of the study (Figure 9) varies from 0.8604 to 0.9697 depending on the sleeper position, its ITI, and the overall ITI (the less the overall SD of ITI is, the less is the R 2), which also indicates a satisfactory accuracy. The section in this study is strategically centralized in the track segment model along 11 consecutive sleepers. The non-linear characteristics of the performed models (smooth and uneven tracks) are shown in Figures 10 and 11. Therefore, the VLL can be updated for each node along the rails based on Eq. (3.2) or (3.3) (new VLL, or nVLL) and their respective coefficients calculated as described in Table 3 for 30 ton axle load and 60 km/h train velocity. It means that each node has its own rate of VLL influenced by its position, ITI, and overall ITI, which is different from the smooth track (each node has the same rate of VLL; there is no influence of ITI).
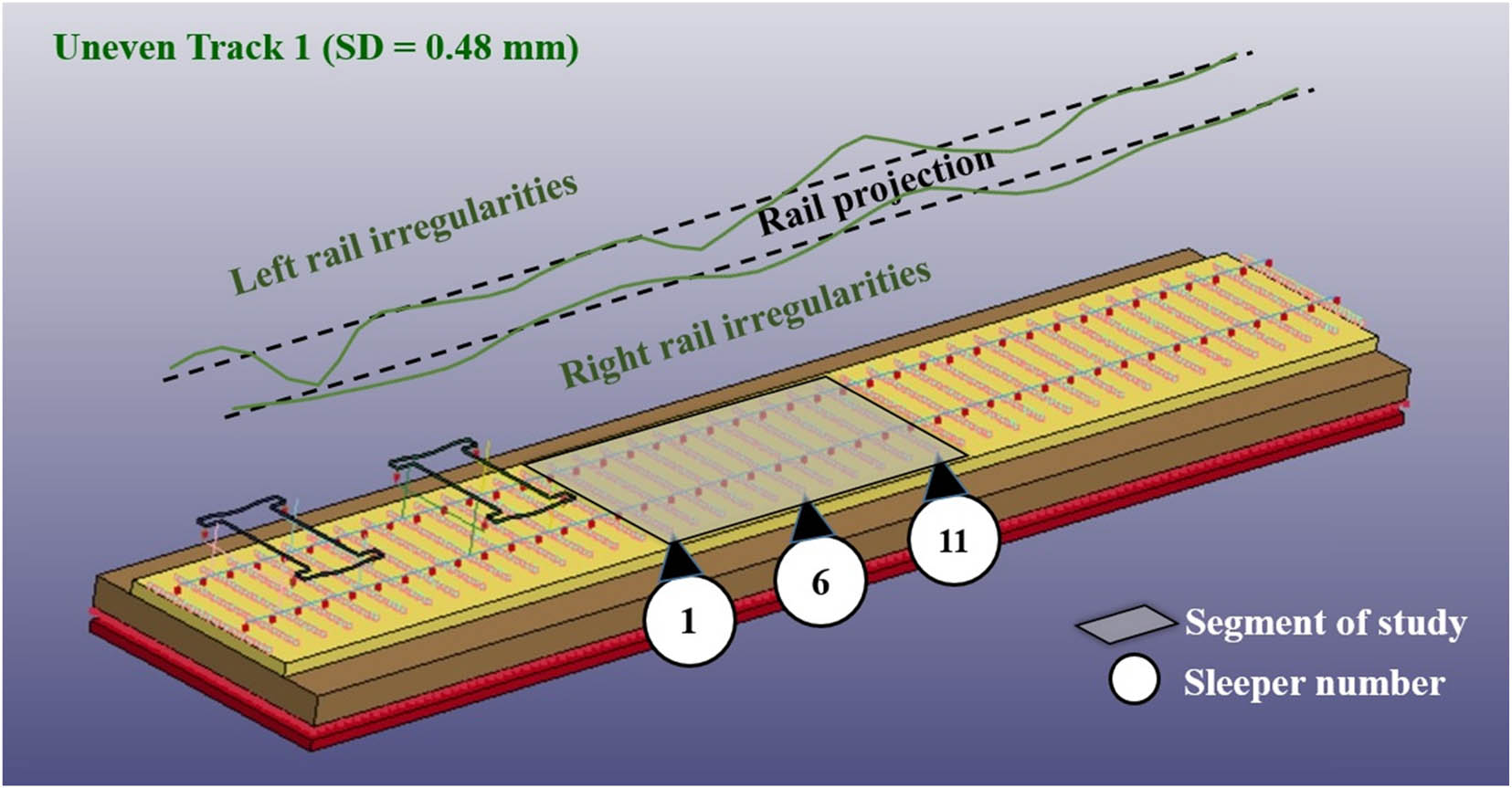
The segment of study to numerically calculate the short-term behaviour of VRD and MaxVRD on FEM under 30 ton axle load and 60 km/h train velocity for both the smooth and uneven (SD = 0.48 mm) tracks.
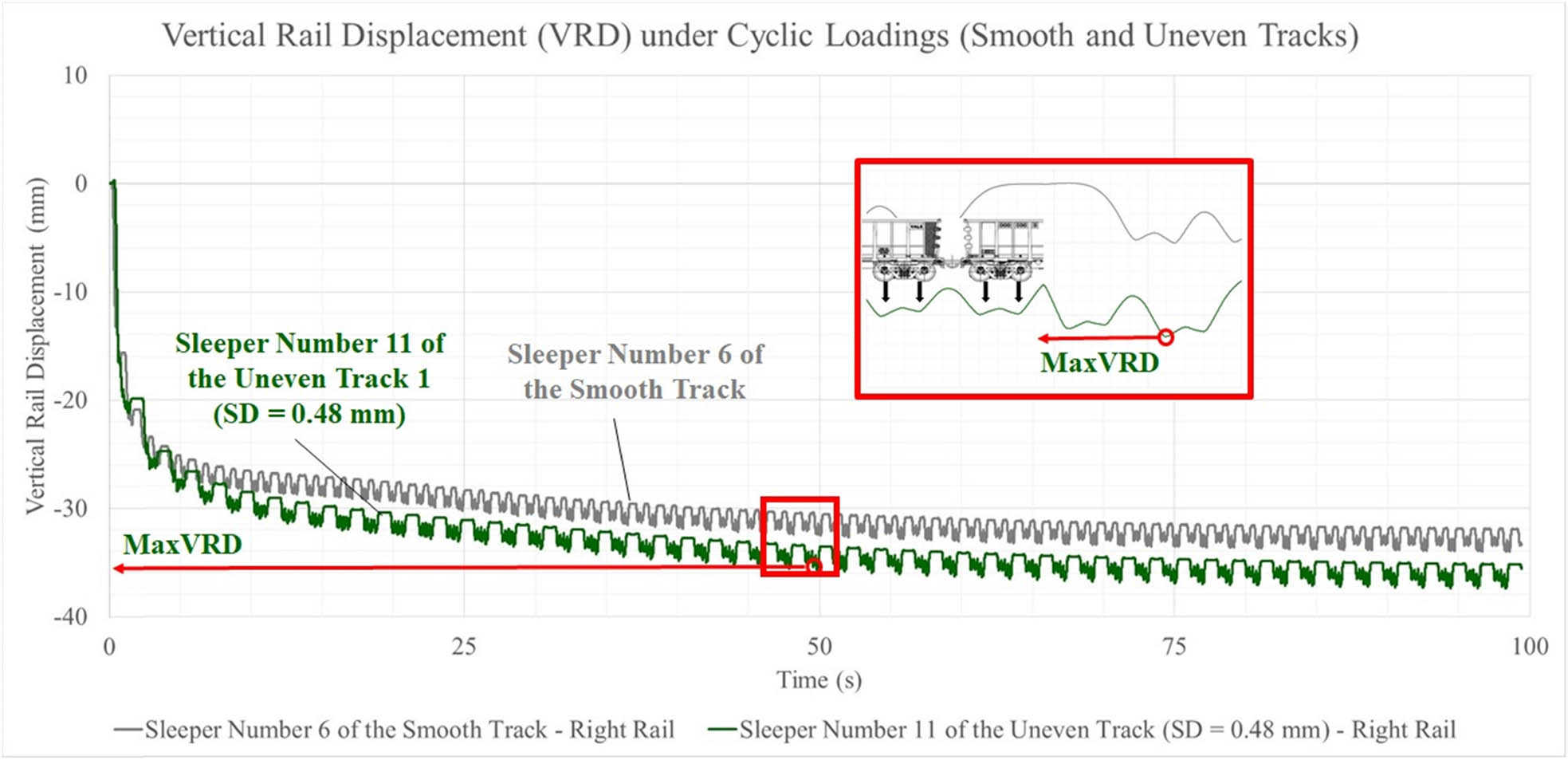
Comparison of VRD on FEM under 30 ton axle load and 60 km/h train velocity for both the smooth and uneven (SD = 0.48 mm) tracks (in detail: the MaxVRD).
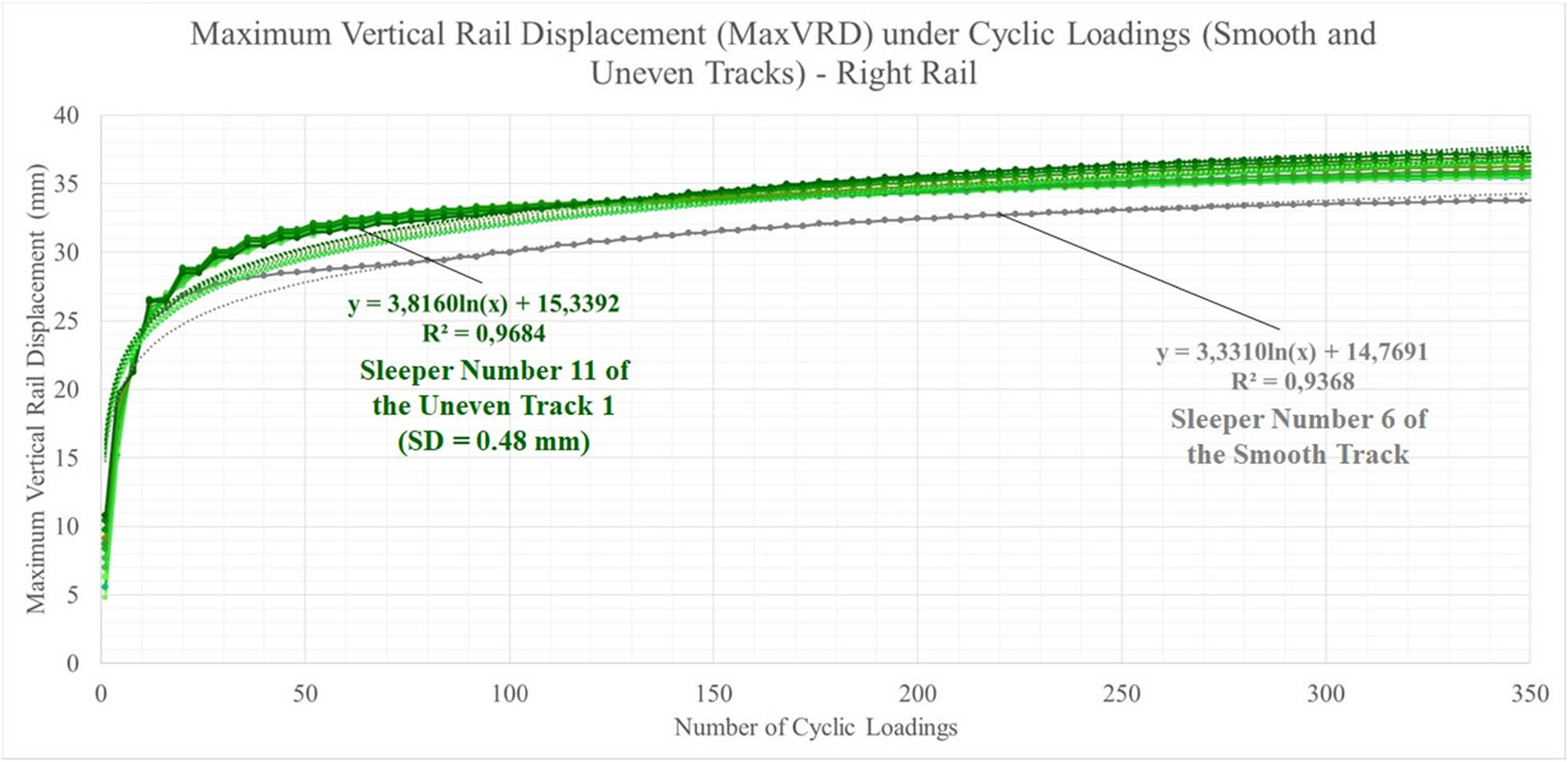
Comparison of MaxVRD on FEM under 30 ton axle load and 60 km/h train velocity for both the smooth and the uneven (SD = 0.48 mm) tracks.
Summary of “a nVLL” coefficients for a regular heavy-haul railway operation (30 tons axle load and 60 km/h train velocity) and two different sets of ITI
| Sleeper number | “a nVLL” | Difference (%) | ||||
|---|---|---|---|---|---|---|
| UT-1 (SD = 0.48 mm) | UT-2 (SD = 3.23 mm) |
|
|
|||
| Left rail (A) | Right rail (B) | Left rail (C) | Right rail (D) | |||
| 1 | 54,324 | 37,403 | 63,284 | 56,574 | 16.49 | 51.26 |
| 2 | 54,050 | 36,665 | 63,357 | 56,552 | 17.22 | 54.24 |
| 3 | 54,279 | 36,387 | 63,472 | 56,451 | 16.94 | 55.14 |
| 4 | 54,604 | 36,105 | 64,900 | 56,908 | 18.86 | 57.62 |
| 5 | 54,798 | 35,616 | 65,564 | 58,300 | 19.65 | 63.69 |
| 6 | 55,023 | 35,101 | 65,771 | 59,409 | 19.53 | 69.25 |
| 7 | 55,372 | 35,004 | 65,133 | 60,317 | 17.63 | 72.31 |
| 8 | 55,914 | 35,262 | 62,730 | 60,022 | 12.19 | 70.22 |
| 9 | 56,919 | 35,849 | 59,371 | 60,339 | 4.31 | 68.31 |
| 10 | 58,498 | 36,744 | 58,957 | 59,301 | 0.78 | 61.39 |
| 11 | 60,684 | 38,160 | 59,161 | 58,224 | −2.51 | 52.58 |
From Figure 10, the effect of ITI on VRD can be observed clearly, which escalates in function of the VP irregularity progress on the top of right rail of the sleeper number 11, for example. This indicates that the wheel–rail contact forces for the uneven track overcome considerably those of smooth track due the variation in dynamic forces (impact loads) generated by the roughness as expected. When bringing two bodies into contact, the existing forces will be transferred over the contact area. The primary objective when analysing such contacts is to calculate the values of forces and deformations at the contact interface. Based on this assumption, the nature of the contact stretch and the wheel–rail contact forces are heavily affected by the rail geometries. They may be determined from the vertical force, the local geometry, and the material properties of both the wheel and the rail. As the roughness does exist in real life, it can be modelled by a load curve giving the vertical deviation of the rail surface from the theoretical centreline of the beam elements as a function of distance along the track from the origin node of the rail. Ideally, roughness profiles measured from both rails of the same piece of track should be used so that the relationship between bump and roll modes is correctly captured. Therefore, the dynamic forces (impact loads) and its variation along the track can be calculated considering the vertical stiffness of wheel–rail contact multiplied by the roughness of the node. These dynamic loadings are transferred from the rails through rail pads and sleepers to damage the ballast beneath the sleepers for each load cycle. Therefore, the ballast under those dynamic forces starts to settle substantially causing the losses of longitudinal level on the top of the rails. It corroborates the effect observed in Augustin et al. [26]; however it has not been proved either numerically or experimentally before. These new findings are considerably better than the previous ones as they can support not only the development of predictive models under diverse operational railway conditions but also fill the gap related to the specification of experiments (numerical, field, or laboratory) to coordinate the track geometrical degradation prediction as pointed out by Melo et al. [2].
Figure 11, in turn, illustrates the influence of ITI on MaxVRD curves, which are captured in function of: (1) the ITI in each right rail node itself, (2) the ITI of the right rail neighbour nodes, and (3) the ITI in each node and neighbour nodes of the opposite rail (left rail). Accordingly, it shows numerically a clear effect of the ITI on MaxVRD, and consequently, on VLL, based on the a (n)VLL coefficients of the right rail (smooth track: 33,310 and uneven track: 38,160). It can also be observed that “a nVLL” coefficients for roughness track are different in each node on the top of rail along the segment of study depending on: (1) the sleeper number position, (2) the initial node irregularity on the top of rail, and (3) the overlapped effect caused by the dynamic forces applied on adjacent sleepers. These effects are attested by Naeimi et al. [35], particularly when the severity of the roughness increases. However, as mentioned above, earlier studies have not calculated the effect of ITI on VLL, which indicates that the new findings can be valuable for track engineers to estimate properly how much a ballasted railway track geometry degrades over time under dynamic cyclic loadings. Table 3 describes a summary of “a nVLL” coefficients for a typical heavy-haul railway operating under 30 tons axle load and 60 km/h train velocity, and two different sets of ITI. It indicates that the set of ITI with the highest SD of VP (uneven track 2 – UT-2) degrades faster (37% on average) than that with the lowest SD (uneven track 1 – UT-1). The exception is sleeper number 11 on the top left rail of the UT-2 (SD = 3.23 mm), which decreases 2.51%. This exceptionality may be explained by the low VP deviation between the left and the right rails on that sleeper reducing significantly the wheel–rail contact force on it as also pointed out by Berawi [32].
Eqs. (2.3) and (2.4) combined with Table 3 permit to calculate the VLL considering the effect of ITI in each node on the top of both left and right rails above the sleepers in the segment of study. From 100 to 3 million cycles, it is possible to predict the VP of each rail along the segment. Figures 12 and 13 illustrate the behaviour of the VLL from its initial stage (ITI by RC, N = 0) to 3 million cycles (approximately 60 MGT in a typical heavy-haul railway) for both low SD of ITI (SD = 0.48 mm) and medium SD of ITI (SD = 3.23 mm). It is observed clearly that the influence of ITI on track geometrical vertical levelling degrades on each rail. An examination of data of rail track roughness calculated over 3 million cycles shows that the SD of VPs increases with the passage of traffic from 0.59 and 0.38 mm at N = 0 (initial stage) to 1.35 and 1.19 mm at 3 million cycles, respectively, for the left and right rails of UT-1 (SD = 0.48 mm) in Figure 11. Our results resonate with the findings by Hawari and Murray [28]. The same behaviour is observed for the UT-2 (SD = 3.23 mm) in Figure 13.
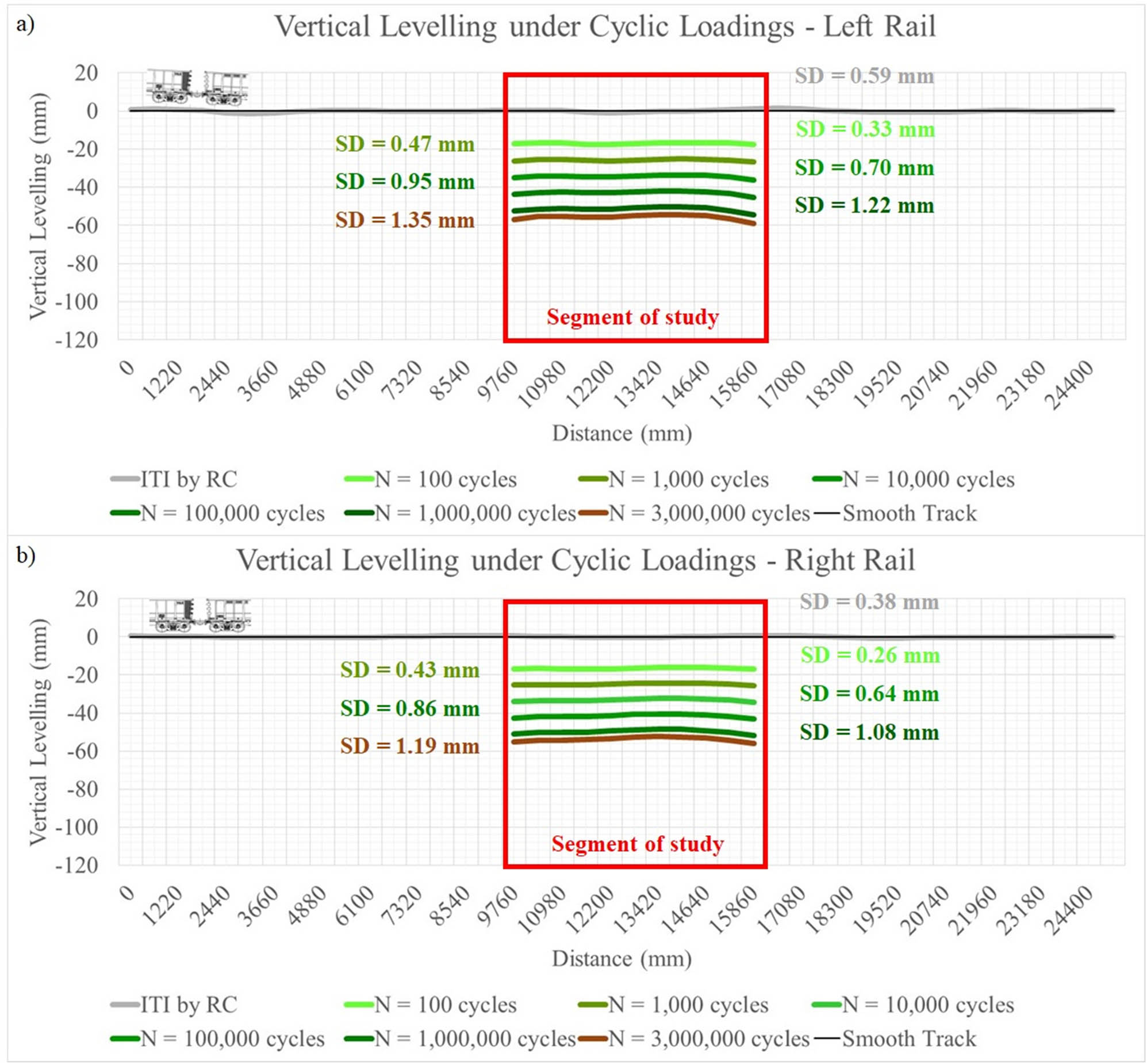
Track geometrical vertical levelling degradation stages for ITI SD of 0.48 mm (UT-1). Note: (a) VLL for the left rail, and (b) VLL for the right rail.
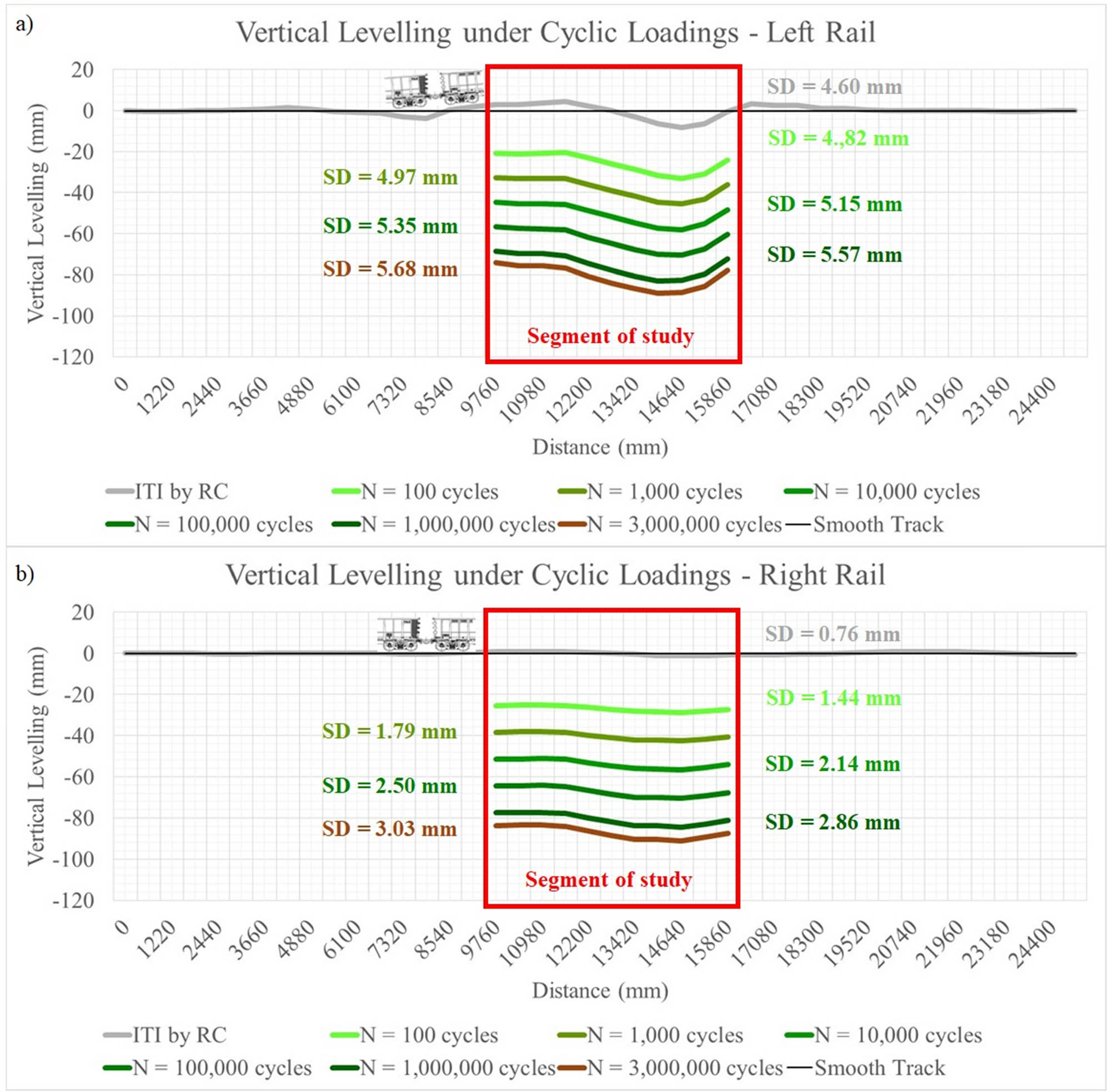
Track geometrical vertical levelling degradation stages for ITI SD of 3.23 mm (UT-2). Note: (a) VLL for the left rail, and (b) VLL for the right rail.
On the other hand, the SD of left rail VP for the UT-1 (SD = 0.48 mm), e.g. increases from 0.59 mm at N = 0 (initial stage) to 1.35 mm at 3 million cycles (approximately 2.2 times) in Figure 12, whereas in Figure 13, the same left rail for the UT-2 (SD = 3.23 mm) rises from 4.60 mm at N = 0 (initial stage) to 5.68 mm at 3 million cycles (∼1.2 times), which indicates that a low SD of ITI does not necessarily mean that over time after millions of cyclic loadings, a track geometrical vertical levelling degradation occurs slower than in a medium SD of ITI track. This is different from a commonly held view that the higher is the SD of ITI, the higher is the rate of increase of roughness with time.
The observed trends suggest that the relationship between track roughness and rate of deterioration of roughness depends on the SD of ITI configuration. For example, in the case of both rails (right and left) presenting a similar partner of SD of ITI (low, medium, or high on both rails), over time and under cyclic loadings, the roughness increases relatively more than that presenting a different partner. It occurs mainly due to the balanced contact force occurring on both rails, and the non-resistance offered by each rail. On the other hand, in the SD of ITI configuration where one rail (e.g. right rail) presents a low SD of ITI and another one (e.g. left rail) presents a medium or high SD of ITI, the rate of deterioration of roughness is less affected as there is a unbalanced impact force, and the right rail with low SD of ITI withstands the effect of contact force caused by the left rail.
In order to extend the investigation of the influence of ITI on VLL, different axel loads and train velocities, and those two sets of ITI are applied on FEM under similar track and vehicle parameters as the previous simulation. Figure 14 shows the comparisons of SD for full track (including both left and right rails in the segment of study) at N = 0 (ITI by RC), N = 100,000, N = 1 million, and N = 3 million cycles for 20, 30, and 40 ton axle loads and 60, 70, and 80 km/h train velocities.
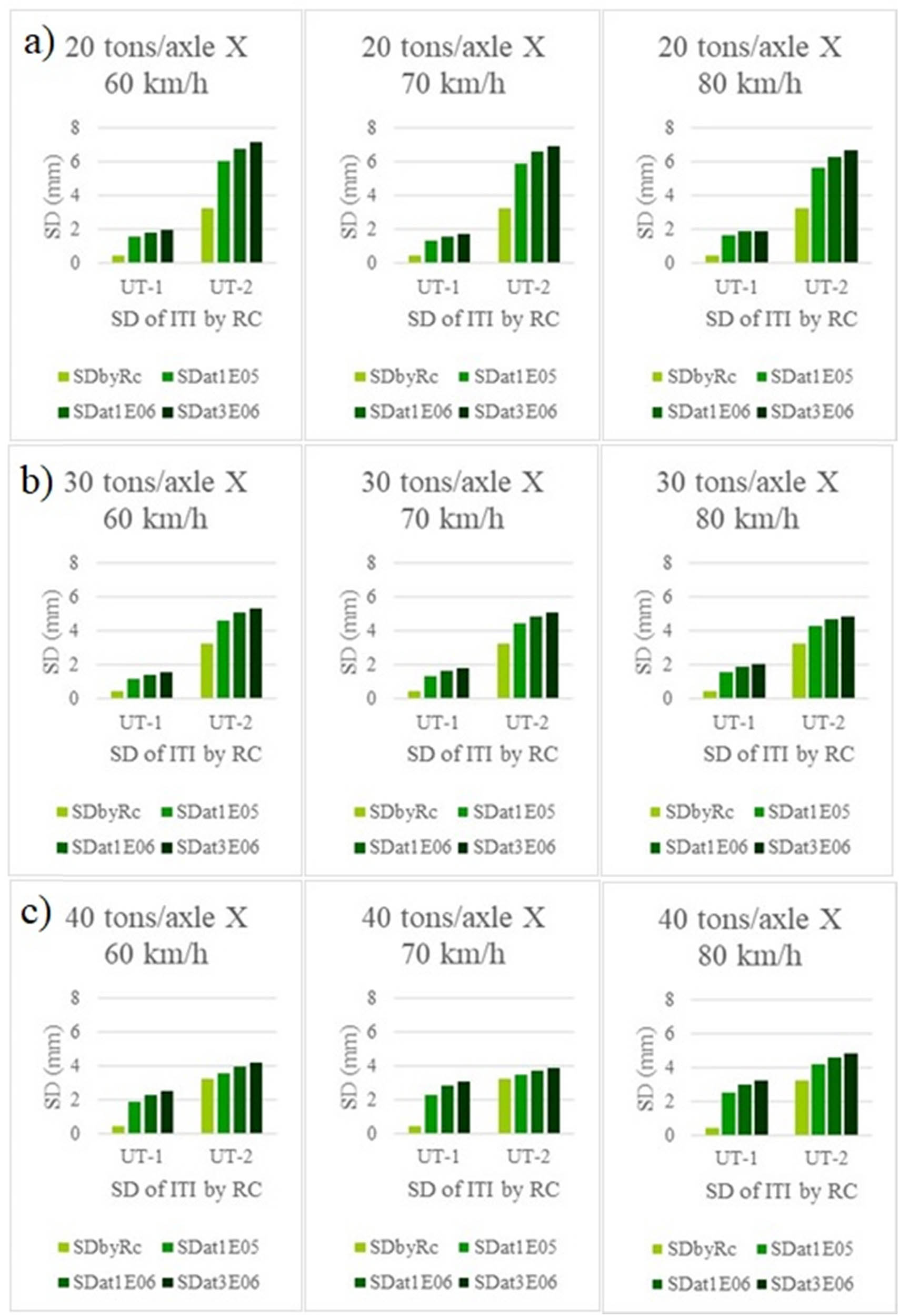
The comparisons of SD of VP for full track (including both left and right rails in the segment of study) at N = 0 (ITI by RC), N = 100,000, 1 million, and 3 million cycles for 20, 30, and 40 tons/axle, and 60, 70, and 80 km/h train velocity.
For a ballasted railway track dominated by 20 ton (a light railway), 30 ton (a typical heavy-haul railway), or 40 ton (an extreme heavy-haul railway) axle loads, both evolutions of SD of VL indicate undoubtedly that the ITI influences the behaviour of VLL. The worst SD of VL escalation scenery occurs at UT-2 for 20 ton axle load and 60 km/h train velocity, in which the SD of VL increases from 3.23 mm at N = 0, ITI, to approximately 7.2 mm at 3 million cycles. It reflects the natural frequency of the ballasted railway track that is influenced not only by both the 20 ton axle load and 60 km/h train velocity but also by the track configuration (ITI). For that same 20 ton axle load, the data in Figure 14 also suggest that a train running at 80 km/h is the best operational configuration for the UT-2 (SD of VL fluctuates from 3.23 mm at N = 0, ITI, to ∼6.7 mm at 3 million cycles) in terms of minimizing the track geometrical degradation. Whereas, for the UT-1, 70 km/h train velocity is the best option (SD of VL increases from 0.48 mm at N = 0, ITI, to ∼1.7 mm at 3 million cycles). These findings are new and can better explain the effect of ITI on VLL than previous investigations. Accordingly, if the axle load increases to 30 tons, an appropriate operational configuration to minimize the escalation of SD of VL at 3 million cycles should be that in which the train runs at 60 km/h at the UT-1 (from 0.48 mm at N = 0, ITI, to ∼1.6 mm). In fact, this configuration is the best one in Figure 14, and it has intuitively been adopted by some heavy-haul railway companies as described above.
On the other hand, if the axle load increases to 40 tons, the effect of ITI on the SD of VP over time increases less than those related to 20 and 30 ton axle load for either UT-2 at 60 km/h train velocity (from 3.23 mm at N = 0, ITI, to ∼4.2 mm) or UT-2 at 70 km/h train velocity (from 3.23 mm at N = 0, ITI, to ∼3.9 mm) at 3 million cycles. However, as it can be observed in Figure 14, one of the best operational configurations for 40 ton axle load is to run the train at 60 km/h at a ballasted railway track similar to UT-1, in which the SD of VL fluctuates from 0.48 mm at N = 0, ITI, to ∼2.5 mm at 3 million cycles. In turn, if the railway company plans to increase the train velocity to 70 km/h, they should run the train on an uneven track with the same ITI characteristics of UT-1. In this case, the SD of VL increases from 0.48 mm at N = 0, ITI, to ∼3,1 mm at 3 million cycles, which indicates a reduction in track geometrical degradation rate. Despite this indicating that the axle load and train velocity influence substantially the VLL, the ITI plays an important role to accelerate it. Other train characteristics can also affect the track geometrical VL degradation such as vehicle suspension stiffness, wheel damping/wheel diameter, and wheel roughness. The wheel defects can be presented as wheel roughness, which can be input on the model of this study and be applied in addition to track roughness [50,51]; however, they have not been discussed in this study. Nevertheless, it is important to highlight that if the ITI increases, the response changes and it can influence considerably the VLL.
As ITI is usually found in all railway track post-construction or maintenance activities around the world, an acceptable SD of ITI can be defined for a minimum effect on VLL (thresholds). Therefore, these new findings are important not only to prove some rationality adopted by the decision-making of railway infrastructure managers but also to support the development of maintenance guidelines by the track engineers. One concrete example related to the mentioned rationality is that the findings can support the decision-makers to simulate different sceneries of SD of ITI configurations. These sceneries can assist the infrastructure managers in predicting the track geometrical degradation, particularly in this study the VLL. A second example, this in reference to the development of maintenance guidelines, can be explored by applying the findings to support the track engineering to define tolerances, thresholds, ranges, and SD of ITI configurations for track maintenance operational standard (post-construction and maintenance activities) to prolong the railway track service life.
4 Conclusion
This research presents new insights into the effect of ITI on a ballasted railway track geometrical degradation, particularly in post-construction or maintenance activities. To investigate this phenomenon, a robust numerical-analytical study has been developed and rigorously validated focusing on the track geometrical VLL under cyclic loadings.
For a roughness track, the research not only suggests that there is a clear response of ITI on VLL as described in previous studies, but also innovatively proposes how to numerically capture that effect. For the railway tracks dominated by different axle loads and train velocities, regardless of SD of ITI, the ITI undoubtedly negatively influences the behaviour of VLL, which reflects the natural frequency of the ballasted railway track. The new findings can be useful for track engineers to predict track geometrical degradation over time under dynamic cyclic loadings.
The research also identifies the worst and the best sceneries of the VP SD evolution in the railway track segment of the study. The worst one is related to the operational configuration of a train running at 60 km/h and carrying a load of 20 tons/axle in an uneven track whose SD of VP evolves from 3.23 mm at N = 0 (ITI) to 7.2 mm, whereas the best scenery corresponds that in which a train runs at 60 km/h transporting a load of 30 tons/axle in an uneven track whose SD of VP downgrades from 0.48 mm at N = 0 (ITI) to 1.5 mm, both sceneries at 3 million cycles. The best scenery has currently been adopted by some heavy-haul railway companies around the world.
Even though the insights demonstrate that the axle load and train velocity effects are evident, the ITI condition plays an important role to accelerate further the track geometrical VLL. As the ITI is usually found in all railway track after maintenance activities (there is no smooth track in an actual railway system), an acceptable configuration for it can be defined for a minimum effect on VLL (thresholds). Therefore, given that this novel improved method can accurately predict numerically the effect of ITI on the track geometrical VLL considering different railway operational conditions and configurations, their findings contribute to obtain new insights into track geometrical degradation, and enhance the development of new practical maintenance and construction guidelines to support the maintenance activities in a ballasted railway track.
Acknowledgements
The first author gratefully appreciates the support Brazilian National Council for Scientific and Technological Development (CNPq), Brazil, Project No. 200359/2018-5, for his Ph.D. scholarship. We are sincerely grateful to the European Commission for the financial sponsorship of the H2020-RISE Project No. 691135 “RISEN: Rail Infrastructure Systems Engineering Network,” which enables a global research network that tackles the grand challenge of railway infrastructure resilience and advanced sensing in extreme environments [52]. The APC is kindly sponsored by the University of Birmingham Library’s Open Access Fund.
-
Funding information: The research has been kindly sponsored by Brazilian National Council for Scientific and Technological Development (CNPq), Brazil, Project No. 200359/2018-5, by the European Commission for H2020-RISE Project No. 691135 (RISEN). The APC is kindly sponsored by the University of Birmingham Library s Open Access Fund.
-
Author contributions: Conceptualization: A.L.O.M., S.K., T.L., and K.G.; data curation: A.L.O.M., T.L., and K.G.; formal analysis: A.L.O.M. and S.K.; investigation, A.L.O.M., S.K. T.L., and K.G.; methodology: A.L.O.M. and S.K.; project administration: S.K.; resources: S.K.; supervision: S.K.; validation: A.L.O.M., T.L., and K.G; visualization: A.L.O.M; writing – original draft: A.L.O.M.; writing – review and editing: A.L.O.M and S.K. All authors have read and agreed to the published version of the manuscript.
-
Conflict of interest: The authors declare that there are no potential conflicts of interest with respect to this study.
-
Data availability statement: Data available upon reasonable request to the corresponding author.
References
[1] Guo Y, Zahi W. Long-term prediction of track geometry degradation in high-speed vehicle-ballastless track system due to differential subgrade settlement. Soil Dyn Earth Eng. 2018;113:1–11.Suche in Google Scholar
[2] Melo ALO, de Kaewunruen S, Papaelias M, Li T. A novel hybrid method for predicting vertical levelling loss of railway track geometry under dynamic cyclic loadings. Int J Struct Stab Dyn. 2022;22(14):2250162.10.1142/S0219455422501620Suche in Google Scholar
[3] Nielsen JCO, Li X. Railway track geometry degradation due to differential settlement of ballast/subgrade – Numerical prediction by an iterative procedure. J Sound Vib. 2018;412:441–56.10.1016/j.jsv.2017.10.005Suche in Google Scholar
[4] Plenge M, Lammering R. The dynamic of railways track and subgrade with respect to deteriorated sleeper support. In: Popp K, Schiehlen W, editors. System dynamics and long-term behaviour of railway vehicles, track and subgrade, Lecture notes in applied mechanics. Vol. 6. Berlin: Springer; 2003. p. 295–314.10.1007/978-3-540-45476-2_18Suche in Google Scholar
[5] Dahlberg T. Track issues. In: Iwnicki S, editor. Handbook of railway vehicle dynamics. Boca Rotan: Taylor and Francis; 2006. p. 143–79.10.1201/9780849333217.ch6Suche in Google Scholar
[6] Selig ET, Waters JM. Track geotechnology and substructure management. London: Thomas Telford; 1994. p. 8.51–4.10.1680/tgasm.20139Suche in Google Scholar
[7] Nguyen K, Villalmanzo DI, Goicolea JM, Gabaldon F. A computational procedure for prediction of ballasted track profile degradation under railway traffic loading. J Rail Rapid Transit. 2016;230(8):1812–27.10.1177/0954409715615374Suche in Google Scholar
[8] Sol-Sánchez Pirozzolo ML, Moreno-Navarro F, Rubio-Gámez MC. A study into the mechanical performance of different configurations for the railway track section: A laboratory approach. Eng Struct. 2016;119:13–23.10.1016/j.engstruct.2016.04.008Suche in Google Scholar
[9] Indraratna B, Salim W, Rujikiatkamjorn C. Advanced rail geotechnology – Ballast track. Boca Rotan: CRC Press; 2018. p. 143–61.Suche in Google Scholar
[10] BS-EN-1348-1. Railway applications — Track — Track geometry quality — Part 1: Characterization of track geometry. London: BSI Standards Publication; 2019.Suche in Google Scholar
[11] Esveld C. Modern railway track. 2nd edn. Zaltbommel: MRT-Productions; 2001.Suche in Google Scholar
[12] Adeagbo MO, Lam HF, Ni YQ. A Bayesian methodology for detection of railway ballast damage using the modified Ludwik nonlinear model. Eng Struct. 2021;236:112047.10.1016/j.engstruct.2021.112047Suche in Google Scholar
[13] Kempfertm HG, Hu Y. Measured dynamic loading of railway underground. Proc. 11th Pan-American Conf. Soil Mechanics and Geotechnical Engineering. Foz do Iguacu, Brazil; 8–12 Nov 1999. p. 843–7.Suche in Google Scholar
[14] Kaewunruen S, Ngamkhanong C, Lim CH. Damage and failure modes of railway prestressed concrete sleepers with holes/web openings subject to impact loading conditions. Eng Struct. 2018;176:840–8.10.1016/j.engstruct.2018.09.057Suche in Google Scholar
[15] Kaewunruen S, Ngamkhanong C. Effects of under sleeper pads on dynamic responses of railway prestressed concrete sleepers subjected to high intensity impact loads. Eng Struct. 2020;214:110604.10.1016/j.engstruct.2020.110604Suche in Google Scholar
[16] Sun Q. An elasto-plastic strain-based approach for analysing the behaviour of ballasted rail track. PhD thesis. Wollongong, Australia: University of Wollongong; 2015.Suche in Google Scholar
[17] Kaewunruen S, Ngamkhanong C, Ng J. Influence of time-dependent material degradation on life cycle serviceability of interspersed railway tracks due to moving train loads. Eng Struct. 2019;199:109625.10.1016/j.engstruct.2019.109625Suche in Google Scholar
[18] Sadeghi J, Seyedkazemi M, Khajehdezfuly A. Nonlinear simulation of vertical behavior of railway fastening system. Eng Struct. 2020;209:110340.10.1016/j.engstruct.2020.110340Suche in Google Scholar
[19] Melo ALO, Kaewunruen S, Papaelias M, Bernucci LLB, Motta R. Methods to monitor and evaluate the deterioration of track and its components in a railway in-service: a systemic review. Front Built Environ. 2020;6:00118.10.3389/fbuil.2020.00118Suche in Google Scholar
[20] Abadi T, Le Pen L, Zervos A, Powrie W. A review and evaluation of ballast settlement models using results from the Southampton Railway Testing Facility (SRTF). Proceedings of the 3rd International Conference on Transportation Geotechnics (ICTG 2016). Vol. 143. 2016. p. 999–1006. Advances in Transportation Geotechnics 3. Procedia Engineering.10.1016/j.proeng.2016.06.089Suche in Google Scholar
[21] Thom NH, Oakley J. Predicting differential settlement in a railway trackbed. Proceedings of Railway Foundation – RailFound 06, 4–8. Birmingham, UK; September 2006. p. 190–200.Suche in Google Scholar
[22] Dahlberg T. Some railroad settlement models: a critical review. Proc IMechE. Part F: J Rail Rapid Transit. 2001;233(1):289–300.10.1243/0954409011531585Suche in Google Scholar
[23] Grossoni I, Andrade AR, Bezin Y, Neves S. The role of track stiffness and its spatial variability on long-term track quality deterioration. Proc IMechE, Part F: J Rail Rapid Transit. 2019;215(4):16–32.10.1177/0954409718777372Suche in Google Scholar
[24] Partington W. TM-TS-097: Track deterioration study – Results of the track laboratory experiments. Derby, UK: British Railway Research; 1979.Suche in Google Scholar
[25] Suiker ASJ, Borst R. A numerical model for the cyclic deterioration of railway tracks. Int J Numer Met Eng. 2003;57:441–70.10.1002/nme.683Suche in Google Scholar
[26] Augustin S, Gudehus G, Huber G, Schünemann A. Numerical model and laboratory tests on settlement of ballast track. In: Popp K, Schiehlen W, editor. System dynamics and long-term behaviour of railway vehicles, track and subgrade, Lecture notes in applied mechanics. Vol. 6. Berlin: Springer; 2003. p. 317–36.10.1007/978-3-540-45476-2_19Suche in Google Scholar
[27] Takemiya H, Bian X. Substructure simulation of inhomogeneous track and layered ground dynamic interaction under train passage. J Eng Mech. 2005;131(7):699–711.10.1061/(ASCE)0733-9399(2005)131:7(699)Suche in Google Scholar
[28] Hawari HM, Murray MH. Deterioration of railway track on heavy haul lines. Proceedings of Conference on Railway Engineering (CORE 2008), Rail – the CORE of Integrated Transports. Perth, Australia; September 2008. p. 273–279.Suche in Google Scholar
[29] Chang H, Liu R, Li Q. A multi-stage linear prediction model for the irregularity of the longitudinal level over unit railway sections. Comput Railw XII WIT Trans Built Environ. 2010;114:641–50.10.2495/CR100591Suche in Google Scholar
[30] Faiz RB. An empirical rail track degradation model based on predictive analysis of rail profile and track geometry. PhD thesis. Loughborough, UK: Loughborough University; 2010.Suche in Google Scholar
[31] Choi IIY, Um JH, Lee JS, Choi HH. The influence of track irregularities on the running behavior of high-speed trains. Proc IMechE Part F: J Rail Rapid Transit. 2012;227(1):94–102.10.1177/0954409712455146Suche in Google Scholar
[32] Berawi ARB. Improving railway track maintenance using power spectral density (PSD). PhD thesis. Porto, Portugal: University of Porto; 2013.Suche in Google Scholar
[33] Guler H. Prediction of railway track geometry deterioration using artificial neural networks: a case study for Turkish state railways. Struct Infra Eng. 2014;10(5):614–26.10.1080/15732479.2012.757791Suche in Google Scholar
[34] Choi J. Qualitative analysis for dynamic behavior of railway ballasted track. PhD thesis. Berlin, Germany: Berlin Institute of Technology; 2014.Suche in Google Scholar
[35] Naeimi M, Zakeri JA, Esmaeili M, Mehrali M. Dynamic response of sleepers in a track with uneven rail irregularities using a 3D vehicle–track model with sleeper beams. Arch Appl Mech. 2015;85:1679–99.10.1007/s00419-015-1012-9Suche in Google Scholar
[36] Shen J, Xu Y, Li H, He Q, Lu Y. Analysis of effect parameters of track settlement in heavy haul railways. Fifth International Conference on Transportation Engineering (ICTE 2015). Dailan, China; 26–27 September 2015. p. 99–105.10.1061/9780784479384.014Suche in Google Scholar
[37] Soleimanmeigouni I, Xiao X, Ahmadi A, Xie M, Nissen A, Kumar U. Modelling the evolution of ballasted railway track geometry by a two-level piecewise model. Struct Infra Eng. 2017;14(1):33–45.10.1080/15732479.2017.1326946Suche in Google Scholar
[38] Guo Y, Zhai W. Long-term prediction of track geometry degradation in high-speed vehicle–ballastless track system due to differential subgrade settlement. Soil Dyn Earthq Eng. 2018;113:1–11.10.1016/j.soildyn.2018.05.024Suche in Google Scholar
[39] De Miguel A, Lau A, Santos I. Numerical simulation of track settlements based on an iterative holistic approach. J Braz Soc Mech Sci Eng. 2018;40(8):381.10.1007/s40430-018-1300-8Suche in Google Scholar
[40] Soleimanmeigouni I, Ahmadi A, Nissen A, Xiao X. Prediction of railway track geometry defects: a case study. Struct Infra Eng. 2020;16(7):987–1001.10.1080/15732479.2019.1679193Suche in Google Scholar
[41] Bednarek WA. Full-scale field experimental investigation on the intended irregularity of CWR track in vertical plane. Energies. 2021;14(22):7477.10.3390/en14227477Suche in Google Scholar
[42] Grossoni I, Powrie W, Zervos A, Bezin Y, Le Pen L. Modelling railway ballasted track settlement in vehicle-track interaction analysis. Transp Geotech, 2021;26:100433.10.1016/j.trgeo.2020.100433Suche in Google Scholar
[43] Kosukegawa K, Mori Y, Suyari H, Kawamoto K. Spatiotemporal forecasting of vertical track alignment with exogenous factors. Sci Rep. 2023;12:2354.10.1038/s41598-023-29303-7Suche in Google Scholar PubMed PubMed Central
[44] Li D, Hyslip J, Sussmann T, Chrismer S. Railway geotechnics. Florida, USA: CRC Press; 2016.10.1201/b18982Suche in Google Scholar
[45] LS-Dyna. LS-DYNA® keywords user’s manual. Vol. 1. Livermore, USA: Livermore Software Technology Corporation (LSTC); 2014.Suche in Google Scholar
[46] LS-Dyna. LS-DYNA® theory manual. Livermore, USA: Livermore Software Technology Corporation (LSTC); 2019.Suche in Google Scholar
[47] Xu L, Lu T. Influence of the finite element type of the sleeper on vehicle-track interaction: a numerical study. Veh Syst Dyn. 2021;59(10):1533–56.10.1080/00423114.2020.1769847Suche in Google Scholar
[48] Gadhave R, Vyas NS. Rail-wheel contact forces and track irregularity estimation from on-board accelerometer data. Veh Syst Dyn. 2022;60(6):2145–66.10.1080/00423114.2021.1899253Suche in Google Scholar
[49] ERRI-B176. Benchmark problem – results and assessment. B176/DT290. Utrecht: International Union of Railway (UIC); 1993.Suche in Google Scholar
[50] Luczak B, Firlik B, Staskievwicz T, Sumelka W. Numerical algorithm for predicting wheel flange war in trams – Validation in a curved track. Proc IMechE Part F: J Rail Rapid Transit. 2020;234(10):1156–69.10.1177/0954409719882807Suche in Google Scholar
[51] Remennikov AM, Kaewunruen S. Determination of dynamic properties of rail pads using an instrumented hammer impact technique. Acoust Aus. 2005;33(2):63–7.Suche in Google Scholar
[52] Kaewunruen S, Sussman JM, Matsumoto A Grand challenges in transportation and transit systems. Front Built Environ. 2016;2:4.10.3389/fbuil.2016.00004Suche in Google Scholar
© 2024 the author(s), published by De Gruyter
This work is licensed under the Creative Commons Attribution 4.0 International License.
Artikel in diesem Heft
- Editorial
- Focus on NLENG 2023 Volume 12 Issue 1
- Research Articles
- Seismic vulnerability signal analysis of low tower cable-stayed bridges method based on convolutional attention network
- Robust passivity-based nonlinear controller design for bilateral teleoperation system under variable time delay and variable load disturbance
- A physically consistent AI-based SPH emulator for computational fluid dynamics
- Asymmetrical novel hyperchaotic system with two exponential functions and an application to image encryption
- A novel framework for effective structural vulnerability assessment of tubular structures using machine learning algorithms (GA and ANN) for hybrid simulations
- Flow and irreversible mechanism of pure and hybridized non-Newtonian nanofluids through elastic surfaces with melting effects
- Stability analysis of the corruption dynamics under fractional-order interventions
- Solutions of certain initial-boundary value problems via a new extended Laplace transform
- Numerical solution of two-dimensional fractional differential equations using Laplace transform with residual power series method
- Fractional-order lead networks to avoid limit cycle in control loops with dead zone and plant servo system
- Modeling anomalous transport in fractal porous media: A study of fractional diffusion PDEs using numerical method
- Analysis of nonlinear dynamics of RC slabs under blast loads: A hybrid machine learning approach
- On theoretical and numerical analysis of fractal--fractional non-linear hybrid differential equations
- Traveling wave solutions, numerical solutions, and stability analysis of the (2+1) conformal time-fractional generalized q-deformed sinh-Gordon equation
- Influence of damage on large displacement buckling analysis of beams
- Approximate numerical procedures for the Navier–Stokes system through the generalized method of lines
- Mathematical analysis of a combustible viscoelastic material in a cylindrical channel taking into account induced electric field: A spectral approach
- A new operational matrix method to solve nonlinear fractional differential equations
- New solutions for the generalized q-deformed wave equation with q-translation symmetry
- Optimize the corrosion behaviour and mechanical properties of AISI 316 stainless steel under heat treatment and previous cold working
- Soliton dynamics of the KdV–mKdV equation using three distinct exact methods in nonlinear phenomena
- Investigation of the lubrication performance of a marine diesel engine crankshaft using a thermo-electrohydrodynamic model
- Modeling credit risk with mixed fractional Brownian motion: An application to barrier options
- Method of feature extraction of abnormal communication signal in network based on nonlinear technology
- An innovative binocular vision-based method for displacement measurement in membrane structures
- An analysis of exponential kernel fractional difference operator for delta positivity
- Novel analytic solutions of strain wave model in micro-structured solids
- Conditions for the existence of soliton solutions: An analysis of coefficients in the generalized Wu–Zhang system and generalized Sawada–Kotera model
- Scale-3 Haar wavelet-based method of fractal-fractional differential equations with power law kernel and exponential decay kernel
- Non-linear influences of track dynamic irregularities on vertical levelling loss of heavy-haul railway track geometry under cyclic loadings
- Fast analysis approach for instability problems of thin shells utilizing ANNs and a Bayesian regularization back-propagation algorithm
- Validity and error analysis of calculating matrix exponential function and vector product
- Optimizing execution time and cost while scheduling scientific workflow in edge data center with fault tolerance awareness
- Estimating the dynamics of the drinking epidemic model with control interventions: A sensitivity analysis
- Online and offline physical education quality assessment based on mobile edge computing
- Discovering optical solutions to a nonlinear Schrödinger equation and its bifurcation and chaos analysis
- New convolved Fibonacci collocation procedure for the Fitzhugh–Nagumo non-linear equation
- Study of weakly nonlinear double-diffusive magneto-convection with throughflow under concentration modulation
- Variable sampling time discrete sliding mode control for a flapping wing micro air vehicle using flapping frequency as the control input
- Error analysis of arbitrarily high-order stepping schemes for fractional integro-differential equations with weakly singular kernels
- Solitary and periodic pattern solutions for time-fractional generalized nonlinear Schrödinger equation
- An unconditionally stable numerical scheme for solving nonlinear Fisher equation
- Effect of modulated boundary on heat and mass transport of Walter-B viscoelastic fluid saturated in porous medium
- Analysis of heat mass transfer in a squeezed Carreau nanofluid flow due to a sensor surface with variable thermal conductivity
- Navigating waves: Advancing ocean dynamics through the nonlinear Schrödinger equation
- Experimental and numerical investigations into torsional-flexural behaviours of railway composite sleepers and bearers
- Novel dynamics of the fractional KFG equation through the unified and unified solver schemes with stability and multistability analysis
- Analysis of the magnetohydrodynamic effects on non-Newtonian fluid flow in an inclined non-uniform channel under long-wavelength, low-Reynolds number conditions
- Convergence analysis of non-matching finite elements for a linear monotone additive Schwarz scheme for semi-linear elliptic problems
- Global well-posedness and exponential decay estimates for semilinear Newell–Whitehead–Segel equation
- Petrov-Galerkin method for small deflections in fourth-order beam equations in civil engineering
- Solution of third-order nonlinear integro-differential equations with parallel computing for intelligent IoT and wireless networks using the Haar wavelet method
- Mathematical modeling and computational analysis of hepatitis B virus transmission using the higher-order Galerkin scheme
- Mathematical model based on nonlinear differential equations and its control algorithm
- Bifurcation and chaos: Unraveling soliton solutions in a couple fractional-order nonlinear evolution equation
- Space–time variable-order carbon nanotube model using modified Atangana–Baleanu–Caputo derivative
- Minimal universal laser network model: Synchronization, extreme events, and multistability
- Valuation of forward start option with mean reverting stock model for uncertain markets
- Geometric nonlinear analysis based on the generalized displacement control method and orthogonal iteration
- Fuzzy neural network with backpropagation for fuzzy quadratic programming problems and portfolio optimization problems
- B-spline curve theory: An overview and applications in real life
- Nonlinearity modeling for online estimation of industrial cooling fan speed subject to model uncertainties and state-dependent measurement noise
- Quantitative analysis and modeling of ride sharing behavior based on internet of vehicles
- Review Article
- Bond performance of recycled coarse aggregate concrete with rebar under freeze–thaw environment: A review
- Retraction
- Retraction of “Convolutional neural network for UAV image processing and navigation in tree plantations based on deep learning”
- Special Issue: Dynamic Engineering and Control Methods for the Nonlinear Systems - Part II
- Improved nonlinear model predictive control with inequality constraints using particle filtering for nonlinear and highly coupled dynamical systems
- Anti-control of Hopf bifurcation for a chaotic system
- Special Issue: Decision and Control in Nonlinear Systems - Part I
- Addressing target loss and actuator saturation in visual servoing of multirotors: A nonrecursive augmented dynamics control approach
- Collaborative control of multi-manipulator systems in intelligent manufacturing based on event-triggered and adaptive strategy
- Greenhouse monitoring system integrating NB-IOT technology and a cloud service framework
- Special Issue: Unleashing the Power of AI and ML in Dynamical System Research
- Computational analysis of the Covid-19 model using the continuous Galerkin–Petrov scheme
- Special Issue: Nonlinear Analysis and Design of Communication Networks for IoT Applications - Part I
- Research on the role of multi-sensor system information fusion in improving hardware control accuracy of intelligent system
- Advanced integration of IoT and AI algorithms for comprehensive smart meter data analysis in smart grids
Artikel in diesem Heft
- Editorial
- Focus on NLENG 2023 Volume 12 Issue 1
- Research Articles
- Seismic vulnerability signal analysis of low tower cable-stayed bridges method based on convolutional attention network
- Robust passivity-based nonlinear controller design for bilateral teleoperation system under variable time delay and variable load disturbance
- A physically consistent AI-based SPH emulator for computational fluid dynamics
- Asymmetrical novel hyperchaotic system with two exponential functions and an application to image encryption
- A novel framework for effective structural vulnerability assessment of tubular structures using machine learning algorithms (GA and ANN) for hybrid simulations
- Flow and irreversible mechanism of pure and hybridized non-Newtonian nanofluids through elastic surfaces with melting effects
- Stability analysis of the corruption dynamics under fractional-order interventions
- Solutions of certain initial-boundary value problems via a new extended Laplace transform
- Numerical solution of two-dimensional fractional differential equations using Laplace transform with residual power series method
- Fractional-order lead networks to avoid limit cycle in control loops with dead zone and plant servo system
- Modeling anomalous transport in fractal porous media: A study of fractional diffusion PDEs using numerical method
- Analysis of nonlinear dynamics of RC slabs under blast loads: A hybrid machine learning approach
- On theoretical and numerical analysis of fractal--fractional non-linear hybrid differential equations
- Traveling wave solutions, numerical solutions, and stability analysis of the (2+1) conformal time-fractional generalized q-deformed sinh-Gordon equation
- Influence of damage on large displacement buckling analysis of beams
- Approximate numerical procedures for the Navier–Stokes system through the generalized method of lines
- Mathematical analysis of a combustible viscoelastic material in a cylindrical channel taking into account induced electric field: A spectral approach
- A new operational matrix method to solve nonlinear fractional differential equations
- New solutions for the generalized q-deformed wave equation with q-translation symmetry
- Optimize the corrosion behaviour and mechanical properties of AISI 316 stainless steel under heat treatment and previous cold working
- Soliton dynamics of the KdV–mKdV equation using three distinct exact methods in nonlinear phenomena
- Investigation of the lubrication performance of a marine diesel engine crankshaft using a thermo-electrohydrodynamic model
- Modeling credit risk with mixed fractional Brownian motion: An application to barrier options
- Method of feature extraction of abnormal communication signal in network based on nonlinear technology
- An innovative binocular vision-based method for displacement measurement in membrane structures
- An analysis of exponential kernel fractional difference operator for delta positivity
- Novel analytic solutions of strain wave model in micro-structured solids
- Conditions for the existence of soliton solutions: An analysis of coefficients in the generalized Wu–Zhang system and generalized Sawada–Kotera model
- Scale-3 Haar wavelet-based method of fractal-fractional differential equations with power law kernel and exponential decay kernel
- Non-linear influences of track dynamic irregularities on vertical levelling loss of heavy-haul railway track geometry under cyclic loadings
- Fast analysis approach for instability problems of thin shells utilizing ANNs and a Bayesian regularization back-propagation algorithm
- Validity and error analysis of calculating matrix exponential function and vector product
- Optimizing execution time and cost while scheduling scientific workflow in edge data center with fault tolerance awareness
- Estimating the dynamics of the drinking epidemic model with control interventions: A sensitivity analysis
- Online and offline physical education quality assessment based on mobile edge computing
- Discovering optical solutions to a nonlinear Schrödinger equation and its bifurcation and chaos analysis
- New convolved Fibonacci collocation procedure for the Fitzhugh–Nagumo non-linear equation
- Study of weakly nonlinear double-diffusive magneto-convection with throughflow under concentration modulation
- Variable sampling time discrete sliding mode control for a flapping wing micro air vehicle using flapping frequency as the control input
- Error analysis of arbitrarily high-order stepping schemes for fractional integro-differential equations with weakly singular kernels
- Solitary and periodic pattern solutions for time-fractional generalized nonlinear Schrödinger equation
- An unconditionally stable numerical scheme for solving nonlinear Fisher equation
- Effect of modulated boundary on heat and mass transport of Walter-B viscoelastic fluid saturated in porous medium
- Analysis of heat mass transfer in a squeezed Carreau nanofluid flow due to a sensor surface with variable thermal conductivity
- Navigating waves: Advancing ocean dynamics through the nonlinear Schrödinger equation
- Experimental and numerical investigations into torsional-flexural behaviours of railway composite sleepers and bearers
- Novel dynamics of the fractional KFG equation through the unified and unified solver schemes with stability and multistability analysis
- Analysis of the magnetohydrodynamic effects on non-Newtonian fluid flow in an inclined non-uniform channel under long-wavelength, low-Reynolds number conditions
- Convergence analysis of non-matching finite elements for a linear monotone additive Schwarz scheme for semi-linear elliptic problems
- Global well-posedness and exponential decay estimates for semilinear Newell–Whitehead–Segel equation
- Petrov-Galerkin method for small deflections in fourth-order beam equations in civil engineering
- Solution of third-order nonlinear integro-differential equations with parallel computing for intelligent IoT and wireless networks using the Haar wavelet method
- Mathematical modeling and computational analysis of hepatitis B virus transmission using the higher-order Galerkin scheme
- Mathematical model based on nonlinear differential equations and its control algorithm
- Bifurcation and chaos: Unraveling soliton solutions in a couple fractional-order nonlinear evolution equation
- Space–time variable-order carbon nanotube model using modified Atangana–Baleanu–Caputo derivative
- Minimal universal laser network model: Synchronization, extreme events, and multistability
- Valuation of forward start option with mean reverting stock model for uncertain markets
- Geometric nonlinear analysis based on the generalized displacement control method and orthogonal iteration
- Fuzzy neural network with backpropagation for fuzzy quadratic programming problems and portfolio optimization problems
- B-spline curve theory: An overview and applications in real life
- Nonlinearity modeling for online estimation of industrial cooling fan speed subject to model uncertainties and state-dependent measurement noise
- Quantitative analysis and modeling of ride sharing behavior based on internet of vehicles
- Review Article
- Bond performance of recycled coarse aggregate concrete with rebar under freeze–thaw environment: A review
- Retraction
- Retraction of “Convolutional neural network for UAV image processing and navigation in tree plantations based on deep learning”
- Special Issue: Dynamic Engineering and Control Methods for the Nonlinear Systems - Part II
- Improved nonlinear model predictive control with inequality constraints using particle filtering for nonlinear and highly coupled dynamical systems
- Anti-control of Hopf bifurcation for a chaotic system
- Special Issue: Decision and Control in Nonlinear Systems - Part I
- Addressing target loss and actuator saturation in visual servoing of multirotors: A nonrecursive augmented dynamics control approach
- Collaborative control of multi-manipulator systems in intelligent manufacturing based on event-triggered and adaptive strategy
- Greenhouse monitoring system integrating NB-IOT technology and a cloud service framework
- Special Issue: Unleashing the Power of AI and ML in Dynamical System Research
- Computational analysis of the Covid-19 model using the continuous Galerkin–Petrov scheme
- Special Issue: Nonlinear Analysis and Design of Communication Networks for IoT Applications - Part I
- Research on the role of multi-sensor system information fusion in improving hardware control accuracy of intelligent system
- Advanced integration of IoT and AI algorithms for comprehensive smart meter data analysis in smart grids


