Abstract
The study aspires to adopt back propagation fuzzy neural networks to solve fuzzy quadratic programming problems. The main motivation behind proposing a back propagation neural network is that it can easily adjust and fine-tune the weights of the network from the error rate obtained at the previous layer. The error rate customarily called the loss function is the dissimilarity between the desired and predicted outputs. The chain and power rules of the derivative allow back propagation and successively update the weights of the network to perform efficiently. Thus, the gradient of the loss function is calculated by iterating backward layer by layer but one at a time to reduce the difference between the desired and the predicted outputs. The research flow is such that first of all the quadratic programming problem is formulated in a fuzzy environment. The problem with fuzzy quadratic programming is formulated as a lower, central, and upper model. The formulated models are then solved with backpropagation fuzzy neural networks. The proposed method is then implemented in the capital market to identify the optimal portfolio for potential investors in the Pakistan Stock Exchange. Six leading stocks traded on the stock exchange from Jan 2016 to Oct 2020 were taken into consideration. At all three levels (lower, central, and upper), the results of identifying the best investment portfolio for investors are consistent. The proposed three models identify the investors to invest in ATHL, MCB and ARPL, whereas, the remaining three IGIHL, INIL and POL are not desirable for investment. In all three cases, the convergence is obtained at 475 iterations which is faster than the previously conducted studies. Moreover, another advantage of the proposed technique is that it brings an improvement of 28.77% in the objective function of mean variance optimization MVO model.
1 Introduction
Neural network was introduced by Rosenblatt (1958) in his seminal paper. The technique was highly appraised by scientists and emerged as an important mechanism for solving the real world’s complex problems [1]. In the field of artificial intelligence and machine learning the neural network plays a significant role. The initial application of the neural network was reported by LeCun et al. [2], where it was adopted for recognizing the handwritten Zip codes. The technique was applied to pattern recognition problem in Bishop [3]. These series of successful implementations motivated researchers to explore the technique keenly and apply it to various real-world scenarios. Research studies have prioritized the steepest descent method of Jacobs over the momentum method of Polyak. The idea of Nesterov accelerated gradient approach evolved as the batch gradient descent and stochastic gradient descent. Moreover, the evolution of support vector machines (SVM) initiated a new era in the domain of machine learning and can be perceived as an extension of perceptron. The technique of SVM has been successfully implemented both for linear and nonlinear classification problems, whereby the problem is categorically divided into separating hyperplanes. Moreover, the SVM classification problems constructed quadratic program problems. Both the primal problem and the dual primal problem can be formulated as quadratic programming problems. The primal-dual method became insufficient as our observations went high, so, for the large-scale optimization LASSO regression method was developed. The importance of quadratic programming increased due to the fact that the LASSO solution developed the problem as an augmented quadratic programming problem.
Initially, very few optimization scientists had expertise with quadratic optimization [4]; like Mann, Markowitz can be justly recognized as the “father of quadratic programming.” In 1956, Markowitz put forward a technique to solve quadratic programming problems [5]. In studies [6,7,8], different approaches were presented to quadratic programming problems.
Quadratic programming problems gained prominence in many areas and played a pivotal role in many scientific and engineering problems. Quadratic programming is a noteworthy approach in which the objective function is quadratic subject to linear constraint. Moré and Toraldo [9], solved quadratic programming problems with bounded constraints. In [10], a complete bibliography of the development of quadratic programming techniques was presented. In the early 90’s, the researchers adopted traditional optimization techniques using artificial neural networks. Linear and quadratic programming problems were solved with the help of neural networks by Maa and Shanblalt and Xia [11,12]. The authors studied bounded quadratic programming problems using the neural network approach [13]. Zak et al. [14] proposed a neural network approach for solving linear programming problems. High-performance neural network was used by Wu et al. [15] for solving linear and quadratic problems. Xia and Wang [16] tried primal neural networks for solving convex quadratic programming problems.
The technique of portfolio optimization theory was first introduced in the seminal paper of Markowitz [17], and after that became a noteworthy topic for emerging researchers. Morkowitz explained the anticipated return of the portfolio as a desiring phenomenon and the fluctuations of the returns undesirable. The mean-variance model of the Markowitz efficiently computed the optimized portfolio [18]. In the study by Richard and Roncalli [19], risk-constrained portfolio optimization problems were addressed. Diversification in investment strategies using maximum entropy approach was addressed by Bera and Park [20]. Brodie et al. [21] addressed the concept of stable investment strategies. The successful and incredible implementations of artificial intelligence and machine learning approaches have attracted researchers to reconsider conventional portfolio optimization. Markowitz proposed a quadratic programming model for solving portfolio optimization problems [22]. Financial specialists proposed models to minimize the risk of returns and maximize their benefits in portfolio optimization problems [23,24,25]. Financial specialists broadly utilized the mean-variance optimization model. Roa’s quadratic entropy [26] maximized portfolio returns by ordering and diversification. Bayesian optimization approach was adopted by Gonzalvez et al. [27]. Lezmi et al. [28] studied portfolio allocation problems with skewed risk. Perrin and Roncalli [29] used the CCD algorithm for solving portfolio optimization problems.
The idea of fuzzy sets proposed by Zadeh [30] has significant applications in the fields of science, technology, engineering, and management. Fuzzy modeling has been applied to optimization problems [31,32,33,34,35].
The idea of fuzzy modeling has been extensively used in the decision-making process. Ala et al. [36] used Multi-Objective Grey Wolf Optimization for the security and efficiency of green energy systems. Riaz et al. [37] studied the efficiency of the supply chain system in a city using a fuzzy decision-making process. Jana et al. [38] evaluated the performance of green sustainable approaches for parcel delivery using fuzzy integral techniques. Alsattar et al. [39] utilized three-stage decision-making process with Pythagorean fuzzy sets for the development of a green sustainable lifestyle. Khan et al. [40] proposed a simplified technique to solve fuzzy linear programming problems. Khan and Khan [41] solved intuitionistic fuzzy linear programming problem using duality properties. In the study by Khan and Karam [42], Data Envelopment Analysis DEA techniques were adopted to measure the efficiency of American Airlines. The study by Faiza and Khalil [43] adopted machine learning techniques to predict flight delay problems. Machine learning techniques were adopted in Zhang et al., [44] for various real world problems. Khan and Aftab [45] utilized dynamic programming problems to address fuzzy linear programming problems. In the study by Silva et al. [46], two-phase approach was used to solve fuzzy quadratic programming problems. Liu [47,48] used fuzzy parameters in solving quadratic programming problems. Quadratic programming problems were addressed by Kheirfam [49] and sensitivity analysis by Kheifam et al. [50]. Molai [51] used fuzzy relational techniques for quadratic programming problems. Probability approaches were adopted by Barik and Biswal [52]. In the study by Gani and Kumar [53], pivoting techniques were used to solve fuzzy quadratic programming problems. The study by Zhou [54] proved the necessary optimality conditions for fuzzy quadratic programming problems. Bai and Bao [55] solved quadratic programming problems in a fuzzy uncertain environment. In the study by Ghanbari and Moghadam [56], an ABS algorithm was adopted to solve the fuzzy quadratic programming problem. Umamaheswari and Ganesan [57] proposed a new method for fuzzy quadratic programming problems. Dasril et al. [58] presented an enhanced constraint method to solve fuzzy quadratic programming problems. Elshafei [59] addressed a fuzzy quadratic programming problem in which the variables were unrestricted. In the studies by Rout et al. and Biswal and De [60,61], multi-objective quadratic programming problems were addressed. In the study by Fathy [62], the multi-objective problem with integer variables was addressed. The study by Khalifa [63] presented an interactive method for multi-objective quadratic programming. In the study by Taghi-Nezhad and Babakordi [64], the problems were decomposed into sub-problems for solution. Fuzzy quadratic programming was successfully applied in irrigation systems [65] and irrigation planning and portfolio optimization [66]. Neural networks were used in the study by Malek and Oskoei [67] to solve constrained quadratic problems. Fuzzy nonlinear programming problems were solved with neural network techniques in [68]. Mansoori et al. [69] utilized neural networks for solving fuzzy quadratic programming problems. In the study by Coelho [70], a dual method is used to solve fuzzy quadratic programming problems.
In this study, a backpropagation fuzzy neural network is used to solve fuzzy quadratic programming problems. The method is applied to the portfolio optimization problem in the Pakistan Stock Exchange. Table 1 presents a summary of the techniques used in the literature and the gap of the proposed back propagation neural network over the existing techniques. It depicts that different methods are used to solve fuzzy quadratic programming problems, and the proposed backpropagation neural network techniques have not been applied so far for the same. Thus, the proposed method has a methodological and population gap with the existing techniques.
Existing methods for fuzzy quadratic programming problems
| Research | Methodology | Gap |
|---|---|---|
| Perrin and Roncalli [29] | CCD for quadratic portfolio optimization | Methodological, population |
| Molai [51] | Fuzzy relational calculus | Methodological, population |
| Barik and Biswal [52] | Probabilistic method | Methodological, population |
| Gani and Kumar [53] | Pivoting technique | Methodological, population |
| Ghanbari and Moghadam [56] | ABS Algo | Methodological, population |
| Darsil et al. [58] | Enhanced constrained technique | Methodological, population |
| Taghi-Nezhad and Babakordi [64] | Decomposition into subproblems | Methodological, population |
| Malek and Oskoei [67] | Neural network | Methodological, population |
| Mansoori et al. [68,69] | Neural network | Methodological, population |
| Coelho [70] | Dual method | Methodological, population |
The statement of the proposed research problem is “How back propagation fuzzy neural network can be utilized to address the quadratic programming problems in fuzzy uncertain environment?”
The objectives of the research are as follows:
To study back propagation fuzzy neural network to solve quadratic programming problems in a fuzzy uncertain environment.
To implement the proposed methodology to the mean-variance Markowitz model in capital market structure.
To solve the model on Python machine learning software using the PyTorch module.
To implement the proposed approach on the datasets of six leading companies in the Pakistan Stock Exchange.
To analyze the results and propose suggestions for optimal portfolio management.
The main contributions of the proposed study are listed as follows:
Incorporation of backpropagation techniques to solve fuzzy quadratic programming problems with the techniques of fuzzy neural network.
Construction of Lagrange’s function in matrix form and chain rule for backpropagation in a fuzzy quadratic programming problem.
Python machine learning software is used to solve the proposed model. The module used is PyTorch.
Implementing the proposed technique for portfolio optimization in the Pakistan Stock Exchange.
Analysis of results and insight into perspective investors in Pakistan Stock Exchange.
The foremost advantages of the proposed technique are listed as follows:
The main advantage of the proposed back propagation neural network is that it can easily adjust and fine-tune the weights of the network from the error rate obtained at the previous layer.
The chain and power rules of the derivative allow backpropagation and successively update the weights of the network to perform efficiently.
Thus, the gradient of the loss function is calculated by iterating backward layer by layer but one at a time to reduce the difference between the desired and the predicted outputs.
The prime utility of the proposed back propagation model is its successful implementation in the Pakistan Stock Exchange. In all three cases of the implementation, the convergence is obtained at 475 iterations. Thus, it is faster than the previous studies.
The proposed technique brings an improvement of 28.77% in the objective function of the mean variance optimization MVO which is greater than reported in the literature.
An epitomic road map of the proposed study is presented below and shown in Figure 1.
Proposition of the fuzzy quadratic programming problem with back propagation neural network.
Formulate the lower model of the proposed fuzzy quadratic programming problem with a back propagation neural network.
Formulate the central model of the proposed fuzzy quadratic programming problem with a back propagation neural network.
Formulate the upper model of the proposed fuzzy quadratic programming problem with a backpropagation neural network.
Implement the proposed fuzzy QP model to mean-variance optimization MVO in the Pakistan Stock Exchange.
Formulate the lower fuzzy QP model for the mean-variance optimization MVO in the Pakistan Stock Exchange.
Formulate the central fuzzy QP model for the mean-variance optimization MVO in Pakistan Stock Exchange.
Formulate the upper fuzzy QP model for the mean-variance optimization MVO in Pakistan Stock Exchange.
Sole all three models (lower, central, and upper) using Python machine learning software and obtain results using the PyTorch module.
Combine the Results of all three models and present a single fuzzy solution.
Compare and contrast the results with existing studies in the literature.
Conclusions and summary of the research.
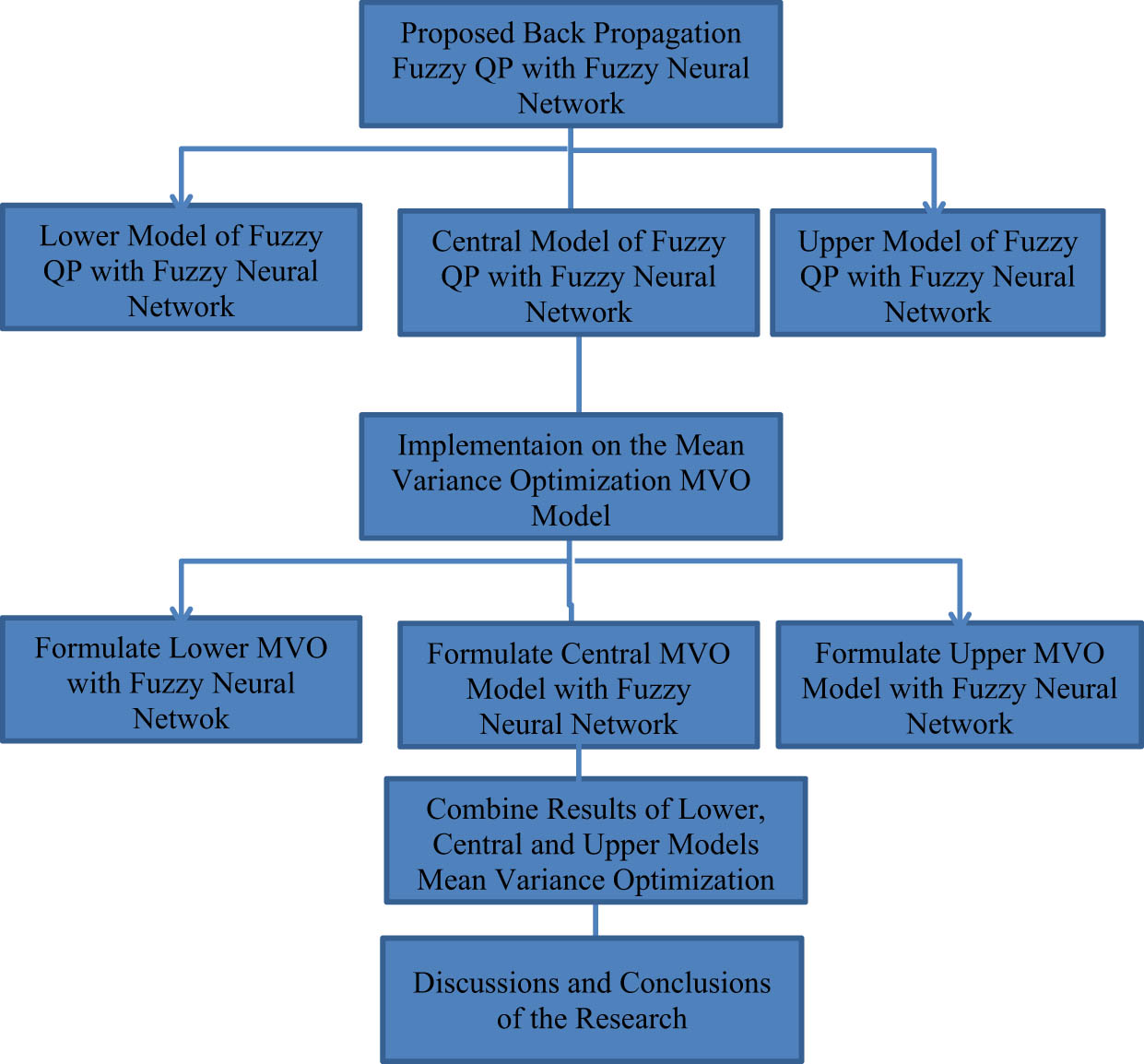
Road map of the proposed study.
This study is organized as follows. After the introduction, the backpropagation method for solving quadratic programming problems with neural networks is given in Section 2. This is followed by Section 3 in which a backpropagation method for solving fuzzy quadratic programming problems with neural networks is proposed. In Section 4, the proposed approach adopted in three is converted into lower, central, and upper models. In Section 5, the proposed methodology is adopted for portfolio optimization problems in Pakistan Stock Exchange. This section has two subsections, 5.1 and 5.2, for the lower and upper models, respectively. Results and discussions are given in Section 6, and the study is concluded in Section 7.
2 Back propagation artificial neural network for quadratic programming problems
A quadratic layer program using a neural network can be defined as (1).
s.t.
where the current layer is
where
Here, D(·) is used for creating the diagonal matrix from the vector. Introducing slacks for inequality constraints in (1) and iteratively minimizing the residuals from KKT conditions over primal and dual problems. The affine scale directions are calculated as (4).
The center and correct direction is given by (6).
Here, µ is the duality gap and
In
The model (9) is obtained by taking the differential of the conditions (8).
Model (9) in matrix form is (10).
Utilizing these equations, we find the Jacobin of z* (or λ* and v*) with regard to any parameters. For example, in the event to compute the Jacobian
Then, with respect to all QP parameters, the relevant gradients can be given by (12).
Whereas all these terms are at most the size of the parameter matrices in standard backpropagation. Finally, system (13) presents the symmetric matrix computing the backpropagated gradient.
where
3 Proposed back propagation fuzzy neural network for fuzzy quadratic programming problems
Fuzzy quadratic layer in a neural network using Klir and Yuan’s study [71] can be presented as (14).
s.t.
where the current layer is
where
Here, D(·) creates the diagonal matrix of the vector, introducing slacks for inequality constraints in (14), and minimizing the residuals from KKT conditions over primal and dual problems. The affine scale directions are calculated as (17).
The matrix K (s, l, r) in (17) is (18).
The center and correct direction is presented (19).
Here, µ is the duality gap and
In
For backpropagation, the KKT of (15) are given (21).
Taking the differentials of (21), gives (22).
Model (22) in matrix form gives (23).
These equations help find the Jacobin of
The gradients are presented in (25).
Finally, (26) presents the symmetric matrix computing the backpropagated gradients.
where
4 The proposed backpropagation fuzzy artificial neural network for lower, central, and upper bounds for quadratic programming problem model
Fuzzy quadratic layer program in triangular fuzzy numbers can be given as follows (27):
s.t.
The current layer is
For backpropagation, it is required to determine the derivative of the solution to the QP problem with respect to the variable parameters. The Lagrangian of the problem is (28).
where
Here,
The value of K (s−l,s,s+r) in (30) is (31).
The center and correct direction is presented (32).
Here,
In the matrix,
The model (35) is obtained by taking the differentials of (34).
Model (35) in matrix form is (36).
These equations help find the Jacobin of
The gradients with respect to QP parameters are presented in (38).
Finally, the system (39) presents the symmetric matrix computing the backpropagated gradients.
Here,
5 Proposed QP model formulation for portfolio optimization in Pakistan stock exchange
In this section, the proposed fuzzy backpropagation neural network is applied to the fuzzy quadratic portfolio optimization problem in the Pakistan Stock Exchange. Markowitz’s MVO model is utilized to formulate the problem. The solutions identify profitable portfolios for potential investors in the Pakistan Stock Exchange based on historical records of the assets. Returns data of the six leading stocks traded in the Pakistan stock exchange are taken into consideration. The companies include Archroma Pakistan Limited (ARPL), IGI Holdings Limited. (IGIHL). International Industries Limited (INIL), Atlas Honda Limited (ATLH), MCB Bank Limited (MCB), and Pakistan Oilfields Limited (POL). For each asset, monthly data between January 2016 and October 2020 of the returns (close price) is obtained from Data Portal, Pakistan Stock Exchange [72]. Table 2 represents the closing prices for the selected stocks from January 2016 to October 2020 [72].
Data of six stocks from Pakistan Stock Exchange from Jan 2016 to Oct 2020
| Date | ARPL | IGIHL | INIL | ATLH | MCB | POL |
|---|---|---|---|---|---|---|
| Jan 2016 | 455.97 | 232.5 | 63.5 | 385 | 192.69 | 213.48 |
| Feb 2016 | 426.06 | 229.72 | 60.75 | 374.99 | 195.88 | 236.19 |
| Mar 2016 | 432.02 | 221 | 65.53 | 377.99 | 206.03 | 258.01 |
| Apr 2016 | 474.58 | 224.53 | 79.96 | 393.36 | 211.53 | 320.37 |
| … | … | … | … | … | … | … |
| Jul 2020 | 559.28 | 212.22 | 122.98 | 440.52 | 177.4 | 407.35 |
| Aug 2020 | 589.9 | 223.98 | 148.31 | 450.2 | 171.07 | 427.94 |
| Sep 2020 | 566.96 | 218.97 | 144.94 | 430 | 173.82 | 421.33 |
| Oct 2020 | 550 | 198.32 | 141.89 | 495 | 166.22 | 318.57 |
Let’s
Rate of Returns of the six stocks from Jan 2016 to Oct 2020
| Date | ARPL | IGIHL | INIL | ATLH | MCB | POL |
|---|---|---|---|---|---|---|
| Feb 2016 | −0.065 | −0.011 | −0.043 | −0.026 | 0.016 | 0.106 |
| Mar 2016 | 0.013 | −0.037 | 0.078 | 0.008 | 0.051 | 0.092 |
| Apr 2016 | 0.098 | 0.015 | 0.220 | 0.040 | 0.026 | 0.241 |
| … | … | … | … | … | … | … |
| Jul 2020 | −0.051 | 0.172 | 0.340 | 0.147 | 0.094 | 0.161 |
| Aug 2020 | 0.054 | 0.055 | 0.205 | 0.021 | −0.035 | 0.050 |
| Sep 2020 | −0.038 | −0.022 | −0.022 | −0.044 | 0.016 | −0.015 |
| Oct 2020 | −0.029 | −0.094 | −0.021 | 0.151 | −0.043 | −0.243 |
From (40), the arithmetic mean and geometric mean for each asset can be calculated (41) and (42) and shown in Table 4.
Arithmetic mean of the stocks
| ARPL | IGIHL | INIL | ATLH | MCB | POL | |
|---|---|---|---|---|---|---|
| Arithmetic mean a i | 0.006 | 0.007 | 0.024 | 0.007 | −0.0006 | 0.0124 |
| G.M g i | 100.32 | 99.72 | 101.42 | 100.44 | 99.74 | 100.70 |
| Volatility | 0.077 | 0.152 | 0.153 | 0.079 | 0.061 | 0.103 |
Covariance and volatility are calculated in (43) and (44) and are shown in Tables 4 and 5, respectively.
Covariance of the stocks
| Covariance | ARPL | IGIHL | INIL | ATLH | MCB | POL |
|---|---|---|---|---|---|---|
| ARPL | 0.006 | 0.003 | 0.004 | 0.002 | 0.001 | 0.002 |
| IGIHL | 0.003 | 0.023 | 0.013 | 0.002 | 0.004 | 0.006 |
| INIL | 0.004 | 0.013 | 0.02356 | 0.006 | 0.004 | 0.007 |
| ATLH | 0.002 | 0.002 | 0.006 | 0.006 | 0.001 | 0.001 |
| MCB | 0.001 | 0.004 | 0.0042 | 0.001 | 0.003 | 0.003 |
| POL | 0.002 | 0.006 | 0.007 | 0.001 | 0.003 | 0.010 |
Correlation matrix of the six stocks
| Correlation | ARPL | IGIHL | INIL | ATLH | MCB | POL |
|---|---|---|---|---|---|---|
| ARPL | 1 | 0.269 | 0.394 | 0.372 | 0.398 | 0.296 |
| IGIHL | 0.269 | 1 | 0.577 | 0.182 | 0.471 | 0.443 |
| INIL | 0.394 | 0.577 | 1 | 0.499 | 0.456 | 0.447 |
| ATLH | 0.372 | 0.182 | 0.499 | 1 | 0.348 | 0.218 |
| MCB | 0.398 | 0.471 | 0.456 | 0.348 | 1 | 0.535 |
| POL | 0.296 | 0.443 | 0.447 | 0.218 | 0.535 | 1 |
The geometric mean is utilized rather than the arithmetic mean because the return rate is multiplicative over period.
Finally the correlation matrix is Table 6.
Ultimately, the central quadratic programming problem for portfolio optimization is constructed.
The proposed central quadratic programming mean-variance model for the portfolio optimization is (45) from Tables 4 and 5.
s.t
After executing the above problem using Python, the following results are obtained. The solution obtained
| Iteration | 0 | Loss | 14.66 |
| Iteration | 25 | Loss | 2.66 |
| Iteration | 50 | Loss | 1.55 |
| Iteration | 75 | Loss | 1.28 |
| Iteration | 100 | Loss | 1.14 |
| Iteration | 125 | Loss | 1.06 |
| Iteration | 150 | Loss | 0.98 |
| Iteration | 175 | Loss | 0.85 |
| Iteration | 200 | Loss | 0.69 |
| Iteration | 225 | Loss | 0.50 |
| Iteration | 250 | Loss | 0.38 |
| Iteration | 275 | Loss | 0.34 |
| Iteration | 300 | Loss | 0.33 |
| Iteration | 325 | Loss | 0.32 |
| Iteration | 350 | Loss | 0.32 |
| Iteration | 375 | Loss | 0.31 |
| Iteration | 400 | Loss | 0.31 |
| Iteration | 425 | Loss | 0.31 |
| Iteration | 450 | Loss | 0.30 |
| Iteration | 475 | Loss | 0.30 |

Errors between the actual and predicted values for the central model.
5.1 Proposed fuzzy QP lower model for portfolio optimization
The proposed lower quadratic programming mean-variance model for the portfolio optimization is (46).
s.t
Executing the problem using Python, the following results are obtained. The solutions obtained
| Iteration | 0 | Loss | = | 15.33 |
| Iteration | 25 | Loss | = | 2.34 |
| Iteration | 50 | Loss | = | 1.25 |
| Iteration | 75 | Loss | = | 0.92 |
| Iteration | 100 | Loss | = | 0.84 |
| Iteration | 125 | Loss | = | 0.83 |
| Iteration | 150 | Loss | = | 0.83 |
| Iteration | 175 | Loss | = | 0.83 |
| Iteration | 200 | Loss | = | 0.83 |
| Iteration | 225 | Loss | = | 0.82 |
| Iteration | 250 | Loss | = | 0.82 |
| Iteration | 275 | Loss | = | 0.82 |
| Iteration | 300 | Loss | = | 0.82 |
| Iteration | 325 | Loss | = | 0.82 |
| Iteration | 350 | Loss | = | 0.81 |
| Iteration | 375 | Loss | = | 0.81 |
| Iteration | 400 | Loss | = | 0.81 |
| Iteration | 425 | Loss | = | 0.80 |
| Iteration | 450 | Loss | = | 0.80 |
| Iteration | 475 | Loss | = | 0.80 |
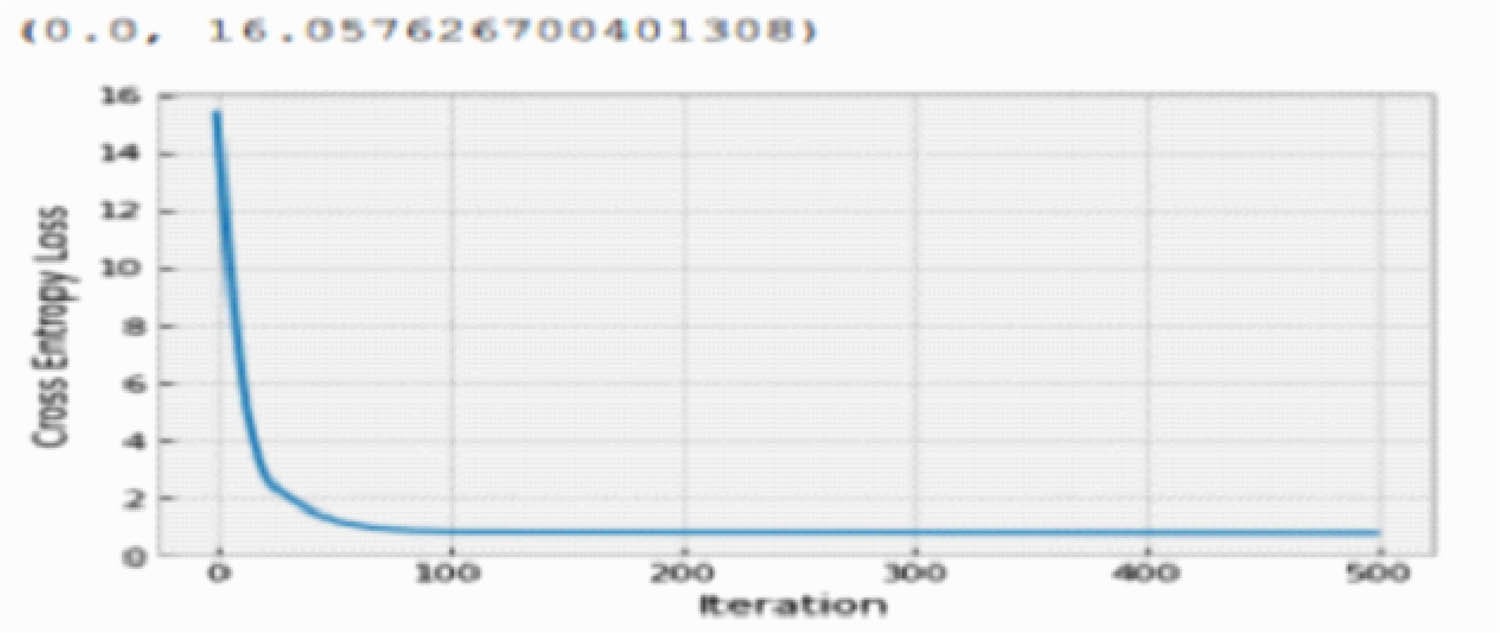
Errors between the actual and predicted values for Lower model.
5.2 Proposed fuzzy QP upper model for portfolio optimization
The proposed upper quadratic programming mean-variance model for portfolio optimization is (47).
s.t
The solutions obtained using the Python machine learning environment are recorded
| Iteration | 0 | Loss | = | 20.80 |
| Iteration | 25 | Loss | = | 4.55 |
| Iteration | 50 | Loss | = | 0.95 |
| Iteration | 75 | Loss | = | 0.61 |
| Iteration | 100 | Loss | = | 0.50 |
| Iteration | 125 | Loss | = | 0.45 |
| Iteration | 150 | Loss | = | 0.42 |
| Iteration | 175 | Loss | = | 0.39 |
| Iteration | 200 | Loss | = | 0.38 |
| Iteration | 225 | Loss | = | 0.38 |
| Iteration | 250 | Loss | = | 0.36 |
| Iteration | 275 | Loss | = | 0.35 |
| Iteration | 300 | Loss | = | 0.34 |
| Iteration | 325 | Loss | = | 0.34 |
| Iteration | 350 | Loss | = | 0.34 |
| Iteration | 375 | Loss | = | 0.33 |
| Iteration | 400 | Loss | = | 0.33 |
| Iteration | 425 | Loss | = | 0.33 |
| Iteration | 450 | Loss | = | 0.33 |
| Iteration | 475 | Loss | = | 0.33 |

Errors between the actual and predicted values for upper model.
6 Results and discussions
The solutions of the lower, central and upper models agree on identifying profitable investment options for potential investors in the stock exchange. All three models identify the investors to invest in ATHL, MCB, and ARPL. Moreover, the remaining three options IGIHL, INIL, and POL are not desirable for investment. The solutions obtained from central model (45), lower model (46) and upper model (47), respectively, are recorded in Table 7 and Figures 5 and 6.
Investment options identified by lower, central, and upper models
| Company | Lower solution | Central solution | Upper solution | Solution (s, l, r) | Solution (s−l, s, s+r) |
|---|---|---|---|---|---|
| ARPL | 0.28 | 0.3 | 0.32 | (0.3, 0,02, −0.02) | (0.28, 0.3, 0.32) |
| IGIHL | 0.07 | 0.05 | 0.01 | (0.05, −0.02, 0.04) | (0.07, 0.05, 0.01) |
| INIL | 0.06 | 0.03 | 0.01 | (0.03–0.03, 0.02) | (0.06, 0.03, 0.01) |
| ATHL | 0.29 | 0.31 | 0.33 | (0.31, 0.02, −0.02) | (0.29, 0.31, 0.33) |
| MCB | 0.28 | 0.3 | 0.32 | (0.3, 0.02, −0.02) | (0.28, 0.3, 0.32) |
| POL | 0.02 | 0.01 | 0.01 | (0.01, −0.01, 0) | (0.02, 0.01, 0.01) |
| Best for investment | ATHL, MCB, ARPL | ATHL, MCB, ARPL | ATHL, MCB, ARPL | ATHL, MCB, ARPL | ATHL, MCB, ARPL |
| Min Mean Variance | 0.6249 | 0.6398 | 0.7594 | (0.6398, 0.0149, −0.1196) | (0.6249, 0.6398, 0.7594) |

Identification of investment options by lower, central, and upper models.

Minimum mean-variance recorded by lower, central, and upper models.
Finally, the results obtained are compared with previously conducted studies. The comparisons are two-folds. Firstly, the improvement it brings in the objective function of mean-variance optimization MVO model and secondly the number of iterations in which the program converges. Table 8 shows a comparison of the proposed method over [15,67,68,69,70]. The table depicts that the proposed method improves the objective of the mean variance optimization MVO model by 28.77%, respectively. Dual of Wu et al. [15] and New model 3 of Malek and Oskoei [67] bring an improvement of 0.004% in the objective function. The proposed study brings an improvement of 28.77% in the objective of the mean-variance optimization MVO model depicting that the proposed results are better than Dual of [15] and New model 3 of [67]. Next, we compare the results obtained with Mansoori et al. [68] and Mansoori et al. [69]. The study [68] brings an improvement of 10% and [69] records an improvement of 15%. The currently proposed study records an improvement of 28.77% in the objective function of the mean-variance optimization MVO model, showing that the results are better than those of Mansoori et al. [68,69]. Moreover, Coelho [70] recorded an improvement of 14%. The proposed study records an improvement of 28.77% in the objective function of the MVO model; thus, the results are better than [70]. The table depicts that the results of the proposed technique are better than the results of the studies [15,67,68,69,70].
Comparisons of the proposed method with existing methods
| Difference | Percent difference (%) | ||
|---|---|---|---|
| Proposed impovement in the objective of the MVO model | At α = 0.0 | 0.00093 | 28.77 |
| 0.002326 | |||
| At α = 1 | |||
| 0.003265 | |||
| Mansoori et al. [69] at uncertainty level α = 0.2,
|
−1.5559 | −0.2441 | 15.6 |
| Mansoori et al. [69] at uncertainty level α = 0.5,
|
−1.8000 | ||
| Primal of the Wu et al. [15] model 5, and Malek and Oskoei [67] New 3 model, Table 5 | −224.99 | −0.01 | 0.004 |
| Dual of the Wu et al. [15] model 5, and Malek and Oskoei [67] New 3 model, Table 5 | −225.02 | ||
| Mansoori et al. [68] at uncertainty level α = 0.0,
|
−18.97 | −2.03 | 10 |
| Mansoori et al. [68] at uncertainty level α = 1,
|
−21.00 | ||
| Coelho [70] at uncertainty level α = 0.0 | 439.57 | 64.54 | 14.68 |
| Coelho [70] at uncertainty level α = 1 | 504.11 |
The efficiency in terms of convergence is compared with existing literature. In terms of convergence, we compare the proposed method with Perrin and Roncalli [29]. Our results presented in Table 9 depict that the minimum loss is obtained at iteration number 475 for all the lower, central, and upper models, respectively. The minimum values for the loss function are 0.30, 0.80, and 0.33 for the lower, central, and upper models, respectively. Perrin and Roncalli [29] pointed out that more than 500 iterative cycles are required for the cyclical coordinate descent CCD algorithm to converge the unconstrained QP problem. In all three proposed cases, the convergence is obtained at 475 iterations; thus, our proposed method is faster and more effective than [29].
Lowest loss of central, lower and upper models
| Iteration number | Lowest loss | Perrin and Roncalli [29] | |
|---|---|---|---|
| Central model | 475 | 0.30 | At least 500 iterations |
| Lower model | 475 | 0.80 | At least 500 iterations |
| Upper model | 475 | 0.33 | At least 500 iterations |
7 Conclusions
In this research, fuzzy quadratic programming problems are solved by utilizing the backpropagation fuzzy artificial neural networks. In backpropagation techniques, the chain and power rules of calculus are utilized to minimize the error of the loss function obtained at the previous layer of the neural network. The quadratic programming problem is formulated in a fuzzy environment. Initially lower, central, and upper models of the problems are formulated then these models are solved with backpropagation fuzzy neural network. The proposed method is then implemented in the capital market to identify the optimal portfolios in the Pakistan Stock Exchange. Six major stocks traded on the stock exchange from Jan 2016 to Oct 2020 are considered. The lower, central, and upper quadratic programming models are constructed and solved. At all three levels (lower, central, and upper), the results are consistent in identifying the best investment portfolio for potential investors. All three models identify to invest in ATHL, MCB, and ARPL. Moreover, the remaining three options IGIHL, INIL, and POL are not desirable for investment. The proposed technique brings an improvement of 28.77% in the objective function of the MVO model. Convergence is obtained at 475 iterations, depicting that the proposed approach is faster than the previous studies. Furthermore, some limitations of the backpropagation are reported. First, backpropagation depends on the data presented to it and is sensitive to noisy data, and irregularity in data can influence its performance. Second, the computation of gradient adds a computational lag at the backpropagation layer. Third, unlike the mini-batch, it is a matrix-based method of calculus and linear algebra.
Acknowledgements
We thank the respectable reviewers and editors for their credible reviews and suggestions.
-
Funding information: This study was funded by no agency/grant.
-
Author contributions: All authors have accepted responsibility for the entire content of this manuscript and approved its submission. IUK: Proposed the main idea, conceptualization, software, writing, supervision, and project management. RUA: Performed data curation, writing, resources, and investigation. MU: Conducted validation, formal analysis, reviewing, editing, and supervision. MSS: Managed resource allocation, software, and visualization.
-
Conflict of interest: The authors declare that they have no conflict of interest.
-
Ethical approval: The article does not contain any studies with human participants performed by any of the authors.
-
Data availability statement: The authors assure the availability of data upon request.
References
[1] Rosenblatt F. The perceptron: a probabilistic model for information storage and organization in the brain. Psychol Rev. 1958;65(6):386–8.10.1037/h0042519Suche in Google Scholar PubMed
[2] LeCun Y, Boser B, Denker JS, Henderson D, Howard RE, Hubbard W, et al. Backpropagation applied to handwritten zip code recognition. Neural Computaion. 1989;1(4):541–51.10.1162/neco.1989.1.4.541Suche in Google Scholar
[3] Bishop CM. Neural networks for pattern recognition. New York, NY, Unitied States: Oxford University press Inc., 189, Madison, Ave; 1995.Suche in Google Scholar
[4] Mann HB. Quadratic forms with linear constraints. Am Math Monthly. 1943;50(7):430–3.10.1080/00029890.1943.11991413Suche in Google Scholar
[5] Markowitz H. The optimization of a quadratic function subject to linear constraints. Nav Res Logist Quartely. 1956;3(1–2):111–33.10.1002/nav.3800030110Suche in Google Scholar
[6] Eaves BC. On quadratic proramming. Manag Sci. 1971;17(11):698–11.10.1287/mnsc.17.11.698Suche in Google Scholar
[7] Frank M, Wolfe P. An algorithm for quadratic programming. Nav Res Logist Q. 1956;3(1–2):95–10.10.1002/nav.3800030109Suche in Google Scholar
[8] Wolfe P. The simplex method for quadratic programming. Econometrica. 1959;27(3):382–98.10.2307/1909468Suche in Google Scholar
[9] Moré JJ, Toraldo G. On the solution of large quadratic programming problems with bound constraints. SIAM J Optim. 1991;1(1):93–13.10.1137/0801008Suche in Google Scholar
[10] Gould NIM, Toint PL. A quadratic programming bibliography. Numerical Analysis Group Interanl Report 1, Rutherford Appleton Laboratory, Chilton, England; 2000.Suche in Google Scholar
[11] Maa CY, Shanblatt MA. Linear and quadratic programming neural network analysis. IEEE Trans Neural Netw. 1992;3(4):580–94.10.1109/72.143372Suche in Google Scholar PubMed
[12] Xia Y. A new neural network for solving linear and quadratic programming problems. IEEE Trans Neural Netw. 1996;7(6):1544–8.10.1109/72.548188Suche in Google Scholar PubMed
[13] Bouzerdoum A, Pattison TR. Neural network for quadratic optimization with bound constraints. IEEE Trans Neural Netw. 1993;4(2):293–4.10.1109/72.207617Suche in Google Scholar PubMed
[14] Zak SH, Upatising V, Hui S. Solving linear programming problems with neural networks: a comparative study. IEEE Trans Neural Netw. 1995;6(1):94.10.1109/72.363446Suche in Google Scholar PubMed
[15] Wu XY, Xia YS, Li J, Chen WK. A high-performance neural network for solving linear and quadratic programming problems. IEEE Trans Neural Netw. 1997;7(3):643–51.10.1109/72.501722Suche in Google Scholar PubMed
[16] Xia Y, Wang J. Primal neural networks for solving convex quadratic programs. International Joint Conference on Neural Networks. Proceedings IEEE (Cat. No. 99CH36339); 1999. p. 582–7.Suche in Google Scholar
[17] Markowitz HM. Foundations of portfolio theory. J Financ. 1991;46(2):469–77.10.1111/j.1540-6261.1991.tb02669.xSuche in Google Scholar
[18] Michaud RO. The Markowitz optimization enigma: Is ‘optimized’optimal? Financial Analyst Journal. 1989;5(1):31–42.10.2469/faj.v45.n1.31Suche in Google Scholar
[19] Richard JC, Roncalli T. Constrained risk budgeting portfolios: Theory, algorithms, applications & puzzles. SSRN Constrained Risk Budgeting Portfolios: Theory, Algorithms, Applications & Puzzles by Jean-Charles Richard, Thierry Roncalli: SSRN; 2019. Accessed 16 April 2021.10.2139/ssrn.3331184Suche in Google Scholar
[20] Bera AK, Park SY. Optimal portfolio diversification using the maximum entropy principle. Econometirc Rev. 2008;27(4–6):484–12.10.1080/07474930801960394Suche in Google Scholar
[21] Brodie J, Daubechies I, De Mol C, Giannone D, Loris I. Sparse and stable Markowitz portfolios. Proc Natl Acad Sci U S A. 2009;106(30):12267–72.10.1073/pnas.0904287106Suche in Google Scholar PubMed PubMed Central
[22] Cottle RW, Infanger G. Harry Markowitz and the early history of quadratic programming. In: Guerard JB, editor. Handbook of portfolio construction. Boston, MA: Springer; 2010. p. 179–11.10.1007/978-0-387-77439-8_8Suche in Google Scholar
[23] Bruder B, Gaussel N, Richard JC, Roncalli T. Regularization of portfolio allocation. SSRN Regularization of Portfolio Allocation by Benjamin Bruder, Nicolas Gaussel, Jean-Charles Richard, Thierry Roncalli: SSRN; 2013. Accessed 10 Feb 2021.10.2139/ssrn.2767358Suche in Google Scholar
[24] Bruder B, Kostyuchyk N, Roncalli T. Risk parity portfolios with skewness risk: An application to factor investing and alternative risk premia. www.thierryroncalli.com/download/Risk_Parity_With_Skewness.pdf; 2016. Accessed 10 March 2021.10.2139/ssrn.2813384Suche in Google Scholar
[25] Choueifaty Y, Froidure T, Reynier J. Properties of the most diversified portfolio. J Invest Strateg. 2013;2(2):49–70.10.21314/JOIS.2013.033Suche in Google Scholar
[26] Carmichael B, Koumou GB, Moran K. Rao’s quadratic entropy maximum Diversif Index. 2018;18(6):1017–31.10.1080/14697688.2017.1383625Suche in Google Scholar
[27] Gonzalvez J, Lezmi E, Roncalli T, Xu J. Financial applications of Gaussian processes and Bayesian optimization. SSRN Financial Applications of Gaussian Processes and Bayesian Optimization by Joan Gonzalvez, Edmond Lezmi, Thierry Roncalli, Jiali Xu: SSRN; 2019. Accessed 10 Feb 2021.10.2139/ssrn.3344332Suche in Google Scholar
[28] Lezmi E, Malongo H, Roncalli T, Sobotka R. Portfolio Allocation with Skewness Risk: A Practical Guide. SSRN Portfolio Allocation with Skewness Risk: A Practical Guide by Edmond Lezmi, Hassan Malongo, Thierry Roncalli, R Sobotka: SSRN; 2018. Accessed 9 Feb 2021.10.2139/ssrn.3201319Suche in Google Scholar
[29] Perrin S, Roncalli T. Machine learning optimization algorithm and portfolio optimization. Arxiv.1909.10233 v1.(q-fin.PM (2019)); 2019.10.2139/ssrn.3425827Suche in Google Scholar
[30] Zadeh LA. Fuzzy sets. Inf Control. 1965;8(3):338–53.10.1016/S0019-9958(65)90241-XSuche in Google Scholar
[31] Khan IU, Ahmad T, Maan N. Feedback fuzzy state space modeling and optimal production planning for steam turbine of a combined cycle power generation plant. Res J Appl Sci. 2012;7(2):100–7.10.3923/rjasci.2012.100.107Suche in Google Scholar
[32] Khan IU, Ahmad T, Maan N. Revised convexity, normality and stability properties of the dynamical feedback fuzzy state space model (FFSSM) of insulin–glucose regulatory system in humans. Soft Comput. 2019;23(21):11247–62.10.1007/s00500-018-03682-wSuche in Google Scholar
[33] Khan IU, Rafique F. Minimum-cost capacitated fuzzy network, fuzzy linear programming formulation, and perspective data analytics to minimize the operations cost of American airlines. Soft Comput. 2021;25(2):1411–29.10.1007/s00500-020-05228-5Suche in Google Scholar
[34] Khan IU, Aftab M. Dynamic programming approach for fuzzy linear programming problems FLPs and its application to optimal resource allocation problems in education system. J Intell Fuzzy Syst. 2022;42(4):3517–35.10.3233/JIFS-211577Suche in Google Scholar
[35] Cui W, Blockley DI. Decision making with fuzzy quadratic programming. Civ Eng Syst. 1990;7(3):140–7.10.1080/02630259008970582Suche in Google Scholar
[36] Ala A, Simic V, Pamucar D, Jana C. A novel neutrosophic-based multi-objective grey wolf optimizer for ensuring the security and resilience of sustainable energy: A case study of belgium. Sustain Cities Soc. 2023;96:104709.10.1016/j.scs.2023.104709Suche in Google Scholar
[37] Riaz M, Farid HM, Jana C, Pal M, Sarkar B. Efficient city supply chain management through spherical fuzzy dynamic multistage decision analysis. Eng Appl Artif Intell. 2023;126:106712.10.1016/j.engappai.2023.106712Suche in Google Scholar
[38] Jana C, Dobrodolac M, Simic V, Pal M, Sarkar B, Stević Ž. Evaluation of sustainable strategies for urban parcel delivery: Linguistic q-rung orthopair fuzzy Choquet integral approach. Eng Appl Artif Intell. 2023;126:106811.10.1016/j.engappai.2023.106811Suche in Google Scholar
[39] Alsattar HA, Qahtan S, Mourad N, Zaidan AA, Deveci M, Jana C, et al. Three-way decision-based conditional probabilities by opinion scores and Bayesian rules in circular-Pythagorean fuzzy sets for developing sustainable smart living framework. Inf Sci. 2023;649:119681.10.1016/j.ins.2023.119681Suche in Google Scholar
[40] Khan IU, Ahmad T, Maan N. A simplified novel technique for solving fully fuzzy linear programming problems. J Optim Theory Appl. 2013;159:536–46.10.1007/s10957-012-0215-2Suche in Google Scholar
[41] Khan IU, Khan M. The notion of duality in fully intuitionistic fuzzy linear programming FIFLP problems. Int J Fuzzy Syst Adv Appl. 2016;20–6.Suche in Google Scholar
[42] Khan IU, Karam FW. Intelligent business analytics using proposed input/output oriented data envelopment analysis DEA and slack based DEA models for US-Airlines. J Intell Fuzzy Syst. 2019;37(6):8207–17.10.3233/JIFS-190641Suche in Google Scholar
[43] Faiza, Khalil K. Airline flight delays using artificial intelligence in covid-19 with perspective analytics. J Intell Fuzzy Syst. 2023;44(4):6631–53.10.3233/JIFS-222827Suche in Google Scholar
[44] Zhang A, Lipton ZC, Li M, Smola AJ. Dive into Deep Learning. Cambridge University Press; 2023.Suche in Google Scholar
[45] Khan IU, Aftab M. Adaptive fuzzy dynamic programming (AFDP) technique for linear programming problems LPs with fuzzy constraints. Soft Comput. 2023;19(27):13931–49.10.1007/s00500-023-08462-9Suche in Google Scholar
[46] Silva RC, Verdegay JL, Yamakami A Two-phase method to solve fuzzy quadratic programming problems. IEEE International Fuzzy Systems Conference; 2007. 10.1109/FUZZY.2007.4295501. Suche in Google Scholar
[47] Liu ST. Quadratic programming with fuzzy parameters: A membership function approach. Chaos, Solitons Fractals. 2009;40(1):237–45.10.1016/j.chaos.2007.07.054Suche in Google Scholar
[48] Liu ST. A revisit to quadratic programming with fuzzy parameters. Chaos, Solitons Fractals. 2009;41(3):1401–7.10.1016/j.chaos.2008.04.061Suche in Google Scholar
[49] Kheirfam B. A method for solving fully fuzzy quadratic programming problems. Acta Univ Apulensis. 2011;27:69–76.Suche in Google Scholar
[50] Kheirfam B, Verdegay JL. Strict sensitivity analysis in fuzzy quadratic programming. Fuzzy Sets Syst. 2012;198:99–11.10.1016/j.fss.2011.10.019Suche in Google Scholar
[51] Molai AA. The quadratic programming problem with fuzzy relation inequality constraints. Comput Ind Eng. 2012;62(1):256–63.10.1016/j.cie.2011.09.012Suche in Google Scholar
[52] Barik SK, Biswal MP. Probabilistic quadratic programming problems with some fuzzy parameters. Adv Oper Res. 2012;635282.10.1155/2012/635282Suche in Google Scholar
[53] Gani AN, Kumar CA. The principal pivoting method for solving fuzzy quadratic programming problems. Int J Pure Appl Math. 2013;85(2):405–14.10.12732/ijpam.v85i2.16Suche in Google Scholar
[54] Zhou X-G, Cao B-Y, Nasseri SH. Optimality conditions for fuzzy number quadratic programming with fuzzy coefficients. J Appl Math. 2014;2014(1):489893.10.1155/2014/489893Suche in Google Scholar
[55] Bai E-D, Bao YE. Study on fuzzy quadratic programming problems. International Conference on Applied Mechanics, Mathematics, Modelling and Simulations; 2018. p. 424–29.10.12783/dtcse/ammms2018/27307Suche in Google Scholar
[56] Ghanbari R, Moghadam KG. Solving fuzzy quadratic programming problems based on ABS algorithm. Soft Comput. 2019;23:11343–9.10.1007/s00500-019-04013-3Suche in Google Scholar
[57] Umamaheswari P, Ganesan K. A new approach for the solution of fuzzy quadratic programming problems. J Adv Res Dyn Control Syst. 2019;11(1):342–9.Suche in Google Scholar
[58] Dasril Y, Muda WHHW, Gamal MDH, Sihwaningrum I. Enhanced constraint exploration on fuzzy quardratic programming problems. Commun Comput Appl Math. 2019;2(1):25–30.Suche in Google Scholar
[59] Elshafei MM. Fully fuzzy quadratic programming with unrestricted fully fuzzy variables and parameters. J Prog Res Math. 2019;15(3):2654–67.Suche in Google Scholar
[60] Rout PK, Nanda S, Acharya S. Muti-objective fuzzy probabilistic quadratic programming problem. Int J Oper Res. 2019;34(3):387–08.10.1504/IJOR.2019.098313Suche in Google Scholar
[61] Biswas A, De AK. Methodology for solving Multi-Objective quadratic programming problems in a fuzzy stochastic environment. In Multi-objective stochastic programming in fuzzy environment. Hershey, PA: IGI Global Publisher; 2019. p. 177–17.10.4018/978-1-5225-8301-1.ch005Suche in Google Scholar
[62] Fathy E. A modified fuzzy approach for the fully fuzzy multi-objective and multi-level integer quadratic programming problems based on a decomposition technique. J Intell and Fuzzy Syst. 2019;37(2):2727–39.10.3233/JIFS-182952Suche in Google Scholar
[63] Khalifa HA. Interactive multiple objective programming in optimization of the fully fuzzy quadratic programming problems. Int J Appl Oper Res. 2020;10(1):21–30.Suche in Google Scholar
[64] Taghi-Nezhad NA, Babakordi F. Fuzzy quadratic programming with non-negative parameters: A solving method based on decomposition. J Decis Oper Res. 2020;3(4):325–32.Suche in Google Scholar
[65] Wang H, Zhang C, Guo P. An interval quadratic fuzzy dependent-chance programming model for optimal irrigation water allocation under uncertainty. Water. 2018;10(6):684. 10.3390/w1006068 Suche in Google Scholar
[66] Wang J, He F, Shi X. Numerical solution of a general interval quadratic programming model for portfolio selection. PLoS ONE. 2019;14(3):e0212913. 10.1371/journal.pone.0212913 Suche in Google Scholar PubMed PubMed Central
[67] Malek A, Oskoei HG. Numerical solutions for constrained quadratic problems using high performance neural networks. Appl Math Comput. 2005;169:451–71.10.1016/j.amc.2004.10.091Suche in Google Scholar
[68] Mansoori A, Effati S, Eshaghnezhad M. An efficient recurrent neural network for solving fuzzy non-linear programming problems. Appl Intell. 2017;46:308–27.10.1007/s10489-016-0837-4Suche in Google Scholar
[69] Mansoori A, Effati, Eshaghnezhad M. A neural network to solve quadratic programming problems with fuzzy parameters. Fuzzy Optim Decis Mak. 2018;17:75–101.10.1007/s10700-016-9261-9Suche in Google Scholar
[70] Coelho R. Solving real-world fuzzy quadratic programming problems by dual parametric approach. In: Melin P, et al., editors. Fuzzy logic in intelligent system design, Advances in intelligent systems and computing. Cham: Springer; 2018. p. 648. 10.1007/978-3-319-67137-6_4.Suche in Google Scholar
[71] Klir GJ, Yuan B. Fuzzy sets and fuzzy logic: Theory and applications. Prentice Hall PTR, Upper Saddle River, New Jersey USA; 1995. p. 414–15.Suche in Google Scholar
[72] Data Portal, Pakistan Stock Exchange. Data Portal - Pakistan Stock Exchange (PSX); 2021. Accessed [30-04-2021].Suche in Google Scholar
© 2024 the author(s), published by De Gruyter
This work is licensed under the Creative Commons Attribution 4.0 International License.
Artikel in diesem Heft
- Editorial
- Focus on NLENG 2023 Volume 12 Issue 1
- Research Articles
- Seismic vulnerability signal analysis of low tower cable-stayed bridges method based on convolutional attention network
- Robust passivity-based nonlinear controller design for bilateral teleoperation system under variable time delay and variable load disturbance
- A physically consistent AI-based SPH emulator for computational fluid dynamics
- Asymmetrical novel hyperchaotic system with two exponential functions and an application to image encryption
- A novel framework for effective structural vulnerability assessment of tubular structures using machine learning algorithms (GA and ANN) for hybrid simulations
- Flow and irreversible mechanism of pure and hybridized non-Newtonian nanofluids through elastic surfaces with melting effects
- Stability analysis of the corruption dynamics under fractional-order interventions
- Solutions of certain initial-boundary value problems via a new extended Laplace transform
- Numerical solution of two-dimensional fractional differential equations using Laplace transform with residual power series method
- Fractional-order lead networks to avoid limit cycle in control loops with dead zone and plant servo system
- Modeling anomalous transport in fractal porous media: A study of fractional diffusion PDEs using numerical method
- Analysis of nonlinear dynamics of RC slabs under blast loads: A hybrid machine learning approach
- On theoretical and numerical analysis of fractal--fractional non-linear hybrid differential equations
- Traveling wave solutions, numerical solutions, and stability analysis of the (2+1) conformal time-fractional generalized q-deformed sinh-Gordon equation
- Influence of damage on large displacement buckling analysis of beams
- Approximate numerical procedures for the Navier–Stokes system through the generalized method of lines
- Mathematical analysis of a combustible viscoelastic material in a cylindrical channel taking into account induced electric field: A spectral approach
- A new operational matrix method to solve nonlinear fractional differential equations
- New solutions for the generalized q-deformed wave equation with q-translation symmetry
- Optimize the corrosion behaviour and mechanical properties of AISI 316 stainless steel under heat treatment and previous cold working
- Soliton dynamics of the KdV–mKdV equation using three distinct exact methods in nonlinear phenomena
- Investigation of the lubrication performance of a marine diesel engine crankshaft using a thermo-electrohydrodynamic model
- Modeling credit risk with mixed fractional Brownian motion: An application to barrier options
- Method of feature extraction of abnormal communication signal in network based on nonlinear technology
- An innovative binocular vision-based method for displacement measurement in membrane structures
- An analysis of exponential kernel fractional difference operator for delta positivity
- Novel analytic solutions of strain wave model in micro-structured solids
- Conditions for the existence of soliton solutions: An analysis of coefficients in the generalized Wu–Zhang system and generalized Sawada–Kotera model
- Scale-3 Haar wavelet-based method of fractal-fractional differential equations with power law kernel and exponential decay kernel
- Non-linear influences of track dynamic irregularities on vertical levelling loss of heavy-haul railway track geometry under cyclic loadings
- Fast analysis approach for instability problems of thin shells utilizing ANNs and a Bayesian regularization back-propagation algorithm
- Validity and error analysis of calculating matrix exponential function and vector product
- Optimizing execution time and cost while scheduling scientific workflow in edge data center with fault tolerance awareness
- Estimating the dynamics of the drinking epidemic model with control interventions: A sensitivity analysis
- Online and offline physical education quality assessment based on mobile edge computing
- Discovering optical solutions to a nonlinear Schrödinger equation and its bifurcation and chaos analysis
- New convolved Fibonacci collocation procedure for the Fitzhugh–Nagumo non-linear equation
- Study of weakly nonlinear double-diffusive magneto-convection with throughflow under concentration modulation
- Variable sampling time discrete sliding mode control for a flapping wing micro air vehicle using flapping frequency as the control input
- Error analysis of arbitrarily high-order stepping schemes for fractional integro-differential equations with weakly singular kernels
- Solitary and periodic pattern solutions for time-fractional generalized nonlinear Schrödinger equation
- An unconditionally stable numerical scheme for solving nonlinear Fisher equation
- Effect of modulated boundary on heat and mass transport of Walter-B viscoelastic fluid saturated in porous medium
- Analysis of heat mass transfer in a squeezed Carreau nanofluid flow due to a sensor surface with variable thermal conductivity
- Navigating waves: Advancing ocean dynamics through the nonlinear Schrödinger equation
- Experimental and numerical investigations into torsional-flexural behaviours of railway composite sleepers and bearers
- Novel dynamics of the fractional KFG equation through the unified and unified solver schemes with stability and multistability analysis
- Analysis of the magnetohydrodynamic effects on non-Newtonian fluid flow in an inclined non-uniform channel under long-wavelength, low-Reynolds number conditions
- Convergence analysis of non-matching finite elements for a linear monotone additive Schwarz scheme for semi-linear elliptic problems
- Global well-posedness and exponential decay estimates for semilinear Newell–Whitehead–Segel equation
- Petrov-Galerkin method for small deflections in fourth-order beam equations in civil engineering
- Solution of third-order nonlinear integro-differential equations with parallel computing for intelligent IoT and wireless networks using the Haar wavelet method
- Mathematical modeling and computational analysis of hepatitis B virus transmission using the higher-order Galerkin scheme
- Mathematical model based on nonlinear differential equations and its control algorithm
- Bifurcation and chaos: Unraveling soliton solutions in a couple fractional-order nonlinear evolution equation
- Space–time variable-order carbon nanotube model using modified Atangana–Baleanu–Caputo derivative
- Minimal universal laser network model: Synchronization, extreme events, and multistability
- Valuation of forward start option with mean reverting stock model for uncertain markets
- Geometric nonlinear analysis based on the generalized displacement control method and orthogonal iteration
- Fuzzy neural network with backpropagation for fuzzy quadratic programming problems and portfolio optimization problems
- B-spline curve theory: An overview and applications in real life
- Nonlinearity modeling for online estimation of industrial cooling fan speed subject to model uncertainties and state-dependent measurement noise
- Quantitative analysis and modeling of ride sharing behavior based on internet of vehicles
- Review Article
- Bond performance of recycled coarse aggregate concrete with rebar under freeze–thaw environment: A review
- Retraction
- Retraction of “Convolutional neural network for UAV image processing and navigation in tree plantations based on deep learning”
- Special Issue: Dynamic Engineering and Control Methods for the Nonlinear Systems - Part II
- Improved nonlinear model predictive control with inequality constraints using particle filtering for nonlinear and highly coupled dynamical systems
- Anti-control of Hopf bifurcation for a chaotic system
- Special Issue: Decision and Control in Nonlinear Systems - Part I
- Addressing target loss and actuator saturation in visual servoing of multirotors: A nonrecursive augmented dynamics control approach
- Collaborative control of multi-manipulator systems in intelligent manufacturing based on event-triggered and adaptive strategy
- Greenhouse monitoring system integrating NB-IOT technology and a cloud service framework
- Special Issue: Unleashing the Power of AI and ML in Dynamical System Research
- Computational analysis of the Covid-19 model using the continuous Galerkin–Petrov scheme
- Special Issue: Nonlinear Analysis and Design of Communication Networks for IoT Applications - Part I
- Research on the role of multi-sensor system information fusion in improving hardware control accuracy of intelligent system
- Advanced integration of IoT and AI algorithms for comprehensive smart meter data analysis in smart grids
Artikel in diesem Heft
- Editorial
- Focus on NLENG 2023 Volume 12 Issue 1
- Research Articles
- Seismic vulnerability signal analysis of low tower cable-stayed bridges method based on convolutional attention network
- Robust passivity-based nonlinear controller design for bilateral teleoperation system under variable time delay and variable load disturbance
- A physically consistent AI-based SPH emulator for computational fluid dynamics
- Asymmetrical novel hyperchaotic system with two exponential functions and an application to image encryption
- A novel framework for effective structural vulnerability assessment of tubular structures using machine learning algorithms (GA and ANN) for hybrid simulations
- Flow and irreversible mechanism of pure and hybridized non-Newtonian nanofluids through elastic surfaces with melting effects
- Stability analysis of the corruption dynamics under fractional-order interventions
- Solutions of certain initial-boundary value problems via a new extended Laplace transform
- Numerical solution of two-dimensional fractional differential equations using Laplace transform with residual power series method
- Fractional-order lead networks to avoid limit cycle in control loops with dead zone and plant servo system
- Modeling anomalous transport in fractal porous media: A study of fractional diffusion PDEs using numerical method
- Analysis of nonlinear dynamics of RC slabs under blast loads: A hybrid machine learning approach
- On theoretical and numerical analysis of fractal--fractional non-linear hybrid differential equations
- Traveling wave solutions, numerical solutions, and stability analysis of the (2+1) conformal time-fractional generalized q-deformed sinh-Gordon equation
- Influence of damage on large displacement buckling analysis of beams
- Approximate numerical procedures for the Navier–Stokes system through the generalized method of lines
- Mathematical analysis of a combustible viscoelastic material in a cylindrical channel taking into account induced electric field: A spectral approach
- A new operational matrix method to solve nonlinear fractional differential equations
- New solutions for the generalized q-deformed wave equation with q-translation symmetry
- Optimize the corrosion behaviour and mechanical properties of AISI 316 stainless steel under heat treatment and previous cold working
- Soliton dynamics of the KdV–mKdV equation using three distinct exact methods in nonlinear phenomena
- Investigation of the lubrication performance of a marine diesel engine crankshaft using a thermo-electrohydrodynamic model
- Modeling credit risk with mixed fractional Brownian motion: An application to barrier options
- Method of feature extraction of abnormal communication signal in network based on nonlinear technology
- An innovative binocular vision-based method for displacement measurement in membrane structures
- An analysis of exponential kernel fractional difference operator for delta positivity
- Novel analytic solutions of strain wave model in micro-structured solids
- Conditions for the existence of soliton solutions: An analysis of coefficients in the generalized Wu–Zhang system and generalized Sawada–Kotera model
- Scale-3 Haar wavelet-based method of fractal-fractional differential equations with power law kernel and exponential decay kernel
- Non-linear influences of track dynamic irregularities on vertical levelling loss of heavy-haul railway track geometry under cyclic loadings
- Fast analysis approach for instability problems of thin shells utilizing ANNs and a Bayesian regularization back-propagation algorithm
- Validity and error analysis of calculating matrix exponential function and vector product
- Optimizing execution time and cost while scheduling scientific workflow in edge data center with fault tolerance awareness
- Estimating the dynamics of the drinking epidemic model with control interventions: A sensitivity analysis
- Online and offline physical education quality assessment based on mobile edge computing
- Discovering optical solutions to a nonlinear Schrödinger equation and its bifurcation and chaos analysis
- New convolved Fibonacci collocation procedure for the Fitzhugh–Nagumo non-linear equation
- Study of weakly nonlinear double-diffusive magneto-convection with throughflow under concentration modulation
- Variable sampling time discrete sliding mode control for a flapping wing micro air vehicle using flapping frequency as the control input
- Error analysis of arbitrarily high-order stepping schemes for fractional integro-differential equations with weakly singular kernels
- Solitary and periodic pattern solutions for time-fractional generalized nonlinear Schrödinger equation
- An unconditionally stable numerical scheme for solving nonlinear Fisher equation
- Effect of modulated boundary on heat and mass transport of Walter-B viscoelastic fluid saturated in porous medium
- Analysis of heat mass transfer in a squeezed Carreau nanofluid flow due to a sensor surface with variable thermal conductivity
- Navigating waves: Advancing ocean dynamics through the nonlinear Schrödinger equation
- Experimental and numerical investigations into torsional-flexural behaviours of railway composite sleepers and bearers
- Novel dynamics of the fractional KFG equation through the unified and unified solver schemes with stability and multistability analysis
- Analysis of the magnetohydrodynamic effects on non-Newtonian fluid flow in an inclined non-uniform channel under long-wavelength, low-Reynolds number conditions
- Convergence analysis of non-matching finite elements for a linear monotone additive Schwarz scheme for semi-linear elliptic problems
- Global well-posedness and exponential decay estimates for semilinear Newell–Whitehead–Segel equation
- Petrov-Galerkin method for small deflections in fourth-order beam equations in civil engineering
- Solution of third-order nonlinear integro-differential equations with parallel computing for intelligent IoT and wireless networks using the Haar wavelet method
- Mathematical modeling and computational analysis of hepatitis B virus transmission using the higher-order Galerkin scheme
- Mathematical model based on nonlinear differential equations and its control algorithm
- Bifurcation and chaos: Unraveling soliton solutions in a couple fractional-order nonlinear evolution equation
- Space–time variable-order carbon nanotube model using modified Atangana–Baleanu–Caputo derivative
- Minimal universal laser network model: Synchronization, extreme events, and multistability
- Valuation of forward start option with mean reverting stock model for uncertain markets
- Geometric nonlinear analysis based on the generalized displacement control method and orthogonal iteration
- Fuzzy neural network with backpropagation for fuzzy quadratic programming problems and portfolio optimization problems
- B-spline curve theory: An overview and applications in real life
- Nonlinearity modeling for online estimation of industrial cooling fan speed subject to model uncertainties and state-dependent measurement noise
- Quantitative analysis and modeling of ride sharing behavior based on internet of vehicles
- Review Article
- Bond performance of recycled coarse aggregate concrete with rebar under freeze–thaw environment: A review
- Retraction
- Retraction of “Convolutional neural network for UAV image processing and navigation in tree plantations based on deep learning”
- Special Issue: Dynamic Engineering and Control Methods for the Nonlinear Systems - Part II
- Improved nonlinear model predictive control with inequality constraints using particle filtering for nonlinear and highly coupled dynamical systems
- Anti-control of Hopf bifurcation for a chaotic system
- Special Issue: Decision and Control in Nonlinear Systems - Part I
- Addressing target loss and actuator saturation in visual servoing of multirotors: A nonrecursive augmented dynamics control approach
- Collaborative control of multi-manipulator systems in intelligent manufacturing based on event-triggered and adaptive strategy
- Greenhouse monitoring system integrating NB-IOT technology and a cloud service framework
- Special Issue: Unleashing the Power of AI and ML in Dynamical System Research
- Computational analysis of the Covid-19 model using the continuous Galerkin–Petrov scheme
- Special Issue: Nonlinear Analysis and Design of Communication Networks for IoT Applications - Part I
- Research on the role of multi-sensor system information fusion in improving hardware control accuracy of intelligent system
- Advanced integration of IoT and AI algorithms for comprehensive smart meter data analysis in smart grids

