Home Bond performance of recycled coarse aggregate concrete with rebar under freeze–thaw environment: A review
Article Open Access

Bond performance of recycled coarse aggregate concrete with rebar under freeze–thaw environment: A review

  • Ting Wang , Xuechao Yang , Weishen Zhang , Qifan Yang , Deqiang Yang , Bangxiang Li , Tian Su EMAIL logo and Xuefeng Mei EMAIL logo
Published/Copyright: May 2, 2024
Download Article (PDF)
Become an author with De Gruyter Brill
Submit Manuscript Author Information
Nonlinear Engineering
From the journal Nonlinear Engineering Volume 13 Issue 1

Abstract

In this article, a review focusing on the frost resistance of recycled coarse aggregate concrete (RAC) and the bond performance of RAC with rebar under freeze–thaw environment is carried out. The results show that there are still some controversies about the advantages and disadvantages of the frost resistance of RAC, and many influencing factors have not been considered. The mass of the RAC pullout specimens shows a trend of first increasing and then decreasing after freeze‒thaw cycles. The failure modes of the RAC pullout specimens after freeze‒thaw cycles include pullout failure, pullout-splitting failure, splitting failure, and rebar yielding failure. The bond performance of RAC with rebar shows a degradation trend after freeze‒thaw cycles, mainly in the decrease in bond strength and the increase in bond slip. The bond performance of RAC specimens is inferior to that of natural aggregate concrete specimens after freeze‒thaw cycles. The bond strength prediction models and the bond–slip constitutive relation prediction models of RAC with rebar after freeze‒thaw cycles have been summarized to ensure that engineers can better understand their applicability. The bond stress distribution between the RAC and rebar in the anchoring area is not uniform and constantly changes with the number of freeze‒thaw cycles. The degradation mechanism of the bond performance of RAC with rebar after freeze‒thaw cycles is analyzed.

Keywords: recycled coarse aggregate concrete; rebar; bond performance; freeze‒thaw cycles; bond–slip curve; degradation mechanism

1 Introduction

Concrete structures have a certain design life, and a large amount of concrete waste will be generated during the demolition process [1,2]. The collapse of concrete buildings caused by natural disasters such as earthquakes also produces a large amount of concrete waste [3,4]. In China, more than 95% of construction waste is transported to the suburbs for stacking or landfilling, which not only occupies a large amount of land resources but also causes a series of environmental pollution problems [5,6,7]. In addition, concrete is composed of sand, stone, and other aggregates, so the contradiction between the increase in the demand for concrete and the lack of aggregate has become increasingly prominent due to the large exploitation of natural sand and stone [5,8]. To realize the sustainable development of society and the effective protection of the environment, a new way is needed to reasonably deal with construction waste [9,10]. Recycled coarse aggregate concrete (RAC) technology is proposed to solve these problems, which can not only solve the shortcomings of traditional treatment methods but also realize the sustainable utilization of resources [11–13]. RAC technology uses broken recycled aggregate as coarse aggregate or fine aggregate to produce new concrete [14–17]. RAC is a kind of green concrete with sustainable development that not only solves the problem of concrete waste treatment but also effectively reduces the exploitation of natural sand and stone resources, which is also conducive to improving environmental pollution [18–21].

The bond performance of concrete with rebar is correlated with the bearing capacity of reinforced concrete structures [22]. Insufficient bond force between concrete and rebar can lead to premature failure of reinforced concrete structures [23]. In addition, freeze–thaw damage of concrete is very common in cold regions [24,25]. Compared with ordinary coarse aggregate, the surface of recycled coarse aggregate (RCA) is attached to old cement mortar so that it has higher porosity and water absorption [26]. The use of RCA will introduce a new interfacial transition zone in concrete [27], as shown in Figure 1, which will affect the frost resistance of concrete and the bond performance between concrete and rebar [28–30]. After freeze–thaw damage, the durability of concrete deteriorates, and the normal use of buildings will be affected. The influence of freeze–thaw damage on the safety of concrete structures is a serious problem in cold regions. Therefore, it is particularly important to study the frost resistance of RAC and the bond performance of RAC with rebar under freeze–thaw environment.

Figure 1 Schematic diagram of the RAC and NAC models. (a) NAC and (b) RAC.
Figure 1

Schematic diagram of the RAC and NAC models. (a) NAC and (b) RAC.

In this article, the frost resistance of RAC, the bond performance indicators (the failure modes, bond strength, bond slip, bond–slip curves), the bond strength prediction models, and the bond–slip constitutive relation prediction models of RAC with rebar after freeze–thaw cycles were reviewed. Furthermore, the degradation mechanism of the bond performance of RAC with rebar after freeze–thaw cycles was analyzed.

2 Frost resistance of RAC

The frost resistance of the RAC was closely related to the bond performance between the RAC and rebar under freeze‒thaw environment. Compared with natural aggregate concrete (NAC), RAC had the characteristics of high water absorption of aggregate and microcracks inside, and the frost resistance of RAC was also different from that of NAC [31]. Some scholars have found through research that the frost resistance of RAC was inferior to that of NAC. Roumiana et al. [32] found that RCA would drain water into the surrounding cement mortar when subjected to freeze‒thaw, resulting in more serious freeze‒thaw damage. Therefore, the frost resistance of RAC was poor, and it was not recommended for use in cold environments. Only when the water–cement ratio was less than 0.55 could it be used in medium cold regions. Cheng et al. [33] analyzed the effect of the RCA content on the frost resistance of RAC and found that the frost resistance of RAC gradually decreased with increasing RCA content. Zhu and Li [34] pointed out that the high water absorption of RCA seriously affected the frost resistance of RAC. The compressive strength, mass, and relative dynamic elastic modulus of RAC after freeze‒thaw cycles were lower than those of NAC. Lu [35] investigated the frost resistance of RAC with different RCA replacement rates in fresh water and 3.5% NaCl solution. The test results show that when the water–cement ratio was the same, the frost resistance of RAC was significantly worse than that of NAC, and the frost resistance of concrete specimens with a 30% RCA replacement rate was the worst.

However, some scholars found that the frost resistance of RAC was comparable to that of NAC or even better than that of NAC. Yildirim et al. [36] showed that the frost resistance of RAC was comparable to that of NAC after 300 freeze‒thaw cycles. Cao et al. [37] reported that when the RCA replacement rate was less than 50%, the basic mechanical properties of RAC after freeze‒thaw cycles were similar to those of NAC. Fan [38] discovered that when the RCA replacement rate was 33%, the frost resistance of RAC was the best, which was similar to that of NAC.

Scholars have also conducted research on improving the frost resistance of RAC. Zhu and Li [34] found that the method of reducing the water cement ratio could improve the frost resistance of RAC. Richardson et al. [39] screened and washed RCA before use, making the grading curve of RCA similar to that of NAC. The test results show that the frost resistance of RAC was better than that of NAC. The reason was that the washing of the RCA before use reduced the content of fine particles, leaving better quality aggregates so that the RAC had a higher compressive strength, thereby improving the frost resistance of the RAC. Chen et al. [40] discovered that adding silica fume or air-entraining agent could significantly improve the frost resistance of RAC. Zhang et al. [41] pointed out that the frost resistance of RAC with an air-entraining agent was even better than that of NAC. Qin et al. [42] showed that the frost resistance of RAC could be improved by adding antifreeze. Gokce et al. [43] pointed out that the frost resistance of RAC prepared by RCA obtained from the original concrete mixed with air-entraining agent was better, and the crack development rate of RAC after freeze‒thaw cycles was even lower than that of NAC; the frost resistance of RAC prepared by RCA obtained from the original concrete mixed without air-entraining agent was poor. This agrees with the findings of Wang [44]. Liu et al. [45] discovered that the frost resistance of RAC prepared by RCA obtained from original concrete with high frost resistance was better, while that prepared by RCA obtained from original concrete with poor frost resistance was poor. The reason was that the freeze‒thaw cycle seriously damaged the original bond mortar inside the RAC, exacerbating crack development.

In addition, Du [46] and Hu and Wu [47] investigated the salt-frost resistance of RAC, and the main conclusions were as follows: with the increase in the number of salt-frost cycles, the cubic compressive strength and the relative dynamic elastic modulus of RAC showed a downward trend; the frost resistance of RAC in salt water was inferior to that in fresh water; and the salt-frost resistance of RAC was inferior to that of NAC.

In summary, scholars have carried out much research on the frost resistance of RAC, but there are still some controversies regarding whether RCA deteriorates the frost resistance of concrete. In addition, there are still few studies on the salt-frost resistance of RAC, and many influencing factors have not been considered. Therefore, it is necessary to further study the salt-frost resistance of RAC.

3 Bond performance of RAC with rebar under freeze‒thaw environment

3.1 Apparent phenomenon and mass loss of RAC pullout specimens

The appearance and mass loss of the RAC pullout specimens after freeze‒thaw cycles are shown in Figures 2 and 3 [48], respectively. As the number of freeze‒thaw cycles increased, the cement mortar and the fine aggregates on the concrete surface slightly peeled off, causing the concrete surface to become rough; as the number of freeze‒thaw cycles continued to increase, the peeling of cement mortar and fine aggregate became more severe, the RCA was exposed, and even coarse aggregate peeling occurred. The surface damage of RAC pullout specimens after salt-freezing cycles was much more severe than that of RAC pullout specimens after freeze‒thaw cycles [48]. This is due to the combined effect of NaCl solution and freeze‒thaw cycles, which increases the water saturation of concrete specimens, making RAC more prone to freeze‒thaw damage, resulting in more severe freeze‒thaw damage to concrete specimens.

Figure 2 Apparent phenomenon after freeze‒thaw cycles.
Figure 2

Apparent phenomenon after freeze‒thaw cycles.

Figure 3 Mass loss of RAC pullout specimens.
Figure 3

Mass loss of RAC pullout specimens.

The mass of the RAC pullout specimens showed a trend of first increasing and then decreasing. The reason is that in the early stage of the freeze‒thaw cycle, external moisture enters the concrete specimen through cracks, leading to an increase in mass; as the number of freeze‒thaw cycles increases, the cement mortar and aggregates on the surface of the concrete specimen peel off, resulting in a decrease in mass. The mass change of RAC pullout specimens after salt-freezing cycles was much more severe than that of RAC pullout specimens after freeze‒thaw cycles [48].

3.2 Pullout failure (PF) mode

The failure modes of the RAC pullout specimens after freeze‒thaw cycles included PF, pullout-splitting failure (PSF), splitting failure (SF), and rebar yielding failure (RYF), as shown in Figure 4 [48,49]. For PF, the free end of the steel bar was trapped in the PVC pipe, and a small amount of concrete debris adhered to the steel bar that was pulled out at the loading end of the steel bar, but the concrete did not undergo significant damage [49]. For PSF, cracks appeared on the concrete surface when PF occurred, but the concrete protective layer was relatively intact, and the steel bars were slowly pulled out from the concrete [50]. For SF, the specimen was suddenly destroyed during the loading process, and longitudinal SF of the concrete occurred. There was no significant displacement between the bonding surface of the rebar and concrete [51]; for RYF, the external tensile force was less than the bond stress between the rebar and concrete, resulting in only relative slip between the rebar and concrete near the loading end of the specimen during the loading process, while no relative slip occurred at the free end. When the pull load reached the yield strength of the rebar, the rebar was pulled off at the loading end, the “necking” phenomenon occurred at the pulling off part, and there were no cracks on the surface of the specimen [52].

Figure 4 Failure modes of RAC pullout specimens.
Figure 4

Failure modes of RAC pullout specimens.

Table 1 lists the failure modes of specimens obtained from the literature [50–58] (d represents steel bar diameter; c represents cover depth; l represents embedment length). The test results of Li [50] showed that for specimens with rebar diameters of 12 and 14 mm, the failure mode after freeze‒thaw cycles was PF; for the specimens with rebar diameters of 18 mm, the failure mode after 25 and 50 freeze‒thaw cycles in salt solution was PF, while the failure mode after 75 freeze‒thaw cycles was SF. Cao [51] pointed out that only the specimen with a large protective layer thickness and an anchorage length of 10d experienced steel bar yielding failure before freeze‒thaw cycles, while the remaining specimens underwent PF. Wang [52,53] found that when the number of freeze‒thaw cycles was less than 175, the failure mode was SF; when the number of freeze‒thaw cycles was more than 200, the failure mode was PSF. When the anchorage length exceeded 10d, the failure mode after freeze‒thaw cycles was RYF. The test results of An [54] showed that the number of freeze‒thaw cycles and the rebar diameter both affected the failure mode of the specimens. The test results of Shang [55] showed that rebar diameter was the key factor affecting the failure mode of the specimen after freeze‒thaw cycles. When the rebar diameter was small, the failure mode was PF; when the rebar diameter was large, the failure mode was SF. Liu [56] found that the number of freeze‒thaw cycles affected the failure mode of the specimens, while Su [58] found that stirrups were a key factor affecting the failure mode of the specimen after freeze‒thaw cycles. The rebar diameter, anchorage length, number of freeze‒thaw cycles, solution type and stirrup both affected the failure mode of the specimens after freeze‒thaw cycles. Therefore, it was necessary to comprehensively consider the impact of various factors on the failure mode of RAC specimens after freeze‒thaw cycles.

Table 1

Factors for determining the failure modes

F–T cycles d (mm) Steel bar type c (mm) Solution l (mm) Failure modes
Li [50] 0–75 12 Plain 69 Fresh water 84 PF
12 Salt solution 84 PF
14/18 Deformed 68/66 Fresh water 98/126 PF
14 68 Salt solution 98 PF
0–50 18 Deformed 66 Salt solution 126 PF
75 18 66 126 SF
Cao et al. [51] 0–100 16 Deformed 67 Fresh water 48 PF
80
128
0 16 Deformed 67 Fresh water 160 RYF
25–100 16 Deformed 67 Fresh water 160 PF
0–100 16 Deformed 55 Fresh water 80 PF
42
Wang et al. [52] 0–175 16 Deformed 67 Fresh water 80 SF
200 PSF
Wang et al. [53] 0–150 16 Deformed 67 Fresh water 80 SF
200 PSF
0–200 16 67 160 RYF
0–200 20 65 100 SF
0–200 20 65 200 SF
An et al. [54] 0–75 12 Deformed 69 Fresh water 60 PF
0–50 16 67 80 PF
75 16 67 80 SF
0–75 20 65 100 SF
Shang et al. [55] 0–75 12 Plain 69 Fresh water 60 PF
14 Deformed 68 70 PF
18 Deformed 66 70 SF
22 Deformed 64 70 SF
Liu et al. [56] 0–150 16 Deformed 42 Fresh water 80 SF
200–300 SF/PF
Ren et al. [57] 0–75 14 Deformed 68 Fresh water 98 SF
0–75 18 66 126 SF
0–75 14 Deformed 68 Salt solution 98 SF
0–75 18 66 126 SF
Su et al. [58] 0–125 18 Deformed (stirrup) 41 Salt solution 100 PSF
0–125 18 Deformed (stirrup) 41 Fresh water 100 PSF
0–125 18 Deformed (no stirrup) 41 Fresh water 100 SF

3.3 Degradation law of the bond performance after freeze‒thaw cycles

After freeze‒thaw cycles, the concrete was damaged from outside to inside [59], which in turn destroyed the bond interface between the concrete and rebar, resulting in the degradation of the bond performance. Figure 5 shows the test results of Li [50], Cao et al. [51], Wang et al. [52,53], and An et al. [54]. The bond performance of RAC with rebar showed a degradation trend after freeze‒thaw cycles, mainly in the decrease in bond strength and the increase in bond slip. An et al. [54] considered that the reason for the decrease in the bond strength and increase in the relative slip after freeze‒thaw cycles was the destruction of the bond interface between concrete and rebar after freeze‒thaw cycles.

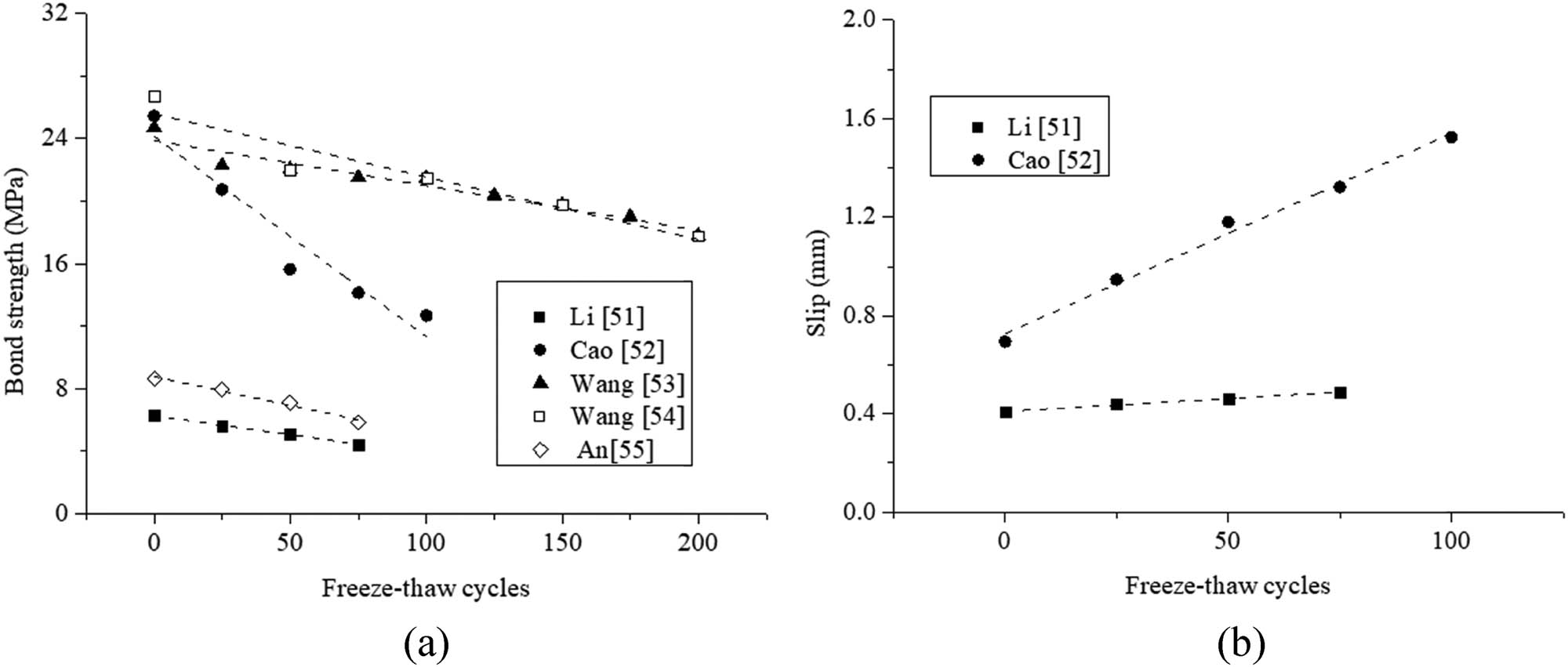
Figure 5 Performance of RAC with rebar after freeze‒thaw cycles: (a) bond strength; (b) slip.
Figure 5

Performance of RAC with rebar after freeze‒thaw cycles: (a) bond strength; (b) slip.

Shang et al. [61] found that the bond strength of RAC with deformed rebar was greater than that with plain rebar after the same number of freeze‒thaw cycles. Cao et al. [62,63] investigated the bond performance of RAC with rebar by using beam-type specimens closer to the actual stress situation, and the results verified the above conclusions. It was also found that the concrete strength, rebar diameter, and anchorage length had a great influence on the bond performance of RAC with rebar after freeze‒thaw cycles, as shown in Figure 6(a–c). Meng [64] conducted an experimental study on the bond performance between rebar and concrete with different RCA replacement rates after freeze‒thaw cycles through pullout tests and found that the degradation of bond performance accelerated with increasing RCA replacement rate, as shown in Figure 6(d). Figure 6 shows that the bond strength of RAC with rebar after freeze‒thaw cycles decreased with increasing anchorage length (rebar diameter and RCA replacement rate), while it increased with increasing concrete strength.

Figure 6 Influencing factors of bond strength: (a) anchorage length, (b) concrete strength, (c) rebar diameter, and (d) RCA replacement rate.
Figure 6

Influencing factors of bond strength: (a) anchorage length, (b) concrete strength, (c) rebar diameter, and (d) RCA replacement rate.

Liu et al. [56] considered the influence of different RCA replacement rates on the bond performance of RAC with rebar under a freeze‒thaw environment and found that the bond strength decreased with increasing RCA replacement rate. In this study, concrete with different RCA replacement rates adopted the same mix proportion, resulting in different initial concrete strengths. Li et al. [60] investigated the bond performance of rebar and RAC with different RCA replacement rates under the premise of ensuring the initial concrete strength and found that when the number of freeze‒thaw cycles was large, the bond strength of RAC specimens was higher than that of NAC specimens, which was different from Liu et al. [56]. Therefore, it was necessary to consider the influence of initial concrete strength when studying the bond performance between rebar and RAC with different RCA replacement rates.

Shang et al. [61], Ren et al. [57], Su et al. [65], and Li et al. [66] conducted a series of studies on the bond performance of RAC with rebar after salt-frost cycles and found that the degradation degree of the bond performance of RAC with rebar after salt-frost cycles was significantly greater than that after freeze‒thaw cycles, which was mainly manifested in the decrease in bond strength and the increase in peak slip, as shown in Figure 7. It can be seen that salt-frost cycling would aggravate the degradation of the bond performance of the RAC with rebar. Shang et al. [61] found that the bond strength of RAC with rebar showed a decreasing trend, while the peak slip showed an increasing trend after freeze‒thaw cycles in freshwater or seawater. Ren et al. [57] discovered that the bond strength of RAC with rebar decreased with increasing rebar diameter; the loss of cube compressive strength of RAC was greater than that of bond strength of RAC with rebar after the same number of freeze‒thaw cycles. Su et al. [65] found that with the increase in salt-frost cycles, the ultimate bond strength and bond stiffness of RAC with rebar decreased continuously, while the peak slip increased continuously; the ultimate bond strength and bond stiffness of RAC with rebar were lower than those of NAC with rebar, while the peak slip of RAC with rebar was larger than that of NAC with rebar.

Figure 7 Bond performance after freeze‒thaw cycles and salt-frost cycles: (a) bond strength; (b) slip.
Figure 7

Bond performance after freeze‒thaw cycles and salt-frost cycles: (a) bond strength; (b) slip.

Su et al. [67,68] investigated the effect of freeze‒thaw and repeated loading on the bond performance of RAC with rebar and found that the bond strength of specimens under repeated loading was lower than that under monotonic loading. As the number of repeated loadings increased, the amount of rebar slip accumulated, leading to an increase in rebar slip, resulting in the peak slip of the specimen under repeated loading being greater than that under monotonic loading, as shown in Figure 8. When the number of repeated loads was small, the slip growth of rebar slip was larger; as the number of repeated loadings increased, the growth of steel bars decreased.

Figure 8 Slip of RAC with rebar under repeated loading.
Figure 8

Slip of RAC with rebar under repeated loading.

3.4 Bond–slip curves

The bond–slip curves of specimens with PF and PSF were relatively complete and divided into the micro slip section, the slip section, the descent section, and the residual section. The descriptions of each section were as follows:

  1. Microslip section: the loading end of the rebar experienced slight sliding, while the free end of the rebar did not experience sliding, indicating that the load was relatively small and had not been transmitted to the free end of the rebar.

  2. Slip section: the free end of the rebar began to slip, and as the ultimate load was about to be reached, the slip of the rebar began to accelerate, and the bond–slip curve exhibited nonlinearity.

  3. Descent section: after reaching the ultimate load, the load began to decrease, and the slip between the loading end and the free end rapidly increased.

  4. Residual section: The bond force between the concrete and rebar remained basically unchanged, and the slip value continued to increase.

The bond–slip curves of specimens with SF only had an ascending segment, which could be divided into microslip sections, slip sections, and splitting sections. The description of the splitting section was as follows:

Splitting section: the concrete around the rebar underwent local damage, and cracks began to appear in the concrete at the loading end, rapidly developing toward the free end and the concrete surface. Finally, the crack penetrated the entire specimen, and the specimen was ultimately split into two–three parts.

As shown in Figure 9 [65], the slope of the ascending section of the bond–slip curve gradually decreased with increasing freeze‒thaw cycles; that is, the stiffness gradually decreased. The reason for this situation is that the concrete strength decreases continuously after freeze‒thaw cycles, and the damage to the bonding surface between the concrete and rebar also increases, which makes the bond performance of the concrete and rebar degrade continuously. While the bond strength decreases continuously, the corresponding slip increases continuously, resulting in the slope of the bond–slip curve decreasing continuously.

Figure 9 Bond–slip curve of RAC with rebar under monotonic loading: (a) pullout SF; (b) SF.
Figure 9

Bond–slip curve of RAC with rebar under monotonic loading: (a) pullout SF; (b) SF.

As shown in Figure 10 [68], the slope of the ascending section of the bond–slip curve under repeated loading was lower than that under monotonic loading. The reason for this situation is that repeated loading exacerbates the degradation of bond strength and increases slip, resulting in a decrease in the slope of the bond–slip curve.

Figure 10 Bond–slip curve of RAC with rebar under repeated loading.
Figure 10

Bond–slip curve of RAC with rebar under repeated loading.

3.5 Bond performance at different anchoring positions

The bond performance of RAC with rebar was usually investigated assuming that the bond stress was uniformly distributed along the anchorage length. Actually, the bond stress and the relative slip between the RAC and rebar were not uniformly distributed along the anchorage length. Cao et al. [62], Meng [64], Liu et al. [56], and Su et al. [58] investigated the effect of freeze‒thaw cycles on the bond performance at different anchoring positions by inserting strain gauges inside the rebar. Meng [64] pointed out that when the load level was low, the distribution of bond stress along the anchorage length was approximately uniform. However, as the load level increased, the bond stress gradually showed a peak point. Su et al. [48,58,67] found that the bond stress distribution between RAC and rebar in the anchoring area was not uniform and constantly changed with the number of freeze‒thaw cycles. Both freeze‒thaw cycles and repeated loading could accelerate the movement of the maximum bond stress from near the loading end to near the free end (as shown in Figure 11).

Figure 11 Bond stress at different anchoring positions: (a) bond stress distribution after 0 freeze‒thaw cycles; (b) bond stress distribution after 75 freeze‒thaw cycles; (c) bond stress distribution after 125 freeze‒thaw cycles; (d) bond stress distribution under repeated loading.
Figure 11

Bond stress at different anchoring positions: (a) bond stress distribution after 0 freeze‒thaw cycles; (b) bond stress distribution after 75 freeze‒thaw cycles; (c) bond stress distribution after 125 freeze‒thaw cycles; (d) bond stress distribution under repeated loading.

3.6 Calculation model of bond performance between RAC and rebar after freeze‒thaw cycles

The bond‒slip constitutive relationship model between the RAC and rebar before freeze‒thaw cycles mainly included Xiao’s model, Prince’s model, and the three-stage model [23]. Based on the mechanical model of the “softened inner layer + elastic outer cylinder” theory (Figure 12), An et al. [54] established the bond strength degradation model of RAC specimens under the freeze‒thaw environment with the splitting tensile strength of RAC as the damage factor; Li et al. [60] proposed the theoretical calculation formula of peak bond strength and yield bond strength of RAC specimens under the freeze‒thaw environment. Niu et al. [69] analyzed the energy damage of the bond interface between RAC and rebar from the perspective of damage mechanics and established the bond–slip damage constitutive model of RAC and rebar after freeze‒thaw cycles.

Figure 12 “Softened inner layer + elastic outer cylinder” model diagram.
Figure 12

“Softened inner layer + elastic outer cylinder” model diagram.

The bond strength calculation model of RAC specimens after freeze‒thaw cycles established by Shang et al. [55] considered the influence of rebar type and diameter on the bond strength:

For plain rebar:

(1) τ = 0.006 N 2 − 0.0644 N + 2.2055 ,

For deformed rebar:

(2) d = 14 mm τ = 0.0015 N 2 − 0.2118 N + 12.967 ,

(3) d = 18 mm τ = 0.0014 N 2 − 0.1936 N + 10.335 ,

(4) d = 12 mm τ = 0.0010 N 2 − 0.1706 N + 9.7381 .

where N is the freeze–thaw cycles, and d is the rebar diameter.

Cao et al. [62] considered the influence of rebar diameter, cubic compressive strength, and anchorage length on the bond performance, and established the bond strength calculation formula and the non-linear bond–slip relationship formula of RAC specimens after freeze–thaw cycles:

(5) τ = 1.1 + 2.6 d l a f c ,

(6) τ = 28.8 S − 30.71 S 2 + 12.46 S 3 − 1.73 S 4 .

where l a is the anchorage length, d is the rebar diameter, f c is the cubic compressive strength of RAC, and S is the rebar slip.

Based on the model proposed by Xiao et al. [71], Ren et al. [57] established the non-linear bond–slip damage constitutive model of RAC specimens after freeze–thaw cycles:

(7) τ / τ 0 = ( S / S 0 ) a , S ≤ S 0 .

where τ 0 is the ultimate bond strength, and S 0 is the slip corresponding to the τ 0 .

The value of a is shown in Table 2

Table 2

Value of a

Freeze–thaw cycles a
25 0.45
50 0.48
75 0.47

Su et al. [65] established the non-linear bond–slip constitutive model of RAC specimens after salt-frost cycles based on the bond–slip constitutive model of NAC specimens proposed by He et al. [72]:

(8) τ = τ 0 , ( s = 0 ) τ 0 + τ u − τ 0 s u s , ( 0 < s ≤ s u ) τ u − τ u − τ i s u − s i ( s − s u ) , ( s u < s ≤ s i ) τ i − τ i − τ r s i − s r ( s − s i ) , ( s i < s ≤ s r ) τ r , ( s > s r ) ,

(9) τ 0 , n = 6.9246 − 0.0461 n , R 2 = 0.9913 ,

(10) τ u , n = − 3 × 10 − 4 n 2 − 0.078 n + 14.703 , R 2 = 0.9992 ,

(11) s u , n = 2 × 10 − 5 n 2 + 0.007 n + 0.1985 , R 2 = 0.9703 ,

(12) τ i , n = 7 × 10 − 6 n 3 + 0.0016 n 2 + 0.0679 n + 8.524 , R 2 = 0.9001 ,

(13) s i , n = 5 × 10 − 6 n 3 + 0.001 n 2 − 0.0414 n + 1.858 , R 2 = 0.8375 ,

(14) τ r , n = 1 × 10 − 6 n 3 + 0.0001 n 2 + 0.0021 n + 1.911 , R 2 = 0.7934 .

where τ 0 is the initial slip bond strength; τ u and s u are the ultimate bond strength and the corresponding slip, respectively; τ i and s i are the acceleration slip bond strength and the corresponding slip, respectively; τ r and s r are the residual bond strength and the corresponding slip; and n is the number of salt-frost cycles.

Su et al. [67] established the ultimate bond strength prediction equation of RAC specimens under salt-frost and repeated loading:

(15) τ u R ( n ) = 2.5 K n K r f cm ( 0 ) ( 1 − 0.124 G / 100 ) = ( 2.978 × 10 − 6 n 2 − 7 .816 × 10 − 3 n + 2.118 ) 0.84 f cu ,

where f cm ( 0 ) is the cylinder compressive strength before the salt-frost cycle; G is the replacement ratio of the RCA; K r is the repeated loading resistance coefficient; K n is the salt-frost resistance coefficient; and n is the number of salt-frost cycles.

It can be seen that there was no unified consensus on the bond strength calculation formula and bond–slip damage constitutive model of RAC specimens after salt-frost cycles, which brought inconvenience to engineering applications.

3.7 Degradation mechanism of bond performance between RAC and rebar after freeze‒thaw cycles

The different stress branches of the bond performance between the RAC and rebar after freeze‒thaw cycles were analyzed as follows:

  1. Microslip section

    In the initial stage of applying the pullout load, the chemical adhesive force was mainly used to resist the pullout load [73], and the bond performance between the concrete and rebar was good. At this stage, the loading end of the steel bar began to produce small slip, while the free end of the steel bar did not slip, the bond surface between the concrete and the rebar was basically not damaged, and the bond–slip curve basically developed linearly.

    With the increase in the number of freeze‒thaw cycles, the chemical adhesive force between the concrete and rebar decreased continuously due to the freeze‒thaw damage of the bond surface between the concrete and steel bar. It was shown in the test that the initial slip bond strength decreased with the increase in freeze‒thaw cycles.

  2. Slip section

    With the increase in the pullout load, the rebar began to deform, the chemical adhesive force decreased continuously until it was completely lost, and the free end of the rebar began to slip. In this stage, the friction and mechanical bite force were mainly used to resist the pullout load. With the continuous increase in the pullout load, the rebar ribs continuously squeezed the surrounding concrete, causing the concrete to produce oblique cracks along the rebar rib.

    After freeze‒thaw cycles, concrete bitten with steel ribs suffered freeze‒thaw damage, the concrete around the rebar ribs was more easily crushed, and the shear resistance continued to decline [74]. It is shown in the test that the ultimate bond strength and the slope of the bond–slip curve decreased with the increase in freeze‒thaw cycles.

  3. Descent section

    When the ultimate load was reached, the mechanical bite force between the rebar and the surrounding concrete and the blocking effect of crushed concrete were mainly used to resist the pullout load. The friction between the concrete and rebar showed a downward trend, the bond strength decreased, and the slip increased.

    After the freeze‒thaw cycles, the mechanical bite force between the rebar and the surrounding concrete and the blocking effect of crushed concrete decreased, resulting in a decrease in the anti-slip ability.

  4. Residual section

    In this stage, friction was mainly used to resist the pullout load. At this time, the friction force was basically in a stable state, and the bond strength was basically stable, while the slip increased continuously.

After freeze‒thaw cycles, the concrete around the rebar became loose, and the friction was reduced. It was shown in the test that the residual bond strength decreased with the increase in the number of freeze‒thaw cycles.

A schematic diagram of the bond performance between the RAC and rebar after freeze‒thaw cycles is shown in Figure 13. Figure 13 shows that the main reasons for the degradation of the bond performance between the RAC and rebar after freeze‒thaw cycles are as follows. On the one hand, due to the damage to the RCA during the crushing process, there are some defects and microcracks in the RAC. Therefore, the freeze‒thaw damage degree of RAC is greater than that of NAC, and there are more internal cracks due to freeze‒thaw damage in RAC, resulting in a relatively small vertical pressure and blocking effect of RAC on rebar. On the other hand, there are weak areas inside the RAC due to the existence of old mortar. When a pullout load is applied, the RAC around the rebar rib is more prone to cracks, and the cracks develop more rapidly, resulting in the RAC around the rebar rib being more easily crushed. As a result, the bond performance between the RAC and rebar after freeze‒thaw cycles is significantly worse than that between the NAC and rebar.

Figure 13 Schematic diagram of the bond performance between RAC and rebar.
Figure 13

Schematic diagram of the bond performance between RAC and rebar.

4 Conclusions

This article presented an overview of the bond performance of RCA concrete with rebar under a freeze‒thaw environment, from which the following conclusions could be drawn:

  1. There are still some controversies regarding whether RCA deteriorates the frost resistance of concrete, there are still few studies on the salt-frost resistance of RAC, and many influencing factors have not been considered. It is necessary to further study the frost resistance of RAC.

  2. The mass of the RAC pullout specimens showed a trend of first increasing and then decreasing after freeze‒thaw cycles. The failure modes of the RAC pullout specimens after freeze‒thaw cycles included PF, PSF, SF, and RYF.

  3. The bond performance of RAC with rebar showed a degradation trend after freeze‒thaw cycles, mainly in the decrease in bond strength and the increase in bond slip. The bond performance of RAC with rebar was inferior to that of NAC with rebar after freeze‒thaw cycles.

  4. The bond strength prediction model and the bond–slip constitutive relation prediction model after freeze‒thaw cycles have been summarized. There is still no unified consensus on the bond strength calculation formula and bond–slip damage constitutive model of RAC with rebar after freeze‒thaw cycles, which brings inconvenience to engineering applications.

  5. The bond stress distribution between the RAC and rebar in the anchoring area was not uniform and constantly changed with the number of freeze‒thaw cycles.

  6. The different stress branches and the degradation mechanism of the bond performance of RAC with rebar after freeze‒thaw cycles were analyzed.

Acknowledgements

The authors thank Zibo Xintiansheng Concrete Co., Ltd. and the Civil Engineering Laboratory of Shandong University of Technology for their support.

  1. Funding information: China Postdoctoral Science Foundation (2022M723687); Shandong Province Natural Science Fundation Youth Branch (ZR2021QE209); Doctoral Science and Technology Startup Foundation of Shandong University of Technology (420048); National Undergraduate Innovation and Entrepreneurship Training Program (202310433045).

  2. Author contributions: Ting Wang: data analysis, writing original draft preparation; Tian Su: investigation, funding acquisition, writing-review and editing; Xuefeng Mei, Bangxiang Li, Weishen Zhang: writing - review & editing, check original draft. Qifan Yang, Xuechao Yang, Deqiang Yang: check original draft.

  3. Conflict of interest: The authors state no conflicts of interest.

  4. Data availability statement: All data, models, and code generated or used during the study appears in the submitted article.

References

[1] Poon CS, Shui ZH, Lam L, Fok H, Kou SC. Influence of moisture states of natural and recycled aggregates on the slump and compressive strength of concrete. Cem Concr Res. 2004;34(1):31–6.10.1016/S0008-8846(03)00186-8Search in Google Scholar

[2] Sadati S, Arezoumandi M, Khayat KH, Volz JS. Shear performance of reinforced concrete beams incorporating recycled concrete aggregate and high-volume fly ash. J Clean Prod. 2016;115(3):284–93.10.1016/j.jclepro.2015.12.017Search in Google Scholar

[3] Lu W, Tam VWY. Construction waste management policies and their effectiveness in Hong Kong: A longitudinal review. Renew Sust Energ Rev. 2013;23(8):214–23.10.1016/j.rser.2013.03.007Search in Google Scholar

[4] Tabsh SW, Abdelfatah AS. Influence of recycled concrete aggregates on strength properties of concrete. Constr Build Mater. 2009;23(2):1163–7.10.1016/j.conbuildmat.2008.06.007Search in Google Scholar

[5] Wang J, Yuan H, Kang X, Lu W. Critical success factors for on-site sorting of construction waste: A China study. Resour Conserv Recy. 2010;54(11):931–6.10.1016/j.resconrec.2010.01.012Search in Google Scholar

[6] Paola VS, Mercedes RM, César PA, Alicia SAG. European legislation and implementation measures in the management of construction and demolition waste. Open Constr Build Technol J. 2011;5(2):156–61.10.2174/1874836801105010156Search in Google Scholar

[7] Shi C, Li Y, Zhang J, Li W, Chong L, Xie Z. Performance enhancement of recycled concrete aggregate-A review. J Clean Prod. 2016;112(1):466–72.10.1016/j.jclepro.2015.08.057Search in Google Scholar

[8] Kulatunga U, Amaratunga D, Haigh R, Rameezdeen R. Attitudes and perceptions of construction workforce on construction waste in Sri Lanka. Manag Environ Qual. 2006;17(1):57–72.10.1108/14777830610639440Search in Google Scholar

[9] Lu W, Yuan H. A framework for understanding waste management studies in construction. Waste Manage. 2011;31(6):1252–60.10.1016/j.wasman.2011.01.018Search in Google Scholar PubMed

[10] Wu J, Jing X, Wang Z. Uni-axial compressive stress‒strain relation of recycled coarse aggregate concrete after freezing and thawing cycles. Constr Build Mater. 2017;134(3):210–9.10.1016/j.conbuildmat.2016.12.142Search in Google Scholar

[11] Xiao JZ, Li JB, Lan Y. Research on recycled aggregate concrete-A review. Concrete. 2003;10:17–20 (in Chinese).Search in Google Scholar

[12] Wagih AM, El-Karmoty HZ, Ebid M, Okba SH. Recycled construction and demolition concrete waste as aggregate for structural concrete. HBRC J. 2013;9(3):193–200.10.1016/j.hbrcj.2013.08.007Search in Google Scholar

[13] Rao A, Jha KN, Misra S. Use of aggregates from recycled construction and demolition waste in concrete. Resour Conserv Recy. 2007;50(1):71–81.10.1016/j.resconrec.2006.05.010Search in Google Scholar

[14] Guo H, Shi C, Guan X, Zhu J, Ding Y, Ling TC, Zhang H, Wang Y. Durability of recycled aggregate concrete-A review. Cem Concr Comp. 2018;89(5):251–9.10.1016/j.cemconcomp.2018.03.008Search in Google Scholar

[15] Xuan D, Zhan B, Poon CS. Assessment of mechanical properties of concrete incorporating carbonated recycled concrete aggregates. Cem Concr Comp. 2016;65(1):67–74.10.1016/j.cemconcomp.2015.10.018Search in Google Scholar

[16] Noritaka M, Tomoyuki S, Kunio Y. Bond splitting strength of high-quality recycled coarse aggregate concrete beams. J Asian Archit Build. 2007;6(2):331–7.10.3130/jaabe.6.331Search in Google Scholar

[17] Arezoumandi M, Volz JS, Khayat KH. An experimental study on flexural strength of reinforced concrete beams with 100% recycled concrete aggregate. Constr Build Mater. 2015;88(2):154–62.10.1016/j.engstruct.2015.01.043Search in Google Scholar

[18] Rahal KN, Alrefaei YT. Shear strength of longitudinally reinforced recycled aggregate concrete beams. Eng Struct. 2017;145(8):273–82.10.1016/j.engstruct.2017.05.028Search in Google Scholar

[19] Marie I, Quiasrawi H. Closed-loop recycling of recycled concrete aggregates. J Clean Prod. 2012;37(4):243–8.10.1016/j.jclepro.2012.07.020Search in Google Scholar

[20] Cardoso R, Silva RV, Brito J, Dhir R. Use of recycled aggregates from construction and demolition waste in geotechnical applications: A literature review. Waste Manage. 2016;49(3):131–45.10.1016/j.wasman.2015.12.021Search in Google Scholar PubMed

[21] Omary S, Ghorbel E, Wardeh G. Relationships between recycled concrete aggregates characteristics and recycled aggregates concretes properties. Constr Build Mater. 2016;108(4):163–74.10.1016/j.conbuildmat.2016.01.042Search in Google Scholar

[22] Shang H, Ren G, Hou D, Zhang P, Zhao T. Bond behaviour between steel bar and concrete under sustained load and dry-wet cycles. Mag Concr Res. 2019;71(13–14):700–9.10.1680/jmacr.18.00048Search in Google Scholar

[23] Su T, Wang CX, Cao FB. An overview of bond behavior of recycled coarse aggregate concrete with steel bar. Rev Adv Mater Sci. 2021;60(1):127–44.10.1515/rams-2021-0018Search in Google Scholar

[24] Cao DF, Zhou KF, Zhou M, Ge WJ, Wang BY. Study on the shear behaviors of RC beams after freeze-thaw cycles. Appl Mech Mater. 2014;488–489(1):750–4.10.4028/www.scientific.net/AMM.488-489.750Search in Google Scholar

[25] Su T, Wu J, Yang G, Jing X, Andrea M. Shear behavior of recycled coarse aggregate concrete beams after freezing and thawing cycles. ACI Struct J. 2019;116(5):67–76.10.14359/51716770Search in Google Scholar

[26] Wang CQ, Xiao JZ. Evaluation of the stress-strain behavior of confined recycled aggregate concrete under monotonic dynamic loadings. Cem Concr Comp. 2018;87:149–63.10.1016/j.cemconcomp.2017.12.012Search in Google Scholar

[27] Bai G, Zhu C, Liu C, Liu B. An evaluation of the recycled aggregate characteristics and the recycled aggregate concrete mechanical properties. Constr Build Mater. 2020;240(2):117978, 1–10.10.1016/j.conbuildmat.2019.117978Search in Google Scholar

[28] Poon CS, Kou SC, Lam L. Influence of recycled aggregate on slump and bleeding of fresh concrete. Mater Struct. 2007;40(9):981–8.10.1617/s11527-006-9192-ySearch in Google Scholar

[29] Rahal K. Mechanical properties of concrete with recycled coarse aggregate. Build Environ. 2007;42(1):407–15.10.1016/j.buildenv.2005.07.033Search in Google Scholar

[30] Kwan WH, Ramli M, Kam KJ, Sulieman MZ. Influence of the amount of recycled coarse aggregate in concrete design and durability properties. Constr Build Mater. 2012;26(1):565–73.10.1016/j.conbuildmat.2011.06.059Search in Google Scholar

[31] Shang YK. The experimental study on the mechanical properties and frost resistance of recycled aggregate concrete. Harbin: Harbin Institute of Technology; 2010 (in Chinese).Search in Google Scholar

[32] Roumiana Z, Francois B, Eric W. Frost resistance of recycled aggregate concrete. Cem Concr Res. 2004;34(10):1927–32.10.1016/j.cemconres.2004.02.025Search in Google Scholar

[33] Cheng Y, Shang X, Zhang Y. Experimental research on durability of recycled aggregate concrete under freeze-thaw cycles. J Phys Conf Ser. 2017;870(1):1–4.10.1088/1742-6596/870/1/012018Search in Google Scholar

[34] Zhu HB, Li X. Experiment on freezing and thawing durability characteristics of recycled aggregate concrete. Key Eng Mater. 2009;400–402(10):447–52.10.4028/www.scientific.net/KEM.400-402.447Search in Google Scholar

[35] Lu XM. The experimental study on the bond behaviour between recycled aggregate concrete and steel bay after freezing and thawing. Qingdao: Qingdao Technological University; 2015 (in Chinese).Search in Google Scholar

[36] Yildirim ST, Meyer C, Herfellner S. Effects of internal curing on the strength, drying shrinkage and freeze-thaw resistance of concrete containing recycled concrete aggregates. Constr Build Mater. 2015;91(8):288–96.10.1016/j.conbuildmat.2015.05.045Search in Google Scholar

[37] Schlebach JP, Cao Z, Bowie JU, Park C. Experimental study on basic mechanical properties of recycled concrete after freeze-thaw cycles. J Nat Disasters. 2012;21(3):184–90 (in Chinese).Search in Google Scholar

[38] Fan YH. Expperiment and study on influence of freeze-thaw cyle on the mechanics behavior of frost-resistant recycled aggregate concrete. Harbin: Harbin Institute of Technology; 2009 (in Chinese).Search in Google Scholar

[39] Richardson A, Coventry K, Bacon J. Freeze/thaw durability of concrete with recycled demolition aggregate compared to virgin aggregate concrete. J Clean Prod. 2011;19(2-3):272–7.10.1016/j.jclepro.2010.09.014Search in Google Scholar

[40] Chen DY, Liu L, Yan Y, Tan KF, Liu H. Effect of different factors on frost resistance of recycled aggregate concrete. J Wuhan Univ Technol. 2011;13(5):54–8 (in Chinese).Search in Google Scholar

[41] Zhang LS, Wang J, Huang QF, Deng Y. Experimental study on frost-resistant durability of recycled concrete. Ind Constr. 2005;35(9):64–6 (in Chinese).Search in Google Scholar

[42] Qin YH, Deng SC, Zhang XB, Liu FH, Peng XH. Frost resistance of recycled concrete. Concrete. 2005;12:49–52 (in Chinese).Search in Google Scholar

[43] Gokce A, Nagataki S, Saeki T, Hisada M. Freezing and thawing resistance of air-entrained concrete incorporating recycled coarse aggregate: The role of air content in demolished concrete. Cem Concr Res. 2004;34(5):799–806.10.1016/j.cemconres.2003.09.014Search in Google Scholar

[44] Wang XR. Experimental study on the effect of air entrainment on mechanical properties and frost resistance of recycled concrete. Harbin: Harbin Institute of Technology; 2011 (in Chinese).Search in Google Scholar

[45] Liu K, Yan J, Hu Q, Sun Y, Zou C. Effects of parent concrete and mixing method on the resistance to freezing and thawing of air-entrained recycled aggregate concrete. Constr Build Mater. 2016;106(3):264–73.10.1016/j.conbuildmat.2015.12.074Search in Google Scholar

[46] Du W. Study on Mechanical Properties and Salt Freezing-resistance of Recycled Aggregate Concrete. Wuhan: Huazhong University of Science and Technology; 2013 (in Chinese).Search in Google Scholar

[47] Hu J, Wu J. Mechanical properties and uni-axial compression stress–strain relation of recycled coarse aggregate concrete subjected to salt-frost cycles. Constr Build Mater. 2019;197(2):652–66.10.1016/j.conbuildmat.2018.11.213Search in Google Scholar

[48] Su T. Bond behavior between recycled coarse aggregate concrete and rebar after salt-frost cycles. Nanjing: Nanjing University of Aeronautics and Astronautics; 2020 (in Chinese).Search in Google Scholar

[49] Wang ZH, Li L, Zhang YX, Wang WT. bond–slip model considering freeze-thaw damage effect of concrete and its application. Eng Struct. 2019;201:109831, 1–12.10.1016/j.engstruct.2019.109831Search in Google Scholar

[50] Li YP. Experimental study on the basic performance of entraining concrete and the bond behavioue between entraining concrete and reinfored after thawing. Qingdao: Qingdao Technological University; 2015 (in Chinese).Search in Google Scholar

[51] Cao FB, Tang LJ, Ding BB, Wang CX. Study on bond–slip properties between steel bars and recycled concrete after freeze-thaw cycles. Eng Mech. 2017;34:244–51 (in Chinese).Search in Google Scholar

[52] Wang CX, Qian JX, Wang H, Xu K, Cao FB. Effect of the freeze-thaw damage the durability of recycled concrete and bonding performance of steel. J Chongqing Univ. 2016;39(2):131–9 (in Chinese).Search in Google Scholar

[53] Wang CX, Tang LJ, Zhang ZB, Wang JJ, Cao FB. Pullout tests research on steel bars and recycled concrete after freeze-thaw cycles. Build Struct. 2018;48(9):97–102 (in Chinese).Search in Google Scholar

[54] An XZ, Yi C, Wang XX, Jiang XP. Study of bond performance between steel bar and recycled aggregate concrete subjected to freeze-thaw cycling. J Exp Mech. 2013;28(2):227–34 (in Chinese).Search in Google Scholar

[55] Shang HS, Zhao TJ, Cao WQ. Bond behavior between steel bar and recycled aggregate concrete after freeze-thaw cycles. Cold Reg Sci Technol. 2015;118:38–44.10.1016/j.coldregions.2015.06.008Search in Google Scholar

[56] Liu K, Yan J, Meng X, Zou C. Bond behavior between deformed steel bars and recycled aggregate concrete after freeze-thaw cycles. Constr Build Mater. 2020;232:117236, 1–12.10.1016/j.conbuildmat.2019.117236Search in Google Scholar

[57] Ren G, Shang H, Zhang P, Zhao T. Bond behaviour of reinforced recycled concrete after rapid freezing-thawing cycles. Cold Reg Sci Technol. 2019;157:133–8.10.1016/j.coldregions.2018.10.005Search in Google Scholar

[58] Su T, Wang T, Wang CG, Yi HH. The influence of salt-frost cycles on the bond behavior distribution between rebar and recycled coarse aggregate concrete. J Build Eng. 2022;45:103568.10.1016/j.jobe.2021.103568Search in Google Scholar

[59] Sun M, Xin DB, Zou CY. Damage evolution and plasticity development of concrete materials subjected to freeze-thaw during the load process. Mech Mater. 2019;139:103192, 1–13.10.1016/j.mechmat.2019.103192Search in Google Scholar

[60] Li Z, Deng Z, Yang H, Wang H. Bond behavior between recycled aggregate concrete and deformed rebar after freeze-thaw damage. Constr Build Mater. 2020;250:118805, 1–11.10.1016/j.conbuildmat.2020.118805Search in Google Scholar

[61] Shang HS, Wang ZH, Zhang P, Zhao TJ, Fan GX, Ren GS. Bond behavior of steel bar in air-entrained RCAC in fresh water and sea water after fast freeze-thaw cycles. Cold Reg Sci Technol. 2017;135(3):90–6.10.1016/j.coldregions.2016.11.005Search in Google Scholar

[62] Cao FB, Yin RP, Wang CX. Beam-type experimental study on bond–slip behavior between recycled concrete and steel bar after freeze-thaw damage. J Archit Structure. 2017;38(4):141–8 (in Chinese).Search in Google Scholar

[63] Cao FB, Lu ZM, Wang CX, Shao JB. Finite element analysis of bond behavior between steel bars and recycled concrete after freeze-thaw cycles in the beam-type test. J Shenyang Archit Univ. 2019;35(6):1099–10 (in Chinese).Search in Google Scholar

[64] Meng XX. Experimental study on bond behavior between steel rebars and recycled concrete after freeze-thaw cycles. Harbin: Harbin Institute of Technology; 2015 (in Chinese).Search in Google Scholar

[65] Su T, Wu J, Yang G, Zou Z. Bond behavior between recycled coarse aggregate concrete and steel bar after salt-frost cycles. Constr Build Mater. 2019;226:673–85.10.1016/j.conbuildmat.2019.07.301Search in Google Scholar

[66] Li XM, Shang HH. Influence of deicer-frosting cycles on bond property of deformed bar and recycled concrete. J Qingdao Univ Technol. 2015;36(4):23–9 (in Chinese).Search in Google Scholar

[67] Yu S, Xing GL, Chen LH, Ben T, Su BL. Bond performance of steel bar in RAC under salt-frost and repeated loading. J Mater Civ Eng. 2020;32(9):04020261, 1–10.10.1061/(ASCE)MT.1943-5533.0003303Search in Google Scholar

[68] Su T, Huang ZF, Yuan JF, Zou ZH, Wang CG, Yi HH. Bond properties of deformed rebar in frost-damaged recycled coarse aggregate concrete under repeated loading. J Mater Civ Eng. 2022;34:04022257. 10.1061/(ASCE)MT.1943-5533.0004401 Search in Google Scholar

[69] Niu JG, Bian Y, Xu Y, Xie CB. Bond performance and interface damage between reinforcement and recycled concrete under freezing-thawing environment. J Yangtze River Sci Res Inst. 2021;38(4):132–7 (in Chinese).Search in Google Scholar

[70] Miranda MP, Morsch IB, Brisotto DS, Bittencourt E, Carvalho EP. Steel-concrete bond behavior: An experimental and numerical study. Constr Build Mater. 2021;271(1):121918, 1–8.10.1016/j.conbuildmat.2020.121918Search in Google Scholar

[71] Xiao JZ, Falkner H. Bond behaviour between recycled aggregate concrete and steel rebars. Constr Build Mater. 2007;21(2):395–401.10.1016/j.conbuildmat.2005.08.008Search in Google Scholar

[72] He SQ, Gong JX, Wang HC. Bond mechanism and degradation model between reinforcement and concrete subjected to deicer-frosting cycles. Ind Archit. 2005;35(12):19–22 (in Chinese).Search in Google Scholar

[73] Zhao J. Study on bonding properties and their damage models between reinforcing bars and concrete in freeze-thaw environment. Harbin: Harbin Institute of Technology; 2006 (in Chinese).Search in Google Scholar

[74] Ji XD, Song YP. Experimental research on bond behaviors between steel bars and concrete after freezing and thawing cycles. J Dalian Univ Technol. 2008;48(2):240–5 (in Chinese).Search in Google Scholar
Received: 2023-04-21
Revised: 2023-08-25
Accepted: 2024-02-27
Published Online: 2024-05-02

© 2024 the author(s), published by De Gruyter

This work is licensed under the Creative Commons Attribution 4.0 International License.

Articles in the same Issue

  1. Editorial
  2. Focus on NLENG 2023 Volume 12 Issue 1
  3. Research Articles
  4. Seismic vulnerability signal analysis of low tower cable-stayed bridges method based on convolutional attention network
  5. Robust passivity-based nonlinear controller design for bilateral teleoperation system under variable time delay and variable load disturbance
  6. A physically consistent AI-based SPH emulator for computational fluid dynamics
  7. Asymmetrical novel hyperchaotic system with two exponential functions and an application to image encryption
  8. A novel framework for effective structural vulnerability assessment of tubular structures using machine learning algorithms (GA and ANN) for hybrid simulations
  9. Flow and irreversible mechanism of pure and hybridized non-Newtonian nanofluids through elastic surfaces with melting effects
  10. Stability analysis of the corruption dynamics under fractional-order interventions
  11. Solutions of certain initial-boundary value problems via a new extended Laplace transform
  12. Numerical solution of two-dimensional fractional differential equations using Laplace transform with residual power series method
  13. Fractional-order lead networks to avoid limit cycle in control loops with dead zone and plant servo system
  14. Modeling anomalous transport in fractal porous media: A study of fractional diffusion PDEs using numerical method
  15. Analysis of nonlinear dynamics of RC slabs under blast loads: A hybrid machine learning approach
  16. On theoretical and numerical analysis of fractal--fractional non-linear hybrid differential equations
  17. Traveling wave solutions, numerical solutions, and stability analysis of the (2+1) conformal time-fractional generalized q-deformed sinh-Gordon equation
  18. Influence of damage on large displacement buckling analysis of beams
  19. Approximate numerical procedures for the Navier–Stokes system through the generalized method of lines
  20. Mathematical analysis of a combustible viscoelastic material in a cylindrical channel taking into account induced electric field: A spectral approach
  21. A new operational matrix method to solve nonlinear fractional differential equations
  22. New solutions for the generalized q-deformed wave equation with q-translation symmetry
  23. Optimize the corrosion behaviour and mechanical properties of AISI 316 stainless steel under heat treatment and previous cold working
  24. Soliton dynamics of the KdV–mKdV equation using three distinct exact methods in nonlinear phenomena
  25. Investigation of the lubrication performance of a marine diesel engine crankshaft using a thermo-electrohydrodynamic model
  26. Modeling credit risk with mixed fractional Brownian motion: An application to barrier options
  27. Method of feature extraction of abnormal communication signal in network based on nonlinear technology
  28. An innovative binocular vision-based method for displacement measurement in membrane structures
  29. An analysis of exponential kernel fractional difference operator for delta positivity
  30. Novel analytic solutions of strain wave model in micro-structured solids
  31. Conditions for the existence of soliton solutions: An analysis of coefficients in the generalized Wu–Zhang system and generalized Sawada–Kotera model
  32. Scale-3 Haar wavelet-based method of fractal-fractional differential equations with power law kernel and exponential decay kernel
  33. Non-linear influences of track dynamic irregularities on vertical levelling loss of heavy-haul railway track geometry under cyclic loadings
  34. Fast analysis approach for instability problems of thin shells utilizing ANNs and a Bayesian regularization back-propagation algorithm
  35. Validity and error analysis of calculating matrix exponential function and vector product
  36. Optimizing execution time and cost while scheduling scientific workflow in edge data center with fault tolerance awareness
  37. Estimating the dynamics of the drinking epidemic model with control interventions: A sensitivity analysis
  38. Online and offline physical education quality assessment based on mobile edge computing
  39. Discovering optical solutions to a nonlinear Schrödinger equation and its bifurcation and chaos analysis
  40. New convolved Fibonacci collocation procedure for the Fitzhugh–Nagumo non-linear equation
  41. Study of weakly nonlinear double-diffusive magneto-convection with throughflow under concentration modulation
  42. Variable sampling time discrete sliding mode control for a flapping wing micro air vehicle using flapping frequency as the control input
  43. Error analysis of arbitrarily high-order stepping schemes for fractional integro-differential equations with weakly singular kernels
  44. Solitary and periodic pattern solutions for time-fractional generalized nonlinear Schrödinger equation
  45. An unconditionally stable numerical scheme for solving nonlinear Fisher equation
  46. Effect of modulated boundary on heat and mass transport of Walter-B viscoelastic fluid saturated in porous medium
  47. Analysis of heat mass transfer in a squeezed Carreau nanofluid flow due to a sensor surface with variable thermal conductivity
  48. Navigating waves: Advancing ocean dynamics through the nonlinear Schrödinger equation
  49. Experimental and numerical investigations into torsional-flexural behaviours of railway composite sleepers and bearers
  50. Novel dynamics of the fractional KFG equation through the unified and unified solver schemes with stability and multistability analysis
  51. Analysis of the magnetohydrodynamic effects on non-Newtonian fluid flow in an inclined non-uniform channel under long-wavelength, low-Reynolds number conditions
  52. Convergence analysis of non-matching finite elements for a linear monotone additive Schwarz scheme for semi-linear elliptic problems
  53. Global well-posedness and exponential decay estimates for semilinear Newell–Whitehead–Segel equation
  54. Petrov-Galerkin method for small deflections in fourth-order beam equations in civil engineering
  55. Solution of third-order nonlinear integro-differential equations with parallel computing for intelligent IoT and wireless networks using the Haar wavelet method
  56. Mathematical modeling and computational analysis of hepatitis B virus transmission using the higher-order Galerkin scheme
  57. Mathematical model based on nonlinear differential equations and its control algorithm
  58. Bifurcation and chaos: Unraveling soliton solutions in a couple fractional-order nonlinear evolution equation
  59. Space–time variable-order carbon nanotube model using modified Atangana–Baleanu–Caputo derivative
  60. Minimal universal laser network model: Synchronization, extreme events, and multistability
  61. Valuation of forward start option with mean reverting stock model for uncertain markets
  62. Geometric nonlinear analysis based on the generalized displacement control method and orthogonal iteration
  63. Fuzzy neural network with backpropagation for fuzzy quadratic programming problems and portfolio optimization problems
  64. B-spline curve theory: An overview and applications in real life
  65. Nonlinearity modeling for online estimation of industrial cooling fan speed subject to model uncertainties and state-dependent measurement noise
  66. Quantitative analysis and modeling of ride sharing behavior based on internet of vehicles
  67. Review Article
  68. Bond performance of recycled coarse aggregate concrete with rebar under freeze–thaw environment: A review
  69. Retraction
  70. Retraction of “Convolutional neural network for UAV image processing and navigation in tree plantations based on deep learning”
  71. Special Issue: Dynamic Engineering and Control Methods for the Nonlinear Systems - Part II
  72. Improved nonlinear model predictive control with inequality constraints using particle filtering for nonlinear and highly coupled dynamical systems
  73. Anti-control of Hopf bifurcation for a chaotic system
  74. Special Issue: Decision and Control in Nonlinear Systems - Part I
  75. Addressing target loss and actuator saturation in visual servoing of multirotors: A nonrecursive augmented dynamics control approach
  76. Collaborative control of multi-manipulator systems in intelligent manufacturing based on event-triggered and adaptive strategy
  77. Greenhouse monitoring system integrating NB-IOT technology and a cloud service framework
  78. Special Issue: Unleashing the Power of AI and ML in Dynamical System Research
  79. Computational analysis of the Covid-19 model using the continuous Galerkin–Petrov scheme
  80. Special Issue: Nonlinear Analysis and Design of Communication Networks for IoT Applications - Part I
  81. Research on the role of multi-sensor system information fusion in improving hardware control accuracy of intelligent system
  82. Advanced integration of IoT and AI algorithms for comprehensive smart meter data analysis in smart grids
https://doi.org/10.1515/nleng-2024-0001
Keywords for this article
recycled coarse aggregate concrete; rebar; bond performance; freeze‒thaw cycles; bond–slip curve; degradation mechanism
Creative Commons
BY 4.0

Articles in the same Issue

  1. Editorial
  2. Focus on NLENG 2023 Volume 12 Issue 1
  3. Research Articles
  4. Seismic vulnerability signal analysis of low tower cable-stayed bridges method based on convolutional attention network
  5. Robust passivity-based nonlinear controller design for bilateral teleoperation system under variable time delay and variable load disturbance
  6. A physically consistent AI-based SPH emulator for computational fluid dynamics
  7. Asymmetrical novel hyperchaotic system with two exponential functions and an application to image encryption
  8. A novel framework for effective structural vulnerability assessment of tubular structures using machine learning algorithms (GA and ANN) for hybrid simulations
  9. Flow and irreversible mechanism of pure and hybridized non-Newtonian nanofluids through elastic surfaces with melting effects
  10. Stability analysis of the corruption dynamics under fractional-order interventions
  11. Solutions of certain initial-boundary value problems via a new extended Laplace transform
  12. Numerical solution of two-dimensional fractional differential equations using Laplace transform with residual power series method
  13. Fractional-order lead networks to avoid limit cycle in control loops with dead zone and plant servo system
  14. Modeling anomalous transport in fractal porous media: A study of fractional diffusion PDEs using numerical method
  15. Analysis of nonlinear dynamics of RC slabs under blast loads: A hybrid machine learning approach
  16. On theoretical and numerical analysis of fractal--fractional non-linear hybrid differential equations
  17. Traveling wave solutions, numerical solutions, and stability analysis of the (2+1) conformal time-fractional generalized q-deformed sinh-Gordon equation
  18. Influence of damage on large displacement buckling analysis of beams
  19. Approximate numerical procedures for the Navier–Stokes system through the generalized method of lines
  20. Mathematical analysis of a combustible viscoelastic material in a cylindrical channel taking into account induced electric field: A spectral approach
  21. A new operational matrix method to solve nonlinear fractional differential equations
  22. New solutions for the generalized q-deformed wave equation with q-translation symmetry
  23. Optimize the corrosion behaviour and mechanical properties of AISI 316 stainless steel under heat treatment and previous cold working
  24. Soliton dynamics of the KdV–mKdV equation using three distinct exact methods in nonlinear phenomena
  25. Investigation of the lubrication performance of a marine diesel engine crankshaft using a thermo-electrohydrodynamic model
  26. Modeling credit risk with mixed fractional Brownian motion: An application to barrier options
  27. Method of feature extraction of abnormal communication signal in network based on nonlinear technology
  28. An innovative binocular vision-based method for displacement measurement in membrane structures
  29. An analysis of exponential kernel fractional difference operator for delta positivity
  30. Novel analytic solutions of strain wave model in micro-structured solids
  31. Conditions for the existence of soliton solutions: An analysis of coefficients in the generalized Wu–Zhang system and generalized Sawada–Kotera model
  32. Scale-3 Haar wavelet-based method of fractal-fractional differential equations with power law kernel and exponential decay kernel
  33. Non-linear influences of track dynamic irregularities on vertical levelling loss of heavy-haul railway track geometry under cyclic loadings
  34. Fast analysis approach for instability problems of thin shells utilizing ANNs and a Bayesian regularization back-propagation algorithm
  35. Validity and error analysis of calculating matrix exponential function and vector product
  36. Optimizing execution time and cost while scheduling scientific workflow in edge data center with fault tolerance awareness
  37. Estimating the dynamics of the drinking epidemic model with control interventions: A sensitivity analysis
  38. Online and offline physical education quality assessment based on mobile edge computing
  39. Discovering optical solutions to a nonlinear Schrödinger equation and its bifurcation and chaos analysis
  40. New convolved Fibonacci collocation procedure for the Fitzhugh–Nagumo non-linear equation
  41. Study of weakly nonlinear double-diffusive magneto-convection with throughflow under concentration modulation
  42. Variable sampling time discrete sliding mode control for a flapping wing micro air vehicle using flapping frequency as the control input
  43. Error analysis of arbitrarily high-order stepping schemes for fractional integro-differential equations with weakly singular kernels
  44. Solitary and periodic pattern solutions for time-fractional generalized nonlinear Schrödinger equation
  45. An unconditionally stable numerical scheme for solving nonlinear Fisher equation
  46. Effect of modulated boundary on heat and mass transport of Walter-B viscoelastic fluid saturated in porous medium
  47. Analysis of heat mass transfer in a squeezed Carreau nanofluid flow due to a sensor surface with variable thermal conductivity
  48. Navigating waves: Advancing ocean dynamics through the nonlinear Schrödinger equation
  49. Experimental and numerical investigations into torsional-flexural behaviours of railway composite sleepers and bearers
  50. Novel dynamics of the fractional KFG equation through the unified and unified solver schemes with stability and multistability analysis
  51. Analysis of the magnetohydrodynamic effects on non-Newtonian fluid flow in an inclined non-uniform channel under long-wavelength, low-Reynolds number conditions
  52. Convergence analysis of non-matching finite elements for a linear monotone additive Schwarz scheme for semi-linear elliptic problems
  53. Global well-posedness and exponential decay estimates for semilinear Newell–Whitehead–Segel equation
  54. Petrov-Galerkin method for small deflections in fourth-order beam equations in civil engineering
  55. Solution of third-order nonlinear integro-differential equations with parallel computing for intelligent IoT and wireless networks using the Haar wavelet method
  56. Mathematical modeling and computational analysis of hepatitis B virus transmission using the higher-order Galerkin scheme
  57. Mathematical model based on nonlinear differential equations and its control algorithm
  58. Bifurcation and chaos: Unraveling soliton solutions in a couple fractional-order nonlinear evolution equation
  59. Space–time variable-order carbon nanotube model using modified Atangana–Baleanu–Caputo derivative
  60. Minimal universal laser network model: Synchronization, extreme events, and multistability
  61. Valuation of forward start option with mean reverting stock model for uncertain markets
  62. Geometric nonlinear analysis based on the generalized displacement control method and orthogonal iteration
  63. Fuzzy neural network with backpropagation for fuzzy quadratic programming problems and portfolio optimization problems
  64. B-spline curve theory: An overview and applications in real life
  65. Nonlinearity modeling for online estimation of industrial cooling fan speed subject to model uncertainties and state-dependent measurement noise
  66. Quantitative analysis and modeling of ride sharing behavior based on internet of vehicles
  67. Review Article
  68. Bond performance of recycled coarse aggregate concrete with rebar under freeze–thaw environment: A review
  69. Retraction
  70. Retraction of “Convolutional neural network for UAV image processing and navigation in tree plantations based on deep learning”
  71. Special Issue: Dynamic Engineering and Control Methods for the Nonlinear Systems - Part II
  72. Improved nonlinear model predictive control with inequality constraints using particle filtering for nonlinear and highly coupled dynamical systems
  73. Anti-control of Hopf bifurcation for a chaotic system
  74. Special Issue: Decision and Control in Nonlinear Systems - Part I
  75. Addressing target loss and actuator saturation in visual servoing of multirotors: A nonrecursive augmented dynamics control approach
  76. Collaborative control of multi-manipulator systems in intelligent manufacturing based on event-triggered and adaptive strategy
  77. Greenhouse monitoring system integrating NB-IOT technology and a cloud service framework
  78. Special Issue: Unleashing the Power of AI and ML in Dynamical System Research
  79. Computational analysis of the Covid-19 model using the continuous Galerkin–Petrov scheme
  80. Special Issue: Nonlinear Analysis and Design of Communication Networks for IoT Applications - Part I
  81. Research on the role of multi-sensor system information fusion in improving hardware control accuracy of intelligent system
  82. Advanced integration of IoT and AI algorithms for comprehensive smart meter data analysis in smart grids
Sign up now to receive a 20% welcome discount
Institutional Access
How does access work?
Have an idea on how to improve our website?
Please write us.
© 2025 De Gruyter Brill
Downloaded on 15.9.2025 from https://www.degruyterbrill.com/document/doi/10.1515/nleng-2024-0001/html
Scroll to top button