Stability analysis of the corruption dynamics under fractional-order interventions

Yasir Nadeem Anjam; Muhammad Imran Aslam; Salman Arif Cheema; Sufian Munawar; Najma Saleem; Mati ur Rahman

doi:10.1515/nleng-2022-0363

Article Open Access

Stability analysis of the corruption dynamics under fractional-order interventions

Yasir Nadeem Anjam , Muhammad Imran Aslam , Salman Arif Cheema , Sufian Munawar , Najma Saleem and Mati ur Rahman

Published/Copyright: February 15, 2024

Published by

Become an author with De Gruyter Brill

Submit Manuscript Author Information

From the journal Nonlinear Engineering Volume 13 Issue 1

Abstract

This article proposes a nonlinear deterministic mathematical model that encapsulates the dynamics of the prevailing degree of corruption in a population. The objectives are attained by exploring the dynamics of the corruption model under fractional-order derivative in the Caputo sense. The outcomes of the research are facilitated by stratifying the population into five compartments: susceptible class, exposed class, corrupted class, recovered class, and honest class. The developed model is validated by proving pivotal delicacies such as positivity, invariant region, basic reproduction number, and stability analysis. The Ulam–Hyers stability technique is used to prove the stable solution. The Adam–Bashforth numerical scheme is employed to estimate the numerical solution. Moreover, the research environment is further enriched by studying each compartment with respect to a wide range of relevant parametric settings. The realizations of this study indicate that susceptible individuals remain subject to being influenced by corrupt individuals. In addition, it is observed that the population of exposed individuals, recovered individuals, and honest individuals asymptotically approach toward the corruption equilibrium point, whereas the magnitudes of susceptible individuals and corrupted individuals decrease asymptotically to the corruption equilibrium state. The compartment dynamics are witnessed to be sensitive for various fractional-orders indicating the utility of the fractional approach. The findings of this study support the fundamental understanding of conceptualizing corruption in accordance with the viral transmission of infectious disease.

Keywords: corruption model; Caputo fractional derivative; Ulam–Hyers stability; Adams–Bashforth method; numerical simulations

1 Introduction

The manifestation of corruption is usually materialized through different definitions comprehending and highlighting the probable ways to execute this deteriorating action. For example, the World Bank defines corruption as “the misuse of public office,” whereas, according to Transparency International, corruption is “the abuse of authority for personal gain” [1]. Many researchers have lamented the multifaceted and drastic impacts of exploiting activity on the socioeconomic and political fabric of societies. Transparency International, in its 2022 corruption report, claimed a loss of $500 billion per annum associated with corruption. More alarmingly, it is documented that in low- and middle-income countries, more than 80% of individuals have experienced healthcare corruption [2]. Vian [3] distinguished seven fundamental areas in the health sector, including construction and rehabilitation of health facilities, purchase of equipment and supplies, distribution and use of drugs, regulation of qualities in products, education of health professionals, medical research, and provision of services by medical personnel where corruption could have pejorative health consequences. Critically, health-related corruption remains distinctively more deteriorating as compared to corruption in conventional economic sectors. Corruption in the health sector possesses the dual burden of restricting economic development and endangering population-level health [4,5]. Furthermore, corruption is found to be a fundamental entity in discouraging taxpayers from paying taxes [6], which then leads to the reduction of resources limiting the efficacy of states in offering social protection and public services to their citizens [7,8]. As long as reasons of the corruption are concerned, Ulain and Hussain [9] nominated limited access to information and exhibition of weak legal frame work as primary factors in this regard. Moreover, Brazys et al. [10] focused on the rule of less professionalism and lack of integrity as defining agents of corruption, whereas Vian [11] accused the prevalence of nepotism as vital element triggering the corrupt practices. The compromised ethical standard and deteriorated moral code have also been discussed in this regard [12]. From a global perspective, corruption is noted as a prominent hurdle in the attainment of the Millennium Development Goals. Aidt [13] explored the existence of a negative correlation between corruption and sustainable development goals and argued that corruption can put a country on an unsustainable path in which its capital base is eroded. Moreover, the corruption is estimated to play the rule of aggravating agent in enhancing the income disparities existent among different socioecnomic classifications of the society [14]. Over time, various fronts have been documented in the literature in concordance with corruption. For example, the study of [15] encapsulating panel data from 126 countries from 1980 to 2007 argued that democratization and media freedom have negative effects on corruption. Similarly, empirical studies neutralizing the effect of other associated factors through laboratory experiments confirmed that women are less likely to be corrupt [16,17]. Moreover, an engaging account provided by Goel and Nelson [18] highlighted the contagious nature of corruption through the aid of US-based data by showing that a 10% increase in the levels of corruption in neighboring states led to increased levels of corruption in a state by 4–11%. This was further sealed by Becker et al. [19] by using multicountry data that the decrement of corruption in one country results in decreased levels of corruption in neighboring countries. A unique epidemiological model of corruption in Nigeria with an immunity provision was proposed by Gweryina et al. [20]. Furthermore, Shah et al. [21] built and analyzed the nonlinear mathematical model to explore the dynamic nature of the corruption flow, whereas Eguda et al. [8] devised a corruption model with a standard incidence that examines the dynamics of corruption as a disease. Crokidakis and Martins [22] suggested and examined a simple model of social contagion describing the dynamics of social influences among politicians in a synthetically corrupt parliament.

Mathematical modeling is a powerful tool for predicting and addressing social issues, and they have been progressively applied in recent eras to alleviate the impact of these issues. Using mathematical models, we can capably control the spread of real-world problems. Many global challenges display quasi-linear characteristics, depending exclusively on linear models can often lead to unrealistic and idealistic consequences. So, nonlinear mathematical models offer a more precise description of real-world issues. In recent years, fractional calculus, regardless of its name, pacts with integrals and derivatives of any positive real order and can be considered a branch of mathematical modeling [23–29]. It has reaped substantial attention from researchers, and various aspects of this subject are well cherished in mathematics and allied disciplines [30–33]. The diverse features of these differential operators lie in their nonlocal nature, which is distracted in integer-order differential operators [26]. Various types of fractional derivatives, such as Riemann and Liouville and Caputo operators, are commonly used in practice.

The last decade has seen an upsurge in the usage of Caputo fractional technique. For example, Yan et al. [34] explored the employment of exponential approximation for the gain of numerical efficiency of the Caputo fractional derivative. Moreover, Odibat and Baleanu [35] introduced the generalized formation of Caputo derivatives and explored their linkages with the classic Adam–Bashforth–Molten method. Furthermore, [36] aimed at the elaborative approximation of the Caputo fractional technique by the employment of the L 1 − 2 formula. Many researchers have employed the fractional approach to model and predict the efficiency of health surveillance synergies. One may consult the account of Farayola et al. [37] aimed at cancer treatment modeling and Baleanu et al. [38] for modeling of the human liver, and Zhang et al. [39] concerned with the evaluation of tuberculosis treatment efficacy. In addition to the aforementioned references, [40] and [41] offered an interesting account of the predictive capability of Caputo fractional methods to encapsulate the transmission of contiguous viral flow. Whereas these fractional derivatives offer better precision in describing real phenomena equated to integer-order derivatives, their kernel functions could end in singularities that lead to computational challenges. Fractional operators have an extensive range of practices in modern mathematics, together with the complex and substantial study of symmetric systems. Moreover, fractional models work better and are more consistent with the real data.

Stirred by the significance of the above-documented issue, this study encapsulates the corruption dynamics through the launch of the Caputo fractional derivative operator and stability analysis by introducing a nonlinear deterministic model for the dynamics of corruption. The whole population is classified into five mutually inclusive classes, namely, susceptible class, exposed class, corrupted class, recovered class, and honest class. First, we will thoroughly examine the developed model to ensure its validity by proving pivotal delicacies such as positivity, invariant region, equilibrium points, reproduction number, and stability analysis. Along with showing complete stability analyses at equilibrium points to evaluate both local and global stability. The idea of Ulam–Hyres (UH) stability is employed to prove that the solution of the devised model is stable. Next, the existence and uniqueness of the solution are proved with the fixed-point theory. Moreover, the Adam–Bashforth iterative numerical scheme is implemented to perform the numerical simulations. Symmetry analysis is a reliable and effective tool that can be employed to derive precise numerical solutions for fractional differential equations. The validity of the issue at hand is also addressed through the simulated results, and the compartment dynamics are witnessed to be sensitive for various fractional-orders indicating the utility of the fractional approach.

This article is mainly partitioned into seven sections. Section 2 is dedicated to the proposed fractional model. Whereas, in Section 3, the theoretical aspects of the considered model including the positivity and boundedness of the solutions, the calculation of equilibrium points, and the determination of the fundamental reproduction number ℛ 0 are discussed. Section 4 reported the stability analysis of the given model. Whereas, Section 5 demonstrates the existence and uniqueness of the solution of the devised model with the use of the fixed-point tool. The numerical evaluations are persuaded in Section 6. Lastly, Section 7 comprehends the major findings of the study along with reporting the future possible research venues.

1.1 Model formulation

In this section, the construction of the suggested model is presented. Let us consider that, for any time t ≥ 0 , the population under study, say N ( t ) , is classified into five groups, such as susceptible individuals S ( t ) , exposed individuals E ( t ) , corrupted individuals C ( t ) , recovered individuals R ( t ) , and honest individuals H ( t ) . Furthermore, the model formulation includes specific parameters: ρ is the probability of corruption being transmitted per contact; susceptible individuals will interact with exposed individuals at a rate β and δ is the rate at which individuals who have been exposed to corruption become corrupted; ε is the rate at which individuals who have recovered become honest; Π is the recruitment rate of susceptible humans; κ is the proportion of individuals who join the honest population from the susceptible population; μ is the mortality rate for the entire human population; α is the proportion of individuals who join the corrupted sub-population from the exposed compartment; and θ is the proportion of individuals who move from the recovered compartment to the honest sub-population. Based on the aforementioned considerations, we have the compartmental flow diagram depicted in Figure 1. Thus, the whole population at any time t is given as follows:

N ( t ) = S ( t ) + E ( t ) + C ( t ) + R ( t ) + H ( t ) .

Therefore, the foundational corruption dynamic model is to be governed through a system of nonlinear differential equations, such that

(1) d S d t = Π + ( 1 − θ ) ε R − ρ β S C − ( κ + μ ) S , d E d t = ρ β S C − ( δ + μ ) E , d C d t = α δ E − ( σ + μ ) C , d R d t = σ C + ( 1 − α ) δ E − ( ε + μ ) R , d H d t = κ S + θ ε R − μ H ,

subject to the following initial conditions:

S ( 0 ) = S 0 ≥ 0 , E ( 0 ) = E 0 ≥ 0 , C ( 0 ) = C 0 ≥ 0 , R ( 0 ) = R 0 ≥ 0 , H ( 0 ) = H 0 ≥ 0 .

Figure 1

Schematic diagram for the transmission of corruption dynamics.

2 Fractional model

Generally, the classical integer-order models are neither vigorous nor more valuable for understanding the dynamical behavior of epidemical disease models. Instead, the fractional-order models work more aptly with the real data. Hence, to generalize the devised system (1) for corruption dynamic, we use the Caputo fractional-order derivative instead of the classical integer-order time derivative D t . This fractional-order formulation will permit us to perceive memory impacts and gain further insight into corruption dynamics. For the fractional formulation, some important concepts and results related to fractional calculus are presented. There are various types of fractional derivatives, but the ones commonly used in mathematical modeling are the Riemann–Liouville derivative and the Caputo derivative [33].

Definition 2.1

The Riemann–Liouville fractional derivative of a function f ( x ) of order α is defined as follows:

D α f ( x ) = 1 Γ ( n − α ) d n d x n ∫ a x f ( t ) ( x − t ) α − n + 1 d t ,

where a is a constant and n is the smallest integer not less than α . Furthermore, Γ ( ⋅ ) denotes the gamma function, which is described as follows:

Γ ( n ) = ∫ 0 ∞ e − t t n − 1 d t .

Definition 2.2

The Riemann–Liouville fractional integral operator I α is defined as follows:

I α f ( x ) = 1 Γ ( α ) ∫ a x ( x − t ) α − 1 f ( t ) d t ,

where f is a real- or complex-valued function on the interval ( a , b ) , α is a positive real number, and Γ ( α ) is the gamma function.

Definition 2.3

The Caputo derivative of a function f ( t ) of order α (in fractional form) is defined as follows:

D t α ( f ( t ) ) = 1 Γ ( n − α ) ∫ a t ( t − ξ ) n α f n ( ξ ) d ξ ,

where n − 1 < α ≤ n . Here, Γ represents the gamma function.

The Caputo fractional derivative is a type of derivative used to calculate noninteger derivatives of functions, particularly for time-dependent systems.

Definition 2.4

The Caputo derivative of a function f ( t ) of order α (in fractional form) for 0 < α < 1 is defined as follows:

D t α ( f ( t ) ) = 1 Γ ( 1 − α ) ∫ 0 t ( t − ξ ) 1 − α f ′ ( ξ ) d ξ ,

such that the integral part on the right-hand side exists.

The proposition is instigated by the introduction of the time derivative of Caputo fractional-order derivative into the system of equations given in Eq. (1). The dimensional imbalance is countered by considering an auxiliary parameter Λ showing the fractionality of the derivative. The new model encapsulating the corruption transmission dynamics for time, t > 0 , and step size, 0 < h ≤ 1 , is written as follows:

(2) 1 Λ 1 − h D t h C ( S ( t ) ) = Π + ( 1 − θ ) ε R − ρ β S C − ( κ + μ ) S , 1 Λ 1 − h D t h C ( E ( t ) ) = ρ β S C − ( δ + μ ) E , 1 Λ 1 − h D t h C ( C ( t ) ) = α δ E − ( σ + μ ) C , 1 Λ 1 − h D t h C ( R ( t ) ) = σ C + ( 1 − α ) δ E − ( ε + μ ) R , 1 Λ 1 − h D t h C ( H ( t ) ) = κ S + θ ε R − μ H .

Here, the initial conditions are given as follows:

S ( 0 ) = S 0 ≥ 0 , E ( 0 ) = E 0 ≥ 0 , C ( 0 ) = C 0 ≥ 0 , R ( 0 ) = R 0 ≥ 0 , H ( 0 ) = H 0 ≥ 0 .

In addition, the system (2) can be written in the following compact form:

(3) 1 Λ 1 − h D t h C G = ψ ( t , G ( t ) ) , for t ∈ [ 0 , T ] , 0 < h ≤ 1 ,

along with

(4) G ( t ) ∣ t = 0 = G 0 ≥ 0 ,

where G : [ 0 , + ∞ ) → ℛ 5 and ψ : ℛ 5 → ℛ 5 are vector-valued functions specified as follows:

(5) G ( t ) = S ( t ) E ( t ) C ( t ) R ( t ) H ( t ) , G 0 = S 0 E 0 C 0 R 0 H 0 , ψ ( G ( t ) ) = Π + ( 1 − θ ) ε R − ρ β S C − ( κ + μ ) S ρ β S C − ( δ + μ ) E α δ E − ( σ + μ ) C σ C + ( 1 − α ) δ E − ( ε + μ ) R κ S + θ ε R − μ H .

3 Theoretical analysis of the proposed model

In this section, we will conduct an extensive theoretical analysis of the proposed fractional model (2). We aim to explore some important characteristics of the devised model and prove that it is well-posed for numerical approximation.

3.1 Positivity

Ensuring the positivity of the initial conditions and parameters is essential in the application of the model. The model focuses on tracking the human population, thus all state variables and related parameters must maintain positivity, specifically, remain ≥ 0 throughout the model. The delicacies such as positivity, invariant feasible region, and the boundedness of the solution of the devised model are demonstrated by considering compartmental space such that

ℛ + 5 = { ( S , E , C , R , H ) ∈ R 5 ; S ( 0 ) ≥ 0 , E ( 0 ) ≥ 0 , C ( 0 ) ≥ 0 , R ( 0 ) ≥ 0 , H ( 0 ) ≥ 0 } ,

where Int ℛ + 5 denotes the interior of ℛ + 5 .

Lemma 3.1

If ( S ( 0 ) , E ( 0 ) , C ( 0 ) , R ( 0 ) , H ( 0 ) ) T ∈ Int ℛ + 5 , then for any t ≥ 0 , the solution of the proposed model is nonnegative.

Proof

As a result, all the solutions to model (2) are nonnegative. Therefore, the following results remain deducible from the first equation of system (2):

1 Λ 1 − h D t h C S ( t ) ∣ S = 0 = Π D t h C S ( t ) ∣ S = 0 = Λ 1 − h Π ≥ 0 .

Similarly, one may note that the second equation of the system given in Eq. (2) provides the following results:

1 Λ 1 − h D t h C E ( t ) ∣ E = 0 = ρ β S C , D t h C E ( t ) ∣ E = 0 = Λ 1 − h ρ β S C ≥ 0 .

It remains trivial to establish the outcomes with respect to the remaining equations of system (2) such that:

D t h C C ( t ) ∣ C = 0 = Λ 1 − h α δ E ≥ 0 , D t h C R ( t ) ∣ R = 0 = Λ 1 − h σ C + ( 1 − α ) δ E ≥ 0 , D t h C H ( t ) ∣ H = 0 = Λ 1 − h ( κ S + θ ε R ) ≥ 0 .

Hence, the nonnegativity of the solutions associated with the system (2) is proved.

3.2 Region of positive invariance

We derived the region of invariance, within which the solution of the devised model remains bounded. This is achieved by stratifying the population into compartments such as

(6) N ( t ) = S ( t ) + E ( t ) + C ( t ) + R ( t ) + H ( t ) .

Now, differentiating Eq. (6) with respect to the solution to model (2) provides

(7) d N d t = d S d t + d E d t + d C d t + d R d t + d H d t .

Therefore, by substituting all the state equations from the model (1) in Eq. (7), one obtains

d N d t = Π − μ N .

The aforementioned character is demonstrated by introducing a region, closed set ℬ such that

ℬ = ( S , E , C , R , H ) ∈ R 5 : S + E + C + R + H ≤ Π μ .

Clearly, ℬ is positively invariant, indicating that the model is considered to be epidemiologically meaningful and mathematically well-posed.

Theorem 3.2

Positive fractional system invariance exists for the closed set ℬ .

Proof

Let us first prove that N = S + E + C + R + H , is a bounded and nonnegative function. Therefore, the total population with the fractional derivative is obtained by adding all the relations compiled in Eq. (2) such that

1 Λ 1 − h D t h C N ( t ) = Π − μ N ( t ) .

Now, by employing the Laplace transform on both sides of the above equation and applying the whole population initial conditions with the assistance of the Mittag–Leffler function, E h , then N ( t ) is written as follows:

N ( t ) = N ( 0 ) E h ( − μ Λ 1 − h t h ) + ∫ 0 t Π Λ 1 − h ξ h − 1 × ∑ j = 0 ∞ ( − 1 ) j μ j Λ j ( 1 − h ) ξ j h Γ ( j h + h ) d ξ , = Π Λ 1 − h ( μ + h ) Λ 1 − h + E h ( − μ Λ 1 − h t h ) ( N ( 0 ) − Π Λ 1 − h ( μ + h ) Λ 1 − h ) , = Π μ + E h ( − μ Λ 1 − h t h ) N ( 0 ) − Π μ .

One may note that for N ( 0 ) ≤ Π μ and t > 0 , N ( t ) ≤ Π μ . This realization establishes the positive invariance of the closed set ℬ in the context of the fractional derivative framework.

3.3 Equilibrium points

This section delineates the calculation of the corruption equilibrium points. The two equilibrium positions related to model (2) are attended by solving 1 Λ 1 − h D t h C ( ⋅ ) = 0 such that

(8) Π + ( 1 − θ ) ε R − ρ β S C − ( k + μ ) S = 0 , ρ β S C − ( δ + μ ) E = 0 , α δ E − ( σ + μ ) C = 0 , σ C + ( 1 − α ) δ E − ( ε + μ ) R = 0 , κ S + θ ε R − μ H = 0 .

Therefore, the corruption-free equilibrium point, E 0 , is obtained by allowing E = 0 , C = 0 , and R = 0 such that

E 0 = Π k + μ , 0 , 0 , 0 , k Π μ ( k + μ ) .

In addition, the endemic equilibrium point E ∗ is written as follows:

E * = ( S ∗ , E ∗ , C ∗ , R ∗ , H ∗ ) ,

where

S ∗ = ( δ + μ ) ( σ + μ ) α β δ ρ , E ∗ = ( σ + μ ) ( ε + μ ) [ 1 − ℛ 0 ] α δ ρ β ϕ ( δ + μ ) ( σ + μ ) ( k + μ ) , C ∗ = ( ε + μ ) [ 1 − ℛ 0 ] ρ β ϕ ( δ + μ ) ( σ + μ ) ( k + μ ) , R ∗ = [ μ ( α − 1 ) − σ ] [ ℛ 0 − 1 ] α ρ β ϕ ( δ + μ ) ( σ + μ ) ( k + μ ) , H ∗ = k ( δ + μ ) ( σ + μ ) μ α β δ ρ + ε θ [ μ ( α − 1 ) − σ ] [ ℛ 0 − 1 ] μ α ρ β ϕ ( δ + μ ) ( σ + μ ) ( k + μ ) ,

and ϕ = α δ μ ( θ − 1 ) − ( ε + μ ) ( δ + μ ) ( σ + μ ) − δ ( 1 + θ ) ( σ + μ ) .

3.4 Basic reproduction number

The reproduction number denoted as ℛ 0 , is a statistical measure used in epidemiology to estimate the transmission potential of corrupted people. It represents the average number of new cases in which one corrupted individual can spread the corruption to a susceptible population. Using the principle of the next-generation matrix [42,43], we gain

F = 0 Π ρ β k + μ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 , V = δ + μ 0 0 0 − α δ σ + μ 0 0 − ( 1 − α ) δ − σ ε + μ 0 0 0 − θ ε μ .

The basic reproduction number is now calculated as the spectral radius of the next-generation matrix F V − 1 such that

F V − 1 = α ρ δ β Π ( δ + μ ) ( σ + μ ) ( k + μ ) Π ρ β ( k + μ ) ( σ + μ ) 0 0 0 0 0 0 0 0 0 0 0 0 0 0 .

Thus, the basic reproduction number, ℛ 0 , is solved as follows:

ℛ 0 = α δ ρ β Π ( δ + μ ) ( σ + μ ) ( k + μ ) .

4 Stability analysis

In this section, we conduct a comprehensive analysis of the proposed model to determine its local and global stability properties. To ascertain local stability, we analyze the signs of the eigenvalues of the Jacobian matrix computed at equilibrium points. To ensure global stability, we employ the Lyapunov theory with the inclusion of the LaSalle invariance principle [44,45] and the Castillo–Chavez theory [46].

4.1 Local stability

We examine the local stability for both the corruption-free and endemic states of the proposed model.

Theorem 4.1

The corruption-free equilibrium point of the said problem is locally asymptotically stable with the condition ℛ 0 < 1 , whereas unstable for ℛ 0 > 1 .

Proof

The Jacobian matrix of corruption-free equilibrium point for the devised model is given as follows:

J ( E 0 ) = − ρ β C − ( κ + μ ) 0 − ρ β S ( 1 − θ ) ε 0 ρ β C − δ − μ ρ β S 0 0 0 α δ − μ − σ 0 0 0 ( 1 − α ) δ σ − ( ε + μ ) 0 κ 0 0 θ ε − μ .

The evaluation of the Jacobian at the corruption-free equilibrium provides,

J ( E 0 ) = − ( κ + μ ) 0 − ρ β Π κ + μ ( 1 − θ ) ε 0 0 − δ − μ ρ β Π κ + μ 0 0 0 α δ − μ − σ 0 0 0 ( 1 − α ) δ σ − ( ε + μ ) 0 κ 0 0 θ ε − μ .

The resultant eigenvalues are λ 1 = − ( κ + μ ) < 0 , λ 2 = − μ < 0 , where

∣ J ( E 0 ) − λ I ∣ = − δ − μ − λ ρ β Π κ + μ 0 α δ − μ − σ − λ 0 ( 1 − α ) δ σ − ( ε + μ ) − λ = 0 ,

∣ J ( E 0 ) − λ I ∣ = − c 1 − λ c 2 0 c 3 − c 4 − λ 0 c 5 σ − c 6 − λ = 0 .

Here,

c 1 = δ + μ , c 2 = ρ β Π κ + μ , c 3 = α δ , c 4 = μ + σ , c 5 = ( 1 − α ) δ , c 6 = ε + μ .

Now, we obtain

λ 3 − ( c 1 + c 4 + c 6 ) λ 2 − ( c 1 c 4 + c 1 c 6 + c 4 c 6 ) λ + ( c 2 c 3 c 6 − c 1 c 4 c 6 ) = 0 .

By using the Routh–Hurwitz [47,48] standards for third-order polynomials, it is verified that, ( c 1 + c 4 + c 6 ) > 0 and ( c 2 c 3 c 6 − c 1 c 4 c 6 ) > 0 , if ( c 2 c 3 c 6 − c 1 c 4 c 6 ) c 2 c 3 c 6 < 1 . On substitution, we obtain

ℛ 0 = α δ ρ β Π ( δ + μ ) ( σ + μ ) ( k + μ ) < 1 ,

and [ c 1 + c 4 + c 6 ] − λ [ c 1 c 4 + c 1 c 6 + c 4 c 6 ] > ( c 2 c 3 c 6 − c 1 c 4 c 6 ) if ℛ 0 < 1 . This completes the proof while highlighting the fact that corruption transmission can be avoided if the initial size of the corrupted people falls inside the corruption-free equilibrium point area of attraction.

Theorem 4.2

The endemic equilibrium, E * , is locally asymptotically stable with the condition ℛ 0 > 1 , whereas it is unstable for ℛ 0 < 1 .

Proof

The Jacobian matrix is computed as follows:

J ( E * ) = − ρ β C − ( κ + μ ) 0 − ρ β S ( 1 − θ ) ε 0 ρ β C − δ − μ p β S 0 0 0 α δ − μ − σ 0 0 0 ( 1 − α ) δ σ − ( ε + μ ) 0 κ 0 0 θ ε − μ .

The eigenvalues are written as λ 1 = − μ < 0 , where

∣ J ( E * ) − λ I ∣ = − ( d 1 + d 2 + λ ) 0 − d 1 d 3 d 1 d 4 − λ d 1 0 0 d 5 − ( d 6 + λ ) 0 0 d 7 σ − ( d 8 + λ ) ,

and

d 1 = ρ β C , d 2 = ( κ + μ ) , d 3 = ( 1 − θ ) ε , d 4 = ( δ + α ) , d 5 = α δ , d 6 = μ + α , d 7 = ( 1 − α ) δ , d 8 = ( ε + μ ) .

On simplification, we obtain

∣ J ( E * ) − λ I ∣ = λ 4 + ( d 1 + d 2 − d 4 + d 6 + d 8 ) λ 3 + ( d 1 d 6 − d 1 d 4 − d 1 d 5 + d 1 d 8 − d 2 d 4 + d 2 d 6 − d 4 d 6 − d 4 d 8 + d 6 d 8 ) λ 2 + ( d 1 d 6 d 8 + d 1 d 2 d 5 − d 1 d 3 d 7 − d 1 d 4 d 6 − d 1 d 4 d 8 − d 1 d 5 d 8 − d 2 d 4 d 6 − d 2 d 4 d 8 + d 2 d 6 d 8 − d 4 d 6 d 8 ) λ − ( d 1 d 2 d 5 d 8 + d 1 d 3 d 5 σ + d 1 d 3 d 6 d 7 + d 1 d 4 d 6 d 8 + d 2 d 4 d 6 d 8 ) = 0 .

Therefore, the above equation can be written as follows:

∣ J ( E * ) − λ I ∣ = n 0 λ 4 + n 1 λ 3 + n 2 λ 2 + n 3 λ 1 + n 4 = 0 ,

where

n 0 = 1 , n 1 = ( d 1 + d 2 − d 4 + d 6 + d 8 ) , n 2 = ( d 1 d 6 − d 1 d 4 − d 1 d 5 + d 1 d 8 − d 2 d 4 + d 2 d 6 − d 4 d 6 − d 4 d 8 + d 6 d 8 ) , n 3 = ( d 1 d 6 d 8 + d 1 d 2 d 5 − d 1 d 3 d 7 − d 1 d 4 d 6 − d 1 d 4 d 8 − d 1 d 5 d 8 − d 2 d 4 d 6 − d 2 d 4 d 8 + d 2 d 6 d 8 − d 4 d 6 d 8 ) , n 4 = ( d 1 d 2 d 5 d 8 + d 1 d 3 d 5 σ + d 1 d 3 d 6 d 7 + d 1 d 4 d 6 d 8 + d 2 d 4 d 6 d 8 ) .

On the employment of Routh–Hurwitz criterion [47] for fourth-order polynomials, n 0 > 0 , n 1 > 0 , n 1 n 2 − n 0 n 3 > 0 , ( n 1 n 2 − n 0 n 3 ) n 3 − n 1 2 n 4 > 0 , and n 4 > 0 only if ℛ 0 > 1 . One may note that the eigenvalues are nonpositive indicating the local asymptotic stability of E * according to Hurwitz criteria.

4.2 Global stability

In this section, we discuss the corruption-free and endemic equilibrium points of the proposed model and prove that they are globally stable.

Theorem 4.3

The aforementioned problem is globally asymptotically stable at corruption-free equilibrium E 0 if ℛ 0 < 1 , but remains unstable otherwise.

Proof

The global stability of the developed model at point E 0 originated through the construct of the Lyapunov function is

(9) V ( t ) = ( S − S * ) + E + C .

Next, the time derivative of Eq. (9) is calculated and applied to the system of the equation given in Eq. (1), then we obtain

d V d t = d S d t + d E d t + d C d t , = Π − ρ β S C − ( κ + μ ) S + ρ β S C − ( δ + μ ) E + α δ E − ( σ + μ ) C , = Π ( μ + κ ) ( μ + κ ) − ( κ + μ ) S − δ E − μ E + α δ E − σ C − μ C , = ( κ + μ ) S * − ( κ + μ ) S − μ ( E + C ) − δ E + α δ E − σ C , = ( κ + μ ) ( S * − S ) − μ ( E + C ) − δ ( E − α E ) − σ C , = − [ ( κ + μ ) ( S − S * ) + μ ( E + C ) + δ ( E − α E ) + σ C ] < 0 .

It is provable that d V d t < 0 for ℛ 0 < 1 . In addition, S = S * and E = C = 0 . The invariant principle of LaSalle’s [44,45] suggests that E 0 is globally asymptotically stable.

Theorem 4.4

The endemic equilibrium state E * = ( S ∗ , E ∗ , C ∗ , R ∗ , H ∗ ) of the model (1) is globally asymptotically stable with the condition ℛ 0 > 1 ; otherwise, it is unstable.

Proof

The global stability is established by defining the Lyapunov function at endemic equilibrium points, such as

(10) Q = 1 2 [ ( S − S * ) + ( E − E * ) ( C − C * ) ] 2 .

After calculating the time derivatives of Eq. (10) and using them in model (1), one obtains

d Q d t = [ ( S − S * ) + ( E − E * ) ( C − C * ) ] × [ Π − ( κ + μ ) S − ( δ + μ ) E + α δ E − ( σ + μ ) C ] , d Q d t = [ ( S − S * ) + ( E − E * ) ( C − C * ) ] × [ ( μ + κ ) ℛ 0 S * − ( κ + μ ) S − ( δ + μ ) E + α δ E − ( σ + μ ) C ] ,

where

δ + μ = η 1 , σ + μ = η 2 , κ + μ = η 3 .

d Q d t = [ ( S − S * ) + ( E − E * ) ( C − C * ) ] × [ η 3 ℛ 0 S * − η 3 S − η 1 E + α δ E − η 2 C ] , d Q d t = [ ( S − S * ) + ( E − E * ) ( C − C * ) ] × [ η 3 ( ℛ 0 S * − S ) − E ( η 1 + α δ ) − η 2 C ] , d Q d t = − [ ( S − S * ) + ( E − E * ) ( C − C * ) ] × [ η 3 ( S − ℛ 0 S * ) + E ( η 1 + α δ ) + η 2 C ] < 0 .

One may note that d Q d t < 0 for all ( S ∗ , E ∗ , C ∗ , R ∗ , H ∗ ) , where as d Q d t = 0 holds only for S ∗ = S , E ∗ = E , C ∗ = C . Subsequently, the endemic equilibrium E * is the only positively invariant set contained in [ ( S , E , C , R , H ) , S ∗ = S , E ∗ = E , C ∗ = C ] . Consequently, the positive E * is asymptotically globally stable.

4.3 Numerical results for stability analysis

In this section, we utilized the fourth-order Runge–Kutta method to numerically solve the proposed deterministic model. This numerical solution provides support for the findings of our analysis. To apply the Runge–Kutta method, we made certain assumptions about the parameter values in the model, and values were chosen in a biologically realistic manner, based on previous studies and empirical evidence. Therefore, with the Runge–Kutta fourth-order method, model (1) yields

(11) S i + 1 − S i l = Π + ( 1 − θ ) ε R i − ρ β S i + 1 C i − ( κ + μ ) S i + 1 , E i + 1 − E i l = ρ β S i C i − ( δ + μ ) E i + 1 , C i + 1 − C i l = α δ E i − ( σ + μ ) C i + 1 , R i + 1 − R i l = σ C i + ( 1 − α ) δ E i − ( ε + μ ) R i + 1 , H i + 1 − H i l = κ S i + θ ε R i − μ H i + 1 .

Next, to solve the considered model numerically, we consider the first equation of model (11) for the susceptible compartment S , and we obtain

S i + 1 − S i = l Π − l ( 1 − θ ) ε R i − l ρ β S i + 1 C i − l ( κ + μ ) S i + 1 , S i + 1 [ 1 + l ρ β C i + l ( κ + μ ) ] = l Π − l ( 1 − θ ) ε R i + S i , S i + 1 = S i − ( 1 − θ ) l ε R i + l Π 1 + l ρ β C i + l ( κ + μ ) .

Similarly, the remaining compartments of system (11) are written in a similar fashion as follows:

E i + 1 − E i l = ρ β S i C i − ( δ + μ ) E i + 1 , E i + 1 − E i = l ρ β S i C i − l ( δ + μ ) E i + 1 , ⋮ E i + 1 = E i + l ρ β C i S i 1 + l ( δ + μ ) . ,

C i + 1 − C i l = α δ E i − ( σ + μ ) C i + 1 , C i + 1 − C i = l α δ E i − l ( σ + μ ) C i + 1 , ⋮ C i + 1 = C i + l δ α E i 1 + l ( σ + μ ) . ,

R i + 1 − R i l = σ C i + ( 1 − α ) δ E i − ( ε + μ ) R i + 1 , R i + 1 − R i = l σ C i + l ( 1 − α ) δ E i − l ( ε + μ ) R i + 1 , ⋮ R i + 1 = R i + l σ C i + l ( 1 − α ) δ E i 1 + l ( ε + μ ) . ,

H i + 1 − H i l = κ S i + θ ε R i − μ H i + 1 , H i + 1 − H i = l κ S i + l θ ε R i − l μ H i + 1 , ⋮ H i + 1 = H i + l κ S i + l θ ε R i 1 + l μ .

4.3.1 Algorithm

The Runge-Kutta method is applied with respect to following steps of the algorithm are given below.

Step 1 : S ( 0 ) = E ( 0 ) = C ( 0 ) = R ( 0 ) = H ( 0 ) = 0 .

Step 2 : for i = 1 , 2 , 3 , … , n − 1

S i + 1 = S i − ( 1 − θ ) l ε R i + l Π 1 + l ρ β C i + l ( κ + μ ) , E i + 1 = E i + l ρ β C i S i 1 + l ( δ + μ ) , C i + 1 = C i + l δ α E i 1 + l ( σ + μ ) , R i + 1 = R i + l σ C i + l ( 1 − α ) δ E i 1 + l ( ε + μ ) , H i + 1 = H i + l κ S i + l θ ε R i 1 + l μ

Step 3: for i = 1 , 2 , 3 , … , n − 1 , write S * ( t i ) = S * , E * ( t i ) = E * , C * ( t i ) = C * , R * ( t i ) = R * , H * ( t i ) = H * .

To graphically represent our results, we will utilize compartmental initial conditions for the developed model. Specifically, we will set S ( 0 ) = 10,000 , E ( 0 ) = 0 , C ( 0 ) = 100 , R ( 0 ) = 0 , and H ( 0 ) = 100 . In addition, we have made biologically reasonable assumptions for the parameter values and utilized the Matlab software to generate the graphs. The detailed description of the parameters influencing the system given in the system of Eq. (1) is documented in Table 1, and the time span considered is from 0 to 250 units, corresponding to days.

Table 1

Description of parameters of model (1)

Parameters	Description	Value of parameters
ρ	Probability of corruption being transmitted per contact	0.036
β	Rate at which susceptible individuals will interact with exposed individuals	0.0234
δ	Rate at which individuals who have been exposed to corruption become corrupted	0.2
ε	Rate at which individuals who have recovered become honest	0.35
Π	Recruitment rate of susceptible humans	85
κ	Proportion of individuals who joins the honest population from susceptible population	0.03
μ	Mortality rate for the entire human population	0.0160
α	Proportion of individuals who join the corrupted subpopulation from the exposed compartment	0.3
θ	Proportion of individuals who move from the recovered compartment to the honest subpopulation	0.1

Figure 2 shows the dynamics of the stability behavior of each class with respect to time and initial conditions. The magnitude of the susceptible class varied for values such as 10,000, 8,000, 6,000, and 4,000. There exists in a positive relationship between the size of the susceptible population and the time to attain stability Figure 2(a). Next, the exposed class is considered for different values, indicating the degree of prevalence such as 0.3, 0.2, 0.1, and 0 in Figure 2(b). First, the population exposed class increases and then after some time decreases. Figure 2(c) depicts the stability attainment for varying sizes of corrupted classes such as 100, 95, 90, and 85. The time to gain stability decreases. After 50 days, the population remains constant. Similar patterns are observed for the recovered class where the magnitude of the class is defined for values such as 0.3, 0.2, 0.1, and 0 in Figure 2(d). The population increases in starting time, after some time, the population decreases rapidly with time. Finally, Figure 2(e) presents the relationship between stability and varying extent of the honest population for values such as 100, 95, 90, and 85. As the size of the honest class increases, the time to achieve stability also increases.

Figure 2

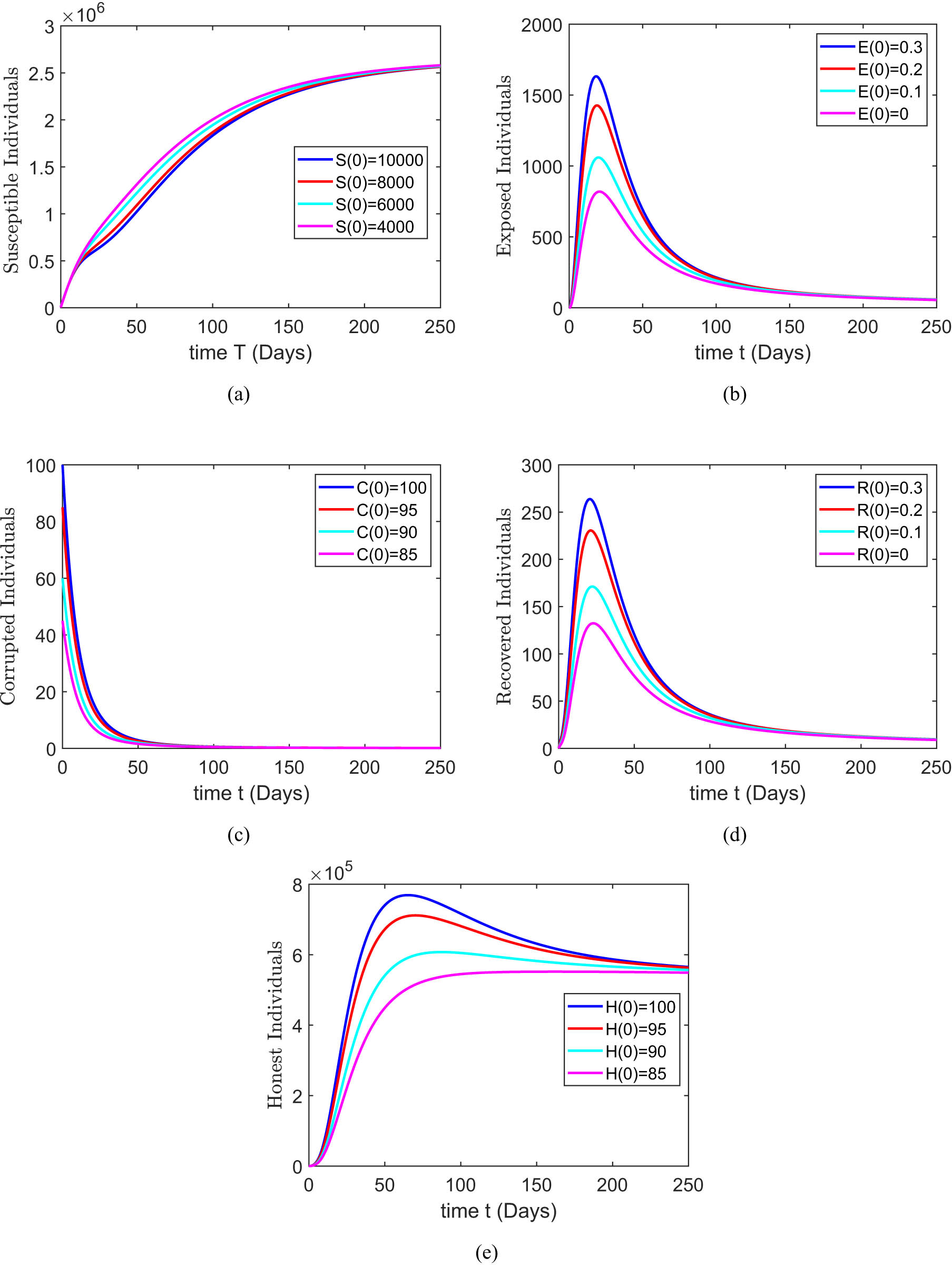
The effects of the variations of simulation results with respect to all compartmental classes of the proposed model (1). (a) Susceptible class; (b) exposed class; (c) corrupted class; (d) projects recovered class; and (e) honest class.

5 Theory of existence

This section is dedicated to demonstrating the existence and uniqueness results of the proposed model through the use of fixed point theory. The system of equations given in Eq. (2) is written as follows:

(12) 1 Λ 1 − h D t h C G = ψ ( t , G ( t ) ) , for t ∈ [ 0 , T ] , 0 < h ≤ 1 , G ( t ) ∣ t = 0 = G 0 ≥ 0

only if

(13) G ( t ) = ( S , E , C , R , H ) T , ψ ( t , G ( t ) ) = ( Y i ( t , S , E , C , R , H ) ) ,

where i = 1 , 2 , 3 , 4 , 5 and Y 1 , Y 2 , Y 3 , Y 4 , Y 5 are defined as follows:

Y 1 = Π + ( 1 − θ ) ε R − ρ β S C − ( k + μ ) S , Y 2 = ρ β S C − ( δ + μ ) E , Y 3 = α δ E − ( σ + μ ) C , Y 4 = σ C + ( 1 − α ) δ E − ( ε + μ ) R , Y 5 = κ S + θ ε R − μ H .

By the application of fractional integral to Eq. (13), we obtain

(14) G ( t ) − G ( 0 ) = Λ 1 − h Γ ( h ) ∫ 0 t ψ ( ξ , G ( ξ ) ) ( t − ξ ) h − 1 d ( ξ ) .

Eq. (14) can be written for each class of the devised model as follows:

(15) S ( t ) − S ( 0 ) = Λ 1 − h Γ ( h ) ∫ 0 t Y 1 ( t − ξ ) h − 1 d ( ξ ) , E ( t ) − E ( 0 ) = Λ 1 − h Γ ( h ) ∫ 0 t Y 2 ( t − ξ ) h − 1 d ( ξ ) , C ( t ) − C ( 0 ) = Λ 1 − h Γ ( h ) ∫ 0 t Y 3 ( t − ξ ) h − 1 d ( ξ ) , R ( t ) − R ( 0 ) = Λ 1 − h Γ ( h ) ∫ 0 t Y 4 ( t − ξ ) h − 1 d ( ξ ) , H ( t ) − H ( 0 ) = Λ 1 − h Γ ( h ) ∫ 0 t Y 5 ( t − ξ ) h − 1 d ( ξ ) .

One may note that to demonstrate that the kernel ψ ( ξ , G ( ξ ) ) satisfies the Lipschitz condition and contraction, it is sufficient to demonstrate that all Y i ; i = 1 , 2 , 3 , 4 , 5 satisfy the Lipschitz condition and contraction.

Theorem 5.1

The kernel Y i satisfies the Lipschitz condition and contraction for the bound function G for i = 1 , 2 , 3 , 4 , 5 if the given inequality such that:

1 > ϒ i ≥ 0 .

Proof

It is verifiable that,

∥ Y 1 ( t , S ) − Y 1 ( t , S 1 ) ∥ = ∥ ρ β S C − ( δ + μ ) E ∥ ≤ ρ β ∥ C ∥ ∥ S ( t ) − S 1 ( t ) ∥ − ( κ + μ ) ∥ S ( t ) − S 1 ( t ) ∥ ≤ ∥ ρ β a ∥ ∥ S ( t ) − S 1 ∥ − ‖ − ( κ + μ ) ∥ S ( t ) − S 1 ∥ ≤ ( ∥ ρ β a − ( κ + μ ) ∥ ) ∥ S − S 1 ∥ .

Let ϒ 1 = ( ∥ ρ β a − ( κ + μ ) ∥ ) , where C ≤ a is a bounded function, thus

(16) ∥ Y 1 ( t , S ) − Y 1 ( t , S 1 ) ∥ = ϒ 1 ∥ S − S 1 ∥ .

As a result, the Lipschitz condition is established for Y 1 , and if 1 > ∥ ρ β a ∥ ≥ 0 , then Y 1 is a contraction. Similarly, one may demonstrate that Y i , i = 2 , 3 , 4 , 5 satisfy the Lipschitz condition, which is then given as follows:

(17) ∥ Y 2 ( t , E ) − Y 2 ( t , E 1 ) ∥ = ϒ 2 ∥ E − E 1 ∥ , ∥ Y 3 ( t , C ) − Y 3 ( t , C 1 ) ∥ = ϒ 3 ∥ C − C 1 ∥ , ∥ Y 4 ( t , R ) − Y 4 ( t , R 1 ) ∥ = ϒ 4 ∥ R − R 1 ∥ , ∥ Y 5 ( t , H ) − Y 5 ( t , H 1 ) ∥ = ϒ 5 ∥ H − H 1 ∥ ,

where ϒ 2 = ( δ + μ ) , ϒ 3 = ( σ + μ ) , ϒ 4 = ( ε + μ ) , and ϒ 5 = μ . Now let us consider the recursive form with respect to system (15) such that

ψ 1 n = S n ( t ) − S n − 1 ( t ) = Λ 1 − h Γ ( h ) ∫ 0 t ( Y 1 ( ξ , S n − 1 ) ) − ( Y 1 ( ξ , S n − 2 ) ) ( t − ξ ) h − 1 d ( ξ ) , ψ 2 n = E n ( t ) − E n − 1 ( t ) = Λ 1 − h Γ ( h ) ∫ 0 t ( Y 2 ( ξ , E n − 1 ) ) − ( Y 2 ( ξ , E n − 2 ) ) ( t − ξ ) h − 1 d ( ξ ) , ψ 3 n = C n ( t ) − C n − 1 ( t ) = Λ 1 − h Γ ( h ) ∫ 0 t ( Y 3 ( ξ , C n − 1 ) ) − ( Y 3 ( ξ , C n − 2 ) ) ( t − ξ ) h − 1 d ( ξ ) , ψ 4 n = R n ( t ) − R n − 1 ( t ) = Λ 1 − h Γ ( h ) ∫ 0 t ( Y 4 ( ξ , R n − 1 ) ) − ( Y 3 ( ξ , R n − 2 ) ) ( t − ξ ) h − 1 d ( ξ ) , ψ 5 n = H n ( t ) − H n − 1 ( t ) = Λ 1 − h Γ ( h ) ∫ 0 t ( Y 5 ( ξ , H n − 1 ) ) − ( Y 5 ( ξ , H n − 2 ) ) ( t − ξ ) h − 1 d ( ξ ) .

The initial condition S ( 0 ) = S 0 , E ( 0 ) = E 0 , C ( 0 ) = C 0 , R ( 0 ) = R 0 , and H ( 0 ) = H 0 . When we apply the norm to the first equation in the above system, we obtain

∥ ψ 1 n ∥ = ∥ S n ( t ) − S n − 1 ( t ) ∥ = Λ 1 − h Γ ( h ) ∫ 0 t ( Y 1 ( ξ , S n − 1 ) ) − ( Y 1 ( ξ , S n − 2 ) ) ( t − ξ ) h − 1 d ( ξ ) , ≤ Λ 1 − h Γ ( h ) ∫ 0 t ∥ ( Y 1 ( ξ , S n − 1 ) ) − ( Y 1 ( ξ , S n − 2 ) ) ( t − ξ ) h − 1 ∥ d ( ξ ) .

The Lipchitz condition gives us

(18) ‖ ψ 1 n ‖ ≤ Λ 1 − h Γ ( h ) ϒ 1 ∫ 0 t ‖ ψ 1 ( n − 1 ) ( ξ ) ‖ d ( ξ ) .

Similarly, it is verifiable that

(19) ∥ ψ 2 n ∥ ≤ Λ 1 − h Γ ( h ) ϒ 2 ∫ 0 t ∥ ψ 2 ( n − 1 ) ( ξ ) ∥ d ( ξ ) , ∥ ψ 3 n ∥ ≤ Λ 1 − h Γ ( h ) ϒ 3 ∫ 0 t ∥ ψ 3 ( n − 1 ) ( ξ ) ∥ d ( ξ ) , ∥ ψ 4 n ∥ ≤ Λ 1 − h Γ ( h ) ϒ 4 ∫ 0 t ∥ ψ 4 ( n − 1 ) ( ξ ) ∥ d ( ξ ) , ∥ ψ 5 n ∥ ≤ Λ 1 − h Γ ( h ) ϒ 5 ∫ 0 t ∥ ψ 5 ( n − 1 ) ( ξ ) ∥ d ( ξ ) .

Hence, we can write

S n ( t ) = ∑ k = 1 n ψ 1 k ( t ) , E n ( t ) = ∑ k = 1 n ψ 2 k ( t ) , C n ( t ) = ∑ k = 1 n ψ 3 k ( t ) , R n ( t ) = ∑ k = 1 n ψ 4 k ( t ) , H n ( t ) = ∑ k = 1 n ψ 5 k ( t )

Theorem 5.2

For a certain amount of time t 1 , the solution to the system of Eq. (2) exists if

Λ 1 − h Γ ( h ) t 1 ϒ 1 < 1 .

Proof

Using the recursive approach along with Eqs. (18) and (19), we derive

(20) ∥ ψ 1 n ∥ ≤ ∥ S n ( 0 ) ∥ Λ 1 − h Γ ( h ) ϒ 1 t n , ∥ ψ 2 n ∥ ≤ ∥ E n ( 0 ) ∥ Λ 1 − h Γ ( h ) ϒ 2 t n , ∥ ψ 3 n ∥ ≤ ∥ C n ( 0 ) ∥ Λ 1 − h Γ ( h ) ϒ 3 t n , ∥ ψ 4 n ∥ ≤ ∥ R n ( 0 ) ∥ Λ 1 − h Γ ( h ) ϒ 4 t n , ∥ ψ 5 n ∥ ≤ ∥ H n ( 0 ) ∥ Λ 1 − h Γ ( h ) ϒ 5 t n .

Consequently, the derived system provides at least one solution and is continuous. Assume that

S ( t ) − S ( 0 ) = S n ( t ) − J 1 n ( t ) , E ( t ) − E ( 0 ) = E n ( t ) − J 2 n ( t ) , C ( t ) − C ( 0 ) = C n ( t ) − J 3 n ( t ) , R ( t ) − R ( 0 ) = R n ( t ) − J 4 n ( t ) , H ( t ) − H ( 0 ) = H n ( t ) − J 5 n ( t ) .

Now,

∥ J 1 n ( t ) ∥ = Λ 1 − h Γ ( h ) ∫ 0 t ( Y 1 ( ξ , S ) ) − ( Y 1 ( ξ , S n − 1 ) ) d ( ξ ) , ≤ Λ 1 − h Γ ( h ) ∫ 0 t ∥ ( Y 1 ( ξ , S ) ) − ( Y 1 ( ξ , S n − 1 ) ) ∥ d ( ξ ) , ≤ Λ 1 − h Γ ( h ) ϒ 1 ∥ S − S n − 1 ∥ t .

After repeating the above-documented process, we have

∥ J 1 n ( t ) ∥ ≤ Λ 1 − h Γ ( h ) t n + 1 ϒ 1 n + 1 h .

At specific time t 1 , we obtain

∥ J 1 n ( t ) ∥ ≤ Λ 1 − h Γ ( h ) t 1 n + 1 ϒ 1 n + 1 h .

When we apply the limit to the above equation such that n → ∞ , we obtain ∥ J 1 n ( t ) ∥ → 0 . Similarly, ∥ J i n ( t ) ∥ for i = 2 , 3 , 4 , 5 is demonstrated as follows:

∥ J 2 n ( t ) ∥ ≤ Λ 1 − h Γ ( h ) t 1 n + 1 ϒ 2 n + 1 h , ∥ J 3 n ( t ) ∥ ≤ Λ 1 − h Γ ( h ) t 1 n + 1 ϒ 3 n + 1 h , ∥ J 4 n ( t ) ∥ ≤ Λ 1 − h Γ ( h ) t 1 n + 1 ϒ 4 n + 1 h , ∥ J 5 n ( t ) ∥ ≤ Λ 1 − h Γ ( h ) t 1 n + 1 ϒ 5 n + 1 h .

Next, to process the uniqueness of the solution of the proposed model (2), let us assume that S 1 ( t ) , E 1 ( t ) , C 1 ( t ) , R 1 ( t ) , and H 1 ( t ) be another solution to the model. Let us write,

(21) S ( t ) − S 1 ( t ) = Λ 1 − h Γ ( h ) ∫ 0 t Y 1 ( ξ , S ) − ( Y 1 ( ξ , S 1 ) ) d ( ξ ) .

By taking the norm of Eq. (21), we have

∥ S ( t ) − S 1 ( t ) ∥ = Λ 1 − h Γ ( h ) ∫ 0 t ∥ Y 1 ( ξ , S ) − ( Y 1 ( ξ , S 1 ) ) ∥ d ( ξ ) .

Utilizing the Lipschitz condition, we obtain

∥ S ( t ) − S 1 ( t ) ∥ = Λ 1 − h Γ ( h ) ϒ 1 t ∥ S ( t ) − S 1 ( t ) ∥ .

Hence,

(22) ∥ S ( t ) − S 1 ( t ) ∥ 1 − Λ 1 − h Γ ( h ) ϒ 1 t ≤ 0 .

Theorem 5.3

If the condition

1 − Λ 1 − h Γ ( h ) ϒ 1 t > 0

is satisfied, then the examined system has a unique solution.

Proof

Let the following condition hold:

∥ S ( t ) − S 1 ( t ) ∥ 1 − Λ 1 − h Γ ( h ) ϒ 1 t ≤ 0 .

Then, ‖ S ( t ) − S 1 ( t ) ‖ = 0 . As a result, we obtain S ( t ) = S 1 ( t ) . The results for other departmental compartments such as E , C , R , and H can be verified similarly.

Definition 5.4

The considered system is said to be UH stable if ∃ some constants δ i > 0 , i ∈ ℛ 5 and for each ℧ i > 0 , for

S ( t ) − Λ 1 − h Γ ( h ) ∫ 0 t ( t − ξ ) h − 1 Y 1 ( ξ , S ( ξ ) ) d ( ξ ) ≤ ℧ 1 , E ( t ) − Λ 1 − h Γ ( h ) ∫ 0 t ( t − ξ ) h − 1 Y 2 ( ξ , E ( ξ ) ) d ( ξ ) ≤ ℧ 2 , C ( t ) − Λ 1 − h Γ ( h ) ∫ 0 t ( t − ξ ) h − 1 Y 3 ( ξ , C ( ξ ) ) d ( ξ ) ≤ ℧ 3 , R ( t ) − Λ 1 − h Γ ( h ) ∫ 0 t ( t − ξ ) h − 1 Y 4 ( ξ , R ( ξ ) ) d ( ξ ) ≤ ℧ 4 , H ( t ) − Λ 1 − h Γ ( h ) ∫ 0 t ( t − ξ ) h − 1 Y 5 ( ξ , H ( ξ ) ) d ( ξ ) ≤ ℧ 5 .

The following conditions are satisfied by constants such as S ˙ , E ˙ , C ˙ , R ˙ , and H ˙ ;

(23) S ˙ ( t ) = Λ 1 − h Γ ( h ) ∫ 0 t ( t − ξ ) h − 1 Y 1 ( ξ , S ˙ ( ξ ) ) d ( ξ ) , E ˙ ( t ) = Λ 1 − h Γ ( h ) ∫ 0 t ( t − ξ ) h − 1 Y 2 ( ξ , E ( ξ ) ) d ( ξ ) , C ˙ ( t ) = Λ 1 − h Γ ( h ) ∫ 0 t ( t − ξ ) h − 1 Y 3 ( ξ , C ( ξ ) ) d ( ξ ) , R ˙ ( t ) = Λ 1 − h Γ ( h ) ∫ 0 t ( t − ξ ) h − 1 Y 4 ( ξ , R ( ξ ) ) d ( ξ ) , H ˙ ( t ) = Λ 1 − h Γ ( h ) ∫ 0 t ( t − ξ ) h − 1 Y 5 ( ξ , H ( ξ ) ) d ( ξ ) .

Hence,

∣ S − S ˙ ∣ ≤ δ 1 ℧ 1 , ∣ E − E ˙ ∣ ≤ δ 2 ℧ 2 , ∣ C − C ˙ ∣ ≤ δ 3 ℧ 3 , ∣ R − R ˙ ∣ ≤ δ 4 ℧ 4 , ∣ H − H ˙ ∣ ≤ δ 5 ℧ 5 .

Assumption. Assume that we have a Banach space ℬ ( U ) for the real-valued functions, where U = [ 0 , b ] and U = ℬ ( U ) × ℬ ( U ) × ℬ ( U ) × ℬ ( U ) × ℬ ( U ) specifies a norm such as ‖ S ˙ , E ˙ , C ˙ , R ˙ , H ˙ ‖ = sup t ∈ U ∣ S ˙ ∣ + sup t ∈ U ∣ E ˙ ∣ + sup t ∈ U ∣ C ˙ ∣ + sup t ∈ U ∣ R ˙ ∣ + sup t ∈ U ‖ H ˙ ∣ .

Theorem 5.5

The considered system is UH stable when the aforementioned assumption holds.

Proof

We have

(24) ∥ S − S ˙ ∥ = Λ 1 − h Γ ( h ) ∫ 0 t ( t − ξ ) h − 1 ∥ ( Y 1 ( ξ , S ) ) − ( Y 1 ( ξ , S ˙ ) ) ∥ d ( ξ ) ≤ ψ 1 ∥ S − S ˙ ∥ .

(25) ∥ E − E ˙ ∥ = Λ 1 − h Γ ( h ) ∫ 0 t ( t − ξ ) h − 1 ∥ ( Y 2 ( ξ , E ) ) − ( Y 2 ( ξ , E ˙ ) ) ∥ d ( ξ ) ≤ ψ 2 ∥ E − E ˙ ∥ .

(26) ∥ C − C ˙ ∥ = Λ 1 − h Γ ( h ) ∫ 0 t ( t − ξ ) h − 1 ∥ ( Y 3 ( ξ , C ) ) − ( Y 3 ( ξ , C ˙ ) ) ∥ d ( ξ ) ≤ ψ 3 ∥ C − C ˙ ∥ .

(27) ∥ R − R ˙ ∥ = Λ 1 − h Γ ( h ) ∫ 0 t ( t − ξ ) h − 1 ‖ ( Y 4 ( ξ , R ) ) − ( Y 4 ( ξ , R ˙ ) ) ‖ d ( ξ ) ≤ ψ 4 ∥ R − R ˙ ∥ .

(28) ∥ H − H ˙ ∥ = Λ 1 − h Γ ( h ) ∫ 0 t ( t − ξ ) h − 1 ∥ ( Y 5 ( ξ , H ) ) − ( Y 5 ( ξ , H ˙ ) ) ∥ d ( ξ ) ≤ ψ 5 ∥ H − H ˙ ∥ .

By using ℧ i = ψ i and Λ 1 − h Γ ( h ) = δ i , we obtained

(29) ∥ S − S ˙ ∥ ≤ ℧ 1 δ 1 .

Similarly, for the remaining classes, we have the following:

(30) ∥ E − E ˙ ∥ ≤ ℧ 2 δ 2 , ∥ C − C ˙ ∥ ≤ ℧ 3 δ 3 , ∥ R − R ˙ ∥ ≤ ℧ 4 δ 4 , ∥ H − H ˙ ∥ ≤ ℧ 5 δ 5 ,

which completes the proof.

6 Numerical simulation

This section is dedicated to the resolution of the system under consideration by using the Adams–Bashforth method. Therefore, the expression given in system (15) is now written as follows:

(31) S ( t ) − S ( 0 ) = Λ 1 − h Γ ( h ) ∫ 0 t ( t − ξ ) h − 1 Y 1 ( ξ , S , E , C , R , H ) d ( ξ ) , E ( t ) − E ( 0 ) = Λ 1 − h Γ ( h ) ∫ 0 t ( t − ξ ) h − 1 Y 2 ( ξ , S , E , C , R , H ) d ( ξ ) , C ( t ) − C ( 0 ) = Λ 1 − h Γ ( h ) ∫ 0 t ( t − ξ ) h − 1 Y 3 ( ξ , S , E , C , R , H ) d ( ξ ) , R ( t ) − R ( 0 ) = Λ 1 − h Γ ( h ) ∫ 0 t ( t − ξ ) h − 1 Y 4 ( ξ , S , E , C , R , H ) d ( ξ ) , H ( t ) − H ( 0 ) = Λ 1 − h Γ ( h ) ∫ 0 t ( t − ξ ) h − 1 Y 5 ( ξ , S , E , C , R , H ) d ( ξ ) .

Let us consider the development of the numerical scheme for the first equation of the above-given system. Moreover, let us define that t ν = ν Δ , ν = 0 , 1 , 2 , … , j , where Δ = T J is the step size and J is the positive integer along with T > 0 . For t = t ν + 1 , ν = 0 , 1 , 2 , … , the first Eq. (31) is given as follows:

(32) S ( t ν + 1 ) − S ( 0 ) = Λ 1 − h Γ ( h ) ∫ 0 t ν + 1 ( t ν + 1 − t ) h − 1 Y 1 ( S , E , C , R , H , t ) d t ,

and

(33) S ( t ν ) − S ( 0 ) = Λ 1 − h Γ ( h ) × ∫ 0 t ν ( t ν − t ) h − 1 Y 1 ( S , E , C , R , H , t ) d t .

By subtracting Eq. (33) from Eq. (32), we obtain

S ( t ν + 1 ) = S ( t ν ) + Λ 1 − h Γ ( h ) ∫ 0 t ν + 1 ( t ν + 1 − t ) h − 1 Y 1 ( S , E , C , R , H , t ) d t − Λ 1 − h Γ ( h ) ∫ 0 t ν ( t ν − t ) h − 1 Y 1 ( S , E , C , R , H , t ) d t .

Let us rewrite the equation as follows:

(34) S ( t ν + 1 ) = S ( t ν ) + ℋ h , 1 − ℋ h , 2 ,

where,

ℋ h , 1 = Λ 1 − h Γ ( h ) ∫ 0 t ν + 1 ( t ν + 1 − t ) h − 1 Y 1 ( S , E , C , R , H , t ) d t ,

ℋ h , 2 = Λ 1 − h Γ ( h ) ∫ 0 t ν ( t ν − t ) h − 1 Y 1 ( S , E , C , R , H , t ) d t .

By using the Lagrange polynomial interpolation, one can obtain an approximate value of the function Y 1 ( S , E , C , R , H , t ) as follows:

(35) Z ( t ) = t − t ν − 1 t v − t ν − 1 Y 1 ( S v , E v , C v , R v , H v , t v ) + t − t v t ν − 1 − t v Y 1 ( S ν − 1 , E ν − 1 , C ν − 1 , R ν − 1 , H ν − 1 , t ν − 1 ) = Y 1 ( S v , E v , C v , R v , H v , t v ) Δ ( t − t ν − 1 ) − Y 1 ( S ν − 1 , E ν − 1 , C ν − 1 , R ν − 1 , H ν − 1 , t ν − 1 ) Δ ( t − t v ) .

Thus,

ℋ h , 1 = Y 1 ( S v , E v , C v , R v , H v , t v ) Δ Γ ( h ) × ∫ 0 t ν + 1 ( t ν + 1 − t ) h − 1 ( t − t ν − 1 ) d t − Y 1 ( S ν − 1 , E ν − 1 , C ν − 1 , R ν − 1 , H ν − 1 , t ν − 1 ) Δ Γ ( h ) × ∫ 0 t ν + 1 ( t ν + 1 − t ) h − 1 ( t − t v ) d t .

By condensing the integral of the above equation, we obtain

ℋ h , 1 = Y 1 ( S v , E v , C v , R v , H v , t v ) Δ Γ ( h ) 2 Δ h t ν + 1 h − t ν + 1 h + 1 h + 1 − Y 1 ( S ν − 1 , E ν − 1 , C ν − 1 , R ν − 1 , H ν − 1 , t ν − 1 ) Δ Γ ( h ) Δ h t ν + 1 h − t ν + 1 h + 1 h + 1 .

Similarly,

ℋ h , 2 = Y 1 ( S v , E v , C v , R v , H v , t v ) Δ Γ ( h ) Δ h t v h − t v h + 1 h + 1 − Y 1 ( S ν − 1 , E ν − 1 , C ν − 1 , R ν − 1 , H ν − 1 , t ν − 1 ) Δ Γ ( h + 1 ) t v h + 1 .

By using the values of ℋ h , 1 and ℋ h , 2 in Eq. (34), we obtain the approximate solution for the first equation as follows:

(36) S ( t ν + 1 ) = S ( t v ) + Λ 1 − h × Y 1 ( S v , E v , C v , R v , H v , t v ) Δ Γ ( h ) × Δ h + 1 2 ( v + 1 ) h + v h h − ( v + 1 ) h + 1 + v h + 1 h + 1 − Y 1 ( S ν − 1 , E ν − 1 , C ν − 1 , R ν − 1 , H ν − 1 , t ν − 1 ) Δ Γ ( h ) Δ h + 1 × ( v + 1 ) h + 1 h − ( v + 1 ) h + 1 h + 1 + ν h h + 1 .

The solutions of the remaining equations of the system (31) are written in a similar fashion, such as

(37) E ( t ν + 1 ) = E ( t v ) + Λ 1 − h Y 2 ( S v , E v , C v , R v , H v , t v ) Δ Γ ( h ) Δ h + 1 × 2 ( v + 1 ) h + v h h − ( v + 1 ) h + 1 + v h + 1 h + 1 − Y 2 ( S ν − 1 , E ν − 1 , C ν − 1 , R ν − 1 , H ν − 1 , t ν − 1 ) Δ Γ ( h ) Δ h + 1 × ( v + 1 ) h + 1 h − ( v + 1 ) h + 1 h + 1 + ν h h + 1 ,

(38) C ( t ν + 1 ) = C ( t v ) + Λ 1 − h × Y 3 ( S v , E v , C v , R v , H v , t v ) Δ Γ ( h ) Δ h + 1 × 2 ( v + 1 ) h + v h h − ( v + 1 ) h + 1 + v h + 1 h + 1 − Y 3 ( S ν − 1 , E ν − 1 , C ν − 1 , R ν − 1 , H ν − 1 , t ν − 1 ) Δ Γ ( h ) Δ h + 1 × ( v + 1 ) h + 1 h − ( v + 1 ) h + 1 h + 1 + ν h h + 1 ,

(39) R ( t ν + 1 ) = R ( t v ) + Λ 1 − h Y 4 ( S v , E v , C v , R v , H v , t v ) Δ Γ ( h ) Δ h + 1 × 2 ( v + 1 ) h + v h h − ( v + 1 ) h + 1 + v h + 1 h + 1 − Y 4 ( S ν − 1 , E ν − 1 , C ν − 1 , R ν − 1 , H ν − 1 , t ν − 1 ) Δ Γ ( h ) Δ h + 1 × ( v + 1 ) h + 1 h − ( v + 1 ) h + 1 h + 1 + ν h h + 1 ,

(40) H ( t ν + 1 ) = H ( t v ) + Λ 1 − h Y 5 ( S v , E v , C v , R v , H v , t v ) Δ Γ ( h ) Δ h + 1 × 2 ( v + 1 ) h + v h h − ( v + 1 ) h + 1 + v h + 1 h + 1 − Y 5 ( S ν − 1 , E ν − 1 , C ν − 1 , R ν − 1 , H ν − 1 , t ν − 1 ) Δ Γ ( h ) Δ h + 1 × ( v + 1 ) h + 1 h − ( v + 1 ) h + 1 h + 1 + ν h h + 1 .

6.1 Results and discussion

This section delineates the dynamics of the proposed fractional model and the effects of model parameters, as well as their combinations in defining the dynamics of transmission of corruption in society. The fundamentals of the analysis are established by the initial conditions, such as S ( 0 ) = 100,00 , E ( 0 ) = 0 , C ( 0 ) = 100 , R ( 0 ) = 0 , and H ( 0 ) = 100 . Moreover, the spirit of consistency is maintained by considering literature-oriented parametric values for the purposed model outlined in Table 1, and the time span considered is from 0 to 70 units, corresponding to days.

Figure 3 depicts the dynamic behavior of the susceptible class S ( t ) with respect to various fractional-orders over time. The features of varying slopes concerning different fractional-orders and stability with respect to time are noticeable. The utility of the fractional-order mechanism in defining the dynamics of susceptible class with respect to corruption transmission can be noted through the varying slope behavior associated with higher and lower fractional-orders. The lower fractional-orders allow the usage of available information more rigorously. Furthermore, the stability of the transmission can be witnessed over time. Similar patterns are observed with respect to exposed individuals, corrupted individuals, recovered individuals, and honest individuals. In general, the employment of lower fractional orders enables more competent encapsulation of corruption dynamics. In addition, the stability of the transmission is found to be associated with time. Figure 4 indicates the enhanced vulnerability of the exposed class at lower fractional-order. Similarly, the corrupted individuals of Figure 5 are more likely to be infected through the corruption transmission when studied with respect to lower fractional-orders. Furthermore, Figure 6 presents the dynamics of recovered individuals with respect to different fractional orders. The relatively sharp rise in the recovery remains associated with lower fractional-orders. Finally, Figure 7 projects the transmission dynamics of honest individuals regarding varying differential orders. The utility of the fractional-order mechanism can be witnessed.

$Figure 3 The adaptive nature of the estimated result for the susceptible class S ( t ) {\mathbb{S}}\left(t) class of the proposed model with respect to arbitrary fractional-orders.$

Figure 3

The adaptive nature of the estimated result for the susceptible class S ( t ) class of the proposed model with respect to arbitrary fractional-orders.

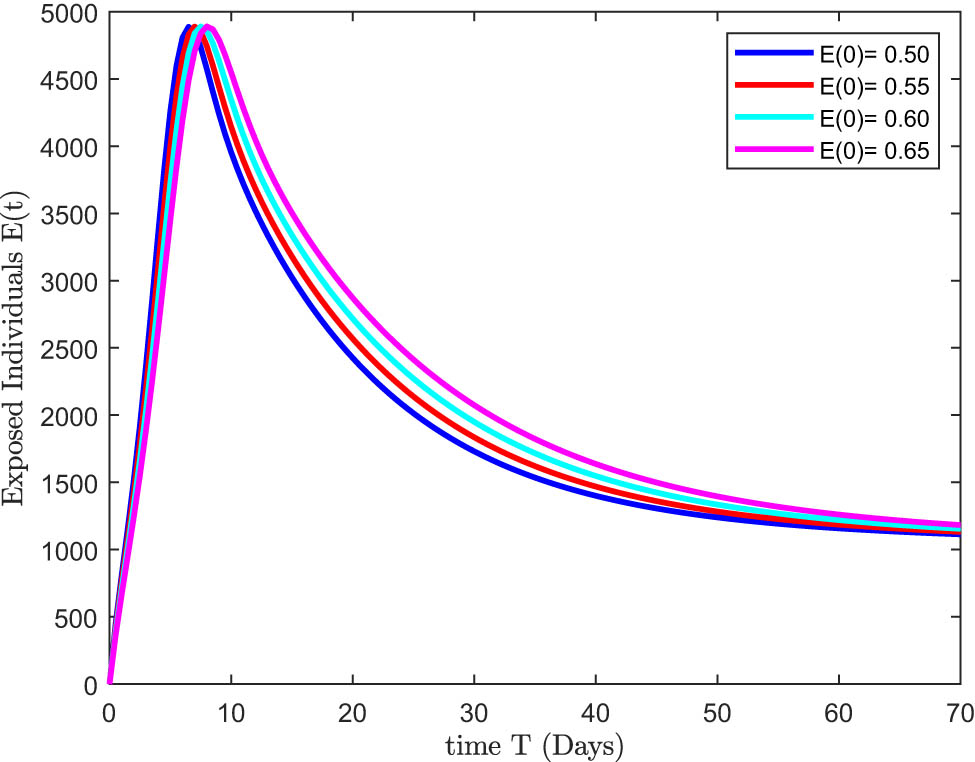
$Figure 4 The adaptive nature of the estimated result for the exposed individuals E ( t ) {\mathbb{E}}\left(t) class of the proposed model with respect to arbitrary fractional-orders.$

Figure 4

The adaptive nature of the estimated result for the exposed individuals E ( t ) class of the proposed model with respect to arbitrary fractional-orders.

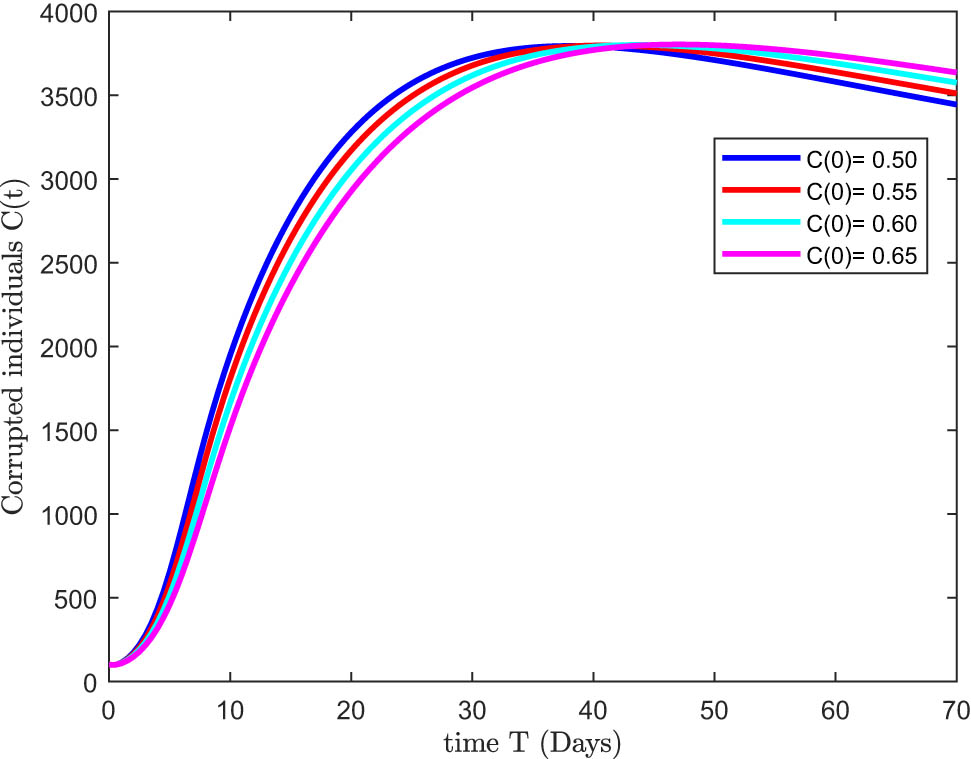
$Figure 5 The adaptive nature of the estimated result for the corrupted individuals C ( t ) {\mathbb{C}}\left(t) class of the proposed model with respect to arbitrary fractional-orders.$

Figure 5

The adaptive nature of the estimated result for the corrupted individuals C ( t ) class of the proposed model with respect to arbitrary fractional-orders.

$Figure 6 The adaptive nature of the estimated result for the recovered individuals R ( t ) {\mathbb{R}}\left(t) class of the proposed model with respect to arbitrary fractional-orders.$

Figure 6

The adaptive nature of the estimated result for the recovered individuals R ( t ) class of the proposed model with respect to arbitrary fractional-orders.

$Figure 7 The adaptive nature of the estimated result for the honest individuals H ( t ) {\mathbb{H}}\left(t) class of the proposed model with respect to arbitrary fractional-orders.$

Figure 7

The adaptive nature of the estimated result for the honest individuals H ( t ) class of the proposed model with respect to arbitrary fractional-orders.

Figure 8(a)--(e) further enforces the above-documented outcomes for the enhanced time of 100 days. One may note the establishment of the already observed realization of the transmission dynamics for various differential orders.

$Figure 8 The time response of all the compartments of proposed model with respect to arbitrary fractional-orders. (a) Belongs to susceptible class; (b) belongs to exposed class; (c) relates to corrupted class; (d) projects recovered class and (e) is associated with honest class.$

Figure 8

The time response of all the compartments of proposed model with respect to arbitrary fractional-orders. (a) Belongs to susceptible class; (b) belongs to exposed class; (c) relates to corrupted class; (d) projects recovered class and (e) is associated with honest class.

Figure 8(a)–(e) shows the establishment of the transmission dynamics across different differential orders. This means that the observed patterns are consistent across various levels of complexity or variability, as represented by the differential orders. This further strengthens the validity and generalizability of the findings.

7 Conclusion

In this study, a nonlinear deterministic mathematical model is proposed to encapsulate the dynamics of corruption transmission in a population. The objectives are achieved by exploiting the corruption dynamics model through the launch of the fractional approach and utilizing fractional calculus. Moreover, the analytical environment is further enriched by stratifying the overall population into five compartments such as susceptible class, exposed class, corrupted class, recovered class, and honest class. The target of generality is maintained by employing a wide range of parametric settings. Over the course of the investigative effort, a comprehensive account of delicacies, including positivity, invariant region, basic reproduction number, equilibrium points, and stability analysis, is provided throughout the article. The UH stability technique has been employed to prove that the solution of the devised model is stable. In addition, the existence and uniqueness of the solution are shown in the framework of the fixed point theory. Moreover, the analysis presented that the population of the exposed individuals, recovered individuals, and honest individuals asymptotically increase toward the corruption-free equilibrium point, whereas the magnitude of susceptible individuals and corrupted individuals decreases asymptotically to the corruption-free equilibrium state. In addition, the introduction of the fractional-order scheme enabled us to study the corruption dynamics more rigorously. Sharper slopes are witnessed to be associated with lower fractions highlighting the utility of the proposed mechanism in using available information more wisely.

In the future, it will be entrusted to extend the proposed scheme for optimal control strategies. The enhanced utility of a fractional-order scheme with various fractional operators under relevant controlled parameters to overcome corruption transmission is anticipated.

Acknowledgements

This research is supported by the Deanship of Research Development, Prince Mohammad Bin Fahd, University, Alkhubar 31952, Saudi Arabia.

Funding information: The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this article.
Author contributions: All the authors contributed equally to the writing of this article.
Conflict of interest: Authors state no conflict of interest.

References

[1] Rose-Ackerman S. The role of the World Bank in controlling corruption. Law Pol’y Int’l Bus. 1997;29:93. Search in Google Scholar

[2] Holmberg S, Rothstein B. Dying of corruption. Health Econ Policy Law. 2011;6(4):529–47. 10.1017/S174413311000023XSearch in Google Scholar PubMed

[3] Vian T. Review of corruption in the health sector: theory, methods and interventions. Health Policy Planning. 2008;23(2):83–94. 10.1093/heapol/czm048Search in Google Scholar PubMed

[4] Mackey TK, Liang BA. Combating healthcare corruption and fraud with improved global health governance. BMC Int Health Human Rights. 2012;12:1–7. 10.1186/1472-698X-12-23Search in Google Scholar PubMed PubMed Central

[5] Hutchinson E, Naher N, Roy P, McKee M, Mayhew SH, Ahmed SM, et al. Targeting anticorruption interventions at the front line: developmental governance in health systems. BMJ Global Health. 2020;5(12):e003092. 10.1136/bmjgh-2020-003092Search in Google Scholar PubMed PubMed Central

[6] Osipov GV, Glotov VI, Karepova SG. Population in the shadow market: petty corruption and unpaid taxes. Entrepreneurship Sustain Issues. 2018;6(2):692. 10.9770/jesi.2018.6.2(16)Search in Google Scholar

[7] Vasilyeva T, Lyulyov O, Pimonenko T. Public Governance efficiency and macroeconomic stability: examining the convergence of social and political determinants. Public Policy Adm. 2019;18(2):241–55. Search in Google Scholar

[8] Eguda FY, James A, Oguntolu FA, Onah D. Mathematical analysis of a model to investigate the dynamics of poverty and corruption. Abacus (Mathematics Science Series). 2019;44(1):352–67. Search in Google Scholar

[9] Ulain N, Hussain F. Fighting governmental corruption in Pakistan: an evaluation of anti-corruption strategies. Hrvatska i komparativna javna uprava: cccasopis za teoriju i praksu javne uprave. 2020;20(3):439–68. 10.31297/hkju.20.3.2Search in Google Scholar

[10] Brazys S, Elkink JA, Kelly G. Bad neighbors? How co-located Chinese and World Bank development projects impact local corruption in Tanzania. Rev Int Organizations. 2017;12(2):227–53. 10.1007/s11558-017-9273-4Search in Google Scholar

[11] Vian T. Anti-corruption, transparency and accountability in health: concepts, frameworks, and approaches. Global Health Action. 2020;13(sup1):1694744. 10.1080/16549716.2019.1694744Search in Google Scholar PubMed PubMed Central

[12] Zhang S. ISMUNHK 2019 United Nations Office on Drugs and Crimes. 2019. Search in Google Scholar

[13] Aidt TS. Corruption and sustainable development. Int Handbook Econom Corruption. 2011;2:3–51. 10.4337/9780857936523.00007Search in Google Scholar

[14] Tanzi V. Corruption around the world: causes, consequences, scope, and cures. Staff Papers. 1998;45(4):559–94. 10.2307/3867585Search in Google Scholar

[15] Bhattacharyya S, Hodler R. Media freedom and democracy in the fight against corruption. Europ J Politic Econ. 2015;39:13–24. 10.1016/j.ejpoleco.2015.03.004Search in Google Scholar

[16] Frank B, Lambsdorff JG, Boehm F. Gender and corruption: Lessons from laboratory corruption experiments. Europ J Develop Res. 2011;23:59–71. 10.1057/ejdr.2010.47Search in Google Scholar

[17] Rivas MF. An experiment on corruption and gender. Bullet Econ Res. 2013;65(1):10–42. 10.1111/j.1467-8586.2012.00450.xSearch in Google Scholar

[18] Goel RK, Nelson MA. Government fragmentation versus fiscal decentralization and corruption. Public Choice. 2011;148:471–90. 10.1007/s11127-010-9666-xSearch in Google Scholar

[19] Becker SO, Egger PH, Seidel T. Common political culture: Evidence on regional corruption contagion. Europ J Politic Econ. 2009;25(3):300–10. 10.1016/j.ejpoleco.2008.12.002Search in Google Scholar

[20] Gweryina RI, Kura MY, Okwu E. An epidemiological model of corruption with immunity clause in Nigeria. World J Modell Simulat. 2019;15(3):262–75. Search in Google Scholar

[21] Shah NH, Yeolekar BM, Patel ZA. Epidemics of corruption using incidence function. Econom Comput Econ Cybernet Stud Res. 2017;51(2):1–16. Search in Google Scholar

[22] Crokidakis N, Sa Martins JS. Can honesty survive in a corrupt parliament?. Int J Mod Phys C. 2018;29(10):1850094.10.1142/S0129183118500948Search in Google Scholar

[23] Evirgen F. Transmission of Nipah virus dynamics under Caputo fractional derivative. J Comput Appl Math. 2023;418:114654. 10.1016/j.cam.2022.114654Search in Google Scholar

[24] Tunç O, Tunç C. Solution estimates to Caputo proportional fractional derivative delay integro-differential equations. Revista de la Real Academia de Ciencias Exactas, Físicas y Naturales. Serie A. Matemáticas. 2023;117(1):12. 10.1007/s13398-022-01345-ySearch in Google Scholar

[25] Matias GS, Lermen FH, Matos C, Nicolin DJ, Fischer C, Rossoni DF, et al. A model of distributed parameters for non-Fickian diffusion in grain drying based on the fractional calculus approach. Biosyst Eng. 2023;226:16–26. 10.1016/j.biosystemseng.2022.12.004Search in Google Scholar

[26] Caponetto R, Dongola G, Fortuna L, Petráš I. Fractional order systems: modeling and control applications. World Scientific; 2010. 10.1142/9789814304207Search in Google Scholar

[27] Tarasov VE. General fractional calculus in multi-dimensional space: Riesz form. Mathematics. 2023;11(7):1651. 10.3390/math11071651Search in Google Scholar

[28] Huai WX, Wang X, Guo Y, Sun ZH, Yang ZH. Investigation of the sediment transport capacity in vegetated open channel flow. J Hydrodynamics. 2021;33:386–9. 10.1007/s42241-021-0021-0Search in Google Scholar

[29] Kilbas A, Marzan S. Cauchy problem for differential equation with Caputo derivative. Fract Calculus Appl Anal. 2004;7(3):297p–321p. Search in Google Scholar

[30] Malinowska AB, Torres DF. Generalized natural boundary conditions for fractional variational problems in terms of the Caputo derivative. Comput Math Appl. 2010;59(9):3110–6. 10.1016/j.camwa.2010.02.032Search in Google Scholar

[31] Baleanu D, Agrawal OP. Fractional Hamilton formalism within Caputo’s derivative. Czechoslovak J Phys. 2006;56(10–11):1087–92. 10.1007/s10582-006-0406-xSearch in Google Scholar

[32] Odionyenma UB, Ikenna N, Bolaji B. Analysis of a model to control the co-dynamics of Chlamydia and Gonorrhea using Caputo fractional derivative. Math Model Numer Simulat Appl. 2023;3(2):111–40. 10.53391/mmnsa.1320175Search in Google Scholar

[33] Miller KS, Ross B. An introduction to the fractional calculus and fractional differential equations. Singapore: Springer; 1993. Search in Google Scholar

[34] Yan Y, Sun ZZ, Zhang J. Fast evaluation of the Caputo fractional derivative and its applications to fractional diffusion equations: a second-order scheme. Commun Comput Phys. 2017;22(4):1028–48. 10.4208/cicp.OA-2017-0019Search in Google Scholar

[35] Odibat Z, Baleanu D. Numerical simulation of initial value problems with generalized Caputo-type fractional derivatives. Appl Numer Math. 2020;156:94–105. 10.1016/j.apnum.2020.04.015Search in Google Scholar

[36] Gao GH, Sun ZZ, Zhang HW. A new fractional numerical differentiation formula to approximate the Caputo fractional derivative and its applications. J Comput Phys. 2014;259:33–50. 10.1016/j.jcp.2013.11.017Search in Google Scholar

[37] Farayola MF, Shafie S, Siam FM, Khan I. Mathematical modeling of radiotherapy cancer treatment using Caputo fractional derivative. Comput Meth Program Biomed. 2020;188:105306. 10.1016/j.cmpb.2019.105306Search in Google Scholar PubMed

[38] Baleanu D, Jajarmi A, Mohammadi H, Rezapour S. A new study on the mathematical modelling of human liver with Caputo-Fabrizio fractional derivative. Chaos Solitons Fractals. 2020;134:109705. 10.1016/j.chaos.2020.109705Search in Google Scholar

[39] Zhang XH, Ali A, Khan MA, Alshahrani MY, Muhammad T, Islam S. Mathematical analysis of the TB model with treatment via Caputo-type fractional derivative. Discrete Dynam Nature Society. 2021;2021:1–5. 10.1155/2021/9512371Search in Google Scholar

[40] Kumar P, Suat Erturk V. The analysis of a time delay fractional Covid-19 model via Caputo type fractional derivative. Math Meth Appl Sci. 2023;46(7):7618–31. 10.1002/mma.6935Search in Google Scholar PubMed PubMed Central

[41] Ali A, Alshammari FS, Islam S, Khan MA, Ullah S. Modeling and analysis of the dynamics of novel coronavirus (COVID-19) with Caputo fractional derivative. Results Phys. 2021;20:103669. 10.1016/j.rinp.2020.103669Search in Google Scholar PubMed PubMed Central

[42] Van den Driessche P, Watmough J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math Biosci. 2002;180(1–2):29–48. 10.1016/S0025-5564(02)00108-6Search in Google Scholar PubMed

[43] Van den Driessche P. Reproduction numbers of infectious disease models. Infect Disease Model. 2017;2(3):288–303. 10.1016/j.idm.2017.06.002Search in Google Scholar PubMed PubMed Central

[44] Ma X, Zhou Y, Cao H. Global stability of the endemic equilibrium of a discrete SIR epidemic model. Adv Differ Equ. 2013;2013:1–9. 10.1186/1687-1847-2013-42Search in Google Scholar PubMed PubMed Central

[45] LaSalle JP. The stability of dynamical systems. Philadelphia (PA), USA: Society for Industrial and Applied Mathematics; 1976. p. 25. Search in Google Scholar

[46] Castillo–Chavez C, Blower S, van den Driessche P, Kirschner D, Yakubu AA, editors. Mathematical approaches for emerging and reemerging infectious diseases: models, methods, and theory. New York (NY), USA: Springer Science & Business Media; 2002. p. 126. 10.1007/978-1-4613-0065-6Search in Google Scholar

[47] Zhang DC, Shi B. Oscillation and global asymptotic stability in a discrete epidemic model. J Math Anal Appl. 2003;278(1):194–202. 10.1016/S0022-247X(02)00717-5Search in Google Scholar

[48] Merkin DR. Introduction to the theory of stability. New York (NY), USA: Springer Science & Business Media; 1996. 10.1007/978-1-4612-4046-4Search in Google Scholar

Received: 2023-09-12

Revised: 2023-11-10

Accepted: 2023-11-21

Published Online: 2024-02-15

This work is licensed under the Creative Commons Attribution 4.0 International License.

Articles in the same Issue

https://doi.org/10.1515/nleng-2022-0363

Keywords for this article

corruption model; Caputo fractional derivative; Ulam–Hyers stability; Adams–Bashforth method; numerical simulations

Creative Commons

BY 4.0