Mathematical model based on nonlinear differential equations and its control algorithm

Xiaohua Yuan

doi:10.1515/nleng-2024-0031

40% Rabatt

auf Fachbücher bei De Gruyter Brill *

Artikel Open Access

Mathematical model based on nonlinear differential equations and its control algorithm

Xiaohua Yuan

Veröffentlicht/Copyright: 19. November 2024

Veröffentlicht von

Veröffentlichen auch Sie bei De Gruyter Brill

Manuskript einreichen Informationen für Autor*innen

Aus der Zeitschrift Nonlinear Engineering Band 13 Heft 1

Abstract

A practical examination of the traditional robotic arm (RA) in operation revealed a significant limitation in its ability to control the position of motion. This underscores the urgent need to enhance the current RA’s position control capabilities. Therefore, this study proposes the use of nonlinear differential equations (NDEs) to establish a mathematical model and the design of NDE-based RA motion control algorithms in conjunction with a central pattern generator neural network. A comparison of the control effects showed that the proposed method was highly fitted to the target trajectory. The joint node (JN) motion tracking trajectories of the three RAs were similar, up to 90–85% to the target trajectories of the JNs. In addition, the control of the motion position was similar up to 95–98% to the target motion position trajectories. The motion control algorithm based on NDEs was effective in improving the average execution time of the Pareto optimal frontier of the RA by 58.29%. The joint velocity and angle changes of the three types of RAs under the NDE control algorithm exhibited a high degree of similarity to the fluctuations observed in the expected and predicted curves. These observations contribute to an understanding of the effectiveness of the system observer in observing the joint angle changes. This indicates that the motion control based on NDEs can effectively enhance the tracking effectiveness of the JN positions of the RA, improve the control ability of the RA motion, and increase the joint stability of the RA.

Keywords: NDE; control algorithms; RAs

1 Introduction

With the rapid development of modern science and technology, the division of traditional science and research methods continues to innovate, and many natural phenomena in today’s society can be transformed into nonlinear differential equations (NDEs) by the model for solving and description [1,2]. Among them, the research objects in the field of physics are mostly nonlinear systems, and the significance of NDEs in physics research is extremely important [3]. Slyn’ko et al. conducted a multifaceted study of NDE around the stability of Lyapunov functions [4]. The method of applying commutative calculus to linear impulse differential variance was proposed to construct quadratic Lyapunov functions using variable matrices. Moreover, stability was achieved for piecewise constant period matrices [5,6]. A robotic arm (RA) is a type of mechanical device in the robotics industry, which has the advantages of high efficiency and adapting to harsh environments. It gradually becomes the main productive force in the fields of industry and agriculture [7]. However, the current social mechanical devices are updated and iterated at an accelerated rate, and user demand is constantly improving. Furthermore, existing research has demonstrated an inability to control the motion position of robotic RA, which has led to a heightened demand for the control of the motion position of the RA [8,9]. In this context, the study proposes the use of NDE to construct control algorithms on the basis of RA motion, aiming to improve the control efficiency of RA. First, mathematical models (M-M) are designed based on NDE. The control algorithm for utilizing M-M with NDE is constructed according to the model. The aim is to provide a theoretical basis for enhancing the position control capability of M-M motion and strengthening the application research of NDE.

The novelty of the study lies in its use of NDE to establish the M-M of RA, which enhances the precision with which complex dynamic behaviors in RA motion can be captured and described. The study combines the NDE with the central pattern generator (CPG) neural network to develop the RA motion control algorithm (RAMCA), which aims to achieve more natural and efficient control of RA motion by leveraging the CPG neural network’s capacity to simulate biological motion. On this basis, the study achieves a seamless connection from theory to application through the established NDE-based M-M and RAMCA, which improves the theoretical depth of the control algorithm and enhances the effectiveness of the control algorithm in practical applications. Furthermore, the study offers theoretical insight and corroborates the efficacy of the proposed method through empirical RA experimentation, thereby enhancing the overall efficiency and precision of RA, which is of paramount importance for the successful completion of intricate tasks.

Through the NDE-based control algorithm, the motion-tracking accuracy of the RA joint nodes (JNs) is significantly improved. Moreover, the joint stability of the RA is enhanced, which provides a guarantee for the stable operation of the RA in complex environments. The NDE-based RAMCA can significantly improve the execution efficiency of the RA, which is of great significance for improving productivity. This study applies NDE to the field of RA control, which provides new perspectives and methods for the application of NDE to engineering and scientific problems and promotes the development of related theories. Overall, the study demonstrates the potential of multidisciplinary cross-fertilization in solving complex engineering problems by combining mechanical engineering, control theory, and neural network technology and provides new ideas for future research.

The study is divided into four sections. Section 2 summarizes the research findings and limitations on NDE and RA motion both domestically and internationally. In Section 3, the NDE-based RAMCA is examined and developed. In Section 4, experimentation and analysis of the proposed NDE-based RAMCA are conducted. Section 5 summarizes the experimental outcomes while also indicating future research directions.

2 Related works

In recent years, NDEs have played an important role in M-M for science and engineering-related problems, and scholars at home and abroad have conducted relevant studies on the analysis of their algorithms. To obtain solutions for higher-order NDEs, Appalanaidu and Deekshitulu proposed a method to solve the delay and expectation problem for higher-order NDEs. That is, the higher-order differential equations with delay and expectation under mixed conditions are transformed into algebraic equations using polynomials and configuration points and the system of algebraic equations is solved using Newton’s method [10]. To solve the nonlinear Schrödinger equation in isolation by computing the differential form of the new isolated solution, Khan transformed the partial differential equation into a dimensionless nonlinear ordinary differential equation by using an appropriate traveling wave variational. This method realized the variational principle for solving the Schrödinger equation in isolation without the Lagrange multiplier method [11]. In order to realize the M-M construction of semiconductor devices, Chen et al. proposed an efficient dual-mesh method on the Newtonian iteration idea by estimating the solutions of hybrid finite element and eigen-finite element methods, thus obtaining near-optimal solutions to the solved linear equations [12]. In order to optimize the model predictive control algorithms, MarusakPiotr proposed a new set of fuzzy and numerically effective algorithms combining analytical and numerical versions of the model predictive control algorithms. It then proved the control system using two nonlinear control devices that led to a significant increase in the model validity [13]. In order to improve the efficiency of solving differential equations, Jing proposed the use of deep neural networks with oscillating function fitting to solve ordinary differential equations. It led to the establishment of an optimal model for the numerical solution of differential equations and the realization of data simulation to a great extent [14].

With the gradual application of NDE in natural science research, many scholars began to use mathematical tools, such as NDE, to solve physical problems. In order to minimize the error in the parameters of the neural network, Okereke and Maliki proposed a feed-forward inverse layer perceptron neural network based on NDE, which effectively reduces the computational complexity of a given problem [15]. To address the problem of poor stability of the driving system, Chen et al. designed to apply a system of Gray differential equations to the model. Moreover, based on this, the study developed a fuzzy neural network combined with a bat algorithm, thus proving the validity of the system model through the Liapunov-like expression and creating a mathematical framework that can be applied [16]. To obtain the trajectory of the cable motion of the 3D end-effector, Arena et al. proposed to solve it using the total Lagrangian equation as well as the compatibility equation that prescribed the connectivity between the cable and the mass of the end-effector, which revealed that the dynamical representation of the end-effector was realized by the balance of the enhanced linear and angular momentum [17]. In order to solve the controller design and vibration damping problems of the flexible single-link manipulator, Cao and Liu described the flexible single-link manipulator using partial differential equations with Nussbaum-type functions and adaptive laws, which in turn led to efficient control results in simulation experiments [18]. Aiming at the adaptive neural tracking control problem of flexible manipulator systems, Li proposed the use of partial differential equations with boundary conditions to model the flexible manipulator system. Moreover, the study used a neural network technique to deal with the unknown nonlinear function and then realized that the system's full state constraints are satisfied and the closed-loop system signal remains bounded [19].

Taken together, current studies on NDE are focused on equation solving and optimization, while studies on NDEs in physical domains such as RA are mainly focused on achieving efficient control of the operating system. Fewer studies use NDEs for investigating RA motion position control. Therefore, this study proposes to use NDEs to establish RA-related M-M and innovatively combines NDEs with a CPG neural network to construct an NDE-based RAMCA algorithm. Through JN control and joint performance verification, the RA motion position control capability has been further improved, providing theoretical reference for the application of NED in the field of physics.

3 NDE-based M-Ms and their control algorithms

The application fields of NDEs are extremely wide, and the current production puts higher demands on the position control of RA. Using NDEs to improve the RA position control effect or a new way, for this reason, the study utilizes NDEs to establish M-M related to RA, and further attempts to introduce neural network technology combined with NDE. The study proposes that the establishment of NDE-based RAMCA has certain positive significance in improving the RA motion position control, which is conducive to enhancing the value of the application of mathematical tools such as NDEs in physics problems.

3.1 NDE-based M-Ms for RA correlation

In order to obtain the unit vector angle and rate of rotation in the RA beam unit view, the study utilizes the NDE to establish the M-M. Among them, the setup of the node coordinate positions in the beam unit view is shown in Figure 1.

Figure 1

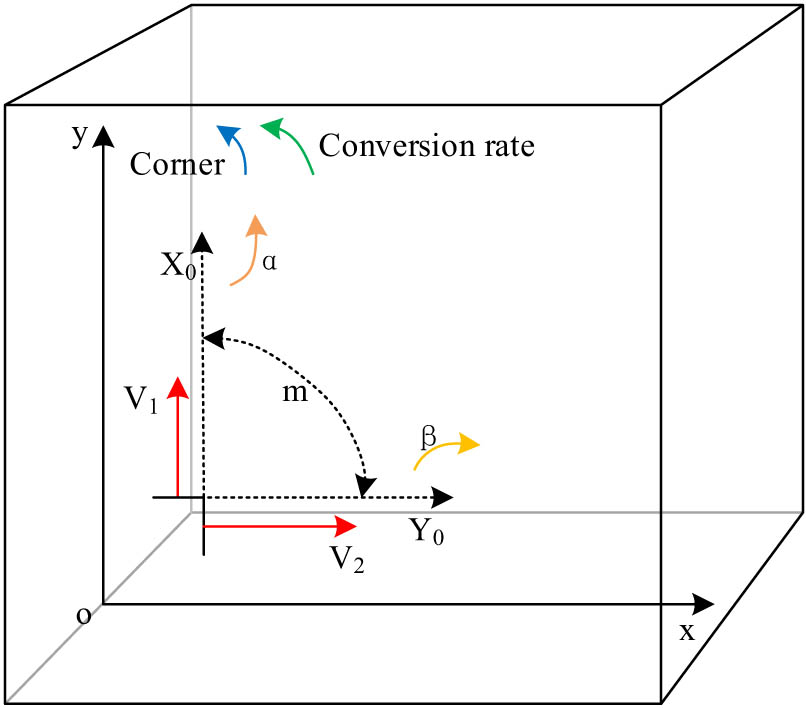
Layout of node coordinate positions from the perspective of beam elements.

In Figure 1, the choice of node coordinate positions is related to the values taken for the unit vector turn angle and turn rate. Therefore, the study begins with the introduction of Lagrange equations (LE) in order to obtain the geometric stiffness of the unit vector turn angle and turn rate [20,21]. The expression for LE is shown in Eq. (1):

(1) T lagrange = λ A t B − λ t i ∑ i = 1 λ A t B T t A − B i A − C t A , i = 1 , … , n .

In Eq. (1), λ denotes the Lagrangian coefficient, A denotes the stiffness vector, B denotes the corner constraint variable of the unit vector, C denotes the turn rate constraint variable of the unit vector, and t denotes the total number of coordinates of nodes within the model involved in obtaining the corner and turn rate of the unit vector. n denotes the total number of internal nodes of the model involved in calculating the unit vector angle and rate of rotation. The geometric stiffness expressions for the unit vector corner and rate of rotation for RA are obtained according to LE, as shown in Eq. (2):

(2) D λ T = E T θ j + E i 2 E T θ j + σ 2 E i 2 ( E T θ j − σ 2 E T θ j ) .

In Eq. (2), E denotes the spatial geometric stiffness per unit vector turn angle, σ denotes the constant of geometric stiffness, and θ denotes the displacement geometric stiffness per unit vector turn rate. Meanwhile, the nonlinear coupling parameters are obtained from the kinetic and potential energies of the model in the unit view of the beam, as shown in Eq. (3):

(3) ( α g ) 2 = E i T i f ( a ) + f ( b ) .

In Eq. (3), f ( a ) denotes the model kinetic energy coefficient. f ( b ) denotes the model potential energy coefficient. And ( α g ) 2 denotes the output results of the nonlinear coupling parameters. To obtain the rigid displacements corresponding to the unit vectors of the RA motion, the study combines the output results of the LE with the nonlinear coupling parameters, as shown in Eq. (4) [22,23]:

(4) F x = β 2 [ sin ( k 0 − k 1 ) + cos ( k 0 + k 1 ) ] F y = β 2 [ tan ( k 0 + k 1 ) − cos ( k 0 − k 1 ) ] .

In Eq. (4), F x denotes the horizontal coordinates of the rigid vector guidance node locations and F y denotes the vertical coordinates of the rigid vector guidance node locations. β denotes the coupling parameter, sin ( k 0 − k 1 ) denotes the rigid distance of the coordinates of the neighboring nodes, and cos ( k 0 + k 1 ) denotes the rigid distance of the coordinates of the guidance nodes. tan ( k 0 + k 1 ) denotes the spacing of unit vector guidance nodes and cos ( k 0 − k 1 ) denotes the spacing of rigid vector nodes. However, the coordinate position arrangement of the nodes inside the RA cannot be fully determined based on the acquired rigid displacements alone. For this reason, the objective function for the dynamics of the RA is determined. The RA is a multi-group three-link structural composite consisting of two rotational joints connected with one translational joint, as shown in Figure 2.

Figure 2

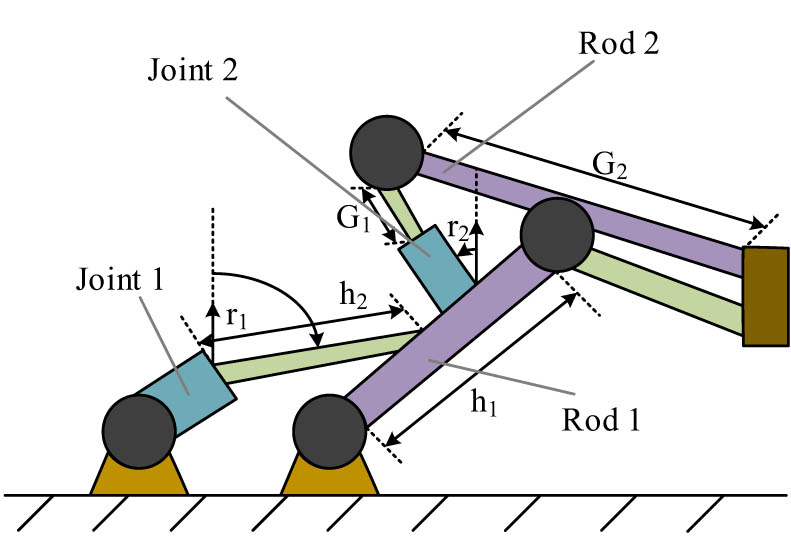
Three-link structure inside the RA.

In Figure 2, the actuation of each joint of the RA is controlled by a hydraulic cylinder at the joint connection. The servo valve of the hydraulic cylinder is closed under normal conditions and opened automatically by the system or manually by hand. The length of the triple link is closely related to the joint angle and the overall motion process of the RA. Therefore, according to the h, G, r motion coordinate system in Figure 2, it is known that the motion trajectory of the random three-link structure inside the RA is shown in Eq. (5):

(5) H ρ x = h 1 cos G 1 + ln r 1 / cos ( G 1 − G 2 ) H ρ y = h 2 cos G 2 + ln r 2 / cos ( G 2 − G 1 ) .

In Eq. (5), H ρ x and H ρ y denote the horizontal and vertical coordinates of the motion trajectories of the three links, respectively. h 1 cos G 1 and h 2 cos G 2 denote the effects of the rotation of link 1 and link 2 on the motion trajectories of the M-M as a whole, respectively. ln r 1 and ln r 2 denote the angles of motion of joints 1 and 2, respectively. Moreover, cos ( G 1 − G 2 ) and cos ( G 2 − G 1 ) denote the motion displacements of link 1 and link 2, respectively. Since the interior of the RA consists of multiple sets of three-link structures operating in concert, the study introduces the principle of redundant RA degrees of freedom to speculate the way the multiple sets of three-link structures in the interior move in concert and the way the endpoints of two sets of three-link structures in close proximity move. The redundant RA degrees of freedom principle is shown in Eq. (6):

(6) g ( x ) = I ( a ) γ e ′ .

In Eq. (6), I ( a ) denotes the movement collaboration relationship matrix of the multi-group three-link structure. γ denotes the moving direction of the neighboring 2-group three-link structure. Among them, the expression of the kinematic collaboration relationship matrix of the multi-group three-link structure is shown in Eq. (7):

(7) I ( a ) = H ( 1 , 1 ) , f 1 sin e 1 , sin ( f 1 + e 1 ) H ( 1 , 2 ) , f 2 sin e 2 , sin ( f 2 + e 2 ) H ( 1 , 3 ) , f 3 sin e 3 , sin ( f 3 + e 3 ) .

On this basis, the study takes the kinematic collaboration relationship matrix as the basis, weights the matrix, thus obtaining the dynamic weights of each joint within the RA, and uses the gradient projection method to refine the kinematic weights of the unit joints. The weighted representation is shown in Eq. (8):

(8) J ( m , n ) = K × M η ∣ N m K − N n K ∣ .

In Eq. (8), J denotes the motion weight coefficient of any joint and K denotes the weighting coefficient of any joint. M denotes the weight value of any joint and η denotes the weighted fusion error. N m K and N n K denote the motion trajectories of joints m and n , respectively. RA is in the motion saturation state that needs to go through the gradient projection method to refine the motion weights of the joints, and the specific refinement expression is shown in Eq. (9):

(9) P o ′ = μ Q l ′ s ⊗ l .

In Eq. (9), μ denotes the gradient projection constant, s denotes the unit joint quantization coefficient, and l denotes the exploration step size. Combining the above, the expression of the RA kinetic objective function is hypothesized, as shown in Eq. (10):

(10) R = ∑ i = 1 [ ( p 0 − p 1 ) / ( q 0 − q 1 ) ] 2 .

In Eq. (10), c denotes the number of RA kinematic joints involved, p denotes the amount of energy consumed by the hydraulic press during RA movement, and q denotes the average value of the kinematic joints’ moving angles. On the basis of the RA dynamic objective function, the coordinate position arrangement of internal nodes is determined using rigid displacement. The matrix weight calculation formula for reusing node coordinates is employed to assign values to the coordinates of internal nodes in sequence, thereby obtaining RAM-M based on NDE. In this case, the coordinate weighting matrix is computed, as shown in Eq. (11):

(11) Δ U ( V π − g ) = W d r ( V π ) i U i − g = W d r ( V π ) i + 2 ℓ W d r ( d π ) U i − π = W d r ( V π ) i d π .

In Eq. (11), U denotes the constant of NDE, V denotes the coordinate weighting coefficient, and W denotes the nonlinear matrix assignment rate. Therefore, the final M-M expression of NDEs is as shown in Eq. (12):

(12) Z = ∑ i = 1 U W ( e − d ) e = ∑ g ≠ 1 i ( U − k i ) .

In Eq. (12), Z denotes the M-M kinetic parameter.

3.2 Construction of NDE-based motion control algorithm for RA

In order to collect the RA motion information of the input data, the study introduces the CPG neural network combined with the M-M of NDEs. The operation of the CPG neural network to control the node regularity of the motion of the input data is determined by the topology of the double-layer level of the third-party neural network [24,25]. In this case, the equation for the topology of the double-layer level of the third-party neural network is shown in Eq. (13):

(13) g ( x ) = φ ( v × w ) g ( y ) = w ( v ) i .

In Eq. (13) v denotes the number of sensing neurons in the bilayer level, and w denotes the RA motion control parameters. Therefore, the study utilizes the NDE to obtain the dynamics parameters of the RA and constructs the RAMCA by adding the parameters as sample data to the topology of the bi-layer level of the third-party neural network. The specific mathematical expression is shown in Eq. (14):

(14) χ = ∑ j = 1 n 2 z i , j cos ( χ i − χ j ) .

In Eq. (14), z i , j denotes the motion stabilization coefficient and cos ( χ i − χ j ) denotes the motion state monitoring period. The specific flow of RAMCA based on NDE is shown in Figure 3.

Figure 3

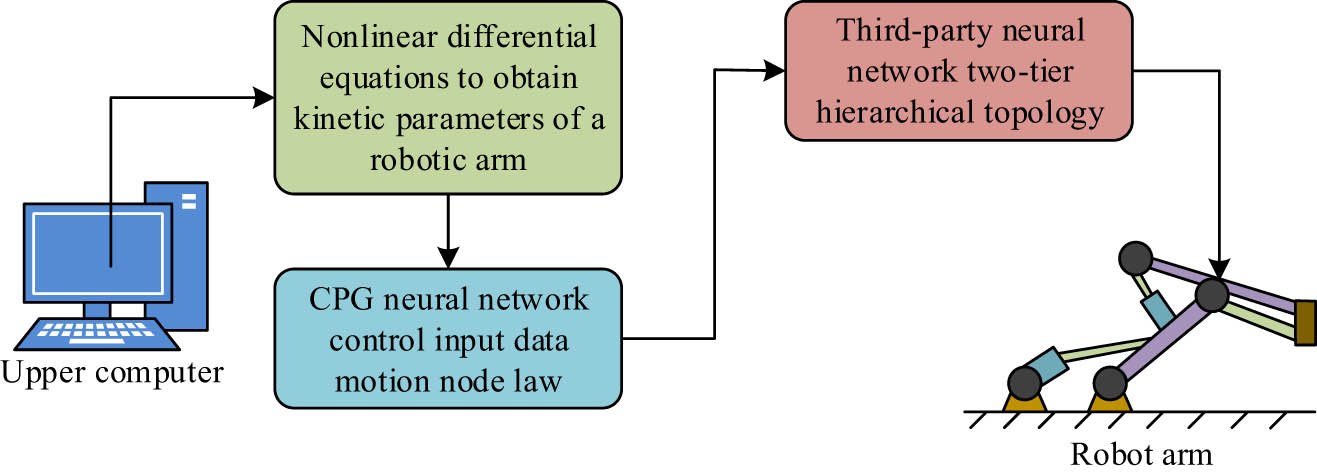
Algorithmic steps for RA motion control on the basis of NDEs.

In Figure 3, RAMCA retains the activation and acquisition functions of the CPG neural network and also adds the motion state detection and stabilization performance. It motivates the RA to be able to control the motion profiles more smoothly, thus correcting the RA dynamics error generated by the motion trajectory deviation. In this regard, the calculation equation for the motion control algorithm to correct the RA motion trajectory offset is shown in Eq. (15):

(15) x ( m ) = ∑ 0 x sin ς y ( m ) = ∑ 0 y cos τ .

In Eq. (15), ς denotes the slope of the RA offset curve, and τ denotes the probability of RA motion trajectory offset recognized by the motion control algorithm. From Eq. (15), the coordinate system function for correcting the RA motion trajectory offset can be derived, as shown in Figure 3.

In Figure 4, the CPG-NDE is able to effectively control the motion position of the RA, which in turn improves the productivity of the RA in practical work.

Figure 4

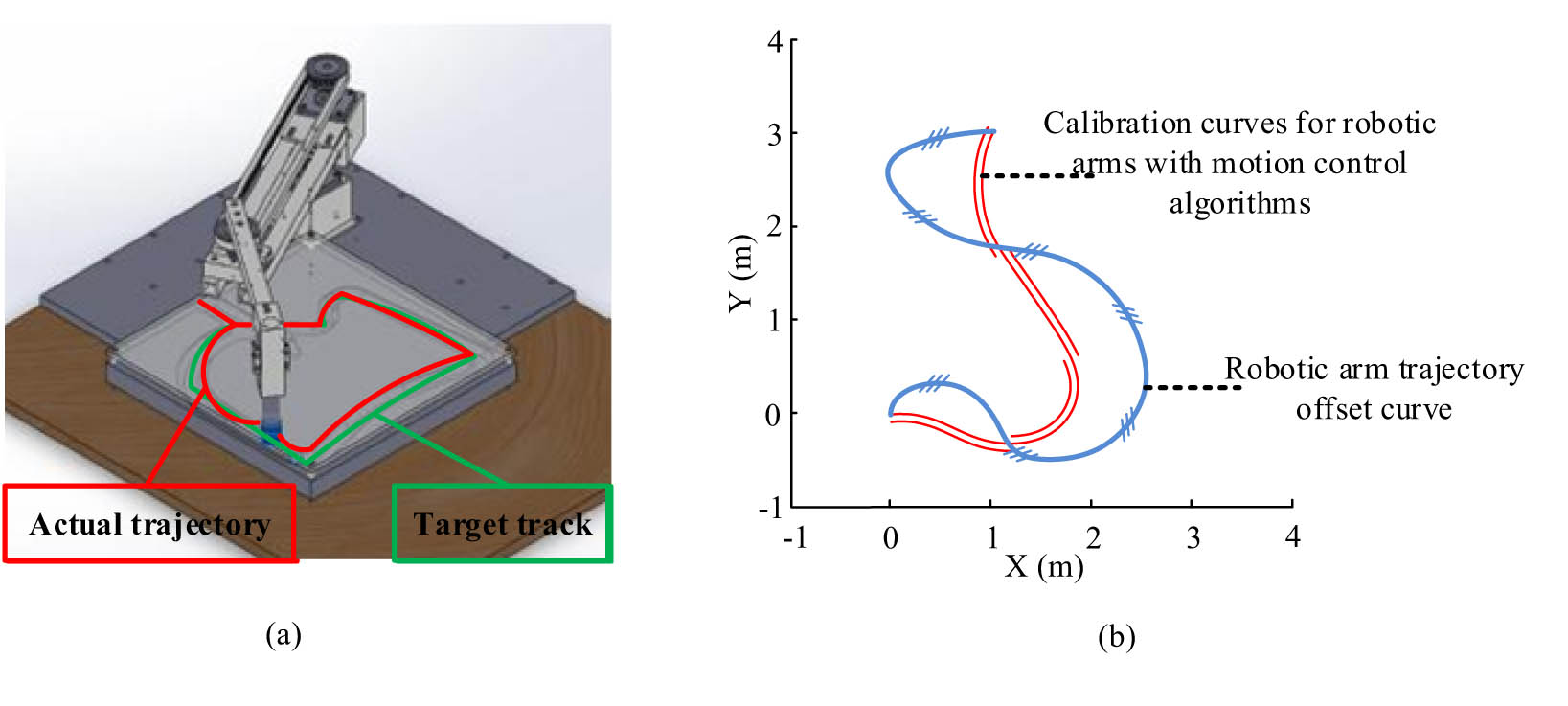
Schematic diagram of motion control algorithm correcting trajectory deviation of RA. (a) Schematic diagram of RA trajectory. (b) Correcting of trajectory deviation using motion control algorithm.

4 Validation of NDE-based motion control algorithm for RA

In order to validate the effectiveness of the proposed NDE-based RAMCA, the study takes three different models of RA as the experimental samples and uses different methods to validate the stability of RA. The main validation contents include the JN of RA, the results of the motion position control as well as the performance of the RA joints, and compares and analyzes the motion control capability of each method based on the validation results.

4.1 Validation of JNs of RA and motion position control results

In order to validate the overall effectiveness of the proposed CPG-NDE, the study first validates the JN control and motion position control results of the RA using three different models of RA as samples with different methods. The study used two RA position control methods proposed by Xu et al. and Chen et al. to compare with CPG-NDE, respectively [26,27]. Among them, the JN motion angle tracking results are shown in Figure 5.

Figure 5

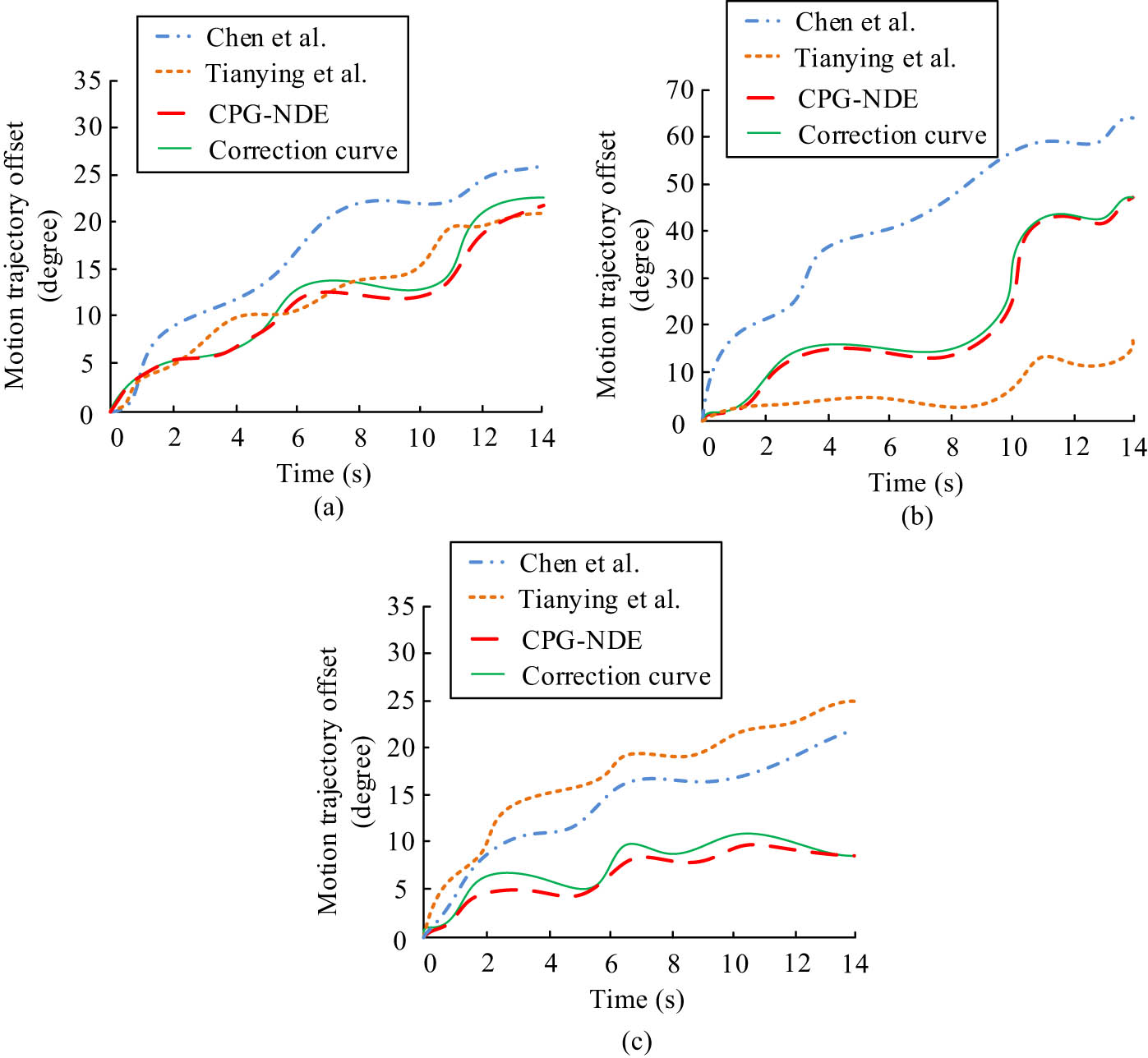
Tracking results of different methods for the motion angle of JNs of RA. (a) Tracking results of joint node motion angles of A-type robotic arms using different methods, (b) tracking results of joint node motion angles of B-type robotic arms using different methods, and (c) Tracking results of joint node motion angles of C-type robotic arms using different methods.

In Figure 5, the tracking results of the research-proposed method for the JN motion angles of the three RAs coincide with the JN motion angles of the actual RAs similarly, whereas the tracking results of the motion angles of the JNs of the other two methods show an overall deviation from that of the actual RAs. This indicates that the proposed method of the study is better for JN position tracking and more effective for controlling the JN of RA. Furthermore, the angle of JN motion for different RA models exhibits varying degrees of fluctuating curves, contingent on the specific RA model under consideration. The proposed method of the study incorporates NDE, which is effective in reducing the error of the average tracking results. This may be the reason leading to its better effect on JN control. Meanwhile, the study further compares the control performance of RA motion position under different methods, and the specific results are shown in Figure 6.

Figure 6

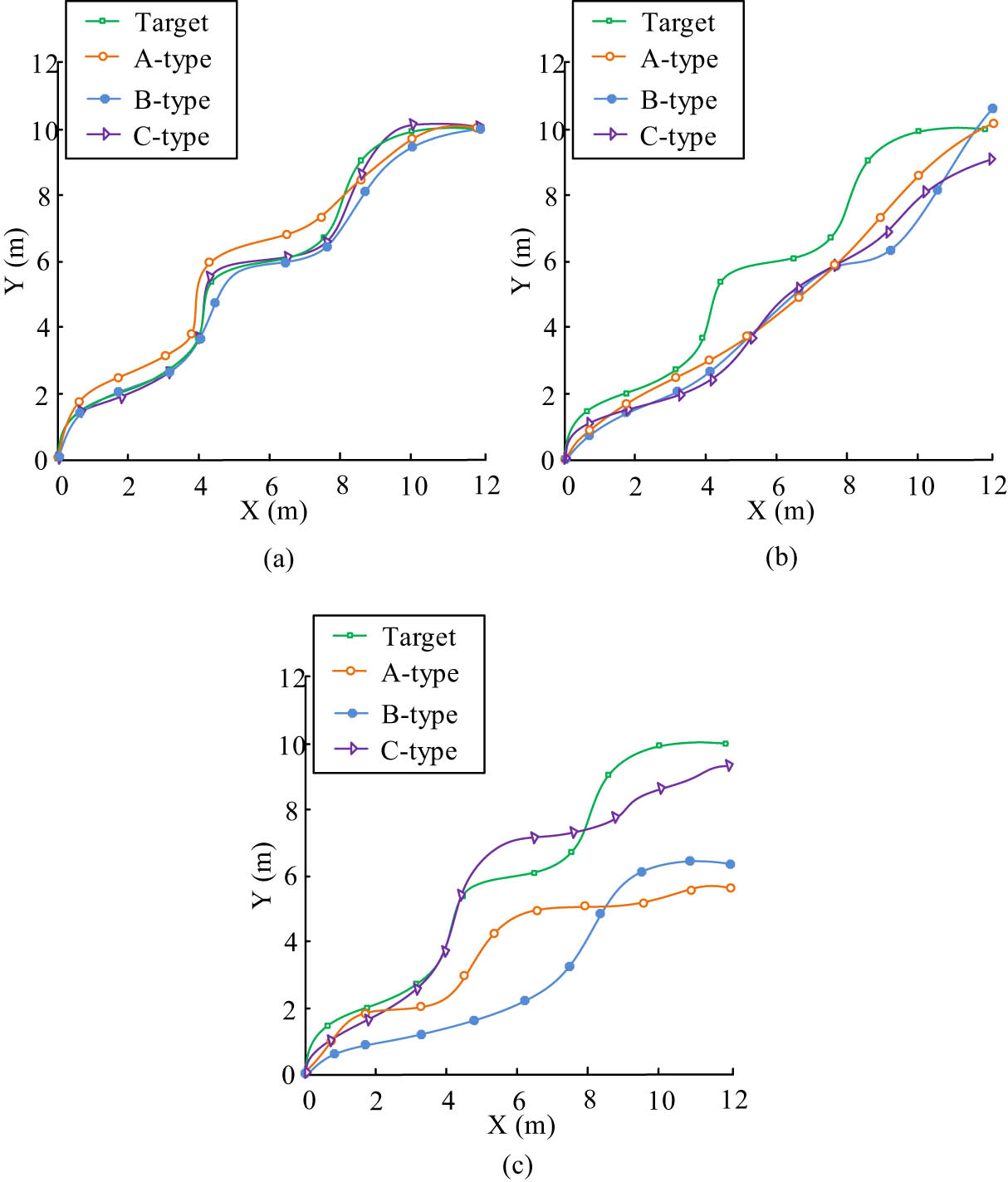
Comparison between the target motion position of the RA and the motion position controlled by three methods. (a) Comparison between the target motion position of the robotic arm and the motion position under CPG-NED control. (b) Comparison between the target motion position of the robotic arm and the motion position under “Tianying et al.” control. (c) Comparison between the target motion position of the robotic arm and the motion position under “Chen et al.” control.

In Figure 6(a), the control of the motion position of the three models of RA under the control of the proposed method of the study is highly consistent with the target motion position, and the motion position of the type C RA is the most effective, which is almost perfectly fitted to the target motion position curve. In Figure 6(b) and (c), the motion positions of the three types of RA under the control of the two methods deviate from the target motion position to a more serious extent, indicating that the effectiveness of the motion position control capability of the two methods is poor. This indicates that the CPG-NDE proposed in the study is more capable of controlling the RA motion position, thus reducing the chance of error in the control system leading to motion trajectory deviation.

4.2 Performance verification of RA joints

In order to verify the joint performance of the RA under CPG-NDE control, we conducted simulation verification experiments in terms of joint velocity variation and joint angle variation. First, the study compares the execution time required to obtain the Pareto-optimal frontier for each of the three types of RA using CPG-NDE and CPG [28]. Moreover, the average execution time curves of the two methods on the three types of RA are obtained by repeating the experiments 30 times with the same desired target position and the attitude of the desired target, and the specific results are shown in Figure 7.

Figure 7

Average execution time curves of different methods on the three types of RAs. (a) CPG-NDE, (b) CPG.

In Figure 7, the execution time of the three RAs under CPG-NDE control to obtain the Pareto-optimal frontier is concentrated in the interval [0.74 s, 0.8 s] and the average execution time is 0.78 s, while the execution time of the three M-Ms under CPG control is concentrated in the interval of [1.8 s, 1.95 s] and the average execution time is 1.87 s, which is higher than the CPG-NBE with a delay of 139.74%. This indicates that RA under CPG-NDE control has a better advantage than CPG in terms of execution time performance. Meanwhile, the study further analyzed the results of CPG-NDE on the three RAs’ joint velocity and angle changes. Among them, the variation of each joint velocity profile of type A RA under CPG-NDE control fed back to the upper computer through the motor is shown in Figure 8.

Figure 8

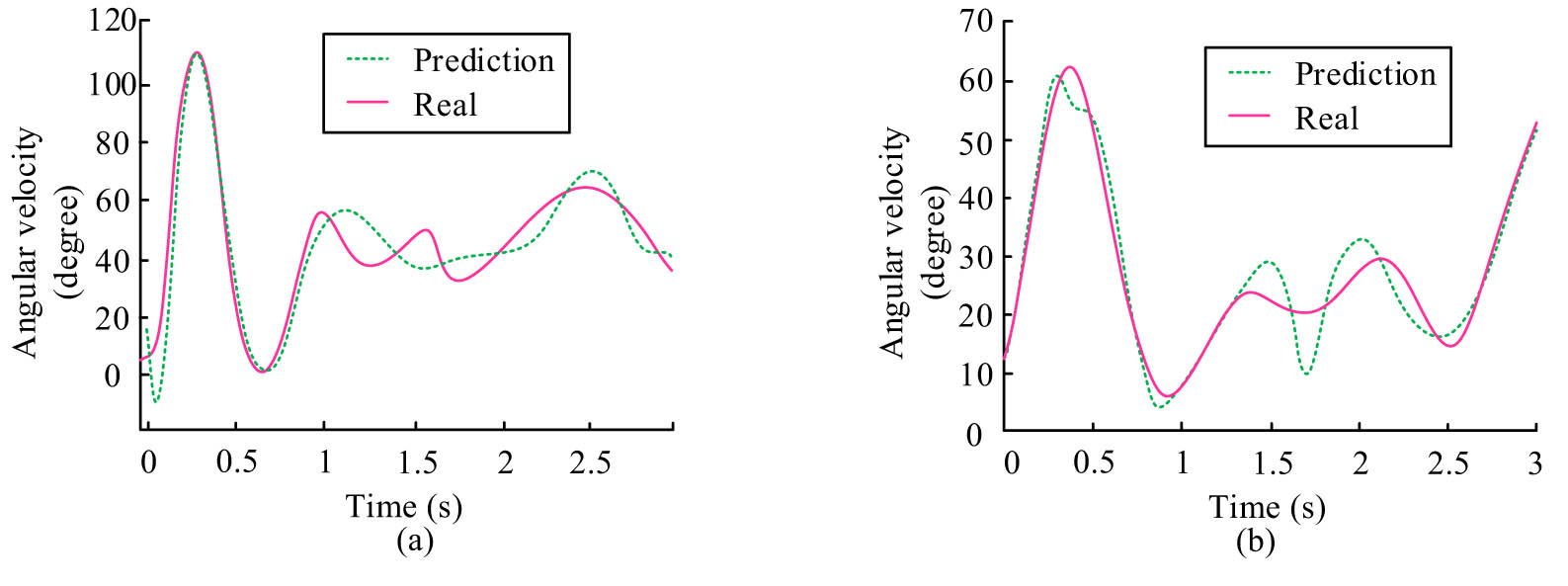
Graph of JN velocity variation of A-type RA. (a) Joint 1 velocity variation diagram. (b) Joint 2 velocity variation diagram.

In Figure 8, the actual change curves of the actual velocities of the two joints of the A-type RA under the control of CPG-NDE fluctuate similarly to the predicted change curves, but there is an error in the range of 0.1–0.5 s. This indicates that the CPG-NDE is effective in controlling the A-type RA. The curve change amplitude of each JN is smooth, and the stability of the RA system is good. The speed change of each joint of the B-type RA under CPG-NDE control is shown in Figure 9.

Figure 9

Graph of JN velocity variation of B-type RA. (a) Joint 1 velocity variation diagram. (b) Joint 2 velocity variation diagram.

In Figure 9, the actual change curves of the velocities of the B-type RA joints under CPG-NDE control have more obvious errors with the predicted results, in which the error range of the velocity change of joint 1 is between 0.2 and 1.0 s. However, the actual change curve of joint 2 almost fits the predicted curve, which indicates that the overall performance of the B-type RA joints under CPG-NDE control is better. The velocity change of each joint of the C-type RA under CPG-NDE control is shown in Figure 10.

Figure 10

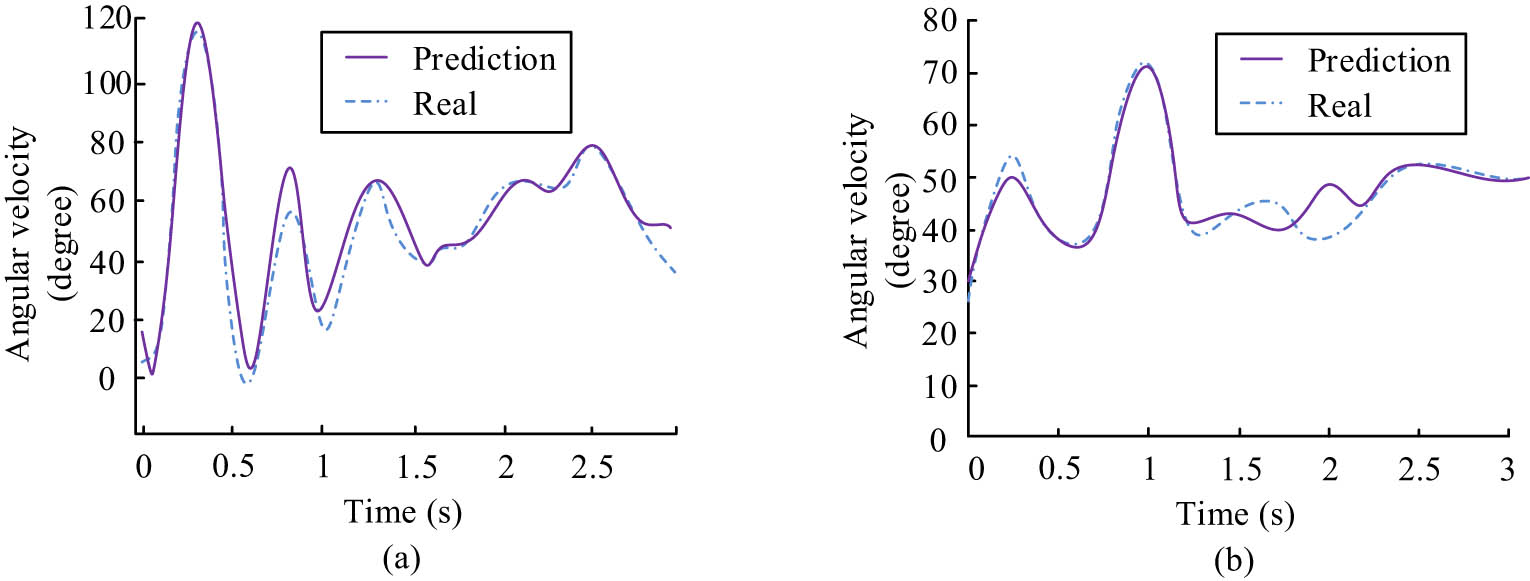
Graph of JN velocity variation of C-type RA. (a) Joint 1 velocity variation diagram. (b) Joint 2 velocity variation diagram.

In Figure 10, the error between the actual change and the predicted change of the joint velocity of type C RA is in the range of 0.1–0.3 s, which indicates that the CPG-NDE is more effective in stabilizing the joints of type C RA. Combining the joint velocity changes of the three types of RA, the research-proposed CPG-NDE is more effective in stabilizing the joint points of RA, and all of the change curves show a smooth and steady phenomenon. This indicates that the control algorithm proposed by the study can meet the stability requirements of RA, and the advantages of RA under CPG-NDE control are more obvious. In addition, the joint angle variation of the A-type RA under CPG-NDE control is shown in Figure 11.

Figure 11

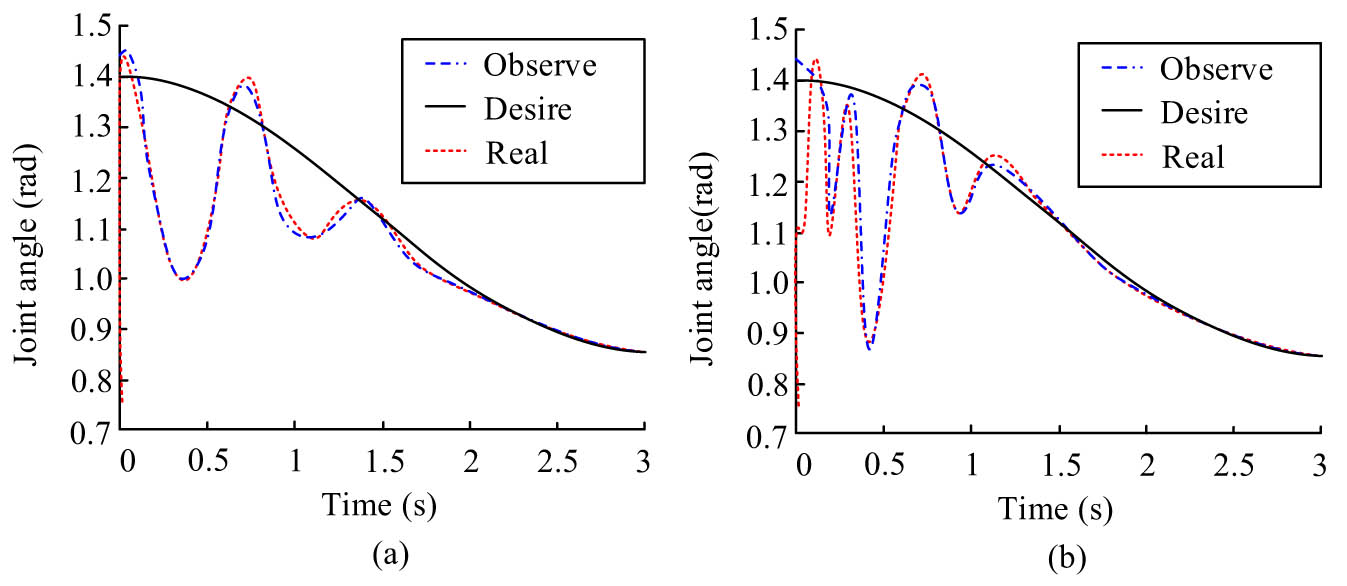
Joint angle changes of A-type RA under CPG-NDE control. (a) Joint 1 angle change curve. (b) Joint 2 angle change curve.

In Figure 11, the joint angle of A-type RA under CPG-NDE control fluctuates significantly in 0–1.5 s, and the fluctuation after 1.5 s almost fits the curve of the desired angle change, which indicates that the stability of the RA joint point is better. Moreover, more than 95% of the curve changes of the actual values have the same trend as the curve changes of the observed values, which indicates that the CPG-NDE is effective in controlling the joints of RA and thus enhances the observation effect of the correlation observer on the changes of the joint angles of RA to a certain extent. The joint angle changes of B-type RA under CPG-NDE control are shown in Figure 12.

Figure 12

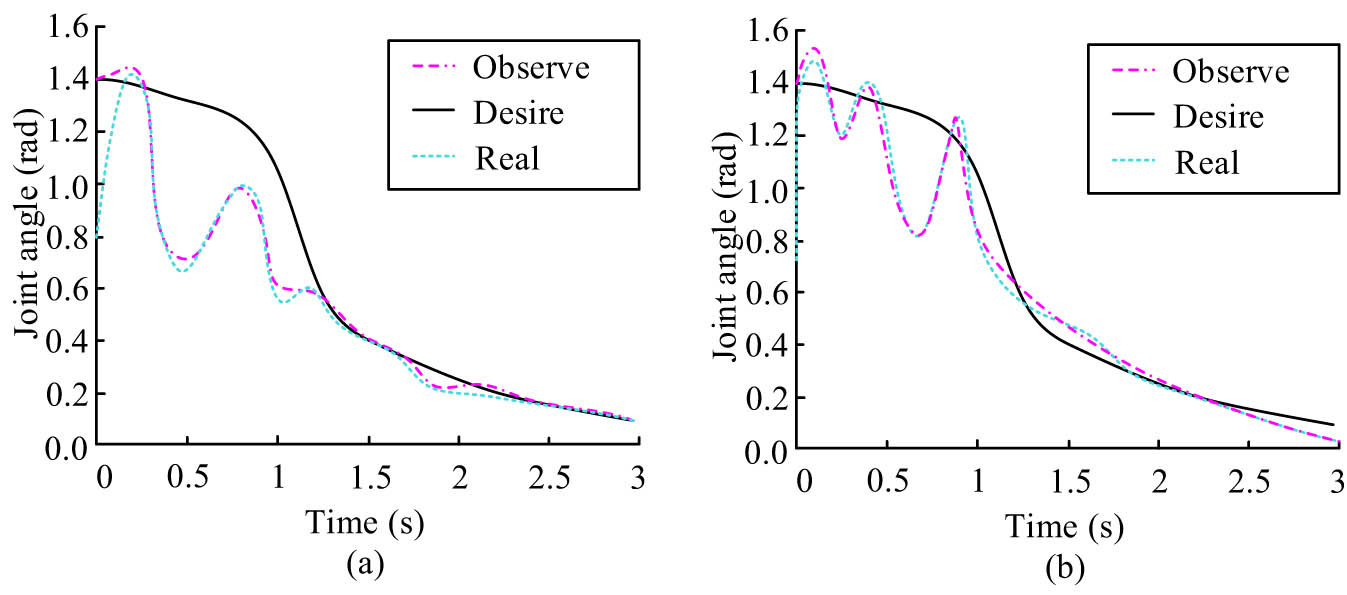
Joint angle changes of B-type RA under CPG-NDE control. (a) Joint 1 angle change curve. (b) Joint 2 angle change curve.

In Figure 12, the CPG-NDE proposed in the study is more effective in controlling the B-type RA, and its joint angle change gradually converges to the desired value after 1 s. The joint angle change of the B-type RA under CPG-NDE control is shown in Figure 13, which indicates that the B-type RA is more stable. With the increase of time, the joint angle change decreases, which indicates that the stability of the B-type RA under CPG-NDE control is better. The joint angle change of the C-type RA under CPG-NDE control is shown in Figure 13.

Figure 13

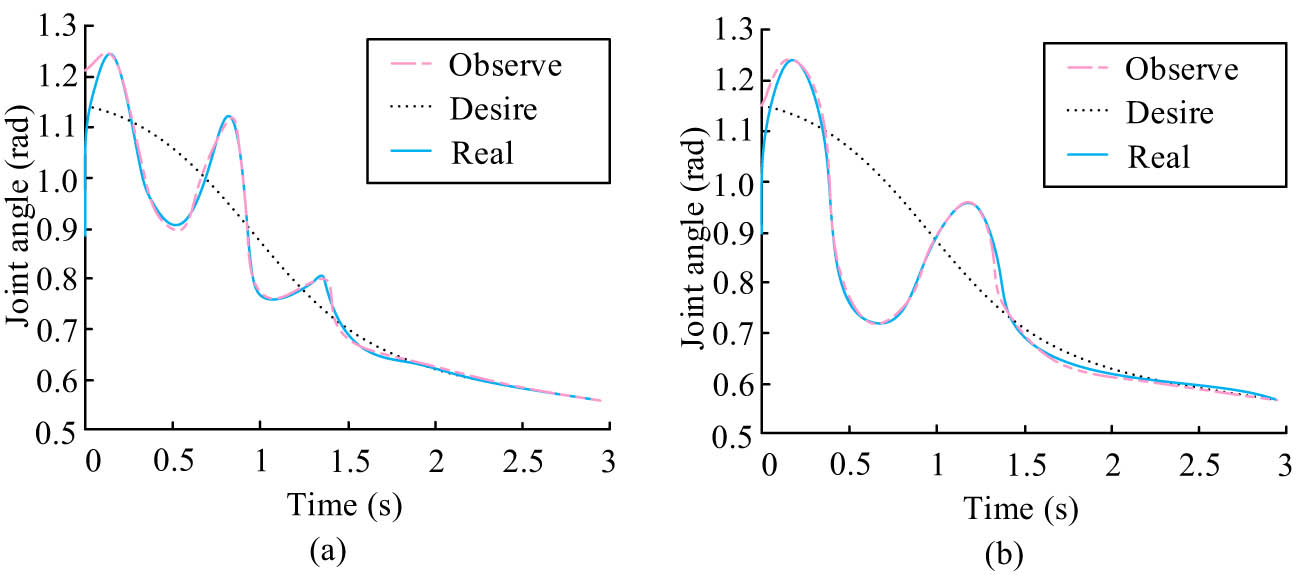
Joint angle changes of B-type RA under CPG-NDE control. (a) Joint 1 angle change curve. (b) Joint 2 angle change curve.

In Figure 13, the joint angle of the C-type RA under CPG-NDE control fluctuates significantly between 0 and 1.3 s compared with the desired value, and the change of its joint angle gradually stabilizes with the increase of time. The above results indicate that the introduction of NDE to control the joint motion position of the RA can effectively enhance the joint stability of the RA, thus obtaining a higher-performance RA operating system.

5 Conclusion

To improve the RA control efficiency, this study designs an algorithm RAMCA for RA motion control by constructing an NDE-based M-M and combining it with a CPG neural network. Experimental validation showed that the algorithm significantly improved the motion control performance of RA in several aspects. The consistency between the JN motion tracking trajectories and the target trajectories of the three types of RAs reached more than 85%, showing good trajectory tracking capability. The motion position control of the RAs had a 98% consistency with the target motion position trajectories. The RAMCA algorithm improved the execution time of the Pareto-optimal frontier of the RAs by 58.29% on average. Under CPG-NDE control, the joint angle and velocity variations of RA of the three robots were highly consistent with the expected and predicted curves. This indicated that the algorithms could effectively enhance the JN position tracking and improve the stability of the robot arm motion control. The above results revealed that the research not only provided a new method for RA motion control but also experimentally verified its effectiveness and superiority in practical applications. In particular, by combining the NDE with the CPG neural network, the study proposed a new control strategy that could improve the motion speed and stability of the robot arm while ensuring position control. Despite the remarkable results of the study, there are still some limitations. For example, the study only analyzes two joints in the structure of a three-link robot arm, and the sample data are analyzed in a narrow range. In the future, the sample data set for the study of RA under CPG-NDE control will be expanded, and the most effective means of increasing the motion speed of the RA machine while maintaining positional control will be investigated. The objective is to enhance the efficiency of production practices.

Funding information: This research was supported by 2023 Ordos Vocational College Research Fund Project: “Research on the Integration of Higher Vocational Mathematics Curriculum and Double-creative Talents Training Mode under the Concept of Three Complete Education” (EJSZY2304).
Author contributions: Xiaohua Yuan conducted experiments, recorded data, analyzed the results, and wrote the manuscript.
Conflict of interest: The author declares no conflict of interest.
Data availability statement: The data are provided within the manuscript.

References

[1] Jan A, Boulaaras S, Abdullah FA, Jan R. Dynamical analysis, infections in plants, and preventive policies utilizing the theory of fractional calculus. Eur Phys J Spec Top. 2023;232(14):2497–512.10.1140/epjs/s11734-023-00926-1Suche in Google Scholar

[2] Alharbi R, Jan R, Alyobi S, Altayeb Y, Khan Z. Mathematical modeling and stability analysis of the dynamics of monkeypox via fractional-calculus. Fractals. 2022;30(10):2240266.10.1142/S0218348X22402666Suche in Google Scholar

[3] Bhatti MM, Sait SM, Ellahi R, Sheremet MA, Oztop H. Thermal analysis and entropy generation of magnetic eyring-powell nanofluid with viscous dissipation in a wavy asymmetric channel. Int J Numer Methods Heat Fluid Flow. 2023;33(5):1609–36.10.1108/HFF-07-2022-0420Suche in Google Scholar

[4] Slyn’ko VI, Tunç O, Bivziuk VO. Application of commutator calculus to the study of linear impulsive systems. Syst Control Lett. 2019;123:160–5.10.1016/j.sysconle.2018.10.015Suche in Google Scholar

[5] Slyn’ko VI, Tunç C, Bivziuk VO. Robust stabilization of non-linear non-autonomous control systems with periodic linear approximation. IMA J Math Control Inf. 2021;38(1):125–42.10.1093/imamci/dnaa003Suche in Google Scholar

[6] Slyn’ko V, Tunç C. Stability of abstract linear switched impulsive differential equations. Automatica. 2019;107:433–41.10.1016/j.automatica.2019.06.001Suche in Google Scholar

[7] Xu WH, Cao LJ, Zhong CL. Review of aerial manipulator and its control. Int J Robot Control Syst. 2021;1(3):308–25.10.31763/ijrcs.v1i3.363Suche in Google Scholar

[8] Srivastava S. A review on design and fabrication of robotic arm. Int J Robot Autom. 2021;7(2):19–21.Suche in Google Scholar

[9] Khan Z, Jawad M, Bonyah E, Khan N, Jan R. Magnetohydrodynamic thin film flow through a porous stretching sheet with the impact of thermal radiation and viscous dissipation. Math Prob Eng. 2022;2022(1):1086847.10.1155/2022/1086847Suche in Google Scholar

[10] Appalanaidu V, Deekshitulu GVSR. Bernstein collocation approach for solving nonlinear differential equations with delay and anticipation. Int J Discontinuity Nonlinearity Complex. 2022;11(3):425–34.10.5890/DNC.2022.09.006Suche in Google Scholar

[11] Khan Y. Novel solitary wave solution of the nonlinear fractal schrdinger equation and its fractal variational principle. Multidiscip Model Mater Struct. 2021;17(3):630–5.10.1108/MMMS-08-2020-0202Suche in Google Scholar

[12] Chen Y, Huang Y, Liu Y, Wang Y. Two-grid method for semiconductor device problem by mixed finite element method and characteristics finite element method. Electron Res Arch. 2021;29(1):1859–80.10.3934/era.2020095Suche in Google Scholar

[13] MarusakPiotr MP. A numerically efficient fuzzy mpc algorithm with fast generation of the control signal. Int J Appl Math Comput Sci. 2021;31(1):59–71.10.34768/amcs-2021-0005Suche in Google Scholar

[14] Jing L. Data simulation of optimal model for numerical solution of differential equations based on deep learning and genetic algorithm. Soft Comput Fusion Found Methodol App. 2023;27(14):10025–32.10.1007/s00500-023-08208-7Suche in Google Scholar

[15] Okereke RN, Maliki OS. Solving riccati-type nonlinear differential equations with novel artificial neural networks. Appl Math. 2021;12(10):919–30.10.4236/am.2021.1210060Suche in Google Scholar

[16] Chen ZY, Wang RY, Meng Y, Chen T. Modeling control and forecasting nonlinear systems based on grey signal theory. Int J Uncertain Fuzz Knowl-B Syst. 2023;31(4):649–68.10.1142/S0218488523500307Suche in Google Scholar

[17] Arena A, Gattulli V, Ottaviano E. Dynamics of cable-driven parallel manipulators with variable length vibrating cables. Int J Non-Linear Mech. 2023;151(5):1–21.10.1016/j.ijnonlinmec.2023.104382Suche in Google Scholar

[18] Cao F, Liu J. Boundary control for pde flexible manipulators: accommodation to both actuator faults and sensor faults. Asian J Control. 2022;24(4):1700–12.10.1002/asjc.2560Suche in Google Scholar

[19] Li XY. Adaptive neural boundary control for state constrained flexible manipulators. Int J Adapt Control Signal Process. 2023;37(8):2184–203.10.1002/acs.3633Suche in Google Scholar

[20] Sheng X, Quan Q, Yu J, Mao X, Jiang W. Tide-induced lagrangian residual velocity and dynamic analysis based on field observations in the inner xiangshan bay, China. Acta Oceanol Sin. 2022;41(10):32–40.10.1007/s13131-022-2007-3Suche in Google Scholar

[21] Yamaguchi T, Takayama K, Hirose N. Quantitative relationships between autumn catches of swordtip squid (uroteuthis edulis) and oceanic conditions to the east of tsushima islands, japan. Am J Mar Sci. 2021;9(1):16–25.Suche in Google Scholar

[22] Arnous AH, Hashemi MS, Nisar KS, Shakeel M, Ahmad J, Ahmad I, et al. Investigating solitary wave solutions with enhanced algebraic method for new extended Sakovich equations in fluid dynamics. Results Phys. 2024;57:107369.10.1016/j.rinp.2024.107369Suche in Google Scholar

[23] Haiour M, Le Hocine MEAB, Jan R, Himadan A, Boulaaras S. Existence and uniqueness for the evolutionary impulse control problem using an asynchronous algorithms. Partial Differ Equ Appl Math. 2024;11:100766.10.1016/j.padiff.2024.100766Suche in Google Scholar

[24] Fu ZT, Wang JY, Liu Y, Xiong JM, Zhang GW. The mechanism of tcm prevention and treatment of heavy covid-19 based on data mining and network pharmacology. Comb Drug Ther. 2023;5(2):30–9.10.53388/DCT20230010Suche in Google Scholar

[25] Wei SX, Wu H, Liu L, Zhang YX, Chen J, Li Q. A cpg-based gait planning and motion performance analysis for quadruped robot. Ind Robot. 2022;49(4):779–97.10.1108/IR-08-2021-0181Suche in Google Scholar

[26] Xu TY, Zhou HB, Tan SX, Li ZQ, Ju X, Peng YC. Mechanical arm obstacle avoidance path planning based on improved artificial potential field method. Ind Robot. 2022;49(2):271–9.10.1108/IR-06-2021-0120Suche in Google Scholar

[27] Chen L, Sun H, Zhao W, Yu T. Ai based gravity compensation algorithm and simulation of load end of robotic arm wrist force. Math Prob Eng. 2021;2021(8):1–11.10.1155/2021/5551544Suche in Google Scholar

[28] Guo S, Geng Z, Yuan J. Single-machine pareto-scheduling with multiple weighting vectors for minimizing the total weighted late works. J Ind Manage Optim.2023;19(1):456–71.10.3934/jimo.2021192Suche in Google Scholar

Received: 2023-12-04

Revised: 2024-07-30

Accepted: 2024-08-12

Published Online: 2024-11-19

This work is licensed under the Creative Commons Attribution 4.0 International License.

Artikel in diesem Heft

https://doi.org/10.1515/nleng-2024-0031

Schlagwörter für diesen Artikel

NDE; control algorithms; RAs

Creative Commons

BY 4.0