On the flow of MHD generalized maxwell fluid via porous rectangular duct

Aamir Farooq; Muhammad Kamran; Yasir Bashir; Hijaz Ahmad; Azeem Shahzad; Yu-Ming Chu

doi:10.1515/phys-2020-0209

Artikel Open Access

On the flow of MHD generalized maxwell fluid via porous rectangular duct

Aamir Farooq , Muhammad Kamran , Yasir Bashir , Hijaz Ahmad , Azeem Shahzad und Yu-Ming Chu

Veröffentlicht/Copyright: 17. Dezember 2020

Veröffentlicht von

Veröffentlichen auch Sie bei De Gruyter Brill

Manuskript einreichen Informationen für Autor*innen Erkunden Sie dieses Fachgebiet

Aus der Zeitschrift Open Physics Band 18 Heft 1

Abstract

The purpose of this proposed investigation is to study unsteady magneto hydrodynamic (MHD) mixed initial-boundary value problem for incompressible fractional Maxwell fluid model via oscillatory porous rectangular duct. Considering the modified Darcy’s law, the problem is simplified by using the method of the double finite Fourier sine and Laplace transforms. As a limiting case of the general solutions, the same results can be obtained for the classical Maxwell fluid. Also, the impact of magnetic parameter, porosity of medium, and the impact of various material parameters on the velocity profile and the corresponding tangential tensions are illuminated graphically. At the end, we will give the conclusion of the whole paper.

Keywords: fractional Maxwell fluid; exact solutions; non-Newtonian fluid; oscillatory rectangular duct; velocity field

1 Introduction

Fluid mechanics is an important branch of applied mathematics; nowadays, the theory of fluid mechanics is growing greatly due to which in various aspects of our life the study of mechanics of fluids has become very significant. The ability of the creatures to move through fluids, i.e., air as well as water, is of vital significance for their way of life. In our real world, all creatures live immersed in fluids (air or water). Significant ways are provided by the circulating fluids systems to distribute the things where they are necessary. For instance, take the example of blood flow which is very important for our body. Likewise, another significant circulation system is ocean which is essentially very crucial for man. Action of flow of fluid on the rotating blades converts different forms of energies like chemical energy, heat energy, or potential energy into kinetic energy in a steam turbine, gas turbine as well as in a water turbine. The efficiency of different types of turbines can be improved by studying this type of flow. Heat is transferred quickly from one part of the engine to the other part by the effective motion of fluid in various cases. The water motion through turbine produces electric power by waves, which is an example of fluid motion. Structures are designed in such a way that they can resist violent sea motions, strong winds, and river erosion, but all these need the understanding of forces exercised by waves, currents as well as winds on these static structures. Therefore, in every case the inclusive information of fluid flow plays the vital role. All these problems are very complicated. The progressive information of turbulence and boundary layer flow can tackle these complicated problems, since the motion of fluid generally propagates in a haphazard manner [1].

Subjects like non-Newtonian flow and rheology are basically interdisciplinary in nature and also get wide applications in many fields. Indeed, non-Newtonian fluids behavior is encountered in almost all the chemical and allied processing industries. Elements determining rheological properties of certain material are very complicated. The active role of applied mathematicians, physicists, and chemists is necessary for the full understanding of these complicated problems. Some of them consider this subject as central to their disciplines. Also, it gets diverse applications in many fields. It also requires an active contribution from chemical and process engineers. They can play their role by processing and handling complicated materials like slurries, polymer melts solutions, foams and emulsions, etc. Similarly, the practicing engineers, scientists, and theoretical mathematicians find this subject very important for them with diverse cultural background [2].

The working and understanding of artificial and natural systems requires the traditional derivative and integral which are important for technology professionals. The derivative operators and calculus integral can be defined by fractional calculus which is the field of mathematics in which the fractional exponents are used in place of integer exponents. In the definition of the non-integer order derivatives there is integral, so it is clear that these derivatives are nonlocal operators, which shows one of their most important uses in applications. The specific information about some function in space or time at some earlier points is contained by the non-integer derivative at some specific point in space or time, respectively. Therefore, non-integer derivatives are characterized by some memory effects that are shared with numerous materials like polymers and viscoelastic materials and also its uses in anomalous diffusions. Many researchers have studied keenly and comprehensively the fractional operators [3,4,5,6,7,8,9,10,23,46,47,48,56]. Due to this, fractional calculus is used in different disciplines [19,20,21,22,49,50,51,52,53]. Many scholars had discussed the dynamics predator-prey model with integer and fractional derivatives (see, e.g., ref. [32,33,34,35,36,37,38,39,40,54,55]). S. Djilali discussed the dynamics of other models (see, e.g., ref. [41,42]) for better understanding. B. Ghanbari et al. and S. Kumar et al. had studied the tumor-immune model for cancer treatment with fractional derivatives [43,44]. Similarities in a fifth-order evolution equation with and with no singular kernel were studied in ref. [45] by E. Goufo. In technological applications, non-Newtonian fluids have vital role as compared to Newtonian fluids. Non-Newtonian fluids are vastly used in industry and they vary from each other in their rheological properties. Due to simplicity of governing equation of the Maxwell fluid model, the scholars have keenly focused on it and elaborated its flow in various geometries. In geo-mechanics, biomechanics, and industry, the most important thing is how the flow takes place via porous media which include flow water through rock regulation of skin and filtration of fluids. Various types of solutions can be obtained by the cross sections of different geometries. It can be wisely used in industry due to its ability to flow via ducts. For the cooling in engineering systems, the porous passages with rectangular cross sections are of prime importance. So, the exact solutions of the classical Maxwell fluid and the generalized Maxwell fluid in different geometries have been thoroughly studied in the literature. Abdulhameed et al. [11] studied the Maxwell fluid via circular tube with the help of Caputo Fabrizio derivative. Aman et al. [12] focused on the thermal properties of Maxwell nanofluids with the fixed wall temperature. Bai et al. [13] studied the numerical analysis of MHD Maxwell fluid over the accelerating with slip condition. With the help of Atangana–Baleanu definition in porous medium, Abro et al. [14] obtained the temperature and velocity fields for the MHD Maxwell model. With the impact of slip and Newtonian heating, Imran et al. [15] focused on the fractional MHD Maxwell fluid flow. Raza and Asad [24] studied the heat transfer of fractional Maxwell fluid. Riaz et al. [25] studied the Maxwell fluid model with different fractional derivatives. Many researchers have studied the flow fluid through porous medium under different factors and conditions [26,27,28,29]. Nazar et al. [16,17] studied the motion of generalized and ordinary Maxwell fluid via an oscillatory rectangular duct and obtained the exact solution for the velocity and tangential stresses. Then, Sultan et al. [18] extended the Nazar et al. [16,17] problem and studied the unsteady flow of a Maxwell fluid in porous rectangular duct. However, to our best knowledge, there were no works on the flow of MHD generalized Maxwell fluid via porous rectangular duct. So, motivated by this, we are interested to find the exact solution for this problem by using integral transform [30].

The remainder of this article is organized as follows. Section 2 provides formulation of the flow problem. In Section 3, we will give the explicit expression of velocity field and the tangential stresses corresponding to MHD flows of a Maxwell fluid with fractional derivatives within an oscillating rectangular duct. In Section 4, we will obtain the explicit expressions for the velocity and the associated tangential stresses of the classical Maxwell fluids and the generalized Maxwell fluid without magnetic and porosity parameters. In Section 5, the obtained results are illuminated by the graphs. In Section 6, we will give the conclusion of the whole article.

2 Formulation of flow problem

Let us suppose the incompressible fractional Maxwell fluid in a duct of rectangular cross section whose sides are at x ̲ = 0 , x ̲ = d , y ̲ = 0 , y ̲ = h . At time t = 0 + , the duct starts to oscillate along the z ̲ -axis. The inner fluid is in a motion due to the oscillation on the boundary of duct.

(2.1) W → ( x ̲ , y ̲ , z ̲ ) = ξ ( x ̲ , y ̲ , t ) k ˆ = ( 0 , 0 , ξ ) , S → = S ( x ̲ , y ̲ , t ) ,

For the velocity field and an extra-stress, we have the following assumptions where k ˆ is the unit vector pointing in z ̲ -direction. According to the first Rivlin–Ericksen kinematic tensor, A → can be defined as

(2.2) A → ≔ ∇ W → + ( ∇ W → ) † ,

where † denotes the transpose operation. The tangential tensor is defined by τ → as

τ → ≔ − p J → + S → ,

in above relation, p is the hydrostatic pressure of the fluid, J → is the identity tensor, and S → is the extra tangential tensor and can be written as

(2.3) ( 1 + λ D t ) [ S → ] = ϖ A → .

Here, ϖ > 0 is the dynamic viscosity, λ is the relaxation time. The operator D t is so-called upper convected derivative and can be written as

(2.4) D t [ S → ] ≔ ∂ ∂ t [ S → ] + ( W → ⋅ ∇ ) S → + ( ∇ W → ) S → + S → ( ∇ W → ) † .

Furthermore, it is obvious to constrain the initial conditions for the fluid initially at rest

(2.5) S ( x ̲ , y ̲ , o ) = 0 = ∂ S ∂ t ( x ̲ , y ̲ , 0 ) .

For the MHD flow, the governing equations for the incompressible fluid will be

(2.6) ∇ ⋅ W → = 0 ρ ∂ W → ∂ t + ( W → ⋅ ∇ ) W → = ∇ ⋅ S → + I → × B → + R → ,

where ρ > o represents the density of the fluid. For the simplicity, the body forces and pressure gradient are ignored.

2.1 Mathematical formulation of the problem

In correspondence to constitutive equations, a fractional Maxwell fluid can be obtained by using appropriate initial and boundary conditions. For this purpose, initially we formulate the constitutive equations for the flow of a classical Maxwell fluid and then revelent reversal are made to get the constitutive equations for the fractional Maxwell fluids. The (2.1) will fulfil the equation of continuity and ( W → ⋅ ∇ ) W → ≡ 0 . With the help of (2.1), (2.2), and (2.4) along with initial conditions (2.5), (2.3) becomes for all t > 0 ,

(2.7) S x ̲ x ̲ = S x ̲ y ̲ = S y ̲ y ̲ = 0 1 + λ ∂ ∂ t S x ̲ z ̲ = ϖ ∂ ξ ∂ x ̲ , 1 + λ ∂ ∂ t S y ̲ z ̲ = ϖ ∂ ξ ∂ y ̲ ,

The momentum (2.6) for an ordinary Maxwell fluid by (2.1) and (2.7) will be

(2.8) ρ 1 + λ ∂ ∂ t ∂ ξ ∂ t = ϖ ∂ 2 ∂ x ̲ 2 + ∂ 2 ∂ y ̲ 2 ξ − σ β 0 2 1 + λ ∂ ∂ t ξ − ϖ ϕ k ξ .

The appropriate IBC’s are

(2.9) ξ ( x ̲ , y ̲ , 0 ) = ∂ ξ ( x ̲ , y ̲ , 0 ) ∂ t = 0 , ξ ( 0 , y ̲ , t ) = ξ ( l , y ̲ , t ) = ξ ( x ̲ , 0 , t ) = ξ ( x ̲ , h , t ) = U 0 cos ( ω t ) , t > 0 ,

(2.10) ξ ( x ̲ , y ̲ , 0 ) = ∂ ξ ( x ̲ , y ̲ , 0 ) ∂ t = 0 , ξ ( 0 , y ̲ , t ) = ξ ( l , y ̲ , t ) = ξ ( x ̲ , 0 , t ) = ξ ( x ̲ , h , t ) = U 0 sin ( ω t ) , t > 0 ,

where U 0 is the amplitude and ω the frequency of the velocity of edge. The IBVP governing the flow of the ordinary Maxwell fluid is given by (2.8)–(2.10). We will obtain the governing equations for the fractional Maxwell fluids by carrying out the same motion by interchanging the inner time derivatives with the Caputo fractional time derivatives ∂ t α for 0 < α ≤ < 1 . Precisely, we entertain the following model with same initial-boundary conditions:

(2.11) ρ ( 1 + λ α D t α ) ∂ ξ ∂ t = ϖ ∂ 2 ∂ x ̲ 2 + ∂ 2 ∂ y ̲ 2 ξ − σ β 0 2 ( 1 + λ α D t α ) ξ − ϖ ϕ k ξ ,

where

D t ℘ f ( t ) = ϖ 1 Γ ( 1 − ℘ ) ∫ 0 t f ' ( τ ) ( t − τ ) ℘ d τ , 0 ≤ ℘ < 1

is the Capouto’s fractional derivative [8] and Γ ( ⋅ ) is the usual Gamma function. Note that the exponent α on λ is written in order to collaborate the dimensions of various terms in (2.11). Introducing the following dimensionless quantities to (2.11)

(2.12) x ̲ ⁎ = x ̲ l , y ̲ ⁎ = y ̲ h , ξ ⁎ = ξ U 0 , t ⁎ = ϖ t ρ l h , λ ⁎ = ϖ λ ρ l h , ω ⁎ = ρ d h ω ϖ , β = l h , 1 K = ϕ l h k , M 2 = σ β 0 2 l h ϖ .

By (2.12), the IBVP (2.11) becomes as, using the same notation for dimensionless quantities and without ⁎ sign,

(2.13) ( 1 + λ α D t α ) ∂ ξ ∂ t = 1 β ∂ 2 ∂ x ̲ 2 + β 2 ∂ 2 ∂ y ̲ 2 ξ − M 2 ( 1 + λ α D t α ) ξ − 1 K ξ ,

(2.14) ξ ( x ̲ , y ̲ , 0 ) = ∂ ξ ( x ̲ , y ̲ , 0 ) ∂ t = 0 , ξ ( 0 , y ̲ , t ) = ξ ( 1 , y ̲ , t ) = ξ ( x ̲ , 0 , t ) = ξ ( x ̲ , 1 , t ) = cos ( ω t ) , t > 0 ,

(2.15) ξ ( x ̲ , y ̲ , 0 ) = ∂ ξ ( x ̲ , y ̲ , 0 ) ∂ t = 0 , ξ ( 0 , y ̲ , t ) = ξ ( 1 , y ̲ , t ) = ξ ( x ̲ , 0 , t ) = ξ ( x ̲ , 1 , t ) = sin ( ω t ) , t > 0 .

3 Calculation for the velocity field

3.1 The case ξ ( 0 , y ̲ , t ) = ξ ( 1 , y ̲ , t ) = ξ ( x ̲ , 0 , t ) = ξ ( x ̲ , 1 , t ) = sin ( ω t )

Multiplying both sides of (2.13) by sin ( α i x ̲ ) sin ( β j y ̲ ) , then integrating with respect to x ̲ and y ̲ over [ 0 , 1 ] × [ 0 , 1 ] , and utilizing the transformed initial and boundary conditions, we obtain

(3.1) ( 1 + λ α D t α ) ∂ ∂ t ξ i j ( t ) + λ i j 2 β ( 1 + λ α D t α ) ξ i j ( t ) + λ i j 2 β ξ i j ( t ) + 1 K ξ i j ( t ) = a i j λ i j 2 β sin ( ω t ) ,

where α r = r π , β s = s π , a r s = [ 1 − ( − 1 ) r ] [ 1 − ( − 1 ) s ] α r β s and λ r s 2 = α r 2 + β 2 β s 2 , and

ξ r s ( t ) = ∫ 0 1 ∫ 0 1 ξ ( x ̲ , y ̲ , t ) sin ( α r x ̲ ) sin ( β s y ¯ ) d x ̲ d y ̲ , r , s = 1 , 2 , 3 …

is the double Fourier transform of ξ ( x ̲ , y ̲ , t ) . Now taking the Laplace transform to (3.1) and utilizing the appropriate transformed conditions, we obtain the expression for ξ ¯ r s ( q ) as

ξ ¯ r s ( q ) = a r s λ r s 2 β ω q 2 + ω 2 × 1 q + λ α q α + 1 + λ r s 2 β + M 2 ( 1 + λ α q α ) + 1 K

(3.2) ξ ¯ r s ( q ) = a r s λ r s 2 β ω q 2 + ω 2 F ¯ r s ( q ) ,

where

F ¯ r s ( q ) = 1 q + λ α q α + 1 + λ r s 2 β + M 2 ( 1 + λ α q α ) + 1 K ,

which can be written as

F ¯ r s ( q ) = β λ r s 2 − 1 + λ α q α + M 2 λ α q α − 1 + M 2 + 1 K q − 1 1 + λ α q α + M 2 + λ r s 2 β + 1 K q − 1 + M 2 λ α q α − 1 β λ r s 2

and ξ ¯ r s ( q ) = ∫ 0 ∞ ξ r s ( t ) e − q t d t is the Laplace transform of ξ r s ( t ) . (3.2) becomes

(3.3) ξ ¯ r s ( q ) = a r s ω q 2 + ω 2 − a r s ω q 2 + ω 2 × 1 + λ α q α + M 2 λ α q α − 1 + M 2 + 1 K q − 1 1 + λ α q α + M 2 + λ r s 2 β + 1 K q − 1 + M 2 λ α q α − 1

Denoting by

U ¯ ( q ) = q ( q − 1 + λ α q α − 1 + M 2 λ α q α − 2 + ( M 2 + 1 K ) q − 2 ) q 2 + ω 2

we get following, by applying the inverse Laplace transform to the above relation,

u ( t ) = L − 1 { U ¯ ( q ) } = λ α Γ ( 1 − α ) ∫ 0 t cos ( ω t ) + M 2 ω sin ( ω t ) ( t − τ ) α d τ + M 2 + 1 K ω 2 ( 1 − cos ( ω t ) ) + sin ( ω t ) ω , 0 < α < 1 .

Taking the following function

A ¯ r s ( q ) = 1 1 + λ α q α + M 2 + λ r s 2 β + 1 K q − 1 + M 2 λ α q α − 1 .

A ¯ r s ( q ) can be written in more simpler form with the help of relations given in the Appendix of ref. [23].

A ¯ r s ( q ) = ∑ l =0 ∞ ∑ m =0 l ( − 1) l l ! ( M 2 λ α ) m M 2 + λ i j 2 β + 1 K l − m m ! ( l − m ) ! λ α ( l + 1) × q α m − l ( q α + λ − α ) l + 1

The inverse Laplace transform of above expression is

a r s ( t ) = ∑ l = 0 ∞ ∑ m = 0 l ( − 1 ) l l ! ( M 2 λ α ) m M 2 + λ i j 2 β + 1 K l − m m ! ( l − m ) ! λ α ( l + 1 ) × G α , α m − l , l + 1 ( − λ − α , t ) ,

where G α , α m − l , l + 1 ( − λ − α , t ) is the generalized G-function and for the explicit expression of the generalized G-function see ref. [7]. The transformed velocity can be rewritten as

(3.4) ξ ¯ r s ( q ) = a r s ω q 2 + ω 2 − a r s ω U ¯ ( q ) A ¯ r s ( q ) .

We will get the following equation by implementing the inverse Laplace transform to the (3.4),

(3.5) ξ r s ( t ) = a r s sin ( ω t ) − a r s ω ( u ( t ) ∗ a r s ( t ) ) ,

where u ( t ) ⁎ a r s ( t ) = ∫ o t u ( t − q ) a r s ( t ) d q denotes the convolution product of u ( t ) and a r s ( t ) . Using the formula from ref. [30,31], velocity field can be written as by implementing the inverse Fourier transform to (3.5)

ξ ( x ̲ , y ̲ , t ) = sin ( ω t ) − 4 ∑ r , s = 1 ∞ a r s ω × sin ( α r x ̲ ) sin ( β s y ̲ ) ( u ( t ) ∗ a r s ( t ) ) ,

in simplifier form it can be,

ξ ( x ̲ , y ̲ , t ) = sin ( ω t ) − 16 ∑ r , s = 0 ∞ ω × sin ( ( 2 r + 1 ) π x ̲ ) ( 2 r + 1 ) π sin ( ( 2 s + 1 ) π y ̲ ) ( 2 s + 1 ) π × u ( t ) ∗ a ( 2 r + 1 ) ( 2 s + 1 ) ( t ) .

The dimensionless tangential stresses T 1 and T 2 corresponding to the fractional Maxwell fluid in such motions are given by

(3.6) ( 1 + λ α D t α ) T 1 ( x ̲ , y ̲ , t ) = ∂ ∂ x ̲ ξ ( x ̲ , y ̲ , t ) ,

(3.7) (1 + λ α D t α ) T 2 ( x ̲ , y ̲ , t ) = ∂ ∂ y ̲ ξ ( x ̲ , y ̲ , t ) ,

where T 1 = l S x ̲ z ̲ ϖ u 0 and T 2 = h S y ̲ z ̲ ϖ u 0 . By implementing the Laplace transform to the (3.6), it yields

T ¯ 1 ( x ̲ , y ̲ , q ) = 1 1 + λ α q α ∂ ∂ x ̲ ξ ̲ ( x ̲ , y ̲ , q ) .

Therefore, T 1 ( x ̲ , y ̲ , q ) can be rewritten as

(3.8) T ¯ 1 ( x ̲ , y ̲ , q ) = 1 − q α q α + λ − α ∂ ∂ x ̲ ξ ̲ ( x ̲ , y ̲ , q ) ,

where

ξ ¯ ( x ̲ , y ̲ , q ) = ω q 2 + ω 2 − 16 ∑ r , s = 0 ∞ ω sin ( ( 2 r + 1 ) π x ̲ ) ( 2 r + 1 ) π × sin ( ( 2 s + 1 ) π y ̲ ) ( 2 s + 1 ) π F ¯ ( q ) A ¯ ( 2 r + 1 ) ( 2 s + 1 ) ( q ) .

Taking the partial derivative of ξ ̲ ( x ̲ , y ̲ , q ) with respect to x ̲ , then putting into the (3.8), we will obtain

(3.9) T ¯ 1 ( x ̲ , y ̲ , q ) = 1 − q α q α + λ − α − 16 ∑ r , s = 0 ∞ ω cos ( ( 2 r + 1 ) π x ̲ ) × sin ( ( 2 s + 1 ) π y ̲ ) ( 2 s + 1 ) π F ¯ ( q ) A ¯ ( 2 r + 1 ) ( 2 s + 1 ) ( q ) .

Following relation can be obtained by implementing the inverse Laplace transform to the (3.9)

T 1 ( x ̲ , y ̲ , t ) = − 16 ∑ r , s = 0 ∞ ω cos ( ( 2 r + 1 ) π x ̲ ) × sin ( ( 2 s + 1 ) π y ̲ ) ( 2 s + 1 ) π f ( t ) ∗ a ( 2 r + 1 ) ( 2 s + 1 ) ( t ) + 16 ∑ r , s = 0 ∞ ω cos ( ( 2 r + 1 ) π x ̲ ) × sin ( ( 2 s + 1 ) π y ̲ ) ( 2 r + 1 ) π f ( t ) ∗ h ( t ) ∗ a ( 2 r + 1 ) ( 2 s + 1 ) ( t ) ,

where h ( t ) = L − 1 q α q α + λ − α = H ( t ) − 1 λ α R α ,0 ( − λ − α , t ) , and R a , b ( c , d , t ) = ∑ n =0 ∞ c n ( t − d ) ( n + 1) a − b − 1 Γ [ ( n + 1) a − b ] .

Similarly, we can calculate T 2 .

3.2 The case ξ ( 0 , y ̲ , t ) = ξ ( 1 , y ̲ , t ) = ξ ( x ̲ , 0 , t ) = ξ ( x ̲ , 1 , t ) = cos ( ω t )

Multiplying both sides of (2.13) by sin ( α r x ̲ ) sin ( β s y ̲ ) , then integrating with respect to x ̲ and y ̲ over [ 0 , 1 ] × [ 0 , 1 ] , and utilizing the transformed initial and boundary conditions yield

(3.10) ( 1 + λ α D t α ) ∂ ∂ t ξ r s ( t ) + λ r s 2 β ( 1 + λ α D t α ) ξ r s ( t ) + λ i j 2 β ξ r s ( t ) + 1 K ξ r s ( t ) = a r s λ r s 2 β cos ( ω t ) ,

we can get the expression for ξ ¯ r s ( q ) by implementing the Laplace transform to (3.10) and utilizing the appropriate transformed conditions,

ξ ¯ r s ( q ) = a r s λ r s 2 β q q 2 + ω 2 × 1 q + λ α q α + 1 + λ r s 2 β + M 2 ( 1 + λ α q α ) + 1 K

(3.11) ξ ¯ r s ( q ) = a r s λ r s 2 β q q 2 + ω 2 F ¯ r s ( q ) .

Then, (3.11) becomes

ξ ¯ r s ( q ) = a r s q q 2 + ω 2 − a r s q q 2 + ω 2 × 1 + λ α q α + M 2 λ α q α − 1 + ( M 2 + 1 K ) q − 1 1 + λ α q α + ( M 2 + λ r s 2 β + 1 K ) q − 1 + M 2 λ α q α − 1

Denoting by

K ¯ ( q ) = q 1 + λ α q α + M 2 λ α q α − 1 + ( M 2 + 1 K ) q − 1 q 2 + ω 2 ,

we get following equation by taking the inverse Laplace transform of the above equation

k ( t ) = L − 1 { F ¯ ( q ) } = λ α Γ ( − α ) ∫ 0 t cos ( ω t ) + M 2 ω sin ( ω t ) ( t − τ ) α d τ + M 2 + 1 K ω sin ( ω t ) + cos ( ω t ) 0 < α < 1

The transformed velocity can be marked as

(3.12) ξ ¯ r s ( q ) = a r s q q 2 + ω 2 − a r s K ¯ ( q ) A ¯ r s ( q )

By implementing the inverse Laplace transform to the (3.12), we will obtain

(3.13) ξ r s ( t ) = a r s sin ( ω t ) − a r s ( k ( t ) ∗ a r s ( t ) ) .

By implementing the inverse Fourier transform to (3.13)

ξ ( x ̲ , y ̲ , t ) = cos ( ω t ) − 4 ∑ r , s = 1 ∞ a r s × sin ( α r x ̲ ) sin ( β s y ̲ ) ( k ( t ) ∗ a r s ( t ) ) .

simply, the above equation can be rewritten as

(3.14) ξ ( x ̲ , y ̲ , t ) = cos ( ω t ) − 16 ∑ r , s = 0 ∞ sin ( ( 2 r + 1 ) π x ̲ ) ( 2 r + 1 ) π × sin ( ( 2 s + 1 ) π y ̲ ) ( 2 s + 1 ) π ( k ( t ) ∗ a ( 2 r + 1 ) ( 2 s + 1 ) ( t ) ) .

We can obtain the associated expressions for the tangential stresses by using the same method of the above section:

T 1 ( x ̲ , y ̲ , t ) = − 16 ∑ r , s = 0 ∞ cos ( ( 2 r + 1 ) π x ̲ ) × sin ( ( 2 s + 1 ) π y ̲ ) ( 2 s + 1 ) π k ( t ) ∗ a ( 2 r + 1 ) ( 2 s + 1 ) ( t ) ) + 16 ∑ r , s = 0 ∞ cos ( ( 2 r + 1 ) π x ̲ ) × sin ( ( 2 s + 1 ) π y ̲ ) ( 2 s + 1 ) π k ( t ) ∗ h ( t ) ∗ a ( 2 r + 1 ) ( 2 s + 1 ) ( t ) .

4 Limiting cases

4.1 Classical Maxwell fluid

Considering α → 1 into (2.13), we can get similar solution [18] of velocity distribution and the associated tangential stresses of both the cases for unsteady flows of an ordinary Maxwell fluid via oscillatory rectangular duct,

ξ s ( x ̲ , y ̲ , t ) = sin ( ω t ) − 16 ∑ r , s = 0 ∞ ω sin ( ( 2 r + 1 ) π x ̲ ) ( 2 s + 1 ) π × sin ( ( 2 s + 1 ) π y ̲ ) ( 2 s + 1 ) π ( f ( t ) ∗ a ( 2 r + 1 ) ( 2 s + 1 ) ( t ) ) ,

ξ c ( x ̲ , y ̲ , t ) = cos ( ω t ) − 16 ∑ r , s = 0 ∞ sin ( ( 2 r + 1 ) π x ̲ ) ( 2 r + 1 ) π × sin ( ( 2 s + 1 ) π y ̲ ) ( 2 s + 1 ) π ( k ( t ) ∗ a ( 2 r + 1 ) ( 2 s + 1 ) ( t ) ) ,

and

T 1 s ( x ̲ , y ̲ , t ) = − 16 ∑ r , s =0 ∞ ω cos ((2 r + 1) π x ̲ ) × sin ((2 s + 1) π y ̲ ) (2 s + 1) π f ( t ) ∗ a (2 r + 1)(2 s + 1) ( t ) + 16 ∑ r , s =0 ∞ ω cos ((2 r + 1) π x ̲ ) × sin ((2 s + 1) π y ̲ ) (2 s + 1) π f ( t ) ∗ h ( t ) ∗ a (2 r + 1)(2 s + 1) ( t ) ) ,

T 1 c ( x , y , t ) = − 16 ∑ r , s = 0 ∞ cos ( ( 2 r + 1 ) π x ¯ ) × sin ( ( 2 s + 1 ) π y ̲ ) ( 2 s + 1 ) π k ( t ) ∗ a ( 2 r + 1 ) ( 2 s + 1 ) ( t ) + 16 ∑ r , s = 0 ∞ cos ( ( 2 r + 1 ) π x ̲ ) × sin ( ( 2 s + 1 ) π y ̲ ) ( 2 s + 1 ) π k ( t ) ∗ h ( t ) ∗ a ( 2 r + 1 ) ( 2 s + 1 ) ( t ) ) ,

where

a (2 r + 1)(2 s + 1) ( t ) = ∑ k =0 ∞ ∑ p =0 k ( − 1) k k ! ( M 2 λ ) p ( M 2 + λ m n 2 β + 1 k ) k − p p ! ( k − p ) ! λ k + 1 × G 1, p − k , k + 1 ( − λ − 1 , t ) , f ( t ) = λ − M 2 + 1 K ω 2 cos ( ω t ) + ( M 2 λ + 1) sin ( ω t ) ω + M 2 + 1 K ω 2 , k ( t ) = λ ( H ( t ) − ω sin ( ω t ) ) + ( M 2 λ + 1) cos ( ω t ) + M 2 + 1 K ω sin ( ω t ) and h ( t ) = L − 1 q q + λ − 1 = H ( t ) − 1 λ R 1,0 ( − λ − 1 , t )

4.2 Generalized Maxwell fluid without magnetic and porosity parameters

Considering M , K = 0 into (2.13), we can get similar solution [16] of velocity distribution and the associated tangential stresses of both the cases for unsteady flows of the generalized Maxwell fluid without magnetic and porosity parameters via oscillatory rectangular duct,

ξ s ( x ̲ , y ̲ , t ) = sin ( ω t ) − 16 ∑ r , s = 0 ∞ ω sin ( ( 2 r + 1 ) π x ̲ ) ( 2 s + 1 ) π × sin ( ( 2 s + 1 ) π y ̲ ) ( 2 s + 1 ) π sin ( ω t ) ∗ q ( 2 r + 1 ) ( 2 s + 1 ) ( t ) ,

ξ c ( x ̲ , y ̲ , t ) = cos ( ω t ) − 16 ∑ r , s = 0 ∞ sin ( ( 2 r + 1 ) π x ̲ ) ( 2 r + 1 ) π × sin ( ( 2 s + 1 ) π y ̲ ) ( 2 s + 1 ) π cos ( ω t ) ∗ q ( 2 r + 1 ) ( 2 s + 1 ) ( t ) ,

and

T 1 s ( x ̲ , y ̲ , t ) = − 16 ∑ r , s = 0 ∞ ω cos ( ( 2 r + 1 ) π x ̲ ) × sin ( ( 2 s + 1 ) π y ̲ ) ( 2 s + 1 ) π sin ( ω t ) ∗ q ( 2 r + 1 ) ( 2 s + 1 ) ( t ) + 16 ∑ r , s = 0 ∞ ω cos ( ( 2 r + 1 ) π x ̲ ) × sin ( ( 2 s + 1 ) π y ̲ ) ( 2 s + 1 ) π sin ( ω t ) ∗ h ( t ) ∗ q ( 2 r + 1 ) ( 2 s + 1 ) ( t ) ) ,

T 1 c ( x , y , t ) = − 16 ∑ r , s =0 ∞ cos ((2 r + 1) π x ¯ ) × sin ((2 s + 1) π y ̲ ) (2 s + 1) π cos ( ω t ) ∗ q (2 r + 1)(2 s + 1) ( t ) + 16 ∑ r , s =0 ∞ cos ((2 r + 1) π x ̲ ) × sin ((2 s + 1) π y ̲ ) (2 s + 1) π cos ( ω t ) ∗ h ( t ) ∗ q (2 r + 1)(2 s + 1) ( t ) ) ,

where

q ( 2 r + 1 ) ( 2 s + 1 ) ( t ) ) = ∑ k = 0 ∞ − λ r s β k ( G α , α − k − 1 , k + 1 ( − λ − α , t ) + λ − α G α , − k − 1 , k + 1 ( − λ − α , t ) ) .

5 Numerical results

The present section aims to show the impact of various physical parameters with respect to time on the flow of MHD generalized Maxwell fluid via porous rectangular duct.

Figure 1 represents the influence of fractional parameter α on the fluid motion with respect to time; from this figure, it is observed that velocity of the fluid increases (absolute values) as fractional derivative parameter approaches to 1 for both sine and cosine oscillation.

$Figure 1 The dimensionless velocity profile of sine and cosine oscillation at ω = π 4 \omega =\tfrac{\pi }{4} , λ = 2 \lambda =2 , K = 0.5 K=0.5 , M = 0.8 M=0.8 , γ = 0.54 \gamma =0.54 , x ̲ = 0.5 \underline{x}=0.5 , and y ̲ = 0.005 . \underline{y}=0.005.$

Figure 1

The dimensionless velocity profile of sine and cosine oscillation at ω = π 4 , λ = 2 , K = 0.5 , M = 0.8 , γ = 0.54 , x ̲ = 0.5 , and y ̲ = 0.005 .

Figure 2 shows the effects of parameter K on the fluid motion with respect to time, as expected fluid velocity increases as value of K increases.

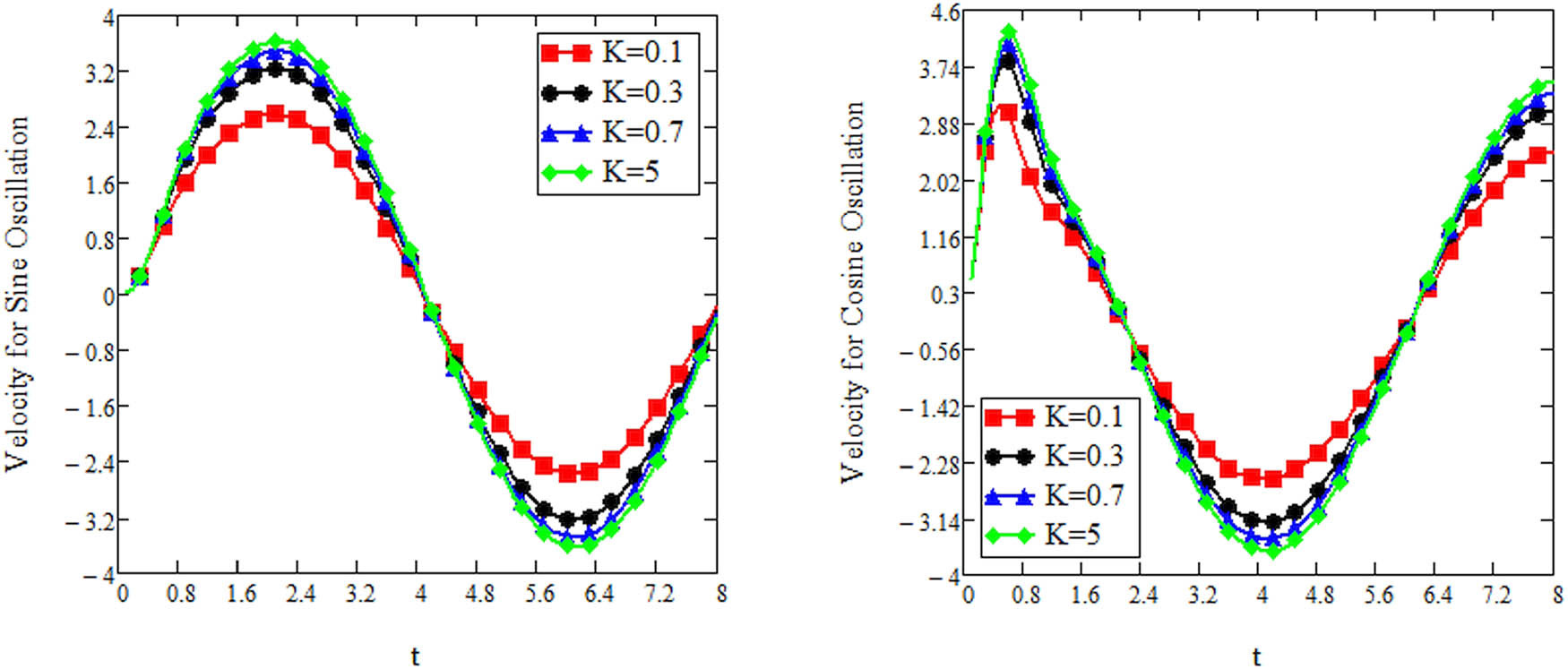
$Figure 2 The dimensionless velocity profile of sine and cosine oscillation at ω = π 4 \omega =\tfrac{\pi }{4} , λ = 2 \lambda =2 , α = 0.7 \alpha =0.7 , M = 0.8 M=0.8 , γ = 0.54 \gamma =0.54 , x ̲ = 0.5 \underline{x}=0.5 , and y ̲ = 0.005 . \underline{y}=0.005.$

Figure 2

The dimensionless velocity profile of sine and cosine oscillation at ω = π 4 , λ = 2 , α = 0.7 , M = 0.8 , γ = 0.54 , x ̲ = 0.5 , and y ̲ = 0.005 .

Figure 3 represents the effect of magnetic parameter M on fluid velocity. From Figure 4, it is clear that velocity of the fluid decreases with the strength of magnetic force.

$Figure 3 The dimensionless velocity profile of sine and cosine oscillation at ω = π 4 \omega =\tfrac{\pi }{4} , λ = 2 \lambda =2 , α = 0.7 \alpha =0.7 , K = 0.5 K=0.5 , γ = 0.54 \gamma =0.54 , x ̲ = 0.5 \underline{x}=0.5 , and y ̲ = 0.005 . \underline{y}=0.005.$

Figure 3

The dimensionless velocity profile of sine and cosine oscillation at ω = π 4 , λ = 2 , α = 0.7 , K = 0.5 , γ = 0.54 , x ̲ = 0.5 , and y ̲ = 0.005 .

$Figure 4 The dimensionless velocity profile of sine and cosine oscillation at ω = π 4 \omega =\tfrac{\pi }{4} , M = 0.8 M=0.8 , α = 0.9 \alpha =0.9 , K = 0.5 K=0.5 , γ = 0.54 \gamma =0.54 , x ̲ = 0.5 \underline{x}=0.5 , and y ̲ = 0.005 . \underline{y}=0.005.$

Figure 4

The dimensionless velocity profile of sine and cosine oscillation at ω = π 4 , M = 0.8 , α = 0.9 , K = 0.5 , γ = 0.54 , x ̲ = 0.5 , and y ̲ = 0.005 .

Figure 4 shows the influence of the relaxation parameter on the fluid motion. From this figure, it is observed that velocity of the fluid decreases for cosine oscillation, but increases for the sine oscillation.

Figure 5 shows the same behavior as that of fractional parameter α on the fluid motion when K , M = 0 .

$Figure 5 The dimensionless velocity profile of sine and cosine oscillation at ω = π 4 \omega =\tfrac{\pi }{4} , M = 0 M=0 , K = 0 K=0 , γ = 0.54 \gamma =0.54 , x ̲ = 0.5 \underline{x}=0.5 , and y ̲ = 0.005 . \underline{y}=0.005.$

Figure 5

The dimensionless velocity profile of sine and cosine oscillation at ω = π 4 , M = 0 , K = 0 , γ = 0.54 , x ̲ = 0.5 , and y ̲ = 0.005 .

In Figures 6 and 7, we show the effect of frequency parameter ω on the dimensionless fluid velocity and shear stress. From Figures 6 and 7, it is clear that the velocity of the fluid and shear stress decreases with the strength of frequency parameter.

$Figure 6 The dimensionless velocity profile of sine and cosine oscillation at λ = 2 \lambda =2 , M = 0.8 M=0.8 , K = 0 , 5 K=0,5 , γ = 0.54 \gamma =0.54 , x ̲ = 0.5 \underline{x}=0.5 , and y ̲ = 0.005 . \underline{y}=0.005.$

Figure 6

The dimensionless velocity profile of sine and cosine oscillation at λ = 2 , M = 0.8 , K = 0 , 5 , γ = 0.54 , x ̲ = 0.5 , and y ̲ = 0.005 .

$Figure 7 The dimensionless tangential stress profile of sine and cosine oscillation at ω = π 4 \omega =\tfrac{\pi }{4} , λ = 2 \lambda =2 , K = 0.5 K=0.5 , M = 0.8 M=0.8 , γ = 0.54 \gamma =0.54 , x ̲ = 0.5 \underline{x}=0.5 , and y ̲ = 0.005 . \underline{y}=0.005.$

Figure 7

The dimensionless tangential stress profile of sine and cosine oscillation at ω = π 4 , λ = 2 , K = 0.5 , M = 0.8 , γ = 0.54 , x ̲ = 0.5 , and y ̲ = 0.005 .

In Figure 8, the dimensionless shear stress represented for different values of fractional parameter α . The stress on the fluid increases for both sine and cosine oscillation as the values of fractional parameter α increase.

$Figure 8 The dimensionless tangential stress profile of sine and cosine oscillation at ω = π 4 \omega =\tfrac{\pi }{4} , λ = 2 \lambda =2 , α = 0.7 \alpha =0.7 , M = 0.8 M=0.8 , γ = 0.54 \gamma =0.54 , x ̲ = 0.5 \underline{x}=0.5 , and y ̲ = 0.005 . \underline{y}=0.005.$

Figure 8

The dimensionless tangential stress profile of sine and cosine oscillation at ω = π 4 , λ = 2 , α = 0.7 , M = 0.8 , γ = 0.54 , x ̲ = 0.5 , and y ̲ = 0.005 .

Figure 9 shows the effects of parameter K on the dimensionless shear stress, as expected fluid velocity increases with the increase in K.

$Figure 9 The dimensionless tangential stress profile of sine and cosine oscillation at ω = π 4 \omega =\tfrac{\pi }{4} , λ = 2 \lambda =2 , α = 0.7 \alpha =0.7 , K = 0.5 K=0.5 , γ = 0.54 \gamma =0.54 , x ̲ = 0.5 \underline{x}=0.5 , and y ̲ = 0.005 . \underline{y}=0.005.$

Figure 9

The dimensionless tangential stress profile of sine and cosine oscillation at ω = π 4 , λ = 2 , α = 0.7 , K = 0.5 , γ = 0.54 , x ̲ = 0.5 , and y ̲ = 0.005 .

In Figures 10 and 11, we show the effect of Magnetic parameter M and relaxation time on the dimensionless shear stress, both sine and cosine oscillation decrease as the Magnetic parameter M and relaxation parameter increase.

$Figure 10 The dimensionless tangential stress profile of sine and cosine oscillation at ω = π 4 \omega =\tfrac{\pi }{4} , M = 0.8 M=0.8 , α = 0.9 \alpha =0.9 , K = 0.5 K=0.5 , γ = 0.54 \gamma =0.54 , x ̲ = 0.5 \underline{x}=0.5 , and y ̲ = 0.005 . \underline{y}=0.005.$

Figure 10

The dimensionless tangential stress profile of sine and cosine oscillation at ω = π 4 , M = 0.8 , α = 0.9 , K = 0.5 , γ = 0.54 , x ̲ = 0.5 , and y ̲ = 0.005 .

$Figure 11 The dimensionless tangential stress profile of sine and cosine oscillation at ω = π 4 \omega =\tfrac{\pi }{4} , M = 0 M=0 , K = 0 K=0 , γ = 0.54 \gamma =0.54 , x ̲ = 0.5 \underline{x}=0.5 , and y ̲ = 0.005 . \underline{y}=0.005.$

Figure 11

The dimensionless tangential stress profile of sine and cosine oscillation at ω = π 4 , M = 0 , K = 0 , γ = 0.54 , x ̲ = 0.5 , and y ̲ = 0.005 .

In Figure 12, the effect of fractional parameter α is shown on dimensionless shear stress when K , M = 0 ; both sine and cosine oscillation increase for the increasing value of α .

$Figure 12 The dimensionless tangential stress profile of sine and cosine oscillation at λ =2 \lambda \mathrm{=2} , M = 0.8 M=0.8 , K = 0 , 5 K=0,5 , γ = 0.54 \gamma =0.54 , x ̲ = 0.5 \underline{x}=0.5 , and y ̲ = 0.005 . \underline{y}=0.005.$

Figure 12

The dimensionless tangential stress profile of sine and cosine oscillation at λ =2 , M = 0.8 , K = 0 , 5 , γ = 0.54 , x ̲ = 0.5 , and y ̲ = 0.005 .

6 Conclusion

In this article, the incompressible, unsteady flow mixed initial-boundary value problem for incompressible fractional Maxwell fluid model through oscillatory porous rectangular duct is studied. The solution is derived by using the techniques of Laplace and double finite sine Fourier transforms for the cosine and sine oscillation of the rectangular duct. The solutions are presented in terms of series form and the generalized G functions. The similar solutions of classical Maxwell fluid and generalized Maxwell fluid without magnetic and porosity parameters are recovered as a limiting case of the general solutions. Finally, the graphical influence of fractional parameters, magnetic parameter, porosity parameter, and relaxation time on the fluid motion is discussed.

Conflict of interest: The authors hereby declare that there is no conflict of interests regarding the publication of this paper.

References

[1] Rahman M. Mechanics of real fluids. UK: WIT Press; 2011.Suche in Google Scholar

[2] Chhabra RP, Richardson JF. Non-Newtonian flow and applied rheology: Engineering applications. Oxford, United Kingdom: BH Publishers; 2008.Suche in Google Scholar

[3] Caputo M, Fabrizio M, New A. Definition of fractional derivative without singular kernel. Prog Fract Differ Appl. 2015;1(2):73–85.Suche in Google Scholar

[4] Ahmad I, Ahmad H, Abouelregal AE, Thounthong P, Abdel-Atay M. Numerical study of integer-order hyperbolic telegraph model arising in physical and related sciences. Eur Phys J Plus. 2020;135:759. 10.1140/epjp/s13360-020-00784-z.Suche in Google Scholar

[5] Atangana A, Baleanu D. New fractional derivatives with nonlocal and non-singular kernel: Theory and application to heat transfermodel. Therm Sci. 2016;20:763–9. 10.2298/tsci160111018a.Suche in Google Scholar

[6] Ahmad H, Akgül A, Khan TA, Stanimirovic PS, Chu Y-M. New perspective on the conventional solutions of the nonlinear time-fractional partial differential equations. Complexity. 2020:1–10. 10.1155/2020/8829017.Suche in Google Scholar

[7] Lorenzo CF, Hartely TT. Generalized functions for fractional calculus. NASA/TP-1999-209424/REV1/; 1999.Suche in Google Scholar

[8] Podlubny I. Fractional differential equations. San Diego: Academic Press; 1999.Suche in Google Scholar

[9] Inc M, Khan MN, Ahmad I, Yao S-W, Ahmad H, Thounthong P. Analysing time-fractional exotic options via efficient local meshless method. Results Phys. 2020;19:103385. 10.1016/j.rinp.2020.103385.Suche in Google Scholar

[10] Hilfer R. Applications of fractional calculus in physics. Singapore: World Scientific Press; 2002.Suche in Google Scholar

[11] Abdulhameed M, Vieru D, Roslan R. Magnetohydrodynamic electroosmotic flow of Maxwell fluids with Caputo–Fabrizio derivatives through circular tubes. Comput Math Appl. 2017;74:2503–19.10.1016/j.camwa.2017.07.040Suche in Google Scholar

[12] Aman S, Salleh M, Ismail Z, Khan I. Exact solution for heat transfer free convection fow of Maxwell nanofuids with graphene nanoparticles. J Phys Conf Ser. 2017;890:012004.10.1088/1742-6596/890/1/012004Suche in Google Scholar

[13] Bai Y, Jiang Y, Liu F, Zhang Y. Numerical analysis of fractional MHD Maxwell fuid with the efects of convection heat transfer condition and viscous dissipation. AIP Adv. 2017;7:125309.10.1063/1.5011789Suche in Google Scholar

[14] Abro K, Khan I, Tassaddiq A. A, Application of Atangana–Baleanu fractional derivative to convection fow of MHD Maxwell fuid in a porous medium over a vertical plate. Math Model Nat Phenom. 2018;13:1.10.1051/mmnp/2018007Suche in Google Scholar

[15] Imran M, Riaz M, Shah N, Zafar A. Boundary layer fow of MHD generalized Maxwell fuid over an exponentially accelerated infnite vertical surface with slip and Newtonian heating at the boundary. Results Phys. 2018;8:1061–7.10.1016/j.rinp.2018.01.036Suche in Google Scholar

[16] Nazar M, Zulqarnain M, Akram MS, Asif M. Flow through an oscillating rectangular duct for generalized maxwell fluid with fractional derivatives. Commun Nonlinear Sci Numer Simulat. 2012;17:3219–34.10.1016/j.cnsns.2011.10.002Suche in Google Scholar

[17] Nazar M, Shahid F, Akram S, Sultan Q. Flow on oscillating rectangular duct for Maxwell fluid. Appl Math Mech. 2012;33:717–30.10.1007/s10483-012-1582-6Suche in Google Scholar

[18] Sultan Q, Nazar M, Akhtar W, Ali U. Unsteady flow of a Maxwell fluid in porous rectangular duct. Sci Int. 2013;25(2):181–94.Suche in Google Scholar

[19] Abro K, Gomez-Aguilar JF, Kolebaje O, Yildirim A. Chaos in a calcium oscillation model via Atangana–Baleanu operator with strong memory. Eur Phys J Plus. 2019;134:140. 10.1140/epjp/i2019-12550-1.Suche in Google Scholar

[20] Khan A, ABdeljawad T, Gomez-Aguilar JF, Khan H. Dynamical study of fractional order mutualism parasitism food web module. Chaos, Solitons Fractals. 2020;134:109685. 10.1016/j.chaos.2020.109685.Suche in Google Scholar

[21] Abouelregal AE, Yao S-W, Ahmad H. Analysis of a functionally graded thermopiezoelectric finite rod excited by a moving heat source. Results Phys. 2020;19:103389. 10.1016/j.rinp.2020.103389.Suche in Google Scholar

[22] Abro KA, Abro IA, Yildirim A. A comparative analysis of sulfate ion concentration via modern fractional derivatives: An industrial application to cooling system of power plant. Physica. 2020;541(C). 10.1016/j.physa.2019.123306.Suche in Google Scholar

[23] Hamid M, Usman M, Zubair T, Haq R, Wang W. Innovative operational matrices based computational scheme for fractional diffusion problems with the Riesz derivative. Eur Phys J Plus. 2019;134:484. 10.1140/epjp/i2019-12871-y.Suche in Google Scholar

[24] Raza N, Asad M. A comparative study of heat transfer analysis of fractional Maxwell fluid by using Caputo and Caputo–Fabrizio derivatives. Can J Phys. 2020;98:89–101. 10.1139/cjp-2018-0602.Suche in Google Scholar

[25] Riaz MB, Atangana A, Iftikhar N. Heat and mass transfer in Maxwell fluid in view of local and non-local differential operators. J Therm Anal Calorim. 2020. 10.1007/s10973-020-09383-7.Suche in Google Scholar

[26] Jamil M, Ahmed A, Khan NA. Some exact traveling wave solutions of MHD Maxwell fluid in porous medium. Int J Appl Comput Math. 2020;6:69. 10.1007/s40819-020-00815-4.Suche in Google Scholar

[27] Singh R, Bishnoi J, Tyagi VK. Triple diffusive convection with Soret–Dufour effects in a Maxwell nanofluid saturated in a Darcy porous medium. SN Appl Sci. 2020;2:704. 10.1007/s42452-020-2462-4.Suche in Google Scholar

[28] Zhang M, Shen M, Liu F, Zhang H. A new time and spatial fractional heat conduction model for Maxwell nanofluid in porous medium. Compu Math Appl. 2019;78(5):1621–36.10.1016/j.camwa.2019.01.006Suche in Google Scholar

[29] Kausar MS, Hussanan A, Mamat M, Ahmad B. Boundary layer flow through Darcy–Brinkman porous medium in the presence of slip effects and porous dissipation. Symmetry. 2019;11:659.10.3390/sym11050659Suche in Google Scholar

[30] Debnath L, Bhatta D. Integral transforms and their applications. Boca Raton, London, New York: Chapman and Hall, CRC; 2007.Suche in Google Scholar

[31] Fetecau C, Fetecau C, Kamran M, D, Vieru. Exact solutions for the flow of a generalized Oldroyd-B fluid induced by a constantly accelerating plate between two side walls perpendicular to the plate. J Non-Newtonian Fluid Mech. 2009;156:189–201.10.1016/j.jnnfm.2008.06.005Suche in Google Scholar

[32] Kumar S, Kumar R, Cattani C, Samet B. Chaotic behaviour of fractional predator-prey dynamical system. Chaos, Solitons Fractals. 2020;135:109811.10.1016/j.chaos.2020.109811Suche in Google Scholar

[33] Djilali S. Herd behavior in a predator-prey model with spatial diffusion: Bifurcation analysis and Turing instability. J Appl Math Comput. 2018;58:125–49.10.1007/s12190-017-1137-9Suche in Google Scholar

[34] Djilali S. Pattern formation of a diffusive predator-prey model with herd behavior and nonlocal prey competition. Math Methods Appl Sci. 2020;43(5):2233–50.10.1002/mma.6036Suche in Google Scholar

[35] Ahmad H, Khan TA, Stanimirovic PS, Chu Y-M, Ahmad I. Modified variational iteration algorithm-II: Convergence and applications to diffusion models. Complexity. 2020;20:8841718. 10.1155/2020/8841718.Suche in Google Scholar

[36] Fethi S, Lakmeche A, Djilali S. Spatiotemporal patterns in a diffusive predator-prey model with protection zone and predator harvesting. Chaos, Solitons Fractals. 2020;140:110180.10.1016/j.chaos.2020.110180Suche in Google Scholar

[37] Souna F, Lakmeche A, Djilali S. The effect of the defensive strategy taken by the prey on predator-prey interaction. J Appl Math Comput. 2020;64:665–90.10.1007/s12190-020-01373-0Suche in Google Scholar

[38] Djilali S, Ghanbari B. Mathematical and numerical analysis of a three-species predator-prey model with herd behavior and time fractional-order derivative. Math Methods Appl Sci. 2020;43(4):1736–52.10.1002/mma.5999Suche in Google Scholar

[39] Ahmad H, Seadawy AR, Khan TA. Numerical solution of Korteweg–de Vries–Burgers equation by the modified variational iteration algorithm-II arising in shallow water waves. Phys Scr. 2020;95(4):045210.10.1088/1402-4896/ab6070Suche in Google Scholar

[40] Yokus A, Durur H, Ahmad H, Yao S-W. Hyperbolic type solutions for the couple Boiti–Leon–Pempinelli system. F U Math Inf. 2020;35(2):523–31.10.22190/FUMI2002523YSuche in Google Scholar

[41] Ahmad I, Khan MN, Inc M, Ahmad H, Nisar KS. Numerical simulation of simulate an anomalous solute transport model via local meshless method. Alexandria, Eng J. 2020;59(4):2827–38.10.1016/j.aej.2020.06.029Suche in Google Scholar

[42] Djilali S, Touaoula TM, Miri SE. A heroin epidemic model: Very general non linear incidence, treat-age, and global stability. Acta Appl Math. 2017;152:171–94.10.1007/s10440-017-0117-2Suche in Google Scholar

[43] Ahmad H, Ahmad I, Stanimirovic PS. Modified variational iteration technique for the numerical solution of fifth order KdV type equations. J Appl Comput Mech. 2020;6(SI):1220–7.Suche in Google Scholar

[44] Kumar S, Kumar A, Samet B, Gomez-Aguilar JF, Osman MS. A chaos study of tumor and effector cells in fractional tumor-immune model for cancer treatment. Chaos, Solitons Fractals. 2020;141:110321.10.1016/j.chaos.2020.110321Suche in Google Scholar

[45] Goufo EFD, Kumar S, Mugisha SB. Similarities in a fifth-order evolution equation with and with no singular kernel. Chaos, Solitons Fractals. 2020;130:109467.10.1016/j.chaos.2019.109467Suche in Google Scholar

[46] Ahmad H, Khan TA, Yao SW. An efficient approach for the numerical solution of fifth-order KdV equations. Open Math. 2020;18(1):738–48.10.1515/math-2020-0036Suche in Google Scholar

[47] Ahmad H, Khan TA, Ahmad I, Stanimirovic PS, Chu Y-M. A new analyzing technique for nonlinear time fractional Cauchy reaction-diffusion model equations. Results Phys. 2020;19:103462. 10.1016/j.rinp.2020.103462.Suche in Google Scholar

[48] Kumar S, Ghosh S, Samet B, Goufo EFD. An analysis for heat equations arises in diffusion process using new Yang–Abdel–Aty–Cattani fractional operator. Math Methods Appl Sci. 2020;43(9):6062–80.10.1002/mma.6347Suche in Google Scholar

[49] Kumar S, Kumar R, Agarwal RP, Samet B. A study of fractional Lotka–Volterra population model using Haar wavelet and Adams–Bashforth–Moulton methods. Math Methods Appl Sci. 2020;43(8):5564–78.10.1002/mma.6297Suche in Google Scholar

[50] Bazighifan O, Ahmad H, Yao S-W. New oscillation criteria for advanced differential equations of fourth order. Mathematics. 2020;8(5):728.10.3390/math8050728Suche in Google Scholar

[51] Khan MN, Ahmad I, Ahmad H. A radial basis function collocation method for space-dependent inverse heat problems. J Appl Comput Mech. 2020;6(SI):1187–99.Suche in Google Scholar

[52] Kumar S, Rashidi MM. New analytical method for gas dynamics equation arising in shock fronts. Comp Phys Commun. 2014;185(7):1947–54.10.1016/j.cpc.2014.03.025Suche in Google Scholar

[53] Kumar S, Kumar A, Baleanu D. Two analytical methods for time-fractional nonlinear coupled Boussinesq–Burger’s equations arise in propagation of shallow water waves. Nonlinear Dyn. 2016;85:699–715.10.1007/s11071-016-2716-2Suche in Google Scholar

[54] Ahmad H, Seadawy AR, Khan TA, Thounthong P. Analytic approximate solutions for some nonlinear Parabolic dynamical wave equations. J Taibah Univ Sci. 2020;14(1):346–58.10.1080/16583655.2020.1741943Suche in Google Scholar

[55] Ahmad I, Ahmad H, Thounthong P, Chu Y-M, Cesarano C. Solution of multi-term time-fractional PDE models arising in mathematical biology and physics by local meshless method. Symmetry. 2020;12(7):1195.10.3390/sym12071195Suche in Google Scholar

[56] Momani S. Analytic solutions of a 3-D propagated wave dynamical equation formulated by conformable calculus. Prog Fract Differ Appl. 2020;1(1):1–10.Suche in Google Scholar

Received: 2020-09-08

Revised: 2020-10-22

Accepted: 2020-11-01

Published Online: 2020-12-17

This work is licensed under the Creative Commons Attribution 4.0 International License.

Artikel in diesem Heft

https://doi.org/10.1515/phys-2020-0209

Schlagwörter für diesen Artikel

fractional Maxwell fluid; exact solutions; non-Newtonian fluid; oscillatory rectangular duct; velocity field

Creative Commons

BY 4.0