Dynamic triaxial constitutive model for rock subjected to initial stress

Junzhe Li; Guang Zhang; Mingze Liu; Shaohua Hu; Xinlong Zhou

doi:10.1515/phys-2020-0014

Article Open Access

Dynamic triaxial constitutive model for rock subjected to initial stress

Junzhe Li , Guang Zhang , Mingze Liu , Shaohua Hu and Xinlong Zhou

Published/Copyright: May 24, 2020

Published by

Become an author with De Gruyter Brill

Submit Manuscript Author Information Explore this Subject

From the journal Open Physics Volume 18 Issue 1

Abstract

Building on the existing model, an improved constitutive model for rock is proposed and extended in three dimensions. The model can avoid the defect of non-zero dynamic stress at the beginning of impact loading, and the number of parameters is in a suitable range. The three-dimensional expansion method of the component combination model is similar to that of the Hooke spring, which is easy to operate and understand. For the determination of model parameters, the shared parameter estimation method based on the Levenberg–Marquardt and the Universal Global Optimization algorithm is used, which can be well applied to models with parameters that do not change with confinement and strain rates. According to the established dynamic constitutive equation, the stress–strain curve of rock under the coupling action of the initial hydrostatic pressure load and constant strain-rate impact load can be estimated theoretically. By comparing the theoretical curve with the test data, it is shown that the dynamic constitutive model is suitable for the rock under the initial pressure and impact load.

Keywords: rock dynamics; initial stress; axial impact load; component combination; three-dimensional constitutive model

1 Introduction

With the massive development of deep earth resources and the wide construction of underground space projects, more and more attention has been paid to study the dynamic constitutive model of deep rock. The fundamental difference between rock statics and dynamics is that the strain rate is in different orders of magnitude, and the strain rate effects that are not negligible at medium to high strain rates will result [1]. Under the dynamic loading such as hard shock, blasting and detonation [2], the stress generated inside rock can be regarded as the summation of static stress and overstress, and the overstress reflects the strain rate effect [3,4]. To simulate the mechanical behavior of rock at medium to high strain rates, many researchers used the mechanical response of the parallel combination of a damaged Hooke spring and a Newton dashpot to simulate dynamic stress [5,6,7,8,9,10,11]. For example, Christensen [5] established a time-dependent damage model to describe the dynamic mechanical properties of rock by introducing damage to modify the Hooke spring in the Kelvin–Voigt model. Shan et al. [6] proposed a time-dependent damage model with statistical damage characteristic for rock under uniaxial impact loading by considering the rock specimen as a parallel combination of the damaged Hooke spring and Newton dashpot. Cao et al. [7] established a dynamic triaxial damage constitutive model of rock based on the Kelvin–Voigt model and Weibull distribution, which consists of the Newton dashpot simulating dynamic stress component and the Hooke spring with statistical damage characteristics simulating the static stress component. Liu et al. [8] performed a series of dynamic triaxial compression tests on amphibolite within a strain rate range of 50–170 s⁻¹ and a confining pressure range of 0–6 MPa, and the aforementioned test results are used to verify the dynamic damage constitutive model of rock established by combining the statistical damage model and the Kelvin–Voigt model. Li et al. [9] proposed a dynamic damage constitutive model based on the Kelvin–Voigt model and Weibull distribution, which was used to describe the mechanical properties and stress–strain curves of concrete under different uniaxial impact loading. Liu et al. [10] proposed a dynamic damage constitutive model based on the Kelvin–Voigt model and Weibull distribution, which was used to describe the dynamic behavior of shale under uniaxial impact loading. In addition, the validity and applicability of the dynamic damage constitutive model based on the Kelvin–Voigt model and Weibull distribution to granite subjected to uniaxial impact load were verified by Wang et al. [11]. These studies show that the damage constitutive model based on the Kelvin–Voigt model can not only describe the dynamic characteristics of rock but also characterize its damage characteristics. However, this model has an obvious drawback that the stress and strain cannot be the same as zero, which is inconsistent with the basic understanding obtained from the mechanical test.

In order to obtain a more reasonable dynamic constitutive model, some researchers had conducted valuable exploration. Li et al. [12,13,14] replaced two Hooke springs in the three-parameter generalized Kelvin–Voigt model (i.e., the Poynting–Thomson model) with two damage bodies, respectively, and established the constitutive model rock subjected to one- or three-dimensional static load under the medium strain rate. The new model obtained by introducing the damage to modify the three-parameter generalized Kelvin–Voigt model can avoid the defect that σ ₁ and ε ₁ cannot be the same as zero. However, the static stress (or static elastic modulus) and the dynamic stress component (or dynamic elastic modulus) in this model cannot be decoupled. Furthermore, it becomes difficult to implement different definitions for damage of different elastic moduli. Wang et al. [15] presented a nonlinear viscoelastic constitutive model (i.e., the Zhu-Wang-Tang (ZWT) model) consisting of a nonlinear spring, a low-frequency Maxwell element and a high-frequency Maxwell element. The low-frequency Maxwell element and the high-frequency Maxwell element were used to describe the viscoelastic response at the low strain rate and the viscoelastic response at the high strain rate, respectively. Dar et al. [16] developed the ZWT model’s incremental equation for triaxial loading based on the Kirchhoff stress tensor and the Green strain tensor. The ZWT model can also avoid the defects in the literature [5,6,7,8,9,10,11]; however, the model cannot reflect the physical fact of rock damage characteristics, and the physical meaning of the nonlinear spring parameters in the model is not clear. In order to solve the aforementioned problems, many scholars [6,17–19] had improved the ZWT model. Ma et al. [17] established a constitutive model describing frozen soil by introducing damage to modify the ZWT model and fitted model parameters. Xie et al. [18] proposed the five-parameter generalized Maxwell model (i.e., the result of replacing the nonlinear spring of the ZWT model with a Hooke spring) to describe the isotropic viscoelasticity of rock-like materials and established a model describing the stress–strain behavior of the soil matrix under uniaxial impact loading by introducing damage to modify the five-parameter generalized Maxwell model. Theoretically, the elastic element may be damaged during deformation, but no damage characteristics appear on the dashpot element [6,19,20]. Therefore, it is unreasonable to introduce damage to correct the entire model. To solve this shortcoming, Xie et al. [19,20] replaced three elastic elements in the ZWT model with three Hooke springs that may be damaged and established a damage-type viscoelastic dynamic constitutive model describing the stress–strain behavior under uniaxial impact loading. However, in the model proposed by Xie et al. [19,20], it is unreasonable to assume that the ratio of the cumulative strain of the Hooke spring that may be damaged to the cumulative strain of the Newton dashpot is constant in the viscoelastic-damage element.

In this study, the following work was carried out. First, the dynamic constitutive model of rock under impact loading is obtained by simplifying the model proposed by Xie et al. [19,20] (i.e., removing the Newton dashpot in the low-frequency viscoelastic-damage element). The simplified model can be considered as a modified three-parameter generalized Maxwell model (i.e., the Zener model) in which two Hooke springs are replaced by different damage bodies. Second, the equivalent stress based on the Mohr–Coulomb criterion in the effective configuration and considering threshold effects is used to measure the damage instead of strain. Finally, a three-dimensional form of the new model under constant strain rate impact loading is developed and verified by dynamic triaxial compression tests. There is a satisfactory agreement between theoretic and experimental results. The model established in this article can provide reference and guidance for the study on the dynamic characteristics of deep rock.

2 Establishment of triaxial dynamic constitutive model

2.1 Model proposed by Xie et al. and its improvement

Figure 1 shows the viscoelastic damage constitutive model proposed by Xie et al. [19,20] to describe the dynamic response of rock. The model consists of one elastic-damage element and two viscoelastic-damage elements in parallel, as expressed below [19]:

(1) { σ = ( 1 − D 0 ) E 0 ε + η 1 ε ̇ ( 1 − exp ( − ( 1 − D 1 ) E 1 ε η 1 ε ̇ ) ) + η 2 ε ̇ ( 1 − exp ( − ( 1 − D 2 ) E 2 ε η 2 ε ̇ ) ) D 0 = 1 − exp ( − ( ε F 0 ) m 0 ) D 1 = 1 − exp ( − ( ε c 1 F 1 ) m 1 ) D 2 = 1 − exp ( − ( ε c 2 F 2 ) m 2 ) ,

where (1 − D ₀)E ₀ ε is the function of strain ε which describes the elastic-damage response (i.e., static response) of rock; E ₀ represents the elastic constant; E 1 ε ̇ θ 1 ( 1 − exp ( − ε ( 1 − D 1 ) / ( ε ̇ θ 1 ) ) ) is the function of strain ε and strain rate ε ̇ , which describes the viscoelastic-damage response of rock under low strain rates (i.e., low-frequency dynamic response); E ₁ and θ ₁ are the elastic constant and relaxation time under low strain rate states; E 2 ε ̇ θ 2 ( 1 − exp ( − ε ( 1 − D 2 ) / ( ε ̇ θ 2 ) ) ) is the function associated with strain ε and strain rate ε ̇ , which describes the viscoelastic-damage response of rock under high strain rates (i.e., high-frequency dynamic response); E ₁ and θ ₁ are the elastic constant and relaxation time under high strain rate states; θ ₁ = η ₁/E ₁ and θ ₂ = η ₂/E ₂, η ₁ and η ₂ are the coefficient of Newton viscosity of the low-frequency viscoelastic-damage element and the high-frequency viscoelastic-damage element, respectively; D ₀, D ₁ and D ₂ are damage variables of the elastic modules E ₀, E ₁ and E ₂, respectively; ε/c ₁ and ε/c ₂ are cumulative strain of the elastic-damage part of the low-frequency viscoelastic-damage element and cumulative strain of the elastic-damage part of the high-frequency viscoelastic-damage element. As the strain accumulates, c ₁ and c ₂ are commonly variable and difficult to determine. However, c ₁ and c ₂ are assumed to be constant by Xie et al. [19,20], which is unreasonable. Obviously, the stresses on the elements in the series are equal. In order to solve the aforementioned problem, effective stress is used to measure the damage in this study.

Figure 1

Viscoelastic-damage constitutive model proposed by Xie et al.

Impact load is a unique type of dynamic load, and its loading time is in the range of 1–100 µs [17]. However, the relaxation time of the low-frequency viscoelastic-damage element varies from 10 to 100 s [17]. There is not enough time for the low-frequency viscoelastic-damage element to relax under impact loading. Therefore, under impact loading, the model proposed by Xie et al. [19,20] can be simplified. The three-dimensional generalization of the simplified model is shown in Figure 2. In the three-dimensional model, strain is no longer a measure of damage. The new damage metric is established based on the Mohr–Coulomb criterion by considering the effect of the threshold.

Figure 2

Improved viscoelastic-damage constitutive model.

2.2 Derivation of constitutive equations

2.2.1 Basic assumptions

The strain rate of impact loading is constant.
Elasticity is simulated with the Hooke springs and it obeys Hooke’s law before damage.
Viscosity is simulated by the Newton dashpot, and the Newton dashpot has no damage characteristic. The Newton dashpot obeys Newton’s law of viscous flow.
Macroscopically, the viscoelasticity of rock is isotropic. In addition, damage efficiency is also isotropic.
There are a lot of micro-defects such as micro-cracks and micro-cavities inside rock, and the distribution direction is uniform [21,22]. Rock can be regarded as a combination of micro-elements, each of which has different strength due to different micro-defects. The strength of the micro-elements inside rock obeys the Weibull distribution law.

2.2.2 Constitutive equation

The model shown in Figure 2 is composed of a quasi-static response element and a dynamic response element in parallel. The quasi-static response element is a damaged Hooke spring, and the dynamic response element is a damaged Maxwell element. The damaged Hooke spring and the damaged Maxwell body are used to simulate the relationship between strain and the quasi-static component of the apparent stress, the relationship between the strain and dynamic component of the apparent stress in the deformation process of rock under impact loading, respectively. The stress relationship between the model in this study and its constituent elements is characterized by the following expression:

(2) σ i = σ i s + σ i d ,

where σ _i represents the apparent stress; σ i s is the stress of the quasi-static response element; σ i d represents the stress of the dynamic response element; and i = 1, 2, 3, i is the three principal directions. The aforementioned equation characterizes the three-dimensional relationship between the apparent stress and strain of rock under impact loading.

For rocks in compression, as shown in Figure 3, A = A ₁ + A ₂, where A is the initial cross-sectional area, A ₁ is the cross-sectional area with the undamaged configuration and A ₂ is the cross-sectional area with the damaged configuration. The damage variable D i s is characterized by the following expression:

(3) D i s = A 2 A 1 + A 2 .

Figure 3

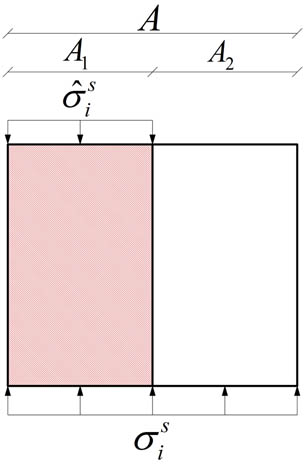
Analysis of microcosmic stress for rock.

The strain equivalent hypothesis [23,24] was presented by Lemaitre in 1971, in which the concept of effective stress was introduced. It was considered that the rock subjected to quasi-static loading consists of two parts, the undamaged and the damage. The former is incapable of carrying the load, and the load on the rock is entirely borne by the later. The relationship between the effective stress and the apparent stress under quasi-static loading can be expressed as follows:

(4) σ i s = ( 1 − D i s ) σ ˆ i s ,

where σ ˆ i s and σ i s represent the effective stress (or true stress, Kirchhoff stress) and the apparent stress (or nominal stress, Cauchy stress) under quasi-static loading, respectively. D i s denotes the damage of elastic modulus under quasi-static loading, which varies from 0 to 1 and corresponds to the undamaged or completely damaged state of rock, respectively. The dynamic response element is not valid under quasi-static loading. Therefore, the relationship between the effective stress and the apparent stress of rock under quasi-static loading denotes the relationship between the effective stress and the apparent stress of the quasi-static response element under impact loading.

According to the strain equivalent hypothesis, it can be concluded that the constitutive relation after damage is in the same form as the constitutive relation before damage, and the former can be obtained by replacing the stress in the later with effective stress. If the constitutive relation of rock before damage is subject to the generalized Hooke’s law, the relationship between the effective stress and strain of the quasi-static response element can be expressed as:

(5) σ ˆ i s = E s 1 + ν ε i + E s ν ( 1 − 2 ν ) ( 1 + ν ) ε V ,

where ε _i is the strain in the principal direction; ε _V = ε ₁ + ε ₂ + ε ₃, ε _V is the volumetric strain; E ^s is the Young modulus of the quasi-static response element; and ν is the Poisson ratio of rock, which is equal to the Poisson ratio of the quasi-static response element.

By substituting equation (5) into equation (4), the constitutive relation of the quasi-static response element can be obtained [25] as follows:

(6) σ i s = ( 1 − D i s ) E s ( ε i 1 + ν + ν ε V ( 1 − 2 ν ) ( 1 + ν ) ) .

If D i s = D j s = D k s = D m s (i.e., isotropic damage), the aforementioned equation can be transformed into:

(7) σ i s = ( 1 − D m s ) E s ε i + ν ( σ j s + σ k s ) .

Equations (6) and (7), respectively, characterize the relationship between the stress and strain of the quasi-static element under impact loading in different forms, i.e., the response of the quasi-static component of the apparent stress to force under impact loading.

The dashpot cannot be damaged, so the Maxwell body with damage is a series combination of damaged body and Newton dashpot, as shown in Figure 4. The load on the damaged body is fully borne by the undamaged part, and the undamaged part is subject to Hooke’s law. The Newton dashpot obeys Newton’s law of viscous flow. It can be seen from equations (5) and (6) that if the strain equivalent hypothesis is adopted, it is determined that the elastic modulus of rock during the loading process is variable and the Poisson ratio is a constant [26]. Therefore, the stress–strain relationship in the damage state can be obtained by replacing the elastic modulus of the stress–strain relationship in the undamaged state with the residual elastic modulus. Based on the above understanding, the relationship between the dynamic component of the apparent stress and the strain of the Maxwell body with damage can be expressed as:

(8) σ ̇ d ( 1 − D d ) E d + σ d η = ε ̇ ,

where the superscript “ ” denotes the time derivative; σ ^d, σ ̇ d , ε and ε ̇ are the stress, stress rate, strain and strain rate of the Maxwell body with damage; E ^d is the increment of elastic modulus caused by rate effect, which is equal to the difference between the elastic modulus under impact loading and the Young modulus under quasi-static loading; D ^d is a variable describing the damage of E ^d.

Figure 4

The Maxwell body with damage.

Under constant strain rate (i.e., ε ̇ = const ) loading, the Laplace transformation is performed on both sides of equation (8). Then, the following equation can be obtained:

(9) s L ( σ d ) − σ d | t = 0 ( 1 − D d ) E d + L ( σ d ) η = ε ̇ s ,

where L(·) represents the result of the Laplace transformation; s is equal to 1 / ∫ 0 + ∞ e − s t d t ; and t represents the loading time (or duration) of the impact load.

The initial condition for the Maxwell body with damage before loading includes σ ^d|_t=0 = 0. Substituting it into equation (9), the following equation can be obtained:

(10) L ( σ d ) = η ε ̇ ( 1 − D d ) E d / η s ( s + ( 1 − D d ) E d / η ) .

The inverse Laplace transformation is performed on both sides of equation (10), and the following equation can be obtained:

(11) σ d = η ( 1 − exp ( − ( 1 − D d ) E d t η ) ) ε ̇ ,

where t is equal to ε / ε ̇ under initial strain zero and constant strain rate loading.

The dynamic response element in this study is represented by the three-dimensional form of the Maxwell body with damage. It is assumed that two elements in the body have the characteristics of Poisson’s effect, and their Poisson ratio is equal to the value of the quasi-static response element. Equation (11) characterizes the relationship between strain and apparent stress of the Maxwell body with damage. Drawing on the idea that the constitutive relation of the Hooke spring is extended from one dimension to three dimensions, the three-dimensional constitutive relation of the Maxwell body with damage can be expressed as follows:

(12) σ i d = η ( 1 − exp ( − ( 1 − D i d ) E d t η ) ) × ε ̇ i 1 + ν + ν ε ̇ V ( 1 + ν ) ( 1 − 2 ν ) .

Similarly, if D i d = D j d = D k d = D m d (i.e., isotropic damage), the aforementioned equation can be transformed into:

(13) σ i d = η ε ̇ i ( 1 − exp ( − ( 1 − D m d ) E d t η ) ) + ν ( σ j d + σ k d ) ,

where ε ̇ i is the strain rate in the principal direction; ε ̇ V = ε ̇ 1 + ε ̇ 2 + ε ̇ 3 , ε ̇ V is the volumetric strain rate; ν is the Poisson ratio of rock, which is equal to the Poisson ratio of the dynamic response element.

Combining equations (2) and (5) with equation (12), the following equation can be obtained:

(14) σ i = 1 1 + ν ( ( 1 − D m s ) E s ε i + η ε ̇ i ( 1 − exp ( − ( 1 − D m d ) E d t η ) ) ) + ν ( 1 − 2 ν ) ( 1 + ν ) ( ( 1 − D m s ) E s ε V + η ε ̇ V ( 1 − exp ( − ( 1 − D m d ) E d t η ) ) ) .

Combining equations (2) and (6) with equation (13), the following equation can be obtained:

(15) σ i = ( 1 − D m s ) E s ε i + η ε ̇ i ( 1 − exp ( − ( 1 − D m d ) E d t η ) ) + ν ( σ j s + σ j d ) + ν ( σ k s + σ k d ) .

According to equation (2), the following two equations are established:

(16) σ j = σ j s + σ j d

(17) σ k = σ k s + σ k d .

Using equations (16) and (17), equation (15) can be transformed into:

(18) σ i = ( 1 − D m s ) E s ε i + η ε ̇ i ( 1 − exp ( − ( 1 − D m d ) E d t η ) ) + ν ( σ j + σ k ) .

Equations (14) and (18) are equivalent without considering the anisotropy of the damage. They characterize the relationship between apparent stress and strain, i.e., the mechanical response of rock under impact loading.

When three orthogonal directions are subjected to loading with the constant strain rate and the initial stress (or initial strain) is zero, the dynamic constitutive relationship of rock can be described by equation (14) or equation (18). Tests that apply shock loads in both directions or in three directions are too difficult to be implemented. For example, Hummeltenberg and Curbach [27] used two orthogonal split Hopkinson pressure bar (SHPB) devices to simultaneously impact the rock specimen to achieve bidirectional simultaneous impact loading. Since synchronization is difficult to achieve, no valid test data have been obtained.

The underground rock is in a triaxial stress state, and the impact load such as blasting is mainly from a certain direction. In order to simulate the mechanical behavior of underground rock under impact loading, Cadoni et al. [28,29] proposed the experimental idea of combining true static triaxial load with the SHPB device. The rock specimen is first loaded into a true triaxial stress state σ 0 and then an impact load is applied in one direction. In this case, the confining pressure remains the same [30,31]. So, the constitutive of the rock can be written as follows:

(19) σ 1 − σ 10 = ( 1 − D m s ) E s ε 1 + η ε ̇ 1 ( 1 − exp ( − ( 1 − D m d ) E d t η ) ) − σ 10 + ν ( σ 20 + σ 30 ) ,

where σ ₁ − σ ₁₀ can be called the deviatoric stress.

It should be noted that the axial strain in the aforementioned equation consists of two parts, the strain caused by the initial triaxial static stress and the strain caused by the impact load, i.e., ε 1 = ε 1 s + ε 1 d , since the load on the rock is loaded in two stages. Correspondingly, ε ̇ 1 = ε ̇ 1 d . It is assumed that the initial compressive stress does not cause rock damage. Therefore, using Hooke’s law, the method for determining the initial strain in the axial direction can be expressed as:

(20) ε 1 s = σ 10 − ν ( σ 20 + σ 30 ) E .

Substituting σ ₁₀ = σ ₂₀ = σ ₃₀ = 0 into equation (19) results in the dynamic constitutive model under uniaxial impact loading as follows:

(21) σ 1 = ( 1 − D m s ) E s ε 1 + η ε ̇ 1 ( 1 − exp ( − ( 1 − D m d ) E d t η ) ) ,

where σ ₁, ε ₁ are the stress and strain under uniaxial impact loading. Substituting ε ₁ = 0 into the aforementioned equation results in σ ₁ = 0, so the model avoids the defect that σ ₁ and ε ₁ cannot be the same as zero. Substituting ε ₁ → 0 (i.e., static loading) into the aforementioned equation results in σ = ( 1 − D m s ) E s ε 1 , so E ^s represents the Young modulus of the rock material. The static elastic modulus (or static stress) and the dynamic elastic modulus (or dynamic stress component) in the model of this study can be decoupled and it is easy to implement different definitions for damage of different elastic moduli.

2.2.3 Evolution equations of damage variables

If it is assumed that rock is a combination of micro-elements, the strength of each micro-element is different from the others because the microscopic defects it contains are different from the others. The damage variable can be defined as the ratio of the number of failure elements to the number of total elements in the rock sample, and the equation for calculation [32] is as follows:

(22) D = N F N ,

where D is the damage variable, N _F is the number of damaged micro-elements and N is the total number of micro-elements contained in the rock sample.

If it is assumed that the strength of the micro-elements obeys the Weibull distribution, the expression of its probability density function [20,33] is as follows:

(23) ω ( F ) = m F 0 ( F F 0 ) m − 1 exp ( − ( F F 0 ) m ) ,

where F is the strength value of the micro-element and m and F ₀ are Weibull distribution parameters. They are based on the shape and properties of rock, respectively. In experiments with fixed conditions, m and F ₀ are constant. According to the definition in the Weibull distribution, m is called the uniformity index and greater than 1.0. As m increases, the generated data are more concentrated.

The failure of rock (i.e., the accumulation of damage) is a gradual process. When load increases from f to f + df, the number of micro-elements that have been destroyed within rock is Nω(f) df. When load increases from 0 to F, the number of micro-elements that have been destroyed within rock can be calculated by:

(24) N F = ∫ 0 F N ω ( f ) d f = N ( 1 − exp ( − ( F / F 0 ) m ) ) .

From equations (22) and (24), the damage variable D can be obtained as follows [33]:

(25) D = 1 − exp ( − ( F / F 0 ) m ) .

The damage variables involved in the model of this study are D m s , D m d , which will be defined separately. Using equation (25), the following equation can be obtained:

(26) D m s = 1 − exp ( − ( F s / F 0 s ) m s )

(27) D m d = 1 − exp ( − ( F d / F 0 d ) m d ) ,

where D m s and D m d represent the isotropic damage of the elastic modulus E ^s and E ^d; E ^s and E ^d represent the effective stress on the static response element and dynamic response element under loading, respectively.

The most critical step in establishing a damage evolution model with the statistical damage theory is to select a scientific method for measuring the strength of rock micro-elements. The strength of rock micro-element is capable of reflecting its failure condition. For D m s in F ^s, Qin et al. [21] proposed to measuring the strength of rock micro-elements with the axial strain and achieved some success. The strength of rock micro-elements is not directly determined by the amount of deformation in a certain direction, but is directly related to the stress state. Therefore, there is still some irrationality in measuring the strength of rock micro-elements with the axial strain [34]. In order to solve the aforementioned problem, many researchers proposed the rock micro-strength measurement method based on the yield criterion (or strength criterion). For example, Zhang et al. [35] established a rock micro-intensity measurement method based on the Von Mises yield criterion. For this method, there is a significant defect, that is, the same magnitude of pressure and tension has the same damage effect. Cao et al. [36] proposed a rock micro-strength measurement method based on the Mohr–Coulomb strength criterion. Similarly, Liu and Dai [37] measured the strength of rock micro-elements using the method based on the Drucker–Prager strength criterion. Although the rock micro-strength measurement method based on the yield criterion (or strength criterion) is more reasonable, there is still some irrationality: the damage evolution model established by this method will damage as long as it bears the load. In fact, damage occurs when the stress within the rock is greater than the yield strength. Later, some researchers proposed improvements (i.e., considering the effect of damage threshold). For example, Cao et al. [38] presented a rock micro-strength measurement method based on the Mohr–Coulomb strength criterion and considering the influence of the damage threshold, as shown in equation (28). Zhao et al. [39] presented a rock micro-strength measurement method based on the Drucker–Prager strength criterion and considering the influence of threshold damage, as shown in equation (29). It should be noted that D m s represents the damage of the static elastic modulus E ^s in the rock triaxial dynamic constitutive model of this study. Therefore, D m s is defined based on the quasi-static yield criterion. In this study, it is specified that the compressive stress and strain are positive. The tensile stress and strain are negative.

(28) F s = 〈 σ ˆ 1 s − 1 + sin φ y 1 − sin φ y σ ˆ 3 s − 2 c y cos φ y 1 − sin φ y 〉 ,

where c _y and φ _y are the cohesive and internal friction angles of the rock under quasi-static loading, respectively. 〈〉 is the Macaulay bracket. If F ^s < 0, 〈F ^s〉 = 0. If F ^s ≥ 0, 〈F ^s〉 = F ^s.

(29) F s = 〈 3 J 2 ( σ ˆ s ) − 2 sin φ y 3 + sin φ y I 1 ( σ ˆ s ) − 6 c y cos φ y 3 + sin φ y 〉 ,

where I 1 ( σ ˆ s ) = tr ( σ ˆ s ) , I 1 ( σ ˆ s ) is the volumetric stress of the effective stress tensor σ ˆ s under quasi-static loading (i.e., the effective volume stress on the quasi-static response element under dynamic loading); J 2 ( σ ˆ s ) = dev ( σ ˆ s ) : dev ( σ ˆ s ) 2 , 3 J 2 ( σ ˆ s ) is the Mises equivalent stress of the effective stress tensor σ ˆ s under quasi-static loading (i.e., the effective Mises equivalent stress on the quasi-static response element under dynamic loading).

It can be viewed in equations (26) and (28) (or equations (26) and (29)) that when F ^s < 0, D m s = 0 and the static response element is in the linear elastic state; when F ^s > 0, D m s > 0 and the quasi-static response element is in the damaged state. In fact, F ^s = 0 is the yield criterion of the static response element, so the starting point of the rock damage under quasi-static loading in the aforementioned method is its yield point. The damage model established by Cao et al. [38] and Zhao et al. [39] reflects the reasonable starting point of rock damage, which is more reasonable than the previous model.

By equation (19), the quasi-static component of apparent stress in the three principal directions can be obtained. Then, the three components are divided by 1 − D m s , and the static components of the effective stress in the three principal directions are obtained, as follows:

(30) σ ˆ 1 s = E s ε 1 + ν ( σ 20 + σ 30 )

(31) σ ˆ 2 s = σ 2 s 1 − D m s = σ 20 1 − D m s

(32) σ ˆ 3 s = σ 3 s 1 − D m s = σ 30 1 − D m s ,

where σ ₁₀, σ ₂₀ and σ ₃₀ are the initial stresses in the three principal directions before impact loading, respectively.

Equation (19) can be transformed into:

(33) 1 − D m s = σ 1 − σ 1 d − ν ( σ 20 + σ 30 ) E s ε 1 ,

where σ 1 d = η ε ̇ 1 ( 1 − exp ( − ( 1 − D m d ) E d t η ) ) .

Substituting equation (34) and σ ₁₀ = σ ₂₀ = σ ₃₀ = p into equations (31) and (32), the following equations can be obtained:

(34) σ ˆ 2 s = p σ 1 − σ 1d − 2 ν p E s ε 1

(35) σ ˆ 3 s = p σ 1 − σ 1d − 2 ν p E s ε 1 ,

where ε 1 = ( 1 − 2 ν ) p E s + ε 1 d .

If the initial stress is hydrostatic pressure, equations (28) and (29) are equivalent, but the form of equation (28) is simpler. The method for measuring the strength of micro-elements represented by equation (28) in this study is selected to describe the damage of rock under quasi-static loading, i.e., the damage of the quasi-static response element.

(36) F s = 〈 ( 1 − p ( 1 + sin φ y ) ( 1 − sin φ y ) ( σ 1 − σ 1 d − 2 ν p ) ) E s ε 1 + 2 ν p − 2 c y cos φ y 1 − sin φ y 〉

In the rock triaxial dynamic constitutive model represented by equation (17), D ^d is the cumulative damage of the elastic modulus E ^d. Thus, F ^d in D ^d cannot be defined based on static strength criteria. In this study, F ^d is measured with the effective dynamic stress component (i.e., the effective stress on the dynamic response element):

(37) F d = σ ˆ 1 d ,

where σ ˆ 1 d = η ε ̇ 1 ( 1 − exp ( − E d t η ) ) . In this article, it is implemented to perform different definitions for D ^s and to overcome the defect that it is unreasonable to define D ^d with strain.

2.3 Parameter determination

Equations (19), (26), (27), (36) and (37) constitute the constitutive equation for rock under impact loading. This equation reflects the implicit-function relationship of stress–strain for rock subjected to initial hydrostatic pressure and axial impact load. The current model contains a total of ten parameters. They are c _y, φ _y, E ^s, ν, F 0 s , m ^s, E ^d, η, F 0 d and m ^d, respectively. The aforementioned parameters can be calculated by uniaxial and/or triaxial compression tests. Depending on the relationship between the quasi-static yield strength obtained by the triaxial compression test and the confinement, the yield surface curve can be drawn. The quasi-static yield strength index (c _y, φ _y) can be obtained by fitting the curve with equation (38) [38]. In this study, the quasi-static yield strength parameters of salt rock are obtained from the results of Cao et al. [38], which are obtained by fitting the test data of Fang et al. [41] Generally, the quasi-static elastic parameters (E ^s, ν) of rock vary with different confinements. However, under low confinement, this change is not obvious for some rocks (such as salt rock). The quasi-static elastic parameters of rock are constants under different low confinements and can be obtained by fitting the linear part of the stress–strain curves of uniaxial and triaxial quasi-static compression tests. In this work, the quasi-static elastic parameters of salt rock are obtained from the test results of Wu and Yang. [40] The other parameters of the constitutive model can be obtained by fitting the stress–strain curve obtained by the dynamic triaxial test with the shared parameter estimation algorithm.

(38) σ 1 y s = 1 + sin φ y 1 − sin φ y p − 2 c y cos φ y 1 − sin φ y ,

where σ 1 y s is the yield stress under quasi-static loading and p is the confining pressure.

The parameter estimation algorithm, including the Levenberg–Marquardt (LM) and the Universal Global Optimization (UGO) algorithm with strong searching ability and robustness, is a powerful tool for processing curve fitting, which is hereinafter referred to as LM-UGO. Many scholars (Xie et al. [19]) believe that the physical quantity η/E ^d reflecting viscoelasticity is an intrinsic characteristic parameter of rock, which does not vary with the loading strain rate. A similar treatment is approved in this study. Thus, the method of sharing parameters can be used to assess the model parameters during the execution of the LM-UGO algorithm.

The current model consists of two parts: quasi-static response element and dynamic response element. The mechanical response of the quasi-static response element simulates the stress–strain relationship of rock under quasi-static loading. The mechanical response of the dynamic response element simulates the strain rate effect of the rock under impact loading. Theoretically, the parameters of the quasi-static response element are only related to material properties and confining pressure, and the parameters of the dynamic response element are only related to material properties and strain rate. The aforementioned characteristics make the variation of the model parameters easy to obtain, which is convenient for application in practice. Taking salt rock as an example, except for c _y, φ _y, E ^s and ν, the values of other parameters in the quasi-static response element under different confinements and the variation with the confining pressure are shown in Figure 5. Except for η/E ^d, the values of other parameters in the dynamic response element under different strains and the variation with strain rate are shown in Figure 6.

$Figure 5 Trend of the quasi-static response element parameters with confining pressure. (a) Trend of parameter F 0 s {F}_{0}^{\text{s}} with confining pressure p and (b) trend of parameter m s with confining pressure p.$

Figure 5

Trend of the quasi-static response element parameters with confining pressure. (a) Trend of parameter F 0 s with confining pressure p and (b) trend of parameter m ^s with confining pressure p.

$Figure 6 Trend of the dynamic response element parameters with strain rate. (a) Trend of parameter E d with strain rate ε ̇ 1 {\dot{\varepsilon }}_{1} ; (b) trend of parameter F 0 d {F}_{0}^{\text{d}} with strain rate ε ̇ 1 {\dot{\varepsilon }}_{1} ; and (c) trend of parameter m d with strain rate ε ̇ 1 {\dot{\varepsilon }}_{1} .$

Figure 6

Trend of the dynamic response element parameters with strain rate. (a) Trend of parameter E ^d with strain rate ε ̇ 1 ; (b) trend of parameter F 0 d with strain rate ε ̇ 1 ; and (c) trend of parameter m ^d with strain rate ε ̇ 1 .

3 Case analysis and discussion

The constitutive model for simulating the deformation process of rock under impact load coupled with initial hydrostatic pressure load has been established, and the method of determining its parameters has been proposed. However, its superiority and applicability are still required to be verified. To this end, the test curves of salt rock reported by Wu and Yang [40] and Fang et al. [41] are discussed in this study. Wu and Yang [40] performed the static triaxial compression tests on salt rock at three initial hydrostatic pressures (5, 15 and 25 MPa) in 2003, and the stress–strain curves were obtained. In order to study the dynamic properties of salt rock, Fang et al. [41] conducted the triaxial impact compression tests at three initial hydrostatic pressures (5, 15 and 25 MPa) with the self-developed triaxial static confining pressure split Hopkinson pressure bar (TSCP-SHPB) in 2012. The TSCP-SHPB included a conventional SHPB and a device of triaxial confining pressure. In the test, equal ring pressure and axial pressure were applied to the columnar rock specimen, then an impact load with constant strain was applied in the axial direction.

In order to simulate the dynamic stress–strain curve in the deformation process of salt rock by using the model, the model parameters must be determined first. According to the stress–strain curves provided by Wu and Yang [40] and Fang et al. [41], the constitutive model parameters of salt rock under different confinements can be obtained, as shown in Tables 1 and 2.

Table 1

Quasi-static yield stresses and strength parameters of salt rock under different confining pressures

p/MPa	Quasi-static yield stress/MPa	c _y/MPa	φ _y/°
5	19.52	6.41	10.3
15	29.62	6.41	10.3
25	41.89	6.41	10.3

Table 2

Parameters of the constitutive model under different confining pressures and strain rates

p/MPa	ε ̇ 1 / s – 1	E ^s/GPa	ν	F 0 s /MPa	m ^s	E ^d/GPa	η/E ^d/µs	F 0 d /MPa	m ^d
5	426	3.83	0.31	229.7389	3.9226	4.1456	66.10	45.6263	1.9922
5	519	3.83	0.31	274.1440	3.0854	4.1100	66.10	63.2775	2.4735
15	476	3.83	0.31	253.6234	3.6775	4.5041	66.10	58.4198	2.4935
15	631	3.83	0.31	304.3146	3.3502	3.4786	66.10	64.0775	4.3489
25	433	3.83	0.31	263.7684	2.0252	4.1000	66.10	47.9476	2.6733
25	513	3.83	0.31	243.5652	3.6538	3.6583	66.10	58.0828	3.2163

In order to verify the rationality and superiority of the proposed three-dimensional model, the current model is compared with some existing models. The element model proposed by Xie et al. [19,20] has not been expanded in three dimensions, so it is unsuitable for the simulation of rock dynamic deformation process under three-dimensional stress. Therefore, only the theoretical curves of the current model and the model proposed by Cao et al. [7] are plotted in Figure 7. As it can be observed in Figure 7, compared against the model of Cao et al. [7], the theoretical curve of the current model is closer to the test curve, especially in the initial deformation stage. The simulated result of the current model is obviously better than that of Cao et al. [7], and the reasons are as follows.

$Figure 7 Comparison of different theoretical curves: (a) p = 5 MPa, ε ̇ 1 = 426 s − 1 {\dot{\varepsilon }}_{1}=426\hspace{.5em}{\text{s}}^{-1} ; (b) p = 5 MPa, ε ̇ 1 = 519 s − 1 {\dot{\varepsilon }}_{1}=519\hspace{.5em}{\text{s}}^{-1} ; (c) p = 15 MPa, ε ̇ 1 = 476 s − 1 {\dot{\varepsilon }}_{1}=476\hspace{.5em}{\text{s}}^{-1} ; (d) p = 15 MPa, ε ̇ 1 = 631 s − 1 {\dot{\varepsilon }}_{1}=631\hspace{.5em}{\text{s}}^{-1} ; (e) p = 25 MPa, ε ̇ 1 = 433 s − 1 {\dot{\varepsilon }}_{1}=433\hspace{.5em}{\text{s}}^{-1} ; and (f) p = 25 MPa, ε ̇ 1 = 513 s − 1 {\dot{\varepsilon }}_{1}=513\hspace{.5em}{\text{s}}^{-1} .$

Figure 7

Comparison of different theoretical curves: (a) p = 5 MPa, ε ̇ 1 = 426 s − 1 ; (b) p = 5 MPa, ε ̇ 1 = 519 s − 1 ; (c) p = 15 MPa, ε ̇ 1 = 476 s − 1 ; (d) p = 15 MPa, ε ̇ 1 = 631 s − 1 ; (e) p = 25 MPa, ε ̇ 1 = 433 s − 1 ; and (f) p = 25 MPa, ε ̇ 1 = 513 s − 1 .

First, the dynamic stress of rock is regarded as the superposition of static stress and inertia force in Cao et al.’s [7] model. However, the inertia force is only related to the dynamic strain rate, so the dynamic stress of rock always contains the inertia force caused by the strain rate when the model is used to simulate the dynamic deformation process of rock. In other words, even at the initial moment of dynamic loading, the dynamic stress of rock is not zero, and the larger the strain rate, the greater the difference between the dynamic stress at the initial moment of dynamic loading and the test results (Figure 7), which is obviously contrary to the actual situation. Second, the static strength criterion is adopted in the dynamic statistical damage constitutive model, which cannot reflect the influence of dynamic change of rock on its strength. Built on the aforementioned two reasons, the model proposed by Cao et al. [7] can only simulate the dynamic deformation process of rock under the condition of low dynamic strain rate at most.

As the most direct method to study the failure process of materials, the test plays a critical role in promoting the research and development of its failure process. However, due to human, material and financial constraints, the failure process test of materials is often limited. One of the most important roles for the constitutive model is tantamount to predict the mechanical response of the rock to strain (or strain rate). Model parameters at different initial quasi-static pressure and strain rates can be calculated by using the trend curve of the parameters. In order to further verify the rationality of the model established in this study, the predicted constitutive curve whose parameters are shown in Table 3 is compared to the test curve, as shown in Figure 8. The coefficient R ² reflecting the degree of agreement between the prediction curve and the test curve is equal to 0.9757, further indicating that the proposed novel model in this study is reasonable and applicable.

Table 3

Predictive value of the constitutive model parameter under p = 15 MPa and ε ̇ 1 = 609 s − 1

p/MPa	ε ̇ 1 / s – 1	E ^s/GPa	F 0 s /MPa	m ^s	E ^d/GPa	η/E ^d/µs	F 0 d /MPa	m ^d
15	609	3.83	262.4694	3.2180	3.6961	66.10	58.0229	3.5142

Figure 8

Comparison of the prediction curve and the test curve.

4 Conclusions

According to the deformation characteristics of rock under initial quasi-static load and constant strain impact, the dynamic triaxial constitutive model of rock is deeply studied. The following conclusions can be drawn:

The current model is obtained by simplifying the component combination model proposed by Xie et al. and has been expanded to three dimensions. The model is suitable for simulating the dynamic deformation process for rock under three-dimensional stress state, and the number of parameters is less, which is more convenient for application. The three-dimensional expansion method of the component combination is similar to that of the Hooke spring, which is easy to operate and understand.
It is a basic fact that the dynamic stress at the initial moment of impact loading should be zero. Using the current model, the defect that the dynamic stress is not zero at the initial stage of impact loading can be avoided. Compared with the element model proposed by Cao et al. [7], the simulation effect is obviously better.
In the current model, the parameters of the quasi-static response element are only related to the material properties and confining pressure, while the parameters of the dynamic response element are only related to the material properties and strain rate. This characteristic makes the variation of the model parameters easy to obtain, which is beneficial to the application of the model in practice. In the determination of model parameters, the shared parameter estimation method based on the LM-UGO algorithm is used, which can be well applied to models with parameters that do not change with confinement and strain rates.
The model can provide reliable prediction results for the dynamic response of rock. The validation, carried out against the test results for salt rock, clearly demonstrated an excellent model performance of rock under the coupling action of low confining pressure and constant strain-rate impact load.

wlkyljz@163.com

Author contributions: Conceptualization was performed by J. Li and G. Zhang; methodology, software and writing – original draft preparation were contributed by J. Li; data curation was performed by M. Liu; writing – review and editing was performed by G. Zhang; supervision was done by S. Hu and X. Zhou; and project administration was performed by G. Zhang.
Funding: This research was supported by the National Natural Science Foundation for Young Scientists of China under Grant No. 51609184 and the National Key Research and Development Program of China under Grant No. 2017YFC0804600.
Conflicts of interest: The authors declare no conflict of interest.

References

[1] Grady DE, Kipp ME. Continuum modelling of explosive fracture in oil shale. Int J Rock Mech Min Sci Geomech Abstr. 1980;17(3):147–57. 10.1016/0148-9062(80)91361-3 Search in Google Scholar

[2] Si X, Gong F, Li X, Wang S, Luo S. Dynamic Mohr–Coulomb and Hoek–Brown strength criteria of sandstone at high strain rates. Int J Rock Mech Min Sci. 2019;115:48–59. 10.1016/j.ijrmms.2018.12.013 Search in Google Scholar

[3] Lindholm US, Yeakley LM, Nagy A. The dynamic strength and fracture properties of dresser basalt. Int J Rock Mech Min Sci Geomech Abstr. 1974;11(5):181–91. 10.1016/0148-9062(74)90885-7 Search in Google Scholar

[4] Zhou Y, Sheng Q, Leng X, Zhu Z, Li N. Preliminary application of dynamic constitutive model with subloading surface for rock materials considering rate effect in rock engineering. Chin J Rock Mech Eng. 2017;36(10):2503–13.Search in Google Scholar

[5] Christensen RM. A nonlinear theory of viscoelasticity for application to elastomers. J Appl Mech. 1980;47(4):762–8. 10.1115/1.3153787 Search in Google Scholar

[6] Shan R, Xue Y, Zhang Q. Time dependent damage model of rock under dynamic loading. Chin J Rock Mech Eng. 2003;22(11):1771–6. 10.3321/j.issn:1000-6915.2003.11.003 Search in Google Scholar

[7] Cao W, Zhao H, Zhang L, Zhang Y. Simulation method of dynamic triaxial deformation process for rock under invariable strain rate. Chin J Geotechnol Eng. 2010;32(11):1658–64. 10.1007/978-94-011-2404-1_16 Search in Google Scholar

[8] Liu J, Xu J, Lv X, Wang Z, Zhang L. Study on dynamic behavior and damage constitutive model of rock under impact loading with confining pressure. Eng Mech. 2012;29(1):55–63.Search in Google Scholar

[9] Li X, Wang S, Weng L, Huang L, Zhou T, Zhou J. Damage constitutive model of different age concretes under impact load. J Cent South Univ. 2015;22(2):693–700. 10.1007/s11771-015-2572-0 Search in Google Scholar

[10] Liu J, Li Y, Zhang H. Study on shale’s dynamic damage constitutive model based on statistical distribution. Shock Vib. 2015;2015:1–8. 10.1155/2015/286097 Search in Google Scholar

[11] Wang ZL, Shi H, Wang JG. Mechanical behavior and damage constitutive model of granite under coupling of temperature and dynamic loading. Rock Mech Rock Eng. 2018;51(10):3045–59. 10.1007/s00603-018-1523-0 Search in Google Scholar

[12] Li X, Zuo Y, Ma C. Constitutive model of rock under coupled static-dynamic loading with intermediate strain rate. Chin J Rock Mech Eng. 2006;25(5):865–74. 10.3321/j.issn:1000-6915.2006.05.001 Search in Google Scholar

[13] Li X, Zuo Y, Ma C. Failure criterion of strain energy density and catastrophe theory analysis of rock subjected to static-dynamic coupling loading. Chin J Rock Mech Eng. 2005;24(16):2814–24. 10.3321/j.issn:1000-6915.2005.16.002 Search in Google Scholar

[14] Li X, Zhou Z, Lok TS, Hong L, Yin T. Innovative testing technique of rock subjected to coupled static and dynamic loads. Int J Rock Mech Min Sci. 2008;45(5):739–48. 10.1016/j.ijrmms.2007.08.013 Search in Google Scholar

[15] Wang L, Labibes K, Azari Z, Pluvinage G. Generalization of split Hopkinson bar technique to use viscoelastic bars. Int J Impact Eng. 1994;15(5):669–86. 10.1016/0734-743x(94)90166-i Search in Google Scholar

[16] Dar UA, Zhang WH, Xu YJ. Numerical implementation of strain rate dependent thermo viscoelastic constitutive relation to simulate the mechanical behavior of PMMA. Int J Mech Mater Des. 2014;10:93–107. 10.1007/s10999-013-9233-y Search in Google Scholar

[17] Ma D, Ma Q, Yuan P. SHPB tests and dynamic constitutive model of artificial frozen sandy clay under confining pressure and temperature state. Cold Reg Sci Technol. 2017;136(APR):37–43. 10.1016/j.coldregions.2017.01.004 Search in Google Scholar

[18] Xie Q, Zhu Z, Kang G. A dynamic micromechanical constitutive model for frozen soil under impact loading. Acta Mech Solida Sin. 2016;29(1):13–21. 10.1016/s0894-9166(16)60003-4 Search in Google Scholar

[19] Xie L, Zhao G, Meng X. Research on damage viscoelastic dynamic constitutive model of soft rock and concrete materials. Chin J Rock Mech Eng. 2013;32(4):857–64. 10.3969/j.issn.1000-6915.2013.04.027 Search in Google Scholar

[20] Fu T, Zhu Z, Zhang D, Liu Z, Xie Q. Research on damage viscoelastic dynamic constitutive model of frozen soil. Cold Reg Sci Technol. 2019;160(APR):209–21. 10.1016/j.coldregions.2019.01.017 Search in Google Scholar

[21] Qin SQ, Jiao JJ, Tang CA, Li Z. Instability leading to coal bumps and nonlinear evolutionary mechanisms for a coal-pillar-and-roof system. Int J Solids Struct. 2006;43(25–26):7407–23. 10.1016/j.ijsolstr.2005.06.087 Search in Google Scholar

[22] Wong TF, Wong RHC, Chau KT, Tang CA. Microcrack statistics, Weibull distribution and micromechanical modeling of compressive failure in rock. Mech Mater. 2006;38(7):664–81. 10.1016/j.mechmat.2005.12.002 Search in Google Scholar

[23] Lemaitre J. A continuous damage mechanics model for ductile fracture. J Eng Mater Technol. 1985;107:335–44. 10.1115/1.3225775 Search in Google Scholar

[24] Chow CL, Wang J. An anisotropic theory of elasticity for continuum damage mechanics. Int J Fract. 1987;33(1):3–16. 10.1007/bf00034895 Search in Google Scholar

[25] Lemaitre J, Dufailly J. Damage measurements. Eng Fract Mech. 1987;28(5–6):643–61. 10.1016/0013-7944(87)90059-2 Search in Google Scholar

[26] Li G, Tang CA. A statistical meso-damage mechanical method for modeling trans-scale progressive failure process of rock. Int J Rock Mech Min Sci. 2015;74:133–50. 10.1016/j.ijrmms.2014.12.006 Search in Google Scholar

[27] Hummeltenberg D, Curbach I. Entwurf und aufbau eines zweiaxialen split-hopkinson-bars. Beton-Stahlbetonbau. 2012;107(6):394–400. 10.1002/best.201200013 Search in Google Scholar

[28] Cadoni E. Dynamic characterization of orthogneiss rock subjected to intermediate and high strain rates in tension. Rock Mech Rock Eng. 2010;43(6):667–76. 10.1007/s00603-010-0101-x Search in Google Scholar

[29] Caverzan A, Cadoni E, Prisco MD. Tensile behaviour of high performance fibre-reinforced cementitious composites at high strain rates. Int J Impact Eng. 2012;45:28–38. 10.1016/j.ijimpeng.2012.01.006 Search in Google Scholar

[30] Xu S, Wang P, Shan J, Zhang M. Dynamic behavior of concrete under static tri-axial loadings. J Vib Shock. 2018;37(15):59–67. 10.13465/j.cnki.jvs.2018.15.008 Search in Google Scholar

[31] Zhang L, He X, Wang X, Kong D. Development of an impact loading test device for concrete under constant confining pressure. J Vib Shock. 2015;34(22):24–7. 10.13465/j.cnki.jvs.2015.22.005 Search in Google Scholar

[32] Chen S, Qiao C, Ye Q, Khan MU. Comparative study on three-dimensional statistical damage constitutive modified model of rock based on power function and Weibull distribution. Environ Earth Sci. 2018;77(3):108. 10.1007/s12665-018-7297-6 Search in Google Scholar

[33] Wang ZL, Li YC, Wang JG. A damage-softening statistical constitutive model considering rock residual strength. Comput Geosci. 2007;33(1):1–9. 10.1016/j.cageo.2006.02.011 Search in Google Scholar

[34] Cao W, Zhao H, Zhang L, Zhang Y. Damage statistical softening constitutive model for rock considering effect of damage threshold and its parameters determination method. Chin J Rock Mech Eng. 2008;27(6):1148–54. 10.3321/j.issn:1000-6915.2008.06.007 Search in Google Scholar

[35] Zhang H, Peng C, Yang G, Ye W, Liu H. Study of damage statistical strength criterion of rock considering the effect of freezing and thawing. J China U Min Technol. 2017;46(5):1066–72. 10.13247/j.cnki.jcumt.000740 Search in Google Scholar

[36] Cao W, Li X, Zhao H. Damage constitutive model for strain-softening rock based on normal distribution and its parameter determination. J Cent South Univ Technol. 2007;14(5):719–24. 10.1007/s11771-007-0137-6 Search in Google Scholar

[37] Liu Y, Dai F. A damage constitutive model for intermittent jointed rocks under cyclic uniaxial compression. Int J Rock Mech Min Sci. 2018;103:289–301. 10.1016/j.ijrmms.2018.01.046 Search in Google Scholar

[38] Cao W, Lin X, Zhan C, Yang S. A statistical damage simulation method of dynamic deformation process for rocks based on nonlinear dynamic strength criterion. Chin J Rock Mech Eng. 2017;36(4):20–8. 10.13722/j.cnki.jrme.2016.0755 Search in Google Scholar

[39] Zhao H, Zhou S, Zhang L. A phenomenological modelling of rocks based on the influence of damage initiation. Environ Earth Sci. 2019;78(5):143. 10.1007/s12665-019-8172-9 Search in Google Scholar

[40] Wu W, Yang C. Experimental study on salt rock under compression and damage model simulation. Chin J Rock Mech Eng. 2006;25:3709–13. 10.3321/j.issn:1000-6915.2006.z2.058 Search in Google Scholar

[41] Fang Q, Ruan Z, Zhai C, Jiang X, Chen L. Split hopkinson pressure bar test and numerical analysis of salt rock under confining pressure and temperature. Chin J Rock Mech Eng. 2012;31(9):1756–65.Search in Google Scholar

Received: 2019-11-12

Revised: 2020-02-22

Accepted: 2020-02-24

Published Online: 2020-05-24

This work is licensed under the Creative Commons Attribution 4.0 International License.

Articles in the same Issue

https://doi.org/10.1515/phys-2020-0014

Keywords for this article

rock dynamics; initial stress; axial impact load; component combination; three-dimensional constitutive model

Creative Commons

BY 4.0