Home Energy equilibrium analysis in the effervescent atomization
Article Open Access

Energy equilibrium analysis in the effervescent atomization

  • Runze Duan , Ziwei Feng , Hongbin Duan , Huiru Qu , Liting Tian , Wenqi Jia , Jakov Baleta , Enyu Wang EMAIL logo , Liansheng Liu EMAIL logo and Liang Tian
Published/Copyright: December 6, 2020
Download Article (PDF)
Open Physics
From the journal Open Physics Volume 18 Issue 1

Abstract

In this paper, the flow characteristics and energy equilibrium analysis of the effervescent atomization had been investigated theoretically and experimentally. The effect of the gas–liquid rate (GLR from 0.04 to 0.15) on the atomization stability was revealed. When the GLR was small, the atomization was unstable. The atomization was gradually stable with an increase in the GLR. The optimal atomization region can be obtained. The Sauter mean diameter (SMD) of the droplets was measured by the phase Doppler analyzer. The SMD decreases with an increase in the GLR. The energy equilibrium analysis was investigated for the swirl atomizer theoretically and experimentally. The results show that the energy dissipation terms are mainly compressed gas expansion, liquid viscosity dissipation, and resistance losses. However, the ratio of the spray kinetic energy and the surface tension energy to the total energy is small.

Keywords: effervescent atomization; energy dissipation analysis; Sauter mean diameter; swirl atomizer; droplets velocity; phase Doppler analyzer

1 Introduction

The effervescent atomization has some advantages such as high atomization quality, low pressure, energy-saving, simple, and reliable. Effervescent atomization technique has been already widely used in many industrial applications, such as liquid fuel combustion, spray cooling, spray irrigation, water mist for fire suppression, medical treatment, and surface spray treatment [1,2,3,4,5]. The main purpose of the atomization is to make the liquid into fragments or small droplets [6,7,8]. The atomization process needs to consume a lot of energy on the inside and outside of the effervescent atomizer [9,10,11]. The effects of energy consumption must be considered when an atomizer is designed and chosen. Hence, it is necessary to investigate energy transfer in the effervescent atomization process.

The process of effervescent atomization has been investigated by Lefebvre et al. in the 1980s [12,13,14]. Using injecting gas into a liquid, bubble flow is formed in the internal-mixing chamber of the atomizer. The effervescent atomization is the result of liquid and gas interaction. When the liquid and gas shear force is greater than the fluid viscous forces and surface tension, the liquid will be deformed and broken into small droplets. When the gas and the droplets continue the interaction, the droplets will be further broken into smaller liquid particles, then the atomization is achieved.

The mean spray droplet size (typically Sauter mean diameter [SMD]), spray cone angle, and the discharge coefficient are the most important performance parameters to atomizer designers. Wade et al. [15] and Wang et al. [16] experimentally investigated the spray characteristics of an effervescent atomizer operating in the MPa injection pressure range. The atomization reason is that the high gas–liquid velocity difference enhances the shear effect. Satapathy et al. [17] continued the work of Wade et al. They found that the ambient gas density is a small influence on SMD. Sovani et al. [18] reinforced the conclusions of Wade et al. and Satapathy et al. They found that the efficiency of the effervescent atomizers is substantially higher than the efficiencies of the conventional twin-fluid atomizers. The same conclusion is obtained by Bayvel and Orzechowski [19]. They indicate that the atomization efficiency of the effervescent atomization is higher than that of other atomizers. The spray quality improvement of the effervescent atomization demands less energy. Karnawat and Kushari [20] thought the spray cone angle is dependent on the GLR. Sovani et al. [21] noted the spray cone angle is widened with an increase in the injection pressure. Chen and Lefebvre [22] found that the spray cone angle increases with a decrease in the liquid viscosity and surface tension. Ochowiak [23] investigated the effect of the discharge coefficient of the effervescent atomizer on the effervescent atomization. The conclusions are that the atomizer construction (mixing chamber and outlet orifice) is very important to discharge coefficient.

All the literature mentioned earlier focuses mainly on the performance parameters of atomization. However, energy consumption in the atomization process is also important to design atomizers and improve atomization quality. Lefebvre et al. [24,25] investigated the energy consideration in twin-fluid atomization. The results are that the ratio of the energy required for atomization to the kinetic energy of the air is a main factor for the atomization. Jedelsky and Jicha [26] systematically investigated the energy conversion process of the effervescent atomization by the experiment. The conclusions are that most of the input energy is spent on the gas expansion work, the air entrainment process, and losses related to the two-phase flow and the discharge. However, viscosity dissipation is not considered. The viscosity has a very important influence on the atomization process and atomization energy consumption.

In this paper, first, the effect of gas–liquid rate (GLR) on the atomization stability is investigated. Second, the effect of two atomizer configuration on the atomization characteristics (velocity and SMD of droplets) is studied. On this basis, the energy equilibrium analysis is investigated for the swirl atomizer in detail. It is hoped that the present work can provide a good scheme for designing effervescent atomizer.

2 Experimental system

The experimental system of the effervescent atomization is illustrated in Figure 1. The pressure of the gas and liquid which was provided by the gas compressor was measured by the pressure gages. The flow rate of the fluid was measured by the mass flow meter, and the gas rate was obtained by the volume flow meter. The gas and liquid are mixed in the atomizer and then flow downstream to the exit orifice. The velocity and size of the droplet were measured by the phase Doppler analyzer (PDA). The spray temperature field was measured by the thermal infrared imager, and the spray stability was analyzed by the high-speed video.

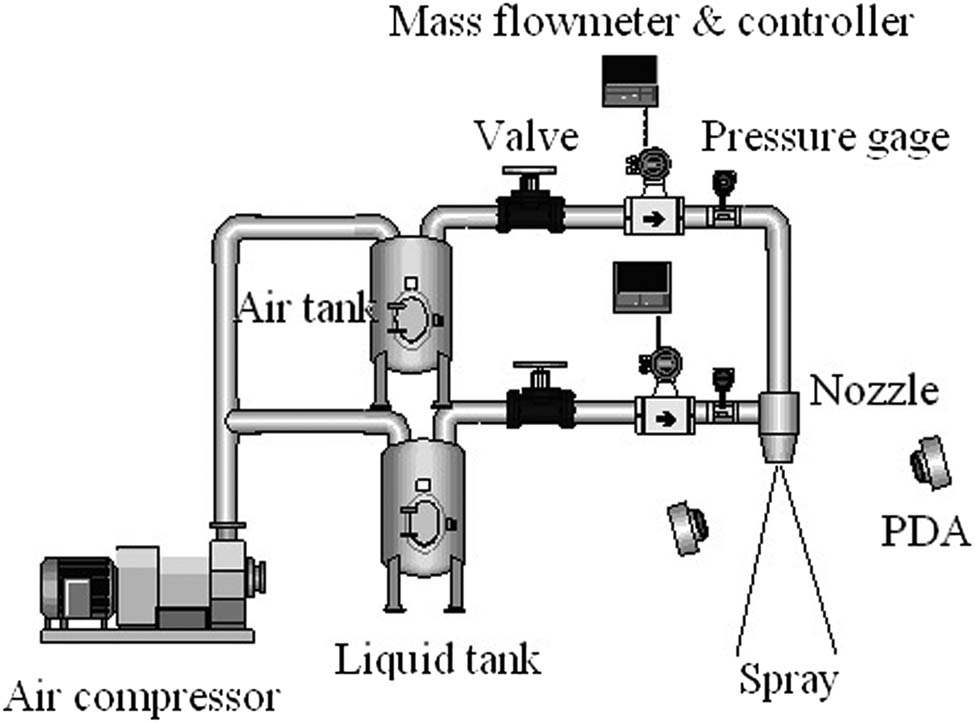
Figure 1 Experimental system.
Figure 1

Experimental system.

Before entering the atomizer, the pressure of the liquid and gas was up to 0.3 MPa. The structure of the swirl atomizer is shown in Figure 2. The diameter of the exit orifice was D = 1.0 mm. The diameter of the mixing chamber was D c = 10 mm. The degrees of mixing and energy interchange between air and water were different in the mixing chamber, then sprayed from the atomizer exit.

Figure 2 Structure of the swirl atomizers.
Figure 2

Structure of the swirl atomizers.

3 Results and discussion

3.1 Characteristic of the atomization in the effervescent atomizer

The characteristic of the atomization in the effervescent atomizer is shown in Figure 3. The pressure of the gas and liquid was changed from 0.26 to 0.32 MPa. The liquid mass flow rate decreases with an increase in the GLR, as shown in Figure 3. The physical mechanisms are revealed as follows: when the GLR is small, the amount of liquid is relatively much more than that of air. The liquid is sprayed from the exit orifice to the stationary atmosphere environment; the restriction of the atomizer wall for the liquid is disappeared. Due to the interaction of gas and liquid, the atomization becomes unstable in the gas–liquid boundary layer. The atomization becomes gradually stable with an increase in the GLR. It is the optimal region for the atomization, as marked by the circle. The spray effect will gradually deteriorate with an increase in the GLR.

Figure 3 Characteristic of the atomization in the effervescent atomizer.
Figure 3

Characteristic of the atomization in the effervescent atomizer.

The effect of the pressure on the liquid mass flow rate is shown in Figure 3 by keeping the GLR constant. The liquid mass flow rate increases with an increase in the gas and liquid pressures. In the terms of physics, the expansion work will increase by increasing the pressure. The velocities of the atomization increases, and the liquid mass flow rate increases. The energy consumption also increases.

3.2 Effect of atomizers configuration on droplets velocity

The effect of swirl atomizer on the atomization characteristics is shown in Figure 4. The gas and liquid pressure was p α = 0.3 MPa (α = 1, 2 represents liquid and gas phase, respectively). The GLR was 0.1. The distance from the discharge orifice (L) was 20–180 mm.

Figure 4 Characteristic of atomization. (a) Radial velocity of droplets, (b) SMD of droplets.
Figure 4

Characteristic of atomization. (a) Radial velocity of droplets, (b) SMD of droplets.

The radial velocity distribution of the droplets is described in Figure 4(a). The velocity of the discharge orifice center is the largest and the velocity becomes gradually small along the radial direction. The velocity radial distribution is approximately symmetrical. The velocities of the droplets will decay gradually with an increase in the distance from the discharge orifice. The SMD radial distribution of the droplets is shown in Figure 4(b). The SMD radial distribution is symmetrical. The SMD of the droplets in the discharge orifice center is the smallest and the SMD of the droplets increases gradually along the radial direction. The SMD of the droplets becomes gradually small with an increase in the distance from the discharge orifice.

3.3 Effect of GLR on droplets velocity

The velocity distribution of the droplets in the different GLR is shown in Figure 5. The GLR was changed from 0.14 to 0.3 by keeping other parameters constant. The variation range (the ellipse) of the droplet velocity is relatively small at the distance from the discharge orifice (20–180 mm) for GLR = 0.1. This is an interesting phenomenon. The physical mechanisms are revealed as follows: many small bubbles are formed in the spray process. The bubbles are compressed in the atomizer interior. When the bubbles flow out of the atomizer, the bubbles would suddenly expand. At the bubble expansion process, the bubbles would deform and burst into droplets under the aerodynamic force. Some energy converts into the droplets’ kinetic energy. The variation range of the droplet velocity becomes big gradually with an increase in the GLR.

Figure 5 Effect of GLR on droplets velocity. (a) GLR = 0.1 (b) GLR = 0.14, (c) GLR = 0.16, (d) GLR = 0.2.
Figure 5

Effect of GLR on droplets velocity. (a) GLR = 0.1 (b) GLR = 0.14, (c) GLR = 0.16, (d) GLR = 0.2.

3.4 Effect of GLR on droplets SMD

The SMD distribution of the droplets in the different GLR from 0.08 to 0.14 by keeping other parameters constant is described in Figure 6. The SMD decreases with an increase in the GLR from 0.08 to 0.12. The reason is that the shearing action in the gas and liquid boundary layer is further enhanced with an increase in the GLR. The liquid droplets become small in the atomization process. The atomization will become unstable with an increase in the GLR, and the size of the droplets will increase. With an increase in the GLR, the input energy also increases in the atomization process. In the following, the energy conversion will be analyzed at the stable atomization conditions.

Figure 6 Effect of GLR on droplets SMD, (a) GLR = 0.08, (b) GLR = 0.1, (c) GLR = 0.12, (d) GLR = 0.14.
Figure 6

Effect of GLR on droplets SMD, (a) GLR = 0.08, (b) GLR = 0.1, (c) GLR = 0.12, (d) GLR = 0.14.

3.5 Energy conversion

For the effervescent atomization process, the liquid and gas mix to form bubbles inside the atomizer and are forced to spray from the atomizer outlet under the action of air pressure. The bubbles will burst near the atomizer outlet. The total input energy is balanced to the summation of the liquid surface tension energy and viscosity dissipation energy, air expansion work, spray kinetic energy and flow resistance loss, and so on, as shown in Figure 7.

Figure 7 Energy consumption of atomizer M L = 6 kg/h, GLR = 0.1, P L = P G = 0.4 MPa, P c = 0.3 MPa.
Figure 7

Energy consumption of atomizer M L = 6 kg/h, GLR = 0.1, P L = P G = 0.4 MPa, P c = 0.3 MPa.

The liquid flux was M L = 6 kg/h. The GLR was 0.1. The gas and liquid pressure was p L = p G = 0.4 MPa . and the mixing chamber pressure was p c = 0.3 MPa . The rated motor power and the rated pressure of the air compressor were 37 kW and 0.8 MPa, respectively. The rated volume flow of the air was 6.3 m3/min. The electric efficiency and the service factor amps were defined 94.7% and 1.15, respectively. The gas compression work per unit mass was 273.16 kJ/kg. The liquid atomization rated power was 7.59 W/kg for this atomizer.

3.5.1 Total input energy

The theoretical energy for the liquid atomization can be obtained as follows:

(1) w = n n − 1 P 1 V 1 P 2 P 1 n − 1 n − 1 ( kJ/kg )

where w is the theoretical energy for the liquid atomization, n is the polytropic index in the compressing process, and P 1 and V 1 denote the pressure and volume for the atmosphere gas, respectively. The gas pressure P 2 can be generated by the compressor. The power of the input energy was calculated as 4.76 W/kg for water.

3.5.2 Gas expansion work

When compressed gas is ejected into the atmospheric environment from the mixing chamber, the gas volume expansion was inevitable. The expansion work can be calculated by

(2) w 1 = 1 n − 1 P 1 V 1 1 − P 1 P c n − 1 n ( kJ/kg )

where w 1 is the gas expansion work and P c is the mixing chamber pressure. The power of the gas expansion work was calculated as 2.244 W/kg. The ratio of the gas expansion work to the total energy was about 47.14%.

3.5.3 Spray kinetic energy

The spray kinetic energy consisted of two parts: gas kinetic energy and liquid kinetic energy.

(3) w 2 = ∑ α = 1 2 1 2 m α v α 2

where w 2 is the spray’s total kinetic energy, α = 1 , 2 represents liquid and gas phase, respectively, m denotes the mass of gas and liquid, and v is the velocity of gas and liquid. The power of the spray kinetic energy was obtained as 0.187 W/kg. The ratio of the spray kinetic energy to the total energy was about 3.93%.

3.5.4 Resistance losses

The atomizer system constituted of three parts, as shown in Figure 8. During the atomization process, the energy losses were mainly caused by the local resistance, especially the inlet region (abrupt contraction) and the outlet region (sudden expansion) of the discharge orifice.

(5) w 3 = ζ v 2 2 g

where w 3 is the local resistance loss, ζ 1 = ζ 3 = 0.5 ζ 2 = 1 denotes the local resistance coefficient, and v is the liquid velocity. Assuming the two-phase flow in discharge orifice was homogeneous and its velocity was nearly equal to that of spray. The power of the local resistance loss was about 0.3 W/kg.

Figure 8 System diagram of atomizer.
Figure 8

System diagram of atomizer.

Considering the energy losses caused by on-way resistance were the same as the local resistance loss, the power of the estimated total energy loss was about 0.6 W/kg. The ratio of the resistance losses energy to the total energy was about 12.6%.

3.5.5 Surface tension energy

(6) w 4 = σ 4 π R 2 N

where w 4 is the liquid surface tension energy, σ is the liquid surface tension coefficient, R denotes the radius of the droplet, and N is the number of the droplets. The power of the surface tension energy was calculated as 0.006 W/kg. The ratio of the surface tension energy to the total energy was about 0.13%.

3.5.6 Viscosity dissipation energy

The viscosity dissipation energy was the difference between total energy and other energy. The viscosity energy can be obtained as follows:

(7) w 5 = w − ∑ m = 1 4 w m

The power of the viscosity dissipation energy was about 0.968–1.05 W/kg. The ratio of the viscous dissipation energy to the total energy was about 20.34–22.06%.

The energy equilibrium analysis results are listed in Table 1. For this effervescent atomizer, the total energy consumption was 4.76 W/kg. The energy dissipation terms were mainly compressed gas expansion (47.14%), viscosity dissipation of liquid (34.48–37.92%), and resistance losses (12.6%). The rate of gas expansion work to the total energy is most. The results are the same as the results of Jedelsky and Jicha [26]. However, the overcoming viscosity dissipation should be about 37% of the total energy. In other words, viscosity has a very important influence on the atomization process and atomization energy consumption. Hence, the viscosity dissipation is not ignored in the atomization process. The expansion cooling and heat release in the atomization process is also very important. The atomization is the process of the liquid changing into the droplets through energy conversion. In this process, expansion cooling and heat release phenomena will inevitably occur. The resistance losses in the atomizer are also an important part of the atomization process. However, the rates of the spray kinetic energy and the surface tension energy to the total energy are relatively small. Based on the above investigation and analysis, it can be concluded that further lessening the expansion work would transfer more energy to overcome liquid viscosity. In other words, the optimization design of the mixing process will be helpful to improve atomization quality.

Table 1

Energy equilibrium analysis results

Amount (W/kg) Ratio (%) Remarks
Total energy consumption 4.760 100.00 Experiments and theories
Rate of gas expansion work 2.244 47.14 Experiments and theories
Rate of viscosity dissipation 1.641–1.805 34.48–37.92 Estimated
Rate of resistance losses 0.6 12.6 Some of the assumptions
Rate of spray kinetic energy 0.187 3.93 Experiments and theories
Rate of surface tension energy 0.006 0.13 Experiments and theories

4 Conclusions

The spray flow characteristics were experimentally diagnosed by the PDA in this article. The two atomizers were introduced and compared. The energy dissipation was analyzed by the experiments and theories. Some results can be obtained:

  1. When the GLR was small, the atomization is unstable work. The atomization effect becomes well gradually with an increase in the GLR. The optimal region of the atomization can be obtained.

  2. The SMD decreases with an increase in the GLR from 0.08 to 0.12. When GLR = 0.14, the atomization is unstable.

  3. The energy dissipation terms are mainly compressed gas expansion, viscosity dissipation of liquid, and resistance losses. However, the rate of the spray kinetic energy and the surface tension energy to the total energy is relatively small.

tel: +86-022-6043-8208

Acknowledgments

The financial support of China National Nature Science Funds (Support No. 51806057 and 51276055), the Nature Science Founds of Hebei (No. E2019202460 and E2019202184)，Science and Technology Plan Project of Tianjin (No. 18YFCZZC00250) and the Industrial Technology Research Institute of Hebei University of Technology (Zhangbei) (No. ZBYJY201902) and Technology Research Project of Hebei Higher Education (No. QN2017050 and QN2018067) are gratefully acknowledged.

References

[1] Jedelsky J, Jicha M, Slama J, Otahal J. Development of an effervescent atomizer for industrial burners. Energy Fuels, 2009;23:6121–30.10.1021/ef900670gSearch in Google Scholar

[2] Kermes V, Belohradsky P. Experimental study on combustion of liquid renewable fuels. In: 13th international conference on process integration, modelling and optimisation for energy saving and pollution reduction; 2010. Vol. 21, p. 457–62.Search in Google Scholar

[3] Daviault S, Ramadan O, Matida E, Hughes P, Hughes R. Atomization performance of petroleum coke and coal water slurries from a twin fluid atomizer. Fuel. 2012;98:183–93.10.1016/j.fuel.2012.02.042Search in Google Scholar

[4] Liu G, Liu F, Yang, J, Mu Y, Hu C, Xu G. Experimental investigations of spray generated by a pressure swirl atomizer. J Energy Inst. 2018;2018:1–12.10.1016/j.joei.2018.01.014Search in Google Scholar

[5] Ochowiak M, Matuszak M, Włodarczak S, Krupińska A, Markowska M, Gościniak A, et al. The concept design and study of twin-fluid effervescent atomizer with air stone aerator. Chem Eng Process Process Intensificat. 2018;124:24–8.10.1016/j.cep.2017.11.020Search in Google Scholar

[6] Mahesh V, Paul E. Spatial droplet velocity and size profiles in effervescent atomizer-produced sprays. Fuel. 1999;78:729–41.10.1016/S0016-2361(98)00192-6Search in Google Scholar

[7] Guido R. Practical and useful tips on discrete wavelet transforms. IEEE Signal Process Mag. 2015;32:162–6.10.1109/MSP.2014.2368586Search in Google Scholar

[8] Gomez J. Influence of bubble size on an effervescent atomization [MSc thesis]. University of Alberta; 2010Search in Google Scholar

[9] Chen Z, Zheng D, Wang J, Chen L, Sundén B. Experimental investigation on heat transfer characteristics of various nanofluids in an indoor electric heater. Renewable Energy. 2020;147:1011–8.10.1016/j.renene.2019.09.036Search in Google Scholar

[10] Guariglia E. Entropy and fractal antennas. Entropy. 2016;18:84.10.3390/e18030084Search in Google Scholar

[11] Berry M, Lewis Z. On the Weierstrass–Mandelbrot fractal function. Proc R Soc A. 1980;370:459–84.Search in Google Scholar

[12] Lefebvre AH, Wang XF, Martin CA. Spray characteristics of aerated-liquid pressure atomizers. J. Propul. Power. 1988;4:293–8.10.2514/3.23066Search in Google Scholar

[13] Zheng D, Wang J, Chen Z, Baleta J, Sundén B. Performance analysis of a plate heat exchanger using various nanofluids. Int J Heat Mass Transfer. 2020;158:119993.10.1016/j.ijheatmasstransfer.2020.119993Search in Google Scholar

[14] Lefebvre AH, Wang XF, Martin CA. Spray characteristics of aerated-liquid pressure atomizers. J Propuls Power. 1988;4:293–8.10.2514/3.23066Search in Google Scholar

[15] Wade RA, Weerts JM, Sojka PE, Gore JP, Eckerle WA. Effervescent atomization at injection pressures in the MPa range. Atomizat Sprays. 1999;9:651–67.10.1615/AtomizSpr.v9.i6.50Search in Google Scholar

[16] Wang J, Tian K, Zhu H, Zeng M, Sundén B. Numerical investigation of particle deposition in film-cooled blade leading edge. Numer Heat Transfer Part A Appl. 2020;77:579–98.10.1080/10407782.2020.1713692Search in Google Scholar

[17] Satapathy MR, Sovani SD, Sojka PE, Gore JP, Eckerle WA, Crofts JD. The effect of ambient density on the performance of an effervescent atomizer operating in the MPa injection pressure range. In: Proceedings of the CSS/CI 1998 technical meeting, 76–80, Lexington, KY (June 1998).Search in Google Scholar

[18] Sovani S, Sojka P, Lefebvre A. Effervescent atomization. Progr Energy Combust Sci. 2001;27:483–521.10.1016/S0360-1285(00)00029-0Search in Google Scholar

[19] Bayvel LP. Liquid atomization. New York: Routledge; 1993.Search in Google Scholar

[20] Karnawat J, Kushari A. Controlled atomization using a twin-fluid swirl atomizer. Exp Fluids. 2006;41:649–63.10.1007/s00348-006-0191-0Search in Google Scholar

[21] Sovani SD, Chou E, Sojka PE, Gore JP, Eckerle WA, Crofts JD. High pressure effervescent atomization: effect of ambient pressure on spray cone angle. Fuel. 2001;80:427–35.10.1016/S0016-2361(00)00105-8Search in Google Scholar

[22] Chen SK, Lefebvre AH. Spray cone angles of effervescent atomizers. Atomizat Spray. 1994;4:291–301.10.1615/AtomizSpr.v4.i3.40Search in Google Scholar

[23] Ochowiak M, Broniarz-Press L, Rozanski J. The discharge coefficient of effervescent atomizers. Exp Therm Fluid Sci. 2010;34:1316–23.10.1016/j.expthermflusci.2010.06.003Search in Google Scholar

[24] Lefebvre AH. Energy considerations in twin-fluid atomization. J Eng Gas Turbines Power Trans ASME. 1992;114:89–96.10.1115/90-GT-003Search in Google Scholar

[25] Beck JE, Lefebvre AH, Koblish TR. Airblast atomization at conditions of low air velocity. J Propuls Power. 1991;7:207–12.10.2514/6.1989-217Search in Google Scholar

[26] Jedelsky J and Jicha M. Energy conversion during effervescent atomization. Fuel. 2013;111:836–44.10.1016/j.fuel.2013.03.053Search in Google Scholar
Received: 2020-09-25
Revised: 2020-11-10
Accepted: 2020-11-12
Published Online: 2020-12-06

© 2020 Runze Duan et al., published by De Gruyter

This work is licensed under the Creative Commons Attribution 4.0 International License.

Articles in the same Issue

  1. Regular Articles
  2. Model of electric charge distribution in the trap of a close-contact TENG system
  3. Dynamics of Online Collective Attention as Hawkes Self-exciting Process
  4. Enhanced Entanglement in Hybrid Cavity Mediated by a Two-way Coupled Quantum Dot
  5. The nonlinear integro-differential Ito dynamical equation via three modified mathematical methods and its analytical solutions
  6. Diagnostic model of low visibility events based on C4.5 algorithm
  7. Electronic temperature characteristics of laser-induced Fe plasma in fruits
  8. Comparative study of heat transfer enhancement on liquid-vapor separation plate condenser
  9. Characterization of the effects of a plasma injector driven by AC dielectric barrier discharge on ethylene-air diffusion flame structure
  10. Impact of double-diffusive convection and motile gyrotactic microorganisms on magnetohydrodynamics bioconvection tangent hyperbolic nanofluid
  11. Dependence of the crossover zone on the regularization method in the two-flavor Nambu–Jona-Lasinio model
  12. Novel numerical analysis for nonlinear advection–reaction–diffusion systems
  13. Heuristic decision of planned shop visit products based on similar reasoning method: From the perspective of organizational quality-specific immune
  14. Two-dimensional flow field distribution characteristics of flocking drainage pipes in tunnel
  15. Dynamic triaxial constitutive model for rock subjected to initial stress
  16. Automatic target recognition method for multitemporal remote sensing image
  17. Gaussons: optical solitons with log-law nonlinearity by Laplace–Adomian decomposition method
  18. Adaptive magnetic suspension anti-rolling device based on frequency modulation
  19. Dynamic response characteristics of 93W alloy with a spherical structure
  20. The heuristic model of energy propagation in free space, based on the detection of a current induced in a conductor inside a continuously covered conducting enclosure by an external radio frequency source
  21. Microchannel filter for air purification
  22. An explicit representation for the axisymmetric solutions of the free Maxwell equations
  23. Floquet analysis of linear dynamic RLC circuits
  24. Subpixel matching method for remote sensing image of ground features based on geographic information
  25. K-band luminosity–density relation at fixed parameters or for different galaxy families
  26. Effect of forward expansion angle on film cooling characteristics of shaped holes
  27. Analysis of the overvoltage cooperative control strategy for the small hydropower distribution network
  28. Stable walking of biped robot based on center of mass trajectory control
  29. Modeling and simulation of dynamic recrystallization behavior for Q890 steel plate based on plane strain compression tests
  30. Edge effect of multi-degree-of-freedom oscillatory actuator driven by vector control
  31. The effect of guide vane type on performance of multistage energy recovery hydraulic turbine (MERHT)
  32. Development of a generic framework for lumped parameter modeling
  33. Optimal control for generating excited state expansion in ring potential
  34. The phase inversion mechanism of the pH-sensitive reversible invert emulsion from w/o to o/w
  35. 3D bending simulation and mechanical properties of the OLED bending area
  36. Resonance overvoltage control algorithms in long cable frequency conversion drive based on discrete mathematics
  37. The measure of irregularities of nanosheets
  38. The predicted load balancing algorithm based on the dynamic exponential smoothing
  39. Influence of different seismic motion input modes on the performance of isolated structures with different seismic measures
  40. A comparative study of cohesive zone models for predicting delamination fracture behaviors of arterial wall
  41. Analysis on dynamic feature of cross arm light weighting for photovoltaic panel cleaning device in power station based on power correlation
  42. Some probability effects in the classical context
  43. Thermosoluted Marangoni convective flow towards a permeable Riga surface
  44. Simultaneous measurement of ionizing radiation and heart rate using a smartphone camera
  45. On the relations between some well-known methods and the projective Riccati equations
  46. Application of energy dissipation and damping structure in the reinforcement of shear wall in concrete engineering
  47. On-line detection algorithm of ore grade change in grinding grading system
  48. Testing algorithm for heat transfer performance of nanofluid-filled heat pipe based on neural network
  49. New optical solitons of conformable resonant nonlinear Schrödinger’s equation
  50. Numerical investigations of a new singular second-order nonlinear coupled functional Lane–Emden model
  51. Circularly symmetric algorithm for UWB RF signal receiving channel based on noise cancellation
  52. CH4 dissociation on the Pd/Cu(111) surface alloy: A DFT study
  53. On some novel exact solutions to the time fractional (2 + 1) dimensional Konopelchenko–Dubrovsky system arising in physical science
  54. An optimal system of group-invariant solutions and conserved quantities of a nonlinear fifth-order integrable equation
  55. Mining reasonable distance of horizontal concave slope based on variable scale chaotic algorithms
  56. Mathematical models for information classification and recognition of multi-target optical remote sensing images
  57. Hopkinson rod test results and constitutive description of TRIP780 steel resistance spot welding material
  58. Computational exploration for radiative flow of Sutterby nanofluid with variable temperature-dependent thermal conductivity and diffusion coefficient
  59. Analytical solution of one-dimensional Pennes’ bioheat equation
  60. MHD squeezed Darcy–Forchheimer nanofluid flow between two h–distance apart horizontal plates
  61. Analysis of irregularity measures of zigzag, rhombic, and honeycomb benzenoid systems
  62. A clustering algorithm based on nonuniform partition for WSNs
  63. An extension of Gronwall inequality in the theory of bodies with voids
  64. Rheological properties of oil–water Pickering emulsion stabilized by Fe3O4 solid nanoparticles
  65. Review Article
  66. Sine Topp-Leone-G family of distributions: Theory and applications
  67. Review of research, development and application of photovoltaic/thermal water systems
  68. Special Issue on Fundamental Physics of Thermal Transports and Energy Conversions
  69. Numerical analysis of sulfur dioxide absorption in water droplets
  70. Special Issue on Transport phenomena and thermal analysis in micro/nano-scale structure surfaces - Part I
  71. Random pore structure and REV scale flow analysis of engine particulate filter based on LBM
  72. Prediction of capillary suction in porous media based on micro-CT technology and B–C model
  73. Energy equilibrium analysis in the effervescent atomization
  74. Experimental investigation on steam/nitrogen condensation characteristics inside horizontal enhanced condensation channels
  75. Experimental analysis and ANN prediction on performances of finned oval-tube heat exchanger under different air inlet angles with limited experimental data
  76. Investigation on thermal-hydraulic performance prediction of a new parallel-flow shell and tube heat exchanger with different surrogate models
  77. Comparative study of the thermal performance of four different parallel flow shell and tube heat exchangers with different performance indicators
  78. Optimization of SCR inflow uniformity based on CFD simulation
  79. Kinetics and thermodynamics of SO2 adsorption on metal-loaded multiwalled carbon nanotubes
  80. Effect of the inner-surface baffles on the tangential acoustic mode in the cylindrical combustor
  81. Special Issue on Future challenges of advanced computational modeling on nonlinear physical phenomena - Part I
  82. Conserved vectors with conformable derivative for certain systems of partial differential equations with physical applications
  83. Some new extensions for fractional integral operator having exponential in the kernel and their applications in physical systems
  84. Exact optical solitons of the perturbed nonlinear Schrödinger–Hirota equation with Kerr law nonlinearity in nonlinear fiber optics
  85. Analytical mathematical schemes: Circular rod grounded via transverse Poisson’s effect and extensive wave propagation on the surface of water
  86. Closed-form wave structures of the space-time fractional Hirota–Satsuma coupled KdV equation with nonlinear physical phenomena
  87. Some misinterpretations and lack of understanding in differential operators with no singular kernels
  88. Stable solutions to the nonlinear RLC transmission line equation and the Sinh–Poisson equation arising in mathematical physics
  89. Calculation of focal values for first-order non-autonomous equation with algebraic and trigonometric coefficients
  90. Influence of interfacial electrokinetic on MHD radiative nanofluid flow in a permeable microchannel with Brownian motion and thermophoresis effects
  91. Standard routine techniques of modeling of tick-borne encephalitis
  92. Fractional residual power series method for the analytical and approximate studies of fractional physical phenomena
  93. Exact solutions of space–time fractional KdV–MKdV equation and Konopelchenko–Dubrovsky equation
  94. Approximate analytical fractional view of convection–diffusion equations
  95. Heat and mass transport investigation in radiative and chemically reacting fluid over a differentially heated surface and internal heating
  96. On solitary wave solutions of a peptide group system with higher order saturable nonlinearity
  97. Extension of optimal homotopy asymptotic method with use of Daftardar–Jeffery polynomials to Hirota–Satsuma coupled system of Korteweg–de Vries equations
  98. Unsteady nano-bioconvective channel flow with effect of nth order chemical reaction
  99. On the flow of MHD generalized maxwell fluid via porous rectangular duct
  100. Study on the applications of two analytical methods for the construction of traveling wave solutions of the modified equal width equation
  101. Numerical solution of two-term time-fractional PDE models arising in mathematical physics using local meshless method
  102. A powerful numerical technique for treating twelfth-order boundary value problems
  103. Fundamental solutions for the long–short-wave interaction system
  104. Role of fractal-fractional operators in modeling of rubella epidemic with optimized orders
  105. Exact solutions of the Laplace fractional boundary value problems via natural decomposition method
  106. Special Issue on 19th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering
  107. Joint use of eddy current imaging and fuzzy similarities to assess the integrity of steel plates
  108. Uncertainty quantification in the design of wireless power transfer systems
  109. Influence of unequal stator tooth width on the performance of outer-rotor permanent magnet machines
  110. New elements within finite element modeling of magnetostriction phenomenon in BLDC motor
  111. Evaluation of localized heat transfer coefficient for induction heating apparatus by thermal fluid analysis based on the HSMAC method
  112. Experimental set up for magnetomechanical measurements with a closed flux path sample
  113. Influence of the earth connections of the PWM drive on the voltage constraints endured by the motor insulation
  114. High temperature machine: Characterization of materials for the electrical insulation
  115. Architecture choices for high-temperature synchronous machines
  116. Analytical study of air-gap surface force – application to electrical machines
  117. High-power density induction machines with increased windings temperature
  118. Influence of modern magnetic and insulation materials on dimensions and losses of large induction machines
  119. New emotional model environment for navigation in a virtual reality
  120. Performance comparison of axial-flux switched reluctance machines with non-oriented and grain-oriented electrical steel rotors
  121. Erratum
  122. Erratum to “Conserved vectors with conformable derivative for certain systems of partial differential equations with physical applications”
https://doi.org/10.1515/phys-2020-0214
Keywords for this article
effervescent atomization; energy dissipation analysis; Sauter mean diameter; swirl atomizer; droplets velocity; phase Doppler analyzer
Creative Commons
BY 4.0

Articles in the same Issue

  1. Regular Articles
  2. Model of electric charge distribution in the trap of a close-contact TENG system
  3. Dynamics of Online Collective Attention as Hawkes Self-exciting Process
  4. Enhanced Entanglement in Hybrid Cavity Mediated by a Two-way Coupled Quantum Dot
  5. The nonlinear integro-differential Ito dynamical equation via three modified mathematical methods and its analytical solutions
  6. Diagnostic model of low visibility events based on C4.5 algorithm
  7. Electronic temperature characteristics of laser-induced Fe plasma in fruits
  8. Comparative study of heat transfer enhancement on liquid-vapor separation plate condenser
  9. Characterization of the effects of a plasma injector driven by AC dielectric barrier discharge on ethylene-air diffusion flame structure
  10. Impact of double-diffusive convection and motile gyrotactic microorganisms on magnetohydrodynamics bioconvection tangent hyperbolic nanofluid
  11. Dependence of the crossover zone on the regularization method in the two-flavor Nambu–Jona-Lasinio model
  12. Novel numerical analysis for nonlinear advection–reaction–diffusion systems
  13. Heuristic decision of planned shop visit products based on similar reasoning method: From the perspective of organizational quality-specific immune
  14. Two-dimensional flow field distribution characteristics of flocking drainage pipes in tunnel
  15. Dynamic triaxial constitutive model for rock subjected to initial stress
  16. Automatic target recognition method for multitemporal remote sensing image
  17. Gaussons: optical solitons with log-law nonlinearity by Laplace–Adomian decomposition method
  18. Adaptive magnetic suspension anti-rolling device based on frequency modulation
  19. Dynamic response characteristics of 93W alloy with a spherical structure
  20. The heuristic model of energy propagation in free space, based on the detection of a current induced in a conductor inside a continuously covered conducting enclosure by an external radio frequency source
  21. Microchannel filter for air purification
  22. An explicit representation for the axisymmetric solutions of the free Maxwell equations
  23. Floquet analysis of linear dynamic RLC circuits
  24. Subpixel matching method for remote sensing image of ground features based on geographic information
  25. K-band luminosity–density relation at fixed parameters or for different galaxy families
  26. Effect of forward expansion angle on film cooling characteristics of shaped holes
  27. Analysis of the overvoltage cooperative control strategy for the small hydropower distribution network
  28. Stable walking of biped robot based on center of mass trajectory control
  29. Modeling and simulation of dynamic recrystallization behavior for Q890 steel plate based on plane strain compression tests
  30. Edge effect of multi-degree-of-freedom oscillatory actuator driven by vector control
  31. The effect of guide vane type on performance of multistage energy recovery hydraulic turbine (MERHT)
  32. Development of a generic framework for lumped parameter modeling
  33. Optimal control for generating excited state expansion in ring potential
  34. The phase inversion mechanism of the pH-sensitive reversible invert emulsion from w/o to o/w
  35. 3D bending simulation and mechanical properties of the OLED bending area
  36. Resonance overvoltage control algorithms in long cable frequency conversion drive based on discrete mathematics
  37. The measure of irregularities of nanosheets
  38. The predicted load balancing algorithm based on the dynamic exponential smoothing
  39. Influence of different seismic motion input modes on the performance of isolated structures with different seismic measures
  40. A comparative study of cohesive zone models for predicting delamination fracture behaviors of arterial wall
  41. Analysis on dynamic feature of cross arm light weighting for photovoltaic panel cleaning device in power station based on power correlation
  42. Some probability effects in the classical context
  43. Thermosoluted Marangoni convective flow towards a permeable Riga surface
  44. Simultaneous measurement of ionizing radiation and heart rate using a smartphone camera
  45. On the relations between some well-known methods and the projective Riccati equations
  46. Application of energy dissipation and damping structure in the reinforcement of shear wall in concrete engineering
  47. On-line detection algorithm of ore grade change in grinding grading system
  48. Testing algorithm for heat transfer performance of nanofluid-filled heat pipe based on neural network
  49. New optical solitons of conformable resonant nonlinear Schrödinger’s equation
  50. Numerical investigations of a new singular second-order nonlinear coupled functional Lane–Emden model
  51. Circularly symmetric algorithm for UWB RF signal receiving channel based on noise cancellation
  52. CH4 dissociation on the Pd/Cu(111) surface alloy: A DFT study
  53. On some novel exact solutions to the time fractional (2 + 1) dimensional Konopelchenko–Dubrovsky system arising in physical science
  54. An optimal system of group-invariant solutions and conserved quantities of a nonlinear fifth-order integrable equation
  55. Mining reasonable distance of horizontal concave slope based on variable scale chaotic algorithms
  56. Mathematical models for information classification and recognition of multi-target optical remote sensing images
  57. Hopkinson rod test results and constitutive description of TRIP780 steel resistance spot welding material
  58. Computational exploration for radiative flow of Sutterby nanofluid with variable temperature-dependent thermal conductivity and diffusion coefficient
  59. Analytical solution of one-dimensional Pennes’ bioheat equation
  60. MHD squeezed Darcy–Forchheimer nanofluid flow between two h–distance apart horizontal plates
  61. Analysis of irregularity measures of zigzag, rhombic, and honeycomb benzenoid systems
  62. A clustering algorithm based on nonuniform partition for WSNs
  63. An extension of Gronwall inequality in the theory of bodies with voids
  64. Rheological properties of oil–water Pickering emulsion stabilized by Fe3O4 solid nanoparticles
  65. Review Article
  66. Sine Topp-Leone-G family of distributions: Theory and applications
  67. Review of research, development and application of photovoltaic/thermal water systems
  68. Special Issue on Fundamental Physics of Thermal Transports and Energy Conversions
  69. Numerical analysis of sulfur dioxide absorption in water droplets
  70. Special Issue on Transport phenomena and thermal analysis in micro/nano-scale structure surfaces - Part I
  71. Random pore structure and REV scale flow analysis of engine particulate filter based on LBM
  72. Prediction of capillary suction in porous media based on micro-CT technology and B–C model
  73. Energy equilibrium analysis in the effervescent atomization
  74. Experimental investigation on steam/nitrogen condensation characteristics inside horizontal enhanced condensation channels
  75. Experimental analysis and ANN prediction on performances of finned oval-tube heat exchanger under different air inlet angles with limited experimental data
  76. Investigation on thermal-hydraulic performance prediction of a new parallel-flow shell and tube heat exchanger with different surrogate models
  77. Comparative study of the thermal performance of four different parallel flow shell and tube heat exchangers with different performance indicators
  78. Optimization of SCR inflow uniformity based on CFD simulation
  79. Kinetics and thermodynamics of SO2 adsorption on metal-loaded multiwalled carbon nanotubes
  80. Effect of the inner-surface baffles on the tangential acoustic mode in the cylindrical combustor
  81. Special Issue on Future challenges of advanced computational modeling on nonlinear physical phenomena - Part I
  82. Conserved vectors with conformable derivative for certain systems of partial differential equations with physical applications
  83. Some new extensions for fractional integral operator having exponential in the kernel and their applications in physical systems
  84. Exact optical solitons of the perturbed nonlinear Schrödinger–Hirota equation with Kerr law nonlinearity in nonlinear fiber optics
  85. Analytical mathematical schemes: Circular rod grounded via transverse Poisson’s effect and extensive wave propagation on the surface of water
  86. Closed-form wave structures of the space-time fractional Hirota–Satsuma coupled KdV equation with nonlinear physical phenomena
  87. Some misinterpretations and lack of understanding in differential operators with no singular kernels
  88. Stable solutions to the nonlinear RLC transmission line equation and the Sinh–Poisson equation arising in mathematical physics
  89. Calculation of focal values for first-order non-autonomous equation with algebraic and trigonometric coefficients
  90. Influence of interfacial electrokinetic on MHD radiative nanofluid flow in a permeable microchannel with Brownian motion and thermophoresis effects
  91. Standard routine techniques of modeling of tick-borne encephalitis
  92. Fractional residual power series method for the analytical and approximate studies of fractional physical phenomena
  93. Exact solutions of space–time fractional KdV–MKdV equation and Konopelchenko–Dubrovsky equation
  94. Approximate analytical fractional view of convection–diffusion equations
  95. Heat and mass transport investigation in radiative and chemically reacting fluid over a differentially heated surface and internal heating
  96. On solitary wave solutions of a peptide group system with higher order saturable nonlinearity
  97. Extension of optimal homotopy asymptotic method with use of Daftardar–Jeffery polynomials to Hirota–Satsuma coupled system of Korteweg–de Vries equations
  98. Unsteady nano-bioconvective channel flow with effect of nth order chemical reaction
  99. On the flow of MHD generalized maxwell fluid via porous rectangular duct
  100. Study on the applications of two analytical methods for the construction of traveling wave solutions of the modified equal width equation
  101. Numerical solution of two-term time-fractional PDE models arising in mathematical physics using local meshless method
  102. A powerful numerical technique for treating twelfth-order boundary value problems
  103. Fundamental solutions for the long–short-wave interaction system
  104. Role of fractal-fractional operators in modeling of rubella epidemic with optimized orders
  105. Exact solutions of the Laplace fractional boundary value problems via natural decomposition method
  106. Special Issue on 19th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering
  107. Joint use of eddy current imaging and fuzzy similarities to assess the integrity of steel plates
  108. Uncertainty quantification in the design of wireless power transfer systems
  109. Influence of unequal stator tooth width on the performance of outer-rotor permanent magnet machines
  110. New elements within finite element modeling of magnetostriction phenomenon in BLDC motor
  111. Evaluation of localized heat transfer coefficient for induction heating apparatus by thermal fluid analysis based on the HSMAC method
  112. Experimental set up for magnetomechanical measurements with a closed flux path sample
  113. Influence of the earth connections of the PWM drive on the voltage constraints endured by the motor insulation
  114. High temperature machine: Characterization of materials for the electrical insulation
  115. Architecture choices for high-temperature synchronous machines
  116. Analytical study of air-gap surface force – application to electrical machines
  117. High-power density induction machines with increased windings temperature
  118. Influence of modern magnetic and insulation materials on dimensions and losses of large induction machines
  119. New emotional model environment for navigation in a virtual reality
  120. Performance comparison of axial-flux switched reluctance machines with non-oriented and grain-oriented electrical steel rotors
  121. Erratum
  122. Erratum to “Conserved vectors with conformable derivative for certain systems of partial differential equations with physical applications”
Sign up now to receive a 20% welcome discount
Institutional Access
How does access work?
Have an idea on how to improve our website?
Please write us.
© 2025 De Gruyter Brill
Downloaded on 15.9.2025 from https://www.degruyterbrill.com/document/doi/10.1515/phys-2020-0214/html
Scroll to top button