Development of a generic framework for lumped parameter modeling

Shuo Yang; Yacine Amara; Wei Hua; Georges Barakat

doi:10.1515/phys-2020-0168

Article Open Access

Development of a generic framework for lumped parameter modeling

Shuo Yang , Yacine Amara , Wei Hua and Georges Barakat

Published/Copyright: July 28, 2020

Published by

Become an author with De Gruyter Brill

Submit Manuscript Author Information Explore this Subject

From the journal Open Physics Volume 18 Issue 1

Abstract

The purpose of this article is to present a generic reluctance network modeling tool dedicated to the modeling of electrical machines. This tool is used for the study of permanent magnet machines. The focus will be on the modeling methodology and software implementation. More precisely, the aspects related to genericity will be discussed. In order to validate the developed tool, the simulation of a 12 slot/10 pole flux-switching permanent magnet machine is conducted, and the results obtained from this generic framework are compared to the corresponding finite element analysis.

Keywords: equivalent circuit modeling; reluctance network; generic framework; permanent magnet machines; flux-switching

1 Introduction

The lumped parameter method (LPM) presents a good compromise between analytical methods, which are known for their reduced computation burden, and numerical methods, mainly the finite element method (FEM), which are known for their relatively good agreement with experimental measurements, when done with the minimum simplifying assumptions. The LPM helps reduce the computation time, while not increasing the number of simplifying assumptions. When used for the modeling of electromagnetic devices, the LPM is known as the magnetic equivalent circuit or the reluctance network (RN) [1,2]. In this contribution, efforts toward the development of a generic framework for the RN approach are presented. As finite element analysis (FEA), the first step in this framework is to mesh the studied domain using reluctance elements and then generate the corresponding algebraic equation system. The following steps are the solving of the generated equation system and exploitation of the obtained results for the analysis of the studied device.

Flux-switching permanent magnet (FSPM) machines are gaining in popularity due to their robustness, wide speed range, high torque, and high power density [3,4,5]. It is shown that FSPM machines have a higher air gap flux density due to the flux focusing effect and fewer mechanical issues in the rotor compared to surface permanent magnet (PM) machines [6]. However, the dual-salient structure results in higher harmonic orders of flux density in the air gap, which require a more refined mesh in FEA. Several studies [7,8,9] have presented a good agreement and a better performance of the mesh-based RN method used in FSPM machine computation, but they only focused on a limited aspect of global quantities, and the saturation is frequently ignored, which is a dominating phenomenon in FSPM machines. In this work, a generic framework for a mesh-based and interpolation coupled RN method is proposed, including a more programming oriented mathematical model and an extensible tool. Then, the global quantities of a 12 slot/10 pole FSPM machine are calculated using the tool. Compared to the method used in ref. [10], a mesh-based pre-processing and the application of the interpolation method on the motion interface avoid the specific knowledge of the investigated machines and increase the genericity of the RN method. Moreover, by using the connectivity matrix, a more programming-suitable formulation is obtained.

In the next sections, the framework will be more thoroughly described. The focus will be on the modeling methodology and software implementation. More precisely, the aspects related to genericity will be discussed. In order to validate the developed tool, the results obtained from this framework are compared to the corresponding FEA.

2 Framework presentation

Aspects related to the mathematical modeling and software implementation of the developed tool are discussed in Sections 2.1 and 2.2 in detail. Compared to previous studies on the subject, where the focus was on mathematical aspects and validation, efforts toward the building of a generic computational model are highlighted.

2.1 Mathematical model

The geometry is discretized in a number of bidirectional elementary reluctance blocks as shown in Figure 1. R _x1, R _x2, and R _y1, R _y2 are the reluctances on the x- and y-axis branches of the block element, respectively. Compared to previous studies, elements are allowed to be attached with two kinds of materials, which enables establishing a more precise model for sloping sides in machines.

(1) R x 1 = 1 μ i T x R x 2 = 1 μ j T x R y 1 = 1 μ i T y R y 2 = 1 μ j T y ,

where T _x and T _y are shape functions in the x- and y-direction, determined by the shape and size of elements. μ _i and μ _j are different permeabilities assigned to the element.

Figure 1

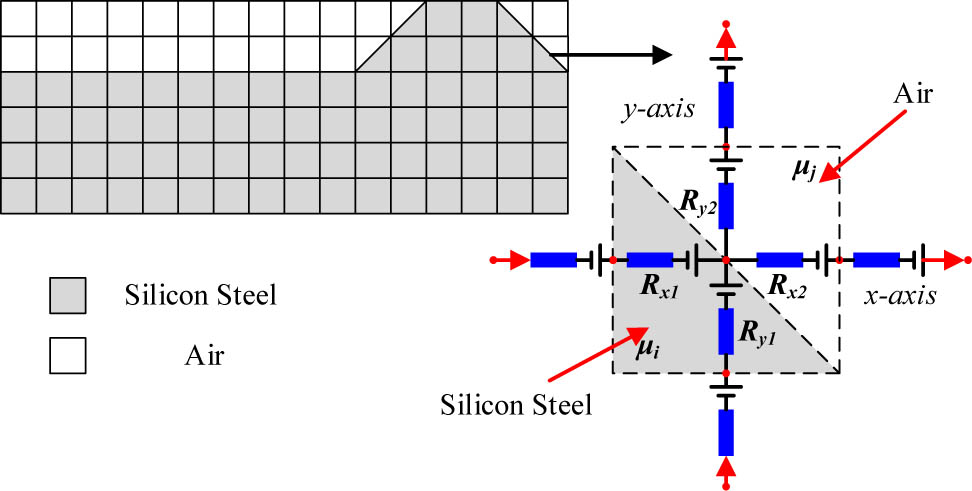
Reluctance block elements.

The circuit solver is developed based on Kirchhoff’s laws [11]. It can be established for a network containing N _n nodes and N _b branches as follows:

(2) C Φ B = − C Φ B s ,

where Φ _B is the vector of the fluxes on branches, Φ B s is the vector of the fluxes generated by current sources, such as a PM and current. C is a connectivity matrix of N _n × N _b size, and the item C _ij is defined as follows:

(3) C i j = 0 if node i and branch j are not connected 1 if branch j flows out of node i − 1 if branch j flows into node i .

According to Ohm’s law, Φ _B and Φ B s can be written as:

(4) Φ B = P U Φ B s = P F ,

where U, P, and F are the voltage vector, the diagonal matrix of permeance, and the magneto-motive force (MMF) source vector, respectively. And the conversion between the voltage U and the node potential V can be expressed as:

(5) U = C T V .

Consequently, equation (2) is transformed into

(6) C P C T V = − C P F .

MMF sources due to the PM need to be placed on the branches of the magnetization direction in the elements through all layers of PM areas, where each source is calculated as shown in equation (7) [12]. H _c is the PM magnetic coercivity, and l _mag is the length along the magnetization direction for each element (Figure 2).

(7) F pm,e = H c l mag,e .

To obey Ampere’s circuital law, MMF sources due to current need to model the distribution of MMF in the air gap first, which is a function of spatial position according to the winding distribution, denoted as F _g(x,t). φ _A(x), φ _B(x), and φ _C(x) are defined as the functions of MMF distribution in the air gap, when the unit current is provided for each phase. x is the x-axis coordinate of each element. Combining the spatial position function with the three-phase input current, we have

(8) F A ( x , t ) = I m cos ( ω t + θ ) φ A ( x ) F B ( x , t ) = I m cos ( ω t + θ − 120 ) φ B ( x ) F C ( x , t ) = I m cos ( ω t + θ + 120 ) φ C ( x ) ,

where F _A, F _B, and F _C are the functions of MMF distribution changing with time. By summing them up, the expression of F _g(x,t) is

(9) F g ( x , t ) = F A ( x , t ) + F B ( x , t ) + F C ( x , t ) .

Figure 2

Modeling of the PM unit.

Figure 3 shows the MMF distribution in the air gap, when setting t = 0 s, θ = 0°. Then, the MMF value contributed by each element should be calculated using the proportion to the whole current area at the corresponding point.

(10) F l,e = l l,e h w F g ( x c,e , t ) ,

where h _w is the height of the winding area and l _l,e is the length along the magnetization direction for each element.

Figure 3

MMF distribution in the air gap.

The main principle of motion handling is to avoid regenerating the mesh in the studied domain with no or little compromise in precision. An interpolation method is employed here, based on the continuity of the scalar magnetic potential and the continuity of the flux density normal component at the sliding interface (Figure 4).

(11) V s i = V r i ′ = x s i − x r i x r ( i + 1 ) − x r i V r i + x s i − x r i + 1 x r i − x r i + 1 V r i + 1 B r i = B s i ' = x r i − x s i x s i − 1 − x s i B s i + x r i − x s i − 1 x s i − x s i − 1 B s i − 1 .

The subscripts s and r are used to denote the values from the stator side and the rotor side. Equation (11) shows a linear interpolation on the interface, and for the interpolation of k orders, the formulation is as follows:

(12) V s i = V r i ′ = ∑ j = 0 k ∏ t = 0 , t ≠ j k x s i − x r t x r j − x r t V r j B r i = B s i ′ = ∑ j = 0 k ∏ t = 0 , t ≠ j k x r i − x s t x s j − x s t B s j .

By using the projection against a specific direction, we can obtain the normal component of the flux density of interface nodes from the connecting branch components.

Figure 4

Interface between the rotor and the stator.

Apart from the sliding interface, the RN is also defined by the Dirichlet boundary condition and the periodic or anti-periodic condition (Figure 5). For node n _Dk, we have

(13) V n D k = 0 .

For node i and node j, no matter what kind of boundary condition is assigned, they are viewed as adjacent elements, so they are connected by a branch, denoted as b. When using the periodic condition, we create the connectivity matrix as per the definition in equation (3). When using the anti-periodic condition, element C _jb in the connectivity matrix is set to 1 rather than −1.

Figure 5

Boundary condition.

The Newton–Raphson method is a technique used for solving nonlinear equations numerically [13]. This method uses an iterative process to approach one root of a function, and this root depends on the initial value. For equation (2), we can write

(14) V k + 1 = V k − J − 1 f ( V k )

knowing that

(15) f ( V k ) = C P ( V k ) C T V k + C P ( V k ) F

(16) J = ∂ f ∂ V = C C T ∘ ∂ P ∂ V V + C ( C T ∘ P ) + C F ∘ ∂ P ∂ V ,

where operator ∘ is the element-wise product.

(17) ∂ P ∂ V = ∂ p 1 ∂ v 1 ⋯ ∂ p 1 ∂ v N n ⋮ ⋱ ⋮ ∂ p N b ∂ v 1 ⋯ ∂ p N b ∂ v N n .

Branch b connects node i and node j, and by considering each part in two adjacent elements of a unique branch separately, the derivative of permeance with respect to node potentials is obtained from the corresponding components based on the expression of permeance calculation.

(18) ∂ p b ∂ v n = 1 l b R b 2 T i μ i 2 μ ̇ i + T j μ j 2 μ ̇ j ∂ V i − V j ∂ V n n = i , j 0 n ≠ i , j ,

where l _b is the length of branch b. Note that the Dirichlet boundary condition and interpolation formulation at the sliding interface modify some values in the coefficient matrix of linear equations, but they have no effect on the calculation of the Jacobian matrix. Accordingly, these items are set to zero after getting the Jacobian matrix using equation (13).

2.2 Tool structure

The framework is developed in four layers to provide genericity, flexibility, and extensibility (Figure 7). The frontal layer is a designing part serviced by widely used mesh tools. Apart from commercial software like ANSYS^® and FLUXTM, GMSH is an open-source toolkit with a powerful and fast mesh function. In this study, an Excel worksheet constructed in a specific format that describes the structure of the machine is used as an input file (Figure 6).

Figure 6

Format of describing the structure of the machine in EXCEL.

Figure 7

Implementation of the tool.

Then, the framework reads the generated file into the circuit generator layer using an adaptor, which decodes the mesh information according to the pre-setting rules. The Excel worksheet in Figure 6 contains dimensions and confined mesh instructs for ExcelAdaptor to decide the concrete mesh scheme. DomainManager helps to manage the geometry properties of the studied domain and generate the size data for each element. Coupled with object Winding and object MaterialManager, DomainManager is processed by object CircuitGenerator, which provides the circuit descriptor encapsulating detailed information of branches that are required in object Assembler during iterations. MaterialManager offers the function of maintaining properties defined by users and helps to manage different types of materials especially nonlinear materials. Also, an interface is opened to accept the customer defined B–H curve fitting function. By default, the program uses an analytic saturation curve with knee adjustment.

(19) B ( H ) = μ 0 H + J s 2 ( 1 − a ) H a + 1 − ( H a + 1 ) 2 − 4 H a ( 1 − a ) ,

where

(20) H a = μ 0 ( μ r − 1 ) H J s .

The implementation of object Winding depends on different configurations of winding, which means that distributed windings and concentrated windings ought to be modeled in two ways. CircuitGenerator calls the unified interface to get the function F _g(x,t) in the air gap when producing an MMF distribution model in the initial state to accelerate the solving process.

Figure 8 shows the main process of simulation at each time step in the circuit solver layer, when users launch a new analysis. Due to the nonlinear properties of materials, the circuit solver layer is developed in two types of iterative methods: fixed-point method and Newton–Raphson method. The Newton–Raphson method approaches a sufficiently precise value much faster than the fixed-point method because of using the tangent of the graph, but sometimes it is unable to reach a convergence as stable as the others. So in the program, both methods are provided. The construction of the Jacobian matrix has been described in the last section. The core solvers of fields are divided in single modules so that users are capable of building their own solver on these stable functions.

Figure 8

Process of the circuit solver layer.

The circuit solver layer inquires the upper layer to obtain the updated magnetic state through the specified interface at each step, which ensures the decoupling between two layers so that users are capable of designing their own modules by utilizing the well-encapsulated modules. Overloading of the default motion and boundary processing function is supported in the program, so a more effective motion handling method like the hybrid analytical method, which performs better in calculating the magnetic field in the air gap, is obtained.

All fields output by the circuit solver layer are registered in the DomainManager and exported to the CSV format, a type of file supported by many programs for post-processing.

3 Validation of the developed tool

In this section, a concrete validation study is described to highlight the good operation and correctness of the developed tool.

3.1 Structure presentation

The structure in Figure 9 is a classical 12/10 FSPM machine with concentrated windings, which has been analyzed in many previous cases. Although the dimensions of the machine were chosen to simplify the modeling study, the values can be set as any number in actual application. Table 1 gives the main machine characteristics.

Figure 9

Studied structure.

Table 1

Machine parameters

Mechanical air-gap (mm)	0.35
r _so, r _si, r _ri (mm)	128, 70.4, 22
θ ₁, θ ₂, θ ₃, θ ₄ (°)	7.5, 15, 7.5, 7.5
l ₁ (mm)	4.6
Magnetization type	Circumferential magnetization
PM magnetic remanence (T)	1.12
Axial length (mm)	75
Speed (rpm)	480
Peak current (A)	10
Coil turns	70

3.2 Validation study

The comparisons shown in Figures 10–14 are between the FEM model meshed with 18,756 nodes and the RN model meshed with 4,800 nodes. Local quantities, such as the tangential and normal component of air gap flux density (Figures 10 and 12); global quantities, such as flux linkage and induced voltage versus time (Figures 11 and 13); torque; and iron loss (Figure 14) are evaluated by the classical method used in FEM. Flux linkage is the sum of fluxes (in the r-axis) passing through all block elements located at slot mid-height spanning one coil pitch. The electromotive force is obtained by the differentiation of the phase flux. The Maxwell stress tensor method is used for the computation of torque. For iron loss estimation, the experimentally verified iron loss model is used here [14]:

(21) P core = P h + P c + P a ,

(22) P h = k h f B m β P c = k c f 2 B m 2 P a = k a f 1.5 B m 1.5 ,

where P _h, P _c, and P _e are, respectively, static hysteresis loss, classical eddy current loss, and excess loss; k _h, k _c, and k _e are the coefficients of the corresponding loss component; f and B _m are the frequency and amplitude of the fundamental flux density; and β is an empirical parameter obtained from experimental measurement.

Figure 10

Air-gap magnetic flux density component comparison, I _m = 0 A. (a) Normal component and (b) tangential component.

Figure 11

Flux linkage and EMF comparison, I _m = 0 A. (a) Flux linkage and (b) induced voltage.

Figure 12

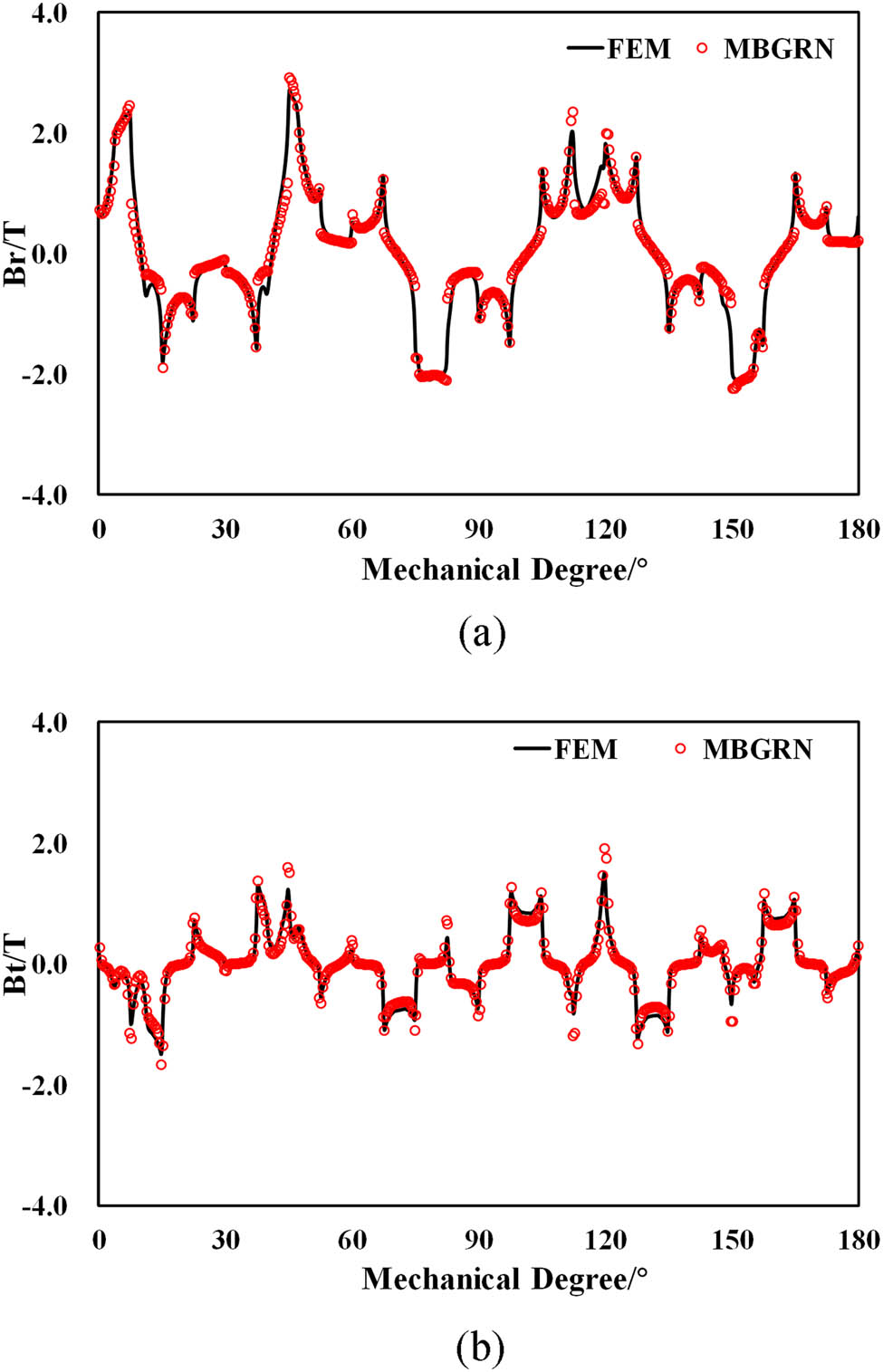
Air-gap magnetic flux density component comparison, I _m = 10 A. (a) Normal component and (b) tangential component.

Figure 13

Flux linkage and EMF comparison, I _m = 10 A. (a) Flux linkage and (b) Induced voltage.

Figure 14

Torque and iron loss versus input current. (a) Torque versus current amplitude. (b) Iron loss versus current amplitude.

Table 2

Errors of the proposed method compared to FEA

I _m (A)	Flux (error %)	Voltage (error %)	Torque (error %)	Iron loss (error %)
0	1.22	1.25	—	1.03
10	1.56	1.78	2.48	2.25

As the FEA model is used as a reference, it is indicated that the RN model achieves a very good agreement with fewer nodes and faster computation speed. The errors of the flux linkages and the voltage waveforms could be obtained by comparing their RMS values obtained from both approaches, and the maximum error is lower than a few percent. For the torque and the core loss, the error is obtained by directly comparing the values of these quantities, and again the error is lower than a few percent (Table 2).

4 Conclusion

In this article, a generic calculating framework for lumped parameter modeling has been presented. The universal mathematical model has been put forward in the matrix format, based on which the structure of a flexible and extensible solver was discussed in detail. The adaptive mesh-based discretization and MMF source distribution techniques allow easy handling of different electromagnetic structures with different properties.

The interpolation method employed in modeling motion components avoids re-meshing at each time-step. Nonlinearities are considered in the solver, by combining the fixed-point method and the Newton–Raphson method. A fairly good agreement between the proposed tool and the commercial FEM software, in terms of flux density, flux linkage, induced voltage, torque, and loss, is obtained. It is a good step toward a powerful and easy-to-use RN tool in the pre-design stage.

Acknowledgments

The authors would like to thank the CNRS (GdR SEEDS 2994 du CNRS), National Natural Science Foundation of China under Grant no. 51825701, Key R&D Program of Jiangsu Province under Grant no. BE2019073, and Université Le Havre Normandie (GREAH) for the funding of this work.

References

[1] Ostovic V. Dynamics of saturated electric machines. New York: Springer-Verlag; 1989.10.1007/978-1-4613-8933-0Search in Google Scholar

[2] Amrhein M, Krein PT. 3-D magnetic equivalent circuit framework for modeling electromechanical devices. IEEE Trans Energy Convers. June 2009;24(2):397–405.10.1109/TEC.2009.2016134Search in Google Scholar

[3] Shao L, Hua W, Zhu ZQ, Zhu X, Cheng M, Wu Z. A novel flux-switching permanent magnet machine with overlapping windings. IEEE Trans Energy Convers. Mar. 2017;32(1):172–83.10.1109/TEC.2016.2611139Search in Google Scholar

[4] Zhu X, Shu Z, Quan L, Xiang Z, Pan X. Multi-objective optimization of an outer-rotor V-shaped permanent magnet flux switching motor based on multi-level design method. IEEE Trans Magn. Oct. 2016;52(10):1–8.10.1109/TMAG.2016.2581767Search in Google Scholar

[5] Hua W, Zhang H, Cheng M, Meng J, Hou C. An outer-rotor flux-switching permanent-magnet-machine with wedge-shaped magnets for in-wheel light traction. IEEE Trans Ind Electron. Jan. 2017;64(1):69–80.10.1109/TIE.2016.2610940Search in Google Scholar

[6] Liu M, Sixel W, Sarlioglu B. Comparative study of 6/4 FSPM and SPM machine for high-speed applications. 2019 IEEE Transportation Electrification Conference and Expo (ITEC). Detroit, MI, USA: 2019. p. 1–7.10.1109/ITEC.2019.8790622Search in Google Scholar

[7] Ouagued S, Amara Y, Barakat G. Comparison of hybrid analytical modelling and reluctance network modelling for pre-design purposes. Math Comp Simul. 2016;130:3–21.10.1016/j.matcom.2016.05.001Search in Google Scholar

[8] Lo DS, Lawali Ali H, Amara Y, Barakat G, Chabour F. Computation of cogging force of a linear tubular flux-switching permanent magnet machine using a hybrid analytical modeling. IEEE Trans Magn. Nov. 2018;54(11):1–5.10.1109/INTMAG.2018.8508771Search in Google Scholar

[9] Benhamida MA, Ennassiri H, Amara Y, Barakat G, Debbah N. Study of switching flux permanent magnet machines using interpolation based reluctance network model. 2016 International Conference on Electrical Sciences and Technologies in Maghreb (CISTEM), Marrakech, 2016. Nov. 2018. p. 1–7.110205.Search in Google Scholar

[10] Zhu ZQ, Pang Y, Howe D, Iwasaki S, Deodhar R, Pride A. Analysis of electromagnetic performance of flux-switching permanent-magnet machines by nonlinear adaptive lumped parameter magnetic circuit model. IEEE Trans Magnet. Nov. 2005;41(11):4277–87.10.1109/TMAG.2005.854441Search in Google Scholar

[11] Delale A, Albert L, Gerbaud L, Wurtz F. Automatic generation of sizing models for the optimization of electromagnetic devices using reluctance networks. IEEE Trans Magn. March 2004;2:830–3.10.1109/TMAG.2004.824908Search in Google Scholar

[12] Asfirane S, Hlioui S, Amara Y, Barriere ODL, Barakat G, Gabsi M. Global quantities computation using mesh-based generated reluctance networks. IEEE Trans Magnetics. Nov. 2018;54(11):1–4. Art 7002304.10.1109/INTMAG.2018.8508215Search in Google Scholar

[13] Yang X, Mittal R. Acceleration of the Jacobi iterative method by factors exceeding 100 using scheduled relaxation. J Comput Phys. October 2014;274:695–708.10.1016/j.jcp.2014.06.010Search in Google Scholar

[14] Lin D, Zhou P, Fu WN, Badics Z, Cendes ZJ. A dynamic core loss model for soft ferromagnetic and power ferrite materials in transient finite element analysis. IEEE Trans Magnet. March 2004;40(2):1318–21.10.1109/TMAG.2004.825025Search in Google Scholar

Received: 2020-01-30

Revised: 2020-05-28

Accepted: 2020-06-03

Published Online: 2020-07-28

This work is licensed under the Creative Commons Attribution 4.0 International License.

Articles in the same Issue

https://doi.org/10.1515/phys-2020-0168

Keywords for this article

equivalent circuit modeling; reluctance network; generic framework; permanent magnet machines; flux-switching

Creative Commons

BY 4.0