Home Uncertainty quantification in the design of wireless power transfer systems
Article Open Access

Uncertainty quantification in the design of wireless power transfer systems

  • Yao Pei , Lionel Pichon EMAIL logo , Mohamed Bensetti and Yann Le-Bihan
Published/Copyright: July 30, 2020
Download Article (PDF)
Open Physics
From the journal Open Physics Volume 18 Issue 1

Abstract

The paper addresses the uncertainty quantification of physical and geometrical material parameters in the design of wireless power transfer systems. For 3D complex systems, a standard Monte Carlo cannot be directly used to extract statistical quantities. So, surrogate models based on Kriging or polynomial chaos expansions are built to study the impact of variable parameters on the radiated magnetic field and efficiency. Such fast prediction of uncertainties in the parameters of the system can improve the design of inductive power transfer systems taking into account human exposure recommendations and variability of the parameters.

Keywords: EMC; wireless transfer; uncertainty quantification; shielding; efficiency

1 Introduction

In recent years, inductive power transfer (IPT) systems have been widely developed in several fields such as biomedical engineering, consumer electronics, and automotive industry. In automotive applications, the coupling between the transmitter, which is placed on the ground, and the receiver, which is placed under the floor of the vehicle, leads to a large gap. This large space implies a high level of stray field near the coils, which can pose a problem of exposure to magnetic fields for passengers or persons likely to approach the vehicle during charging operations [1,2,3,4,5]. The stray field depends on the power level and shielding effectiveness (SE) of the charging pads. It is therefore important to evaluate the efficiency of the system and the SE. The properties of shields are very dependent on many parameters (thickness, number of layers, electromagnetic properties, etc.) [6] and these parameters may be affected by uncertainties (measurements errors, approximations) having a significant impact on the performances of the system.

For such uncertainty propagation studies, statistical methods based on Monte Carlo approaches are used [7]. For example, analytical simulations illustrate in ref. [8] the influence of material properties on the SE of planar sheets with a Monte Carlo technique. Two simple standard configurations were analyzed. The first case considers a source loop in a low frequency range of 0–100 kHz. Such standard geometry is a basic situation in IPT [9]. The second one deals with a plane wave in a high frequency range of 0–10 GHz which is relevant to general electromagnetic compatibiliy (EMC) studies involving composite materials [10].

However, with such a Monte Carlo approach, a large set of inputs are considered and many evaluations of a model response are needed. This leads to a heavy computational cost in case of complex system configurations. To avoid the computational burden and deal with a large variability of data, it can be very useful to build adequate metamodels (or surrogate models). A metamodel is an approximated model, built with a reduced set of input data, and whose behavior is representative of the original model for all data. Metamodeling is a well-known procedure in reliability and uncertainty propagation in mechanics. It is based on stochastic techniques (Kriging, polynomial chaos expansions [PCE]). In electromagnetics, similar approaches have been developed in electromagnetic compatibility problems and human exposure evaluation [11,12,13]. Recently, the quantification of uncertainty relevant to electrical parameters of a simple wireless transfer system was studied using a PCE [14]: both the transmitter and receiver units have simple shapes and only consist of a resonant coil (helical or spiral) and a matching loop. In ref. [15] Kriging was combined with a finite element software for the design of an IPT system.

This paper presents the study of uncertainty propagation in the design of 3D wireless power systems taking into account the shielding structures. It extends the work presented in ref. [16] where preliminary results dealing with the stray field emitted from an IPT system were considered. A Monte Carlo approach cannot be applicable because of too heavy computational cost. Instead, surrogate models based on Kriging and PCE are presented and applied to two simplified but realistic 3D IPT systems. The first one was built in Politecnico di Torino [16,17] and the second one in GeePs [18]. The stochastic techniques easily take into account the variability of different parameters defining the 3D configurations. In particular, the results show that with a reduced set of input data, accurate predictions relevant to the stray field or mutual inductance can be obtained over a wide range of parameters. This allows making easier any sensitivity analysis when designing the system with appropriate shielding structural parts.

2 Wireless power system (Polito di Torino)

2.1 Studied configuration

The structure considered in this section contains two rectangular coils (the transmitter and the receiver) and two ferrite plates. This test case corresponds to an existing inductive power system that has been built in Politecnico di Torino, Italy [17]. Preliminary results have been published in ref. [16]. The design includes a steel plate that represents the chassis of the electric vehicle (Figure 1). The dimensions of the system are shown in Table 1. The relative permeability of ferrite is 2,200. This system has been designed for dynamic charging but only static charging is considered in this study. The power electronics controls and keeps the rms value of the current in the transmitter at 36 A and the current in the receiver at 75 A.

Figure 1 Studied configuration of the wireless transfer system.
Figure 1

Studied configuration of the wireless transfer system.

Table 1

Dimensions of the wireless power transfer system

Width (m) Length (m)
Transmitter 0.5 1.5
Receiver 0.5 0.3
Ferrite 0.2 0.25
Frame 1.5 0.5

2.2 Kriging

Kriging is a stochastic interpolation algorithm which assumes that the model output M(x) is a realization of a Gaussian process indexed by the inputs x [19]:

(1) M ( x ) ∼ M K ( x ) = β T f ( x ) + σ 2 Z ( x , ω )

The first term in (1) is the mean value of the Gaussian process (trend) and it consists of the regression coefficients β j (j = 1,…,P) and the basis functions f j (j = 1,…,P). The second term in (1) consists of σ 2, the (constant) variance of the Gaussian process and Z(x, ω), a zero mean, unit variance, stationary Gaussian process. The underlying probability space is represented by ω and is defined in terms of a correlation function. The correlation function describes the correlation between two samples of the input space and depends on the hyperparameters. In the context of metamodeling, it is of interest to calculate a prediction M K (x) for a new point x, given X = (x 1,…,x n ), the experimental design and y = (y 1 = M(x 1),…,y n = M(x n )), the corresponding (noise-free) model responses. A Kriging metamodel (Kriging predictor) provides such predictions based on the Gaussian properties of the process.

2.3 Polynomial chaos expansion

The polynomial chaos is a spectral method and consists in the approximation of the system output in a suitable finite-dimensional basis Ψ(X) made of orthogonal polynomials. A truncation of this polynomial expansion can be written as follows:

(2) M ( x ) ∼ M PC ( x ) = ∑ j = 0 P − 1 ∝ j Ψ j ( X )

where M(x) is the system output, X is the random input vector made of the input parameters x i , Ψ j are the multivariate polynomials belonging to Ψ(X), α j are the coefficients to be estimated, and P is the size of the polynomial basis Ψ(X). Each multivariate polynomial Ψ j is built as a tensor product of univariate polynomials orthogonal with respect to the probability density function of each input parameter x i .

2.4 Numerical results – three parameters (chassis conductivity and misalignment between emitter and receiver)

Kriging has been applied in the configuration of Figure 5 in order to check the compliance regarding the maximum admissible values of the radiated magnetic field. For the frequency of interest (85 kHz), the maximum admissible value of the magnetic flux density is 27 µT according to the ICNIRP Guidelines (2010) [5]. The experimental design is evaluated by the finite element method (Figure 2). The magneto-dynamic problem is solved with a 3D vector potential formulation using the software COMSOL.

Figure 2 Finite element mesh used for computing sampling data.
Figure 2

Finite element mesh used for computing sampling data.

Figure 3 IPT system [18].
Figure 3

IPT system [18].

The accuracy of the metamodel is checked thanks to the leave-one-out (LOO) cross-validation defined according to [19]:

(3) LOO = ∑ i = 1 N ( M ( x i ) − M − i ( x i ) ) 2 / Var [ Y ]

This quantity involves in each sampling point x i the error between the value provided by the model and the Kriging prediction by using all the sampling points except x i . If the LOO is close to 1, the metamodel is highly modified if one data point is erased, whereas the smallest it is, the least it will be modified.

In this example, the variability regarding the frame conductivity, distance between coils and length of reception coil is investigated. Here, σ, d, and L are the chassis conductivity, distance between coils, and length of reception coil, respectively. The range of variation is shown in Table 2.

Table 2

Parameters: range of variations

Parameter Min Max
σ (S/m) 104 106
d (m) 0 1
L (m) 0.2 0.3

Regarding the conductivity, the range includes typical values relevant to composite materials which are used in automotive applications. These three parameters are important for such analysis since once a park or a road is equipped with defined transmitter coils, different kinds of vehicle may be charged by the system. The level of radiated field then depends on the type of the receiver system (L and d) and car body (σ). They may strongly vary according to the vehicle.

For the studied case, the metamodel is constructed with 10 randomly selected data points out of 27 (three samples for each of the three parameters). The computing cost for one simulation (three given parameters) is less than 2 min on a work station DELL XEON E5-1630 V3 (64 Go). The number of 27 data inputs points (full wave computations) was chosen as a compromise between accuracy and reasonable computing time in view of an engineering-oriented tool. The accuracy of the metamodel is then calculated on the remaining 17 points out of 27 to get the LOO (Table 3). Regarding Kriging, a significant lower LOO is obtained using a linear or quadratic term compared to an ordinary trend.

Table 3

Comparison of different metamodels

LOO
Kriging (ordinary trend) 2.1 × 10−4
Kriging (linear trend) 1.7 × 10−6
Kriging (quadratic trend) 1.3 × 10−5
PCE 1 × 10−6

In order to study the influence of the number of samples on the predictions, the metamodels were constructed on 8, 10, and 15 randomly selected points out of 27 data points. The values of LOO for different methods and for the three given cases are shown in Table 4. In practice, it was shown that using more than 10 points is unnecessary to get a sufficiently accurate surrogate model.

Table 4

LOO values for different numbers of samples

8 points 10 points 15 points
Kriging (ordinary trend) 8.8 × 10−6 2 × 10−4 1.6 × 10−4
Kriging (linear trend) 1.3 × 10−3 1.7 × 10−6 1.2 × 10−8
Kriging (quadratic trend) 5 × 10−3 1.3 × 10−5 8.8 × 10−7
PCE 2.2 × 10−3 1 × 10−6 8.1 × 10−7

3 Wireless power system (GeePs)

3.1 Studied configuration

The IPT system considered in this section has been studied in GeePs and is presented in ref. [18] (Figure 3). There are two squared coils and rectangular ferrite plates. The power transfer efficiency can be expressed as [15]:

(4) η ∝ 1 1 + R 1 R L ω L 12 2

where ω is the angular frequency, R 1 is the series transmitter coil resistance, R L is the series load resistance, and L 12 is the mutual inductance between the two coils.

Figure 4 log(LOO) error versus different number of samples.
Figure 4

log(LOO) error versus different number of samples.

It is clear from (4) that when the structure of the coils and the frequency of the IPT system have been fixed, the efficiency is directly related to the mutual inductance.

The dimensions of the IPT systems are shown in Table 5. The design of the ferrites plates of a IPT system has a relatively strong effect on the power transfer efficiency. Here, the uncertainty lies in the distance between the ferrite plate and the coil (d), the thickness (w), and the relative permeability (µ r) of the ferrite plate. A surrogate model is built in order to study the influence on the mutual inductance in the IPT system.

Table 5

Dimensions of the IPT system

Parameter Value
Coil length 468 mm
Coil height 13 mm
Ferrite width 600 mm
Ferrite length 500 mm
Ferrite height 2 mm
Distance between coils 150 mm
Frequency 85 kHz
Current in one coil 42 A rms

3.2 Sensitivity analysis

A PCE is used to find the most influential parameters and to perform a first sensitivity analysis. To illustrate, the metamodel is built with 120 samples, each sample including three values corresponding to the three parameters. The parameters are chosen uniformly distributed over the range of variations (Table 6). As Figure 4 shows, the LOO error rapidly decreases with the number of these datapoints. Around 20 datapoints is a sufficient number to obtain a value of M with less than 5% compared to the value computed with the 3D finite element model.

Table 6

Parameters: range of variation

Parameter Min Max
μ r 1,000 3,000
d (mm) 0 10
w (mm) 0 2
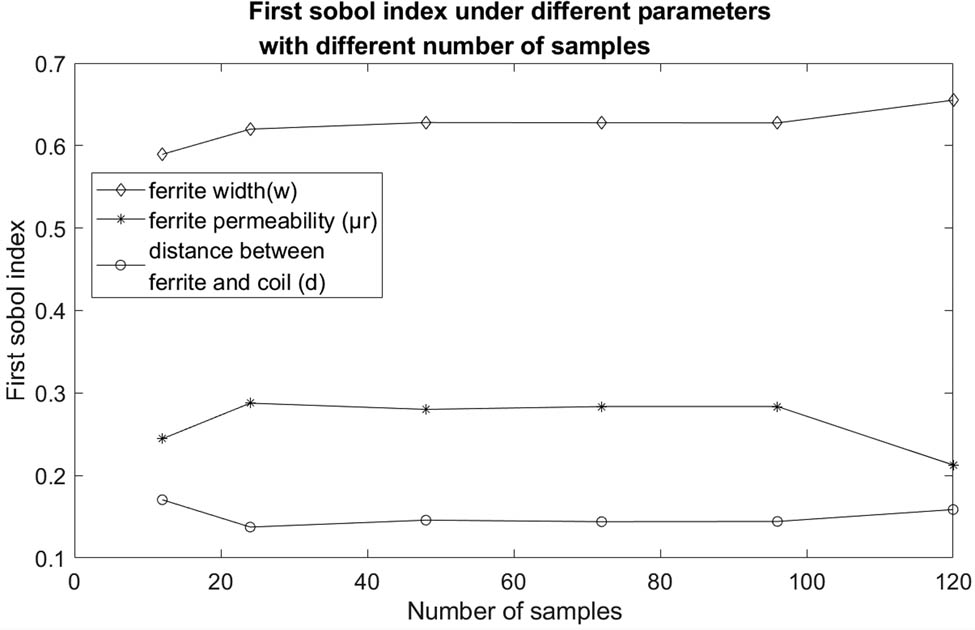
Figure 5 First Sobol index versus number of samples.
Figure 5

First Sobol index versus number of samples.

In order to perform a sensitivity analysis regarding the mutual inductance L 12, the Sobol indices [20] are determined. These Sobol indices are statistical quantities that can be obtained at low cost using the metamodels instead of a classical Monte Carlo approach. They are known analytically with a PCE metamodel. The first order Sobol index related to the parameter p is defined as in ref. [21] with the first statistical moments:

(5) S p = Var ( E { L 12 | p } ) / Var[ L 12 ]

If S i is close to one, it describes the highest impact on the mutual inductance L 12. Figure 5 contains the first-order Sobol index for the three parameters. It is clear that no matter how the number of samples changes, the Sobol index for each parameter is nearly the same and the thickness of the ferrite plate appears to influence the most. Therefore, this parameter should be paid more attention when designing the system.

4 Conclusion

Predictions of magnetic field and related quantities have been obtained from a statistic approach Monte Carlo and stochastic models. In case of a 3D complex configuration, metamodels based on Kriging or PCE provide efficient approaches to consider the uncertainties regarding different physical or geometrical parameters. The interest of such surrogate models was demonstrated in case of two simplified but realistic inductive power systems. With a reduced number of samples, a metamodel can be used as a fast predictor to check if reference levels fit the guidelines for human exposure, for example, or to improve the efficiency of the transfer. The paper has validated the approach with synthetic numerical data: In a next step, predictions of the metamodels will be compared with measured values. The work will also be extended to investigate more complex configurations involving a higher number of parameters and taking into account the global structure of the vehicle.

Acknowledgments

The results presented here are developed in the framework of the 16ENG08 MICEV Project. The latter received funding from the EMPIR program co-financed by the Participating States and from the European Union’s Horizon 2020 research and innovation program.

References

[1] Cirimele V, Diana M, Freschi F, Mitolo M. Inductive power transfer for automotive applications: state-of-the-art and future trends. IEEE Trans Ind Appl. 2018;54(5):4069.10.1109/IAS.2016.7731966Search in Google Scholar

[2] Park S. Evaluation of electromagnetic exposure during 85 kHz wireless power transfer for electric vehicles. IEEE Trans Magnet. 2018;53(1):5100208.10.1109/TMAG.2017.2748498Search in Google Scholar

[3] Cirimele V, Freschi F, Giaccone L, Pichon L, Repetto M. Human exposure assessment in dynamic inductive power transfer for automotive applications. IEEE Trans Magnet. 2017;53(6):5000304.10.1109/CEFC.2016.7816121Search in Google Scholar

[4] Feliziani M, Cruciani S, Campi T, Maradei F. Near field shielding of a wireless power transfer (WPT) current coil. Progr Electromagnet Res C. 2017;77:39–48.10.2528/PIERC17042804Search in Google Scholar

[5] ICNIRP guidelines for limiting exposure to time varying electric and magnetic fields (1 Hz–100 KHz). Health Phys. 2010;99:818–36.10.1097/HP.0b013e3181f06c86Search in Google Scholar PubMed

[6] Al Achkar G, Pichon L, Benjelloun N, Daniel L. A broadband electromagnetic homogenization method for composite materials. IEEE Trans Magnet. 2018;54(3):9400304.10.1109/TMAG.2017.2759224Search in Google Scholar

[7] Kroese D, Taimre T, Botev Z. Handbook of Monte Carlo Methods. New York: Wiley Series in Probability and Statistics; 2011.10.1002/9781118014967Search in Google Scholar

[8] Krauth V-L, Pichon L. Uncertainty Quantification in the Shielding Effectiveness Evaluation of Planar Sheets. ISEF 2019, 19th International Symposium on Electromagnetic Fieldsin Mechatronics, Electrical and Electronic Engineering, Aug 2019, Nancy, France.10.1109/ISEF45929.2019.9097029Search in Google Scholar

[9] Ryan CM. Computer expression for predicting shielding effectiveness for the low-frequency plane shield case. IEEE Trans Electromagnet Compat. 1967;9(2):83–94.10.1109/TEMC.1967.4307468Search in Google Scholar

[10] Stratton JA. Electromagnetic theory. New York: McGraw-Hill; 1941.Search in Google Scholar

[11] Lefebvre J, Roussel H, Walter E, Lecointe D, Tabbara W. Prediction from wrong models: the Kriging approach. IEEE Antennas Propag Mag. 1996;38(4):35–45.10.1109/74.537364Search in Google Scholar

[12] Voyer D, Musy F, Nicolas L, Perrussel R. Probabilistic methods applied to 2D electromagnetic numerical dosimetry. COMPEL. 2008;27(3):651–67.10.1108/03321640810861098Search in Google Scholar

[13] Silly-Carette J, Lautru D, Wong M-F, Gati A, Wiart J, Fouad Hanna V. Variability on the propagation of a plane wave using stochastic collocation methods in a bio electromagnetic application. IEEE Microw Wirel Compon Lett. 2009;19(4):185–87.10.1109/LMWC.2009.2015481Search in Google Scholar

[14] Bilicz S, Gyimóthy S, Pávó J, Horváth P, Marák K. Uncertainty quantification of wireless power transfer systems, IEEE Wireless Power Transfer Conference (WPTC); 2016.10.1109/WPT.2016.7498861Search in Google Scholar

[15] Knaisch K, Gratzfeld P. Gaussian process surrogate model for the design of circular, planar coils used in inductive power transfer for electric vehicles. IET Power Electron. 2016;9(15):2786–94.10.1049/iet-pel.2016.0392Search in Google Scholar

[16] Lagouanelle P, Krauth V-L, Pichon L. Uncertainty Quantification in the Assessment of Human Exposure near Wireless Power Transfer Systems in Automotive Applications. Automotive 2019, Turin, Italy, 2019.10.23919/EETA.2019.8804593Search in Google Scholar

[17] Cirimele V. Design and integration of a dynamic IPT system for automotive applications [PhD dissertation]. Politecnico di Torino and University Paris-Saclay; 2017.Search in Google Scholar

[18] Caillierez A. Etude et mise en oeuvre du transfert de l'énergie électrique par induction: application à la route électrique pour véhicule en mouvement [PhD thesis]. Université Paris-Saclay; 2015.Search in Google Scholar

[19] Marelli S, Sudret B. UQLab: A framework for uncertainty quantification in Matlab, Proc. 2nd Int. Conf. on Vulnerability, Risk Analysis and Management (ICVRAM2014), Liverpool, United Kingdom; 2014, p. 2554–63.10.1061/9780784413609.257Search in Google Scholar

[20] Sobol IM. Sensitivity estimates for nonlinear mathematical models. Math Modell Comput Exp. 1993;1(4):407–14.Search in Google Scholar

[21] Larbi M, Stievano IS, Canavero FG, Besnier P. Variability impact of many design parameters: the case of a realistic electronic link. IEEE Trans Electromagn Compat. 2018;60(1):34–41.10.1109/TEMC.2017.2727961Search in Google Scholar
Received: 2020-01-30
Revised: 2020-05-31
Accepted: 2020-06-29
Published Online: 2020-07-30

© 2020 Yao Pei et al., published by De Gruyter

This work is licensed under the Creative Commons Attribution 4.0 International License.

Articles in the same Issue

  1. Regular Articles
  2. Model of electric charge distribution in the trap of a close-contact TENG system
  3. Dynamics of Online Collective Attention as Hawkes Self-exciting Process
  4. Enhanced Entanglement in Hybrid Cavity Mediated by a Two-way Coupled Quantum Dot
  5. The nonlinear integro-differential Ito dynamical equation via three modified mathematical methods and its analytical solutions
  6. Diagnostic model of low visibility events based on C4.5 algorithm
  7. Electronic temperature characteristics of laser-induced Fe plasma in fruits
  8. Comparative study of heat transfer enhancement on liquid-vapor separation plate condenser
  9. Characterization of the effects of a plasma injector driven by AC dielectric barrier discharge on ethylene-air diffusion flame structure
  10. Impact of double-diffusive convection and motile gyrotactic microorganisms on magnetohydrodynamics bioconvection tangent hyperbolic nanofluid
  11. Dependence of the crossover zone on the regularization method in the two-flavor Nambu–Jona-Lasinio model
  12. Novel numerical analysis for nonlinear advection–reaction–diffusion systems
  13. Heuristic decision of planned shop visit products based on similar reasoning method: From the perspective of organizational quality-specific immune
  14. Two-dimensional flow field distribution characteristics of flocking drainage pipes in tunnel
  15. Dynamic triaxial constitutive model for rock subjected to initial stress
  16. Automatic target recognition method for multitemporal remote sensing image
  17. Gaussons: optical solitons with log-law nonlinearity by Laplace–Adomian decomposition method
  18. Adaptive magnetic suspension anti-rolling device based on frequency modulation
  19. Dynamic response characteristics of 93W alloy with a spherical structure
  20. The heuristic model of energy propagation in free space, based on the detection of a current induced in a conductor inside a continuously covered conducting enclosure by an external radio frequency source
  21. Microchannel filter for air purification
  22. An explicit representation for the axisymmetric solutions of the free Maxwell equations
  23. Floquet analysis of linear dynamic RLC circuits
  24. Subpixel matching method for remote sensing image of ground features based on geographic information
  25. K-band luminosity–density relation at fixed parameters or for different galaxy families
  26. Effect of forward expansion angle on film cooling characteristics of shaped holes
  27. Analysis of the overvoltage cooperative control strategy for the small hydropower distribution network
  28. Stable walking of biped robot based on center of mass trajectory control
  29. Modeling and simulation of dynamic recrystallization behavior for Q890 steel plate based on plane strain compression tests
  30. Edge effect of multi-degree-of-freedom oscillatory actuator driven by vector control
  31. The effect of guide vane type on performance of multistage energy recovery hydraulic turbine (MERHT)
  32. Development of a generic framework for lumped parameter modeling
  33. Optimal control for generating excited state expansion in ring potential
  34. The phase inversion mechanism of the pH-sensitive reversible invert emulsion from w/o to o/w
  35. 3D bending simulation and mechanical properties of the OLED bending area
  36. Resonance overvoltage control algorithms in long cable frequency conversion drive based on discrete mathematics
  37. The measure of irregularities of nanosheets
  38. The predicted load balancing algorithm based on the dynamic exponential smoothing
  39. Influence of different seismic motion input modes on the performance of isolated structures with different seismic measures
  40. A comparative study of cohesive zone models for predicting delamination fracture behaviors of arterial wall
  41. Analysis on dynamic feature of cross arm light weighting for photovoltaic panel cleaning device in power station based on power correlation
  42. Some probability effects in the classical context
  43. Thermosoluted Marangoni convective flow towards a permeable Riga surface
  44. Simultaneous measurement of ionizing radiation and heart rate using a smartphone camera
  45. On the relations between some well-known methods and the projective Riccati equations
  46. Application of energy dissipation and damping structure in the reinforcement of shear wall in concrete engineering
  47. On-line detection algorithm of ore grade change in grinding grading system
  48. Testing algorithm for heat transfer performance of nanofluid-filled heat pipe based on neural network
  49. New optical solitons of conformable resonant nonlinear Schrödinger’s equation
  50. Numerical investigations of a new singular second-order nonlinear coupled functional Lane–Emden model
  51. Circularly symmetric algorithm for UWB RF signal receiving channel based on noise cancellation
  52. CH4 dissociation on the Pd/Cu(111) surface alloy: A DFT study
  53. On some novel exact solutions to the time fractional (2 + 1) dimensional Konopelchenko–Dubrovsky system arising in physical science
  54. An optimal system of group-invariant solutions and conserved quantities of a nonlinear fifth-order integrable equation
  55. Mining reasonable distance of horizontal concave slope based on variable scale chaotic algorithms
  56. Mathematical models for information classification and recognition of multi-target optical remote sensing images
  57. Hopkinson rod test results and constitutive description of TRIP780 steel resistance spot welding material
  58. Computational exploration for radiative flow of Sutterby nanofluid with variable temperature-dependent thermal conductivity and diffusion coefficient
  59. Analytical solution of one-dimensional Pennes’ bioheat equation
  60. MHD squeezed Darcy–Forchheimer nanofluid flow between two h–distance apart horizontal plates
  61. Analysis of irregularity measures of zigzag, rhombic, and honeycomb benzenoid systems
  62. A clustering algorithm based on nonuniform partition for WSNs
  63. An extension of Gronwall inequality in the theory of bodies with voids
  64. Rheological properties of oil–water Pickering emulsion stabilized by Fe3O4 solid nanoparticles
  65. Review Article
  66. Sine Topp-Leone-G family of distributions: Theory and applications
  67. Review of research, development and application of photovoltaic/thermal water systems
  68. Special Issue on Fundamental Physics of Thermal Transports and Energy Conversions
  69. Numerical analysis of sulfur dioxide absorption in water droplets
  70. Special Issue on Transport phenomena and thermal analysis in micro/nano-scale structure surfaces - Part I
  71. Random pore structure and REV scale flow analysis of engine particulate filter based on LBM
  72. Prediction of capillary suction in porous media based on micro-CT technology and B–C model
  73. Energy equilibrium analysis in the effervescent atomization
  74. Experimental investigation on steam/nitrogen condensation characteristics inside horizontal enhanced condensation channels
  75. Experimental analysis and ANN prediction on performances of finned oval-tube heat exchanger under different air inlet angles with limited experimental data
  76. Investigation on thermal-hydraulic performance prediction of a new parallel-flow shell and tube heat exchanger with different surrogate models
  77. Comparative study of the thermal performance of four different parallel flow shell and tube heat exchangers with different performance indicators
  78. Optimization of SCR inflow uniformity based on CFD simulation
  79. Kinetics and thermodynamics of SO2 adsorption on metal-loaded multiwalled carbon nanotubes
  80. Effect of the inner-surface baffles on the tangential acoustic mode in the cylindrical combustor
  81. Special Issue on Future challenges of advanced computational modeling on nonlinear physical phenomena - Part I
  82. Conserved vectors with conformable derivative for certain systems of partial differential equations with physical applications
  83. Some new extensions for fractional integral operator having exponential in the kernel and their applications in physical systems
  84. Exact optical solitons of the perturbed nonlinear Schrödinger–Hirota equation with Kerr law nonlinearity in nonlinear fiber optics
  85. Analytical mathematical schemes: Circular rod grounded via transverse Poisson’s effect and extensive wave propagation on the surface of water
  86. Closed-form wave structures of the space-time fractional Hirota–Satsuma coupled KdV equation with nonlinear physical phenomena
  87. Some misinterpretations and lack of understanding in differential operators with no singular kernels
  88. Stable solutions to the nonlinear RLC transmission line equation and the Sinh–Poisson equation arising in mathematical physics
  89. Calculation of focal values for first-order non-autonomous equation with algebraic and trigonometric coefficients
  90. Influence of interfacial electrokinetic on MHD radiative nanofluid flow in a permeable microchannel with Brownian motion and thermophoresis effects
  91. Standard routine techniques of modeling of tick-borne encephalitis
  92. Fractional residual power series method for the analytical and approximate studies of fractional physical phenomena
  93. Exact solutions of space–time fractional KdV–MKdV equation and Konopelchenko–Dubrovsky equation
  94. Approximate analytical fractional view of convection–diffusion equations
  95. Heat and mass transport investigation in radiative and chemically reacting fluid over a differentially heated surface and internal heating
  96. On solitary wave solutions of a peptide group system with higher order saturable nonlinearity
  97. Extension of optimal homotopy asymptotic method with use of Daftardar–Jeffery polynomials to Hirota–Satsuma coupled system of Korteweg–de Vries equations
  98. Unsteady nano-bioconvective channel flow with effect of nth order chemical reaction
  99. On the flow of MHD generalized maxwell fluid via porous rectangular duct
  100. Study on the applications of two analytical methods for the construction of traveling wave solutions of the modified equal width equation
  101. Numerical solution of two-term time-fractional PDE models arising in mathematical physics using local meshless method
  102. A powerful numerical technique for treating twelfth-order boundary value problems
  103. Fundamental solutions for the long–short-wave interaction system
  104. Role of fractal-fractional operators in modeling of rubella epidemic with optimized orders
  105. Exact solutions of the Laplace fractional boundary value problems via natural decomposition method
  106. Special Issue on 19th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering
  107. Joint use of eddy current imaging and fuzzy similarities to assess the integrity of steel plates
  108. Uncertainty quantification in the design of wireless power transfer systems
  109. Influence of unequal stator tooth width on the performance of outer-rotor permanent magnet machines
  110. New elements within finite element modeling of magnetostriction phenomenon in BLDC motor
  111. Evaluation of localized heat transfer coefficient for induction heating apparatus by thermal fluid analysis based on the HSMAC method
  112. Experimental set up for magnetomechanical measurements with a closed flux path sample
  113. Influence of the earth connections of the PWM drive on the voltage constraints endured by the motor insulation
  114. High temperature machine: Characterization of materials for the electrical insulation
  115. Architecture choices for high-temperature synchronous machines
  116. Analytical study of air-gap surface force – application to electrical machines
  117. High-power density induction machines with increased windings temperature
  118. Influence of modern magnetic and insulation materials on dimensions and losses of large induction machines
  119. New emotional model environment for navigation in a virtual reality
  120. Performance comparison of axial-flux switched reluctance machines with non-oriented and grain-oriented electrical steel rotors
  121. Erratum
  122. Erratum to “Conserved vectors with conformable derivative for certain systems of partial differential equations with physical applications”
https://doi.org/10.1515/phys-2020-0174
Keywords for this article
EMC; wireless transfer; uncertainty quantification; shielding; efficiency
Creative Commons
BY 4.0

Articles in the same Issue

  1. Regular Articles
  2. Model of electric charge distribution in the trap of a close-contact TENG system
  3. Dynamics of Online Collective Attention as Hawkes Self-exciting Process
  4. Enhanced Entanglement in Hybrid Cavity Mediated by a Two-way Coupled Quantum Dot
  5. The nonlinear integro-differential Ito dynamical equation via three modified mathematical methods and its analytical solutions
  6. Diagnostic model of low visibility events based on C4.5 algorithm
  7. Electronic temperature characteristics of laser-induced Fe plasma in fruits
  8. Comparative study of heat transfer enhancement on liquid-vapor separation plate condenser
  9. Characterization of the effects of a plasma injector driven by AC dielectric barrier discharge on ethylene-air diffusion flame structure
  10. Impact of double-diffusive convection and motile gyrotactic microorganisms on magnetohydrodynamics bioconvection tangent hyperbolic nanofluid
  11. Dependence of the crossover zone on the regularization method in the two-flavor Nambu–Jona-Lasinio model
  12. Novel numerical analysis for nonlinear advection–reaction–diffusion systems
  13. Heuristic decision of planned shop visit products based on similar reasoning method: From the perspective of organizational quality-specific immune
  14. Two-dimensional flow field distribution characteristics of flocking drainage pipes in tunnel
  15. Dynamic triaxial constitutive model for rock subjected to initial stress
  16. Automatic target recognition method for multitemporal remote sensing image
  17. Gaussons: optical solitons with log-law nonlinearity by Laplace–Adomian decomposition method
  18. Adaptive magnetic suspension anti-rolling device based on frequency modulation
  19. Dynamic response characteristics of 93W alloy with a spherical structure
  20. The heuristic model of energy propagation in free space, based on the detection of a current induced in a conductor inside a continuously covered conducting enclosure by an external radio frequency source
  21. Microchannel filter for air purification
  22. An explicit representation for the axisymmetric solutions of the free Maxwell equations
  23. Floquet analysis of linear dynamic RLC circuits
  24. Subpixel matching method for remote sensing image of ground features based on geographic information
  25. K-band luminosity–density relation at fixed parameters or for different galaxy families
  26. Effect of forward expansion angle on film cooling characteristics of shaped holes
  27. Analysis of the overvoltage cooperative control strategy for the small hydropower distribution network
  28. Stable walking of biped robot based on center of mass trajectory control
  29. Modeling and simulation of dynamic recrystallization behavior for Q890 steel plate based on plane strain compression tests
  30. Edge effect of multi-degree-of-freedom oscillatory actuator driven by vector control
  31. The effect of guide vane type on performance of multistage energy recovery hydraulic turbine (MERHT)
  32. Development of a generic framework for lumped parameter modeling
  33. Optimal control for generating excited state expansion in ring potential
  34. The phase inversion mechanism of the pH-sensitive reversible invert emulsion from w/o to o/w
  35. 3D bending simulation and mechanical properties of the OLED bending area
  36. Resonance overvoltage control algorithms in long cable frequency conversion drive based on discrete mathematics
  37. The measure of irregularities of nanosheets
  38. The predicted load balancing algorithm based on the dynamic exponential smoothing
  39. Influence of different seismic motion input modes on the performance of isolated structures with different seismic measures
  40. A comparative study of cohesive zone models for predicting delamination fracture behaviors of arterial wall
  41. Analysis on dynamic feature of cross arm light weighting for photovoltaic panel cleaning device in power station based on power correlation
  42. Some probability effects in the classical context
  43. Thermosoluted Marangoni convective flow towards a permeable Riga surface
  44. Simultaneous measurement of ionizing radiation and heart rate using a smartphone camera
  45. On the relations between some well-known methods and the projective Riccati equations
  46. Application of energy dissipation and damping structure in the reinforcement of shear wall in concrete engineering
  47. On-line detection algorithm of ore grade change in grinding grading system
  48. Testing algorithm for heat transfer performance of nanofluid-filled heat pipe based on neural network
  49. New optical solitons of conformable resonant nonlinear Schrödinger’s equation
  50. Numerical investigations of a new singular second-order nonlinear coupled functional Lane–Emden model
  51. Circularly symmetric algorithm for UWB RF signal receiving channel based on noise cancellation
  52. CH4 dissociation on the Pd/Cu(111) surface alloy: A DFT study
  53. On some novel exact solutions to the time fractional (2 + 1) dimensional Konopelchenko–Dubrovsky system arising in physical science
  54. An optimal system of group-invariant solutions and conserved quantities of a nonlinear fifth-order integrable equation
  55. Mining reasonable distance of horizontal concave slope based on variable scale chaotic algorithms
  56. Mathematical models for information classification and recognition of multi-target optical remote sensing images
  57. Hopkinson rod test results and constitutive description of TRIP780 steel resistance spot welding material
  58. Computational exploration for radiative flow of Sutterby nanofluid with variable temperature-dependent thermal conductivity and diffusion coefficient
  59. Analytical solution of one-dimensional Pennes’ bioheat equation
  60. MHD squeezed Darcy–Forchheimer nanofluid flow between two h–distance apart horizontal plates
  61. Analysis of irregularity measures of zigzag, rhombic, and honeycomb benzenoid systems
  62. A clustering algorithm based on nonuniform partition for WSNs
  63. An extension of Gronwall inequality in the theory of bodies with voids
  64. Rheological properties of oil–water Pickering emulsion stabilized by Fe3O4 solid nanoparticles
  65. Review Article
  66. Sine Topp-Leone-G family of distributions: Theory and applications
  67. Review of research, development and application of photovoltaic/thermal water systems
  68. Special Issue on Fundamental Physics of Thermal Transports and Energy Conversions
  69. Numerical analysis of sulfur dioxide absorption in water droplets
  70. Special Issue on Transport phenomena and thermal analysis in micro/nano-scale structure surfaces - Part I
  71. Random pore structure and REV scale flow analysis of engine particulate filter based on LBM
  72. Prediction of capillary suction in porous media based on micro-CT technology and B–C model
  73. Energy equilibrium analysis in the effervescent atomization
  74. Experimental investigation on steam/nitrogen condensation characteristics inside horizontal enhanced condensation channels
  75. Experimental analysis and ANN prediction on performances of finned oval-tube heat exchanger under different air inlet angles with limited experimental data
  76. Investigation on thermal-hydraulic performance prediction of a new parallel-flow shell and tube heat exchanger with different surrogate models
  77. Comparative study of the thermal performance of four different parallel flow shell and tube heat exchangers with different performance indicators
  78. Optimization of SCR inflow uniformity based on CFD simulation
  79. Kinetics and thermodynamics of SO2 adsorption on metal-loaded multiwalled carbon nanotubes
  80. Effect of the inner-surface baffles on the tangential acoustic mode in the cylindrical combustor
  81. Special Issue on Future challenges of advanced computational modeling on nonlinear physical phenomena - Part I
  82. Conserved vectors with conformable derivative for certain systems of partial differential equations with physical applications
  83. Some new extensions for fractional integral operator having exponential in the kernel and their applications in physical systems
  84. Exact optical solitons of the perturbed nonlinear Schrödinger–Hirota equation with Kerr law nonlinearity in nonlinear fiber optics
  85. Analytical mathematical schemes: Circular rod grounded via transverse Poisson’s effect and extensive wave propagation on the surface of water
  86. Closed-form wave structures of the space-time fractional Hirota–Satsuma coupled KdV equation with nonlinear physical phenomena
  87. Some misinterpretations and lack of understanding in differential operators with no singular kernels
  88. Stable solutions to the nonlinear RLC transmission line equation and the Sinh–Poisson equation arising in mathematical physics
  89. Calculation of focal values for first-order non-autonomous equation with algebraic and trigonometric coefficients
  90. Influence of interfacial electrokinetic on MHD radiative nanofluid flow in a permeable microchannel with Brownian motion and thermophoresis effects
  91. Standard routine techniques of modeling of tick-borne encephalitis
  92. Fractional residual power series method for the analytical and approximate studies of fractional physical phenomena
  93. Exact solutions of space–time fractional KdV–MKdV equation and Konopelchenko–Dubrovsky equation
  94. Approximate analytical fractional view of convection–diffusion equations
  95. Heat and mass transport investigation in radiative and chemically reacting fluid over a differentially heated surface and internal heating
  96. On solitary wave solutions of a peptide group system with higher order saturable nonlinearity
  97. Extension of optimal homotopy asymptotic method with use of Daftardar–Jeffery polynomials to Hirota–Satsuma coupled system of Korteweg–de Vries equations
  98. Unsteady nano-bioconvective channel flow with effect of nth order chemical reaction
  99. On the flow of MHD generalized maxwell fluid via porous rectangular duct
  100. Study on the applications of two analytical methods for the construction of traveling wave solutions of the modified equal width equation
  101. Numerical solution of two-term time-fractional PDE models arising in mathematical physics using local meshless method
  102. A powerful numerical technique for treating twelfth-order boundary value problems
  103. Fundamental solutions for the long–short-wave interaction system
  104. Role of fractal-fractional operators in modeling of rubella epidemic with optimized orders
  105. Exact solutions of the Laplace fractional boundary value problems via natural decomposition method
  106. Special Issue on 19th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering
  107. Joint use of eddy current imaging and fuzzy similarities to assess the integrity of steel plates
  108. Uncertainty quantification in the design of wireless power transfer systems
  109. Influence of unequal stator tooth width on the performance of outer-rotor permanent magnet machines
  110. New elements within finite element modeling of magnetostriction phenomenon in BLDC motor
  111. Evaluation of localized heat transfer coefficient for induction heating apparatus by thermal fluid analysis based on the HSMAC method
  112. Experimental set up for magnetomechanical measurements with a closed flux path sample
  113. Influence of the earth connections of the PWM drive on the voltage constraints endured by the motor insulation
  114. High temperature machine: Characterization of materials for the electrical insulation
  115. Architecture choices for high-temperature synchronous machines
  116. Analytical study of air-gap surface force – application to electrical machines
  117. High-power density induction machines with increased windings temperature
  118. Influence of modern magnetic and insulation materials on dimensions and losses of large induction machines
  119. New emotional model environment for navigation in a virtual reality
  120. Performance comparison of axial-flux switched reluctance machines with non-oriented and grain-oriented electrical steel rotors
  121. Erratum
  122. Erratum to “Conserved vectors with conformable derivative for certain systems of partial differential equations with physical applications”
Sign up now to receive a 20% welcome discount
Institutional Access
How does access work?
Have an idea on how to improve our website?
Please write us.
© 2025 De Gruyter Brill
Downloaded on 15.9.2025 from https://www.degruyterbrill.com/document/doi/10.1515/phys-2020-0174/html
Scroll to top button