Architecture choices for high-temperature synchronous machines

Ewa Napieralska Juszczak; Daniel Roger; Krzysztof Komeza; Marcin Lefik; Piotr Napieralski

doi:10.1515/phys-2020-0154

Article Open Access

Architecture choices for high-temperature synchronous machines

Ewa Napieralska Juszczak , Daniel Roger , Krzysztof Komeza , Marcin Lefik and Piotr Napieralski

Published/Copyright: October 27, 2020

Published by

Become an author with De Gruyter Brill

Submit Manuscript Author Information Explore this Subject

From the journal Open Physics Volume 18 Issue 1

Abstract

The article proposes an analysis of the possible architectures of synchronous machines with an ability to operate at high temperatures of over 200°C in their environment. Two machine principles have been considered: the permanent magnet synchronous machine and the synchronous reluctance machine. The numerical analyses are carried out with 3D-coupled electromagnetic-fluid-thermal models; the electromagnetic one provides the local losses that give the input data to the coupled thermal-fluid analysis model for computing the temperatures inside the machines. The simulation results are used for estimating the temperature limit of each machine architecture, considering the characteristics of their critical parts.

Keywords: high temperatures; permanent magnet synchronous machine; synchroreluctant machine; thermal analysis; fluid dynamics; HT° materials

1 Introduction

In recent years, the aeronautical industry has started implementing the concept of more electric aircraft based on the replacement of mechanical, hydraulic, and pneumatic actuators and systems by electrical drives [1,2,3,4,5]. For getting good propulsion efficiencies, the airliners are equipped with high-bypass turbofan engines. The electric generators are located in the outer part of the turbofan propulsion engines; the bypass cold air flux insulates them from the central hot turbine. For improving the propulsion efficiency, it is increase the bypass air flux, creating an open rotor propulsion engine without any outer part [6]. For this application, the electric generators must be situated near the turbine, where the ambient temperature can be over 200°C with a low air pressure. A conventional machine operating in this environment requires the use of extreme heat insulation and a liquid (oil) cooling. Therefore, the concept of high-temperature (HT°) machines, with an ability to operate at very high ambient temperature, becomes interesting. The HT° electrical machines are designed for being used in hot environments where the ambient temperature is much higher than typical ones. The machine losses cause a natural increase in the temperatures inside the motor housing. Fluid cooling systems are very difficult to use in such harsh conditions; therefore, the internal temperature gradient must be high and the internal temperature much over 200°C, even up to 500°C. For high power densities and high ambient temperature, the hottest points of the machine are over the capabilities of the best available polymers, which can operate at more or less than 240°C for a lifetime of 2,000 h [7,8,9]. For operating continuously at higher internal temperatures, significant machine changes must be made. First of all, it is necessary to use an inorganic electrical insulation system and adapt the machine geometry to this inorganic insulation technology [10,11,12,13]. The inorganic materials do not the flexibility of polymers: the machine coils cannot be wound in semi-closed stator slots as it is usually made. The windings must be made of simple-shaped coils, which are rigid objects placed on stator teeth separated by opened slots. The coils are connected by HT° wires. This specific stator winding with one coil per slot requires a specific electromagnetic design for limiting the cogging torque. The opened stator slots create flux density harmonics in the air gap and additional losses due to eddy currents that change the thermal balance [14,15,16,17,18,19]. These drawbacks can be mitigated by magnetic wedges closing the stator slots. During the design process of HT° permanent magnet synchronous machines (PMSMs), a particular attention must be paid to the thermal stress in windings and the operating temperatures of permanent magnets [20,21]. Specific SmCo permanent magnets must be used. However, these only available magnets have a higher electric conductivity than the standard ones. The machine design must take these effects into consideration. Thus, the design calculations of these electromechanical transducers require specific electromagnetic and thermal analyses, which also calculate the thermal effects of the power losses.

This article is about the general frame of research works on electrical machines with an ability to operate at high ambient temperatures; it is an extension of the communication presented at a conference [22]. The heart of the article, developed in the following sections, consists of numerical simulations of three machine architectures, namely, two for the HT° PMSM and one for the synchronous reluctance machine (SRM). The electromagnetic simulations produce data for the 3D thermal-fluid numerical computation, which estimates the temperatures of the critical parts of machines. Results are used to define HT° machine prototypes.

The overall objective of the research project is to broaden the field of application of electric machines toward HT° environments. The article concerns a stage of the project that consists of defining a prototype able to verify the proposed solutions. The presented simulations allow to estimate the performance of various design options for the same basic sizes. The prototype size is as follows:

effective length: 50 mm;
stator diameter: 122 mm;
air gap thickness: 0.3 mm;
speed 5,000 rpm;
Phase-to-phase voltage: 400 V.

The rated power and the efficiency depend on the machine topology and the ambient temperature. At lower ambient temperatures compatible with magnet capabilities, the expected efficiency and rated power are higher for PMSM than for SRM, but this solution is not available for hither ambient temperatures.

2 Possible HT° materials for rotating machines and associated architectures

2.1 Choice of topologies for HT° machines

For studying the feasibility of a machine with an ability to operate durably in a hot environment, the characteristics of the active parts materials limit the choices for the machine architecture. For windings, the standard organic insulation made of polymer cannot be used at very HT°; inorganic materials, without any polymer in their composition, must be used. The ceramic insulated wire has the required thermal characteristics and an oxidation protection of copper by a nickel layer; but it has not the excellent electrical and mechanical properties of the standard enameled wires. These weaknesses must be compensated by an HT° encapsulation cement [13,23]. Consequently, the inorganic HT° coils are rigid objects; their mechanical characteristics must be considered by designing specific stator cores. A prototype of an HT° inorganic coil, with an ability to operate up to 500°C, is presented in Figure 1 [24]. The windings of the prototypes are made of simple-shaped coils, which are rigid objects encapsulated with an HT° cement. Cements used to build the coil insulation can work up to 800°C. Tests at such HT° have been made on simple coils.

Figure 1

Prototype of an HT° inorganic insulated coil with an ability to operate continuously up to 800°C.

The stator core geometry must be compatible with such simple rectangular rigid coils. The structure of the motor winding must have only one rigid coil per stator tooth, an no complex end-winding connections. This structure corresponds to a concentrated winding, which has fractional slot number per pole and phase [25]. The concentrated winding architecture excludes dc and induction machine. The only possible topologies are PMSMs and SRMs. The HT° prototype was designed with methods widely described in textbooks and in scientific literature for standard temperatures. However, the design must be adapted to the physical characteristics of inorganic HT° coils that are rigid objects. The rectangular slots must be opened toward the air gap. The number of teeth must be as high as possible to get a good slot filing factor with rectangular teeth.

Moreover, the stator must be designed with rectangular opened teeth for making the assembly possible; this geometry is far from the usual stator core one made with semi-closed slots [26]. Therefore, a detailed electromagnetic study, with high-performance numeric tools, is required for analyzing the consequences of such unusual slot shapes on the cogging torque and on eddy current additional losses.

For PMSMs, several combinations of a number of stator teeth/number of poles are possible. The combination 12 teeth/10 poles (12/10) is widespread for this kind of machine operating at standard temperatures [26]. This topology produces an electromotive force with low harmonics when the machine operates as a three-phase generator and smooth torque when it works as a motor. We opt for this topology but with 24 teeth and 20 poles (24/20) for achieving a better slot-filling factor, with rigid coils requiring rectangular slots. This topology also reduces the height of the stator yoke that facilitates the heat exchanges toward the motor external frame. For the HT° machine, two-rotor topologies are possible: the magnets can be mounted on the surface of a cylinder of soft magnetic material or inside this cylinder [27]. The first option is easier to achieve, but it places the magnets near the opened slots of the stator that induce eddy currents in magnets during the rotation. They are also near the coils that operate at HT°. The second solution places the magnets inside the motor core, and the flux is concentrated toward the air gap by the more complex shapes of the soft magnetic rotor poles. With this solution, the magnet temperatures are lower. In both cases, the design of the rotor must provide a direct evacuation of the heat caused by eddy currents in the magnets. For surface magnet rotor, a particular attention must be paid for estimating the eddy current losses in magnets. The segmentation of each magnet reduces the losses without increasing the complexity of manufacturing and assembly [28]. It is true that segmentation increases the workload, although not significantly, but it is the only effective method of reducing losses in magnets, which are important in the case of permanent magnets with the addition of cobalt with increased electrical conductivity used due to increased Currie temperature.

One of the major problems of HT° machine design is the correct choice of permanent magnets. The manufacturers’ documentation summarizes the technologies available in HT°. The excellent magnets made of neodymium, iron, and boron alloys usually used to build synchronous machines do not tolerate very HT°. The AlNiCo, which accepts temperatures of the order of 450°C, cannot be used to build synchronous machines because it requires a magnetization in situ because of its very weak coercive field. Only a few samarium–cobalt alloys have a high coercive field of temperatures slightly over 300°C. The magnet is, therefore, a critical element that constitutes a technological lock to reach higher temperatures [27,29].

The SRM can be seen as a special case of a salient-pole synchronous machine with a zero dc field created by the rotor. The same number of stator teeth and rotor poles can be used (24/20). The magnets are no longer needed, which is very interesting for eliminating the technological lock. However, this topology requires a very small air gap and full magnetization by the stator, which corresponds to a lower power factor [29].

The mechanical part of such machines is fairly simple up to medium speeds; the bearings are the most complex parts. HT° bearings were developed a longtime ago for aircraft turbines. The motor frame must be made of steel for avoiding differential dilatation relative to the soft magnetic core. The Okayama University (Japan) studied the behavior of soft FeSi magnetic materials at HT° [30,31].

In order to properly adjust the machine parameters, we carried out several simulations examining three 24/20 architectures with an ability to receive prefabricated inorganic rigid HT° coils:

a 24/20 PMSM with surface HT° SmCo magnets (Figure 2),
a 24/20 PMSM with interior HT° SmCo magnets (Figure 3), and
a 24/20 SRM (Figure 4).

Figure 2

Surface magnet rotor for the 24/20 PMSM.

Figure 3

Interior magnet rotor for the 24/20 PMSM.

Figure 4

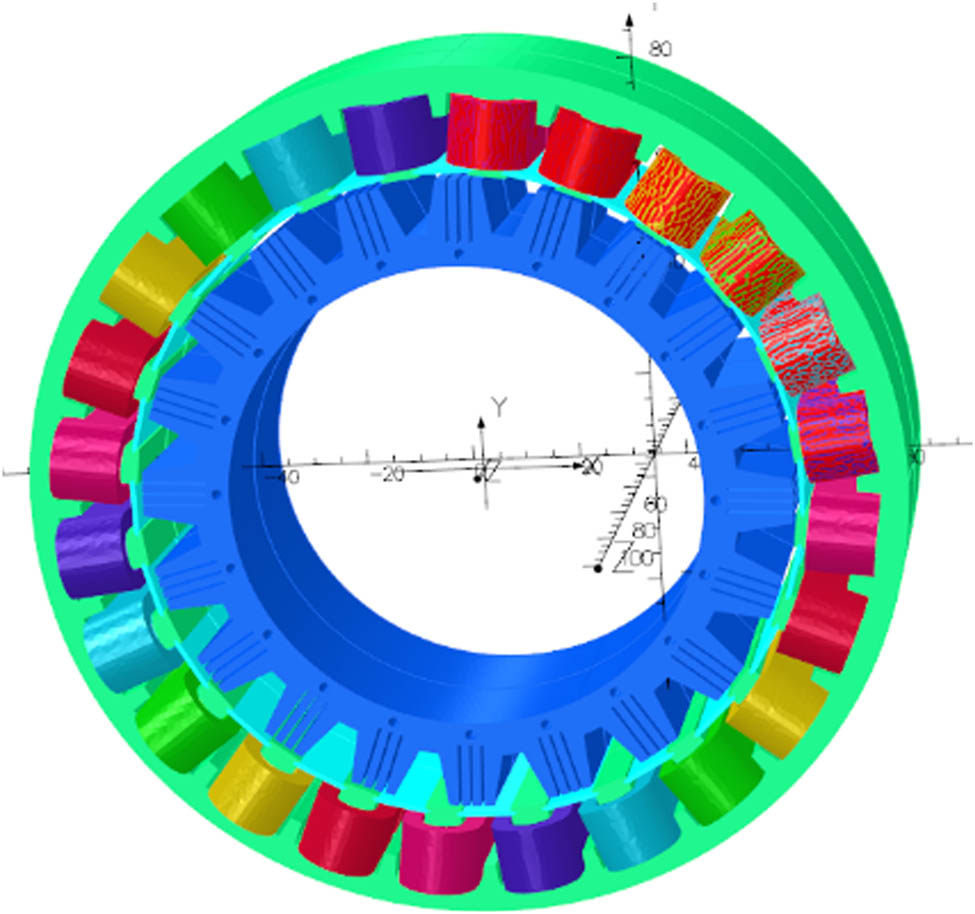
Full 24/20 SRM with the same stator than PMSMs.

Figure 2 presents the architecture of the surface magnet rotor and Figure 3 interior magnet rotor. For the second architecture, slots are made inside the rotor soft magnetic core for inserting the magnets; they are opened toward the internal side in contact with the nonmagnetic shaft. A narrow isthmus of soft magnetic material closes the external side of each slot on the air gap side. This isthmus must resist the centrifugal force applied to the magnets; it must also be saturated for limiting the flux leakages. In the same way as for surface magnet rotor, the interior magnets are also subdivided into four for limiting eddy currents and corresponding losses. Naturally, the interior magnet topology yields a better protection of the magnets that are not directly exposed to the slotting effects.

Figure 4 shows that SRMs have a simpler architecture. The rotor, made of soft magnetic material, has 20 salient poles. Additional radial narrow air gaps cross each salient pole for increasing the transverse reluctance. The rotor can be made of massive soft magnetic steel that provides a very high mechanical resistance. Another solution is to build the rotor with laminated sheets. The natural oxidation of magnetic sheets limits eddy currents [32].

2.2 Method of determination of heat sources

The temperature computation requires the determination of heat sources, which are losses in the windings as well as in the laminated core and losses from eddy currents in the massive conductive elements of the machine. Software used for electromagnetic field analysis was Opera 3D and Opera 2D (originally from Vector Fields, which is today known as Dassault Systèmes UK Limited). As commonly known, the 3D time-stepping finite element method (FEM) is very time-consuming; thus, the use of 2D analysis is preferred. Furthermore, losses in the core, only in a certain part are caused by the fundamental field but also by high-rank harmonics caused by both excitation and the change in magnetic reluctance along the perimeter of the machine [33]. For the calculation of core losses, which are less affected by 3D phenomena due to the lack of a skew, the 2D time-stepping analysis was performed over approximately 20 cycles until the steady state was reached. Next, the core losses are calculated from 2D simulation results as a value taken from all available time snapshots according to the method described in [32,34] and previously used for induction motors. A number of sample points in time were chosen to allow for the subsequent discrete Fourier transform (DFT) analysis. Using the values of components of magnetic flux density in each mesh element at any time snapshot, the DFT analysis was performed in order to assess the contribution of higher harmonics, which are important. The number of calculated harmonics was selected according to the Nyquist–Shannon sampling theorem as half of the number of sample points. The calculation of losses necessitated the extrapolation of the specific loss characteristic of the material for frequencies above 5,000 Hz. This extrapolation used the measured values in the range 20–5,000 Hz and had the form (1)

(1) w Fe = k e f 2 B α + k h f B β

where k _e and k _h are the coefficients of eddy currents and hysteresis, f is frequency, and α and β the extrapolation coefficients. For a fixed value of the peak flux density B, the graph of specific loss divided by the frequency should have the form of a straight line relatively to the frequency (2).

(2) w Fe f = k e B α f + k h B β

In order to obtain good accuracy, approximation of the frequency range has been divided into ranges.

The 3D calculations are necessary in the case of machine simulations with permanent magnets, especially due to the calculation of losses from eddy currents. The 2D model assuming the infinite length of the machine for eddy currents generates significant errors. The more so applies to machines with segmented magnets, where eddy currents have to close within each segment. For the purpose of the 3D simulation, a quarter of the machine was considered to benefit from the magnetic symmetry. The windings are modelled by connections to external resistances. The time-stepping analysis was performed, assuming constant speed of rotation of the rotor with adaptive time-step length. The 3D mesh contains a total of 4.26 million edge elements. In the conductive areas, the element size was chosen to be less than one third of the penetration depth. Moreover, the distribution of the density of the mesh is greater than that required to correctly reproduce the effect of rotation of the rotor relative to the stator. To reduce the computation times, the simulations were performed on a virtual machine with eight cores.

2.3 Method of the coupled thermal fluid analysis in 3D

The coupled thermal-fluid and electromagnetic models are able to compute the temperature distributions outside and inside the machine [33,34]. They are used for PMSM and SRM topologies. Three solid models of analyzed machines were prepared: PMSM – variant 1, PMSM – variant 2, and SRM model. The Ansys Fluent package with finite volume method for calculations was used. The discretization mesh for machine models has 7,012,326 elements for PMSM variant 1; 9,216,970 elements for PMSM variant 2; and 4,475,389 elements for SRM. For the solid regions, only the heat equation was solved; whereas for the fluid regions, the mass transport had to be considered. This was done by utilizing a Reynolds-averaged Navier–Stokes (RANS model) approach with a k–ε turbulence model [35] and nonlinear mixed boundary condition for external housing’s faces for convective and radiative heat flow. The inputs are the average powers in any machine part computed with the electromagnetic model previously described.

3 Results of analysis

Simulations were carried out for three topologies: PMSM with surface-mounted magnets (variant 1), PMSM with embedded magnets (variant 2), and SRM. In the first row, we conducted simulations of the impact of permanent magnet segmentation on the distribution of eddy currents and losses in a permanent magnet machine. We examined the effect of machine structure on the cogging torque and the stator voltage. The numbers of poles and slots were carefully chosen to reduce the high-frequency slotting effects on PM losses and torque ripples [18.35-38]. A popular method to limit the ripple torque and eddy current losses in PMs involves the use of magnetic wedges. Three different designs have been considered: without magnetic wedges (NM), with magnetic wedges build from the same material as the stator core (M), and semi-magnetic wedges made of a composite material (SM). The influence of magnetic wedges between the stator teeth on the losses in the magnets were tested. Then, based on the results of calculated losses in the machine, simulation of temperature distribution was carried out for all topologies [39,40,41,42].

3.1 Results of the electromagnetic field simulation

First, the impact of magnet segmentation on the distribution of current density is examined. Figure 5 shows current density distribution on the surface of PM without segmentation (left part) and with segmentation in the axial direction (right part). The segmentation of the magnets and the use of magnetic wedges make it possible to reduce losses in surface-mounted permanent magnets.

Figure 5

Current density distribution [A/mm²] on the surface of PM left – without segmentation and right – with segmentation in the axial direction.

The following simulations concern the impact of configuration on the distribution of the electromagnetic field. Figure 6 shows the torque versus time and stator voltage when the PMSM is used as a generator connected to three resistances for both rotor topologies. Due to field leakage through the isthmus (even despite its saturation as seen in Figure 12), the induced voltage and torque are smaller for the embedded structure for the same load. This figure shows also that the interior magnet topology produces much smaller cogging torques. This result shows that benefits of the interior magnet rotor well-known for classical designee (smoother voltage and smaller cogging torque) exist also for the shapes required by the HT° design.

Figure 6

Comparison of torque instantaneous values for embedded (1) and surface magnets (2) working in generator mode with the same external load resistance in each phase.

Figure 12

Distribution of magnitude of magnetic flux density for model with embedded magnets and nonmagnetic wedges from 3D simulation.

Figure 7 shows the torque versus time and stator voltage when the PMSM is used as a generator connected to three resistances for both rotor topologies. The advantage of the embedded magnets construction is much smaller cogging torque shown in Figure 6 at no-load for the same cases.

Figure 7

PMSM left: stator voltages for interior magnets (1) and surface magnets (2) right: cogging torque for interior magnets (1) and surface magnets (2).

Three types of wedges were tested. Figure 8 shows the results of cogging torque at no-load for three types of wedges.

Figure 8

Cogging torque at no load, 1 = without magnetic wedges (NM), 2 = with magnetic wedges build from the same material as the stator core (M), and semi-magnetic wedges made of a composite material (SM).

Similar results have been obtained for the rated load condition. In this case, the machine was run as a generator with a purely resistive load, where each phase was connected to a resistor with a value of 24.3 Ω. The influence of the stator winding leakage flux on the saturation of the wedges is not significant because of a high value of the coercivity of the permanent magnet. Magnetic material we use is Vacoflux 48 manufactured by Vacuumschmelze (CoFe Alloys with 17–50% Co with 2.35 T saturation polarization). From producer we obtained BH curve up to 2.3 T. Because dynamic relative permeability for that point is still equal to 5.97, further extrapolation was necessary. For this purpose, we as usually use the Froelich method consisting of approximation of the inverse of permeability as a function of field strength H using a linear function. Then this extrapolation is used to generate the BH curve after 2.3 T until the dynamic relative permeability is equal to 1.

Figure 9 shows the comparison of the moduli of the magnetic flux density between the no-load and full-load cases for the variant with magnetic wedges.

Figure 9

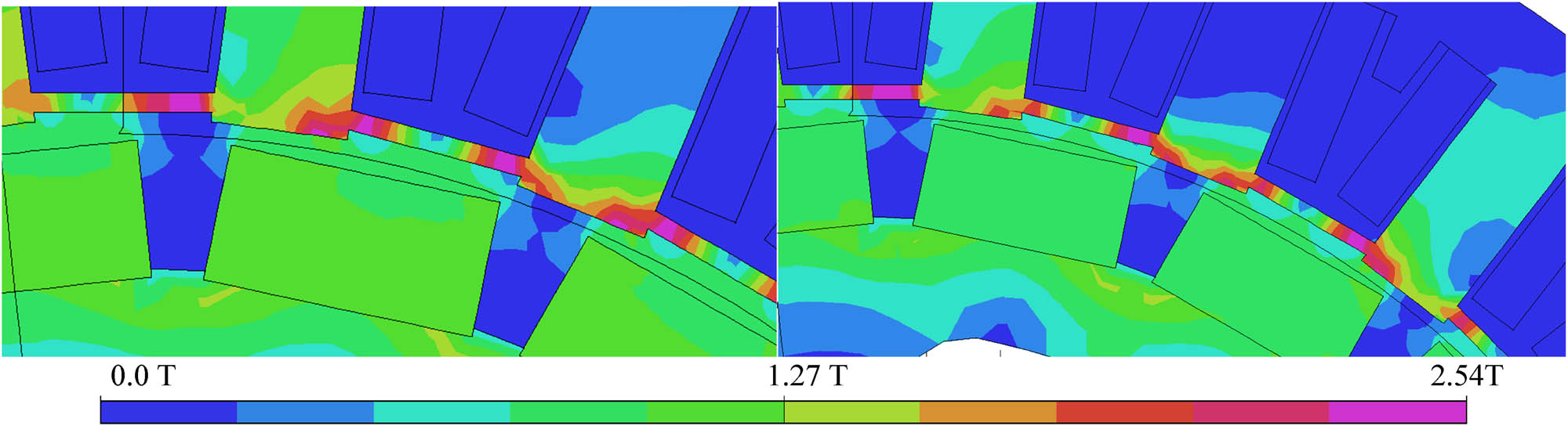
Comparison of the moduli of the magnetic flux density between the no-load and full-load cases for the variant with magnetic wedges.

Figure 10 provides a comparison of the relative values of the torque ripple (related to the average value of the torque) for the three types of the wedges.

Figure 10

Comparison of the relative values of the torque ripple (related to the average value of the torque) for the three types of the wedges 1-(NM), 2-(M), and 3-(SM).

Figure 11 shows the magnitude of magnetic flux density for surface-mounted magnets and nonmagnetic wedges from 3D simulation. For comparison next Figure 12 shows the magnitude of magnetic flux density for model with embedded magnets.

Figure 11

Distribution of magnitude of magnetic flux density for surface-mounted magnets and nonmagnetic wedges.

All constructions are characterized by a similar use of the magnetic circuit. Similar calculations were made for the SRM working as a motor. Results are obtained for the stator current offset angle corresponding to the maximum reluctance torque. It was assumed that the stator winding currents are sine. The HT° coils are the same as the PMSM. On Figure 13, the distribution of magnetic field density for reluctance machine is presented.

Figure 13

Distribution of magnitude of magnetic flux density [T] for reluctance model with laminated rotor from 3D simulation.

Based on the results presented on Figure 14, it can be concluded that, for currents over 8 A, the relationship between torque and current is practically linear.

Figure 14

Torque current curve for a constant internal angle.

The difference between the 2D and 3D solutions in the case of a reluctance motor with laminated rotor is small (about 5.3%). For the 2D model, the electrical conductivity of the stator wedges was not taken into account, but it has little effect on the solution. Figure 15 shows the comparison of torque calculated by 2D and 3D models. To reduce transient phenomena, the voltage increases linearly over the first two periods.

Figure 15

Comparison of 2D and 3D torque calculation.

Because in this simulation we assume that the motor is powered from a current source, the current was sinusoidal, but of course the voltage induced in the windings is distorted (Figure 16). Also, in this case, the 2D solution gives satisfactory accuracy.

Figure 16

Induced voltage in motor winding vs. time.

Based on the presented results, we decided to use the 2D simulation for the calculations of electromagnetic field in the reluctance machine. Figure 17 presents the analysis of the stator and rotor losses from higher harmonics for a reluctance machine from 2D simulation and methods described in the previous paragraph. These losses are negligible.

Figure 17

Losses in the stator and rotor of cores SRM due to harmonics.

3.2 Coupled thermal-fluid analysis in 3D

The electromagnetic and thermal-fluid models yield temperature distributions outside and inside the machine for several architectures and materials [18]. The cooling system in the machine is as simple as possible, i.e., natural convection of air cooling. The convective heat transfer coefficient for external surface of the motor’s housing was determined from empirical formula based on dimensionless Rayleigh and Nusselt numbers.

(3) Nu = C ⋅ Ra n

where Nu is the Nusselt number, Ra is the Rayleigh number, and C and n are parameters depended on the value of the Rayleigh number and the shape of the body. For analyzed case was assumed that the motor’s housing is cylindrical.

Finally, the convective heat transfer coefficient from the following formula:

(4) h c = Nu ⋅ κ d

where κ is a thermal conductivity of the fluid (air) and d is a housing diameter.

In the mathematical model, combined boundary condition was used. This boundary conditions is given by following formula [18]:

(5) κ ∂ T ∂ n = h c ( T w − T ∞ ) + ε r σ T w 4 − T ext 4

where h _c is a convective heat transfer coefficient, T _∞ is the temperature of the ambient air, T _w is the surface temperature of the wall, T _ext is the ambient temperature, and σ is the Stefan–Boltzmann constant. The convective heat transfer coefficient h _c can be determined from empirical formula which is based on dimensionless Rayleigh and Nusselt numbers.

The CFD model is based on Reynolds-averaged Navier–Stokes equations (RANS equations). This model includes mass, momentum, and energy equations for turbulent fluid flow. In analyzed case k−ε Realizable turbulent model was used. Radiation was included by discrete ordinates radiation model. This model gives temperature distribution and velocity vector of the fluid flow.

Figure 18 shows the temperature distributions in the whole PMSM computed for two architectures: the surface-mounted magnets and embedded magnets for an ambient external air at 200°C. These results were obtained with and without slot magnetic wedges. Figure 19 shows the temperatures on the outside surface of the PMSM housing.

Figure 18

Temperature distribution in the PMSM cross section. (a) surface-magnet rotor stator slot magnetic wedges, (b) surface-magnet rotor no stator slot magnetic wedges, (c) embedded-magnet rotor stator slot magnetic wedges, (d) embedded-magnet rotor no stator slot magnetic wedges.

Figure 19

The temperature distributions outside HT° PMSM. (a) Surface-magnet rotor stator slot magnetic wedges, (b) surface-magnet rotor no stator slot magnetic wedges, (c) embedded-magnet rotor stator slot magnetic wedges, (d) embedded-magnet rotor stator no slot magnetic wedges.

The average temperature values of selected machine components for both variants and versions with and without wedges were calculated. The results of these calculations are presented in Table 1.

Table 1

Average temperatures of the main PMSM parts for both architectures at 200°C ambient

Temperatures in the main motor parts (°C)	Surface magnet rotor		Embedded magnet rotor
Temperatures in the main motor parts (°C)	Wedges (magnetic slot closing wedge)	No wedge (nonmagnetic slot closing wedge)	Wedges (magnetic slot closing wedge)	No wedgd (nonmagnetic slot closing wedge)
Magnets	307.3	283.0	281.1	239.6
Wedges	321.0	270.9	300.3	245.8
Rotor package	305.4	281.0	281.4	239.7
Stator package	307.0	266.6	288.6	245.9
Winding	312.6	273.1	293.6	250.0

Figure 20 shows the temperature distributions inside and outside the SRM for an ambient temperature of 200°C. Figure 21 is similar but for an air temperature of 500°C.

Figure 20

Temperature distribution for SRM in an ambient air at 200°C. (a) Temperature inside the machine 3D vues and coil ends, (b) temperature in the transverse cross section, (c) temperatures in a longitudinal cross section, (d) external housing temperatures.

Figure 21

Temperature distribution for SRM in an ambient air at 500°C. (a) Temperatures inside the machine 3D vues and coils ends, (b) temperatures in the transverse cross section, (c) temperatures in a longitudinal cross section, (d) external housing temperatures.

4 Discussion

4.1 Main results interpretation

The simulation results open discussions on several topics of HT° synchronous machine possible architectures. For both PMSMs and SRMs, the concentrated winding machines with opened slots have better functional characteristics with magnetic wedges closing the slots: voltages are smoother when the machine operates as a generator; the cogging torque is lower when it is used as a motor. Three solutions were tested. The best results are obtained with wedges made of a magnetic steel, which characteristics are similar to the magnetic material of the core. For wedges of low permeability, the cogging torque is higher. For the tested geometry, it is possible to reduce the losses in the surface magnet to a value of 22.9 W and to of 0.72 W in embedded magnets.

For PMSMs, the rotor embedded magnet structure, also known as interior PM rotor, has a lower torque ripple than the rotor surface magnet structure because the soft magnetic core protects permanent magnet from pulsating fields mainly due to the stator slots. However, this rotor structure is much more difficult to build because of the complex shape of the soft core. The weak mechanical point is the saturated isthmus between the air gap and the embedded magnet. Because of the complex shape of the soft magnetic core, the nonmagnetic shaft is also more difficult to machine. Consequently, this structure is much more expensive than the case of the rotor with surface magnets made with a quasi-cylindrical shape with flat surfaces intended to receive the magnets. At HT°, the bonding of the magnets is not suitable, they must be fixed securely by an external carbon fiber or titanium thin shrink ring. With these structure the eddy currents exist mainly in the region of the upper corners of magnets.

For both PMSM architectures, the technological lock for operating at higher temperature is situated at the level of the magnets because the only available ones are specific Samarium and Cobalt alloys. Manufacturers give interesting characteristics up to 340°C but with lower coercive fields than at standard temperatures. Therefore, the high-speed operations requiring to weaken the magnet field by acting on the command must be limited for avoiding a permanent rotor demagnetization. With such metallic magnets, the internal losses due to eddy current are higher than in PMSM operating at standard temperatures. Such PMSMs can be used with ambient temperature limited to more or less 200°C. For higher temperatures, the SRM architecture, made without any magnet, is required.

Similar simulations were made for SRMs for stator 3-phase sine currents. The internal angle corresponds to the maximum reluctant torque. Thermal calculations were carried out for two ambient temperatures: 200°C and 500°C. The results of these calculations as the average temperature values of selected machine components are presented in Table 2.

Table 2

Temperature of the main SRM components for the considered geometry

	Ambient	Housing	Rotor core	Stator core	Stator winding
Temperature (°C)	200	335.3	354.5	350.6	393.6
Temperature (°C)	500	580.6	605.3	603.6	652.8

The results are obtained for a stator current of 8A RMS at a frequency corresponding to 5,000 rpm. The torque is 2 Nm, coil losses 610 W, stator iron losses 69 W, losses in the rotor iron losses 35 W, and losses in the stator wedges 2.5 W. These results show that the efficiency of this HT° SRM is rather low (59%). The coil losses are also unacceptable, and the HT° coil design is more critical than for the HT° PMSM. Special care must be taken on the coil filling factor. For the PMSM with the embedded magnets and with wedges, the efficiency is 85.6%.

4.2 Definition of prototypes

The simulations made on PMSMs show that both options with embedded and surface magnets have advantages and disadvantages; therefore, we decided to check both in practice. Based on simulation results, three prototypes of HT° machines will be built. The first one is a PMSM with surface-mounted magnets on the rotor. The second one is made with interior magnets. Both PMSM prototypes will be made with SmCo magnets [11]. The third prototype will be an SRM with a salient-pole FeSi-laminated rotor. The rotor will be a simple stack of laser-cut FeSi laminations insulated by their natural oxidation and pressed between two stainless steel flanges fixed to the shaft.

For the surface magnet rotor, the available glues are limited to 280°C. This technological lock will be overcome using a thin carbon shrink ring around the magnets. The complex shape of the soft magnetic of the interior magnet rotor core will be obtained by electro-erosion with a mechanical isthmus of 0.3 mm between each magnet side and the air gap, which will be saturated by the magnet flux. The rotor mechanical fixing will be made by a nonmagnetic stainless steel shaft providing rotor rigidity.

The stator design will be identical for the three prototypes. The 24 inorganic HT° stator coils will be placed on the stator teeth with a thin glass fiber textile placed between each stator tooth and the coil for providing a mechanical damping. The stator slots will be closed by metallic wedges for reducing the cogging torque and the magnet losses. Electric connections between coils will be made using silver brazing. The stator core with the 24 HT° coils will be placed in stainless steel housing, which ensures the centering of the flanges.

4.3 Prototype testing preparation

Electric machines with an ability to operate at ambient temperatures over 200°C are at the very beginning of their development; no angular position sensors are still available on the market. Consequently, specific methods are required for testing the HT° synchronous machines without any angular sensor. Sensorless PMSM drives exist for a long-time, but they need a good knowledge of the PMSM under tests parameter, which is not the case for a prototype operating on a wide temperature range. Large coil resistances variations are expected. Moreover, with a standard sensorless control, the lack of control can damage the machine under tests. For avoiding this drawback, the machine will be fed by a current source PWM inverter placed outside the oven used for imposing an elevated ambient temperature. The inverter will provide a sine 3 sine currents, with a phase lag of ± 2 π / 3 forming a balanced 3-phase system with a controlled magnitude (I _M) and frequency (f). This three-phase current system will produce several rotating magnetomotive force (mmf) because of the concentrated winding architecture. These rotating fmm can be described by Fourier series. For a 24/20 PMSM made following the standard rules of the concentrated windings [26], the first fmm harmonic rotates at a speed of f/10 rps. An average torque is produced only when the 20-rotor poles are synchronized with the rotating fmm first harmonic; the other rotating fmm creates only the cogging torque. Therefore, for starting the machine from zero-speed in opened loop, the frequency must be f = 0.

The operation procedure consists of slowly increasing the current magnitude for f = 0, while the rotor position is unknown. The stator creates a zero-speed first harmonic fmm and many others of lower magnitudes that create no average torque. For a current magnitude estimated to be more or less I L = 2 A (2 A in the first phase and 1A in the other ones), the rotor free of any mechanical load torque will move toward a mechanical balance position where the rotor poles are in front of the zero-speed stator mmf ones. In a second time, the current will be increased in achieving enough static torque. From this mechanical equilibrium, the frequency will be slowly increase to attain the rated speed. This method is valid for a PMSM or for an SRM.

For a synchronous motor fed by a PWM inverter controlled in current, the feeding system provides the motor safety when synchronism is lost because of a too large load angle between the stator rotating mmf pole rotor ones. When the stability limit will be reached, the electromagnetic average torque falls to zero and the motor stops without damage because the current magnitude is controlled by the inverter independently of the voltage. However, the synchronous machine must be restarted from zero frequency.

With an ac source controlled in current, the motor voltage magnitude and phase lag depend on the angle between the rotating mmf first harmonic and the rotor. The active and reactive powers will be deduced from the voltage magnitude and phase lag measurements. The stator losses will be computed from the actual coil temperature and current measurements, considering the temperature coefficient of the copper wires.

Tests will be made in the oven that impose the required ambient temperature. The mechanical load will be a simple additional inertia equal to four times the rotor one for getting a large global inertia. The electromagnetic torque will be estimated from the time derivative of the frequency imposed by the converter control system and the global inertia.

Currently we are working on the preparation of prototypes and test bench. We plan to carry out measurements for both versions of PMSM at an ambient temperature of 200°C and for a reluctance machine at ambient temperatures of 200°C and 500°C for checking in practice the results obtained by simulation.

5 Conclusion

The article presents a classification of several possible architectures of HT° machines made with inorganic coils with an ability to operate at high ambient temperatures and with high internal thermal gradients. With such inorganic coils, made without any polymer, the limitation parameter is the permanent magnet maximum temperature for the PMSM.

The design of an HT° motor requires rigid coils and, consequently, a specific design of the stator core with rectangular teeth and opened slots are required for making possible the assembly of the coils. Therefore, the slotting effect is much higher than for classical designs made with conventional flexible organic enameled wires in semi-closed slots. Eddy currents in surface-mounted magnets and corresponding losses are much higher than for standard architectures. Moreover, the only available magnets with an ability to operate over 300°C have a higher electric conductivity. The machine architecture must take these effects into consideration. A solution consists of closing the stator slots by magnetic wedges. The two PMSM rotor investigated architectures show that, with surface magnets, the eddy currents losses are much higher than for the interior magnet rotor. The interior magnet PMSM also provides a smoother torque.

The SRM is made without any magnet; this architecture can operate at much higher temperature. The limit comes from the decrease in the machine global performance due to the stator coil resistance large increase at HT°. Generally speaking, SRMs have a lower efficiency than comparable size PMSMs at classical temperatures. This drawback increases with the ambient temperature, but the SRM architectures, associated with inorganic stator coils and a mechanical design valid for HT°, are the only solution for an electric machine placed in an ambient air over 350°C.

Several general points must be considered for designing HT° machines:

The conventional FeSi of FeCo magnetic sheets with their natural oxidation as insulating layers can be used for the soft core. However, a slightly lower rated air gap flux density must be chosen. The iron losses are lower than that at conventional temperatures because of the lower electric conductivity of the core sheets.
For PMSMs, the maximum temperature depends on SmCo magnets and the motor demagnetization for overspeed capabilities because of the lower coercive fields at HT°. Slot magnetic wedges used for closing the opened stator slots reduce the cogging torque and the magnet losses.
For SRMs made with HT° inorganic coils, the internal temperature limit is much higher. However, the practical limit for the user is linked with the reduction in the efficiency caused by the natural increase in the stator coil resistances.
The numerical electromagnetic and thermal numerical studies provide data useful for the design of three prototypes that are now being implemented and will be tested. Works in progress concern their full comparative tests in a hot environment and with high internal temperature gradients. The detailed experimental result will be presented in a further article.

References

[1] Aeronautics and Air Transport: Beyond Vision 2020 Towards 2050, Jun. 2010, Available online: http://www.acare4europe.org/docs/towards2050.pdf.Search in Google Scholar

[2] Munuswamy I, Wheeler PW. Electric DC WIPS: all electric aircraft. Innovations in 2017Power and Advanced Computing Technologies (i-PACT); 2017. p. 1–5.10.1109/IPACT.2017.8244883Search in Google Scholar

[3] Wheeler PW. Technology for the more and all electric aircraft of the future. 2016 IEEE International Conference on Automatica (ICA-ACCA) Curico, Chile. October 2016.10.1109/ICA-ACCA.2016.7778519Search in Google Scholar

[4] Chen J, Wang Ch, Chen J. Investigation on the selection of electric power system architecture for future more electric aircraft. IEEE Trans Trans Elect. 2018;4(2):563–76.10.1109/TTE.2018.2792332Search in Google Scholar

[5] Gong G, Heldwein ML, Drofenik U, Minibock J, Mino K, Kola JW. Comparative evaluation of three-phase high-power-factor AC-DC converter concepts for application in future more electric aircraft. IEEE Trans Ind Electron. 2005;52(3):727–37.10.1109/APEC.2004.1295968Search in Google Scholar

[6] Available online: https://www.safran-group.com/fr/media/safran-celebre-le-debut-des-essais-du-demonstrateur-open-rotor-sur-le-nouveau-banc-lair-libre-distres-20171003.Search in Google Scholar

[7] Ho J, Jow T. Effect of crystallinity and morphology on dielectric properties of peek at elevated temperature. 2013 IEEE International Conference on Solid Dielectrics (ICSD). June 2013. p. 385–8.10.1109/ICSD.2013.6619864Search in Google Scholar

[8] Hoang ATT, Serdyuk YVV, Gubanski SM. Electrical characterization of a new enamel insulation. IEEE Trans Dielectr Electr Insulation. June 2014;21(3):1291–301.10.1109/TDEI.2014.6832277Search in Google Scholar

[9] Raminosoa T, El-Refaie A, Torrey D, Grace K, Pan D, Grubic S, et al. Test results for a high temperature non-permanent-magnet traction motor. IEEE Trans Ind Appl. 2017;53(4):3496–504.10.1109/ECCE.2016.7855495Search in Google Scholar

[10] Iosif V, Roger D, Duchesne S, Malec D. An insulation solution for coils of high temperature motors (500°C). 2016 IEEE Int Conf Dielectr (ICD). 2016;1:297–300.10.1109/ICD.2016.7547603Search in Google Scholar

[11] Liu J, Walmer M. Thermal stability and performance data for SmCo 2:17 high-temperature magnets on ppm focusing structures. IEEE Trans ElectrDevices. 2005;52(5):899–902.10.1109/TED.2005.845868Search in Google Scholar

[12] Cozonac D, Lecointe JP, Duchesne S, Velu G. Materials characterization and geometry of a high temperature induction machine. 2014 International Conference on Electrical Machines (ICEM); 2014. p. 2499–505.10.1109/ICELMACH.2014.6960538Search in Google Scholar

[13] Iosif V, Roger D, Duchesne S, Malec D. Assessment and improvements of inorganic insulation for high temperature low voltage motors. IEEE Trans Dielectr Electr Insulati. 2016;23(5):2534–42.10.1109/TDEI.2016.7736810Search in Google Scholar

[14] Hua H, Zhu ZQ, Wang C, Zheng M, Wu Z, Wu D, et al. Partitioned stator machines with NdFeB and ferrite magnets. IEEE Trans Ind Appl. 2017;53(3):1870–82.10.1109/TIA.2016.2645899Search in Google Scholar

[15] Widme JD, Martin R, Mecrow BC. Optimization of an 80 kW segmental rotor switched reluctance machine for automotive traction. IEEE Trans Ind Appl. 2015;51(4):2990–9.10.1109/TIA.2015.2405051Search in Google Scholar

[16] Boglietti A, Cossale M, Vaschetto S, Dutra T. Thermal conductivity evaluation of fractional-slot concentrated-winding machines. IEEE Trans Ind Appl. 2017;53(3):2059–65.10.1109/ECCE.2016.7855511Search in Google Scholar

[17] El-Refaie AM. Fractional-slot concentrated-windings synchronous permanent magnet machines: opportunities and challenges. IEEE Trans Ind Electr. 2010;57(1):107–21.10.1109/TIE.2009.2030211Search in Google Scholar

[18] El-Refaie AM, Jahns TM. Optimal flux weakening in surface PM machines using fractional-slot concentrated windings. IEEE Trans Ind Appl. 2005;41(3):790–800. 10.1109/TIA.2005.847312.Search in Google Scholar

[19] Gagas BS, Sasaki K, Athavale A, Kato T, Lorenz RD. Magnet temperature effects on the useful properties of variable flux PM synchronous machines and a mitigating method for magnetization changes. IEEE Trans Ind Appl. 2017;53(3):2189–99.10.1109/ECCE.2016.7855228Search in Google Scholar

[20] Zhu ZQ, Lee B, Liu X. Integrated field and armature current control strategy for variable flux reluctance machine using open winding. IEEETrans IndAppl. 2016;52(2):1519–29.10.1109/EVER.2015.7112947Search in Google Scholar

[21] Hyung-Kyu K, Hur J. Dynamic characteristic analysis of irreversible demagnetization in SPM- and IPM-Type BLDC motors. IEEE Trans Ind Appl. 2017;53(2):982–90.10.1109/TIA.2016.2619323Search in Google Scholar

[22] Lefik M, Komeza K, Napieralska-Juszczak E, Roger D, Napieralski P. Comparison of the reluctance and permanent magnet synchronous machine operating at high temperatures. IEEE Transportation Electrification Conference and Expo (ITEC). Long Beach, USA: 2018, June 13-15. p. 418–23.10.1109/ITEC.2018.8450087Search in Google Scholar

[23] Cotronics, Adhesifs, ciments, revetements ceramiques hautes temperatures 1000-3000°C.; Fiche technique, www.cotronics.com.Search in Google Scholar

[24] Elmadah H, Roger D, Takorabet N. Design of inorganic coils for high temperature electrical machines. Open Phys. 2019;17:698–708.10.1515/phys-2019-0072Search in Google Scholar

[25] EL-Refaie AM. Fractional-slot concentrated-windings synchronous permanent magnet machines: opportunities and challenges. IEEE Trans Ind Electron. 2010;57(1):107–21. 10.1109/TIE.2009.2030211.Search in Google Scholar

[26] Pyrhonen J, Jokien T, Hrabovcova V. Design of rotating electrical machines. 2nd edn., John Whiley & Sons; 2014.Search in Google Scholar

[27] Komeza K, Lefik M, Roger D, Juszczak E, Elmadah H, Napieralski P, et al. High temperature permanent magnet synchronous machine analysis of thermal field. Open Phys. 2019;17(1):631–42. 10.1515/phys-2019-0065.Search in Google Scholar

[28] Bianchi N, Degano M, Fornasiero E. Sensitivity analysis of torque ripple reduction of synchronous reluctance and interior PM motors. IEEE Trans Ind Appl. 2015;51(1):187–95.10.1109/ECCE.2013.6646932Search in Google Scholar

[29] Dogan H, Wurtz F, Foggia A, Garbuio L. Analysis of slot-pole combination of fractional-slots PMSM for embedded applications. IEEE International Conference on Electrical Machines and Power Electronics (ACEMP); Sept 2011.10.1109/ACEMP.2011.6490669Search in Google Scholar

[30] Ying HW, Bettayeb A, Kaczmarek R, Vannier JC. Optimization of magnet segmentation for reduction of Eddy–Current losses in permanent magnet synchronous machine. IEEE Trans Energy Convers. 2010;25(2):381–7.10.1109/TEC.2009.2036250Search in Google Scholar

[31] Takahashi N, Morishit M, Miyagi D, Nakano M. Examination of magnetic properties of magnetic materials at high temperature using a ring specimen. IEEE Trans Magnetics. 2010;46(2):548–51.10.1109/TMAG.2009.2033122Search in Google Scholar

[32] Takahashi N, Morishit M, Miyagi D, Nakano M. Comparison of magnetic properties of magnetic materials at high temperature. IEEE Trans Magnetics. 2011;47(10):4352–5.10.1109/TMAG.2011.2158517Search in Google Scholar

[33] Lefik M, Komeza K, Napieralska-Juszczak E, Roger D, Napieralsk P. Comparison of the reluctance laminated and solid rotor synchronous machine operating at high temperatures. COMPEL. 2019;38(4):1111–9.10.1108/COMPEL-10-2018-0405Search in Google Scholar

[34] Bertotti G. General properties of power losses in soft ferromagnetic materials. IEEE Trans Magn. 1988;24(1):621–30.10.1109/20.43994Search in Google Scholar

[35] Dems M, Komeza K. Performance characteristics of a high-speed energy-saving induction motor with an amorphous stator core. IEEE Trans Ind Electron. 2014;61(6):3046–55.10.1109/ICElMach.2012.6350228Search in Google Scholar

[36] Li S, Sarlioglu B, Jurkovic S, Patel NR, Savagian P. Analysis of temperature effects on performance of interior permanent magnet machines for high variable temperature applications. IEEE Trans Ind Appl. 2017;53(5):4923–33.10.1109/TIA.2017.2700473Search in Google Scholar

[37] Melka B, Smolka J, Bulinski Z, Ryf A, Hetmanczyk J, Makiela D. A validated numerical model of heat and mass transfer in a PM BLDC electric motor. International Symposium on Power Electronics, Electrical Drives, Automation and Motion (SPEEDAM); Aug. 2016.10.1109/SPEEDAM.2016.7525885Search in Google Scholar

[38] Reddy P, El-Refaie A. Comparison of interior and surface PM machines equipped with fractional-slot concentrated windings for hybrid traction applications. IEEE Trans Energy Convers. 2012;27(3):593–602.10.1109/ECCE.2011.6064067Search in Google Scholar

[39] Tang Ch, Soong WL, Jahns TM, Ertugrul N. Analysis of iron loss in interior PM machines with distributed windings under deep field weakening. IEEE Trans Ind Appl. 2015;51(5):3761–72.10.1109/ECCE.2014.6953969Search in Google Scholar

[40] Pfister PD, Xin Y, Youtong F. Slotted permanent-magnet machines: general analytical model of magnetic fields, torque, eddy currents, and permanent-magnet power losses including the diffusion effect. IEEE Trans Magnetics. 2016;52(5).10.1109/TMAG.2015.2512528Search in Google Scholar

[41] Staton RD, Lock R, Booker J, Drury D. Winding design for minimum power loss and low-cost manufacture in application to fixed-speed PM generator. IEEE Trans Ind Appl. 2015;51(5):3773–82.10.1109/TIA.2015.2434802Search in Google Scholar

[42] Ruoho S, Haavisto M, Takala F, Santa-Nokki T, Paju M. Temperature dependence of resistivity of sintered rare-earth permanent-magnet materials. IEEE Trans Magnetics. 2010;46(1):15–20.10.1109/TMAG.2009.2027815Search in Google Scholar

Received: 2020-04-30

Revised: 2020-05-26

Accepted: 2020-06-04

Published Online: 2020-10-27

This work is licensed under the Creative Commons Attribution 4.0 International License.

Articles in the same Issue

https://doi.org/10.1515/phys-2020-0154

Keywords for this article

high temperatures; permanent magnet synchronous machine; synchroreluctant machine; thermal analysis; fluid dynamics; HT° materials

Creative Commons

BY 4.0