Home Phragmén-Lindelöf alternative results and structural stability for Brinkman fluid in porous media in a semi-infinite cylinder
Article Open Access

Phragmén-Lindelöf alternative results and structural stability for Brinkman fluid in porous media in a semi-infinite cylinder

  • Yuanfei Li EMAIL logo and Xuejiao Chen
Published/Copyright: December 23, 2022
Download Article (PDF)
Open Mathematics
From the journal Open Mathematics Volume 20 Issue 1

Abstract

This article investigates the spatial behavior of the solutions of the Brinkman equations in a semi-infinite cylinder. We no longer require the solutions to satisfy any a priori assumptions at infinity. Using the energy estimation method and the differential inequality technology, the differential inequality about the solutions is derived. By solving this differential inequality, it is proved that the solutions grow polynomially or decay exponentially with spatial variables. In the case of decay, the structural stability of Brinkman fluid is also proved.

Keywords: Phragmén-Lindelöf alternative results; Brinkman equations; energy estimation; structural stability
MSC 2010: 35B40; 35K50; 35Q35

1 Introduction

The Brinkman equations are often used to describe flow in a porous medium, which have been discussed in the books of Nield and Bejan [1], Straughan [2], and Hewitt [3]. Many scholars in the literature have paid attention to the spatial attenuation of Brinkman equations on a semi-infinite cylinder. Payne and Song [4] considered the fluid in porous media controlled by Brinkman equations. The Saint-Venant-type decay of the solutions on a semi-infinite cylinder is obtained. For more works on fluid equations, one can see [5,6, 7,8,9, 10,11]. These articles need to assume that the solutions satisfy certain a priori assumptions at the infinity of the cylinder.

However, the classical Phragmén-Lindelöf alternative theorem does not need such a priori assumption, but proves that the solutions either decay exponentially or increase exponentially with the distance from the finite end of the cylinder. In the past few decades, the Phragmén-Lindelöf alternative research has received a lot of attention (see [12,13,14, 15,16,17]). The above articles mainly focus on linear problems.

In this article, we suppose that a porous medium occupies the interior of a semi-infinite cylindrical pipe of arbitrary cross-section and generators parallel to the x 3 axis. We let R denote the semi-infinite cylinder, i.e.,

R = { x = ( x 1 , x 2 , x 3 ) ∣ ( x 1 , x 2 ) ∈ D , x 3 ≥ 0 } ,

where D is the cross section of the cylinder (Figure 1).

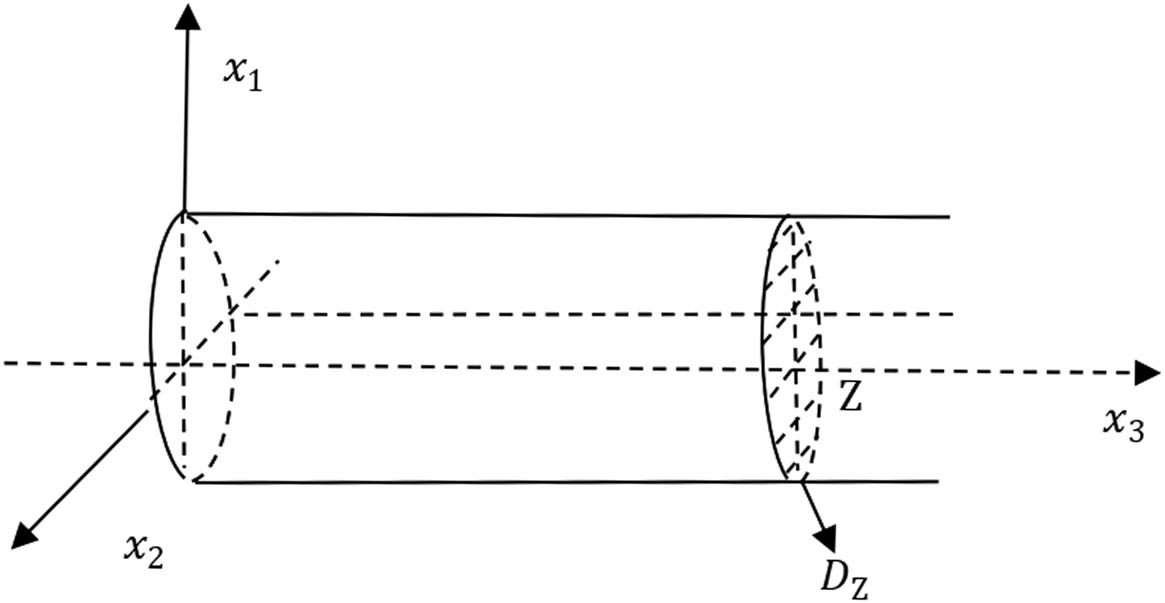
Figure 1 Cylindrical pipe.
Figure 1

Cylindrical pipe.

The Brinkman equations we consider in this article can be written as follows:

(1.1) − ν Δ u i + u i = − p i + g i T , in R × ( 0 , t ) ,

(1.2) u i , i = 0 , in R × ( 0 , t ) ,

(1.3) ∂ t T + u i T i = Δ T , in R × ( 0 , t ) ,

where i = 1 , 2 , 3 ; u i is the velocity field; T is the temperature of the fluid; p is the pressure; ν > 0 represents the Brinkman coefficient; and g = ( g 1 , g 2 , g 3 ) is the gravity field, which are prescribed functions. For simplicity, we assume that g satisfies

(1.4) ∣ g ∣ ≤ 1 , ∣ ∇ g ∣ ≤ 1 .

We use commas for derivation, repeated English subscripts for summation from 1 to 3, and repeated Greek subscripts for summation from 1 to 2, e.g., u i , j u i , j = ∑ i , j = 1 3 ∂ u i ∂ x j 2 and u α , β u α , β = ∑ α , β = 1 2 ∂ u α ∂ x β 2 .

Equations (1.1)–(1.3) also satisfy the following initial-boundary conditions:

(1.5) u i ( x 1 , x 2 , x 3 , t ) = 0 , T ( x 1 , x 2 , x 3 , t ) = 0 , on ∂ D × { x 3 > 0 } × ( 0 , t ) ,

(1.6) u i ( x 1 , x 2 , 0 , t ) = f i ( x 1 , x 2 , t ) , T ( x 1 , x 2 , 0 , t ) = h ( x 1 , x 2 , t ) , on D × ( 0 , t ) ,

(1.7) u i ( x 1 , x 2 , x 3 , 0 ) = 0 , T ( x 1 , x 2 , x 3 , 0 ) = 0 , in R ,

where f i and h are continuously differentiable and ∂ D is the boundary of D .

We also introduce the following notations:

R z = { ( x 1 , x 2 , x 3 ) ∣ ( x 1 , x 2 ) ∈ D , x 3 > z ≥ 0 } ,

D z = { ( x 1 , x 2 , x 3 ) ∣ ( x 1 , x 2 ) ∈ D , x 3 = z ≥ 0 } ,

where z is a running variable along the x 3 axis.

This article studies the Phragmén-Lindelöf-type alternative theorem of equations (1.1)–(1.7) on R . Because our model contains nonlinear terms and pressure terms that are difficult to deal with, how to set the energy function is the key. As far as we know, there are few relevant results on the Phragmén-Lindelöf-type alternative results of such nonlinear equations. The second work of this article is to study the structural stability of Brinkman equations in the case of decay. This type of structural stability is proposed by Hirsch and Smale in their book [18], which mainly studies whether small changes in the coefficients of the equations can cause great changes in the solution. A large number of results have been achieved in the past few decades, see [19,20,21, 22,23,24, 25,26,27, 28,29]. However, these results only considered the bounded region and have not paid enough attention to the structural stability of the solutions of partial differential equations in a semi-infinite cylinder. Therefore, the research of this article is very meaningful and can provide a reference for the alternative research of other types of nonlinear equations.

2 Preliminary

Here are some lemmas that will be often used.

Lemma 2.1

[4] If w ∣ ∂ D = 0 , then

λ 1 ∫ D w 2 d A ≤ ∫ D w α w α d A ,

where λ 1 is the smallest positive eigenvalue of

Δ 2 φ + λ φ = 0 , in D , φ = 0 , on ∂ D ,

where Δ 2 is a two-dimensional Laplace operator.

Lemma 2.2

[30] There exists a positive constant k 1 depending on region D such that

∫ D w 4 d A 1 2 ≤ k 1 ∫ D w 2 d A + ∫ D w α w α d A .

Lemma 2.3

[31] If g is a continuously differentiable function on D and ∫ D g d A = 0 , then there exists a vector function w = ( w 1 , w 2 ) such that

w α , α = g , in D , w α = 0 , on ∂ D ,

and a positive constant C depending only on the geometry of D such that

∫ D w α , β w α , β d A ≤ C ∫ D w α , α w α , α d A .

To obtain the Phragmén-Lindelöf-type alternative result of the solutions to (1.1)–(1.3), we define

(2.1) F ( z , t ) = δ 1 F 1 ( z , t ) + F 2 ( z , t ) + F 3 ( z , t ) ,

where δ 1 is a positive constant and F i ( z , t ) ( i = 1 , 2 , 3 ) are defined as follows:

(2.2) F 1 ( z , t ) = − ∫ 0 t ∫ D z e − ω η p u 3 d A d η + ν ∫ 0 t ∫ D z e − ω η u i , 3 u i d A d η ,

(2.3) F 2 ( z , t ) = ν ∫ 0 t ∫ D z e − ω η u i , 33 u i , 3 d A d η + ∫ 0 t ∫ D z e − ω η p 3 u 3 , 3 d A d η − ∫ 0 t ∫ D z e − ω η g i T u i , 3 d A d η ,

(2.4) F 3 ( z , t ) = − 1 2 ∫ 0 t ∫ D z e − ω η u 3 T 2 d A d η + ∫ 0 t ∫ D z e − ω η T 3 T d A d η .

In (2.2)–(2.4), ω is a positive constant. Let z 0 be a positive constant that satisfies z > z 0 ≥ 0 . Using the divergence theorem, equations (1.1)–(1.3), and the initial-boundary conditions (1.5)–(1.7), we have

(2.5) F 1 ( z , t ) − F 1 ( z 0 , t ) = − ∫ 0 t ∫ z 0 z ∫ D ξ e − ω η u i p i d A d ξ d η + ν ∫ 0 t ∫ z 0 z ∫ D ξ e − ω η [ u i Δ u i + u i , j u i , j ] d A d ξ d η = ∫ 0 t ∫ z 0 z ∫ D ξ e − ω η [ ν u i , j u i , j + u i u i ] d A d ξ d η − ∫ 0 t ∫ z 0 z ∫ D ξ e − ω η g i u i T d A d ξ d η .

Second, differentiating equation (1.1) with respect to x 3 , we have

− ν Δ u i , 3 + u i , 3 + p i 3 − [ g i T ] 3 = 0 .

Therefore, we have

(2.6) ∫ 0 t ∫ z 0 z ∫ D ξ e − ω η [ − ν Δ u i , 3 + u i , 3 + p i 3 − [ g i T ] 3 ] u i , 3 d A d η = 0 .

By the divergence theorem, we have from (2.6)

(2.7) ν ∫ 0 t ∫ z 0 z ∫ D ξ e − ω η u i , j 3 u i , j 3 d A d ξ d η + ∫ 0 t ∫ z 0 z ∫ D ξ e − ω η u i , 3 u i , 3 d A d ξ d η = ν ∫ 0 t ∫ D z e − ω η u i , 33 u i , 3 d A d η − ν ∫ 0 t ∫ D z 0 e − ω η u i , 33 u i , 3 d A d η + ∫ 0 t ∫ D z e − ω η p 3 u 3 , 3 d A d η − ∫ 0 t ∫ D z 0 e − ω η p 3 u 3 , 3 d A d η − ∫ 0 t ∫ D z e − ω η g i T u i , 3 d A d η + ∫ 0 t ∫ D z 0 e − ω η g i T u i , 3 d A d η + ∫ 0 t ∫ z 0 z ∫ D ξ e − ω η g i T u i , 33 d A d ξ d η .

We have, from (2.7) and (2.3),

(2.8) F 2 ( z , t ) − F 2 ( z 0 , t ) = ν ∫ 0 t ∫ z 0 z ∫ D ξ e − ω η u i , j 3 u i , j 3 d A d ξ d η + ∫ 0 t ∫ z 0 z ∫ D ξ e − ω η u i , 3 u i , 3 d A d ξ d η − ∫ 0 t ∫ z 0 z ∫ D ξ e − ω η g i T u i , 33 d A d ξ d η .

Similar to (2.5), we have

(2.9) F 3 ( z , t ) − F 3 ( z 0 , t ) = − ∫ 0 t ∫ z 0 z ∫ D ξ e − ω η T u i T i d A d ξ d η + ∫ 0 t ∫ z 0 z ∫ D ξ e − ω η ( T i T ) i d A d η = ∫ 0 t ∫ z 0 z ∫ D ξ e − ω η T i T i + 1 2 ω T 2 d A d ξ d η + 1 2 e − ω t ∫ z 0 z ∫ D ξ T 2 d A d ξ .

Combining (2.2), (2.3), and (2.4), we have

(2.10) F ( z , t ) − F ( z 0 , t ) = − δ 1 ∫ 0 t ∫ D z e − ω η p u 3 d A d η + ∫ 0 t ∫ D z e − ω η p 3 u 3 , 3 d A d η + ν ∫ 0 t ∫ D z e − ω η u i , 33 u i , 3 d A d η + δ 1 ν ∫ 0 t ∫ D z e − ω η u i , 3 u i d A d η − ∫ 0 t ∫ D z e − ω η g i T u i , 3 d A d η − 1 2 ∫ 0 t ∫ D z e − ω η u 3 T 2 d A d η + ∫ 0 t ∫ D z e − ω η T 3 T d A d η ≐ ∑ i = 1 7 I i .

Combining (2.5), (2.8), and (2.9), we have

(2.11) F ( z , t ) − F ( z 0 , t ) = ∫ 0 t ∫ z 0 z ∫ D ξ e − ω η δ 1 ν u i , j u i , j + δ 1 u i u i + ν u i , j 3 u i , j 3 + u i , 3 u i , 3 + T i T i + 1 2 ω T 2 d A d ξ d η + 1 2 e − ω t ∫ z 0 z ∫ D ξ T 2 d A d ξ − δ 1 ∫ 0 t ∫ z 0 z ∫ D ξ e − ω η g i u i T d A d ξ d η − ∫ 0 t ∫ z 0 z ∫ D ξ e − ω η g i T u i , 33 d A d ξ d η .

From (2.11), we have

(2.12) ∂ ∂ z F ( z , t ) = ∫ 0 t ∫ D z e − ω η δ 1 ν u i , j u i , j + δ 1 u i u i + ν u i , j 3 u i , j 3 + u i , 3 u i , 3 + T i T i + 1 2 ω T 2 d A d η + 1 2 e − ω t ∫ D z T 2 d A − δ 1 ∫ 0 t ∫ D z e − ω η g i u i T d A d η − ∫ 0 t ∫ D z e − ω η g i T u i , 33 d A d η .

We have the following lemma.

Lemma 2.4

For the function F ( z , t ) defined in (2.1) and ∫ D f 3 d A = 0 , the following differential inequality is satisfied:

(2.13) ∣ F ( z , t ) ∣ ≤ b 1 ∂ F ∂ z ( z , t ) + b 2 ∂ F ∂ z ( z , t ) 3 2 ,

where b 1 = max 2 C λ 1 , 1 δ 1 + ν 2 δ 1 + 2 ω , ν 2 + ν δ 1 + 1 ω and b 2 = 1 2 k 1 max 4 ω , 1 .

Proof

Using the Hölder inequality and the Young inequality, we have

(2.14) − δ 1 ∫ 0 t ∫ D z e − ω η g i u i T d A d η ≤ 1 2 δ 1 ∫ 0 t ∫ D z e − ω η u i u i d A d η + 1 2 δ 1 ∫ 0 t ∫ D z e − ω η T 2 d A d η ,

(2.15) ∫ 0 t ∫ D z e − ω η g i T u i , 33 d A d η ≤ 1 2 ν ∫ 0 t ∫ D z e − ω η u i , 33 u i , 33 d A d η + 1 2 ν ∫ 0 t ∫ D z e − ω η T 2 d A d η .

Inserting (2.14) into (2.15) and choosing δ 1 + 1 ν ≤ 1 2 ω , we have

(2.16) ∂ ∂ z F ( z , t ) ≥ ∫ 0 t ∫ D z e − ω η δ 1 ν u i , j u i , j + 1 2 δ 1 u i u i + ν u i , j 3 u i , j 3 + 1 2 u i , 3 u i , 3 + T i T i + 1 4 ω T 2 d A d η + 1 2 e − ω t ∫ D z T 2 d A ,

and

(2.17) ∂ ∂ z F ( z , t ) ≤ ∫ 0 t ∫ D z e − ω η δ 1 ν u i , j u i , j + 3 2 δ 1 u i u i + ν u i , j 3 u i , j 3 + 3 2 u i , 3 u i , 3 + T i T i + 3 4 ω T 2 d A d η + 1 2 e − ω t ∫ D z T 2 d A .

Next, we will bound I i ( i = 1 , 2 , … , 7 ) by ∂ ∂ z F ( z , t ) . To do this, we note that

∫ D z u 3 d A = ∫ D u 3 d A + ∫ 0 z ∫ D ξ u 3 , 3 d A d ξ = ∫ D u 3 d A − ∫ 0 z ∫ D ξ u α , α d A d ξ = ∫ D f 3 d A .

This shows that the area mean value of u 3 over each cross section is the same as that over D . Since ∫ D f 3 d A = 0 , we have ∫ D z u 3 d A = 0 . According to Lemma 2.3, there exists a vector function v = ( v 1 , v 2 ) such that

v α , α = u 3 , in D ; v α = 0 , on ∂ D .

Therefore, using (1.1), we have

(2.18) I 1 = − δ 1 ∫ 0 t ∫ D z e − ω η p v α , α d A d η = δ 1 ∫ 0 t ∫ D z e − ω η p α v α d A d η = δ 1 ∫ 0 t ∫ D z e − ω η [ ν Δ u α + g α T − u α ] v α d A d η = − δ 1 ν ∫ 0 t ∫ D z e − ω η u α , β v α , β d A d η + δ 1 ν ∫ 0 t ∫ D z e − ω η u α , 33 v α d A d η + δ 1 ∫ 0 t ∫ D z e − ω η g α v α T d A d η − δ 1 ∫ 0 t ∫ D z e − ω η u α v α d A d η ≐ I 11 + I 12 + I 13 + I 14 .

Using the Hölder inequality, the Young inequality, and Lemmas 2.1 and 2.3, we have

(2.19) ∣ I 11 ∣ ≤ δ 1 ν ∫ 0 t ∫ D z e − ω η v α , β v α , β d A d η ∫ 0 t ∫ D z e − ω η u α , β u α , β d A d η 1 2 ≤ δ 1 ν C ∫ 0 t ∫ D z e − ω η v α , α v α , α d A d η ∫ 0 t ∫ D z e − ω η u α , β u α , β d A d η 1 2 ≤ δ 1 ν C ∫ 0 t ∫ D z e − ω η u 3 2 d A d η ∫ 0 t ∫ D z e − ω η u α , β u α , β d A d η 1 2 ≤ δ 1 ν C λ 1 ∫ 0 t ∫ D z e − ω η u 3 , α u 3 , α d A d η ∫ 0 t ∫ D z e − ω η u α , β u α , β d A d η 1 2 ≤ 1 2 δ 1 ν C λ 1 ∫ 0 t ∫ D z e − ω η u i , j u i , j d A d η ,

(2.20) ∣ I 12 ∣ ≤ δ 1 ν ∫ 0 t ∫ D z e − ω η v α v α d A d η ∫ 0 t ∫ D z e − ω η u α , 33 u α , 33 d A d η 1 2 ≤ 1 2 δ 1 C λ 1 δ 1 ν ∫ 0 t ∫ D z e − ω η u 3 , α u 3 , α d A d η + ν ∫ 0 t ∫ D z e − ω η u α , 33 u α , 33 d A d η ,

(2.21) ∣ I 13 ∣ ≤ δ 1 ∫ 0 t ∫ D z e − ω η v α v α d A d η ∫ 0 t ∫ D z e − ω η T 2 d A d η 1 2 ≤ δ 1 1 λ 1 ∫ 0 t ∫ D z e − ω η v α , β v α , β d A d η ∫ 0 t ∫ D z e − ω η T 2 d A d η 1 2 ≤ δ 1 C λ 1 ∫ 0 t ∫ D z e − ω η v α , α v α , α d A d η ∫ 0 t ∫ D z e − ω η T 2 d A d η 1 2 ≤ δ 1 C λ 1 ∫ 0 t ∫ D z e − ω η u 3 2 d A d η ∫ 0 t ∫ D z e − ω η T 2 d A d η 1 2 ≤ 2 C δ 1 λ 1 ω 1 2 δ 1 ∫ 0 t ∫ D z e − ω η u 3 2 d A d η + 1 4 ω ∫ 0 t ∫ D z e − ω η T 2 d A d η ,

(2.22) ∣ I 14 ∣ ≤ δ 1 ∫ 0 t ∫ D z e − ω η v α v α d A d η ∫ 0 t ∫ D z e − ω η u α u α d A d η 1 2 ≤ δ 1 C λ 1 ∫ 0 t ∫ D z e − ω η u 3 2 d A d η ∫ 0 t ∫ D z e − ω η u α u α d A d η 1 2 ≤ 1 2 δ 1 C λ 1 ∫ 0 t ∫ D z e − ω η u i u i d A d η .

Inserting (2.19)–(2.22) into (2.18) and noting (2.16), we have

(2.23) ∣ I 1 ∣ ≤ 2 C λ 1 ∂ ∂ z F ( z , t ) ,

where we have used the condition δ 1 + 1 < 1 2 ω .

For I 2 , we use (1.1) and (1.2) to have

(2.24) I 2 = ∫ 0 t ∫ D z e − ω η [ ν Δ u 3 + g 3 T − u 3 ] u 3 , 3 d A d η = ν ∫ 0 t ∫ D z e − ω η u 3 , α α u 3 , 3 d A d η + ν ∫ 0 t ∫ D z e − ω η u 3 , 33 u 3 , 3 d A d η + ∫ 0 t ∫ D z e − ω η g 3 T u 3 , 3 d A d η − ∫ 0 t ∫ D z e − ω η u 3 u 3 , 3 d A d η = − ν ∫ 0 t ∫ D z e − ω η u 3 , α u 3 , α 3 d A d η + ν ∫ 0 t ∫ D z e − ω η u 3 , 33 u 3 , 3 d A d η + ∫ 0 t ∫ D z e − ω η g 3 T u 3 , 3 d A d η − ∫ 0 t ∫ D z e − ω η u 3 u 3 , 3 d A d η ≐ I 21 + I 22 + I 23 + I 24 .

Using the Hölder inequality and the Young inequality, we have

(2.25) ∣ I 21 ∣ ≤ ν ∫ 0 t ∫ D z e − ω η u 3 , α u 3 , α d A d η ∫ 0 t ∫ D z e − ω η u 3 , α 3 u 3 , α 3 d A d η 1 2 ≤ 1 2 δ 1 δ 1 ν ∫ 0 t ∫ D z e − ω η u 3 , α u 3 , α d A d η + ν ∫ 0 t ∫ D z e − ω η u 3 , α 3 u 3 , α 3 d A d η ,

(2.26) ∣ I 22 ∣ ≤ ν ∫ 0 t ∫ D z e − ω η u 3 , 33 2 d A d η ∫ 0 t ∫ D z e − ω η u 3 , 3 2 d A d η 1 2 ≤ ν 2 δ 1 δ 1 ν ∫ 0 t ∫ D z e − ω η u 3 , 33 2 d A d η + 1 2 ∫ 0 t ∫ D z e − ω η u 3 , 3 2 d A d η ,

(2.27) ∣ I 23 ∣ ≤ 2 ω 1 4 ω ∫ 0 t ∫ D z e − ω η T 2 d A d η + 1 2 ∫ 0 t ∫ D z e − ω η u 3 , 3 2 d A d η ,

(2.28) ∣ I 24 ∣ ≤ 1 2 δ 1 1 2 δ 1 ∫ 0 t ∫ D z e − ω η u 3 2 d A d η + 1 2 ∫ 0 t ∫ D z e − ω η u 3 , 3 2 d A d η .

Inserting (2.25)–(2.28) into (2.24), we have

(2.29) ∣ I 2 ∣ ≤ 1 δ 1 + ν 2 δ 1 + 2 ω ∂ ∂ z F ( z , t ) .

Using the Hölder inequality and the Young inequality, we have

(2.30) ∣ I 3 ∣ ≤ ν 2 ν ∫ 0 t ∫ D z e − ω η u i , 33 u i , 33 d A d η + 1 2 ∫ 0 t ∫ D z e − ω η u i , 3 u i , 3 d A d η ,

(2.31) ∣ I 4 ∣ ≤ ν δ 1 1 2 ∫ 0 t ∫ D z e − ω η u i , 3 u i , 3 d A d η + 1 2 δ 1 ∫ 0 t ∫ D z e − ω η u i u i d A d η ,

(2.32) ∣ I 5 ∣ ≤ 1 ω 1 2 ∫ 0 t ∫ D z e − ω η u i , 3 u i , 3 d A d η + 1 2 ω ∫ 0 t ∫ D z e − ω η T 2 d A d η ,

(2.33) ∣ I 7 ∣ ≤ 1 ω ∫ 0 t ∫ D z e − ω η T 3 2 d A d η + 1 4 ω ∫ 0 t ∫ D z e − ω η T 2 d A d η .

Combining (2.30)–(2.33), we have

(2.34) ∣ I 3 ∣ + ∣ I 4 ∣ + ∣ I 5 ∣ + ∣ I 7 ∣ ≤ ν 2 + ν δ 1 + 1 ω ∂ ∂ z F ( z , t ) .

Using the Hölder inequality, the Young inequality, and Lemma 2.2, we have

(2.35) ∣ I 6 ∣ ≤ 1 2 ∫ 0 t ∫ D z e − ω η T 4 d A d η ∫ 0 t ∫ D z e − ω η u 3 u 3 d A d η 1 2 ≤ 1 2 k 1 ∫ 0 t ∫ D z e − ω η T 2 d A d η + ∫ 0 t ∫ D z e − ω η T α T α d A d η ∫ 0 t ∫ D z e − ω η u 3 u 3 d A d η 1 2 ≤ 1 2 k 1 max 4 ω , 1 ∂ ∂ z F ( z , t ) 3 2 .

Inserting (2.23), (2.29), (2.34), and (2.35) into (2.10), we can obtain Lemma 2.4.□

3 Main result

Based on Lemma 4, we can obtain the following theorem.

Theorem 3.1

Let ( u i , T ) be a solution of equations (1.1)–(1.3) with the initial-boundary conditions (1.5) and (1.6) in R , then for fixed t, either

(3.1) lim z → ∞ z − 3 ∫ 0 t ∫ z 0 z ∫ D ξ e − ω η δ 1 ν u i , j u i , j + 3 2 δ 1 u i u i + T i T i + 3 4 ω T 2 d A d ξ d η + 1 2 e − ω t ∫ z 0 z ∫ D ξ T 2 d A d ξ ≥ C 1

holds or

(3.2) ∫ 0 t ∫ z ∞ ∫ D ξ e − ω η δ 1 ν u i , j u i , j + 1 2 δ 1 u i u i + T i T i + 1 4 ω T 2 d A d ξ d η + 1 2 e − ω t ∫ z ∞ ∫ D ξ T 2 d A d ξ ≤ b 6 Q 2 ( 0 , t ) e − 2 z b 5 + b 5 Q ( 0 , t ) e − z b 5

holds, where C 1 , b 5 , and b 6 are positive constants and Q ( 0 , t ) will be defined in (3.16).

Proof

We consider (2.1) for two cases.

Case I. ∃ z 0 ≥ 0 such that F ( z 0 , t ) ≥ 0 .

From (2.11), we know that ∂ ∂ z F ( z , t ) ≥ 0 . So, we have F ( z , t ) ≥ F ( z 0 , t ) ≥ 0 , z ≥ z 0 . Therefore, (2.1) can be written as

(3.3) F ( z , t ) ≤ b 1 ∂ F ∂ z ( z , t ) + b 2 ∂ F ∂ z ( z , t ) 3 2 , z ≥ z 0 .

Using the Young inequality, we have

(3.4) ∂ F ∂ z ( z , t ) = ∂ F ∂ z ( z , t ) 3 4 ⋅ 2 3 ∂ F ∂ z ( z , t ) 3 2 ⋅ 1 3 ≤ 2 3 ∂ F ∂ z ( z , t ) 3 4 + 1 3 ∂ F ∂ z ( z , t ) 3 2 .

Inserting (3.4) into (3.3), we have

F ( z , t ) ≤ b 3 ∂ F ∂ z ( z , t ) 3 4 + b 4 ∂ F ∂ z ( z , t ) 3 2 , z ≥ z 0 ,

where b 3 = 2 3 b 1 and b 4 = 1 3 b 1 + b 2 . Therefore, we have

(3.5) F ( z , t ) + b 3 2 4 b 4 ≤ b 4 ∂ F ∂ z ( z , t ) 3 4 + b 3 2 b 4 2 , z ≥ z 0 .

From (3.5), it follows that

∂ F ∂ z ( z , t ) ≥ 1 b 4 F ( z , t ) + b 3 2 4 b 4 2 − b 3 2 b 4 4 3 , z ≥ z 0 .

So, we have

(3.6) 2 b 4 1 1 b 4 F ( z , t ) + b 3 2 4 b 4 2 − b 3 2 b 4 1 3 + b 3 1 1 b 4 F ( z , t ) + b 3 2 4 b 4 2 − b 3 2 b 4 4 3 ⋅ d 1 b 4 F ( z , t ) + b 3 2 4 b 4 2 − b 3 2 b 4 ≥ 1 , z ≥ z 0 .

Integrating (3.6) from z 0 to z , we have

(3.7) 3 b 4 1 b 4 F ( z , t ) + b 3 2 4 b 4 2 − b 3 2 b 4 2 3 − 1 b 4 F ( z 0 , t ) + b 3 2 4 b 4 2 − b 3 2 b 4 2 3 − 3 b 3 1 b 4 F ( z , t ) + b 3 2 4 b 4 2 − b 3 2 b 4 − 1 3 − 1 b 4 F ( z 0 , t ) + b 3 2 4 b 4 2 − b 3 2 b 4 − 1 3 ≥ z − z 0 , z ≥ z 0 .

We discard the second and third terms at the left end of (3.7). In the first term of (3.7), we use the following inequality:

a + b ≤ a + b , a , b ≥ 0 ,

to have

3 b 4 1 b 4 F ( z , t ) 2 3 ≥ z − z 0 − 3 b 3 1 b 4 F ( z 0 , t ) + b 3 2 4 b 4 2 − b 3 2 b 4 − 1 3 .

Therefore, we have

(3.8) F ( z , t ) ≥ 1 3 b 4 2 3 ( z − z 0 ) − b 3 b 4 2 3 1 b 4 F ( z 0 , t ) + b 3 2 4 b 4 2 − b 3 2 b 4 − 1 3 3 .

On the other hand, we integrate (2.12) from z 0 to z to obtain

(3.9) F ( z , t ) − F ( z 0 , t ) ≤ ∫ 0 t ∫ z 0 z ∫ D ξ e − ω η δ 1 ν u i , j u i , j + 3 2 δ 1 u i u i + T i T i + 3 4 ω T 2 d A d ξ d η + 1 2 e − ω t ∫ z 0 z ∫ D ξ T 2 d A d ξ .

Combining (3.8) and (3.9), we can obtain (3.1).

Case II. ∀ z ≥ 0 such that F ( z , t ) < 0 , then we have from (2.1)

(3.10) − F ( z , t ) ≤ b 1 ∂ F ∂ z ( z , t ) + b 2 ∂ F ∂ z ( z , t ) 3 2 , z ≥ 0 .

Using the Young inequality again, we have

(3.11) ∂ F ∂ z ( z , t ) 3 2 = ∂ F ∂ z ( z , t ) 1 2 ∂ F ∂ z ( z , t ) 2 ⋅ 1 2 ≤ 1 2 ∂ F ∂ z ( z , t ) + 1 2 ∂ F ∂ z ( z , t ) 2 .

Inserting (3.11) into (3.10), we have

(3.12) − F ( z , t ) ≤ b 5 ∂ F ∂ z ( z , t ) + b 6 ∂ F ∂ z ( z , t ) 2 , z ≥ 0 ,

where b 5 = b 1 + 1 2 b 2 and b 6 = 1 2 b 2 . It follows from (3.12) that

∂ F ∂ z ( z , t ) ≥ − F ( z , t ) b 6 + b 5 2 4 b 6 2 − b 5 2 b 6 .

So, we have

(3.13) − 2 b 6 − b 5 1 − F ( z , t ) b 6 + b 5 2 4 b 6 2 − b 5 2 b 6 d − F ( z , t ) b 6 + b 5 2 4 b 6 2 − b 5 2 b 6 ≥ 1 , z ≥ 0 .

Integrating (3.13) from 0 to z , we have

(3.14) 2 b 6 − F ( z , t ) b 6 + b 5 2 4 b 6 2 − − F ( 0 , t ) b 6 + b 5 2 4 b 6 2 + b 5 l n − F ( z , t ) b 6 + b 5 2 4 b 6 2 − b 5 2 b 6 − b 5 l n − F ( 0 , t ) b 6 + b 5 2 4 b 6 2 − b 5 2 b 6 ≤ − z .

Dropping the first term on the left of (3.14), we have

b 5 ln − F ( z , t ) b 6 + b 5 2 4 b 6 2 − b 5 2 b 6 ≤ − z + 2 b 6 − F ( 0 , t ) b 6 + b 5 2 4 b 6 2 + b 5 ln − F ( 0 , t ) b 6 + b 5 2 4 b 6 2 − b 5 2 b 6 .

Therefore, we obtain

(3.15) − F ( z , t ) b 6 + b 5 2 4 b 6 2 ≤ Q ( 0 , t ) e − z b 5 + b 5 2 b 6 ,

where

(3.16) Q ( 0 , t ) = − F ( 0 , t ) b 6 + b 5 2 4 b 6 2 − b 5 2 b 6 e 2 b 6 b 5 − F ( 0 , t ) b 6 + b 5 2 4 b 6 2 .

Squaring (3.15), we have

(3.17) − F ( z , t ) ≤ b 6 Q 2 ( 0 , t ) e − 2 z b 5 + b 5 Q ( 0 , t ) e − z b 5 .

So, we have lim z → ∞ [ − F ( z , t ) ] = 0 . Now, we integrate (2.11) from z to ∞ to obtain

(3.18) − F ( z , t ) ≥ ∫ 0 t ∫ z ∞ ∫ D ξ e − ω η δ 1 ν u i , j u i , j + 1 2 δ 1 u i u i + T i T i + 1 4 ω T 2 d A d ξ d η + 1 2 e − ω t ∫ z ∞ ∫ D ξ T 2 d A d ξ .

Combining (3.17) and (3.18), we can obtain (3.2).□

Remark 3.2

Theorem 3.1 shows that the solution of equations (1.1)–(1.3) grows polynomially or decays exponentially as z → ∞ , and the growth rate is at least as fast as z − 3 .

Remark 3.3

To make the decay estimate explicit, we have to derive the upper bounds for − F ( 0 , t ) . To do this, we let

f ˜ ( x , t ) = f ( x , t ) e − σ z , σ > 0 .

Using a similar methods of [4, 5], it is easy to derive that − F ( 0 , t ) can be bounded in terms of known data.

4 Continuous dependence result

In this section, we derive the continuous dependence on the Brinkman coefficient ν in the case of decay. To do this, we first give a useful lemma.

Lemma 4.1

(See [32]) Let R be a bounded simply connected region in R 3 with the Lipschitz boundary ∂ R . Then, given any Dirichlet integrable function v satisfying ∫ R v d x = 0 , there exist a vector field with components w ¯ i ( i = 1 , 2 , 3 ) , which is Dirichlet integrable and vanishes on ∂ R , and a dimensionless constant k 3 depending only on the geometry of R such that

w ¯ i , i = v , in R ,

and

∫ R w ¯ i , j w ¯ i , j d x ≤ k 3 ∫ R [ w ¯ j , j ] 2 d x .

Suppose that u i , p , T and u i ∗ , p ∗ , T ∗ be the solutions of equations (1.1)–(1.7) but corresponding to deferent ν and ν ∗ , respectively. Let

(4.1) v i = u i − u i ∗ , Σ = T − T ∗ , π = p − p ∗ , ν ˜ = ν − ν ∗ ,

then v i , Σ , and π satisfy the following system:

(4.2) − ν ˜ Δ u i − ν ∗ Δ v i + v i = − π i + g i Σ , in R × ( 0 , τ ) ,

(4.3) v i , i = 0 , in R × ( 0 , τ ) ,

(4.4) ∂ t Σ + u i Σ i + v i T i ∗ = Δ Σ , in R × ( 0 , τ ) ,

(4.5) v i ( x 1 , x 2 , x 3 , t ) = 0 , Σ ( x 1 , x 2 , x 3 , t ) = 0 , on ∂ D × { x 3 > 0 } × ( 0 , τ ) ,

(4.6) v i ( x 1 , x 2 , 0 , t ) = 0 , Σ ( x 1 , x 2 , 0 , t ) = 0 , on D × ( 0 , τ ) ,

(4.7) v i ( x 1 , x 2 , x 3 , 0 ) = 0 , Σ ( x 1 , x 2 , x 3 , 0 ) = 0 , in R .

Next, we derive the continuous dependence result.

We multiply (4.2) with ( ξ − z ) e − ω η v i and integrate in R z × [ 0 , t ] to obtain

∫ 0 t ∫ R z ( ξ − z ) e − ω η [ − ν ˜ Δ u i − ν ∗ Δ v i + v i + π i − g i Σ ] v i d x d η = 0 ,

from which it follows that

(4.8) ∫ 0 t ∫ R z ( ξ − z ) e − ω η [ ν ∗ v i , j v i , j + v i v i ] d x d η = − ν ˜ ∫ 0 t ∫ R z e − ω η u i , 3 v i d x d η − ν ∗ ∫ 0 t ∫ R z e − ω η v i , 3 v i d x d η + ∫ 0 t ∫ R z e − ω η π v 3 d x d η − ν ˜ ∫ 0 t ∫ R z ( ξ − z ) e − ω η u i , j v i , j d x d η + ∫ 0 t ∫ R z ( ξ − z ) e − ω η g i Σ v i d x d η ≐ ∑ i = 1 5 J i .

Using the Schwarz inequality and (3.2), we obtain

(4.9) J 1 ≤ ∫ 0 t ∫ R z e − ω η ν ˜ 2 u i , 3 u i , 3 d x d η 1 2 ∫ 0 t ∫ R z e − ω η v i v i d x d η 1 2 ≤ δ 1 ν ν ˜ 2 ∫ 0 t ∫ R z e − ω η u i , 3 u i , 3 d x d η + 1 4 δ 1 ν ∫ 0 t ∫ R z e − ω η v i v i d x d η ,

(4.10) J 2 ≤ ν ∗ 2 ∫ 0 t ∫ R z e − ω η ν ∗ v i , 3 v i , 3 d x d η + ν ∗ 2 ∫ 0 t ∫ R z e − ω η v i v i d x d η .

Obviously, ∫ D v 3 d A = 0 . So, according to Lemma 4.1, there exists a vector function w ¯ = ( w ¯ 1 , w ¯ 2 , w ¯ 3 ) such that

w ¯ i , i = v 3 , in R , w ¯ i = 0 , on ∂ R .

(4.11) J 3 = ∫ 0 t ∫ R z e − ω η π w ¯ i , i d x d η = − ∫ 0 t ∫ R z e − ω η π i w ¯ i d x d η = ∫ 0 t ∫ R z e − ω η [ − ν ˜ Δ u i − ν ∗ Δ v i + v i − g i Σ ] w ¯ i d x d η = ν ˜ ∫ 0 t ∫ R z e − ω η u i , j w ¯ i , j d x d η + ν ∗ ∫ 0 t ∫ R z e − ω η v i , j w ¯ i , j d x d η + ∫ 0 t ∫ R z e − ω η v i w ¯ i d x d η − ∫ 0 t ∫ R z e − ω η g i Σ w ¯ i d x d η ≐ J 31 + J 32 + J 33 + J 34 .

Using the Schwarz inequality and Lemma 4.1, we obtain

(4.12) J 31 ≤ ν ˜ ∫ 0 t ∫ R z e − ω η u i , j u i , j d x d η 1 2 ∫ 0 t ∫ R z e − ω η w ¯ i , j w ¯ i , j d x d η 1 2 ≤ ν ˜ k 3 ∫ 0 t ∫ R z e − ω η u i , j u i , j d x d η 1 2 ∫ 0 t ∫ R z e − ω η v 3 2 d x d η 1 2 ≤ ν ˜ 2 δ 1 ν ∫ 0 t ∫ R z e − ω η u i , j u i , j d x d η + k 3 4 δ 1 ν ∫ 0 t ∫ R z e − ω η v 3 2 d x d η ,

(4.13) J 32 ≤ k 3 ν ∗ 2 ν ∗ ∫ 0 t ∫ R z e − ω η v i , j v i , j d x d η + ∫ 0 t ∫ R z e − ω η v 3 2 d x d η ,

(4.14) J 33 ≤ k 3 h 2 π ∫ 0 t ∫ R z e − ω η v i v i d x d η + ∫ 0 t ∫ R z e − ω η v 3 2 d x d η ,

(4.15) J 34 ≤ k 3 h 2 π ∫ 0 t ∫ R z e − ω η Σ 2 d x d η + ∫ 0 t ∫ R z e − ω η v 3 2 d x d η .

Inserting (4.12)–(4.15) into (4.11), we have

(4.16) J 3 ≤ ν ˜ 2 δ 1 ν ∫ 0 t ∫ R z e − ω η u i , j u i , j d x d η + k 3 h 2 π ∫ 0 t ∫ R z e − ω η Σ 2 d x d η + k 3 4 δ 1 ν + k 3 ν ∗ 2 + k 3 h π × ∫ 0 t ∫ R z e − ω η v i v i d x d η + k 3 ν ∗ 2 ν ∗ ∫ 0 t ∫ R z e − ω η v i , j v i , j d x d η .

Using the Schwarz inequality, we obtain

(4.17) J 4 ≤ 1 2 ν ∗ ν ˜ 2 ∫ 0 t ∫ R z ( ξ − z ) e − ω η u i , j u i , j d x d η + 1 2 ν ∗ ∫ 0 t ∫ R z ( ξ − z ) e − ω η v i , j v i , j d x d η ,

(4.18) J 5 ≤ 1 2 ∫ 0 t ∫ R z ( ξ − z ) e − ω η Σ 2 d x d η + 1 2 ∫ 0 t ∫ R z ( ξ − z ) e − ω η v i v i d x d η .

Inserting (4.9), (4.10), and (4.16)–(4.18) into (4.8), we have

(4.19) 1 2 ∫ 0 t ∫ R z ( ξ − z ) e − ω η [ ν ∗ v i , j v i , j + v i v i ] d x d η ≤ 1 2 ∫ 0 t ∫ R z ( ξ − z ) e − ω η Σ 2 d x d η + k 3 h 2 π ∫ 0 t ∫ R z e − ω η Σ 2 d x d η + 1 4 δ 1 ν + ν ∗ 2 + k 3 4 δ 1 ν + k 3 ν ∗ 2 + k 3 h π ∫ 0 t ∫ R z e − ω η v i v i d x d η + ν ∗ 2 + k 3 ν ∗ 2 ν ∗ ∫ 0 t ∫ R z e − ω η v i , j v i , j d x d η + 1 2 ν ∗ ν ˜ 2 ∫ 0 t ∫ R z ( ξ − z ) e − ω η u i , j u i , j d x d η + 2 ν ˜ 2 δ 1 ν ∫ 0 t ∫ R z e − ω η u i , j u i , j d x d η .

Now, we multiply (4.4) with ( ξ − z ) e − ω η Σ and integrate in R z × [ 0 , t ] to obtain

∫ 0 t ∫ R z ( ξ − z ) e − ω η [ ∂ η Σ + u i Σ i + v i T i ∗ − Δ Σ ] Σ d x d η = 0 ,

from which it follows that

(4.20) 1 2 ∫ R z ( ξ − z ) e − ω t Σ 2 d x ∣ η = t + ∫ 0 t ∫ R z ( ξ − z ) e − ω η 1 2 ω Σ 2 + Σ i Σ i d x d η = − ∫ 0 t ∫ R z e − ω η Σ 3 Σ d x d η + 1 2 ∫ 0 t ∫ R z e − ω η u 3 Σ 2 d x d η + ∫ 0 t ∫ R z e − ω η T ∗ Σ v 3 d x d η + ∫ 0 t ∫ R z ( ξ − z ) e − ω η v i T ∗ Σ i d x d η ≐ ∑ i = 1 4 J ^ i .

Using the Schwarz inequality, we obtain

(4.21) J ^ 1 ≤ 2 ω ∫ 0 t ∫ R z e − ω η 1 2 ω Σ 2 d x d η 1 2 ∫ 0 t ∫ R z e − ω η Σ 3 2 d x d η 1 2 ≤ 2 ω ∫ 0 t ∫ R z e − ω η 1 2 ω Σ 2 d x d η + ∫ 0 t ∫ R z e − ω η Σ 3 2 d x d η .

Using Lemma 2.2, we have

(4.22) J ^ 2 ≤ ∫ 0 t ∫ z ∞ ∫ D ξ e − ω η u 3 2 d A 1 2 ∫ D ξ e − ω η Σ 4 d A 1 2 d ξ d η ≤ k 1 ∫ 0 t ∫ z ∞ − 2 ∫ R ξ e − ω η u 3 u 3 , 3 d x 1 2 ∫ D ξ e − ω η Σ 2 d A + ∫ D ξ e − ω η Σ α Σ α d A d ξ d η ≤ 2 k 1 max t ∈ [ 0 , τ ] ∫ R z e − ω η u 3 2 d x ∫ R z e − ω η u 3 , 3 2 d x 1 4 × ∫ 0 t ∫ R z e − ω η Σ 2 d x d η + ∫ 0 t ∫ R z e − ω η Σ α Σ α d A d x d η .

Let

T M = max R × [ 0 , τ ] { h ( x 1 , x 2 , t ) } ,

we have

(4.23) J ^ 3 ≤ 2 ω T M ∫ 0 t ∫ R z e − ω η 1 2 ω Σ 2 d x d η 1 2 ∫ 0 t ∫ R z e − ω η v 3 2 d x d η 1 2 ≤ 2 ω T M ∫ 0 t ∫ R z e − ω η 1 2 ω Σ 2 d x d η + ∫ 0 t ∫ R z e − ω η v 3 2 d x d η ,

(4.24) J ^ 4 ≤ 1 2 ∫ 0 t ∫ R z ( ξ − z ) e − ω η Σ i Σ i d x d η + 1 2 T M 2 ∫ 0 t ∫ R z ( ξ − z ) e − ω η v i v i d x d η .

Inserting (4.21)–(4.24) into (4.20), we have

(4.25) 1 2 ∫ R z ( ξ − z ) e − ω t Σ 2 d x η = t + ∫ 0 t ∫ R z ( ξ − z ) e − ω η 1 2 ω Σ 2 + 1 2 Σ i Σ i d x d η ≤ 2 ω + 2 k 1 2 ω max t ∈ [ 0 , τ ] ∫ R z e − ω η u 3 2 d x ∫ R z e − ω η u 3 , 3 2 d x 1 4 + 2 ω T M ∫ 0 t ∫ R z e − ω η 1 2 ω Σ 2 d x d η + 2 ω + 2 k 1 2 ω max t ∈ [ 0 , τ ] ∫ R z e − ω η u 3 2 d x ∫ R z e − ω η u 3 , 3 2 d x 1 4 × ∫ 0 t ∫ R z e − ω η Σ i Σ i d x d η + 2 ω T M ∫ 0 t ∫ R z e − ω η v 3 2 d x d η + 1 2 T M 2 ∫ 0 t ∫ R z ( ξ − z ) e − ω η v i v i d x d η .

If we define

(4.26) Ψ ( z , t ) = ∫ R z ( ξ − z ) e − ω t Σ 2 d x ∣ η = t + ∫ 0 t ∫ R z ( ξ − z ) e − ω η [ ω Σ 2 + Σ i Σ i ] d x d η + 1 2 ω ∫ 0 t ∫ R z ( ξ − z ) e − ω η [ ν ∗ v i , j v i , j + v i v i ] d x d η ,

then we have

(4.27) − ∂ ∂ z Ψ ( z , t ) = ∫ R z e − ω t Σ 2 d x ∣ η = t + ∫ 0 t ∫ R z e − ω η [ ω Σ 2 + Σ i Σ i ] d x d η + 1 2 ω ∫ 0 t ∫ R z e − ω η [ ν ∗ v i , j v i , j + v i v i ] d x d η .

Combining (4.19) and (4.25) and choosing ω ≥ 4 T M 2 , we have

(4.28) Ψ ( z , t ) ≤ b 7 − ∂ ∂ z Ψ ( z , t ) + 1 2 ν ∗ ν ˜ 2 ω ∫ 0 t ∫ R z ( ξ − z ) e − ω η u i , j u i , j d x d η + 2 ν ˜ 2 δ 1 ν ω ∫ 0 t ∫ R z e − ω η u i , j u i , j d x d η ,

where

(4.29) b 7 = max 2 2 ω + 2 k 1 4 ω max t ∈ [ 0 , τ ] ∫ R z e − ω η u 3 2 d x ∫ R z e − ω η u 3 , 3 2 d x 1 4 + 2 2 ω T M + 2 k 3 h h ω , 1 4 δ 1 ν + ν ∗ 2 + k 3 4 δ 1 ν + k 3 ν ∗ 2 + k 3 h π + 2 2 ω T M .

In view of (3.2), we have

(4.30) ∫ 0 t ∫ R z e − ω η u i , j u i , j d x d η ≤ b 6 ν δ 1 Q 2 ( 0 , t ) e − 2 z b 5 + b 5 ν δ 1 Q 2 ( 0 , t ) e − z b 5 .

Therefore,

(4.31) ∫ 0 t ∫ R z ( ξ − z ) e − ω η u i , j u i , j d x d η = ∫ 0 t ∫ z ∞ ∫ R ξ e − ω η u i , j u i , j d x d ξ d η ≤ b 6 b 5 2 ν δ 1 Q 2 ( 0 , t ) e − 2 z b 5 + b 5 2 ν δ 1 Q 2 ( 0 , t ) e − z b 5 .

Inserting (4.30) and (4.31) into (4.28), we have

(4.32) Ψ ( z , t ) ≤ b 7 − ∂ ∂ z Ψ ( z , t ) + b 8 ν ˜ 2 e − 2 z b 5 + b 9 ν ˜ 2 e − z b 5 ,

where b 8 = b 6 b 5 4 ν ∗ ν δ 1 Q 2 ( 0 , t ) ω + b 6 Q 2 ( 0 , t ) ω and b 9 = b 5 2 2 ν ∗ ν δ 1 Q 2 ( 0 , t ) ω + b 5 Q 2 ( 0 , t ) ω . It follows that from (4.32)

(4.33) ∂ ∂ z Ψ ( z , t ) e z b 7 ≤ b 8 ν ˜ 2 e − 2 z b 5 + z b 7 + b 9 ν ˜ 2 e − z b 5 + z b 7 .

If b 5 ≠ 2 b 7 and b 5 ≠ b 7 , then we integrate (4.33) from 0 to z to obtain

(4.34) Ψ ( z , t ) ≤ Ψ ( 0 , t ) e − z b 7 + b 8 − 2 b 5 + 1 b 7 ν ˜ 2 e − 2 z b 5 − e − z b 7 + b 9 − 1 b 5 + 1 b 7 ν ˜ 2 e − z b 5 − e − z b 7 .

If b 5 = 2 b 7 , then we integrate (4.33) from 0 to z to obtain

(4.35) Ψ ( z , t ) ≤ Ψ ( 0 , t ) e − z b 7 + b 8 ν ˜ 2 z e − z b 7 + 2 b 9 b 7 ν ˜ 2 e − z 2 b 7 − e − z b 7 .

If b 5 = b 7 , then we integrate (4.33) from 0 to z to obtain

(4.36) Ψ ( z , t ) ≤ Ψ ( 0 , t ) e − z b 7 + b 8 b 7 ν ˜ 2 e − z b 7 − e − 2 z b 7 + b 9 ν ˜ 2 z e − z b 7 .

To obtain the main result, we have to derive the upper bound for Ψ ( 0 , t ) . In (4.32), we choose z = 0 to have

(4.37) Ψ ( 0 , t ) ≤ b 7 − ∂ ∂ z Ψ ( 0 , t ) + b 8 ν ˜ 2 + b 9 ν ˜ 2 .

Therefore, we only need to derive the bound for − ∂ ∂ z Ψ ( 0 , t ) . In (4.27), we choose z = 0 to have

(4.38) − ∂ ∂ z Ψ ( 0 , t ) = ∫ R e − ω t Σ 2 d x η = t + ∫ 0 t ∫ R e − ω η [ ω Σ 2 + Σ i Σ i ] d x d η + 1 2 ω ∫ 0 t ∫ R e − ω η [ ν ∗ v i , j v i , j + v i v i ] d x d η .

On the other hand, combining (4.8) and (4.20) and using the initial-boundary conditions (4.5)–(4.7), we obtain

(4.39) − ∂ ∂ z Ψ ( 0 , t ) ≤ − 1 2 ν ˜ ω ∫ 0 t ∫ R z e − ω η u i , j v i , j d x d η + 1 2 ω ∫ 0 t ∫ R z e − ω η g i Σ v i d x d η + ∫ 0 t ∫ R z e − ω η v i T Σ i d x d η ≤ 1 4 ν ∗ ν ˜ 2 ω ∫ 0 t ∫ R z e − ω η u i , j v i , j d x d η + 1 4 ω ν ∗ ∫ 0 t ∫ R z e − ω η v i , j v i , j d x d η + 1 2 ω ∫ 0 t ∫ R z e − ω η Σ 2 d x d η + 1 8 ω ∫ 0 t ∫ R z e − ω η v i v i d x d η + 2 ω T M 2 ∫ 0 t ∫ R z e − ω η Σ i Σ i d x d η + 1 8 ω ∫ 0 t ∫ R z e − ω η v i v i d x d η .

Since ω ≥ 4 T M 2 , we combine (4.30), (4.38), and (4.39) to have

− ∂ ∂ z Ψ ( 0 , t ) ≤ 1 2 − ∂ ∂ z Ψ ( 0 , t ) + ν ˜ 2 ω b 6 4 ν ∗ ν δ 1 Q 2 ( 0 , t ) e − 2 z b 5 + ν ˜ 2 ω b 5 4 ν ∗ ν δ 1 Q 2 ( 0 , t ) e − z b 5 .

Therefore, we have

(4.40) − ∂ ∂ z Ψ ( 0 , t ) ≤ ν ˜ 2 ω b 6 2 ν ∗ ν δ 1 Q 2 ( 0 , t ) + ν ˜ 2 ω b 5 2 ν ∗ ν δ 1 Q 2 ( 0 , t ) .

Inserting (4.40) into (4.37), we have

(4.41) Ψ ( 0 , t ) ≤ b 10 ν ˜ 2 ,

where b 10 = ω b 6 b 7 2 ν ∗ ν δ 1 Q 2 ( 0 , t ) + ω b 5 b 7 2 ν ∗ ν δ 1 Q 2 ( 0 , t ) + b 8 + b 9 . Inserting (4.41) into (4.34)–(4.35) and combining with (4.26), we can obtain the following theorem.

Theorem 4.1

Let ( u , T ) and ( u ∗ , T ∗ ) be solutions of (1.1)–(1.7) corresponding to the coefficients ν and ν ∗ , respectively. If ∀ z ≥ 0 such that F ( z , t ) < 0 and ∫ D 0 f 3 d A = 0 , then the solutions of equations (1.1)–(1.7) depend continuously on the effective viscosity coefficient ν . Specifically, if b 5 ≠ 2 b 7 and b 5 ≠ b 7 , then we obtain

∫ R z ( ξ − z ) e − ω t Σ 2 d x η = t + ∫ 0 t ∫ R z ( ξ − z ) e − ω η [ ω Σ 2 + Σ i Σ i ] d x d η + 1 2 ω ∫ 0 t ∫ R z ( ξ − z ) e − ω η [ ν ∗ v i , j v i , j + v i v i ] d x d η ≤ b 10 ν ˜ 2 e − z b 7 + b 8 − 2 b 5 + 1 b 7 ν ˜ 2 e − 2 z b 5 − e − z b 7 + b 9 − 1 b 5 + 1 b 7 ν ˜ 2 e − z b 5 − e − z b 7 .

If b 5 = 2 b 7 , then we obtain

∫ R z ( ξ − z ) e − ω t Σ 2 d x η = t + ∫ 0 t ∫ R z ( ξ − z ) e − ω η [ ω Σ 2 + Σ i Σ i ] d x d η + 1 2 ω ∫ 0 t ∫ R z ( ξ − z ) e − ω η [ ν ∗ v i , j v i , j + v i v i ] d x d η ≤ b 10 ν ˜ 2 e − z b 7 + b 8 b 7 ν ˜ 2 z e − z b 7 + 2 b 9 ν ˜ 2 e − z 2 b 7 − e − z b 7 .

If b 5 = b 7 , then we obtain

∫ R z ( ξ − z ) e − ω t Σ 2 d x η = t + ∫ 0 t ∫ R z ( ξ − z ) e − ω η [ ω Σ 2 + Σ i Σ i ] d x d η + 1 2 ω ∫ 0 t ∫ R z ( ξ − z ) e − ω η [ ν ∗ v i , j v i , j + v i v i ] d x d η ≤ b 10 ν ˜ 2 e − z b 7 + b 8 ν ˜ 2 e − z b 7 − e − 2 z b 7 + b 9 b 7 ν ˜ 2 z e − z b 7 .

5 Conclusion

In this article, we define the Brinkman equations (1.1)–(1.3) in a semi-infinite cylinder and the Phragmén-Lindelöf alternative result and the continuous dependence result on ν are obtained. However, there are still some deeper problems to be studied in this article. We note that Quintanilla [13] considered the spatial selectivity of solutions of several kinds of partial differential equations with a radius defined in the outer region of the sphere for the first time, in which the so-called outer region of the sphere is

Ω = { ( x 1 , x 2 , x 3 ) ∣ x 1 2 + x 2 2 + x 3 2 ≥ R 0 2 , R 0 > 0 } .

Li et al. [17,33] studied the selectivity of the wave equations in the region Ω , and obtained the rapid attenuation rate and growth rate. However, this type of research has not received sufficient attention. Therefore, it will be a meaningful topic to study the spatial properties of solutions of Brinkman equations on Ω .

  1. Funding information: This work is supported by the Key projects of universities in Guangdong Province (Natural Science) (2019KZDXM042) and the Research team project of Guangzhou Huashang College(2021HSKT01).

  2. Author contributions: All authors have accepted responsibility for the entire content of this manuscript and approved its submission.

  3. Conflict of interest: The authors state that there is no conflict of interest.

  4. Data availability statement: This article focuses on theoretical analysis, not involving experiments and data.

References

[1] D. A. Nield and A. Bejan, Convection in Porous Media, Springer-Verlag, New York, 1992. 10.1007/978-1-4757-2175-1Search in Google Scholar

[2] B. Straughan, Mathematical aspects of penetrative convection, Pitman Res. Notes Math. Vol. 288, Longman, Harlow, 1993. Search in Google Scholar

[3] D. R. Hewitt, Vigorous convection in porous media, Proc. R. Soc. A: Math. Phys. Eng. Sci. 476 (2020), no. 2239, 20200111, https://doi.org/10.1098/rspa.2020.0111. Search in Google Scholar PubMed PubMed Central

[4] L. E. Payne and J. C. Song, Spatial decay estimates for the Brinkman and Darcy flows in a semi-infinite cylinder, Contin. Mech. Thermodyn. 9 (1997), 175–190, https://doi.org/10.1007/s001610050064. Search in Google Scholar

[5] Y. F. Li, Y. Liu, S. Luo, and C. Lin, Decay Estimates for the Brinkman-Forchheimer equations in a semi-infinite pipe, ZAMM Z. Angew. Math. Mech. 92 (2012), no. 2, 160–176, https://doi.org/10.1002/zamm.201000202. Search in Google Scholar

[6] Y. F. Li, Y. Liu, and C. Lin, Decay estimates for homogeneous Boussinesq equations in a semi-infinite pipe, Nonlinear Anal. 74 (2011), no. 13, 4399–4417, https://doi.org/10.1016/j.na.2011.03.062. Search in Google Scholar

[7] Y. F. Li and C. H. Lin, Spatial decay for solutions to 2-D Boussinesq system with variable thermal diffusivity, Acta Appl. Math. 154 (2018), 111–130, https://doi.org/10.1007/s10440-017-0136-z. Search in Google Scholar

[8] R. J. Knops and R. Quintanilla, Spatial decay in transient heat conduction for general elongated regions, Quart. Appl. Math. 76 (2018), 611–625, https://doi.org/10.1090/qam/1497. Search in Google Scholar

[9] C. H. Lin and L. E. Payne, Spatial decay bounds in the channel flow of an incompressible viscous fluid, Math. Models Methods Appl. Sci. 14 (2004), no. 6, 795–818, https://doi.org/10.1142/S0218202504003453. Search in Google Scholar

[10] C. H. Lin and L. E. Payne, Spatial decay bounds in time dependent pipe flow of an incompressible viscous fluid, SIAM J. Appl. Math. 65 (2005), 458–475, https://doi.org/10.1137/040606326. Search in Google Scholar

[11] Y. Liu, Y. F. Li, Y. Lin, and Z. Yao, Spatial decay bounds for the channel flow of the Boussinesq equations, J. Math. Anal. Appl. 381 (2011), 87–109, https://doi.org/10.1016/j.jmaa.2011.02.066. Search in Google Scholar

[12] J. C. Song, Phragmén-Lindelöf and continuous dependence type results in a Stokes flow, Appl. Math. Mech. (English Ed.) 31 (2010), no. 7, 875–882, https://doi.org/10.1007/s10483-010-1321-z. Search in Google Scholar

[13] R. Quintanilla, Some remarks on the fast spatial growth/decay in exterior regions, Z. Angew. Math. Phys. 70 (2019), 83, https://doi.org/10.1007/s00033-019-1127-x. Search in Google Scholar

[14] M. C Leseduartea and R. Quintanilla, Phragmén-Lindelöf of alternative for the Laplace equation with dynamic boundary conditions, J. Appl. Anal. Comput. 7 (2017), no. 4, 1323–1335, https://doi.org/10.11948/2017081. Search in Google Scholar

[15] Y Liu and C. H. Lin, Phragmén-Lindelöf-type alternative results for the stokes flow equation, Math. Inequal. Appl. 9 (2006), no. 4, 671–694, https://doi.org/10.7153/mia-09-60. Search in Google Scholar

[16] L. E. Payne and J. C. Song, Phragmén-Lindelöf and continuous dependence type results in generalized heat conduction, Z. Angew. Math. Phys. 47 (1996), 527–538, https://doi.org/10.1007/BF00914869. Search in Google Scholar

[17] J. Jiménez-Garrido, J. Sanz, and G. Schindl, A Phragmén-Lindelöf Theorem via proximate orders, and the propagation of asymptotics, J. Geom. Anal. 30 (2020), 3458–483, https://doi.org/10.1007/s12220-019-00203-5. Search in Google Scholar PubMed PubMed Central

[18] M. W. Hirsch and S. Smale, Differential Equations, Dynamical Systems, and Linear Algebra, Academic Press, New York, 1974. Search in Google Scholar

[19] Y. F. Li and P. Zeng, Continuous dependence on the heat source of 2D large-scale primitive equations in oceanic dynamics, Symmetry 13 (2021), no. 10, 1961, https://doi.org/10.3390/sym13101961. Search in Google Scholar

[20] Y. Liu, X. L. Qin, J. C. Shi, and W. J. Zhi, Structural stability of the Boussinesq fluid interfacing with a Darcy fluid in a bounded region in R2, Appl. Math. Comput. 411 (2021), 126488, https://doi.org/10.1016/j.amc.2021.126488. Search in Google Scholar

[21] Y. Liu, Y. F. Li, and J. C. Shi, Estimates for the linear viscoelastic damped wave equation on the Heisenberg group, J. Differential Equations 285 (2021), 663–685, https://doi.org/10.1016/j.jde.2021.03.026. Search in Google Scholar

[22] Y. Liu, S. Z. Xiao, and Y. W. Lin, Continuous dependence for the Brinkman-Forchheimer fluid interfacing with a Darcy fluid in a bounded domain, Math. Comput. Simulation 150 (2018), 66–82, https://doi.org/10.1016/j.matcom.2018.02.009. Search in Google Scholar

[23] Y. F. Li, X. J. Chen, and J. C. Shi, Structural stability in resonant penetrative convection in a Brinkman-Forchheimer fluid interfacing with a Darcy fluid, Appl. Math. Optim. 84 (2021), no. 1, 979–999, https://doi.org/10.1007/s00245-021-09791-7. Search in Google Scholar

[24] W. H. Chen, Cauchy problem for thermoelastic plate equations with different damping mechanisms, Commun. Math. Sci. 18 (2020), no. 2, 429–457, https://doi.org/10.4310/CMS.2020.v18.n2.a7. Search in Google Scholar

[25] Y. F. Li, S. Z. Xiao, and P. Zeng, The applications of some basic mathematical inequalities on the convergence of the primitive equations of moist atmosphere, J. Math. Inequal. 15 (2021), no. 1, 293–304, https://doi.org/10.7153/jmi-2021-15-22. Search in Google Scholar

[26] M. Ciarletta, B. Straughan, and V. Tibullo, Structural stability for a thermal convection model with temperature-dependent solubility, Nonlinear Anal. Real World Appl. 22 (2015), 34–43, https://doi.org/10.1016/j.nonrwa.2014.07.012 Search in Google Scholar

[27] N. L. Scott and B. Straughan, Continuous dependence on the reaction terms in porous convection with surface reactions, Quart. Appl. Math. 71 (2013), no. 3, 501–508, https://www.jstor.org/stable/43645925. Search in Google Scholar

[28] B. Straughan, Continuous dependence on the heat source in resonant porous penetrative convection, Stud. Appl. Math. 127 (2011), 302–314, https://doi.org/10.1111/j.1467-9590.2011.00521.x. Search in Google Scholar

[29] F. Franchi and B. Straughan, Continuous dependence and decay for the Forchheimer equations, Proc. R. Soc. A: Math. Phys. Eng. Sci. 459 (2003), no. 2040, 3195–3202, https://doi.org/10.1098/rspa.2003.1169. Search in Google Scholar

[30] Y. F. Li, S. Z. Xiao, and X. J. Chen, Spatial alternative and stability of-type III Thermoelastic equations, Adv. Appl. Math. Mech. 42 (2021), no.4, 431–440, https://doi.org/10.21656/1000-0887.410270. Search in Google Scholar

[31] I. Babuska and A. K Aziz, Survey lectures on the mathematical foundations of the finite element method, In: A. K. Aziz (eds), The Mathematical Foundations of the Finite Element Method with Applications to Partial Differential Equations, Academic Press, New York, 1972, pp. 5–359, https://doi.org/10.1016/C2013-0-10319-4. Search in Google Scholar

[32] O. A. Ladyzhenskaya and V. A. Solonnikov, Some problems of vector analysis and generalized formulations of boundary-value problems for the Navier-Stokes equations, J. Sov. Math. 10 (1978), 257–86, https://doi.org/10.1007/BF01566606. Search in Google Scholar

[33] Y. F. Li, J. C. Shi, H. S. Zhu, and S. Q. Huang, Fast growth or decay estimates of thermoelastic equations in an external domain, Acta Math. Sci. Ser. A (Chinese Ed.) 41 (2021), no. 4, 1042–1052, http://caod.oriprobe.com/articles/61851590/Fast_Growth_or_Decay_Estimates_of_Thermoelastic_Eq.htm. Search in Google Scholar
Received: 2022-01-30
Revised: 2022-10-30
Accepted: 2022-11-15
Published Online: 2022-12-23

© 2022 the author(s), published by De Gruyter

This work is licensed under the Creative Commons Attribution 4.0 International License.

Articles in the same Issue

  1. Regular Articles
  2. A random von Neumann theorem for uniformly distributed sequences of partitions
  3. Note on structural properties of graphs
  4. Mean-field formulation for mean-variance asset-liability management with cash flow under an uncertain exit time
  5. The family of random attractors for nonautonomous stochastic higher-order Kirchhoff equations with variable coefficients
  6. The intersection graph of graded submodules of a graded module
  7. Isoperimetric and Brunn-Minkowski inequalities for the (p, q)-mixed geominimal surface areas
  8. On second-order fuzzy discrete population model
  9. On certain functional equation in prime rings
  10. General complex Lp projection bodies and complex Lp mixed projection bodies
  11. Some results on the total proper k-connection number
  12. The stability with general decay rate of hybrid stochastic fractional differential equations driven by Lévy noise with impulsive effects
  13. Well posedness of magnetohydrodynamic equations in 3D mixed-norm Lebesgue space
  14. Strong convergence of a self-adaptive inertial Tseng's extragradient method for pseudomonotone variational inequalities and fixed point problems
  15. Generic uniqueness of saddle point for two-person zero-sum differential games
  16. Relational representations of algebraic lattices and their applications
  17. Explicit construction of mock modular forms from weakly holomorphic Hecke eigenforms
  18. The equivalent condition of G-asymptotic tracking property and G-Lipschitz tracking property
  19. Arithmetic convolution sums derived from eta quotients related to divisors of 6
  20. Dynamical behaviors of a k-order fuzzy difference equation
  21. The transfer ideal under the action of orthogonal group in modular case
  22. The multinomial convolution sum of a generalized divisor function
  23. Extensions of Gronwall-Bellman type integral inequalities with two independent variables
  24. Unicity of meromorphic functions concerning differences and small functions
  25. Solutions to problems about potentially Ks,t-bigraphic pair
  26. Monotonicity of solutions for fractional p-equations with a gradient term
  27. Data smoothing with applications to edge detection
  28. An ℋ-tensor-based criteria for testing the positive definiteness of multivariate homogeneous forms
  29. Characterizations of *-antiderivable mappings on operator algebras
  30. Initial-boundary value problem of fifth-order Korteweg-de Vries equation posed on half line with nonlinear boundary values
  31. On a more accurate half-discrete Hilbert-type inequality involving hyperbolic functions
  32. On split twisted inner derivation triple systems with no restrictions on their 0-root spaces
  33. Geometry of conformal η-Ricci solitons and conformal η-Ricci almost solitons on paracontact geometry
  34. Bifurcation and chaos in a discrete predator-prey system of Leslie type with Michaelis-Menten prey harvesting
  35. A posteriori error estimates of characteristic mixed finite elements for convection-diffusion control problems
  36. Dynamical analysis of a Lotka Volterra commensalism model with additive Allee effect
  37. An efficient finite element method based on dimension reduction scheme for a fourth-order Steklov eigenvalue problem
  38. Connectivity with respect to α-discrete closure operators
  39. Khasminskii-type theorem for a class of stochastic functional differential equations
  40. On some new Hermite-Hadamard and Ostrowski type inequalities for s-convex functions in (p, q)-calculus with applications
  41. New properties for the Ramanujan R-function
  42. Shooting method in the application of boundary value problems for differential equations with sign-changing weight function
  43. Ground state solution for some new Kirchhoff-type equations with Hartree-type nonlinearities and critical or supercritical growth
  44. Existence and uniqueness of solutions for the stochastic Volterra-Levin equation with variable delays
  45. Ambrosetti-Prodi-type results for a class of difference equations with nonlinearities indefinite in sign
  46. Research of cooperation strategy of government-enterprise digital transformation based on differential game
  47. Malmquist-type theorems on some complex differential-difference equations
  48. Disjoint diskcyclicity of weighted shifts
  49. Construction of special soliton solutions to the stochastic Riccati equation
  50. Remarks on the generalized interpolative contractions and some fixed-point theorems with application
  51. Analysis of a deteriorating system with delayed repair and unreliable repair equipment
  52. On the critical fractional Schrödinger-Kirchhoff-Poisson equations with electromagnetic fields
  53. The exact solutions of generalized Davey-Stewartson equations with arbitrary power nonlinearities using the dynamical system and the first integral methods
  54. Regularity of models associated with Markov jump processes
  55. Multiplicity solutions for a class of p-Laplacian fractional differential equations via variational methods
  56. Minimal period problem for second-order Hamiltonian systems with asymptotically linear nonlinearities
  57. Convergence rate of the modified Levenberg-Marquardt method under Hölderian local error bound
  58. Non-binary quantum codes from constacyclic codes over 𝔽q[u1, u2,…,uk]/⟨ui3 = ui, uiuj = ujui⟩
  59. On the general position number of two classes of graphs
  60. A posteriori regularization method for the two-dimensional inverse heat conduction problem
  61. Orbital stability and Zhukovskiǐ quasi-stability in impulsive dynamical systems
  62. Approximations related to the complete p-elliptic integrals
  63. A note on commutators of strongly singular Calderón-Zygmund operators
  64. Generalized Munn rings
  65. Double domination in maximal outerplanar graphs
  66. Existence and uniqueness of solutions to the norm minimum problem on digraphs
  67. On the p-integrable trajectories of the nonlinear control system described by the Urysohn-type integral equation
  68. Robust estimation for varying coefficient partially functional linear regression models based on exponential squared loss function
  69. Hessian equations of Krylov type on compact Hermitian manifolds
  70. Class fields generated by coordinates of elliptic curves
  71. The lattice of (2, 1)-congruences on a left restriction semigroup
  72. A numerical solution of problem for essentially loaded differential equations with an integro-multipoint condition
  73. On stochastic accelerated gradient with convergence rate
  74. Displacement structure of the DMP inverse
  75. Dependence of eigenvalues of Sturm-Liouville problems on time scales with eigenparameter-dependent boundary conditions
  76. Existence of positive solutions of discrete third-order three-point BVP with sign-changing Green's function
  77. Some new fixed point theorems for nonexpansive-type mappings in geodesic spaces
  78. Generalized 4-connectivity of hierarchical star networks
  79. Spectra and reticulation of semihoops
  80. Stein-Weiss inequality for local mixed radial-angular Morrey spaces
  81. Eigenvalues of transition weight matrix for a family of weighted networks
  82. A modified Tikhonov regularization for unknown source in space fractional diffusion equation
  83. Modular forms of half-integral weight on Γ0(4) with few nonvanishing coefficients modulo ℓ
  84. Some estimates for commutators of bilinear pseudo-differential operators
  85. Extension of isometries in real Hilbert spaces
  86. Existence of positive periodic solutions for first-order nonlinear differential equations with multiple time-varying delays
  87. B-Fredholm elements in primitive C*-algebras
  88. Unique solvability for an inverse problem of a nonlinear parabolic PDE with nonlocal integral overdetermination condition
  89. An algebraic semigroup method for discovering maximal frequent itemsets
  90. Class-preserving Coleman automorphisms of some classes of finite groups
  91. Exponential stability of traveling waves for a nonlocal dispersal SIR model with delay
  92. Existence and multiplicity of solutions for second-order Dirichlet problems with nonlinear impulses
  93. The transitivity of primary conjugacy in regular ω-semigroups
  94. Stability estimation of some Markov controlled processes
  95. On nonnil-coherent modules and nonnil-Noetherian modules
  96. N-Tuples of weighted noncommutative Orlicz space and some geometrical properties
  97. The dimension-free estimate for the truncated maximal operator
  98. A human error risk priority number calculation methodology using fuzzy and TOPSIS grey
  99. Compact mappings and s-mappings at subsets
  100. The structural properties of the Gompertz-two-parameter-Lindley distribution and associated inference
  101. A monotone iteration for a nonlinear Euler-Bernoulli beam equation with indefinite weight and Neumann boundary conditions
  102. Delta waves of the isentropic relativistic Euler system coupled with an advection equation for Chaplygin gas
  103. Multiplicity and minimality of periodic solutions to fourth-order super-quadratic difference systems
  104. On the reciprocal sum of the fourth power of Fibonacci numbers
  105. Averaging principle for two-time-scale stochastic differential equations with correlated noise
  106. Phragmén-Lindelöf alternative results and structural stability for Brinkman fluid in porous media in a semi-infinite cylinder
  107. Study on r-truncated degenerate Stirling numbers of the second kind
  108. On 7-valent symmetric graphs of order 2pq and 11-valent symmetric graphs of order 4pq
  109. Some new characterizations of finite p-nilpotent groups
  110. A Billingsley type theorem for Bowen topological entropy of nonautonomous dynamical systems
  111. F4 and PSp (8, ℂ)-Higgs pairs understood as fixed points of the moduli space of E6-Higgs bundles over a compact Riemann surface
  112. On modules related to McCoy modules
  113. On generalized extragradient implicit method for systems of variational inequalities with constraints of variational inclusion and fixed point problems
  114. Solvability for a nonlocal dispersal model governed by time and space integrals
  115. Finite groups whose maximal subgroups of even order are MSN-groups
  116. Symmetric results of a Hénon-type elliptic system with coupled linear part
  117. On the connection between Sp-almost periodic functions defined on time scales and ℝ
  118. On a class of Harada rings
  119. On regular subgroup functors of finite groups
  120. Fast iterative solutions of Riccati and Lyapunov equations
  121. Weak measure expansivity of C2 dynamics
  122. Admissible congruences on type B semigroups
  123. Generalized fractional Hermite-Hadamard type inclusions for co-ordinated convex interval-valued functions
  124. Inverse eigenvalue problems for rank one perturbations of the Sturm-Liouville operator
  125. Data transmission mechanism of vehicle networking based on fuzzy comprehensive evaluation
  126. Dual uniformities in function spaces over uniform continuity
  127. Review Article
  128. On Hahn-Banach theorem and some of its applications
  129. Rapid Communication
  130. Discussion of foundation of mathematics and quantum theory
  131. Special Issue on Boundary Value Problems and their Applications on Biosciences and Engineering (Part II)
  132. A study of minimax shrinkage estimators dominating the James-Stein estimator under the balanced loss function
  133. Representations by degenerate Daehee polynomials
  134. Multilevel MC method for weak approximation of stochastic differential equation with the exact coupling scheme
  135. Multiple periodic solutions for discrete boundary value problem involving the mean curvature operator
  136. Special Issue on Evolution Equations, Theory and Applications (Part II)
  137. Coupled measure of noncompactness and functional integral equations
  138. Existence results for neutral evolution equations with nonlocal conditions and delay via fractional operator
  139. Global weak solution of 3D-NSE with exponential damping
  140. Special Issue on Fractional Problems with Variable-Order or Variable Exponents (Part I)
  141. Ground state solutions of nonlinear Schrödinger equations involving the fractional p-Laplacian and potential wells
  142. A class of p1(x, ⋅) & p2(x, ⋅)-fractional Kirchhoff-type problem with variable s(x, ⋅)-order and without the Ambrosetti-Rabinowitz condition in ℝN
  143. Jensen-type inequalities for m-convex functions
  144. Special Issue on Problems, Methods and Applications of Nonlinear Analysis (Part III)
  145. The influence of the noise on the exact solutions of a Kuramoto-Sivashinsky equation
  146. Basic inequalities for statistical submanifolds in Golden-like statistical manifolds
  147. Global existence and blow up of the solution for nonlinear Klein-Gordon equation with variable coefficient nonlinear source term
  148. Hopf bifurcation and Turing instability in a diffusive predator-prey model with hunting cooperation
  149. Efficient fixed-point iteration for generalized nonexpansive mappings and its stability in Banach spaces
https://doi.org/10.1515/math-2022-0531
Keywords for this article
Phragmén-Lindelöf alternative results; Brinkman equations; energy estimation; structural stability
Creative Commons
BY 4.0

Articles in the same Issue

  1. Regular Articles
  2. A random von Neumann theorem for uniformly distributed sequences of partitions
  3. Note on structural properties of graphs
  4. Mean-field formulation for mean-variance asset-liability management with cash flow under an uncertain exit time
  5. The family of random attractors for nonautonomous stochastic higher-order Kirchhoff equations with variable coefficients
  6. The intersection graph of graded submodules of a graded module
  7. Isoperimetric and Brunn-Minkowski inequalities for the (p, q)-mixed geominimal surface areas
  8. On second-order fuzzy discrete population model
  9. On certain functional equation in prime rings
  10. General complex Lp projection bodies and complex Lp mixed projection bodies
  11. Some results on the total proper k-connection number
  12. The stability with general decay rate of hybrid stochastic fractional differential equations driven by Lévy noise with impulsive effects
  13. Well posedness of magnetohydrodynamic equations in 3D mixed-norm Lebesgue space
  14. Strong convergence of a self-adaptive inertial Tseng's extragradient method for pseudomonotone variational inequalities and fixed point problems
  15. Generic uniqueness of saddle point for two-person zero-sum differential games
  16. Relational representations of algebraic lattices and their applications
  17. Explicit construction of mock modular forms from weakly holomorphic Hecke eigenforms
  18. The equivalent condition of G-asymptotic tracking property and G-Lipschitz tracking property
  19. Arithmetic convolution sums derived from eta quotients related to divisors of 6
  20. Dynamical behaviors of a k-order fuzzy difference equation
  21. The transfer ideal under the action of orthogonal group in modular case
  22. The multinomial convolution sum of a generalized divisor function
  23. Extensions of Gronwall-Bellman type integral inequalities with two independent variables
  24. Unicity of meromorphic functions concerning differences and small functions
  25. Solutions to problems about potentially Ks,t-bigraphic pair
  26. Monotonicity of solutions for fractional p-equations with a gradient term
  27. Data smoothing with applications to edge detection
  28. An ℋ-tensor-based criteria for testing the positive definiteness of multivariate homogeneous forms
  29. Characterizations of *-antiderivable mappings on operator algebras
  30. Initial-boundary value problem of fifth-order Korteweg-de Vries equation posed on half line with nonlinear boundary values
  31. On a more accurate half-discrete Hilbert-type inequality involving hyperbolic functions
  32. On split twisted inner derivation triple systems with no restrictions on their 0-root spaces
  33. Geometry of conformal η-Ricci solitons and conformal η-Ricci almost solitons on paracontact geometry
  34. Bifurcation and chaos in a discrete predator-prey system of Leslie type with Michaelis-Menten prey harvesting
  35. A posteriori error estimates of characteristic mixed finite elements for convection-diffusion control problems
  36. Dynamical analysis of a Lotka Volterra commensalism model with additive Allee effect
  37. An efficient finite element method based on dimension reduction scheme for a fourth-order Steklov eigenvalue problem
  38. Connectivity with respect to α-discrete closure operators
  39. Khasminskii-type theorem for a class of stochastic functional differential equations
  40. On some new Hermite-Hadamard and Ostrowski type inequalities for s-convex functions in (p, q)-calculus with applications
  41. New properties for the Ramanujan R-function
  42. Shooting method in the application of boundary value problems for differential equations with sign-changing weight function
  43. Ground state solution for some new Kirchhoff-type equations with Hartree-type nonlinearities and critical or supercritical growth
  44. Existence and uniqueness of solutions for the stochastic Volterra-Levin equation with variable delays
  45. Ambrosetti-Prodi-type results for a class of difference equations with nonlinearities indefinite in sign
  46. Research of cooperation strategy of government-enterprise digital transformation based on differential game
  47. Malmquist-type theorems on some complex differential-difference equations
  48. Disjoint diskcyclicity of weighted shifts
  49. Construction of special soliton solutions to the stochastic Riccati equation
  50. Remarks on the generalized interpolative contractions and some fixed-point theorems with application
  51. Analysis of a deteriorating system with delayed repair and unreliable repair equipment
  52. On the critical fractional Schrödinger-Kirchhoff-Poisson equations with electromagnetic fields
  53. The exact solutions of generalized Davey-Stewartson equations with arbitrary power nonlinearities using the dynamical system and the first integral methods
  54. Regularity of models associated with Markov jump processes
  55. Multiplicity solutions for a class of p-Laplacian fractional differential equations via variational methods
  56. Minimal period problem for second-order Hamiltonian systems with asymptotically linear nonlinearities
  57. Convergence rate of the modified Levenberg-Marquardt method under Hölderian local error bound
  58. Non-binary quantum codes from constacyclic codes over 𝔽q[u1, u2,…,uk]/⟨ui3 = ui, uiuj = ujui⟩
  59. On the general position number of two classes of graphs
  60. A posteriori regularization method for the two-dimensional inverse heat conduction problem
  61. Orbital stability and Zhukovskiǐ quasi-stability in impulsive dynamical systems
  62. Approximations related to the complete p-elliptic integrals
  63. A note on commutators of strongly singular Calderón-Zygmund operators
  64. Generalized Munn rings
  65. Double domination in maximal outerplanar graphs
  66. Existence and uniqueness of solutions to the norm minimum problem on digraphs
  67. On the p-integrable trajectories of the nonlinear control system described by the Urysohn-type integral equation
  68. Robust estimation for varying coefficient partially functional linear regression models based on exponential squared loss function
  69. Hessian equations of Krylov type on compact Hermitian manifolds
  70. Class fields generated by coordinates of elliptic curves
  71. The lattice of (2, 1)-congruences on a left restriction semigroup
  72. A numerical solution of problem for essentially loaded differential equations with an integro-multipoint condition
  73. On stochastic accelerated gradient with convergence rate
  74. Displacement structure of the DMP inverse
  75. Dependence of eigenvalues of Sturm-Liouville problems on time scales with eigenparameter-dependent boundary conditions
  76. Existence of positive solutions of discrete third-order three-point BVP with sign-changing Green's function
  77. Some new fixed point theorems for nonexpansive-type mappings in geodesic spaces
  78. Generalized 4-connectivity of hierarchical star networks
  79. Spectra and reticulation of semihoops
  80. Stein-Weiss inequality for local mixed radial-angular Morrey spaces
  81. Eigenvalues of transition weight matrix for a family of weighted networks
  82. A modified Tikhonov regularization for unknown source in space fractional diffusion equation
  83. Modular forms of half-integral weight on Γ0(4) with few nonvanishing coefficients modulo ℓ
  84. Some estimates for commutators of bilinear pseudo-differential operators
  85. Extension of isometries in real Hilbert spaces
  86. Existence of positive periodic solutions for first-order nonlinear differential equations with multiple time-varying delays
  87. B-Fredholm elements in primitive C*-algebras
  88. Unique solvability for an inverse problem of a nonlinear parabolic PDE with nonlocal integral overdetermination condition
  89. An algebraic semigroup method for discovering maximal frequent itemsets
  90. Class-preserving Coleman automorphisms of some classes of finite groups
  91. Exponential stability of traveling waves for a nonlocal dispersal SIR model with delay
  92. Existence and multiplicity of solutions for second-order Dirichlet problems with nonlinear impulses
  93. The transitivity of primary conjugacy in regular ω-semigroups
  94. Stability estimation of some Markov controlled processes
  95. On nonnil-coherent modules and nonnil-Noetherian modules
  96. N-Tuples of weighted noncommutative Orlicz space and some geometrical properties
  97. The dimension-free estimate for the truncated maximal operator
  98. A human error risk priority number calculation methodology using fuzzy and TOPSIS grey
  99. Compact mappings and s-mappings at subsets
  100. The structural properties of the Gompertz-two-parameter-Lindley distribution and associated inference
  101. A monotone iteration for a nonlinear Euler-Bernoulli beam equation with indefinite weight and Neumann boundary conditions
  102. Delta waves of the isentropic relativistic Euler system coupled with an advection equation for Chaplygin gas
  103. Multiplicity and minimality of periodic solutions to fourth-order super-quadratic difference systems
  104. On the reciprocal sum of the fourth power of Fibonacci numbers
  105. Averaging principle for two-time-scale stochastic differential equations with correlated noise
  106. Phragmén-Lindelöf alternative results and structural stability for Brinkman fluid in porous media in a semi-infinite cylinder
  107. Study on r-truncated degenerate Stirling numbers of the second kind
  108. On 7-valent symmetric graphs of order 2pq and 11-valent symmetric graphs of order 4pq
  109. Some new characterizations of finite p-nilpotent groups
  110. A Billingsley type theorem for Bowen topological entropy of nonautonomous dynamical systems
  111. F4 and PSp (8, ℂ)-Higgs pairs understood as fixed points of the moduli space of E6-Higgs bundles over a compact Riemann surface
  112. On modules related to McCoy modules
  113. On generalized extragradient implicit method for systems of variational inequalities with constraints of variational inclusion and fixed point problems
  114. Solvability for a nonlocal dispersal model governed by time and space integrals
  115. Finite groups whose maximal subgroups of even order are MSN-groups
  116. Symmetric results of a Hénon-type elliptic system with coupled linear part
  117. On the connection between Sp-almost periodic functions defined on time scales and ℝ
  118. On a class of Harada rings
  119. On regular subgroup functors of finite groups
  120. Fast iterative solutions of Riccati and Lyapunov equations
  121. Weak measure expansivity of C2 dynamics
  122. Admissible congruences on type B semigroups
  123. Generalized fractional Hermite-Hadamard type inclusions for co-ordinated convex interval-valued functions
  124. Inverse eigenvalue problems for rank one perturbations of the Sturm-Liouville operator
  125. Data transmission mechanism of vehicle networking based on fuzzy comprehensive evaluation
  126. Dual uniformities in function spaces over uniform continuity
  127. Review Article
  128. On Hahn-Banach theorem and some of its applications
  129. Rapid Communication
  130. Discussion of foundation of mathematics and quantum theory
  131. Special Issue on Boundary Value Problems and their Applications on Biosciences and Engineering (Part II)
  132. A study of minimax shrinkage estimators dominating the James-Stein estimator under the balanced loss function
  133. Representations by degenerate Daehee polynomials
  134. Multilevel MC method for weak approximation of stochastic differential equation with the exact coupling scheme
  135. Multiple periodic solutions for discrete boundary value problem involving the mean curvature operator
  136. Special Issue on Evolution Equations, Theory and Applications (Part II)
  137. Coupled measure of noncompactness and functional integral equations
  138. Existence results for neutral evolution equations with nonlocal conditions and delay via fractional operator
  139. Global weak solution of 3D-NSE with exponential damping
  140. Special Issue on Fractional Problems with Variable-Order or Variable Exponents (Part I)
  141. Ground state solutions of nonlinear Schrödinger equations involving the fractional p-Laplacian and potential wells
  142. A class of p1(x, ⋅) & p2(x, ⋅)-fractional Kirchhoff-type problem with variable s(x, ⋅)-order and without the Ambrosetti-Rabinowitz condition in ℝN
  143. Jensen-type inequalities for m-convex functions
  144. Special Issue on Problems, Methods and Applications of Nonlinear Analysis (Part III)
  145. The influence of the noise on the exact solutions of a Kuramoto-Sivashinsky equation
  146. Basic inequalities for statistical submanifolds in Golden-like statistical manifolds
  147. Global existence and blow up of the solution for nonlinear Klein-Gordon equation with variable coefficient nonlinear source term
  148. Hopf bifurcation and Turing instability in a diffusive predator-prey model with hunting cooperation
  149. Efficient fixed-point iteration for generalized nonexpansive mappings and its stability in Banach spaces
Sign up now to receive a 20% welcome discount
Institutional Access
How does access work?
Have an idea on how to improve our website?
Please write us.
© 2025 De Gruyter Brill
Downloaded on 17.10.2025 from https://www.degruyterbrill.com/document/doi/10.1515/math-2022-0531/html
Scroll to top button